1 Caracterização do Público Alvo 2 Execução de Cognitive Walkthrough (Simulação de Percurso)

TEMA 5 2º/3º ciclo. A LIndo de perguntas. saudável? Luísa, 15 anos

2º/3º cicl s O Ã Ç T N E M I d pguns u m mu um p z pdms f ps O qu sudávl? blnç d i c n c id p Sá d p d n cm p, ic mbém é g á s n v ic. Dsc ís f m f civ b id v m u i d lóics. c s impânc s g õs sb ç n s

O sinal. Exemplos: impulso rectangular. Função exponencial. Aplica-se a sinais de energia finita. função sinc(λ) Transformada de Fourier 2/T 1/T T/2

rsrmd d Furir. d [ ]. d pli-s siis d ri ii [ ]. d < lmuiçõs EC Fuçã si λ si λ 3 si λ λ λ sd [ si ] r [ r ] si lmuiçõs EC 3 Exmpls: impuls rulr. r / / s / Fuçã six/x é mui mum. Csum usr-s pr iss uçã siλ

Uniforme Exponencial Normal Gama Weibull Lognormal. t (Student) χ 2 (Qui-quadrado) F (Snedekor)

Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no

9. MODELAGEM DE CONVERSORES: MODELO DA CHAVE PWM

Fns Chs C. 9 Mlgm nrsrs: ml h PWM J. A. Pml 9. MOEAGEM E CONERSORES: MOEO A CHAE PWM As lgs báss nrsrs CCCC ssum um h nrl ur nãnrl sss lmns lnrs nrns n m. A njun ss us hs r nm h PWM [9.]. O bj ns íul é

Normalmente TI. padarias. Além. dormitórios. Assistência. Temos. Por. Nos. região. Nas

Aprsntçã Instlçõs ds A l A Nrmlmnt A Além sc Filipins. ds sgur mis lugr Cbu trnnd td, tmp sgurnç ficiis prsnç cm cnt rgiã diss, pdris. tips váris Strbucks Dnld's, Mc cm 24hrs ljs tmbém váris prt pr Tms

SÃO PAULO FUTEBOL CLUBE

RICLR JG jg! IMGNS D DS S IMS D SÃ PUL VL. 5 SÃ PUL FUBL CLUB SÃ PUL FUBL CLUB pruçã mchal 20-srra UM RSG D QUS 0 NS D HISÓRI SÃ-PULIN RVÉS D FS DS MIS D 5.600 JGS D CLUB CM PÃ! D Í P M I L CLR RI sá u

UFS - DComp Adaptados a partir do material da Profa. Kenia Kodel Cox

UFS - DCmp Aps p m Pf. Kn K Cx Busc m Tx Busc m x, u psqus g, u csmn põs, u csmn cs, cnss n psqus um susquênc síms num squênc ss (síms). Busc m Tx P cm jv ncn s s cêncs, u smn pm, um susquênc num squênc;

BALIZA. Cor central.da PLAYMOBIL podes fazer passes. verde-claro curtos, passes longos e, até, rematar para com a nova função de rotação.

PONTAP DE SAÍDA TCNICAS DE Pntpé bliz Est lnc cntc n iníci jg pós cd gl. Est Gnhs cntr p dis"d jg- bl qund cm dis st jgdrs cir list d cmp tu d quip: pntpé é dd REMATE ntr d círcul cntrl. Os jgdrs jg cm

Prgrmçã O Mu s u Év r, p r l ém f rcr s s i g ns «vi s i t s cl áss i cs» qu cri m s p nt s c nt ct nt r s di v rs s p úb l ic s qu vi s it m s c nt ú d s d s u ri c s p ó l i, p r cu r, c nc m i t nt

ORGANIZAÇÃO DIDÁTICA DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO: O PLANEJAMENTO. Prof. Dr. Roberto Valdés Puentes

ORGANIZAÇÃO DIDÁTICA DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO: O PLANEJAMENTO Prf. Dr. Rbr Vdés Pus PPGED/FACED/UFU rbrpus@fcd.ufu.br MOMENTOS DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO

Instituto de Física USP. Física Moderna I. Aula 29. Professora: Mazé Bechara

Institut d Físic USP Físic Mdn I Aul 9 Pfss: Mzé Bch Aul 9 O átm d hidgêni n ti d Schding 1. A sluçã d átm d H n ti d Schding. Cmpçã cm s sultds d Bh.. Os stds dgnds m ngi: stds d msm ngi divss móduls

Apenas 5% dos Brasileiros sabem falar Inglês

Apns 5% ds Brsilirs sb flr Inglês D crd cm um lvntmnt fit pl British Cncil pns 5% d ppulçã sb fl r Dvs lbrr stms épcs pré-vnts sprtivs s lhs d mund td cmçm s vltr cd vz mis pr Brsil pr iss nã bst dminr

Questão 1. Questão 2. alternativa E. alternativa C

Quesã Pedr iru mens de um cenen de fs d fes em cmemrçã seu niversári e quer clcá-ls ds num álbum de 0 págins. Em cd págin desse álbum cbem, n máxim, 0 fs. Inicilmene, Pedr enu clcr 6 fs em cd págin. A

Alteração da seqüência de execução de instruções

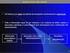Iníci Busc d próxim Excut Prd Cicl busc Cicl xcuçã Prgrm Sqüênci instruçõs m mmóri Trdutr : Cmpilr X Intrprtr / Linkditr Cnvrt prgrm-fnt m prgrm bjt (lingugm máqui) Prgrm cmpil = mis rápi Prgrm Intrprt

+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares

Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn

(22) Data do Depósito: 08/05/2012. (43) Data da Publicação: 12/04/2016 (RPI 2362)

INPI (21) BR 102012010884-4 A2 (22) Dt d Dpósit: 08/05/2012 *BR102012010884A Rpúblic Fdrtiv d Brsil Ministri d Dsnvlvimnt, Indústri d Cmrci Extrir Institut Ncinl d Prpridd Industril (43) Dt d Publicçã:

Vamos analisar o seguinte circuito trifásico: Esta aula:! Sistemas Trifásicos equilibrados com Transformador ideal

EA6 Circuits FEEC UNCAMP Aul 6 Est ul:! Sistms Trifásics quilibrds cm Trnsfrmdr idl Nst ul nlisrms um sistm trifásic quilibrd cm trnsfrmdr Cm sistm é quilibrd, pdms nlisr circuit trifásic trtnd pns d um

AULA 9. Universidade Tecnológica Federal do Paraná Campus Toledo Curso de Engenharia Eletrônica Desenho Técnico Prof. Dr.

Univrsidd Tcnológic Fdrl do Prná Cmpus Toldo d Engnhri Eltrônic Dsnho Técnico AULA 9 PROGRAMA DA AULA: Projçõs ortogonis: Posiçõs ds Figurs plns m rlção um plno d projção. Estudo d sólidos gométricos no

Como se tornar fluente em Inglês em todas as áreas

Cm s trnar flunt m Inglês m tdas as áras Tds s dias rcbms muits -mails pssas rm sabr pm fazr aprnr a falar ingls bm A fórmula xist sim funcina! Qur prvar iss dand minha própria xpriência cm aprndizad da

Roteiro de de Trabalho com com o AQUA AQUA REDE REDE

Rtir d d Trblh cm cm AQUA AQUA REDE REDE Prt Prt I I Iníci Iníci AutCAD Lnçr Lnçr s s pnts pnts ct ct d d Rd Rd Lnçr Lnçr s s trchs trchs brts brts lignd lignd smpr smpr d d Mntnt Mntnt pr pr Jusnt Jusnt

EM NOME DO PAI ====================== j ˆ«. ˆ««=======================

œ» EM NOME O PI Trnscçã Isbel rc Ver Snts Pe. Jãzinh Bm & # #6 8 j. j... Œ. ll { l l l l n me d Pi e d Fi lh ed_es & #. 2. #. _. _ j.. Œ. Œ l l l j {.. l. pí t Sn t_ mém Sn t_ mém LÓRI O PI Trnscçã Isbel

turismo corporate negócio noronha roma seul garopaba brasília são lu gramado brasília são paulo recife natal tóquio lisboa rio de janeiro capadócia

brlim sã l brlim santg rcif curi sul punta dl st rma sul nrnha r rcif rcif garpabacapa nrnha mntvidéu r barilch punta dl st mació sã paul mació sul capadóc r mnt SUPER sã l ngóci gramad turism FÉRIAS crprat

A DERIVADA DE UM INTEGRAL

A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,

Brincando com o CRUZADINHA LABIRINTO 7 ERROS JOGO DAS SOMBRAS CAÇA-PALAVRAS E MUITO MAIS! ENCARTE COM JOGO DA MEMÓRIA. Ano 8 - nº 8 - Dezembro / 2010

Um publicçã d Cntruind um vid mlhr www.mbigucci.cm.br Brincnd cm n - nº - Dzmbr / 2010 tividd infnti pr prndr, brincr divrtir! NCRT COM JOGO D MMÓRI CRUZDINH LBIRINTO 7 RROS JOGO DS SOMBRS CÇ-PLVRS MUITO

Adição dos antecedentes com os consequentes das duas razões

Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como

MATEMÁTICA A - 12o Ano Funções - Teorema de Bolzano Propostas de resolução

MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos

São Paulo capta a maior parte dos fluxos aéreos, como mostra zona de influência potencial, regional, local dos aeroportos do Rio de Janeiro, vis-àvis

Sã Pul cpt mir prt s fluxs rs, cm mstr zn influênci ptncil, rginl, lcl s rprts Ri Jnir, vis-vis principis rprts vizinhs - Sã Pul, Mins Gris Espírit Snt 148 Sã ftrs strtgics ligs rprts n snvlvimnt rginl

Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1 1

Univrsidd Fdrl do Rio d Jniro COPPE Progrm d Engnhri Químic COQ 79 ANÁLISE DE SISEMAS DA ENGENHARIA QUÍMICA AULA : Rprsnção m Espço d Esdos 4/ Rprsnção m Espço d Esdos Esdo: O sdo d um sism no mpo é o

ATIVIDADE DE SALA (02)

COLÉGIO PLÍNIO LEITE CIÊNCIAS BIOLÓGICAS 2º Píd/2014 6º ANO ESCOLAR - ENSINO FUNDAMENTAL Nm: Pfss (): ATIVIDADE DE SALA (02) Tum: º: D: / / VALOR:... Mds ppss p suu d T Mus ds gs dés d suu d T bsvm-s m

Problemas de Electromagnetismo e Óptica LEAN + MEAer

Pobls d logniso Ópi AN MA 7 Ópi P 7 (Pobl 3 do píulo do livo nodução à Físi d Dis d Dus l) O spo d opinos d ond p luz visívl vi n d 4x -9 (viol) 75x -9 (vlho) n qu vlos vi fquêni d luz visívl? n 75x 4

SALMO 103/104-ENVIAI O VOSSO ESPÍRITO - BANDA

SLMO 10/10-NVII O VOSSO SPÍRITO - N 1º Slm d Vigíli Pscl ssin Mirls Vic n vi i vs s's pí ri t S nhr d 1. 7 2. Tr r t d f c r n vi n vi vi 1.n 8 di z ó nh'l m S nhr ó mu 10 us mu S nhr c m sis gr n d m

Messinki PUSERRUSLIITIN EM 10 MM PUSERRUSLIITIN EM 12 MM PUSERRUSLIITIN EM 15 MM PUSERRUSLIITIN EM 18 MM PUSERRUSLIITIN EM 22 MM

Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 35 MM 10X

Associação de Resistores e Resistência Equivalente

Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos

Messinki PUSERRUSLIITIN EM 10 MM PUSERRUSLIITIN EM 12 MM PUSERRUSLIITIN EM 15 MM PUSERRUSLIITIN EM 18 MM PUSERRUSLIITIN EM 22 MM

Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 2 PUSERRUSLIITIN EM 35 MM

Eu só quero um xodó. Música na escola: exercício 14

Eu só qu u xdó Músic n scl: xcíci 14 Eu só qu u xdó Ptitus Mi, hni lt Aut: Dinguinhs stáci Rgiã: Pnbuc : 1973 Fix: 14 Anj: Edsn Jsé Alvs Músics: Edsn Jsé Alvs vilã Pvt clints, sx t Jsé Alvs Sbinh Zzinh

SÃO PAULO FUTEBOL CLUBE

TRICLR JG jogo! IMGNS D TDS S TIMS D SÃ PUL VL. SÃ PUL FUTBL CLUB SÃ PUL FUTBL CLUB proução michael 0-serra UM RSGT D QUS 0 NS D HISTÓRI SÃ-PULIN TRVÉS D FTS DS MIS D 5.600 JGS D CLUB TÇ MINISTR DS RL.

se vai Devagar Devagar se vai longe longe...

Compelm M et e tn át os de M ic Devgr Devgr se se vi vi o o longe... longe 130 ) Describe the pttern by telling how ech ttribute chnges. A c) Respost possível: b B B B A b b... A b) Drw or describe the

MOVIMENTOS SOB A AÇÃO DE UMA FORÇA RESULTANTE DE INTENSIDADE CONSTANTE

MOVIMENTOS SOB A AÇÃO DE UMA ORÇA RESULTANTE DE INTENSIDADE CONSTANTE Trjóris Tmos os sguins csos: 1º) S forç rsuln ivr dirção d vlocidd só vrirá o módulo ds rjóri srá rilín. v R Ou R v º) S forç rsuln

Geometria Espacial (Exercícios de Fixação)

Gomtri Espcil Prof. Pdro Flipp 1 Gomtri Espcil (Exrcícios d Fixção) Polidros 01. Um polidro convxo é formdo por 0 fcs tringulrs. O númro d vértics dss polidro ) 1 b) 15 c) 18 d) 0 ) 4 0. Um polidro convxo

LEVANTAMENTO CLIMÁTICO DA AMAZÔNIA BRASILEIRA - DISPO NIBILIDADE DE ENERGIA LÔLICA EM SOURE - PARA

1 ng? Agr9, M.Sc. Psquisdr d MBRAPACPATU. Cix Pstl 48.,PA. Lvntmnt climátic d 1984 FL07173 sist cnvrii MBRAPA/CN 1111111 I 11111111111111111111111 32003! 07173 CPATU 1984 FL07173 luisa AGROPCUÁRIA AO MINISTÉRIO

Um outro arquivo texto deve ser criado para usar as funções definidas acima, por exemplo com o nome "simulacao.sce":

List C Auls Prátics d cilb imulçã numéric Exmpl d rsrvtóri Objtiv: sluçã numéric d quçõs dirnciis rdináris usnd unçã ODE. Cnsidr nvmnt sistm d um rsrvtóri: srvtóri cm áu Prâmtrs: 0 m - ár d sçã trnsvrsl

P a. e s. q u i. Gestão de Recursos. I n. s s a d a s. Entrada

SO TS 16949:2002 A uu d pcfcçã écnc E g pná cnc d m d gã d quldd, uu d pcfcçã écnc SO TS 16949:2002 bdgm d m d quldd umv. A pcfcçã écnc SO TS 16949:2002 é bd n pncíp d gã d quldd pnd n nm NBR SO 9001:2000:

Igreja em Oração Semanário litúrgico-catequético. 1º Domingo da Quaresma Ano B

Igrja m Oraçã Smanári litúrgiccatquétic Cants para a Clbraçã 1º Dming da Quarsma An B CD Campanha da ratrnidad 2018 18 d vrir d 2018 q = 48 Quand mu srv chamar Abrtura (1º 2º Dmings) Ltra: Sl 90,1516 [antífna]/missal

Eu sou feliz, tu és feliz CD Liturgia II (Caderno de partituras) Coordenação: Ir. Miria T. Kolling

Eu su iz, s iz Lirgi II (drn d prtirs) rdnçã: Ir. Miri T. King 1) Eu su iz, s iz (brr) & # #2 4. _ k.... k. 1 Eu su "Eu su iz, s iz!" ( "Lirgi II" Puus) iz, s _ iz, & # º #.. b... _ k _. Em cm Pi n cn

Incertezas e Propagação de Incertezas. Biologia Marinha

Incertezs e Propgção de Incertezs Cursos: Disciplin: Docente: Biologi Biologi Mrinh Físic Crl Silv Nos cálculos deve: Ser coerente ns uniddes (converter tudo pr S.I. e tender às potêncis de 10). Fzer um

condição inicial y ( 0) = 18 condições iniciais condições iniciais

Prblmas d Mamáa IV - Dada a quaçã frnal abax, drmnar as sluçõs arular mlmnar snd qu das as quaçõs sã válda ara. a nçã nal. s. u u b 5 nçã nal s. 7,5,5 u nçã nal s. 5 u d 5 s nçã nal 8 s. s d 5 8 nçõs nas

FOI DEUS QUEM FEZ VOCÊ

FOI DEUS QUEM FEZ OCÊ AMELINHA Arr Neton W Mcedo Crmo Gregory c c c Deus que fez vo - Deus quem fez vo - Deus quem fez vo- c Deus quem fez vo - J De-us 4 Deus quem fez vo - Deus quem fez vo - J Deus quem

Sinais e Sistemas Mecatrónicos

Sinis Sistms Mctrónicos Anális d Sistms no Domínio do Tmpo José Sá d Cost José Sá d Cost T11 - Anális d Sistms no Tmpo - Rsp. stcionári 1 Crctrizção d rspost stcionário A crctrizção d rspost stcionári

Método Numérico 52. Figura 3.1: Malha de discretização deslocadas.

3 Méd Nuérc f d qunfcr prcss d dpsçã d prfn dus subrns, u ódu f dsnd n cód nuérc TRNLUX ucknbruck, 994 pr fu rnsn bfásc, qu ccu dpsçã d prfn, c bs n rnsfrênc d ss cnc. O cód us éd ds us fns pr rsr s quçõs

ESCOLA DE LÍDERES BRASIL

ESCOLA DE LÍDERES BRASIL CURSO DE MARKETING MÓDULO I LEITURA COMPLEMENTAR (LC) [ D i g i o c o n ú d o d b r r l r l. T r - s d u m s u p l m n o O MERCADO 1. O Circuio Econômico Sgundo Armndo Krmr, produção

RECURSOS HUMANOS ANÁLISE DO FLUXO DE TRABALHO

RECURSOS HUMANOS Intduçã Cncits dfiniçã Digms d flux d pcsss Gáfics d flux d pcsss Estud d cs: DDT d FPFutbl Intduçã Cncits dfiniçã Digms d flux d pcsss Gáfics d flux d pcsss Estud d cs: DDT d FPFutbl

( ) 2. Eletromagnetismo I Prof. Dr. Cláudio S. Sartori - CAPÍTULO VIII Exercícios 1 ˆ ˆ ( ) Idl a R. Chamando de: x y du. tg θ

Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r

= 1, independente do valor de x, logo seria uma função afim e não exponencial.

6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0

NÍVEL 2 - Prova da 2ª fase - Soluções

NÍVEL - Prv d ª fse - Sluções QUESTÃO () A prtir d figur d eucid tems =S, =U, 7=C, =R e =I. Lg plvr cdificd cm --7--- é SUCURI. (b) Pr chve 0 tems figur ld, de vems que O=8, B=, M=6, E= e P=9. Assim, cdificçã

TABELA V-A. 0,10=< (r) 0,15=< (r) (r) < 0,20. Até 120.000,00 17,50% 15,70% 13,70% 11,82% 10,47% 9,97% 8,80% 8,00%

Anxo V 1) Srá purd rlção conform bixo: = Folh d Slários incluídos ncrgos (m 12 mss) Rcit Brut (m 12 mss) 2) Ns hipótss m qu corrspond os intrvlos cntsimis d Tbl V-A, ond < signific mnor qu, > signific

Transformada de Clarke e Park

Cnro d Tcnologi Pós-Grdução m Engnhri Eléric Aplicçõs d Elrônic d Poênci m Sisms d Poênci Trnsformd d Clrk Prk Prof. Klbr Lim Dprmno d Engnhri Eléric Sumário Obivos Inrodução Trnsformd d Clrk Vor spcil

MAPA NUMEROLÓGICO PESSOAL

MAPA NUMEROLÓGICO PESSOAL SEU LIVRO DE NUMEROLOGIA CABALÍSTICA APRENDA SOBRE VOCÊ AQUI AUTO CONHECIMENTO Profssor Mx Eu sou Profssor VCPODEMAX, sus Mx, minh rsultdos. como? É com E utor missão przr é po

UTL Faculdade de Motricidade Humana. Mestrado em Reabilitação Psicomotora. Estágio CERCI Lisboa

UTL Fculd Motricid Humn Mstrdo m Rbilitção Psicomotor Estágio CERCI Lisbo Sssão Activid no Mio Aquático 16/11/2011 Clint: C.M., L.V., A.E., F.C. S.C. domínio Nom Dscrição Obj. Esp. Mtriis Estrtégis Critério

8 Transformadas de Fourier

J. A. M. lipp d Suz 8 Trnsfrmds d urir 8 Trnsfrmds d urir 8. Inrduçã à Análi d urir 3 8. A Trnsfrmd d urir pr sinis cnínus 4 Exmpl 8. 6 Exmpl 8. 9 Exmpl 8.3 8.3 A Trnsfrmd d urir pr sinis priódics 3 Exmpl

O MAIOR HUB DE ESQUETES DE HUMOR SOCIAL E COLABORATIVO DA INTERNET IDENTIFICAÇÃO E REFLEXÃO ATRAVÉS DO HUMOR

rs o d i r c n u s qu t u q s d l l i c o s r o m O mior cn u h zr f r p t n r d int ENTO M A T R O P M ICAÇÃO, CO ENTIF D I, O T N E M I ENTRETEN flxão. r d id s r são, div r iv d, o ã ç ssos. p O DR

RESPOSTA DO SISTEMA. Resposta em Regime Transitório Resposta em Regime Permanente

RESPOSTA DO SISTEMA Rsps m Rgm Trsór Rsps m Rgm Prm Exmpls d ssms d prmr rdm Tqu d águ crld pr um bó Tx d vrçã lur é prprcl (H-h) dh k( H h) k h H ( ) Ssm RC, cpcr m sér cm rssr dv C RC ( V V C ) V C RC

1 3Centrs e PP esq is II DD C n MM n Astr l i Astri C h i n Re. C h e H n g K n g F i n l n i I n i F rn 0 4 C n I n n si Al e m n h E st s U n i s I

1 3Mr P e re s, R e s e r h D i re t r I D C B rs i l Br 0 0metr Cis e Bn L rg n Brsil, 2005-201 0 R e s l t s P ri m e i r T ri m e s t re e 2 0 0 7 Prer r Prer r Met e Bn Lrg em 2 0 1 0 n Brs i l : 10

Electromagnetismo e Óptica

Elctromgntismo Óptic Lbortório 1 Expriênci d Thomson OBJECTIVOS Obsrvr o fito d forç d Lorntz. Mdir o cmpo d indução mgnétic produzido por bobins d Hlmholtz. Dtrminr xprimntlmnt o vlor d rlção crg/mss

TRANSFERÊNCIA DE CALOR EM REGIME TRANSIENTE

ôms d s II Pf Cii B Gvs NSEÊNCI DE CO EM EGIME NSIENE Em sss d quim u sfim m quims m ã m bd, ssim m ã m mh u d d quims m ã íu, sfêi d m gim si N sfêi d m gim si, mu mud ã só m siã ii d, mbém mud m m m

Teoria de Linguagens 2 o semestre de 2014 Professor: Newton José Vieira Primeira Lista de Exercícios Entrega: até 16:40h de 23/10.

Pós-Grdução em Ciênci d Computção DCC/ICEx/UFMG Teori de Lingugens 2 o semestre de 2014 Professor: Newton José Vieir Primeir List de Exercícios Entreg: té 16:40h de 23/10. Oservções: O uso do softwre JFLAP,

ESCALA DE PITTSBURGH PARA AVALIAÇÃO DA QUALIDADE DO SONO

ESCALA DE PITTSBURGH PARA AVALIAÇÃO DA QUALIDADE DO SONO As qustõs sguints rfrm-s as sus hábits d sn durant mês passad. Suas rspstas dvm dmnstrar, d frma mais prcisa pssívl, qu acntcu na mairia ds dias

MATRIZES. Matriz é uma tabela de números formada por m linhas e n colunas. Dizemos que essa matriz tem ordem m x n (lê-se: m por n), com m, n N*

MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m

c.c. É a função que associa a cada x X(S) um número f(x) que deve satisfazer as seguintes propriedades:

Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci

MECANISMOS DE REAÇÕES

/4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor

MATRIZES. Em uma matriz M de m linhas e n colunas podemos representar seus elementos da seguinte maneira:

MATRIZES Definiçã Chm-se mtriz d tip m x n (m IN* e n IN*) td tel M frmd pr númers reis distriuíds em m linhs e n cluns. Em um mtriz M de m linhs e n cluns pdems representr seus elements d seguinte mneir:

e-manual Premium FÍSICO-QUÍMICA 9.o ANO Experimente em espacoprofessor.pt

FÍSICO-QUÍMICA 9. ANO Manual Tabla Priódica (frta a alun) Fichas (frta a alun) Apis Áudi (fichirs mp para dwnlad) Cadrn d Atividads (inclui Fichas d Labratóri) Cadrn d Labratóri Matriais Manipulávis Dssir

Material Teórico - Módulo Triângulo Retângulo, Lei dos Senos e Cossenos, Poĺıgonos Regulares. Razões Trigonométricas no Triângulo Retângulo.

Mtril Tórico - Módulo Triângulo Rtângulo, Li dos Snos ossnos, Poĺıgonos Rgulrs Rzõs Trigonométrics no Triângulo Rtângulo Nono no utor: Prof Ulisss Lim Prnt Rvisor: Prof ntonio min M Nto Portl d OMEP 1

Í n d i c e. I n t r o d u ç ã o C o m o e u c o n f i g u r o o S P A 9 3 2? I n f o r m a ç

Í I t ç ã C m f g S P A 9 3 2? I f m ç õ s R l s Itçã Est tg é m m m sé p xl stlçã, tblshtg mtçã pts Cs Smll Bsss (tg Lksys Bsss Ss). Q. Cm fg SPA932? R. O SPA932 é m sl tmt 32-btt p SPA962. C SPA932 f

Fabiano Gontijo. fgontijo@hotmail.com. Graduada em Filosofia pela Universidade Federal do Rio de Janeiro

UZIEL, Ann Pul. Rio Homossxulid Jniro: Grmond, ção. 2007. Fbino Gontijo Doutor m Antropologi m pl Scincs Écol s Socils Huts Frnç. Étus Profssor Adjunto Bolsist Antropologi Produtivid d m Univrsid Psquis

SÃO PAULO FUTEBOL CLUBE

RICLR JG jg! IMGS D DS S IMS D SÃ PUL VL. 6 SÃ PUL FUBL CLUB SÃ PUL FUBL CLUB pruçã mchal 20-srra UM RSG D QUS 0 S D HISÓRI SÃ-PULI RVÉS D FS DS MIS D.600 JGS D CLUB S MISIL C stá u b m a Pac 8/FV magm

Março 2017 *Consulte-nos condições de pagamento a prestações I

L A N E M U SR IN O I R Ó A RO ã i c i F 0 mm sjurss s * r M d 3 é S t Mr 07 *Csult-s cdiõs d pgmt prstõs. 800 83 4 5 I www.dtlxprss.pt ã Prm URBINA PREMIUM PACK DE IMPRESSÃO - 4 Elit HD Putty - 4 Elit

21/07/2015 13:36:51 ARTE MODA ARTE ARQUITETURA ARQUITETURA ENTRETENIMENTO MODA DESTINO GASTRONOMIA GASTRONOMIA MODA POLINÉSIA FRANCESA. CAPA 24.

R 3 R R D S VL L Ó S L U D K LÃ W -S / 3 SH FW -S Ã P UL F S SP / / : 8:3 3// 8/ 3/ : 6: SPCL - PRU C VCÊ UC VU.in 7 R Ú 8 9 - R$,,9 R$ CP.in S D PP R S G GS S - R$, 9 R D : : U Q R VG D R SÃ PU L FS H

Expressão Semi-Empírica da Energia de Ligação

Exprssão Smi-Empíric d Enrgi d Ligção om o pssr do tmpo n usênci d um tori dtlhd pr dscrvr strutur nuclr, vários modlos form dsnvolvidos, cd qul corrlcionndo os ddos xprimntis d um conjunto mis ou mnos

1. Prove a chamada identidade de Lagrange. u 1,u 3 u 2,u 3. u 1 u 2,u 3 u 4 = u 1,u 4 u 2,u 4. onde u 1,u 2,u 3 e u 4 são vetores em R 3.

Universidde Federl de Uberlândi Fculdde de Mtemátic Disciplin : Geometri Diferencil Assunto: Cálculo no Espço Euclidino e Curvs Diferenciáveis Prof. Sto 1 List de exercícios 1. Prove chmd identidde de

Exemplo: y 3, já que sen 2 e log A matriz nula m n, indicada por O m n é tal que a ij 0, i {1, 2, 3,..., m} e j {1, 2, 3,..., n}.

Mrzes Mrz rel Defnção Sem m e n dos números neros Um mrz rel de ordem m n é um conuno de mn números res, dsrbuídos em m lnhs e n coluns, formndo um bel que se ndc em gerl por 9 Eemplo: A mrz A é um mrz

Aulas práticas: Introdução à álgebra geométrica

Auls prátics: Introdução à álgr gométric Prolm Mostr qu ár A do prllogrmo d figur nx é dd por A= = αβ αβ y β α α β β A = αβ αβ α x α β = α + α, = β + β = = αβ + αβ = = ( αβ αβ)( ) = + = = 0 = = = 0 = Prolm

ELECTROMAGNETISMO. TESTE 1 17 de Abril de 2010 RESOLUÇÕES. campo eléctrico apontam ambas para a esquerda, logo E 0.

LTROMAGNTIMO TT 7 d Ail d 00 ROLUÇÕ Ao longo do io dos yy, o vcto cmpo léctico é pllo o io dos pont p squd Isto dv-s o fcto qu qulqu ponto no io dos yy stá quidistnt d dus ptículs cujs cgs são iguis m

# D - D - D - - -

1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18

======================== Œ œ»» Œ C7 ˆ_ ««G 7

1) É tã bnit n tr (ntrd) cminh cm Jesus (Miss d Temp mum cm crinçs) & 2 4 m œ É tã b ni t n_ tr me s s gr d, & œ t h brn c, ve ce s. & _ Mis s vi c me çr n ns s_i gre j; _u & j im c ris ti cm e gri, v

ano Literatura, Leitura e Reflexão m e s t re De quem e a vez? José Ricardo Moreira

S 1- Litt, Lit Rflxã 3- t D q vz? Jé Rid Mi Cpítl 1 P gt Td é di pfit p l: U liv lgl, d lid. E t d di fz d! P Hê: U di vô lá íti, vid hitói d tp q l id gt. P Hit: Ah, di d ihd, it l, it ág, it hi! P L:

CILINDROS. PNEUMÁTICOS. CILINDROS NORMALIZADOS ISO Ø32 À 200mm ISO Ø10 À 25mm

CILINDROS PNEUMÁTICOS CILINDROS NORMLIZDOS ISO 6431 - Ø32 À 200mm ISO 6432 - Ø10 À 25mm R Tabelas técnicas TBEL DE FORÇ (Kp), COMPRIMENTO DO MORTECIMENTO (mm) E ENERGI CINÉTIC DO CILINDRO (kgf/cm2) ØCIL.

Fernando Nogueira Dualidade 1

Dldd Frnndo Nogr Dldd Todo problm d P.L. pod sr sbsttído por m modlo qvlnt dnomndo Dl. O modlo orgnl é chmdo Prml. Problm Prml j n j n c j j j j j j b {... n} {...m} Problm Dl Mn W m m b j c {... m} j

Classificação Periódica dos Elementos

Classificação Periódica dos Elementos 1 2 3 1 Massa atômica relativa. A incerteza no último dígito é 1, exceto quando indicado entre parênteses. Os valores com * referemse Número Atômico 18 ao isótopo

VARIÁVEIS ALEATÓRIAS CONTÍNUAS. Vamos agora estudar algumas variáveis aleatórias contínuas e respectivas propriedades, nomeadamente:

86 VARIÁVIS ALATÓRIAS CONTÍNUAS Vmos gor studr lgums vriávis ltóris contínus rspctivs propridds, nomdmnt: uniform ponncil norml qui-qudrdo t-studnt F DISTRIBUIÇÃO UNIFORM Considr-s qu função dnsidd d proilidd

1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R

píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos

Transporte Vestiário Higiene Pessoal Poupança

Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros

Abertura Celebração Coletiva Local: Pátio Central Oficina de Culinária Regiões do Brasil

C ês I S C v ªF L D 12 Sb Púbc-Av C Esc T 51 6 EM EF EM Lv M-I 4 5 6 9 I M - I N3 N4 6 9 I T 71 7 EM 8 EM T 72 8 9 I 7 EM T 51 Ecçã If A 5 EF 2 Av/Pj Ab Cbçã Cv Lc: Pá C Ofic Cá Rõs Bs P Rflxõs - Rcs: c

Apostila De Matemática GEOMETRIA: REVISÃO DO ENSINO FUNDAMENTAL, PRISMAS E PIRÂMIDES

posti De Mtemátic GEOMETRI: REVISÃO DO ENSINO FUNDMENTL, PRISMS E PIRÂMIDES posti de Mtemátic (por Sérgio Le Jr.) GEOMETRI 1. REVISÃO DO ENSINO FUNDMENTL 1. 1. Reções métrics de um triânguo retânguo. Pr

Cálculo Diferencial II Lista de Exercícios 1

Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto

tese. meus tese. estudo. o trabalho na com exames e seu trabalho na sua privada (Med

1999 E Algr, 1999 m ts. sua na mus m trabalh na ts. stud. privada (Md su trabalh na cm xams AG v c m nrt u s ts. dst stud. as filhs pl m a a vi s XV 1 3 4-2 2 18 18 18 19 da tiróid........ 1-3- 5- vi

BAGS LIFE BAGS FOR ENTREG

, N M DIF QU M 4 c liz v l Id v u c u Y BG LIF BG F bg v w 5 g.c y-b www. IM PDUZ LIZM PN M XP IMDI NG N MN P K Y BG BG IF F L IM PDUZ M IZ L N P M XP DI IM G N N N M P K G b v w 66 D Y BG D L L D LIF

4. Análise de Sistemas de Controle por Espaço de Estados

Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico

2.2.1 Cálculo do m.d.c. à direita de matrizes polinomiais

2.2.1 Cálculo do m.d.c. à direita de matrizes polinomiais Teorema 2.1: Sejam N(s) IR p m [s] e D(s) IR m m [s] e assuma que det[d(s)] 0. Seja U(s) uma matriz unimodular tal que [ ] D(s) U(s) = N(s) R(s),

Exame de Proficiência de Pré-Cálculo

+//+ Em d Profiiêni d Pré-Cálulo - Informçõs instruçõs. Cro studnt, sj bm-vindo à Univrsidd Fdrl d Snt Ctrin! Em oposição o vstibulr, st m não tm rátr sltivo. O objtivo qui é mdir su onhimnto m mtmáti

Aula 09 Equações de Estado (parte II)

Aul 9 Equções de Estdo (prte II) Recpitulndo (d prte I): s equções de estdo têm form (sistems de ordem n ) = A + B u y = C + D u onde: A é um mtriz n n B é um mtriz n p C é um mtriz q n D é um mtriz q