Um outro arquivo texto deve ser criado para usar as funções definidas acima, por exemplo com o nome "simulacao.sce":

Algoritmo de integração numérica - Euler: Considerando a seguinte equação diferencial:

Lista B Aulas Práticas d Scilab Equaçõs difrnciais Introdução: Considr um corpo d massa m fito d um matrial cujo calor spcífico à prssão constant sja c p. Est corpo stá inicialmnt a uma tmpratura T 0,

Cálculo Diferencial II Lista de Exercícios 1

Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto

Roteiro de de Trabalho com com o AQUA AQUA REDE REDE

Rtir d d Trblh cm cm AQUA AQUA REDE REDE Prt Prt I I Iníci Iníci AutCAD Lnçr Lnçr s s pnts pnts ct ct d d Rd Rd Lnçr Lnçr s s trchs trchs brts brts lignd lignd smpr smpr d d Mntnt Mntnt pr pr Jusnt Jusnt

Sinais e Sistemas Mecatrónicos

Sinis Sistms Mctrónicos Anális d Sistms no Domínio do Tmpo José Sá d Cost José Sá d Cost T11 - Anális d Sistms no Tmpo - Rsp. stcionári 1 Crctrizção d rspost stcionário A crctrizção d rspost stcionári

log5 log 5 x log 2x log x 2

mta unção rítmic. Indiqu o vlor d:.. 6.. 7 49...5..6. 5 ln.7. 9.4. ln.8..9. 46.. 4 4 6 6 8 8. Dtrmin o vlor d... 4 8.. 8.. 8.4. 5.5..9. 5.6. 9.7.,8.8... 6 5 8 4 5..... Rsolv cd um ds quçõs:.... 5.. ln

4.21 EXERCÍCIOS pg. 176

78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s

MATEMÁTICA A - 12o Ano Funções - Teorema de Bolzano Propostas de resolução

MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos

1) Determine o domínio das funções abaixo e represente-o graficamente: 1 1

) Dtrmin dmíni das funçõs abai rprsnt- graficamnt: z + z 4.ln( ) z ln z z arccs( ) f) z g) z ln + h) z ( ) ) Dtrmin dmíni, trac as curvas d nívl sbc gráfic das funçõs: f (, ) 9 + 4 f (, ) 6 f (, ) 6 f

ESCOLA SUPERIOR DE TECNOLOGIA

Dprtnto Mtátic Disciplin Anális Mtátic II Curso Engnhri do Abint º Sstr º Fich nº 6: Equçõs difrnciis d vriávis sprds správis, totis cts, co fctor intgrnt hoogéns d ª ord. Coptição ntr spécis E hbitts

c.c. É a função que associa a cada x X(S) um número f(x) que deve satisfazer as seguintes propriedades:

Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci

Vamos analisar o seguinte circuito trifásico: Esta aula:! Sistemas Trifásicos equilibrados com Transformador ideal

EA6 Circuits FEEC UNCAMP Aul 6 Est ul:! Sistms Trifásics quilibrds cm Trnsfrmdr idl Nst ul nlisrms um sistm trifásic quilibrd cm trnsfrmdr Cm sistm é quilibrd, pdms nlisr circuit trifásic trtnd pns d um

Cálculo Diferencial e Integral 1

NOTAS DE AULA Cálculo Dirncil Intgrl Drivds Prossor: Luiz Frnndo Nuns, Dr. 8/Sm_ Cálculo ii Índic Drivds.... Dinição.... Função drivd.... Drivds ds unçõs composts.... Rgrs d drivção.... A Drivd como T

ANEXO I DA LEI COMPLEMENTAR Nº123, DE 14 DE DEZEMBRO DE 2006 (vigência: 01/01/2012)

ANEO I DA LEI COMPLEMENTAR Nº123, DE 14 DE DEZEMBRO DE 2006 (vigênci: 01/01/2012) (Rdção dd pl Li Complmntr nº 139, d 10 d novmbro d 2011) Alíquots Prtilh do Simpls Ncionl - Comércio Rcit Brut m 12 mss

( ) 2. Eletromagnetismo I Prof. Dr. Cláudio S. Sartori - CAPÍTULO VIII Exercícios 1 ˆ ˆ ( ) Idl a R. Chamando de: x y du. tg θ

Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r

TABELA V-A. 0,10=< (r) 0,15=< (r) (r) < 0,20. Até 120.000,00 17,50% 15,70% 13,70% 11,82% 10,47% 9,97% 8,80% 8,00%

Anxo V 1) Srá purd rlção conform bixo: = Folh d Slários incluídos ncrgos (m 12 mss) Rcit Brut (m 12 mss) 2) Ns hipótss m qu corrspond os intrvlos cntsimis d Tbl V-A, ond < signific mnor qu, > signific

MECANISMOS DE REAÇÕES

/4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor

D e atribuamos a x o acréscimo x e a y o acréscimo y, tais que o ponto ( x + x,

DERIVADAS PARCIAIS ACRÉSCIMOS Acréscimo totl Sj unção dinid n rgião D R Tommos o ponto D tribumos o créscimo o créscimo tis qu o ponto D O créscimo d unção qundo pssmos do ponto o ponto é s chm créscimo

MESTRADO INTEGRADO EM ENGENHARIA INFORMÁTICA E COMPUTAÇÃO EIC0011 MATEMÁTICA DISCRETA

1. Tm 40 livros irnts qu vi gurr m 4 ixs ors irnts, olono 10 livros m ix.. Qunts possiilis tm istriuir os livros pls ixs irnts? Justiiqu.. Suponh gor qu tinh 60 livros. Qunts possiilis pr os olor ns 4

Material Teórico - Módulo Triângulo Retângulo, Lei dos Senos e Cossenos, Poĺıgonos Regulares. Razões Trigonométricas no Triângulo Retângulo.

Mtril Tórico - Módulo Triângulo Rtângulo, Li dos Snos ossnos, Poĺıgonos Rgulrs Rzõs Trigonométrics no Triângulo Rtângulo Nono no utor: Prof Ulisss Lim Prnt Rvisor: Prof ntonio min M Nto Portl d OMEP 1

Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1 1

Univrsidd Fdrl do Rio d Jniro COPPE Progrm d Engnhri Químic COQ 79 ANÁLISE DE SISEMAS DA ENGENHARIA QUÍMICA AULA : Rprsnção m Espço d Esdos 4/ Rprsnção m Espço d Esdos Esdo: O sdo d um sism no mpo é o

RESPOSTA DO SISTEMA. Resposta em Regime Transitório Resposta em Regime Permanente

RESPOSTA DO SISTEMA Rsps m Rgm Trsór Rsps m Rgm Prm Exmpls d ssms d prmr rdm Tqu d águ crld pr um bó Tx d vrçã lur é prprcl (H-h) dh k( H h) k h H ( ) Ssm RC, cpcr m sér cm rssr dv C RC ( V V C ) V C RC

AULA 9. Universidade Tecnológica Federal do Paraná Campus Toledo Curso de Engenharia Eletrônica Desenho Técnico Prof. Dr.

Univrsidd Tcnológic Fdrl do Prná Cmpus Toldo d Engnhri Eltrônic Dsnho Técnico AULA 9 PROGRAMA DA AULA: Projçõs ortogonis: Posiçõs ds Figurs plns m rlção um plno d projção. Estudo d sólidos gométricos no

Derivadas parciais de ordem superior à primeira. Teorema de Schwarz.

Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,

A Função Densidade de Probabilidade

Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj X um vriávl ltóri com conjunto d vlors X(S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. A Função Dnsidd

Alteração da seqüência de execução de instruções

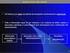Iníci Busc d próxim Excut Prd Cicl busc Cicl xcuçã Prgrm Sqüênci instruçõs m mmóri Trdutr : Cmpilr X Intrprtr / Linkditr Cnvrt prgrm-fnt m prgrm bjt (lingugm máqui) Prgrm cmpil = mis rápi Prgrm Intrprt

+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares

Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn

RESOLUÇÃO DE EQUAÇÕES POR MEIO DE DETERMINANTES

RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.

8 = 1 GRUPO II. = x. 1 ln x

Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim

ELECTROMAGNETISMO. TESTE 1 17 de Abril de 2010 RESOLUÇÕES. campo eléctrico apontam ambas para a esquerda, logo E 0.

LTROMAGNTIMO TT 7 d Ail d 00 ROLUÇÕ Ao longo do io dos yy, o vcto cmpo léctico é pllo o io dos pont p squd Isto dv-s o fcto qu qulqu ponto no io dos yy stá quidistnt d dus ptículs cujs cgs são iguis m

CAPÍTULO 3. Exercícios é contínua, decrescente e k 2 positiva no intervalo [ 3, [. De ln x 1 para x 3, temos. dx 3.

CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)

Aulas práticas: Introdução à álgebra geométrica

Auls prátics: Introdução à álgr gométric Prolm Mostr qu ár A do prllogrmo d figur nx é dd por A= = αβ αβ y β α α β β A = αβ αβ α x α β = α + α, = β + β = = αβ + αβ = = ( αβ αβ)( ) = + = = 0 = = = 0 = Prolm

Estruturas cristalinas - aplicações [6]

[6] Questã 1: Clcule númer de átms existentes em um grm de chumb (Pb), sbend-se que su mss tômic crrespnde 07,. Resluçã: cm mss tômic crrespnde um ml de átms, de um regr de três simples tem-se 6,0. 10

FLUXO EM SOLOS SOB CONDIÇÃO SATURADA. Análise Numérica Método das Diferenças Finitas

FLUXO EM SOLOS SOB CONDIÇÃO SATURADA Análise Numéric Métd ds Diferençs Finits CONTEÚDO. ANÁLISE NUMÉRICA MÉTODO DAS FIFERENÇAS FINITAS..... CONDIÇÕES ESPECIAIS... 5... Superfície impermeável... 5... Diferentes

VARIÁVEIS ALEATÓRIAS CONTÍNUAS. Vamos agora estudar algumas variáveis aleatórias contínuas e respectivas propriedades, nomeadamente:

86 VARIÁVIS ALATÓRIAS CONTÍNUAS Vmos gor studr lgums vriávis ltóris contínus rspctivs propridds, nomdmnt: uniform ponncil norml qui-qudrdo t-studnt F DISTRIBUIÇÃO UNIFORM Considr-s qu função dnsidd d proilidd

TÉCNICAS DE INTEGRAÇÃO. 1.1 Integrais por Substituição Mudança de Variáveis

UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis

4 Modelos para rochas consolidadas e não consolidadas

4 Molos para rochas consoliaas não consoliaas No capítulo antrior, aprsntou-s um molo física rochas calibrávl para o rsrvatório m qustão, qu é o molo proposto para ralizar stimativas prssõs poros, qu srá

Associação de Resistores e Resistência Equivalente

Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos

Instituto de Física USP Física V - Aula 7

Institut d Física USP Física V - Aula 7 Prfssra: Mazé Bchara Aula 07 Mvimnts na atmfsfra ns cnstituints ds sólids.. A distribuiçã spacial ds gass da atmsfra: (a) dsprzand a frça da gravidad; (b) cnsidrand

Análise e Síntese de Algoritmos

Anális Sínts Aloritmos Aloritmos Elmntrs m Gros [CLRS, Cp. 22] 2014/2015 Contxto Rvisão [CLRS, Cp.1-13] Funmntos; notção; xmplos Aloritmos m Gros [CLRS, Cp.21-26] Aloritmos lmntrs Árvors rnnts Cminos mis

10.7 Área da Região Limitada por duas Funções Nesta seção, consideraremos a região que está entre os gráficos de duas funções.

0.7 Ár d Rgião Limitd por dus Funçõs Nst sção, considrrmos rgião qu stá ntr os gráficos d dus funçõs. S f g são contínus f () g() 0 pr todo m [,], ntão ár A d rgião R, limitd plos gráficos d f, g, = =,

MOVIMENTOS SOB A AÇÃO DE UMA FORÇA RESULTANTE DE INTENSIDADE CONSTANTE

MOVIMENTOS SOB A AÇÃO DE UMA ORÇA RESULTANTE DE INTENSIDADE CONSTANTE Trjóris Tmos os sguins csos: 1º) S forç rsuln ivr dirção d vlocidd só vrirá o módulo ds rjóri srá rilín. v R Ou R v º) S forç rsuln

Lista 3 - Resolução. 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os.

GN7 Introução à Álgr Linr Prof n Mri Luz List - Rsolução Vrifiqu s os proutos ixo stão m finios, m so firmtivo, lul-os ) [ / ] / ) / [ / ] ) ) Solução ) orm primir mtriz é x sgun é x, logo o prouto stá

Definição de Área entre duas curvas - A área A entre região limitada pelas curvas. x onde f e g são contínuas e x g x

Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para

= 1, independente do valor de x, logo seria uma função afim e não exponencial.

6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0

ln xdx 1 TÉCNICAS DE INTEGRAÇÃO

Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr

1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R

píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos

5.10 EXERCÍCIO pg. 215

EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção

3 Freqüências Naturais e Modos de Vibração

3 Frqüêncis Nturis Modos d Vibrção Aprsnt-s nst cpítulo ddução ds quçõs difrnciis prciis d movimnto com s rspctivs condiçõs d contorno prtir do funcionl d nrgi.3. Tm-s ssim um problm d vlor d contorno

BALIZA. Cor central.da PLAYMOBIL podes fazer passes. verde-claro curtos, passes longos e, até, rematar para com a nova função de rotação.

PONTAP DE SAÍDA TCNICAS DE Pntpé bliz Est lnc cntc n iníci jg pós cd gl. Est Gnhs cntr p dis"d jg- bl qund cm dis st jgdrs cir list d cmp tu d quip: pntpé é dd REMATE ntr d círcul cntrl. Os jgdrs jg cm

Instituto de Física USP. Física Moderna I. Aula 29. Professora: Mazé Bechara

Institut d Físic USP Físic Mdn I Aul 9 Pfss: Mzé Bch Aul 9 O átm d hidgêni n ti d Schding 1. A sluçã d átm d H n ti d Schding. Cmpçã cm s sultds d Bh.. Os stds dgnds m ngi: stds d msm ngi divss móduls

Resoluções de Exercícios

sluçõs Ecícis MTEMÁTI IV LOO 0 nhcimnts lgébics pítul 0 Funçõs Tignmétics 0 p.( p-)( p-b).( p- c), n + b+ c 8+ + p 8 8.0...9..... LOO 0 0 D + D sn cs tg 0 + 0... sn +.,8.,8. sn 0. +,.,8. +, cm. sn 0 0

(22) Data do Depósito: 08/05/2012. (43) Data da Publicação: 12/04/2016 (RPI 2362)

INPI (21) BR 102012010884-4 A2 (22) Dt d Dpósit: 08/05/2012 *BR102012010884A Rpúblic Fdrtiv d Brsil Ministri d Dsnvlvimnt, Indústri d Cmrci Extrir Institut Ncinl d Prpridd Industril (43) Dt d Publicçã:

MATRIZES. Matriz é uma tabela de números formada por m linhas e n colunas. Dizemos que essa matriz tem ordem m x n (lê-se: m por n), com m, n N*

MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m

Adição dos antecedentes com os consequentes das duas razões

Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como

O sinal. Exemplos: impulso rectangular. Função exponencial. Aplica-se a sinais de energia finita. função sinc(λ) Transformada de Fourier 2/T 1/T T/2

rsrmd d Furir. d [ ]. d pli-s siis d ri ii [ ]. d < lmuiçõs EC Fuçã si λ si λ 3 si λ λ λ sd [ si ] r [ r ] si lmuiçõs EC 3 Exmpls: impuls rulr. r / / s / Fuçã six/x é mui mum. Csum usr-s pr iss uçã siλ

Exame de Proficiência de Pré-Cálculo

+//+ Em d Profiiêni d Pré-Cálulo - Informçõs instruçõs. Cro studnt, sj bm-vindo à Univrsidd Fdrl d Snt Ctrin! Em oposição o vstibulr, st m não tm rátr sltivo. O objtivo qui é mdir su onhimnto m mtmáti

Resolução da Prova 1 de Física Teórica Turma C2 de Engenharia Civil Período

Rsolução da Prova d Física Tórica Turma C2 d Engnharia Civil Príodo 2005. Problma : Qustõs Dados do problma: m = 500 kg ; v i = 4; 0 m=s ;! a = 5! g d = 2 m. Trabalho ralizado por uma força constant: W

tese. meus tese. estudo. o trabalho na com exames e seu trabalho na sua privada (Med

1999 E Algr, 1999 m ts. sua na mus m trabalh na ts. stud. privada (Md su trabalh na cm xams AG v c m nrt u s ts. dst stud. as filhs pl m a a vi s XV 1 3 4-2 2 18 18 18 19 da tiróid........ 1-3- 5- vi

CAPÍTULO 3 - CÁLCULO DIFERENCIAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS

CAPÍTULO - CÁLCULO DIFERENCIAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS. Introdução A dinição d unção d um vriávl indpndnt pod sr dd por: é um unção d vriávl ou sj é um unção d vriávl dpndnt s cd vlor d corrspond

(22) Data do Depósito: 11/02/2015. (43) Data da Publicação: 24/01/2017

INPI (21) BR 102015003018-5 A2 (22) Dt do Dpósito: 11/02/2015 *BR102015003018A Rpúblic Fdrtiv do Brsil Ministério d Indústri, Comércio Extrior Srviços Instituto Ncionl d Propridd Industril (43) Dt d Publicção:

INFORMATIVO 02 / 2009 LEI COMPLEMENTAR 128/08 - SIMPLES NACIONAL - CONTRIBUIÇÃO PREVIDENCIÁRIA PARA CERTOS PRESTADORES DE SERVIÇO

2inf08 HMF (23.01.29) INFORMATIVO 02 / 29 LEI COMPLEMENTAR 128/08 - SIMPLES NACIONAL - CONTRIBUIÇÃO PREVIDENCIÁRIA PARA CERTOS PRESTADORES DE SERVIÇO Em 22.12.28 foi publicd Li Complmntr 128. El ltrou

CAPÍTULO 9 COORDENADAS POLARES

Luiz Frncisco d Cruz Drtmnto d Mtmátic Uns/Buru CAPÍTULO 9 COORDENADAS POLARES O lno, tmbém chmdo d R, ond R RR {(,)/, R}, ou sj, o roduto crtsino d R or R, é o conjunto d todos os rs ordndos (,), R El

Taxi: Opção mais rápida e cara. Deve ser evitada, a não ser que você privilegie o conforte

Vi vijr pr? Situ-s com nosss dics roportos trns mtrôs Chgd m Avião: Aroporto Hthrow: Situdo crc 20 km ost um dos mis movim ntdos d Europ possui cinco trminis Dpois pssr pls formlids imigrção pgr su bggm

J. A. M. Felippe de Souza 7 Séries de Fourier

7 Séris d Furir 7. Itrduçã à Aális d Furir 3 7. Séri trigmétri d Furir pr siis tíus 5 7.3 rm d Furir 6 Exmpl 7. 7 7. Um itrprtçã d Séri d Furir 3 7.5 Séri xpil d Furir pr siis tíus 7 Exmpl 7. 9 7.6 Equivlêi

Análises de sistemas no domínio da frequência

prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico

Prgrmçã O Mu s u Év r, p r l ém f rcr s s i g ns «vi s i t s cl áss i cs» qu cri m s p nt s c nt ct nt r s di v rs s p úb l ic s qu vi s it m s c nt ú d s d s u ri c s p ó l i, p r cu r, c nc m i t nt

ELEMENTOS ELETROMECÂNICOS

ELEMENTOS ELETROMECÂNICOS Ptenciôetr Mtr elétric Gerdr Eleent Ptenciôetr Mtr elétric Gerdr Entrd Psiçã d cntt desliznte Diferenç de ptencil Rtçã d eix Síd Diferenç de ptencil Rtçã d tr Diferenç de ptencil

Notas sobre Integrais Impróprios em R. Pedro Lopes Departamento de Matemática Instituto Superior Técnico 1o. Semestre 2009/2010

Nots sobr Intris Impróprios m R Pdro Lops Dprtmnto d Mtmátic Instituto Suprior Técnico o. Smstr 29/2 Ests nots constitum um mtril d poio o curso d Cálculo Dirncil Intrl II pr s licnciturs m Ennhri Inormátic,

UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ

PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Prof Mc ARMANDO PAULO DA SILVA Prof Mc JOSÉ DONIZETTI DE LIMA INTEGRAIS IMPRÓPRIAS A TRANSFORMADA DE LAPLACE g ()d = lim R R g()d o limit it Qudo o limit it

TÓPICOS. Melhor aproximação. Projecção num subespaço. Mínimo erro quadrático.

Not m: litur dsts pontmntos não dispns d modo lgum litur tnt d iliogrfi principl d cdir Chm-s tnção pr importânci do trlho pssol rlizr plo luno rsolvndo os prolms prsntdos n iliogrfi, sm consult prévi

ERROS ESTACIONÁRIOS. Controle em malha aberta. Controle em malha fechada. Diagrama completo. Análise de Erro Estacionário CONSTANTES DE ERRO

ERROS ESTACIONÁRIOS Control Mlh Abrt Fhd Constnts d rro Tios d sistms Erros unitários Exmlo Control m mlh brt Ação bási, sm rlimntção A ntrd do ontroldor é um sinl d rrêni A síd do ontroldor é o sinl d

Prova de Conhecimentos Específicos 1 a QUESTÃO: (3,0 pontos)

Prov de Conhecimentos Específicos 1 QUESTÃO: (3,0 pontos) Um mol de um gás idel é comprimido, isotermicmente, de modo que su pressão e volume vrim do estdo pr o estdo b, de cordo com o gráfico o ldo. Ddos:

Lista de Exercícios 4 Cálculo I

Lista d Ercícis 4 Cálcul I Ercíci 5 página : Dtrmin as assínttas vrticais hrizntais (s istirm) intrprt s rsultads ncntrads rlacinand-s cm cmprtamnt da funçã: + a) f ( ) = Ants d cmçar a calcular s its

Microeconomia II. Prof. Elaine Toldo Pazello. Capítulo 24

Microconomia II Rsolução 4 a Lista d Exrcícios Prof. Elain Toldo Pazllo Capítulo 24 1. Exrcícios 2, 3, 4, 7, 8, 9, 11 12 do Capítulo 24 do Varian. s no final do livro. 2. Uma mprsa monopolista opra com

MOVIMENTO RELATIVO. Não existe um referencial absoluto. Velocidade Relativa. v B. v A. Velocidades de A e B medidas pelo observador O B = A = dr

1 MOVIMEO ELIVO O mimen é um cncei reli cu descriçã depende de um referencil específic esclhid pel bserdr. Diferenes bserdres usnd sisems referenciis diferenes bém diferenes descrições de um mesm mimen.

VILANCICOS. José Alberto Kaplan. Sesc Partituras

VILANCICOS Jsé Albrt Kaplan NOTA As mldias ds Vilancics: Anunciaçã; Ofrta, frta pastra; Gl xcl fram xtraídas, cm s rspctivs txts, da bra Aut das pastrhas, cligid rcnstituíd pr Ciçã d Barrs Barrt. Obs:

Módulo 03. Determinantes. [Poole 262 a 282]

Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost

Metodologia de Walker e Skogerboe para avaliação de irrigação por sulcos

UNIERSIDADE FEDERA DO CEARÁ CENTRO DE CIÊNCIAS AGRÁRIAS DEPARTAMENTO DE ENGENHARIA AGRÍCOA CURSO DE MESTRADO EM IRRIGAÇÃO E DRENAGEM DISCIPINA: AD 73 - IRRIGAÇÃO POR SUPERFÍCIE Prof.: Rimundo Nonto Távor

PROPRIEDADES DO ELIPSÓIDE

. Elis grdor N Godsi é o lisóid d rvolução (ª roximção) qu srv como rfrênci no osicionmnto godésico; N mior rt dos cálculos d Godsi Gométric é usd gomtri do Elisóid d volução; O Elisóid é formdo l rvolução

Problema do Caixeiro Viajante. Solução força bruta. Problema do Caixeiro Viajante. Projeto e Análise de Algoritmos. Problema do Caixeiro Viajante

Projto Anális Aloritmos Prolm o Cixiro Vijnt Altirn Sors Silv Univrsi Frl o Amzons Instituto Computção Prolm o Cixiro Vijnt Um vim (tour) m um ro é um ilo qu pss por toos os vértis. Um vim é simpls quno

a, pois dois vértices desse triângulo são pontos

UFJF MÓDULO DO PSM TRÊNO 0-0 REFERÊNC DE CORREÇÃO D PROV DE MTEMÁTC PR O DESENVOLVMENTO E RESPOST DS QUESTÕES, SÓ SERÁ DMTDO USR CNET ESFEROGRÁFC ZUL OU PRET Questão Um empres promoveu um concurso pr que

Capítulo 9. Chopper(conversor CC-CC)

píulo 9 onrsor nrodução hoppr(conrsor rg Alimnção: nsão ix rg: nsão riál Equiln d um rnsormdor A A nsão d síd do conrsor pod sr mior ou mnor qu nsão d nrd Normlmn uilizdos m limnção d disposiios lromcânicos

O sinal Impulso Unitário 1. Definição

O sinl mpuls Uniári. Dfiniçã mpuls uniári mp iscr [n] [ n], n, cs cnrári mpuls uniári mp cnínu, 2. Hisóric O sinl l Dirc fi cri pl físic inglês Pul A. Muric Dirc 92-984 p sr is cm quiln cnínu l Krnckr

Transformada de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior

Trormd d plc Pro. Eg. oio Crlo mo Júior GEND Diição d Trormd d plc Trormd d plc d lgu ii Propridd d Trormd d plc Exrcício Corol d Sm Mcâico Trormd d plc Obivo: O obivo d ção é zr um irodução à Trormd d

Corrected. Exame de Proficiência de Pré-Cálculo (2018.2)

Em d Profiiêni d Pré-Cálulo (. Informçõs instruçõs. Cro studnt, sj m-vindo à Univrsidd Fdrl d Snt Ctrin! Em oposição o vstiulr, st m não tm rátr sltivo. O ojtivo qui é mdir su onhimnto m mtmáti dqur sus

Prova de Conhecimentos Específicos. 1 a QUESTÃO: (1,5 ponto) PROAC / COSEAC - Gabarito. Considere a função f definida por. f(x)=.

Prova d Conhcimntos Espcíficos 1 a QUESTÃO: (1,5 ponto) Considr a função f dfinida por Dtrmin: -x f(x). a) as quaçõs das assíntotas horizontais vrticais, caso xistam; b) as coordnadas dos pontos d máximo

Mecânica & Ondas. Módulo 10: O Oscilador harmónico. J. Seixas

Mcânc & Onds Oscldor hrónco Spls Co ro Forçdo Oscldors copldos qução ds onds Módulo : O Oscldor hrónco J. Ss Prlnr: Poncs U forç dz - s consrv v s s u l qu du F d Por plo, grvdd é consrv v dgz F g F -

MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ - UTFPR CAMPUS CORNÉLIO PROCÓPIO

MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS

09. Se. 10. Se. 12. Efetue: 13. Calcule C. a é:, determine a matriz X

LIST DE EER MTRIZES E DETERMINNTES PROF ROGERINHO º ENSINO MÉDIO NOME Nº TURM Rrsn n for d l rz, co s, s, Dd rz, co, scrv rz (M O rço d u rz qudrd é so dos lnos d su dgonl rncl O rço d rz ) (, l qu é:

Eletromagnetismo I. Eletromagnetismo I - Eletrostática. Equação de Laplace (Capítulo 6 Páginas 119 a 123) Eq. de Laplace

Eletromgnetismo I Prof. Dniel Orquiz Eletromgnetismo I Prof. Dniel Orquiz de Crvlo Equção de Lplce (Cpítulo 6 Págins 119 123) Eq. de Lplce Solução numéric d Eq. de Lplce Eletromgnetismo I 2 Prof. Dniel

AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº 0B Funções exponenciais e logarítmicas - 12º ano

AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Fich d Trblho nº B Funçõs ponnciis logrítmics - º no Mts (C.A.). Clcul os sguints limits: n n.. lim.. lim.. lim n n n n n n n n.. lim.. lim.6. lim n n n n. Clcul, m,

INTEGRAÇÃO MÉTODO DA SUBSTITUIÇÃO

INTEGRAÇÃO MÉTODO DA UBTITUIÇÃO o MUDANÇA DE VARIAVEL PARA INTEGRAÇÃO Emplos Ercícios MÉTODO DA INTEGRAÇÃO POR PARTE Emplos Ercícios7 INTEGRAL DEFINIDA8 Emplos Ercícios REFERÊNCIA BIBLIOGRÁFICA INTRODUÇÃO:

Série de Fourier tempo contínuo

Fculdd d Engnhri Séri d Fourir mpo conínuo.5.5.5.5 -.5 - -.5 - -.5.5.5 SS MIEIC 7/8 Séri d Fourir m mpo conínuo ul d hoj Fculdd d Engnhri Rspos d SLIs conínuo ponnciis Eponnciis imgináris hrmonicmn rlcionds

Cosmologia quântica sem singularidades

13 rtig grl VOL. 40 - N. 2 Csmlgi quântic s singulrids Jsé M. Vlhinh Univrsid d Bir Intrir, R. Mrquês D Ávil Blm, 6201-001 Cvilhã jvlhi@ubi.pt Rsum A Rltivid Grl plicd univrs cm um td cnduz à chmd tri

UFS - DComp Adaptados a partir do material da Profa. Kenia Kodel Cox

UFS - DCmp Aps p m Pf. Kn K Cx Busc m Tx Busc m x, u psqus g, u csmn põs, u csmn cs, cnss n psqus um susquênc síms num squênc ss (síms). Busc m Tx P cm jv ncn s s cêncs, u smn pm, um susquênc num squênc;

Métodos Computacionais em Engenharia DCA0304 Capítulo 4

Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d

Uniforme Exponencial Normal Gama Weibull Lognormal. t (Student) χ 2 (Qui-quadrado) F (Snedekor)

Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no

Material envolvendo estudo de matrizes e determinantes

E. E. E. M. ÁREA DE CONHECIMENTO DE MATEMÁTICA E SUAS TECNOLOGIAS PROFESSORA ALEXANDRA MARIA º TRIMESTRE/ SÉRIE º ANO NOME: Nº TURMA: Mteril envolvendo estudo de mtrizes e determinntes INSTRUÇÕES:. Este

Eu sou feliz, tu és feliz CD Liturgia II (Caderno de partituras) Coordenação: Ir. Miria T. Kolling

Eu su iz, s iz Lirgi II (drn d prtirs) rdnçã: Ir. Miri T. King 1) Eu su iz, s iz (brr) & # #2 4. _ k.... k. 1 Eu su "Eu su iz, s iz!" ( "Lirgi II" Puus) iz, s _ iz, & # º #.. b... _ k _. Em cm Pi n cn

Temática Circuitos Eléctricos Capítulo Sistemas Trifásicos LIGAÇÃO DE CARGAS INTRODUÇÃO

www.-l.nt Tmática Circuitos Eléctricos Capítulo Sistmas Trifásicos GAÇÃO DE CARGAS NTRODÇÃO Nsta scção, studam-s dois tipos d ligação d cargas trifásicas (ligação m strla ligação m triângulo ou dlta) dduzindo