Sumário e Objectivos. Método dos Elementos Finitos 11ªAula e 12ªAula. Novembro
|
|
|
- Célia de Oliveira de Sá
- 5 Há anos
- Visualizações:
Transcrição
1 Sumário e Objectivos Sumário: Dependência do Tempo. Equações de Equilíbrio. Matriz de Massa para alguns Elementos. Vibrações Livres e Forçadas. Métodos de Resolução das Equações Diferenciais de Equilíbrio. Objectivos da Aula: Apreensão dos Aspectos mais relevantes para efeitos de análise de Problemas que envolvam Vibrações e Solicitações Dinâmicas no contexto do. 1
2 Aplicações
3 Princípio dos Trabalhos Virtuais δu δu δε σ V V T T T ρ u+ cu+ dv= TBdV T u FdS n T u i F i S i= 1 = δu + δ + δ δu deslocamento Virtual ρ massa específica c parâmetro de Amortecimento Trabalho realizado pelas Forças Exteriores iguala o trabalho absorvido pelas forças de Inércia, de amortecimento e esforços internos. B representa as forças de Volume, F representa as forças de superfície e F i representa as forças nodais. 3
4 Discretização por Elementos Finitos u = Nd u = Nd u = Nd ε = Bd σ = Dε T T T T dv c dv dv δd BDB d+ NN d + ρ NN d = V V V n T = dv + ds δd NB NF + Fi V S i= 1 K = B DB C N N M ρn N e ext e T T T dv e = c dv e= dv V V V n T T i dv dv Fe V V i= 1 F = N b + N F + 4
5 Discretização por Elementos Finitos Kd+Cd+Md=F ext e e e e Sendo: K = ( ) K e, C= ( ) C e,m= ( ) M e, Δ= ( ) d e e F ext =( ) F e ext obtém-se K Δ+C Δ +M Δ =F e ext 5
6 Matrizes de Massa Elemento Triangular Linear T T T M = ρn NdV = dzρn NdA= tρn NdA e 0 V A A t e e e N N 0 N 0 N = 0 N1 0 N 0 N 3 Nó 1 Nó Nó 3 y, v 1 (x 1, y 1 ) (u 1, v 1 ) 3 (x 3, y 3 ) (u 3, v 3 ) A f y f x (x, y ) (u, v ) x, u 1 N = [(y - y )(x - x ) + (x - x )(y - y )] Ae 1 N = [(y - y )(x - x ) + (x - x )(y - y )] Ae 1 N = [(y - y )(x - x ) + (x - x )(y - y )] Ae 6
7 Matrizes de Massa Elemento Triangular Linear M tρ e NN NN 1 0 NN N N 0 N N 0 N N NN 0 NN 0 NN e = 0 NN1 0 NN 0 NN A 3 A NN NN 3 0 NN N N 0 N N 0 N N m n p m!n!p! N1 NNdA 3 = A (m + n + p + )! M e da ρta = sim. 0 7
8 Elemento Rectangular Linear 4 ( 1, +1) η 3 (1, +1) N N 0 N 0 N 0 N = 0 N1 0 N 0 N3 0 N 4 Nó 1 Nó Nó 3 Nó 4 ξ N = (1 +ξξ )(1 +ηη) 1 j 4 j j 1 ( 1, 1) (1, 1) T t T e dv dx da 0 V A M = ρ N N = ρ N N = = ρ = ρ ξ η T T t NNdA abt d d 1 NN 1 A y, v b 4 (x 4, y 4 ) (u 4, v 4 ) 1 (x 1, y 1 ) (u 1, v 1 ) a η ξ = xa, η= yb ξ 3 (x 3, y 3 ) (u 3, v 3 ) (x, y ) (u, v ) x, u 8
9 Elemento Rectangular Linear M e = ρtab sim
10 Elemento Linear Isoparamétrico Plano y 4 (x 4, y 4 ) 3 (x 3, y 3 ) 4 ( 1, +1) η 3 (1, +1) ξ 1 (x 1, y 1 ) (x, y ) x 1 ( 1, 1) (1, 1) h u ( ξη, ) = N( ξη, ) de x( ξ, η) = N( ξ, η) x e 10
11 Elemento Linear Isoparamétrico Matriz de Massa T t T T e = ρ = ρ = 0 ρ V A A M N NdV dx N NdA t N NdA T 1 1 = tρnndet Jdξdη 11
12 Elemento Hexaédrico de 8 Nós N d N 0 0 N 0 0 N i 8 = 0 N Ni N8 0 ei N i 0 0 N 0 0 N 0 0 N 1 i 8 ui = v i ( i = 1,,,8) w i = 1 8 (1 + ξξ )(1 + ηη )(1 + ζζ ) i i x i z y 3 1
13 Elemento Hexaédrico M = N T N d = N T ρ V ρ N det [J] dξdηdζ e V e det[j] = abc = Ve Sub - matrizes ij 1 1 NN 1 i j M = ρabc dξdηdζ N 0 0 N 0 0 i j i j = ρabc 0 N 0 0 N 0 dξdηdζ 0 0 N 0 0 N i j NN 0 0 i j i j =ρabc 0 N N 0 dξdηdζ 0 0 NiN j 13
14 Elemento Hexaédrico Matriz de Massa sendo Mij 0 0 Mij 0 M M = ij ij Ou seja: ij 1 1 i j M =ρabc N N dξdηdζ ρabc = (1 +ξξ 1 i )(1 +ξξ j )d ξ (1 1 i )(1 j )d (1 1 i )(1 j )d +ηη +ηη η +ζζ + ζζ ζ 64 ρhab ( = + 3ξξ i j )(1 + 3ηη i j )(1 + 3ζζ i j ) 8 14
15 Elemento Hexaédrico Matriz de Massa (direcção x) M e x = ρabc sim
16 Elemento de Placa de Mindlin com 4 Nós w = 4 i= 1 N i w i, θ x = 4 i= 1 N θ i x i, θ y = 4 i= 1 N θ i y i sendo N = 1 (1 + ξ ξ )(1 + η η ) i 4 i i Matriz das Funções de Forma N N 0 0 N 0 0 N 0 0 N = N N N N 0 0 N 0 0 N 0 0 N 0 0 N Nó 1 Nó Nó 3 Nó 4 16
17 Matriz de Massa Elemento de Placa de Mindlin de 4 Nós M e = A e T N I N da I ρt ρt = ρt
18 Matriz de Amortecimento A existência de amortecimento implica a diminuição da amplitude de vibração com o tempo. O Amortecimento pode ser provocado ou estar inerente ao problema em causa. Em muitos problemas o amortecimento é suficiente pequeno (as forças de amortecimento são da ordem dos 10% das outras forças)para poder ser considerado como viscoso. Amortecimento de Rayleigh C=α K+βM 18
19 Diagonalização da Matriz de Massa A matriz de massa acabada de obter para alguns elementos é a Matriz de Massa Consistente que representa uma discretização de uma distribuição de Massa Contínua e esta matriz não é Diagonal. É conveniente nalguns casos e sobretudo por questões numéricas associadas aos tempos de execução a consideração de uma Matriz de Massa Diagonal. O processo mais conhecido de diagonalização da Matriz de Massa é designado por HRZ e é devido a Hinton, Rock e Zienkiewicz. 19
20 Diagonalização HRZ 1. Calcular os Elementos de Massa da Diagonal da Matriz de Massa Consistente M ii.. Para cada direcção em que se considera o movimento possível de acordo com o número de graus de Liberdade por nó: a) Determinar a soma dos elementos da diagonal associados a essa direcção (S) b) Multiplicar M ii por M/S sendo M a massa do Elemento 0
21 Vibrações Livres Na ausência de Amortecimento e Carregamento Exterior as Equações de Equilíbrio Dinâmico tomam a forma: K Δ+M Δ =0 Nestas Condições todos os graus de Liberdade se movem em fase e à mesma frequência ω. O movimento devido às Vibrações consiste numa amplitude nodal Ū que varia sinusoidalmente com o tempo em relação aos deslocamentos que correspondem ao equilíbrio estático Δ st produzido por Cargas independentes do tempo. 1
22 Vibrações Livres No caso das cargas serem nulas Δ st =0 e Ū representam amplitudes em relação à configuração de tensão nula. Δ = Usenωt e Δ= ω ω As equações de equilíbrio tomam a forma ( K ) Usen t ω M U=0 Onde ω éum valor próprio e ω éa frequência natural. A matriz dos coeficientes de Ū, é por vezes designada por Matriz de Rigidez Dinâmica.
23 Vibrações Livres Escrevendo a equação seguinte: Com a forma: KU =ω MU ( K ) ω M U=0 Pode-se dizer que os modos de vibração correspondem a configurações em que existe equilíbrio entre as resistências elásticas e as forças de Inércia. No caso de Ū conter graus de liberdade que são não nulos após a supressão dos modos de corpo rígido e mecanismos, a matriz K é positiva definida. No caso da matriz de massa ter elementos diagonais só positivos então a Matriz de Massa é também positiva definida. 3
24 Vibrações Livres O número de valores não nulos da frequência natural ω i, é igual ao número de graus de liberdade em Ū. Ocorre por vezes a existência de valores iguais de ω i. Estruturas sem restrições ou com mecanismos têm uma Matriz de Rigidez positiva semidefinida e um valor próprio nulo associado a cada movimento de corpo rígido ou mecanismo. As formas de vibração correspondentes descrevem o movimento de corpo rígido ou o mecanismo. No caso de existirem valores nulos na diagonal da Matriz de Massa corresponde-lhe um valor próprio infinito. No caso de existência de valores nulos na diagonal eles podem ser eliminados através de um processo de condensação estática antes da obtenção dos valores próprios. 4
25 Vibrações Livres Considerando a equação KU =ω MU Para cada modo i e multiplicando à esquerda por Ū T i obtém-se: T T Ui KUi = ωi Ui MUi Resolvendo em ordem a w i obtém-se: Conhecido por Coeficiente de Rayleigh ω i = U U T i T i KU i MU i 5
26 Vibrações Livres A Redução de Guyan é utilizada para reduzir o número de Graus de Liberdade ao número de graus relevantes para a obtenção da Solução. Kmm Kms Mmm Mms Um 0 Ksm K ω = ss Msm M ss U s 0 A consideração de um processo de condensação estática pura e simples conduziria a matrizes no sistema final que são dependentes da frequência. Para obter uma transformação independente da frequência Guyan e Irons sugeriram que a relação entre graus de liberdade escravos e graus de liberdade principais fosse inteiramente dominada pela rigidez. 6
27 Redução de Guyan Ignorando a massa nos coeficientes dos graus de liberdade escravos obtém-se: { } 1 T U { } s = Kss Kms Um U m I m 1 T s Kss K ms U = = TU sendo T= U Problema de valores próprios reduzido T KrUm ω MrUm = 0 onde Kr = T KT M r = T T MT 7
28 Equações de Equilíbrio Dinâmico Reduzidas A redução de Guyan pode considerar-se aplicada também ao sistema de equilíbrio dinâmico global e não só ao problema de valores próprios. K Δ+C Δ +M Δ =F e ext T KrΔ m + CrΔ m + MrΔ m = R r onde Kr = T KT T Mr = T MT T Cr = T CT ext 8
29 Determinação da Resposta em Função do Tempo Métodos de Sobreposição Modal Métodos de Integração Directa: Implícitos Explícitos 9
30 { } { Δ ( )} Δ( ) Sistema de Equações diferenciais a resolver Após Discretização, Assemblagem e Minimização da Energia Total obtém-se o Sistema de Equações Diferenciais de Equilíbrio seguinte no caso da Dinâmica K Δ+C Δ +M Δ =R 0, 0 Condições Iniciais conhecidas M Matriz de Massa Global C - Matriz de Amortecimento Global K Matriz de Rigidez Global R ext Vector da Solicitação Exterior Global ext 30
31 Matriz de Amortecimento D=Δ D=Δ Representa o vector das Acelerações Representa o vector das Velocidades D=Δ Representa o Vector dos Deslocamentos A matriz de Amortecimento pode ser considerada como uma combinação linear das Matrizes de Rigidez e de Massa, ou seja: C= α K+βM 31
32 Métodos de Solução A forma de solução do sistema de equações diferenciais recorre à integração directa das equações de equilíbrio dinâmico. Sendo conhecida a solução no instante inicial, t=0, procuram-se soluções que verifiquem as equações de equilíbrio num conjunto discreto de posições no tempo. A maior parte dos métodos usa intervalos de tempo iguais, Dt, Dt, 3DT,, ndt. Os métodos utilizados podem ser classificados em explícitos e implícitos. 3
33 Métodos Explícitos Nos métodos explícitos não há necessidade de resolução de um sistema de equações. Estes métodos utilizam a solução das equações diferenciais no instante t para prever a solução no instante t+dt. Na maior parte dos casos intervalos de tempo muito pequenos são necessários de modo a obter-se uma solução estável. Estes métodos são condicionalmente estáveis no que respeita ao intervalo de tempo. A dimensão do intervalo de tempo é inversamente proporcional à frequência mais elevada do sistema discreto. 33
34 Métodos Implícitos Nos métodos Implícitos o sistema de equações diferenciais deve ser verificado no instante t+dt conhecida a solução no instante t. Estes métodos exigem a solução de um sistema de equações em cada intervalo de tempo. Os intervalos podem ser mais elevados que no caso dos métodos explícitos. Os métodos implícitos podem ter estabilidade condicional e incondicional. 34
35 Método das Diferenças Centrais Considerando um desenvolvimento em Série de Taylor para o deslocamento D nos instantes t+δt (D n+1 )e t-δt (D n-1 ), obtém-se: 3 Δt Δt Dn+ 1= Dn+Δ t D n+ D n+ Dn Δt Δt Dn 1= Dn Δ t D n+ D n Dn
36 Método das Diferenças Centrais Velocidade A diferença das duas equações anteriores é: D D D 3 n+ 1 n 1= n + O( Δt ) Resolvendo em ordem à velocidade obtém-se: D n Dn+ 1 Dn 1 3 = + O( Δt ) Δt 36
37 Método das Diferenças Centrais Aceleração A soma das duas equações do desenvolvimento em série de Taylor dos deslocamentos nos instantes t n+1 e t n-1 permite obter a aceleração: D 1 = D D + D Δt n { } n+ 1 n n 1 37
38 Método das Diferenças Centrais Considerando a equação de equilíbrio no instante t que é KDn + CD n+ MD n = Substituindo nesta equação as expressões para a velocidade e aceleração obtém-se: 1 1 KDn+ C ( Dn+ 1 Dn 1) + M ( Dn+ 1 Dn+ Dn 1) = R Δt Δt R ext ext 38
39 Método das Diferenças Centrais Esta última equação pode ser escrita com a seguinte forma: M+ C t t = K M M C Δ t t Δt Δ Δ Δ ext Dn + 1 R Dn Dn 1 Por resolução deste sistema de equações podem obter-se os deslocamentos D n+1. No caso das matrizes M e C serem diagonais os valores dos deslocamentos D n+1 obtém-se sem necessidade de resolução de um sistema de equações. Ver: Concepts and Applications of Finite Element Analysis,COOK, R. D; MALKUS, D. S. and PLESHA, M. E., John Wiley & Sons,third edition,
40 Método das Diferenças Centrais { D(0) } Condições iniciais { D( 0 )},{ D( 0) } podendo obter-se Para iniciar o processo é preciso conhecer-se D (-Δt) que pode ser determinado a partir de { D ( 0 )} e { D ( 0) }. Este Método é condicionalmente estável sendo necessário considerar um intervalo de tempo crítico Δt cr = T n /π sendo T n o menor dos períodos do sistema com n graus de liberdade. Para mais informação ver: Concepts and Applications of Finite Element Analysis,COOK, R. D; MALKUS, D. S. and PLESHA, M. E., John Wiley & Sons,third edition,
41 Método de Newmark Newmark apresentou um conjunto de Métodos para a solução de problemas em Dinâmica Estrutural e estes métodos têm sido muito utilizados. Considere-se as equações de equilíbrio no instante t+δt, considerando U=D: KUn+ 1+ CU n+ 1+ MU n+ 1= R + ext n 1 41
42 Método de Newmark O desenvolvimento em Série de Taylor do deslocamento e da velocidade fornece as equações seguintes: 3 Δt Δt Un+ 1= Un+Δ t U n+ U n+ Un Δt Un+ 1= U n+δ t U n+ Un+... 4
43 Método de Newmark Newmark truncou estas séries e deu-lhe a seguinte forma: Δt 3 n+ 1= n+δ t n+ n+βδ n U U U U t U U n+ 1= U n+δ tu n+γδt Un Admitindo que a aceleração é linear no intervalo de tempo Δt 1 U = U n+ ( U n+ 1 U n) τ sendo 0 τ Δt Δt U n+ 1 U n U = Δt 43
44 Método de Newmark Substituindo esta última equação nas equações anteriores obtém-se: 1 n+ 1= n+δ t n+ ( β) Δt n+βδ n+ 1 U U U U t U U n+ 1= U n+ (1 γ) Δ tu n+γδt U n+ 1 Resolvendo a 1ª equação em ordem à aceleração no instante t+δt obtém-se: U = ( U U ) U 1 U βδt βδt β n+ 1 n+ 1 n n n 44
45 Método de Newmark Substituindo o valor obtido para a aceleração no instante t+δt na expressão que fornece a velocidade no mesmo instante obtém-se: γ γ γ U = ( U U ) + 1 U +Δt 1 U βδt β β n+ 1 n+ 1 n n n 45
46 Método de Newmark Substituindo os valores obtidos para a aceleração e velocidade no instante t+δt nas equações de equilíbrio no referido instante obtém-se: γ γ γ KUn+ 1+ C ( Un+ 1 Un) + C 1 U n+ CΔt 1 U n+ βδt β β M M 1 ext + ( n 1 n) U + U U n M 1 U n = R n+ 1 βδt βδt β 46
47 Método de Newmark Resolvendo em ordem ao deslocamento no instante t+δt obtém-se γ M ext M γ K+ C + Un+ 1= R n C Un+ βδt βδt βδt βδt M γ 1 γ + C 1 U n+ M 1 C Δ t 1 U βδt β β β Conhecido o deslocamento no instante t+δt é fácil obter a velocidade e a aceleração no mesmo instante. n 47
48 Método de Newmark Os parâmetros γ e β podem ser considerados de acordo com a tabela seguinte Versão γ β Estabilidade Aceleração Média Aceleração Linear Fox-Goodwin Amortecimento Algorítmico 1/ 1/4 Incondicional 1/ 1/6 1/ 1/1 Condicional 1/ 1/4(γ+1/) Incondicional 48
49 Método de Newmark Para mais informação ver: Concepts and Applications of Finite Element Analysis,COOK, R. D; MALKUS, D. S. and PLESHA, M. E., John Wiley & Sons,third edition, (Ver algumas das referências indicadas neste texto) 49
50 Método de Wilson θ O Método de Wilson θ é um método implícito e é essencialmente uma extensão do Método da Aceleração Linear. No Método de Wilson θ a aceleração admite-se linear no intervalo t a t+ θδt sendo θ 1. Considerando τ tal que 0 τ θδt a aceleração toma a forma 1 U = U t+ ( U t+θδt U t) τ θδt Integrando 1 U = U tτ+ ( U t+θδt U t) τ + C1 θδt 50
51 Método de Wilson θ A constante C 1 obtém-se considerando que U = U t para τ =0 ou seja C1 = U Consequentemente 1 U = U t + U tτ+ ( U t+ θδt U t) τ θδt Integrando 1 1 U = U + U τ + U + U U 6θΔt t ( ) 3 t t tτ t+ θδt t τ 51
52 Método de Wilson θ Usando estas expressões para obter o deslocamento e a velocidade no instante t+θδt tem-se: θδt U ( ) t+θδt = U t + U t+ θδt U t θδt U = U + θδ tu + U + U 6 ( ) t+θδt t t t+ θδt t 5
53 Método de Wilson θ Considere-se as equações de equilíbrio no instante t+θδt ou seja: ( ) +θδ KUt+θΔ t+ CU t+θδ t+ MU t+θδt = R +θ R R ext ext ext t t t t Das equações anteriores (acetato anterior) pode obter-se U 6 6 = ( Ut+ θδt Ut) U U θδt θδt U 3 θδt = ( Ut+ θδt Ut) U U θδt t+ θδt t t t+θδt t t 53
54 Método de Wilson θ Substituindo estas expressões para a velocidade e aceleração no instante t+θδt nas equações de equilíbrio obtém-se 3 6 ext ext ext K+ C+ M U t+θδt = Rt +θ( Rt+θΔt Rt ) + θδt θδt θδt + C+ M C M C M U + + U + + U t t t θδ θδ θδ t t t Este sistema de equações resolve-se obtendo-se U t+θδt 54
55 Método de Wilson θ Conhecido U t+θδt obtém-se a aceleração no instante t+θδt que é: 6 6 U t+ θδ t = ( t+ t t) U θδ U U t U t θδt θδt Este valor é utilizado nas expressões seguintes para obter os respectivos valores no instante t+δt 1 1 U = U + U τ + U U U τ + θδ 6θΔt 1 U = U ( ) t + U tτ+ Ut+ θδt Ut τ θδt ( ) 3 t t t t+ t t τ 1 U = U t+ ( U t+θδt U t) τ θδt 55
56 Método de Wilson θ Os valores da Aceleração, Velocidade e Deslocamento no instante t+δtsão: U = ( Ut+θΔt Ut) U + 1 U θδt θδt θ t+δt t t Δt U = U + U + U ( ) t+δt t t+ Δt t Δt U = U + U Δ t+ U + U 6 ( ) t+δ t t t t+δt t 56
57 Método de Hilber Hughes and Taylor O Método α Considerem-se as equações de equilíbrio nos instantes t e t+δt, ou seja: ext KU t+δ t+ CU t+δ t+ MU t+δt = R t+δ KU t + CU t+ MU t = R ext t Subtraindo as duas equações e multiplicando por α obtém-se: ext ext αk( Ut+Δ t Ut) +αc( U t+δ t U t) +αm( U t+δt U t) =α( Rt+Δt Rt ) t 57
58 Método de Hilber Hughes and Taylor O Método α Desprezando a variação da aceleração nestas últimas equações e adicionando às equações de equilíbrio no instante t+δt obtém-se: (1 + α )K U t+δ t+ (1 +α )CU t+δ t+ MU t+δt = ext ext = (1 +α) Rt+Δ t α Rt+Δt+α CU t +αku t As expressões para o deslocamento e velocidade são análogas ao Método de Newmark 1 t+δ t = t+δ t t+ ( β) Δt t+βδ t+δt U U U U t U U t+δ t = U t+ (1 γ) Δ tu t+γδt U t+δt 58
59 Método de Hilber Hughes and Taylor O Método α O Método de solução das equações de equilíbrio é semelhante ao Método de Newmark considerando: 1 α γ= (1 α ) 1 β= (1 α ) 4 59
Simulação da Deformação de Objectos em Imagens Segundo Princípios Físicos. Patrícia C. T. Gonçalves Raquel R. Pinho João Manuel R. S.
 Simulação da Deformação de Objectos em Imagens Segundo Princípios Físicos Patrícia C. T. Gonçalves Raquel R. Pinho João Manuel R. S. Tavares Objectivo Dadas duas imagens de um objecto em instantes distintos
Simulação da Deformação de Objectos em Imagens Segundo Princípios Físicos Patrícia C. T. Gonçalves Raquel R. Pinho João Manuel R. S. Tavares Objectivo Dadas duas imagens de um objecto em instantes distintos
Aplicação de Princípios Físicos na Simulação da Deformação de Objectos Em Imagens
 Aplicação de Princípios Físicos na Simulação da Deformação de Objectos Em Imagens Patrícia C. T. Gonçalves, João Manuel R. S. Tavares, Renato M. Natal Jorge IDMEC Instituto de Engenharia Mecânica Pólo
Aplicação de Princípios Físicos na Simulação da Deformação de Objectos Em Imagens Patrícia C. T. Gonçalves, João Manuel R. S. Tavares, Renato M. Natal Jorge IDMEC Instituto de Engenharia Mecânica Pólo
Integração Numérica- continuação
 Integração Numérica- continuação McGraw-Hill 1 Cambridge University Press Prentice-Hall 2 Métodos Explícitos em Dinâmica:. O equilíbrio no instante t usa-se para calcular o deslocamento em t+δt Instabilidade
Integração Numérica- continuação McGraw-Hill 1 Cambridge University Press Prentice-Hall 2 Métodos Explícitos em Dinâmica:. O equilíbrio no instante t usa-se para calcular o deslocamento em t+δt Instabilidade
Sumário e Objectivos. Método dos Elementos Finitos 3ªAula. Setembro
 Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Sumário e Objectivos. Setembro. Elementos Finitos 2ªAula
 Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]
![η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ] η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]](/thumbs/100/144288148.jpg) BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
2 Amortecimento Amortecimento viscoso ou proporcional Sistemas de um grau de liberdade
 2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
3 IMPLEMENTAÇÃO DO ELEMENTO FINITO
 3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
Sumário e Objectivos. Mecânica dos Sólidos não Linear Capítulo 2. Lúcia Dinis 2005/2006
 Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Vibrações Mecânicas. Sistemas com 2 Graus de Liberdade DEMEC/CTG/UFPE. Ramiro Brito Willmersdorf
 Vibrações Mecânicas Sistemas com 2 Graus de Liberdade DEMEC/CTG/UFPE Ramiro Brito Willmersdorf 2015.1 Introdução Sistemas que requerem 2 coordenadas generalizadas para especificar unicamente sua configuração;
Vibrações Mecânicas Sistemas com 2 Graus de Liberdade DEMEC/CTG/UFPE Ramiro Brito Willmersdorf 2015.1 Introdução Sistemas que requerem 2 coordenadas generalizadas para especificar unicamente sua configuração;
Aerodinâmica I. Cálculo Numérico do Escoamento em Torno de Perfis Método dos paineis Γ S
 ( P) σ Aerodinâmica I [ ln( r( P, q) )] σ ( q) ds + ( V ) + γ ov np = vwp + Γ S π np O método dos paineis transforma a equação integral de Fredholm da segunda espécie num sistema de equações algébrico,
( P) σ Aerodinâmica I [ ln( r( P, q) )] σ ( q) ds + ( V ) + γ ov np = vwp + Γ S π np O método dos paineis transforma a equação integral de Fredholm da segunda espécie num sistema de equações algébrico,
ESTRUTURAS PARA LINHAS DE TRANSMISSÃO 6 MÉTODO DOS ELEMENTOS FINITOS
 LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
Licenciatura em Engenharia Civil MECÂNICA II
 NOME: Não esqueça 1) (4 VAL.) de escrever o nome a) Uma partícula descreve um movimento no espaço definido pelas seguintes trajectória e lei horária: z + y 1 = 2 t = y = x + y 1 = (... e ) y s = 2 t Caracterize-o
NOME: Não esqueça 1) (4 VAL.) de escrever o nome a) Uma partícula descreve um movimento no espaço definido pelas seguintes trajectória e lei horária: z + y 1 = 2 t = y = x + y 1 = (... e ) y s = 2 t Caracterize-o
FEP Física para Engenharia II
 FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
Departamento de Engenharia Mecânica ENG Mecânica dos Sólidos II. Teoria de Vigas. Prof. Arthur Braga
 Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Física para Engenharia II - Prova P a (cm/s 2 ) -10
 4320196 Física para Engenharia II - Prova P1-2012 Observações: Preencha todas as folhas com o seu nome, número USP, número da turma e nome do professor. A prova tem duração de 2 horas. Não somos responsáveis
4320196 Física para Engenharia II - Prova P1-2012 Observações: Preencha todas as folhas com o seu nome, número USP, número da turma e nome do professor. A prova tem duração de 2 horas. Não somos responsáveis
Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff.
 Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
ANÁLISE DINÂMICA DE ESTRUTURAS POR INTERMÉDIO DE MARCHA NO TEMPO COM PARAMETRIZAÇÃO LOCAL ASSOCIADA AO MÉTODO DOS ELEMENTOS FINITOS
 ANÁLISE DINÂMICA DE ESTRUTURAS POR INTERMÉDIO DE MARCHA NO TEMPO COM PARAMETRIZAÇÃO LOCAL ASSOCIADA AO MÉTODO DOS ELEMENTOS FINITOS Tales Vieira Sofiste Dissertação de Mestrado apresentada ao Programa
ANÁLISE DINÂMICA DE ESTRUTURAS POR INTERMÉDIO DE MARCHA NO TEMPO COM PARAMETRIZAÇÃO LOCAL ASSOCIADA AO MÉTODO DOS ELEMENTOS FINITOS Tales Vieira Sofiste Dissertação de Mestrado apresentada ao Programa
2 Formulação do Problema
 Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
7 Exemplos Numéricos do Caso Não-Linear
 84 7 Exemplos Numéricos do Caso Não- Neste capítulo é apresentada uma série de exemplos numéricos mostrando a influência da não-linearidade da fundação na resposta do sistema, tanto para o caso de resposta
84 7 Exemplos Numéricos do Caso Não- Neste capítulo é apresentada uma série de exemplos numéricos mostrando a influência da não-linearidade da fundação na resposta do sistema, tanto para o caso de resposta
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
ANÁLISE SÍSMICA DE PÓRTICOS PLANOS METÁLICOS UTILIZANDO O MÉTODO DOS ELEMENTOS FINITOS
 UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA CIVIL E AMBIENTAL ANÁLISE SÍSMICA DE PÓRTICOS PLANOS METÁLICOS UTILIZANDO O MÉTODO DOS ELEMENTOS FINITOS VICTOR ULYSSES SOUSA
UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA CIVIL E AMBIENTAL ANÁLISE SÍSMICA DE PÓRTICOS PLANOS METÁLICOS UTILIZANDO O MÉTODO DOS ELEMENTOS FINITOS VICTOR ULYSSES SOUSA
Disciplina de Cálculo Automático de Estruturas. 5º ano da Licenciatura em Engenharia Civil
 ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide 1 Slide 1 Sobre Modelos para SLIT s Introdução
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide 1 Slide 1 Sobre Modelos para SLIT s Introdução
Vibrações Mecânicas. Sistemas Contínuos. DEMEC UFPE Ramiro Willmersdorf
 Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:
![1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com: 1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:](/thumbs/68/59802332.jpg) Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
MECÂNICA DO CONTÍNUO. Tópico 3. Método dos Trabalhos Virtuais
 MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
1. Estudo do pêndulo
 Objectivos odelizar um pêndulo invertido rígido de comprimento e massa, supondo uma entrada de binário. Simular em computador. entar estabilizar o pêndulo em ciclo aberto por manipulação directa do binário.
Objectivos odelizar um pêndulo invertido rígido de comprimento e massa, supondo uma entrada de binário. Simular em computador. entar estabilizar o pêndulo em ciclo aberto por manipulação directa do binário.
Vibrações de sistemas com um grau de liberdade 1
 Vibrações de sistemas com um grau de liberdade 1 DEFINIÇÕES Vibração mecânica movimento de uma partícula ou de um corpo que oscila em torno de uma posição de equilíbrio. Período de vibração intervalo de
Vibrações de sistemas com um grau de liberdade 1 DEFINIÇÕES Vibração mecânica movimento de uma partícula ou de um corpo que oscila em torno de uma posição de equilíbrio. Período de vibração intervalo de
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Introdução ao Método dos Elementos Finitos
 Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
ESCOAMENTOS VARIÁVEIS EM PRESSÃO (Choque Hidráulico)
 ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
Elementos Finitos 2014/2015 Colectânea de trabalhos, exames e resoluções
 Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
O método convencional consistente dos elementos de contorno
 3 Método convencional consistente dos elementos de contorno O método convencional consistente dos elementos de contorno (MCCEC) [10] baseia-se na adequada consideração das constantes de corpo rígido da
3 Método convencional consistente dos elementos de contorno O método convencional consistente dos elementos de contorno (MCCEC) [10] baseia-se na adequada consideração das constantes de corpo rígido da
Capítulo Integração de Newton-Cotes
 Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
Professor: Juan Julca Avila. Site:
 Professor: Juan Julca Avila Site: http://professor.ufabc.edu.br/~juan.avila Bibliografia Cook, R.; Malkus, D.; Plesha, M., Concepts and Applications of Finite Element Analysis, John Wiley, New York, Fourth
Professor: Juan Julca Avila Site: http://professor.ufabc.edu.br/~juan.avila Bibliografia Cook, R.; Malkus, D.; Plesha, M., Concepts and Applications of Finite Element Analysis, John Wiley, New York, Fourth
Método dos Elementos Finitos Aplicado à Problemas Planos
 Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
UENF - COORDENAÇÃO ACADÊMICA -
 UENF - COORDENAÇÃO ACADÊMICA - Universidade Estadual do Norte Fluminense Darcy Ribeiro PROGRAMA ANALÍTICO DE DISCIPLINA (PÓS-GRADUAÇÃO) Centro CCT IDENTIFICAÇÃO Laboratório LECIV Pré-requisito Co-requisito
UENF - COORDENAÇÃO ACADÊMICA - Universidade Estadual do Norte Fluminense Darcy Ribeiro PROGRAMA ANALÍTICO DE DISCIPLINA (PÓS-GRADUAÇÃO) Centro CCT IDENTIFICAÇÃO Laboratório LECIV Pré-requisito Co-requisito
Sumário e Objectivos. Placas e Cascas 3ªAula. Março
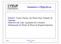 Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Análise dinâmica de sólidos elásticos pelo método dos elementos finitos
 Análise dinâmica de sólidos elásticos pelo método dos elementos finitos Vítor Hugo Amaral Carreiro Dissertação para obtenção do Grau de Mestre em Engenharia Civil Júri Presidente: Doutor Pedro Guilherme
Análise dinâmica de sólidos elásticos pelo método dos elementos finitos Vítor Hugo Amaral Carreiro Dissertação para obtenção do Grau de Mestre em Engenharia Civil Júri Presidente: Doutor Pedro Guilherme
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
 Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Unidade V - Desempenho de Sistemas de Controle com Retroação
 Unidade V - Desempenho de Sistemas de Controle com Retroação Introdução; Sinais de entrada para Teste; Desempenho de um Sistemas de Segunda Ordem; Efeitos de um Terceiro Pólo e de um Zero na Resposta Sistemas
Unidade V - Desempenho de Sistemas de Controle com Retroação Introdução; Sinais de entrada para Teste; Desempenho de um Sistemas de Segunda Ordem; Efeitos de um Terceiro Pólo e de um Zero na Resposta Sistemas
UNIVERSIDADE FEDERAL DO ABC
 UNIVERSIDADE FEDERAL DO ABC BC49 Cálculo Numérico - LISTA - sistemas lineares de equações Profs André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda Métodos diretos Analise os sistemas
UNIVERSIDADE FEDERAL DO ABC BC49 Cálculo Numérico - LISTA - sistemas lineares de equações Profs André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda Métodos diretos Analise os sistemas
Actividade Formativa 1
 Actividade Formativa 1 Resolução 1. a. Dada a função y 3+4x definida no conjunto A {x R: 2 x < 7} represente graficamente A e a sua imagem; exprima a imagem de A como um conjunto. b. Dada a função y 3
Actividade Formativa 1 Resolução 1. a. Dada a função y 3+4x definida no conjunto A {x R: 2 x < 7} represente graficamente A e a sua imagem; exprima a imagem de A como um conjunto. b. Dada a função y 3
Cinemática da partícula fluida
 Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Técnicas de Desenho de Filtros Digitais
 Técnicas de Desenho de Filtros Digitais Luís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Técnicas de Desenho de Filtros Digitais p1/38 Resumo Desenho de filtros discretos com base em filtros
Técnicas de Desenho de Filtros Digitais Luís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Técnicas de Desenho de Filtros Digitais p1/38 Resumo Desenho de filtros discretos com base em filtros
Antenas e Propagação. Artur Andrade Moura.
 1 Antenas e Propagação Artur Andrade Moura amoura@fe.up.pt 2 Equações de Maxwell e Relações Constitutivas Forma diferencial no domínio do tempo Lei de Faraday Equações de Maxwell Lei de Ampére Lei de Gauss
1 Antenas e Propagação Artur Andrade Moura amoura@fe.up.pt 2 Equações de Maxwell e Relações Constitutivas Forma diferencial no domínio do tempo Lei de Faraday Equações de Maxwell Lei de Ampére Lei de Gauss
Capítulo 5 Carga Axial
 Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
2 ANÁLISE ESTÁTICA DA ESTABILIDADE MÉTODO ANALÍTICO.
 ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
Sumário e Objectivos. Resistência dos Materiais 18ªAula. Lúcia M.J.S. Dinis 2005/2006
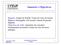 Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Objectivos da Aula: Apreensão dos conceitos Fundamentais associados
Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Objectivos da Aula: Apreensão dos conceitos Fundamentais associados
PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA EXPERIÊNCIA 10: REDES DE SEGUNDA ORDEM
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA Edição 2017 E.Galeazzo / L.Yoshioka
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA Edição 2017 E.Galeazzo / L.Yoshioka
4 e 6/Maio/2016 Aulas 17 e 18
 9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
2 ANÁLISE LIMITE NUMÉRICA
 AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
PEF 3302 Mecânica das Estruturas I Segunda Prova (22/11/2016) - duração: 160 minutos Resolver cada questão em uma folha de papel almaço distinta
 Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Estabilidade Dinâmica
 Estabilidade Dinâmica João Oliveira Departamento de Engenharia Mecânica, Área Científica de Mecânica Aplicada e Aeroespacial Instituto Superior Técnico Estabilidade de Voo, Eng. Aeroespacial Versão de
Estabilidade Dinâmica João Oliveira Departamento de Engenharia Mecânica, Área Científica de Mecânica Aplicada e Aeroespacial Instituto Superior Técnico Estabilidade de Voo, Eng. Aeroespacial Versão de
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um
 As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
SIMULAÇÃO DA DEFORMAÇÃO DE OBJECTOS EM IMAGENS SEGUNDO PRINCÍPIOS FÍSICOS
 2º ENCONTRO NACIONAL DE BIOMECÂNICA H. Rodrigues et al. (Eds.) Évora, Portugal, 8 e 9 de Fevereiro, 2007 SIMULAÇÃO DA DEFORMAÇÃO DE OBJECTOS EM IMAGENS SEGUNDO PRINCÍPIOS FÍSICOS Patrícia C. T. Gonçalves,
2º ENCONTRO NACIONAL DE BIOMECÂNICA H. Rodrigues et al. (Eds.) Évora, Portugal, 8 e 9 de Fevereiro, 2007 SIMULAÇÃO DA DEFORMAÇÃO DE OBJECTOS EM IMAGENS SEGUNDO PRINCÍPIOS FÍSICOS Patrícia C. T. Gonçalves,
Resposta: (A) o traço é positivo (B) o determinante é negativo (C) o determinante é nulo (D) o traço é negativo (E) o traço é nulo.
 MESTRADO INTEGRADO EM ENG. INFORMÁTICA E COMPUTAÇÃO 201/2018 EIC0010 FÍSICA I 1º ANO, 2º SEMESTRE 12 de junho de 2018 Nome: Duração 2 horas. Prova com consulta de formulário e uso de computador. O formulário
MESTRADO INTEGRADO EM ENG. INFORMÁTICA E COMPUTAÇÃO 201/2018 EIC0010 FÍSICA I 1º ANO, 2º SEMESTRE 12 de junho de 2018 Nome: Duração 2 horas. Prova com consulta de formulário e uso de computador. O formulário
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Método dos trabalhos virtuais. Jacob Bernoulli (também James ou Jacques) (Suiça, 27 December August 1705)
 Método dos trabalhos virtuais Jacob ernoulli (também James ou Jacques) (Suiça, 7 December 1654 16 ugust 1705) Trabalho mecânico de uma força num deslocamento infinitesimal (trabalho elementar) x z 0 Trabalho
Método dos trabalhos virtuais Jacob ernoulli (também James ou Jacques) (Suiça, 7 December 1654 16 ugust 1705) Trabalho mecânico de uma força num deslocamento infinitesimal (trabalho elementar) x z 0 Trabalho
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Sistemas com N GDL 1 Prof. Paulo S. Varoto Objetivos Objetivo
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Sistemas com N GDL 1 Prof. Paulo S. Varoto Objetivos Objetivo
INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 2007/2008 Semestre: 1 o
 INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 27/28 Semestre: o MATEMÁTICA COMPUTACIONAL Exercícios [4 Sendo A M n (C) mostre que: (a) n A 2 A n A 2 ; (b)
INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 27/28 Semestre: o MATEMÁTICA COMPUTACIONAL Exercícios [4 Sendo A M n (C) mostre que: (a) n A 2 A n A 2 ; (b)
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS. Professores: Ronny Calixto Carbonari
 Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Programa de Pós-graduação em Engenharia Mecânica da UFABC. Disciplina: Fundamentos de Mecânica dos Sólidos II. Lista 2
 Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Vibrações 1º EE Questão 1
 Vibrações º EE 2052 Questão O sistema claramente tem um grau de liberdade, e é mais facilmente tratável, na minha opinião, considerado como um sistema rotativo A coordenada generalizada empregada será
Vibrações º EE 2052 Questão O sistema claramente tem um grau de liberdade, e é mais facilmente tratável, na minha opinião, considerado como um sistema rotativo A coordenada generalizada empregada será
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial
 Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
Flavio Torres da Fonseca
 SISTEMA COMPUTACIONAL PARA ANÁLISE DINÂMICA GEOMETRICAMENTE NÃO-LINEAR ATRAVÉS DO MÉTODO DOS ELEMENTOS FINITOS Flavio Torres da Fonseca UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA PROGRAMA
SISTEMA COMPUTACIONAL PARA ANÁLISE DINÂMICA GEOMETRICAMENTE NÃO-LINEAR ATRAVÉS DO MÉTODO DOS ELEMENTOS FINITOS Flavio Torres da Fonseca UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA PROGRAMA
de equações diferenciais
 Método de otimização para resolução de equações diferenciais José Mario Martínez Fedor Pisnitchenko Sandra Augusta Santos Matemática Aplicada - IMECC/UNICAMP, 13083-859 Campinas, SP, Brasil E-mail: martinez@ime.unicamp.br,
Método de otimização para resolução de equações diferenciais José Mario Martínez Fedor Pisnitchenko Sandra Augusta Santos Matemática Aplicada - IMECC/UNICAMP, 13083-859 Campinas, SP, Brasil E-mail: martinez@ime.unicamp.br,
Aula # 8 Vibrações em Sistemas Contínuos Modelo de Segunda Ordem
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA Laboratório de Dinâmica SEM 504 DINÂMICA ESTRUTURAL Aula # 8 Vibrações em Sistemas Contínuos Modelo de Segunda
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA Laboratório de Dinâmica SEM 504 DINÂMICA ESTRUTURAL Aula # 8 Vibrações em Sistemas Contínuos Modelo de Segunda
Matrizes e sistemas de equações algébricas lineares
 Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
Exame Final de EDI-38 Concreto Estrutural I Prof. Flávio Mendes Neto Dezembro de 2006 Sem consulta (duração máxima: 4 horas)
 1 Exame Final de EDI-38 Concreto Estrutural I rof. Flávio Mendes Neto Dezembro de 2006 Sem consulta (duração máxima: 4 horas) Esta prova tem 4 páginas e 5 questões (divididas em 9 itens). Considere os
1 Exame Final de EDI-38 Concreto Estrutural I rof. Flávio Mendes Neto Dezembro de 2006 Sem consulta (duração máxima: 4 horas) Esta prova tem 4 páginas e 5 questões (divididas em 9 itens). Considere os
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional = 4200 knm²
 CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
Método dos trabalhos virtuais. Jacob Bernoulli (também James ou Jacques) (Suiça, 27 December August 1705)
 Método dos trabalhos virtuais Jacob ernoulli (também James ou Jacques) (Suiça, 7 December 1654 16 ugust 1705) Trabalho mecânico de uma força num deslocamento infinitesimal (trabalho elementar) x z 0 Trabalho
Método dos trabalhos virtuais Jacob ernoulli (também James ou Jacques) (Suiça, 7 December 1654 16 ugust 1705) Trabalho mecânico de uma força num deslocamento infinitesimal (trabalho elementar) x z 0 Trabalho
Seção 9: EDO s lineares de 2 a ordem
 Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
1. Movimento Harmônico Simples
 Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
1 [30] A figura ao lado mostra o zoom da discretização de uma função
![1 [30] A figura ao lado mostra o zoom da discretização de uma função 1 [30] A figura ao lado mostra o zoom da discretização de uma função](/thumbs/92/110361962.jpg) TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
MESTRADO INTEGRADO EM ENG. INFORMÁTICA E COMPUTAÇÃO 2015/2016
 MESTRADO INTEGRADO EM ENG. INFORMÁTICA E COMPUTAÇÃO 015/016 EIC0010 FÍSICA I 1o ANO, o SEMESTRE 1 de julho de 016 Nome: Duração horas. Prova com consulta de formulário e uso de computador. O formulário
MESTRADO INTEGRADO EM ENG. INFORMÁTICA E COMPUTAÇÃO 015/016 EIC0010 FÍSICA I 1o ANO, o SEMESTRE 1 de julho de 016 Nome: Duração horas. Prova com consulta de formulário e uso de computador. O formulário
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
Anexo 1 - Revisões de Teoria das Probabilidades e Processos Estocásticos
 1 Anexo 1 - Revisões de Teoria das Probabilidades e Processos Estocásticos Documento auxiliar à disciplina de Modelação, Identificação e Controlo Digital Alexandre Bernardino IST-Secção de Sistemas e Controlo
1 Anexo 1 - Revisões de Teoria das Probabilidades e Processos Estocásticos Documento auxiliar à disciplina de Modelação, Identificação e Controlo Digital Alexandre Bernardino IST-Secção de Sistemas e Controlo
Transformada de Laplace
 Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Camada Limite Laminar
 Camada Limite Laminar Profa. Mônica F. Naccache PUC- Rio Profa. Mônica Naccache PUC- Rio 1 Camada Limite Hipótese de Ludwig Prandtl (194): região do fluido em escoamento pode ser dividida em partes: Camada
Camada Limite Laminar Profa. Mônica F. Naccache PUC- Rio Profa. Mônica Naccache PUC- Rio 1 Camada Limite Hipótese de Ludwig Prandtl (194): região do fluido em escoamento pode ser dividida em partes: Camada
Algoritmos Numéricos I. Lucia Catabriga 1
 Algoritmos Numéricos I Problema de Valor no Contorno (PVC) Método das Diferenças Finitas Lucia Catabriga 1 1 DI/UFES - Brazil Novembro 2014 Introdução Introdução A solução de Problemas de Valor no Contorno
Algoritmos Numéricos I Problema de Valor no Contorno (PVC) Método das Diferenças Finitas Lucia Catabriga 1 1 DI/UFES - Brazil Novembro 2014 Introdução Introdução A solução de Problemas de Valor no Contorno
Resistência dos Materiais
 - Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
- Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
B e sabendo que.( ) = 0 B = A (A é o vector potencial magnético) ( A) A t
 Campos variáveis no tempo e equações de Maxwell - 1 o Funções potenciais A divergência de um campo magnético é zero. 0 podemos escrever: B e sabendo que.( ) 0 B A (A é o vector potencial magnético) ( A)
Campos variáveis no tempo e equações de Maxwell - 1 o Funções potenciais A divergência de um campo magnético é zero. 0 podemos escrever: B e sabendo que.( ) 0 B A (A é o vector potencial magnético) ( A)
MÉTODOS DE ENERGIA 1 INTRODUÇÃO
 MÉTODOS DE ENERGIA 1 INTRODUÇÃO Quando não ocorre dissipação de energia, o trabalho realizado pelas cargas aplicadas e a energia são iguais, sendo o trabalho um produto vetorial da força pelo deslocamento.
MÉTODOS DE ENERGIA 1 INTRODUÇÃO Quando não ocorre dissipação de energia, o trabalho realizado pelas cargas aplicadas e a energia são iguais, sendo o trabalho um produto vetorial da força pelo deslocamento.
Aula do cap. 16 MHS e Oscilações
 Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Controlo Em Espaço de Estados. Trabalho de Laboratório nº 3
 Mestrado em Engenharia Electrotécnica e de Computadores Controlo Em Espaço de Estados 2008/09 Trabalho de Laboratório nº 3 Controlo Adaptativo do Nível de um Tanque J. Miranda Lemos e Alexandre Bernardino
Mestrado em Engenharia Electrotécnica e de Computadores Controlo Em Espaço de Estados 2008/09 Trabalho de Laboratório nº 3 Controlo Adaptativo do Nível de um Tanque J. Miranda Lemos e Alexandre Bernardino
Solução Numérica de EDOs
 Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Capítulo 1. Esquema de diferenças finitas e a equação do Oscilador Harmônico
 Capítulo 1 Esquema de diferenças finitas e a equação do Oscilador Harmônico Embora a maior parte dos Modelos Atmosféricos (MA) seja resolvida por uma série de equações diferencias parciais (EDP), em algumas
Capítulo 1 Esquema de diferenças finitas e a equação do Oscilador Harmônico Embora a maior parte dos Modelos Atmosféricos (MA) seja resolvida por uma série de equações diferencias parciais (EDP), em algumas
