Elementos Finitos para a Análise Elástica de Lajes
|
|
|
- Esther Correia Bergmann
- 6 Há anos
- Visualizações:
Transcrição
1 Elementos Finitos para a Análise Elástica de Lajes Luís Manuel Santos Castro 27 de Novembro de 27 Introdução Nestes apontamentos sobre Elementos Finitos de Laje encontram-se sumarizados os conceitos apresentados nas aulas da cadeira de Análise de Estruturas II. Na primeira parte deste texto são definidas as grandezas em função das quais se descreve o comportamento das lajes - deslocamentos, deformações e esforços -, assim como as equações que as permitem relacionar - compatibilidade, equilíbrio e elasticidade. São tratadas em separado a teoria das lajes finas (teoria de Kirchhoff) e a teoria das lajes espessas (teoria de Reissner-Mindlin). A teoria das lajes finas já foi estudada na cadeira de Análise de Estruturas I []. Como foi referido na altura, a teoria de Kirchhoff não permite considerar o efeito da deformabilidade por esforço transverso. A teoria de Reissner-Mindlin já permite a consideração deste efeito. A sua utilização é desta forma aconselhável sempre que a espessura da laje ultrapassa os limites que a permitem classificar como laje fina. Tal sucede sempre que a influência do esforço de corte se torna não desprezável e as hipóteses sobre as quais se baseia a teoria de Kirchhoff deixam de ser válidas. Em geral, costuma considerar-se uma laje como espessa quando a relação vão/espessura é menor que. Uma vez sumarizadas as teorias de lajes, é discutida a forma através da qual se podem definir as aproximações para o campo de deslocamentos quando se formulam elementos finitos para efectuar a análise de lajes finas. Para ilustrar alguns dos aspectos focados, são definidos dois dos elementos finitos utilizados na análise deste tipo de estruturas. É ainda estudado um exemplo de aplicação, com base no qual é ilustrada a utilização do método dos elementos finitos na análise de lajes finas. Numa primeira etapa é obtida a equação de equilíbrio global, utilizando-se para o efeito a sequência de cálculo já estudada no caso dos problemas de placas (elasticidade plana). Depois de obtidos os deslocamentos independentes é efectuado o pós-processamento, sendo definida a solução aproximada para o campo de deslocamentos transversais em cada um dos elementos da malha. Com base nas condições de compatibilidade e nas relações constitutivas, são calculadas de seguida as aproximações para os campos de deformações e para os campos de esforços. Especial atenção é dedicada à caracterização das soluções aproximadas obtidas. Finalmente, é definida a forma através da qual se podem obter elementos finitos para a análise de lajes espessas, sendo salientados alguns cuidados a ter na sua utilização. É também apresentado um exemplo de aplicação no qual se discutem fundamentalmente os aspectos referentes ao pós-processamento, uma vez que no caso das lajes espessas o tipo de elementos finitos
2 2 TEORIA DE KIRCHHOFF 2 a utilizar se assemelha bastante ao utilizado no caso das placas. A análise da aproximação obtida permitirá caracterizar a solução que este tipo de elementos permite obter. É chamada a atenção para as diferenças fundamentais existentes entre as soluções obtidas com elementos finitos desenvolvidos para as teorias de Reissner-Mindlin e de Kirchhoff, respectivamente. 2 Teoria de Kirchhoff O domínio de uma laje pode ser descrito na forma, Ω = {(x,y,z) R 3 : z [ h/2,h/2], (x,y) V R 2 }, onde V e h denotam o plano médio e a espessura da laje, respectivamente. Na figura encontra-se representado o sistema de eixos utilizado e em relação ao qual se encontram escritas as relações fundamentais do problema. Figura : Sistema de eixos O campo de deslocamentos num ponto qualquer do elemento de laje pode ser determinado através das igualdades: u x (x,y,z) = z θ x (x,y) u y (x,y,z) = z θ y (x,y) u z (x,y,z) = w(x,y) onde w(x,y), θ x (x,y) e θ y (x,y) representam os deslocamentos transversais, as rotações no plano (x,z) e as rotações no plano (y,z) dos pontos pertencentes ao plano médio da laje. As deformações de corte podem ser obtidas através das igualdades: γ xz = u x z + u z x = θ x(x,y) + w(x,y) ; () x γ yz = u y z + u z y = θ y(x,y) + w(x,y). (2) y
3 2 TEORIA DE KIRCHHOFF 3 Quando se despreza a deformabilidade por corte, as expressões anteriores permitem obter de imediato: θ x (x,y) = w(x,y) (3) x θ y (x,y) = w(x,y) (4) y A relação entre o campo de rotações θ x e o campo de deslocamentos transversais w encontra-se representada graficamente na figura 2. Figura 2: Definição das rotações; teoria de Kirchhoff. Verifica-se então que os campos θ x (x,y) e θ y (x,y) não são independentes do campo de deslocamentos transversais, w(x, y). Este é por consequência o único campo de deslocamentos a determinar para se poder caracterizar de forma completa os campos de deslocamentos numa laje fina. Resulta daqui que quando se formulam elementos finitos para a análise deste tipo de elementos estruturais, deverá ser necessário definir apenas uma aproximação conveniente para o campo de deslocamentos transversais. As restantes componentes do tensor das deformações são definidas pelas seguintes igualdades: ε xx (x,y,z) = ε yy (x,y,z) = γ xy (x,y,z) = u x x = z θ x(x,y) x u y y = z θ y(x,y) y u x y + u y x = z As igualdades (3) e (4) permitem agora escrever: ε xx (x,y,z) = z 2 w(x,y) x 2 ε yy (x,y,z) = z 2 w(x,y) y 2 ( θx (x,y) y = z χ x (x,y) = z χ y (x,y) + θ ) y(x,y) x
4 2 TEORIA DE KIRCHHOFF 4 γ xy (x,y,z) = 2 z 2 w(x,y) x y = 2 z χ xy (x,y) Para caracterizar de forma completa o estado de deformação numa laje fina são então necessárias duas curvaturas de flexão, χ x (x,y) e χ y (x,y), e uma curvatura de torção, χ xy (x,y). As condições de compatibilidade que permitem relacionar as componentes independentes do tensor das curvaturas e o campo de deslocamentos na laje podem ser escritas na forma genérica, e = Au (5) onde se define e = χ x (x,y) χ y (x,y) 2χ xy (x,y), A = 2 x 2 2 y x y, u = {w(x,y)}. (6) Para se caracterizarem os esforços existentes no elemento de laje são definidos dois momentos flectores, m x (x,y) e m y (x,y), e um momento torsor, m xy (x,y). As relações constitutivas permitem relacionar as componentes independentes do tensor dos momentos com as componentes independentes do tensor das curvaturas. Esta relação linear pode ser escrita na forma: s = De (7) onde neste caso se define s = m x (x,y) m y (x,y) m xy (x,y), D = D f ν ν ( ν)/2 e onde D f, a rigidez de flexão do elemento de laje, tem a definição habitual: (8) D f = E h 3 2( ν 2 ) (9) Uma vez definidos os campos de momentos flectores, os campos de esforços transversos podem ser obtidos através das igualdades v x (x,y) = m x(x,y) x v y (x,y) = m xy(x,y) x + m xy(x,y) y + m y(x,y) y As condições de equilíbrio estabelecem a relação que deve existir entre o carregamento aplicado ao elemento de laje e os esforços que nele se instalam. Esta condição pode ser escrita genericamente na forma: A s + f = ()
5 2 TEORIA DE KIRCHHOFF 5 No caso das lajes finas tem-se: { A 2 = 2 x 2 y x y }, f = {q(x,y)} () onde q(x, y) denota a carga distribuída que actua segundo a direcção perpendicular à superfície média do elemento de laje. Na tabela encontram-se especificadas as condições de fronteira a verificar em cada um dos bordos existentes na laje a analisar. A rotação normal a um dado bordo, ou seja a rotação no plano definido pela normal ao bordo e pelo eixo z, é denotada por θ n. O momento flector em cada bordo, m n, corresponde ao momento que se desenvolve exactamente no mesmo plano. Na figura 3 encontram-se representadas, para um bordo genérico AB, as rotações θ n e θ t, assim como os momentos m n e m t. Na tabela, g denota o valor especificado para a grandeza g envolvida na definição da condição de fronteira em causa. Saliente-se que regra geral são nulos os valores especificados para essas grandezas. Figura 3: Definição das rotações θ n e θ t. Recorde-se ainda que na teoria das lajes finas sempre que se define um bordo livre, as condições de fronteira envolvem a definição do esforço transverso efectivo [], denotado na tabela por v en. Bordo encastrado Bordo simplesmente apoiado Bordo livre w = w w = w v en = v en θ n = θ n m n = m n m n = m n Tabela : Condições de fronteira para as lajes de Kirchhoff Para finalizar, refira-se que quando se desenvolve uma formulação de elementos finitos que passa pela definição de uma aproximação para o campo de deslocamentos transversais, especial atenção deverá ser colocada na forma como se impõem as condições de fronteira cinemática, ou seja, aquelas onde o valor dos deslocamentos é prescrito.
6 3 TEORIA DE REISSNER-MINDLIN 6 3 Teoria de Reissner-Mindlin A teoria de lajes de Reissner-Mindlin permite considerar o efeito da deformabilidade por esforço transverso. Tal como se encontra ilustrado na figura 4, considera-se que fibras inicialmente perpendiculares ao plano médio da laje permanecem rectas após deformação do elemento estrutural, mas não continuam necessariamente a ser ortogonais àquele mesmo plano. Figura 4: Definição das rotações; teoria de Mindlin Como as deformações por corte deixam de ser nulas, as equações () e (2) permitem verificar que os campos de rotações θ x (x,y) e θ y (x,y) deixam de se poder calcular directamente a partir do campo de deslocamentos transversais. Desta forma, para se caracterizar o campo de deslocamentos numa laje espessa, torna-se necessário determinar três campos independentes, o campo de deslocamentos transversais, e os dois campos de rotações. Para caracterizar o estado de deformação num elemento de laje, para além da definição das curvaturas utilizadas na caracterização do comportamento das lajes finas, passa a ser necessário conhecer o valor das deformações de corte, γ x (x,y) e γ y (x,y). Os operadores intervenientes nas equações de compatibilidade (5) passam agora a ser definidos através das igualdades: χ x (x,y) γ x (x,y) γ y (x,y) χ y (x,y) e = 2 χ xy (x,y) ; A = x x y y y x w(x, y) ; u = θ x (x,y) θ y (x,y) (2)
7 3 TEORIA DE REISSNER-MINDLIN 7 As relações de elasticidade continuam a poder ser escritas na forma (7), mas agora tem-se m x (x,y) D f ν D f m y (x,y) ν D f D f s = m xy (x,y) ; D = Gh 3 (3) 2 v x (x,y) φgh v y (x,y) φgh onde o factor de corte φ tem como finalidade corrigir o efeito da distribuição não-uniforme das tensões tangenciais ao longo da espessura da laje. É usual admitir-se que φ = A /A = 5/6, onde A corresponde à área reduzida do rectângulo. Os operadores intervenientes nas equações de equilíbrio definidas em () vêm agora dados pelas seguintes igualdades: A = x y y x x y q(x, y) ; f = m x (x,y) m y (x,y) (4) Na definição do vector de forças aplicadas, f, q(x,y) continua a denotar a distribuição de cargas aplicadas na perpendicular ao plano médio da laje. As grandezas m x (x,y) e m y (x,y) correspondem a campos de momentos distribuídos, aplicados nos planos (x, z) e (y, z), respectivamente. Na teoria de Reissner-Mindlin são três as condições de fronteira que se torna necessário especificar para cada um dos bordos da laje. Na tabela 2 sumarizam-se estas condições para o caso dos bordos encastrados, simplesmente apoiados e livres. Bordo encastrado Bordo simplesmente apoiado Bordo livre w = w w = w v n = v n θ n = θ n m n = m n m n = m n θ t = θ t θ t = θ t m t = m t w = w m n = m n m t = m t Tabela 2: Condições de fronteira para as lajes de Reissner-Mindlin
8 4 ELEMENTOS FINITOS PARA LAJES FINAS 8 Nos bordos encastrados é necessário impor directamente o valor dos deslocamentos transversais, w, e das rotações θ n e θ t. Tal como no caso das lajes finas, a rotação θ n {θ t } corresponde à rotação no plano definido pela normal {tangente} ao bordo em causa e pela direcção z. Nos bordos livres considera-se que são especificados o esforço transverso, v n, e os momentos flector e torsor, m n e m t, respectivamente. Note-se que na teoria das lajes espessas já não se definem os campos de esforços transversos efectivos. Quando se têm bordos simplesmente apoiados, há duas formas alternativas para se definirem as condições de fronteira. A primeira alternativa passa pela imposição do valor dos deslocamentos transversais, w, e das rotações tangenciais, θ t. É também especificado o valor do momento flector, m n. Na segunda alternativa, apenas se especifica o valor do campo de deslocamentos transversais, permitindo-se que as rotações θ t possam tomar valores não-nulos. Sublinhe-se que esta forma de impor as condições de fronteira se torna possível porque na teoria das lajes espessas se desfaz a dependência directa entre deslocamentos transversais e rotações. Saliente-se ainda que as duas restantes condições de fronteira no mesmo bordo envolvem a especificação do valor dos momentos flector e torsor. Das duas formas alternativas existentes para tratar os bordos simplesmente apoiados, a que mais se utiliza é a primeira, uma vez que se encontra mais próximo da percepção física do comportamento do elemento estrutural em análise. A segunda alternativa é utilizada sempre que se torna complicado impor a condição θ t = θ t, o que acontece por exemplo quando se estudam lajes circulares simplesmente apoiadas. É ainda utilizada quando se pretende tornar o modelo numérico mais flexível. De facto, como se impõem apenas os valores dos deslocamentos transversais há uma quantidade menor de deslocamentos especificados, o que torna menos rígido o modelo adoptado, conduzindo à obtenção de valores ligeiramente maiores para os diferentes campos de deslocamentos. 4 Elementos finitos para lajes finas Como foi referido na secção 2, quando se desenvolve uma formulação de elementos finitos para a análise de lajes finas é o campo de deslocamentos transversais que importa aproximar. Uma vez obtida uma solução aproximada para w(x, y), a aproximação para todas as outras grandezas envolvidas na caracterização do comportamento da laje pode ser obtida a partir da aplicação sucessiva das condições de compatibilidade, elasticidade e equilíbrio. Quando se baseia a formulação de elementos finitos de laje na teoria de Kirchhoff, torna-se necessário garantir a continuidade dos deslocamentos transversais, w, e das suas derivadas, w/ n, entre elementos adjacentes. Esta é uma diferença muito importante em relação ao que foi estudado para os problemas de placas, onde apenas se tem que garantir a continuidade dos deslocamentos interpolados [2]. Para justificar de uma forma muito simplista esta imposição, recorde-se que existe uma grande analogia entre as equações das lajes de Kirchhoff e as equações das vigas. Recorde-se ainda que quando se impõe a continuidade dos deslocamentos entre elementos de viga adjacentes, é necessário garantir não só a continuidade dos deslocamentos transversais, mas também a
9 4 ELEMENTOS FINITOS PARA LAJES FINAS 9 continuidade da sua derivada, o que corresponde a assegurar a continuidade das rotações. De um ponto de vista mais formal, pode dizer-se que quando no operador diferencial de compatibilidade A existem segundas derivadas, a definição das aproximações deve ter em conta que as funções de interpolação a utilizar devem ter continuidade C (continuidade das funções e suas derivadas). É o que se passa no caso das vigas e das lajes finas. A necessidade de garantir a continuidade dos deslocamentos e das suas derivadas dificulta significativamente a tarefa de obtenção das funções para efectuar a aproximação dos campos cinemáticos. Torna-se bastante complexa e trabalhosa a obtenção de elementos que permitam verificar por completo as equações de compatibilidade. A utilização de funções polinomiais simples e a utilização dos deslocamentos nodais como incógnitas do problema (situação típica dos elementos finitos de placa) conduz, regra geral, à obtenção de elementos em que pelo menos uma das condições de compatibilidade/continuidade é violada. Este dilema coloca-se com frequência a quem pretende desenvolver elementos de lajes finas. Se por um lado as construções mais simples não permitem verificar a priori todas as condições de compatibilidade, os elementos que permitem satisfazer todos aqueles requisitos são mais complexos, o seu desenvolvimento muito mais trabalhoso e por vezes a sua aplicação bem mais restrita. Aos elementos em que todas as condições de compatibilidade são verificadas, é habitual chamar-se elementos conformes. Caso contrário, são designados elementos não-conformes. É importante salientar que alguns dos elementos não-conformes são frequentes vezes utilizados na análise de lajes finas. A validade da sua aplicação não pode ser posta em causa, uma vez que o seu comportamento e a sua convergência se encontram convenientemente estudados e demonstrados. É importante salientar que em muitos casos estes elementos permitem mesmo obter resultados de melhor qualidade do que os que são obtidos com a utilização de elementos conformes. 4. Exemplo de um elemento não-conforme Um dos elementos não-conformes mais utilizado é o elemento ACM. O seu nome reune as iniciais dos nomes dos investigadores que participaram no seu desenvolvimento (Adini-Clough- Melosh). Trata-se de um elemento rectangular de quatro nós, em cada um dos quais são considerados três deslocamentos independentes; o deslocamento transversal, w i, e as duas rotações, θ xi e θ yi. Em cada elemento define-se desta forma um total de 2 graus de liberdade, como se encontra ilustrado na figura 5. A aproximação para o campo de deslocamentos transversais pode ser escrita na forma: w(x,y) = 2 i= ψ i (x,y)u i. (5) Matricialmente, pode escrever-se: u = Ψu (e) (6)
10 4 ELEMENTOS FINITOS PARA LAJES FINAS Figura 5: Elemento ACM. onde, [ Ψ = ψ (x,y) ψ 2 (x,y) ψ (x,y) ψ 2 (x,y) ] u (e) = u u 2. (7) u u 2 Fisicamente, a função de interpolação ψ i (x,y) corresponde ao campo de deslocamentos transversais que surge quando se impõe o deslocamento elementar u i com valor unitário e se garante que todos os restantes são nulos (u j =, se j i), assim como se garante que não existe qualquer carga distribuída aplicada. Cada função de interpolação terá a seguinte expressão geral [4]: ψ i (x,y) = c + c 2 x + c 3 y + c 4 x 2 + c 5 xy + c 6 y 2 +c 7 x 3 + c 8 x 2 y + c 9 xy 2 + c y 3 + c x 3 y + c 2 xy 3. (8) Para se conseguirem determinar as 2 constantes envolvidas na definição da função ψ i (x,y), basta escrever e resolver o sistema linear de 2 equações e 2 incógnitas que pode ser obtido quando se impõe o campo de deslocamentos pretendido, ou seja u i = e u j = quando j i [4]. Considere-se, como exemplo, que se pretende determinar a função ψ 4 (x,y). As equações que permitem obter os valores dos coeficientes c i presentes na definição (8) são as seguintes: ψ 4 (,) = ; ψ 4 (a,) = ; ψ 4 (a,b) = ; ψ 4 (,b) = ψ 4 (,) x ψ 4 (,) y = ; = ; ψ 4 (a,) x ψ 4 (a,) y = ; = ; ψ 4 (a,b) x ψ 4 (a,b) y = ; = ; ψ 4 (,b) x ψ 4 (,b) y = = Seguindo este procedimento, obter-se-á a seguinte definição para cada uma das funções de
11 4 ELEMENTOS FINITOS PARA LAJES FINAS interpolação [4]: ψ (x,y) = 3x2 a 2 + 2x3 a 3 xy ab + 3x2 y a 2 b 2x3 y a 3 b 3y2 b 2 + 3xy2 ab 2 + 2y3 b 3 2xy3 ab 3 ψ 2 (x,y) = x 2x2 a + x3 a 2 xy b + 2x2 y x3 y ab a 2 b ψ 3 (x,y) = y xy a 2y2 + 2xy2 + y3 b ab b 2 xy3 ab 2 ψ 4 (x,y) = 3x2 a 2 2x3 a 3 + xy ab 3x2 y a 2 b + 2x3 y a 3 b 3xy2 ab 2 + 2xy3 ab 3 ψ 5 (x,y) = x2 a + x3 a 2 + x2 y ab x3 y a 2 b ψ 6 (x,y) = xy a 2xy2 + xy3 ab ab 2 ψ 7 (x,y) = xy ab + 3x2 y a 2 b 2x3 y a 3 b + 3xy2 ab 2 2xy3 ab 3 ψ 8 (x,y) = x2 y ab + x3 y a 2 b ψ 9 (x,y) = xy2 ab + xy3 ab 2 ψ (x,y) = ψ (x,y) = xy ab 3x2 y a 2 b + 2x3 y a 3 b + 3y2 b 2 3xy2 ab 2 2y3 b 3 + 2xy3 ab 3 xy b 2x2 y + x3 y ab a 2 b ψ 2 (x,y) = y2 b + xy2 ab + y3 b 2 xy3 ab 2 As definições apresentadas para as funções de interpolação permitem verificar que a equação (5) define uma aproximação cúbica para o campo de deslocamentos transversais no elemento de laje. Saliente-se que devido à existência dos termos c x 3 y e c 2 xy 3, o campo de deslocamentos transversais ao longo de segmentos de recta oblíquos em relação ao sistema de eixos coordenados terá um andamento do 4 o grau. Na figura 6 encontram-se representadas cada uma das funções de interpolação definidas anteriormente. O elemento ACM é dito não-conforme porque não garante a continuidade das rotações θ n entre elementos adjacentes. A análise da situação representada na figura 7 permite esclarecer o porquê dessa não-conformidade. Considere-se o elemento i e a fronteira definida por x = a. Ao longo desse bordo, a aproximação para o campo de deslocamentos transversais
12 4 ELEMENTOS FINITOS PARA LAJES FINAS ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ (x,y) ϕ 8 (x,y) ϕ (x,y) ϕ (x,y) ϕ 2 (x,y) Figura 6: Funções de aproximação do elemento ACM.
13 4 ELEMENTOS FINITOS PARA LAJES FINAS 3 pode ser escrita na forma genérica, w(a,y) = a + a 2 y + a 3 y 2 + a 4 y 3, enquanto que os campos de rotações vêm dados por: θ x (a,y) = θ y (a,y) = ( w(x,y) ) = a 5 + a 6 y + a 7 y 2 + a 8 y 3, x x=a ( w(x,y) ) = a 2 2a 3 y 3a 4 y 2. y x=a Para que os campos de deslocamentos transversais e rotações pudessem ser definidos de forma única ao longo desse bordo, seria necessário estabelecer oito condições que permitissem calcular os oito coeficientes a i presentes nas definições anteriores. Ora acontece que ao longo do bordo em causa apenas se conseguem estabelecer seis equações, correspondentes aos valores dos deslocamentos nodais nos dois nós que definem o lado. Figura 7: Não-conformidade do elemento ACM. Pode observar-se que na definição de w(a,y) e de θ y (a,y) intervêm as mesmas quatro constantes a i, com i a variar de até 4. Verifica-se desta forma que os deslocamentos transversais w e as rotações θ y nos nós (2) e (3) do elemento i permitem definir, de forma única, a expressão para os correspondentes campos cinemáticos. Se se pensar no que se passa no elemento i+ e no bordo x =, conclui-se também que w e θ y vêm definidos de forma única em função dos deslocamentos dos nós () e (4). Quando se impõe que estes nós tenham os mesmos deslocamentos que os nós (2) e (3) do elemento i, garante-se a continuidade do campo de deslocamentos transversais e do campo de rotações θ y (que neste bordo correspondem às rotações θ t ) na fronteira comum a ambos os elementos. No que respeita à rotação θ n, não é difícil concluir que os dois deslocamentos nodais q 3 e q 6 (ver figura 7) não são suficientes para se conseguir determinar de forma única a expressão do campo de rotações θ x (a,y). Assim, e mesmo garantindo que os deslocamentos nos nós partilhados pelos elementos i e i+ são os mesmos, poderão surgir descontinuidades no campo de rotações normais na fronteira comum àqueles elementos.
14 4 ELEMENTOS FINITOS PARA LAJES FINAS 4 Esta não-conformidade na definição das rotações normais, θ n, faz também com que a solução aproximada não respeite de forma integral todas as condições de fronteira cinemática. Deste modo, sempre que existir um bordo encastrado, mesmo sendo nulo o valor de θ n nos nós da discretização, o campo de rotações poderá tomar valores diferentes de zero nos restantes pontos do bordo em causa. Uma vez definida a matriz das funções de interpolação, Ψ, a matriz de rigidez elementar pode ser obtida através da definição geral: K (e) = B t DB dv = (AΨ) t D(AΨ) dv (9) V A matriz de rigidez elementar do elemento ACM pode ser escrita na forma genérica, K K 2 K 3 K (e) = D f K 2 K 22 K 23, (2) K t 3 K t 23 K 33 onde a definição de cada um dos blocos é dada por: 4 a b b + 4 b a 3 4 ν b 5 b + 2 b a ν 5 b + 2 a b ν K = 5 b + 2 b a ν 4 a 5 b 5 b + 4 b 3 a 4 a ν ν 5 b + 2 a b ν 4 a ν 3 b + 4 b 4 b ν 2 a b 3 4 b 4 b a ν b 5 b 2 b a 2 + ν 5 b + a b 2 4 ν V 2 a b 3 4 b 4 b a ν b 5 b 2 b a 2 + ν 5 b + a b 2 4 ν 4 a b b + 4 b a 3 4 ν b K 2 = 5 b + 2 b a 2 ν 5 b a 5 b + 2 b 3 a + a ν 5 b 5 b 2 b a 2 4 ν 5 b + a b 2 4 ν 2 a 4 b ( + ν) + 3 b + 2 a b ν 2 a b b 2 b a 3 4 ν b 5 b b a 2 ν 5 b a b 2 + ν 4 a b 3 4 b + 2 b a ν b 5 b + b a 2 + ν 5 b a 5 b + b 3 a a ν 5 b 5 b b a ν 5 b a b ν K 3 = a b ( + ν) 3 b 2 a b 2 + ν 4 a b 3 4 b + 2 b a ν b 5 b + b a 2 4 ν 5 b 2 a b 2 + ν 2 a b b 2 b a 3 4 ν b 5 b + b a 2 4 ν 5 b 4 a 5 b + 2 b 3 a + 4 a ν 5 b 5 b b a 2 ν 5 b + 2 a b 2 ν 2 a 3 b b + b ν a b ν K 22 = 4 a 5 b + 4 b 3 a 4 a ν 5 b ν 5 b b a ν 5 b 4 a 5 b + 2 b 3 a + 4 a ν 5 b ν 4 a 4 b ( + ν) 3 b 2 a b ν 5 b b a ν 5 b 2 a b ν 4 a b b + 4 b a 3 4 ν b 5 b 2 b a 2 4 ν 5 b 4 a 5 b + 2 b 3 a + 4 a ν 5 b 5 b 2 b a 2 4 ν 5 b 4 a 5 b + 4 b 3 a 4 a ν 5 b
15 4 ELEMENTOS FINITOS PARA LAJES FINAS 5 2 a b ( + ν) + K 23 = 3 b 2 a b 2 4 ν ν 5 b + b a 2 + ν 5 b a b 2 + ν b 4 b 2 a b 3 4 a ν b 5 b + 2 b a 2 ν 5 b a 5 b + b 3 a a ν 5 b 5 b 2 b a 2 + ν 5 b a 5 b + 2 b 3 a + a ν 5 b a 3 b b ( + ν) a b ν 4 a 4 b ( + ν) 3 b K 33 = a b ν 2 a 4 b ( + ν) + 3 b a b ν 4 a b b + 4 b a 3 4 ν b 5 b + 2 b a ν 5 b 2 a b 2 4 ν 5 b + 2 b a ν 5 b 4 a 5 b + 4 b 3 a 4 a ν 5 b ν 2 a 4 b ( + ν) + 3 b 2 a b 2 4 ν ν 4 a 3 b + 4 b 4 b ν O vector da forças nodais elementares pode ser obtido através da definição geral: F (e) = Ψ t f dv. (2) V Utilizando as definições (7) e () e considerando-se uma carga uniformemente distribuída, q, obtémse: a b 4 a 2 b 24 a b 2 24 a b 4 ( a 2 b ) 24 a b 2 F = q 24 a b (22) 4 ( a 2 b ) 24 ( a b 2) 24 a b 4 a 2 b 24 ( a b 2) Exemplo de aplicação A resolução do problema apresentado na figura 8 vai permitir ilustrar a aplicação do elemento ACM na análise elástica linear de lajes finas. Considera-se que o material que constitui a
16 4 ELEMENTOS FINITOS PARA LAJES FINAS 6 estrutura tem um coeficiente de Poisson ν =.3. O módulo de elasticidade, E, e a espessura da laje, h, são tais que a rigidez de flexão, D f, tem um valor unitário. A laje está sujeita a uma carga uniformemente distribuída q(x,y) =.kn/m 2. Figura 8: Definição do problema Discretização da estrutura e identificação dos deslocamentos independentes A laje é discretizada em 2 elementos finitos rectangulares do tipo ACM. Os deslocamentos independentes correspondentes a esta discretização encontram-se identificados na figura 9. Figura 9: Discretização adoptada Definição da aproximação Como os dois elementos considerados têm a mesma geometria, as funções de aproximação (escritas no referencial local) a considerar na análise têm a mesma definição em ambos. Assim, substituindo a = e b = nas definições dadas anteriormente para as funções de interpolação obtém-se: ψ (x,y) = 3x 2 + 2x 3 xy + 3x 2 y 2x 3 y 3y 2 + 3xy 2 + 2y 3 2xy 3
17 4 ELEMENTOS FINITOS PARA LAJES FINAS 7 ψ 2 (x,y) = x 2x 2 + x 3 xy + 2x 2 y x 3 y ψ 3 (x,y) = y xy 2y 2 + 2xy 2 + y 3 xy 3 ψ 4 (x,y) = 3x 2 2x 3 + xy 3x 2 y + 2x 3 y 3xy 2 + 2xy 3 ψ 5 (x,y) = x 2 + x 3 + x 2 y x 3 y ψ 6 (x,y) = xy 2xy 2 + xy 3 ψ 7 (x,y) = xy + 3x 2 y 2x 3 y + 3xy 2 2xy 3 ψ 8 (x,y) = x 2 y + x 3 y ψ 9 (x,y) = xy 2 + xy 3 ψ (x,y) = xy 3x 2 y + 2x 3 y + 3y 2 3xy 2 2y 3 + 2xy 3 ψ (x,y) = xy 2x 2 y + x 3 y ψ 2 (x,y) = y 2 + xy 2 + y 3 xy 3 As incidências para os elementos e 2 encontram-se definidas nas tabelas 3 e 4, respectivamente. Local Global Tabela 3: Tabela de incidências do elemento. Local Global Tabela 4: Tabela de incidências do elemento 2. Obtenção das equações de equilíbrio elementares Tendo uma geometria semelhante e sendo constituídos pelo mesmo material, os elementos e 2 partilham a mesma matriz de rigidez elementar. Substituindo na definição (2) os valores a =, b =, ν =.3 e D f =., obtém-se:
18 4 ELEMENTOS FINITOS PARA LAJES FINAS 8 K () = Como a carga distribuída aplicada em ambos os elementos é igual, o vector de forças nodais elementares é partilhado pelos elementos e 2. De (22) vem de imediato: F () = Reunião das equações elementares Para efectuar o processo de reunião das equações elementares, é utilizada da forma habitual a informação contida nas tabelas de incidências definidas para cada um dos elementos. Desta forma, a matriz de rigidez global é obtida através de: K = K (), K (),2 K (), K (),7 K (),9 K (),8 K () 2,2 K () 2, K () 2,7 K () 2,9 K () 2,8 K (), K (),7 K (),9 K (),8 K () 7,7 + K(2), K () 7,9 + K(2),2 K () 7,8 + K(2) K () 9,9 + K(2) 2,2 K () 9,8 + K(2), 2, K () 8,8 + K(2), Utilizando as matrizes de rigidez elementares definidas anteriormente, é possível determinar
19 4 ELEMENTOS FINITOS PARA LAJES FINAS 9 o valor numérico dos elementos da matriz de rigidez da estrutura. Obtém-se: K = O vector das forças nodais é obtido da seguinte forma: F () F () 2 F () F = F () 7 + F (2) F () 9 + F (2) 2 F () 8 + F (2) Utilizando a informação referente a cada um dos elementos, torna-se possível obter: F = Resolução da equação de equilíbrio nodal A resolução da equação de equilíbrio global, K q = F, permite determinar o valor dos deslocamentos independentes. Obtém-se:.9987 (m).3757 (rad).2383 (rad) q =.725 (m).82 (rad).764 (rad) Análise da solução obtida Uma vez determinados os deslocamentos independentes e utilizando de novo a informação contida nas tabelas de incidências, é possível escrever a aproximação obtida para o campo de deslocamentos transversais em cada um dos elementos. Para o elemento é possível escrever: w () (x,y) = ψ 7 (x,y) q 4 + ψ 8 (x,y) q 6 + ψ 9 (x,y) q 5 +ψ (x,y) q + ψ (x,y) q 3 + ψ 2 (x,y) q 2
20 4 ELEMENTOS FINITOS PARA LAJES FINAS 2 Substituindo na expressão anterior as definições para as funções de forma e os valores dos deslocamentos independentes, obtém-se: w () (x,y) =.5345xy.6488x 2 y +.43x 3 y +.624y 2 (23).333xy 2.627y xy 3 Para o elemento 2 vem: w (2) (x,y) = ψ (x,y) q 4 + ψ (x,y) q 6 + ψ 2 (x,y) q 5 o que permite definir: w (2) (x,y) =.39xy.6747x 2 y x 3 y y xy y xy 3 Confirma-se que ao longo de segmentos de recta paralelos aos sistemas de eixos se obtém uma aproximação cúbica para o campo de deslocamentos transversais. Já ao longo de rectas não paralelas a x ou a y, a expressão para o deslocamento transversal aproximado é do 4 o grau. Uma vez obtidas as aproximações para o campo de deslocamentos transversais, as expressões (3) e (4) permitem determinar as aproximações para os campos de rotações θ x e θ y. Para o elemento obtêm-se as seguintes igualdades: θ () x = w(x,y) x =.5345y xy.3429x 2 y +.333y 2.368y 3 (24) θ () y = w(x,y) y =.5345x x 2.43x y (25) +.666xy +.865y 2.4xy 2 É importante averigurar neste instante se a solução obtida para os campos de deslocamentos no elemento respeita as condições de fronteira cinemática. No bordo com y =, tanto os deslocamentos transversais quanto os campos de rotações deveriam ser nulos, tendo em conta o encastramento existente. A partir de (23) e (24) não é difícil verificar que w(x,) = e θ x (x,) =. Já quanto à rotação normal, θ y (x,), verifica-se que se anula apenas nos nós e 2 (onde o seu valor foi directamente prescrito), tomando valores diferentes de zero na restante parte do bordo encastrado. A variação de θ y (x,) encontra-se ilustrada no gráfico representado na figura. Fica desta forma ilustrado que a utilização do elemento ACM conduz a soluções aproximadas que não verificam de forma total as condições de fronteira do problema sempre que se especifica o valor das rotações normais num determinado bordo da laje. Os campos de rotações no elemento 2 são dados pelas igualdades: θ x (x,y) (2) =.39y xy.2658x 2 y y y 3
21 4 ELEMENTOS FINITOS PARA LAJES FINAS 2.E E-3-4.E-3-6.E-3 Elemento -8.E-3 -.E-2 -.2E-2 -.4E-2 Figura : Distribuição das rotações θ y no bordo superior - y = - do elemento. θ y (x,y) (2) =.39x x x y xy y xy 2 É agora possível verificar que não há continuidade para o campo de rotações θ x ao longo da fronteira entre os elementos e 2. Dadas as expressões definidas atrás, não é difícil verificar que: θ x () (,y) θ(2) x (,y). Esta mesma conclusão pode ser retirada da análise da figura, onde se representam os campos de rotações θ x no bordo x = (referencial global) obtidos através das aproximações definidas para os elementos e 2. Os campos de curvaturas no elemento podem ser obtidos através da aplicação das equações de compatibilidade definidas em (6). Obtém-se: χ () x = 2 w(x,y) x 2 =.2976y.6858xy χ () y = 2 w(x,y) y 2 = x y.228xy χ () xy = 2 w(x,y) x y = x.3429x y.4y 2 Os campos de momentos podem agora ser calculados com o recurso às relações constitutivas
22 4 ELEMENTOS FINITOS PARA LAJES FINAS 22 8.E-2 7.E-2 6.E-2 5.E-2 4.E-2 Elemento Elemento 2 3.E-2 2.E-2.E-2.E Figura : Distribuição das rotações θ x na interface entre os elementos e 2. definidas em (8): m () x = D f (χ x (x,y) + νχ y (x,y)) = x y.7524xy m () y = D f (νχ x (x,y) + χ y (x,y)) = x y.42654xy m () xy = D f ( ν)χ xy (x,y) = x.243x y.7728y 2 A aproximação definida para os campos de momentos flectores é bilinear, o que faz com que os respectivos diagramas ao longo de segmentos de recta paralelos aos sistemas de eixos coordenados sejam lineares. Por sua vez, é obtida uma aproximação quadrática para o campo de momentos torsores, m xy. Importa agora verificar se a distribuição de momentos obtida verifica as condições de equilíbrio no domínio e na fronteira. Para se verificar o equilíbrio no domínio, a distribuição de cargas aplicadas q(x, y) obtida aplicando a condição () à aproximação obtida para os campos de momentos, deve corresponder ao carregamento inicialmente aplicado à estrutura. Ora a aplicação da equação () permite verificar que a solução de momentos aproximada obtida para o elemento equilibra uma carga distribuída nula, q(x,y) =, o que faz com que o equilíbrio no domínio não venha verificado. Para haver equilíbrio na fronteira, é necessário que a solução obtida para os esforços permita recuperar as condições de carregamento nos bordos da laje (condições de fronteira estática). Repare-se agora o que se passa, por exemplo, na fronteira definida por x =. O diagrama
23 4 ELEMENTOS FINITOS PARA LAJES FINAS 23 de momentos flectores ao longo desse bordo é dado por: m n = m () x (,y) = y. Esta expressão permite concluir que não há equilíbrio na fronteira em causa, uma vez que o momento flector toma valores não nulos, o que contraria as condições de fronteira inicialmente especificadas. O diagrama representado na figura 2 permite reforçar esta ideia. 2.E-.5E-.E- 5.E-2.E E-2 -.E- Elemento -.5E- Figura 2: Distribuição dos momentos flectores no bordo x = do elemento. No elemento 2, os campos de curvaturas e os campos de momentos são dados pelas seguintes igualdades: χ x (x,y) (2) χ y (x,y) (2) =.3494y.436xy = x y.3594xy χ xy (x,y) (2) = x.2658x y.7547y 2 m x (x,y) (2) m y (x,y) (2) = x y.58442xy = x y xy m xy (x,y) (2) = x.4466x y.22829y 2 Para haver equilíbrio de esforços na fronteira inter-elementar, será necessário que a distribuição de momentos flectores obtida com base na solução aproximada definida para o elemento seja igual à distribuição obtida com base na aproximação referente ao elemento 2. A figura 3, onde se traçam aquelas duas distribuições, permite verificar que também não há equilíbrio na fronteira entre elementos. Conclui-se desta forma que a solução aproximada obtida não verifica as condições de equilíbrio nem no domínio, nem na fronteira, o que constitui uma das características gerais das formulações clássicas (de deslocamento) do método dos elementos finitos.
24 4 ELEMENTOS FINITOS PARA LAJES FINAS 24 2.E-.5E-.E- Elemento Elemento 2 5.E-2.E E-2 -.E- Figura 3: Distribuição dos momentos flectores no bordo comum aos dois elementos finitos. 4.2 Exemplo de um elemento conforme Apresenta-se agora de forma muito sucinta o exemplo de um elemento conforme. Trata-se também de um elemento rectangular com quatro nós, e é conhecido geralmente por elemento BFS (Bogner-Fox-Schmit) [4]. Para justificar o tipo de funções de interpolação utilizadas na definição do elemento BFS, mais uma vez se recorre à semelhança existente entre as equações que regem o comportamento das lajes finas e dos elementos de viga. Recorde-se então que quando se formula este tipo de elemento se aproxima o campo de deslocamentos transversais através da expansão w(x) = h (x)δ i + h 2 (x)θ i + h 3 (x)δ j + h 4 (x)θ j, onde δ i{j} e θ i{j} representam o deslocamento transversal e a rotação do nó inicial{final} da barra, respectivamente. Para assegurar a continuidade da função (deslocamentos transversais) e das suas derivadas (rotações) entre elementos adjacentes, são utilizadas as seguintes funções, h (x) = 3x2 L 2 + 2x3 L 3 h 2 (x) = x 2x2 L + x3 L 2 h 3 (x) = 3x2 L 2 2x3 L 3 h 4 (x) = x2 L + x3 L 2 conhecidas geralmente por funções de Hermite e cuja representação gráfica se encontra na figura 4. A passagem para os elementos de laje é agora simples. Intuitivamente, compreender-se-á que se as funções de Hermite permitem verificar as condições de continuidade em domínios
25 4 ELEMENTOS FINITOS PARA LAJES FINAS h(x).2..8 h2(x) h3(x) h4(x) Figura 4: Funções de hermite unidimensionais unidimensionais, o produto de duas funções de Hermite, uma definida em x e a outra definida em y, deverá conduzir à construção de uma função de interpolação conforme num domínio bidimensional. As funções de aproximação do elemento BFS são construídas desta forma. Consideram-se quatro polinómios de Hermite definidos em x e quatro polinómios de Hermite definidos em y. O produto cruzado dessas funções unidimensionais permite a construção de um total de 6 funções bidimensionais, que correspondem precisamente às funções de interpolação procuradas. Define-se então: ψ (x,y) = h (x) h (y) ψ 2 (x,y) = h 2 (x) h (y) ψ 3 (x,y) = h (x) h 2 (y) ψ 4 (x,y) = h 2 (x) h 2 (y) ψ 5 (x,y) = h 3 (x) h (y) ψ 6 (x,y) = h 4 (x) h (y) ψ 7 (x,y) = h 3 (x) h 2 (y) ψ 8 (x,y) = h 4 (x) h 2 (y) ψ 9 (x,y) = h 3 (x) h 3 (y) ψ (x,y) = h 4 (x) h 3 (y) ψ (x,y) = h 3 (x) h 4 (y) ψ 2 (x,y) = h 4 (x) h 4 (y) ψ 3 (x,y) = h (x) h 3 (y) ψ 4 (x,y) = h 2 (x) h 3 (y) ψ 5 (x,y) = h (x) h 4 (y) ψ 6 (x,y) = h 2 (x) h 4 (y) Obtém-se desta forma um elemento com 6 graus de liberdade, sendo quatro as incógnitas associadas a cada um dos nós. Assim, para além dos graus de liberdade habituais (o deslocamento transversal e as duas rotações), há um outro deslocamento nodal independente
26 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 26 a ter em conta. O significado físico deste quarto grau de liberdade corresponde ao valor da curvatura de torção no nó em causa. Na figura 5 encontram-se representados os graus de liberdade elementares a considerar quando se utiliza um elemento BFS. A aproximação para o campo de deslocamentos transversais pode agora ser escrita na forma: 6 w(x,y) = ψ i (x,y)u i (26) i= A utilização deste elemento resulta bastante limitada, uma vez que a sua aplicabilidade se resume a domínios rectangulares. Figura 5: Elemento BFS As dezasseis funções de aproximação utilizadas na definição do elemento BFS encontram-se representadas na figura 6. Repare-se na forma pouco habitual que as funções de interpolação associadas aos deslocamentos nodais correspondentes às curvaturas de torção apresentam (ver por exemplo o gráfico de ψ 4 (x,y)). 5 Elementos finitos para lajes espessas Na teoria de Mindlin, o campo de deslocamentos transversais, w(x, y), é independente dos campos de rotações, θ x (x,y) e θ y (x,y). Torna-se desta forma necessário interpolar de uma forma independente cada um destes campos. Para assegurar a continuidade dos deslocamentos transversais e de todas as rotações, é suficiente neste caso garantir a continuidade das funções de interpolação utilizadas. Este facto faz com que venha muito facilitado o desenvolvimento de elementos finitos para a análise de lajes espessas. Note-se que no operador diferencial de compatibilidade definido em (2) apenas intervêm derivadas de primeira ordem, o que implica que apenas seja necessário garantir continuidade C para as funções de aproximação.
27 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS ϕ (x,y) ϕ (x,y) 5 ϕ (x,y) 9 ϕ (x,y) 3 ϕ (x,y) 2 ϕ (x,y) 6 ϕ (x,y) ϕ (x,y) 4 ϕ (x,y) 3 ϕ (x,y) 7 ϕ (x,y) ϕ (x,y) 5 ϕ (x,y) 4 ϕ (x,y) 8 ϕ 2 (x,y) ϕ (x,y) Figura 6: Funções de aproximação do elemento BFS.
28 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 28 Ao contrário do que sucede nas lajes finas, é então possível a definição de elementos muito semelhantes aos que foram estudados no caso dos problemas de elasticidade plana [2, 3]. As funções de interpolação são semelhantes, diferindo apenas os graus de liberdade que devem ser considerados em cada um dos nós. Como deslocamentos nodais independentes consideram-se os deslocamentos transversais, w, e as duas rotações, θ x e θ y. As interpolações em cada elemento finito podem ser então escritas na forma, w(x,y) = θ x (x,y) = θ y (x,y) = nnos i= nnos i= nnos i= ψ i (x,y)w i, (27) ψ i (x,y)(θ x ) i, (28) ψ i (x,y)(θ y ) i, (29) onde nnos denota o número de nós do elemento finito utilizado. As aproximações podem ser expressas matricialmente na forma (6), mas onde agora se define: Ψ = ψ (x, y)... ψ nnos (x, y) ψ (x, y)... ψ nnos (x, y)... (3) ψ (x, y)... ψ nnos (x, y) e u = w(x, y) θ x (x,y) θ y (x,y) w. w nnos (θ x ) u (e) =. (θ x ) nnos (θ y ). (θ y ) nnos Se se utilizar um elemento finito rectangular com 4 nós, os deslocamentos nodais elementares a considerar são os que se encontram representados na figura 7. Recorde-se que para elementos de forma rectangular com lados paralelos ao sistema de eixos coordenados, as funções de interpolação têm a seguinte definição: ψ (x,y) = x a y b + xy ab ψ 2 (x,y) = ψ 3 (x,y) = ψ 4 (x,y) = x a xy ab xy ab y b xy ab (3)
29 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 29 Figura 7: Elemento rectangular de 4 nós para a análise de lajes de Reissner-Mindlin ϕ (x,y) ϕ (x,y) ϕ (x,y) 3 ϕ (x,y) Figura 8: Funções de aproximação para o elemento rectangular de 4 nós.
30 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 3 Na figura 8 representa-se graficamente cada uma destas quatro funções de interpolação. Conhecida a matriz das funções de interpolação, Ψ, e o operador diferencial de compatibilidade A definido em (2), a matriz de rigidez elementar pode ser calculada com recurso à expressão geral (9), onde agora a matriz das constantes elásticas D é definida em (3). O vector das forças nodais elementares pode ser determinado utilizando-se a definição (2). No caso das lajes espessas, o vector f corresponde à definição apresentada em (4). 5. Cuidados a ter na utilização deste tipo de elementos Dada a sua simplicidade e facilidade de utilização, os modelos de elementos finitos para lajes espessas são os mais utilizados, mesmo em situações para as quais se pode deixar de considerar a laje como espessa. Costuma considerar-se que um bom elemento de Reissner-Mindlin deve conseguir recuperar os resultados fornecidos pela teoria de Kirchhoff quando a espessura da laje começa a diminuir. Embora esta afirmação seja verdadeira em muitos dos casos, situações há em que a diminuição da espessura da laje coloca alguns problemas no que toca à utilização de elementos baseados na implementação da teoria de Reissner-Mindlin. Um dos fenómenos mais gravosos que podem surgir nesta circunstância é o chamado locking. Este fenómeno pode destruir por completo a solução, tornando muito pequenos (ou mesmo nulos) os valores calculados para o campo de deslocamentos. O fenómeno de locking surge porque na definição dos elementos da matriz de rigidez há coeficientes que têm parcelas que vêm multiplicadas por h 3 (parcela de flexão) e parcelas que vêm multiplicadas apenas por h (parcela de corte). Quando a espessura da laje começa a diminuir, a parcela de corte começa a predominar sobre a parcela de flexão, o que faz com que a influência desta última tenda a desaparecer. Uma vez que o fenómeno de locking está associado a uma rigidez excessiva do modelo numérico utilizado, a sua resolução passa pela sub-avaliação dos elementos das matrizes de rigidez elementares. Assim, no cálculo numérico de cada um dos coeficientes que compõem essa matriz, em vez de se utilizar o número de pontos de Gauss necessário para se efectuar uma integração exacta [2, 3], utiliza-se um número inferior, o que vai permitir fazer desaparecer o locking. A integração diz-se reduzida quando se considera um número de pontos de Gauss inferior ao necessário para efectuar as integrações tanto das parcelas de corte quanto das parcelas de flexão. A integração dir-se-à selectiva quando se integra a parcela de flexão de forma exacta e se utiliza sub-integração apenas para a parcela de corte, que é no fundo a principal reponsável pelo locking. Para diferentes tipos de elementos finitos, encontra-se representada na tabela 5 o número de pontos de Gauss que permite efectuar a integração exacta, assim como o número de pontos de Gauss que permitem definir integrações reduzidas e selectivas. Para ilustrar o fenómeno de locking, considere-se uma laje quadrada simplesmente apoiada em todo o seu contorno e sujeita à acção de uma carga uniformemente distribuída, q. Consi-
31 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 3 Tipo de integração Exacta Reduzida Selectiva 2 2 (flexão) 3 3 (flexão) 4 4 (flexão) (corte) 2 2 (corte) 3 3 (corte) Tabela 5: Tipos de integração para elementos isoparamétricos derando a teoria de lajes finas, a solução exacta para o valor do deslocamento transversal no ponto central da laje é dado por: w e =.4644 q L 4 D f, onde L corresponde ao comprimento do bordo da laje. O valor exato do momento flector nesse mesmo ponto é dado pela igualdade: m e = q L2 Na figura 9 encontra-se representada a evolução do valor do deslocamento transversal do ponto central da laje à medida que se diminui a espessura da laje. Em abcissas representa-se a relação L/h e em ordenadas o valor normalizado para o deslocamento em causa, w/w e. A malha utilizada na análise é sempre a mesma e é constituída por elementos isoparamétricos de 4 nós. Seria de esperar que à medida que a espessura da laje fosse diminuindo, os resultados se aproximassem dos resultados fornecidos pela teoria de Kirchhoff, muito embora os elementos utilizados resultem da implementação da teoria de Reissner-Mindlin. Os gráficos representados na figura 9 permitem verificar que quando se utiliza uma integração reduzida ou uma integração selectiva este é de facto o comportamento verificado. Já quando se utiliza a integração total, é bem visível a activação do fenómeno de locking a partir de uma dada relação L/h. Este mesmo efeito pode ser recuperado na análise dos gráficos representados na figura 2, onde agora se representa, exactamente para os mesmos casos testados anteriormente, a evolução do valor do momento flector normalizado, m/m e. Quando se utilizam malhas constituídas por elementos de ordem superior, é de esperar que o fenómeno de locking comece a ser activado para valores de espessuras inferiores. Este aspecto
32 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 32 W/We.4.2. Reduzida e Selectiva.8 Completa Reduzida.6 Selectiva.4.2 Completa..E+ 2.E+ 4.E+ 6.E+ 8.E+.E+2.2E+2 Figura 9: Efeito de locking no valor do deslocamento transversal; elementos de 4 nós. L/h M/Me.2. Reduzida e Selectiva Completa.8 Reduzida Selectiva.6.4 Completa.2..E+ 2.E+ 4.E+ 6.E+ 8.E+.E+2.2E+2 Figura 2: Efeito de locking no valor dos momentos flectores; elementos de 4 nós. L/h
33 5 ELEMENTOS FINITOS PARA LAJES ESPESSAS 33 é visível através da análise da figura 2, onde na análise da mesma laje, mas considerando agora uma discretização envolvendo elementos rectangulares com 8 nós, o locking só começa a surgir para valores mais elevados da relação L/h. W/We.4E+.2E+.E+ 8.E- 6.E- Completa 4.E- Reduzida 2.E-.E+.E+ 2.E+2 4.E+2 6.E+2 8.E+2.E+3.2E+3 Figura 2: Efeito de locking no valor do deslocamento transversal; elementos de 8 nós. L/h Embora os exemplos que aqui são apresentados não o permitem observar, pode afirmar-se que os elementos rectangulares com nove e dezasseis nós são menos sensíveis ao locking que os elementos com oito e doze nós, respectivamente. 5.2 Exemplo de aplicação Retome-se o exemplo de aplicação definido na figura 8. Considere-se de novo uma discretização com dois elementos, mas onde agora são utilizados os elementos isoparamétricos de 4 nós obtidos com a implementação da teoria de lajes espessas. Note-se que os graus de liberdade são os mesmos que anteriormente, e encontram-se identificados na figura 9. Considerou-se nesta análise uma espessura h =. m. O valor do módulo de elasticidade foi escolhido por forma a garantir que a rigidez de flexão da laje, D f, tenha um valor unitário. Para evitar o fenómeno de locking foi utilizada uma integração selectiva. De seguida apenas se efectua a análise crítica da solução aproximada obtida. O processo de obtenção da equação de equilíbrio global não encerra qualquer novidade em relação ao que foi discutido no caso das placas e também no caso da aplicação do elemento ACM. Utilizando o programa de cálculo automático LAJE32, obtiveram-se os seguintes valores para
Elementos Finitos 2014/2015 Colectânea de trabalhos, exames e resoluções
 Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
TESTE FINAL. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 TESTE FINAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARTAMENTO DE ENGENHARIA CIVIL SECÇÃO DE ESTRUTURAS Duração: h00m 1 - (.0 val.) Considere a laje de betão armado
TESTE FINAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARTAMENTO DE ENGENHARIA CIVIL SECÇÃO DE ESTRUTURAS Duração: h00m 1 - (.0 val.) Considere a laje de betão armado
ESTRUTURAS PARA LINHAS DE TRANSMISSÃO 6 MÉTODO DOS ELEMENTOS FINITOS
 LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
2 Teoria de Placas. Figura Placa plana retangular submetida a uma carga de superfície q z. Ref. Brush e Almroth (1975)
 2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]
![η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ] η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]](/thumbs/100/144288148.jpg) BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
EXAME NORMAL. x 2 B D. x 1 C. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Exame de. Licenciatura em Engenharia Civil 21 de Junho de ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre
 Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
Modelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff
 Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
TESTE FINAL. x =2. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
Luís Manuel Santos Castro
 Modelação de Lajes com Elementos de Grelha Luís Manuel Santos Castro 1 Introdução A resolução analítica da equação de Lagrange só é possível nos casos em que a laje apresenta geometria, condições de fronteira
Modelação de Lajes com Elementos de Grelha Luís Manuel Santos Castro 1 Introdução A resolução analítica da equação de Lagrange só é possível nos casos em que a laje apresenta geometria, condições de fronteira
Estruturas de Betão Armado II. 3 Lajes - Análise
 Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
Sumário e Objectivos. Placas e Cascas 3ªAula. Março
 Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Introdução ao Método dos Elementos Finitos
 Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
3 IMPLEMENTAÇÃO DO ELEMENTO FINITO
 3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
Caso mais simples MÉTODO DOS ELEMENTOS FINITOS. Álvaro Azevedo. Faculdade de Engenharia Universidade do Porto
 MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
PEF 3302 Mecânica das Estruturas I Segunda Prova (22/11/2016) - duração: 160 minutos Resolver cada questão em uma folha de papel almaço distinta
 Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Resistência dos Materiais, MA, IST,
 11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
6 MÉTODO DE ELEMENTOS FINITOS - MEF
 6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
ANÁLISE DE ESTRUTURAS II
 DECivil ANÁLISE DE ESTRUTURAS II INTRODUÇÃO À ANÁLISE LIMITE DE LAJES Orlando J B A ereira 005 1 Introdução Em geral, pretende-se que as estruturas tenham um comportamento linear nas situações usuais de
DECivil ANÁLISE DE ESTRUTURAS II INTRODUÇÃO À ANÁLISE LIMITE DE LAJES Orlando J B A ereira 005 1 Introdução Em geral, pretende-se que as estruturas tenham um comportamento linear nas situações usuais de
Peça linear em equilíbrio estático sob a acção de um carregamento genérico e uma secção transversal S:
 Esforços em peças lineares. Peça linear em equilíbrio estático sob a acção de um carregamento genérico e uma secção transversal S: Orientação do eixo e seccionamento da peça e através da secção de corte
Esforços em peças lineares. Peça linear em equilíbrio estático sob a acção de um carregamento genérico e uma secção transversal S: Orientação do eixo e seccionamento da peça e através da secção de corte
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486
 0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
Sumário e Objectivos. Setembro. Elementos Finitos 2ªAula
 Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Teoria Clássica das Placas
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada.
 Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
MÉTODO DOS ELEMENTOS FINITOS
 MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.alvaroazevedo.com Setembro 2017 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.alvaroazevedo.com Setembro 2017 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada.
 Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Análise Matricial de Estruturas com orientação a objetos
 Análise Matricial de Estruturas com orientação a objetos Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto...
Análise Matricial de Estruturas com orientação a objetos Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto...
4. Avaliação dos Resultados
 4. Avaliação dos Resultados 4.1. Introdução Neste capítulo, são mostradas as análises que foram realizadas com a utilização do programa Ansys [19] com o intuito de testar, no âmbito deste programa, a eficiência
4. Avaliação dos Resultados 4.1. Introdução Neste capítulo, são mostradas as análises que foram realizadas com a utilização do programa Ansys [19] com o intuito de testar, no âmbito deste programa, a eficiência
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS. Professores: Ronny Calixto Carbonari
 Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1
 PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
2.1 Translação, rotação e deformação da vizinhança elementar Variação relativa do comprimento (Extensão)
 Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Módulo de elasticidade ou módulo de Young
 CAPÍTULO FLEXÃO DE VIGA Antecedendo a apresentação da formulação de diversos tipos de elementos de viga, efectua-se em seguida uma revisão dos fundamentos da flexão de vigas. Apenas são consideradas as
CAPÍTULO FLEXÃO DE VIGA Antecedendo a apresentação da formulação de diversos tipos de elementos de viga, efectua-se em seguida uma revisão dos fundamentos da flexão de vigas. Apenas são consideradas as
Sumário e Objectivos. Método dos Elementos Finitos 3ªAula. Setembro
 Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Universidade de Coimbra Faculdade de Ciências e Tecnologia 2001/02 Estruturas II (aulas teóricas)
 Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Sumário e Objectivos. Mecânica dos Sólidos 8ªAula. Lúcia M.J.S. Dinis 2007/2008
 Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Perfis Tubulares Objectivos da Aula: Apreensão dos conceitos
Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Perfis Tubulares Objectivos da Aula: Apreensão dos conceitos
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
3 Implementação Computacional
 3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
4 Esforços em Cascas Conoidais
 4 Esforços em Cascas Conoidais Uma das principais vantagens do emprego de cascas esbeltas em engenharia e arquitetura é a sua capacidade de resistir às cargas aplicadas principalmente através de esforços
4 Esforços em Cascas Conoidais Uma das principais vantagens do emprego de cascas esbeltas em engenharia e arquitetura é a sua capacidade de resistir às cargas aplicadas principalmente através de esforços
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia
 Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Prof. Dr. Eduardo Lenz Cardoso
 Elementos Finitos I Análise Estática Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Sumário Revisão de trabalho e energia; Definição de Energia Potencial Total; Princípio da Mínima Energia Potencial
Elementos Finitos I Análise Estática Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Sumário Revisão de trabalho e energia; Definição de Energia Potencial Total; Princípio da Mínima Energia Potencial
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Aula 04 MÉTODO DAS FORÇAS. Classi cação das estruturas quanto ao seu equilíbrio estático. ² Isostática:
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Elementos finitos triangulares compatíveis na análise estrutural de lajes finas
 Elementos finitos triangulares compatíveis na análise estrutural de lajes finas Pedro Miguel de Matos Sanches Dissertação para obtenção do Grau de Mestre em Engenharia Civil Presidente: Orientador: Vogal:
Elementos finitos triangulares compatíveis na análise estrutural de lajes finas Pedro Miguel de Matos Sanches Dissertação para obtenção do Grau de Mestre em Engenharia Civil Presidente: Orientador: Vogal:
Sumário e Objectivos. Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares
 Sumário e Objectivos Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares 1 Vigas 2 Camião 3 Bicicleta 4 Função de Tensão de Prandtl A solução do problema
Sumário e Objectivos Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares 1 Vigas 2 Camião 3 Bicicleta 4 Função de Tensão de Prandtl A solução do problema
Comparação do Comportamento de Elementos Finitos de Equilíbrio para Lajes de Kirchhoff e para Lajes de Reissner-Mindlin
 Comparação do Comportamento de Elementos Finitos de Equilíbrio para Lajes de Kirchhoff e para Lajes de Reissner-Mindlin António Pedro Cartaxo Urmal Dissertação para obtenção do Grau de Mestre em Engenharia
Comparação do Comportamento de Elementos Finitos de Equilíbrio para Lajes de Kirchhoff e para Lajes de Reissner-Mindlin António Pedro Cartaxo Urmal Dissertação para obtenção do Grau de Mestre em Engenharia
2 Casca cilíndrica delgada
 Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
6 Formulação para Problemas da Mecânica da Fratura Linear Elástica
 58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
Prefácio... Notação... XIII
 Sumário Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto... 3 1.1.3. Modelo computacional... 1.2. Organização
Sumário Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto... 3 1.1.3. Modelo computacional... 1.2. Organização
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/ Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 14ª Aula Duração - Horas Data - 13 de Novembro de 003 Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão
1/ Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 14ª Aula Duração - Horas Data - 13 de Novembro de 003 Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Sumário e Objectivos. Mecânica dos Sólidos não Linear Capítulo 2. Lúcia Dinis 2005/2006
 Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
LEIS CONSTITUTIVAS 4.1 INTRODUÇÃO
 LEIS CONSTITUTIVAS 4. INTRODUÇÃO As tensões foram estabelecidas como grandezas quantificadoras dos esforços transmitidas de ponto para ponto num sólido sujeito a acções exteriores e foram utilizadas no
LEIS CONSTITUTIVAS 4. INTRODUÇÃO As tensões foram estabelecidas como grandezas quantificadoras dos esforços transmitidas de ponto para ponto num sólido sujeito a acções exteriores e foram utilizadas no
ANÁLISE DE ESTRUTURAS I Ano lectivo de 2015/2016 2º Semestre
 Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 05/06 º Semestre Problema (5 de Novembro de 000) onsidere a estrutura representada na figura. ssuma que todas as barras apresentam a mesma
Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 05/06 º Semestre Problema (5 de Novembro de 000) onsidere a estrutura representada na figura. ssuma que todas as barras apresentam a mesma
Análise de Vigas em Fundação Elástica
 Análise de Vigas em Fundação Elástica uís Manuel Santos Castro 1 Introdução Nestes apontamentos é efectuada uma breve descrição das principais metodologias utilizadas na resolução de problemas de vigas
Análise de Vigas em Fundação Elástica uís Manuel Santos Castro 1 Introdução Nestes apontamentos é efectuada uma breve descrição das principais metodologias utilizadas na resolução de problemas de vigas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
CONTEÚDOS PROGRAMADOS. (Análise Computacional de Tensões EEK 533)
 (Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
(Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
Sumário e Objectivos. Lúcia M.J.S. Dinis 2007/2008. Mecânica dos Sólidos 7ª Aula
 Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Análise de Tensões em Placas, Cascas e Reservatórios
 Análise de Tensões em Placas, Cascas e Reservatórios J.F. Silva Gomes Professor Catedrático Faculdade de Engenharia, Universidade do Porto Edições INEGI Porto, 2007 Edição e Distribuição INEGI-Instituto
Análise de Tensões em Placas, Cascas e Reservatórios J.F. Silva Gomes Professor Catedrático Faculdade de Engenharia, Universidade do Porto Edições INEGI Porto, 2007 Edição e Distribuição INEGI-Instituto
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1
 PME-235 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1 6.1. Introdução O objetivo destas notas é apresentar, de forma um pouco mais detalhada,
PME-235 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1 6.1. Introdução O objetivo destas notas é apresentar, de forma um pouco mais detalhada,
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Secção de Estruturas do DECivil MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL 18 de Janeiro de 1999 1ª Chamada PARTE TEÓRICA 1a) Diga como podem ser obtidas as
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Secção de Estruturas do DECivil MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL 18 de Janeiro de 1999 1ª Chamada PARTE TEÓRICA 1a) Diga como podem ser obtidas as
Sergio Persival Baroncini Proença
 ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
Eletromagnetismo I. Prof. Daniel Orquiza. Eletromagnetismo I. Prof. Daniel Orquiza de Carvalho
 Eletromagnetismo I Prof. Daniel Orquiza Eletromagnetismo I Prof. Daniel Orquiza de Carvalo Equação de Laplace (Capítulo 6 Páginas 160 a 172) Eq. de Laplace Solução numérica da Eq. de Laplace Eletromagnetismo
Eletromagnetismo I Prof. Daniel Orquiza Eletromagnetismo I Prof. Daniel Orquiza de Carvalo Equação de Laplace (Capítulo 6 Páginas 160 a 172) Eq. de Laplace Solução numérica da Eq. de Laplace Eletromagnetismo
DISCIPLINA DE ESTRUTURAS METÁLICAS
 DECivil Departamento de Engenharia Civil e Arquitectura DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 INDÍCE 1. Esforço axial e flexão em regime elástico. Revisão
DECivil Departamento de Engenharia Civil e Arquitectura DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 INDÍCE 1. Esforço axial e flexão em regime elástico. Revisão
Sumário e Objectivos. Resistência dos Materiais 18ªAula. Lúcia M.J.S. Dinis 2005/2006
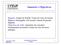 Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Objectivos da Aula: Apreensão dos conceitos Fundamentais associados
Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Objectivos da Aula: Apreensão dos conceitos Fundamentais associados
Cap. 3. Tensão. 1. Existência das forças internas. 2. Princípio das tensões de Euler e Cauchy. 3. Vector das tensões no ponto P
 Cap. 3. Tensão 1. Existência das forças internas 2. Princípio das tensões de Euler e Cauchy 3. Vector das tensões no ponto P 3.1 Componentes cartesianas 3.2 Componentes intrínsecas 4. Tensor das tensões
Cap. 3. Tensão 1. Existência das forças internas 2. Princípio das tensões de Euler e Cauchy 3. Vector das tensões no ponto P 3.1 Componentes cartesianas 3.2 Componentes intrínsecas 4. Tensor das tensões
UFABC - Universidade Federal do ABC. ESTO Mecânica dos Sólidos I. as deformações principais e direções onde elas ocorrem.
 UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff.
 Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
Deflexão em vigas de eixo reto
 10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos
 2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
Programa de Pós-graduação em Engenharia Mecânica da UFABC. Disciplina: Fundamentos de Mecânica dos Sólidos II. Lista 2
 Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial.
 Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Esforços Elementares em Peças Lineares
 CAPÍTULO III Esforços Elementares em Peças Lineares SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/13 Capitulo III Esforços Elementares em Peças Lineares 3.1 Definição dos esforços elementares Uma estrutura
CAPÍTULO III Esforços Elementares em Peças Lineares SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/13 Capitulo III Esforços Elementares em Peças Lineares 3.1 Definição dos esforços elementares Uma estrutura
Licenciatura em Engenharia Electrotécnica e de Computadores. 1 a chamada Ou seja,
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1 a chamada 00-01-08 Resolução da Parte Prática 1 (a) O valor aproximado de w é obtido a partir dos valores aproximados de x,
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1 a chamada 00-01-08 Resolução da Parte Prática 1 (a) O valor aproximado de w é obtido a partir dos valores aproximados de x,
Antenas e Propagação. Artur Andrade Moura.
 1 Antenas e Propagação Artur Andrade Moura amoura@fe.up.pt 2 Equações de Maxwell e Relações Constitutivas Forma diferencial no domínio do tempo Lei de Faraday Equações de Maxwell Lei de Ampére Lei de Gauss
1 Antenas e Propagação Artur Andrade Moura amoura@fe.up.pt 2 Equações de Maxwell e Relações Constitutivas Forma diferencial no domínio do tempo Lei de Faraday Equações de Maxwell Lei de Ampére Lei de Gauss
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
Prof. Alfredo Gay Neto Prof. Miguel Bucalem PEF 5716
 Prof. Alfredo Gay Neto Prof. Miguel Bucalem PEF 5716 017 Um modelo é uma representação aproximada da realidade Problema físico Modelo físico Modelo matemático Idealização Abstração Regras de representação
Prof. Alfredo Gay Neto Prof. Miguel Bucalem PEF 5716 017 Um modelo é uma representação aproximada da realidade Problema físico Modelo físico Modelo matemático Idealização Abstração Regras de representação
Questionário de Física IV
 Questionário de Física IV LEFT-LEA-LMAC-LCI 2 Semestre 2002/2003 Amaro Rica da Silva, Teresa Peña Alfredo B. Henriques Profs. Dep.Física - IST Questão 1 Na figura junta representam-se as linhas de campo
Questionário de Física IV LEFT-LEA-LMAC-LCI 2 Semestre 2002/2003 Amaro Rica da Silva, Teresa Peña Alfredo B. Henriques Profs. Dep.Física - IST Questão 1 Na figura junta representam-se as linhas de campo
Equações diferenciais
 Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
ANÁLISE DE ESTRUTURAS I Ano lectivo de 2014/2015 2º Semestre
 Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 20/205 2º Semestre Problema (28 de Janeiro de 999) onsidere a estrutura representada na figura. a) Indique qual o grau de indeterminação
Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 20/205 2º Semestre Problema (28 de Janeiro de 999) onsidere a estrutura representada na figura. a) Indique qual o grau de indeterminação
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO
 4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
UNIVERSIDADE NOVA DE LISBOA FACULDADE DE CIÊNCIAS E TECNOLOGIA CURSO DE LICENCIATURA EM ENGENHARIA GEOLÓGICA
 UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
4. Tensores cartesianos em 3D simétricos
 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
Disciplina de Cálculo Automático de Estruturas. 5º ano da Licenciatura em Engenharia Civil
 ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
ENTECA 2003 IV ENCONTRO TECNOLÓGICO DA ENGENHARIA CIVIL E ARQUITETURA
 508 ENTECA 003 ANÁLISE DE SAPATA DE FUNDAÇÃO PELO MÉTODO DAS DIFERENÇAS FINITAS Bolsista: Márcia Regina Lima Rizzo Orientador: Fábio Armando Botelho Cordovil UNIVERSIDADE ESTADUAL DE MARINGÁ RESUMO A sapata
508 ENTECA 003 ANÁLISE DE SAPATA DE FUNDAÇÃO PELO MÉTODO DAS DIFERENÇAS FINITAS Bolsista: Márcia Regina Lima Rizzo Orientador: Fábio Armando Botelho Cordovil UNIVERSIDADE ESTADUAL DE MARINGÁ RESUMO A sapata
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I. Capítulo 6 Flexão
 Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
$QiOLVHHDQiOLVHGHVHQVLELOLGDGHGHHVWUXWXUDVUHWLFXODGDV
 $QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
$QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
Torção de uma Barra Prismática
 Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Prof. Dr. Eduardo Lenz Cardoso
 Introdução ao Método dos Elementos Finitos Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Breve Curriculo Dr. Eng Mecânica UFRGS/DTU Prof. Subst. UFRGS (Mecânica dos Sólidos I/ MEF/ Mecânica dos
Introdução ao Método dos Elementos Finitos Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Breve Curriculo Dr. Eng Mecânica UFRGS/DTU Prof. Subst. UFRGS (Mecânica dos Sólidos I/ MEF/ Mecânica dos
5 Implementação da Metodologia
 5 Implementação da Metodologia A implementação da metodologia proposta no Capítulo 4 é possível devido ao importante avanço que os métodos numéricos e a capacidade de processamento computacional atuais
5 Implementação da Metodologia A implementação da metodologia proposta no Capítulo 4 é possível devido ao importante avanço que os métodos numéricos e a capacidade de processamento computacional atuais
DEPARTAMENTO DE ENGENHARIA MECÂNICA. ) uma base ortonormal positiva de versores de V. Digamos que a lei de transformação do operador T seja dada por:
 PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
ESCOAMENTOS VARIÁVEIS EM PRESSÃO (Choque Hidráulico)
 ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
