Prof. Dr. Eduardo Lenz Cardoso
|
|
|
- Sebastião Corte-Real Madureira
- 5 Há anos
- Visualizações:
Transcrição
1 Elementos Finitos I Análise Estática Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br
2 Sumário Revisão de trabalho e energia; Definição de Energia Potencial Total; Princípio da Mínima Energia Potencial (PMEP);
3 Trabalho Mecânico Incremento do trabalho provocado por uma força depende, em cada instante, da direção relativa entre a força e o deslocamento; f(t) du dw t = f t.du= f du cos u W tot = dw t = 0 f t du
4 Trabalho Caso Particular No caso de uma mola no regime linear: Assim, considerando uma mola com deslocamento u, teremos: F=Ku W tot = 0 u Kudu=K 0 u udu=0.5ku 2 F u
5 Energia Interna O conceito de material elástico pode ser associado a conservação de energia (termodinâmica): dq (troca de calor) dw (trabalho mecânico) du (energia interna) dk (energia cinética) F Volume de controle dw dq=du dk
6 Energia interna Se o comportamento é elástico: Consideramos que não ocorre troca de calor ao longo da fronteira (e nem geração no interior do volume de controle); Se o problema é estático: Consideramos que não existe energia cinética (cargas aplicadas de forma estática);
7 Energia Interna Assim, da termodinâmica: dw dq=du dk E verificamos que, com estas hipóteses, todo o trabalho aplicado é armazenado na forma de energia interna. Por isso, o material elástico tem energia para realizar o trabalho inverso ao aplicado, retornando a configuração original.
8 Energia de Deformação Este armazenamento de energia se dá em cada ponto do material, e, assim, dizemos que está relacionado a deformação que o material sofre ao aplicarmos trabalho. Por isso, a energia interna, nestes casos, é chamada de energia de deformação.
9 Energia de Deformação Como vimos no módulo I, podemos associar o conceito de rigidez axial de uma mola com o de uma barra. Assim: IMPORTANTE F=Ku= EA L u W tot =U=0.5 EA L u2 x = u L u= x L W tot =U=0.5 EA L 2 x L 2 W tot =U=0.5 E x x AL W tot =U=0.5 x x V
10 Energia de Deformação Específica É a que ocorre em cada ponto do volume do corpo. No caso geral varia ponto a ponto W tot =U=0.5 x x V U 0[ J ] m 3 x Em cada ponto do corpo U= V U 0 dv x
11 Energia Potencial Total de um corpo elástico Define se como Energia Potencial Total de um corpo elástico o trabalho necessário para modificar o estado do corpo, da configuração final (deformada) para a configuração inicial (indeformada); Nesta definição consideramos que os carregamentos externos aplicados na configuração final se mantém constantes no processo de reversão do movimento.
12 Energia Potencial Total de um corpo elástico Assim, a Energia Potencial Total pode ser escrita como: Energia interna armazenada na configuração final Trabalho das forças externas (no retorno) =U
13 Energia Potencial Total de um corpo elástico U= 2 Ku2 =Pucos = P u = 2 Ku2 Pu
14 Princípio da Mínima Energia Potencial (PMEP) A Energia Potencial Total de um corpo elástico está associada a um potencial termodinâmico. Assim sendo, sabemos que todo o sistema em equilíbrio deve apresentar uma quantidade mínima de energia;
15 Princípio da Mínima Energia Potencial (PMEP) Para encontrarmos a mínima energia que o sistema pode assumir (o que equivale a um sistema em equilíbrio), estudamos o extremo da Energia Potencial Total: Min u =0 u = U = U u u P=0
16 Princípio da Mínima Energia Potencial (PMEP) Aplicando este conceito para uma barra, verificamos que: u = 2 EAu 2 L Pu u = EAu L P=0 P= EA L u Ou seja: de todos os deslocamentos possíveis que uma estrutura pode assumir, somente o que leve a um mínimo valor da Energia Potencial Total equivale ao equilíbrio
17 Princípio da Mínima Energia Potencial (PMEP) Somente um apresenta o valor mínimo da Energia Potencial Total: corresponde ao que a estrutura vai assumir se for aplicado o carregamento.
18 Sumário 2 Dedução do elemento finito de barra utilizando o PMEP
19 Elemento Finito de Barra (PMEP) Aplicando diretamente o conceito do PMEP: P A P2 =U =U P U P 2 U 2 nó nó 2 U= V 2 x x dv P B P2 mas como estes termos variam ao U U2 longo da barra??
20 Elemento Finito de Barra (PMEP) Assumimos que os deslocamentos variam linearmente ao longo do elemento, tendo como referência os valores nodais: P P2 U U2 u x =N x U N 2 x U 2 =[ N N 2 ]{ U U 2} =N U N x = x L N 2 x = x L Funções de Interpolação
21 Elemento Finito de Barra (PMEP) Com esta hipótese, podemos agora calcular a deformação e a tensão em cada ponto do volume da barra: x = u x = N x U N x U 2 2 x = N x x U N 2 x x U 2 Matriz com derivadas das funções de interpolação Vetor de deslocamentos nodais = N x x x N 2 x { U 2} x U = L L { U U 2} BU
22 Elemento Finito de Barra (PMEP) E, da lei de Hooke, considerando ainda que o material é homogêneo: x =E x =E BU Assim, voltando para a expressão da energia de deformação: U= V 2 x x dv = 2 V E BU BU dv
23 Elemento Finito de Barra (PMEP) Agora podemos avaliar todos os termos da Energia Potencial Total conjuntamente: =U =U P U P 2 U 2 = 2 V E BU BU dv {U U 2 } { P P 2} = 2 V E BU BU dv U T P = 2 V U T B T E BU dv U T P
24 Elemento Finito de Barra E aplicar o PMEP: (PMEP) U = V 2 U T B T E BU dv U U T P U =0 V B T E B dv U=P V L L E L L dv { U U 2} = { P P 2} E V L 2 dv V L 2 dv V L 2 dv V L 2 dv 2} {U U = { P 2} P
25 Elemento Finito de Barra (PMEP) Calculando os termos da matriz: E V L 2 dv V L 2 dv V L 2 dv V L 2 dv 2} {U U = { P 2} P V L dv A L A 2 = L 2 = L E A L { U 2} U = { P 2} P
26 Elemento Finito de Barra (PMEP) Resumindo o procedimento detalhado aqui: Utilização do PMEP para determinar o equilíbrio de uma barra; Hipótese sobre a variação dos deslocamentos dentro do elemento, baseado nos valores nodais.
27 Elemento Finito de Barra (PMEP) Uma característica importante, comum a todos os elementos finitos, é o fato de que as tensões são obtidas baseadas nos deslocamentos nodais. Assim, em cada elemento: x =E x =E BU e verificamos que a tensão terá uma variação com um grau menor do que os deslocamentos: será constante!
28 Preparação para a dedução de elementos finitos de elasticidade Utilização de coordenadas naturais; Integração Numérica;
29 Coordenadas Naturais Quanto mais complicada a geometria do elemento, maior a dificuldade em definir as funções de interpolação e maior a dificuldade em calcular as integrais e, portanto, calcular a matriz de rigidez.
30 Coordenadas Naturais Objetivo: mapear a geometria do elemento para uma que seja mais fácil de descrever e de integrar
31 Coordenadas Naturais Elemento Mestre y r = 2x L Elemento em coordenadas naturais s x r L x=l r 2 r= r= J = dx dr = L 2 relação entre os diferenciais
32 Coordenadas Naturais Assim, como existe uma relação entre as coordenadas originais e as naturais, podemos escrever o deslocamento axial ao longo do elemento como: u x =N x U N 2 x U 2 N x = x L N 2 x = x L u r =N r U N 2 r U 2 N r = x L = r 2 N 2 r = x L =r 2
33 Coordenadas Naturais No entanto, queremos calcular as grandezas no elemento master: x = u x = N r U N r U 2 2 x = N r r dr dx U N r 2 r dr dx U 2 N r = r 2 N 2 r = r 2 dr dx = 2 L x = 2 2 L U 2 correção das derivadas = 2 L U = 2 L J L { U U 2} =BU
34 Coordenadas Naturais Para integrar o termo que dá origem a matriz de rigidez: V B T E B dv U =P devemos lembrar que estamos trabalhando em coordenadas naturais: V n L dv = 2 n r L 2 A da Jdr = A 2A L 2 dr J= L 2 correção das dimensões dos domínios de integração L 2 = A L
35 Integração Numérica Em elementos finitos mais complicados, nem sempre podemos realizar as integrais analiticamente; Nestes casos utilizamos procedimentos numéricos > importante entender as propriedades destes métodos!
36 Integração Numérica Quadratura de Gauss f x f r 0 L f x dx x f r Jdr r = r = r
37 Integração Numérica f r Ponto de Gauss Correção entre os diferenciais 0 L f x dx=f r W J f r 2 W 2 J r r 2 r Peso de correção
38 Integração Numérica Com n pontos de Gauss podemos integrar exatamento um polinômio de grau 2n ; Se forem utilizados menos pontos de Gauss, o resultado é aproximado; Se a função não for um polinômio, então o resultado é sempre aproximado e devemos utilizar um grande número de pontos;
39 Tabela de Pontos de Gauss n= r =0.0 W =2 n=2 r = 3 W = r 2 = 3 W = 2 r = 3 5 W =5 9 n=3 r 2 =0.0 W 2 = 8 9 r 3= 3 5 W 3 =5 9
40 Integração Numérica Exemplo: 0 4 x 3 3x dx=88.0 Primeiro, mudamos a variável: x=l r 4r r 4 2 Jdr Agora temos o seguinte polinômio: Com 2 pontos, podemos integrar um polinomio de grau 4: 8r 3 24r 2 30r dr r = 3 W = r 2 = 3 W 2 =
41 Integração Numérica Assim, podemos trocar a integral por 8r 3 24r 2 30r dr 8 r 3 24 r 2 30 r r r r =88.0
42 Integração Numérica Se usarmos somente um ponto de Gauss: 8r 3 24r 2 30r dr r =0.0 W =2 8 r 3 24 r 2 30 r 4 W 4 2 =56!!
43 Integração Numérica Se quisermos integrar uma função não polinomial: 0 5 e x dx=47.43 n= r e 2 Jdr n= n=
44 Integração Numérica Para funções de mais de uma variável, utilizamos uma quadratura para cada variável: r 2 3s 2 5dr ds= r 2 3s 2 5 W W 2 r 2 3s W W 2 r 2 2 3s 2 5 W W 2 r 2 2 3s W W 2 [ 3 [ ] ]=
45 Integração Numérica Cuidado: estes pontos não são ótimos para mais de uma variável!!
46 Sumário 2 Dedução do elemento finito de viga longa utilizando coordenadas naturais e integração numérica
47 Energia de Deformação na Teoria de Vigas Longas O conceito de energia de deformação específica não muda. Assim: Ainda, da lei de Hooke: Considerando agora todo o volume da viga, obtemos: x =E x U 0 = V 2 E 2 x dv U 0 = 2 x x
48 Energia de Deformação na Teoria de Vigas Longas Agora vamos utilizar duas equações do primeiro módulo: My x = I z U= V 2 E 2 x dv = v 2 E My I z 2 dv 2 v x 2 = M EI U= My v 2 E I z 2 dv = V 2 E v'' 2 y 2 dv
49 Energia de Deformação na Teoria de Vigas Longas Transformando a integral de volume em uma integral de área mais uma de comprimento: U= V 2 E v '' 2 y 2 dv = L [ E v '' 2 2 A y 2 da]dx Lembrando que a integral na área corresponde ao momento de inéricia, Iz. Assim: E v '' U= 2 L I 2 z dx
50 Energia Potencial Total em uma viga Longa A energia potencial total é definida por =U Em uma viga submetida a um carregamento distribuído p(x), temos que Assim: = L p x v x dx E v '' = 2 L I 2 z dx L p x v x dx
51 Elemento Finito de Viga Longa (PMEP) v x =f V,, V 2, 2
52 Elemento Finito de Viga Longa (PMEP) Para utilizar todos os tópicos abordados até agora, vamos utilizar coordenadas naturais para deduzir o elemento. Assim, ao invés de x usaremos r v r =N r V N 2 r N 3 r V 2 N 4 r 2 v r =N r U r [,]
53 Elemento Finito de Viga Longa (PMEP) Onde o menor grau de interpolação que permite esta descrição é dado por um conjunto de polinômios cúbicos, chamados de Polinômios de Hermite. N r = r 3 N 2 r = r 3 4 r 2 N 3 r = r 3 4 3r 4 2 N 4 r = r 3 4 r 2 4 r r r 4 4
54 Elemento Finito de Viga Longa (PMEP) Considerando agora a expressão da Energia Potencial Total em coordenadas naturais: E v'' r = 2 2 I z Jdr p r v r Jdr E introduzindo as aproximações: E N '' r U = 2 2 I z Jdr p r N r U Jdr
55 Elemento Finito de Viga Longa Onde (PMEP) N '' r =B= 2 N r r 2 dr dx dr dx 2 N 2 r r 2 dr dx dr dx 2 N 3 r r 2 dr dx dr dx 2 N 4 r r 2 dr dx dr dx B= 2 L 2 3r 2 2 3r 3r 2 2 3r Assim: EI = z B r U 2 2 Jdr p r N r U Jdr
56 Elemento Finito de Viga Longa (PMEP) Aplicando o PMEP para esta expressão: Min v =0 U = U U =0 EI z B T r B r Jdr U p r N r Jdr =0
57 Elemento Finito de Viga Longa (PMEP) Estudando o termo que dá origem a matriz de rigidez: EI z B T r B r Jdr U Por exemplo, o primeiro termo resulta em: K = EI z 36r 2 L 4 L 2 dr
58 Elemento Finito de Viga Longa (PMEP) Portanto com 2 pontos de Gauss obtemos a solução exata para cada posição da matriz de rigidez da viga longa: EI z B T r B r Jdr U EI z B T r B r W J EI z B T r 2 B r 2 W 2 J 2 36r K =EI z L 4 L 2 EI z 36r 2 2 L 4 L 2 =2EI z L 3
59 Carregamento Distribuído O segundo termo do PMEP está associado ao carregamento distribuído. Neste caso, devemos assumir um comportamento para p(r). Como temos 2 nós: p r =N r P N 2 r P 2 p r N r Jdr= N r T N r P Jdr
60 Esforços Internos na Viga Longa Da teoria de viga longa sabemos que: EI z v'' x =M x E, considerando a interpolação do deslocamento transversal: M r =E I z B r U Como assumimos funções cúbicas para v(r), teremos no máximo uma variação linear de momento fletor.
61 EXERCÍCIO Deduza, utilizando PMEP e coordenadas naturais, a matriz de rigidez de um eixo com seção transversal circular. Dica: utilize as mesmas funções de interpolação de barra. Algumas relações úteis: U 0 = 2 xy x xy =G x x = d x dx A 2 d A = J 0 W =T
62 EXERCÍCIO 2 A divisão de dois polinômios não necessáriamente resulta em um polinômio. Verifique a precisão da quadratura de Gauss para a integral da seguinte expressão: 0 00 x 2 5 x 2 30 dx=
63 Sumário 3 Uma breve revisão das equações do contínuo; Estado plano de tensões; Estado plano de deformações; Elemento Bilinear Isoparamétrico / Mapeamento Isoparamétrico; Elemento Triangular de Deformações Constantes (CST);
64 Equações da Elasticidade Tridimensional Os modelos estruturais utilizados até aqui eram baseados em hipóteses (primeiro módulo); Aqui, iremos relaxar as hipóteses sobre geometria, carregamento e comportamento, mas vamos continuar com as hipóteses de material isotrópico, com comportamento elástico e linear.
65 Equações da Elasticidade Tridimensional O estado de tensões em um ponto de um corpo 3D é dado por y x xy xz = xy y zz z yz xz yz xz xz x yz xy
66 Equações da Elasticidade Tridimensional Sendo que em um material com comportamento elástico e linear, o estado de tensões se relaciona com o estado de deformações através de uma relação constitutiva: Forma compacta { x y z xy xz yz}= E 2 =C x y { z 2 xy 2 xz 2 yz} Forma compacta
67 Equações da Elasticidade Tridimensional Outra hipótese importante que será considerada aqui é a de deformações infinitesimais. Nesta caso, em cada ponto do corpo, temos as seguintes relações: u x x = x u x u y xy = 2 y x Operador diferencial u y y = y u x u z xz = 2 z x =Lu u z z = z u z u y yz = 2 y z
68 Equações da Elasticidade Tridimensional A equação fundamental da mecânica do contínuo é a que relaciona a variação de tensão ao longo do corpo com as forças aplicadas (na verdade, um sistema de equações): x x xy y xz z b x = a x xy x y y yz z b y = a y xz x yz y z z b z = a z
69 Energia de Deformação Específica Caso Geral No início deste módulo vimos que em uma barra com comportamento elástico e linear: u 0 =0.5 x x Quando consideramos todas as componentes de tensão e deformação em um ponto obtemos: u 0 =0.5 x x y y z z xy xy xz xz yz yz =0.5 T
70 Energia Potencial Total Caso Geral Considerando agora todas as componentes de tensão e de deformação, temos que = V 0.5 T dv E podemos utilizar o mesmo procedimento de barras e vigas: ) Assumir uma forma para o deslocamento; 2) Aplicar as relações def< >desloc; 3) Aplicar a relação constitutiva; 4) Utilizar o PMEP.
71 Estado Plano de Tensões Particularização das equações tridimensionais, por meio de duas hipóteses: Geometria: assumimos uma peça que esteja contida no plano XY, com pequena espessura na direção Z; Carregamento: somente forças aplicadas no plano z x y
72 Estado Plano de Tensões Como consequência, não teremos tensões com índice Z (espessura) e, com isso, teremos uma relação constitutiva mais simples: { x y xy}= E 2 0 x { y 2 xy} z = y x
73 Estado Plano de Deformações Particularização das equações tridimensionais, por meio de duas hipóteses: Geometria: assumimos uma peça tenha a dimensão Z muito maior do que as demais; Carregamento: somente forças aplicadas no plano XY x y z
74 Estado Plano de Deformações Como consequência, não teremos deformações com índice Z e, com isso, teremos uma relação constitutiva mais simples: { x y xy}= 0 E { x y 2 xy} z = x y
75 Estado Plano Em ambos os casos teremos um número menor de componentes de tensão e de deformação, além de termos uma relação constitutiva mais simples e de menor dimensão.
76 Elemento Finito Bilinear Isoparamétrico Quadrilateral V 3 s V 4,, 3 U 3 4 U 4 V r U x, y V 2 2 U 2,,
77 Elemento Finito Bilinear Isoparamétrico Quadrilateral Vamos assumir que os deslocamentos no interior do elemento tem variação linear em cada direção (bilinear). Em coordenadas naturais: u r, s =N r, s U N 2 r, s U 2 N 3 r, s U 3 N 4 r, s U 4 v r, s =N r, s V N 2 r, s V 2 N 3 r, s V 3 N 4 r, s V 4
78 Elemento Finito Bilinear Isoparamétrico Quadrilateral As funções de interpolação em coordenadas naturais são dadas por: N r, s = 4 r s N r, s = 4 r s N 3 r,s = 4 r s N 4 r, s = 4 r s
79 Elemento Finito Bilinear Isoparamétrico Quadrilateral Na forma matricial: V U 2 V 2 0 N 0 N 2 0 N 3 0 N 4 r, s {U { u = N 0 N 2 0 N 3 0 N 4 0 v} r, s U 3 V 3 U 4 V 4}=N U
80 Elemento Finito Bilinear Isoparamétrico Quadrilateral Utilizando agora o conceito de estado plano e as relações entre deformação e deslocamento: =L u = { x y 0 2 xy} r, s x y 0 y x {u v} r, s
81 Elemento Finito Bilinear Isoparamétrico Quadrilateral e, introduzindo as aproximações para o deslocamento: = { x y 0 2 xy} r, s x y V 0 U 2 N 0 N 2 0 N 3 0 N 4 0 V y 0 N 0 N 2 0 N 3 0 N 4 r, s {U 4} 2 U 3 V 3 x U r, s =B r, s U 4 V r, s =C B r, s U
82 Elemento Finito Bilinear Isoparamétrico Quadrilateral onde N x 0 B= 0 N y N 2 x 0 0 N 2 y N 3 x 0 0 N 3 y N 4 x 0 0 N 4 y N y N x N 2 y N 2 x N 3 y N 3 x N 4 y N 4 x r, s
83 Elemento Finito Bilinear Isoparamétrico Quadrilateral No entanto, temos que considerar que as funções de interpolação são descritas em coordenadas naturais. Utilizando a regra da cadeia: N r = N x N s = N x d x dr N y d x d s N y d y dr d y d s }= { N r N s dx dr dx ds dy N dr dy { } x N ds y
84 Elemento Finito Bilinear Isoparamétrico Quadrilateral A matriz é chamada de Jacobiana, relacionando os diferenciais de (x,y) com (r,s): }= { N r N s dx dr dx ds dy N dr dy { } x N ds y J
85 Elemento Finito Bilinear Isoparamétrico Quadrilateral Isolando as incógnitas: }= { N x N y dx dr dx ds dy dr dy ds { N } r N s
86 Formulação Isoparamétrica IsoParamétrica = mesma parametrização Só podemos determinar J se conhecermos a variação de x e de y com r e com s. Para isso, assumimos que x r, s =N r, s x N 2 r, s x 2 N 3 r, s x 3 N 4 r, s x 4 y r, s =N r, s y N 2 r,s y 2 N 3 r, s y 3 N 4 r, s y 4 com as mesmas funções utilizadas para os deslocamentos.
87 Formulação Isoparamétrica Assim, por exemplo, calculamos o primeiro termo da matriz J com: dx dr = d N r, s x N r, s x N r, s x N r,s x dr dx dr = dn r, s dr x dn 2 r, s dr x 2 dn 3 r,s dr x 3 dn 4 r, s dr x 4
88 Elemento Bilinear Isoparamétrico Resumindo: Para calcularmos a deformação (e a tensão), precisamos da matriz B que, por sua vez, depende da inversa da matriz J. Para calcularmos J precisamos de uma expressão para as coordenadas no interior do elemento em função de r e de s > mesma interpolação dos deslocamentos.
89 Elemento Bilinear Isoparamétrico Interpretação da matriz Jacobiana (J) Em D J = dx dr = L 2 Em 2D = dx J dr dx ds dy dr dy ds r, s
90 Elemento Bilinear Isoparamétrico Interpretação da matriz Jacobiana (J) Em D x = N r r dr dx U N r 2 r dr dx U 2 Em 2D { N x N y }= dx dr dx ds dy dr dy ds { N } r N s
91 Elemento Bilinear Isoparamétrico Interpretação da matriz Jacobiana (J) Em D J = dx dr = L 2 relação entre os comprimentos Em 2D dx dr J =det J =det dx ds dy dr dy ds relação entre as áreas
92 Elemento Bilinear Isoparamétrico Exemplo 0,4 4,4 x r, s =0 4 r s 4 r s y r, s =0 0 4 r s 4 r s 4 4 0,0 4,0 J =[ ] det J = =4
93 Elemento Bilinear Isoparamétrico Para obtermos a matriz de Rigidez, utilizamos o PMEP: V 0.5 T dv U = V 0.5 CB r, s U T B r, s U dv U = V 0.5U T B T r, s C B r, s dv U U tal que: Espessura V B T C B dv U =t B T C B det J drdsu=k e U
94 Elemento Bilinear Isoparamétrico Para estudarmos a integração, verificamos que a matriz B depende da inversa de J e que na matriz K temos ainda um produto por det(j). Assim, teremos uma razão entre polinômios. V B T C B dv U =t B T C B det J drdsu=k e U
95 Elemento Bilinear Isoparamétrico A integral deve ser realizada por quadratura de Gauss 2x2: s,, t B T C B det J drds r,,
96 Elemento Bilinear Isoparamétrico Expandindo a integral nos pontos de Gauss: t B T C B det J drds=t B T r, s C B r, s det J r, s B T r 2, s C B r 2, s det J r 2, s B T r, s 2 C B r, s 2 det J r, s 2 B T r 2, s 2 C B r 2, s 2 det J r 2, s 2 ou seja, temos que montar as matrizes e calcular o determinante 4 vezes, além de calcular os produtos: demorado.
97 Elemento Bilinear Isoparamétrico Quanto ao termo do trabalho externo, temos 3 possibilidades: ) Forças concentradas nos nós; 2) Forças distribuídas nas faces; 3) Forças de corpo (no volume do elemento)
98 Elemento Bilinear Isoparamétrico Forças Concentradas Este é o caso mais simples, onde o trabalho é dado por: C = F x U F y V F x2 U 2 F y2 V2 F x3 U 3 F y3 V3 F x4 U 4 F y4 V4=U T F C Com contribuição para o PMEP de: C U = F C
99 Elemento Bilinear Isoparamétrico Forças Distribuídas Quando temos um carregamento distribuído em uma face: p r, s= =N 3 r, s= p 3x N 4 r, s= p 4x N 3 r, s= p 3y N 4 r, s= p 4y p 4 p 3 = pu r, s= det J dr = p U T N T det J Com contribuição para o PMEP de: P U = F = t d p N T dr
100 Elemento Bilinear Isoparamétrico Forças de Corpo Assumindo a força peso: P = t gu r, s det J dr ds= t g N U det J dr ds t gu T N T det J dr ds Com contribuição para o PMEP de: P U = F = t b g N T det J dr ds
101 Elemento Bilinear Isoparamétrico Conclusão Assim, do PMEP: K e U =F c F d F b sendo que a superposição das matrizes, para formar o sistema global, é realizada da mesma forma que em barra, eixos e vigas, apenas com um número maior de graus de liberdade.
102 Exemplo 00 N V 4 V 5 V 6 00 N 4 U 4 5 U 5 6 U 6 V 2 V 3 V U 2 U 2 3 U 3
103 {F x x F y F y F x2 F x2 F y2 F y2 F x3 0 F y3 0 F x4 F x4 F y4 F y4 F x5 F x3 F y5 F y3 F x6 0 F y6}={f } { F x 2 F y 2 F x2 2 F y2 0 2 F x4 2 F y4 2 F x3 2 F y3 }= k Exemplo k k k 0 0 k k k k {U k k k k 0 0 k k k k 0 0 V k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 U 2 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 V k 2 k 2 k 2 k k 2 k 2 k 2 k 2 U 6} k 2 k 2 k 2 k k 2 k 2 k 2 k 2 V 3 k k k k 0 0 k k k k 0 0 U 4 k k k k 0 0 k k k k 0 0 V 4 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 U 5 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 V k 2 k 2 k 2 k k 2 k 2 k 2 k 2 U k 2 k 2 k 2 k k 2 k 2 k 2 k V
104 Exemplo { k }= k k k 0 0 k k k k {U k k k k 0 0 k k k k 0 0 V k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 U 2 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 V k 2 k 2 k 2 k k 2 k 2 k 2 k 2 U 6} k 2 k 2 k 2 k k 2 k 2 k 2 k 2 V 3 k k k k 0 0 k k k k 0 0 U 4 k k k k 0 0 k k k k 0 0 V 4 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 U 5 k k k k 2 k k 2 k 2 k 2 k k k k 2 k k 2 k 2 k 2 V k 2 k 2 k 2 k k 2 k 2 k 2 k 2 U k 2 k 2 k 2 k k 2 k 2 k 2 k V
105 Exemplo O resultado da simulação são os deslocamentos nodais. Se quisermos calcular as tensões, devemos utilizar a relação: Com um três cuidados especiais: r, s =C B r, s U Obtido anteriormente no sistema global ) o grau de representação das tensões é menor do que o dos deslocamentos; 2) Existem posições (r,s) onde o erro no cálculo das tensões é menor > Pontos de Barlow; 3) Não existe continuidade de tensão entre elementos vizinhos.
106 Exemplo No caso do bilinear isoparamétrico, coincidem com os pontos de Gauss.
107 Cisalhamento Parasita Quando submetido a um carregamento que provoca flexão, o elemento responde com um modo errado de deformação, que é mais rígido do que o de flexão.
108 Cisalhamento Parasita Soluções ) Sub integração: utilizam se 4 pontos de Gauss > Aparecimento de modos espúrios; 2) Sub integração + correção: disponível em vários códigos; 3) Uso de modos adicionais de deformação: método da bolha (enhanced strain); 4) Uso de elementos com maior grau de interpolação; 5) Refino de malha.
109 Distorção do Elemento Deve se tomar os seguintes cuidados com a geração da malha: det(j)<0! b a b 4 a
110 Elemento Finito Triangular de Deformação Constante (CST) V 3 3,4 3 U 3 Quadrilateral degenerado V V 2 U 2 U 2 2
111 Elemento Finito Triangular de Deformação Constante (CST) Como os nós 3 e 4 são colapsados, verificamos que dos 8 graus de liberdade, teremos 6 independentes. Ainda: x r, s =N x N 2 x 2 N 3 N 4 x 3 y r, s =N y N 2 y 2 N 3 N 4 y 3 Ou seja, na prática teremos uma modificação na terceira função de interpolação: x r,s =N x N 2 x 2 N a 3 x 3 y r,s =N y N 2 y 2 N a 3 y 3
112 Elemento Finito Triangular de Deformação Constante (CST) onde: N 3 a = 2 s Como resultado desta degeneração, verificamos que a matriz B se torna independente de x e de y (constante). Assim, ao calcularmos a matriz de rigidez, verificamos que: Ke=t B T C B det J drdr =4 B T C Bdet J drds
113 Elemento Finito Triangular de Deformação Constante (CST) e, como a matriz B é constante ao longo do elemento, verificamos que tanto a deformação quanto a tensão são constantes: =BU =C BU o que torna este elemento muito limitado se a malha for pouco refinada. No entanto, como não temos que integrar, ele é muito rápido.
114 Elemento Finito Triangular de Deformação Constante (CST) Anisotropia Numérica: em malhas feitas com o CST, deve se evitar orientar os elementos em uma direção preferencial. Isto provoca um efeito numérico e artificial, conhecido como anisotropia (no caso, rigidez dependente da direção) numérica (pois não tem relação com a realidade, sendo um efeito da discretização).
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS. Professores: Ronny Calixto Carbonari
 Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Prof. Dr. Eduardo Lenz Cardoso
 Introdução ao Método dos Elementos Finitos Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Breve Curriculo Dr. Eng Mecânica UFRGS/DTU Prof. Subst. UFRGS (Mecânica dos Sólidos I/ MEF/ Mecânica dos
Introdução ao Método dos Elementos Finitos Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Breve Curriculo Dr. Eng Mecânica UFRGS/DTU Prof. Subst. UFRGS (Mecânica dos Sólidos I/ MEF/ Mecânica dos
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Programa de Pós-graduação em Engenharia Mecânica da UFABC. Disciplina: Fundamentos de Mecânica dos Sólidos II. Lista 2
 Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Análise Matricial de Estruturas com orientação a objetos
 Análise Matricial de Estruturas com orientação a objetos Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto...
Análise Matricial de Estruturas com orientação a objetos Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto...
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Introdução ao Método dos Elementos Finitos
 Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
Introdução ao Método dos Elementos Finitos Estruturas Aeroespaciais II (10373) 2014 1. Introdução O Método dos Elementos Finitos (MEF), cuja génese se verificou por volta de 1940, é uma ferramenta matemática
ESTRUTURAS PARA LINHAS DE TRANSMISSÃO 6 MÉTODO DOS ELEMENTOS FINITOS
 LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
$QiOLVHHDQiOLVHGHVHQVLELOLGDGHGHHVWUXWXUDVUHWLFXODGDV
 $QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
$QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
Teoria das Estruturas - Aula 08
 Teoria das Estruturas - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
EXAME NORMAL. x 2 B D. x 1 C. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
MECÂNICA DO CONTÍNUO. Tópico 3. Método dos Trabalhos Virtuais
 MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
, Equação ESFORÇO NORMAL SIMPLES 3.1 BARRA CARREGADA AXIALMENTE
 3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
Prefácio... Notação... XIII
 Sumário Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto... 3 1.1.3. Modelo computacional... 1.2. Organização
Sumário Prefácio... IX Notação... XIII Capítulo 1 Introdução... 1 1.1. Processo de análise... 2 1.1.1. Modelo estrutural... 2 1.1.2. Modelo discreto... 3 1.1.3. Modelo computacional... 1.2. Organização
2 Teoria de Placas. Figura Placa plana retangular submetida a uma carga de superfície q z. Ref. Brush e Almroth (1975)
 2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
Capítulo 5 Carga Axial
 Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Capítulo Integração de Newton-Cotes
 Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
5 CISALHAMENTO SIMPLES
 5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
POTENCIAL ELÉTRICO. Prof. Bruno Farias
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III POTENCIAL ELÉTRICO Prof. Bruno Farias Introdução Um dos objetivos da Física é determinar
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III POTENCIAL ELÉTRICO Prof. Bruno Farias Introdução Um dos objetivos da Física é determinar
2 Casca cilíndrica delgada
 Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
3 Revisão da literatura II: Fluxo em meios porosos
 46 3 Revisão da literatura II: Fluxo em meios porosos 3.1. Meio poroso saturado e parcialmente saturado O solo na sua estrutura apresenta duas zonas em função do seu conteúdo de umidade, zona saturada
46 3 Revisão da literatura II: Fluxo em meios porosos 3.1. Meio poroso saturado e parcialmente saturado O solo na sua estrutura apresenta duas zonas em função do seu conteúdo de umidade, zona saturada
3 Implementação Computacional
 3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
Objetivo: Determinar a equação da curva de deflexão e também encontrar deflexões em pontos específicos ao longo do eixo da viga.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
PEF 3302 Mecânica das Estruturas I Segunda Prova (22/11/2016) - duração: 160 minutos Resolver cada questão em uma folha de papel almaço distinta
 Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
MÉTODOS DE ENERGIA 1 INTRODUÇÃO
 MÉTODOS DE ENERGIA 1 INTRODUÇÃO Quando não ocorre dissipação de energia, o trabalho realizado pelas cargas aplicadas e a energia são iguais, sendo o trabalho um produto vetorial da força pelo deslocamento.
MÉTODOS DE ENERGIA 1 INTRODUÇÃO Quando não ocorre dissipação de energia, o trabalho realizado pelas cargas aplicadas e a energia são iguais, sendo o trabalho um produto vetorial da força pelo deslocamento.
CONTEÚDOS PROGRAMADOS. (Análise Computacional de Tensões EEK 533)
 (Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
(Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
Deflexão em vigas e eixos
 Capítulo 12: Deflexão em vigas e eixos Adaptado pela prof. Dra. Danielle Bond Deflexão em Vigas e Eixos Muitas vezes é preciso limitar o grau de deflexão que uma viga ou eixo pode sofrer quando submetido
Capítulo 12: Deflexão em vigas e eixos Adaptado pela prof. Dra. Danielle Bond Deflexão em Vigas e Eixos Muitas vezes é preciso limitar o grau de deflexão que uma viga ou eixo pode sofrer quando submetido
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I. Capítulo 6 Flexão
 Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Universidade de Coimbra Faculdade de Ciências e Tecnologia 2001/02 Estruturas II (aulas teóricas)
 Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Figura 4.1: a)elemento Sólido Tetraédrico Parabólico. b)elemento Sólido Tetraédrico Linear.
 4 Método Numérico Foi utilizado o método dos elementos finitos como ferramenta de simulação com a finalidade de compreender e avaliar a resposta do tubo, elemento estrutural da bancada de teste utilizada
4 Método Numérico Foi utilizado o método dos elementos finitos como ferramenta de simulação com a finalidade de compreender e avaliar a resposta do tubo, elemento estrutural da bancada de teste utilizada
Análise de Suporte para Televisão e DVD
 Universidade Federal de Minas Gerais Elementos Finitos para Análise de Estruturas Professor Estevam as Casas Análise de Suporte para Televisão e DVD Carlos Secundino Heleno Santos ucia ima obo eite Willer
Universidade Federal de Minas Gerais Elementos Finitos para Análise de Estruturas Professor Estevam as Casas Análise de Suporte para Televisão e DVD Carlos Secundino Heleno Santos ucia ima obo eite Willer
Atuador Eletrotermomecânico. Operam no modo quasi-estático
 Atuador Eletrotermomecânico Operam no modo quasi-estático Equações Constitutivas Equação de Condutividade Elétrica Equação de Termoelasticidade Equação de Condutividade Térmica q 1 1 1 2 1 I 2 em ; em
Atuador Eletrotermomecânico Operam no modo quasi-estático Equações Constitutivas Equação de Condutividade Elétrica Equação de Termoelasticidade Equação de Condutividade Térmica q 1 1 1 2 1 I 2 em ; em
CIV 1127 ANÁLISE DE ESTRUTURAS II 2º Semestre Primeira Prova Data: 04/09/2002 Duração: 2:45 hs Sem Consulta
 CIV 27 ANÁLISE DE ESRUURAS II 2º Semestre 2002 Primeira Prova Data: 04/09/2002 Duração: 2:45 hs Sem Consulta ª Questão (6,0 pontos) Considere a estrutura hiperestática abaixo, onde também está indicado
CIV 27 ANÁLISE DE ESRUURAS II 2º Semestre 2002 Primeira Prova Data: 04/09/2002 Duração: 2:45 hs Sem Consulta ª Questão (6,0 pontos) Considere a estrutura hiperestática abaixo, onde também está indicado
Exame de. Licenciatura em Engenharia Civil 21 de Junho de ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre
 Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
3 IMPLEMENTAÇÃO DO ELEMENTO FINITO
 3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
Aula 04 MÉTODO DAS FORÇAS. Classi cação das estruturas quanto ao seu equilíbrio estático. ² Isostática:
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Maio, 2016. 5 Análise e projeto de vigas em flexão Conteúdo Introdução Diagramas de Força Cortante e Momento Fletor Problema
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Maio, 2016. 5 Análise e projeto de vigas em flexão Conteúdo Introdução Diagramas de Força Cortante e Momento Fletor Problema
η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]
![η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ] η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]](/thumbs/100/144288148.jpg) BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
MÉTODO DOS ELEMENTOS FINITOS
 MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.alvaroazevedo.com Setembro 2017 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.alvaroazevedo.com Setembro 2017 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
6 MÉTODO DE ELEMENTOS FINITOS - MEF
 6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
Caso mais simples MÉTODO DOS ELEMENTOS FINITOS. Álvaro Azevedo. Faculdade de Engenharia Universidade do Porto
 MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
Turma/curso: 5º Período Engenharia Civil Professor: Elias Rodrigues Liah, Engº Civil, M.Sc.
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS I Código: ENG2032 Tópico: ENERGIA DE DEFORMAÇÃO E PRINCÍPIO DA CONSERVAÇÃO DE ENERGIA Turma/curso:
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS I Código: ENG2032 Tópico: ENERGIA DE DEFORMAÇÃO E PRINCÍPIO DA CONSERVAÇÃO DE ENERGIA Turma/curso:
1 Transformada de Legendre
 1 Transformada de Legendre No caso da parede porosa a pressão constante a quantidade se conserva. Além disso H = U + P V dh = du + P dv + V dp du = dq + dw = dq dh = dq + V dp P dv escrevendo H = H (P;
1 Transformada de Legendre No caso da parede porosa a pressão constante a quantidade se conserva. Além disso H = U + P V dh = du + P dv + V dp du = dq + dw = dq dh = dq + V dp P dv escrevendo H = H (P;
CAPÍTULO VI FLEXÃO ELÁSTICA EM VIGAS
 1 CAPÍTULO VI FLEXÃO ELÁSTICA EM VIGAS I. ASPECTOS GERAIS As vigas empregadas nas edificações devem apresentar adequada rigidez e resistência, isto é, devem resistir aos esforços sem ruptura e ainda não
1 CAPÍTULO VI FLEXÃO ELÁSTICA EM VIGAS I. ASPECTOS GERAIS As vigas empregadas nas edificações devem apresentar adequada rigidez e resistência, isto é, devem resistir aos esforços sem ruptura e ainda não
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
Torção de uma Barra Prismática
 Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
2 ANÁLISE ESTÁTICA DA ESTABILIDADE MÉTODO ANALÍTICO.
 ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
4 ESFORÇO DE FLEXÃO SIMPLES
 4 ESFORÇO DE FLEXÃO SIMPLES O esforço de flexão simples é normalmente resultante da ação de carregamentos transversais que tendem a curvar o corpo e que geram uma distribuição de tensões aproximadamente
4 ESFORÇO DE FLEXÃO SIMPLES O esforço de flexão simples é normalmente resultante da ação de carregamentos transversais que tendem a curvar o corpo e que geram uma distribuição de tensões aproximadamente
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
Resistência dos Materiais, MA, IST,
 11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
TESTE FINAL. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 TESTE FINAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARTAMENTO DE ENGENHARIA CIVIL SECÇÃO DE ESTRUTURAS Duração: h00m 1 - (.0 val.) Considere a laje de betão armado
TESTE FINAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARTAMENTO DE ENGENHARIA CIVIL SECÇÃO DE ESTRUTURAS Duração: h00m 1 - (.0 val.) Considere a laje de betão armado
Exercícios de Análise Matricial de Estruturas 1. 1) Obter a matriz de rigidez [ ] K da estrutura abaixo para o sistema de coordenadas estabelecido.
![Exercícios de Análise Matricial de Estruturas 1. 1) Obter a matriz de rigidez [ ] K da estrutura abaixo para o sistema de coordenadas estabelecido. Exercícios de Análise Matricial de Estruturas 1. 1) Obter a matriz de rigidez [ ] K da estrutura abaixo para o sistema de coordenadas estabelecido.](/thumbs/59/43741778.jpg) Exercícios de Análise Matricial de Estruturas ) Obter a matriz de rigidez [ ] K da estrutura abaixo para o sistema de coordenadas estabelecido. Dicas: - Obtenção da energia de deformação do sistema estrutural
Exercícios de Análise Matricial de Estruturas ) Obter a matriz de rigidez [ ] K da estrutura abaixo para o sistema de coordenadas estabelecido. Dicas: - Obtenção da energia de deformação do sistema estrutural
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos
 2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
4 Análise de elementos unidimensionais
 4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
Elementos Finitos 2014/2015 Colectânea de trabalhos, exames e resoluções
 Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Cinemática da partícula fluida
 Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Proposta para o cálculo da frequência natural de vibração sob não-linearidade geométrica
 4 Proposta para o cálculo da frequência natural de vibração sob não-linearidade geométrica A formulação analítica que leva em conta a rigidez geométrica dos sistemas elásticos no cálculo de suas frequências,
4 Proposta para o cálculo da frequência natural de vibração sob não-linearidade geométrica A formulação analítica que leva em conta a rigidez geométrica dos sistemas elásticos no cálculo de suas frequências,
26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia
 Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Teoria Clássica das Placas
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Sumário e Objectivos. Setembro. Elementos Finitos 2ªAula
 Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO
 TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO APRESENTAÇÃO Contatos: victor.silva@progeto.com.br victormsilva.com PLANO DE AULA Apresentação do Plano de Aula Forma de Avaliação Faltas e Atrasos UNIDADE
TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO APRESENTAÇÃO Contatos: victor.silva@progeto.com.br victormsilva.com PLANO DE AULA Apresentação do Plano de Aula Forma de Avaliação Faltas e Atrasos UNIDADE
Introdução 21. Figura 1 Descontinuidades num modelo estrutural
 1 Introdução O Método dos Elementos Finitos (MEF) estabeleceu-se como a principal ferramenta de análise estrutural a partir dos anos 70 e, com o passar do tempo, seu uso se disseminou amplamente, tanto
1 Introdução O Método dos Elementos Finitos (MEF) estabeleceu-se como a principal ferramenta de análise estrutural a partir dos anos 70 e, com o passar do tempo, seu uso se disseminou amplamente, tanto
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO
 Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II
 Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 21 Flávia
Nota de aula 13 - Estudo da Energia de Deformação - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 2o. semestre de 21 Flávia
As equações governantes do problema poroelástico têm duas parcelas:
 4 POROELASTICIDADE 4.1. Introdução Esta teoria que descreve o comportamento acoplado entre os fluidos e sólidos em meios porosos foi primeiramente descrita por Biot que teve início com uma série de artigos
4 POROELASTICIDADE 4.1. Introdução Esta teoria que descreve o comportamento acoplado entre os fluidos e sólidos em meios porosos foi primeiramente descrita por Biot que teve início com uma série de artigos
= P = 9 6 = 3 2 = 1 1 2,
 Exame 1 Resolução A distribuição da cotação total (0 valores pelos oito grupos de questões é a seguinte: Grupo 1 4 5 6 7 8 Cotação Exame 15 5 5 5 Cotação P-fólio 5 5 Q d = Q s 1 Dado o modelo de mercado
Exame 1 Resolução A distribuição da cotação total (0 valores pelos oito grupos de questões é a seguinte: Grupo 1 4 5 6 7 8 Cotação Exame 15 5 5 5 Cotação P-fólio 5 5 Q d = Q s 1 Dado o modelo de mercado
Sumário e Objectivos. Método dos Elementos Finitos 3ªAula. Setembro
 Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
MAC de outubro de 2009
 MECÂNICA MAC010 26 de outubro de 2009 1 2 3 4 5. Equiĺıbrio de Corpos Rígidos 6. Treliças 7. Esforços internos Esforços internos em vigas VIGA é um elemento estrutural longo e delgado que é apoiado em
MECÂNICA MAC010 26 de outubro de 2009 1 2 3 4 5. Equiĺıbrio de Corpos Rígidos 6. Treliças 7. Esforços internos Esforços internos em vigas VIGA é um elemento estrutural longo e delgado que é apoiado em
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1
 PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
Carga axial. Princípio de Saint-Venant
 Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
CAPÍTULO 3 DINÂMICA DA PARTÍCULA: TRABALHO E ENERGIA
 CAPÍLO 3 DINÂMICA DA PARÍCLA: RABALHO E ENERGIA Neste capítulo será analisada a lei de Newton numa de suas formas integrais, aplicada ao movimento de partículas. Define-se o conceito de trabalho e energia
CAPÍLO 3 DINÂMICA DA PARÍCLA: RABALHO E ENERGIA Neste capítulo será analisada a lei de Newton numa de suas formas integrais, aplicada ao movimento de partículas. Define-se o conceito de trabalho e energia
ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO:
 Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
Professor: Estevam Las Casas. Disciplina: MÉTODOS DE ELEMENTOS FINITOS MEF TRABALHO
 UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA GRADUAÇÃO EM ENGENHARIA MECÂNICA Professor: Estevam Las Casas Disciplina: MÉTODOS DE ELEMENTOS FINITOS MEF TRABALHO Análise de deformação de um
UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA GRADUAÇÃO EM ENGENHARIA MECÂNICA Professor: Estevam Las Casas Disciplina: MÉTODOS DE ELEMENTOS FINITOS MEF TRABALHO Análise de deformação de um
Conceitos fundamentais em uma dimensão Bases
 fundamentais em uma dimensão PME5425 Métodos de Elementos Finitos de Alta Ordem com Aplicações em Mecânica dos Fluidos e Transferência de Calor Prof. Programa de Pós-Graduação em Engenharia Mecânica Escola
fundamentais em uma dimensão PME5425 Métodos de Elementos Finitos de Alta Ordem com Aplicações em Mecânica dos Fluidos e Transferência de Calor Prof. Programa de Pós-Graduação em Engenharia Mecânica Escola
Comparação de Desempenho entre o Método dos Elementos de Contorno com Integração Direta e o Método dos Elementos Finitos em problemas de Poisson
 Trabalho apresentado no III CMAC - SE, Vitória-ES, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Comparação de Desempenho entre o Método dos Elementos de Contorno
Trabalho apresentado no III CMAC - SE, Vitória-ES, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Comparação de Desempenho entre o Método dos Elementos de Contorno
Determinação dos Deslocamentos em Vigas Segundo o Método dos Elementos Finitos A.L. Christoforo1; A. B. Monteiro 2 ; T.H. Panzera 3 ; G. C. L.
 Universidade Federal de São João Del-Rei MG 26 a 28 de maio de 200 Associação Brasileira de Métodos Computacionais em Engenharia Determinação dos Deslocamentos em igas Segundo o Método dos Elementos Finitos
Universidade Federal de São João Del-Rei MG 26 a 28 de maio de 200 Associação Brasileira de Métodos Computacionais em Engenharia Determinação dos Deslocamentos em igas Segundo o Método dos Elementos Finitos
AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO. Eletromagnetismo - Instituto de Pesquisas Científicas
 ELETROMAGNETISMO AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO Se um carga elétrica se move de um ponto à outro, qual é o trabalho realizado sobre essa carga? A noção de mudança de posição nos remete
ELETROMAGNETISMO AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO Se um carga elétrica se move de um ponto à outro, qual é o trabalho realizado sobre essa carga? A noção de mudança de posição nos remete
TRELIÇA C/ SISTEMA TENSOR DE CABO
 Q) RESPOSTA TRELIÇA C/ SISTEMA TENSOR DE CABO Obtidas as matrizes de rigidez dos elementos estruturais, deve-se remanejar tais coeficientes para a matriz de rigidez da estrutura (graus de liberdade ordenados).
Q) RESPOSTA TRELIÇA C/ SISTEMA TENSOR DE CABO Obtidas as matrizes de rigidez dos elementos estruturais, deve-se remanejar tais coeficientes para a matriz de rigidez da estrutura (graus de liberdade ordenados).
pelo sistema de coordenadas Cartesianas. Podemos utilizar também o sistema de coordenadas
 A. Coordenadas Curvilineares. Teorema de Gauss em coordenadas curvilineares Para especificar a posição, utilizamos a base e x, e y, e z e x r = y z pelo sistema de coordenadas Cartesianas. Podemos utilizar
A. Coordenadas Curvilineares. Teorema de Gauss em coordenadas curvilineares Para especificar a posição, utilizamos a base e x, e y, e z e x r = y z pelo sistema de coordenadas Cartesianas. Podemos utilizar
TESTE FINAL. x =2. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
Capítulo 1 MÉTODOS DE ENERGIA
 Capítulo 1 MÉTODOS DE ENERGIA 1.1. INTRODUÇÃO Em geral, o estudo da mecânica dos sólidos (corpos rígidos e deformáveis) baseia-se no Método Newtoniano, apoiando-se nas análises vetoriais, sob diversas
Capítulo 1 MÉTODOS DE ENERGIA 1.1. INTRODUÇÃO Em geral, o estudo da mecânica dos sólidos (corpos rígidos e deformáveis) baseia-se no Método Newtoniano, apoiando-se nas análises vetoriais, sob diversas
CIV 1127 ANÁLISE DE ESTRUTURAS II 2º Semestre Terceira Prova 25/11/2002 Duração: 2:30 hs Sem Consulta
 CIV 1127 ANÁISE DE ESTRUTURAS II 2º Semestre 02 Terceira Prova 25/11/02 Duração: 2:30 hs Sem Consulta 1ª Questão (4,0 pontos) Para uma viga de ponte, cujo modelo estrutural é apresentado abaixo, calcule
CIV 1127 ANÁISE DE ESTRUTURAS II 2º Semestre 02 Terceira Prova 25/11/02 Duração: 2:30 hs Sem Consulta 1ª Questão (4,0 pontos) Para uma viga de ponte, cujo modelo estrutural é apresentado abaixo, calcule
MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Secção de Estruturas do DECivil MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL 18 de Janeiro de 1999 1ª Chamada PARTE TEÓRICA 1a) Diga como podem ser obtidas as
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Secção de Estruturas do DECivil MÉTODOS NUMÉRICOS DE ANÁLISE ESTRUTURAL 18 de Janeiro de 1999 1ª Chamada PARTE TEÓRICA 1a) Diga como podem ser obtidas as
Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada.
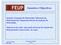 Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
Engenharia Biomédica
 Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS Professores: Ronny Calixto Carbonari Maria Elizete Kunkel Janeiro de 2013 2 Introdução a Modelagem: Solução Analítica
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS Professores: Ronny Calixto Carbonari Maria Elizete Kunkel Janeiro de 2013 2 Introdução a Modelagem: Solução Analítica
Análise de assentamento do terreno
 Manual de engenharia No. 21 Atualização: 01/2019 Análise de assentamento do terreno Programa: Arquivo: MEF Demo_manual_21.gmk Este exemplo contém a análise do assentamento do terreno sob o carregamento
Manual de engenharia No. 21 Atualização: 01/2019 Análise de assentamento do terreno Programa: Arquivo: MEF Demo_manual_21.gmk Este exemplo contém a análise do assentamento do terreno sob o carregamento
Solução: Um esboço da região pode ser visto na figura abaixo.
 Instituto de Matemática - IM/UFRJ Gabarito prova final - Escola Politécnica / Escola de Química - 29/11/211 Questão 1: (2.5 pontos) Encontre a área da região do primeiro quadrante limitada simultaneamente
Instituto de Matemática - IM/UFRJ Gabarito prova final - Escola Politécnica / Escola de Química - 29/11/211 Questão 1: (2.5 pontos) Encontre a área da região do primeiro quadrante limitada simultaneamente
UENF - COORDENAÇÃO ACADÊMICA -
 UENF - COORDENAÇÃO ACADÊMICA - Universidade Estadual do Norte Fluminense Darcy Ribeiro PROGRAMA ANALÍTICO DE DISCIPLINA (PÓS-GRADUAÇÃO) Centro CCT IDENTIFICAÇÃO Laboratório LECIV Pré-requisito Co-requisito
UENF - COORDENAÇÃO ACADÊMICA - Universidade Estadual do Norte Fluminense Darcy Ribeiro PROGRAMA ANALÍTICO DE DISCIPLINA (PÓS-GRADUAÇÃO) Centro CCT IDENTIFICAÇÃO Laboratório LECIV Pré-requisito Co-requisito
5 Análise experimental e numérica de membranas cilíndricas hiperelásticas
 5 Análise experimental e numérica de membranas cilíndricas hiperelásticas 5.1. Análise experimental para aferição da formulação apresentada: Ensaio de tração e pressão interna uniforme em membranas cilíndricas
5 Análise experimental e numérica de membranas cilíndricas hiperelásticas 5.1. Análise experimental para aferição da formulação apresentada: Ensaio de tração e pressão interna uniforme em membranas cilíndricas
Renato Martins Assunção
 Análise Numérica Erros, Extrapolação de Richardson e Quadratura Gaussiana Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 40 Análise do erro Sabemos
Análise Numérica Erros, Extrapolação de Richardson e Quadratura Gaussiana Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 40 Análise do erro Sabemos
Deformação. - comportamento de um material quando carregado
 Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Equações diferenciais
 Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
