NÚMEROS RACIONAIS OPERAÇÕES
|
|
|
- Fernanda Prada Camarinho
- 7 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: NÚMEROS RACIONAIS OPERAÇÕES Prof. Adriano Vargas Freitas
2 Noção de número racional Já sabemos que entre os números naturais não é possível efetuar determinadas divisões como, por exemplo, a divisão de 1 por 8. No entanto, na prática, essa divisão pode ser possível? É possível dividir uma pizza em 8 partes iguais?
3 Diferentes significados dos números racionais SIGNIFICADO PARTE-TODO: Um todo é dividido em partes iguais e são consideradas algumas dessas partes QUOCIENTE: Refere-se à divisão entre dois números naturais, sendo o segundo diferente de zero. RAZÃO: Relação entre duas grandezas. OPERADOR: Operador em um cálculo. SITUAÇÕES-PROBLEMA Uma pizza pequena será dividida igualmente em três pedaços. Você comeu 2 pedaços. Quanto da pizza você comeu? Duas pizzas serão divididas igualmente entre 3 irmãos. Quanto das pizzas caberá a cada um? Os meninos correspondem a 2/3 da turma. Por quanto devemos multiplicar 2 para obter o número 5?
4 Os números racionais podem ser representados de duas formas: Fracionária: Ex.: 2/5 Decimal: Ex.: 1,25 Transformação: Para transformar frações em números decimais, basta efetuar a divisão indicada. Ex.: 2/5 = 0,4 ; 1/3 = 0,33... ; 1/10 = 0,10
5 Observações: Se a e b são números naturais, com b diferente de zero, então a/b é um número fracionário. O número colocado acima do traço (a) chama-se numerador e indica quantas partes foram tomadas do inteiro. O número colocado abaixo do traço (b) chama-se denominador e indica em quantas partes iguais o inteiro foi dividido. O numerador e o denominador são chamados termos da fração.
6 Como se lêem as frações Se o denominador for: 2 - meio 3 - terço 4 - quarto 5 - quinto 6 - sexto 7 - sétimo 8 - oitavo 9 - nono 10 décimos centésimos milésimos Nos demais casos, lê-se o denominador acompanhado da palavra avos. Exemplos.: ½ - um meio 1/3 um terço 3/10 três décimos 2/15 dois quinze avos
7 Como se lêem os decimais Cada número racional escrito na sua forma decimal tem sua leitura de acordo com a posição que ocupam os algarismos: Parte inteira Parte decimal centenas dezenas unidades décimos centésimos milésimos Décimos milésimos Centésimos milésimos Milionésimos Lê-se a parte inteira, seguida da parte decimal, acompanhada das palavras. Décimos, centésimos, etc... Exemplos.: 2,3 = dois inteiros e três décimos 0,07 = sete centésimos 13,12 = treze inteiros e doze centésimos 1,302 = um inteiro e trezentos e dois milésimos 4, 3415 = quatro inteiros e três mil quatrocentos e quinze décimos milésimos Obs.: Quando representa uma quantidade de dinheiro: R$ 6,71 = seis reais e setenta e um centavos
8 Representação de decimais no material dourado:
9 Representação de decimais no ábaco:
10 Tipos de Frações Frações equivalentes: São frações que representam a mesma quantidade Propriedade fundamental: quando multiplicamos ou dividimos os termos de uma fração por um mesmo número, diferente de zero, obtemos uma fração equivalente a ela.
11
12 Atividade: Corrida das frações Material necessário: - Dados - Régua das frações - Carrinhos
13 Comparação de frações de mesmo denominador Duas frações com mesmo denominador podem ser comparadas pelos valores dos seus numeradores. Ex.: 1/4 < 3/4 pois 1< 3
14 Comparação de frações de denominadores diferentes Para comparar duas frações de denominadores diferentes, é necessário reduzi-las a um mesmo denominador. Ex.: 3/4 e 1/2 ½ pode ser escrito como 2/4 (frações equivalentes) Comparando ¾ e 2/4, temos: 3/4 > 2/4, pois 3 > 2.
15 O que é e como se calcula o MMC? Dados dois ou mais números naturais diferentes de zero, chama-se mínimo múltiplo comum desses números o menor de seus múltiplos comuns diferentes de zero. Ex.: Vamos determinar o MMC entre os números 12, 18 e 24 (Método 1): 12 = (12, 24, 36, 48, 60, 72, 84, 96,...) 18 = (18, 36, 54, 72, 90, 108,...) 24 = (24, 48, 72, 96, 120, 144,...)
16 O que é e como se calcula o MMC? Dados dois ou mais números naturais diferentes de zero, chama-se mínimo múltiplo comum desses números o menor de seus múltiplos comuns diferentes de zero. Método 2: Ex.: 12 = = = m.m.c.= = 72
17 O que é e como se calcula o MMC? Dados dois ou mais números naturais diferentes de zero, chama-se mínimo múltiplo comum desses números o menor de seus múltiplos comuns diferentes de zero. Processo prático para o cálculo do MMC: Decomposição simultânea Método 3: M.M.C. (12, 18, 24) = 2 x 2 x 2 x 3 x 3 = 72 O mínimo múltiplo comum dos números 12, 18 e 24 é igual a 72. Atividades: Calcule o mmc entre: a) 64 e 40 b) 4, 6, 9 e 30
18 Redução de frações ao mesmo denominador pelo m.m.c. Ex.: a) 1/2 e 2/3 b) 1/4, 3/6 e 1/5
19 Comparação de números decimais O maior número decimal é aquele que tem maior parte inteira. Ex.: 12,435 ; 5,7 e 32,73 32,73 > 12,435 > 5,7
20 Dificuldades na aprendizagem de números racionais Algumas ideias válidas para os números naturais não são válidas para números racionais. Sendo os racionais trabalhados como extensão do conceito de número inteiro, fica fácil compreender que os alunos queiram transferir para os números racionais o que já foi aprendido sobre os números naturais. Por isso há algumas dificuldades na aprendizagem de números racionais para os quais o professor deve estar atento. Uma das dificuldades é a forma de representação. Se para os números naturais, cada número tem representação única, para os racionais há infinitas formas fracionárias de representar um mesmo numero e uma única forma decimal. Outra dificuldade é a comparação entre números racionais. No caso da escrita fracionária, quando se compara, por exemplo, ½ e 1/3, alguns alunos tendem a pensar, pelo menos num primeiro momento, que ½ é menor que 1/3, pois 2 é menor que 3 (2<3). Quando na verdade ½ é maior que 1/3. No caso da escrita decimal, também surgem dificuldades na comparação de números racionais. Os alunos aprendem na comparação de números naturais que, quanto mais dígitos tem um número, maior ele é. (SILVEIRA, 2010).
21
22 Adição e Subtração de números fracionários de mesmo denominador Obs.: Na educação básica é importante o uso de materiais concretos, que permitam visualizar as operações, tais como tiras de papel retangular, onde será destacada a parte-todo. Ex.: 1/3 + 1/3 2/3 1/3 2/4 + 1/4
23 Adição e Subtração de números fracionários de denominadores diferentes Para somar e subtrair frações com denominadores diferentes, utiliza-se o conceito de frações equivalentes. Ex.: 2/3 + 1/6 1 1/3
24 Ex.: modo para encontrar soma entre os decimais 2, ,152 utilizando o Ábaco.
25 Multiplicação e Divisão de números fracionários Podemos usar representações geométricas para compreender os resultados: Ex.: 2 x 1/3 ½ : 2 ¼. 1/3 ¼ : 1/3
26 Multiplicação e Divisão de números decimais Para que os alunos melhor compreendam o algoritmo da multiplicação de número decimais podemos utilizar, por exemplo, o material dourado ou o ábaco. Ex.: 4. 0,10 0,10. 0,12 1,56 : 3 6,45 : 0,5
27 1) Comprei duas barras iguais de chocolate, uma de chocolate branco e outra de chocolate preto. Comi 1/2 de chocolate branco e 1/3 de chocolate preto. Quanto de chocolate eu comi ao todo? 2 ) Eu comi 1/2 de uma barra de chocolate branco e meu amigo 1/3 de uma barra igual, de chocolate preto. Quem comeu mais? Quanto a mais? 3) Meu pai comeu 2 pedaços de 2/8 de chocolate. Qual a fração que representa o total comido por ele?
28 É importante, também, propor situações em que a criança perceba que trabalhar com material concreto, qualquer que seja ele, se torna pesaroso e, portanto, há necessidade de um algoritmo que possa ser utilizado em qualquer situação. Essa é a forma que acreditamos que os algoritmos devem ser apresentados aos alunos nos primeiros ciclos do ensino fundamental: devem ser construídos com a participação deles e a partir da necessidade de generalizações (SILVEIRA, 2010).
NÚMEROS RACIONAIS. operações
 UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2018.2 NÚMEROS RACIONAIS operações Prof. Adriano Vargas Freitas Noção de número
UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2018.2 NÚMEROS RACIONAIS operações Prof. Adriano Vargas Freitas Noção de número
FRAÇÕES. O QUE É UMA FRAÇÃO? Fração é um número que exprime uma ou mais partes iguais em que foi dividida uma unidade ou um inteiro.
 FRAÇÕES O QUE É UMA FRAÇÃO? Fração é um número que exprime uma ou mais partes iguais em que foi dividida uma unidade ou um inteiro. Assim, por exemplo, se tivermos uma pizza inteira e a dividimos em quatro
FRAÇÕES O QUE É UMA FRAÇÃO? Fração é um número que exprime uma ou mais partes iguais em que foi dividida uma unidade ou um inteiro. Assim, por exemplo, se tivermos uma pizza inteira e a dividimos em quatro
3. Números Racionais
 . Números Racionais O conjunto dos números racionais, representado por Q, é o conjunto dos números formado por todos os quocientes de números inteiros (mas não pode dividir por zero). O uso do símbolo
. Números Racionais O conjunto dos números racionais, representado por Q, é o conjunto dos números formado por todos os quocientes de números inteiros (mas não pode dividir por zero). O uso do símbolo
MATEMÁTICA PROF. JOSÉ LUÍS FRAÇÕES
 FRAÇÕES I- INTRODUÇÃO O símbolo a / b significa a : b, sendo a e b números naturais e b diferente de zero. Chamamos: a / b de fração; a de numerador; b de denominador. Se a é múltiplo de b, então a / b
FRAÇÕES I- INTRODUÇÃO O símbolo a / b significa a : b, sendo a e b números naturais e b diferente de zero. Chamamos: a / b de fração; a de numerador; b de denominador. Se a é múltiplo de b, então a / b
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se
 Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
Prepara a Prova Final Matemática 4.º ano
 Nem todos os números representam quantidades inteiras e existem, por isso, diferentes formas de representar as partes da unidade. Os números decimais e fracionários representam essas partes da unidade.
Nem todos os números representam quantidades inteiras e existem, por isso, diferentes formas de representar as partes da unidade. Os números decimais e fracionários representam essas partes da unidade.
Fração. Parte ou pedaço de um inteiro.
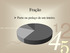 Fração Parte ou pedaço de um inteiro. Exemplos do Uso da Fração no Dia-a-Dia Ao dividir uma pizza; Exemplos do Uso da Fração no Ao dividir um bolo; Dia-a-Dia Milhões Exemplos do Uso da Fração no Dia-a-Dia
Fração Parte ou pedaço de um inteiro. Exemplos do Uso da Fração no Dia-a-Dia Ao dividir uma pizza; Exemplos do Uso da Fração no Ao dividir um bolo; Dia-a-Dia Milhões Exemplos do Uso da Fração no Dia-a-Dia
Revisão de Frações. 7º ano Professor: André
 Revisão de Frações 7º ano Professor: André FRAÇÃO COMO PARTE DE UMA FIGURA OU OBJETO. O CÍRCULO ACIMA QUE ESTAVA INTEIRO FOI DIVIDIDO EM QUATRO PARTES IGUAIS. CADA UMA DESTAS PARTES REPRESENTA UM PEDAÇO
Revisão de Frações 7º ano Professor: André FRAÇÃO COMO PARTE DE UMA FIGURA OU OBJETO. O CÍRCULO ACIMA QUE ESTAVA INTEIRO FOI DIVIDIDO EM QUATRO PARTES IGUAIS. CADA UMA DESTAS PARTES REPRESENTA UM PEDAÇO
Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração.
 Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração. numerador 1 6 traço de fração ( : ) denominador Uma fração envolve a seguinte
Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração. numerador 1 6 traço de fração ( : ) denominador Uma fração envolve a seguinte
NÚMEROS RACIONAIS. FRAÇÕES. Ano letivo
 NÚMEROS RACIONAIS. FRAÇÕES Ano letivo 203-4 Fração é um número que exprime uma ou mais partes, em que foi dividida a unidade. Numerador 2 Denominador Termos da fracção é o numerador, representa o número
NÚMEROS RACIONAIS. FRAÇÕES Ano letivo 203-4 Fração é um número que exprime uma ou mais partes, em que foi dividida a unidade. Numerador 2 Denominador Termos da fracção é o numerador, representa o número
PROJETO KALI MATEMÁTICA B AULA 3 FRAÇÕES
 PROJETO KALI - 20 MATEMÁTICA B AULA FRAÇÕES Uma ideia sobre as frações Frações são partes de um todo. Imagine que, em uma lanchonete, são vendidos pedaços de pizza. A pizza é cortada em seis pedaços, como
PROJETO KALI - 20 MATEMÁTICA B AULA FRAÇÕES Uma ideia sobre as frações Frações são partes de um todo. Imagine que, em uma lanchonete, são vendidos pedaços de pizza. A pizza é cortada em seis pedaços, como
MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco
 MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco MÓDULO 3 Números Racionais e Operações com Frações 1.INTRODUÇÃO Quando dividimos um objeto em partes iguais, uma dessas partes ou a reunião de várias delas
MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco MÓDULO 3 Números Racionais e Operações com Frações 1.INTRODUÇÃO Quando dividimos um objeto em partes iguais, uma dessas partes ou a reunião de várias delas
Frações. Números Racionais. Conceito de Fração:
 Frações Números Racionais Consideremos a operação 4 : 5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números naturais porque
Frações Números Racionais Consideremos a operação 4 : 5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números naturais porque
TUTORIAL DE OPERAÇÕES BÁSICAS
 TUTORIAL DE OPERAÇÕES BÁSICAS MULTIPLICAÇÃO POR E SEUS MÚLTIPLOS Para multiplicar multiplicar por, 0, 00,... basta deslocar a vírgula para a direita tantas casas quantos forem os zeros.,6,6 (desloca a
TUTORIAL DE OPERAÇÕES BÁSICAS MULTIPLICAÇÃO POR E SEUS MÚLTIPLOS Para multiplicar multiplicar por, 0, 00,... basta deslocar a vírgula para a direita tantas casas quantos forem os zeros.,6,6 (desloca a
MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS
 MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS Multiplicação com números decimais Há duas maneiras de efetuarmos a multiplicação envolvendo números decimais: multiplicação de número natural por decimal e multiplicação
MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS Multiplicação com números decimais Há duas maneiras de efetuarmos a multiplicação envolvendo números decimais: multiplicação de número natural por decimal e multiplicação
ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES 1A
 ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES A Exemplos: 9 7 9 9 7 7 9 0 0 0 0 0 0 Denominadores iguais: Na adição e subtração de duas ou mais frações que têm denominadores iguais, conservamos o denominador comum e somamos
ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES A Exemplos: 9 7 9 9 7 7 9 0 0 0 0 0 0 Denominadores iguais: Na adição e subtração de duas ou mais frações que têm denominadores iguais, conservamos o denominador comum e somamos
AGENTE ADMINISTRATIVO FEDERAL
 FRAÇÕES SÍNTESE TEÓRICA O que é uma fração? Fração é um número que exprime uma ou mais partes iguais em que foi dividida uma unidade ou um inteiro. Assim, por exemplo, se tivermos uma pizza inteira e a
FRAÇÕES SÍNTESE TEÓRICA O que é uma fração? Fração é um número que exprime uma ou mais partes iguais em que foi dividida uma unidade ou um inteiro. Assim, por exemplo, se tivermos uma pizza inteira e a
REVISÃO DE MATEMÁTICA BÁSICA
 REVISÃO DE MATEMÁTICA BÁSICA AULA 2 Frações Profe. Kátia FRAÇÕES Uma fração é a representação de uma ou mais partes de algo que foi dividido em partes iguais. Partes de um inteiro. Todo objeto original
REVISÃO DE MATEMÁTICA BÁSICA AULA 2 Frações Profe. Kátia FRAÇÕES Uma fração é a representação de uma ou mais partes de algo que foi dividido em partes iguais. Partes de um inteiro. Todo objeto original
4. Números Racionais (continuação)
 4. Números Racionais (continuação) Quando falamos em números, com as pessoas comuns, estamos nos referindo a uma classe bem especial de números racionais (Q) os chamados números decimais. Números Decimais
4. Números Racionais (continuação) Quando falamos em números, com as pessoas comuns, estamos nos referindo a uma classe bem especial de números racionais (Q) os chamados números decimais. Números Decimais
DECIMAIS. Definições e operações
 DECIMAIS Definições e operações A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète. O uso
DECIMAIS Definições e operações A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète. O uso
SOCIEDADE EDUCACIONAL DO AMANHÃ. Profª: EDNALVA DOS SANTOS
 SOCIEDADE EDUCACIONAL DO AMANHÃ Profª: EDNALVA DOS SANTOS 1 Frações O que são? 2 Para representar os números fracionários foi criado um símbolo, que é a fração. Sendo a e b números naturais e b 0 (b diferente
SOCIEDADE EDUCACIONAL DO AMANHÃ Profª: EDNALVA DOS SANTOS 1 Frações O que são? 2 Para representar os números fracionários foi criado um símbolo, que é a fração. Sendo a e b números naturais e b 0 (b diferente
D 7 C 4 U 5. MATEMÁTICA Revisão Geral Aula 1 - Parte 1. Professor Me. Álvaro Emílio Leite. Valor posicional dos números. milésimos décimos.
 MATEMÁTICA Revisão Geral Aula 1 - Parte 1 Professor Me. Álvaro Emílio Leite O que é um algarismo? É um símbolo que utilizamos para formar e representar os números. Exemplo: Os algarismos que compõem o
MATEMÁTICA Revisão Geral Aula 1 - Parte 1 Professor Me. Álvaro Emílio Leite O que é um algarismo? É um símbolo que utilizamos para formar e representar os números. Exemplo: Os algarismos que compõem o
MATEMÁTICA PROF. JOSÉ LUÍS NÚMEROS DECIMAIS
 NÚMEROS DECIMAIS Em todo numero decimal: CONVENÇÃO BÁSICA DO SISTEMA DECIMAL a parte inteira é separada da parte decimal por uma vírgula; um algarismo situado a direita de outro tem um valor significativo
NÚMEROS DECIMAIS Em todo numero decimal: CONVENÇÃO BÁSICA DO SISTEMA DECIMAL a parte inteira é separada da parte decimal por uma vírgula; um algarismo situado a direita de outro tem um valor significativo
Representação: 2 5. Resposta: Cada pessoa receberá R$ 6,25 (seis reais e vinte e cinco centavos)
 MATEMÁTICA FRAÇÕES E NÚMEROS DECIMAIS Fração quer dizer pedaços do mesmo tamanho. Você tem um chocolate dividido em 5 partes iguais. Dessas 5 partes você comeu 2. A fração que representa essa situação
MATEMÁTICA FRAÇÕES E NÚMEROS DECIMAIS Fração quer dizer pedaços do mesmo tamanho. Você tem um chocolate dividido em 5 partes iguais. Dessas 5 partes você comeu 2. A fração que representa essa situação
Frações. Veja um exemplo: A fração 8 é igual a 8 :2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos 2
 Frações O símolo a significa a:, sendo a e números naturais e diferente de zero Chamamos: a a de fração; de numerador: Frações de denominador: Se a é múltiplo de, então a é um número natural ( números
Frações O símolo a significa a:, sendo a e números naturais e diferente de zero Chamamos: a a de fração; de numerador: Frações de denominador: Se a é múltiplo de, então a é um número natural ( números
R.: b) Crie um título para o texto lido, usando o nome desse elemento.
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL 0- Leia o texto a seguir. Nosso planeta tem muito mais água do que terra: apenas a fração de é terra. É nos
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL 0- Leia o texto a seguir. Nosso planeta tem muito mais água do que terra: apenas a fração de é terra. É nos
Adição de números decimais
 NÚMEROS DECIMAIS O número decimal tem sempre uma virgula que divide o número decimal em duas partes: Parte inteira (antes da virgula) e parte decimal (depois da virgula). Ex: 3,5 parte inteira 3 e parte
NÚMEROS DECIMAIS O número decimal tem sempre uma virgula que divide o número decimal em duas partes: Parte inteira (antes da virgula) e parte decimal (depois da virgula). Ex: 3,5 parte inteira 3 e parte
Matéria: Matemática Assunto: Frações Prof. Dudan
 Matéria: Matemática Assunto: Frações Prof. Dudan Matemática FRAÇÕES Definição Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem do latim fractus
Matéria: Matemática Assunto: Frações Prof. Dudan Matemática FRAÇÕES Definição Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem do latim fractus
Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um
 FRAÇÕES Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria
FRAÇÕES Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria
Frações racionais. Matemática - UEL Compilada em 26 de Março de 2010.
 Matemática Essencial Frações racionais Conteúdo Matemática - UEL - 2010 - Compilada em 26 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Elementos Históricos
Matemática Essencial Frações racionais Conteúdo Matemática - UEL - 2010 - Compilada em 26 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Elementos Históricos
invés de dizermos, por exemplo, um seis, para a fração, dizemos um sexto. Os
 FRAÇÕES Os números naturais {0,,, 3,...} são uteis para realizar contagens de objetos, por exemplo. No entanto, eles não dão conta de algumas situações do cotidiano, como quantificar partes de um todo.
FRAÇÕES Os números naturais {0,,, 3,...} são uteis para realizar contagens de objetos, por exemplo. No entanto, eles não dão conta de algumas situações do cotidiano, como quantificar partes de um todo.
Roteiro de trabalho para o 4o ano
 Roteiro de trabalho para o 4o ano No volume do 4º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Roteiro de trabalho para o 4o ano No volume do 4º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Os números decimais. Centenas Dezenas Unidades, Décimos Centésimos Milésimos. 2 Centenas 4 dezenas 0 unidades, 7 décimos 5 centésimos 1 milésimo
 Os números decimais Leitura e escrita de números decimais A fração 6/10 pode ser escrita na forma 0,6, em que 10 é a parte inteira e 6 é a parte decimal. Aqui observamos que este número decimal é menor
Os números decimais Leitura e escrita de números decimais A fração 6/10 pode ser escrita na forma 0,6, em que 10 é a parte inteira e 6 é a parte decimal. Aqui observamos que este número decimal é menor
Definimos como conjunto uma coleção qualquer de elementos.
 Conjuntos Numéricos Conjunto Definimos como conjunto uma coleção qualquer de elementos. Exemplos: Conjunto dos números naturais pares; Conjunto formado por meninas da 6ª série do ensino fundamental de
Conjuntos Numéricos Conjunto Definimos como conjunto uma coleção qualquer de elementos. Exemplos: Conjunto dos números naturais pares; Conjunto formado por meninas da 6ª série do ensino fundamental de
PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Habilidades Avaliação
 Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
unidade de milhar Centena dezena unidade ordem
 1 REPRESENTAÇÃO NA FORMA DECIMAL A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète. O uso
1 REPRESENTAÇÃO NA FORMA DECIMAL A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète. O uso
Matemática. Frações. Professor Dudan.
 Matemática Frações Professor Dudan www.acasadoconcurseiro.com.br Matemática FRAÇÕES Definição Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem
Matemática Frações Professor Dudan www.acasadoconcurseiro.com.br Matemática FRAÇÕES Definição Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem
UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL COUSINIERE
 Sociedade Brasileira de Matemática Matemática na Contemporaneidade: desafios e possibilidades UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL
Sociedade Brasileira de Matemática Matemática na Contemporaneidade: desafios e possibilidades UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL
NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO
 NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO PROFESSOR:Ardelino R Puhl Ano 2015 MÓDULO- 3 ( QUINTA SÉRIE ) PROBLEMAS ENVOLVENDO AS QUATRO OPERAÇÕES 1-A um teatro compareceram
NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO PROFESSOR:Ardelino R Puhl Ano 2015 MÓDULO- 3 ( QUINTA SÉRIE ) PROBLEMAS ENVOLVENDO AS QUATRO OPERAÇÕES 1-A um teatro compareceram
Pró-letramento Matemática Estado de Minas Gerais
 Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
Resposta: b) Se você adicionar o mesmo número 6 vezes, obterá Qual é esse número? Cálculo. Resposta:
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - º ANO - ENSINO FUNDAMENTAL ========================================================================== 0- Problemas para você resolver Leia
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - º ANO - ENSINO FUNDAMENTAL ========================================================================== 0- Problemas para você resolver Leia
Números Decimais. Esse método, modernizado, é utilizado até hoje.
 Números Decimais O francês Viète (1540-1603) desenvolveu um método para escrever as frações decimais; no lugar de frações,viète escreveria números com vírgula. Esse método, modernizado, é utilizado até
Números Decimais O francês Viète (1540-1603) desenvolveu um método para escrever as frações decimais; no lugar de frações,viète escreveria números com vírgula. Esse método, modernizado, é utilizado até
PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Habilidades Avaliação
 Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
ADIÇÃO mesma natureza homogêneas Como fazer Exemplo heterogêneas Como fazer Exemplo
 ADIÇÃO É a operação que tem por fim determinar uma fração que contenha todas as unidades e partes de unidades de várias parcelas de mesma natureza. Entende-se por mesma natureza as frações que exprimem
ADIÇÃO É a operação que tem por fim determinar uma fração que contenha todas as unidades e partes de unidades de várias parcelas de mesma natureza. Entende-se por mesma natureza as frações que exprimem
Planejamento de Curso de Matemática para a 5º serie.
 Planejamento de Curso de Matemática para a 5º serie. 1º O conteúdo trabalhado no ano será: Obs: Todos os conteúdos antes de serem iniciados devem ter o contexto histórico passado. 1º Modulo Conjuntos:
Planejamento de Curso de Matemática para a 5º serie. 1º O conteúdo trabalhado no ano será: Obs: Todos os conteúdos antes de serem iniciados devem ter o contexto histórico passado. 1º Modulo Conjuntos:
01- Verifique se o número é múltiplo de 29. R.: a) D (25) = b) D (17) = c) D (20) = d) D (18) =
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL ========================================================================== 01- Verifique se o número 8 437 é
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL ========================================================================== 01- Verifique se o número 8 437 é
= 0,333 = 0, = 0,4343 = 0, = 1,0222 = 1,02
 1 1.1 Conjuntos Numéricos Neste capítulo, serão apresentados conjuntos cujos elementos são números e, por isso, são denominados conjuntos numéricos. 1.1.1 Números Naturais (N) O conjunto dos números naturais
1 1.1 Conjuntos Numéricos Neste capítulo, serão apresentados conjuntos cujos elementos são números e, por isso, são denominados conjuntos numéricos. 1.1.1 Números Naturais (N) O conjunto dos números naturais
NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO MÓDULO - 3 ( QUINTA SÉRIE ) PROFESSOR:Ardelino R Puhl
 NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO MÓDULO - 3 ( QUINTA SÉRIE ) PROFESSOR:Ardelino R Puhl PROBLEMAS ENVOLVENDO AS QUATRO OPERAÇÕES 1-A um teatro compareceram
NEEJA: NÚCLEO ESTADUAL DE EDUCAÇÃO DE JOVENS E ADULTOS CONSTRUINDO UM NOVO MUNDO MÓDULO - 3 ( QUINTA SÉRIE ) PROFESSOR:Ardelino R Puhl PROBLEMAS ENVOLVENDO AS QUATRO OPERAÇÕES 1-A um teatro compareceram
Prof. a : Patrícia Caldana
 CONJUNTOS NUMÉRICOS Podemos caracterizar um conjunto como sendo uma reunião de elementos que possuem características semelhantes. Caso esses elementos sejam números, temos então a representação dos conjuntos
CONJUNTOS NUMÉRICOS Podemos caracterizar um conjunto como sendo uma reunião de elementos que possuem características semelhantes. Caso esses elementos sejam números, temos então a representação dos conjuntos
MATEMÁTICA 5º ANO UNIDADE 1. 1 NÚMEROS, PROBLEMAS E SOLUÇÕES Sistema de numeração Operações com números grandes
 MATEMÁTICA 5º ANO UNIDADE 1 CAPÍTULOS 1 NÚMEROS, PROBLEMAS E SOLUÇÕES Sistema de numeração Operações com números grandes 2 IMAGENS E FORMAS Ângulos Ponto, retas e planos Polígono Diferenciar o significado
MATEMÁTICA 5º ANO UNIDADE 1 CAPÍTULOS 1 NÚMEROS, PROBLEMAS E SOLUÇÕES Sistema de numeração Operações com números grandes 2 IMAGENS E FORMAS Ângulos Ponto, retas e planos Polígono Diferenciar o significado
Deixando de odiar Matemática Parte 5
 Deixando de odiar Matemática Parte Adição e Subtração de Frações Multiplicação de frações Divisão de Frações 7 1 Adição e Subtração de Frações Para somar (ou subtrair) duas ou mais frações de mesmo denominador,
Deixando de odiar Matemática Parte Adição e Subtração de Frações Multiplicação de frações Divisão de Frações 7 1 Adição e Subtração de Frações Para somar (ou subtrair) duas ou mais frações de mesmo denominador,
Frações e porcentagens. Prof. Marcelo Freitas
 Frações e porcentagens Prof. Marcelo Freitas FRAÇÃO A fração representa a idéia da divisão de um inteiro (objeto, figura, número, etc) em partes iguais e destas partes pegamos uma ou mais, conforme o nosso
Frações e porcentagens Prof. Marcelo Freitas FRAÇÃO A fração representa a idéia da divisão de um inteiro (objeto, figura, número, etc) em partes iguais e destas partes pegamos uma ou mais, conforme o nosso
Frações significa a:b, sendo a e b números naturais e b diferente de zero. Chamamos: de fração; a de numerador; b de denominador.
 O símbolo Frações significa a:b, sendo a e b números naturais e b diferente de zero. Chamamos: de fração; a de numerador; b de denominador. Se a é múltiplo de b, então é um número natural. Veja um exemplo:
O símbolo Frações significa a:b, sendo a e b números naturais e b diferente de zero. Chamamos: de fração; a de numerador; b de denominador. Se a é múltiplo de b, então é um número natural. Veja um exemplo:
a) Em quantas partes iguais o retângulo foi dividido? R.: b) Cada uma dessas partes representa que fração do retângulo? R.:
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - º ANO - ENSINO FUNDAMENTAL ====================================================================== 0- Observe a figura: Em quantas partes
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - º ANO - ENSINO FUNDAMENTAL ====================================================================== 0- Observe a figura: Em quantas partes
Frações Decimais. Matemática - UEL Compilada em 26 de Março de 2010.
 Matemática Essencial Frações Decimais Conteúdo Matemática - UEL - 2010 - Compilada em 26 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 O papel das frações
Matemática Essencial Frações Decimais Conteúdo Matemática - UEL - 2010 - Compilada em 26 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 O papel das frações
LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS
 LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS Prof. Maria José Ferreira da Silva zeze@pucsp.br Porque as dificuldades no ensino? Porque as dificuldades na aprendizagem? GRANDEZAS Quantificar significa
LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS Prof. Maria José Ferreira da Silva zeze@pucsp.br Porque as dificuldades no ensino? Porque as dificuldades na aprendizagem? GRANDEZAS Quantificar significa
AUTOR: PROF. PEDRO A. SILVA lê-se: 2 inteiros e cinco sextos. Exs.:, 2 3 Fração aparente É aquela cujo numerador é múltiplo do denominador.
 I - NÚMEROS RACIONAIS lê-se: inteiros e cinco sextos. a Dois números a e b ( b 0 ), quando escritos na forma b representam uma fração, onde : b (denominador) e a (numerador). O numerador e o denominador
I - NÚMEROS RACIONAIS lê-se: inteiros e cinco sextos. a Dois números a e b ( b 0 ), quando escritos na forma b representam uma fração, onde : b (denominador) e a (numerador). O numerador e o denominador
Preparação para a Prova Final de Matemática 2.º Ciclo do Ensino Básico Olá, Matemática! 6.º Ano
 Números e operações Números racionais não negativos Noção e representação de número racional Comparação e ordenação de números racionais Operações com números racionais Valores aproximados Percentagens
Números e operações Números racionais não negativos Noção e representação de número racional Comparação e ordenação de números racionais Operações com números racionais Valores aproximados Percentagens
MATEMÁTICA 4º ANO COLEÇÃO INTERAGIR E CRESCER
 CONTEÚDOS MATEMÁTICA 4º ANO COLEÇÃO INTERAGIR E CRESCER UNIDADE 1 1. Sistema de numeração decimal - Unidade; - Dezena; - Centena; - Unidade de milhar; - Dezena de milhar; - Centena de milhar; - Milhões.
CONTEÚDOS MATEMÁTICA 4º ANO COLEÇÃO INTERAGIR E CRESCER UNIDADE 1 1. Sistema de numeração decimal - Unidade; - Dezena; - Centena; - Unidade de milhar; - Dezena de milhar; - Centena de milhar; - Milhões.
REVISÃO DOS CONTEÚDOS
 REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
AGRUPAMENTO de ESCOLAS Nº1 de SANTIAGO do CACÉM Ano Letivo 2013/2014 PLANIFICAÇÃO ANUAL
 AGRUPAMENTO de ESCOLAS Nº1 de SANTIAGO do CACÉM Ano Letivo 2013/2014 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa e Metas Curriculares de Matemática 1º CICLO MATEMÁTICA 4º ANO TEMAS/DOMÍNIOS
AGRUPAMENTO de ESCOLAS Nº1 de SANTIAGO do CACÉM Ano Letivo 2013/2014 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa e Metas Curriculares de Matemática 1º CICLO MATEMÁTICA 4º ANO TEMAS/DOMÍNIOS
Matemática lógica. 7,5 2=15 x 8 +5,4=13,4
 Central de Treinamento e Aperfeiçoamento em Eletrônica 9 Apostila 7,5 2=5 x 0 3 2 8 8 +5,=3, 5 7 6 Matemática lógica www.ctaeletronica.com.br Deus amou o mundo de tal maneira que Deu Seu Filho unigênito,
Central de Treinamento e Aperfeiçoamento em Eletrônica 9 Apostila 7,5 2=5 x 0 3 2 8 8 +5,=3, 5 7 6 Matemática lógica www.ctaeletronica.com.br Deus amou o mundo de tal maneira que Deu Seu Filho unigênito,
Colégio Motiva Jardim Ambiental. Professor: Rivaildo Alves da Silva. Turmas de 9º Anos ETAPA II
 Colégio Motiva Jardim Ambiental Professor: Rivaildo Alves da Silva Turmas de 9º Anos ETAPA II 2019 CONJUNTO DOS NÚMEROS REAIS (Operações com números Reais) Adição Considere a seguinte adição: 1,28 + 2,6
Colégio Motiva Jardim Ambiental Professor: Rivaildo Alves da Silva Turmas de 9º Anos ETAPA II 2019 CONJUNTO DOS NÚMEROS REAIS (Operações com números Reais) Adição Considere a seguinte adição: 1,28 + 2,6
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL FARROUPILHA CAMPUS ALEGRETE PIBID
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Natauan Bianchin de Lima 1.2 Público alvo: 6 ao 9 ano do Ensino Fundamental e Curso Magistério 1.3 Duração: 5 horas 1.4 Conteúdo desenvolvido:
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Natauan Bianchin de Lima 1.2 Público alvo: 6 ao 9 ano do Ensino Fundamental e Curso Magistério 1.3 Duração: 5 horas 1.4 Conteúdo desenvolvido:
PRÓ-LETRAMENTO MATEMÁTICA ESTADO DE MINAS GERAIS
 SUGESTÕES DE ESTUDO PARA FRAÇÕES o ENCONTRO Neste momento de trabalho, vamos explorar algumas das diversas maneiras de se compreender as frações, todas importantes para nosso cotidiano. O texto complementar
SUGESTÕES DE ESTUDO PARA FRAÇÕES o ENCONTRO Neste momento de trabalho, vamos explorar algumas das diversas maneiras de se compreender as frações, todas importantes para nosso cotidiano. O texto complementar
Professor: Fábio Soares - Disciplina: Métodos Quantitativos ADMINISTRAÇÃO
 Unidade 1 - Números Reais: representações O principal motivo para que a maioria dos cursos comecem por um breve estudo dos números reais é o fato de no Cálculo e na Análise, estuda-se o comportamento de
Unidade 1 - Números Reais: representações O principal motivo para que a maioria dos cursos comecem por um breve estudo dos números reais é o fato de no Cálculo e na Análise, estuda-se o comportamento de
FRAÇÕES. Professora: Gianni Leal 6ºBM
 FRAÇÕES Professora: Gianni Leal 6ºBM IDEIA INTUITIVA DE INTEIRO E O QUEBRADO Frases comuns no dia a dia: Perdi o ônibus por uma fração de segundos Paguei 7 reais e uns quebrados. São quatro horas e meia.
FRAÇÕES Professora: Gianni Leal 6ºBM IDEIA INTUITIVA DE INTEIRO E O QUEBRADO Frases comuns no dia a dia: Perdi o ônibus por uma fração de segundos Paguei 7 reais e uns quebrados. São quatro horas e meia.
Sinais iguais, soma e conserva o sinal. Sinais diferentes, subtrai e conserva o sinal do maior.
 Curso preparatório SEED-PR Data Escolaridade: Nível médio; Possíveis organizadoras: COPS.UEL, NC.UFPR ou PUC.PR Início do curso: 29/01 Término: 03/05 Aulas: Segunda a quinta-feira MATEMÁTICA 1-Sistema
Curso preparatório SEED-PR Data Escolaridade: Nível médio; Possíveis organizadoras: COPS.UEL, NC.UFPR ou PUC.PR Início do curso: 29/01 Término: 03/05 Aulas: Segunda a quinta-feira MATEMÁTICA 1-Sistema
CURRÍCULO DA DISCIPLINA MATEMÁTICA / CRITÉRIOS DE AVALIAÇÃO 2013/2014 1º Ciclo Matemática 3º Ano Metas / Objetivos Instrumentos de Domínios e
 de Avaliação Números e Operações Números Sistema de decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até ao milhão Conhecer a romana Descodificar o sistema de decimal Adicionar
de Avaliação Números e Operações Números Sistema de decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até ao milhão Conhecer a romana Descodificar o sistema de decimal Adicionar
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO
 PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
PROGRAMA DE NIVELAMENTO 2011 MATEMÁTICA
 PROGRAMA DE NIVELAMENTO 0 MATEMÁTICA I - CONJUNTOS NUMÉRICOS Z {..., -, -, -, 0,,,,...} Não há números inteiros em fração ou decimais Q Racionais São os números que representam partes inteiras ou divisões,
PROGRAMA DE NIVELAMENTO 0 MATEMÁTICA I - CONJUNTOS NUMÉRICOS Z {..., -, -, -, 0,,,,...} Não há números inteiros em fração ou decimais Q Racionais São os números que representam partes inteiras ou divisões,
Monster. Concursos. Matemática 1 ENCONTRO
 Monster Concursos Matemática 1 ENCONTRO CONJUNTOS NUMÉRICOS Conjuntos numéricos podem ser representados de diversas formas. A forma mais simples é dar um nome ao conjunto e expor todos os seus elementos,
Monster Concursos Matemática 1 ENCONTRO CONJUNTOS NUMÉRICOS Conjuntos numéricos podem ser representados de diversas formas. A forma mais simples é dar um nome ao conjunto e expor todos os seus elementos,
MÓDULO II. Operações Fundamentais em Z. - Sinais iguais das parcelas, somam-se conservando o sinal comum. Exemplo: 2 4 = 6
 1 MÓDULO II Nesse Módulo vamos aprofundar as operações em Z. Para introdução do assunto, vamos percorrer a História da Matemática, lendo os textos dispostos nos links a seguir: http://www.vestibular1.com.br/revisao/historia_da_matematica.doc
1 MÓDULO II Nesse Módulo vamos aprofundar as operações em Z. Para introdução do assunto, vamos percorrer a História da Matemática, lendo os textos dispostos nos links a seguir: http://www.vestibular1.com.br/revisao/historia_da_matematica.doc
UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL COUSINIERE
 UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL COUSINIERE Lucas Dechem Calanca Instituto Federal de Educação, Ciência e Tecnologia/câmpus
UMA PROPOSTA CONSTRUTIVISTA PARA O ENSINO DE NÚMEROS RACIONAIS POSITIVOS E SUAS OPERAÇÕES UTILIZANDO O MATERIAL COUSINIERE Lucas Dechem Calanca Instituto Federal de Educação, Ciência e Tecnologia/câmpus
1º período. Conhecer os algarismos que compõem o SND (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Diferenciar algarismos e números.
 1º período Os números naturais: Sistema de Numeração Decimal. (SND). Pág.30 a 32. Um pouco de história: sistema de numeração dos romanos. Pág. 33 a 35 Os números naturais. Pág. 36 e 37 Sistema de Numeração
1º período Os números naturais: Sistema de Numeração Decimal. (SND). Pág.30 a 32. Um pouco de história: sistema de numeração dos romanos. Pág. 33 a 35 Os números naturais. Pág. 36 e 37 Sistema de Numeração
Pré-Cálculo. Camila Perraro Sehn Eduardo de Sá Bueno Nóbrega. FURG - Universidade Federal de Rio Grande
 Pré-Cálculo Camila Perraro Sehn Eduardo de Sá Bueno Nóbrega Projeto Pré-Cálculo Este projeto consiste na formulação de uma apostila contendo os principais assuntos trabalhados na disciplina de Matemática
Pré-Cálculo Camila Perraro Sehn Eduardo de Sá Bueno Nóbrega Projeto Pré-Cálculo Este projeto consiste na formulação de uma apostila contendo os principais assuntos trabalhados na disciplina de Matemática
LIGA DE ENSINO DO RIO GRANDE DO NORTE CENTRO UNIVERSITÁRIO DO RIO GRANDE DO NORTE
 Matemática Básica Módulo 01 Introdução. Hoje em dia temos a educação presencial, semi-presencial e educação a distância. A presencial é a dos cursos regulares, onde professores e alunos se encontram sempre
Matemática Básica Módulo 01 Introdução. Hoje em dia temos a educação presencial, semi-presencial e educação a distância. A presencial é a dos cursos regulares, onde professores e alunos se encontram sempre
Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES
 Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS
Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS
REVISÃO DOS CONTEÚDOS
 REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
Em nossas aulas, estudamos sobre múltiplos e divisores. Vamos explorá-las nas questões que seguem.
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL ================================================================= Em nossas aulas, estudamos sobre múltiplos
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 5º ANO - ENSINO FUNDAMENTAL ================================================================= Em nossas aulas, estudamos sobre múltiplos
FRAÇÕES. Professor Dudan
 FRAÇÕES Professor Dudan Frações Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem do latim fractus e significa "partido", dividido ou "quebrado
FRAÇÕES Professor Dudan Frações Fração é um modo de expressar uma quantidade a partir de uma razão de dois números inteiros. A palavra vem do latim fractus e significa "partido", dividido ou "quebrado
Roteiro de trabalho para o 5o ano
 Roteiro de trabalho para o 5o ano No volume do 5º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Roteiro de trabalho para o 5o ano No volume do 5º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
AULA 8. Conteúdo: Equivalência de Frações. Objetivo: Compreender o significado e o processo de obtenção de frações equivalentes.
 AULA 8 Conteúdo: Equivalência de Frações. Objetivo: Compreender o significado e o processo de obtenção de frações equivalentes. 8.1 Tarefa 1: Problema Gerador Na terça-feira, a turma dividiu um bolo pequeno
AULA 8 Conteúdo: Equivalência de Frações. Objetivo: Compreender o significado e o processo de obtenção de frações equivalentes. 8.1 Tarefa 1: Problema Gerador Na terça-feira, a turma dividiu um bolo pequeno
Capítulo 1: Fração e Potenciação
 1 Capítulo 1: Fração e Potenciação 1.1. Fração Fração é uma forma de expressar uma quantidade sobre o todo. De início, dividimos o todo em n partes iguais e, em seguida, reunimos um número m dessas partes.
1 Capítulo 1: Fração e Potenciação 1.1. Fração Fração é uma forma de expressar uma quantidade sobre o todo. De início, dividimos o todo em n partes iguais e, em seguida, reunimos um número m dessas partes.
Matemática. Operações Básicas. Professor Dudan.
 Matemática Operações Básicas Professor Dudan www.acasadoconcurseiro.com.br Matemática OPERAÇÕES MATEMÁTICAS Observe que cada operação tem nomes especiais: Adição: + 4 = 7, em que os números e 4 são as
Matemática Operações Básicas Professor Dudan www.acasadoconcurseiro.com.br Matemática OPERAÇÕES MATEMÁTICAS Observe que cada operação tem nomes especiais: Adição: + 4 = 7, em que os números e 4 são as
SISTEMA DE EQUAÇÕES DO 1º GRAU COM DUAS VARIÁVEIS. Como se trata de dois números, representamos por duas letras diferentes x e y.
 SISTEMA DE EQUAÇÕES DO 1º GRAU COM DUAS VARIÁVEIS Equação do 1º grau com duas variáveis Ex: A soma de dois números é 10. Quais são esses números? Como se trata de dois números, representamos por duas letras
SISTEMA DE EQUAÇÕES DO 1º GRAU COM DUAS VARIÁVEIS Equação do 1º grau com duas variáveis Ex: A soma de dois números é 10. Quais são esses números? Como se trata de dois números, representamos por duas letras
Concurso Público 2017
 Concurso Público 017 Conteúdo I Frações frações equivalentes, simplificação de frações, comparação de frações, números fracionários, operações com frações (adição, subtração, multiplicação, divisão e potenciação).
Concurso Público 017 Conteúdo I Frações frações equivalentes, simplificação de frações, comparação de frações, números fracionários, operações com frações (adição, subtração, multiplicação, divisão e potenciação).
TEMA / CONTEÚDOS OBJETIVOS / DESCRITORES DE DESEMPENHO AVALIAÇÃO GESTÃO DO TEMPO Contar até ao bilião (mil milhões).
 Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de Matemática de 4ª Série Fundamental
 Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de Matemática de 4ª Série Fundamental TEMA III - NÚMEROS E OPERAÇÕES / ÁLGEBRA E FUNÇÕES Este é o tema de maior prioridade para a Matemática
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de Matemática de 4ª Série Fundamental TEMA III - NÚMEROS E OPERAÇÕES / ÁLGEBRA E FUNÇÕES Este é o tema de maior prioridade para a Matemática
TREINAMENTO MATEMÁTICA BÁSICA 1ª ETAPA
 TREINAMENTO MATEMÁTICA BÁSICA 1ª ETAPA 1 Adição, subtração, multiplicação e divisão de números naturais e decimais Números Naturais Nos dias de hoje, em lugar das pedrinhas, utilizam-se, em todo o mundo,
TREINAMENTO MATEMÁTICA BÁSICA 1ª ETAPA 1 Adição, subtração, multiplicação e divisão de números naturais e decimais Números Naturais Nos dias de hoje, em lugar das pedrinhas, utilizam-se, em todo o mundo,
OPERAÇÕES COM FRAÇÕES
 OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL FARROUPILHA CAMPUS ALEGRETE PIBID
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Fabielli Vieira de July 1.2 Público alvo: alunos do 6º e 7º anos 1.3 Duração: 2 h 1.4 Conteúdo desenvolvido: Frações 2. Objetivos da proposta
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Fabielli Vieira de July 1.2 Público alvo: alunos do 6º e 7º anos 1.3 Duração: 2 h 1.4 Conteúdo desenvolvido: Frações 2. Objetivos da proposta
Conhecendo as Frações!!! 2013
 ANEXO HQ Vamos cortar uma pizza em fatias da seguinte maneira: Se comermos as três fatias menores, que fração indica o que sobrou da pizza? Matemática em quadrinhos Conhecendo as Frações!!! or S io do
ANEXO HQ Vamos cortar uma pizza em fatias da seguinte maneira: Se comermos as três fatias menores, que fração indica o que sobrou da pizza? Matemática em quadrinhos Conhecendo as Frações!!! or S io do
NOTAS SOBRE A VISUALIZAÇÃO GEOMÉTRICA DE FRAÇÕES. Notes on viewing fraction of geometric
 9 NOTAS SOBRE A VISUALIZAÇÃO GEOMÉTRICA DE FRAÇÕES Notes on viewing fraction of geometric Eudes Antônio da Costa Introdução Nestas notas consideraremos o conjunto dos números naturais (inteiros positivos)
9 NOTAS SOBRE A VISUALIZAÇÃO GEOMÉTRICA DE FRAÇÕES Notes on viewing fraction of geometric Eudes Antônio da Costa Introdução Nestas notas consideraremos o conjunto dos números naturais (inteiros positivos)
Provão. Matemática 4 o ano
 Provão Matemática 4 o ano 21 Com base em seus estudos sobre sistema de numeração decimal, marque a alternativa correta para escrevermos por extenso, os números: 1.423 94 195 a) Mil quatrocentos e vinte
Provão Matemática 4 o ano 21 Com base em seus estudos sobre sistema de numeração decimal, marque a alternativa correta para escrevermos por extenso, os números: 1.423 94 195 a) Mil quatrocentos e vinte
- Plano Anual 4º Ano de Escolaridade -
 Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
PLANEJAMENTO ANUAL / TRIMESTRAL 2012 Conteúdos Habilidades Avaliação
 COLÉGIO LA SALLE BRASÍLIA Disciplina: Matemática Trimestre: 1º Números Naturais: - Sistema de numeração - Adição e subtração - Multiplicação e divisão - Traduzir em palavras números representados por algarismos
COLÉGIO LA SALLE BRASÍLIA Disciplina: Matemática Trimestre: 1º Números Naturais: - Sistema de numeração - Adição e subtração - Multiplicação e divisão - Traduzir em palavras números representados por algarismos
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015
 Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
Roteiro de trabalho para o 3o ano
 Roteiro de trabalho para o 3o ano No volume do 3º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Os números e sua história
Roteiro de trabalho para o 3o ano No volume do 3º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Os números e sua história
Geometria e Medida. Números e Operações. Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação. - Atenção.
 Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
