SISTEMAS DE NUMERAÇÃO
|
|
|
- Alessandra Aranha de Almeida
- 8 Há anos
- Visualizações:
Transcrição
1 Atualizado em Prof. Rui Mano E mail: rmano@tpd.puc rio.br SISTEMAS DE NUMERAÇÃO Sistemas de Numer ação Posicionais Desde quando se começou a registrar informações sobre quantidades, foram criados diversos métodos de representar as quantidades. Esse histórico pode ser encontrado em Representação da Informação. O método ao qual estamos acostumados usa um sistema de numeração posicional. Isso significa que a posição ocupada por cada algarismo em um número altera seu valor de uma potência de 10 (na base 10) para cada casa à esquerda. Por exemplo, no sistema decimal (base 10), no número 125 o algarismo 1 representa 100 (uma centena ou 10 2 ), o 2 representa 20 (duas dezenas ou 1x10 1 ) e o 5 representa 5 mesmo (5 unidades ou 5x10 0 ). Assim, em nossa notação, 125 = 1x x x10 0 Base de um Sistema de Numeração A base de um sistema é a quantidade de algarismos disponível na representação. A base 10 é hoje a mais usualmente empregada, embora não seja a única utilizada. No comércio pedimos uma dúzia de rosas ou uma grosa de parafusos (base 12) e também marcamos o tempo em minutos e segundos (base 60). Os computadores utilizam a base 2 (sistema binário) e os programadores, por facilidade, usam em geral uma base que seja uma potência de 2, tal como 2 4 (base 16 ou sistema hexadecimal) ou eventualmente ainda 2 3 (base 8 ou sistema octal). Na base 10, dispomos de 10 algarismos para a representação do número: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Na base 2, seriam apenas 2 algarismos: 0 e 1. Na base 16, seriam 16: os 10 algarismos aos quais estamos acostumados, mais os símbolos A, B, C, D, E e F, representando respectivamente 10, 11, 12, 13, 14 e 15 unidades. Generalizando, temos que uma base b qualquer disporá de b algarismos, variando entre 0 e (b 1). A representação 125,38 10 (base 10) significa 1x x x x x10 2 : Generalizando, representamos uma quantidade N qualquer, numa dada base b, com um número tal como segue: N b = a n.b n a 2.b 2 + a 1.b 1 + a 0.b 0 + a 1.b 1 + a 2.b a n.b n sendo que
2 a n.b n a 2.b 2 + a 1.b 1 + a 0.b 0 é a parte inteira e a 1.b 1 + a 2.b a n.b n é a parte fracionária. Intuitivamente, sabemos que o maior número que podemos representar, com n algarismos, na base b, será o número composto n vezes pelo maior algarismo disponível naquela base (ou seja, b 1). Por exemplo, o maior número que pode ser representado na base 10 usando 3 algarismos será 999 (ou seja, = 999). Generalizando, podemos ver que o maior número inteiro N que pode ser representado, em uma dada base b, com n algarismos (n "casas"), será N = b n 1. Assim, o maior número de 2 algarismos na base 16 será FF 16 que, na base 10, equivale a = Representação Binária Os computadores modernos utilizam apenas o sistema binário, isto é, todas as informações armazenadas ou processadas no computador usam apenas DUAS grandezas, representadas pelos algarismos 0 e 1. Essa decisão de projeto deve se à maior facilidade de representação interna no computador, que é obtida através de dois diferentes níveis de tensão (ver discussão em Bits & Bytes). Havendo apenas dois algarismos, portanto dígitos binários, o elemento mínimo de informação nos computadores foi apelidado de bit (uma contração do inglês binary digit). Na base 2, o número "10" vale dois. Mas se 10 2 = 2 10, então dez é igual a dois? Não, dez não é e nunca será igual a dois! Na realidade, "10" não significa necessariamente "dez". Nós estamos acostumados a associar "10" a "dez" porque estamos acostumados a usar o sistema de numeração decimal. O número 10 2 seria lido "um zero" na base 2 e vale 2 10 (convertido para "dois" na base dez), 10 5 seria lido "um zero" na base 5 e vale 5 10 (convertido para "cinco" na base dez), pode ser lido como "um zero" na base 10 ou então como "dez" na base dez, seria lido "um zero" na base 16 e vale (convertido para "dezesseis" na base dez), etc. Portanto, 10 só será igual a dez se e somente se o número estiver representado na base dez! Uma curiosidade: o número "10 b" vale sempre igual à base, porque em uma dada base b os algarismos possíveis vão sempre de 0 a (b 1)! Como o maior algarismo possível em uma dada base b é igual a (b 1), o próximo número será (b = b) e portanto será sempre 10 e assim, numa dada base qualquer, o valor da base será sempre representado por " 10"! Obs.: Toda vez que um número for apresentado sem que seja indicado em qual sistema de numeração ele está representado, estenderemos que a base é dez. Sempre que outra base for utilizada, a base será obrigatoriamente indicada. Um dia pode ser que os computadores se tornem obrigatórios e sejamos todos forçados por lei a estudar a aritmética em binário! Mas, mesmo antes disso, quem programa
3 computadores precisa conhecer a representação em binário! Vamos começar entendendo as potências de dois (calma, isso é só o começo, depois piora!): Repr.Binária Potência Repr.Decimal Depois (e só depois) de compreender bem a tabela acima, fazendo a devida correlação com a representação decimal, é conveniente decorar (aaaaaarrrrrrggggggghhhhhh!!!!!) os valores da tabela. As conversões entre base dois e base dez e as potências de dois são utilizadas a todo momento e seria perda de tempo estar toda hora convertendo. Da mesma forma que, uma vez entendido o mecanismo da multiplicação, decoramos a taboada, é muito mais efetivo saber de cor a tabela acima que fazer as contas de conversão toda vez que for necessário. A representação binária é perfeitamente adequada para utilização pelos computadores. No entanto, um número representado em binário apresenta muitos bits, ficando longo e passível de erros quando manipulado por seres humanos normais como por exemplo os programadores, analistas e engenheiros de sistemas (bem, não tão normais assim...). Para facilitar a visualização e manipulação por programadores de grandezas processadas em computadores, são usualmente adotadas as representações octal (base 8) e principalmente hexadecimal (base 16). Ressaltamos mais uma vez que o computador opera apenas na base 2 e as representações octal e hexadecimal não são usadas no computador, elas se destinam apenas à manipulação de grandezas pelos programadores. Representação em Octal e em Hexadecimal Em projetos de informática (isto é, nos trabalhos realizados pelos programadores, analistas e engenheiros de sistemas), é usual representar quantidades usando sistemas em potências do binário (octal e principalmente hexadecimal), para reduzir o número de algarismos da representação e conseqüentemente facilitar a compreensão da grandeza e evitar erros. No sistema octal (base 8), cada tres bits são representados por apenas um algarismo octal (de 0 a 7). No sistema hexadecimal (base 16), cada quatro bits são representados por apenas um algarismo hexadecimal (de 0 a F). A seguir, apresentamos uma tabela com os números em decimal e sua representação correspondente em binário, octal e hexadecimal:
4 Base 10 Base 2 Base 8 Base A B C D E F Nota: a base 16 ou sistema hexadecimal pode ser indicada também por um "H" ou "h" após o número; por exemplo: FFH significa que o número FF (ou 255 em decimal) está em hexadecimal. Não confundir o "H" ou "h" com mais um dígito, mesmo porque em hexadecimal só temos algarismos até "F" e portanto não existe um algarismo "H". Exemplo: Como seria a representação do número em binário, octal e hexadecimal? Solução: Seria respectivamente , 20 8 e Conver sões entre Bases Vamos analisar agora as regras gerais para converter números entre duas bases quaisquer. Conversões entre as bases 2, 8 e 16 As conversões mais simples são as que envolvem bases que são potências entre si. Vamos exemplificar com a conversão entre a base 2 e a base 8. Como 2 3 = 8, separando os bits de um número binário em grupos de tres bits (começando sempre da direita para a esquerda!) e convertendo cada grupo de tres bits para seu equivalente em octal, teremos a representação do número em octal. Por exemplo: = (separando em grupos de 3, sempre começando da direita para a esquerda) Sabemos que = 2 8 ; = 5 8 ; = 1 8 portanto = 251 8
5 Se você ainda não sabe de cor, faça a conversão utilizando a regra geral. Vamos agora exemplificar com uma conversão entre as bases 2 e 16. Como 2 4 = 16, basta separarmos em grupos de 4 bits (começando sempre da direita para a esquerda!) e converter. Por exemplo: = (separando em grupos de 4 bits, sempre começando da direita para a esquerda) Sabemos que = 6 16; = A 16 ; = D 16 ; portanto = 6AD 16 Vamos agora exercitar a conversão inversa. Quanto seria 3F5H (lembrar que o H está designando "hexadecimal") em octal? O método mais prático seria converter para binário e em seguida para octal. 3F5H = (convertendo cada dígito hexadecimal em 4 dígitos binários) = = (agrupando de tres em tres bits) = = (convertendo cada grupo de tres bits para seu valor equivalente em octal). Conversão de Números em uma base b qualquer para a base 10 Vamos lembrar a expressão geral já apresentada: N b = a n.b n a 2.b 2 + a 1.b 1 + a 0.b 0 + a 1.b 1 + a 2.b a n.b n A melhor forma de fazer a conversão é usando essa expressão. Tomando como exemplo o número , vamos calcular seu valor representado na base dez. Usando a expressão acima, fazemos: = 1x x x x x x2 0 = = Podemos fazer a conversão de números em qualquer base para a base 10 usando o algoritmo acima. Exemplos: a) Converter 4F5H para a base 10. Solução: Lembramos que o H significa que a representação é hexadecimal (base 16). Sabemos ainda que F 16= Então: 4x x x16 0 = 4x x = = b) Converter para a base 10. Solução: 3x x x x9 0 = 3x x81 + 8x9 + 5 = = c) Converter 7G 16 para a base 10. Solução: Uma base b dispõe dos algarismos entre 0 e (b 1). Assim, a base 16 dispõe dos algarismos 0 a F e portanto o símbolo G não pertence à representação hexadecimal. d) Converter 1001,01 2 para a base 10. Solução: 1x x x x x x2 2 = ,25 = 9,25 10 e) Converter 34,3 5 para a base 10. Solução: 3x x x5 1 = ,6 = 19,6 10
6 f) Converter 38,3 8 para a base 10. Solução: Uma base b dispõe dos algarismos entre 0 e (b 1). Assim, a base 8 dispõe dos algarismos 0 a 7 e portanto o algarismo 8 não existe nessa base. A representação 38,3 não existe na base 8. Conversão de Números da Base 10 para uma Base b qualquer A conversão de números da base dez para uma base qualquer emprega algoritmos que serão o inverso dos acima apresentados. Os algoritmos serão melhor entendidos pelo exemplo que por uma descrição formal. Vamos a seguir apresentar os algoritmos para a parte inteira e para a parte fracionária: Parte Inteira: O número decimal será dividido sucessivas vezes pela base; o resto de cada divisão ocupará sucessivamente as posições de ordem 0, 1, 2 e assim por diante até que o resto da última divisão (que resulta em qüociente zero) ocupe a posição de mais alta ordem. Veja o exemplo da conversão do número para a base 2: Experimente fazer a conversão contrária (retornar para a base 10) e ver se o resultado está correto. Parte Fracionária Se o número for fracionário, a conversão se fará em duas etapas distintas: primeiro a parte inteira e depois a parte fracionária. Os algoritmos de conversão são diferentes. O algoritmo para a parte fracionária consiste de uma série de multiplicações sucessivas do número fracionário a ser convertido pela base; a parte inteira do resultado da primeira multiplicação será o valor da primeira casa fracionária e a parte fracionária será de novo multiplicada pela base; e assim por diante, até o resultado dar zero ou até encontrarmos o número de casas decimais desejado. Por exemplo, vamos converter 15,65 10 para a base 2, com 5 e com 10 algarismos fracionários:
7 Obs.: Em ambos os casos, a conversão foi interrompida quando encontramos o número de algarismos fracionários solicitadas no enunciado. No entanto, como não encontramos resultado 0 em nenhuma das multiplicações, poderíamos continuar efetuando multiplicações indefinidamente até encontrar (se encontrarmos) resultado zero. No caso de interrupção por chegarmos ao número de dígitos especificado sem encontramos resultado zero, o resultado encontrado é aproximado e essa aproximação será função do número de algarismos que calcularmos. Fazendo a conversão inversa, encontraremos: Com 5 algarismos fracionários: Parte inteira: = Parte fracionária: 0, = 1x x x x x2 5 = 0,5 + 0,125 = 0, Com 10 algarismos fracionários: Parte inteira: = Parte fracionária: 0, = 1x x x x x x x x x x2 10 = 1/2 + 1/8 + 1/64 + 1/ /1024 = 0,5 + 0, , , , = 0, Ou seja, podemos verificar (sem nenhuma surpresa) que, quanto maior número de algarismos forem considerados, melhor será a aproximação. Conversão de Números entre duas Bases quaisquer Para converter números de uma base b para uma outra base b' quaisquer (isso é, que não sejam os casos particulares anteriormente estudados), o processo prático utilizado é converter da base b dada para a base 10 e depois da base 10 para a base b' pedida. Exemplo: Converter 43 5 para ( ) = (4 x 5 + 3) 10 = ==> 23/9 = 2 (resto 5) logo 43 5 = = 25 9 Ar itmética em Binár io A taboada da soma aritmética em binário é muito simples. São poucas regras: = = = = 0 (e " vai 1" para o dígito de ordem superior) = 1 (e " vai 1" para o dígito de ordem superior) Exemplo: Efetuar Obs.: 1) Lembre se: soma se as colunas da direita para a esquerda, tal como uma soma em decimal. Obs.: 2) No exemplo, são usadas, em seqüência, da direita para a esquerda, todas as regrinhas acima. Obs.: 3) Na primeira linha, em azul, é indicado o "vai um". Obs.: 4) Por simplicidade, no exemplo estamos considerando os dois números positivos. Solução: 11 > "vai um"
8 Vamos ver agora a taboada da subtração: 0 0 = = 1 (" vem um do próximo" ) 1 0 = = 0 Obs.: Como é impossível tirar 1 de zero, o artifício é "pedir emprestado" 1 da casa de ordem superior. Ou seja, na realidade o que se faz é subtrair 1 de 10 e encontramos 1 como resultado, devendo então subtrair 1 do dígito de ordem superior (aquele 1 que se "pediu emprestado"). Vamos lembrar que esse algoritmo é exatamente o mesmo da subtração em decimal a que já estamos acostumados desde o curso primério. Exemplo: Efetuar Obs.: 1) Lembre se: subtrai se as colunas da direita para a esquerda, tal como uma subtração em decimal. Obs.: 2) No exemplo, são usadas, em seqüência, da direita para a esquerda, todas as regrinhas acima. Obs.: 3) Na primeira linha, em vermelho, é indicado o "vem um". Obs.: 4) Por simplicidade, no exemplo estamos considerando os dois números positivos. Solução: 02 > "vem um" Complemento a Base A implementação do algoritmo da subtração em computadores é complexa, requerendo vários testes. assim, em computadores a subtração em binário é feita por um artifício. O método utilizado é o " Método do Complemento a Base" que consiste em encontrar o complemento do número em relação à base e depois somar os números. Os computadores funcionam sempre na base 2, portanto o complemento à base será complemento a dois. Computadores encontram o complemento a dois de um número através de um algoritmo que pode ser assim descrito: se o número é positivo, mantenha o número (o complemento de um número positivo é o próprio número) se o número é negativo: inverta o número negativo ou o subtraendo na subtração (todo 1 vira zero, todo zero vira um) some 1 ao número em complemento some as par celas (na subtração, some o minuendo ao subtraendo)
9 se a soma em complemento acarretar " vai um" ao resultado, ignore o transporte final) Como exemplo, vamos usar o algoritmo acima na subtração = 0001 mantém o minuendo > 1101 inverte o subtraendo > 0011 soma minuendo e subtraendo > soma 1 > ignora o "vai um" > 0001 Este algoritmo será analisado em detalhes na seção Representação de Números Negativos em Complemento. Vamos ver agora a taboada da multiplicação: 0 x 0 = 0 0 x 1 = 0 1 x 0 = 0 1 x 1 = 1 No entanto, também a multiplicação em computadores é feita por um artifício: para multiplicar um número A por n, basta somar A com A, n vezes. Por exemplo, 4 x 3 = E a divisão também pode ser feita por subtrações sucessivas! O que concluímos? Que qualquer operação aritmética pode ser realizada em computadores apenas através de somas (diretas ou em complemento)! Legal, mas para que serve isso? Por enquanto, ficamos por aqui. No capítulo sobre Circuitos Lógicos veremos como essas propriedades serão úteis para os engenheiros que projetam os computadores! Uns exercícios um pouco diferente, para desenvolver o raciocínio: a) Durante uma exploração, a arqueóloga Lar Acroft encontrou numa escavação uma pedra gravada com os seguintes caracteres: %@#% # # # & %&#&% Concluindo brilhantemente (e com uma boa dose de adivinhação) que os símbolos correspondiam a uma operação de adição entre dois números positivos e que todos os algarismos usados pela antiga civilização estão presentes na gravação, determine a base de numeração utilizada, o algarismo arábico correspondente a cada símbolo e a representação das parcelas e do resultado da adição, convertidas para a base 10. b) O Sr. M. recebeu certo dia um e mail de seu agente Jaime Bonde, que estava em missão. O e mail continha apenas o seguinte texto: SEND MORE MONEY
10 Concluindo (também) brilhantemente (e também com uma boa dose de adivinhação) que os símbolos correspondiam a uma operação de adição entre dois números positivos representados em decimal (Jaime NÃO era forte em informática!), o Sr. M. raciocinou e então enviou ao agente uma determinada quantia. Quanto o Sr. M. enviou para seu agente J. Bonde?
Conversões em Sistemas de Numeração. José Gustavo de Souza Paiva
 Conversões em Sistemas de Numeração José Gustavo de Souza Paiva 1 Conversões entre bases que são potências entre si Primeiro caso base binária para base octal Como 2 3 = 8, podemos separar os bits de um
Conversões em Sistemas de Numeração José Gustavo de Souza Paiva 1 Conversões entre bases que são potências entre si Primeiro caso base binária para base octal Como 2 3 = 8, podemos separar os bits de um
3 Sistemas de Numeração:
 3 Sistemas de Numeração: Os computadores eletrônicos têm como base para seu funcionamento a utilização de eletricidade. Diferente de outras máquinas que a presença ou ausência de eletricidade apenas significam
3 Sistemas de Numeração: Os computadores eletrônicos têm como base para seu funcionamento a utilização de eletricidade. Diferente de outras máquinas que a presença ou ausência de eletricidade apenas significam
Sistemas de Numerações.
 Matemática Profº: Carlos Roberto da Silva; Lourival Pereira Martins. Sistema de numeração: Binário, Octal, Decimal, Hexadecimal; Sistema de numeração: Conversões; Sistemas de Numerações. Nosso sistema
Matemática Profº: Carlos Roberto da Silva; Lourival Pereira Martins. Sistema de numeração: Binário, Octal, Decimal, Hexadecimal; Sistema de numeração: Conversões; Sistemas de Numerações. Nosso sistema
Aritmética Binária e. Bernardo Nunes Gonçalves
 Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Sistemas de Numeração. Professor: Rogério R. de Vargas INFORMÁTICA 2014/2
 INFORMÁTICA Sistemas de Numeração Professor: Rogério R. de Vargas 2014/2 Sistemas de Numeração São sistemas de notação usados para representar quantidades abstratas denominadas números. Um sistema numérico
INFORMÁTICA Sistemas de Numeração Professor: Rogério R. de Vargas 2014/2 Sistemas de Numeração São sistemas de notação usados para representar quantidades abstratas denominadas números. Um sistema numérico
1. Sistemas de numeração
 1. Sistemas de numeração Quando mencionamos sistemas de numeração estamos nos referindo à utilização de um sistema para representar uma numeração, ou seja, uma quantidade. Sistematizar algo seria organizar,
1. Sistemas de numeração Quando mencionamos sistemas de numeração estamos nos referindo à utilização de um sistema para representar uma numeração, ou seja, uma quantidade. Sistematizar algo seria organizar,
ARQUITETURA DE COMPUTADORES. Sistemas de Numeração. 1 Arquitetura de Computadores
 ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
Organização de Computadores. Cálculos Binários e Conversão entre Bases Aritmética Binária
 Organização de Computadores Capítulo 4 Cálculos Binários e Conversão entre Bases Aritmética Binária Material de apoio 2 Esclarecimentos Esse material é de apoio para as aulas da disciplina e não substitui
Organização de Computadores Capítulo 4 Cálculos Binários e Conversão entre Bases Aritmética Binária Material de apoio 2 Esclarecimentos Esse material é de apoio para as aulas da disciplina e não substitui
Escola Secundária c/3º CEB José Macedo Fragateiro. Curso Profissional de Nível Secundário. Componente Técnica. Disciplina de
 Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
Sistemas de Numeração
 Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Sistemas de Numeração. Engenharia da Computação 3 Período Alex Vidigal Bastos
 UNIPAC Sistemas Digitais Sistemas de Numeração Engenharia da Computação 3 Período Alex Vidigal Bastos 1 Agenda Objetivos Introdução Sistema Binário Sistema Octal Sistema Hexadecimal Aritméticas no Sistema
UNIPAC Sistemas Digitais Sistemas de Numeração Engenharia da Computação 3 Período Alex Vidigal Bastos 1 Agenda Objetivos Introdução Sistema Binário Sistema Octal Sistema Hexadecimal Aritméticas no Sistema
Unidade 3: Sistemas de Numeração Conversões Entre Quaisquer Bases e Aritmética em Bases Alternativas Prof. Daniel Caetano
 Arquitetura e Organização de Computadores 1 Unidade 3: Sistemas de Numeração Conversões Entre Quaisquer Bases e Aritmética em Bases Alternativas Prof. Daniel Caetano Objetivo: Apresentar métodos genéricos
Arquitetura e Organização de Computadores 1 Unidade 3: Sistemas de Numeração Conversões Entre Quaisquer Bases e Aritmética em Bases Alternativas Prof. Daniel Caetano Objetivo: Apresentar métodos genéricos
Sistemas de Numeração
 Universidade Tecnológica Federal do Paraná Bacharelado em Ciência da Computação IC3A Introdução à Ciência da Computação Sistemas de Numeração Marcos Silvano O. Almeida Baseado no material do prof. Rogério
Universidade Tecnológica Federal do Paraná Bacharelado em Ciência da Computação IC3A Introdução à Ciência da Computação Sistemas de Numeração Marcos Silvano O. Almeida Baseado no material do prof. Rogério
Trabalho compilado da Internet Prof. Claudio Passos. Sistemas Numéricos
 Trabalho compilado da Internet Prof. Claudio Passos Sistemas Numéricos A Informação e sua Representação O computador, sendo um equipamento eletrônico, armazena e movimenta as informações internamente sob
Trabalho compilado da Internet Prof. Claudio Passos Sistemas Numéricos A Informação e sua Representação O computador, sendo um equipamento eletrônico, armazena e movimenta as informações internamente sob
Eletrônica Digital 1 Módulo1 Capítulo 1 Sistemas Numéricos. Prof. Nilton Costa Junior
 Eletrônica Digital 1 Módulo1 Capítulo 1 Sistemas Numéricos Prof. Nilton Costa Junior Sistemas Numéricos Existem vários sistemas numéricos: Decimal Binário Octal Hexadecimal Sistema Decimal representado
Eletrônica Digital 1 Módulo1 Capítulo 1 Sistemas Numéricos Prof. Nilton Costa Junior Sistemas Numéricos Existem vários sistemas numéricos: Decimal Binário Octal Hexadecimal Sistema Decimal representado
ORGANIZAÇÃO DE COMPUTADORES MÓDULO 13
 ORGANIZAÇÃO DE COMPUTADORES MÓDULO 13 Índice 1. Circuitos Digitais - Continuação...3 1.1. Por que Binário?... 3 1.2. Conversão entre Bases... 3 2 1. CIRCUITOS DIGITAIS - CONTINUAÇÃO 1.1. POR QUE BINÁRIO?
ORGANIZAÇÃO DE COMPUTADORES MÓDULO 13 Índice 1. Circuitos Digitais - Continuação...3 1.1. Por que Binário?... 3 1.2. Conversão entre Bases... 3 2 1. CIRCUITOS DIGITAIS - CONTINUAÇÃO 1.1. POR QUE BINÁRIO?
Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Engenharia Disciplina de Lógica Computacional Aplicada. Prof. Dr.
 Índice 1. SISTEMAS NUMÉRICOS 1.1 Caracterização dos Sistemas Numéricos 1.2 Sistemas Numéricos em uma Base B Qualquer 1.2.1 Sistema de Numeração Decimal 1.2.2. Sistema de Numeração Binário 1.2.3 Sistema
Índice 1. SISTEMAS NUMÉRICOS 1.1 Caracterização dos Sistemas Numéricos 1.2 Sistemas Numéricos em uma Base B Qualquer 1.2.1 Sistema de Numeração Decimal 1.2.2. Sistema de Numeração Binário 1.2.3 Sistema
Aula 3 - Sistemas de Numeração
 UEM Universidade Estadual de Maringá DIN - Departamento de Informática Disciplina: Fundamentos da Computação Profª Thelma Elita Colanzi Lopes thelma@din.uem.br Aula 3 - Sistemas de Numeração O ser humano,
UEM Universidade Estadual de Maringá DIN - Departamento de Informática Disciplina: Fundamentos da Computação Profª Thelma Elita Colanzi Lopes thelma@din.uem.br Aula 3 - Sistemas de Numeração O ser humano,
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade
 REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
Curso: Técnico de Informática Disciplina: Redes de Computadores. 1- Apresentação Binária
 1- Apresentação Binária Os computadores funcionam e armazenam dados mediante a utilização de chaves eletrônicas que são LIGADAS ou DESLIGADAS. Os computadores só entendem e utilizam dados existentes neste
1- Apresentação Binária Os computadores funcionam e armazenam dados mediante a utilização de chaves eletrônicas que são LIGADAS ou DESLIGADAS. Os computadores só entendem e utilizam dados existentes neste
Exemplo de Subtração Binária
 Exemplo de Subtração Binária Exercícios Converta para binário e efetue as seguintes operações: a) 37 10 30 10 b) 83 10 82 10 c) 63 8 34 8 d) 77 8 11 8 e) BB 16 AA 16 f) C43 16 195 16 3.5.3 Divisão binária:
Exemplo de Subtração Binária Exercícios Converta para binário e efetue as seguintes operações: a) 37 10 30 10 b) 83 10 82 10 c) 63 8 34 8 d) 77 8 11 8 e) BB 16 AA 16 f) C43 16 195 16 3.5.3 Divisão binária:
2. Sistemas de Numeração, Operações e Códigos. 2. Sistemas de Numeração, Operações e Códigos 1. Números Decimais. Objetivos.
 Objetivos 2. Sistemas de Numeração, Operações e Códigos Revisar o sistema de numeração decimal Contar no sistema de numeração binário Converter de decimal para binário e vice-versa Aplicar operações aritméticas
Objetivos 2. Sistemas de Numeração, Operações e Códigos Revisar o sistema de numeração decimal Contar no sistema de numeração binário Converter de decimal para binário e vice-versa Aplicar operações aritméticas
Representação de Dados
 Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Sistemas de Numeração
 Sistemas de Numeração Um numeral é um símbolo ou grupo de símbolos que representa um número em um determinado instante da evolução do homem. Tem-se que, numa determinada escrita ou época, os numerais diferenciaram-se
Sistemas de Numeração Um numeral é um símbolo ou grupo de símbolos que representa um número em um determinado instante da evolução do homem. Tem-se que, numa determinada escrita ou época, os numerais diferenciaram-se
Sistemas de Numeração
 Sistemas de Numeração Representação da Informação para seres humanos Números (1,2,3,4...) Letras (a,a,b,b,c,c...) Sinais de pontuação (:,;...) Operadores aritméticos (+,-,x,/) Representação da Informação
Sistemas de Numeração Representação da Informação para seres humanos Números (1,2,3,4...) Letras (a,a,b,b,c,c...) Sinais de pontuação (:,;...) Operadores aritméticos (+,-,x,/) Representação da Informação
Introdução à Engenharia de
 Introdução à Engenharia de Computação Tópico: Sistemas de Numeração José Gonçalves - LPRM/DI/UFES Introdução à Engenharia de Computação Introdução O número é um conceito abstrato que representa a idéia
Introdução à Engenharia de Computação Tópico: Sistemas de Numeração José Gonçalves - LPRM/DI/UFES Introdução à Engenharia de Computação Introdução O número é um conceito abstrato que representa a idéia
Lista de Exercícios Sistemas de Numeração
 Lista de Exercícios Sistemas de Numeração 1- (Questão 5 BNDES Profissional Básico Análise de Sistemas - Suporte ano 010) Um administrador de sistemas, ao analisar o conteúdo de um arquivo binário, percebeu
Lista de Exercícios Sistemas de Numeração 1- (Questão 5 BNDES Profissional Básico Análise de Sistemas - Suporte ano 010) Um administrador de sistemas, ao analisar o conteúdo de um arquivo binário, percebeu
Sistemas de Numeração. Introdução ao Computador 2010/1 Renan Manola
 Sistemas de Numeração Introdução ao Computador 2010/1 Renan Manola Introdução Em sistemas digitais o sistema de numeração binário é o mais importante, já fora do mundo digital o sistema decimal é o mais
Sistemas de Numeração Introdução ao Computador 2010/1 Renan Manola Introdução Em sistemas digitais o sistema de numeração binário é o mais importante, já fora do mundo digital o sistema decimal é o mais
Representação de Dados e Sistemas de Numeração
 1 Representação de Dados e Sistemas de Numeração Sistema de numeração decimal e números decimais (base 10) Sistema de numeração binário e números binários (base 2) Conversão entre binário e decimal Sistema
1 Representação de Dados e Sistemas de Numeração Sistema de numeração decimal e números decimais (base 10) Sistema de numeração binário e números binários (base 2) Conversão entre binário e decimal Sistema
Matemática Aplicada à Informática
 Matemática Aplicada à Informática Unidade 3.0 Sistemas numéricos Curso Técnico em Informática Aline Maciel Zenker SUMÁRIO SUMÁRIO... 2 CONVERSÃO DE BASE NUMÉRICA... 3 1 DECIMAL X BINÁRIO... 3 1.1 Onde
Matemática Aplicada à Informática Unidade 3.0 Sistemas numéricos Curso Técnico em Informática Aline Maciel Zenker SUMÁRIO SUMÁRIO... 2 CONVERSÃO DE BASE NUMÉRICA... 3 1 DECIMAL X BINÁRIO... 3 1.1 Onde
Vamos exemplificar o conceito de sistema posicional. Seja o número 1303, representado na base 10, escrito da seguinte forma:
 Nova bibliografia: Título: Organização e projeto de computadores a interface Hardware/Software. Autor: David A. Patterson & John L. Hennessy. Tradução: Nery Machado Filho. Editora: Morgan Kaufmmann Editora
Nova bibliografia: Título: Organização e projeto de computadores a interface Hardware/Software. Autor: David A. Patterson & John L. Hennessy. Tradução: Nery Machado Filho. Editora: Morgan Kaufmmann Editora
ELETRÔNICA DIGITAL 1
 CENTRO FEDERAL DE ENSINO TECNOLÓGICO DE SANTA CATARINA UNIDADE SÃO JOSÉ ÁREA DE TELECOMUNICAÇÕES ELETRÔNICA DIGITAL 1 CAPÍTULO 1 SUMÁRIO INTRODUÇÃO...2 1. SISTEMAS DE NUMERAÇÃO...4 1.1 Introdução...4
CENTRO FEDERAL DE ENSINO TECNOLÓGICO DE SANTA CATARINA UNIDADE SÃO JOSÉ ÁREA DE TELECOMUNICAÇÕES ELETRÔNICA DIGITAL 1 CAPÍTULO 1 SUMÁRIO INTRODUÇÃO...2 1. SISTEMAS DE NUMERAÇÃO...4 1.1 Introdução...4
Ano letivo: 2012/2013. Sistemas de numeração. Pág.: 1/11. Escola profissional de Fafe SDAC. Trabalho elaborado por: Ana Isabel, nº905 TURMA 7.
 Pág.: 1/11 Escola profissional de Fafe SDAC Trabalho elaborado por: Ana Isabel, nº905 TURMA 7.5 Pág.: 2/11 Índice Introdução... 3 Sistemas de numeração posicionais... 4 Representação na base 2... 4 Representação
Pág.: 1/11 Escola profissional de Fafe SDAC Trabalho elaborado por: Ana Isabel, nº905 TURMA 7.5 Pág.: 2/11 Índice Introdução... 3 Sistemas de numeração posicionais... 4 Representação na base 2... 4 Representação
Introdução. A Informação e sua Representação (Parte III) Universidade Federal de Campina Grande Departamento de Sistemas e Computação
 Universidade Federal de Campina Grande Departamento de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte III) Prof.a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
Universidade Federal de Campina Grande Departamento de Sistemas e Computação Introdução à Computação A Informação e sua Representação (Parte III) Prof.a Joseana Macêdo Fechine Régis de Araújo joseana@computacao.ufcg.edu.br
2. Representação Numérica
 2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
Sistemas de numeração
 E Sistemas de numeração Aqui estão apenas números ratificados. William Shakespeare A natureza tem algum tipo de sistema de coordenadas geométrico-aritmético, porque a natureza tem todos os tipos de modelos.
E Sistemas de numeração Aqui estão apenas números ratificados. William Shakespeare A natureza tem algum tipo de sistema de coordenadas geométrico-aritmético, porque a natureza tem todos os tipos de modelos.
Sistemas de Numeração
 Professor Menezes SISTEMA DE NUMERAÇÃO 1-1 Sistemas de Numeração Observe que alguns números decimais a possuem uma representação muito curiosa no sistema binário: 1 decimal = 1 binário; 2 decimal = 10
Professor Menezes SISTEMA DE NUMERAÇÃO 1-1 Sistemas de Numeração Observe que alguns números decimais a possuem uma representação muito curiosa no sistema binário: 1 decimal = 1 binário; 2 decimal = 10
Codificação 1. Introdução. C 2 R r {! + codificação
 Codificação 1. Introdução A unidade básica de memória é o digito binário (bit). Para representar diferentes em memória é necessário que o bit armazene pelo menos 2 valores. A informação pode ser armazenada
Codificação 1. Introdução A unidade básica de memória é o digito binário (bit). Para representar diferentes em memória é necessário que o bit armazene pelo menos 2 valores. A informação pode ser armazenada
Sistemas Numéricos e a Representação Interna dos Dados no Computador
 Capítulo 2 Sistemas Numéricos e a Representação Interna dos Dados no Computador 2.0 Índice 2.0 Índice... 1 2.1 Sistemas Numéricos... 2 2.1.1 Sistema Binário... 2 2.1.2 Sistema Octal... 3 2.1.3 Sistema
Capítulo 2 Sistemas Numéricos e a Representação Interna dos Dados no Computador 2.0 Índice 2.0 Índice... 1 2.1 Sistemas Numéricos... 2 2.1.1 Sistema Binário... 2 2.1.2 Sistema Octal... 3 2.1.3 Sistema
centena dezena unidade 10 2 10 1 10 0 275 2 7 5 200 + 70 + 5 275
 A. Sistemas de Numeração. Para se entender a linguagem do computador (o Código de Máquina), é necessário conhecer um pouco da teoria dos números. Não é uma tarefa tão difícil quanto pode parecer. Sabendo-se
A. Sistemas de Numeração. Para se entender a linguagem do computador (o Código de Máquina), é necessário conhecer um pouco da teoria dos números. Não é uma tarefa tão difícil quanto pode parecer. Sabendo-se
Conversão de Bases e Aritmética Binária
 Conversão de Bases e Aritmética Binária Prof. Glauco Amorim Sistema de Numeração Decimal Dígitos Decimais: 0 2 3 4 5 6 7 8 9 Potências de base 0 0 0 2 0 0 3 4 0 0 00 000 0 000 Sistema de Numeração Binário
Conversão de Bases e Aritmética Binária Prof. Glauco Amorim Sistema de Numeração Decimal Dígitos Decimais: 0 2 3 4 5 6 7 8 9 Potências de base 0 0 0 2 0 0 3 4 0 0 00 000 0 000 Sistema de Numeração Binário
Notas de aula #1 SISTEMAS NUMÉRICOS
 UTFPR Disciplina: EL66J Prof. Gustavo B. Borba Notas de aula #1 SISTEMAS NUMÉRICOS - Notação posicional Definição: A posição de cada algarismo no número indica a sua magnitude. A magnitude também é chamada
UTFPR Disciplina: EL66J Prof. Gustavo B. Borba Notas de aula #1 SISTEMAS NUMÉRICOS - Notação posicional Definição: A posição de cada algarismo no número indica a sua magnitude. A magnitude também é chamada
Principais códigos utilizados. Codificação. Código binário puro. Codificação binária. Codificação Binária. Código Binário puro e suas variantes
 Codificação Principais códigos utilizados Computadores e Equipamentos de Comunicações Digitais trabalham com representação e códigos. A codificação binária de sinais é largamente utilizada em Sistemas
Codificação Principais códigos utilizados Computadores e Equipamentos de Comunicações Digitais trabalham com representação e códigos. A codificação binária de sinais é largamente utilizada em Sistemas
Em um sistema de numeração de base b qualquer, um número positivo é representado pelo polinômio:
 ELETRÔNICA DIGITAl I 1 SISTEMAS DE NUMERAÇÃO INTRODUÇÃO A base dos sistemas digitais são os circuitos de chaveamento (switching) nos quais o componente principal é o transistor que, sob o ponto de vista
ELETRÔNICA DIGITAl I 1 SISTEMAS DE NUMERAÇÃO INTRODUÇÃO A base dos sistemas digitais são os circuitos de chaveamento (switching) nos quais o componente principal é o transistor que, sob o ponto de vista
Hardware de Computadores
 Sistema Binário Hardware de Computadores O sistema binário é um sistema de numeração posicional em que todas as quantidades são representadas, utilizando-se como base as cifras: zero e um (0 e 1). Os computadores
Sistema Binário Hardware de Computadores O sistema binário é um sistema de numeração posicional em que todas as quantidades são representadas, utilizando-se como base as cifras: zero e um (0 e 1). Os computadores
SISTEMAS DIGITAIS Prof. Ricardo Rodrigues Barcelar http://www.ricardobarcelar.com
 - Aula 1 - SISTEMA DE NUMERAÇÃO BINÁRIA E DECIMAL Todos os computadores são formados por circuitos digitais, onde as informações e os dados são codificados com dois níveis de tensão, pelo que o seu sistema
- Aula 1 - SISTEMA DE NUMERAÇÃO BINÁRIA E DECIMAL Todos os computadores são formados por circuitos digitais, onde as informações e os dados são codificados com dois níveis de tensão, pelo que o seu sistema
ICC - Aula 6. Ivan da Silva Sendin. November 17, 2014. Bits, portas logicas, flip-flops,... Numeros e Simbolos Exercicios
 ICC - Aula 6 Ivan da Silva Sendin November 17, 2014 Só existem 10 tipos de pessoas: as que entendem números binários e as que não entendem Bits 0 e 1 portas logicas operadores lógicos Circuitos f : {0,
ICC - Aula 6 Ivan da Silva Sendin November 17, 2014 Só existem 10 tipos de pessoas: as que entendem números binários e as que não entendem Bits 0 e 1 portas logicas operadores lógicos Circuitos f : {0,
Arquitetura de Rede de Computadores
 TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
Capítulo 2. Representação de dados em sistemas computacionais
 Capítulo 2 Representação de dados em sistemas computacionais Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos [1] Compreender o conceito
Capítulo 2 Representação de dados em sistemas computacionais Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos [1] Compreender o conceito
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
O número é algo abstrato que representa a idéia de quantidade, expressos através de símbolos previamente acordados.
 Sistemas Numéricos Nos primórdios os homens primitivos não tinham a necessidade de contar, porém este conceito foi se transformando com o decorrer da história, o surgindo a escrita e do comércio nas civilizações
Sistemas Numéricos Nos primórdios os homens primitivos não tinham a necessidade de contar, porém este conceito foi se transformando com o decorrer da história, o surgindo a escrita e do comércio nas civilizações
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara. Carga Horária: 60h
 Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação da Informação Um dispositivo eletrônico, armazena e movimenta as informações internamente
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação da Informação Um dispositivo eletrônico, armazena e movimenta as informações internamente
UNIBRATEC Ensino Superior e Técnico em Informática DHD Desenvolvimento em Hardware
 UNIBRATEC Ensino Superior e Técnico em Informática DHD Desenvolvimento em Hardware 1 Francisco Fechine Borges quinta-feira, 24 de agosto de 2006 UNIBRATEC Ensino Superior e Técnico em Informática DHD Desenvolvimento
UNIBRATEC Ensino Superior e Técnico em Informática DHD Desenvolvimento em Hardware 1 Francisco Fechine Borges quinta-feira, 24 de agosto de 2006 UNIBRATEC Ensino Superior e Técnico em Informática DHD Desenvolvimento
Capítulo UM Bases Numéricas
 Capítulo UM Bases Numéricas 1.1 Introdução Quando o homem aprendeu a contar, ele foi obrigado a desenvolver símbolos que representassem as quantidades e grandezas que ele queria utilizar. Estes símbolos,
Capítulo UM Bases Numéricas 1.1 Introdução Quando o homem aprendeu a contar, ele foi obrigado a desenvolver símbolos que representassem as quantidades e grandezas que ele queria utilizar. Estes símbolos,
Organização e Arquitetura de Computadores I
 Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
CAPÍTULO 6 ARITMÉTICA DIGITAL
 CAPÍTULO 6 ARITMÉTICA DIGITAL Introdução Números decimais Números binários positivos Adição Binária Números negativos Extensão do bit de sinal Adição e Subtração Overflow Aritmético Circuitos Aritméticos
CAPÍTULO 6 ARITMÉTICA DIGITAL Introdução Números decimais Números binários positivos Adição Binária Números negativos Extensão do bit de sinal Adição e Subtração Overflow Aritmético Circuitos Aritméticos
Sistemas de Numeração e Conversão de Base
 1 No estudo de sistemas digitais recorre-se a diferentes sistemas de numeração. Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,...,9. Números superiores a 9; convencionamos o significado da posição
1 No estudo de sistemas digitais recorre-se a diferentes sistemas de numeração. Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,...,9. Números superiores a 9; convencionamos o significado da posição
Sistemas de Numeração. 1 Introdução aos sistemas numeração
 Sistemas de Numeração 1 Introdução aos sistemas numeração Sistemas de Numeração Base Decimal Base Binária Base Octal Base Hexadecimal Sistemas de numeração ria\base Oct tal\ Base He exadecimal l\base Biná
Sistemas de Numeração 1 Introdução aos sistemas numeração Sistemas de Numeração Base Decimal Base Binária Base Octal Base Hexadecimal Sistemas de numeração ria\base Oct tal\ Base He exadecimal l\base Biná
Sistemas de Numeração. Bases Numéricas e Conversão entre bases
 Sistemas de Numeração Bases Numéricas e Conversão entre bases Objetivos Contar em binário, octal, hexadecimal Conversões: DECIMAL BINÁRIO OCTAL HEXADECIMAL Histórico A origem dos conceitos sobre números
Sistemas de Numeração Bases Numéricas e Conversão entre bases Objetivos Contar em binário, octal, hexadecimal Conversões: DECIMAL BINÁRIO OCTAL HEXADECIMAL Histórico A origem dos conceitos sobre números
LÓGICA DE PROGRAMAÇÃO PARA ENGENHARIA INTRODUÇÃO À ORGANIZAÇÃO DE COMPUTADORES
 LÓGICA DE PROGRAMAÇÃO PARA ENGENHARIA INTRODUÇÃO À ORGANIZAÇÃO DE COMPUTADORES Prof. Dr. Daniel Caetano 2012-1 Objetivos Apresentar o funcionamento do computador Apresentar a função da memória e dos dispositivos
LÓGICA DE PROGRAMAÇÃO PARA ENGENHARIA INTRODUÇÃO À ORGANIZAÇÃO DE COMPUTADORES Prof. Dr. Daniel Caetano 2012-1 Objetivos Apresentar o funcionamento do computador Apresentar a função da memória e dos dispositivos
Sistema de Numeração e Códigos. Sistemas de Informação CPCX UFMS Prof. Renato F. dos Santos
 Sistema de Numeração e Códigos Sistemas de Informação CPCX UFMS Prof. Renato F. dos Santos Objetivos Converter um número de um sistema de numeração (decimal, binário ou hexadecimal) no seu equivalente
Sistema de Numeração e Códigos Sistemas de Informação CPCX UFMS Prof. Renato F. dos Santos Objetivos Converter um número de um sistema de numeração (decimal, binário ou hexadecimal) no seu equivalente
Circuitos Digitais. Conteúdo. Sistema de Numeração e Códigos :: Conversões de Binário para Decimal SISTEMA DE NUMERAÇÃO E CÓDIGOS
 Ciência da Computação Sistemas de Numeração e Conversões Prof. Sergio Ribeiro Material adaptado das aulas do Prof. José Maria da UFPI Conteúdo Conversões de binário para decimal. Conversões de decimal
Ciência da Computação Sistemas de Numeração e Conversões Prof. Sergio Ribeiro Material adaptado das aulas do Prof. José Maria da UFPI Conteúdo Conversões de binário para decimal. Conversões de decimal
REVISÃO E AVALIAÇÃO DA MATEMÁTICA
 2 Aula 45 REVISÃO E AVALIAÇÃO DA 3 Vídeo Arredondamento de números. 4 Arredondamento de números Muitas situações cotidianas envolvendo valores destinados à contagem, podem ser facilitadas utilizando o
2 Aula 45 REVISÃO E AVALIAÇÃO DA 3 Vídeo Arredondamento de números. 4 Arredondamento de números Muitas situações cotidianas envolvendo valores destinados à contagem, podem ser facilitadas utilizando o
Fabio Bento fbento@ifes.edu.br
 Fabio Bento fbento@ifes.edu.br Eletrônica Digital Sistemas de Numeração e Códigos 1. Conversões de Binário para Decimal 2. Conversões de Decimal para Binário 3. Sistema de Numeração Hexadecimal 4. Código
Fabio Bento fbento@ifes.edu.br Eletrônica Digital Sistemas de Numeração e Códigos 1. Conversões de Binário para Decimal 2. Conversões de Decimal para Binário 3. Sistema de Numeração Hexadecimal 4. Código
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES
 CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
Sistemas de Numeração
 Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Sistemas de Numeração Nuno Pombo / Miguel Neto Arquitectura Computadores I 2014/2015 1 Conversão
Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Sistemas de Numeração Nuno Pombo / Miguel Neto Arquitectura Computadores I 2014/2015 1 Conversão
Conversão de Bases Numéricas
 Disciplina: Circuitos Digitais Conversão de Bases Numéricas Prof. a Dra. Carolina Davanzzo Gomes dos Santos Email: profcarolinadgs@gmail.com Página: profcarolinadgs.webnode.com.br Sistemas de Numeração
Disciplina: Circuitos Digitais Conversão de Bases Numéricas Prof. a Dra. Carolina Davanzzo Gomes dos Santos Email: profcarolinadgs@gmail.com Página: profcarolinadgs.webnode.com.br Sistemas de Numeração
Aula 2 Modelo Simplificado de Computador
 Aula 2 Modelo Simplificado de Computador Um computador pode ser esquematizado de maneira bastante simplificada da seguinte forma: Modelo Simplificado de Computador: Memória Dispositivo de Entrada Processador
Aula 2 Modelo Simplificado de Computador Um computador pode ser esquematizado de maneira bastante simplificada da seguinte forma: Modelo Simplificado de Computador: Memória Dispositivo de Entrada Processador
Arquitetura de Computadores
 Arquitetura de Computadores Prof. Fábio M. Costa Instituto de Informática UFG 1S/2004 Representação de Dados e Aritimética Computacional Roteiro Números inteiros sinalizados e nãosinalizados Operações
Arquitetura de Computadores Prof. Fábio M. Costa Instituto de Informática UFG 1S/2004 Representação de Dados e Aritimética Computacional Roteiro Números inteiros sinalizados e nãosinalizados Operações
Lógica Combinacional Aula 01 Sistema de Numeração. Felipe S. L. G. Duarte Felipelageduarte+fatece@gmail.com
 Lógica Combinacional Aula 01 Sistema de Numeração Felipe S. L. G. Duarte Felipelageduarte+fatece@gmail.com Sistema de Numeração Um numeral é um símbolo ou grupo de símbolos que representa um número em
Lógica Combinacional Aula 01 Sistema de Numeração Felipe S. L. G. Duarte Felipelageduarte+fatece@gmail.com Sistema de Numeração Um numeral é um símbolo ou grupo de símbolos que representa um número em
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Notação Posicional. Introdução à Computação. Bases. Bases. Sistemas de Numeração. Exemplo:
 Notação Posicional Introdução à Computação Sistas de Numeração O objetivo principal de qualquer base numérica é a de representar números É a posição do algarimo (dígito) que determina seu valor Ex: número
Notação Posicional Introdução à Computação Sistas de Numeração O objetivo principal de qualquer base numérica é a de representar números É a posição do algarimo (dígito) que determina seu valor Ex: número
Computadores XII: Aprendendo a Somar A4 Texto 3
 Computadores XII: Aprendendo a Somar A4 Texto 3 http://www.bpiropo.com.br/fpc20051017.htm Sítio Fórum PCs /Colunas Coluna: B. Piropo Publicada em 17/10/2005 Autor: B.Piropo Na coluna anterior, < http://www.forumpcs.com.br/viewtopic.php?t=131250
Computadores XII: Aprendendo a Somar A4 Texto 3 http://www.bpiropo.com.br/fpc20051017.htm Sítio Fórum PCs /Colunas Coluna: B. Piropo Publicada em 17/10/2005 Autor: B.Piropo Na coluna anterior, < http://www.forumpcs.com.br/viewtopic.php?t=131250
ELETRÔNICA. Changed with the DEMO VERSION of CAD-KAS PDF-Editor (http://www.cadkas.com). INTRODUÇÃO
 0010100111010101001010010101 CURSO DE 0101010100111010100101011101 1010011001111010100111010010 ELETRÔNICA 1010000111101010011101010010 DIGITAL INTRODUÇÃO Os circuitos equipados com processadores, cada
0010100111010101001010010101 CURSO DE 0101010100111010100101011101 1010011001111010100111010010 ELETRÔNICA 1010000111101010011101010010 DIGITAL INTRODUÇÃO Os circuitos equipados com processadores, cada
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara. Carga Horária: 60h
 Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação de grandeza com sinal O bit mais significativo representa o sinal: 0 (indica um número
Sistema de Numeração e Conversão entre Sistemas. Prof. Rômulo Calado Pantaleão Camara Carga Horária: 60h Representação de grandeza com sinal O bit mais significativo representa o sinal: 0 (indica um número
REDES DE COMPUTADORES - I UNI-ANHANGUERA. CURSO DE ANÁLISE E DESENVOLVIMENTO DE SISTEMAS PROF. MARCIO BALIAN
 1 REDES DE COMPUTADORES - I UNI-ANHANGUERA. CURSO DE ANÁLISE E DESENVOLVIMENTO DE SISTEMAS PROF. MARCIO BALIAN ENDEREÇAMENTO IP O IP é um protocolo da Camada de rede É um endereço lógico único em toda
1 REDES DE COMPUTADORES - I UNI-ANHANGUERA. CURSO DE ANÁLISE E DESENVOLVIMENTO DE SISTEMAS PROF. MARCIO BALIAN ENDEREÇAMENTO IP O IP é um protocolo da Camada de rede É um endereço lógico único em toda
Laboratório - Uso da calculadora do Windows com endereços de rede
 Laboratório - Uso da calculadora do Windows com endereços de rede Objetivos Parte 1: Acesso à Calculadora do Windows Parte 2: Converter entre os sistemas numéricos Parte 3: Converter endereços IPv4 de
Laboratório - Uso da calculadora do Windows com endereços de rede Objetivos Parte 1: Acesso à Calculadora do Windows Parte 2: Converter entre os sistemas numéricos Parte 3: Converter endereços IPv4 de
SISTEMAS DE NUMERAÇÃO
 Universidade do Contestado Campus Concórdia Curso de Sistemas de Informação Prof.: Maico Petry SISTEMAS DE NUMERAÇÃO DISCIPLINA: Fundamentos em Informática SISTEMAS DE NUMERAÇÃO E REPRESENTAÇÃO DE DADOS
Universidade do Contestado Campus Concórdia Curso de Sistemas de Informação Prof.: Maico Petry SISTEMAS DE NUMERAÇÃO DISCIPLINA: Fundamentos em Informática SISTEMAS DE NUMERAÇÃO E REPRESENTAÇÃO DE DADOS
Aula 2 Sistemas de Numeração (Revisão)
 Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
Jeandervall. Roteamento
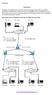 Roteamento Configurar um roteador parece um tanto quanto complicado, porem não é uma tarefa impossível. O detalhe é que é preciso tomar muita a atenção na ora de configurar as rotas. Recomenda-se que antes
Roteamento Configurar um roteador parece um tanto quanto complicado, porem não é uma tarefa impossível. O detalhe é que é preciso tomar muita a atenção na ora de configurar as rotas. Recomenda-se que antes
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO LUÍS PAULO REIS
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO LUÍS PAULO REIS LICENCIATURA EM CIÊNCIA DA INFORMAÇÃO DISCIPLINA DE INFORMÁTICA BÁSICA - 1º ANO SETEMBRO
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO LUÍS PAULO REIS LICENCIATURA EM CIÊNCIA DA INFORMAÇÃO DISCIPLINA DE INFORMÁTICA BÁSICA - 1º ANO SETEMBRO
13 Números Reais - Tipo float
 13 Números Reais - Tipo float Ronaldo F. Hashimoto e Carlos H. Morimoto Até omomentonoslimitamosaouso do tipo inteiro para variáveis e expressões aritméticas. Vamos introduzir agora o tipo real. Ao final
13 Números Reais - Tipo float Ronaldo F. Hashimoto e Carlos H. Morimoto Até omomentonoslimitamosaouso do tipo inteiro para variáveis e expressões aritméticas. Vamos introduzir agora o tipo real. Ao final
Genericamente qualquer sistema de numeração pode ser caracterizado por:
 SISTEMAS NUMÉRICOS 1 Genericamente qualquer sistema de numeração pode ser caracterizado por: Sistema de Base N - Possui N dígitos e o maior é (N-1) - Qualquer número maior que (N-1) pode ser expresso como
SISTEMAS NUMÉRICOS 1 Genericamente qualquer sistema de numeração pode ser caracterizado por: Sistema de Base N - Possui N dígitos e o maior é (N-1) - Qualquer número maior que (N-1) pode ser expresso como
Unidade 5: Sistemas de Representação
 Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
ANALÓGICA X DIGITAL. Vamos começar essa aula estabelecendo os dois tipos de eletrônica: Eletrônica Analógica. Eletrônica Digital
 ANALÓGICA X DIGITAL Vamos começar essa aula estabelecendo os dois tipos de eletrônica: Eletrônica Analógica Eletrônica Digital ANALÓGICA X DIGITAL A eletrônica analógica é caracterizada por um sinal que
ANALÓGICA X DIGITAL Vamos começar essa aula estabelecendo os dois tipos de eletrônica: Eletrônica Analógica Eletrônica Digital ANALÓGICA X DIGITAL A eletrônica analógica é caracterizada por um sinal que
Curso de Hardware Aula 01 Tema: Sistema de Medidas Por: Edmilson de Oliveira Reis Revisado em: 02/03/2012
 Curso de Hardware Aula 01 Tema: Sistema de Medidas Por: Edmilson de Oliveira Reis Revisado em: 02/03/2012 Unidades de Medida de Armazenamento Esses detalhes refletem na quantidade de informação armazenada
Curso de Hardware Aula 01 Tema: Sistema de Medidas Por: Edmilson de Oliveira Reis Revisado em: 02/03/2012 Unidades de Medida de Armazenamento Esses detalhes refletem na quantidade de informação armazenada
REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO
 REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO Profs. M.Sc. Lucio M. Duarte e Ph.D. Avelino Zorzo 1 Faculdade de Informática - PUCRS 1 REPRESENTAÇÃO DE DADOS Acredita-se que a criação de números veio com
REPRESENTAÇÃO DE DADOS E SISTEMAS DE NUMERAÇÃO Profs. M.Sc. Lucio M. Duarte e Ph.D. Avelino Zorzo 1 Faculdade de Informática - PUCRS 1 REPRESENTAÇÃO DE DADOS Acredita-se que a criação de números veio com
PC Fundamentos Revisão 4
 exatasfepi.com.br PC Fundamentos Revisão 4 André Luís Duarte...mas os que esperam no Senhor renovarão as suas forças; subirão com asas como águias; correrão, e não se cansarão; andarão, e não se fatigarão.is
exatasfepi.com.br PC Fundamentos Revisão 4 André Luís Duarte...mas os que esperam no Senhor renovarão as suas forças; subirão com asas como águias; correrão, e não se cansarão; andarão, e não se fatigarão.is
Aula 6 Aritmética Computacional
 Aula 6 Aritmética Computacional Introdução à Computação ADS - IFBA Representação de Números Inteiros Vírgula fixa (Fixed Point) Ponto Flutuante Para todos, a quantidade de valores possíveis depende do
Aula 6 Aritmética Computacional Introdução à Computação ADS - IFBA Representação de Números Inteiros Vírgula fixa (Fixed Point) Ponto Flutuante Para todos, a quantidade de valores possíveis depende do
Aula 2: Conversão entre Bases, Aritmética
 Aula 2: Conversão entre Bases, Aritmética Circuitos Digitais Rodrigo Hausen CMCC UFABC 25 de janeiro de 2013 http://compscinet.org/circuitos Rodrigo Hausen (CMCC UFABC) Aula 2: Conversão entre Bases, Aritmética
Aula 2: Conversão entre Bases, Aritmética Circuitos Digitais Rodrigo Hausen CMCC UFABC 25 de janeiro de 2013 http://compscinet.org/circuitos Rodrigo Hausen (CMCC UFABC) Aula 2: Conversão entre Bases, Aritmética
PROGRAMAÇÃO ESTRUTURADA. CC 2º Período
 PROGRAMAÇÃO ESTRUTURADA CC 2º Período PROGRAMAÇÃO ESTRUTURADA Aula 06: Ponteiros Declarando e utilizando ponteiros Ponteiros e vetores Inicializando ponteiros Ponteiros para Ponteiros Cuidados a serem
PROGRAMAÇÃO ESTRUTURADA CC 2º Período PROGRAMAÇÃO ESTRUTURADA Aula 06: Ponteiros Declarando e utilizando ponteiros Ponteiros e vetores Inicializando ponteiros Ponteiros para Ponteiros Cuidados a serem
20-10-2014. Sumário. Arquitetura do Universo
 Sumário Das Estrelas ao átomo Unidade temática 1 Diferenças entre medir, medição e medida duma grandeza. Modos de exprimir uma medida. Algarismos significativos: Regras de contagem e operações. Esclarecimento
Sumário Das Estrelas ao átomo Unidade temática 1 Diferenças entre medir, medição e medida duma grandeza. Modos de exprimir uma medida. Algarismos significativos: Regras de contagem e operações. Esclarecimento
INTRODUÇÃO AOS SISTEMAS LÓGICOS
 1 INTRODUÇÃO AOS SISTEMAS LÓGICOS SISTEMA NUMÉRICO PROF. ANDRÉ MONTEVECCHI ANDRE.MONTEVECCHI@PROF.UNIBH.BR 19/02/2014 Prof. André Montevecchi / Profa. Anna Tostes 2 SUMÁRIO Sistemas Numéricos Notação Posicional
1 INTRODUÇÃO AOS SISTEMAS LÓGICOS SISTEMA NUMÉRICO PROF. ANDRÉ MONTEVECCHI ANDRE.MONTEVECCHI@PROF.UNIBH.BR 19/02/2014 Prof. André Montevecchi / Profa. Anna Tostes 2 SUMÁRIO Sistemas Numéricos Notação Posicional
ORGANIZAÇÃO DE COMPUTADORES MÓDULO 12
 ORGANIZAÇÃO DE COMPUTADORES MÓDULO 12 Índice 1. Circuitos Digitais...3 1.1. Sistemas de Numeração... 3 1.2. Tema de Números-Base... 4 2 1. CIRCUITOS DIGITAIS 1.1. SISTEMAS DE NUMERAÇÃO O que quer dizer
ORGANIZAÇÃO DE COMPUTADORES MÓDULO 12 Índice 1. Circuitos Digitais...3 1.1. Sistemas de Numeração... 3 1.2. Tema de Números-Base... 4 2 1. CIRCUITOS DIGITAIS 1.1. SISTEMAS DE NUMERAÇÃO O que quer dizer
Números base 2, 8, 10, 16. Sistemas da Computação Prof. Rossano Pablo Pinto, Msc. rossano at gmail com 2 semestre 2007
 Números base 2, 8, 10, 16 Sistemas da Computação Prof. Rossano Pablo Pinto, Msc. rossano at gmail com 2 semestre 2007 Tópicos Números binário, decimal, octal, hexadecimal Conversões entre bases Números
Números base 2, 8, 10, 16 Sistemas da Computação Prof. Rossano Pablo Pinto, Msc. rossano at gmail com 2 semestre 2007 Tópicos Números binário, decimal, octal, hexadecimal Conversões entre bases Números
Fundamentos em Informática (Sistemas de Numeração e Representação de Dados)
 1 UNIVERSIDADE DO CONTESTADO / UnC CAMPUS CONCÓRDIA/SC CURSO DE SISTEMAS DE INFORMAÇÃO Fundamentos em Informática (Sistemas de Numeração e Representação de Dados) (Apostila da disciplina elaborada pelo
1 UNIVERSIDADE DO CONTESTADO / UnC CAMPUS CONCÓRDIA/SC CURSO DE SISTEMAS DE INFORMAÇÃO Fundamentos em Informática (Sistemas de Numeração e Representação de Dados) (Apostila da disciplina elaborada pelo
Informática Sistemas de Numeração. Profª. Me. Valéria Espíndola Lessa lessavaleria@gmail.com Valeria-lessa@uergs.edu.br
 Sistemas de Numeração Profª. Me. Valéria Espíndola Lessa lessavaleria@gmail.com Valeria-lessa@uergs.edu.br Outros Sistemas de Numeração Já sabemos que existem outros tipos de sistemas de numeração, além
Sistemas de Numeração Profª. Me. Valéria Espíndola Lessa lessavaleria@gmail.com Valeria-lessa@uergs.edu.br Outros Sistemas de Numeração Já sabemos que existem outros tipos de sistemas de numeração, além
EFA / S13 SIS Ricardo Castanhinha / Nº 21322 STC / Formadoras Alexandra Formosinho & Isabel Carvalho. Sistema Binário
 EFA / S13 SIS Sistema Binário SISTEMA BINÁRIO Estamos acostumados a utilizar o SISTEMA DECIMAL DE NUMERAÇÃO. Esse sistema usa 10 algarismos para formar todos os números: 0, 1, 2, 3, 4, 5, 6, 7, 8, e 9.
EFA / S13 SIS Sistema Binário SISTEMA BINÁRIO Estamos acostumados a utilizar o SISTEMA DECIMAL DE NUMERAÇÃO. Esse sistema usa 10 algarismos para formar todos os números: 0, 1, 2, 3, 4, 5, 6, 7, 8, e 9.
Bases Numéricas e Conversão. DCC 122 - Circuitos Digitais
 Bases Numéricas e Conversão DCC 122 - Circuitos Digitais Objetivos Bases numéricas utilizadas em sistemas computacionais. Conversões: DECIMAL BINÁRIO HEXADECIMAL Sistemas de Numeração Não posicional Ex.
Bases Numéricas e Conversão DCC 122 - Circuitos Digitais Objetivos Bases numéricas utilizadas em sistemas computacionais. Conversões: DECIMAL BINÁRIO HEXADECIMAL Sistemas de Numeração Não posicional Ex.
Prof. Rafael Gross. rafael.gross@fatec.sp.gov.br
 Prof. Rafael Gross rafael.gross@fatec.sp.gov.br Todo protocolo define um tipo de endereçamento para identificar o computador e a rede. O IP tem um endereço de 32 bits, este endereço traz o ID (identificador)
Prof. Rafael Gross rafael.gross@fatec.sp.gov.br Todo protocolo define um tipo de endereçamento para identificar o computador e a rede. O IP tem um endereço de 32 bits, este endereço traz o ID (identificador)
