Oscilações de Grandes Amplitudes num Corpo que se Move com Velocidade Constante
|
|
|
- Cássio Neto Tavares
- 5 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Oscilações de Grandes Amplitdes nm Corpo qe se Move com Velocidade Constante Ator: Jan Novaes Recicar Orientador: Prof. Dr. Liz Antonio Alcântara Pereira Co-orientador: Prof. Ph.D. Migel Hiroo Hirata Itabá, Abril de 007
2 UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Oscilações de Grandes Amplitdes nm Corpo qe se Move com Velocidade Constante Ator: Jan Novaes Recicar Orientador: Prof. Dr. Liz Antonio Alcântara Pereira Co-orientador: Prof. Ph.D. Migel Hiroo Hirata Crso: Mestrado em Engenharia Mecânica Área de Concentração: Dinâmica dos Flidos e Máqinas de Flxo Dissertação sbmetida ao Programa de Pós-Gradação em Engenharia Mecânica como parte dos reqisitos para obtenção do Títlo de Mestre em Engenharia Mecânica. Itabá, Abril de 007 M.G. Brasil
3 UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Oscilações de Grandes Amplitdes nm Corpo qe se Move com Velocidade Constante Ator: Jan Novaes Recicar Orientador: Prof. Dr. Liz Antonio Alcântara Pereira Co-orientador: Prof. Ph.D. Migel Hiroo Hirata Composição da Banca Examinadora: Prof. Dr. Sérgio Viçosa Möller - UFRGS Prof. Dra. Ana Lcia Fernandes de Lima e Silva - UNIFEI Prof. Ph.D. Migel Hiroo Hirata (Co-orientador) - UNIFEI Prof. Dr. Liz Antonio Alcântara Pereira (Orientador) - UNIFEI
4 Dedicatória Aos mes pais, Votech e Maria Lygia, qe sempre me incentivaram na formação e no desenvolvimento cltral.
5 Agradecimentos Ao me Orientador, Professor Dr. Liz Antonio Alcântara Pereira, pela competência, dedicação, paciência e amizade. Ao Professor Ph.D. Migel Hiroo Hirata, pela sa valiosa ada na co-orientação deste trabalho. Ao Professor Dr. José Egênio Rios Ricci, por se apoio e por me apresentar ao grpo de trabalho de Método de Vórtices.
6 O rio atinge ses obetivos porqe aprende a contornar obstáclos (Lao-Tsé)
7 Resmo RECICAR, J. N. (007), Oscilações de Grandes Amplitdes nm Corpo qe se Move com Velocidade Constante, Itabá, 9p. Dissertação (Mestrado em Máqinas de Flxo) - Institto de Engenharia Mecânica, Universidade Federal de Itabá. Este trabalho analisa o escoamento de m flido Newtoniano com propriedades constantes ao redor de m corpo oscilante qe se move com velocidade constante. A oscilação do corpo é perpendiclar à direção do escoamento. São apresentados resltados referentes à análise da inflência da freqüência e da amplitde de oscilação de m cilindro circlar sobre o cálclo das cargas aerodinâmicas e sobre o número de Strohal. A simlação nmérica é realizada tilizando-se o Método de Vórtices Discretos. Para cada incremento de tempo da simlação, m número de vórtices discretos de Lamb é gerado próximo à sperfície do corpo; a intensidade dos vórtices nascentes é calclada para satisfazer a condição de escorregamentonlo. As cargas aerodinâmicas são calcladas tilizando ma formlação integral derivada de ma eqação de Poisson para a pressão. Três tipos de regimes de escoamento são identificados drante m amento na freqüência de oscilação do corpo. O primeiro tipo é observado para baixas freqüências de oscilação do corpo; nesta sitação o número de Strohal permanece qase constante correspondendo ao número de Strohal de m corpo sem oscilação. O segndo tipo corresponde a m regime de transição, onde aparentemente a freqüência de emissão de vórtices não correlaciona com a freqüência de oscilação do corpo. Finalmente para altas freqüências de oscilação do corpo a freqüência de emissão de vórtices coincide com a freqüência de oscilação do corpo denominada de freqüência de lock-in. Palavras-chave Método de vórtices, método dos painéis, cargas aerodinâmicas, número de Strohal, corpo oscilante.
8 Abstract RECICAR, J. N. (007), Large Amplitde Oscillation in a Body which Moves with Constant Velocity, Itabá, 9p. MSc. Dissertation - Institto de Engenharia Mecânica, Universidade Federal de Itabá. The flow arond a heaving body which moves with constant velocity in a qiescent Newtonian flid with constant properties is analyzed. For the circlar cylinder is presented the inflences of the freqency and amplitde oscillation on the aerodynamics loads and on the Strohal nmber. For the nmerical simlations, the Discrete Vortex Method is sed. In the vortex method the vorticity generated on the body srface is discretized and represented by a clod of particles carrying vorticity. Lamb vortices with a viscos core are sed for that matter. For each time step of the simlation, a nmber of discrete vortices are placed close to the body srface; the intensity of them is determined sch as to satisfy the no-slip bondary condition. The aerodynamics loads are obtained sing an integral eqation derived from the pressre Poisson eqation. It is also possible to identify three different types of flow regime as the cylinder oscillation freqency increases. The first type is observed for low freqency range of the cylinder oscillation; in this sitation the Strohal nmber remains almost constant. The first type is followed by an intermediate range of freqency, the transition regime, where apparently the shedding freqency does not correlate to the freqency of the cylinder oscillation. Finally in the third type, high freqency of cylinder oscillation, the vortex shedding freqency is locked-in with the cylinder oscillation freqency. Keywords Vortex method, panels method, aerodynamics loads, Strohal nmber, oscillating blff body.
9 i Smário SUMÁRIO I LISTA DE FIGURAS IV LISTA DE TABELAS VI SIMBOLOGIA VII LETRAS LATINAS VII LETRAS GREGAS VIII SUPERESCRITOS IX SUBSCRITOS IX SIGLAS X CAPÍTULO INTRODUÇÃO CAPÍTULO 6 REVISÃO BIBLIOGRÁFICA 6. ESCOAMENTO AO REDOR DE UM CORPO OSCILANTE O QUAL SE MOVE COM VELOCIDADE CONSTANTE Referências Utilizadas Referências Gerais O MÉTODO DE VÓRTICES CAPÍTULO 3 3 FORMULAÇÃO GERAL DO PROBLEMA E O MÉTODO DE VÓRTICES 3 3. INTRODUÇÃO FORMULAÇÃO GERAL DO MÉTODO
10 ii 3.3 HIPÓTESES SIMPLIFICADORAS EQUAÇÕES E CONDIÇÕES DE CONTORNO QUE DEFINEM O MODELO ADIMENSIONALIZAÇÃO DAS EQUAÇÕES O MÉTODO DE VÓRTICES Eqação do Transporte da Vorticidade A Separação dos Efeitos Viscosos Convecção da Vorticidade Difsão da Vorticidade Geração da Vorticidade Conservação da Circlação Cargas Aerodinâmicas CAPÍTULO 4 37 IMPLEMENTAÇÃO NUMÉRICA INTRODUÇÃO ALGORÍTMO GERAL DO MÉTODO CAPÍTULO 5 46 ANÁLISE DOS RESULTADOS DA SIMULAÇÃO NUMÉRICA INTRODUÇÃO PARÂMETROS UTILIZADOS NA SIMULAÇÃO NUMÉRICA CILINDRO CIRCULAR Cilindro circlar sem oscilação Cilindro circlar oscilando CAPÍTULO 6 7 CONCLUSÕES E SUGESTÕES 7 6. INTRODUÇÃO CONCLUSÕES E SUGESTÕES REFERÊNCIAS BIBLIOGRÁFICAS 76 APÊNDICE A 8 OBTENÇÃO DA EQUAÇÃO DO TRANSPORTE DE VORTICIDADE 3D E D 8 APÊNDICE B 86 DETALHES DO CÁLCULO DAS VELOCIDADES 86 APÊNDICE C 9
11 iii DISTRIBUIÇÃO DA VORTICIDADE E DA VELOCIDADE INDUZIDA 9 C. O VÓRTICE POTENCIAL C. O VÓRTICE LAMB APÊNDICE D 98 VELOCIDADE INDUZIDA POR UMA NUVEM DE VORTICES 98
12 iv Lista de Figras Figra Definição do problema Figra Distribição de fontes com densidade niforme Figra 3 Representação de m painel genérico do corpo Figra 4 Velocidade indzida pelo corpo Figra 5 Flxo de vorticidade através da parede Figra 6 Vórtice de Lamb Figra 7 Algoritmo de implementação do programa OSCILLATION.FOR Figra 8 Detalhe da distribição de painéis no cilindro circlar Figra 9 Determinação da freqüência de emissão de vórtices Figra 0 Cálclo da amplitde média de C L Figra Comparação dos resltados médios de coeficiente de pressão ( C P ) Figra Cargas aerodinâmicas integradas (sem oscilação) Figra 3 Evolção da vorticidade após 800 iterações (sem oscilação) Figra 4 Campo de velocidades e manchas de vorticidade Figra 5 Campo de velocidade e vorticidade (trecho a - b ) Figra 6 Campo de velocidades e vorticidade ( C máximo negativo) Figra 7 Campo de velocidades e vorticidade (trecho b - c ) Figra 8 Amplitde média do C L em fnção da amplitde de oscilação para λ = 0, Figra 9 Amplitde média do C L em fnção da amplitde de oscilação para λ =, Figra 0 Cargas aerodinâmicas integradas ( λ =, 0 e A = 0, 3) Figra Distribição do coeficiente de pressão ( λ =, 0 e A = 0, 3) Figra Número de Strohal de emissão de vórtices em fnção do Strohal do corpo L
13 Figra 3 Número de Strohal para amplitde de oscilação A = 0, Figra 4 Número de Strohal para amplitde de oscilação A = 0, Figra 5 Freqüência de lock-in em fnção da amplitde de oscilação do corpo Figra 6 Esteira para corpo parado (a) e corpo oscilando (b) Figra 7 Esteira para t = 33, A = 0, 5 e λ =, Figra 8 Campo de velocidades e mancha de vorticidade Figra 9 Esteira para t = 8, 3, A = 0, 5 e λ =, Figra 30 Campo de velocidades e manchas de vorticidade Figra 3 Padrão da esteira para t = 3, 4, A = 0, 5 e λ =, Figra 3 Campo de velocidades e manchas de vorticidade Figra 33 Oscilação, velocidade, aceleração e sstentação para λ =, 5 e A = 0, Figra 34 Velocidade indzida sobre o ponto de controle do painel Figra 35 Painéis tilizados nas verificações das velocidades indzidas Figra 36 Painel sperior frontal Figra 37 Painel inferior frontal Figra 38 Painel traseiro sperior Figra 39 Painel inferior traseiro Figra 40 Painel horizontal sperior Figra 4 Painel horizontal inferior Figra 4 Velocidade indzida pelo escoamento incidente niforme Figra 43 Velocidade indzida pelo vórtice potencial Figra 44 Velocidade indzida pelo vórtice de Lamb v
14 vi Lista de Tabelas Tabela Parâmetros tilizados na simlação nmérica Tabela Cilindro circlar sem oscilação Tabela 3 Estdo para baixas velocidades anglares de oscilação Tabela 4 Estdo para altas velocidades anglares de oscilação Tabela 5 Corpo sem oscilação Tabela 6 Corpo com oscilação de peqena amplitde Tabela 7 Corpo com oscilação de grande amplitde Tabela 8 Corpo com oscilação de média amplitde
15 vii Simbologia Letras Latinas A b C D C L Cp d D f Amplitde da oscilação do corpo Comprimento característico Coeficiente de arrasto Coeficiente de sstentação Coeficiente de pressão Diâmetro do cilindro circlar Força de arrasto Freqüência associada a emissão de vórtices f Freqüência de oscilação do corpo C K KC L M Nv p Elemento da matriz de inflência Número de Kelegan-Carpenter Força de sstentação Número de painéis planos Número total de vórtices discretos presentes na esteira Campo de pressões Re Número de Reynolds S S C S Define fronteira da região flida Sperfície do corpo Sperfície a grandes distâncias
16 St T 0 t U i c v v V V x V y x y x d y d y 0 y& 0 Y Z d Número de Strohal Tempo característico Referente ao tempo Velocidade do escoamento incidente Campo de velocidades Vetor velocidade do escoamento incidente Vetor velocidade indzida pelo corpo Vetor velocidade indzida pela nvem de vórtices Componente em x da velocidade Componente em y da velocidade Vetor velocidade do corpo Componente em x do vetor velocidade do corpo Componente em y do vetor velocidade do corpo Coordenada em x da partícla Coordenada em y da partícla Coordenada em x do vetor avanço randômico Coordenada em y do vetor avanço randômico Posição instantânea, em y, do corpo oscilante Componente em y do vetor velocidade do corpo Trabalho específico total Vetor avanço randômico viii Letras Gregas λ Velocidade anglar da oscilação do corpo π Constante Pi ( π = ) η Referente ao contorno do corpo ρ ν Massa específica Viscosidade cinemática
17 μ Δ t σ σ 0 γ Γ Σ ω ω Ω Δ s θ ε Viscosidade dinâmica Incremento de tempo Densidade de fontes Raio do núcleo do vórtice de Lamb Densidade de vórtices Intensidade do vórtice Representa m somatório Campo de vorticidades Componente do vetor vorticidade Domínio do escoamento Comprimento do painel Ânglo do painel Posição de desprendimento dos vórtices discretos Operador Nabla Operador Laplaciano ix Sperescritos Designa variável adimensional Sbscritos τ n Denota componente tangencial Referente a direção normal Denota condições de escoamento não-pertrbado
18 Siglas x UNIFEI Universidade Federal de Itabá
19 Capítlo INTRODUÇÃO O estdo do escoamento incompressível e em regime não-permanente de m flido Newtoniano com propriedades constantes ao redor de m corpo oscilante movendo-se com velocidade constante é de grande importância para as análises aerodinâmicas e hidrodinâmicas em várias áreas da engenharia. As oscilações de peqena amplitde são importantes na análise de corpos imersos tais como trocadores de calor, pás de trbomáqinas e asas de avião; e ma atenção especial deve ser tomada na condição de lock-in, o sea, na região onde a freqüência de emissão de vórtices é a mesma da freqüência de oscilação do corpo. As oscilações de grandes amplitdes, por otro lado, são relevantes em corpos localizados em ondas e correntes tais como risers, linhas de transmissão, pás de helicópteros, etc. O movimento oscilatório de peqena amplitde modifica, principalmente, o campo próximo à sperfície do corpo tendo, como conseqüência, m importante efeito nas forças aerodinâmicas e na distribição de pressão. Se o movimento oscilatório for de grande amplitde observa-se, adicionalmente, a inflência do movimento na esteira do corpo, o qal pode ser importante no estdo com vários corpos o na presença de ma sperfície.
20 O crescente avanço na área comptacional tem permitido a realização de simlações nméricas mais refinadas ao redor de geometrias complexas levando-se em conta os efeitos viscosos. Como geometrias complexas aqi se entendem: ma asa se movimentando nas proximidades de ma sperfície plana, o escoamento ao redor de m connto de prédios residenciais, o escoamento ao redor de cabos de ma rede de transmissão de energia, o movimento das pás no interior da volta de ma máqina de flxo, etc. Neste contexto, o Grpo de Método de Vórtices da UNIFEI vem analisando desde 997 sitações qe envolvem: interferência entre fronteiras sólidas podendo o não existir movimento relativo entre elas; efeitos de oscilação de corpos e aspectos relacionados com transferência de calor. Para a análise das sitações anteriormente mencionadas tiliza-se ma classe geral de métodos nméricos denominados de Métodos de Partíclas. O Método de Vórtices Discretos, tema central deste trabalho, é o representante mais conhecido dos Métodos de Partíclas; neste método a vorticidade presente no meio flido é discretizada e representada por ma nvem de vórtices discretos. Cada vórtice discreto presente na nvem de vórtices tem a sa traetória acompanhada individalmente ao longo de toda a simlação, o qe caracteriza ma descrição pramente lagrangeana. Vea, por exemplo, os trabalhos de Chorin (973), Lewis (999), Kamemoto (994), Sarpkaya (989), Alcântara Pereira et al. (00), Hirata et al. (003) e Kamemoto (004). O presente trabalho se insere dentro das atividades qe vem sendo desenvolvidas pelo Grpo de Método de Vórtices da UNIFEI contribindo para o esclarecimento de ma classe importante dos fenômenos físicos: a oscilação de corpos imersos nm meio flido. Em m trabalho anterior, Silva (004) tilizo o Método de Vórtices Discretos para estdar as propriedades aerodinâmicas de m escoamento ao redor de m corpo com a restrição de peqenas amplitdes de oscilação. Diferentemente do presente trabalho, a presença da oscilação do corpo foi considerada fazendo-se ma transferência das condições de contorno de ma posição atal do corpo para ma posição média por ele ocpada. Mstto et al. (998) apresentaram resltados para m cilindro girante considerando altos números de Reynolds e baixas freqüências de rotação, prevendo a ocorrência do Efeito Magns. Utilizaram o Método de Vórtices Discretos para o cálclo dos avanços difsivos e convectivos; o processo de geração de vorticidade satisfaz a condição de escorregamento-nlo e o Teorema do Círclo é tilizado para satisfazer a condição de impenetrabilidade. O cálclo
21 das cargas aerodinâmicas é feito com a tilização das fórmlas generalizadas de Blasis, independente do conhecimento da distribição das pressões na sperfície do corpo. 3 Uma abordagem mais simples para este problema seria considerar o corpo fixo e deixar oscilar o escoamento incidente, conforme o trabalho de Bodstein (005). No entanto, a restrição qe se faz a esta abordagem é qe o flido inteiro oscila com a mesma freqüência e amplitde, o qal não é verdade nma sitação real, principalmente na região da esteira do corpo. O presente trabalho tem como obetivo principal analisar o escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano com propriedades constantes qe se realiza ao redor de m corpo, o qal apresenta m movimento de oscilação de amplitde qalqer sperposto ao movimento principal. O movimento de oscilação do corpo é transversal à direção do escoamento, embora a metodologia desenvolvida possa ser generalizada para ma oscilação qalqer. Escolhe-se m cilindro de seção circlar como a geometria a ser analisada. Deste modo tem-se como finalidades: (a) definir os parâmetros nméricos qe são variáveis na simlação nmérica; (b) calclar a evolção no tempo dos coeficientes de arrasto e sstentação para o cilindro circlar fixo e qando apresenta m movimento de oscilação transversal à direção do escoamento; (c) comparar os resltados nméricos obtidos nesta simlação com valores experimentais e com otros resltados nméricos disponíveis na literatra; (d) preparar o algoritmo desenvolvido neste trabalho, a fim de qe ele sea ma referência para o desenvolvimento de trabalhos ftros. Os resltados para m cilindro circlar fixo são apresentados e comparados com os resltados experimentais e nméricos disponíveis na literatra. No caso do cilindro circlar oscilando transversalmente ao escoamento incidente, a comparação dos resltados é feita apenas considerando os resltados nméricos disponíveis na literatra. É importante salientar qe apesar do número de Reynolds tilizado nas simlações ser alto, nenhma tentativa foi feita de se inclir ma modelagem de trblência, o qe pode ser considerado de acordo com Alcântara Pereira et al. (00). Para o cálclo das cargas aerodinâmicas é tilizada a formlação apresentada por Shintani & Akamats (994), qe leva em consideração a contribição de todos os vórtices presentes na esteira. Nas simlações efetadas as cargas aerodinâmicas integradas, tais como
22 4 os coeficientes de arrasto e de sstentação, a distribição de pressão e o número de Strohal apresentam ma boa concordância com os resltados experimentais. Devido à emissão alternada dos vórtices, o coeficiente de sstentação oscila ao redor de zero, drante toda a simlação nmérica. A amplitde de oscilação deste coeficiente, porém, amenta com a oscilação do cilindro. É possível identificar três tipos de regimes de escoamento relacionados com a freqüência de oscilação. O primeiro tipo, tipo I, é observado para baixas freqüências de oscilação do cilindro; nesta sitação o número de Strohal permanece qase constante. O segndo tipo, tipo II, ocorre para valores intermediários de freqüência de oscilação do cilindro; nesta sitação, aparentemente a freqüência de emissão de vórtices não se correlaciona com a freqüência de oscilação do cilindro. Finalmente, no tipo III observa-se o fenômeno de lock-in onde a freqüência de emissão de vórtices é igalada com a freqüência de oscilação do cilindro. O capítlo apresenta ma revisão bibliográfica referente a movimento de oscilação de corpos e ma revisão sobre a evolção do Método de Vórtices. O capítlo 3 apresenta o modelo tilizado para a simlação do escoamento de m flido viscoso, bidimensional, incompressível e em regime não-permanente em torno de m corpo de forma arbitrária e conhecida, qe se desloca nma região flida de grandes dimensões e qe apresenta m movimento de oscilação transversal à direção do escoamento. A solção nmérica para o modelo proposto é obtida com a tilização do Método de Vórtices Discretos. No capítlo 4 encontra-se o algoritmo de implementação do Método de Vórtices Discretos, com comentários sobre os parâmetros nméricos tilizados na simlação nmérica. Apresenta-se, também, a estrtra do programa comptacional desenvolvido em lingagem FORTRAN, podendo-se encontrar descrições sobre as fnções das rotinas de cálclo tilizadas, qe axiliam o programa principal. No capítlo 5 são apresentados e disctidos os resltados de simlações nméricas feitas com o cilindro circlar. Os resltados nméricos encontrados são comparados com otros resltados nméricos e com resltados experimentais disponíveis na literatra. As conclsões sobre os resltados obtidos nas simlações nméricas e as sgestões para trabalhos ftros estão no capítlo 6.
23 5 No apêndice A apresenta-se a obtenção da Eqação do Transporte da Vorticidade a partir da eqação da continidade e das eqações de Navier-Stokes. Além disso, é feita ma interpretação física da Eqação do Transporte da Vorticidade bidimensional e tridimensional. No apêndice B são mostrados detalhes do cálclo das velocidades indzidas nos painéis planos considerando a oscilação do corpo em estdo. No apêndice C são apresentados os gráficos da distribição de velocidades tangenciais indzidas e vorticidade, dos modelos potencial e de Lamb. Uma das etapas do Método de Vórtices consiste na determinação do campo de velocidades em cada vórtice discreto. Para isto é necessário conhecer a velocidade indzida pelos vórtices discretos ns nos otros, a velocidade devido ao escoamento incidente e a inflência do corpo no campo de velocidades. O número de operações envolvidas no cálclo das velocidades indzidas pelos vórtices, ns nos otros, é da ordem de N V (sendo N V o número de vórtices discretos na nvem). No apêndice D é apresentado m algoritmo eficaz para o cálclo da interação vórtice-vórtice (Alcântara Pereira, 999).
24 Capítlo REVISÃO BIBLIOGRÁFICA. ESCOAMENTO AO REDOR DE UM CORPO OSCILANTE O QUAL SE MOVE COM VELOCIDADE CONSTANTE Neste capítlo são realizados comentários e apresentados os resmos de algns trabalhos disponíveis na literatra, relacionados ao escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano com propriedades constantes ao redor de m corpo oscilante. Primeiramente são citadas as referências tilizadas no desenvolvimento do presente trabalho e posteriormente as referências gerais, qe pela sa importância no estdo, são comentadas... Referências Utilizadas Meneghini & Bearman (995) simlaram nmericamente o escoamento oscilatório de grandes amplitdes sobre m cilindro circlar, porém, limitando o número de Reynolds em 00. O método tilizado para a simlação foi a formlação de vórtices em céllas incorporando ma difsão viscosa.
25 7 Mstto et al. (998) estdaram o escoamento ao redor de m cilindro circlar com e sem rotação. Os resltados apresentados dos coeficientes de arrasto e sstentação e o número de Strohal estão de acordo qando comparados com os valores nméricos e experimentais disponíveis na literatra, porém, a oscilação do corpo transversal à direção do escoamento não foi considerada. Morghental (000) realizo estdos aerodinâmicos em pontes extensas tilizando dois métodos nméricos: o Método de Vórtices Discretos e o Método de Elementos Finitos. O obetivo do trabalho foi verificar a viabilidade e a aplicabilidade das das abordagens nméricas para determinar as propriedades básicas aerodinâmicas e simlar os efeitos da interação flido-estrtra. Concli qe o Método de Vórtices Discretos tem m potencial de se tornar ma ferramenta poderosa para a análise aerodinâmica de corpos rombdos, porém, m tempo adicional será gasto para calibração dos parâmetros nméricos envolvidos na simlação. Silva (004) estdo o escoamento sobre m corpo oscilante com a restrição de peqenas amplitdes de oscilações. Como a relação entre a amplitde de oscilação e o comprimento característico do corpo tende à zero, as condições de contorno impostas sobre a sperfície do corpo foram transferidas para ma posição média da sperfície discretizada do corpo facilitando, assim, a implementação nmérica do problema. As cargas aerodinâmicas distribídas e integradas foram calcladas para m aerofólio NACA 00 e foi realizado m estdo da inflência dos parâmetros nméricos sobre a oscilação do corpo. O presente trabalho em relação ao da Silva (004) considera os efeitos de oscilação de qalqer amplitde sem mdar as matrizes de inflência. A técnica tilizada consiste na mdança de coordenadas do corpo drante a simlação nmérica... Referências Gerais Vários estdos sobre a vorticidade gerada em corpos oscilantes foram realizados nas últimas décadas. Dalton & Chantranvatana (980) estdaram o movimento oscilatório de m cilindro circlar sob o ponto de vista da distribição de pressão média no cilindro. Eles mostraram qe as características do escoamento dependem do número de Kelegan-Carpenter, KC, definido
26 πa na forma KC =. À medida qe o cilindro se move em ma direção, ma esteira de d vórtices é formada; para peqenos valores de KC (inferiores a 0,38) a separação do escoamento não ocorre e não há formação de vórtices. Para valores de KC speriores a 5, m par de vórtices é formado e permanece simétrico não se espalhando drante o movimento. Entretanto, à medida qe o cilindro reverte a direção, o par de agrpamentos se move em direção ao cilindro, e se dissipa rapidamente, devido ao rápido amento da velocidade relativa entre o cilindro e flido. Em segida, m novo par de vórtices é formado e o processo se repete. Para valores de KC entre 5 e 5, m dos agrpamentos de vórtices se torna mais largo qe o otro, mas o espalhamento convencional e alternado ainda ocorre. Este estdo mostra qe a presença da esteira de vórtices no escoamento reverso afeta a distribição de pressão de ma maneira compreensível e previsível. O trabalho concli qe para peqenos valores de KC os resltados da distribição de pressão não se eqivalem aos resltados para o caso do cilindro sem oscilação e com o amento de KC há ma diminição da pressão na parte traseira do cilindro e na esteira. 8 Williamson & Rosko (988) classificaram vários padrões de nvens de vórtices relacionando com dois parâmetros, o comprimento de onda do movimento oscilatório e a amplitde de oscilação do cilindro circlar. Ambos os parâmetros foram adimensionalizados pelo diâmetro do cilindro. Vários padrões de nvens foram observados experimentalmente e foram classificados em termos de vórtices, tais como, dois agrpamentos simples, dois pares de agrpamentos, dois pares de agrpamentos e m agrpamento simples, e etc. Os principais experimentos descritos no artigo foram efetados com número de Reynolds baixos, mais precisamente, Re = 39. Badr et al. (995) estdaram o caso de m cilindro circlar colocado em m flido viscoso oscilando na direção normal ao eixo do cilindro, o qal é considerado em reposo. Assmem-se qe o escoamento se inicio de maneira repentina, a partir do reposo, e permanecem simétrico sobre a direção do movimento. O método tilizado pelos atores para obtenção da solção é baseado na integração das eqações de Navier-Stokes através de m procedimento nmérico. A simlação nmérica foi feita para grandes valores de tempo e para números de Reynolds moderados e altos. A comparação entre os resltados obtidos para escoamentos viscosos e não-viscosos mostram ma melhor concordância para valores maiores de número de Reynolds e número de Strohal. O escoamento médio para grandes tempos foi calclado e apresento boa concordância com previsões anteriores baseadas na teoria da
27 camada limite. Nesse estdo, os resltados mostraram qe a contribição das forças de atrito para o coeficiente de arrasto total C D é relativamente peqena e qe a diferença de fase entre as solções para escoamentos viscosos e não-viscosos é peqena no início do movimento e amenta com o passar do tempo. A razão para isto é qe o campo de escoamento distante do cilindro é livre de vórtices para peqenos incrementos de tempo. Com o amento dos incrementos de tempo, os vórtices são espalhados a partir do cilindro casando mdanças na estrtra do campo de escoamento. Essas mdanças fazem com qe o escoamento distante do cilindro desvie do escoamento potencial. 9. O MÉTODO DE VÓRTICES Vários métodos nméricos aplicam-se na simlação e na análise do escoamento de m flido viscoso ao redor de corpos. Existem métodos qe tilizam descrição eleriana, por exemplo, o Método das Diferenças Finitas e o Método dos Elementos Finitos. Métodos qe tilizam a descrição lagrangeana, por exemplo, o Método de Vórtices e métodos baseados nas descrições eleriana e lagrangeana, ntas (Fronteira Imersa). Estes métodos, com vantagens e desvantagens, são sempre adeqados para ma determinada faixa de aplicação. O Método de Vórtices apresenta algmas características marcantes das qais se destacam: (a) a não necessidade de se criar ma malha de discretização da região flida, (b) o escoamento é descrito apenas nas regiões de interesse, o sea, onde a vorticidade se encontra concentrada: na camada limite e na esteira do corpo e (c) o método não exige ma consideração explícita das condições de contorno a grandes distâncias do corpo. Rosenhead (93) estabelece os fndamentos da metodologia para simlar nmericamente a evolção da vorticidade nm meio flido. Mitos avanços e refinamentos do método, desde então, foram realizados. Ashrst (977), tilizando ma nvem de vórtices discretos, analiso e simlo nmericamente o comportamento e o desenvolvimento de camadas cisalhantes. Lewis (98), Araúo (994a) e Araúo (997b) em ses trabalhos consideraram o escoamento em corpos rombdos, com arestas vivas. Assim, a simlação nmérica tilizando o método de vórtices torna-se bastante simplificada, pois, em primeiro lgar, para estes corpos
28 os pontos de separação estão bem definidos permitindo qe os desprendimentos da vorticidade seam fixados nas adacências dos mesmos e como conseqüência o número de vórtices presentes na nvem é peqeno. 0 A simlação nmérica do escoamento sobre corpos com sperfícies saves (círclos, aerofólios, etc.) apresenta ma dificldade associada ao fato de não se conhecer o ponto de separação, qe pode mdar drante a simlação. Para sperar esta dificldade é necessário simlar os processos de geração e de transporte de vorticidade ao longo de toda a sperfície do corpo, o sea, torna-se necessário simlar o desenvolvimento da camada limite. Vários atores apresentaram alternativas para simlar o escoamento ao redor de m corpo. Uma destas alternativas se baseia no Método dos Painéis (Katz & Plotkin, 99) para o cálclo da inflência do corpo no campo de velocidades no interior da esteira. Nesta linha de estdo Lewis (98) tiliza painéis, sobre os qais, distribem-se vórtices (Método de Martensen). Na simlação nmérica, esta distribição é representada por m único vórtice no ponto médio dos painéis. Este procedimento apresenta imprecisões em mitas sitações. Para contornar parcialmente estas imprecisões Lewis (99) desenvolve m esqema qe tiliza sb-painéis, Kamemoto et al. (995) preferem distribir fontes sobre os painéis e Alcântara Pereira (999) em se trabalho tiliza painéis planos sobre os qais são distribídos vórtices com densidade constante. De acordo com o algoritmo de separação da parte viscosa proposto por Chorin (973), nm mesmo incremento de tempo, assme-se qe os fenômenos de convecção e de difsão da vorticidade podem ser tratados independentemente m do otro. Assim sendo, o transporte da vorticidade por convecção é feito conhecendo-se o campo de velocidades. De ma maneira geral, o campo de velocidades sobre os vórtices discretos é composto pelas contribições do escoamento incidente, pela velocidade indzida pelo corpo e pela velocidade indzida pela nvem de vórtices presente na região flida. A velocidade indzida pelo corpo é determinada tilizando-se o Método dos Painéis. Todos os trabalhos citados até aqi tilizam a Lei de Biot-Savart modificada para o cálclo da velocidade indzida pela vorticidade presente na região flida. Este cálclo representa a parcela dominante dos esforços comptacionais reqeridos nas simlações nméricas. Mstto (998) e Alcântara Pereira (999) desenvolveram m algoritmo qe redzi mito este esforço comptacional. Detalhes deste algoritmo se encontram no apêndice D.
29 Para simlar o processo de difsão da vorticidade tiliza-se o Método do Avanço Randômico. As bases teóricas qe fndamentam o Método de Vórtice, tilizando este método para a simlação da difsão de vorticidade, são apresentadas no trabalho de Einstein (956). Vários trabalhos tilizam o Método do Avanço Randômico para simlar nmericamente os efeitos difsivos (Porthose & Lewis (98); Smith & Stansby (988); Kamemoto et al. (995); Mstto et al. (998); Hirata & Hirata (998); Hirata & Alcântara Pereira (999); etc.). Um problema qe srge relacionado com a conservação da circlação refere-se aos vórtices qe migram para o interior do corpo. Vários esqemas foram propostos para contornar esta dificldade. Algns atores preferem eliminar os vórtices qe migram para o interior do corpo e tilizar a lei de Conservação da Circlação para compensar a vorticidade perdida, como pode ser visto nos trabalhos de Mstto (998), Malta (998) e Alcântara Pereira (999). Ricci (00) preferi refletir para o interior do flido os vórtices discretos qe atravessam a sperfície do corpo. As cargas aerodinâmicas classificam-se, de ma maneira geral, em cargas distribídas (por exemplo, a pressão) e cargas integradas (por exemplo, as forças de arrasto e de sstentação). Lewis (99) determino o coeficiente de pressão pela integração do termo de pressão das eqações de Navier-Stokes. As cargas aerodinâmicas integradas são calcladas integrando-se o campo de pressões. Mstto et al. (998) apresentaram m algoritmo qe permite separar o termo de pressão nas eqações de Navier-Stokes; este algoritmo completa aqele tilizado para a separação dos efeitos viscosos (Chorin, 973). He & S (999) apresentaram ma nova formlação para a determinação da distribição de pressões isolando o termo de pressão das eqações de Navier-Stokes e acrescentando o termo de aceleração convectiva, não considerado por Lewis (99). O cálclo das cargas aerodinâmicas integradas pode, no entanto, ser efetado sem qe haa a necessidade da integração da pressão sobre a sperfície de m corpo isolado. Utilizando-se ma forma estendida das fórmlas de Blasis para escoamento em regime nãopermanente, pode-se obter estas cargas de maneira bastante elegante a partir de elementos conhecidos drante a simlação nmérica, o sea, a intensidade dos vórtices discretos presentes na esteira e as componentes da velocidade nos pontos por eles ocpados (Graham, 980; Sarpkaya, 989).
30 Shintani & Akamats (994) apresentaram m método simples para calclar a distribição de pressões em m escoamento de m flido viscoso em regime não-permanente, baseado no Método dos Elementos de Contorno. Tomando o divergente das eqações de Navier-Stokes, aplicáveis ao escoamento bidimensional, eles obtêm ma eqação de Poisson, em termos da pressão. Em segida mltiplicam esta eqação pela fnção de Green e integram no domínio do escoamento. As integrais são discretizadas e resolvidas nmericamente, em fnção de valores pertinentes ao campo do escoamento como, velocidade, posição dos vórtices no campo e vorticidade gerada sobre a sperfície e a presente na nvem. Alcântara Pereira et al. (00) apresentaram simlações nméricas mais refinadas envolvendo os aspectos de trblência. Como contribições principais deste trabalho tem-se: ma modelagem sb-malha de trblência tilizando-se m modelo de Fnção Estrtra de Velocidade de Segnda Ordem adaptada ao Método de Vórtices Discretos e o desenvolvimento e implementação de m algoritmo nmérico, para inclir, no contexto do Método de Vórtices, a modelagem de trblência. Foram apresentados os resltados para o escoamento ao redor de m cilindro de seção circlar e feitas comparações entre os resltados nméricos obtidos, com e sem modelagem de trblência, com resltados nméricos e experimentais disponíveis na literatra, para valores do coeficiente de arrasto e do número de Strohal.
31 Capítlo 3 FORMULAÇÃO GERAL DO PROBLEMA E O MÉTODO DE VÓRTICES 3. INTRODUÇÃO Este capítlo apresenta a formlação matemática necessária para a simlação nmérica de m escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano, com propriedades constantes, em torno de m corpo de forma arbitrária e conhecida, qe se desloca nma região flida de grandes dimensões. O movimento do corpo é composto de m movimento retilíneo com velocidade constante sperposto m movimento oscilatório de amplitde finita constante λ, vea a figra. U sobre o qal é A e velocidade anglar O Método de Vórtices Discretos é tilizado na simlação nmérica deste fenômeno. Além de simlar o processo de geração, convecção e difsão da vorticidade o algoritmo desenvolvido do Método de Vórtices permite o cálclo das cargas aerodinâmicas atantes sobre m corpo oscilante. Para a simlação do corpo, o algoritmo tiliza o Método de Painéis de fontes com densidade niforme e para simlar a vorticidade são tilizados vórtices discretos de Lamb. Um esqema de avanço de Eler de primeira ordem simla a convecção da vorticidade, ao passo qe o Método de Avanço Randômico é empregado para simlar a difsão da vorticidade. Para o cálclo das cargas aerodinâmicas é tilizada a formlação
32 proposta por Shintani & Akamats (994), qe leva em consideração a contribição de todos os vórtices presentes na esteira FORMULAÇÃO GERAL DO MÉTODO Considere na figra m sistema de coordenadas ( ξ Oη) fixo ao corpo. Nestas condições a sperfície do corpo S C é definida pela eqação escalar: ( ξ, η) 0 F = (3.) Considere em segida m sistema de coordenadas inerciais ( xoy) fixo, em relação à ma posição média ocpada pelo corpo. y η Q(x, y) U y o = Acos( λt) η c O o R 0 ξc x = ξ y = η + A cos ξ ( λt) x ( ) S :F ξ, η =ξ +η R = 0 C 0 S= Sc US S : r0 = x + y Figra Definição do problema
33 Assim sendo, a eqação (3.) pode ser reescrita como: 5 F (, η) ( ξ) ( ξ) ηs ξ = ηc = 0 (3.) ηi Com a finalidade de simplificar os desenvolvimentos e a implementação nmérica assme-se qe o corpo oscila na direção perpendiclar à direção da velocidade incidente. Assim sendo tem-se: y o ( λt) = A cos (3.3) λ = πf C (3.4) onde f C é a freqüência de oscilação do corpo. A sperfície do corpo é definida nas coordenadas inerciais por: [ y (t) + η(x) ] 0 Sc : Fc (x, y, t) = y c 0 = (3.5) e no caso particlar de m corpo simétrico com relação à ξ, tem-se: Fc c 0 = (x, y, t) = y y (t) m η(x) 0 (3.6) Um observador fixo no sistema (,o, y) velocidade V cos componentes são: x deverá observar qe o corpo oscila com ma V x = 0 (3.7a) Vy 0 ( λ t) = y& = A λsin (3.7b) Note qe a adição de otros movimentos oscilatórios lineares o rotacionais não apresenta dificldades conceitais.
34 A grandes distâncias, a montante ( x ), o flido move-se tal qe: 6 = U (3.8a) v = 0 (3.8b) A grandes distâncias, transversalmente ao corpo ( = 0 e y ± ) x o movimento do flido casado pela oscilação do corpo deve decair em intensidade e deve-se ver praticamente: U (3.9a) v 0 (3.9b) A grandes distâncias, a sante ( x + ), tem-se a esteira do corpo qe é inflenciada pela oscilação do mesmo. Nas vizinhanças do corpo a inflência da oscilação do corpo se faz sentir, principalmente, na direção transversal. A energia transferida ao flido, pela oscilação do corpo, é observada pela velocidade indzida nas partíclas de flido. Mesmo desprezando os efeitos da compressibilidade, a intensidade da velocidade indzida deve decair com a distância porqe se observa o espalhamento da energia transferida em todas as direções. A sante espera-se qe os efeitos casados pela oscilação seam somados aos efeitos convectivos associados à velocidade U. Para simlar as sitações descritas anteriormente tiliza-se m caso particlar do Método de Partíclas, qe é o Método de Vórtices. Este método apresenta ma série de vantagens, como a inexistência de ma malha de discretização da região flida, ma exigência dos métodos elerianos, e ses problemas associados como a difsão e instabilidades nméricas. Otra vantagem é a não especificação de condições na esteira, pois o comportamento da esteira é estabelecido atomaticamente e a atenção do estdo é dirigida exclsivamente para as regiões onde a vorticidade se faz presente, o sea, o método não considera as regiões onde nenhma atividade importante acontece. O item 3.6 disctirá mais vantagens deste método sobre os tradicionais métodos elerianos.
35 3.3 HIPÓTESES SIMPLIFICADORAS 7 A formlação matemática desenvolvida baseia-se nas segintes hipóteses simplificadoras, qe se relacionam com a geometria, as propriedades dos flidos e as propriedades do escoamento: H Escoamento bidimensional. O escoamento realiza-se em das dimensões e a região flida é infinita estendendo-se a grandes distâncias do corpo. H Escoamento incompressível. Os efeitos da compressibilidade são desprezados, isto é, o número de Mach assme valores mito menores qe a nidade (em geral, Mach < 0,3). H3 Flido é Newtoniano com propriedades constantes. Como conseqüência tem-se: O desenvolvimento da camada limite e, desde qe haa condições apropriadas, o escoamento descola e há a formação da esteira; A eqação do movimento, qe exprime o Princípio da Conservação da Qantidade de Movimento Linear (PCQML), é representada pelas eqações de Navier-Stokes; A condição de contorno especificada sobre a sperfície do corpo é a condição de aderência qe, por sa vez, pode ser dividida em condição de impenetrabilidade e condição de escorregamento-nlo. H4 A formlação assme qe o escoamento é laminar. Embora as análises qe serão feitas considerem número de Reynolds elevado, os aspectos de trblência não serão levados em consideração. O modelo da Fnção Estrtra de Velocidade de Segnda Ordem poderá ser incorporado à formlação do problema, vea Alcântara Pereira et al. (00) para se levar em conta estes aspectos. H5 A análise será restrita para o escoamento ao redor de m cilindro circlar, embora qalqer otra forma de geometria conhecida possa ser analisada.
36 3.4 EQUAÇÕES E CONDIÇÕES DE CONTORNO QUE DEFINEM O MODELO 8 As eqações qe governam o fenômeno físico descrito no item 3. são representadas pelas expressões matemáticas qe representam os princípios de conservação. O Princípio da Conservação da Massa (Eqação da Continidade) é expresso por: ρ Dρ + ρ = + ρ = 0 (3.0) t Dt A hipótese H (escoamento incompressível) permite qe a eqação da continidade sea simplificada, assmindo a forma: = 0 (3.) Considerando as hipóteses anteriores, o Princípio de Conservação da Qantidade de Movimento Linear é dado pelas eqações de Navier-Stokes: + = p + ν t ρ (3.) onde (, v) é o vetor velocidade, p representa o campo de pressões, ρ é a massa específica e ν o coeficiente de viscosidade cinemática. As condições de contorno na sperfície do corpo são fixadas através da condição de aderência. Desta maneira, a condição de impenetrabilidade exige qe o componente normal da velocidade da partícla sea igal ao componente normal da velocidade da sperfície e a condição de escorregamento-nlo impõe qe o mesmo deve acontecer com os componentes tangenciais destas velocidades: ( n) = ( V n) sobre S C, representa a condição de impenetrabilidade (3.3a) ( τ) = ( V τ) sobre S C, representa a condição de escorregamento-nlo (3.3b)
37 onde n e τ são, respectivamente, os vetores nitários normal e tangencial a sperfície S C em cada ponto e o vetor V (Vx,Vy ) refere-se à velocidade da sperfície do corpo. 9 A grandes distâncias, em S, assme-se qe o escoamento em estdo tende para o escoamento não pertrbado: U (3.4) 3.5 ADIMENSIONALIZAÇÃO DAS EQUAÇÕES A adimensionalização das eqações governantes e das condições de contorno em estdo é importante, pois contribi na formlação e na solção do modelo indicando a dependência entre grandezas e adando na apresentação dos resltados, o sea, mostrando ma relação fncional entre as grandezas e sgerindo como as grandezas devem ser apresentadas. Inicialmente definem-se as grandezas características do fenômeno estdado. Em geral, tem-se qe: b é o comprimento característico, adota-se o diâmetro do cilindro circlar - d -. U é a velocidade característica, adota-se a velocidade do escoamento incidente. T 0 é o tempo característico, onde T 0 = b U Com a tilização das grandezas características, as eqações e sas condições de contorno podem ser adimensionalizadas. As grandezas, adimensionalizadas, tornam-se: x x = coordenadas adimensionalizadas b y y = coordenadas adimensionalizadas b UT0 T0 = tempo adimensionalizado b
38 UΔt Δ t = incremento de tempo adimensionalizado b 0 = componente da velocidade na direção do eixo dos x adimensionalizada U v v = componente da velocidade na direção do eixo dos y adimensionalizada U p ρu p = pressão adimensionalizada Γ Γ = intensidade de m vórtice adimensionalizada bu bλ λ = velocidade anglar adimensionalizada U σ 0 σ 0 = raio do núcleo do vórtice de Lamb adimensionalizado b ρub Re = número de Reynolds μ = b operador Nabla adimensionalizado = b operador Laplaciano adimensionalizado bω ω = vorticidade adimensionalizada U O significado de algmas grandezas ficará mais claro com o desenvolvimento do texto. Com estas definições, as condições de contorno, expressas pelas eqações (3.3a) e (3.3b) e (3.4), podem ser escritas na forma adimensional. ( n) = ( V n) ( τ) = ( V τ) sobre S C sobre S C (3.5a) (3.5b)
39 U (3.5c) como: Do mesmo modo, as eqações (3.) e (3.) são escritas em termos adimensionais = 0 (3.6) t + = p + Re (3.7) Observa-se qe o asterisco () tilizado para indicar ma grandeza adimensionalizada será doravante omitido por comodidade de digitação e apresentação das eqações. 3.6 O MÉTODO DE VÓRTICES O Método de Vórtices, m caso particlar dos Métodos de Partíclas, caracteriza-se pela tilização de m esqema pramente lagrangeano. Este método consiste no acompanhamento individalizado das partíclas, os vórtices discretos, drante toda a simlação nmérica. O Método de Vórtices possi ma série de vantagens qe o tornam atraente em sitações como a do problema proposto. A primeira destas vantagens refere-se ao fato da vorticidade presente na região flida ser discretizada e simlada nmericamente com a tilização de ma nvem de vórtices discretos. A cada incremento de tempo da simlação nmérica, novos vórtices são gerados na fronteira sólida S c da figra. Como conseqüência, dispensa-se a tilização de ma malha, o qe é exigido pelos métodos elerianos clássicos como Método de Diferenças Finitas, Método dos Volmes Finitos e Métodos de Elementos Finitos. Nestes métodos tradicionais ma malha deve ser gerada para discretizar a região o domínio de interesse em sb-regiões, onde as eqações qe definem o modelo devem ser satisfeitas. A segnda vantagem está associada ao fato de qe cada partícla é segida individalmente desde sa geração até o fim da simlação nmérica. Desta maneira, não há a
40 necessidade de se especificar explicitamente as condições de contorno nas fronteiras onde a vorticidade não é gerada. Otra vantagem reside no fato de qe os cálclos são direcionados apenas para as regiões onde a nvem de vórtices se faz presente, o sea, na camada limite e na esteira viscosa. A conservação da circlação deve ser obedecida drante toda a simlação e as intensidades dos vórtices nascentes são determinadas de tal modo qe a condição de escorregamento-nlo dada pela eqação (3.3b) sea satisfeita. Maiores detalhes serão disctidos no algoritmo geral do método descrito no capítlo Eqação do Transporte da Vorticidade O Método de Vórtices é m método nmérico tilizado para a simlação do escoamento de m flido Newtoniano ao redor de m corpo. Este escoamento é governado pelas eqações da continidade simplificada (eqação 3.) e Navier-Stokes (eqação 3.). A análise das eqações de Navier-Stokes, definida pela eqação (3.) mostra a presença do termo de pressão, qe representa certa dificldade na maniplação das eqações, qando se tenta obter ma solção. Tomando-se o rotacional em ambos os lados da eqação e em segida tilizando-se da definição da vorticidade, da eqação da continidade e da hipótese H (escoamento bidimensional), obtém-se a eqação do transporte da vorticidade (Batchelor, 970): ω + ω = ω (3.8) t Re onde é o vetor velocidade do escoamento incidente, Re = Ud é o número de Reynolds ν baseado no diâmetro do cilindro e ω representa, em das dimensões, o único componente não-nlo do vetor vorticidade, qe é definido como: ω = (3.9) Nota-se qe o termo correspondente à variação da vorticidade devido à deformação das linhas de vorticidade, não se faz presente. Vea detalhes no apêndice A.
41 A evolção da vorticidade é governada pela eqação (3.8). O lado esqerdo desta eqação representa a variação temporal da vorticidade, o sea, contém os termos qe representam o fenômeno da convecção da vorticidade, enqanto qe o lado direito representa os efeitos da viscosidade nesta evolção, o sea, contém os termos necessários para descrever a difsão da vorticidade A Separação dos Efeitos Viscosos Nmericamente, cada incremento de tempo, Δ t, é feito de maneira discreta. O Algoritmo de Separação da Parte Viscosa, Viscos Splitting Algorithm, inicialmente proposto por Chorin (973), assme qe, dentro do mesmo incremento de tempo, a difsão da vorticidade pode ser aproximadamente calclada independentemente da sa convecção. Com esta aproximação, a implementação nmérica do Método de Vórtices passa a ser bastante simplificada se a intensidade e a posição dos vórtices forem conhecidas. Assim sendo, o fenômeno da convecção da vorticidade é governado pela eqação: ω + ω = 0 (3.0) t e o fenômeno da difsão da vorticidade é governado pela eqação: t = Re ω ω (3.) Os processos de convecção e de difsão realizam-se scessivamente, dentro de m mesmo intervalo de tempo Δ t e no limite, qando Δt 0, convergem para a eqação (3.8) Convecção da Vorticidade A análise da eqação (3.0) qe governa a convecção da vorticidade mostra qe esta é convectada materialmente, o sea, a vorticidade é transportada por convecção como se fosse ma partícla de flido (Helmholtz, 858):
42 4 Dω ω = + ω = 0 (3.) Dt t Deste modo para a convecção da nvem de vórtices deve-se calclar o campo de velocidades e conseqüentemente, o movimento de m vórtice arbitrário ( i) pode ser calclado integrando-se a eqação para a sa traetória. Assim sendo, o transporte da vorticidade por convecção é escrito em sa forma lagrangeana como: d x dt (i) onde (i) ( x, t) (i) = (3.3) (i) x é o vetor posição do vórtice arbitrário i) (i) (i) ( no instante t e ( x, t) representa a velocidade indzida por todo o escoamento na posição x (i) ocpada pelo vórtice neste instante. Tem-se i =, Nv ; Nv é o número total de vórtices na nvem. (i) (i) Conhecendo-se a velocidade ( x, t), a solção nmérica da eqação (3.3) pode ser obtida pelo esqema de avanço de primeira ordem de Eler qe corresponde a ma primeira aproximação à solção da eqação do avanço convectivo: (i) (i) (i) (i) x (t + Δt) = x (t) + ( x, t)δt (3.4) A velocidade é formada pelas contribições do escoamento incidente, i, pela velocidade indzida pelo corpo, c, e pela velocidade indzida pela nvem de vórtices discretos presente na região flida, v. = + + (3.5) i c v No caso mais comm, o escoamento incidente, i, é representado pelo escoamento niforme, na direção do eixo x. Em termos de componentes, tem-se i = e v i = 0. A contribição do corpo é simlada tilizando o Método dos Painéis (Katz & Plotkin, 99), qe permite simlar corpos de formas arbitrárias e conhecidas. O Método dos Painéis consiste em se discretizar a sperfície de m corpo com a tilização de segmentos (o painéis planos) sobre os qais são distribídas singlaridades. Neste trabalho a sperfície do corpo é
43 simlada por m connto de painéis planos sobre os qais se distribem fontes com densidade niforme, σ ( x), vea a figra (Katz & Plotkin, 99). 5 y σ( x ) = niforme x Figra Distribição de fontes com densidade niforme Para m sistema de coordenadas fixo nm painel, conforme a figra 3 (Katz & Plotkin, 99), os componentes e v da velocidade indzida por ma distribição niforme de fontes sobre m ponto P são: σ r σ r = ln (3.6a) π r 4π r ln = σ v = ( θ θ ) (3.6b) π
44 6 y P ( x, y) r r θ θ x A seginte eqação: Figra 3 Representação de m painel genérico do corpo [ ]{ SIGMA} { RHSS} COUPS = (3.7a) o a sa forma matricial eqivalente: 0.5 K K 3... K m K K K m Km σ RHSS K m σ RHSS K 3m σ 3 = RHSS σ m RHSS 3 m (3.7b) constiti m sistema linear de eqações algébricas, ca incógnita representa a densidade de fontes, onde: [ COUPS ]: é a matriz de inflência. Os coeficientes K i, representam a velocidade normal indzida no ponto de controle de m painel genérico i por ma distribição niforme de fontes com densidade nitária localizada sobre o painel ; { SIGMA }: é o vetor incógnita;
45 { RHSS }: é o vetor colna lado direito, vea mais detalhes no capítlo 4 e no apêndice B. 7 O cálclo da velocidade indzida pelo corpo é feito no sistema de coordenadas fixas ao corpo ( ξoη). Portanto, a velocidade do escoamento na sperfície do corpo é escrita como: ξ,η; t) = Ui y& (t) (3.8) ( 0 A eqação (3.8) mostra qe o efeito da oscilação do corpo, representado pelo componente, provoca ma distribição de singlaridades adicional na sperfície do corpo. Natralmente, as velocidades indzidas devido a estas singlaridades, também inflenciam no cálclo dos efeitos convectivos e das cargas aerodinâmicas. A velocidade indzida pelo corpo, de acordo com os cálclos do Método dos Painéis, é c (ξ, η), vc(ξ, η), qe representa a velocidade indzida no vórtice ( i), indicada por [ ] localizado em ( ξ,η), conforme mostrado na figra 4. y η η (i) vc(ξ,η) c(ξ,η) U y o = Acos( λt) O o ξ ξ x Figra 4 Velocidade indzida pelo corpo Mas como ( (t) = ξ e (i) (t) = y (t) + η, escreve-se qe: x i) y 0 c i) ( (x, y, t) = c(ξ,η;t) (3.9a)
46 i) vc (x, y, t) = vc( ξ, η; t) + y 0 (t) (3.9b) ( & 8 O cálclo da velocidade indzida pela nvem de vórtices discretos presente na região flida é a etapa qe consome maior tempo de CPU, pois o número de operações realizadas pelo processador é da ordem do qadrado do número de vórtices discretos presentes no escoamento. De maneira geral, os componentes nas direções x e y da velocidade total, indzida no vórtice k pelos demais vórtices são calclados pelas expressões: N = V k Γ NV U Vk, = k (3.30a) N = V k Γ NV VV k, = k v (3.30b) As expressões acima revelam qe m vórtice não indz velocidade sobre ele mesmo. O componente x da velocidade indzida em m vórtice k por m vórtice (de intensidade nitária), é igal ao componente x da velocidade indzida no vórtice pelo vórtice k, com sinal contrário. De forma análoga, o componente y da velocidade indzida em m vórtice k por m vórtice (de intensidade nitária), é igal ao componente y da velocidade indzida no vórtice pelo vórtice k, com sinal contrário. Observando esta particlaridade, Mstto et al. (998) e Alcântara Pereira (999) desenvolveram m algoritmo qe calcla apenas os componentes em x e em y da velocidade indzida no vórtice k pelo vórtice. Maiores detalhes são apresentados no apêndice D. As solções para as eqações (3.30a) e (3.30b) implicam na tilização de m modelo de vórtice qe incorpora m núcleo de raio σ o, ao vórtice livre. Vários modelos podem ser adotados com esta finalidade os qais foram bastante explorados por (Hirata & Alcântara Pereira, 999). O modelo adotado no presente trabalho é o vórtice de Lamb (Panton, 984) o qal assme ma distribição normal para a vorticidade no interior do núcleo do vórtice. Mais
47 detalhes podem ser vistos no trabalho de Mstto, (998) e de Alcântara Pereira, (999). Também, no apêndice C são apresentados os gráficos da distribição de velocidades tangenciais indzidas e vorticidades dos modelos potencial e de Lamb Difsão da Vorticidade O processo de difsão da vorticidade é o responsável pela manifestação dos efeitos da viscosidade. Na eqação (3.) este fato está implícito através do número de Reynolds. A solção da eqação qe governa a difsão da vorticidade é obtida através de m esqema pramente lagrangeano. A alternativa tilizada é representada pelo Método de Avanço Randômico, qe foi inicialmente obtida por Einstein (956) e tilizado por vários pesqisadores como, por exemplo, Lewis (99). Com este método o processo de difsão da vorticidade deixa de ser estritamente determinístico, aliás, ma característica dos escoamentos com número de Reynolds elevado. Considere m vórtice ( i) da nvem, qe no instante ( t), encontra-se localizado em (i) x (t). O Método de Avanço Randômico exige qe cada vórtice da nvem sofra m avanço randômico definido por Z ( x, ) d d y d. Se o avanço convectivo for calclado tilizando-se o esqema de avanço de primeira ordem de Eler dado pela eqação (3.4), o vórtice ( i) deverá ser posicionado como (i) (i) (i) (i) x (t + Δt) = x (t) + ( x, t)δt + Z d (3.3) Os componentes x d e definidos como (Alcântara Pereira, 00): y d do vetor avanço randômico Z d, na forma adimensional, são 4Δt ( d = ln [ cos( πq) ] (3.3a) Re P x i) 4Δt ( d = ln [ sin( πq) ] (3.3b) Re P y i) onde P e Q são números randômicos tal qe 0 ( P e Q) < <.
48 3.6.5 Geração da Vorticidade 30 A vorticidade é também gerada sempre qe m flido viscoso se movimenta nto a ma fronteira sólida. As eqações de Navier-Stokes (3.) podem ser colocadas na seginte forma: D Dt = p υ ω ρ (3.33) Como o escoamento é bidimensional (hipótese H) e spondo qe o escoamento realiza-se no semi-plano sperior e qe o eixo real representa ma das sperfícies sólidas ( y = 0), onde a condição de aderência é especificada, tem-se: p x ω = μ y (3.34) A eqação (3.34) governa a geração da vorticidade nma sperfície sólida coincidente com o eixo dos x. A derivada do lado direito da eqação representa o flxo de vorticidade em y = 0. Como não existe flido para y < 0, este flxo de vorticidade representa a qantidade de vorticidade qe está sendo gerada na sperfície. A eqação (3.34) permite qe esta vorticidade gerada sea qantificada pelo se lado esqerdo. Em otras palavras, se o gradiente de pressão é favorável haverá ma geração de vorticidade, á qe o flxo passa a ser positivo. Alternativamente, se o gradiente de pressão é desfavorável haverá ma destrição de vorticidade, á qe o flxo passa a ser negativo. A figra 5 ilstra graficamente este processo.
49 3 y Flxo de vorticidade através da fronteira ω y aderência x Sperfície sólida y = 0 Gradiente de pressão ao longo da fronteira p x Figra 5 Flxo de vorticidade através da parede Na implementação nmérica este processo é eqivalente à tilização da condição de escorregamento-nlo dada pela eqação (3.3b). Para garantir a condição de escorregamento-nlo sobre o ponto de controle de cada painel distribem-se vórtices nascentes de Lamb, (vea apêndice C), de acordo com a figra 6: Vórtice de Lamb σ 0 Painél ε Ponto de Controle Figra 6 Vórtice de Lamb Além da posição de geração dos vórtices, otras variáveis importantes são: a camada protetora (pro) e o percental de deslocamento da posição de geração dos vórtices em relação à sperfície discretizada (gap). A camada protetora consiste em envolver o corpo de forma a determinar ma região dentro da qal não é permitida a permanência de vórtices. Esta camada é localizada dentro de ma região retanglar e, qalqer vórtice qe ltrapassar esta região tem sa posição investigada com a finalidade de averigar se o mesmo se encontra no interior
50 da camada protetora o não; em caso positivo, a singlaridade é deslocada para fora do corpo de ma posição determinada pelo valor + ( ε gap) ε em relação à sperfície discretizada. 3 Algns atores, como Ricci (00), tilizam-se de ma camada protetora próxima à sperfície do corpo, qe em princípio evitaria qe os vórtices discretos migrassem para o interior do corpo. Otros atores preferem eliminar os vórtices e tilizar a Lei de Conservação da Circlação para compensar a vorticidade perdida (Alcântara Pereira, 00). A alternativa qe é adotada neste trabalho consiste na tilização de ma camada protetora e reflexão dos vórtices de volta ao escoamento. É importante frisar qe qalqer qe sea o esqema adotado, o Princípio da Conservação da Circlação não pode ser violado. O balanço da vorticidade na região flida deve ser constante drante toda a simlação nmérica. De maneira similar à montagem da eqação matricial de fontes, a seginte eqação: [ ]{ GAMMA} { RHSV} COUPV = (3.35a) o a sa forma matricial eqivalente: K K K... K 3 m K K K K 3... m K K K K m m 3m... mm Γ RHSV Γ RHSV Γ3 = RHSV Γm RHSV 3 m (3.35b) constiti m sistema linear de eqações algébricas, ca incógnita representa a intensidade de vórtices, onde: [ COUPV ]: é a matriz de inflência. Os coeficientes K i, representam a velocidade tangencial indzida no ponto de controle de m painel genérico i, por m vórtice de Lamb com intensidade nitária, localizado sobre o painel ; { GAMMA }: é o vetor incógnita;
51 { RHSV }: é o vetor colna lado direito, qe para o escoamento potencial, leva em conta a contribição do escoamento incidente. A partir da presença de vórtices livres no meio flido, este vetor é atalizado conforme descrito no capítlo Conservação da Circlação Na teoria potencial a condição de conservação da circlação é imposta ao longo do domínio flido Ω, e é expressa por: Γ = ds = 0 (3.36) C Considerando a nvem de vórtices, a conservação global da circlação é calclada pela eqação (4.5) conforme apresentado no capítlo Cargas Aerodinâmicas Entende-se como carga aerodinâmica, a ação qe o flido em movimento ao redor de m corpo, exerce sobre sa sperfície. As grandezas de maior interesse relacionadas com as cargas aerodinâmicas são: a distribição de pressões sobre a sperfície do corpo (cargas distribídas) e as forças de arrasto e de sstentação (cargas integradas). O cálclo do campo de pressões é feito considerando a metodologia proposta por Kamemoto (993), onde se aplica o operador divergente nas eqações de Navier-Stokes e com o axílio da eqação da continidade obtém-se ma eqação de Poisson para a pressão, qe é resolvida tilizando-se m Método de Painéis. Com este procedimento, o campo de pressões, em qalqer ponto da região flida, pode ser calclado integrando-se a fnção de Bernolli, definida por Uhlman (99) como: Y = p +, = (3.37)
52 Shintani & Akamats (994) apresentaram otra formlação qe pode ser melhor combinada com o Método de Vórtices Discretos, ma vez qe torna-se necessário conhecer apenas o campo de velocidades e o campo de vorticidade. A eqação é dada por: 34 HY i SC Y G i n ds = G i ( ω) dω ( G i ω) nds (3.38) Ω Re SC onde: H = em Ω (no domínio do escoamento) o H = 0.5 em S C (na sperfície do corpo) e G corresponde à solção fndamental da eqação de Laplace. As integrais presentes na eqação (3.38) são resolvidas nmericamente. No trabalho de Ricci (00) pode-se encontrar a dedção da eqação qe permite determinar o valor da pressão no ponto i : HY i + S π n x ( x x i ) + n y ( y yi ) ( x x ) + ( y y ) i i YdS = Ω π v( x x i ) ( y yi ) ( x x ) + ( y y ) i i ωdω Re S π n y ( x x i ) n x ( y yi ) ( x x ) + ( y y ) i i ωds (3.39) qe discretizada, para ser resolvida nmericamente, toma a forma: HY i + π M = ; i n x( x x i ) + n y( y yi ) ( x x ) + ( y y ) i i ΔS Y = π ( x x i ) ( y yi ) ( x x ) + ( y y ) v πre ( x x ) n ( y y ) Nv M y i x Γ + = i i = ; i i n i i ( x x ) + ( y y ) ΔS γ (3.40)
53 35 A eqação (3.39) pode ser resolvida pelo Método de Painéis agrpando o primeiro e o último somatório nas matrizes de inflência Ap (matriz de pressão) e Ad (matriz lado direito), respectivamente. Assim, a eqação (3.40) pode ser escrita do seginte modo: π M = Ap v ( x x i ) ( y yi ) ( x x ) + ( y y ) Nv M i, Y = Γ + Adi, γ π = i i = (3.4) O lado direito da eqação anterior, por sa vez, pode ser escrito da seginte forma: ( x x i ) ( y yi ) ( x x ) + ( y y ) v Ld i = Adi, γ (3.4) π Nv M Γ + = i i = A aplicação da eqação (3.4) nos M painéis qe discretizam a sperfície do corpo condz ao seginte sistema de eqações matriciais: [ ]{ Y} { Ld} Ap = (3.43) Uma vez conhecidos os valores da incógnita Y para os M painéis, obtêm-se os valores do coeficiente de pressão para cada segmento: C = Y (3.44) P i i + á qe a velocidade sobre a sperfície do corpo é nla. As forças aerodinâmicas são obtidas pela integração da pressão ao longo do corpo. A força de arrasto ata em cada painel na direção do escoamento incidente, ao passo qe a força de sstentação ata em cada painel na direção normal a este. Assim, as referidas forças são dadas por: M ( p p ) D = ΔS sinθ (3.45) = M ( p p ) = L = ΔS cosθ (3.46)
54 onde p é a pressão no ponto de controle do painel e p é a pressão do escoamento não pertrbado. A adimensionalização das eqações anteriores leva à obtenção dos coeficientes de arrasto e sstentação, respectivamente dados por: 36 M = M ( p p ) ΔS sinθ = C = C ΔS sinθ (3.47) D = P M = M ( p p ) ΔS cosθ = C = C ΔS cosθ (3.48) L = P
55 Capítlo 4 IMPLEMENTAÇÃO NUMÉRICA 4. INTRODUÇÃO Este capítlo apresenta o algoritmo de implementação do Método de Vórtices Discretos tilizado para a simlação nmérica do escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano, com propriedades constantes em torno de m corpo oscilante de forma arbitrária e conhecida, qe se desloca nma região flida de grandes dimensões. Apresenta-se, também, a estrtra do programa comptacional desenvolvido em lingagem FORTRAN e as descrições sobre as fnções das rotinas de cálclo tilizadas, qe axiliam o programa principal. 4. ALGORÍTMO GERAL DO MÉTODO Para a simlação nmérica do problema formlado no capítlo 3 foi desenvolvido o programa comptacional OSCILLATION.FOR em lingagem FORTRAN, baseado no programa Método de Vórtices Discretos desenvolvido por Alcântara Pereira (999). As principais modificações foram a inclsão das singlaridades do tipo fontes, m novo sistema de eqações matriciais para a geração dos vórtices de Lamb e as rotinas de transferência de
56 coordenadas. O diagrama em blocos do algoritmo qe implementa esta solção é mostrado na figra INDATA DATAPREP COUPS RHSS COUPV RHSV MODCOUP GAUSSPIV (S) GAUSSPIV (V) GENERATION POS_BODY COMP_UM_VM M A I N. F 5 O R DIFUSION CONVEC POS_BODY REFLECTION POS_INERTIAL PRINT POS_BODY COMP_UM_VM RHSV CONSERV RHSS 3 7 GAUSSPIV (V) GAUSSPIV (S) 4 8 MOD_M COMP UC VC 5 ITERATIVO PRESSURE 6 9 AVERAGE ITERATIVO Figra 7 Algoritmo de implementação do programa OSCILLATION.FOR A segir será explicada a finalidade de cada rotina tilizada no programa OSCILLATION.FOR para qe ele possa ser compreendido por m sário.
57 Rotina INDATA 39 Esta rotina tem como finalidade a leitra de todos os dados necessários para a simlação nmérica do escoamento ao redor de m corpo oscilante de forma qalqer e conhecida. O arqivo de entrada INPUT.DAT é aberto pela rotina para a leitra dos segintes parâmetros tilizados no programa comptacional: M => número de painéis planos qe representam a sperfície discretizada do corpo stop => número total de incrementos de tempo save => intervalo de tempo para salvar os arqivos de saída start => instante de tempo para o início do cálclo das cargas aerodinâmicas U α Δt ε pro => velocidade do escoamento incidente => ânglo de ataqe do escoamento incidente => incremento de tempo => posição de desprendimento dos vórtices sobre cada painel plano => espessra da camada protetora gap => deslocamento de cada ponto de controle em direção a sperfície real σ 0 => raio do núcleo do vórtice de Lamb Re A λ => número de Reynolds => amplitde de oscilação => velocidade anglar Em segida, no arqivo PANELS.DAT são lidas as coordenadas dos pontos extremos de cada painel do corpo em análise.
58 Rotina DATAPREP.FOR 40 A rotina DATAPREP.FOR recebe o valor dos pontos extremos de cada painel e a partir deles calcla para cada painel o valor do ponto de controle, do ânglo de orientação, o comprimento do painel e os pontos de desprendimento do vórtice discreto de Lamb. Esta rotina também imprime no arqivo DISCRET.DAT a geometria discretizada do corpo. Rotina COUPS.FOR A próxima etapa consiste do cálclo dos coeficientes da matriz de inflência de fontes pela rotina COUPS.FOR. Estes coeficientes são mostrados na eqação matricial (3.7b), qe pode ser escrita como: M [ K( Sk,S )]{ σ } = { RHSS(Sk )} = (4.) Na eqação matricial acima ( S, ) K é ma matriz de inflência, onde cada elemento k S da matriz representa a indção de velocidade normal sobre o ponto de controle do painel genérico k por todos os otros painéis de fontes. Para a montagem dos coeficientes assmese qe a densidade de cada fonte é igal a nidade. Os coeficientes da matriz de inflência de fontes não sofrem variação ao longo da simlação nmérica, porqe dependem apenas da geometria do corpo. No presente trabalho os coeficientes da matriz de inflência de fontes são calclados no sistema de coordenadas fixo ao corpo. A matriz de inflência é montada impondo-se a condição de impenetrabilidade (condição de Nemann) sobre o ponto de controle de cada painel. Rotina RHSS.FOR O lado direito da eqação matricial é m vetor colna de M elementos, qe leva em consideração a velocidade normal indzida pelo escoamento incidente e pela nvem de vórtices discretos sobre o ponto de controle de cada painel. Para m painel genérico M, o valor de (S ) RHSS k na primeira vez em qe ele é calclado, no instante t = 0( Δt), considera apenas a indção de velocidade normal do escoamento incidente, ma vez qe não existe vórtice livre no meio flido.
59 Drante o processo iterativo, o vetor colna lado direito da eqação matricial (4.) corresponde ao somatório da velocidade normal indzida pelo escoamento incidente (, v), vea apêndice B, e pelos vórtices discretos de Lamb ( k,, v k, ) no ponto de controle do painel genérico k com ânglo de inclinação θ k. No problema analisado tem-se a seginte eqação para o vetor colna lado direito de fontes: { sin(θ ) ( v + y ) cos(θ ) + sin(θ ) v cos(θ )} RHSS(S ) = & (4.) k k o k k, k k, k 4 A inflência da oscilação do corpo está representada na eqação (4.) pelo termo y& 0 co valor é calclado pela eqação (3.7b). Rotina COUPV.FOR A próxima etapa consiste do cálclo dos coeficientes da matriz de inflência dos vórtices nascentes de Lamb pela rotina COUPV.FOR. Estes coeficientes são mostrados na eqação matricial (3.35b), qe pode ser escrita como: M [ K( Sk,S )]{ Γ} = { RHSV(Sk )} = (4.3) Na eqação matricial acima ( S, ) K é ma matriz de inflência, onde a linha k k S representa a indção de velocidade tangencial sobre o ponto de controle do painel genérico k por todos os vórtices de Lamb nascentes. Estes vórtices discretos de Lamb são posicionados tangenciando o ponto de controle dos painéis de acordo com ma linha normal ao ponto de controle do painel e qe passa pelo centro do núcleo do vórtice, conforme mostra a figra 6. No instante inicial, 0( Δt) t =, e a cada novo incremento de tempo, Δ t, há a geração de vorticidade sobre a sperfície discretizada do corpo. Deste modo, o sistema de M eqações algébricas e M incógnitas mostrado na eqação (4.3), deve ser resolvido. Os coeficientes da matriz de inflência de vórtices não sofrem variação ao longo da simlação, porqe dependem apenas da geometria do corpo. No presente trabalho os coeficientes da matriz de inflência de vórtices são calclados no sistema de coordenadas fixo ao corpo. A matriz de inflência é montada impondo-se a condição de escorregamento-nlo sobre o ponto de controle de cada painel.
60 Rotina RHSV.FOR 4 O lado direito da eqação matricial é m vetor colna de M elementos. Para m painel genérico k, o valor de RHSV(S k ) na primeira vez em qe ele é calclado, no instante t = 0( Δt), considera apenas a indção de velocidade tangencial do escoamento incidente, vea apêndice B, ma vez qe não existe vórtice livre no meio flido. Em todos os incrementos de tempo segintes, este vetor é atalizado devido aos z vórtices discretos de Lamb qe indzem velocidade ( k,, v k, ) sobre o ponto de controle do painel genérico k com ânglo de inclinação θ k. No problema analisado tem-se a seginte eqação para o vetor colna lado direito de vórtices: RHSV(S k { cos( θ ) ( v + y ) sin( θ ) cos( θ ) v sin( θ )} ) = & (4.4) k o k k, k k, k Novamente, a inflência da oscilação do corpo representada na eqação (4.4) pelo termo y& 0 tem se valor calclado pela eqação (3.7b). Rotina MODCOUP.FOR Esta rotina acrescenta linha e colna na matriz de inflência de vórtices, dada pela eqação (4.3), para imposição da conservação da circlação global, obedecendo a seginte eqação: M NV ( Γ ) + ( Γk ) = 0 vórtices nascentes vórtices livres = k= (4.5) Aproveita-se esta rotina para o cálclo dos coeficientes da matriz de pressão COUPP. Esta matriz corresponde ao termo do lado esqerdo da eqação (3.40) representado por Ap i,. Rotina GAUSSPIV.FOR As eqações matriciais (3.4), (4.) e (4.3) são então resolvidas pela rotina GAUSSPIV.FOR, qe tiliza o Método de Eliminação de Gass com Condensação Pivotal
61 Parcial, fornecendo para o programa principal o vetor colna incógnita com as densidades fontes e intensidades de vórtices sobre cada painel. 43 Rotina GENERATION.FOR A vorticidade gerada sobre a sperfície do painel plano genérico, em cada incremento de tempo, sofre m processo de agltinação instantânea formando m vórtice discreto. Cada vórtice discreto qe é gerado localiza-se a ma peqena distância ε sobre ma normal qe passa pelo ponto de controle do painel (figra 6). Este processo é denominado de difsão primária (Alcântara Pereira, 999). O vórtice discreto formado possi m núcleo viscoso e o modelo qe vem sendo tilizado é o modelo original do vórtice de Lamb (Panton, 984). A rotina GENERATION realiza o processo de desprendimento dos vórtices discretos. Rotina COMP_UM_VM.FOR A rotina COMP_UM_VM.FOR é acionada para calclar os componentes da velocidade indzida no ponto de controle dos painéis planos devidos à presença dos vórtices discretos desprendidos e dos vórtices discretos presentes na nvem de vórtices, para a correção dos vetores colna das eqações (4.) e (4.4). Rotina COMP_UC_VC.FOR A COMP_UC_VC.FOR realiza o cálclo dos componentes da velocidade total indzida em cada vórtice discreto de Lamb da nvem, levando-se em conta a inflência do escoamento incidente, do corpo presente no escoamento (representado por painéis de fontes com distribição niforme de densidade) e de todos os vórtices discretos qe formam a nvem em cada instante de tempo. Nesta rotina tem-se o cálclo, portanto, do campo de velocidades. Rotina PRESSURE.FOR O cálclo das cargas aerodinâmicas integradas e das distribídas é feito pela rotina PRESSURE.FOR, qe calcla a pressão instantânea atante no ponto de controle de cada painel mais as forças instantâneas resltantes de arrasto e sstentação. Este cálclo é baseado na formlação de Shintani & Akamats (994), descrita no Capítlo 3.
62 Rotina DIFFUS.FOR 44 A rotina DIFFUS.FOR realiza o processo de difsão dos vórtices através do Método de Avanço Randômico. Em cada instante de tempo, cada vórtice discreto da nvem tem associado dois números randômicos P e Q entre 0.0 e.0. Vea as eqações (3.3a) e (3.3b). Rotina CONVEC.FOR De posse do campo de velocidades (cálclo dos componentes da velocidade indzida em cada vórtice discreto da nvem) o avanço convectivo de cada vórtice discreto é simlado com a tilização de m esqema de avanço de primeira ordem de Eler mostrado pela eqação (3.4). Rotina REFLECTION.FOR As velocidades indzidas pelo corpo não estarão corretamente calcladas para pontos de controle extremamente próximos ao corpo. Ricci (00) em se trabalho mostro qe ao se tilizar painéis de fontes com densidade niforme os erros conservam-se da ordem de %, qando o ponto de controle é deslocado para 3% ( gap = 0. 3) da distância entre o painel e a sperfície do corpo, para pontos sitados fora de ma camada protetora qe corresponde a ma distância ao painel igal o sperior a 40% do se comprimento ( pro = 0. 40). Ao se realizar a simlação nmérica dos efeitos da difsão e da convecção da vorticidade algns vórtices discretos podem migrar para o interior do corpo. O reposicionamento (reflexão) destes vórtices discretos na região flida é realizado pela rotina REFLEC.FOR, ma rotina axiliar. Rotina PRINT.FOR A rotina PRINT.FOR realiza a gravação em arqivos de saída dos resltados instantâneos importantes da simlação nmérica. Estes arqivos contêm a posição de cada vórtice da nvem, à distribição instantânea de pressões ao redor da sperfície discretizada do corpo e os valores das cargas aerodinâmicas integradas (força de arrasto e força de sstentação).
63 Rotina CONSERV.FOR 45 Para realizar a conservação da circlação do escoamento, a rotina CONSERV.FOR acrescenta zero em RHSV (M + ) do vetor colna do lado direito vórtice e faz M = M +. Rotina MODM.FOR Após a resolção da eqação (4.3) com as novas condições descritas, a rotina MOD_M.FOR é acionada para realizar a correção do número M de painéis, qe foi alterado pela rotina anterior (CONSERV.FOR). Esta rotina, também imprime no arqivo CONTROL.DAT, os valores do instante de tempo (step) e do valor extra obtido na resolção da eqação matricial de vórtices devido à imposição da conservação da circlação conforme a eqação (4.5). Rotina POS_BODY.FOR Esta rotina é responsável por modificar as coordenadas de todos os vórtices para o referencial do corpo (coordenadas fixas ao corpo). (t) = η y (t) (4.6) (i) y 0 Rotina POS_INERTIAL.FOR Esta rotina é responsável por modificar as coordenadas de todos os vórtices para o referencial inercial, conforme a eqação (4.6): (t) = η + y (t) (4.7) (i) y 0 Rotina AVERAGE.FOR Assim qe o último incremento de tempo for conclído, a rotina AVERAGE.FOR é acionada. Ela é responsável pelo cálclo e impressão dos coeficientes de arrasto e sstentação médios atantes sobre o corpo e da distribição de pressão média sobre o corpo (entre START e STOP).
64 46 Capítlo 5 ANÁLISE DOS RESULTADOS DA SIMULAÇÃO NUMÉRICA 5. INTRODUÇÃO Neste capítlo apresentam-se os resltados da simlação nmérica do escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano de propriedades constantes em torno de m corpo oscilante, qe se desloca nma região flida de grandes dimensões. Embora a metodologia desenvolvida se apliqe a corpos de qalqer forma e modo de oscilação, os resltados apresentados referem-se a m cilindro circlar oscilando na direção perpendiclar ao movimento. Os resltados obtidos para m cilindro circlar fixo são apresentados e comparados com os resltados da literatra (experimentais e nméricos) e esta comparação servi para ma validação inicial do algoritmo proposto no capítlo 4. A inflência da oscilação foi analisada comparando-se o número de Strohal em diversas faixas de freqüências, o qe reslto na identificação de três tipos de regime de escoamento, à medida qe a freqüência de oscilação amenta.
65 5. PARÂMETROS UTILIZADOS NA SIMULAÇÃO NUMÉRICA 47 Em todas as simlações nméricas consideram-se das classes de parâmetros nméricos. Uma relacionada com o método nmérico e otra relacionada com o fenômeno físico. No presente estdo, os parâmetros relacionados com o fenômeno físico são: a) Número de Reynolds: Re Altos valores de números de Reynolds compreendem a faixa de interesse prático. Para esta faixa a escolha apropriada para a difsão da vorticidade é o Método de Avanço Randômico. Os valores adotados para o número de Reynolds devem ser altos e sficientes para os efeitos de simlação nmérica pelo Método de Vórtices Discretos. Valores da ordem 5 6 de 0 < Re < 0 mostram-se apropriados para esta formlação proposta, no caso do cilindro circlar. b) Ânglo de ataqe (α) O ânglo de ataqe (α) é considerado nas simlações de perfis aerodinâmicos. No presente estdo (cilindro circlar) considera-se α = 0. c) Raio do Núcleo do Vórtice de Lamb ( σ 0 ) Em todas as simlações nméricas feitas decidi-se pela escolha de valores igais para o raio do núcleo do vórtice de Lamb ( σ 0 ) e para a posição de nascimento dos vórtices discretos ( ε), ao longo da sperfície do cilindro circlar. Esta escolha permite qe m vórtice discreto, qe é gerado, se localize a ma peqena distância ( ε) sobre ma normal qe passa pelo ponto de controle do painel (Alcântara Pereira, 999), vea a figra 6. O raio do núcleo do vórtice de Lamb pode ser estimado através da eqação (5.), (Mstto, 998). Vea apêndice C. Δt σ 0 = 4,48364 (5.) Re
66 Considerando Δ t = 0, 05 e 48 5 Re = 0 temos para o cilindro circlar o valor do raio do núcleo do vórtice de Lamb de σ 0 = 0, 003. Os parâmetros relacionados com a simlação nmérica são: a) Número de painéis A sperfície do cilindro circlar é discretizada e representada por m número M finito de painéis planos, sobre os qais se distribem singlaridades do tipo fontes. Em todos os casos analisados neste capítlo são tilizados M = 00 painéis inscritos para a discretização da sperfície do corpo sendo qe todos os painéis possem comprimentos igais adimensionalizados pelo diâmetro do cilindro, conforme mostrado na figra 8. η Painél Painél 0 ξ Painél 00 Figra 8 Detalhe da distribição de painéis no cilindro circlar b) Incremento de Tempo Nas simlações nméricas apresentadas opto-se por fixar m valor para o incremento de tempo compatível com a ordem de grandeza do esqema de avanço de primeira ordem de Eler tilizado no processo convectivo da vorticidade. O valor adotado é de Δ t = 0, 05 (adimensional). O incremento de tempo foi calclado pela expressão fornecida por (Mstto et al., 998): kπ Δt = (5.) M
67 49 onde 0 k e M é o número de painéis qe discretizam a sperfície do corpo e a sperfície plana. c) Posição de Desprendimento dos Vórtices Discretos ( ε) Conforme disctido nos parâmetros associados ao fenômeno físico, a posição de nascimento dos vórtices discretos ( ε) apresenta o mesmo valor nmérico do raio do núcleo do vórtice de Lamb ( σ 0 ), permitindo assim, qe os vórtices nascentes esteam sempre posicionados tangenciando o ponto de controle dos painéis planos, conforme mostrado na figra 6. Logo, tem-se ε = σ 0 = 0, 003. Resmindo, na tabela são apresentados os segintes valores adotados como dados de entrada: Tabela Parâmetros tilizados na simlação nmérica Parâmetro M = 00 stop = 800 save = 8 start = 00 U = α = 0 Δt = 0,05 ε = 0,003 pro = 0,40 gap = 0,3 σ 0 = 0,003 Re = Descrição Número de painéis inscritos distribidos no corpo Número total de avanços de tempo na simlação Número de avanços de tempo para gerar o arqivo da nvem de vórtices, o sea, a cada 8 passos da simlação é gerado m arqivo com as posições dos vórtices Avanço de tempo inicial para o cálclo da distribição de pressão Velocidade incidente adimensionalizada Ânglo de ataqe Incremento de tempo Posição de Desprendimento dos Vórtices Discretos Camada protetora Aste do ponto de controle do painel Raio do Núcleo do Vórtice de Lamb Número de Reynolds
68 5. CILINDRO CIRCULAR Cilindro circlar sem oscilação Inicialmente o programa OSCILLATION.FOR foi tilizado para a simlação nmérica do escoamento bidimensional, incompressível e em regime não-permanente de m flido Newtoniano de propriedades constantes em torno de m cilindro circlar sem oscilação, qe se desloca nma região flida de grandes dimensões. Os resltados nméricos obtidos para as cargas aerodinâmicas integradas (forças de arrasto e de sstentação) e para as cargas aerodinâmicas distribídas (campo de pressões) foram comparados com otros resltados nméricos e experimentais disponíveis na literatra. O número de Strohal é tilizado como m parâmetro associado com a freqüência de emissão de vórtices e, qando o corpo oscila define-se também, m número de Strohal associado à freqüência de oscilação do corpo. fd St = (associado à freqüência de emissão de vórtices, f ) U f d St = C C U (associado à freqüência de oscilação do corpo, f C ) (5.3) A freqüência de emissão de vórtices é calclada a partir do gráfico da força de sstentação em fnção do tempo, conforme mostrado na figra 9. Primeiro é calclado o período médio da crva da força de sstentação e posteriormente a freqüência de emissão de vórtices: T + T TN T = (5.4) N f = (5.5) T
69 5.00 Forca de Sstentacao Cargas Aerodinamicas Integradas T T T N Tempo Figra 9 Determinação da freqüência de emissão de vórtices A freqüência de oscilação do corpo é calclada a partir da velocidade anglar -λ - o qal é m parâmetro tilizado nas simlações. λ f C = (5.6) π A amplitde média do coeficiente de sstentação corresponde ao valor médio das amplitdes positivas e negativas do mesmo e é obtida a partir do gráfico da força de sstentação em fnção do tempo, conforme mostra a figra 0. A + A A N A + = N (5.7) ' ' ' A + A A N' A = ' N (5.8) A CL A A = (5.9) + +
70 5.00 Forca de Sstentacao Cargas Aerodinamicas Integradas A A AN C L A A A N Tempo Figra 0 Cálclo da amplitde média de C L A tabela contém as comparações entre os resltados nméricos e experimentais para as cargas aerodinâmicas integradas e para o número de Strohal. Os resltados médios foram calclados entre os instantes adimensionais t = 0 e t = 40. O resltado experimental de Blevins (984) apresenta 0 % de incerteza. Os resltados apresentados por Mstto et al. (998) foram obtidos tilizando o Método de Vórtices Discretos em associação com o Teorema do Círclo (Milne-Thompson, 955) para simlar a sperfície do cilindro. Alcântara Pereira et al. (00) tilizaram o Método de Painéis com distribição niforme de vórtices sobre os painéis planos. Silva (004) tilizo m algoritmo para simlar a oscilação do corpo com peqenas amplitdes, onde, nma primeira aproximação, as condições de contorno do corpo são transferidas de ma posição atal para ma posição média da sperfície discretizada do corpo. Os resltados de Silva (004) na tabela são sem oscilação.
71 Tabela Cilindro circlar sem oscilação 53 Re = 0 5, A = 0, λ = 0 C L C D St A CL Blevins (984) ---,0 0,9 --- Mstto et al. (998) ---, 0, --- Alcântara Pereira et al. (00) 0,04, 0, --- Silva (004) -0,03,3 0,0 --- Simlação Atal 0,07, 0,0,058 Os resltados mostrados na tabela apresentam ma boa concordância, pois tanto o número de Strohal qanto o coeficiente de arrasto de todas as simlações nméricas se aproximam do valor experimental. Como era de se esperar o coeficiente de arrasto está m poco acima do valor experimental (exceto aqele obtido por Alcântara Pereira et al. (00) qe incorpora na sa simlação nmérica ma modelagem de trblência), pois os efeitos tridimensionais não são considerados no presente trabalho. O Número de Strohal encontrado, no entanto, está mito próximo do valor experimental, o qe demonstra não ser inflenciado ao se negligenciar o efeito tridimensional. A figra apresenta ma distribição de pressão média sobre a sperfície discretizada do cilindro. Observa-se qe os valores encontrados na presente simlação apresentam ma boa concordância com os dados experimentais, sendo speriores àqeles apresentados por (Mstto,998). No entanto, apresentam ainda m peqeno desvio na região de descolamento da camada limite sitada entre 60 e 80. Acredita-se qe m refinamento na distribição de painéis nesta região associado a ma adeqada modelagem de trblência podem minimizar esta discrepância. Otra alternativa para ma melhoria dos resltados nesta região consiste em se realizar m tratamento mais adeqado para os vórtices nascentes. Na presente simlação todos os vórtices discretos de Lamb nascem tangenciando a sperfície dos painéis planos com m mesmo valor para o raio do núcleo viscoso.
72 54.00 M = Simlação Atal Experimental (Blevins, 984) Teoria Potencial Solção Nmérica (Mstto,988) θ Δt = 0,05 ε = 0,003 σ 0 = 0, Re = Cp Theta Figra Comparação dos resltados médios de coeficiente de pressão ( C P ) Os resltados médios para os coeficientes de sstentação e de arrasto foram calclados entre os instantes t = 0 e t = 40. A figra mostra a evolção no tempo destes coeficientes aerodinâmicos. Forca de Arrasto M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = Cargas Aerodinamicas Integradas Forca de Sstentacao a c b Tempo Figra Cargas aerodinâmicas integradas (sem oscilação)
73 Observa-se qe: 55 - o coeficiente de sstentação oscila em torno do valor zero, como esperado, pois o cilindro está sendo estdado como m corpo isolado; - a crva qe representa o coeficiente de arrasto oscila com o dobro da freqüência da crva qe representa o coeficiente de sstentação, o qe é ma característica intrínseca do cilindro circlar; A figra 3 apresenta a posição dos vórtices na esteira do caso simlado no instante t = 40, qe corresponde a 800 avanços no tempo da simlação. De cada lado de ma linha passando pelo centro do cilindro observa-se a formação de grandes estrtras constitídas por agrpamento de vórtices qe são alternadamente despreendidos formando a esteira de Von Kármán. M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = Figra 3 Evolção da vorticidade após 800 iterações (sem oscilação) Doravante estes aglomerados serão referidos como grandes estrtras vorticosas. A freqüência de emissão destas estrtras é aqela tilizada para o cálclo do número de Strohal. Observo-se ainda qe ela é a responsável pela oscilação dos coeficientes de arrasto e de sstentação drante a simlação nmérica vea a figra. A figra 3, embora bastante ilstrativa, fornece apenas ma informação semiqantitativa do comportamento da esteira, o sea, ela apresenta a posição dos vórtices sem levar em consideração as intensidades dos mesmos. A figra 4 mostra o campo de velocidades e as manchas de vorticidade na condição de força de sstentação máxima, ponto a indicado no gráfico da figra. A legenda da primeira figra refere-se ao componente v da velocidade indzida em cada vórtice e a legenda da segnda figra refere-se à intensidade dos aglomerados de vórtices.
74 56 V Figra 4 Campo de velocidades e manchas de vorticidade A figra 5 mostra o campo de velocidades e as manchas referentes ao trecho compreendido entre os pontos a e b do gráfico do coeficiente de sstentação (figra ). V Figra 5 Campo de velocidade e vorticidade (trecho a - b ) Nota-se a formação de estrtras vorticosas no sentido horário devido a forte inflência do componente v positivo da velocidade indzida. A figra 6 mostra o comportamento do campo de velocidades e as manchas de vorticidade na condição de força de sstentação máxima negativa, ponto b do gráfico da figra.
75 57 Na figra 7 é mostrada a formação, no trecho compreendido entre os pontos b e c, de estrtras vorticosas no sentido anti-horário devido a inflência do componente v negativo da velocidade indzida. V Figra 6 Campo de velocidades e vorticidade ( C máximo negativo) L V Figra 7 Campo de velocidades e vorticidade (trecho b - c )
76 5.. Cilindro circlar oscilando 58 A tabela 3 apresenta os resltados obtidos na simlação nmérica considerando ma baixa velocidade anglar da oscilação do cilindro circlar ( λ = 0, 05 ) e diferentes valores para as amplitdes de oscilação. Tabela 3 Estdo para baixas velocidades anglares de oscilação Velocidade Anglar (λ) 0,05 Amplitde (A) C L C D 0,0-0,05,33 0,96 0,008,7 0,05 0,069,95 0,98 0,008,7 0, 0,07,84 0,07 0,008,00 0,5 0,067,58 0,08 0,008, 0, 0,4,85 0,9 0,008,070 0,3 0,6,09 0,0 0,008,04 0,5 0,69,5 0, 0,008 0,97 St St C A CL M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = Nota-se qe nestas sitações o Número de Strohal fica mito próximo ao valor encontrado para o corpo parado ( St = 0, 9 ), porém, deve-se observar qe ele praticamente independente da amplitde de oscilação. Observa-se, também, qe o amento da amplitde de oscilação poco afeta na amplitde média da crva do coeficiente de sstentação, conforme mostrado no gráfico da figra 8. O valor do coeficiente de sstentação apresenta valores razoáveis à medida qe os valores de amplitdes de oscilação do corpo amentam. O valor médio do coeficiente de arrasto se manteve insensível às variações da amplitde de oscilação do corpo qando a freqüência de oscilação é baixa.
77 59. M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = AC L λ = A Figra 8 Amplitde média do C L em fnção da amplitde de oscilação para λ = 0, 05 A tabela 4 apresenta os resltados obtidos na simlação nmérica considerando ma velocidade anglar maior da oscilação do corpo ( λ =, 5) para várias amplitdes. Tabela 4 Estdo para altas velocidades anglares de oscilação Velocidade Anglar (λ),5 Amplitde (A) C L C D 0,0 0,08,78 0,03 0,39,77 0,05-0,009,095 0,40 0,39,094 0, 0,054 0,886 0,40 0,39, 0,5 0,03 0,63 0,40 0,39,34 0, 0,008 0,347 0,39 0,39,467 0,3 0,044 0,7 0,38 0,39,805 0,5 0,0-0,35 0,39 0,39,3 St St C A CL M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = O aspecto qe chama mais atenção nesta tabela é observado nas colnas qe apresentam o número de Strohal do corpo e de emissão de vórtices. Para valores mais elevados da amplitde de oscilação do corpo, verifica-se claramente o fenômeno de lock-in onde as freqüências de emissão de vórtices são praticamente as mesmas das freqüências de oscilação do corpo. Para amplitdes mito peqenas este fenômeno não é claramente observado.
78 Nota-se neste caso qe com o amento da amplitde de oscilação, a amplitde média do coeficiente de sstentação amenta, conforme mostrado na figra O valor médio do coeficiente de sstentação ( C amplitde de oscilação do corpo mantendo-se praticamente nlo. L ) é insensível às variações da O valor médio do coeficiente de arrasto ( C D ), no entanto, dimini sensivelmente com o amento da amplitde de oscilação do corpo mostrando claramente a importância do fenômeno de lock-in..5 M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = AC L.5 λ = A Figra 9 Amplitde média do C L em fnção da amplitde de oscilação para λ =, 5 De forma análoga à sitação de corpo parado ( λ = 0 e A = 0), a figra 0 apresenta o comportamento das cargas aerodinâmicas entre os instantes t = 0 e t = 40 para ma amplitde de oscilação de A = 0, 3 e ma velocidade anglar de λ =, 0. Nesta sitação o gráfico da distribição do coeficiente de pressão sobre a sperfície discretizada do corpo é formado a partir dos valores instantâneos de pressão conforme apresentado na figra. Qando o movimento do corpo é de sbida e atinge a posição máxima, ponto A, a maior pressão é observada na sperfície sperior do cilindro ( θ = 90 ) e, por otro lado, qando o
79 movimento do corpo é de descida e atinge a posição mínima, ponto C, a maior pressão ocorrerá na sperfície inferior do cilindro ( θ = 70 ) C L C D θ Coeficientes de Arrasto e Sstentação A B C D Tempo Figra 0 Cargas aerodinâmicas integradas ( λ =, 0 e A = 0, 3) Figra Distribição do coeficiente de pressão ( λ =, 0 e A = 0, 3)
80 6 As análises anteriores motivaram ma investigação sobre a relação entre o Número de Strohal do corpo (associado à oscilação do corpo) e o Número de Strohal (associado à emissão de vórtices). Para isto qatro simlações foram analisadas. A primeira simlação refere-se ao corpo parado e os resltados obtidos são mostrados na tabela 5. Tabela 5 Corpo sem oscilação Amplitde (A) Velocidade Anglar (λ) C L C D St St C A CL 0 0 0,069,5 0,03 0,058 A segnda simlação analisa o comportamento do corpo oscilante com baixa amplitde ( A = 0, 5) para ma faixa de velocidades anglares qe se estende de λ = 0, 0 até λ =, 5. Os resltados são mostrados na tabela 6 e na figra. Tabela 6 Corpo com oscilação de peqena amplitde Amplitde (A) Velocidade Anglar (λ) C L C D St St C A CL 0,5 0,0 0,047,47 0,07 0,00,36 0,0 0,050,56 0,08 0,003,095 0,05 0,067,58 0,08 0,008, 0, 0,8,9 0,9 0,06,94 0, 0,046,07 0, 0,03,074 0,3-0,064,4 0,05 0,048 0,869 0,4 0,008,047 0,05 0,064,0 0,6 0,039 0,877 0,096 0,096,749 0,7 0,56 0,9 0, 0,,889 0,8-0,55 0,90 0,3 0,7,533 0,9 0,036,094 0,4 0,43,774,0-0,09,04 0,60 0,59,63, -0,003,006 0,9 0,9,,3-0,03 0,904 0,07 0,07,89,5 0,03 0,63 0,40 0,39,34 M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = 00000
81 Na figra observa-se o comportamento do número de Strohal referente ao movimento oscilatório de corpo ( St ) em fnção do Strohal referente à freqüência de C emissão dos vórtices (St ). Uma análise do número de Strohal indica qe para ma baixa freqüência de oscilação do corpo o número de Strohal de emissão de vórtices está próximo de 0, 0, o qal é o mesmo valor encontrado na simlação do corpo parado, conforme mostrado na tabela 5. Por otro lado, o lock-in, o sea, a sincronização entre a freqüência de emissão de vórtices e a freqüência de oscilação do corpo, ocorre nas freqüências mais altas de oscilação do corpo III 0. II St I 0. A = Figra Número de Strohal de emissão de vórtices em fnção do Strohal do corpo A terceira simlação analisa o comportamento do corpo oscilante de grande amplitde ( A = 0, 50 ) para ma faixa de velocidades anglares qe se estende de λ = 0, 0 até λ =, 5. Os resltados são mostrados na tabela 7 e na figra 3. Uma análise cidadosa do número de Strohal mostra três diferentes regimes de escoamento. Para baixa freqüência de oscilação do corpo (baixo valor do número de Strohal do corpo, St ) o número de Strohal de emissão de vórtices está próximo de 0, 0, o qal é o C Stc mesmo valor encontrado na simlação do corpo parado, conforme mostrado na tabela 5 e indicado na figra 3 por I. No otro extremo, para alto valor do número de Strohal do corpo, ocorre o fenômeno de lock-in onde a freqüência de emissão de vórtices se igala à freqüência de oscilação do corpo. Este comportamento é indicado na figra 3 pela região III.
82 64 Entre estes dois extremos há m regime de transição com m comportamento indefinido. Nota-se qe isto ocorre nos movimentos oscilatórios de grandes amplitdes, conforme mostrado na região II das figras e 3. Tabela 7 Corpo com oscilação de grande amplitde Amplitde (A) Velocidade Anglar (λ) CL C D St St C A CL 0,5 0,0 0,004,5 0,07 0,00,5 0,0 0,050,70 0,09 0,003,55 0,05 0,69,5 0, 0,008 0,97 0, 0,94,44 0,0 0,06,35 0, -0,076 0,90 0,6 0,03 0,70 0,3-0,53 0,488 0,048 0,048,0 0,4 0,050 0,36 0,064 0,064 3,06 0,6 0,84 0,433 0,096 0,096 4,44 0,7 0,99 0,449 0, 0, 3,976 0,8-0,008 0,46 0,7 0,7 3,608 0,9 0,4 0,343 0,43 0,43 3,76,0-0, 0,48 0,60 0,59,938, 0,03-0,096 0,9 0,9,470,3-0,009-0,44 0,08 0,07,36,5 0,0-0,35 0,39 0,39,3 M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = 00000
83 III 0. II St I 0. A = 0, Stc Figra 3 Número de Strohal para amplitde de oscilação A = 0, 5 A última simlação analisa o comportamento do corpo oscilante considerando ma amplitde de valor intermediário ( A = 0, 30 ) para ma faixa de velocidades anglares qe se estende de λ = 0, 0 até λ =, 5. Os resltados são mostrados na tabela 8 e na figra 4. Novamente ma análise cidadosa do número de Strohal mostra três diferentes regimes de escoamento. Para baixa freqüência de oscilação do corpo (baixo valor do número de Strohal do corpo, St C ) o número de Strohal de emissão de vórtices está próximo de 0,0, conforme indicado na figra 4 por I. No otro extremo a freqüência de emissão de vórtices se igala a freqüência de oscilação do corpo. Este comportamento é indicado na figra 4 pela região III. Entre estes dois extremos há m regime de transição com m comportamento indefinido identificado no gráfico por II.
84 Tabela 8 Corpo com oscilação de média amplitde 66 Amplitde (A) Velocidade Anglar (λ) C L C D St St C A CL 0,3 0,0 0,36,08 0,03 0,00,60 0,0 0,048,89 0,99 0,003,07 0,05 0,6,09 0,0 0,008,04 0, 0,86,36 0,0 0,06,379 0, 0,07,0 0,07 0,03,057 0,3-0,36 0,93 0, 0,048 0,57 0,4 0,064 0,698 0,069 0,064,04 0,6 0,9 0,58 0,095 0,096 3,7 0,7 0,30 0,76 0, 0, 3,564 0,8-0,053 0,79 0,7 0,7 3,43 0,9 0,03 0,800 0,45 0,43 3,09,0-0,7 0,69 0,6 0,59,84, 0,03 0,495 0,9 0,9,0,3-0,03 0,49 0,06 0,07,99,5 0,044 0,7 0,38 0,39,805 M = 00 Δt = 0,05 ε = 0,003 σ 0 = 0,003 Re = III 0. II St I 0. A = 0, Stc Figra 4 Número de Strohal para amplitde de oscilação A = 0, 3
85 67 A análise das três sitações de amplitdes de oscilação do corpo mostra a dependência da freqüência de lock-in com esta amplitde de oscilação do corpo. Qanto maior a amplitde de oscilação do corpo menor a freqüência de lock-in, conforme indica a figra Freqência de Lock-in Amplitde de Oscilação Figra 5 Freqüência de lock-in em fnção da amplitde de oscilação do corpo Para m melhor entendimento analisa-se a esteira de vórtices formada nestes corpos oscilantes. Para ma freqüência baixa de oscilação o comportamento da esteira é qase o mesmo do mostrado na figra 3, para m cilindro sem oscilação, com exceção dos agrpamentos de vórtices qe acompanham a amplitde de oscilação do corpo. A figra 6 mostra este padrão de emissão de vórtices para m corpo oscilando com peqena amplitde e freqüência baixa comparado com ma esteira de m corpo sem oscilação.
86 68 M = 00 Δt = 0,05 (a) A = 0,0 e λ = 0,0 ε = 0,003 σ0 = 0,003 Re = (b) A = 0,05 e λ =,5 Figra 6 Esteira para corpo parado (a) e corpo oscilando (b) Para o cilindro oscilando na região de transição a estrtra da esteira torna-se intermitente e os agrpamentos de vórtices são emitidos irreglarmente do cilindro. Na região de lock-in m forte agrpamento de vórtices é observado a sante do cilindro qando o mesmo atravessa ma linha simétrica. Esta sitação é ilstrada na figra 7, onde o cilindro está movendo-se do topo para baixo. A figra 8 mostra, para esta sitação, o campo de velocidade e as manchas de vorticidade. M = 00 Δt = 0,05 ε = 0,003 σ0 = 0,003 Re = Figra 7 Esteira para t = 33, A = 0,5 e λ =,0
87 69 V Figra 8 Campo de velocidades e mancha de vorticidade Nota-se qe este agrpamento, denominado de agrpamento atal, apresenta ma rotação baixa na direção anti-horária, o qe desacelera o escoamento na parte sperior do cilindro e acelera o escoamento na parte inferior. Além disso, a vorticidade é indzida nm novo agrpamento de vórtices qe se forma na parte sperior do cilindro. Este novo agrpamento de vórtices emprra o agrpamento atal e qando o cilindro atinge a posição mais inferior da oscilação ele tende a separar-se para a nvem de vórtices. A figra 9 ilstra esta sitação e a figra 30 mostra o campo de velocidades e as manchas de vorticidade. M = 00 Δt = 0,05 ε = 0,003 σ0 = 0,003 Re = Figra 9 Esteira para t = 8,3, A = 0,5 e λ =,0 V Figra 30 Campo de velocidades e manchas de vorticidade
88 70 Natralmente o oposto é observado qando o cilindro está se movendo de sa posição mais baixa para a posição sperior. A figra 3 mostra a sitação onde o cilindro encontra-se na parte sperior e a figra 3 mostra o comportamento do campo de velocidades e das manchas de vorticidade. M = 00 Δt = 0,05 ε = 0,003 σ0 = 0,003 Re = Figra 3 Padrão da esteira para t = 3,4, A = 0,5 e λ =,0 V Figra 3 Campo de velocidades e manchas de vorticidade A figra 33 apresenta m estdo comparando as formas de onda da oscilação do corpo, da velocidade do corpo, da aceleração do corpo e do coeficiente de sstentação. Como pode ser observado o coeficiente de sstentação oscila com a mesma freqüência de oscilação do corpo e sa amplitde alcança valores altos, em torno de,5 e,0. Observa-se, também, qe a forma de onda do coeficiente de sstentação é igal à da aceleração do corpo. Isto ocorre porqe na velocidade anglar considerada ( λ =,5 ) ocorre o fenômeno de lock-in.
Análise do Escoamento ao Redor de um Corpo Oscilante na Presença de uma Superfície Plana
 UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Análise do Escoamento ao Redor de m Corpo Oscilante na Presença
UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Análise do Escoamento ao Redor de m Corpo Oscilante na Presença
4 Análise dimensional para determinação da frequência e fator de amplificação do pico máximo
 4 Análise dimensional para determinação da freqência e fator de amplificação do pico máimo A análise cidadosa das eqações qe regem o escoamento pode fornecer informações sobre os parâmetros importantes
4 Análise dimensional para determinação da freqência e fator de amplificação do pico máimo A análise cidadosa das eqações qe regem o escoamento pode fornecer informações sobre os parâmetros importantes
2 a Prova de Mecânica dos Fluidos II PME /05/2012 Nome: No. USP
 a Prova de Mecânica dos Flidos II PME 8/5/ Nome: No. USP ª. Qestão (. pontos). Vamos admitir m escoamento trblento de ar (ρ=,kg/m ; ν=,6-5 m /s) sobre m aerofólio esbelto em regime permanente. Medidas
a Prova de Mecânica dos Flidos II PME 8/5/ Nome: No. USP ª. Qestão (. pontos). Vamos admitir m escoamento trblento de ar (ρ=,kg/m ; ν=,6-5 m /s) sobre m aerofólio esbelto em regime permanente. Medidas
3 Teoria de Ondas Marítimas
 3 Teoria de Ondas Marítimas 3.1. Introdção Ondas do mar resltam da ação de forças sobre m flido de maneira a pertrbar o se estado inicial, isto é, deformá-lo. Estas forças são provocadas por diversos agentes
3 Teoria de Ondas Marítimas 3.1. Introdção Ondas do mar resltam da ação de forças sobre m flido de maneira a pertrbar o se estado inicial, isto é, deformá-lo. Estas forças são provocadas por diversos agentes
Capítulo 4. Convecção Natural
 Capítlo 4 Convecção Natral eitra e Exercícios (Incropera & DeWitt) 6ª Edição Seções: 9. a 9.9 Exercícios: Cap. 9 6, 9, 3, 8, 5, 7, 30, 36, 45, 58, 75, 88, 9, 94, 05, 0 5ª Edição Seções: 9. a 9.9 Exercícios:
Capítlo 4 Convecção Natral eitra e Exercícios (Incropera & DeWitt) 6ª Edição Seções: 9. a 9.9 Exercícios: Cap. 9 6, 9, 3, 8, 5, 7, 30, 36, 45, 58, 75, 88, 9, 94, 05, 0 5ª Edição Seções: 9. a 9.9 Exercícios:
5 Exemplos de análise determinística 5.1. Introdução
 5 Exemplos de análise determinística 5.1. Introdção Para validação dos modelos nméricos determinísticos e comparações entre os procedimentos de solção, são efetadas análises de qatro exemplos. O primeiro
5 Exemplos de análise determinística 5.1. Introdção Para validação dos modelos nméricos determinísticos e comparações entre os procedimentos de solção, são efetadas análises de qatro exemplos. O primeiro
Métodos Numéricos para Mecânica dos Fluidos
 Métodos Nméricos para Mecânica dos Flidos Professores: Antônio Castelo Filho Fernando Marqes Federson Leandro Franco de Soza Lis Gstavo Nonato Michael George Mansell Métodos Nméricos para Mecânica dos
Métodos Nméricos para Mecânica dos Flidos Professores: Antônio Castelo Filho Fernando Marqes Federson Leandro Franco de Soza Lis Gstavo Nonato Michael George Mansell Métodos Nméricos para Mecânica dos
ANÁLISE DE SENSIBILIDADE DE ESTRUTURAS VIA ANSYS
 3 ANÁLISE DE SENSIBILIDADE DE ESRUURAS VIA ANSYS Geralmente o MEF é o método nmérico de análise tilizado pare se obter os valores das fnções objetivo e das restrições, no qe diz respeito à maioria dos
3 ANÁLISE DE SENSIBILIDADE DE ESRUURAS VIA ANSYS Geralmente o MEF é o método nmérico de análise tilizado pare se obter os valores das fnções objetivo e das restrições, no qe diz respeito à maioria dos
Escoamentos Internos
 Escoamentos Internos Os escoamentos internos e incompressíveis, onde os efeitos da viscosidade são consideráveis, são de extrema importância para os engenheiros! Exemplos, Escoamento em tbo circlar: veias
Escoamentos Internos Os escoamentos internos e incompressíveis, onde os efeitos da viscosidade são consideráveis, são de extrema importância para os engenheiros! Exemplos, Escoamento em tbo circlar: veias
6 Análise dos Resultados
 6 Análise dos Resltados 6.. Introdção Neste capítlo são apresentados e analisados os resltados obtidos nos ensaios das sete vigas e a determinação dos ses índices de dctilidade. As resistências das vigas
6 Análise dos Resltados 6.. Introdção Neste capítlo são apresentados e analisados os resltados obtidos nos ensaios das sete vigas e a determinação dos ses índices de dctilidade. As resistências das vigas
Capítulo 1 Introdução
 Capítlo 1 Introdção Nas últimas décadas, o Método de Elementos Finitos tem sido ma das principais ferramentas da mecânica comptacional na representação dos mais diversos tipos de fenômenos físicos presentes
Capítlo 1 Introdção Nas últimas décadas, o Método de Elementos Finitos tem sido ma das principais ferramentas da mecânica comptacional na representação dos mais diversos tipos de fenômenos físicos presentes
2 - ELEMENTOS FINITOS DE BARRA ARTICULADA. CONCEITOS BÁSICOS
 Método dos elementos finitos aplicado a estrtras reticladas Capítlo - EEMETOS FIITOS DE BARRA ARTICUADA. COCEITOS BÁSICOS. - Introdção este capítlo o método dos elementos finitos (MEF vai ser aplicado
Método dos elementos finitos aplicado a estrtras reticladas Capítlo - EEMETOS FIITOS DE BARRA ARTICUADA. COCEITOS BÁSICOS. - Introdção este capítlo o método dos elementos finitos (MEF vai ser aplicado
CONVECÃO NATURAL. É o processo de transferência de calor induzido por forças gravitacionais, centrífugas ou de Coriolis.
 CONVECÃO NAURA É o processo de transferência de calor indzido por forças gravitacionais, centrífgas o de Coriolis. A convecção natral ocorre na circlação atmosférica e oceânica, sistemas de refrigeração
CONVECÃO NAURA É o processo de transferência de calor indzido por forças gravitacionais, centrífgas o de Coriolis. A convecção natral ocorre na circlação atmosférica e oceânica, sistemas de refrigeração
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2015/16
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 05/6 Exame de ª época, 5 de Janeiro de 06 Nome : Hora : :30 Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : Consulta limitada
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 05/6 Exame de ª época, 5 de Janeiro de 06 Nome : Hora : :30 Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : Consulta limitada
7 Conclusões e Sugestões para Trabalhos Futuros
 7 Conclsões e Sgestões para Trabalhos Ftros Este trabalho experimental estda a inflência do parâmetro dctilidade em sete vigas retanglares de concreto armado reforçadas à flexão com tecidos de fibra de
7 Conclsões e Sgestões para Trabalhos Ftros Este trabalho experimental estda a inflência do parâmetro dctilidade em sete vigas retanglares de concreto armado reforçadas à flexão com tecidos de fibra de
IX CONGRESSO BRASILEIRO DE ENGENHARIA E CIÊNCIAS TÉRMICAS
 IX CONGRESSO BRASILEIRO DE ENGENHARIA E CIÊNCIAS TÉRMICAS 9th BRAZILIAN CONGRESS OF THERMAL ENGINEERING AND SCIENCES Paper CIT0-016 COMPORTAMENTO HIRODINÂMICO DE UMA PELÍCULA LÍQUIDA DESCENDENTE EM PLACA
IX CONGRESSO BRASILEIRO DE ENGENHARIA E CIÊNCIAS TÉRMICAS 9th BRAZILIAN CONGRESS OF THERMAL ENGINEERING AND SCIENCES Paper CIT0-016 COMPORTAMENTO HIRODINÂMICO DE UMA PELÍCULA LÍQUIDA DESCENDENTE EM PLACA
Escoamento em Regime Turbulento Perfil de velocidade média, U
 Escoamento em Regime Trblento Camada da parede: - Zona de eqilíbrio local. Prodção de k Dissipação de k (ε) - Na parede, 0, a eqação de balanço de qantidade de movimento na direcção x redz-se a T dp dx
Escoamento em Regime Trblento Camada da parede: - Zona de eqilíbrio local. Prodção de k Dissipação de k (ε) - Na parede, 0, a eqação de balanço de qantidade de movimento na direcção x redz-se a T dp dx
Cálculo Vetorial. Geometria Analítica e Álgebra Linear - MA Aula 04 - Vetores. Profa Dra Emília Marques Depto de Matemática
 Cálclo Vetorial Estdaremos neste tópico as grandezas etoriais, sas operações, propriedades e aplicações. Este estdo se jstifica pelo fato de, na natreza, se apresentarem 2 tipo de grandezas, as escalares
Cálclo Vetorial Estdaremos neste tópico as grandezas etoriais, sas operações, propriedades e aplicações. Este estdo se jstifica pelo fato de, na natreza, se apresentarem 2 tipo de grandezas, as escalares
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA
 AA-220 AERODINÂMICA NÃO ESTACIONÁRIA Aerofólio fino em regime incompressível não estacionário (baseado nas Notas de Aula do Prof Donizeti de Andrade) Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Relembrando
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA Aerofólio fino em regime incompressível não estacionário (baseado nas Notas de Aula do Prof Donizeti de Andrade) Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Relembrando
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2014/15
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 4/5 Exame de ª época, 3 de Janeiro de 5 Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 4/5 Exame de ª época, 3 de Janeiro de 5 Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2016/17
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 6/ Exame de ª época, 4 de Janeiro de Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 6/ Exame de ª época, 4 de Janeiro de Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2015/16
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 8 de Janeiro de 6 Nome : Hora : 8:3 Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 8 de Janeiro de 6 Nome : Hora : 8:3 Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
ALBERT EINSTEIN INSTITUTO ISRAELITA DE ENSINO E PESQUISA CENTRO DE EDUCAÇÃO EM SAÚDE ABRAM SZAJMAN
 ALBERT EINSTEIN INSTITUTO ISRAELITA DE ENSINO E PESQUISA CENTRO DE EDUCAÇÃO EM SAÚDE ABRAM SZAJMAN CURSO DE ESPECIALIZAÇÃO EM ENGENHARIA CLÍNICA DISCIPLINA: GESTÃO DE TECNOLOGIAS MÉDICAS TEMA:REGULAÇÃO
ALBERT EINSTEIN INSTITUTO ISRAELITA DE ENSINO E PESQUISA CENTRO DE EDUCAÇÃO EM SAÚDE ABRAM SZAJMAN CURSO DE ESPECIALIZAÇÃO EM ENGENHARIA CLÍNICA DISCIPLINA: GESTÃO DE TECNOLOGIAS MÉDICAS TEMA:REGULAÇÃO
Conceitos Fundamentais 1.1
 Conceitos Fndamentais. Capítlo Conceitos Fndamentais. Introdção Um sólido deformável sob a acção de forças eternas, deformar-se-á e no sólido desenvolver-se-ão esforços internos. Estes esforços serão em
Conceitos Fndamentais. Capítlo Conceitos Fndamentais. Introdção Um sólido deformável sob a acção de forças eternas, deformar-se-á e no sólido desenvolver-se-ão esforços internos. Estes esforços serão em
2 Modelagem Matemática do Problema
 2 Modelagem Matemática do Problema O escoamento de uma gota imersa em um fluido através de um capilar é um problema transiente, não linear, bifásico com superfície livre e descrito pela equação de Navier
2 Modelagem Matemática do Problema O escoamento de uma gota imersa em um fluido através de um capilar é um problema transiente, não linear, bifásico com superfície livre e descrito pela equação de Navier
Antenas de Tanguá (RJ)
 Antenas de Tangá (RJ) Composição de movimentos y P(x,y) y(t) O x(t) X descoberta de Galile Uma grande parte da discssão qe sege visa o caso particlar em qe temos m movimento nma direção X e otro na direção
Antenas de Tangá (RJ) Composição de movimentos y P(x,y) y(t) O x(t) X descoberta de Galile Uma grande parte da discssão qe sege visa o caso particlar em qe temos m movimento nma direção X e otro na direção
Fenômeno de Transportes A PROFª. PRISCILA ALVES
 Fenômeno de Transportes A PROFª. PRISCILA ALVES PRISCILA@DEMAR.EEL.USP.BR Proposta do Curso Critérios de Avaliação e Recuperação Outras atividades avaliativas Atividades experimentais: Será desenvolvida
Fenômeno de Transportes A PROFª. PRISCILA ALVES PRISCILA@DEMAR.EEL.USP.BR Proposta do Curso Critérios de Avaliação e Recuperação Outras atividades avaliativas Atividades experimentais: Será desenvolvida
Curso de Análise Matricial de Estruturas 1
 Crso de Análise Matricial de Estrtras IV MÉODO DA IIDEZ IV. Solção eral A modelagem de m sistema estrtral para sa resolção através do método da rigidez deve preferencialmente apretar m número de coordenadas
Crso de Análise Matricial de Estrtras IV MÉODO DA IIDEZ IV. Solção eral A modelagem de m sistema estrtral para sa resolção através do método da rigidez deve preferencialmente apretar m número de coordenadas
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2015/16
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 9 de Julho de 6 Nome : Hora : 4: Número: Duração : horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 9 de Julho de 6 Nome : Hora : 4: Número: Duração : horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13 Exame de 3ª época, 19 de Julho de 2013 Nome : Hora : 15:00 Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13 Exame de 3ª época, 19 de Julho de 2013 Nome : Hora : 15:00 Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Osciladores lineares contínuos
 Osciladores lineares contínos Apontamentos da Disciplina de Dinâmica e Engenharia Sísmica Mestrado em Engenharia de Estrtras Institto Sperior Técnico ís Gerreiro Março de 1999 Osciladores ineares Contínos
Osciladores lineares contínos Apontamentos da Disciplina de Dinâmica e Engenharia Sísmica Mestrado em Engenharia de Estrtras Institto Sperior Técnico ís Gerreiro Março de 1999 Osciladores ineares Contínos
Dedução da Equação de Orr-Sommerfeld para um Fluido Viscoelástico do tipo Giesekus
 Dedção da Eqação de Orr-Sommerfeld para m Flido Viscoelástico do tipo Gieseks Laison J. da S. Frlan Pós-Gradação em Matemática Aplicada e Comptacional Uniersidade Estadal Palista - UNESP Presidente Prdente,
Dedção da Eqação de Orr-Sommerfeld para m Flido Viscoelástico do tipo Gieseks Laison J. da S. Frlan Pós-Gradação em Matemática Aplicada e Comptacional Uniersidade Estadal Palista - UNESP Presidente Prdente,
UNIVERSIDADE FEDERAL DE SANTA CATARINA CURSO DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA
 UNIVERSIDADE FEDERAL DE SANTA CATARINA CURSO DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA IMPLEMENTAÇÃO DE UM MÉTODO DE VOLUMES FINITOS COM SISTEMA DE COORDENADAS LOCAIS PARA A SOLUÇÃO ACOPLADA DAS EQUAÇÕES
UNIVERSIDADE FEDERAL DE SANTA CATARINA CURSO DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA IMPLEMENTAÇÃO DE UM MÉTODO DE VOLUMES FINITOS COM SISTEMA DE COORDENADAS LOCAIS PARA A SOLUÇÃO ACOPLADA DAS EQUAÇÕES
Composição de movimentos. P(x,y) y(t) x(t) descoberta de Galileu
 Composição de movimentos P(,) (t) O (t) X descoberta de Galile Uma grande parte da discssão qe sege visa o caso particlar em qe temos m movimento nma direção X e otro na direção Y, e no qal o qe acontece
Composição de movimentos P(,) (t) O (t) X descoberta de Galile Uma grande parte da discssão qe sege visa o caso particlar em qe temos m movimento nma direção X e otro na direção Y, e no qal o qe acontece
FATOR DE CONCENTRAÇÃO DE TENSÃO À FADIGA - COMPARAÇÃO ENTRE VALORES EXPERIMENTAIS E OBTIDOS COM A UTILIZAÇÃO DE UM SOFTWARE DE ELEMENTOS FINITOS
 FATOR DE CONCENTRAÇÃO DE TENSÃO À FADIGA - COMPARAÇÃO ENTRE VALORES EXPERIMENTAIS E OBTIDOS COM A UTILIZAÇÃO DE UM SOFTWARE DE EMENTOS FINITOS Liz Daré Neto Gstavo Tietz Cazeri Edardo Carlos Bianchi Rodrigo
FATOR DE CONCENTRAÇÃO DE TENSÃO À FADIGA - COMPARAÇÃO ENTRE VALORES EXPERIMENTAIS E OBTIDOS COM A UTILIZAÇÃO DE UM SOFTWARE DE EMENTOS FINITOS Liz Daré Neto Gstavo Tietz Cazeri Edardo Carlos Bianchi Rodrigo
Introdução aos Fluidos em Movimento Tipos de Escoamentos
 Introdução aos Fluidos em Movimento Tipos de Escoamentos Aula 3 de PME3230 Descrição Euleriana e Lagrangeana Linhas de Corrente e de Trajetória Aceleração Prof. Marcos Tadeu Pereira Classificações possíveis
Introdução aos Fluidos em Movimento Tipos de Escoamentos Aula 3 de PME3230 Descrição Euleriana e Lagrangeana Linhas de Corrente e de Trajetória Aceleração Prof. Marcos Tadeu Pereira Classificações possíveis
2 Formulação Matemática e Modelagem Computacional
 2 Formulação Matemática e Modelagem Computacional 2.1. Formulação Matemática A análise do escoamento através de tubos capilares foi desenvolvida utilizando-se o código CFD que vem sendo desenvolvido e
2 Formulação Matemática e Modelagem Computacional 2.1. Formulação Matemática A análise do escoamento através de tubos capilares foi desenvolvida utilizando-se o código CFD que vem sendo desenvolvido e
Escoamento potencial
 Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
PROV O ENGENHARIA QUÍMICA. Questão nº 1. h = 0,1 m A. Padrão de Resposta Esperado: a) P AB = P A B. Sendo ρ água. >> ρ ar. Em B : P B. .
 PRO O 00 Qestão nº ar A B h = 0, m A B a) P AB = P A B Sendo ρ ága >> ρ ar : Em B : P B = (ρ ága. g) h + P A P A B = P B P A =.000 x 9,8 x 0, = 980 Pa (valor:,5 pontos) b) P ar = P man = 0 4 Pa Em termos
PRO O 00 Qestão nº ar A B h = 0, m A B a) P AB = P A B Sendo ρ ága >> ρ ar : Em B : P B = (ρ ága. g) h + P A P A B = P B P A =.000 x 9,8 x 0, = 980 Pa (valor:,5 pontos) b) P ar = P man = 0 4 Pa Em termos
Departamento de Engenharia Mecânica. ENG 1011: Fenômenos de Transporte I
 Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Universidade Federal do Paraná
 Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Os escoamentos turbulentos
Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Os escoamentos turbulentos
Capítulo 5. TERMOELASTICIDADE LINEAR 1D PERMANENTE
 Capítlo 5. ermoelasticidade linear D permanente 65 Capítlo 5. RMOASICIDAD INAR D RMANN Neste capítlo, o modelo matemático é composto por das eações diferenciais: a problema térmico; e a problema elástico.
Capítlo 5. ermoelasticidade linear D permanente 65 Capítlo 5. RMOASICIDAD INAR D RMANN Neste capítlo, o modelo matemático é composto por das eações diferenciais: a problema térmico; e a problema elástico.
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2013/14
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 013/14 Exame de 3ª época, 15 de Julho de 014 Nome : Hora : 9:00 Número: Duração : 3 horas 1ª Parte : Sem consulta ª Parte : onsulta limitada
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 013/14 Exame de 3ª época, 15 de Julho de 014 Nome : Hora : 9:00 Número: Duração : 3 horas 1ª Parte : Sem consulta ª Parte : onsulta limitada
EM34B Transferência de Calor 2
 EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Convecção Forçada Escoamento Externo 2 Convecção Forçada: Escoamento Externo Escoamento Externo É definido como um escoamento
EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Convecção Forçada Escoamento Externo 2 Convecção Forçada: Escoamento Externo Escoamento Externo É definido como um escoamento
Transferência de Calor
 Transferência de Calor Introdução à Convecção Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Transferência de Calor Introdução à Convecção Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Arrasto e sustentação
 Arrasto e sustentação J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Arrasto e sustentação 1 / 16 Sumário 1 Noção de camada limite 2 Separação do escoamento e esteira
Arrasto e sustentação J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Arrasto e sustentação 1 / 16 Sumário 1 Noção de camada limite 2 Separação do escoamento e esteira
Fundamentos da Mecânica dos Fluidos
 Fundamentos da Mecânica dos Fluidos 1 - Introdução 1.1. Algumas Características dos Fluidos 1.2. Dimensões, Homogeneidade Dimensional e Unidades 1.2.1. Sistemas de Unidades 1.3. Análise do Comportamentos
Fundamentos da Mecânica dos Fluidos 1 - Introdução 1.1. Algumas Características dos Fluidos 1.2. Dimensões, Homogeneidade Dimensional e Unidades 1.2.1. Sistemas de Unidades 1.3. Análise do Comportamentos
4 Estudos sobre Ductilidade de Vigas Reforçadas
 4 Estdos sobre Dctilidade de Vigas Reforçadas 4.1. Introdção Este capítlo apresenta algns estdos teóricos e experimentais encontrados na literatra sobre vigas de concreto armado reforçadas com compósitos
4 Estdos sobre Dctilidade de Vigas Reforçadas 4.1. Introdção Este capítlo apresenta algns estdos teóricos e experimentais encontrados na literatra sobre vigas de concreto armado reforçadas com compósitos
Escoamentos Externos
 Escoamentos Externos O estudo de escoamentos externos é de particular importância para a engenharia aeronáutica, na análise do escoamento do ar em torno dos vários componentes de uma aeronave Entretanto,
Escoamentos Externos O estudo de escoamentos externos é de particular importância para a engenharia aeronáutica, na análise do escoamento do ar em torno dos vários componentes de uma aeronave Entretanto,
3 SPH. 3.1 Introdução
 3 SPH 3.1 Introdução Smoothed Particle Hydrodynamics (SPH) é um método puramente Lagrangiano desenvolvido por Lucy (1977) e Gingold (1977) em um estudo do campo da astrofísica voltado para colisão entre
3 SPH 3.1 Introdução Smoothed Particle Hydrodynamics (SPH) é um método puramente Lagrangiano desenvolvido por Lucy (1977) e Gingold (1977) em um estudo do campo da astrofísica voltado para colisão entre
Química. Bioprocessos e Biotecnologia para contato:
 SIMULAÇÃO DO COMPORTAMENTO DE REATORES CONTÍNUOS DE MISTURA PERFEITA CONTENDO ENZIMAS IMOBILIZADAS EM MATRIZES POROSAS PARA A CINÉTICA COM INIBIÇÃO POR SUBSTRATO PROBLEMA ENVOLVENDO MÚLTIPLOS ESTADOS ESTACIONÁRIOS
SIMULAÇÃO DO COMPORTAMENTO DE REATORES CONTÍNUOS DE MISTURA PERFEITA CONTENDO ENZIMAS IMOBILIZADAS EM MATRIZES POROSAS PARA A CINÉTICA COM INIBIÇÃO POR SUBSTRATO PROBLEMA ENVOLVENDO MÚLTIPLOS ESTADOS ESTACIONÁRIOS
SIMULAÇÃO NUMÉRICA DE UM TUBO DE CALOR AXIALMENTE ROTATIVO COM ESTRUTURA POROSA PARA BOMBEAMENTO CAPILAR DO CONDENSADO
 SIMULAÇÃO NUMÉRICA DE UM TUBO DE CALOR AXIALMENTE ROTATIVO COM ESTRUTURA POROSA PARA BOMBEAMENTO CAPILAR DO CONDENSADO Lís E. Saraia saraia@pf.tche.br Uniersidade de Passo Fndo, Facldade de Engenharia
SIMULAÇÃO NUMÉRICA DE UM TUBO DE CALOR AXIALMENTE ROTATIVO COM ESTRUTURA POROSA PARA BOMBEAMENTO CAPILAR DO CONDENSADO Lís E. Saraia saraia@pf.tche.br Uniersidade de Passo Fndo, Facldade de Engenharia
Camada limite laminar
 Camada limite laminar J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Camada limite laminar 1 / 24 Sumário 1 Introdução 2 Equações da camada limite laminar 3 Solução
Camada limite laminar J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Camada limite laminar 1 / 24 Sumário 1 Introdução 2 Equações da camada limite laminar 3 Solução
PEF Projeto de Estruturas Marítimas ESFORÇOS NA PLATAFORMA FIXA
 PEF 506 - Projeto de Estruturas Marítimas ESFORÇOS NA PLATAFORMA FIXA 1. Introdução O principal esforço agente em uma plataforma fixa é aquele advindo do movimento do meio fluido. evido à complexidade
PEF 506 - Projeto de Estruturas Marítimas ESFORÇOS NA PLATAFORMA FIXA 1. Introdução O principal esforço agente em uma plataforma fixa é aquele advindo do movimento do meio fluido. evido à complexidade
ESCOAMENTO INCOMPRESSÍVEL TRIDIMENSIONAL
 6 ESCOAMENTO INCOMPRESSÍVEL TRIDIMENSIONAL 6.1. Introdução Até agora foram analisados escoamentos bidiemensionais. Os escoamentos em torno dos corpos e perfis dos capítulos anteriores envolvem apenas duas
6 ESCOAMENTO INCOMPRESSÍVEL TRIDIMENSIONAL 6.1. Introdução Até agora foram analisados escoamentos bidiemensionais. Os escoamentos em torno dos corpos e perfis dos capítulos anteriores envolvem apenas duas
Tabela Número de Strouhal obtido nas simulações e resultados experimentais.
 105 Tabela 6.3 - Número de Strouhal obtido nas simulações e resultados experimentais. Número de Strouhal (St) Número de Reynolds Presente trabalho Roshko (1967) URANS DES LES Eq. (6.1) 1 10 4 0, 1877 0,
105 Tabela 6.3 - Número de Strouhal obtido nas simulações e resultados experimentais. Número de Strouhal (St) Número de Reynolds Presente trabalho Roshko (1967) URANS DES LES Eq. (6.1) 1 10 4 0, 1877 0,
Prof. Antônio F M Santos
 Prof. Antônio F M Santos Profa. Rosenda Valdés Arencibia Maio, 011 Sexo: Masclino, Feminino Calvície: Calvo, Não calvo A associação entre das o mais variáveis implica qe o conhecimento de ma altera a
Prof. Antônio F M Santos Profa. Rosenda Valdés Arencibia Maio, 011 Sexo: Masclino, Feminino Calvície: Calvo, Não calvo A associação entre das o mais variáveis implica qe o conhecimento de ma altera a
5 Conclusões e recomendações para trabalhos futuros
 5 Conclusões e recomendações para trabalhos futuros 154 5 Conclusões e recomendações para trabalhos futuros 5.1. Conclusões O presente trabalho combinou o estudo experimental com o numérico para uma geometria
5 Conclusões e recomendações para trabalhos futuros 154 5 Conclusões e recomendações para trabalhos futuros 5.1. Conclusões O presente trabalho combinou o estudo experimental com o numérico para uma geometria
3 Metodologia e Confiabilidade da Simulação Numérica
 3 Metodologia e Confiabilidade da Simlação Nmérica No presente trabalho, o medidor ltrassônico é simlado como m dispositivo qe mede velocidades médias em retas inclinadas com relação ao eixo do dto. lém
3 Metodologia e Confiabilidade da Simlação Nmérica No presente trabalho, o medidor ltrassônico é simlado como m dispositivo qe mede velocidades médias em retas inclinadas com relação ao eixo do dto. lém
MALHAS COMPUTACIONAIS PARA SIMULAÇÃO NUMÉRICA DE ESCOAMENTOS DE FLUIDOS ENTRE CILINDROS COM EXCENTRICIDADE
 0 a 05 de jnho de 009, Ijí/RS MALHAS COMPUACIONAIS PARA SIMULAÇÃO NUMÉRICA DE ESCOAMENOS DE FLUIDOS ENRE CILINDROS COM EXCENRICIDADE G 04 Modelagem Matemática Ricardo Vargas Del Frari URI/Erechim ricardodf@hotmail.com
0 a 05 de jnho de 009, Ijí/RS MALHAS COMPUACIONAIS PARA SIMULAÇÃO NUMÉRICA DE ESCOAMENOS DE FLUIDOS ENRE CILINDROS COM EXCENRICIDADE G 04 Modelagem Matemática Ricardo Vargas Del Frari URI/Erechim ricardodf@hotmail.com
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2017/18
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 217/18 Exame de 1ª época, 2 de Janeiro de 218 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta livre
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 217/18 Exame de 1ª época, 2 de Janeiro de 218 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta livre
SOLUÇÃO NUMÉRICA PARA O PROBLEMA DE FILTRAÇÃO TANGENCIAL COM MALHAS NÃO- UNIFORMES
 SOLUÇÃO NUMÉRICA PARA O PROBLEMA DE FILTRAÇÃO TANGENCIAL COM MALHAS NÃO- UNIFORMES D. E. N. LIMA e J. M. SILVA Universidade Federal de Alfenas, Instituto de Ciência e Tecnologia E-mail para contato: douglasales33@gmail.com
SOLUÇÃO NUMÉRICA PARA O PROBLEMA DE FILTRAÇÃO TANGENCIAL COM MALHAS NÃO- UNIFORMES D. E. N. LIMA e J. M. SILVA Universidade Federal de Alfenas, Instituto de Ciência e Tecnologia E-mail para contato: douglasales33@gmail.com
05/08/2014. RM = (RB ± IM) unidade. Como usar as informações disponíveis sobre o processo de medição e escrever corretamente o resultado da medição?
 6 Resltados de Medições Diretas Fndamentos da Metrologia Científica e Indstrial Slides do livrofmci Motivação definição do mensrando procedimento de medição resltado da medição condições ambientais operador
6 Resltados de Medições Diretas Fndamentos da Metrologia Científica e Indstrial Slides do livrofmci Motivação definição do mensrando procedimento de medição resltado da medição condições ambientais operador
Capítulo 3 Comportamento mecânico dos materiais = = = =
 apítlo omportamento mecânico dos materiais Problema Uma peça prismática de comprimento L e secção transversal rectanglar de altra 0cm e largra 0cm foi sjeita ao ensaio de tracção. variação de comprimento
apítlo omportamento mecânico dos materiais Problema Uma peça prismática de comprimento L e secção transversal rectanglar de altra 0cm e largra 0cm foi sjeita ao ensaio de tracção. variação de comprimento
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Transferência de Calor
 Transferência de Calor Convecção Natural - Parte 1 Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Transferência de Calor Convecção Natural - Parte 1 Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Estudo do comportamento da análise isogeométrica para o problema de Hemker
 Trabalho apresentado no CNMAC, Gramado - RS, 26. Proceeding Series of the Brazilian Society of Comptational and Applied Mathematics Estdo do comportamento da análise isogeométrica para o problema de Hemker
Trabalho apresentado no CNMAC, Gramado - RS, 26. Proceeding Series of the Brazilian Society of Comptational and Applied Mathematics Estdo do comportamento da análise isogeométrica para o problema de Hemker
Formação de Vórtices em um Corpo que Oscila na mesma Direção do Escoamento Incidente
 UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Formação de Vórtices em um Corpo que Oscila na mesma Direção do
UNIVERSIDADE FEDERAL DE ITAJUBÁ INSTITUTO DE ENGENHARIA MECÂNICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA DISSERTAÇÃO DE MESTRADO Formação de Vórtices em um Corpo que Oscila na mesma Direção do
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA. Inércia Térmica de Sensores.
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA Inércia Térmica de Sensores por Tiago Roberto Borges de Moraes Trabalho Final da Disciplina de Medições
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA Inércia Térmica de Sensores por Tiago Roberto Borges de Moraes Trabalho Final da Disciplina de Medições
CÁLCULO DE CARGAS AERODINÂMICAS (Simulação numérica utilizando uma nuvem de vórtices)
 CÁCUO E CARGAS AEROINÂMICAS (Simulação numérica utilizando uma nuvem de vórtices) uiz Antonio A. Pereira Miguel H. Hirata Waldir de Oliveira epartamento de Engenharia Mecânica - EFEI, Av. BPS n 1303 CEP.
CÁCUO E CARGAS AEROINÂMICAS (Simulação numérica utilizando uma nuvem de vórtices) uiz Antonio A. Pereira Miguel H. Hirata Waldir de Oliveira epartamento de Engenharia Mecânica - EFEI, Av. BPS n 1303 CEP.
MAP INTRODUÇÃO MATEMÁTICA À MECÂNICA DOS FLUIDOS 2 o semestre de 2006 ESPIRAL DE EKMAN KLEITON BLANE
 MAP - 431 INTRODUÇÃO MATEMÁTICA À MECÂNICA DOS FLUIDOS o semestre de 006 ESPIRAL DE EKMAN KLEITON BLANE Introdção No final do séclo XIX (1898) o noregês Fridjod Nansen (1861-1930) verifico qe os icebergs
MAP - 431 INTRODUÇÃO MATEMÁTICA À MECÂNICA DOS FLUIDOS o semestre de 006 ESPIRAL DE EKMAN KLEITON BLANE Introdção No final do séclo XIX (1898) o noregês Fridjod Nansen (1861-1930) verifico qe os icebergs
Estudo refinado da aerodinâmica e desempenho do Alpha One
 Anais do 4 O Encontro de Iniciação Científica e ós-gradação do IA XV ENCIA / 9 Institto ecnológico de Aeronática, São José dos Campos, S, Brasil, Otbro, 9 a, 9. Estdo refinado da aerodinâmica e desempeno
Anais do 4 O Encontro de Iniciação Científica e ós-gradação do IA XV ENCIA / 9 Institto ecnológico de Aeronática, São José dos Campos, S, Brasil, Otbro, 9 a, 9. Estdo refinado da aerodinâmica e desempeno
2 Fundamentos Teóricos
 Fundamentos Teóricos.1.Propriedades Físicas dos Fluidos Fluidos (líquidos e gases) são corpos sem forma própria; podem se submeter a variações grandes da forma sob a ação de forças; quanto mais fraca a
Fundamentos Teóricos.1.Propriedades Físicas dos Fluidos Fluidos (líquidos e gases) são corpos sem forma própria; podem se submeter a variações grandes da forma sob a ação de forças; quanto mais fraca a
Introdução Equações médias da turbulência Estrutura turbulenta de cisalhamento Transporte de energia cinética turbulenta. Turbulência. J. L.
 Turbulência J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Turbulência 1 / 29 Sumário 1 Introdução 2 Equações médias da turbulência 3 Estrutura turbulenta de cisalhamento
Turbulência J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Turbulência 1 / 29 Sumário 1 Introdução 2 Equações médias da turbulência 3 Estrutura turbulenta de cisalhamento
UNIVERSIDADE FEDERAL DE SANTA CATARINA - UFSC CENTRO DE ENGENHARIAS DA MOBILIDADE CEM. Bruno Zagoto Toscan
 UNIVERSIDADE FEDERAL DE SANTA CATARINA - UFSC CENTRO DE ENGENHARIAS DA MOBILIDADE CEM Bruno Zagoto Toscan Simulação de Escoamento em um Aerofólio NACA 0012 Joinville, 2014 1 INTRODUÇÃO A dinâmica dos fluidos
UNIVERSIDADE FEDERAL DE SANTA CATARINA - UFSC CENTRO DE ENGENHARIAS DA MOBILIDADE CEM Bruno Zagoto Toscan Simulação de Escoamento em um Aerofólio NACA 0012 Joinville, 2014 1 INTRODUÇÃO A dinâmica dos fluidos
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13 Exame de 1ª época, 18 de Janeiro de 2013 Nome : Hora : 8:00 Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13 Exame de 1ª época, 18 de Janeiro de 2013 Nome : Hora : 8:00 Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
EM34B Transferência de Calor 2
 EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Parte II: 2 Estudo da Transferência de Calor por Convecção 02 Objetivos 1. Mecanismo físico: o o o Origem física; Parâmetros
EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Parte II: 2 Estudo da Transferência de Calor por Convecção 02 Objetivos 1. Mecanismo físico: o o o Origem física; Parâmetros
3. MODELOS MATEMÁTICOS PARA FORÇAS DE CONTATO E DE REMOÇÃO
 3. MODELOS MATEMÁTICOS PARA FORÇAS DE CONTATO E DE REMOÇÃO Conforme mencionado na revisão bibliográfica, pesquisadores da PUC-Rio desenvolveram alguns modelos simplificados para previsão das forças de
3. MODELOS MATEMÁTICOS PARA FORÇAS DE CONTATO E DE REMOÇÃO Conforme mencionado na revisão bibliográfica, pesquisadores da PUC-Rio desenvolveram alguns modelos simplificados para previsão das forças de
Mecânica dos Fluidos Formulário
 Fluxo volúmétrico através da superfície Mecânica dos Fluidos Formulário Fluxo mássico através da superfície Teorema do transporte de Reynolds Seja uma dada propriedade intensiva (qtd de por unidade de
Fluxo volúmétrico através da superfície Mecânica dos Fluidos Formulário Fluxo mássico através da superfície Teorema do transporte de Reynolds Seja uma dada propriedade intensiva (qtd de por unidade de
Corpos Não-Fuselados
 Escoamentos com esteiras de grandes dimensões (ordem de grandeza da dimensão transversal do corpo), com alterações significativas do escoamento relativamente à situação de fluido perfeito (elevados δ *
Escoamentos com esteiras de grandes dimensões (ordem de grandeza da dimensão transversal do corpo), com alterações significativas do escoamento relativamente à situação de fluido perfeito (elevados δ *
Capítulo 1. INTRODUÇÃO
 Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
3. Hidráulica dos escoamentos em canais de leito fixo Classificação dos escoamentos
 3. Hidrálica dos escoamentos em canais de leito ixo Revisão de conceitos de Hidrálica Geral 3.1. Classiicação dos escoamentos Número de Reynolds: exprime a importância das orças de viscosidade em relação
3. Hidrálica dos escoamentos em canais de leito ixo Revisão de conceitos de Hidrálica Geral 3.1. Classiicação dos escoamentos Número de Reynolds: exprime a importância das orças de viscosidade em relação
IMPLEMENTAÇÃO DO MÉTODO DOS PAINÉIS PARA O ESTUDO DE PROPRIEDADES AERODINÂMICAS DE AEROFÓLIOS
 IMPLEMENTAÇÃO DO MÉTODO DOS PAINÉIS PARA O ESTUDO DE PROPRIEDADES AERODINÂMICAS DE AEROFÓLIOS João de Sá Brasil Lima joaobrasil.lima@gmail.com Resumo. Este artigo trata da implementação computacional do
IMPLEMENTAÇÃO DO MÉTODO DOS PAINÉIS PARA O ESTUDO DE PROPRIEDADES AERODINÂMICAS DE AEROFÓLIOS João de Sá Brasil Lima joaobrasil.lima@gmail.com Resumo. Este artigo trata da implementação computacional do
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2013/14
 Mestrado Integrado em Engenhia Mecânica Aerodinâmica 1º Semestre 13/14 Exame de ª época, 9 de Janeiro de 14 Nome : Hora : 8: Número: Duração : 3 horas 1ª Pte : Sem consulta ª Pte : onsulta limitada a livros
Mestrado Integrado em Engenhia Mecânica Aerodinâmica 1º Semestre 13/14 Exame de ª época, 9 de Janeiro de 14 Nome : Hora : 8: Número: Duração : 3 horas 1ª Pte : Sem consulta ª Pte : onsulta limitada a livros
Capítulo 6: Escoamento Externo Hidrodinâmica
 Capítulo 6: Escoamento Externo Hidrodinâmica Arrasto viscoso e de pressão Arrasto total Campo de escoamento Linhas de corrente: definidas como a linha contínua que é tangente aos vetores velocidade ao
Capítulo 6: Escoamento Externo Hidrodinâmica Arrasto viscoso e de pressão Arrasto total Campo de escoamento Linhas de corrente: definidas como a linha contínua que é tangente aos vetores velocidade ao
Álgumas palavras sobre as Equações de Navier-Stokes
 Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
Introdução aos Métodos Quase-Experimentais
 Técnicas Econométricas para Avaliação de Impacto Introdção aos Métodos Qase-Experimentais Rafael Perez Ribas Centro Internacional de Pobreza Brasília, 23 de abril de 28 Introdção Breve descrição de métodos
Técnicas Econométricas para Avaliação de Impacto Introdção aos Métodos Qase-Experimentais Rafael Perez Ribas Centro Internacional de Pobreza Brasília, 23 de abril de 28 Introdção Breve descrição de métodos
FENÔMENOS DE TRANSPORTES
 FENÔMENOS DE TRANSPORTES AULA 6 CINEMÁTICA DOS FLUIDOS PROF.: KAIO DUTRA Conservação da Massa O primeiro princípio físico para o qual nós aplicamos a relação entre as formulações de sistema e de volume
FENÔMENOS DE TRANSPORTES AULA 6 CINEMÁTICA DOS FLUIDOS PROF.: KAIO DUTRA Conservação da Massa O primeiro princípio físico para o qual nós aplicamos a relação entre as formulações de sistema e de volume
a. com fontes emissoras pontuais (chaminés); b. com fontes emissoras lineares (estradas);
 MODELAÇÃO DE POLUIÇÃO ATMOSFÉRIA A fnção dos modelos de qalidade do ar é representar matematicamente os processos de dilição, transporte e mistra dos polentes emitidos para o ar. Eistem vários tipos de
MODELAÇÃO DE POLUIÇÃO ATMOSFÉRIA A fnção dos modelos de qalidade do ar é representar matematicamente os processos de dilição, transporte e mistra dos polentes emitidos para o ar. Eistem vários tipos de
Vicente Luiz Scalon. Disciplina: Transmissão de Calor
 Convecção Forçada Externa Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Método Empírico Camada Limite Teoria de Prandtl Solução de Blasius Convecção Laminar
Convecção Forçada Externa Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Método Empírico Camada Limite Teoria de Prandtl Solução de Blasius Convecção Laminar
2 Métodos Experimentais
 Métodos Experimentais.1. Eqipamentos Este capítlo trata da descrição dos eqipamentos tilizados neste estdo, princípios de fncionamento e aspectos metrológicos referentes aos mesmos..1.1.densímetro Fabricado
Métodos Experimentais.1. Eqipamentos Este capítlo trata da descrição dos eqipamentos tilizados neste estdo, princípios de fncionamento e aspectos metrológicos referentes aos mesmos..1.1.densímetro Fabricado
Capítulo 4 Equilíbrio de Radiação (RE) e Equilíbrio de Partículas Carregadas (CPE)
 Física das Radiações e Dosimetria Capítlo 4 Eqilíbrio de Radiação (RE) e Eqilíbrio de Partíclas Carregadas (CPE) Dra. Lciana Torinho Campos Programa Nacional de Formação em Radioterapia Introdção Introdção
Física das Radiações e Dosimetria Capítlo 4 Eqilíbrio de Radiação (RE) e Eqilíbrio de Partíclas Carregadas (CPE) Dra. Lciana Torinho Campos Programa Nacional de Formação em Radioterapia Introdção Introdção
Transferência de Calor
 Transferência de Calor Escoamento Sobre uma Placa Plana Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Escoamento Sobre uma Placa Plana Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
0.5 setgray0 0.5 setgray1. Mecânica dos Fluidos Computacional. Aula 3. Leandro Franco de Souza. Leandro Franco de Souza p.
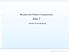 Leandro Franco de Souza lefraso@icmc.usp.br p. 1/2 0.5 setgray0 0.5 setgray1 Mecânica dos Fluidos Computacional Aula 3 Leandro Franco de Souza Leandro Franco de Souza lefraso@icmc.usp.br p. 2/2 Fluido
Leandro Franco de Souza lefraso@icmc.usp.br p. 1/2 0.5 setgray0 0.5 setgray1 Mecânica dos Fluidos Computacional Aula 3 Leandro Franco de Souza Leandro Franco de Souza lefraso@icmc.usp.br p. 2/2 Fluido
4.3 Ondas de Gravidade de Superfície
 4.3 Ondas de Gravidade de Serfície As ondas de gravidade serficial se desenvolvem qando eiste ma serfície livre o ma descontinidade de densidade. A força restaradora é das ondas de gravidade é a gravidade,
4.3 Ondas de Gravidade de Serfície As ondas de gravidade serficial se desenvolvem qando eiste ma serfície livre o ma descontinidade de densidade. A força restaradora é das ondas de gravidade é a gravidade,
Os vórtices da turbulência bidimensional
 file:///c:/users/utilizador/documents/ficheiros%20universidade/diversos/bolsa%20gulbenkian/2008.09/hurricane%5b1%5d.jpg Os vórtices da turbulência bidimensional Seminário Diagonal 27/05/2009 José Ricardo
file:///c:/users/utilizador/documents/ficheiros%20universidade/diversos/bolsa%20gulbenkian/2008.09/hurricane%5b1%5d.jpg Os vórtices da turbulência bidimensional Seminário Diagonal 27/05/2009 José Ricardo
MECÂNICA DOS FLUIDOS II. Introdução à camada limite. Introdução à camada limite. Conceitos:
 MECÂNICA DOS FLIDOS II Conceitos: Camada limite; Camada limite confinada e não-confinada; Escoamentos de corte livre e Esteira; Camadas limites laminares e turbulentas; Separação da camada limite; Equações
MECÂNICA DOS FLIDOS II Conceitos: Camada limite; Camada limite confinada e não-confinada; Escoamentos de corte livre e Esteira; Camadas limites laminares e turbulentas; Separação da camada limite; Equações
Notas de aula prática de Mecânica dos Solos I (parte 12)
 1 Notas de ala prática de Mecânica dos Solos I (parte 1) Hélio Marcos Fernandes Viana Tema: Exercícios de permeabilidade dos solos evolvendo a aplicação das leis de Bernoilli e Darcy 1. o ) Considerando-se
1 Notas de ala prática de Mecânica dos Solos I (parte 1) Hélio Marcos Fernandes Viana Tema: Exercícios de permeabilidade dos solos evolvendo a aplicação das leis de Bernoilli e Darcy 1. o ) Considerando-se
h coeficiente local de transferência de calor por convecção h coeficiente médio de transferência de calor por convecção para toda a superfície
 \CONVECÇÃO FORÇADA EXTERNA " Fluxo térmico: q h(tsup T ) h coeficiente local de transferência de calor por convecção Taxa de transferência de calor q ha sup (T sup T ) h coeficiente médio de transferência
\CONVECÇÃO FORÇADA EXTERNA " Fluxo térmico: q h(tsup T ) h coeficiente local de transferência de calor por convecção Taxa de transferência de calor q ha sup (T sup T ) h coeficiente médio de transferência
5 Análise dos Resultados
 5 Análise dos Resultados Neste capítulo é apresentada a análise dos resultados obtidos mediante o uso do código computacional existente, levando-se em conta as modificações que foram feitas. Nesta análise
5 Análise dos Resultados Neste capítulo é apresentada a análise dos resultados obtidos mediante o uso do código computacional existente, levando-se em conta as modificações que foram feitas. Nesta análise
