IMPLEMENTAÇÃO DE ALGORITMOS DE INTEGRAÇÃO IMPLÍCITA PARA MODELOS CONSTITUTIVOS ELASTO- PLÁSTICOS NA SIMULAÇÃO GEOMECÂNICA.
|
|
|
- Bernardo Lagos
- 5 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS DEPARTAMENTO DE ENGENHARIA CIVIL IMPLEMENTAÇÃO DE ALGORITMOS DE INTEGRAÇÃO IMPLÍCITA PARA MODELOS CONSTITUTIVOS ELASTO- PLÁSTICOS NA SIMULAÇÃO GEOMECÂNICA. LEILA BRUNET DE SÁ BESERRA Recife, PE Agosto de 00
2 IMPLEMENTAÇÃO DE ALGORITMOS DE INTEGRAÇÃO IMPLÍCITA PARA MODELOS CONSTITUTIVOS ELASTO-PLÁSTICOS NA SIMULAÇÃO GEOMECÂNICA. LEILA BRUNET DE SÁ BESERRA Dissertação submetida ao corpo docete do programa de pós-graduação em egeharia civil da Uiversidade Federal de Perambuco como parte itegrate dos requisitos ecessários à obteção do grau de Mestre em Egeharia Civil. Área de cocetração: Egeharia Geotécica. ORIENTADOR: LEONARDO JOSÉ NASCIMENTO GUIMARÃES CO-ORIENTADOR: IVALDO DÁRIO DA SILVA PONTES FILHO Recife, PE Agosto de 00
3 Catalogação a fote Bibliotecária Rosieide Mesquita Goçalves Luz / CRB4-36 (BCTG) B554i Beserra, Leila Bruet de Sá. Implemetação de algoritmos de itegração implícita para modelos costitutivos Elasto-Plásticos a simulação geomecâica / Leila Bruet de Sá Beserra. - Recife: O Ator, 0. Vii,80f., figs., tabs., gráfs. Orietador: Prof. Dr. Leoardo José Nascimeto Guimarães. Co-Orietador. Prof. Dr. Ivaldo Dário da Silva Potes Filho. Dissertação (Mestrado) Uiversidade Federal de Perambuco. CTG. Programa de Pós-Graduação em Egeharia Civil, 0. Icui Referêcias..Egeharia Civil.. Elasto -Plasticidade. 3. Elemetos Fiitos. 4. Itegração Implícita. 5. Permeabilidade. 6. Acoplameto Hidro Geomecâico. I. Guimarães, Leoardo José Nascimeto (Orietador). II. Potes Filho, Ivaldo Dário da Silva (Co-Orietador). I. Título. 64 CDD (. Ed.) UFPE/BCTG06/0
4 IMPLEMENTAÇÃO DE ALGORITMOS DE INTEGRAÇÃO IMPLÍCITA PARA MODELOS CONSTITUTIVOS ELASTO-PLÁSTICOS NA SIMULAÇÃO GEOMECÂNICA. Leila Bruet de Sá Beserra DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DO PROGRAMA DE PÓS- GRADUAÇÃO EM ENGENHARIA CIVIL DA UNIVERSIDADE FEDERAL DE PERNAMBUCO COMO PARTE INTEGRANTE DOS REQUISITOS NECESSÁRIOS À OBTENÇÃO DO GRAU DE MESTRE EM ENGENHARIA CIVIL. Leoardo José do Nascimeto Guimarães Orietador, Ph. D. Ivaldo Dário da Silva Potes Filho Co-Orietador, D. Sc. Osvaldo Luís Mazoli Examiador Extero, Ph. D. Nestor Alberto Zouai Pereira Examiador Extero, Ph. D. Recife, PE Agosto de 00
5 AGRADECIMENTOS Aos professores Leoardo Guimarães e Ivaldo Potes, por todos os esiametos, explicações e orietações tão importates para a realização e coclusão desta dissertação. Ao Vitor e a miha mãe Sâia pelo esforço e sacrifício em coviver com a miha ausêcia ao logo do período do mestrado, a miha mãe Clara que sempre foi um suporte técico para todos da ossa casa e aos meus pais Bety e Jarbas que mesmo um pouco loge sempre torceram pelo meu sucesso. A todos os meus amigos do LMCG, Julliaa, Igor, Nayra, Ialdo, Viícius, Thiago, Joatha e Luciaa pela costate compahia, amizade e icetivo, e em especial às mihas queridas amigas, Marcela, por compartilhar a casa comigo, e Débora, com sua eergia sempre estimulate, todos me ajudaram a fazer o mestrado a UFPE. A todos os fucioários da UFPE pelo apoio, em especial à Rose, que é capaz de resolver qualquer problema, e a Brito com seus cafés a hora certa. A todos os professores que cotribuíram para a miha formação, desde a escola até a pósgraduação, em especial ao prof. Gilso da UFPB, que me ajudou os meus primeiros passos da vida cietífica. Ao CNPq e a ANP, por meio do PRH-6, pelo apoio fiaceiro oferecido durate o desevolvimeto de miha pesquisa. i
6 RESUMO A previsão do comportameto dos solos e rochas, pricipalmete quado submetidos a variações o estado de tesões, ecessita de uma modelagem que leve em cota o fato do meio poroso ser deformável. Para resolver problemas dessa atureza, é ecessária a adoção de modelos costitutivos mecâicos e hidráulicos que cosiderem a variação da permeabilidade itríseca da rocha (parâmetro chave do problema hidráulico) em fução da porosidade, que por sua vez poderá variar devido à deformação do meio (parâmetro do modelo costitutivo mecâico). Uma etapa importate o processo de simulação de meios porosos cosiste a escolha de um algoritmo para a itegração das relações costitutivas que seja eficiete do poto de vista computacioal, este setido foram implemetados o código de elemetos fiitos CODE_BRIGHT algoritmos implícitos de itegração de tesões para os modelos costitutivos elasto-plásticos de vo Mises (Simo & Hughes, 998) e de Drucker-Prager. (Souza Neto et al, 008). Também foi proposta uma modificação o algoritmo de itegração implícita com projeção explícita do multiplicador plástico, deomiado IMPLEX (Oliver et al., 008), resultado uma melhor aproximação deste. Na etapa de validação dos algoritmos implemetados foram simulados, um caso de expasão de cavidade cilídrica com solução exata cohecida e dois casos em escala de campo, o escorregameto de um talude, ode somete o modelo mecâico pode ser testado e um caso de perfuração de poço, ode o acoplameto hidro-mecâico é avaliado. Foi modelado aida, um esaio triaxial, ode foi observada a modificação proposta para o IMPLEX. A aálise dos resultados obtidos mostrouse satisfatória. Palavras-chave: Plasticidade, Elemetos fiitos, Itegração implícita, Permeabilidade, Acoplameto hidro-geomecâico. ii
7 ABSTRACT Predictig the behavior of oil reservoirs, especially whe they are uder variable effective stresses, requires a model that takes ito accout the deformatio of porous media. This lik is doe cosiderig permeability ad porosity variatios as a fuctio of stress-strai state. The umerical tool used i this paper was the fiite elemet code CODE_BRIGHT which solves the equilibrium ad fluid flow equatios i a coupled way. I this kid of problem, a importat compoet of the fiite elemet code is the algorithm for the itegratio of stressstrai relatioships, which geerally are based o highly o-liear elastic-plastic costitutive laws. A ew versio of the implicit algorithm with a explicit predictio of the plastic multiplier, called IMPLEX (Oliver et al., 008), was adopted i this paper. This algorithm improves the efficiecy ad robustess of the umerical code, allowig solvig bigger ad more complex problems. A simulatio of well stability was carried out ad the results showed the performace of the implemeted algorithm. Key-words: Plasticity, Fiite Elemet Methods, Implicit itegratio, Permeability, Hydromechaical coupled iii
8 LISTA DE FIGURAS Figura. - Superfície de Fluêcia (Ges & Prats, 003)... Figura. - Material elasto-plástico perfeito, com edurecimeto e com amolecimeto, respectivamete... 3 Figura.3 - Potecial plástico e vetor de deformações plásticas (Ges & Prat, 003)... 4 Figura.4 - Edurecimeto isotrópico e ciemático, respectivamete (Medoça, 005)... 5 Figura.5- Superfície de fluêcia de vo Mises (Gomes, 006)... 9 Figura.6 - Superfície de fluêcia de Drucker Prager (Sousa, 004)... Figura 3. - Algoritmo de retoro ao vértice (Souza Neto et al, 008)... 4 Figura 4. - Geometria do problema de cavidade cilídrica Figura 4. - Malha de elemetos fiitos Figura Curva carga-deslocameto Figura Esquema do esaio triaxial Figura Trajetória de tesões (tesão média x tesão de vo Mises) Figura Trajetória de tesões (tesão média x tesão de vo Mises) Figura 4.7 -Geometria e codições de cotoro do problema Figura Malha de elemetos fiitos... 6 Figura Variação da altura crítica do talude com o fator de gravidade... 6 Figura Evolução dos deslocametos horizotais com o fator de gravidade... 6 Figura 4. - Evolução dos deslocametos verticais com o fator de gravidade Figura 4. - Evolução das deformações plásticas cisalhates com o fator de gravidade Figura Evolução das deformações plásticas volumétricas com o fator de gravidade. 64 Figura Distribuição dos deslocametos Figura Vetores de deslocameto Figura Deformações plásticas cisalhates iv
9 Figura Deformações plásticas volumétricas Figura 4.8 Distribuição de porosidade Figura Trajetória de tesões para o caso do talude vertical Figura Geometria do problema e malha de elemetos fiitos Figura 4. - Deformações plásticas desviadoras Figura 4. - Imagem ultrasôica de perfil de poço apresetado breakout a direção da tesão pricipal meor o plao ormal ao poço Figura Variação de porosidade... 7 Figura Variação de permeabilidade... 7 Figura Distribuição da pressão de líquido Figura Trajetória de tesões v
10 LISTA DE TABELAS Tabela 4. - Parâmetros do material do cilidro Tabela 4. -Propriedades do material do esaio triaxial Tabela 4 3 Parâmetros do Problema de Talude Vertical Tabela Parâmetros do material do maciço escavado vi
11 SUMÁRIO.Itrodução..... Itrodução..... Objetivos Orgaização da Dissertação... 3.Caracterização hidromecâica e relações costitutivas Ciemática e Equilíbrio Modelo Costitutivo Elasto-plásticos Ivariates Decomposição Aditiva do Tesor de Deformações Resposta Elástica Resposta Plástica Potecial Plástico Lei de Edurecimeto Matriz Costitutiva Elasto-plástica Critério de Plastificação de vo Mises Critério de Plastificação de Drucker Prager Modelo Costitutivo Hidráulico Equação da Coservação de massa Relação etre Permeabilidade e Porosidade... 3 vii
12 .3.3. Deformações Plásticas e Variação da Permeabilidade Formulação Numérica Algoritmo de Itegração Implícita para o Modelo de Vo Mises com Edurecimeto Estado de tesões Edurecimeto Liear Módulo Tagete Cosistete Elasto-Plástico Algoritmo Básico Implemetado Algoritmo de Itegração Implícita para o Modelo de Drucker Prager Equações Costitutivas Algoritmo de Retoro para o Modelo de Drucker Prager Retoro à Superfície do Coe Retoro ao Poto de Sigularidade (Vértice) Escolha do Retoro Apropriado Matriz Tagete Cosistete Algoritmo Básico Implemetado Algoritmo de Itegração Implícita-Explícita (IMPLEX) para o Modelo de Drucker Prager Algoritmo Básico Implemetado Casos Aalisados Expasão de Cavidade Cilídrica Esaio Triaxial Aálise de Talude Vertical viii
13 4.4. Perfuração de Poço Coclusões Sugestões Para Trabalhos Futuros Referêcias Bibliográficas ix
14 . INTRODUÇÃO.. INTRODUÇÃO A dispoibilidade crescete de recursos computacioais cada vez mais robustos e dissemiados abre espaço para a utilização de ferrametas de trabalho mais poderosas e alavaca o desevolvimeto de teorias e modelos cada vez mais complexos para a represetação dos diversos feômeos e comportametos. Essa realidade ão é diferete para a Egeharia Geotécica, que tradicioalmete esteve apoiada os coceitos da Mecâica dos Solos desevolvidas por Terzaghi, a Teoria da Elasticidade e as teorias de plasticidade. A partir das observações em campo e em esaios de laboratório, diversos modelos costitutivos foram desevolvidos com ituito de represetar o comportameto dos solos. Esses modelos são costruídos como simplificação das codições reais mediate a adoção de hipóteses simplificadoras que visam dimiuir o grau de complexidade matemática da formulação bem como possibilitar a resolução do sistema de equações resultates. Com o adveto da modelagem computacioal pode-se aproveitar ao máximo as vatages oferecidas pelos modelos costitutivos mais avaçados, porém tais modelos ão devem possuir um grau de complexidade que iviabilize sua aferição ou iterpretação de seus resultados. O modo como os parâmetros do problema variam o espaço e o tempo assim como as relações existetes etre as gradezas relevates a aálise devem ser cotempladas a etapa de descrição feomeológica, de maeira a validar o modelo proposto. Durate a etapa de simulação matemática do comportameto de um material sob solicitação mecâica, devem ser cosideradas suas propriedades físicas e estruturais, além de sua costituição físicomieralógica, resposáveis pela maeira particular com a qual se verifica a resposta do meio solicitado (Vascocelos, 007). Os materiais ormalmete estudados os campos da Egeharia Geotécica e de Reservatórios de Petróleo apresetam uma estrutura porosa, cujos vazios podem estar total ou
15 parcialmete preechidos por líquidos. O estado de deformação e as codições de resistêcia de tais meios ecessitam, para sua total compreesão, de recursos teóricos que vão além dos fudametos básicos da Mecâica dos Sólidos. Costata-se que a preseça de fluido os poros e sua iteração com e as partículas sólidas iflueciam a resposta global do meio poroso (Lambe & Whitma, 976). Para resolver problemas dessa atureza, é ecessária a adoção de modelos costitutivos mecâicos e hidráulicos que levem em cota o fato do meio poroso ser deformável. Neste caso, a permeabilidade itríseca (ou absoluta) da rocha, um dos parâmetros chave do problema hidráulico, será cosiderada em fução da porosidade, que por sua vez poderá variar quado o meio se deforma. Esta deformação ocorre quado há variações o estado de tesões efetivas, dadas pelo tesor de tesões totais meos o tesor esférico das poro-pressões. Do poto de vista matemático, este problema acoplado hidro-mecâico é represetado por um sistema de equações ão-lieares em derivadas parciais que, quado discretizado, resulta um sistema de equações algébricas ão-lieares ode as equações de fluxo são modificadas através da icorporação do termo de deformação da matriz porosa, equato que a equação mecâica passa a icluir um termo de pressão e saturação, proveietes das equações de fluxo. Diferetes esquemas de solução podem ser usados, a depeder do tamaho e ível de acoplameto etre os problemas hidráulico e geomecâico. Nesse cotexto se isere a ferrameta CODE_BRIGHT (COupled DEformatio, BRIe, Gas ad Heat Trasport), utilizada este trabalho, e que se presta a modelar problemas em até três dimesões, caracterizados por feômeos de atureza mecâica, hidráulica, térmica e química, permitido aida o acoplameto etre duas ou mais destas modalidades... OBJETIVOS O presete trabalho tem como pricipal objetivo acrescetar à ferrameta CODE_BRIGHT uma família de algoritmos de itegração implícita para leis costitutivas tesão-deformação.
16 Visado um gaho de eficiêcia computacioal e uma simulação umérica mais satisfatória. Especificamete podemos listar os seguites objetivos pricipais. - Desevolver implemetações uméricas de algoritmos de itegração implícita e implícito-explícita (IMPLEX) para o cálculo das tesões e deformações segudo os modelos elasto-plásticos de vo Mises e Drucker Prager. - Simular os esaios de laboratório, permitido que os resultados destes sejam extrapolados para a escala de campo através da modelagem umérica. - Simular problemas acoplado fluxo e deformação em problemas que iteressam a egeharia geotécica e a idústria de petróleo..3. ORGANIZAÇÃO DA DISSERTAÇÃO A presete dissertação é composta de cico capítulos. Iicialmete, o capítulo, são apresetados os objetivos que se pretede alcaçar com o trabalho e também as motivações que levaram a escolha do tema a ser desevolvido. No capítulo são descritas brevemete as teorias e formulações matemáticas que caracterizam a modelagem do problema acoplado hidro-mecâico. São apresetados os modelos costitutivos mecâico e hidráulicos adotados o desevolvimeto do trabalho e também uma breve revisão sobre algus aspectos da teoria da plasticidade que cocerem ao tema desevolvido a dissertação. No capítulo 3 estão descritos os algoritmos que foram iseridos o código em elemetos fiitos CODE_BRIGHT. Para itegração de tesões foi implemetado o algoritmo de itegração implícita apresetado por Simo & Hughes (998) para o modelo de vo Mises, equato para o modelo de Drucker Prager foi utilizado o algoritmo proposto por de Souza Neto et al (008) e aida foi acrescetada uma simplificação do algoritmo implícito proposta por Oliver et al(008). 3
17 No capítulo 4 são apresetados algus exemplos de validação dos algoritmos implemetados através de simulações de esaios de laboratórios e problemas com soluções cohecidas. São também mostradas as aálises da modelagem de dois problemas que iteressam à egeharia geotécica, o estudo de estabilidade de taludes verticais e a perfuração de poços em rochas frágeis. Fialmete, o capítulo 5 são apresetadas as coclusões da dissertação e etão são sugeridas futuras lihas de pesquisa a serem desevolvidas tedo em vista a cotiuidade do trabalho, bem como a melhora dos modelos utilizados para simular o comportameto do meio poroso e da eficiêcia computacioal da ferrameta CODE_BRIGHT. 4
18 . CARACTERIZAÇÃO HIDROMECÂNICA E RELAÇÕES CONSTITUTIVAS Neste capítulo serão apresetados os coceitos e as hipóteses básicas adotadas a modelagem hidro-mecâica que descreve o comportameto de solos saturados, deformáveis e comportameto elasto-plástico, quado submetidos a programas cargas quasi-estáticas. Os solos e rochas são materiais trifásicos costituídos por partículas sólidas e vazios que podem estar total ou parcialmete preechidos por líquidos. Os movimetos e o estado de equilíbrio destes sólidos porosos ecessitam, para sua total compreesão, dos fudametos básicos e recursos teóricos da Mecâica dos Sólidos e dos Fluidos, para solicitações quaseestáticas e fluxo de baixa velocidade. A iteração do fluido os vazios e o esqueleto sólido iflueciam a resposta global do meio (Skempto, 96; Lambe & Whitma, 976; Sousa Pito, 000). Nesta modelagem serão cosideradas as seguites hipóteses (Maier e Cocchetti, 00): SATURAÇÃO COMPLETA DO ESQUELETO SÓLIDO POR UM ÚNICO FLUIDO; PERMEABILIDADE CONSTANTE COM O TEMPO; HIPÓTESE DE PEQUENAS DEFORMAÇÕES, OU SEJA, RELAÇÃO CINÉTICA LINEAR; PROGRAMA DE CARGAS QUASI-ESTÁTICO, ISTO É, PROGRAMA DE CARGAS EXTERNAS LENTO E SEM EFEITOS INERCIAIS, MAS RÁPIDO O SUFICIENTE COM RELAÇÃO AO PROCESSO DE FLUXO; VALIDADE DO PRINCÍPIO DAS TENSÕES EFETIVAS, COMO DESCRITO A SEGUIR. Em meados da década de 90, Karl Terzaghi itroduziu o coceito de tesões efetivas com o ituito de explicar a resposta de um meio poroso saturado quado submetido a solicitações exteras. Ele observou experimetalmete que as deformações produzidas estes meios saturados são depedetes de um estado de tesões efetivas atuates sobre o meio. Quado há uma solicitação em termos de tesões totais () e existe uma fase líquida a qual ocorre uma 5
19 pressão o líquido p l., etão o tesor de tesões efetivas defiido por Terzaghi é caracterizado a partir da seguite relação: ' p I (.) l ode represeta o tesor de tesões totais, ' o tesor de tesões efetivas, e p l a pressão exercida pelo fluido cotido os poros e I é o tesor uitário de seguda ordem. É importate assialar que as variações de movimeto (deslocameto, deformações, variação volumétrica) o corpo são devidas exclusivamete a variações as tesões efetivas (Bishop & Blight, Atkiso & Brasby, 978; Lacellotta, 995). A equação (.) descreve satisfatoriamete o comportameto dos solos saturados quado são observadas as codições de icompressibilidade dos grãos. Quado esta codição ão é satisfeita a resposta mecâica dos solos e das rochas é mais precisamete cotrolada por uma tesão efetiva que é fução da tesão total aplicada e da poro-pressão, de acordo com a seguite expressão: ' αpi (.) que correspode a uma reformulação do modelo de Terzaghi com a itrodução do parâmetro α (coeficiete de Biot) relacioado à compressibilidade do meio (Biot, 94), sedo α : α K K s (.3) ode, K e K s são os módulos volumétricos da matriz porosa e dos grãos, respectivamete... CINEMÁTICA E EQUILÍBRIO Vamos cosiderar etão, um meio saturado com domíio Ω e uma froteira Γ, composta por duas partes disjutas e complemetares Γ u e Γ f as quais são prescritos os deslocametos e as 6
20 forças exteras, tais que (Γ u U Γ f Γ) e (Γ u Γ f Ø). Aalogamete Γ p e Γ q são as partes de Γ as quais estão prescritas a pressão do fluido p l e o fluxo q, tais que (Γ pl U Γ q Γ) e (Γ pl Γ q Ø), com Γ regular. Algus aspectos difereciam o solo de outros materiais, a exemplo da plastificação sob carregameto exclusivo das tesões médias. Para uma determiada massa de solo, uma parcela cosiderável de seu volume é composta por vazios que podem ou ão estar preechidos de líquido. Para que haja uma mudaça o volume desta massa de solo é preciso que haja movimeto da fase fluida (ar e água) existete os vazios. Esse movimeto volumétrico vai depeder das restrições impostas pelo esqueleto sólido. As variáveis que relacioam a proporção etre os vazios e as partículas sólidas são o ídice de vazios: V V v e (.4) t e a porosidade: φ e e (.5) ode V v é o volume de vazios e V t o volume total. As compoetes do tesor de deformações podem ser cosideradas como fuções cotíuas das compoetes de deslocameto. Para o caso de pequeas deformações, tal relação assume uma cofiguração liear coforme represetada pela seguite equação: ε T ( u u ) em Ω (.6) Equato o equilíbrio fica caracterizado por: div b 0 em Ω (.7) 7
21 .. MODELO CONSTITUTIVO ELASTO-PLÁSTICO A teoria da plasticidade descreve o comportameto de uma classe de materiais bastate relevate para a egeharia geotécica, rochas, argilas e solos de uma maeira geral. Esses materiais, após serem submetidos a um carregameto, apresetam uma deformação permaete (ou plástica) mesmo quado completamete descarregados. Em particular, este trabalho, a teoria da plasticidade está restrita à pequeas deformações e à descrição de materiais para os quais a deformação ão é depedete da taxa de aplicação do carregameto. Segudo Sousa (004) são critérios esseciais para a formulação de um modelo elastoplástico, a relação elástica, o critério de plastificação, a existêcia de um potecial plástico e as leis de edurecimeto e amolecimeto... INVARIANTES Devido à ifluêcia que a deformação volumétrica exerce o comportameto dos solos, é coveiete, o tratameto de problemas geotécicos, trabalhar com ivariates que possibilitem separar os efeitos associados à variação de volume daqueles associados à mudaça de forma (distorção). Para melhor compreesão dos coceitos que serão apresetados, faz-se ecessária a defiição de algus ivariates, como se segue. O tesor de tesões é defiido como: 8
22 x τ xy τ xz τ τ xy y yz τ xz τ yz z (.8) e o tesor desviador é defiido como: S pi (.9) ode I é o tesor idetidade e p a tesão média, defiido como: p tr( ) ( 3) ( x y z ) 3 3 (.0) Portato: S x τ xy τ xz p τ y τ xy yz p τ τ z xz yz p (.) O segudo ivariate adotado é defiido como: J S (.) J ( x p) ( y p) ( ( ) τ xz τ xz τ yz z p) (.3) Segudo Che & Baladi (985) os ivariates p e J relacioam-se com a eergia associada à variação volumétrica e à eergia associada à distorção respectivamete. 9
23 ... DECOMPOSIÇÃO ADITIVA DO TENSOR DE DEFORMAÇÕES. Uma das pricipais hipóteses da teoria da plasticidade para pequeas deformações é a decomposição do tesor de deformações totais ε em um tesor de deformações elásticas (ou reversíveis) ε e e um tesor de deformações plásticas (ou irreversíveis), ε p. e ε ε ε p (.4)..3. RESPOSTA ELÁSTICA A elasticidade liear idepede do tempo e da história de carregameto, e cosidera que todas as mudaças de deformação em fução das variações do estado tesioal são istatâeas e o sistema é completamete reversível, ou seja, a eergia absorvida é totalmete recuperada o processo de descarregameto. A deformação elástica pode ser defiida através do pricípio da decomposição aditiva, que decompõe a deformação total em uma parcela elástica e outra plástica (Eq..4). e ε ε ε p (.5) Nesse caso, a lei costitutiva para a tesão pode ser expressa como: D e ε e (.6) ode D e é a matriz de rigidez elástica. 0
24 ..4. RESPOSTA PLÁSTICA De acordo com Ges & Prat (003) a teoria da Plasticidade a superfície de fluêcia é uma fução das tesões e de outros parâmetros que separa, o espaço das tesões, a região ode o material possui comportameto elástico da região ode o comportameto é plástico, também deomiada região das tesões plasticamete admissíveis. A expressão geral que defie a superfície de fluêcia se escreve como: f (, h) 0 (.7) ode h é um vetor de parâmetros de estado que cotrolam o edurecimeto. A região ode o material se comporta elasticamete deomia-se domíio elástico e é defiida por: Ε e { f (, h) < 0} (.8) A fução de fluêcia delimita uma região fechada o espaço, através de uma superfície de fluêcia, descrita como: Ε { f (, h) 0} (.9) Quado o material está em regime plástico, ou seja, deformado-se de maeira irreversível, o estado de tesões sempre deve estar sobre a superfície de fluêcia, sedo o exterior da superfície a região das tesões iadmissíveis, como mostra a Figura..
25 Figura. - Superfície de Fluêcia (Ges & Prats, 003) Em geral a superfície é depedete das tesões atuates e seu tamaho varia como uma fução dos parâmetros de estado h. Para plasticidade perfeita h é costate e a superfície de fluêcia ão muda de tamaho durate o carregameto. Para plasticidade com edurecimeto ou amolecimeto h varia com as deformações plásticas e a superfície de fluêcia se expade ou dimiui durate o carregameto. Na Figura. é possível observar o comportameto dos materiais elasto-plásticos perfeitos, com edurecimeto e com amolecimeto. Na plasticidade perfeita, os materiais apresetam patamar de escoameto defiido pela tesão de escoameto y, parâmetro do material para determiado sistema de cargas e codições de cotoro, que se matém costate. Para materiais com edurecimeto a tesão de escoameto iicial é excedida e em materiais com amolecimeto a tesão de escoameto decresce.
26 Figura. - Material elasto-plástico perfeito, com edurecimeto e com amolecimeto, respectivamete (uiaxial.)..5. POTENCIAL PLÁSTICO Sob codição uiaxial é cosiderado implicitamete que a direção das deformações plásticas icremetais é coicidete com a direção da tesão imposta. Cotudo em um caso multiaxial a situação se tora mais complexa devido à existêcia de seis compoetes de tesões e deformações. É ecessário se estabelecer a direção de deformação plástica em qualquer estado de tesão. Assim para defiir as direções das deformações plásticas icremetais recorre-se a existêcia de um potecial plástico g, tal que, a lei de escoameto plástico é caracterizada por: dε ij g λ (.0) ij Ode dε ij represeta as seis compoetes da deformação plástica icremetal, λ é chamado de multiplicador plástico e é um escalar que forece a magitude da deformação plástica. A direção é dada pelo gradiete de g, a fução potecial plástica, que é expressa como, g (, ξ) 0 (.) Ode ξ é um vetor característico dos parâmetros do material. 3
27 A direção da deformação plástica é paralela a direção do gradiete do potecial plástico e, portato, perpedicular a superfície determiada por g, como mostra a figura.3. Quado a superfície de fluêcia e o potecial plástico coicidem (fg), trata-se de plasticidade associada, o caso cotrário trata-se plasticidade ão-associada (Ges e Prat, 003). Figura.3 - Potecial plástico e vetor de deformações plásticas (Ges & Prat, 003)..6. LEI DE EDURECIMENTO Com o iício da plastificação, poderá ocorrer um aumeto ou dimiuição da superfície de fluêcia e são as leis de edurecimeto ou amolecimeto, respectivamete, que regulam este feômeo. A defiição dessas leis pode ser feita estabelecedo-se a variação do parâmetro h, quado defiidas tais leis permitem descrever as mudaças de posição e de tamaho da superfície de plastificação. Podem ser cosiderados dois tipos de edurecimeto: isotrópico,quado apeas o tamaho da superfície é alterado; e ciemático, quado a superfície é deslocada sem sofrer variação de 4
28 forma ou tamaho sofredo apeas traslação a direção do fluxo plástico. A figura.4 ilustra os dois comportametos. Figura.4 - Edurecimeto isotrópico e ciemático, respectivamete (Medoça, 005) Para cotrolar tal variação do tamaho, forma ou posição da superfície de fluêcia devem ser defiidos os parâmetros de edurecimeto h, que por sua vez são fuções da deformação plástica acumulada como a seguir. h h( ε p ) (.)..7. TENSOR CONSTITUTIVO ELASTO-PLÁSTICO É preciso defiir a relação etre as tesões e deformações icremetais para sua coseqüete utilização os modelos costitutivos elasto-plásticos.. As equações são apresetadas em fução das taxas (derivadas em relação ao tempo) de tesão e de deformação. Defiido D ep como sedo o tesor costitutivo elasto-plástico, em cotraposição à matriz elástica D e, a relação etre as tesões e deformações para um material elasto-plástico, pode ser escrita da seguite forma. ep & D ε& (.3) 5
29 6 ode & é o icremeto do tesor de tesões e ε& o icremeto do tesor de deformações. O icremeto total de deformação pode ser dividido em duas parcelas, a elástica ( e ε& ) e a plástica ( p ε& ) como mostrado a seguir, De acordo com (.6) e (.0) tem-se que, Combiado (.6) e (.5) com (.4), pode-se escrever Coforme visto ateriormete, os materiais em regime plástico devem satisfazer a codição F(,h)0. Além disso, para ateder a codição de cosistêcia, o diferecial de F deve ser igual a zero (Medoça, 005), de ode se deduz que, e o multiplicador plástico resulta em: p e ε ε ε & & & (.4) D ε & & e e (.5) Ψ ε ), g( p λ & (.6) Ψ D Dε ), g( e e e λ & & (.7) 0 ), ( ), ( ), ( h h h h h & & & T T f f f (.8) A g f f T e T e T Ψ D h Dε h ), ( ), ( ), ( & λ (.9)
30 7 Ode, O parâmetro A varia de acordo com a codição de plasticidade do material. Para plasticidade perfeita, h é uma costate e A0. Para o caso de edurecimeto ou amolecimeto, (.30) é reescrita como, Devido à relação liear etre h e ε p, o parâmetro λ pode ser cacelado e A tora-se determiado. Caso a relação seja ão-liear o parâmetro escalar ão é cacelado e A se tora idetermiado. Tal dificuldade é estedida à determiação da matriz elasto-plástica. Na prática todos os modelos assumem uma relação liear etre o parâmetro de estado h e as deformações plásticas ε p (Sousa, 004). Substituido (.9) em (.7) obtém-se, E por fim, substituido (.3) em (.3), tem-se a expressão da matriz costitutiva elastoplástica, h h h & T f A ), ( λ (.30) p p T f A ε ε h h h & ), ( λ (.3) A g f f g T e T e T e e Ψ D h Dε h Ψ D Dε ), ( ), ( ), ( ), ( & & & (.3)
31 D ep D e e g(, Ψ) f (, h) e D D T T f (, h) e g(, Ψ) D A T (.33) CRITÉRIO DE PLASTIFICAÇÃO DE VON MISES De acordo com (Souza Neto et al, 008) este modelo, que é mais apropriado a descrição do comportameto elasto-plástico dos metais, foi proposto por vo Mises em 93. De acordo com o critério de Vo Mises, a plastificação se iicia quado o tesor das tesões desviadoras S atige um valor crítico. Tal modelo ão cosidera que a parte esférica do tesor de tesões teha ifluêcia as deformações plásticas. A superfície de fluêcia para este modelo pode ser escrita como, f (, h) S y 3 (.34) Ode y é a tesão de escoameto e varia para cada material. A superfície de fluêcia de vo Mises tem a forma de um cilidro circular o espaço das tesões pricipais, coforme ilustra a Figura.5. A superfície é idepedete da tesão média p e a parcela represeta seu y 3 raio. As deformações plásticas ocorrem ormalmete à superfície de fluêcia o setido do espaço de tesões iadmissíveis. Neste trabalho será cosiderado o modelo de vo Mises associado, portato fg. 8
32 Figura.5- Superfície de fluêcia de vo Mises (Gomes, 006)..8. CRITÉRIO DE PLASTIFICAÇÃO DE DRUCKER PRAGER O modelo proposto por Drucker e Prager, como uma suavização do modelo de Mohr- Coulomb (Souza Neto et al, 008), cosiste a modificação do critério de vo Mises ode um termo é itroduzido para que o modelo se tore sesível às variações volumétricas. O modelo de Drucker Prager prevê que a plastificação tem iício quado o ivariate de tesões desviadoras, J, e a tesão média, p, atigem uma combiação de valores críticos. Para este modelo podemos defiir a fução de fluêcia da seguite forma, f (, h) J ηp ξc (.35) Sedo, η(, ϕ) ; ξ ( c, ϕ) c (.36) 9
33 Ode a coesão (c) e o âgulo de atrito (ϕ) são parâmetros do material. A superfície de plastificação de Drucker Prager é um coe cilídrico como mostrado a figura.6 e os parâmetros η e ξ são escolhidos de acordo com a aproximação à superfície de Mohr-Coulomb. Duas das mais comus aproximações são obtidas fazedo-se coicidir os vértices iteros ou exteros da superfície de Mohr-Coulomb. A coicidêcia dos vértices exteros é dada por 6 si φ η (.37) 3(3 si φ) 6 cos φ ξ (.38) 3(3 si φ) E a coicidêcia dos vértices iteros é dada por, 6 si φ η (.39) 3(3 si φ) 6 cos φ ξ (.40) 3(3 si φ) Os coes exteros e iteros são cohecidos respectivamete como coe de compressão e coe de extesão. Uma seção do plao-π de ambas as superfícies é mostrada a figura.6. 0
34 Figura.6 - Superfície de fluêcia de Drucker Prager (Sousa, 004) Uma lei de fluxo plástico ão associada pode ser obtida para o modelo de Drucker Prager adotado-se como fução do potecial plástico a mesma fução de fluêcia ode o âgulo de atrito (ϕ) é substituído pelo âgulo de dilatâcia (ψ) sedo escrito da forma a seguir, g(, h) J η p (.4) ode, para o coe extero: 6 siψ η (.4) 3(3 siψ ) e, para o coe itero: 6 siψ η (.43) 3(3 siψ ).3. MODELO CONSTITUTIVO HIDRÁULICO
35 Um aspecto particular que diferecia o solo de outros materiais é que para uma determiada massa de solo, uma parcela cosiderável de seu volume é composta por vazios que podem ou ão estar preechidos de líquido. É coseso que para que haja uma mudaça o volume desta massa de solo é preciso que a fase fluida (ar e água) existete os vazios se movimete. Esse movimeto dos fluidos vai depeder da restrição que o esqueleto sólido impõe, e a variável utilizada para mesurar a dificuldade que a fase fluida tem de se movimetar etre os vazios do solo é a permeabilidade. A permeabilidade depede da forma e do tamaho das partículas sólidas e também da proporção em volume existete etre os vazios e os grãos, deomiado de ídice de vazios..3.. EQUAÇÃO DA CONSERVAÇÃO DE MASSA Para o problema hidráulico, as equações de coservação de quatidade de movimeto das fases fluidas são substituídas pela lei de Darcy geeralizada, cuja validade restrige-se a uma codição de fluxo lamiar (Bear, 988). Cosiderado o meio poroso como saturado por um úico fluido, a água, a coservação de massa da fase líquida é expressa como, ( ρ ) ( q u& lφ ρl l φρ l ) 0 (.44) t ode ρ l é a desidade do líquido e q l é o fluxo volumétrico de líquido, dado pela Lei de Darcy da seguite forma, q l k( pl ρlg) (.45) sedo k é o tesor de codutividade hidráulica, defiido como κ k (.46) µ l
36 ode g é o vetor de gravidade, κ o tesor de permeabilidade itríseca para o meio saturado e µ l a viscosidade do fluido..3.. RELAÇÃO ENTRE PERMEABILIDADE E POROSIDADE O acoplameto hidromecâico pode ser obtido por meio de uma relação direta etre a variação de uma variável mecâica e a evolução de uma propriedade do comportameto hidráulico e vice-versa. Na literatura as tetativas focam uma relação direta etre a permeabilidade itríseca com o estado de tesões, porém, essa tarefa, em termos práticos ecotra limitações decorretes da complexidade relativa ao problema. Sedo assim, as relações comumete ecotradas permitem determiar as variações de permeabilidade itríseca através de leis que relacioam esta gradeza com a porosidade (Sousa, 004). Sabe-se que a permeabilidade do meio poroso ão depede uicamete da porosidade, porém de uma série de fatores que devem ser cosiderados (tamaho e distribuição dos poros, percetual de fios, diâmetro efetivos dos grãos, etc). Em decorrêcia da complexidade cocerete à determiação de uma relação simples e geral, comumete são utilizadas relações experimetais que se prestam para uma estimativa aproximada da variação de tais parâmetros. No programa de elemetos fiitos CODE_BRIGHT, que resolve de maeira acoplada as equações do problema hidromecâico (Sousa et al, 005) há uma equação que expressa a depedêcia da permeabilidade itríseca com a porosidade por meio de uma lei expoecial empírica (Febex, 00), descrita como, [ ( φ )] κ κ 0. exp b φ0 (.47) Ode b é um parâmetro de ajuste que serve pra regular a amplitude da ifluêcia da variação da porosidade do meio sobre a permeabilidade. A magitude dos valores assumidos por este parâmetro se justifica pela maior ou meor desidade da rocha, visto que tais características 3
37 iflueciam a maeira como o ídice de vazios varia (e coseqüetemete, a porosidade também). Em geral valores elevados de b são empregados para rochas desas devido a pequea magitude da variação da porosidade (Sousa, 004). Essa lei permite represetar, de maeira aproximada, o comportameto hidromecâico de diversas classes de meios porosos, mediate a escolha de valor adequado para o parâmetro de ajuste DEFORMAÇÕES PLÁSTICAS E VARIAÇÃO DA PERMEABILIDADE As compoetes do tesor de deformações podem ser cosideradas como fuções cotíuas das compoetes de deslocameto, que para pequeas deformações, assume a forma: ε T ( u u ) (.48) Sedo o meio poroso um sistema costituído por várias fases, além da equação da coservação de massa da fase líquida deve ser cosiderada a coservação de massa da fase sólida, que uma vez admitida a hipótese de deformabilidade do meio, pode ser expressa como: t [( φ ) ρ ] [ ( φ) ρ ] s s u& (.49) Sedo u& o vetor de velocidade da fase sólida devido à deformabilidade do meio poroso. Defiido-se a derivada material de uma variável qualquer φ(x,y,z,t) como (Ferreira, 996 e Oller, 00): dϕ ϕ u& ϕ dt t (.50) tora-se possível estabelecer a variação da porosidade em fução da deformação volumétrica, 4
38 dφ dt ( φ ) dρ s ( φ v (.5) ρ s dt )ε& Ode ε& v é a taxa de deformação volumétrica e dρ s é o termo de compressibilidade da fase dt sólida. Quado se admite a icompressibilidade da fase sólida, o primeiro termo da equação (.49) se aula, de modo que a variação da porosidade é iflueciada apeas pela variação a deformação volumétrica. De acordo com a formulação matemática do problema hidromecâico, a determiação do estado de tesão em cada poto do meio poroso possibilita a atualização do campo de deformação por meio da relação costitutiva característica do meio. Isso proporcioa a determiação do campo de deslocameto correspodete (icógita do problema mecâico) pela equação (.48), por outro lado a equação da coservação de massa da matriz porosa (.5) jutamete com a equação que caracteriza o acoplameto hidromecâico (.47) determia a atualização das respectivas variáveis de tal modo a se obter a icógita do problema hidráulico (pressão de líquido). (Vascocelos, 007) 5
39 3. FORMULAÇÃO NUMÉRICA A seguir estão descritos os algoritmos que foram implemetados o programa de elemetos fiitos CODE_BRIGHT, que é capaz de resolver problemas acoplados termo-hidromecâicos e geoquímicos em meios porosos. Este programa foi desevolvido por Olivella et al (995) e a primeira versão foi apresetada com o propósito de solucioar problemas relacioados a materiais salios um cotexto de disposição de resíduos ucleares. Posteriormete, sua aplicação estedeu-se à modelagem de sistemas de barreiras de proteção ambietal, trasporte de solutos, aterros, escavações, barrages de terra, pavimetação, solos colapsíveis e solos expasivos (Nóbrega, 008). O presete trabalho trata da implemetação de algoritmos de itegração implícita de modelos costitutivos elasto-plásticos, aplicados a problemas acoplados hidro-mecâicos em meios porosos Segudo Sousa (004) as aplicações do método dos elemetos fiitos a plasticidade evolvem a solução de dois cojutos de equações difereciais: (a) Relação icremetal tesão-deformação, em ível de poto de Gauss. (b) Equação global carga-deslocameto, em ível de toda malha de elemetos fiitos. No problema de itegração da lei costitutiva tesão-deformação, a escolha dos algoritmos totalmete implícitos foi pricipalmete motivado por estes serem icodicioalmete estáveis, por ão possuírem grade restrição em relação ao tamaho do passo de tempo e possibilitarem a dedução de um operador tagete cosistete, essecial para o uso em cojução com um procedimeto global de Newto-Raphso (covergêcia quadrática). Portato, tais algoritmos permitem torar o CODE_BRIGHT uma ferrameta computacioalmete mais eficiete. 6
40 3.. ALGORITMO DE INTEGRAÇÃO IMPLÍCITA PARA O MODELO DE VON MISES COM ENDURECIMENTO Neste trabalho, a implemetação do modelo de vo Mises, tem por base a formulação apresetada em Simo & Hughes (998). No capítulo aterior foram apresetadas as equações coceretes ao problema tesão-deformação, para itegrar essas equações umericamete é coveiete adotar um itervalo de tempo fictício, defiido como: t t t (3.) Assim as equações apresetadas podem ser reescritas em termos icremetais. Pode-se listar como as equações básicas adotadas a implemetação do modelo de vo Mises: (a) Lei elástica D e ε e (3.) ode D e é o tesor elastico isotrópico (b) Fução de fluêcia f (, y ) S (3.3) y 3 ode p ( ε ) (3.4) y y 7
41 p é a tesão de escoameto do material e é uma fução da deformação plástica acumulada, ε. (c) Lei de fluxo associada p f 3 S & ε γ γ (3.5) S (d) Lei de edurecimeto, ode a equação para evolução da variável itera de edurecimeto é dada por & 3 p ε (3.6) ε& 3... ESTADO DE TENSÕES TRIAL Dado o icremeto de deformação: ε ε ε (3.7) ode ε correspodete a deformação o tempo t e e aida cohecidas variáveis de estado { ε, ε p } deformação plástica acumulada são dadas por: ε a deformação o tempo t. Sedo em t. A deformação elástica e a e e ε ε ε (3.8) p ε ε p (3.9) 8
42 A tesão correspodete é calculada como: e e D : ε (3.0) ode, a tesão média, p, e o tesor desviador S, são calculados, respectivamete, como: e Gε d S (3.) e p Kεv (3.) ode ε d e ε v são, respectivamete, as compoetes desviadoras e volumétrica da deformação, equato que G é o módulo elástico cisalhate e K o módulo elástico volumétrico, defiidos como: E G ( ν ) (3.3) E K 3 ν (3.4) ( ) sedo E o módulo de elasticidade e ν o coeficiete de Poisso. A tesão de escoameto é defiida como: p y y ( ε ) y (3.5) Uma vez determiado o estado elástico, o próximo passo do algoritmo é verificar se o estado de tesões está cotido ou ão a superfície de fluêcia. Se estiver o iterior da superfície de fluêcia, portato f (!, ) 0 (3.6) y 9
43 Etão o passo do itervalo [t, t ] é puramete elástico e o estado elástico é a solução para a problema de itegração, esse caso as variáveis são atualizadas como se segue. e ε e ε (3.7) ε ε ε p p p (3.8) (3.9) y y y (3.0) Se o estado de tesões estiver o exterior da superfície defiida pela fução f o espaço das tesões pricipais, etão o passo [t, t ] é elasto-plástico e o algoritmo de retoro a superfície de fluêcia deve ser aplicado. Para o modelo de vo Mises, o algoritmo de retoro correspode a resolver o seguite sistema de equações ão lieares: 3 S e e ε ε γ (3.) S ε p ε p γ (3.) p S y ( ε ) 0 (3.3) 3 O qual deve ser resolvido para ε ε e, p atualizado de acordo com a seguite fórmula: e γ e o tesor de deformação plástica pode ser 3 S p p ε ε γ (3.4) S O sistema apresetado acima pode ser simplificado e o algoritmo de retoro à superfície de fluêcia do modelo de vo Mises pode ser reduzido a uma úica equação ão liear, sedo o icremeto do multiplicador plástico a icógita do problema. Essa redução o úmero de 30
44 equações é de extrema importâcia o setido de fazer o cálculo do estado de tesões atual mais eficiete do poto de vista computacioal e melhorar o desempeho do esquema de elemetos fiitos como um todo. Ates da simplificação das equações (3.), (3.) e (3.3) deve-se otar que o vetor de fluxo de vo Mises é puramete desviador, portato (3.), (3.) e (3.3) podem ser divididas em: e ε e v v ε (3.5) 3 S e e εd ε d γ (3.6) S o que equivale, em termos de tesão, a: p p (3.7) 3 S S S γ G (3.8) S Este é o algoritmo de retoro apeas para a compoete desviadora da tesão. A tesão média, p, tem o valor computado o passo elástico e pode ser elimiada do sistema de equações. A simplificação a seguir decorre do rearrajo da equação de atualização das tesões desviadoras (3.8), obtedo-se: 3 γ G S S S (3.9) As tesões desviadoras e as elasto-plásticas se relacioam da seguite forma: S S S S (3.30) 3
45 Etão o vetor de fluxo e o estado de tesões atualizado coicidem, substituido a idetidade acima em (3.8) temos a seguite fórmula de atualização simplificada para as tesões desviadoras: 3 G γ γ 3G S S S S q (3.3) ode, 3 S (3.3) q é a tesão de vo Mises, calculada a tetativa elástica. Desde que S seja um tesor costate o algoritmo de retoro, a tesão desviador S é fução liear do γ apeas a formula de atualização acima. Da expressão (3.3) pode-se deduzir que o algoritmo totalmete implícito do modelo de vo Mises, a atualização da tesão desviadora é obtida dividido a tesão desviadora pelo fator 3G / q γ. Fialmete substituido (3.3) em (3.) detro da codição de cosistêcia plástica (3.3), o sistema das equações (3.), (3.) e (3.3) do algoritmo de retoro a superfície de fluêcia para o modelo de vo Mises se reduz a seguite equação escalar (geralmete ão liear) tedo o icremeto do multiplicador plástico como sua úica icógita: ~ p f ( γ ) q 3G γ ( ε γ ) 0 (3.33) y A equação acima é etão resolvida em um esquema Newto-Raphso e, com a solução de γ, as variáveis de estado são atualizadas como se segue: γ 3G S S S q p I (3.34) (3.35) 3
46 e e [ D ] ε e : S v ε (3.36) G 3 p p ε ε γ (3.37) Se requerido, o tesor de deformações plásticas é atualizado por (3.4) ENDURECIMENTO LINEAR A úica fote de ão liearidade o algoritmo de retoro de vo Mises (3.33) é a curva de edurecimeto, defiida pela equação (3.4). Para materiais com edurecimeto liear esta fução é expressa como p p y ( ε ) 0 Hε (3.38) Ode 0 é a tesão de escoameto iicial do material virgem e H é a costate de edurecimeto do material, este caso(3.33) trasforma-se em, f p γ ) q 3G γ [ ( ε γ ) H ] 0 (3.39) ( 0 E o icremeto do multiplicador plástico pode ser obtido, a forma fechada, f γ (3.40) 3G H No caso de plasticidade perfeita (H0), a expressão para γ recai em, f γ (3.4) 3G 33
47 Para este caso a atualização da tesão é a simples projeção do passo elástico a superfície de fluêcia ao logo de rua direção radial. Esta é a projeção do poto mais próximo do estado de tesões a superfície de fluêcia MÓDULO TANGENTE CONSISTENTE ELASTO-PLÁSTICO Detro do cotexto dos elemetos fiitos icremetais, usamos o operador tagete cosistete dado pela equação (3.4). ε D (3.4) Sob fluxo plástico, ou seja, quado o algoritmo de retoro é usado etão a tesão é atualizada como: e γ 6G D I d : ε q e (3.43) ode γ é a solução da seguite equação. p f ( γ ) q 3G γ ( ε γ ) 0 (3.44) y Na equação (3.44), a tesão elástica de vo Mises, elástica segudo a equação: q, é fução da deformação 34
48 3 ε (3.45) e q G d E o módulo tagete cosistete elasto-plástico para o presete modelo é obtido pela difereciação de (3.4) sedo, ε e D e γ 6G q I d 6G q ε e d γ ε e γ 6G ( q ) ε e d q ε e (3.46) Da equação (3.45), com alguma maipulação, obtém-se: q G ε 3 e N (3.47) ode foi, coveietemete defiido, o vetor de fluxo uitário: e d S ε N Ν (3.48) 3 S ε e d fazedo uso da idetidade ε e e d ε d : I d, quado aplicada a regra da cadeia. Da difereciação da equação implícita (3.44) para o γ, cosiderado (3.47), temos: γ ε q G e 3 e G H 3G H ε 3 Ν (3.49) ode H é a costate de edurecimeto do material. 35
49 36 Fialmete, substituido (3.47) e (3.49) em (3.46) obtém após alguma maipulação, a seguite expressão para o operador tagete elasto-plástico cosistete com o algoritmo de retoro implícito para o modelo de vo Mises com edurecimeto isotrópico: É importate ressaltar que para este modelo em particular e este algoritmo de itegração, o operador D ep é simétrico ALGORITMO BÁSICO IMPLEMENTADO Algoritmo implícito Backward Euler. ) Base de Dados. Cálculo dos módulos elásticos volumétrico e cisalhate: I I N N I N N I D D K H G q G q G G H G q G q G d d e ep γ γ γ γ (3.50) p ε ε ε ; ; ; ; ε (3.5) K H E y ; ; ; ; ν (3.5) ) ( ν E G (3.53) ) ( 3 ν E K e (3.54)
50 ) Estado Trial. e D : ε (3.55) q Kε (3.56) 3 q Hε (3.57) 3 ( q ) f β y (3.58) β S q β β (3.58) (3.59) 3) Verifica se Passo é Elástico ou Elasto-plástico. f Se 0 (3.60) Etão ε ε p ε ε ε ε p (3.6) 37
51 38 Fim 4) Matriz Tagete Cosistete vo Mises Verifica se matriz elástica ou elasto-plástica: Seão [ ] 3 3 ) / ( p p G K H G f ε ε ε ε γ γ γ ε ε γ γ (3.6) Se 0 γ (3.63) Etão 0 0 δ δ (3.64) Seão [ ] ( ) K H G G 3 β β β δ δ γ δ (3.65) (3.66)
52 Calcula matriz tagete cosistete: D ep ep D : ε ε D ep Gδ I Gδ 3 K e (3.67) 3.. ALGORITMO DE INTEGRAÇÃO IMPLÍCITA PARA O MODELO DE DRUCKER PRAGER Na presete seção é apresetado o algoritmo para o modelo de Drucker Prager que foi implemetado o código em elemetos fiitos, para esta implemetação foi tomada como referêcia o algoritmo de itegração implícita descrito por Souza Neto et al (008) EQUAÇÕES CONSTITUTIVAS A superfície de plastificação de Drucker Prager é defiida pela seguite fução de fluêcia. f, (3.68) ( c) S ηp ξc Ode p é a tesão hidrostática e c é a coesão do material. As costates η e ξ são escolhidas de acordo com a aproximação à superfície de Mohr-Coulomb adotada, segudo as seguites equações. 39
53 Para coicidêcia dos vértices exteros (coe de compressão) η ξ 6siφ 3(3 siφ) 6 cos φ 3(3 si φ) (3.69) Para coicidêcia dos vértices iteros (coe de tração) η ξ 6siφ 3(3 siφ) 6cosφ 3(3 si φ ) (3.70) Para coicidêcia do eixo de ruptura η ξ 3si φ 3 cosφ 3 (3.7) Para o modelo implemetado foi adotada uma regra de fluxo ão associado, ode a fução potecial é defiida como. g S η p (3.7) Ode η é fução do âgulo de dilatâcia ψ e pode ser calculado de acordo com as seguites equações. Para o coe extero 6 si φ η (3.73) 3(3 si φ) Para o coe itero 6si φ η (3.74) 3(3 si φ) 40
54 Para coicidêcia do 3siφ η (3.75) eixo de ruptura 3 Para a superfície do coe de Drucker Prager, o vetor de fluxo é dado como, g S η S 3 (3.76) Para o poto de sigularidade do coe (vértice), o vetor de fluxo é o subgradiete de f, ou seja, é um vetor cotido o coe complemetar, como mostra a Figura 3.. Figura 3. - Algoritmo de retoro ao vértice (Souza Neto et al, 008) 3... ALGORITMO DE RETORNO PARA O MODELO DE DRUCKER PRAGER O algoritmo de itegração para o modelo de Drucker Prager é relativamete simples, primeiramete devido à existêcia de uma úica sigularidade em sua superfície, o vértice. E também porque a superfície de fluêcia, é totalmete simétrica em relação ao eixo hidrostático. 4
55 A forma geral de atualização do tesor de tesões é: e γd : (3.77) e ode γ D : é o vetor de retoro à superfície de fluêcia 3... RETORNO À SUPERFÍCIE DO CONE Para a porção suave do coe, ode o vetor de fluxo é defiido por (3.76), o icremeto de deformação plástica é calculado como. ε p γ S η γ S 3 (3.78) E correspode à seguite fórmula de atualização das tesões. S γ G Kη S (3.79) I Que equivale às seguites equações, em termos das compoetes desviadora e hidrostática. G S S S (3.80) p p Kη γ 4
56 A codição de cosistêcia para o caso presete é dada por. f S ηp ξc 0 (3.8) Substituido (3.80) em (3.8) resulta a seguite equação para o multiplicador plástico. ~ f ( γ ) S G γ η( p Kη γ ) ξc 0 (3.8) Com alguma maipulação, chegamos em: f γ G Kηη (3.83) Após a solução da equação acima, a tesão é atualizada coforme (3.79) RETORNO AO PONTO DE SINGULARIDADE (VÉRTICE) No vértice, o vetor de retoro, deve estar cotido o coe complemetar esquematicamete ilustrado a Figura 3..A codição de cosistêcia (3.8) é reduzida a: ξ c η p p K ε v 0 (3.84) 43
57 As tesões são atualizadas segudo a equação: p p K ε )I ( v (3.85) ESCOLHA DO RETORNO APROPRIADO Iicialmete, adota-se o algoritmo de retoro a superfície do coe, uma vez determiado o γ,procede-se a seguite verificação: Se S G γ 0 (3.86) Etão algoritmo de retoro é validado, seão deve-se aplicar o retoro ao vértice MATRIZ TANGENTE CONSISTENTE A determiação implícita da matriz tagete cosistete elasto-plástica é dado pela expressão: D ep G Gγ I Gγ S G GA d d 3 S (3.87) GAK ( η η ) K ( Kηη A) d d 44
58 Se o estado de tesões estiver o domíio elástico (γ 0), recupera-se a matriz elástica: D e G I K (3.88) ALGORITMO BÁSICO IMPLEMENTADO Algoritmo implícito Backward-Euler: ) Base de Dados, ε, p ε E, ν, c, φ, ψ (3.89) Cálculo dos módulos elásticos volumétrico e cisalhate: E K 3( ν ) E G ( ν ) (3.90) ) Estado Trial e D : ε (3.9) 45
59 f S ηp ξc (3.9) 3) Verifica se Passo é Elástico ou Elasto-plástico Se f 0 (3.93) Etão ε p 0 (3.94) Seão γ ε p f ( G Kηη ) γ g D ep : ε p (3.95) 4) Verifica tesão o vértice Se S < γ (3.96) Etão ε p cξ η ep D : ( ) (3.97) Fim 46
60 3.3. ALGORITMO DE INTEGRAÇÃO IMPLÍCITA-EXPLÍCITA (IMPLEX) PARA O MODELO DE DRUCKER PRAGER Oliver et al. (008) propuseram um algoritmo de itegração de tesões bastate robusto que é uma simplificação do algoritmo implícito apresetado a seção aterior. A idéia é dimiuir a ão liearidade do algoritmo de retoro estimado o multiplicador plástico a partir das tesões, deformações e variáveis de história do passo aterior. Desta forma ão é mais ecessário calcular as derivadas do multiplicador plástico, simplificado o algoritmo de itegração e a obteção da matriz tagete cosistete. Claro, com esta simplificação paga-se o preço de ão se cumprir exatamete a codição de cosistêcia, o que pode ser miimizado com a adoção de icremeto de carga (ou passos de tempo) meores. Também para problemas ode se tem estados de tesões uiformes a malha, como os casos de reprodução de esaios, o algoritmo proposto por Oliver et al. (008) apreseta oscilações que os autores também mostram que podem ser cotroladas com o tamahos de passos de tempo dados durate a aálise de elemetos fiitos. No presete trabalho o algoritmo de Oliver et al. (008) foi modificado e propõe-se uma ova maeira de estimar o multiplicador plástico, que permaece costate o algoritmo de retoro (ão precisado ser derivado), e elimia as oscilações observadas pelos autores do algoritmo origial para problemas de estados de tesões uiformes. Essa melhor aproximação do multiplicador plástico o algoritmo de retoro também resulta uma meor violação da codição de cosistêcia. No algoritmo proposto por Oliver et al. (008), o algoritmo de retoro é o mesmo da seção aterior para itegração implícita, porém faz-se uma extrapolação explícita do multiplicador plástico do passo atual ( γ ) escaloado pelos icremetos de tempos dos passos atual ( t ) e aterior ( t ). Da seguite forma: γ t t γ (3.98) 47
61 No algoritmo proposto este trabalho, calcula-se a estimativa do multiplicador plástico a partir da projeção das deformações totais do tempo aterior: * t ε ε t (3.99) Posteriormete, com esta projeção das deformações totais estima-se um estado de tesões : * e * D : ε (3.00) Vale ressaltar que este estado de tesões é projetado a partir do estado de tesões *, covergido do passo de tempo aterior, o que irá melhorar a estimativa do multiplicador com relação ao proposto por Oliver et al. (008) a equação (3.99). Assim, com base o estado de tesões verifica-se o estado de plastificação do material: * f * S * * ηp ξc (3.0) e, caso haja violação da superfície de fluêcia, obtém-se o multiplicador plástico para o passo de tempo atual: γ * f ( G Kηη ) (3.0) Todo o resto do algoritmo para o método IMPLEX é igual à itegração implícita apresetada a seção aterior. Porém, a matriz tagete cosistete tem seu cálculo bastate simplificado uma vez que o multiplicador plástico foi calculado com valores do passo de tempo aterior 48
62 (covergido) e sua derivada é zero (Oliver et al., 008), torado o sistema muito mais robusto do poto de vista computacioal. Com a simplificação itroduzida pelo algoritmo IMPLEX, a matriz cosistete elasto-plástica resulta em: D ep e [ D ] γ S I 3 S S S S (3.03) E, ovamete, se elástico γ 0 e recupera-se a matriz elástica ALGORITMO BÁSICO IMPLEMENTADO O algoritmo implícito Backward-Euler com as alterações sugeridas para as estimativas simplificadas do multiplicador plástico é resumido a seguir: ) Base de Dados ; ; ε ; ε ε E, ν, c, φ, ψ p ; γ (3.04) Cálculo dos módulos elásticos volumétrico e cisalhate: 49
63 E K 3( ν ) E G ( ν ) (3.05) ) Se IMPLEX, estima-se o multiplicador plástico Oliver et al. (008): γ t t γ (3.03) Presete trabalho f * * t ε ε t * e D ε * : S * γ * f ( G Kηη ) * ηp ξc (3.04) 3) Estado defiitivo para ambos algoritmos (Implícito e IMPLEX) (3.05) e D : ε f S ηp ξc 4) Se implícito, calcula multiplicador plástico. (3.06) 50
64 γ f ( G Kηη ) (3.03) 5) Verifica se passo é elástico ou elasto-plástico. Se f 0 (3.04) Etão ε p 0 (3.05) Seão γ ε p f ( G Kηη ) γ g D ep : ε p (3.06) 6) Verifica tesão o vértice. Se Etão ε p S cξ η ep [ D ] < γ : ( ) (3.07) (3.08) Fim 5
65 4. CASOS ANALISADOS Os casos aalisados este capítulo têm como objetivo verificar a fucioalidade e eficiêcia dos algoritmos implemetados. Primeiramete foi simulado um exemplo de um cilidro sujeito a uma pressão itera, segudo o modelo de vo Mises, para este caso os resultados obtidos foram comparados com uma solução prevista a literatura. Em seguida foram simulados um esaio triaxial e dois problemas característicos da mecâica dos solos, o estudo da estabilidade de um talude vertical e uma perfuração de poço horizotal em rocha frágil. Estes problemas foram simulados segudo o critério de Drucker Prager implemetado, o modelo Drucker Prager escolhido para as simulação foi o que se aproxima à superfície de Mohr Coulomb pela coicidêcia dos vértices exteros (coe de compressão). 4.. EXPANSÃO DE CAVIDADE CILÍNDRICA Na presete seção serão apresetados os resultados de um exemplo umérico obtido pelo algoritmo de itegração implícita para o modelo de vo Mises. Possibilitado, etão, a verificação do seu desempeho e fucioalidade. O exemplo umérico aalisado cosiste a simulação do comportameto de um cilidro metálico com as paredes espessas sujeitas a uma pressão itera. A pressão P, prescrita a superfície itera é aumetada gradualmete até a carga de colapso (carga limite) ser alcaçada. A plastificação começa a superfície itera e desevolve-se gradualmete a forma de uma frete de plastificação cilídrica em direção a face extera do cilidro. O colapso ocorre quado a frete de plastificação alcaça a face extera e o cilidro tora-se 5
66 iteiramete plastificado. Ao atigir a carga limite, o cilidro pode expadir-se idefiidamete sem qualquer acréscimo de carga aplicada. Hill (950) propõe uma solução aalítica fechada para este problema, ode a carga aplicada para um determiado raio c da frete de plastificação pode ser expresso por: P Y c c l a b (4.) ode, para o modelo de vo Mises: Y y 3 (4.) A carga limite pode ser determiada pela equação: P lim y b l 3 a (4.3) A simulação umérica deste problema foi obtida por meio do algoritmo de itegração implícita implemetado para o critério de plastificação de vo Mises, este caso foi cosiderada plasticidade perfeita. A geometria e codições de cotoro do problema estão esquematizadas a figura 4. e as propriedades do material estão listadas a tabela 4.. A malha de elemetos fiitos adotada é mostrada afigura 4.. Devido à simetria, apeas um quarto da geometria do problema foi discretizado, com as devidas restrições de movimeto impostas os ós exteros. 53
67 Figura 4. - Geometria do problema de cavidade cilídrica Tabela 4. - Parâmetros do material do cilidro Parâmetros Módulo de Elasticidade (E) Coeficiete de Poisso (ν) Tesão de escoameto ( y ) b a 0 GPa 0,3 0,4 GPa 00 mm 00 mm 400 elemetos do tipo quadrilátero com quatro ós (potos de itegração de Gauss). Total de 45 ós. Figura 4. - Malha de elemetos fiitos 54
68 Para as dimesões e parâmetros do problema, obtém-se o seguite valor da carga limite, calculado por meio da equação (4.3): P 0,9 GPa (4.4) lim Na figura 4.3 são plotados os resultados uméricos obtidos, bem como uma projeção do valor da carga limite (Equação 4.4), pode ser observado que a carga de colapso da solução umérica atige um valor que se aproxima razoavelmete daquele previsto pela solução de Hill (950). P 0,0 GPa (4.5) umérico lim A solução em elemetos fiitos utilizada atige o colapso quado as codições de equilíbrio ão podem mais serem alcaçadas e as iterações globais do algoritmo ão covergem. 0, 0,5 Pressão itera (GPa) 0, 0,05 Solução umérica Projeção da carga limite 0 0,0 0, 0, 0,3 0,4 0,5 0,6 0,7 Deslocameto radial (mm) Figura Curva carga-deslocameto 55
69 Com base os resultados obtidos, verifica-se que o algoritmo de itegração implícita utilizado apreseta uma aproximação satisfatória em relação à solução aalítica para o valor de carga limite. 4.. ENSAIO TRIAXIAL Para ilustrar o melhorameto proporcioado pelo algoritmo proposto este trabalho, que modificou o algoritmo IMPLEX origial apresetado por Olivier et al, 008, realizou-se um esaio triaxial CU (cosolidado e ão dreado) para uma material com os parâmetros apresetados a tabela 4.. A geometria do problema e a malha de elemetos fiitos utilizada são mostradas a figura 4.4, a malha costa de 5 elemetos quadrático e 36 potos odais, cosiderado a simetria do problema, apeas um quarto da amostra é modelado. Figura Esquema do esaio triaxial 56
70 Neste esaio a amostra saturada de água é cofiada a uma tesão de célula de 0,3 MPa e 7 posteriormete aplica-se uma taxa de deslocameto vertical de x 0 m / s comprimido a amostra. Tabela 4. -Propriedades do material do esaio triaxial Parâmetros Módulo de Elasticidade (E) Coeficiete de Poisso (ν) Âgulo de atrito Âgulo de dilatacia Coesão 00 MPa 0, ,30 MPa Nas figuras 4.5 e 4.6 observa-se o espaço das tesões médias efetivas versus tesões de vo Mises que há uma fase iicial elástica ão dreada, ode a trajetória de tesões é vertical, paralela ao eixo das tesões de vo Mises. Posteriormete, quado o estado de tesões atige a evoltória de Drucker Prager, o efeito de dilatacia deste modelo, sob codição ão dreada, iduz uma geração de poso-pressões egativas que fazem com que o estado se tesões siga a evoltória o setido positivo da tesão média efetiva. Olivier et al (008) com Olivier et al (008) com Presete trabalho com t 5x0 t 5x0 t 5x s s s Figura Trajetória de tesões (tesão média x tesão de vo Mises) 57
71 4 Olivier et al (008) com t 5x0 s 3 Olivier et al (008) com t 5x0 s 4 Presete trabalho com t 5x0 s 3 Presete trabalho com t 5x0 s Figura Trajetória de tesões (tesão média x tesão de vo Mises) Observa-se as figuras 4.5 e 4.6 que os resultados da simulação do esaio com o algoritmo IMPLEX origial proposto por Olivier et al (008) depedem claramete do tamaho do passo de tempo. Quado cosiderados maiores valores de icremetos de tempo, a trajetória de tesões viola sigificativamete a evoltória de Drucker Prager. O mesmo esaio, foi simulado segudo a alteração proposta pelo presete trabalho para o IMPLEX (Olivier et al, 008) e, para este caso, o algoritmo ão apresetou sesibilidade sigificativa em relação ao tamaho do passo de tempo, e a trajetória de tesões ão viola a superfície de fluêcia mesmo para maiores valores de icremetos de tempo 4.3. ANÁLISE DE TALUDE VERTICAL Segudo Caputo (987) o termo talude compreede qualquer superfície que limita um maciço de solo ou rocha. O estudo da estabilidade de taludes costituem um dos maiores problemas da Mecâica dos Solos o que se refere a previsão do seu mecaismo de evolução com o tempo. 58
72 As forças devido ao peso próprio dos solos são resposáveis por causar istabilidade os diversos tipos de taludes. No caso estudado é feita uma aálise de estabilidade, quato à ruptura, de um talude vertical com de 0 metros de altura, através do modelo elasto-plástico de Drucker Prager implemetado de forma a verificar sua eficiêcia, pois se trata de um problema que exige um grade custo computacioal. A aálise é feita verificado a formação da superfície de ruptura do talude através da distribuição das deformações plásticas. A simulação do carregameto do material do talude é feita através do aumeto, com o tempo, da força de gravidade aplicada. Para esta aálise foi adotado um fator de gravidade (F g ) variado etre zero 0 e 4,5. 0 F 4,5 (4.6) g A altura crítica do talude é calulada pela expressão aalítica (4.7) defiida por Terzaghi (Caputo, 987) para taludes verticais, em fução do peso próprio e que leva em cota o aparecimeto de fedas de tração o topo do talude.,67c φ H crit ta 45 (4.7) γ Neste caso a ruptura deverá ter iício quado a codição de altura crítica ão for mais satisfeita. O problema físico está esquematizado a figura 4.7 e as propriedades do material estão descritos a tabela
73 Figura Geometria e codições de cotoro do problema Tabela 4 3 Parâmetros do Problema de Talude Vertical Parâmetros porosidade E (MPa) c (MPa) φ ψ ν ρ s(kg/m³) 0,0 5x0 4 0, ,30 87,5 A malha discretizada para o programa de elemetos fiitos, mostrada a figura 4.8, é composta por 500 elemetos quadráticos de quatro ós, que somam 60 ós. 60
74 Figura Malha de elemetos fiitos O fator F g represeta o fator de gravidade aplicado ao logo do tempo. Este fator leva ao aumeto icremetal do peso próprio do material defiido pela equação (4.8). γ ρ. Fg g (4.8) t s. Ode γ t é o peso próprio do talude, ρ s é o peso específico do solo e g é a aceleração da gravidade, cujo valor de referêcia é de 0,0m/s². Segudo a solução aalítica de Terzaghi para determiação da altura crítica de taludes verticais, o caso aalisado apresetaria comportameto de ruptura para um fator Fg de,5, como pode ser observado a figura 4.9. Para o Fg de,5 a altura crítica atige o valor de 0 metros (altura do talude), portato para valores de Fg maiores que,5 a altura crítica será meor do que a altura do talude. 6
75 Altura Crítica (m) ,5,5,5 3 3,5 4 4,5 5 Fator de Gravidade (Fg) Figura Variação da altura crítica do talude com o fator de gravidade Os resultados obtidos com a simulação umérica mostraram-se coeretes com a previsão da solução aalítica. As figuras 4.0 e 4. apresetam as evoluções dos deslocametos horizotais e verticais, respectivamete. Podemos observar que, para o fator de gravidade de,5, corre um aumeto brusco dos deslocametos, decorrete do processo de ruptura do material. 0,00E00 Fator de Gravidade Deslocameto Horizotal (m),00e-03,00e-03 3,00E-03 4,00E-03 Nó Nó 9 Nó 85 Figura Evolução dos deslocametos horizotais com o fator de gravidade 6
76 Fator de Gravidade 0,00E Deslocameto Vertical (m) -5,00E-04 -,00E-03 -,50E-03 -,00E-03 -,50E-03-3,00E-03 Nó Nó 9 Nó 85 Figura 4. - Evolução dos deslocametos verticais com o fator de gravidade O mesmo comportameto pode ser observado a evolução das deformações plásticas cisalhates e volumétricas mostradas as figuras 4. e
77 8,00E-03 Deformações Plásticas Cisalhates 7,00E-03 6,00E-03 5,00E-03 4,00E-03 3,00E-03,00E-03,00E-03 0,00E00 Elemeto 70 Elemeto 445 Elemeto Fator de Gravidade Figura 4. - Evolução das deformações plásticas cisalhates com o fator de gravidade 0,006 Deformações Plásticas Volumétricas 0,005 0,004 0,003 0,00 0,00 0 Elemeto 70 Elemeto 445 Elemeto Fator de Gravidade Figura Evolução das deformações plásticas volumétricas com o fator de gravidade A seguir serão apresetados os resultados gráficos obtidos por meio do pós-processador GiD. As figuras 4.4 e 4.5 ilustram os deslocametos totais e os vetores de deslocameto, respectivamete. 64
78 Figura Distribuição dos deslocametos Figura Vetores de deslocameto A formação da superfície de ruptura pode ser observada as figuras 4.6 e 4.7, que mostram a distribuição das deformações plásticas cisalhates e volumétricas, respectivamete. Figura Deformações plásticas cisalhates Figura Deformações plásticas volumétricas A variação da porosidade do material segue a forma da superfície de colapso, como mostra a figura 4.8, aumetado as áreas plastificadas devido ao comportameto dilatate do material. 65
79 Figura 4. 8 Distribuição de porosidade A figura 4.9 apreseta a aálise das trajetórias de tesões em termos de tesão média e tesão de vo Mises, bem como a evoltória de Drucker Prager. Em todos os elemetos aalisados, a trajetória de tesões toca a superfície de fluêcia, cofirmado que o material está sob regime plástico. É possível observar também que, para o caso aalisado segudo o algoritmo IMPLEX com modificação proposta por este trabalho, as trajetórias de tesões ão violam a superfície de fluêcia. 66
80 6,00E00 5,00E00 4,00E00 Tesão Desviadora (MPa) 3,00E00,00E00,00E00 Elemeto 70 Elemeto 445 Elemeto 499 Evoltória de Drucker-Prager 0,00E00 -,00E00 0,00E00,00E00,00E00 3,00E00 4,00E00 5,00E00 Tesão média (MPa) Figura Trajetória de tesões para o caso do talude vertical Para o problema do talude vertical, o algoritmo implemetado apresetou resultados satisfatórios, sedo coerete com a solução aalítica proposta por Therzaghi. O algoritmo também ão apresetou problemas de covergêcia, mesmo sedo um caso que leva a ruptura do material PERFURAÇÃO DE POÇO A istabilidade de poços durate o processo de perfuração é uma questões de grade relevâcia para a egeharia de petróleo. De acordo com Steiger & Leug (99) 90 % dos problemas em poços ocorrem quado se perfura folhelhos, rochas sedimetares bastate 67
81 abudates as regiões produtoras e que geralmete apresetam baixas resistêcia mecâica e permeabilidade. (Sousa et al, 005). De acordo com Souley et al (00) e Hajiabdolmajid et al (00), o processo de escavação em meios rochosos iduzem uma redistribuição do estado de tesões o maciço que acarreta o fissurameto das regiões próximas à execução da perfuração. O aparecimeto de fissuras coduz a um aumeto a permeabilidade da rocha que, por sua vez, afeta da redistribuição das poro-pressões. Na presete seção, foi executada a modelagem da perfuração de um poço horizotal em maciço rochoso frágil (folhelho) cujos parâmetros físicos estão listados a Tabela a geometria do problema (discretizada para o programa de elemetos fiitos em 066 elemetos quadráticos de quatro ós, que somam 35 potos de itegração de Gauss) bem como as codições de cotoro e de carregameto são mostradas a Figura 4.0 a relação etre variações a permeabilidade em fução das alterações da porosidade é determiada pela equação (.49) Para simular tal problema de forma acoplada (equações hidráulicas e mecâicas) foi utilizado o algoritmo de itegração IMPLEX para o modelo de Drucker Prager. 68
82 Figura Geometria do problema e malha de elemetos fiitos Tabela Parâmetros do material do maciço escavado Parâmetros Módulo de Youg 5400 MPa Coeficiete de Poisso 0,35 Parâmetro de Biot-Willis,00 Permeabilidade itríseca iicial 0-7 cm/s Porosidade iicial 0,0 Coesão Pressão de poros iicial (P 0 ) Pressão de fluido aplicada a perfuração,0 MPa 5 MPa 30 MPa Âgulo de atrito (ϕ) 30 Âgulo de dilatâcia (ψ) 30 69
83 É importate ressaltar que o estado de pressão do fluido ijetado é superior ao valor iicial característico da formação. Sousa & Guimarães (005) relatam que a ijeção de um fluido pressurizado durate o processo de perfuração de um poço costitui-se como uma codição de cotoro mecâica e hidráulica. A figura 4. mostra a evolução da frete de plastificação do material, ota-se que devido ao estado geoestático a zoa plastificada ão se distribui uiformemete ao logo da parede do poço. Tal comportameto iflueciará a redistribuição da porosidade e permeabilidade o meio e o regime de fluxo em toro do poço. Figura 4. - Deformações plásticas desviadoras Devido a essa distribuição ão uiforme de tesões pode ocorrer o break-out, que segudo Rocha et al (007) são zoas de desmoroameto e ruptura por cisalhameto em lados opostos do poço que se dá o poto de maior diferecial de tesão e a direção da meor tesão, que para o caso deste poço a tesão pricipal meor é a horizotal. A figura 4. mostra uma imagem de ultrassom de um poço que sofreu break-out, tal feômeo muda a seção do poço de circular para elíptica. 70
84 Figura 4. - Imagem ultrasôica de perfil de poço apresetado breakout a direção da tesão pricipal meor o plao ormal ao poço. Na figura 4.3 é mostrada a variação de porosidade e a figura 4.4 apreseta a variação do campo de permeabilidade para o caso aalisado, ode é possível visualizar a formação de um camiho preferecial de fluxo a direção horizotal, ode houve aumeto da permeabilidade. Coforme apresetado a figura 4.5, a frete de avaço das poro-pressões se desevolve mais rápido as zoas plastificadas do meio poroso. Por esta razão a cosideração da permeabilidade como depedete do estado tesão-deformação do material cosiste em um importate acoplameto etre os comportametos hidráulico e mecâico da rocha. 7
85 Figura Variação de porosidade Figura Variação de permeabilidade 7
86 Figura Distribuição da pressão de líquido A figura 4.6 apreseta a aálise das trajetórias de tesões em termos de tesão média efetiva e tesão de vo Mises, bem como a evoltória de Drucker Prager para os parâmetros cosiderados o problema. 9,00E0 8,00E0 7,00E0 Tesão cisalhate (MPa) 6,00E0 5,00E0 4,00E0 3,00E0 Elemeto 690 Elemeto 8,00E0 Elemeto,00E0 Elemeto 5 Evoltória 0,00E00 0,00E00,00E0,00E0 3,00E0 4,00E0 5,00E0 6,00E0 7,00E0 Tesão média (MPa) Figura Trajetória de tesões 73
Sumário e Objectivos. Objectivos da Aula: Apreensão de alguns aspectos associados à solução de problemas elasto-plásticos.
 Sumário e Objectivos Sumário: Plasticidade. Métodos de Solução do Sistema de Equações ão Lieares. Programa para aálise elasto - plástica de problemas bidimesioais Objectivos da Aula: Apreesão de algus
Sumário e Objectivos Sumário: Plasticidade. Métodos de Solução do Sistema de Equações ão Lieares. Programa para aálise elasto - plástica de problemas bidimesioais Objectivos da Aula: Apreesão de algus
étodos uméricos MÉTODO DOS MOMENTOS - MOM Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON 5.1 MODELO MATEMÁTICO E SOLUÇÃO ANALÍTICA
 Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA
 ISBN 978-85-7846-516-2 UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA Resumo Alisso Herique dos Satos UEL Email: alisso_hs612@hotmail.com Ferada Felix Silva UEL Email: ferada.f.matematica@gmail.com
ISBN 978-85-7846-516-2 UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA Resumo Alisso Herique dos Satos UEL Email: alisso_hs612@hotmail.com Ferada Felix Silva UEL Email: ferada.f.matematica@gmail.com
Mecânica dos Sólidos II
 Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA DEPARTAMENTO DE ENGENHARIA QUÍMICA ENG 008 Fenômenos de Transporte I A Profª Fátima Lopes
 Tipos de fluidos: Os vários tipos de problemas ecotrados em Mecâica dos Fluidos podem ser classificados com base a observação de características físicas do campo de fluxo. Uma possível classificação é
Tipos de fluidos: Os vários tipos de problemas ecotrados em Mecâica dos Fluidos podem ser classificados com base a observação de características físicas do campo de fluxo. Uma possível classificação é
1 Amintas engenharia
 1 Amitas egeharia 2 Cálculo Numérico 1. Itrodução Amitas Paiva Afoso 3 1. Itrodução O que é o Cálculo Numérico? 4 1. Itrodução O Cálculo Numérico correspode a um cojuto de ferrametas ou métodos usados
1 Amitas egeharia 2 Cálculo Numérico 1. Itrodução Amitas Paiva Afoso 3 1. Itrodução O que é o Cálculo Numérico? 4 1. Itrodução O Cálculo Numérico correspode a um cojuto de ferrametas ou métodos usados
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO
 EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO Miquéias Gomes dos Satos 1 ; Douglas Azevedo Castro 2 1 Aluo do Curso de Egeharia de Bioprocessos e Biotecologia; Campus de Gurupi; e-mail:miqueias@uft.edu.br PIVIC/UFT
EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO Miquéias Gomes dos Satos 1 ; Douglas Azevedo Castro 2 1 Aluo do Curso de Egeharia de Bioprocessos e Biotecologia; Campus de Gurupi; e-mail:miqueias@uft.edu.br PIVIC/UFT
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
1. Definição e conceitos básicos de equações diferenciais
 Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO. Dr. Sivaldo Leite Correia
 PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
4 Teoria da Probabilidade
 48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO
 5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
6 Resultados Experimentais
 6 Resultados Experimetais O propósito deste capítulo é validar experimetalmete a metodologia apresetada os capítulos ateriores através do programa computacioal desevolvido. O estudo é focado o comportameto
6 Resultados Experimetais O propósito deste capítulo é validar experimetalmete a metodologia apresetada os capítulos ateriores através do programa computacioal desevolvido. O estudo é focado o comportameto
2- Resolução de Sistemas Não-lineares.
 MÉODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 2- Resolução de Sistemas Não-lieares. 2.- Método de Newto. 2.2- Método da Iteração. 2.3- Método do Gradiete. 2- Sistemas Não Lieares de Equações Cosidere
MÉODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 2- Resolução de Sistemas Não-lieares. 2.- Método de Newto. 2.2- Método da Iteração. 2.3- Método do Gradiete. 2- Sistemas Não Lieares de Equações Cosidere
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS
 4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO. PME Mecânica dos Sólidos I 2 a Lista de Exercícios
 PME- - Mecâica dos Sólidos I a Lista de Eercícios ) Determie o tesor das tesões, escrito em relação à base b = e, e, e ), para cada um dos ( casos idicados (as tesões estão em MPa). Utilie a coveção de
PME- - Mecâica dos Sólidos I a Lista de Eercícios ) Determie o tesor das tesões, escrito em relação à base b = e, e, e ), para cada um dos ( casos idicados (as tesões estão em MPa). Utilie a coveção de
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
n ) uma amostra aleatória da variável aleatória X.
 - Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
- Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos
 Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
ELECTROMAGNETISMO E ÓPTICA
 ELECTROMAGNETISMO E ÓPTICA NOTAS DE CURSO Prof. Resposável: Mário J. Piheiro Istituto Superior Técico 008 1 O electromagetismo estuda o efeito das cargas eléctricas em repouso ou em movimeto. Eistem dois
ELECTROMAGNETISMO E ÓPTICA NOTAS DE CURSO Prof. Resposável: Mário J. Piheiro Istituto Superior Técico 008 1 O electromagetismo estuda o efeito das cargas eléctricas em repouso ou em movimeto. Eistem dois
2.3 Dimensionamento segundo as normas de outros países
 Cap. 2 Revisão bibliográfica 30 2.3 Dimesioameto segudo as ormas de outros países A seguir estão apresetados os critérios de dimesioameto, referete ao assuto em questão, de ormas de países com larga tradição
Cap. 2 Revisão bibliográfica 30 2.3 Dimesioameto segudo as ormas de outros países A seguir estão apresetados os critérios de dimesioameto, referete ao assuto em questão, de ormas de países com larga tradição
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
UNIVERSIDADE DE SÃO PAULO ENGENHARIA QUÍMICA LOQ 4016 OPERAÇÕES UNITÁRIAS EXPERIMENTAL I
 UNIVERSIAE E SÃO PAULO ENGENHARIA QUÍMICA LOQ 4016 OPERAÇÕES UNITÁRIAS EXPERIMENTAL I Profa. Lívia Chaguri E-mail: lchaguri@usp.br 1- Redução de Tamaho - Fudametos/Caracterização graulométrica - Equipametos:
UNIVERSIAE E SÃO PAULO ENGENHARIA QUÍMICA LOQ 4016 OPERAÇÕES UNITÁRIAS EXPERIMENTAL I Profa. Lívia Chaguri E-mail: lchaguri@usp.br 1- Redução de Tamaho - Fudametos/Caracterização graulométrica - Equipametos:
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS. 1 a Edição
 BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
Resposta de Sistemas de 2 a Ordem à Excitação Periódica Não Harmônica
 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS
 UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-44 Cálculo Diferecial e Itegral II (Escola Politécica) Terceira Lista de Exercícios - Professor: Equipe de Professores 0.1. Vide Lista,
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-44 Cálculo Diferecial e Itegral II (Escola Politécica) Terceira Lista de Exercícios - Professor: Equipe de Professores 0.1. Vide Lista,
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
2 - PRINCÍPIO DE FUNCIONAMENTO DO GERADOR DE CORRENTE CONTINUA
 2 - PRICÍPIO D FUCIOAMTO DO GRADOR D CORRT COTIUA 2.1 - A FORÇA LTROMOTRIZ IDUZIDA O pricípio de fucioameto do gerador de correte cotíua tem por base a Lei de Faraday que estabelece que, se o fluxo magético
2 - PRICÍPIO D FUCIOAMTO DO GRADOR D CORRT COTIUA 2.1 - A FORÇA LTROMOTRIZ IDUZIDA O pricípio de fucioameto do gerador de correte cotíua tem por base a Lei de Faraday que estabelece que, se o fluxo magético
4 Modelagem Numérica. φ φ
 4 Modelagem Numérica O modelo matemático apresetado o capítulo aterior foi resolvido com o código comercial FLUENT, o ual é baseado o método de Volumes Fiitos (Patakar, 1980). Para resolver umericamete
4 Modelagem Numérica O modelo matemático apresetado o capítulo aterior foi resolvido com o código comercial FLUENT, o ual é baseado o método de Volumes Fiitos (Patakar, 1980). Para resolver umericamete
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
5 Teoria dos Valores Extremos
 Teoria dos Valores Extremos 57 5 Teoria dos Valores Extremos A Teoria dos Valores Extremos vem sedo bastate utilizada em campos ligados a evetos raros. Sua estatística é aplicada a estimação de evetos
Teoria dos Valores Extremos 57 5 Teoria dos Valores Extremos A Teoria dos Valores Extremos vem sedo bastate utilizada em campos ligados a evetos raros. Sua estatística é aplicada a estimação de evetos
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA
 1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
A DESIGUALDADE DE CHEBYCHEV
 A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
FORMAS QUADRÁTICAS. Esta forma quadrada pode ser reescrita em forma matricial, segundo:
 PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
Bombas industriais. 1 Torr = 1 mmhg. Bombas industriais
 Codições (especificações) de carga: Para água ao ível do mar 1 Torr = 1 mmhg Codições (especificações) de carga: Carga de Pressão (h p ) A carga de pressão é cosiderada quado um sistema de bombeameto começa,
Codições (especificações) de carga: Para água ao ível do mar 1 Torr = 1 mmhg Codições (especificações) de carga: Carga de Pressão (h p ) A carga de pressão é cosiderada quado um sistema de bombeameto começa,
RESOLUÇÃO DE SISTEMAS NÃO LINEARES
 87 RESOLUÇÃO DE SISTEMAS NÃO LINEARES Uma equação que coteha uma epressão do tipo, -,,, se(), e +z, z etc, é chamada ão-liear em,, z,, porque ela ão pode ser escrita o que é uma equação liear em,, z, a
87 RESOLUÇÃO DE SISTEMAS NÃO LINEARES Uma equação que coteha uma epressão do tipo, -,,, se(), e +z, z etc, é chamada ão-liear em,, z,, porque ela ão pode ser escrita o que é uma equação liear em,, z, a
3 0 Exercício Programa de PMR 2420 Data de entrega: 21/06/2012 (até as 17:00hs) Método de Elementos Finitos (MEF)
 ,3 m,8 m 3 Exercício Programa de PMR 242 Data de etrega: 21/6/212 (até as 17:hs) Método de Elemetos Fiitos (MEF) 1) Cosidere a estrutura da figura abaixo sujeita a uma carga cocetrada F 3 variado o tempo
,3 m,8 m 3 Exercício Programa de PMR 242 Data de etrega: 21/6/212 (até as 17:hs) Método de Elemetos Fiitos (MEF) 1) Cosidere a estrutura da figura abaixo sujeita a uma carga cocetrada F 3 variado o tempo
Universidade Federal de Mato Grosso Probabilidade e Estatística - Curso: Engenharia Civil Introdução à Inferência Estatística - Prof a Eveliny
 1 Itrodução Uiversidade Federal de Mato Grosso Probabilidade e Estatística - Curso: Egeharia Civil Itrodução à Iferêcia Estatística - Prof a Eveliy Vimos o iício do curso como resumir descritivamete variáveis
1 Itrodução Uiversidade Federal de Mato Grosso Probabilidade e Estatística - Curso: Egeharia Civil Itrodução à Iferêcia Estatística - Prof a Eveliy Vimos o iício do curso como resumir descritivamete variáveis
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL INTRODUÇÃO ROTEIRO POPULAÇÃO E AMOSTRA. Estatística Aplicada à Engenharia
 ROTEIRO DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL 1. Itrodução. Teorema Cetral do Limite 3. Coceitos de estimação potual 4. Métodos de estimação potual 5. Referêcias Estatística Aplicada à Egeharia 1 Estatística
ROTEIRO DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL 1. Itrodução. Teorema Cetral do Limite 3. Coceitos de estimação potual 4. Métodos de estimação potual 5. Referêcias Estatística Aplicada à Egeharia 1 Estatística
Transporte Iônico e o Potencial de Membrana
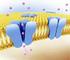 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
( ) III) ESPAÇOS VETORIAIS REAIS. Definição: Denomina-se espaço vetorial sobre os Reais (R) ao conjunto não vazio. 1) Existe uma adição:
 Elemetos de Álgebra Liear ESPAÇOS VETORIAIS REAIS III) ESPAÇOS VETORIAIS REAIS Defiição: Deomia-se espaço vetorial sobre os Reais (R) ao cojuto ão vazio + : V V V ) Existe uma adição: com as seguites propriedades:
Elemetos de Álgebra Liear ESPAÇOS VETORIAIS REAIS III) ESPAÇOS VETORIAIS REAIS Defiição: Deomia-se espaço vetorial sobre os Reais (R) ao cojuto ão vazio + : V V V ) Existe uma adição: com as seguites propriedades:
Figura 4.53 Sinais coletados para as componentes da velocidade (a) u, (b) v e (c) w na sonda 1 estação A do escoamento a Re =
 90 a) b) c) Figura 4.53 Siais coletados para as compoetes da velocidade (a) u, (b) v e (c) w a soda 1 estação A do escoameto a Re = 1.000. 91 Figura 4.54 Variação do úmero de Strouhal em fução do úmero
90 a) b) c) Figura 4.53 Siais coletados para as compoetes da velocidade (a) u, (b) v e (c) w a soda 1 estação A do escoameto a Re = 1.000. 91 Figura 4.54 Variação do úmero de Strouhal em fução do úmero
Experimento 1 Estudo da Lei de Hooke
 Experimeto 1 Estudo da Lei de Hooke 1.1 Objetivos Físicos Verificação experimetal da lei de Hooke para uma mola helicoidal: Medida experimetal do módulo de rigidez do material μ. 1. Objetivos Didáticos
Experimeto 1 Estudo da Lei de Hooke 1.1 Objetivos Físicos Verificação experimetal da lei de Hooke para uma mola helicoidal: Medida experimetal do módulo de rigidez do material μ. 1. Objetivos Didáticos
CONHECIMENTOS ESPECÍFICOS
 CESPE/UB FUB/0 fa 5 4 CONHECIMENTOS ESPECÍFICOS 60 As distribuições B e C possuem os mesmos valores para os quartis Q e Q, e o quartil superior em B correspode ao quartil cetral (Q ) da distribuição A.
CESPE/UB FUB/0 fa 5 4 CONHECIMENTOS ESPECÍFICOS 60 As distribuições B e C possuem os mesmos valores para os quartis Q e Q, e o quartil superior em B correspode ao quartil cetral (Q ) da distribuição A.
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Cálculo Diferencial e Integral I Resolução do 2 ō Teste - LEIC
 Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Mas o que deixou de ser abordado na grande generalidade desses cursos foi o estudo dos produtos infinitos, mesmo que só no caso numérico real.
 Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Ajuste de Curvas pelo Método dos Quadrados Mínimos
 Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Método do Lugar das Raízes
 Método do Lugar das Raízes Coceito de Lugar das Raízes; O Procedimeto do Lugar das Raízes; Projeto de Parâmetros pelo Método do Lugar das Raízes; Sesibilidade e Lugar das Raízes; Cotrolador de Três Termos
Método do Lugar das Raízes Coceito de Lugar das Raízes; O Procedimeto do Lugar das Raízes; Projeto de Parâmetros pelo Método do Lugar das Raízes; Sesibilidade e Lugar das Raízes; Cotrolador de Três Termos
ABORDAGEM PARA A SOLUÇÃO DE DESIGUALDADES VARIACIONAIS: A FUNÇÃO GAP
 ABORDAGEM PARA A SOLUÇÃO DE DESIGUALDADES VARIACIONAIS: A FUNÇÃO GAP SARA MEIRA MOUTTA RABELO (UESC) saramoutta@hotmail.com gudelia g. morales de arica (UENF) gudelia@uef.br O trabalho apreseta uma descrição
ABORDAGEM PARA A SOLUÇÃO DE DESIGUALDADES VARIACIONAIS: A FUNÇÃO GAP SARA MEIRA MOUTTA RABELO (UESC) saramoutta@hotmail.com gudelia g. morales de arica (UENF) gudelia@uef.br O trabalho apreseta uma descrição
Análise da Resposta Livre de Sistemas Dinâmicos de 2 a Ordem
 Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
CF358 Física BásicaExperimental I
 CF358 Física BásicaExperimetal I CONFIGURAÇÃO MÓDULO TEÓRICO MÓDULO EXPERIMENTAL => BLOCO 1-4 EXPERIMENTOS => BLOCO 2-4 EXPERIMENTOS PRESENÇA (muito importate) NO MÍNIMO 75% AVALIAÇÃO 01 PROVA -BLOCO TEÓRICO
CF358 Física BásicaExperimetal I CONFIGURAÇÃO MÓDULO TEÓRICO MÓDULO EXPERIMENTAL => BLOCO 1-4 EXPERIMENTOS => BLOCO 2-4 EXPERIMENTOS PRESENÇA (muito importate) NO MÍNIMO 75% AVALIAÇÃO 01 PROVA -BLOCO TEÓRICO
6.1 Estimativa de uma média populacional: grandes amostras. Definição: Um estimador é uma característica amostral (como a média amostral
 6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 4
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 4 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 4 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
Séquências e Séries Infinitas de Termos Constantes
 Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Estudando complexidade de algoritmos
 Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
FILAS PARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING PROBABILÍSTICO
 CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
binomial seria quase simétrica. Nestas condições será também melhor a aproximação pela distribuição normal.
 biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO
 O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
Interpolação. Interpolação Polinomial
 Iterpolação Iterpolação Poliomial Objetivo Iterpolar uma fução f(x) cosiste em aproximar essa fução por uma outra fução g(x), escolhida etre uma classe de fuções defiidas (aqui, usaremos poliômios). g(x)
Iterpolação Iterpolação Poliomial Objetivo Iterpolar uma fução f(x) cosiste em aproximar essa fução por uma outra fução g(x), escolhida etre uma classe de fuções defiidas (aqui, usaremos poliômios). g(x)
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Estacionariedade e correlação temporal em dados financeiros
 Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
AULA Subespaço, Base e Dimensão Subespaço.
 Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM
 6 AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM Quado se pretede estudar uma determiada população, aalisam-se certas características ou variáveis dessa população. Essas variáveis poderão ser discretas
6 AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM Quado se pretede estudar uma determiada população, aalisam-se certas características ou variáveis dessa população. Essas variáveis poderão ser discretas
AULA 17 A TRANSFORMADA Z - DEFINIÇÃO
 Processameto Digital de Siais Aula 7 Professor Marcio Eisecraft abril 0 AULA 7 A TRANSFORMADA Z - DEFINIÇÃO Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Siais e Sistemas, a edição, Pearso, 00. ISBN 9788576055044.
Processameto Digital de Siais Aula 7 Professor Marcio Eisecraft abril 0 AULA 7 A TRANSFORMADA Z - DEFINIÇÃO Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Siais e Sistemas, a edição, Pearso, 00. ISBN 9788576055044.
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
Uma relação entre sincronização no mapa do círculo e os números racionais
 Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
5. O algoritmo dos mínimos quadrados
 Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA
 Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
Representação em espaço de estado de sistemas de enésima ordem. Função de perturbação não envolve termos derivativos.
 VARIÁVEIS DE ESTADO Defiições MODELAGEM E DINÂMICA DE PROCESSOS Profa. Ofélia de Queiroz Ferades Araújo Estado: O estado de um sistema diâmico é o cojuto míimo de variáveis (chamadas variáveis de estado)
VARIÁVEIS DE ESTADO Defiições MODELAGEM E DINÂMICA DE PROCESSOS Profa. Ofélia de Queiroz Ferades Araújo Estado: O estado de um sistema diâmico é o cojuto míimo de variáveis (chamadas variáveis de estado)
Sumário. 2 Índice Remissivo 17
 i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
Séries de Fourier. As séries de Fourier são séries cujos termos são funções sinusoidais.
 Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
2. COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES
 CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
O PARADOXO DE SIMPSON
 O PARADOXO DE SIMPSON Valmir R. Silva Adre Toom PIBIC-UFPE-CNPq Itrodução A aálise cietífica de dados através da modelagem matemática é uma atividade idispesável a Teoria de Decisão. O mesmo coceito é
O PARADOXO DE SIMPSON Valmir R. Silva Adre Toom PIBIC-UFPE-CNPq Itrodução A aálise cietífica de dados através da modelagem matemática é uma atividade idispesável a Teoria de Decisão. O mesmo coceito é
Aplicação de Métodos Espectrais ao Cálculo Numérico de Escoamentos Compressíveis
 Aplicação de Métodos Espectrais ao Cálculo umérico de Escoametos Compressíveis Adré Rosale Istituto Tecológico de Aeroáutica Praça Marechal Eduardo Gomes, 50 - Vila das Acácias São José dos Campos São
Aplicação de Métodos Espectrais ao Cálculo umérico de Escoametos Compressíveis Adré Rosale Istituto Tecológico de Aeroáutica Praça Marechal Eduardo Gomes, 50 - Vila das Acácias São José dos Campos São
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
CARTA DE CONTROLE PARA MONITORAMENTO DE FRAÇÃO DE CONFORMES UTILIZANDO UM NOVO ESTIMADOR
 XXIX ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO. CARTA DE CONTROLE PARA MONITORAMENTO DE FRAÇÃO DE CONFORMES UTILIZANDO UM NOVO ESTIMADOR Ruth Pereira Loureço (USP) ruth.p.loureco@gmail.com Lida Lee Ho
XXIX ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO. CARTA DE CONTROLE PARA MONITORAMENTO DE FRAÇÃO DE CONFORMES UTILIZANDO UM NOVO ESTIMADOR Ruth Pereira Loureço (USP) ruth.p.loureco@gmail.com Lida Lee Ho
4 Modelo Constitutivo de Drucker-Prager para materiais rochosos
 4 Modelo Constitutivo de Drucker-Prager para materiais rochosos Os modelos constitutivos são parte essencial nas análises de distribuição de tensões e deformações em problemas complexos de Engenharia Geotécnica.
4 Modelo Constitutivo de Drucker-Prager para materiais rochosos Os modelos constitutivos são parte essencial nas análises de distribuição de tensões e deformações em problemas complexos de Engenharia Geotécnica.
Exercício: Mediu-se os ângulos internos de um quadrilátero e obteve-se 361,4. Qual é o erro de que está afetada esta medida?
 1. Tratameto estatísticos dos dados 1.1. TEORIA DE ERROS O ato de medir é, em essêcia, um ato de comparar, e essa comparação evolve erros de diversas origes (dos istrumetos, do operador, do processo de
1. Tratameto estatísticos dos dados 1.1. TEORIA DE ERROS O ato de medir é, em essêcia, um ato de comparar, e essa comparação evolve erros de diversas origes (dos istrumetos, do operador, do processo de
SINAIS E SISTEMAS DE TEMPO DISCRETO
 SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
Características dinâmicas
 Características diâmicas As características diâmicas, descrevem o seu comportameto durate o itervalo de tempo em que a gradeza medida varia até o mometo em que o seu valor medido é apresetado. Resposta
Características diâmicas As características diâmicas, descrevem o seu comportameto durate o itervalo de tempo em que a gradeza medida varia até o mometo em que o seu valor medido é apresetado. Resposta
Material Teórico - Módulo de ESTATÍSTICA. As Diferentes Médias. Primeiro Ano do Ensino Médio
 Material Teórico - Módulo de ESTATÍSTICA As Diferetes Médias Primeiro Ao do Esio Médio Autor: Prof Atoio Camiha Muiz Neto Revisor: Prof Fracisco Bruo Holada Nesta aula, pausamos a discussão de Estatística
Material Teórico - Módulo de ESTATÍSTICA As Diferetes Médias Primeiro Ao do Esio Médio Autor: Prof Atoio Camiha Muiz Neto Revisor: Prof Fracisco Bruo Holada Nesta aula, pausamos a discussão de Estatística
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS.
 TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
1 Distribuições Amostrais
 1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
MÉTODO DE NEWTON RESUMO
 MÉTODO DE NEWTON Iácio de Araujo Machado Roaldo Ribeiro Alves RESUMO Este trabalho teve por objetivo apresetar o método iterativo de Newto bastate importate por sua fácil aplicabilidade. O objetivo pricipal
MÉTODO DE NEWTON Iácio de Araujo Machado Roaldo Ribeiro Alves RESUMO Este trabalho teve por objetivo apresetar o método iterativo de Newto bastate importate por sua fácil aplicabilidade. O objetivo pricipal
ESTUDO DA SECAGEM DE BANANAS ATRAVÉS DO MODELO DE DIFUSÃO USANDO SOLUÇÕES ANALÍTICAS
 WWWCONVIBRAORG ESTUDO DA SECAGEM DE BANANAS ATRAVÉS DO MODELO DE DIFUSÃO USANDO SOLUÇÕES ANALÍTICAS ANDRÉA F RODRIGUES 1, WILTON P SILVA 2, JOSIVANDA P GOMES 3, CLEIDE M D P S SILVA 4, ÍCARO CARVALHO RAMOS
WWWCONVIBRAORG ESTUDO DA SECAGEM DE BANANAS ATRAVÉS DO MODELO DE DIFUSÃO USANDO SOLUÇÕES ANALÍTICAS ANDRÉA F RODRIGUES 1, WILTON P SILVA 2, JOSIVANDA P GOMES 3, CLEIDE M D P S SILVA 4, ÍCARO CARVALHO RAMOS
