Virgílio Mendonça da Costa e Silva
|
|
|
- Pedro Damásio Quintanilha
- 8 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça da Costa e Silva Jaeiro 08
2 3. Vibrações Livres com Amortecimeto de Sistemas com GL No sistema de vibração com amortecimeto a força de amortecimeto é resposável pela dissipação de eergia do sistema. Embora seja difícil a descrição real da força de amortecimeto é possível à admissão de modelos ideais de amortecimeto, que muitas vezes resultam o progostico satisfatório da resposta. Detre esses modelos, a força de amortecimeto viscoso, proporcioal à velocidade, coduz a um tratameto matemático mais simples. 3. Coceito Físico de Amortecimeto A força de amortecimeto viscoso é expressa pela seguite equação: Ode: C - Coeficiete de amortecimeto em [N.s/m] & - Velocidade da massa em [m/s] F d = C & (3.) 3. Determiação da Equação Diferecial do Movimeto 3.. Método de Somatório de Forças (Newto) Cosidere um sistema de um grau de liberdade, composto de uma massa M, uma mola de massa desprezível e rigidez K e um amortecedor de massa desprezível e coeficiete de amortecimeto C, represetado pela Figura 3.: Posição sem Deflexão K Diagrama de Corpo livre K C K M C M Peso C & M K ( +) & && Peso Sistema em Equilibrio Estático Sistema em Movimeto Figura 3. Sistema de Vibração Livre com Amortecimeto de GL
3 Aplicado somatório de forças (Seguda Lei do Movimeto de Newto), ao modelo físico da Figura 3., obtém-se: ou ( ) M && = Peso - C & - K + M && + C & + K = 0 (3.) 3.. Método de Eergia Usado Equação de Lagrage Os sistemas mecâicos com força de amortecimeto, para efeito de coservação de eergia, são cosiderados sistemas ão coservativos por cota da dissipação de eergia. Assim, a determiação da E.D.M. - Equação Diferecial do Movimeto ão pode ser obtida pela aplicação do pricípio de Coservação de Eergia, como feito para sistemas com vibrações livres sem amortecimeto. Etretato, podemos obter a E.D.M. usado as expressões de eergias ciética, potecial e dissipada do sistema mecâico através da Equação de Lagrage, desevolvida e apresetada pelo matemático italiao Joseph Louis Lagrage (736 83) a sua obra-prima Mechaique. A Equação de Lagrage é muito utilizada os estudos de vibrações de sistemas mecâicos com múltiplos graus de liberdade. A Equação de Lagrage pode ser deduzida a partir de pricípios de trabalho virtual e pricípios itegrais, como detalhado o Capítulo V. Neste Capítulo mostramos apeas a sua aplicação a determiação da Equação Diferecial do Movimeto de Sistemas Mecâicos de um Grau de Liberdade com Amortecimeto. A equação de Lagrage é represetada por: d T T D U = Q d t q & q q & q (3.3) ode: T é a eergia ciética do sistema U é a eergia potecial do sistema D é a eergia dissipada do sistema Q é a -éssima força extera geeralizada aplicada ao sistema q é a -éssima coordeada geeralizada do sistema Para um sistema de um grau de liberdade com amortecimeto temos apeas uma coordeada geeralizada q =. As equações de eergia para o sistema são:
4 Eergia Ciética: Eergia Potecial: Eergia Dissipada: T = M & (3.4) U = K ( + ) - Mg (3.5) D = C & (3.6) Calculado as parcelas da equação (3.3) com base as equações (3.4), (3.5) e (3.6), temos: T T = = M & q & & (3.7) d T d T = = M && d t q& d t & (3.8) T T = = 0 q (3.9) D D = = C & = C & q & & (3.0) U U = = K + K - Mg = K q (3.) Q = 0 (3.) obtém-se: Substituido as equações (3.8), (3.9), (3.0), (3.) e (3.) a equação (3.3), M && + C & + K = 0 (3.3) 3.3 Solução e Aálise da Equação Diferecial do Movimeto A equação (3.3) é uma equação diferecial ordiária, de seguda ordem, homogêea com coeficietes costates. Portato, sua solução é do tipo:
5 s t ( t ) = e (3.4) Substituido a solução dada pele equação (3.4) a equação (3.3), obtém-se: s t ( M s + C s + K ) e = 0 (3.5) A codição para que a equação (3.5) seja igual a zero é que o termo etre parêteses seja igual a zero, ou seja: M s + C s + K = 0 (3.6) De ode se obtém: - C C K s, = ± - M M M (3.7) Como a equação diferecial (3.3) tem duas soluções, a solução geral é a combiação geral das duas soluções, ou seja: ou s t ( ) s t t = A e + B e (3.8a) ( t ) = e A e + B e C C K C K t + - t - t M M M M M (3.8b) O primeiro termo da equação (3.8b) é simplesmete uma fução de tempo expoecialmete decrescete. Etretato, o comportameto do termo etre parêteses depede do valor umérico do radical, que pode ser positivo, ulo ou egativo, o que defie se o sistema é respectivamete superamortecido, subamortecido ou com amortecimeto crítico Sistemas Superamortecidos Se o amortecimeto presete o sistema é tal que: C K > M M (3.9) os expoetes a equação (3.8b) são úmeros reais. Neste caso ão há oscilação possível. Referimo-os a este caso como sistema superamortecido.
6 3.3. Sistemas Sub Amortecidos Se o amortecimeto presete o sistema é tal que: C K < M M (3.0) os expoetes a equação (3.8b) são úmeros complexos. Neste caso podemos trasformá-los através das equações de Euler em fuções seoidais ou cosseoidais. Assim o sistema oscilará. Referimo-os a este caso como sistema subamortecido Sistemas com Amortecimeto Crítico Se o amortecimeto presete o sistema é tal que: C K = M M (3.) dizemos que o valor de C = C C (Coeficiete de Amortecimeto Crítico) reduz o radical da equação (3.8b) a zero. Temos o caso limite etre movimeto oscilatório e ão oscilatório. Referimo-os a este caso como sistema com amortecimeto crítico. 3.4 Fator de Amortecimeto e Frequêcia Natural Amortecida Com base o item 3.3.3, podemos escrever a equação (3.) a forma: CC K = = ω M M (3.) ou C = K M = M (3.3) C ω É coveiete se expressar o valor de qualquer amortecimeto de um sistema em termos do amortecimeto que é crítico para o mesmo, por meio de uma fração ão mesurável, ζ C = C (3.4) C que é chamada de fator ou fração de amortecimeto.
7 Podemos agora escrever as soluções da equação diferecial do movimeto, dada pela equação (3.7), em termos de ζ. Notado que se C ζ C = C = ζ ω M M (3.5) a equação (3.7) pode ser escrita como: ( ) s = ζ ± ζ - ω (3.6), Com este ovo coceito, podemos classificar o sistema de vibração livre com amortecimeto como: ζ = - Sistema Amortecido Criticamete. Neste caso a quatidade de amortecimeto presete o sistema está a codição limite etre vibrar e ão vibrar. ζ > - Sistema Superamortecido. Neste caso a quatidade de amortecimeto presete o sistema é tão alta que faz com que o sistema ão oscile. ζ < - Sistema Subamortecido. Neste caso a quatidade de amortecimeto presete o sistema ão impede o mesmo de ter um movimeto oscilatório. A Figura 3. mostra a equação (3.6) traçada um plao complexo, com ζ ao logo do eixo horizotal. Se = 0 ζ, a equação (3.6) fica reduzida a: s = i ω ± (3.7), de modo que as raízes o eixo imagiário correspodem ao caso de ão amortecimeto. Para 0< ζ < a equação (3.6) pode ser escrita da forma: ( ) s = - ζ i - ζ ω ± (3.8), As raízes s e s são etão potos complexos cojugados sobre um arco circular covergido o poto s ω, = - (3.9) A medida que ζ cresce acima da uidade, as raízes separam-se ao logo do eixo horizotal e permaecem úmeros reais. Tedo presete este diagrama,
8 estamos aptos a examiar a solução dada pela equação (3.7) para cada caso. Figura 3. Lugar das Raízes de um Sistema de Vibração Livre com Amortecimeto de GL Apesar de estarmos iteressados apeas os sistemas subamortecidos (sistemas oscilatórios), examiaremos os três casos em detalhes em termos de quatidades usadas a prática. Começamos com movimeto oscilatório. Movimeto Oscilatório - ζ < Substituido a equação (3.8) a equação (3.8a), a solução geral pode ser escrita como: - ζ ω t + i - ζ ω t i - ζ ω t ( ) ( ) t = e A e + B e (3.30) Aplicado Euler, temos: ( ) t = e - ζ ω t ( ζ ω ) + ( ζ ω ) A cos - t i se - t + B cos ( - ζ ω t) - i se ( - ζ ω t ) (3.3a) ou ζ ω ( ) ( ) ( ζ ω ) ( ) ( ζ ω ) - t t = e A B cos - t A B i se - t (3.3b) Aplicado as codições de cotoro:
9 t = 0 ( ) ( ) ( ) & ( ) t = 0 & t = 0 (3.3) Chega-se à: ( ) ( ) + ζ ω ( ) & 0 0 ( ζ ω ) + ( ) ( ζ ω ) - ζ ω t t = e se - t 0 cos - t ω - ζ (3.33a) ou ζ ω ( ) ( ζ ω φ) - t t = e se - t + (3.33b) ode: é a amplitude do movimeto dada por: ( ) + ζ ω ( ) & 0 0 = + 0 ω - ζ ( ) (3.34) φ é a fase do movimeto dada por: ( ) ω ζ ( ) + ζ ω ( ) 0 - φ = tg & 0 0 (3.35) Sabemos que um sistema vibratório é periódico, assim podemos calcular o período de vibração amortecida T d, usado a equação: ( t + T ) = ( t) (3.36) Aplicado a equação (3.36) a parte periódica de (3.33b), obtém-se: ( ζ ω ( ) φ) ( ζ ω φ) se - t + T + = se - t + (3.37a) ou ( ) - ζ ω t + T + φ = - ζ ω t + φ + π (3.37b)
10 De ode se obtém, para = (Um ciclo): π π T d = = ω - ζ ωd (3.38) ode: ω = ω - ζ é a frequêcia atural amortecida. d 3.5 Determiação do Coeficiete de Amortecimeto Uma das maeiras mais prática de determiar o coeficiete de amortecimeto de um sistema de um GL é excitá-lo por impulso ou retirá-lo da sua posição de equilíbrio forçado-o a oscilar, medir a taxa de decréscimo de duas oscilações cosecutivas e utilizar a fórmula do decremeto logarítmico Decremeto Logarítmico A medida da taxa de decréscimo das oscilações livres é um meio coveiete para se determiar a quatidade de amortecimeto presete um sistema. Quato maior for o amortecimeto, maior será a taxa de decréscimo. Cosidere uma vibração amortecida represetada pela equação (3.33b) ζ ω ( ) ( ζ ω φ) - t t = e se - t + (3.39) que é idicada graficamete a Figura 3.3. Itroduzimos aqui uma expressão deomiada decremeto logarítmico que é defiida como o logaritmo atural da razão de duas quaisquer amplitudes cosecutivas. A fórmula do decremeto será: = l = ( ζ ω φ) ( ζ ω ( + d ) φ) - ζ ω t e se - t + - ζ ω ( t Td ) e + se - t T + (3.40)
11 Figura 3.3 Taxa de Decréscimo da Oscilação medida pelo Decremeto Logarítmo Uma vez que os valores dos seos são iguais (fução periódica) quado o tempo é aumetado de um período de amortecimeto, a equação (3.40) fica reduzida a: e - ζ ω t ζ ω Td = l = l e = ζ ω - ζ ω ( t Td ) T + d e (3.4) Substituido o valor do período amortecido a equação (3.4), obtém-se: ou = π ζ - ζ (3.4a) ζ = 4 π + (3.4b) A equação (3.4a) é uma solução exata. Quado o amortecimeto é muito pequeo ζ 0 - ζ, logo a equação (3.4a) se aproxima a: (3.43) π ζ A Figura 3.4 mostra um gráfico dos valores, exatos e aproximados de em fução de ζ.
12 Figura 3.4 Decremeto Logaritmo em Fução de ζ Movimeto Não Oscilatório - ζ > Quado ζ é maior que a uidade, as duas raízes permaecem o eixo real, ver Figura 3., e separadas, uma aumetado e a outra dimiuido. A expressão da solução geral é etão: ζ + ζ ω ζ ζ ω ( ) t = A e + B e - t - - t (3.44) Aplicado as codições de cotoro: t = 0 ( ) ( ) ( ) & ( ) t = 0 & t = 0 Chega-se à: A = B = ( ) ( ζ ζ ) ω ( ) & ω ζ - ( ) ( ζ ζ ) ω ( ) & ω ζ - (3.45) (3.46) O movimeto é fução do tempo expoecialmete e decrescete, deomiado de aperiódico.
13 Movimeto Amortecido Criticamete - ζ = Para ζ =, obtemos uma raiz dupla s = s = - ω, e os dois termos da equação (3.8a) combiam para formar apeas um, ou seja: ω ω ( ) ( ) t = A B e = C e t t + (3.47) Observe que esta codição ão tem úmero de costate requerido para satisfazer as duas codições iiciais. Fazedo ζ e aplicado as codições de cotoro: Chega-se à: t = 0 ( ) ( ) ( ) & ( ) t = 0 & t = 0 { } ( ) - ζ ω t & ( ) ω ( ) ( ) t = e t + 0 (3.48) A Figura 3.7 mostra três tipos de resposta com deslocameto iicial ( 0 ). As partes móveis de muitos medidores elétricos e istrumetos são amortecidos criticamete, a fim de evitar a ultrapassagem e a oscilação. 3.6 Represetação Gráfica do Movimeto Movimeto Oscilatório - ζ < Solução da E.D.M. - C t M ( ) ( ζ ω φ) t = e se - t + Figura 3.5 Oscilação Amortecida ζ <
14 Movimeto Não Oscilatório - ζ > Solução da E.D.M. ζ + ζ ω ζ ζ ω ( ) t = A e + B e - t - - t Figura 3.6 Oscilação Não Amortecida ζ > Movimeto Amortecido Criticamete - ζ = Solução da E.D.M. { } ω ( ) t & ( ) ω ( ) ( ) t = e t + 0 Figura 3.7 Movimeto Amortecido Criticamete ζ =
15 Exercício 3.: Mostrar que o decremeto logaritmo é dado também pela equação = l 0 ode represeta a amplitude após decorridos ciclos. Traçar uma curva dado o úmero de ciclos decorridos em fução de ζ para que a amplitude dimiua de 50 por ceto. Solução: Para duas quaisquer amplitudes cosecutivas a razão é: 0 = = = L = = e 3 Podemos escrever a razão 0 da seguite forma: 0 0 = L = e 3 de ode obtém-se a requerida equação: = l 0 Para obtermos o umero de ciclos decorridos para a redução de 50 por ceto a amplitude π ζ = l = Segue a seguir a Figura 3.8 traçada. Figura 3.8 Referete ao Exemplo 3.
16 Exercício 3. Mostrar que o decremeto logaritmo, o caso de amortecimeto pequeo, pode ser expresso em termos da eergia de vibração U e da eergia U discipada em cada ciclo. Solução: A figura abaixo mostra uma vibração amortecida com amplitude cosecutivas,, 3, L Baseados a defiição de decremeto logaritmo = l 0 escrevemos a relação de amplitudes a forma expoecial = e - = - +! A eergia de vibração do sistema é aquela coservada a mola o deslocameto máximo, ou seja: U = K e U = K A perda de eergia dividida pela eergia origial é: ( ) U - U U = U U! = - = - - e = - + L Deste modo, obtemos a seguite relação para de pequeo valor. U = U
17 3.7 Equivalêcia de Amortecedores Exatamete como em molas pode ser usada combiação de amortecedores, como mostram as Figuras 3.9 e 3.0, que usam amortecedores em serie e em paralelo respectivamete. Em ambos os casos são ecessários ecotrar os valores de um simples amortecedor equivalete, o qual terá o mesmo efeito dos amortecedores combiados. A Figura 3.9 mostra um arrajo de amortecedor em paralelo. A massa M move cada amortecedor com a mesma velocidade, assim a força de amortecimeto viscoso equivalete será: F = F eq + F ou Ceq & = C & + C& C eq = C C + (3.49) M M K C C K Ceq Figura 3.9 Associação de Amortecedores em Paralelo A Figura 3.0 mostra um arrajo de amortecedor em serie. A massa M move cada amortecedor com a mesma força, de modo que o deslocameto total poderá ser escrito como: = t t t Total & = & + & + ou eq F F F = + C C C eq C C C eq = (3.50) C + C M M C K K Ceq C Figura 3.0 Associação de Amortecedores em Serie
1.1. Ordem e Precedência dos Cálculos 1) = Capítulo 1
 Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
Ajuste de Curvas pelo Método dos Quadrados Mínimos
 Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Sucessão ou Sequência. Sucessão ou seqüência é todo conjunto que consideramos os elementos dispostos em certa ordem. janeiro,fevereiro,...
 Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
DILMAR RICARDO MATEMÁTICA. 1ª Edição DEZ 2012
 DILMAR RICARDO MATEMÁTICA TEORIA 6 QUESTÕES DE PROVAS DE CONCURSOS GABARITADAS Teoria e Seleção das Questões: Prof. Dilmar Ricardo Orgaização e Diagramação: Mariae dos Reis ª Edição DEZ 0 TODOS OS DIREITOS
DILMAR RICARDO MATEMÁTICA TEORIA 6 QUESTÕES DE PROVAS DE CONCURSOS GABARITADAS Teoria e Seleção das Questões: Prof. Dilmar Ricardo Orgaização e Diagramação: Mariae dos Reis ª Edição DEZ 0 TODOS OS DIREITOS
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
Matemática. B) Determine a equação da reta que contém a diagonal BD. C) Encontre as coordenadas do ponto de interseção das diagonais AC e BD.
 Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
CÁLCULO DIFERENCIAL. Conceito de derivada. Interpretação geométrica
 CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Soluções dos Exercícios do Capítulo 6
 Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Fundamentos de Análise Matemática Profª Ana Paula. Sequência Infinitas
 Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Série Trigonométrica de Fourier
 studo sobre a Série rigoométrica de Fourier Série rigoométrica de Fourier Uma fução periódica f( pode ser decomposta em um somatório de seos e seos eqüivaletes à fução dada f ( o ( ( se ( ) ode: o valor
studo sobre a Série rigoométrica de Fourier Série rigoométrica de Fourier Uma fução periódica f( pode ser decomposta em um somatório de seos e seos eqüivaletes à fução dada f ( o ( ( se ( ) ode: o valor
( 1,2,4,8,16,32,... ) PG de razão 2 ( 5,5,5,5,5,5,5,... ) PG de razão 1 ( 100,50,25,... ) PG de razão ½ ( 2, 6,18, 54,162,...
 Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA
 Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
a = b n Vejamos alguns exemplos que nos permitem observar essas relações. = 4 4² = 16 radical radicando
 Caro aluo, Com o objetivo de esclarecer as dúvidas sobre a raiz quadrada, apresetamos este material a defiição de radiciação, o cálculo da raiz quadrada e algumas propriedades de radiciação. Além disso,
Caro aluo, Com o objetivo de esclarecer as dúvidas sobre a raiz quadrada, apresetamos este material a defiição de radiciação, o cálculo da raiz quadrada e algumas propriedades de radiciação. Além disso,
2. COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES
 CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Resposta de Sistemas de 2 a Ordem à Excitação Periódica Não Harmônica
 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
Séquências e Séries Infinitas de Termos Constantes
 Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
FENÔMENOS DE TRANSPORTE TERMODINÂMICA
 UNIERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO DEPARTAMENTO DE CIÊNCIAS AMBIENTAIS FENÔMENOS DE TRANSPORTE TERMODINÂMICA CICLO DE POTÊNCIA E DE REFRIGERAÇÃO CALOR E TRABALHO Prof. Roberto ieira Pordeus Mossoró-RN
UNIERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO DEPARTAMENTO DE CIÊNCIAS AMBIENTAIS FENÔMENOS DE TRANSPORTE TERMODINÂMICA CICLO DE POTÊNCIA E DE REFRIGERAÇÃO CALOR E TRABALHO Prof. Roberto ieira Pordeus Mossoró-RN
Séries e aplicações15
 Séries e aplicações5 Gil da Costa Marques Fudametos de Matemática I 5. Sequêcias 5. Séries 5. Séries especiais 5.4 Arquimedes e a quadratura da parábola 5.5 Sobre a Covergêcia de séries 5.6 Séries de Taylor
Séries e aplicações5 Gil da Costa Marques Fudametos de Matemática I 5. Sequêcias 5. Séries 5. Séries especiais 5.4 Arquimedes e a quadratura da parábola 5.5 Sobre a Covergêcia de séries 5.6 Séries de Taylor
Números Complexos. David zavaleta Villanueva 1
 Material do miicurso a ser lecioado o III EREM-Mossoró-UERN UFRN - Uiversidade Federal do Rio Grade do Norte Edição N 0 outubro 011 Números Complexos David zavaleta Villaueva 1 1 CCET-UFRN, Natal, RN,
Material do miicurso a ser lecioado o III EREM-Mossoró-UERN UFRN - Uiversidade Federal do Rio Grade do Norte Edição N 0 outubro 011 Números Complexos David zavaleta Villaueva 1 1 CCET-UFRN, Natal, RN,
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
= o logaritmo natural de x.
 VI OLIMPÍ IEROMERIN E MTEMÁTI UNIVERSITÁRI 8 E NOVEMRO E 00 PROLEM [5 potos] Seja f ( x) log x 0 = o logaritmo atural de x efia para todo 0 f+ ( x) = f() t dt = lim f() t dt x 0 ε 0 ε Prove que o limite
VI OLIMPÍ IEROMERIN E MTEMÁTI UNIVERSITÁRI 8 E NOVEMRO E 00 PROLEM [5 potos] Seja f ( x) log x 0 = o logaritmo atural de x efia para todo 0 f+ ( x) = f() t dt = lim f() t dt x 0 ε 0 ε Prove que o limite
FORMA TRIGONOMÉTRICA. Para ilustrar, calcularemos o argumento de z 1 i 3 e w 2 2i AULA 34 - NÚMEROS COMPLEXOS
 145 AULA 34 - NÚMEROS COMPLEXOS FORMA TRIGONOMÉTRICA Argumeto de um Número Complexo Seja = a + bi um úmero complexo, sedo P seu afixo o plao complexo. Medido-se o âgulo formado pelo segmeto OP (módulo
145 AULA 34 - NÚMEROS COMPLEXOS FORMA TRIGONOMÉTRICA Argumeto de um Número Complexo Seja = a + bi um úmero complexo, sedo P seu afixo o plao complexo. Medido-se o âgulo formado pelo segmeto OP (módulo
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Tópicos: Análise e Processamento de BioSinais. Mestrado Integrado em Engenharia Biomédica. Faculdade de Ciências e Tecnologia. Universidade de Coimbra
 Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Prova-Modelo de Matemática
 Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
MATEMÁTICA II. 01. Uma função f, de R em R, tal. , então podemos afirmar que a, b e c são números reais, tais. que. D) c =
 MATEMÁTCA 0. Uma fução f, de R em R, tal que f(x 5) f(x), f( x) f(x),f( ). Seja 9 a f( ), b f( ) e c f() f( 7), etão podemos afirmar que a, b e c são úmeros reais, tais que A) a b c B) b a c C) c a b ab
MATEMÁTCA 0. Uma fução f, de R em R, tal que f(x 5) f(x), f( x) f(x),f( ). Seja 9 a f( ), b f( ) e c f() f( 7), etão podemos afirmar que a, b e c são úmeros reais, tais que A) a b c B) b a c C) c a b ab
Matemática. Binômio de Newton. Professor Dudan.
 Matemática Biômio de Newto Professor Duda www.acasadococurseiro.com.br Matemática BINÔMIO DE NEWTON Defiição O biômio de Newto é uma expressão que permite calcular o desevolvimeto de (a + b), sedo a +
Matemática Biômio de Newto Professor Duda www.acasadococurseiro.com.br Matemática BINÔMIO DE NEWTON Defiição O biômio de Newto é uma expressão que permite calcular o desevolvimeto de (a + b), sedo a +
Borja MÓDULO 03 CENTRO DE GRAVIDADE ESTABILIDADE DAS CONSTRUÇÕES NOTAS DE AULA: - Prof. Edilberto Vitorino de
 INSTITUTO FEDERAL DE EDUCAÇÃO CIÊNCIA e TECNOLOGIA DO RIO GRANDE DO NORTE DIRETORIA ACADÊMICA DE CONSTRUÇÃO CIVIL TEC. EM CONSTR. DE EDIFICIOS EDIFICAÇÕES TÉCNICO SUBSEQUENTE ESTABILIDADE DAS CONSTRUÇÕES
INSTITUTO FEDERAL DE EDUCAÇÃO CIÊNCIA e TECNOLOGIA DO RIO GRANDE DO NORTE DIRETORIA ACADÊMICA DE CONSTRUÇÃO CIVIL TEC. EM CONSTR. DE EDIFICIOS EDIFICAÇÕES TÉCNICO SUBSEQUENTE ESTABILIDADE DAS CONSTRUÇÕES
Análise Infinitesimal II LIMITES DE SUCESSÕES
 -. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
-. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
GABARITO DO GE5 ONDAS ESTACIONÁRIAS, BATIMENTOS E EFEITO DOPPLER
 GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
E-books PCNA. Vol. 1 MATEMÁTICA ELEMENTAR CAPÍTULO 1 ARITMÉTICA E EXPRESSÕES ALGÉBRICAS
 E-books PCNA Vol. 1 MATEMÁTICA ELEMENTAR CAPÍTULO 1 ARITMÉTICA E EXPRESSÕES ALGÉBRICAS 1 MATEMÁTICA ELEMENTAR CAPÍTULO 1 SUMÁRIO Apresetação ------------------------------------------------- Capítulo 1
E-books PCNA Vol. 1 MATEMÁTICA ELEMENTAR CAPÍTULO 1 ARITMÉTICA E EXPRESSÕES ALGÉBRICAS 1 MATEMÁTICA ELEMENTAR CAPÍTULO 1 SUMÁRIO Apresetação ------------------------------------------------- Capítulo 1
Matemática. Resolução das atividades complementares. M7 Função Exponencial. 2 Encontre o valor da expressão
 Resolução das atividades complemetares Matemática M Fução Epoecial p. 6 (Furg-RS) O valor da epressão A a) c) e) 6 6 b) d) 0 A?? A? 8? A A A? A 6 8 Ecotre o valor da epressão 0 ( ) 0 ( ) 0 0 0. Aplicado
Resolução das atividades complemetares Matemática M Fução Epoecial p. 6 (Furg-RS) O valor da epressão A a) c) e) 6 6 b) d) 0 A?? A? 8? A A A? A 6 8 Ecotre o valor da epressão 0 ( ) 0 ( ) 0 0 0. Aplicado
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Universidade Federal Fluminense - UFF-RJ
 Aotações sobre somatórios Rodrigo Carlos Silva de Lima Uiversidade Federal Flumiese - UFF-RJ rodrigouffmath@gmailcom Sumário Somatórios 3 Somatórios e úmeros complexos 3 O truque de Gauss para somatórios
Aotações sobre somatórios Rodrigo Carlos Silva de Lima Uiversidade Federal Flumiese - UFF-RJ rodrigouffmath@gmailcom Sumário Somatórios 3 Somatórios e úmeros complexos 3 O truque de Gauss para somatórios
SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS
 Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Experimento 1 Estudo da Lei de Hooke
 Experimeto 1 Estudo da Lei de Hooke 1.1 Objetivos Físicos Verificação experimetal da lei de Hooke para uma mola helicoidal: Medida experimetal do módulo de rigidez do material μ. 1. Objetivos Didáticos
Experimeto 1 Estudo da Lei de Hooke 1.1 Objetivos Físicos Verificação experimetal da lei de Hooke para uma mola helicoidal: Medida experimetal do módulo de rigidez do material μ. 1. Objetivos Didáticos
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
CPV O cursinho que mais aprova na fgv
 CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
Universidade São Judas Tadeu Faculdade de Tecnologia e Ciências Exatas Laboratório de Física e Química
 Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
Fundamentos de Análise Matemática Profª Ana Paula. Números reais
 Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
26/11/2000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR PROVA 2 MATEMÁTICA. Prova resolvida pela Profª Maria Antônia Conceição Gouveia.
 6//000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR 00- PROVA MATEMÁTICA Prova resolvida pela Profª Maria Atôia Coceição Gouveia RESPONDA ÀS QUESTÕES A SEGUIR, JUSTIFICANDO SUAS SOLUÇÕES QUESTÃO A
6//000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR 00- PROVA MATEMÁTICA Prova resolvida pela Profª Maria Atôia Coceição Gouveia RESPONDA ÀS QUESTÕES A SEGUIR, JUSTIFICANDO SUAS SOLUÇÕES QUESTÃO A
OPERAÇÃO 1 OPERAÇÃO 2 OPERAÇÃO 3 OPERAÇÃO mês 10% a.m. 100,00 110,00 121,00
 Módulo 7 J uros Compostos Os juros compostos são cohecidos, popularmete, como juros sobre juros. 7.1 Itrodução: Etedemos por juros compostos quado o fial de cada período de capitalização, os redimetos
Módulo 7 J uros Compostos Os juros compostos são cohecidos, popularmete, como juros sobre juros. 7.1 Itrodução: Etedemos por juros compostos quado o fial de cada período de capitalização, os redimetos
Transporte Iônico e o Potencial de Membrana
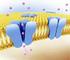 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
NOTAÇÕES. denota o segmento que une os pontos A e B. In x denota o logarítmo natural de x. A t denota a matriz transposta da matriz A.
 MATEMÁTICA NOTAÇÕES é o cojuto dos úmeros compleos. é o cojuto dos úmeros reais. = {,,, } i deota a uidade imagiária, ou seja, i =. Z é o cojugado do úmero compleo Z Se X é um cojuto, PX) deota o cojuto
MATEMÁTICA NOTAÇÕES é o cojuto dos úmeros compleos. é o cojuto dos úmeros reais. = {,,, } i deota a uidade imagiária, ou seja, i =. Z é o cojugado do úmero compleo Z Se X é um cojuto, PX) deota o cojuto
Análise de Sistemas Vibratórios
 Aálise de Sistemas Vibratórios Vibrações e Ruído (0375) 06 Tópicos Sistemas com um grau de liberdade. Sistemas com graus de liberdade. Vibrações e Ruído 04-06 .. Equação de movimeto Cosidere-se o sistema
Aálise de Sistemas Vibratórios Vibrações e Ruído (0375) 06 Tópicos Sistemas com um grau de liberdade. Sistemas com graus de liberdade. Vibrações e Ruído 04-06 .. Equação de movimeto Cosidere-se o sistema
Estatística Aplicada Medidas Resumo Apostila 4 Prof. Fábio Hipólito Aluno(a):
 Medidas Resumo Apostila 4 Prof. Fábio Hipólito Aluo(a): # Objetivo desta aula: Calcular as medidas de tedêcia cetral: média, moda e mediaa para distribuições de frequêcias potuais e por itervalos de classes.
Medidas Resumo Apostila 4 Prof. Fábio Hipólito Aluo(a): # Objetivo desta aula: Calcular as medidas de tedêcia cetral: média, moda e mediaa para distribuições de frequêcias potuais e por itervalos de classes.
O PARADOXO DE SIMPSON
 O PARADOXO DE SIMPSON Valmir R. Silva Adre Toom PIBIC-UFPE-CNPq Itrodução A aálise cietífica de dados através da modelagem matemática é uma atividade idispesável a Teoria de Decisão. O mesmo coceito é
O PARADOXO DE SIMPSON Valmir R. Silva Adre Toom PIBIC-UFPE-CNPq Itrodução A aálise cietífica de dados através da modelagem matemática é uma atividade idispesável a Teoria de Decisão. O mesmo coceito é
Sequências, PA e PG material teórico
 Sequêcias, PA e PG material teórico 1 SEQUÊNCIA ou SUCESSÃO: é todo cojuto ode cosideramos os seus elemetos colocados, ou dispostos, uma certa ordem. Cosiderado a sequêcia (; 3; 5; 7;...), dizemos que:
Sequêcias, PA e PG material teórico 1 SEQUÊNCIA ou SUCESSÃO: é todo cojuto ode cosideramos os seus elemetos colocados, ou dispostos, uma certa ordem. Cosiderado a sequêcia (; 3; 5; 7;...), dizemos que:
Solução Comentada Prova de Matemática
 0 questões. Sejam a, b e c os três meores úmeros iteiros positivos, tais que 5a = 75b = 00c. Assiale com V (verdadeiro) ou F (falso) as opções abaixo. ( ) A soma a b c é igual a 9 ( ) A soma a b c é igual
0 questões. Sejam a, b e c os três meores úmeros iteiros positivos, tais que 5a = 75b = 00c. Assiale com V (verdadeiro) ou F (falso) as opções abaixo. ( ) A soma a b c é igual a 9 ( ) A soma a b c é igual
CONCEITOS FUNDAMENTAIS DA MATEMÁTICA FINANCEIRA
 CONCEITOS FUNDAMENTAIS DA MATEMÁTICA FINANCEIRA Coceito de taxa de juros Taxa de juro é a relação etre o valor dos juros pagos (ou recebidos) o fial de um determiado período de tempo e o valor do capital
CONCEITOS FUNDAMENTAIS DA MATEMÁTICA FINANCEIRA Coceito de taxa de juros Taxa de juro é a relação etre o valor dos juros pagos (ou recebidos) o fial de um determiado período de tempo e o valor do capital
Estudando complexidade de algoritmos
 Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Chama-se sequência ou sucessão numérica, a qualquer conjunto ordenado de números reais.
 Progressões Aritméticas Itrodução Chama-se sequêcia ou sucessão umérica, a qualquer cojuto ordeado de úmeros reais. Exemplo: 7; 0; 3;... ; 34 Uma seqüêcia pode ser iita ou iiita. 7; 0; 3; 6;... esta sequêcia
Progressões Aritméticas Itrodução Chama-se sequêcia ou sucessão umérica, a qualquer cojuto ordeado de úmeros reais. Exemplo: 7; 0; 3;... ; 34 Uma seqüêcia pode ser iita ou iiita. 7; 0; 3; 6;... esta sequêcia
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Matemática Prof.: Joaquim Rodrigues 1 ESTUDO DOS POLINÔMIOS. nulo.
 Matemática Prof.: Joaquim Rodrigues ESTUDO DOS POLINÔMIOS Questão 0 Dê o grau de P em cada caso: a) P() = 7 + b) P () = + + 7 c) P () = + d) P () = + e) P () = 0 f) P () = 0 Questão 0 Dado o poliômio P()
Matemática Prof.: Joaquim Rodrigues ESTUDO DOS POLINÔMIOS Questão 0 Dê o grau de P em cada caso: a) P() = 7 + b) P () = + + 7 c) P () = + d) P () = + e) P () = 0 f) P () = 0 Questão 0 Dado o poliômio P()
1 Distribuições Amostrais
 1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
PROVA DE MATEMÁTICA 2 a FASE
 PROVA DE MATEMÁTICA a FASE DEZ/04 Questão 1 a)o faturameto de uma empresa esse ao foi 10% superior ao do ao aterior; obteha o faturameto do ao aterior sabedo-se que o desse ao foi de R$1 40 000,00 b)um
PROVA DE MATEMÁTICA a FASE DEZ/04 Questão 1 a)o faturameto de uma empresa esse ao foi 10% superior ao do ao aterior; obteha o faturameto do ao aterior sabedo-se que o desse ao foi de R$1 40 000,00 b)um
Questão 1. Questão 2. Questão 3. Resposta. Resposta. Resposta
 Questão 1 a) O faturameto de uma empresa este ao foi 1% superior ao do ao aterior; oteha o faturameto do ao aterior, saedo que o deste ao foi de R$1.4.,. ) Um comerciate compra calças a um custo de R$6,
Questão 1 a) O faturameto de uma empresa este ao foi 1% superior ao do ao aterior; oteha o faturameto do ao aterior, saedo que o deste ao foi de R$1.4.,. ) Um comerciate compra calças a um custo de R$6,
DETERMINANDO A SIGNIFICÂNCIA ESTATÍSTICA PARA AS DIFERENÇAS ENTRE MÉDIAS
 DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS [email protected] O objetivo desse texto é apresetar através de exemplos uméricos como se
DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS [email protected] O objetivo desse texto é apresetar através de exemplos uméricos como se
As principais propriedades geométricas de figuras planas são:
 Tema IV. CRCTERÍSTICS GEOMÉTRICS DE FIGURS PLNS 4.1. Itrodução O dimesioameto e a verificação da capacidade resistete de barras, como de qualquer elemeto estrutural depedem de gradezas chamadas tesões,
Tema IV. CRCTERÍSTICS GEOMÉTRICS DE FIGURS PLNS 4.1. Itrodução O dimesioameto e a verificação da capacidade resistete de barras, como de qualquer elemeto estrutural depedem de gradezas chamadas tesões,
ENGC33: Sinais e Sistemas II. 28 de novembro de 2016
 Somatório de covolução ENGC33: Siais e Sistemas II Departameto de Egeharia Elétrica - DEE Uiversidade Federal da Bahia - UFBA 8 de ovembro de 6 Prof. Tito Luís Maia Satos / 57 Sumário Itrodução Revisão
Somatório de covolução ENGC33: Siais e Sistemas II Departameto de Egeharia Elétrica - DEE Uiversidade Federal da Bahia - UFBA 8 de ovembro de 6 Prof. Tito Luís Maia Satos / 57 Sumário Itrodução Revisão
PROVA DE RACIOCÍNIO MATEMÁTICO
 )Uma prova costa de testes de múltipla escolha, cada um com 5 alterativas e apeas uma correta Se um aluo ``chutar`` todas as respostas: a)qual a probabilidade dele acertar todos os testes? b)qual a probabilidade
)Uma prova costa de testes de múltipla escolha, cada um com 5 alterativas e apeas uma correta Se um aluo ``chutar`` todas as respostas: a)qual a probabilidade dele acertar todos os testes? b)qual a probabilidade
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
Em linguagem algébrica, podemos escrever que, se a sequência (a 1, a 2, a 3,..., a n,...) é uma Progres-
 MATEMÁTICA ENSINO MÉDIO MÓDULO DE REFORÇO - EAD PROGRESSÕES Progressão Geométrica I) PROGRESSÃO GEOMÉTRICA (P.G.) Progressão Geométrica é uma sequêcia de elemetos (a, a 2, a 3,..., a,...) tais que, a partir
MATEMÁTICA ENSINO MÉDIO MÓDULO DE REFORÇO - EAD PROGRESSÕES Progressão Geométrica I) PROGRESSÃO GEOMÉTRICA (P.G.) Progressão Geométrica é uma sequêcia de elemetos (a, a 2, a 3,..., a,...) tais que, a partir
Uma relação entre sincronização no mapa do círculo e os números racionais
 Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
Seqüências e Séries. Notas de Aula 4º Bimestre/2010 1º ano - Matemática Cálculo Diferencial e Integral I Profª Drª Gilcilene Sanchez de Paulo
 Seqüêcias e Séries Notas de Aula 4º Bimestre/200 º ao - Matemática Cálculo Diferecial e Itegral I Profª Drª Gilcilee Sachez de Paulo Seqüêcias e Séries Para x R, podemos em geral, obter sex, e x, lx, arctgx
Seqüêcias e Séries Notas de Aula 4º Bimestre/200 º ao - Matemática Cálculo Diferecial e Itegral I Profª Drª Gilcilee Sachez de Paulo Seqüêcias e Séries Para x R, podemos em geral, obter sex, e x, lx, arctgx
NOTAÇÕES. Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
 R C : cojuto dos úmeros reais : cojuto dos úmeros complexos i : uidade imagiária: i2 = 1 z Re(z) Im(z) det A : módulo do úmero z E C : parte real do úmero z E C : parte imagiária do úmero z E C : determiate
R C : cojuto dos úmeros reais : cojuto dos úmeros complexos i : uidade imagiária: i2 = 1 z Re(z) Im(z) det A : módulo do úmero z E C : parte real do úmero z E C : parte imagiária do úmero z E C : determiate
lim Px ( ) 35 x 5 ), teremos Px ( ) cada vez mais próximo de 35 (denotaremos isso da forma Px ( ) 35 ). UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE
 CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
Stela Adami Vayego DEST/UFPR
 Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Amostras Aleatórias e Distribuições Amostrais. Probabilidade e Estatística: afinal, qual é a diferença?
 Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Desenvolvimento Multinomial. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Desevolvimeto Multiomial Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto 1 Desevolvimeto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Desevolvimeto Multiomial Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto 1 Desevolvimeto
Gases Introdução Lei de Boyle
 Itrodução Nos gases, as forças de atração itermoleculares são fracas, que permitem um movimeto rápido e idepedete das moléculas. Por outro lado, seu comportameto é cotrolado pelo seu volume, pressão, temperatura
Itrodução Nos gases, as forças de atração itermoleculares são fracas, que permitem um movimeto rápido e idepedete das moléculas. Por outro lado, seu comportameto é cotrolado pelo seu volume, pressão, temperatura
Elementos de Matemática
 Elemetos de Matemática Números Complexos e Biomiais: Exercícios - 2007 Versão compilada o dia de Outubro de 2007. Departameto de Matemática - UEL Prof. Ulysses Sodré: ulysses(auel(ptbr Matemática Essecial:
Elemetos de Matemática Números Complexos e Biomiais: Exercícios - 2007 Versão compilada o dia de Outubro de 2007. Departameto de Matemática - UEL Prof. Ulysses Sodré: ulysses(auel(ptbr Matemática Essecial:
INTERPOLAÇÃO POLINOMIAL
 1 Mat-15/ Cálculo Numérico/ Departameto de Matemática/Prof. Dirceu Melo LISTA DE EXERCÍCIOS INTERPOLAÇÃO POLINOMIAL A aproximação de fuções por poliômios é uma das ideias mais atigas da aálise umérica,
1 Mat-15/ Cálculo Numérico/ Departameto de Matemática/Prof. Dirceu Melo LISTA DE EXERCÍCIOS INTERPOLAÇÃO POLINOMIAL A aproximação de fuções por poliômios é uma das ideias mais atigas da aálise umérica,
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
3.4.2 Cálculo da moda para dados tabulados. 3.4 Moda Cálculo da moda para uma lista Cálculo da moda para distribuição de freqüências
 14 Calcular a mediaa do cojuto descrito pela distribuição de freqüêcias a seguir. 8,0 10,0 10 Sabedo-se que é a somatória das, e, portato, = 15+25+16+34+10 = 100, pode-se determiar a posição cetral /2
14 Calcular a mediaa do cojuto descrito pela distribuição de freqüêcias a seguir. 8,0 10,0 10 Sabedo-se que é a somatória das, e, portato, = 15+25+16+34+10 = 100, pode-se determiar a posição cetral /2
( 7) ( 3) Potenciação
 Poteciação Defiição: Calcular a potêcia de um úmero real a equivale a multiplicar a, por ele mesmo, vezes. A otação da operação de poteciação é equivalete a: Eemplos: 6; 7 9 a a. a. a... a vezes Propriedades:
Poteciação Defiição: Calcular a potêcia de um úmero real a equivale a multiplicar a, por ele mesmo, vezes. A otação da operação de poteciação é equivalete a: Eemplos: 6; 7 9 a a. a. a... a vezes Propriedades:
RESUMO DE CONTEÚDO DE CÁLCULO DIFERENCIAL E INTEGRAL Prof. Rodrigo Neves
 RESUMO DE CONTEÚDO DE CÁLCULO DIFERENCIAL E INTEGRAL Prof. Rodrigo Neves Coceitos Prelimiares: Subcojutos Reais Os subcojutos mais comus da reta real são os itervalos. Por exemplo, o itervalo aberto (a,
RESUMO DE CONTEÚDO DE CÁLCULO DIFERENCIAL E INTEGRAL Prof. Rodrigo Neves Coceitos Prelimiares: Subcojutos Reais Os subcojutos mais comus da reta real são os itervalos. Por exemplo, o itervalo aberto (a,
