CEEJA MAX DADÁ GALLIZZI

Transcrição

1 CEEJA MAX DADÁ GALLIZZI MATEMÁTICA ENSINO MÉDIO APOSTILA 20 Página 1

2 Parabéns!!! Você já é um vencedor! Voltar a estudar é uma vitória que poucos podem dizer que conseguiram. É para você, caro aluno, que desenvolvemos esse material. Foi pensando em seu sucesso e em auxiliá-lo nas redescobertas da arte matemática que elaboramos o conteúdo e os exercícios contidos nesta coleção de apostilas. Ela foi escrita em linguagem simples e com a preocupação de transmitir os assuntos importantes de matemática da forma mais clara possível. Todos nós usamos matemática diariamente, mesmo sem perceber. Em uma compra, ao pagar e ao receber o troco, estamos fazendo matemática. Até para utilizarmos corretamente uma máquina de calcular, precisamos saber matemática. Para isto, em cada aula, você encontrará ferramentas matemáticas que passarão a fazer parte da sua vida para enriquecê-la e facilitála. A matemática não é um conjunto de regras que devam ser decoradas. O importante é compreender o que está por trás de cada regra; é compreender os conceitos. Assim você poderá utilizar os seus conhecimentos em situações novas, resolvendo os problemas que surgirem na sua casa, no seu trabalho, na sua vida. Uma parte fundamental dessa apostila são os Exercícios. Não se aprende matemática apenas lendo um texto. É preciso praticar. É preciso gastar lápis e papel resolvendo exercícios. Só assim ganhamos segurança no que aprendemos e ficamos preparados para a aula seguinte. Portanto, tente fazer os exercícios de cada aula. Talvez você não consiga resolver todos, mas o importante é tentar fazer. Também aprendemos muito com nossos próprios erros. Resolva todos os exercícios em seu caderno (não responder na apostila, pois a mesma será utilizada por outros alunos no decorrer do curso). Procure-nos assim que surgirem as primeiras dificuldades, nós estaremos sempre prontos para ajudálo. No fim do curso você terá adquirido uma série de conhecimentos de matemática que serão suas ferramentas para compreender melhor o mundo que nos cerca, tornando-o um cidadão mais seguro e respeitado. Mas, acima de tudo, você vai descobrir que pensar é divertido. Raciocinar é estimulante. Resolver desafios, questionar, encontrar soluções nos dá prazer, desenvolve a nossa mente e torna mais ágil o nosso raciocínio. Adquirindo o hábito de pensar de forma organizada, você terá aprendido a mais importante das lições e nós teremos cumprido o nosso objetivo. Página 2

3 Geometria Espacial Introdução A preocupação com o cálculo de volumes é bastante antiga. Há milhares de anos a civilização egípcia já conhecia alguns processos para esse cálculo. Os habitantes da Grécia Antiga aprimoraram esses processos e desenvolveram outros. Destaca-se o trabalho do matemático e físico Arquimedes, que viveu no século III a.c. Desenvolvendo raciocínios bastante criativos, Arquimedes mostrou como calcular o volume de diversas figuras geométricas. Conta-se que, enquanto tomava banho, constatou que a água subia quando ele mergulhava. Essa quantidade de água que subia era seu volume. Página 3

4 Com esta aula iniciamos o estudo da Geometria Espacial. Nesta unidade você estudará as propriedades de figuras espaciais, tais como: o cubo, o paralelepípedo, a esfera, o cilindro etc. Aprenderá também a calcular o volume dessas e de outras figuras. Para o cálculo de um volume podemos usar diferentes unidades de medida. Certamente você já conhece o litro e o metro cúbico. Portanto, vamos aprofundar esses conceitos. Página 4

5 Volume ou Capacidade Podemos ter muitas definições para a palavra volume, mas para a Matemática é o espaço ocupado por um corpo. Todo sólido geométrico possui volume e ocupa espaço. Volume ou capacidade de um corpo (ou recipiente) é a quantidade de espaço que esse corpo ocupa ou que ele dispõe para armazenar alguma coisa. Por exemplo: Esses recipientes têm a capacidade de armazenar 1 litro de líquido, conforme a indicação em cada embalagem. Podemos dizer que o volume ou a capacidade de cada um desses recipientes é de 1 litro. Vejamos um outro exemplo: diariamente nos portos brasileiros, navios são carregados ou descarregados com mercadorias que serão transportadas para outros lugares. Em geral, essas mercadorias são armazenadas em grandes caixas chamadas de container. Existem dois tipos de container: o de 20 pés (cuja capacidade é de 32,88 metros cúbicos) e o de 40 pés (cuja capacidade é de 66, 92 metros cúbicos). Página 5

6 Unidade de Volume ou de Capacidade O litro(l) Litro (simbolo: l) é uma unidade de medida de volume que obedece ao sistema métrico decimal e é aceito pelo Sistema Internacional de Unidades. O litro é a quantidade de líquido capaz de encher completamente um cubo oco, com 10 cm de aresta. Quantos litros cabem num metro cúbico? Para responder a essa pergunta vamos imaginar uma caixa cúbica com 1 metro de aresta e muitos cubinhos com 10 cm de aresta. Cada um desses cubinhos corresponde a 1 litro de água. Podemos arrumar os cubinhos dentro da caixa grande em fileiras de 10, de forma que o fundo da caixa fique com = 100 cubinhos. Como podemos formar 10 camadas, temos: = cubinhos Página 6

7 O mililitro(ml) Em algumas situações práticas, o volume a ser medido é tão pequeno que o litro se torna uma unidade inadequada. Isso acontece, por exemplo, quando queremos indicar a quantidade de líquido de um vidro de remédio. Nesse caso usamos o mililitro (ml). O mililitro é a quantidade de líquido que cabe num cubo oco com 1 cm de aresta. 1 cm 1 cm 1 cm As latas de refrigerante e cerveja costumam ter em seu rótulo a indicação em mililitros de seu volume. Repare: Muitas vezes é importante que saibamos relacionar duas unidades. Da mesma forma que relacionamos a hora com o minuto, o metro com o quilômetro ou com o centímetro, da mesma forma precisamos relacionar as unidades de volume. Página 7

8 Outras unidades de volume muito usuais. Nos exemplos anteriores utilizamos o litro (cuja abreviatura é l) e o metro cúbico (cuja abreviatura é m 3 ) como unidades de medida. Além dessas unidades, temos também o centímetro cúbico (cm³), o decímetro cúbico (dm³), o mililitro (ml) etc. A escolha da unidade de medida adequada depende do tamanho do que se vai medir. O metro cúbico, por exemplo, é adequado para medir grandes volumes, como no caso de um container. Nesse caso iremos representá-lo usando a seguinte unidade: 1m³ (metro cúbico) = 1000 litros Para medir pequenos volumes costumamos usar o litro(l) e o mililitro(ml) como no caso da caixa de leite. Em situações em que o volume é muito pequeno podemos usar: 1cm³ = 1 ml (mililitro) Em situações cotidianas usamos: 1 litro = 1000cm³ (centímetro cúbico) = 1dm³ (decímetro cúbico) Podemos concluir que as principais unidades usuais de m³ (metros cúbicos) são: 1m³ = 1000 litros 1cm³ = 1 ml (mililitro) 1 dm³ = 1 litro Página 8

9 Exercícios Questão 01: Que unidade de medida você usaria para indicar a quantidade de líquido em: a) um copo de chopp; b) uma lata de óleo; c) uma piscina; d) uma ampola. Questão 02: Responda: a) Quantos cm 3 contém um litro (l)? b) Quantos cm 3 contém um mililitro (ml)? c) Quantos litros contém um m 3? d) 2000 cm 3 equivalem a quantos litros? e) 5 m 3 equivalem a quantos litros? Questão 03: Uma outra unidade para medir volumes, muito usada na vida prática, é a garrafa. Sabendo que a garrafa vale de litro indique sua capacidade em mililitros. Questão 04: Uma lata de óleo tem, em geral 900 ml. Quantas latas correspondem a um galão de 45l de óleo? Questão 05: Com um barril de vinho de 360 litros, quantas garrafas de vinho de 750ml podemos completar? Questão 06: Como você explicaria para uma criança o que é um litro de água? Página 9

10 Veja alguns exemplos de prismas. Prismas Prismas são sólidos geométricos que possuem as seguintes características: bases paralelas são iguais; arestas laterais iguais e paralelas e que ligam as duas bases. Nomenclatura: Os prismas são desiguais pelo número de lados das bases, que lhes dão o nome: Veremos a seguir os volumes de alguns dos prismas mais utilizados em nosso cotidiano. Página 10

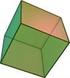
11 O Cubo Cubo é um prisma em que todas as faces são quadradas. O cubo é um prisma quadrangular regular cuja altura é igual à medida da aresta da base. É, de entre todos os poliedros, talvez o mais conhecido, por existirem muitos objetos de uso diário de forma cúbica, como por exemplo um dado. O cubo é um poliedro regular pois as suas faces são geometricamente iguais. O cubo tem os seguintes elementos: 6 faces, que são quadrados geometricamente iguais; 12 arestas iguais, que são segmentos de reta; 8 vértices, que são pontos. Para construir um cubo basta conhecer a medida de uma aresta. Aresta é o nome que se dá à linha que separa uma face da outra. Os lados dos quadrados que formam o cubo são as arestas do cubo. Página 11

12 O Volume do Cubo O volume de um cubo depende da medida de sua aresta, consideramos apenas uma medida, pois o cubo possui todas as arestas de tamanhos iguais e seu volume é apresentado pela expressão, onde a corresponde à medida da aresta. EXEMPLO: Quantos litros cabem no reservatório abaixo? Solução: l l Página 12

13 O Paralelepípedo Uma caixa de fósforos, uma embalagem de detergente, um tijolo, algumas caixas de medicamentos, um livro, uma pedra de dominó são objetos com os quais lidamos diariamente e cuja forma se associa a um sólido geométrico a que chamamos paralelepípedo retângulo. Paralelepípedo é um prisma que possui em suas bases um paralelogramo. Sendo que o paralelepípedo é configurado pela reunião dos seis paralelogramos que o constituem. Este sólido geométrico tem os seguintes elementos: 6 faces (são retângulos iguais dois a dois); 12 arestas (iguais quatro a quatro); 8 vértices. Para a construção de um paralelepípedo é necessário conhecer os comprimentos das três arestas concorrentes a um mesmo vértice. Página 13

14 O Volume do Paralelepípedo O volume de um paralelepípedo é o produto das medidas de suas arestas. Matematicamente dizemos que: ou EXEMPLO: Quantos litros de água são necessários para encher completamente uma caixa d água cujas dimensões são: 0,90 m de comprimento, 0,80 m de largura e 0,70 m de altura? Como l, teremos então: x 1000 l São necessários 504l para encher, completamente, essa caixa d água. Página 14

15 Exercícios Questão 07: Os cubos seguintes têm, respectivamente, arestas 1, 2 e 3 cm. Calcule o valor de cada um dos cubos. Questão 08: A piscina de um clube tem 2 m de profundidade, 12 m de comprimento e 8 m de largura. Quantos litros de água são necessários para enchê-la? Questão 09: Uma caixa cúbica tem 50 cm de aresta e será totalmente enchida de água. Determine: a) Qual o seu volume? b) Quantas garrafas de 500 ml cada uma podem ser enchidas com a água desta caixa? Questão 10: Precisamos construir uma caixa d água com o formato de um paralelepípedo. Quais podem ser as dimensões dessa caixa para que sua capacidade seja de litros? Página 15

16 Questão 11: Uma caixa de vinho tem as seguintes dimensões: 30 cm de altura, 40 cm de comprimento e 25 cm de largura. Um comerciante importou um container de 20 pés (32,88 m 3 ) de caixas de vinho. Quantas caixas de vinho ele encomendou? Questão 12: Um supermercado vende pedaços de goiabada. Os pedaços têm a forma aproximada de paralelepípedos. Um pedaço mede 6 cm x 5 cm x 8 cm e custa R$ 0,72. Um outro pedaço, de 8 cm x 6 cm x 9 cm, é vendido a R$ 1,35. Qual dos dois pedaços será mais vantajoso comprar? Questão 13: O doce de leite é vendido, em um supermercado, em dois tipos de embalagem: um tijolo, cujas medidas são 8 cm x 10 cm x 9 cm e que custa R$ 4,80. pequenas unidades, medindo 1,5 cm x 3 cm x 1,0 cm. Por quanto deve ser vendida cada uma das pequenas unidades, de modo a não haver vantagem de uma embalagem sobre a outra? Página 16

17 Introdução Pirâmide A pirâmide é considerada um dos mais antigos sólidos geométricos construídos pelo homem. Uma das mais famosas é a pirâmide de Quéops, construída em a.c., com 150 m de altura, aproximadamente - o que pode ser comparado a um prédio de 50 andares. Quando pensamos numa pirâmide, vem-nos à cabeça a imagem da pirâmide egípcia, cuja base é um quadrado. Contudo, o conceito geométrico de pirâmide é um pouco mais amplo: sua base pode ser formada por qualquer polígono. As figuras abaixo representam pirâmides: Página 17

18 Elementos da Pirâmide Uma pirâmide é um sólido geométrico, cuja base é um polígono e cujas faces laterais são triângulos que possuem um vértice comum. Em uma pirâmide, podemos identificar vários elementos: Base: A base da pirâmide é a região plana poligonal sobre a qual se apoia a pirâmide. Vértice: O vértice da pirâmide é o ponto isolado P mais distante da base da pirâmide. Eixo: Quando a base possui um ponto central, isto é, quando a região poligonal é simétrica ou regular, o eixo da pirâmide é a reta que passa pelo vértice e pelo centro da base. Altura: Distância do vértice da pirâmide ao plano da base. Faces laterais: São regiões planas triangulares que passam pelo vértice da pirâmide e por dois vértices consecutivos da base. Arestas Laterais: São segmentos que têm um extremo no vértice da pirâmide e outro extremo num vértice do polígono situado no plano da base. Apótema: É a altura de cada face lateral. Superfície Lateral: É a superfície poliédrica formada por todas as faces laterais. Aresta da base: É qualquer um dos lados do polígono da base. Página 18

19 O Volume da Pirâmide O volume de uma pirâmide pode ser obtido como um terço do produto da área da base pela altura da pirâmide, isto é: EXEMPLO 01: Qual o volume de uma pirâmide quadrangular, cuja altura mede 5 cm e a aresta da base, 3 cm? Resolução: O volume dessa pirâmide é de 15 cm 3. EXEMPLO 02: Uma indústria irá fabricar uma peça no formato de uma pirâmide de base triangular com as medidas indicadas na figura. Sabendo que serão fabricadas peças maciças de aço, determine o volume de aço gasto na produção dessa peça. Resolução: O volume dessa pirâmide é de 45 cm 3. Página 19

20 Exercícios Questão 14: Uma pirâmide de base quadrangular possui altura medindo 2 metros e cada lado da base com medida igual a 3 metros. Determine o volume dessa pirâmide. Questão 15: Juliana tem um perfume contido em um frasco com a forma de uma pirâmide regular com base quadrada. A curiosa Juliana quer saber o volume de perfume que o frasco contém. Para isso ela usou uma régua e tirou duas informações: a medida da aresta da base de 4cm e a medida da altura do frasco que é de 6cm. Quantos ml de perfume há nesse frasco? Página 20

21 Corpos Redondos Introdução Você sabia que: Três quartos da superfície da Terra são cobertos de água? A linha do Equador mede, aproximadamente, km? Pense agora nas seguintes questões, relativas ao planeta Terra: Qual é o seu volume de sua superfície? Qual é a área coberta de água em sua superfície? As respostas a essas questões são possíveis com o estudo dos corpos redondos, que faremos nesse capítulo. Veja exemplos de corpos redondos: Cilindro Cone Esfera Página 21

22 O Cilindro O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas. Aplicações práticas Os cilindros abaixo sugerem alguma aplicação importante em sua vida? O Volume do Cilindro Podemos imaginar um cilindro formado por círculos de cartolina, todos do mesmo tamanho, empilhados. Por isso, temos que o volume do cilindro é também igual ao produto da área da base pela altura. Onde: r h = altura r = raio d = diâmetro d Como a base do cilindro é circular, utilizamos a área do círculo para calcular a área da base, sendo assim,onde. Assim, teremos: Página 22

23 EXEMPLO 01: Um galão de vinho de forma cilíndrica tem o raio da base igual a 2m e sua altura é 5m e está completamente cheio. Qual é a quantidade de vinho existente, em litros, nesse galão? Resolução: l x 1000 Nesse galão há 62800l de vinho. EXEMPLO 02: Um reservatório tem as dimensões e a forma da figura abaixo. Quantos litros de combustível ele pode armazenar? Resolução: l l 1000 Ele poderá armazenar 14,130l de combustível. Página 23

24 Exercícios Questão 16: São comuns os objetos em forma cilíndrica. Num supermercado, se você observar as embalagens, vai identificar facilmente essa forma. Uma pessoa dispõe de dois recipientes cilíndricos: um tem raio de 20 cm e altura de 12 cm; o outro tem a metade do raio, porém o dobro da altura. Qual o recipiente de maior capacidade? Questão 17: Uma lata de óleo tem a forma de um cilindro. Seu diâmetro mede 8,4 cm e, sua altura, 18,2 cm. Será que ela comporta 1000 ml de óleo? Questão 18: Uma seringa tem a forma cilíndrica com 1cm de diâmetro, quando o êmbolo estiver a 5cm da extremidade da seringa próxima à agulha, qual o volume aproximado, em ml, de remédio líquido que a seringa pode conter? Página 24

25 Questão 19: Para fabricar uma caixa de lápis de cor, é preciso saber inicialmente qual é o volume de cada lápis. a) Calcule então o volume de um lápis (sem apontar) que tem 0,8cm de diâmetro e 8cm de comprimento. b) Determine agora o volume aproximado de uma caixa que contém 12 desses lápis. Questão 20: Uma panela caseira tem a forma de um cilindro; sua altura é 12cm e o diâmetro, 20cm. Deve-se enchê-la com cubos de gelo de 2cm de aresta, de tal forma que não transborde ao derreter o gelo. Qual a quantidade máxima de cubos de gelo necessária para encher a panela? Questão 21: As bebidas normalmente, são vendidas em embalagens diferentes. É preciso ter sempre atenção na hora de decidir qual comprar. Veja o exemplo: Certa bebida é vendida em dois tipos de embalagem: em garrafa de 600 ml, por R$ 0,78. em lata de 350 ml, por R$ 0,49. Qual das duas embalagens é mais vantajosa? Página 25

26 O Cone Quando falamos em cone logo vem em nossa mente a imagem do instrumento utilizado no trânsito, além desse exemplo, temos outros como as casquinhas de sorvetes, chapeuzinho de aniversário, entre outros. O Volume do Cone O volume, V, de um cone de altura, h, e base com raio, r, é 1/3 do volume do cilindro com as mesmas dimensões, assim, teremos: Onde: h = altura r = raio d = diâmetro Como a base do cone é circular, utilizamos a área do círculo para calcular a área da base, sendo assim,onde. Assim, teremos: Página 26

27 EXEMPLO 01: Qual é o volume de um cone de raio 5cm e altura 12cm? Resolução: l O volume desse cone é de 314 ml. EXEMPLO 02: Qual é o volume de um cone de diâmetro 6cm e altura 8cm? Resolução: l O volume desse cone é de aproximadamente 75 ml. Página 27

28 Exercícios Questão 22: Qual é a capacidade de uma casquinha de sorvete de forma cônica cujo raio é 3cm e cuja altura é 10cm? Questão 23: Um tanque cônico tem 4m de profundidade e seu topo circular tem 6m de diâmetro. Qual é o volume máximo, em litros, que esse tanque pode conter de líquido? Questão 24: Uma taça de champanhe, no formato de um cone, tem 8cm de diâmetro e 12cm de altura. Qual a capacidade dessa taça? Questão 25: Há um pirulito em forma de guarda-chuvinha sabor chocolate, com 6cm de altura e 2cm de diâmetro. a) Qual é o volume desse pirulito? b) Uma fábrica fez uma encomenda de 1000 desses pirulitos, quantos litros de chocolate serão necessários para fazê-los? Página 28

29 A Esfera Sem dúvida alguma, a esfera é considerada um dos sólidos mais curiosos que existem, e sua forma tem sido extremamente útil ao homem. É possível que os homens tenham criado a forma esférica a partir da observação e do estudo dos corpos celestes, como o Sol e a Lua. Ou da verificação de fenômenos como a sombra da Terra projetada sobre a Lua. O formato de nosso planeta foi reproduzido em diversos objetos até chegar às bolas de futebol, vôlei e outros. Matematicamente, a esfera pode ser definida como "um sólido geométrico formado por uma superfície curva contínua cujos pontos estão eqüidistantes de um outro fixo e interior chamado centro"; ou seja, é uma superfície fechada de tal forma que todos os pontos dela estão à mesma distância de seu centro, ou ainda, de qualquer ponto de vista de sua superfície, a distância ao centro é a mesma. O Volume da Esfera A fórmula que dá o volume da esfera foi demonstrada pelo matemático grego Arquimedes, no século III a.c., em seu livro sobre a esfera e o cilindro. Usando o método de exaustão, inventado por outro matemático grego chamado Eudoxo, Arquimedes provou que o volume de uma esfera é igual a quatro vezes o volume do cone, cujo raio é o raio da esfera e cuja altura é também o raio da esfera. Assim, o volume da esfera é: Página 29

30 EXEMPLO 01: Qual é o volume de uma esfera cujo raio mede 5 cm? Resolução: l O volume dessa esfera é de aproximadamente 523 ml. EXEMPLO 02: Qual é o volume de uma esfera cujo diâmetro mede 6 cm? Resolução: l O volume dessa esfera é de aproximadamente 113 ml. Página 30

31 Exercícios Questão 26: O raio de uma esfera de ferro fundido é 4 cm. Qual é o volume aproximado dessa esfera? Questão 27: Qual é o volume de uma bola de basquete cujo diâmetro mede 26 cm? Questão 28: Uma fábrica de suco de laranja confeccionou suas embalagens em dois formatos: uma esférica de 8 cm de diâmetro e outra cilíndrica. Sabendo que as duas embalagens têm a mesma altura e a mesma largura, calcule seus volumes. Lembre-se: Página 31

32 Gabarito Questão 01: a) ml b) ml c) l d) ml Questão 02: a) 1000cm 3 b) 1cm 3 c) 1000l d) 2l e) 5000l Questão 03: 750ml Questão 04: 50 latas Questão 05: 480 garrafas Questão 06: resposta pessoal Questão 07: V 1 = 1cm 3 ; V 2 = 8cm 3 ; V 3 = 27cm 3 Questão 08: l Questão 09: a) V= cm 3 = 125l b) V= 250 garrafas Questão 10: l = 1m; c = 5m; a = 1m Questão 11: 1096 caixas Questão 12: O segundo pedaço Questão 13: R$0,03 Questão 14: 6 m 3 Questão 15: 32 ml Questão 16: Recipiente 1 Questão 17: Sim, V=1008,09cm 3 Questão 18: 3,9 ml Questão 19: a) V= 4,0192cm 3 b) V= 48,23 cm 3 Página 32

33 Questão 20: 471 cubos Questão 21: Garrafa Questão 22: V= 94,20cm 3 Questão 23: V= 37,68m 3 Questão 24: V= 200,96cm 3 Questão 25: a) V= 6,28cm 3 b) 6,28 litros Questão 26: V= 267,94 cm 3 Questão 27: V= 9198,10 cm 3 Questão 28: V cilindro = 401,92cm 3 ; V esfera = 267,94cm 3 Página 33

34 Bibliografia Os textos e os exercícios foram retirados e/ou pesquisados nos seguintes livros: Telecurso 2000 Matemática: Volumes 1,2 e 3 Ensino Médio. - São Paulo: Editora Globo, Matemática: Aula por Aula: Volume Único: Ensino Médio / Benigno Barreto Filho, Cláudio Xavier Barreto. - São Paulo: FTD, Matemática: Contexto & Aplicações: Volumes 1, 2 e 3: Ensino Médio. - São Paulo: Ática,1999. Matemática Fundamental, 2º grau: Volume Único / José Ruy Giovanni, José Roberto Bonjorno, José Ruy Giovanni Jr. São Paulo: FTD, Coleção Base: Matemática: Volume Único / Manoel Paiva. São Paulo: Moderna, Curso Prático de Matemática: Volumes 1, 2 e 3 Ensino Médio / Paulo Bucchi. São Paulo: Moderna, Matemática: Temas e Metas: Volumes 1,2 e 3 / Antônio dos Santos Machado. São Paulo: Atual, Praticando Matemática: 6º ao 9º ano /Álvaro Andrini, Maria José Vasconcellos. São Paulo: Editora do Brasil, A Conquista da Matemática Nova: 6º ao 9º ano / José Ruy Giovanni, Benedito Castrucci, José Ruy Giovanni Jr. São Paulo: FTD, Página 34

35 Este conjunto de apostilas foi elaborado pelos professores da Área de Matemática do CEEJA Max Dadá Gallizzi, com base nos livros didáticos descritos na Bibliografia, ora transcrevendo exercícios e teorias, ora criando com base nos conteúdos observados. Professores Ednilton Feliciano Francis Mara C. Sirolli Paulo Teles de Araújo Jr Satie Sandra Soares Taira 2010 Página 35