= {números irracionais} = {números reais positivos} = {números reais negativos} = {números reais não positivos} = {números reais não negativos}

MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução

MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como 2 1, 1414 e 3 1, 7321, representando na reta real o intervalo

Escola Secundária de Lousada

Escola Secundária de Lousada Ficha de Trabalho de Matemática do 9º ano N.º Assunto: Números reais e inequações-exercícios de exames nacionais e testes intermédios Lições nº e Data: /02 /2012 1 Qual das

MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução

MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o conjunto A Z tem sete elementos, os sete elemento são três

Escola EB 2,3 de Ribeirão (Sede) ANO LECTIVO 2010/2011 Números Reais + Inequações Outubro 2010

Escola EB, de Ribeirão (Sede) ANO LECTIVO 00/0 Números Reais + Inequações Outubro 00 Nome: N.º: Turma: 9.º Ano Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios(TI) Tema: Números

Conjuntos Numéricos Conjunto dos números naturais

Conjuntos Numéricos Conjunto dos números naturais É indicado por Subconjuntos de : N N e representado desta forma: N N 0,1,2,3,4,5,6,... - conjunto dos números naturais não nulos. P 0,2,4,6,8,... - conjunto

Exercícios de provas nacionais e testes intermédios

Exercícios de provas nacionais e testes intermédios 1. Considera o conjunto A = [ π[ Qual é o menor número inteiro que pertence ao conjunto A (A) 3 (B) 4 (C) π (D) π 1 2. Qual dos conjuntos seguintes é

Escola Básica de Ribeirão (Sede) ANO LETIVO 0/0 Ficha de Trabalho outubro 0 Nome: N.º: Turma: 9.º Ano Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Números Reais

AO VIVO MATEMÁTICA Professor Haroldo Filho 3 de maio, 2016 EQUAÇÕES IRRACIONAIS

MATEMÁTICA Professor Haroldo Filho de maio, 016 EQUAÇÕES IRRACIONAIS Na resolução das equações irracionais, onde a incógnita se encontra sob um radical de índice dois, seremos obrigados a elevar ao quadrado

MATEMÁTICA - 3o ciclo

MATEMÁTICA - o ciclo Números Reais - Dízimas Propostas de resolução. Como o ponto O é a origem da reta e a abcissa do ponto A é 5, então OA = 5, e o diâmetro da circunferência é: d = 2 OA = 2 5 2. Recorrendo

Matemática. Resolução das atividades complementares. M3 Conjuntos

Resolução das atividades complementares 1 Matemática M3 Conjuntos p. 52 1 Considere os conjuntos A 5 {x M* x é par e x. 6}, 5 {x M* x é ímpar e x, 21} e C 5 {x M* x é par}. Então: a) A tem 2 elementos

Definição: Um ou mais elementos que tenham características iguais ou atendam a uma regra que lhes permitam fazer parte de um mesmo meio.

CONJUNTOS Definição: Um ou mais elementos que tenham características iguais ou atendam a uma regra que lhes permitam fazer parte de um mesmo meio. Exemplos: A = {a, e, i, o, u} (conjunto das vogais do

Números Reais e Inequações. Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI)

A G R U P A M E N T O D E E S C O L A S 172 303 MÃES D ÁGUA SEDE - Escola Básica e Secundária Mães d Água Números Reais e Inequações Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios

Função exponencial e logarítmica

Função exponencial e logarítmica Laura Goulart UESB 17 de Fevereiro de 2019 Laura Goulart (UESB) Função exponencial e logarítmica 17 de Fevereiro de 2019 1 / 1 "É melhor um bocado seco, e com ele a tranquilidade,

Quinta-feira, 04.02.16

7º Ano - C 7º Ano - B 7º Ano - A Português Xadrez Quinta-feira, 04.02.16 7º ano A - Antes de executar suas tarefas, revise a parte teórica Atividade complementar no caderno Adição dos números inteiros

Ficha de trabalho n.º 1 (com resolução) Assunto: Lógica

Ficha de trabalho n.º 1 (com resolução) Assunto: Lógica 10.º ano Parte I - Escolha múltipla (Selecione a opção correta) 1. Considere a proposição: O quadrado de qualquer número real é um número real positivo.

Este material é apenas um resumo de parte do conteúdo da disciplina.

Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 1 - Seção 1.3 do livro texto da disciplina: Números e Funções Reais,

ATIVIDADE. b) A diferença de dois números inteiros é sempre um número inteiro. c) Existe número natural que não é número inteiro.

ATIVIDADE 1. Considere os números a seguir e responda: 5; -8; 0; 14; -100; 57; -18; 2/3; -0,4; -1 a) Quais deles são números naturais? b) Quais deles são números inteiros? c) Todo número natural é um número

Universidade Federal Fluminense Escola de Engenharia de Volta Redona. Alunos: Darlei e Maria Carolina. Possíveis formatos de hipociclóides.

Universidade Federal Fluminense Escola de Engenharia de Volta Redona Alunos: Darlei e Maria Carolina Possíveis formatos de hipociclóides. > xt:=t->(a-b)*cos(theta)+b*cos((a-b)/b*theta); xt := t ( A B )

Pré-Cálculo. Humberto José Bortolossi. Aula de junho de Departamento de Matemática Aplicada Universidade Federal Fluminense

Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Aula 14 17 de junho de 2011 Aula 14 Pré-Cálculo 1 Funções da forma x elevado a menos n Aula 14 Pré-Cálculo

PROCESSAMENTO DE DADOS / SISTEMAS DE INFORMAÇÃO TRABALHO SEMESTRAL DE MATEMÁTICA:LÓGICA MATEMÁTICA

PROCESSAMENTO DE DADOS / SISTEMAS DE INFORMAÇÃO TRABALHO SEMESTRAL DE MATEMÁTICA:LÓGICA MATEMÁTICA EQUIPE DE MATEMÁTICA 1) Sejam as proposições: p : Marcos é alto. q : Marcos é elegante. r : Marcos é inteligente.

Existem conjuntos em todas as coisas e todas as coisas são conjuntos de outras coisas.

MÓDULO 3 CONJUNTOS Saber identificar os conjuntos numéricos em diferentes situações é uma habilidade essencial na vida de qualquer pessoa, seja ela um matemático ou não! Podemos dizer que qualquer coisa

Lista das Principais Funções

Lista das Principais Funções Laura Goulart UESB 24 de Maio de 2016 Laura Goulart (UESB) Lista das Principais Funções 24 de Maio de 2016 1 / 21 1)Função constante f (x) = c(c : cte ) Laura Goulart (UESB)

2 - Conjunto: conceito primitivo; não necessita, portanto, de definição. Exemplo: conjunto dos números pares positivos: P = {2,4,6,8,10,12,... }.

ASSUNTO DE MATEMATICA=CONJUNTOS REAIS E ETC. 2 - Conjunto: conceito primitivo; não necessita, portanto, de definição. Exemplo: conjunto dos números pares positivos: P = {2,4,6,8,10,12,... }. Esta forma

AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO. Matemática

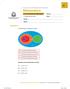GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 9 o ano do Ensino Fundamental Turma o Bimestre de 206 Data / / Escola Aluno EF Questão Considerando

MATEMÁTICA - 3o ciclo Números Reais - Dízimas (8 o ano) Propostas de resolução

MATEMÁTICA - 3o ciclo Números Reais - Dízimas (8 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios. Como o ponto O é a origem da reta e a abcissa do ponto A é 5, então OA

Polinômios (B) 4 (C) 2 (D) 1 3 (E). 2

Polinômios. (ITA 2005) No desenvolvimento de (ax 2 2bx + c + ) 5 obtém-se um polinômio p(x) cujos coeficientes somam 32. Se 0 e são raízes de p(x), então a soma a + b + c é igual a (A) 2 (B) 4 (C) 2 (D)

6º ANO ARGENTINA 6º ANO CANADÁ

6º ANO ARGENTINA 1º Horário: História Análise do capítulo 16: O Império Macedônico, Filipe II e Alexandre o grande. e dialogada. 2º Horário: Geografia Os tipos de chuvas, frontal, Folha xerocada com questões

SE18 - Matemática. LMAT 6B2-1- Polinômios (Operações com polinômios) Questão 1

SE18 - Matemática LMAT 6B2-1- Polinômios (Operações com polinômios) Questão 1 (Eear 2017) Considere P(x) = 2x 3 + bx 2 + cx, tal que P(1) = -2 e P(2) = 6. Assim, os valores de b e c são, respectivamente,

1) (UFV) Seja A uma matriz invertível de ordem 2. Se det (2A) det (A ), então o valor de det A é: a) 2 b) 1 c) 3. e) 4

) (UFV) Seja uma matriz invertível de ordem. Se det () det ( ), então o valor de det é: e) 4 ) (UFV) Na matriz quadrada ( a ij ) de ordem, os elementos a, a, a e a, nesta ordem, apresentam a seguinte propriedade:

E.E SENADOR LUIZ NOGUEIRA MARTINS

6º A/B Decompor um número natural nas unidades das diversas ordens, de acordo com seu valor posicional. 79,31% FÁCIL Decompor um número natural nas unidades das diversas ordens, de acordo com seu valor

Mat 9 Números Reais. . π Cláudia Maria Diegues Araújo 1/23

.. 1 2... 2, 05050505050505....-3-2-10123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100....

MATRIZ DE REFERÊNCIA PARA AVALIAÇÃO EM MATEMÁTICA 9º ANO DO ENSINO FUNDAMENTAL SISTEMA PERMANENTE DE AVALIAÇÃO DA EDUCAÇÃO BÁSICA DO CEARÁ SPAECE

MATRIZ DE REFERÊNCIA PARA AVALIAÇÃO EM MATEMÁTICA 9º ANO DO ENSINO FUNDAMENTAL SISTEMA PERMANENTE DE AVALIAÇÃO DA EDUCAÇÃO BÁSICA DO CEARÁ SPAECE TEMA I: INTERAGINDO COM OS NÚMEROS E FUNÇÕES N DESCRITOR

2ª série do Ensino Médio

2ª série do Ensino Médio Geometria Plana Cálculo de Áreas e Relações na Circunferência. Polígonos Regulares, Polígonos Inscritos na Circunferência e Trigonometria. Relações Métricas no Triângulo Retângulo

Funções Racionais, Exponenciais e Logarítmicas

Funções Racionais, Exponenciais e Logarítmicas Aula 3 590253 Plano da Aula Definição de Função Racional Função Exponencial e Logarítmica Função Inversa Exercícios Referências James Stewart Cálculo Volume

1.2 Axioma do Supremo

1.2 Axioma do Supremo EXERCÍCIOS RESOLVIDOS 1. Verifique que se n N é ímpar, então n 2 é também ímpar. O que pode concluir de n N sabendo que n 2 é par? RESOLUÇÃO Seja n N ímpar, com n = 2k+1, para algum

UFJF ICE Departamento de Matemática Cálculo I Primeira Avaliação 12/01/2013 FILA A Aluno (a): Matrícula: Turma:

UFJF ICE Departamento de Matemática Cálculo I Primeira Avaliação /0/03 FILA A Aluno (a): Matrícula: Turma: Instruções Gerais: - A prova pode ser feita a lápis, exceto o quadro de respostas das questões

O valor de que torna a expressão verdadeira é:

Exercício 1. (FUVEST SP/1994) O número real x que satisfaz a equação é: a) b) c) 2 e) Resposta: e Tags: Logaritmos, Funções, Ensino Médio, Álgebra, Matemática, FUVEST SP, 1994, Logarítmos Exercício 2.

Lógica Proposicional Fórmulas e Precedência de Operadores

Lógica Proposicional Fórmulas e Precedência de Operadores Prof. Marcos A. Schreiner Disciplina de Introdução à Lógica 23 de março de 2015 Prof. Marcos A. Schreiner (UFPR) 23 de março de 2015 1 / 18 1 Introdução

exemplos O conjunto das letras do nosso alfabeto; L= {a, b, c, d,..., z}. O conjunto dos dias da semana: S= {segunda, terça,... domingo}.

CONJUNTOS Conjunto: Representa uma coleção de objetos, geralmente representado por letras MAIÚSCULAS; não interessando a ordem e quantas vezes os elementos estão listados na coleção, e sempre são representados

Função Exponencial. 1.Definição 2.Propriedades 3.Imagem 4.Gráfico 5.Equações exponenciais 6.Inequações exponenciais

UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função Eponencial Prof.:

( ) Função Exponencial. Função Exponencial. x = 0 f(0) = a 0 = 1. x 1 < x 2 f(x 1 ) > f(x 2 ) x a. 1 a ) Na função exponencial f(x) = a x, temos:

UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função Eponencial. Propriedades

Resoluções das atividades de Matemática

Resoluções das atividades de Matemática Sumário Capítulo Equação do o grau I... Capítulo Equação do o grau II... Capítulo Equação do o grau III... Capítulo 9 Sistemas de equações...9 Capítulo Relação inária...

PROFESSOR: ALEXSANDRO DE SOUSA

E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO Conjuntos Numéricos PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net MATEMÁTICA, 9º Ano Pontos no plano cartesiano/pares ordenados

MATEMÁTICA BÁSICA SUMÁRIO

MATEMÁTICA BÁSICA SUMÁRIO 1 Operações com frações 2 Divisão de frações 3 Operações com números relativos 4 Resolução de equações do 1º grau (1º tipo) 5 Resolução de equações do 1º grau (2º tipo) 6 Resolução

Humberto José Bortolossi [01] (a) (1.0) Escreva infinitos números racionais que pertençam ao intervalo

PRIMEIRA VERIFICAÇÃO DE APRENDIZAGEM Pré-Cálculo Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Nome legível: Assinatura: [0] (a) (.0) Escreva infinitos números racionais que pertençam

Funções Exponenciais

UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Funções Exponenciais

9,43 9,40 7,77 9,28 5,20 3,63 6,08 3,02 2,05 4,59 2,45 5,83 9,42 8,52 4,41 3,30 3,52

RELATORIO MA11 Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 1,0 1,0 1,0 1,0 1,0 1,0 0,5 0,5 1,0 1,0 1,0 NOTA 9,43 9,40 7,77 9,28 5,20 3,63 6,08 3,02 2,05 4,59 2,45 5,83 9,42 8,52 4,41 3,30 3,52 %

RADICIAÇÃO, POTENCIAÇÃO, LOGARITMAÇÃO. Potência POTENCIAÇÃO, RADICIAÇÃO E LOGARITMAÇÂO NOS NÚMEROS REAIS. Potenciação 1

RADICIAÇÃO, POTENCIAÇÃO, LOGARITMAÇÃO Potência POTENCIAÇÃO, RADICIAÇÃO E LOGARITMAÇÂO NOS NÚMEROS REAIS Potenciação 1 Neste texto, ao classificarmos diferentes casos de potenciação, vamos sempre supor

FICHA DE TRABALHO N.º 2 MATEMÁTICA A - 10.º ANO CONJUNTOS E CONDIÇÕES

FICHA DE TRABALHO N.º MATEMÁTICA A - 10.º ANO CONJUNTOS E CONDIÇÕES Conhece a Matemática e dominarás o Mundo. Galileu Galilei GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Considere a condição px : x é um número

Acadêmico(a) Turma: Capítulo 7: Limites

Acadêmico(a) Turma: Capítulo 7: Limites 7.1. Noção Intuitiva de ite Considere a função f(), em que f() = 2 + 1. Para valores de que se aproima de 1, por valores maiores que 1 (Direita) e por valores menores

1 Números Reais (Soluções)

Números Reais (Soluções). a) x2 4 b) x c) x d) x e) x f) 2 x+2 g) 2 x(x+2) h) x i) x 2 4 j) x(x + ) + x k) log(x) l) 2 log ( x 2 + x 2). 2. a) x = x 2 b) 2 x c) x d) x 0 x = e) x = 4 x = 2 f) x = x = 2

Curso de Administração Centro de Ciências Sociais Aplicadas Universidade Católica de Petrópolis. Matemática 1. Revisão - Conjuntos e Relações v. 0.

Curso de Administração Centro de Ciências Sociais Aplicadas Universidade Católica de Petrópolis Matemática 1 Revisão - Conjuntos e Relações v. 0.1 Baseado nas notas de aula de Matemática I da prof. Eliane

Razões Trigonométricas

Curso Preparatório - PROFMAT 2014 Germán Ignacio Gomero Ferrer gigferrer@uesc.br 13 de Agosto de 2013 Problema 13 (The New York City Contest - Outono 1983) No triângulo ABC, sin 2 A + sin 2 B = 1. Encontre

1 Números Reais. 1. Simplifique as seguintes expressões (definidas nos respectivos domínios): b) x+1. d) x 2, f) 4 x 4 2 x, g) 2 x2 (2 x ) 2, h)

Números Reais. Simplifique as seguintes expressões (definidas nos respectivos domínios): x a), x b) x+ +, x c) +x + x +x, d) x, e) ( x ), f) 4 x 4 x, g) x ( x ), h) 3 x 6 x, i) x x +, j) x x+ x, k) log

Números e Operações. Nome: N.ª: Ano: Turma:

MATEMÁTICA 3º CICLO FICHA 3 Números e Operações Números Reais Dízimas Finitas e Infinitas Nome: N.ª: Ano: Turma: Data: / / 20 Um número diz-se racional quando pode ser representado por uma fração entre

CANDIDATO: DATA: 20 / 01 / 2010

UNIVERSIDADE ESTADUAL DO CEARÁ - UECE SECRETARIA DE EDUCAÇÃO A DISTÂNCIA - SEaD Universidade Aberta do Brasil UAB LICENCIATURA PLENA EM MATEMÁTICA SELEÇÃO DE TUTORES PRESENCIAIS CANDIDATO: DATA: 0 / 0

Números - Aula 03. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil

Números - Aula 03 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 28 de Fevereiro de 2014 Primeiro Semestre de 2014 Turma 2013106 - Engenharia Mecânica Corpos Vimos que o

CONJUNTOS EXERCÍCIOS DE CONCURSOS

CONJUNTOS EXERCÍCIOS DE CONCURSOS E0626 (IBEG Merendeira Prefeitura de Uruaçu GO). Sendo os conjuntos A = {2, 4, 6, 8, 10, 12}; B = {1, 3, 5, 7, 9, 11}; C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. I A

Exercícios de Revisão de Conceitos Fundamentais

Eercícios de Revisão de Conceitos Fundamentais. Números.. Números inteiros e números raccionários. Operações com números raccionários. Percentagens. ) Escreva as seguintes racções impróprias na orma de

Números e Funções Reais, E. L. Lima, Coleção PROFMAT.

1/12 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 4 - Seções 4.1 e 4.2 do livro texto da disciplina: Números e Funções

Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos

Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não

Números Reais. Jairo Menezes e Souza 19/09/2013 UFG/CAC

UFG/CAC 19/09/2013 Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Chamamos de Z o conjunto dos números

CONTROLE DIÁRIO DE CONTEÚDOS E ATIVIDADES TURNO MATUTINO

G.01 CAP.02 INTRODUÇÃO AOS ESTUDOS HISTORICOS ATIVIDADE COMPLEMENTAR NO CADERNO ESTUDAR CONTEUDO PARA A P3 G.01 CAP.01 RENASCIMENTO PAG.219 Nº 04 ESTUDAR PAG. 219 GLADSON G.01 CAP.01 GLOBALIZAÇÃO E MEIO

CURSO DE MATEMÁTICA. Conjuntos dos números naturais, inteiros, racionais e irracionais. (propriedades e operações) Josimar Padilha

CURSO DE MATEMÁTICA Conjuntos dos números naturais, inteiros, racionais e irracionais. (propriedades e operações) Josimar Padilha Qual a importância de conhecer os CONJUNTOS NUMÉRICOS? Meu querido aluno,

5. (UFJF-MG) Os pontos A(2, 6) e B(3, 7) são

p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br ( ) 4t 1. Para que valores 5 + 1, 2t 4 pertence ao eixo das ordenadas? A linguagem das funções Sistema de coordenadas Conceito de função

Professor: Fábio Soares - Disciplina: Métodos Quantitativos ADMINISTRAÇÃO

Unidade 1 - Números Reais: representações O principal motivo para que a maioria dos cursos comecem por um breve estudo dos números reais é o fato de no Cálculo e na Análise, estuda-se o comportamento de

PROF. LUIZ CARLOS MOREIRA SANTOS. Questão 01)

Questão 0) Um recipiente com capacidade para 5 litros está completamente cheio de leite puro. Uma pessoa retira 3 litros desse leite e completa o recipiente com 3 litros de água. Em seguida, retira 3 litros

6º ANO CANADÁ 6º ANO ARGENTINA. 1º Horário: Matemática Conteúdo: Correção de tarefa, revisão das atividades Atividade: Atividade 16 Tarefa: ***

6º ANO ARGENTINA 1º Horário: Geografia Conteúdo: Correção da tarefa 2º Horário: Artes * 3º Horário: Geografia Conteúdo: Aula expositiva sobre a lua e suas importâncias para terra 4º Horário: Português

Divisibilidade e Números primos. George Darmiton da Cunha Cavalcanti CIn - UFPE

Divisibilidade e Números primos George Darmiton da Cunha Cavalcanti CIn - UFPE Divisibilidade de inteiros Sejam a e b dois inteiros. Dizemos que a divide b, a é um divisor de b ou b é um múltiplo de a

Cálculo I - Lista 1: Números reais. Desigualdades. Funções.

Faculdade de Zootecnia e Engenharia de Alimentos Universidade de São Paulo Cálculo I - Lista : Números reais Desigualdades Funções Prof Responsável: Andrés Vercik Um inteiro positivo n é par se n k para

Introdução à Teoria dos Números - Notas 1 Os Princípios da Boa Ordem e de Indução Finita

Introdução à Teoria dos Números - Notas 1 Os Princípios da Boa Ordem e de Indução Finita 1 Preliminares Neste curso, prioritariamente, estaremos trabalhando com números inteiros mas, quando necessário,

Conjunto dos números irracionais (I)

MATEMÁTICA Revisão Geral Aula - Parte 1 Professor Me. Álvaro Emílio Leite Conjunto dos números irracionais (I) {... π; ; ; ; 7; π + } I =... Q Z N I Número pi ( π) Diâmetro Perímetro π =,14196897984664...

LISTA DE EXERCÍCIOS. Demonstrações diretas e por absurdo

LISTA DE EXERCÍCIOS Matemática Básica Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ 02 Demonstrações diretas e por absurdo Diga se cada uma das sentenças abaixo é verdadeira ou falsa.

AV1 - MA UMA SOLUÇÃO. d b =. 3q 2 = 2p 2,

AV1 - MA 11-01 Questão 1. Prove que se a, b, c e d são números racionais tais que a + b 3 = c + d 3 então a = c e b = d. A igualdade a + b 3 = c + d 3 implica que (a c) = (d b) 3. Suponha que tenhamos

Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão Lista 2. Sequências de Números Reais

Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 0 Lista Sequências de Números Reais. Dê o termo geral de cada uma das seguintes sequências: a,, 3, 4,... b, 4, 9, 6,... c,,

Sexta Feira. Cálculo Diferencial

Sexta Feira Cálculo Diferencial 15/0/013 Funções Reais Domínio, imagem e gráficos Código: EXA37 A Turmas: ELE1AN, MEC1AN Prof. HANS-ULRICH PILCHOWSKI Prof. Hans-Ulrich Pilchowski Notas de aula Cálculo

DOS REAIS AOS DECIMAIS

DOS REAIS AOS DECIMAIS Número é a sua representação Na sua origem, número é resultado dos processos de contagem ou de medida. Tais números precisam ter algum tipo de representação, para possibilitar as

Matemática Instrumental Prof.: Luiz Gonzaga Damasceno

1 Matemática Instrumental 2008.1 Aula 1 Introdução Hoje em dia temos a educação presencial, semi-presencial e educação a distância. A presencial é a dos cursos regulares, onde professores e alunos se encontram

Conteúdo Ensino Fund. II

Conteúdo Ensino Fund. II Data: 07/03/19 Turma: 6º ano I Ens. Fund. II Matutino Tempo Disc./Professor Conteúdo(s) do dia Dever (es) de- casa Correção, pág.38. Págs.39, 40 e 41 - Conto maravilhoso - Leitura

Gabarito da lista de Exercícios sobre Técnicas de Demonstração

Universidade Federal Fluminense Curso: Sistemas de Informação Disciplina: Fundamentos Matemáticos para Computação Professora: Raquel Bravo Gabarito da lista de Exercícios sobre Técnicas de Demonstração

Capítulo 1 Números Reais

Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 1 Números Reais Conjuntos Numéricos Conjunto dos naturais: N = {1,, 3, 4,... } Conjunto dos inteiros: Z = {..., 3,, 1, 0, 1,, 3,... } {

ATIVIDADE DE AVALIAÇÃO FINAL - Valor : 2,0

Matemática I Márcia 8º 19/12/2018 ATIVIDADE DE AVALIAÇÃO FINAL - Valor : 2,0 1.Em relação aos principais conjuntos numéricos é correto afirmar: a) Todo número inteiro é natural, mas nem todo número natural

Nome do aluno: N.º: Turma:

Teste de Matemática A 2017 / 2018 Teste N.º 1 Matemática A Duração do Teste: 90 minutos NÃO É PERMITIDO O USO DE CALCULADORA 10.º Ano de Escolaridade Nome do aluno: N.º: Turma: Na resposta aos itens de

Funções Polinomiais com Coeficientes Complexos. Teorema do Resto. 3 ano E.M. Professores Cleber Assis e Tiago Miranda

Funções Polinomiais com Coeficientes Complexos Teorema do Resto 3 ano E.M. Professores Cleber Assis e Tiago Miranda Funções Polinomiais com Coeficientes Complexos Teorema do Resto 1 Exercícios Introdutórios

QUESTÕES OBJETIVAS. ) é uma Progressão Aritmética (P.A.) de razão 2 e com a 1 Considere uma função f : dada por f ( x) = ax+ b.

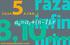QUESTÕES OBJETIVAS Questão 9: Se y x= π, pode-se afirmar que: a) sen y sen x= 0 b) sen ( y π ) = 2.sen x c) cos y = cos x d) cos cos sen 2 2 y = x x e) cos 2x = cos y Questão : A seqüência ( a1, a2,...,

» Potenciação e Radiciação

-* Nome: nº Ano: 9º Ano/EF Data: 30/06/2013 Exercícios de Matemática Professor: Hélio N. Informações Importantes: Não é permitido o uso de calculadora ou qualquer material eletrônico; Esta lista não tem

6º ANO ARGENTINA 6º ANO CANADÁ

6º ANO ARGENTINA 6º ANO CANADÁ 1º Horário: História 2º Horário: Português Conteúdo: Apresentação de trabalho 3º Horário: Português Conteúdo: Apresentação de trabalho 4º Horário: Matemática Atividade: Correção

Segmento: Pré-vestibular. Coleção: Alfa, Beta e Gama. Disciplina: Matemática. Unidade 1: Série 17. Conjuntos

Segmento: Pré-vestibular Coleção: Alfa, Beta e Gama Disciplina: Matemática Volume: 1 Unidade 1: Série 17 Resoluções Conjuntos 1. A = {1, } O Conjunto A possui dois elementos: 1 e. O total de subconjuntos

Roteiro de Estudo para a Recuperação Semestral MATEMÁTICA 1ºEM

Roteiro de Estudo para a Recuperação Semestral MATEMÁTICA 1ºEM NOME: IMPRIMA AS FOLHAS. RESOLVA AS QUESTÕES DISSERTATIVAS EM FOLHA DE PAPEL ALMAÇO OU FOLHA DE FICHÁRIO; OS TESTES PODERÃO SER RESPONDIDOS

MATEMÁTICA Conjuntos. Professor Marcelo Gonzalez Badin

MATEMÁTICA Conjuntos Professor Marcelo Gonzalez Badin Alguns símbolos importantes Œ Pertence / Tal que œ Não Pertence : Tal que $ " fi Existe Não existe Qualquer (para todo) Portanto Se, e somente se,...(equivalência)

Plano de Trabalho. Conjuntos

Matemática 1º Ano 1º Bimestre/2013 Plano de Trabalho Conjuntos Tarefa 1 Cursista: Emanuel Angelo Alves Série: 1ª série do Ensino Médio Grupo: 7 Tutor: Ligia Vitória de Azevedo Telles Introdução O presente

Prova Escrita de Matemática 3.º Ciclo do ensino Básico ; 9ºAno de escolaridade

ESCOLA SECUNDÁRIA C/3º CICLO DO ENSINO BÁSICO DE LOUSADA Prova Escrita de Matemática 3.º Ciclo do ensino Básico ; 9ºAno de escolaridade Duração da Prova: 90 minutos A PREENCHER PELO ALUNO Nome completo

CONJUNTOS NUMÉRICOS. O que são?

CONJUNTOS NUMÉRICOS O que são? Os Naturais Os números Naturais surgiram da necessidade de contar as coisas. Eles são todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula

PROVA DE MATEMÁTICA MÓDULO III DO PISM (triênio )

QUESTÕES OBJETIVAS PROVA DE MATEMÁTICA MÓDULO III DO PISM (triênio 004-006) 09. Num determinado jogo, cada participante recebe uma ficha circular (tipo uma moeda) com um número impresso em cada uma das

Medidas em geometria. Pontos em discussão na preparação de um eventual documento

Medidas em geometria Pontos em discussão na preparação de um eventual documento Estes pontos em discussão surgiram a partir das ideias para um texto que alguns já comentaram; são apresentados em sequência

Funções potência da forma f (x) =x n, com n N

Folha 1 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções potência da forma f (x) =x n, com n N Parte 08 Parte 8 Matemática Básica 1

3 pode ser associado a letra C.

PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - ÁLGEBRA - 8º ANO - ENSINO FUNDAMENTAL ============================================================================ 01- Na figura a seguir foram representados

Matemática 1 INTRODUÇÃO 1 TEOREMA DAS RAÍZES COMPLEXAS 3 TEOREMA DAS RAÍZES RACIONAIS 2 TEOREMA DAS RAÍZES IRRACIONAIS. Exercício Resolvido 2

Matemática Frente II CAPÍTULO 22 EQUAÇÕES POLINOMIAIS 1 INTRODUÇÃO Nos capítulos anteriores, durante o estudo de polinômios, já estudamos alguns teoremas que nos ajudam a encontrar as raízes de polinômios.

Conjuntos Numéricos { } { } { } Conjunto dos Números Naturais

0/0/0 Conjuntos uméricos Conjunto dos úmeros aturais Chama-se conjunto dos números naturais,,o conjunto formado pelos números 0,,,,... {,,,,...} = 0 As duas operações fundamentais, a adição e a multiplicação,

LISTA ZERO - Potenciação em Reais

LISTA ZERO - Potenciação em Reais 1. (FGV 003) Se x = 300000 e y = 0,0000, então x.y vale: a) 0,64 b) 6,4 c) 64 d) 640 e) 6400. (UNESP 199) O valor da expressão a) 0,3 b ) -0,1 c ) -0, d) 0, e) 0 3. (FUVEST