Capitulo 7 Ótica de partículas carregadas
|
|
|
- Sílvia Mirandela Garrau
- 6 Há anos
- Visualizações:
Transcrição
1 Capitulo 7 Ótica de partículas carregadas versão 008. O que há em comum etre um cahão de elétros de um osciloscópio ou de um tubo de TV com sistemas óticos como maquia fotográfica, microscópios, etc...? Todos os sistemas citados acima fucioam seguido os mesmos pricípios de um sistema ótico, que o desig dos aceleradores de partículas carregadas também se baseia os mesmos fudametos, além dos microscópicos óticos e eletrôicos. Em várias situações práticas faz-se ecessário trasportar e cotrolar feixes de partículas carregadas, o que pode ser feito com o auxílio de letes. As letes possuem uma ação focalizadora que maximiza a eficiêcia de trasmissão do sistema de trasporte. Letes podem ser costituídas de campos elétricos e/ou magéticos. Trataremos aqui apeas de letes eletrostáticas. Elas são apropriadas para várias aplicações, são fáceis de costruir e operar. A faixa de velocidades das partículas que trataremos aqui é da ordem de algus kev, e efeitos relativísticos serão desprezados. A equação diferecial que descreve a deflexão de partículas carregadas por campos puramete eletrostáticos ão iclui em a massa em a carga da partícula. Assim, com as voltagem e polaridade apropriadas,um sistema eletrostático de letes pode igualmete ser utilizado para qualquer partícula, idepedete da sua carga e massa. Os íos são mais pesados do que elétros, etão viajarão muito mais letamete do que os elétros, mas seguirão as mesmas trajetórias. Refração de um feixe de partículas Em uma lete eletrostática, a distribuição de poteciais ão pode ser geralmete expressa em termos de uma fução exata, em é possível deduzir matematicamete a trajetória do elétro mesmo que o campo teha sido experimetalmete mapeado. Nestes casos, é útil itroduzir a idéia de refração de um feixe de elétros uma froteira de potecial. Já sabemos de cursos elemetares que o elétro tete a se mover a direção oposta ao campo elétrico. Vamos agora pesar em termos de lihas (ou superfícies) de potecial e discutir a deflexão de elétros em termos de estágios sucessivos de refração quado passado de uma região equipotecial para outra. O campo a verdade variar de forma ão abrupta, sem descotiuidades. Um meio com ídice de refração que varia cotiuamete ão é fácil de tratar, etão é mais fácil trocá-lo por uma série de camadas com uma desidade crescete, como se faz quado tratamos refração a atmosfera. Um campo elétrico exerce uma forca sobre uma partícula de carga q v r r F qe q φ que e sempre perpedicular a superfície ϕcostate. 08
2 d E 0 E 0 v y v y θ r v x θ i v y v x V V V V E (V V )/d O espaço etre qualquer eletrodo é etão represetado como preechido por uma série de superfícies equipoteciais cuja distribuição de desidades pode ser ajustada de acordo com a precisão desejada. Supoha que um elétro de velocidade v o se aproxima de uma equipotecial que divide dois meios de poteciais V e V. Os âgulos de icidêcia i e de refração são defiidos com em ótica com respeito à perpedicular o poto de icidêcia. Supodo que o elétro foi acelerado a partir do repouso q(v V o ) ½ mv Quado cruza a superfície equipotecial, a compoete tagecial de sua velocidade (v o seθ i ) ão mudará, mas a compoete ormal (v o cosθ i ) mudará para v o cos(θ r ). Etão v seθi v seθ r seθ i seθ r v v ( V ( V Vo ) V ) o ode e são defiidos como ídices de refração. Esta razão é costate para qualquer elétro e é aáloga à lei de Sell para a refração ótica. Exercício 7.. Mostre que fazedo V V V e V V Vo a razão etre os ídices de V refração e escrito por +, mostrado que / depede somete da difereça V de potecial etre os meios e e a eergia ciética iicial da partícula. 09
3 0 Revisão de ótica geométrica Vamos começar ilustrado a propriedade focalizadora de uma lete devido a curvatura de sua superfície limite. A figura abaixo mostra duas regiões, tedo ídice de refração e, separadas por um cotoro de raio R. Raios de luz icidem paralelamete ao eixo, e para pequeas distacias h e h são refratados o limite de tal modo que cruzam o eixo os potos F e F, respectivamete. Estes são o primeiro e segudo potos focais desta lete simples ode as distacias são medidas a partir do limite. Supomos h<<r de tal modo que os seos e tagetes dos âgulos podem ser aproximados pelos próprios âgulos. Etão f h f h R h R h α α α α α α α α α α elimiado os âgulos ecotramos R f R f ou aida f f O sial e uma coseqüêcia da defiição de distacia focal medida a partir do limite da superfície.
4 α h α F F R h α 4 α 3 Fig. - Refração da luz em cotoro esférico etre dois meios. O detalhe mostra a coveção de siais. Os âgulos α e α são positivos assim como os âgulos etre os raios e o eixo os potos focais. A coveção dos âgulos e que medidos a partir do eixo ao raio são positivos se a rotação e horária. Estas coveções faz com que os âgulos teham o sial de suas tagetes.
5 lete delgada p f f q + p q f Aalogia com letes óticas
6 Qualquer campo eletrostático com simetria rotacioal possui propriedades para formar images. Partículas carregadas com a mesma eergia, partido de potos em um plao objeto, são focalizadas em potos em um plao imagem, se suas trajetórias são paraxiais, ou seja, se elas são bastate próximas ao eixo e sempre possuem uma icliação pequea em relação a ele. Tais raios geram uma imagem estigmática (correta poto a poto) magificada ou dimiuída. Magificação e posição de uma imagem depedem da eergia das partículas: Há uma dispersão em eergia; a formação da imagem é perturbada por uma aberração cromática. Uma lete eletrostática cosiste de dois ou mais eletrodos matidos em poteciais diferetes. Quado plaejado sistemas de letes eletrostáticas é freqüetemete útil relembrar a aalogia que existe etre estas letes e os sistemas óticos mais familiares em ótica geométrica. No etato, o caso de letes eletrostáticas, ao cotrário da ótica geométrica, a focalização pode ser alcaçada com a mudaça da eergia ciética do feixe. Outra difereça é que letes eletrostáticas possuem muito mais aberrações do que as suas cotrapartidas óticas. Isto sigifica que a abertura, ou o úmero f ( f# ) de uma lete eletrostática é usualmete limitada de modo a mater estas aberrações um ível tolerável. Raios fora do eixo, ao cotrário do raios paraxiais, ão são focalizados em um mesmo poto. O cojuto de poto de iterseção de todos os raios adjacetes, partido do mesmo poto objeto forma uma camada cáustica: A imagem é afetada por aberrações geométricas. Para ossa sorte, este problema ão é tão fudametal a maioria dos casos, uma vez que estas letes são utilizadas para o trasporte de partículas e ão para a formação de images. Outra difereça é a repulsão coulombiaa o caso de feixes carregados, que pode limitar a correte de partículas, mas pode ser desprezado para feixes pouco itesos ( da ordem de A). Para focalizar um feixe com simetria rotacioal, a área em toro do eixo é utilizada. Com a demada crescete a qualidade da imagem (como em um microscópio eletrôico, por exemplo), requer uma abertura, tão pequea, que a difração a borda do buraco do diafragma ifluêcia a qualidade da imagem. Para aalisadores eletrostáticos (aalisadores de velocidade), o etato, há vatagem o fato de ocorrer uma aberração cromática forte. Letes eletrostáticas também podem atuar como filtros para selecioar um certo itervalo de eergias do feixe. Colimação e defiição de um feixe de partículas carregadas Em qualquer aplicação é ecessário defiir a extesão espacial e agular do feixe. Isto pode ser feito defiido duas aberturas físicas, coforme ilustrado a Fig.. A primeira abertura, A, defie o tamaho radial do feixe e é chamada de a jaela (widow) do sistema. As partículas são supostamete emitidas isotropicamete de cada poto detro da jaela. A seguda abertura, A, determia a extesão agular do feixe e é chamada de pupila. Cada poto detro da jaela dá origem a um picel ( pecil) de raios, cujo meio âgulo, θ P, é dado por θ P r p /L, ode r p é o raio da abertura da pupila e L a distâcia etre a jaela e a pupila. 3
7 A A r j θ P θ F rp jaela pupila Fig. defiição radial e agular de um feixe por uma jaela e pupila. Brilho O brilho β de um poto sobre um objeto lumioso é determiado pela correte diferecial I, que passa através de um elemeto de área A em toro de um poto, e ilumia em um âgulo sólido Ω: I β (µacm - sr - ) () A Ω A jaela é geralmete uiformemete ilumiada pelo feixe de partículas. Fica como exercício (exercício ) mostrar que o brilho do objeto descrito pela jaela A lei de Helmhotltz-Lagrage Uma lete eletrostática produz images de aberturas físicas que defiem o feixe, e o plaejameto de letes pode ser cosiderado em termos destas jaelas e pupilas. Isto é ilustrado a Fig., ode a lete produz uma imagem da jaela: tais images são chamadas de jaelas virtuais. O raio da imagem r, relacioa-se com o raio da jaela, r, por uma magificação liear da lete, M r /r. Passado através da lete, do potecial V para o potecial V, ocorre também uma mudaça a eergia da partícula e uma 4
8 mudaça o âgulo do picel (θ). A lei de Helmholtz-Lagrage relacioa estas quatidades / / rθ V rθ () V ou seja, o produto rθv / é uma gradeza coservada. É importate otar que os âgulos esta relação são os âgulos do picel e ão os âgulos do feixe. Uma vez que o âgulo do picel seja determiado em algum poto do sistema ótico pelas aberturas físicas, estará automaticamete determiado em um outro poto pela lei de Helmholtz-Lagrage. Na Fig. 3 a pupila foi posicioada o plao focal da lete. Isto faz com que a imagem da pupila vá para o ifiito e produz um âgulo de feixe ulo a imagem. A Eq. mostra que o âgulo do picel aumeta se a eergia do feixe dimiui. V V F r r L jaela pupila Imagem da jaela Fig. - Uma ilustração da lei de Helmholtz-Lagrage e o posicioameto da pupila para produzir um âgulo de feixe zero. Defiições e medidas das tesões das letes É essecial que as tesões aplicadas V, V, etc... sejam medidas com respeito à uma referêcia correta que freqüetemete ão é zero. A referecia correta é eergia 5
9 6 ciética zero da partícula, ou seja, a referecia é escolhida tal que a partícula terá eergia ciética igual à qv quado está uma região de potecial V. Ótica de partículas em campos axialmete simétricos Na ausêcia de campos magéticos, a equação do movimeto de uma partícula carregada e escrita como x q dt x d m φ x q dt x d m φ x q dt x d m φ Na ausêcia de fotes, a equação de Lapace pode ser escrita como z y x φ φ φ De modo geral, ão há solução aalítica para a maioria dos casos, mas pode-se resolver umericamete. A maioria das letes eletrostáticas, sao feitas por campos elétricos com simetria axial, obtidas por tubos ou aberturas cilídricas.
10 Fig. Lete eletrostática cosistido de dois tubos cilidricos. a) represetação esquemática, b) o potecial e sua seguda derivada, c) aalogia com a ótica geométrica. O sistema de coordeadas apropriado e o cilídrico, r, z, φ. Como o sistema e axialmete simétrico, o potecial ão depede do agulo, mas somete de r e z. Para r 0 a primeira derivada do potecial é ula, o que ão acotece para r diferete de zero. Ou seja, a força atua aquelas partículas que se movem fora do eixo de simetria da lete. Na figura acima, elétros proveietes da esquerda, são atraídos em direção ao eixo de simetria (ote que a força é sempre perpedicular a lihas equipoteciais). Para φ > φ, os elétros são acelerados quado se movem do primeiro para o segudo tubo. Sua velocidade é maior o tubo a direita do que o da esquerda. Isto sigifica que o efeito divergete da direita é meor do que o efeito focalizador da esquerda. O sistema fucioa como uma lete focalizadora. Para φ < φ o sistema fucioa como uma lete divergete. Represetação de uma lete espessa Em ótica elemetar, a refração de um raio de luz por uma lete supostamete ocorre abruptamete em um plao que situa-se o cetro da lete. No caso de uma lete eletrostática, a refração ocorre através de uma distâcia ão ula, e a lete é descrita como espessa. Esta descrição é ilustrada a Fig. 3. A lete é represetada por dois plaos pricipais, P e P, cada qual tem um comprimeto focal correspodete, f e f com potos focais F e F, respectivamete. As posições dos plaos pricipais, dos potos focais e também do objeto (P) e imagem (Q), são medidas com respeito ao plao de referêcia que é usualmete escolhido ser o plao de simetria da lete. As trajetórias assitóticas das partículas podem ser determiadas como se segue: i) A partícula etrado a lete paralela ao eixo ótico segue uma liha reta até o plao pricipal P, ode a trajetória é refratada de tal modo que passa pelo poto focal F. ii) A partícula passado pelo poto focal F segue uma liha reta até o plao pricipal P e é etão refratada de tal modo que deixa a lete paralela ao eixo ótico. iii) Trajetórias paralelas a etrada, se cruzam o poto focal F. Algumas relações úteis podem ser obtidas a partir da lete espessa: ( P F Q F f f () )( ) f ( Q F ) M (3) ( P f) f ode M é a magificação liear (r /r ). Para uma imagem real, M é egativa, mas é comum referir à magificação como se fosse positiva. 7
11 P Plao de referêcia P P objeto F imagem F f f Q F F Fig. 3 Represetação de uma lete espessa. Geometria de letes 8
12 Os dois tipos mais comus de letes eletrostática são as letes cilídricas e as letes de abertura circular, cuja simetria cilídricas são bem apropriadas para feixes cilídricos. As propriedades focais das letes depedem do úmero de eletrodos que ela cotém, além das dimesões e voltages aplicadas. Letes cilídricas tedem a ser mais fortes e a produzir meos aberrações do que as de abertura circular. De modo geral, quato mais eletrodos possuir uma lete, maior será o grau de cotrole sobre suas propriedades focais. Discutiremos aqui somete letes cilídricas, embora os mesmos pricípios s e apliquem a letes de abertura circular. V V D 0. D V V V 3 D 0. D V V V 3 V 4 D 0. D 0. D Fig.4 Letes de, 3 e 4 elemetos. Letes com dois elemetos 9
13 Fig. 5 Tais letes cosistem de dois cilidros separados por uma distâcia (gap), g, que é tipicamete 0.D (D diâmetro da lete). O comprimeto de cada cilidro deve ser com este diâmetro, de tal forma que o potecial axial possa alcaçar seu valor assitótico (sem efeitos de borda). Na prática, isto sigifica que cada comprimeto deva ser maior do que.5 D. Os parâmetros focais f, f, F e F, depedem da razão das voltages V /V, aplicadas aos eletrodos. Parâmetros para vários valores de V /V são apresetados em [3]. Estes parâmetros são apresetados freqüetemete a forma de curvas PQ. Em ótica elemetar de letes, as distâcias do objetos e imagem estão relacioadas por hipérboles, ou seja, /P + /Q /f, ode f é a distâcia focal. De forma similar, curvas PQ para letes são represetadas por hipérboles, cada correspodedo a um valor particular de V /V. Tal família de curvas PQ para uma lete de dois elemetos é mostrada a figura abaixo. Estas curvas também forecem diretamete a magificação M. A desvatagem de uma lete de dois elemetos é que, para uma posição do objeto fixa, a posição da imagem mudará se V /V mudar. Este problema é resolvido como uma lete de três elemetos. 0
14 Fig.6 Curvas PQ para uma lete de dois elemetos. Referecia [4] Letes com três elemetos Fig. 7 As letes com três elemetos são mostradas a Fig. 4. O comprimeto do elemeto cetral é tipicamete 0,5 ou,0 D, sedo que o valor maior forece uma faixa maior de razões etre as voltages. As propriedades focais deste tipo de lete depede da razão etre as voltages, ou seja, V 3 /V e V /V, o que dá a esta lete uma propriedade muito útil: a razão V 3 /V pode ser variada matedo fixas as distâcias do objeto e da
15 imagem, simplesmete mudado a voltagem de focalização V /V. Por causa desta propriedade estas letes são as vezes chamadas de letes zoom. Esta é uma propriedade muito importate porque a prática os objetos e as images, ou seja, fotes de partículas, detetores, e aalisadores de eergia, são freqüetemete fixos. O valor V 3 /V pode ser maior, meor ou igual a uidade, quado esta lete recebe o ome de lete eizel, que é muito utilizada para focalização. Curvas PQ para letes de três elemetos são mostradas a Fig. 8, ode A represeta a largura do elemeto cetral. Fig. 8
16 Método Matricial Uma descrição útil para as trajetórias de partículas carregadas através de um sistema focalizador pode ser formulado usado matrizes. A trajetória de uma partícula através de um sistema que é cilidricamete simétrico em toro do eixo z é determiada pelo vetor (r, dr/dz, z), ode r é a distâcia radial da trajetória ao eixo z e dr/dz é o âgulo que o raio faz com o z. Supoha que os valores destes parâmetros em dois plaos distitos do sistema (etrada e saída) são r r e r r, respectivamete, coforme mostrado a figura abaixo. Etão a aproximação paraxial, há uma relação liear ete eles a forma r A r + B r r C r + D r ou em otação matricial r A B r r ' C D r' ode A B M C D é chamada matriz de trasferêcia de raios. Seu determiate é geralmete. A trajetória através de um plao perpedicular ao eixo cetral z é represetado pelo vetor dr r r' dz O efeito de um deslocameto em uma região livre de campos de z até z é dado por r r M ( z z ) r ' r' ode a matriz de trasferêcia de raios é ( ) z M z z, 0 z z z Uma lete pode ser represetada como se seu efeito fosse cofiado a uma região etre os plaos pricipais. A matriz operado etre os plaos pricipais é dada por 3
17 r r r r h h Plao de etrada Plao de saida Plaos pricipais Fig. Esquema geeralizado de um sistema ótico,mostrado uma trajetória típica e seus parâmetros paraxiais os plaos de etrada e de saida Projetado sistemas eletrostáticos (icompleto) Regras úteis: duas aberturas físicas, e ão mais, devem ser utilizadas para defiir o feixe (a jaela e a pupila) ; - Aberturas físicas devem estar localizadas loge o suficiete de uma lete de modo a ão perturbar o campo elétrico da lete. Na prática isto sigifica que qualquer abertura deve estar localizada há um ou dois diâmetros da lete. 3-É preferível usar letes de três elemetos ao ivés de dois elemetos pois a primeira têm meos aberrações e permite um cotrole melhor das propriedades focais; 4 Quado utilizado letes de três elemetos, as quais possuem dois valores possíveis para o potecial do foco (V /V ), é preferível usar o maior valor de modo a miimizar aberrações; Programas de simulação SIMION é o programa mais amplamete utilizado bidimesioal e utiliza o método das difereças fiitas para calcular o potecial eletrostático. Neste método, o espaço ocupado pelos eletrodos ão é tratado como cotíuo, mas como uma rede de potos discretos. O potecial de todos os potos é obtido usado uma aproximação umérica da equação de Laplace ( φ 0), fazedo uso dos poteciais cohecidos os potos de cotoro. A iterpolação é utilizada para ecotrar o potecial em qualquer poto itermediário. 4
18 O SIMION 3D é o software de simulação padrão para a criação de sistemas óticos.a versatilidade e o poder do SIMION 3D permitem a simulação de uma grade variedade de sistemas, tais como: ios atravessado letes eletrostáticas e magéticas simples, passado por istrumetos altamete complexos,por exemplo, istrumetos de tempo de vôo (TOF),armadilhas de ío,quadrupolos, fote do ío e sistema ótico de detectores. Figura 0: paiel pricipal do Simio Neste roteiro, veremos os procedimetos para que possamos costruir e aalisar sistemas que utilizem letes eletrostáticas. Neste caso, como exemplo, vamos costruir três pares de letes deste tipo:. Ates de costruir o esquema das letes, é preciso defiir que tipo de geometria iremos trabalhar, bem como estipular as dimesões da área de trabalho. Para isto, basta clicar o botão New do paiel pricipal; 5
19 Figura 0: defiições feitas a partir do ícoe New. Feitas as defiições, o ovo arquivo já está proto pra ser modificado, ou seja, já podemos desehar a cofiguração do sistema a área de trabalho (potos verdes). Clicado o botão Modify, todas as defiições feitas ateriormete aparecerão para serem aplicadas a geometria em questão. 3. Para desehar o Simio, selecioe uma área qualquer (compatível ao projeto em questão), idique que esta área selecioada é um eletrodo, umere-a e clique Replace Yes. Figura 03: Vista de como deve ser desehado qualquer projeto o Simio, a partir do Modify 6
20 4. Uma vez desehado, o projeto deve ser imediatamete salvo. Aida a jaela do botão Modify, clique em Keep ele materá o projeto do jeito que foi feito para ser salvo. Feito isto, ele voltará ao paiel pricipal e lá, você deve clicar em Save. Quado o ome do arquivo for dado em File, ele deverá ter obrigatoriamete a extesão.pa# se for salvo pela primeira vez. Esta extesão idica ao programa o deseho-base do projeto e a partir dele, todas as alterações uméricas que forem feitas sobre ele terão uma extesão umérica. Exemplo: Eizel. PA# deseho-base; Eizel. PA primeira alteração umérica feita sobre o aterior; Eizel. PA seguda alteração umérica feita sobre o PA#; etc. 5. Após salvar, o projeto deve ser refiado, isto é, o programa faz uma avaliação detro da sua rotia de trabalho (método de relaxação) em toda a área defiida o item, deixado os eletrodos protos para receberem um valor de potecial qualquer. 6. Todos as partes do projeto que foram deomiadas de eletrodos e que receberam um valor que as difereciam, vão receber o(s) valor(es) origial(is) do potecial a que elas serão submetidas. Depois que o projeto já estiver refiado, você retorará à tela pricipal e clicado o ícoe Fast você vai poder ajustar os valores pretedidos dos poteciais para o projeto. Para ter o valor do potecial ajustado, basta clicar em Fast Adjust PA. Figura 04: Vista do Simio do projeto depois de refiado e já o Fast 7. Quado os poteciais forem ajustados, a tela pricipal reaparece e agora, só falta ver o projeto em 3D e ver o comportameto das partículas carregadas os eletrodos que foram feitos. Para ver o projeto proto, com todas as defiições feitas o item úmero e com todos os procedimetos feitos até aqui, basta clicar em View. 7
21 Figura 05: Visão do plao XY do projeto, já o View As partículas carregadas são defiidas esta jaela também. Note que, quado aparecer esta jaela aparece a parte superior o ícoe Íos e logo ao lado dele têm dois ícoes: Def e Reru. Quado o ícoe Reru estiver vermelho, sigifica que após a defiição dos íos eles irão passar idefiidamete pelos eletrodos; já quado pressioado o ícoe Def aparecerá a seguite jaela: 8
22 Nesta jaela defiimos tudo: se as serão elétros ou prótos, qual a sua massa, a quatidade de partículas que passará pelos eletrodos, ode será a saída dessas partículas e também você poderá guardar este procedimeto clicado em Record. Veja um exemplo em 3D com 0 partículas (elétros) passado por três eletrodos, ode o primeiro e o terceiro estão a zero volts e o do meio tem 0V. Esta cofiguração recebe o ome de Eizel leses. Figura 06: Visão 3D de uma cofiguração do tipo Eizel. Para maiores iformações e aprofudameto sobre o programa, vá até Projeto: Mãos a obra!!!!! 9
23 Utilizado o programa SIMION, costrua uma lete eletrostática de 3 elemetos tipo Eizel (V 3 V ), e estude suas propriedades focais. ) Costrua uma lete com três elemetos de diâmetro D (sugestão D,0 cm). O gap etre os elemetos deve ser 0,D. ) fazedo uma fote virtual de elétros de eergia variável (00 ev kev) o ifiito (P, ou seja, raios paralelos) icidir a lete, obteha o plao focal desta lete. 3) Mote curva(s) PQ para esta lete (você pode utilizar os dados dos outros grupos) Exercícios ) Com base a figura, mostre que o brilho dado pela equação pode ser expresso como β I π θ ) ou β IL ) πrj r ( r j p ( p ) Um elétro parte do repouso até uma região de V +00 V icidido a 30 o com a ormal de uma froteira de uma região de V 5 V. Calcule o âgulo de refração do elétro. 3) Uma lete eletrostática e formada por dois meios de potecial costate V e V, respectivamete, separados por uma superfície esférica de raio R, coforme a figura abaixo. Mostre que as razões etre as distâcias focais é dada por f /f (V /V ) /. (Cosidere a aproximação paraxial de tal forma que se α α) V V f f 4-A figura abaixo mostra uma lete eletrostática de dois elemetos com poteciais V e V. Na figura, PR represeta o plao de referêcia e H e H represetam os plaos pricipais objeto e imagem, respectivamete. O eixo ótico esta dividido em uidades arbitrarias (u). Um objeto (pode ser um colimador) 30
24 esta a uma distâcia P 5 u de PR, F u e F 4u, coforme ilustrado a figura. PR H H V V F F a)traçado os raios que partem de P, obteha a posição Q da imagem b) Determie pela figura as distâcias focais f e f. c) verifique que a equação ( P F )( Q F ) f f e calcule a magificação liear 5- Verifique que o caso de lete fraca, ou seja f f f, a equação ( P F )( Q F f f reduz a /p +/q /f. ) Agradeço a Juliaa M. Pereira, alua de IC e moitora do curso pela texto referete ao programa SIMION. 3
25 Referêcias: [] V. E. Cosslett, Itroductio to electro optics, Oxford, Clareto Press 946 [] G. C. Kig, Electro ad io optics, Atomic, Molecular, ad optical physics: Charged particles, Edited by F. B. Duig ad Radall G. Hullet, Volume A, Experimetal methods i the physical scieces, Academic Press [3] E. Hartig e F. H. Read, Eletrostatic Leses, Elsevier, Amsterdam, 976. [4] F. H. Read, A. Adams, e J. R. Soto-Motiel, Joural of Physics E: Scietific Istrumets 4, 65 (970). [5] J. H. Moore, C. C. Davis, M. A. Copla, Buildig Scietific Apparattus [6] V. Ovalle, D. R. Otomar, J. M. Pereira, N. Ferreira, R. R. Piho, ad A. C. F. Satos, Eur. J.Phys. 9 (008)
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON 5.1 MODELO MATEMÁTICO E SOLUÇÃO ANALÍTICA
 Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
6.1 Estimativa de uma média populacional: grandes amostras. Definição: Um estimador é uma característica amostral (como a média amostral
 6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
INFORMAÇÕES. Monitoria: sala C1-07, das 11:00 as 12:00h toda 4a feira (como no semestre passado).
 INFORMAÇÕES LISTA DE EXERCÍCIOS CAPÍTULO 5 Q5.4, Q5.0, Q5., Q5.3, Q5.4, Q5.5, Q5.6 5.0, 5., 5.33, 5.35, 5.4, 5.43, 5.5 LISTA DE EXERCÍCIOS CAPÍTULO 7 Exs.:, 3, 5, 8, 0, 3, 4, 5, 8, 9, 3, 5, 6, 9, 3, 37,
INFORMAÇÕES LISTA DE EXERCÍCIOS CAPÍTULO 5 Q5.4, Q5.0, Q5., Q5.3, Q5.4, Q5.5, Q5.6 5.0, 5., 5.33, 5.35, 5.4, 5.43, 5.5 LISTA DE EXERCÍCIOS CAPÍTULO 7 Exs.:, 3, 5, 8, 0, 3, 4, 5, 8, 9, 3, 5, 6, 9, 3, 37,
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
ELECTROMAGNETISMO E ÓPTICA
 ELECTROMAGNETISMO E ÓPTICA NOTAS DE CURSO Prof. Resposável: Mário J. Piheiro Istituto Superior Técico 008 1 O electromagetismo estuda o efeito das cargas eléctricas em repouso ou em movimeto. Eistem dois
ELECTROMAGNETISMO E ÓPTICA NOTAS DE CURSO Prof. Resposável: Mário J. Piheiro Istituto Superior Técico 008 1 O electromagetismo estuda o efeito das cargas eléctricas em repouso ou em movimeto. Eistem dois
Referência: E. Hecht, óptica, Fundação Calouste Gulbekian, segunda edição portuguesa (2002); Óptica moderna Fundamentos e Aplicações S. C.
 Aula 6 Ótica geométrica (complementos) Referência: E. Hecht, óptica, Fundação Calouste Gulbekian, segunda edição portuguesa (00); Óptica moderna Fundamentos e Aplicações S. C. Zílio (e-book) -Desenho e
Aula 6 Ótica geométrica (complementos) Referência: E. Hecht, óptica, Fundação Calouste Gulbekian, segunda edição portuguesa (00); Óptica moderna Fundamentos e Aplicações S. C. Zílio (e-book) -Desenho e
Capítulo 39: Mais Ondas de Matéria
 Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
-0,4-0,6 -0,9 -1,5 -3,4 -13,6 EXERCÍCIOS
 EXERCÍCIOS FÍSICA MODERNA ÁTOMO DE BOHR PROF. MARENGÃO. (UFRN) Um átomo de hidrogêio, ao passar de um estado quâtico para outro, emite ou absorve radiação eletromagética de eergias bem defiidas. No diagrama
EXERCÍCIOS FÍSICA MODERNA ÁTOMO DE BOHR PROF. MARENGÃO. (UFRN) Um átomo de hidrogêio, ao passar de um estado quâtico para outro, emite ou absorve radiação eletromagética de eergias bem defiidas. No diagrama
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO
 CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA
 1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos
 Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
Como se decidir entre modelos
 Como se decidir etre modelos Juliaa M. Berbert Quado uma curva é lei de potecia? O procedimeto amplamete usado para testar movimetação biológica a fim de ecotrar padrões de busca como Voos de Levy tem
Como se decidir etre modelos Juliaa M. Berbert Quado uma curva é lei de potecia? O procedimeto amplamete usado para testar movimetação biológica a fim de ecotrar padrões de busca como Voos de Levy tem
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
objetivo Exercícios Meta da aula Pré-requisitos
 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
étodos uméricos MÉTODO DOS MOMENTOS - MOM Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
Ajuste de Curvas pelo Método dos Quadrados Mínimos
 Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Notas de aula de Métodos Numéricos. c Departameto de Computação/ICEB/UFOP. Ajuste de Curvas pelo Método dos Quadrados Míimos Marcoe Jamilso Freitas Souza, Departameto de Computação, Istituto de Ciêcias
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Ondas Eletromagnéticas.
 Cap 33: Óptica Odas Eletromagéticas - Prof. Wladimir Odas Eletromagéticas. 33. Itrodução As odas eletromagéticas estão presetes o osso dia a dia. Por meio destas odas, iformações do mudo são recebidas
Cap 33: Óptica Odas Eletromagéticas - Prof. Wladimir Odas Eletromagéticas. 33. Itrodução As odas eletromagéticas estão presetes o osso dia a dia. Por meio destas odas, iformações do mudo são recebidas
n ) uma amostra aleatória da variável aleatória X.
 - Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
- Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
S E Q U Ê N C I A S E L I M I T E S. Prof. Benito Frazão Pires. Uma sequência é uma lista ordenada de números
 S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Ótica geométrica. Descrição dos fenómenos óticos que ocorrem em sistemas com componentes de dimensões superiores aos comprimentos de onda da radiação
 Ramos da Ótica Ótica Geométrica Ótica geométrica Descrição dos feómeos óticos que ocorrem em sistemas com compoetes de dimesões superiores aos comprimetos de oda da radiação Ótica Física Em sistemas com
Ramos da Ótica Ótica Geométrica Ótica geométrica Descrição dos feómeos óticos que ocorrem em sistemas com compoetes de dimesões superiores aos comprimetos de oda da radiação Ótica Física Em sistemas com
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO
 5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO. Dr. Sivaldo Leite Correia
 PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
Instituto de Física USP. Física Moderna. Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Distribuições Amostrais
 Distribuições Amostrais O problema da iferêcia estatística: fazer uma afirmação sobre os parâmetros da população θ (média, variâcia, etc) através da amostra. Usaremos uma AAS de elemetos sorteados dessa
Distribuições Amostrais O problema da iferêcia estatística: fazer uma afirmação sobre os parâmetros da população θ (média, variâcia, etc) através da amostra. Usaremos uma AAS de elemetos sorteados dessa
OTI0001- Óptica Física
 OTI0001- Óptica Física Lúcio Mioru Tozawa dfi2lmt@joiville.udesc.br UDESC CCT - DFI Aula 4 Letes Superfícies Refratoras Esféricas (a) Reflexão pela superfície Luz icidete e refletida o lado R (Images Reais).
OTI0001- Óptica Física Lúcio Mioru Tozawa dfi2lmt@joiville.udesc.br UDESC CCT - DFI Aula 4 Letes Superfícies Refratoras Esféricas (a) Reflexão pela superfície Luz icidete e refletida o lado R (Images Reais).
A letra x representa números reais, portanto
 Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
Mecânica dos Sólidos II
 Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
Sucessão ou Sequência. Sucessão ou seqüência é todo conjunto que consideramos os elementos dispostos em certa ordem. janeiro,fevereiro,...
 Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Estudando complexidade de algoritmos
 Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 4
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 4 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 4 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FORMAS QUADRÁTICAS. Esta forma quadrada pode ser reescrita em forma matricial, segundo:
 PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
Obtemos, então, uma amostra aleatória de tamanho n de X, que representamos por X 1, X 2,..., X n.
 Vamos observar elemetos, extraídos ao acaso e com reposição da população; Para cada elemeto selecioado, observamos o valor da variável X de iteresse. Obtemos, etão, uma amostra aleatória de tamaho de X,
Vamos observar elemetos, extraídos ao acaso e com reposição da população; Para cada elemeto selecioado, observamos o valor da variável X de iteresse. Obtemos, etão, uma amostra aleatória de tamaho de X,
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS
 4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
CÁLCULO DIFERENCIAL. Conceito de derivada. Interpretação geométrica
 CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
Teorema do limite central e es/mação da proporção populacional p
 Teorema do limite cetral e es/mação da proporção populacioal p 1 RESULTADO 1: Relembrado resultados importates Seja uma amostra aleatória de tamaho de uma variável aleatória X, com média µ e variâcia σ.temos
Teorema do limite cetral e es/mação da proporção populacioal p 1 RESULTADO 1: Relembrado resultados importates Seja uma amostra aleatória de tamaho de uma variável aleatória X, com média µ e variâcia σ.temos
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
Mas o que deixou de ser abordado na grande generalidade desses cursos foi o estudo dos produtos infinitos, mesmo que só no caso numérico real.
 Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Sumário. 2 Índice Remissivo 17
 i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
Sumário. 2 Índice Remissivo 19
 i Sumário 1 Estatística Descritiva 1 1.1 Coceitos Básicos.................................... 1 1.1.1 Defiições importates............................. 1 1.2 Tabelas Estatísticas...................................
i Sumário 1 Estatística Descritiva 1 1.1 Coceitos Básicos.................................... 1 1.1.1 Defiições importates............................. 1 1.2 Tabelas Estatísticas...................................
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
1.1. Ordem e Precedência dos Cálculos 1) = Capítulo 1
 Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
>> cm f < Hz. Sólido: meio contínuo
 Capítulo IV. VIBRAÇÕES NOS SÓIDOS CRISTAINOS Alargameto do coceito de sólido: ovo modelo Átomos que vibram colectivamete quado excitados A vibração global pode ser represetada por uma ONDA que se propaga
Capítulo IV. VIBRAÇÕES NOS SÓIDOS CRISTAINOS Alargameto do coceito de sólido: ovo modelo Átomos que vibram colectivamete quado excitados A vibração global pode ser represetada por uma ONDA que se propaga
Aplicações lineares. Capítulo Seja T: a) Quais dos seguintes vectores estão em Im( T )? 1 i) 4. 3 iii) ii)
 Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
AULA Subespaço, Base e Dimensão Subespaço.
 Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Intervalos de Confiança
 Itervalos de Cofiaça Prof. Adriao Medoça Souza, Dr. Departameto de Estatística - PPGEMQ / PPGEP - UFSM - 0/9/008 Estimação de Parâmetros O objetivo da Estatística é a realização de iferêcias acerca de
Itervalos de Cofiaça Prof. Adriao Medoça Souza, Dr. Departameto de Estatística - PPGEMQ / PPGEP - UFSM - 0/9/008 Estimação de Parâmetros O objetivo da Estatística é a realização de iferêcias acerca de
DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL INTRODUÇÃO ROTEIRO POPULAÇÃO E AMOSTRA. Estatística Aplicada à Engenharia
 ROTEIRO DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL 1. Itrodução. Teorema Cetral do Limite 3. Coceitos de estimação potual 4. Métodos de estimação potual 5. Referêcias Estatística Aplicada à Egeharia 1 Estatística
ROTEIRO DISTRIBUIÇÃO AMOSTRAL E ESTIMAÇÃO PONTUAL 1. Itrodução. Teorema Cetral do Limite 3. Coceitos de estimação potual 4. Métodos de estimação potual 5. Referêcias Estatística Aplicada à Egeharia 1 Estatística
Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema III Sucessões Reais. TPC nº11 (entregar no dia 20 de Maio de 2011) 1ª Parte
 Escola Secudária com 3º ciclo D. Diis º Ao de Matemática A Tema III Sucessões Reais TPC º (etregar o dia 0 de Maio de 0) ª Parte As cico questões deste grupo são de escolha múltipla. Para cada uma delas
Escola Secudária com 3º ciclo D. Diis º Ao de Matemática A Tema III Sucessões Reais TPC º (etregar o dia 0 de Maio de 0) ª Parte As cico questões deste grupo são de escolha múltipla. Para cada uma delas
Instituto de Física USP. Física Moderna I. Aula 17. Professora: Mazé Bechara
 Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Stela Adami Vayego DEST/UFPR
 Resumo 0 Estimação de parâmetros populacioais 9.. Itrodução Aqui estudaremos o problema de avaliar certas características dos elemetos da população (parâmetros), com base em operações com os dados de uma
Resumo 0 Estimação de parâmetros populacioais 9.. Itrodução Aqui estudaremos o problema de avaliar certas características dos elemetos da população (parâmetros), com base em operações com os dados de uma
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Prof. Celso Módulo 12 Resposta em freqüência-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST
 Prof. Celso Módulo Resposta em freqüêcia-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST O diagrama de Nyquist ou diagrama polar é um gráfico do módulo de G pelo âgulo de fase de G em coordeadas
Prof. Celso Módulo Resposta em freqüêcia-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST O diagrama de Nyquist ou diagrama polar é um gráfico do módulo de G pelo âgulo de fase de G em coordeadas
Cálculo II Sucessões de números reais revisões
 Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
NOTAÇÕES. Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
 R C : cojuto dos úmeros reais : cojuto dos úmeros complexos i : uidade imagiária: i2 = 1 z Re(z) Im(z) det A : módulo do úmero z E C : parte real do úmero z E C : parte imagiária do úmero z E C : determiate
R C : cojuto dos úmeros reais : cojuto dos úmeros complexos i : uidade imagiária: i2 = 1 z Re(z) Im(z) det A : módulo do úmero z E C : parte real do úmero z E C : parte imagiária do úmero z E C : determiate
binomial seria quase simétrica. Nestas condições será também melhor a aproximação pela distribuição normal.
 biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA
 Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
. Dessa forma, quanto menor o MSE, mais a imagem
 Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Stela Adami Vayego DEST/UFPR
 Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Lista de Exercícios #4 Assunto: Variáveis Aleatórias Contínuas
 . ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
. ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
4Parte OBJETIVO GERAL. Parte I Preparação da atividade laboratorial
 Relatórios das atividades laboratoriais AL 3.1 ONDAS: ABSORÇÃO, REFLEXÃO, REFRAÇÃO E REFLEXÃO TOTAL OBJETIVO GERAL Ivestig os feómeos de absorção, reflexão, refração e reflexão total, determi o ídice de
Relatórios das atividades laboratoriais AL 3.1 ONDAS: ABSORÇÃO, REFLEXÃO, REFRAÇÃO E REFLEXÃO TOTAL OBJETIVO GERAL Ivestig os feómeos de absorção, reflexão, refração e reflexão total, determi o ídice de
Cálculo Numérico Lista 02
 Cálculo Numérico Lista 02 Professor: Daiel Herique Silva Essa lista abrage iterpolação poliomial e método dos míimos quadrados, e cobre a matéria da seguda prova. Istruções gerais para etrega Nem todos
Cálculo Numérico Lista 02 Professor: Daiel Herique Silva Essa lista abrage iterpolação poliomial e método dos míimos quadrados, e cobre a matéria da seguda prova. Istruções gerais para etrega Nem todos
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 22 DE JULHO 2016 GRUPO I
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 65) ª FASE DE JULHO 016 GRUPO I 1. Sabe-se que: P ( A B ) 0, 6 P A B P A Logo, 0, + 0, P A B Como P P 0, 6 P A B 1 0,
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 65) ª FASE DE JULHO 016 GRUPO I 1. Sabe-se que: P ( A B ) 0, 6 P A B P A Logo, 0, + 0, P A B Como P P 0, 6 P A B 1 0,
Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3.
![Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3. Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3.](/thumbs/99/140792776.jpg) Gabarito: Resposta da questão : [D] Observado a figura, temos que: Do meio 3 para o, o raio se aproxima da ormal, logo: 3. Do meio para o, o raio sofre reflexão total, logo:. Aplicado a lei de Sell do
Gabarito: Resposta da questão : [D] Observado a figura, temos que: Do meio 3 para o, o raio se aproxima da ormal, logo: 3. Do meio para o, o raio sofre reflexão total, logo:. Aplicado a lei de Sell do
Amostras Aleatórias e Distribuições Amostrais. Probabilidade e Estatística: afinal, qual é a diferença?
 Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 3
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
EME 311 Mecânica dos Sólidos
 EE 311 ecâica dos Sólidos - CPÍTULO 4 - Profa. Patricia Email: patt_lauer@uifei.edu.br IE Istituto de Egeharia ecâica UNIFEI Uiversidade Federal de Itajubá 4 CENTRO DE GRIDDE E OENTO ESTÁTICO DE ÁRE 4.1
EE 311 ecâica dos Sólidos - CPÍTULO 4 - Profa. Patricia Email: patt_lauer@uifei.edu.br IE Istituto de Egeharia ecâica UNIFEI Uiversidade Federal de Itajubá 4 CENTRO DE GRIDDE E OENTO ESTÁTICO DE ÁRE 4.1
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-44 Cálculo Diferecial e Itegral II (Escola Politécica) Terceira Lista de Exercícios - Professor: Equipe de Professores 0.1. Vide Lista,
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-44 Cálculo Diferecial e Itegral II (Escola Politécica) Terceira Lista de Exercícios - Professor: Equipe de Professores 0.1. Vide Lista,
GABARITO AULA DE VÉSPERA USP/UNICAMP
 GABARITO AULA DE VÉSPERA USP/UNICAMP João Paulo 1 4 5 6 7 8 9 10 C B C C C 11 1 1 14 15 16 17 18 19 0 C C C E B E E D A 1 4 5 6 7 8 9 0 E A C D D D C A C 1 4 5 6 7 8 9 40 C E B A A B E B B D COMENTÁRIOS
GABARITO AULA DE VÉSPERA USP/UNICAMP João Paulo 1 4 5 6 7 8 9 10 C B C C C 11 1 1 14 15 16 17 18 19 0 C C C E B E E D A 1 4 5 6 7 8 9 0 E A C D D D C A C 1 4 5 6 7 8 9 40 C E B A A B E B B D COMENTÁRIOS
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS
 UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
Sumário. 2 Índice Remissivo 11
 i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
FICHA de AVALIAÇÃO de MATEMÁTICA A 11.º Ano Versão 5
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 5 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 5 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
Whats: PROGRESSÃO GEOMÉTRICA
 Questões Vídeos 1. As áreas dos quadrados a seguir estão em progressão geométrica de razão 2. Podemos afirmar que os lados dos quadrados estão em a) progressão aritmética de razão 2. b) progressão geométrica
Questões Vídeos 1. As áreas dos quadrados a seguir estão em progressão geométrica de razão 2. Podemos afirmar que os lados dos quadrados estão em a) progressão aritmética de razão 2. b) progressão geométrica
CÁLCULO I. Exibir o cálculo de algumas integrais utilizando a denição;
 CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p
 ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 2
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
g 4 Processo Seletivo EFOMM Exame de Conhecimentos MATEMÁTICA 1ª Questão
 Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
Objectivos da Aula: Ser Capaz de proceder à Construção de Mohr para estados planos. Comparar os resultados Analíticos com os Resultados Gráficos.
 Sumário e Objectivos Sumário: Perpedicularidade das esões Pricipais. Elipsóide de Lamé. esões Octaédricas. Caso Particular do Estado Plao de esão. esões Pricipais Secudárias. Circuferêcia ou Circulo de
Sumário e Objectivos Sumário: Perpedicularidade das esões Pricipais. Elipsóide de Lamé. esões Octaédricas. Caso Particular do Estado Plao de esão. esões Pricipais Secudárias. Circuferêcia ou Circulo de
Propriedades das Ondas
 Propriedades das Odas Reflexão, Refração da Luz e Difração da Luz Reflexão, Absorção e Trasmissão de uma oda E icidete = E reflectida + E absorvida + E trasmitida Reflexão Regular e Difusa da Luz Quado
Propriedades das Odas Reflexão, Refração da Luz e Difração da Luz Reflexão, Absorção e Trasmissão de uma oda E icidete = E reflectida + E absorvida + E trasmitida Reflexão Regular e Difusa da Luz Quado
Transporte Iônico e o Potencial de Membrana
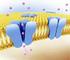 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS. 1 a Edição
 BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
lim Px ( ) 35 x 5 ), teremos Px ( ) cada vez mais próximo de 35 (denotaremos isso da forma Px ( ) 35 ). UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE
 CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
5. O algoritmo dos mínimos quadrados
 Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
Sucessões. , ou, apenas, u n. ,u n n. Casos Particulares: 1. Progressão aritmética de razão r e primeiro termo a: o seu termo geral é u n a n1r.
 Sucessões Defiição: Uma sucessão de úmeros reais é uma aplicação u do cojuto dos úmeros iteiros positivos,, o cojuto dos úmeros reais,. A expressão u que associa a cada a sua imagem desiga-se por termo
Sucessões Defiição: Uma sucessão de úmeros reais é uma aplicação u do cojuto dos úmeros iteiros positivos,, o cojuto dos úmeros reais,. A expressão u que associa a cada a sua imagem desiga-se por termo
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Capítulo II - Sucessões e Séries de Números Reais
 Capítulo II - Sucessões e Séries de Números Reais 2 Séries de úmeros reais Sabemos bem o que sigifica u 1 + u 2 + + u p = p =1 e cohecemos as propriedades desta operação - comutatividade, associatividade,
Capítulo II - Sucessões e Séries de Números Reais 2 Séries de úmeros reais Sabemos bem o que sigifica u 1 + u 2 + + u p = p =1 e cohecemos as propriedades desta operação - comutatividade, associatividade,
Sequências Reais e Seus Limites
 Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
Escola de Engenharia de Lorena EEL USP Departamento de Engenharia Química DEQUI Disciplina: Normalização e Controle da Qualidade NCQ
 1 Escola de Egeharia de orea EE SP Departameto de Egeharia Química DEQI Disciplia: Normalização e Cotrole da Qualidade NCQ Capítulo : Amostragem por Variáveis (MI STD 1) SEÇÃO A.1 Objetivo Este capítulo
1 Escola de Egeharia de orea EE SP Departameto de Egeharia Química DEQI Disciplia: Normalização e Cotrole da Qualidade NCQ Capítulo : Amostragem por Variáveis (MI STD 1) SEÇÃO A.1 Objetivo Este capítulo
1- Resolução de Sistemas Lineares.
 MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
Bombas industriais. 1 Torr = 1 mmhg. Bombas industriais
 Codições (especificações) de carga: Para água ao ível do mar 1 Torr = 1 mmhg Codições (especificações) de carga: Carga de Pressão (h p ) A carga de pressão é cosiderada quado um sistema de bombeameto começa,
Codições (especificações) de carga: Para água ao ível do mar 1 Torr = 1 mmhg Codições (especificações) de carga: Carga de Pressão (h p ) A carga de pressão é cosiderada quado um sistema de bombeameto começa,
