Transformações Conformes: 15 Aplicações
|
|
|
- Luiz Fernando Camarinho
- 5 Há anos
- Visualizações:
Transcrição
1 AULA Transformações Conformes: 15 Aplicações META: Aplicar transformações conformes. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Aplicar transformações conformes na determinação da distribuição de velocidade em alguns escoamentos estacionários laminares planos. PRÉ-REQUISITOS Aula14 de Variáveis Complexas.
2 Transformações Conformes: Aplicações 15.1 Introdução Caros alunos concluímos aqui nosso curso de Variáveis Complexa com Algumas Aplicações das Transformações Conformes. Em particular faremos aplicações ao escoamento laminar, não viscoso e potencial de fluidos Problemas de Dirichlet e de Neumann Vários problemas da Física e da Engenharia são modelados matematicamente por equações diferenciais parciais às quais são associadas condições adicionais denominadas condições de contorno. Denominamos Problema de Valor de Contorno ao problema de determinar uma solução que satisfaça ao mesmo tempo as equações diferenciais e as condições de contorno. Estaremos interessados basicamente na solução de problemas cuja modelagem recaiam em equações de Laplace bi-dimensional i.e. Problemas onde desejamos determinar uma função ux, u que satisfaça a equação de Laplace: u + u = 0 no interior de uma região B sujeita a certas condições na fronteira B. Os problemas de Dirichlet e de Neumann podem ser resolvidos em uma região B simplesmente conexa que, através de aplicações conformes, possam ser transformadas na região limitada pelo semi-plano superior ou o círculo unitário. Neste caso é muito útil o teorema da transformação de Riemmann enunciado sem demonstração na aula anterior. As idéias por trás da solução de tais problemas são: 206
3 Variáveis Complexas i Usar uma aplicação conforme que leve a região B no semiplano superior ou o círculo unitário. AULA 15 ii Resolver o problema no semi-plano superior ou no círculo unitário. Uma vez resolvidos a tarefa principal recai em determinar a transformação conforme adequada citada no ítem anterior. iii Usar a solução obtida semi-plano ou círculo unitário para resolver o problema original na região B usando a inversa da aplicação conforme. O processo descrito baseia-se nos seguintes teoremas: Teorema Seja B uma região simplesmente conexa e f : B C holomorfa tal que f z 0 z B então existe uma única função f 1 : Imgf B. OBS Este teorema assegura que tanto f quanto f 1 são aplicações conformes. Sua demonstração não será feita aqui. Os interessados poderão busca-la em outras referências ou adaptar o teorema da função inversa no caso especial de R 2, para o plano complexo. Teorema Sejam B z e B w abertos simplesmente conexos dos plano z e plano w respectivamente e f : B z B w uma aplicação conforme tal que f z 0 z B z então se Φ é harmônica em B w, Φ f é harmônica em B z. A demonstração deste teorema segue imediatamente do seguinte teorema: 207
4 Transformações Conformes: Aplicações Teorema Sejam w = u + vı = fz = fx + yı analítica onde f z 0 então: 2 Φ Φ 2 = f z 2 2 Φ u Φ v 2 PROVA: Podemos escrever x = xu, v e y = yu, v desta forma Φx, y = Φxu, v, yu, v. Usando a regra da cadeia temos: Φ = Φ u u + Φ v v e Φ = Φ u u + Φ v v Para a segunda derivada, usando a regra da cadeia a derivada de um produto, temos: 2 Φ 2 = Φ 2 u u 2 + Φ u u + Φ v 2 v 2 + Φ v v 2 Φ 2 = Φ 2 u u 2 + u Φ u u u + Φ v v u + Φ 2 v v 2 + u Φ u u v + Φ v v v = Φ 2 u u 2 + u 2 Φ u u Φ v v u 2 Φ u u v + 2 Φ v v 2 + Φ 2 v v 2 + u Do mesmo modo, calculando 2 Φ 2 2 Φ 2 = Φ u 2 u 2 + u + Φ 2 v v 2 + u temos: 2 Φ u u Φ v v u 2 Φ u u v + 2 Φ v v 2 Somando 2 Φ 2 com 2 Φ 2 temos: 208
5 Variáveis Complexas 2 Φ Φ 2 = Φ 2 u u u 2 + Φ 2 v v v [ 2 u + 2 Φ 2 ] [ u 2 u Φ v 2 v Φ u v u v + u v ] v 2 AULA 15 Como w = u + vı = fz é analítica temos que u e v satisfazem as equações de Cauchy-Riemann: u = v e v = u. Daí, temos: u v + u v = v v v = 0. O que elimina a última v parte da equação acima e temos: 2 Φ Φ 2 = Φ 2 u u u [ 2 u + 2 Φ 2 u Φ v ] 2 u 2 v v [ Φ v 2 v 2 + ] v 2 Por outro lado, u e v são também são harmônicas logo: 2 u u 2 = 0 e 2 v v = 0, o que elimina os dois primeiros 2 termos da equação e temos: 2 Φ Φ 2 = 2 Φ u 2 [ u 2 + ] u Φ v 2 [ v 2 + ] v 2 Usando as equações de Cauchy-Riemann u = v e v = u temos: u v + u v = v v v = 0. O que elimina a última v 209
6 Transformações Conformes: Aplicações parte da equação acima e temos: u 2 u 2 + = v 2 + v E a equação acima toma a forma: 2 = u 2 v 2 + = f z 2 2 Φ Φ 2 = f z 2 2 Φ u Φ v 2 Teorema Sejam B z e B w abertos simplesmente conexos dos plano z e plano w respectivamente e f : B z B w uma aplicação conforme tal que f mapeia B z em B w então se Φ satisfaz: Φu, v = c, u, v B w ou Φ n n n u, v = 0, u, v B w Φ f satisfaz: Φ fx, y = c, x, y B z ou Φ f x, y = 0, x, y B z n n n Problemas de Dirichlet Vejamos a definição: Definição O problema de Dirichlet consiste em determinar uma função Φx, y contínua com derivadas parciais contínuas que satisfaçam: Φ + Φ = 0 Φx, y = c, x, y B, x, y B onde c R Problemas de Neumann Vejamos a definição: 210
7 Variáveis Complexas Definição O problema de Neumann consiste em determinar uma função Φx, y contínua com derivadas parciais contínuas que satisfaçam: Φ + Φ = 0, x, y B Φ n n n x, y = 0, x, y B onde n n n é a normal unitária a B orientada para fora de B e Φ n n n a derivada direcional de Φ na direção da normal. AULA Aplicações ao Escoamento de Fluidos Muitos problemas de hidráulica, dinâmica dos fluidos ou aerodinâmica dos fluidos podem ser resolvidos por métodos de variáveis complexas, em especial com aplicações conformes, como veremos nesta subseção. Para este fim são necessárias algumas considerações que simplificaram tremendamente a nossa tarefa. As hipóteses básicas são as seguintes: i O escoamento é bi-dimensional. As características básicas do escoamento de fluidos são as mesmas independente do plano en consideração. Isso permite aplicação dos teoremas na solução de problemas de escoamento en redor de objetos. ii Escoamento estacionário. A velocidade do fluido depende apenas das coordenadas espaciais x, y e não do tempo. iii Fluido não viscoso. O fluido não tem viscosidade, escoa sem atrito. iv Escoamento potencial. A velocidade do fluido deriva de um campo potencial i.e. se v x e v y são as componentes da velocidade na direção x e na direção y respectivamente, existe uma 211
8 Transformações Conformes: Aplicações função Φx, y tal que: v x = Φ v y = Φ v Fluido incompressível. Equivale a dizer que a densidade do fluido é constante e o campo de velocidade satisfaz: v x + v y OBS Substituindo eqn e eqn temos: 2 Φ Φ logo o potencial de velocidade Φ é uma função harmônica. Se Ψ é a harmônica conjugada de Φ definimos o potencial complexo Ω por: Ωz = Φx, y + Ψx, yı. Daí, temos: Ω z = dω dz = Φ + Ψ ı = Φ Φ ı = v x v y ı OBS As famílias de curvas a um parâmetro: Φx, y = α Ψx, y = β onde α e β são constante são denominadas curvas eqüipotenciais e curvas de fluxo respectivamente. Em escoamentos estacionários curvas de fluxo representam trajetória reais das partículas do fluido. 212
9 Variáveis Complexas Escoamento em Torno de Obstáculos AULA 15 Um problema importante em dinâmica dos fluidos é determinar como um fluido, inicialmente escoando com velocidade constante v 0, é perturbado pela introdução de obstáculos. A intenção é obter um potencial complexo da forma: Ωz = v 0 z + Gz tal que lim Gz = 0 garantindo que longe do obstáculo a velocidade tem módulo z constante. y plano z w plano w a x u Figura 15.1: Transformação fz = z + a2 z Exemplo Estudar o potencial complexo de escoamento Ωz = v 0 z + a2. z SOLUÇÃO: Pela figura 15.1 a transformação conforme fz = z + a2 z leva o exterior do semi-círculo de raio a centrado em z 0 = 0 do semiplano superior do plano z no semiplano superior do plano w. Portanto podemos usa-la para descrever o escoamento de um fluido incompressível, não viscoso, estacionário em torno do semicírculo. Daí, fazendo z = re θı podemos reescrever o potencial 213
10 Transformações Conformes: Aplicações complexo na forma: Ωz = Φ + Ψı = v 0 re θı + a2 = v 0 r + a2 r De eqn temos: re θı cosθ + v 0 r a2 r Φr, θ = v 0 r + a2 r Ψr, θ = v 0 r a2 r cosθ sinθ sinθı Então as curvas Ψr, θ = β ver figura 15.2 representam as linhas de corrente i.e. as trajetórias reais das partículas do fluido. y x Figura 15.2: Linhas de corrente Por outro lado, derivando o potencial complexo Ω para obter a velocidade complexa temos: V = Ω z = v 0 1 a2 z 2 = v 0 1 a2 re θı = v 0 1 a2 r 2 cosθ v 0a 2 sinθı
11 Variáveis Complexas distante do semi-círculo, lim r V = v 0 i.e. o fluido está escoando na direção do semi-eixo real positivo com velocidade constante v 0. AULA Conclusão Na aula de hoje, vimos que é possível usar aplicações conformes para resolver alguns tipos de problemas de escoamento de fluidos. RESUMO No nosso resumo da Aula 15 constam os seguintes tópicos: Problemas de Dirichlet e de Neumann A solução de problemas de Dirichlet e de Neumann baseia-se nos seguintes teoremas: Teorema 1: Seja B uma região simplesmente conexa e f : B C holomorfa tal que f z 0 z B então existe uma única função f 1 : Imgf B. Teorema 2: Sejam B z e B w abertos simplesmente conexos dos plano z e plano w respectivamente e f : B z B w uma aplicação conforme tal que f z 0 z B z então se Φ é harmônica em B w, Φ f é harmônica em B z. Teorema 3: Sejam B z e B w abertos simplesmente conexos dos plano z e plano w respectivamente e f : B z B w uma aplicação conforme tal que 215
12 Transformações Conformes: Aplicações f mapeia B z em B w então se Φ satisfaz: Φu, v = c, u, v B w ou Φ n n n u, v = 0, u, v B w Φ f satisfaz: Φ fx, y = c, x, y B z ou Φ f x, y = 0, x, y B z n n n Definição: Problema de Dirichlet O problema de Dirichlet consiste em determinar uma função Φx, y contínua com derivadas parciais contínuas que satisfaçam: Φ + Φ = 0, x, y B Φx, y = c, x, y B onde c R. Definição: Problema de Neumann O problema de Neumann consiste em determinar uma função Φx, y contínua com derivadas parciais contínuas que satisfaçam: Φ + Φ = 0, x, y B Φ n n n x, y = 0, x, y B onde n n n é a normal unitária a B orientada para fora de B e Φ n n n a derivada direcional de Φ na direção da normal. PRÓXIMA AULA Caros alunos esta é nossa última aula portanto, não haverá próxima aula pois, esta é a última aula do nosso curso de Variáveis Complexa. Espero que este curso tenha dado bons frutos. 216
13 Variáveis Complexas Ele é apenas um introdução ao maravilhoso mundo das Variáveis Complexas. A Leitura complementar fornece material adicional para quem desejar mais informações. AULA 15 ATIVIDADES Deixamos como atividades as seguintes questões: ATIV Considere o potencial complexo de escoamento Ωz = v 0 z + a2 e determine os pontos de estagnação do fluido. z Comentário: Lembre-se que os pontos de estagnação em um escoamento são pontos onde a velocidade complexa é nula. ATIV Considere o potencial complexo de escoamento Ωz = v 0 z + a2 e mostre que as curvas ae ıt, t [0, π], t, t, a] z e t, t [a, são linhas de corrente. Comentário: corrente. Volte ao exemplo e estude a equação das linhas de LEITURA COMPLEMENTAR SPIEGEL, Murray R., Variáveis Complexas, Coleção Schaum, Editora McGraw-Hill do Brasil, SOARES, Márcio G., Cálculo em uma Variável Complexa, Coleção Matemática Universitária, Editora SBM, BROWN, James W. and CHURCHILL, Ruel R., Complex Variables and Applications Editora McGraw Hill,
14 Transformações Conformes: Aplicações FERNANDEZ, Cecília S. e BERNARDES Jr, Nilson C. Introdução às Funções de uma Variável Complexa. Editora SBM,
Mais Alguns Aspectos da Derivação Complexa
 Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Cálculo de Resíduos AULA 12
 AULA 2 META: Apresentar cálculo de resíduos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir resíduo de uma função de variáveis complexas em um ponto dado e calcular o resíduo de uma
AULA 2 META: Apresentar cálculo de resíduos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir resíduo de uma função de variáveis complexas em um ponto dado e calcular o resíduo de uma
META: Introduzir o conceito de derivada de funções de variáveis complexas.
 AULA 3 META: Introduzir o conceito de derivada de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir derivada de funções de variáveis complexas e determinar
AULA 3 META: Introduzir o conceito de derivada de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir derivada de funções de variáveis complexas e determinar
Limites de Funções de Variáveis Complexas
 Limites de Funções de Variáveis Complexas AULA 2 META: Introduzir o conceito de limite de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir limites de
Limites de Funções de Variáveis Complexas AULA 2 META: Introduzir o conceito de limite de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir limites de
Funções Elementares do Cálculo Complexos 1
 Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
Convergência de Séries de Números Complexos
 Convergência de Séries de Números Complexos META: Apresentar o conceito de convergência de séries de números complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir convergência
Convergência de Séries de Números Complexos META: Apresentar o conceito de convergência de séries de números complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir convergência
Funções Elementares do Cálculo Complexos 2
 Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Teoremas de Cauchy AULA 8
 Teoremas de auchy META: Introduzir os principais teoremas de auchy sobre integração de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Enunciar os principais
Teoremas de auchy META: Introduzir os principais teoremas de auchy sobre integração de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Enunciar os principais
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Escoamento potencial
 Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Transformações Conformes
 META: Introduzir o conceito de transformações conforme. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir transformações conformes e exemplificar transformações conformes. PRÉ-REQUISITOS
META: Introduzir o conceito de transformações conforme. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir transformações conformes e exemplificar transformações conformes. PRÉ-REQUISITOS
Cálculo II Lista 4. com respostas
 Cálculo II Lista 4. com respostas Exercício 1. Esboce a curva de nível de f(x, ) que passa pelo ponto P e desenhe o vetor gradiente de f em P: (a) f(x, ) = x ; P = ( 2, 2); 2 (b) f(x, ) = x 2 + 4 2 ; P
Cálculo II Lista 4. com respostas Exercício 1. Esboce a curva de nível de f(x, ) que passa pelo ponto P e desenhe o vetor gradiente de f em P: (a) f(x, ) = x ; P = ( 2, 2); 2 (b) f(x, ) = x 2 + 4 2 ; P
Fichas de Análise Matemática III
 Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
Singularidades de Funções de Variáveis Complexas
 Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Variáveis Complexas. José Carlos Leite
 Variáveis Complexas José Carlos Leite São Cristóvão/SE 2011 Variaveis Complexas Elaboração de Conteúdo José Carlos Leite Projeto Gráfico Neverton Correia da Silva Nycolas Menezes Melo Capa Hermeson Alves
Variáveis Complexas José Carlos Leite São Cristóvão/SE 2011 Variaveis Complexas Elaboração de Conteúdo José Carlos Leite Projeto Gráfico Neverton Correia da Silva Nycolas Menezes Melo Capa Hermeson Alves
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
3 Superfícies Spacelike em IR 2,1
 Superfícies Spacelike em IR,. Fórmula de Representação para Spacelike no espaço de Lorentz.. O espaço de Minkowski Seja IR, = IR, ḡ o espaço de Minkowski de dimensão com a métrica de Lorentz ḡ =(dx ) +(dx
Superfícies Spacelike em IR,. Fórmula de Representação para Spacelike no espaço de Lorentz.. O espaço de Minkowski Seja IR, = IR, ḡ o espaço de Minkowski de dimensão com a métrica de Lorentz ḡ =(dx ) +(dx
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
Curso: Engenharia Industrial Elétrica. Análise de variáveis Complexas Data: 27/08/2013. Turma: 01 Semestre:
 Professora: Edmary S B Araújo Aluno(a): Fontes e poços São pontos singulares de f( Linhas de fontes e linhas de poços são linhas no fluido nos quais o fluido aparece e desaparece, respectivamente Alguns
Professora: Edmary S B Araújo Aluno(a): Fontes e poços São pontos singulares de f( Linhas de fontes e linhas de poços são linhas no fluido nos quais o fluido aparece e desaparece, respectivamente Alguns
Lista 1 - Métodos Matemáticos II Respostas
 Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
14 AULA. Vetor Gradiente e as Derivadas Direcionais LIVRO
 1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais 2 ō Semestre 2009/2010
 Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais Guia 6 João Pedro Boavida. 19 a 28 de Outubro
 19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
38 a Aula AMIV LEAN, LEC Apontamentos
 38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
Capítulo 2. Ortogonalidade e Processo de Gram-Schmidt. Curso: Licenciatura em Matemática
 Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Universidade Federal de Goiás. Plano de Ensino
 01: Dados de Identificação da Disciplina: Plano de Ensino Disciplina: Funções de uma Variável Complexa Cod. da Disciplina: 2733 Curso: Matematica Licenciatura Cod. do Curso: Turma: Matemática: Licenciatura
01: Dados de Identificação da Disciplina: Plano de Ensino Disciplina: Funções de uma Variável Complexa Cod. da Disciplina: 2733 Curso: Matematica Licenciatura Cod. do Curso: Turma: Matemática: Licenciatura
Teoria Escalar da Difração
 Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
PROVAS DE ANÁLISE COMPLEXA
 PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
Lista 2 - Métodos Matemáticos II Respostas
 Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
SUMÁRIO CAPÍTULO 1 CAPÍTULO 2
 SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
Seção 29 Ortogonalidade das funções de Bessel Membrana circular
 Seção 9 Ortogonalidade das funções de Bessel Membrana circular Vamos considerar o problema de determinar vibrações livres de uma membrana presa pelo bordo tambor), conhecidos o deslocamento e a velocidade
Seção 9 Ortogonalidade das funções de Bessel Membrana circular Vamos considerar o problema de determinar vibrações livres de uma membrana presa pelo bordo tambor), conhecidos o deslocamento e a velocidade
ALVARO ANTONIO OCHOA VILLA
 UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS DEPARTAMENTO DE ENGENHARIA MECÂNICA PÓS-GRADUAÇÃO. DOUTORADO EM ENERGIA. ANÁLISE DIMENSIONAL E SEMELHANÇA ALVARO ANTONIO OCHOA VILLA
UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS DEPARTAMENTO DE ENGENHARIA MECÂNICA PÓS-GRADUAÇÃO. DOUTORADO EM ENERGIA. ANÁLISE DIMENSIONAL E SEMELHANÇA ALVARO ANTONIO OCHOA VILLA
Teorema de Divergência
 Teorema de ivergência META: Apresentar o teorema de Gauss e algumas de suas aplicações. OBJETIVO: Ao fim da aula os alunos deverão ser capazes de: Enunciar o teorema de Gauss. eterminar o divergente de
Teorema de ivergência META: Apresentar o teorema de Gauss e algumas de suas aplicações. OBJETIVO: Ao fim da aula os alunos deverão ser capazes de: Enunciar o teorema de Gauss. eterminar o divergente de
Fenômenos de Transferência FEN/MECAN/UERJ Prof Gustavo Rabello 2 período 2014 lista de exercícios 06/11/2014. Conservação de Quantidade de Movimento
 Fenômenos de Transferência FEN/MECAN/UERJ Prof Gustavo Rabello 2 período 2014 lista de exercícios 06/11/2014 Conservação de Quantidade de Movimento 1. A componente de velocidade v y de um escoamento bi-dimensional,
Fenômenos de Transferência FEN/MECAN/UERJ Prof Gustavo Rabello 2 período 2014 lista de exercícios 06/11/2014 Conservação de Quantidade de Movimento 1. A componente de velocidade v y de um escoamento bi-dimensional,
Fundamentos da Eletrostática Aula 11 Sobre a solução de problemas eletrostáticos
 Fundamentos da Eletrostática Aula 11 Sobre a solução de problemas eletrostáticos Prof. Alex G. Dias Prof. Alysson F. Ferrari Solução de problemas eletrostáticos via Equação de Laplace Especicada a distribuição
Fundamentos da Eletrostática Aula 11 Sobre a solução de problemas eletrostáticos Prof. Alex G. Dias Prof. Alysson F. Ferrari Solução de problemas eletrostáticos via Equação de Laplace Especicada a distribuição
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER
 TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
6 AULA. Equações Paramétricas LIVRO. META Estudar funções que a cada ponto do domínio associa um par ordenado
 1 LIVRO Equações Paramétricas 6 AULA META Estudar funções que a cada ponto do domínio associa um par ordenado de R 2 OBJETIVOS Estudar movimentos de partículas no plano. PRÉ-REQUISITOS Ter compreendido
1 LIVRO Equações Paramétricas 6 AULA META Estudar funções que a cada ponto do domínio associa um par ordenado de R 2 OBJETIVOS Estudar movimentos de partículas no plano. PRÉ-REQUISITOS Ter compreendido
Mecânica dos Fluidos II (MEMec) Aula de Resolução de Problemas n o 3
 Mecânica dos Fluidos II (MEMec) Aula de Resolução de Problemas n o 3 (Método das imagens, escoamento em torno de um cilindro com circulação, transformação conforme) EXERCÍCIO 1 [Problema 6 das folhas do
Mecânica dos Fluidos II (MEMec) Aula de Resolução de Problemas n o 3 (Método das imagens, escoamento em torno de um cilindro com circulação, transformação conforme) EXERCÍCIO 1 [Problema 6 das folhas do
GABARITO. 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan
 GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
A integral definida Problema:
 A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
1 Diferenciabilidade e derivadas direcionais
 UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2015/16
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 9 de Julho de 6 Nome : Hora : 4: Número: Duração : horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 5/6 Exame de ª época, 9 de Julho de 6 Nome : Hora : 4: Número: Duração : horas ª Parte : Sem consulta ª Parte : Consulta limitada a livros
Departamento de Engenharia Mecânica. ENG 1011: Fenômenos de Transporte I
 Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Fenômeno de Transportes A PROFª. PRISCILA ALVES
 Fenômeno de Transportes A PROFª. PRISCILA ALVES PRISCILA@DEMAR.EEL.USP.BR Proposta do Curso Critérios de Avaliação e Recuperação Outras atividades avaliativas Atividades experimentais: Será desenvolvida
Fenômeno de Transportes A PROFª. PRISCILA ALVES PRISCILA@DEMAR.EEL.USP.BR Proposta do Curso Critérios de Avaliação e Recuperação Outras atividades avaliativas Atividades experimentais: Será desenvolvida
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Variável Complexa
 Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
CÁLCULO II - MAT Em cada um dos seguintes campos vetoriais, aplicar o resultado do exercício 3 para mostrar que f
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERIANA Instituto Latino-Americano de iências da Vida e da Natureza entro Interdisciplinar de iências da Natureza 1. Dado um campo vetorial bidimensional ÁLULO
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERIANA Instituto Latino-Americano de iências da Vida e da Natureza entro Interdisciplinar de iências da Natureza 1. Dado um campo vetorial bidimensional ÁLULO
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
Lista 6: CDCI2 Turmas: 2AEMN e 2BEMN. 1 Divergente e Rotacional de Campos Vetoriais
 Lista 6: CDCI Turmas: AEMN e BEMN Prof. Alexandre Alves Universidade São Judas Tadeu Divergente e Rotacional de Campos Vetoriais Exercício : Calcule a divergência e o rotacional dos seguintes campos vetoriais:
Lista 6: CDCI Turmas: AEMN e BEMN Prof. Alexandre Alves Universidade São Judas Tadeu Divergente e Rotacional de Campos Vetoriais Exercício : Calcule a divergência e o rotacional dos seguintes campos vetoriais:
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA
 AA-22 AERODINÂMICA NÃO ESTACIONÁRIA Aerodinâmica Linearizada Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Linearização da Equação do Potencial Completo - proposta ( φ φ) 2 2 1 φ φ ( φ φ) φ 2 + + =
AA-22 AERODINÂMICA NÃO ESTACIONÁRIA Aerodinâmica Linearizada Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Linearização da Equação do Potencial Completo - proposta ( φ φ) 2 2 1 φ φ ( φ φ) φ 2 + + =
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA
 AA-220 AERODINÂMICA NÃO ESTACIONÁRIA Aerofólio fino em regime incompressível não estacionário (baseado nas Notas de Aula do Prof Donizeti de Andrade) Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Relembrando
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA Aerofólio fino em regime incompressível não estacionário (baseado nas Notas de Aula do Prof Donizeti de Andrade) Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Relembrando
Análise Complexa e Equações Diferenciais 1 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
PROBLEMAS DIRETO E INVERSO. A Teoria do Potencial admite um: Problema DIRETO: determinação do potencial a partir das massas geradoras
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA SUL DE MINAS GERAIS Câmpus Inconfidentes TEORIA DO POTENCIAL Aula 06 PROBLEMAS DIRETO E INVERSO A Teoria do Potencial admite um: Problema DIRETO: determinação
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA SUL DE MINAS GERAIS Câmpus Inconfidentes TEORIA DO POTENCIAL Aula 06 PROBLEMAS DIRETO E INVERSO A Teoria do Potencial admite um: Problema DIRETO: determinação
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
15 AULA. Máximos e Mínimos LIVRO. META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais.
 1 LIVRO Máximos e Mínimos 1 AULA META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais. OBJETIVOS Maximizar e/ou minimizar função de duas variáveis a valores reais.
1 LIVRO Máximos e Mínimos 1 AULA META Encontrar os pontos de máximo e mínimo de uma função de duas variáveis a valores reais. OBJETIVOS Maximizar e/ou minimizar função de duas variáveis a valores reais.
Algumas Aplicações das Integrais tríplas
 Algumas Aplicações das Integrais tríplas META: Apresentar algumas aplicações das integrais triplas de funções de valores reais e domínio em R 3. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes
Algumas Aplicações das Integrais tríplas META: Apresentar algumas aplicações das integrais triplas de funções de valores reais e domínio em R 3. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes
Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados
 Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados Cecília S. Fernandez UFF Neste trabalho vamos apresentar uma demonstração elementar de um resultado envolvendo
Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados Cecília S. Fernandez UFF Neste trabalho vamos apresentar uma demonstração elementar de um resultado envolvendo
Utilização do princípio da Simetria de Riemann-Schwarz para transformações conformes de algumas regiões*
 Utilização do princípio da Simetria de Riemann-Schwarz para transformações conformes de algumas regiões* Ludmila Bourchtein, Adriana Neumann de Oliveira ** Departamento de Matemática, Universidade Federal
Utilização do princípio da Simetria de Riemann-Schwarz para transformações conformes de algumas regiões* Ludmila Bourchtein, Adriana Neumann de Oliveira ** Departamento de Matemática, Universidade Federal
Solução: Um esboço da região pode ser visto na figura abaixo.
 Instituto de Matemática - IM/UFRJ Gabarito prova final - Escola Politécnica / Escola de Química - 29/11/211 Questão 1: (2.5 pontos) Encontre a área da região do primeiro quadrante limitada simultaneamente
Instituto de Matemática - IM/UFRJ Gabarito prova final - Escola Politécnica / Escola de Química - 29/11/211 Questão 1: (2.5 pontos) Encontre a área da região do primeiro quadrante limitada simultaneamente
Exercícios resolvidos P3
 Exercícios resolvidos P3 Questão 1 Calcule a área da superfície obtida pela revolução da curva α(t) (R cos t,, R sin t + a), t [, 2π], < R < a, em torno do eixo x. Esta superfície é chamada de Toro. Resposta:
Exercícios resolvidos P3 Questão 1 Calcule a área da superfície obtida pela revolução da curva α(t) (R cos t,, R sin t + a), t [, 2π], < R < a, em torno do eixo x. Esta superfície é chamada de Toro. Resposta:
Variável Complexa
 Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano
 Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
LOQ Fenômenos de Transporte I
 LOQ 4083 - Fenômenos de Transporte I FT I 07 Equações básicas na forma integral para o volume de controle Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas
LOQ 4083 - Fenômenos de Transporte I FT I 07 Equações básicas na forma integral para o volume de controle Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
x 2 (2 x) 2 + z 2 = 1 4x + z 2 = 5 x = 5 z2 4 Como y = 2 x, vem que y = 3+z2
 Turma A Questão 1: (a Calcule Instituto de Matemática e Estatística da USP MAT55 - Cálculo Diferencial e Integral III para Engenharia a. Prova - 1o. Semestre 15-19/5/15 e z dx + xz dy + zy dz sendo a curva
Turma A Questão 1: (a Calcule Instituto de Matemática e Estatística da USP MAT55 - Cálculo Diferencial e Integral III para Engenharia a. Prova - 1o. Semestre 15-19/5/15 e z dx + xz dy + zy dz sendo a curva
AMIII - Exercícios Resolvidos Sobre Formas Diferenciais e o Teorema de Stokes
 AIII - Exercícios Resolvidos obre Formas Diferenciais e o Teorema de tokes 4 de Dezembro de. eja a superfície Calcule: a) A área de ; b) O centróide de ; { x, y, z) R 3 : z cosh x, x
AIII - Exercícios Resolvidos obre Formas Diferenciais e o Teorema de tokes 4 de Dezembro de. eja a superfície Calcule: a) A área de ; b) O centróide de ; { x, y, z) R 3 : z cosh x, x
Análise Matemática IV Problemas para as Aulas Práticas
 Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
x = u y = v z = 3u 2 + 3v 2 Calculando o módulo do produto vetorial σ u σ v : 9u 2 + 9v 2
 MAT 255 - Cálculo Diferencial e Integral para Engenharia III a. Prova - 22/6/21 - Escola Politécnica Questão 1. a valor: 2, Determine a massa da parte da superfície z 2 x 2 + y 2 que satisfaz z e x 2 +
MAT 255 - Cálculo Diferencial e Integral para Engenharia III a. Prova - 22/6/21 - Escola Politécnica Questão 1. a valor: 2, Determine a massa da parte da superfície z 2 x 2 + y 2 que satisfaz z e x 2 +
META: Introduzir o conceito de integração de funções de variáveis complexas.
 Integrção omplex AULA 7 META: Introduzir o conceito de integrção de funções de vriáveis complexs. OBJETIVOS: Ao fim d ul os lunos deverão ser cpzes de: Definir integrl de um função complex. lculr integrl
Integrção omplex AULA 7 META: Introduzir o conceito de integrção de funções de vriáveis complexs. OBJETIVOS: Ao fim d ul os lunos deverão ser cpzes de: Definir integrl de um função complex. lculr integrl
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES. (UFG) RESUMO
 A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES Fernando Ricardo Moreira 1, Esdras Teixeira Costa 2, Marcio Koetz 3, Samanta Andressa Santos Dumke Teixeira 4, Henrique Bernardes da Silva 5 1 Professor Mestre
A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES Fernando Ricardo Moreira 1, Esdras Teixeira Costa 2, Marcio Koetz 3, Samanta Andressa Santos Dumke Teixeira 4, Henrique Bernardes da Silva 5 1 Professor Mestre
Introdução às superfícies de Riemann
 Introdução às superfícies de Riemann Sylvain Bonnot Fevereiro 2015 Nessa primeira aula vamos apresentar o conteúdo do curso, os principais resultados e as definições basicas com primeiros examplos de superfícies
Introdução às superfícies de Riemann Sylvain Bonnot Fevereiro 2015 Nessa primeira aula vamos apresentar o conteúdo do curso, os principais resultados e as definições basicas com primeiros examplos de superfícies
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
DERIVADAS PARCIAIS. y = lim
 DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
Eletromagnetismo I. Prof. Daniel Orquiza. Eletromagnetismo I. Prof. Daniel Orquiza de Carvalho
 Eletromagnetismo I Prof. Daniel Orquiza Eletromagnetismo I Prof. Daniel Orquiza de Carvalo Equação de Laplace (Capítulo 6 Páginas 160 a 172) Eq. de Laplace Solução numérica da Eq. de Laplace Eletromagnetismo
Eletromagnetismo I Prof. Daniel Orquiza Eletromagnetismo I Prof. Daniel Orquiza de Carvalo Equação de Laplace (Capítulo 6 Páginas 160 a 172) Eq. de Laplace Solução numérica da Eq. de Laplace Eletromagnetismo
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO:
 Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
Professor: Edney Melo ALUNO(A): Nº TURMA: TURNO: DATA: / / COLÉGIO: 1. Cálculo Diferencial Em vários ramos da ciência, é necessário algumas vezes utilizar as ferramentas básicas do cálculo, inventadas
LISTA DE EXERCÍCIOS SOBRE TEOREMA DE GREEN, FLUXO (CONT.), DIVERGÊNCIA E ROTACIONAL DE UM CAMPO ESPAÇO, LAPLACIANO, FUNÇÕES HARMÔNICAS (CONT)
 LISTA DE EXEÍIOS SOBE TEOEMA DE GEEN, FLUXO (ONT.), DIVEGÊNIA E OTAIONAL DE UM AMPO ESPAÇO, LAPLAIANO, FUNÇÕES HAMÔNIAS (ONT) POFESSO: IADO SÁ EAP () Sejam F (x, y, ) e G(x, y, ) campos vetoriais definidos
LISTA DE EXEÍIOS SOBE TEOEMA DE GEEN, FLUXO (ONT.), DIVEGÊNIA E OTAIONAL DE UM AMPO ESPAÇO, LAPLAIANO, FUNÇÕES HAMÔNIAS (ONT) POFESSO: IADO SÁ EAP () Sejam F (x, y, ) e G(x, y, ) campos vetoriais definidos
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2012/13
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 212/13 Exame de 2ª época, 2 de Fevereiro de 213 Nome : Hora : 8: Número: Duração : 3 horas 1ª Parte : Sem consulta 2ª Parte : Consulta
Processamento de Malhas Poligonais
 Processamento de Malhas Poligonais Tópicos Avançados em Computação Visual e Interfaces I Prof.: Marcos Lage www.ic.uff.br/~mlage mlage@ic.uff.br Conteúdo: Notas de Aula Curvas 06/09/2015 Processamento
Processamento de Malhas Poligonais Tópicos Avançados em Computação Visual e Interfaces I Prof.: Marcos Lage www.ic.uff.br/~mlage mlage@ic.uff.br Conteúdo: Notas de Aula Curvas 06/09/2015 Processamento
Revisão do Teorema de Green
 Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então
 Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Integrais Sobre Caminhos e Superfícies. Teoremas de Integração do Cálculo Vectorial.
 Capítulo 5 Integrais Sobre Caminhos e Superfícies. Teoremas de Integração do Cálculo Vectorial. 5.1 Integral de Um Caminho. Integral de Linha. Exercício 5.1.1 Seja f(x, y, z) = y e c(t) = t k, 0 t 1. Mostre
Capítulo 5 Integrais Sobre Caminhos e Superfícies. Teoremas de Integração do Cálculo Vectorial. 5.1 Integral de Um Caminho. Integral de Linha. Exercício 5.1.1 Seja f(x, y, z) = y e c(t) = t k, 0 t 1. Mostre
1 Primeira lista de exercícios
 1 Primeira lista de exercícios Números complexos, derivadas e integrais. 1. Ache todos os valores das seguintes raízes: (a) (2i) 1=2 (b) ( i) 1=3 (c) 8 1=6 2. Descreva geometricamente cada uma das regiões
1 Primeira lista de exercícios Números complexos, derivadas e integrais. 1. Ache todos os valores das seguintes raízes: (a) (2i) 1=2 (b) ( i) 1=3 (c) 8 1=6 2. Descreva geometricamente cada uma das regiões
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
1 Números Complexos e Plano Complexo
 UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
Análise Complexa e Equações Diferenciais
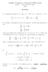 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Exercícios de revisão
 Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
Cálculo Diferencial e Integral de Campos Vetoriais
 Capítulo 1 Cálculo Diferencial e Integral de Campos Vetoriais Conteúdo 1.1 Breve Interlúdio........................... 8 1.2 Noções básicas de campo escalar e vetorial........... 9 1.3 Divergência de um
Capítulo 1 Cálculo Diferencial e Integral de Campos Vetoriais Conteúdo 1.1 Breve Interlúdio........................... 8 1.2 Noções básicas de campo escalar e vetorial........... 9 1.3 Divergência de um
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
