Introdução às superfícies de Riemann
|
|
|
- Edite Moreira Salgado
- 6 Há anos
- Visualizações:
Transcrição
1 Introdução às superfícies de Riemann Sylvain Bonnot Fevereiro 2015 Nessa primeira aula vamos apresentar o conteúdo do curso, os principais resultados e as definições basicas com primeiros examplos de superfícies de Riemann. Algumas informações necessárias: Meu sylvain@ime.usp.br Endereço do meu site: Superfícies de Riemann Seja X um espaço topológico separado. X é uma superfície topológica se todo ponto de X tem uma vizinhança homeomorfa a um aberto de R 2. Seja n N. Uma carta holomorfa de X é um homeomorfismo ϕ de um aberto U (chamado o domínio da carta ϕ) de X sobre um aberto de C n. Sejam ϕ e ψ duas cartas de X de domínios respectivos U e V. Então γ := ψ ϕ 1 é um homeomorfismo do aberto ϕ(u V) até ψ(u V), chamado função de transição. Figura 1: Um espaço que não é separado: a linha com duas origens é obtido com a colagem de duas copias de R ao longo de R {0}. Definição 1. Um atlas holomorfo no espaço topológico X é uma familia (ϕ i ) i I de cartas holomorfas com domínios U i tal que: (a) As cartas cobram X: isto é X = i U i (b) As funções de transições ϕ ij são holomorfas, onde ϕ ij = ϕ i ϕ 1 j : ϕ j (U i U j ) ϕ i (U i U j ). Uma variedade complexa é um espaço topológico X, Hausdorff 1 e com base enumerável, equipado com um atlas holomorfo maximal. O número n é chamado de dimensão complexa de X. Porque pedir uma base enumerável? Simplesmente para poder utilizar partições diferenciáveis da unidade: Teorema. Uma variedade diferenciável M possui uma partição diferenciável da unidade se e só se toda componente conexa de M é de Hausdorff e tem base enumerável. Lembra que uma partição diferenciável da unidade é uma família ( f i ) i I de funções diferenciáveis f i : X R tal que: 1. Para todo i I, f i 0 e o suporte Supp( f i ) é contido no domínio U i de uma carta diferenciável de X; 2 Figura 2: Função de transição ψ ϕ 1 : ϕ(u V) ψ(u V). 1 Lembra que um espaço separado é também chamado "espaço de Hausdorff". 2 Uma família de abertos (U i ) i I tal que X = i I U i é localmente finita se todo ponto p X possui uma vizinhança V tal que V U i = apenas para um número finito de indíces.
2 introdução às superfícies de riemann 2 2. A família (U i ) i I é localmente finita; 3. i I f i (p) = 1 para todo p X. 3 3 Essa soma tem um número finito de termos diferentes de 0. A esfera de Riemann O primeiro examplo de superfície de Riemann é a esfera de Riemann. No espaço R 3 com coordenadas (x, y, t) podemos considerar a esfera unitária S 2, x 2 + y 2 + t 2 = 1. Seja N = (0, 0, 1) o polo Norte da esfera e S = (0, 0, 1) o polo Sul. A projeção estereográfica associada à N associa a cada ponto M S 2 N a interseção da reta (NM) com o plano t = 0. A coordenada complexa deste ponto é z = x + iy 1 t. Assim a aplicação (x, y, t) z é um homeomorfismo de S 2 N sobre C, isto é uma carta holomorfa. Podemos também definir uma outra carta holomorfa S 2 S sobre C: a composta da projeção estereográfica associada a S com depois a conjugação complexa (i.e z z). O resultado é w = x iy 1 + u. Uma observação importante é que z.w = 1. A esfera S 2 com este atlas holomorfo é chamada esfera de Riemann, denotada por Ĉ. Funções holomorfas em Ĉ. Seja U Ĉ um conjunto aberto. Uma função f é holomorfa em U se: para todo ponto M = N f pode ser escrita numa vizinhança de M distinta de N como uma função holomorfa em z, e para todo ponto M = S, f pode ser escrita numa vizinhança de M distinta de S como uma função de w. Para um aberto U Ĉ {N, S}, uma função holomorfa em z é também holomorfa em w (lembra da relação: z.w = 1). A esfera de Riemann pode ser vista como uma compactificação 4 do plano complexo C, i.e como o resultado de acrescentar um ponto no plano. Conjuntos do tipo U = {z C; z > R} { } formam uma base de vizinhanças de, e uma função f definida em U é holomorfa perto de se e somente se Figura 3: Projeção estereográfica associada à N. 4 Um mergulho f : X Y com imagem densa e Y compactificação X de um espaço topológico X é um mergulho tal que f (X) é denso em X. é holomorfa perto de w = 0. w 1 f (1/w)
3 introdução às superfícies de riemann 3 Extensão de um polinômio complexo na esfera de Riemann. Seja P : C C um polinômio complexo. Então P tem uma extensão P : Ĉ Ĉ na esfera de Riemann, dada por P : (isto é, o infinito é u ponto fixo de P). Para simplificar, o seguinte lema considera somente um polinômio de grau 2. Lema 1. Seja P c : C C um polinômio quadrático dado pela formula P c (z) = z 2 + c. Então existe uma extensão P c : Ĉ Ĉ de P c na esfera de Riemann Ĉ tal que o ponto Ĉ é um super-atrator. Demonstração. A mudança de variável w = 1 z manda até 0: Um ponto fixo x 0 de uma aplicação holomorfa definida perto de x 0 é um super-atrator se f (x 0 ) = 0. w z = w 1 w cw 2 z2 + c = 1 w 2 + c Com essa nova variável, a aplicação é agora dada por : w w2 1 + cw 2 = w2 (1 cw ) = w 2 cw Nessa expansão não tem um termo de grau 1, então w = 0 é um super-atrator. Agora é fácil ver que a bacia do ponto contem um disco aberto D(, R) de raio R > 0: Lema 2. Seja P(z) = z d + a d 2 z d a 0. Então existe um R > 0 tal que z > R = z n. Demonstração. Simplesmente temos que P(z) = z d ( 1 + a d 2 z a 0 z d ), então P(z) z d. 1 2 > K. z para um K > 1 e z grande. Por indução temos P n (z) K n. z e o resultado é uma consequência imediata. A condição a d 1 = 0 pode ser sempre obtida depois de uma conjugação com uma função linear. Figura 4: Polinômio na esfera de Riemann, com a bacia de atração do infinito em cinza. Teorema 1. Seja P(z) um polinômio de grau k 2. Então para R suficientemente grande, existe uma aplicação φ : { z > R} C, biholomorfa de V := { z > R} até φ(v) tal que φ(p(z)) = (φ(z)) k. Essa aplicação é única a menos de uma multiplicação por uma raiz (k 1) ésima da unidade.
4 introdução às superfícies de riemann 4 Demonstração. É facil ver que para R grande temos que P(V) V e que ψ(z) := log P(z) é bem definida e limitada em V. Podemos então z k escrever P(z) como P(z) = z k. exp ψ(z). Por indução temos que ( ) P n (z) = z kn. exp k n 1 ψ(z) ψ(p n 1 (z)). Assim podemos definir um ramo de kn P n (z), simplesmente como ( 1 φ n (z) := z. exp k ψ(z) ) k n ψ(pn 1 (z)). Agora ψ é limitada em V então j=1 1 k j ψ(p j 1 (z)) converge uniformemente em V, então φ n também converge uniformemente para um limite φ analítica em V. A equação funcional φ P = φ k é consequência da seguinte equação, fácil de verificar: φ n (P(z)) = (φ n+1 (z)) k. Essa nova coordenada w = φ(z) é chamada coordenada de Böttcher perto do infinito, e é fundamental no assunto da dinâmica holomorfa. Funções meromorfas Definição 2. Uma função meromorfa numa variedade complexa X é uma função f : X Ĉ holomorfa. Funções meromorfas na esfera de Riemann Teorema 2. Cada função meromorfa na esfera de Riemann é uma fração racional. Demonstração. Seja f uma função meromorfa em Ĉ. Podemos supor que não é um pólo de f (se não, podemos considerar 1 f ).Assim, f é limitada perto do infinito.para cada pólo finito a = de f podemos escrever localmente A expressão k=1 N f (z) = N k=1 c k + h(z), com h holomorfa perto de a. (z a) k c k (z a) é chamada a k parte polar de f no pólo finito a. Sejam a 1,... a n os pólos de f, então a função g = f (partes polares) é holomorfa em C e limitada, então é constante (teorema de Liouville). Lembra que f é limitada perto do infinito,num disco D(, r).
5 introdução às superfícies de riemann 5 Automorfismos de Ĉ Teorema 3. Cada automorfismo de Ĉ é uma função de Möbius z com ad bc = 0. az+b cz+d Demonstração. O automorfismo f pode ser escrito como f = Q P (P e Q sem raiz comum). Agora P não tem mais de um zero (simples), então P é de grau 0 ou 1. O mesmo é verdadeiro para Q. Assim f pode ser escrito como cz+d az+b. Necessariamente, ad bc = 0 (se não f é constante). Proposição 1. Seja X ume superfície de Riemann. Então o conjunto M(X) das funções meromorfas em X é um corpo. Funções analíticas entre superfícies de Riemann Uma função f meromorfa, diferente de zero, tem zeros que são isolados, então 1/ f é meromorfa também. Lema de Weyl O problema de Dirichlet Definição 3. Seja U C um aberto, uma função u : U R é dita harmônica se: u é de classe C 2 e u = 0, onde = x 2 y 2 Definição 4. Seja U C um aberto, uma função u : U R é dita harmônica se: para todo disco D(z, r) U, u(z) = 2π 1 2π 0 u(z + re iθ )dθ. Lema 3. Se u : D R é harmônica num disco D C, então existe uma função holomorfa f : D C tal que u = Re( f ). Demonstração. Queremos uma função v tal que u + iv : D C seja holomorfa, i.e queremos: v x = u v e também y y = u x (equações de Cauchy-Riemann). Utilizando a fórmula de Stokes, a forma diferencial Pdx + Qdy é exata (i.e = d f ) se isto é: ( u ) y y P y = Q x, = ( ) u x x, mas isso é uma consequência imediata de u = 0.
6 introdução às superfícies de riemann 6 Lema 4. Seja u : U R uma função definida num aberto U de C e tal que para todo z U, existe um disco D(z, r) U e uma função holomorfa f com u = Re f. Então u é harmônica em U. Demonstração. Consequência imediata das equações de Cauchy- Riemann: u = 2 u x u y 2 = ( ) v + ( v ) = 0. x y y x E facil ver que uma função harmônica tem que ser de classe C. Proposição 2. Seja u : U aberto R harmônica, com D(z, r) U, então: Se u = Re( f ), com f holomorfa, já sabemos que f é C e então u também. u(z) = 1 2π u(z + re iθ )dθ. 2π 0 Demonstração. Num disco maior D(z, s) U, s > r, a função u pode ser escrita como u = Re f onde f = u + iv é holomorfa. A fórmula de Cauchy implica: (u + iv)(z) = f (z) = 1 2πi D(z,r) f (ζ ζ z dζ = 1 2π 2πi 0 Tomando as partes reais dessa equação dá o resultado. Princípio do máximo para funções analíticas e harmônicas f (z + re iθ ) z + re iθ z ireiθ dθ. Teorema 4 (Comportamento local das aplicações holomorfas). Sejam X e X duas superfícies de Riemann e f : X X uma aplicação holomorfa não constante. Seja a X e a = f (a). Então existe um inteiro k 1 que depende de a e duas cartas holomorfas φ : U V em X e φ : U V em Y tais que: 1. a U com φ(a) = 0 e a U com φ (a ) = 0; 2. f (U) U e o seguinte diagrama comuta: U X V f U X z z k V 3. φ f φ(z) = z k, para cada z V. Uma consequência imediata é que as funções holomorfas são abertas. Também f holomorfa satisfaz o príncipio do máximo: se f é holomorfa, não constante num aberto conexo U, então f não tem um máximo em U. Lembra que f é aberta significa f (aberto) = aberto.
7 introdução às superfícies de riemann 7 Proposição 3. Uma função harmônica u satisfaz o príncipio do máximo: num aberto conexo, ou u é constante, ou u não tem um máximo. Demonstração. u harmônica = localmente u = Re( f ), f holomorfa. Suponhamos que u tem um máximo em z 0 e u não constante. Então f é aberta e existe z perto de z 0 tal que Re f (z) > Re f (z 0 ), uma contradição. Núcleo de Poisson Sejam ζ, z C, então o núcleo de Poisson no disco D de raio 1 é P(z, ζ) := ζ 2 z 2 ( ) ζ + z z ζ 2 = Re. ζ z A seguinte observação (consequência do teorema do resíduo)vai ser útil : 1 2π ( ) 1 P(e iθ ζ + z dζ, z)dθ = Re = 1. 2π 0 2πi ζ =1 ζ z ζ Seja f (θ), θ R uma função contínua 2π-périodica. O problema de Dirichlet para o disco D(0, r) é de encontrar uma função F contínua no disco fechado D(0, r), harmônica no disco aberto z < r e tal que no bordo: F(re iθ ) = f (θ). Teorema 5. O problema de Dirichlet para um disco possui uma única solução. Demonstração. Unicidade da solução. Sejam u 1 e u 2 duas soluções. Então u 1 u 2 é contínua no disco fechado, harmônica no interior e zero no bordo. O princípio do máximo mostra que u 1 u 2 tem que ser zero no disco inteiro. Existência da solução. Para cada z < r, seja F(z) = 1 2π f (θ)p(re iθ, z)dθ. 2π 0 Vamos mostrar que F é harmônica e que f (θ) = lim F(z). z reiθ F é harmônica, porque ela é a parte real da seguinte função holomorfa em z < r: 1 2π f (θ) reiθ + z 2π 0 re iθ z dθ. Para ver que essa função é holomorfa, podemos derivar a função sob o sinal de integral.
8 introdução às superfícies de riemann 8 Lema 5. A integral I := 1 r 2 z 2 2π θ θ 0 >η re iθ z 2 dθ converge para 0 quando z re iθ 0 com z < r. Demonstração do lema. Seja z = ρe iα. Se α θ 0 η 2, temos α θ η 2 para todo θ tal que θ θ 0 η 2. Isso implica re iθ z rsen η 2, e então a integral I é menor que r2 ρ 2 quando ρ r. r 2 sen 2 η 2 que converge para zero Agora vamos mostrar Podemos escrever F(z) f (θ 0 ) = 1 2π + 1 2π lim F(z) = f (θ 0 ). z re iθ 0 z <r θ θ 0 η θ θ 0 >η ( f (θ) f (θ 0 )) r2 z 2 re iθ z 2 dθ ( f (θ) f (θ 0 )) r2 z 2 re iθ z 2 dθ Seja ɛ > 0. A primeira integral é menor que sup θ θ0 η f (θ) f (θ 0 ). A continuidade de f implica que podemos escolher η tal que a primeira integral seja menor que 2 ɛ. Com essa escolha de η, um majorante da segunda integral é 2. sup f (θ). 1 r 2 z 2 θ R 2π θ θ 0 >η re iθ z 2 dθ 0, quando z reiθ 0, Lembra que 1 2π r 2 z 2 2π 0 re iθ z 2 dθ = 1 isto é, para z suficientemente perto de re iθ 0, essa segunda integral será ɛ 2 e então F(z) f (θ 0 ) ɛ, que mostra o resultado. Sequências de funções harmônicas e convergência Proposição 4. Seja u n : D(0, R) R, n N uma sequência de funções harmônicas que converge uniformemente sobre compactos para uma função u : D(0, R) R. Então u é harmônica também.
9 introdução às superfícies de riemann 9 Demonstração. Para todo r < R, no disco z < r temos u n (z) = 1 2π P(z, re iθ )u n (re iθ )dθ. 2π 0 Pela convergência uniforme de u n no bordo D(0, r) temos que a mesma fórmula fica valida para u, mas isso significa que u é harmônica. Teorema 6. Seja M R e u 0 u 1... M uma sequência de funções harmônicas u n : D(0, R) R. Então essa sequência converge uniformemente sobre compactos para uma função harmônica u : D(0, R) R. Demonstração. Seja K um compacto de D(0, R). Então existe ρ < r < R tais que K { z ρ}. Dado ɛ > 0, seja ɛ := ɛ r ρ r+ρ. A sequência u n (0) é crescente e limitada então existe N tal que n m N = u n (0) u m (0) ɛ. Agora podemos observar que para z ρ temos 0 P(z, re iθ ) r + z r z r + ρ r ρ, então a aplicação da fórmula de Poisson para a função u n u m dá, para todo z K: u n (z) u m (z) = 1 2π P(r, e iθ )(u n (re iθ ) u m (re iθ ))dθ 2π 0 r + ρ 1 2π (u n (re iθ ) u m (re iθ ))dθ r ρ 2π 0 r + ρ r ρ (u n(0) u m (0)) ɛ. Assim, a sequência (u n ) n N converge uniformemente sobre K e o limite é uma função harmônica. Funções subharmônicas Definição 5. Seja X uma superfície de Riemann. Uma função contínua u : X R é subharmônica se para todo domínio D de X e toda função v : D R harmônica, a diferença u v é constante, ou sem máximo. Isto é uma conseqüência da proposição sobre a convergência uniforme das funções harmônicas. Um domínio é um aberto conexo de X
10 introdução às superfícies de riemann 10 Modificação harmônica. Seja D um disco analítico de X (i.e a preimagem φ 1 (D) de um disco D C por uma carta holomorfa φ). Para cada função contínua u : X R podemos definir a modificação harmônica em D de u como a única função u D contínua em X, igual a u em X D e harmônica em D. Proposição 5. Seja u : X R contínua. As seguintes proposições são equivalentes: 1. u é sub-harmônica. 2. para todo disco analítico D, u u D. 3. para todo disco analítico D, u 1 2π D u. Demonstração. 1 = 2 A função u u D é zero em X D e subharmônica em D, então ela é ou constante (e essa constante só pode ser zero) ou sem máximo em D (mas isso implica que a função é 0). 2 = 3 Temos u(0) u D (0) que é a média de u D no bordo do disco, mas essa média é também a média de u no bordo do disco (porque u = u D em D). 3 = 1 Seja v harmônica num domínio D tal que u v tem um máximo M em D. O conjunto D M := {P D; u(p) v(p) = M} é fechado, não vazio. E suficiente mostrar que ele é aberto também para concluir, porque D é conexo. Seja P D M e D r D um disco analítico com centro em P, então M = (u v)(p) média de (u v) no bordo M, então u v = M no bordo (e então numa vizinhança de P). Aqui podemos mudar o valor de r > 0. Proposição 6 (Perron). Seja F uma família = de funções subharmônicas em X tal que a) para cada disco analítico D, u F = u D F, b) se u, v F, então existe w F tal que w max(u, v) em X. Então, se a função u := sup F u é finita em cada ponto, ela é harmônica. Demonstração. Podemos trabalhar localmente num disco analítico D. Seja x 0 D. Podemos escrever u (x 0 ) = lim u n (x 0 ) com u n F. Também podemos supor que a sequência u n é crescente (se não, max i n u i ) e que as funções u n são harmônicas introduzir u n (se não utilizar u n := u n,d ). Nessa situação o teorema de Harnack implica a existência de um limite u harmônica. Vamos mostrar que u = u. Seja x qualquer ponto de D. Da mesma maneira podemos
11 introdução às superfícies de riemann 11 escrever u (x) como um limite lim v n (x) com v n F. Também o teorema de Harnack implica a existência de um limite harmônica v. Podemos também supor v n u n, então u v u. Mas agora u v é harmônica em D, é 0 em D e zero em x 0. O princípio do máximo implica que u v = 0 em D e então u = v = u. O objetivo vai ser agora de obter a solução do problema de Dirichlet geral como um supremo de uma família de funções subharmônicas. Seja Y um aberto de uma superfície de Riemann X e f : Y R uma função contínua limitada. Vamos denotar por F f a família de funções F f := {u : Y R contínua e u sup Y e u f f, sub-harmônica em Y, f em Y}, = sup F f u em Y. Podemos observar que u f é harmônica. A função u f só tem uma extensão contínua até Y se a fronteira Y é suficientemente regular: Definição 6. Um ponto x Y é chamado regular se existe uma vizinhança aberta U de x e uma função β (chamada barreira) contínua em Y U e tal que: 1. β é sub-harmônica em Y U, 2. β(x) = 0 e β(y) < 0 para todo y (Y U) {x}. A existência de uma barreira num ponto x é um problema local. Nos precisamos um critério simples para definir barreiras: Teorema 7. Seja Y um aberto de C e a Y. Suponhamos que tem um disco D := {z C; z m < r}, onde m C, r > 0, tal que a D e D Y =. Então a é um ponto regular do bordo de Y. Demonstração. Podemos escolher c = (a + m)/2. Então, β(z) := log r log z c 2 defina uma barreira no ponto a. Isto é, a é um ponto regular. Figura 5: A condição do "disco exterior"para existência de barreira. Lema 6. Sejam m, c R tais que m c. Seja x Y um ponto regular e V uma vizinhança de x. Então existe uma função v : Y R contínua com as seguintes propriedades: (i) a restrição v Y é sub-harmônica, (ii) v(x) = c, e a restrição de v em Y V é c, (iii) a restrição de v em Y V é = m.
12 introdução às superfícies de riemann 12 Demonstração. Podemos supor c = 0. Seja U uma vizinhança aberta de x e β : Y U R uma barreira em x. Podemos reduzir V e supor que o fecho V seja um compacto de U. Então sup{β(y); y V Y} < 0. Então existe uma constante k > 0 tal que A função β é < 0 no compacto V Y. kβ V Y < m. Vamos definir agora max(m, kβ) em Y V v := m em Y V. Então essa função v é contínua em Y e sub-harmônica em Y e satisfaz as condições (ii) e (iii). O seguinte lema mostra porque pontos regulares são importantes: Lema 7. Seja f contínua e limitada no bordo de um aberto Y de X.Se x é regular, então lim y x u f (y) = f (x). Demonstração. A função f é contínua e limitada em Y, então k f (x) K. Seja ɛ > 0 e x Y. A continuidade de f implica f (x) ɛ f (y) f (x) + ɛ, para todo y Y V, onde V é uma vizinhança de x.podemos aplicar o lema com m = k ɛ, c = f (x) ɛ e obter assim uma função v F tal que: 1. v é sub-harmônica, 2. v(x) = f (x) ɛ e v f (x) ɛ em Y V, 3. v é igual a k ɛ em Y V. Em particular v F f (e então v u f ). Isso implica lim inf u f (y) v(x) = f (x) ɛ. y x Da mesma maneira, utilizando o mesmo lema podemos encontrar Seja Y X e a Y então lim inf y x := lim ɛ 0 (inf{ f (t) : t Y D(x, ɛ) {x}}). uma função contínua w : Y R, sub-harmônica em Y e tal que: 5 5 Aplicar o lema com K = m c = 1. w(x) = f (x) f (x) 2. w Y V f (x)
13 introdução às superfícies de riemann w Y V = K. Para qualquer função u F f e y Y V temos que u(y) f (x) + ɛ. Então u(y) + w(y) ɛ para todo y Y V. Também temos u(z) + w(z) K K = 0 para todo z Y V. Agora a função u + w é sub-harmônica em Y V então podemos aplicar o principio do máximo e obter u + w ɛ em Y V. Assim para qualquer função u F f temos e isso implica u Y V ɛ w Y V, lim sup u f (y) ɛ w(x) = f (x) + ɛ. y x y Y A demonstração acima utilizou Lema 8. Seja u : D R uma função contínua e sub-harmônica que tem um máximo no domínio D, então u é constante. Demonstração. Seja S := sup(u(z); z D) e A = u 1 (S). A é fechado (porque u é contínua). Vamos mostrar que A é aberto também. Seja z 0 A e φ : U V uma carta holomorfa com φ(z 0 ) = 0. Então v = u φ 1 : V R é contínua, sub-harmônica com um máximo S no ponto 0. Seja r > 0 tal que D(0, r) {z; z r} V: Assim, como o domínio é conexo, A aberto e fechado = A = ou A = D. S = v(0) 1 2π v(re iθ dθ 1 2π Sdθ = S. 2π 0 2π 0 Isso implica, pela continuidade de v, que v(re iθ ) = S para todo θ. Assim v é constante numa vizinhança de 0. O seguinte teorema é agora uma conseqüência imediata. Teorema 8. Seja Y um aberto de uma superfície de Riemann X tal que todos os pontos de Y sejam regulares. Então para cada função contínua limitada f : Y R o problema de Dirichlet pode ser resolvido.
14 introdução às superfícies de riemann 14 Funções de Green e superfícies hiperbólicas Definição 7. Uma superfície de Riemann X é dita elíptica se ela é compacta, hiperbólica se existe uma função u < 0 sub-harmônica e não constante em X, e parabólica nos outros casos. Lema 9. Seja X uma superfície de Riemann hiperbólica, D um domínio com bordo regular em X, com complemento K compacto não vazio. Então existe uma função contínua ω : D R tal que Observe que uma superfície elíptica não pode ser compacta por causa do principio do máximo. 1. ω = 1 em D; 2. ω é harmônica e satisfaz 0 < ω < 1. Demonstração. X é hiperbólica então existe u > 0 super-harmônica não constante em X. Podemos supor min K u = 1. A função u não tem um minimo em X então existe P D tal que u(p) < 1. Podemos trocar u com min(1, u) e assim supor u = 1 em K. Seja Figura 6: A função harmônica ω. u super-harmônica u subharmônica F := {v contínua em D, sub-harmônica e u em D}. Então F é uma família de Perron. 6 Isso significa que ω := sup F v é harmônica. Vamos mostrar que essa função ω é a solução do problema. Seja então K D X um domínio com bordo regular e com fecho compacto. Seja v uma solução do problema de Dirichlet tal que 1 em K v := 0 em D 6 Para todo disco e v F então u v = u v 0 em e subharmônica então v F. estendida por zero fora de D. Então v u é sub-harmônica e 0 fora de D então também 0 em D (o máximo dela acontece no bordo). Assim, v F e isso implica v ω u. Agora ω é contínua em D, 0 ω 1 em D, ω 1 em K, ω não é constante (porque ω(p) < 1) então não tem máximo nem mínimo em D: isso implica 0 < ω < 1 em D. Definição 8. Uma função de Green num ponto P de X é uma função g harmônica e > 0 em X {P} tal que g(z) + log z seja harmônica perto de P numa carta holomorfa z em P,e minimal (no sentido que g g para outra função candidata). Em particular se g existe, ela é única. Teorema 9. X é hiperbólica se e somente se existe uma função de Green num ponto (ou em qualquer ponto) de X.
Funções analíticas LISTA DE EXERCÍCIOS
 LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
Introdução às superfícies de Riemann
 LISTA DE EXERCÍCIOS Introdução às superfícies de Riemann 1. Mostre que toda curva plana é uma superfície de Riemann não-compacta. 2. Seja F : C 3 C um polinômio homogêneo de grau d, isto é, cada monômio
LISTA DE EXERCÍCIOS Introdução às superfícies de Riemann 1. Mostre que toda curva plana é uma superfície de Riemann não-compacta. 2. Seja F : C 3 C um polinômio homogêneo de grau d, isto é, cada monômio
Fichas de Análise Matemática III
 Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Exercícios de revisão
 Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
MAT Cálculo Avançado - Notas de Aula
 bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Séries de Laurent e Teoremas de Cauchy
 Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor
 Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor Roberto Imbuzeiro Oliveira 6 de Abril de 20 Preliminares Nestas notas, U C sempre será um aberto e f : U C é contínua. Duas curvas
Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor Roberto Imbuzeiro Oliveira 6 de Abril de 20 Preliminares Nestas notas, U C sempre será um aberto e f : U C é contínua. Duas curvas
PROVAS DE ANÁLISE COMPLEXA
 PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
SUMÁRIO CAPÍTULO 1 CAPÍTULO 2
 SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
MAT ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS
 MAT 5818 - ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS 1) Mostre que M n (C) munida da norma ((a jk )) 1 j,k n = k=1 2) Defina na álgebra C[X] dos polinômios complexos na variável X a
MAT 5818 - ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS 1) Mostre que M n (C) munida da norma ((a jk )) 1 j,k n = k=1 2) Defina na álgebra C[X] dos polinômios complexos na variável X a
Variedades diferenciáveis e grupos de Lie
 LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
Análise Complexa e Equações Diferenciais 2 ō Semestre 2009/2010
 Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Análise Complexa e Equações Diferenciais 1 o Semestre de 2011/ o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2011, 10h,
 Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
ACED Análise Complexa e Equações Diferenciais. 17 a Aula Teorema de Cauchy. Michael Paluch 1 o Semestre 2018/2019
 ACED Análise Complexa e Equações Diferenciais MEC Michael Paluch 1 o Semestre 2018/2019 17 a Aula 17.1 Teorema de Cauchy Recordamos que a imagem de um caminho seccionalmente de classe C 1 chamase uma curva
ACED Análise Complexa e Equações Diferenciais MEC Michael Paluch 1 o Semestre 2018/2019 17 a Aula 17.1 Teorema de Cauchy Recordamos que a imagem de um caminho seccionalmente de classe C 1 chamase uma curva
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
LISTA DE EXERCÍCIOS SOBRE TEOREMA DE GREEN, FLUXO (CONT.), DIVERGÊNCIA E ROTACIONAL DE UM CAMPO ESPAÇO, LAPLACIANO, FUNÇÕES HARMÔNICAS (CONT)
 LISTA DE EXEÍIOS SOBE TEOEMA DE GEEN, FLUXO (ONT.), DIVEGÊNIA E OTAIONAL DE UM AMPO ESPAÇO, LAPLAIANO, FUNÇÕES HAMÔNIAS (ONT) POFESSO: IADO SÁ EAP () Sejam F (x, y, ) e G(x, y, ) campos vetoriais definidos
LISTA DE EXEÍIOS SOBE TEOEMA DE GEEN, FLUXO (ONT.), DIVEGÊNIA E OTAIONAL DE UM AMPO ESPAÇO, LAPLAIANO, FUNÇÕES HAMÔNIAS (ONT) POFESSO: IADO SÁ EAP () Sejam F (x, y, ) e G(x, y, ) campos vetoriais definidos
3 ā Prova de MAT Cálculo IV - IFUSP 2 ō semestre de /12/2009 Prof. Oswaldo Rio Branco de Oliveira
 3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
Minicurso Colóquio de Matemática da Região Norte 2014
 Minicurso Colóquio de Matemática da Região Norte 2014 Comitê Científico Flávia Morgana de O. Jacinto (UFAM) - Coordenadora Hugo Alex Carneiro Diniz (UFOPA) Jorge Herbert Soares de Lira (UFC) Marcelo Miranda
Minicurso Colóquio de Matemática da Região Norte 2014 Comitê Científico Flávia Morgana de O. Jacinto (UFAM) - Coordenadora Hugo Alex Carneiro Diniz (UFOPA) Jorge Herbert Soares de Lira (UFC) Marcelo Miranda
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n
 Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos
 MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos Prof. Edson de Faria 30 de Março de 2014 Observação: O objetivo desta lista é motivar uma revisão dos conceitos e fatos básicos sobre
MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos Prof. Edson de Faria 30 de Março de 2014 Observação: O objetivo desta lista é motivar uma revisão dos conceitos e fatos básicos sobre
MAT 1351 : Cálculo para Funções de Uma Variável Real I. Sylvain Bonnot (IME-USP)
 MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
LISTA 5 DE GEOMETRIA RIEMANNIANA 2007
 LISTA 5 DE GEOMETRIA RIEMANNIANA 2007 RICARDO SA EARP (1) Considere S 3 = {(z 1, z 2 ) C 2 ; z 1 2 + z 2 2 = 1}. seja q um inteiro q > 1. Seja Γ = {1, e 2π1/q,..., e 2π(q 1)/q }, o grupo finito agindo
LISTA 5 DE GEOMETRIA RIEMANNIANA 2007 RICARDO SA EARP (1) Considere S 3 = {(z 1, z 2 ) C 2 ; z 1 2 + z 2 2 = 1}. seja q um inteiro q > 1. Seja Γ = {1, e 2π1/q,..., e 2π(q 1)/q }, o grupo finito agindo
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
1 Aula do dia 08/08/2005
 Inclui até a aula de 17/10/2005 Referências básicas do curso: [1, 3] 1 Aula do dia 08/08/2005 Teorema 1.1 (de Bernstein-Cantor). Sejam X e Y conjuntos. Suponha que existam f : X Y e g : Y X funções injetoras.
Inclui até a aula de 17/10/2005 Referências básicas do curso: [1, 3] 1 Aula do dia 08/08/2005 Teorema 1.1 (de Bernstein-Cantor). Sejam X e Y conjuntos. Suponha que existam f : X Y e g : Y X funções injetoras.
Prova Substitutiva de MAT Cálculo IV - IFUSP 2 ō semestre de /12/2009 Prof. Oswaldo Rio Branco de Oliveira
 Prova Substitutiva de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009-8/2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : GABARITO Q 2 3 4 5 6 7 8 9 0 2 Total N JUSTIFIQUE TODAS AS PASSAGENS
Prova Substitutiva de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009-8/2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : GABARITO Q 2 3 4 5 6 7 8 9 0 2 Total N JUSTIFIQUE TODAS AS PASSAGENS
x B A x X B B A τ x B 3 B 1 B 2
 1. Definição e exemplos. Bases. Dar uma topologia num conjunto X é especificar quais dos subconjuntos de X são abertos: Definição 1.1. Um espaço topológico é um par (X, τ) em que τ é uma colecção de subconjuntos
1. Definição e exemplos. Bases. Dar uma topologia num conjunto X é especificar quais dos subconjuntos de X são abertos: Definição 1.1. Um espaço topológico é um par (X, τ) em que τ é uma colecção de subconjuntos
Revisão do Teorema de Green
 Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
MAT 1351 : Cálculo para Funções de Uma Variável Real I. Sylvain Bonnot (IME-USP)
 MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
13 de novembro de 2007
 13 de novembro de 2007 Objetivos - Definição Subgrupos Axiomas de Separação Bases e Sistema fundamental de vizinhanças para a identidade Euclidianos e o Quinto Problema de Hilbert Objetivos - Medida de
13 de novembro de 2007 Objetivos - Definição Subgrupos Axiomas de Separação Bases e Sistema fundamental de vizinhanças para a identidade Euclidianos e o Quinto Problema de Hilbert Objetivos - Medida de
Análise Complexa e Equações Diferenciais Guia 6 João Pedro Boavida. 19 a 28 de Outubro
 19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
Estrutura complexa do Espaço de Teichmüller
 Estrutura complexa do Espaço de Teichmüller Minoru Akiyama A teoría de Teichmüller estuda as diferentes estruturas conformes que têm uma superfície topológica dada. Específicamente, se S é uma superfície
Estrutura complexa do Espaço de Teichmüller Minoru Akiyama A teoría de Teichmüller estuda as diferentes estruturas conformes que têm uma superfície topológica dada. Específicamente, se S é uma superfície
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
Variável Complexa
 Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Transformada Z. A transformada Z de uma sequência x n é definida como:
 Transformada Z Vimos que as DTFTs de algumas sequências não convergem uniformemente para funções contínuas de ω, porque as sequências não são absolutamente somáveis. A transformada Z permitirá a análise
Transformada Z Vimos que as DTFTs de algumas sequências não convergem uniformemente para funções contínuas de ω, porque as sequências não são absolutamente somáveis. A transformada Z permitirá a análise
Lista 2 - Métodos Matemáticos II Respostas
 Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
Continuidade de processos gaussianos
 Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
Aula vinte e quatro: Sequências de funções contínuas e limites
 Aula vinte e quatro: Sequências de funções contínuas e limites Na semana passada a gente viu que: 1. Se f : M N é função contínua e K M é compacto, f K é uniformemente continua. Idea da prova: Fixado ɛ
Aula vinte e quatro: Sequências de funções contínuas e limites Na semana passada a gente viu que: 1. Se f : M N é função contínua e K M é compacto, f K é uniformemente continua. Idea da prova: Fixado ɛ
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
CÁLCULO II - MAT Em cada um dos seguintes campos vetoriais, aplicar o resultado do exercício 3 para mostrar que f
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERIANA Instituto Latino-Americano de iências da Vida e da Natureza entro Interdisciplinar de iências da Natureza 1. Dado um campo vetorial bidimensional ÁLULO
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERIANA Instituto Latino-Americano de iências da Vida e da Natureza entro Interdisciplinar de iências da Natureza 1. Dado um campo vetorial bidimensional ÁLULO
Sobre a dinâmica de aplicações do círculo e do toro
 Sobre a dinâmica de aplicações do círculo e do toro Fernando Oliveira U. F. de Minas Gerais EMALCA 2010 Fernando Oliveira (U. F. de Minas Gerais) Sobre a dinâmica de aplicações do círculo e do toro EMALCA
Sobre a dinâmica de aplicações do círculo e do toro Fernando Oliveira U. F. de Minas Gerais EMALCA 2010 Fernando Oliveira (U. F. de Minas Gerais) Sobre a dinâmica de aplicações do círculo e do toro EMALCA
Cálculo Diferencial e Integral II Resolução do Exame/Teste de Recuperação 02 de Julho de 2018, 15:00h - versão 2 Duração: Exame (3h), Teste (1h30)
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
DANIEL V. TAUSK. se A é um subconjunto de X, denotamos por A c o complementar de
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
ANÁLISE E TOPOLOGIA. 1 o semestre. Estudaremos neste curso alguns dos conceitos centrais da análise matemática: números reais, derivadas,
 ANÁLISE E TOPOLOGIA 1 o semestre Estudaremos neste curso alguns dos conceitos centrais da análise matemática: números reais, derivadas, séries e integrais. 1. Espaços topológicos e métricos Todos estes
ANÁLISE E TOPOLOGIA 1 o semestre Estudaremos neste curso alguns dos conceitos centrais da análise matemática: números reais, derivadas, séries e integrais. 1. Espaços topológicos e métricos Todos estes
{ 1 se x é racional, 0 se x é irracional. cos(k!πx) = cos(mπ) = ±1. { 1 se x Ak
 Solução dos Exercícios Capítulo 0 Exercício 0.: Seja f k : [0, ] R a função definida por Mostre que f k (x) = lim j (cos k!πx)2j. { f k (x) = se x {/k!, 2/k!,..., }, 0 senão e que f k converge pontualmente
Solução dos Exercícios Capítulo 0 Exercício 0.: Seja f k : [0, ] R a função definida por Mostre que f k (x) = lim j (cos k!πx)2j. { f k (x) = se x {/k!, 2/k!,..., }, 0 senão e que f k converge pontualmente
LISTA 3 DE INTRODUÇÃO À TOPOLOGIA 2011
 LISTA 3 DE INTRODUÇÃO À TOPOLOGIA 2011 RICARDO SA EARP Limites e continuidade em espaços topológicos (1) (a) Assuma que Y = A B, onde A e B são subconjuntos abertos disjuntos não vazios. Deduza que A B
LISTA 3 DE INTRODUÇÃO À TOPOLOGIA 2011 RICARDO SA EARP Limites e continuidade em espaços topológicos (1) (a) Assuma que Y = A B, onde A e B são subconjuntos abertos disjuntos não vazios. Deduza que A B
Transformações Conformes: 15 Aplicações
 AULA Transformações Conformes: 15 Aplicações META: Aplicar transformações conformes. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Aplicar transformações conformes na determinação da distribuição
AULA Transformações Conformes: 15 Aplicações META: Aplicar transformações conformes. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Aplicar transformações conformes na determinação da distribuição
3 Superfícies Spacelike em IR 2,1
 Superfícies Spacelike em IR,. Fórmula de Representação para Spacelike no espaço de Lorentz.. O espaço de Minkowski Seja IR, = IR, ḡ o espaço de Minkowski de dimensão com a métrica de Lorentz ḡ =(dx ) +(dx
Superfícies Spacelike em IR,. Fórmula de Representação para Spacelike no espaço de Lorentz.. O espaço de Minkowski Seja IR, = IR, ḡ o espaço de Minkowski de dimensão com a métrica de Lorentz ḡ =(dx ) +(dx
Noções (básicas) de Topologia Geral, espaços métricos, espaços normados e espaços com produto interno. André Arbex Hallack
 Noções (básicas) de Topologia Geral, espaços métricos, espaços normados e espaços com produto interno André Arbex Hallack Setembro/2011 Introdução O presente texto surgiu para dar suporte a um Seminário
Noções (básicas) de Topologia Geral, espaços métricos, espaços normados e espaços com produto interno André Arbex Hallack Setembro/2011 Introdução O presente texto surgiu para dar suporte a um Seminário
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Instituto de Matemática e Estatística da USP. Ano Professor Oswaldo R. B. de Oliveira. Capítulo 8 - Teorema de Cauchy Homotópico e Logaritmo
 MAT 225 - FUNÇÕES ANALÍTICAS Instituto de Matemática e Estatística da USP Ano 2015 Professor Oswaldo R. B. de Oliveira http://www.ime.usp.br/~oliveira oliveira@ime.usp.br Capítulo 8 - Teorema de Cauchy
MAT 225 - FUNÇÕES ANALÍTICAS Instituto de Matemática e Estatística da USP Ano 2015 Professor Oswaldo R. B. de Oliveira http://www.ime.usp.br/~oliveira oliveira@ime.usp.br Capítulo 8 - Teorema de Cauchy
VARIÁVEIS COMPLEXAS UNIVERSIDADE FEDERAL DE SÃO CARLOS CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA
 UNIVERSIDADE FEDERAL DE SÃO CARLOS CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA TÓPICOS SOBRE FUNÇÕES DE VÁRIAS VARIÁVEIS COMPLEXAS Joel Rogelio Portada Coacalle São
UNIVERSIDADE FEDERAL DE SÃO CARLOS CENTRO DE CIÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA TÓPICOS SOBRE FUNÇÕES DE VÁRIAS VARIÁVEIS COMPLEXAS Joel Rogelio Portada Coacalle São
2 Hiperbolicidade e estabilidade
 2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
Variável Complexa
 Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Algumas Caracterizações do Catenóide
 Universidade Federal da Bahia Instituto de Matemática Curso de Pós-graduação em Matemática Dissertação de Mestrado Algumas Caracterizações do Catenóide Adson Sampaio Melo Salvador Bahia Julho 2006 Algumas
Universidade Federal da Bahia Instituto de Matemática Curso de Pós-graduação em Matemática Dissertação de Mestrado Algumas Caracterizações do Catenóide Adson Sampaio Melo Salvador Bahia Julho 2006 Algumas
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
e i $ p = K1, a teoria de funções de variáveis
 TEOREMA DA UNIFORMIZAÇÃO DE RIEMANN Aluno: Ricardo Lomba de Araujo Junior Orientador: Flávio Erthal Abdenur Introdução O Teorema de Riemann é um dos mais importantes resultados obtidos em Análise Complexa,
TEOREMA DA UNIFORMIZAÇÃO DE RIEMANN Aluno: Ricardo Lomba de Araujo Junior Orientador: Flávio Erthal Abdenur Introdução O Teorema de Riemann é um dos mais importantes resultados obtidos em Análise Complexa,
MAT 2110 : Cálculo para Química. Sylvain Bonnot (IME-USP)
 MAT 2110 : Cálculo para Química Sylvain Bonnot (IME-USP) 2014 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver o link para MAT 2110 na
MAT 2110 : Cálculo para Química Sylvain Bonnot (IME-USP) 2014 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver o link para MAT 2110 na
O Teorema de Peano. f : D R n. uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e uma função ϕ : I R n tais que
 O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
Teoremas fundamentais dos espaços normados
 Capítulo 9 Teoremas fundamentais dos espaços normados 9.1 Teorema de Hahn-Banach O próximo teorema, conhecido como teorema de Hahn-Banach, é uma generalização do Teorema 4.12, o qual, recordamos para conveniência
Capítulo 9 Teoremas fundamentais dos espaços normados 9.1 Teorema de Hahn-Banach O próximo teorema, conhecido como teorema de Hahn-Banach, é uma generalização do Teorema 4.12, o qual, recordamos para conveniência
Teoremas de uma, duas e três séries de Kolmogorov
 Teoremas de uma, duas e três séries de Kolmogorov 13 de Maio de 013 1 Introdução Nestas notas Z 1, Z, Z 3,... é uma sequência de variáveis aleatórias independentes. Buscaremos determinar condições sob
Teoremas de uma, duas e três séries de Kolmogorov 13 de Maio de 013 1 Introdução Nestas notas Z 1, Z, Z 3,... é uma sequência de variáveis aleatórias independentes. Buscaremos determinar condições sob
Análise I Solução da 1ª Lista de Exercícios
 FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
Lista de exercícios 1 Grupos e Topológia
 Universidade Federal do Paraná 1 semestre 2017. Programa de Pós-Graduação em Matemática Grupos de Lie Prof. Olivier Brahic Lista de exercícios 1 Grupos e Topológia Exercício 1. (Propriedades topológicas
Universidade Federal do Paraná 1 semestre 2017. Programa de Pós-Graduação em Matemática Grupos de Lie Prof. Olivier Brahic Lista de exercícios 1 Grupos e Topológia Exercício 1. (Propriedades topológicas
Curso de Mestrado em Matemática Aplicada Tópicos de Topologia - Monopólos e Curvas Algébricas 1 a Série de Problemas - Outubro 1999
 Secção de Álgebra e Análise - Departamento de Matemática - IST Curso de Mestrado em Matemática Aplicada Tópicos de Topologia - Monopólos e Curvas Algébricas 1 a Série de Problemas - Outubro 1999 Os conceitos
Secção de Álgebra e Análise - Departamento de Matemática - IST Curso de Mestrado em Matemática Aplicada Tópicos de Topologia - Monopólos e Curvas Algébricas 1 a Série de Problemas - Outubro 1999 Os conceitos
Lista 1 - Métodos Matemáticos II Respostas
 Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
! " # $ % & ' # % ( # " # ) * # +
 a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
Escoamento potencial
 Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
Resumos de CDI-II. 1. Topologia e Continuidade de Funções em R n. 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto
 Resumos de CD- 1. Topologia e Continuidade de Funções em R n 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto B r (a) = {x R n : x a < r}. 2. Seja A R n um conjunto. m ponto a A diz-se: (i)
Resumos de CD- 1. Topologia e Continuidade de Funções em R n 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto B r (a) = {x R n : x a < r}. 2. Seja A R n um conjunto. m ponto a A diz-se: (i)
38 a Aula AMIV LEAN, LEC Apontamentos
 38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
1 Primos em uma PA? 2 Pequeno teorema de Dirichlet
 Pequeno teorema de Dirichlet Primos em uma PA? O famoso teorema de Dirichlet, também conhecido como PCP princípio das casas dos primos), diz: Teorema. Dirichlet) Sejam a e n dois inteiros com a, n). Então
Pequeno teorema de Dirichlet Primos em uma PA? O famoso teorema de Dirichlet, também conhecido como PCP princípio das casas dos primos), diz: Teorema. Dirichlet) Sejam a e n dois inteiros com a, n). Então
COORDENADAS DO ESPAÇO DE
 UNIVERSIDADE FEDERAL DE MINAS GERAIS INSTITUTO DE CIÊNCIAS EXATAS Departamento de Matemática Dissertação de Mestrado COORDENADAS DO ESPAÇO DE TEICHMÜLLER. Bruno Zanotelli Felippe Orientador: Francisco
UNIVERSIDADE FEDERAL DE MINAS GERAIS INSTITUTO DE CIÊNCIAS EXATAS Departamento de Matemática Dissertação de Mestrado COORDENADAS DO ESPAÇO DE TEICHMÜLLER. Bruno Zanotelli Felippe Orientador: Francisco
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Teorema de Riemann-Roch
 Campus de São José do Rio Preto Rafael Lucas de Arruda Teorema de Riemann-Roch e Aplicações São José do Rio Preto, 25 de fevereiro de 2011 RAFAEL LUCAS DE ARRUDA Teorema de Riemann-Roch e Aplicações Dissertação
Campus de São José do Rio Preto Rafael Lucas de Arruda Teorema de Riemann-Roch e Aplicações São José do Rio Preto, 25 de fevereiro de 2011 RAFAEL LUCAS DE ARRUDA Teorema de Riemann-Roch e Aplicações Dissertação
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA
 ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
Topologia e Análise Linear. Maria Manuel Clementino, 2013/14
 Maria Manuel Clementino, 2013/14 2013/14 1 ESPAÇOS MÉTRICOS Espaço Métrico Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições,
Maria Manuel Clementino, 2013/14 2013/14 1 ESPAÇOS MÉTRICOS Espaço Métrico Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições,
Cálculo avançado. 1 TOPOLOGIA DO R n LISTA DE EXERCÍCIOS
 LISTA DE EXERCÍCIOS Cálculo avançado 1 TOPOLOGIA DO R n 1. Considere o produto interno usual, no R n. ostre que para toda aplicação linear f : R n R existe um único vetor y R n tal que f (x) = x, y para
LISTA DE EXERCÍCIOS Cálculo avançado 1 TOPOLOGIA DO R n 1. Considere o produto interno usual, no R n. ostre que para toda aplicação linear f : R n R existe um único vetor y R n tal que f (x) = x, y para
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
[À funç~ao d chama-se métrica e aos elementos de X pontos do espaço métrico; a condiç~ao (3) designa-se por desigualdade triangular.
 Aula I - Topologia e Análise Linear 1 Espaços Métricos ESPAÇO MÉTRICO Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições, quaisquer
Aula I - Topologia e Análise Linear 1 Espaços Métricos ESPAÇO MÉTRICO Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições, quaisquer
Análise Matemática IV Problemas para as Aulas Práticas
 Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Imersões e Mergulhos. 4 a aula,
 4 a aula, 12-04-2007 Imersões e Mergulhos Um mapa entre variedades f : X Y diz-se um mergulho sse (1) é uma imersão, i.e., Df x : T x X T f(x) Y é injectiva, para todo x X, (2) é injectiva, e (3) a inversa
4 a aula, 12-04-2007 Imersões e Mergulhos Um mapa entre variedades f : X Y diz-se um mergulho sse (1) é uma imersão, i.e., Df x : T x X T f(x) Y é injectiva, para todo x X, (2) é injectiva, e (3) a inversa
O espaço das Ordens de um Corpo
 O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
3.1 Limite & Continuidade
 3. FUNÇÕES CONTÍNUAS ANÁLISE NO CORPO R - 2018.1 3.1 Limite & Continuidade 1. Mostre que a função valor absoluto f (x) = jxj é contínua em qualquer ponto x 2 R: 2. A função de Dirichlet ' : R! R é de nida
3. FUNÇÕES CONTÍNUAS ANÁLISE NO CORPO R - 2018.1 3.1 Limite & Continuidade 1. Mostre que a função valor absoluto f (x) = jxj é contínua em qualquer ponto x 2 R: 2. A função de Dirichlet ' : R! R é de nida
1 Limites e Conjuntos Abertos
 1 Limites e Conjuntos Abertos 1.1 Sequências de números reais Definição. Uma sequência de números reais é uma associação de um número real a cada número natural. Exemplos: 1. {1,2,3,4,...} 2. {1,1/2,1/3,1/4,...}
1 Limites e Conjuntos Abertos 1.1 Sequências de números reais Definição. Uma sequência de números reais é uma associação de um número real a cada número natural. Exemplos: 1. {1,2,3,4,...} 2. {1,1/2,1/3,1/4,...}
1 Distância entre dois pontos do plano
 Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Exercícios de topologia geral, espaços métricos e espaços vetoriais
 Exercícios de topologia geral, espaços métricos e espaços vetoriais 9 de Dezembro de 2009 Resumo O material nestas notas serve como revisão e treino para o curso. Estudantes que nunca tenham estudado estes
Exercícios de topologia geral, espaços métricos e espaços vetoriais 9 de Dezembro de 2009 Resumo O material nestas notas serve como revisão e treino para o curso. Estudantes que nunca tenham estudado estes
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Fabio Augusto Camargo
 Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Análise Complexa e Equações Diferenciais
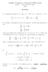 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
