MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz. EST Setúbal / IPS Maio 2012
|
|
|
- João Gabriel das Neves Correia
- 6 Há anos
- Visualizações:
Transcrição
1 MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
2 Congruências Lineares De nição A congruência da forma ax b (mod m), diz-se uma congruência linear. Teorema mdc(a, m) = 1 =) 9x 0 2 Z : ax 0 b (mod m) Todas as outras soluções de ax b (mod m) são da forma x 0 + km, k 2 Z. Demonstração 1 a parte: Como mdc(a, m) = 1, existem inteiros s e t tais que as + mt = 1. Então, as 1 (mod m), donde, multiplicando ambos os membros por b, vem a(sb) b (mod m). Considerando x 0 = sb, tem-se que x 0 é solução de ax b (mod m). 2 a parte: Ver Sebenta. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
3 Algoritmo de Resolução 0. Dados: ax b (mod m) com mdc(a, m) = Determinar uma combinação linear inteira de a e m que seja igual a 1, isto é, inteiros s e t tais que as + mt = 1 (os coe cientes da combinação linear podem ser calculados a partir da retrosubstituição dos restos fornecidos pelo algoritmo de Euclides); 2. Utilizar o coe ciente s obtido no passo acima para calcular a solução da congruência x 0 = sb. Resolver a congruência linear 33x 38 (mod 280) e indicar o conjunto das suas soluções. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
4 Caso Geral Teorema Seja mdc(a, m) = d. Então, ax b (mod m) tem solução sse djb. Nesta situação, x 0 é solução de ax b (mod m) () x 0 é solução de a d x b d mod m d 6x 9 (mod 15) tem solução porque mdc(6, 15) = 3 e 3j9. As soluções coincidem com as da congruência 6 3 x 9 mod 15, 2x 3 (mod 5). 3 3 Dado que x 0 = 4 é solução de 2x 3 (mod 5), o conjunto das soluções de 6x 9(mod 15) é f4 + 5k : k 2 Zg. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
5 Observação Prova-se que o conjunto x 0 + k m d : k 2 Z das soluções da congruência ax b (mod m) é a união dos conjuntos das soluções das congruências x x 0 (mod m), x x 0 + m (mod m), d x x m (mod m),..., x x 0 + (d 1) m (mod m). d d Estes últimos conjuntos são disjuntos dois a dois, pelo que é costume dizer que, por exemplo, x 0, x 0 + m d,..., x 0 + (d 1) m d são soluções distintas módulo m da congruência ax b (mod m). Vimos no exemplo anterior que o conjunto das soluções da congruência 6x 9 (mod 15) é f4 + 5k : k 2 Zg. De acordo com a nota anterior, este conjunto é a união dos conjuntos das soluções de x 4 (mod 15), x 9 (mod 15) e x 14 (mod 15). Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
6 Teorema Chinês dos Restos Existe um número natural que, quando dividido por 3, dá resto 2, quando dividido por 5, dá resto 4 e que, quando dividido por 7, dá resto 6? Teorema Sejam m 1, m 2,..., m k números naturais primos entre si dois a dois e a 1, a 2,..., a k inteiros quaisquer. Então, existe uma solução x que resolve simultaneamente as congruências 8 x a 1 (mod m 1 ) >< x a 2 (mod m 2 ) >:. x a k (mod m k ) Quaisquer duas soluções são congruentes módulo M = m 1 m 2 m k.. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
7 Algoritmo de Resolução de um Sistema de Congruências 1 Calcular M = m 1 m 2 m k, M 1 = M m 1, M 2 = M m 2,..., M k = M m k ; 2 Determinar soluções particulares s i de cada uma das congruências M i x 1 (mod m i ), i = 1, 2,..., k. 3 Formar a solução particular x 0 = M 1 s 1 a 1 + M 2 s 2 a M k s k a k. 4 As soluções do sistema são os valores de x tais que x x 0 (mod M). Resolver o sistema 8 < : x 2 (mod 3) x 4 (mod 5) x 6 (mod 7). Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
8 Resolução 1 Sejam M = = 105 e M 1 = = 35, M 2 = = 21 e M 3 = = Procuremos então soluções particulares das congruências 8 < : 35x 1 (mod 3) 21x 1 (mod 5) 15x 1 (mod 7) Soluções procuradas: s 1 = 2, s 2 = 1 e s 3 = 1; 3 x 0 = (35 2 2) + (21 1 4) + (15 1 6) = 314; 4 O conjunto solução é f k : k 2 Zg ou equivalentemente, f k : k 2 Zg.. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
9 Função de Euler S n = fr 2 N 0 : 0 r n 1 ^ mdc(r, n) = 1g. De nição Função de Euler: φ : N! N n! φ(n) = js n j s n S n φ(n) 1 f0g 1 2 f1g 1 3 f1, 2g 2 4 f1, 3g 2 n S n φ(n) 5 f1, 2, 3, 4g 4 6 f1, 5g 2 7 f1, 2, 3, 4, 5, 6g 6 8 f1, 3, 5, 7g 4 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
10 Observações 1 Se p é um número primo, então todos os inteiros 1, 2,..., p 1 são relativamente primos com p. Logo, Mais geralmente: φ(p) = p 1. φ(p k ) = p k p k 1 = p k 1 1. p 2 Se m e n são números naturais primos entre si, então φ(mn) = φ(m)φ(n). Por exemplo, φ(341) = φ(11 31) = φ(11)φ(31) = = Das obs. 1 e 2 conclui-se mais geralmente que, se n = p e 1 1 φ(n) = n 1. r k=1 Se n = 108 = , φ(108) = p k 1 pe = 36. r, 2 pe r Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
11 Teorema (de Euler) Sejam n 2 N e a 2 Z. Se mdc(a, n) = 1, então a φ(n) 1 (mod n). Calcular o resto da divisão de 2 60 por 77. O número 77 é composto pois 77 = Então, visto que 7 e 11 são primos entre si, φ(77) = φ(7)φ(11) = (7 1) (11 1) = 60. Como 2 é invertível módulo 77, isto é, mdc(2, 77) = 1, tem-se pelo teorema de Euler: 2 φ(77) 1(mod 77), (mod 77). Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
12 (Pequeno) Teorema de Fermat Teorema Seja a um número inteiro e p um número primo. Se p - a então a p 1 1 (mod p). Vejamos a aplicação do teorema de Fermat ao cálculo do resto da divisão de por 101. Visto que 101 é primo e não divide 2, tem-se (mod 101) pelo teorema de Fermat. Como = , vem, pelas propriedades das congruências: = = (mod 101). Portanto, o resto requerido é 8. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
13 Corolário Se a é um número inteiro e p é um número primo, então a p por p, isto é, a p a (mod p). a é divisível Demonstração Consideremos os casos p - a e pja. No primeiro caso, o teorema de Fermat garante que a p 1 1 (mod p) ; então, multiplicando ambos os membros desta congruência por a, obtém-se a p a (mod p). No segundo cado, isto é, se pja, p também divide a p a e, portanto, a congruência a p a (mod p) é igualmente válida. Exercício Mostre que para todo o inteiro a, o número a 3 + (a + 1) 3 + (a + 2) 3 é divisível por 3. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
14 Calcular o resto da divisão de 2 40 por 77. Como 77 = 7 11 e 7 e 11 são primos entre si, vamos utilizar o resultado: 2 40 x(mod 7) 2 40 ) 2 x(mod 11) 40 x(mod 77) Pelo pequeno teorema de Fermat, 2 6 1(mod 7) ) 2 40 = = (mod 7) (mod 11) ) 2 40 = (mod 11). Recorrendo ao teorema chinês dos restos, podemos resolver x 2(mod 7). Obtém-se então x 23(mod 77) donde x 1(mod 11) (mod 7) (mod 11) ) (mod 77). Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
15 De nição Os números naturais compostos n que satifazem a congruência a n 1 1 (mod n), para algum a, designam-se por pseudoprimos de Fermat relativos à base a. O número composto 341 = é um pseudoprimo de Fermat relativamente à base 2 pois veri ca De nição (mod 341). Os números compostos n que que satisfazem a congruência a n a (mod n), qualquer que seja o natural a, dizem-se números de Carmichael. s Os números compostos 561, 1105 e 1729 são os primeiros números de Carmichael. Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) Maio / 15
Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 42
 1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
Note-se que pelo Teorema de Euler. a φ(n) 1 (mod n) logo existe k nas condições da definição acima e. Raízes Primitivas. Ordem de um elemento
 Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
, com k 1, p 1, p 2,..., p k números primos e α i, β i 0 inteiros, as factorizações de dois números inteiros a, b maiores do que 1.
 Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA
 Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (2/6) Carlos Luz. EST Setúbal / IPS Abril 2012
 MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (2/6) Carlos Luz EST Setúbal / IPS 16 22 Abril 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (2/6) 16 22 Abril 2012 1 / 15 Divisão Inteira Teorema Sendo
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (2/6) Carlos Luz EST Setúbal / IPS 16 22 Abril 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (2/6) 16 22 Abril 2012 1 / 15 Divisão Inteira Teorema Sendo
Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r. n = qd + r
 Matemática Discreta September 18, 2018 1 1 Divisão de inteiros Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r {0,..., d 1} tal que n = qd + r Dizemos que a
Matemática Discreta September 18, 2018 1 1 Divisão de inteiros Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r {0,..., d 1} tal que n = qd + r Dizemos que a
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Matemática Discreta. Introdução à Teoria de Números - Exercícios 1 o ano /2011
 Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
MAT Álgebra I para Licenciatura 2 a Lista de exercícios
 MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MATEMÁTICA MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira
 Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ
 NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL
 1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 30 de março de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. Calcule uma estimativa
1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 30 de março de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. Calcule uma estimativa
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Teorema Chinês dos Restos. Tópicos Adicionais
 Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
1 Congruência. 2. m mmc(n, m) m a b. De 1) e 2) segue que: a b mod n e a b mod m.
 1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
Universidade do Minho
 Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
MA14 - Aritmética Unidade 20 Resumo. Teoremas de Euler e de Wilson
 MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Primeiro Desao Mestre Kame
 Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Se mdc(a,m) = 1, como a é invertível módulo m, a equação. ax b (mod m)
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
1. O que podemos dizer sobre a imagem da função. f : Z Z, f(x) = x 2 + x + 1?
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Existem infinitos números de Carmichael, mas não provaremos isso neste curso.
 6 Pseudoprimos 6.1 O Pequeno Teorema de Fermat nos diz que, se n é primo, então temos b n b (mod n) para todo b Z. Portanto, a contrapositiva diz que se temos b n b (mod n) ( ) para algum b Z, então n
6 Pseudoprimos 6.1 O Pequeno Teorema de Fermat nos diz que, se n é primo, então temos b n b (mod n) para todo b Z. Portanto, a contrapositiva diz que se temos b n b (mod n) ( ) para algum b Z, então n
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Notas sobre teoria dos números (2)
 1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
Polos Olímpicos de Treinamento. Aula 9. Curso de Teoria dos Números - Nível 2. O Teorema de Euler. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
XIX Semana Olímpica de Matemática. Nível 3. Polinômios Ciclotômicos e Congruência Módulo p. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
Álgebra A - Aula 12 Sistemas de congruências
 Álgebra A - Aula 12 Sistemas de congruências Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Equações lineares ax b (mod n) Se a possui um inverso α em Z n, então: α(ax) αb
Álgebra A - Aula 12 Sistemas de congruências Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Equações lineares ax b (mod n) Se a possui um inverso α em Z n, então: α(ax) αb
1 Potências e raízes em Aritmética Modular. Seja p primo e a um inteiro primo com p; a aplicação
 1 Potências e raízes em Aritmética Modular 1.1 Os Teoremas de Fermat e Euler Seja p primo e a um inteiro primo com p; a aplicação Z /p Z /p, x ax definida pela multiplicação por a (ou mais precisamente
1 Potências e raízes em Aritmética Modular 1.1 Os Teoremas de Fermat e Euler Seja p primo e a um inteiro primo com p; a aplicação Z /p Z /p, x ax definida pela multiplicação por a (ou mais precisamente
Elementos de Matemática Finita ( ) Exercícios resolvidos
 Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Proposição 0 (Divisão Euclidiana): Dados a b, b b * existem q, r b unicamente determinados tais que 0 r < b e a = bq + r
 "!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
"!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
MA14 - Aritmética Unidade 15 - Parte 1 Resumo. Congruências
 MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
NÚMEROS INTEIROS. Álgebra Abstrata - Verão 2012
 NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c.
 Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Este material é apenas um resumo de parte do conteúdo da disciplina.
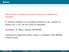 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
Aritmética dos Restos. Problemas com Congruências. Tópicos Adicionais
 Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
Programa Combinatória Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 52
 1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
Resposta:
 Gabarito - Dia 1 Exercício 1. Utilizando a Cifra de ATBASH decifre a mensagem VHHV VCVIXRXRL V UZXRO. Esse exercício é fácil. Exercício 2. Utilize o código de Políbio para codicar a mensagem Pensar é um
Gabarito - Dia 1 Exercício 1. Utilizando a Cifra de ATBASH decifre a mensagem VHHV VCVIXRXRL V UZXRO. Esse exercício é fácil. Exercício 2. Utilize o código de Políbio para codicar a mensagem Pensar é um
MATEMÁTICA 1 MÓDULO 2. Divisibilidade. Professor Matheus Secco
 MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
Álgebra I. Volume 3 Módulo 1. Adilson Gonçalves Luiz Manoel Figueiredo. Apoio:
 . Álgebra I Volume 3 Módulo 1 Adilson Gonçalves Luiz Manoel Figueiredo Apoio: Fundação Cecierj / Consórcio Cederj Rua Visconde de Niterói, 1364 Mangueira Rio de Janeiro, RJ CEP 20943-001 Tel.: (21) 2334-1569
. Álgebra I Volume 3 Módulo 1 Adilson Gonçalves Luiz Manoel Figueiredo Apoio: Fundação Cecierj / Consórcio Cederj Rua Visconde de Niterói, 1364 Mangueira Rio de Janeiro, RJ CEP 20943-001 Tel.: (21) 2334-1569
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
 Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
Teorema Chinês dos Restos. Sistema de Congruências. Tópicos Adicionais
 Teorema Chinês dos Restos Sistema de Congruências Tópicos Adicionais Teorema Chinês dos Restos Sistema de Congruências 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre todos
Teorema Chinês dos Restos Sistema de Congruências Tópicos Adicionais Teorema Chinês dos Restos Sistema de Congruências 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre todos
Resolução do EXAME da ÉPOCA de RECURSO
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA DISCRETA Resolução do EXAME da ÉPOCA de RECURSO Curso: LEI o Semestre / Data: 8 de Julho de Duração: hm I Diga, justificando
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA DISCRETA Resolução do EXAME da ÉPOCA de RECURSO Curso: LEI o Semestre / Data: 8 de Julho de Duração: hm I Diga, justificando
MA14 - Aritmética Lista 1. Unidades 1 e 2
 MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
Gabarito e Pauta de Correção ENQ
 Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
PLANO DE ENSINO E APRENDIZAGEM
 SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO DE E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR DA DISCIPLINA:
SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO DE E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR DA DISCIPLINA:
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
5 Congruências lineares. Programa. 1 Parte 1 - Conjuntos e Aplicações. 1 Conjuntos. 4 Indução matemática e divisibilidade
 Matemática Discreta 2008/09 Jorge André & Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Programa 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução matemática
Matemática Discreta 2008/09 Jorge André & Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Programa 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução matemática
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
 Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
UNIVERSIDADE FEDERAL DO MATO GROSSO DO SUL INSTITUTO DE MATEMÁTICA MATEMÁTICA EM REDE NACIONAL MESTRADO PROFISSIONAL. Nivaldo Alves de Souza Marques
 UNIVERSIDADE FEDERAL DO MATO GROSSO DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO MATEMÁTICA EM REDE NACIONAL MESTRADO PROFISSIONAL FATORAÇÃO DE INTEIROS Nivaldo Alves de Souza Marques CAMPO
UNIVERSIDADE FEDERAL DO MATO GROSSO DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO MATEMÁTICA EM REDE NACIONAL MESTRADO PROFISSIONAL FATORAÇÃO DE INTEIROS Nivaldo Alves de Souza Marques CAMPO
3.3 Congruências e aritmética modular
 40 CHAPTER 3. ELEMENTOS DE ARITMÉTICA DOS INTEIROS 3.3 Congruências e aritmética modular Consideremos primeiro o seguinte exemplo: o que podemos dizer sobre a imagem da função f : Z Z, f(x) =x 2 + x +
40 CHAPTER 3. ELEMENTOS DE ARITMÉTICA DOS INTEIROS 3.3 Congruências e aritmética modular Consideremos primeiro o seguinte exemplo: o que podemos dizer sobre a imagem da função f : Z Z, f(x) =x 2 + x +
S. C. COUTINHO. = 2n 2 r 2 m 1. Como 2 n 2 r = 2 r (2 n r 1) = 2 r (2 mq 1), então 2 n 2 r 2 m 1 = 2r (2 m 1)(2 mq ) Q = (2n 1) (2 r 1) 2 m 1
 DEPARTAMENTO DE CIÊNCIA DA COMPUTAÇÃO UFRJ NÚMEROS INTEIROS E CRIPTOGRAFIA RSA S. C. COUTINHO 1. Respostas dos exercícios do capítulo 1 (1) (a) mdc(14, 35) = 7; α = 2 e β = 1; (b) mdc(252, 180) = 36, α
DEPARTAMENTO DE CIÊNCIA DA COMPUTAÇÃO UFRJ NÚMEROS INTEIROS E CRIPTOGRAFIA RSA S. C. COUTINHO 1. Respostas dos exercícios do capítulo 1 (1) (a) mdc(14, 35) = 7; α = 2 e β = 1; (b) mdc(252, 180) = 36, α
4.1 Preliminares. No exemplo acima: Dom(R 1 ) = e Im(R 1 ) = Dom(R 2 ) = e Im(R 2 ) = Dom(R 3 ) = e Im(R 3 ) = Diagrama de Venn
 4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
MA14 - Aritmética Unidade 22 Resumo. Aritmética das Classes Residuais
 MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA. Ministério da Educação
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA Ministério da Educação Instituto Federal de Educação, Ciência e Tecnologia da Paraíba - Campus Cajazeiras Diretoria de Ensino / Coord. do Curso
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E tecnologia PARAÍBA Ministério da Educação Instituto Federal de Educação, Ciência e Tecnologia da Paraíba - Campus Cajazeiras Diretoria de Ensino / Coord. do Curso
1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).
![1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n). 1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).](/thumbs/98/136620653.jpg) Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
CIC 111 Análise e Projeto de Algoritmos II
 CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
ax + by 347 = 0 k = text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: DOCENTES: Gilda Ferreira e Ana Nunes
 text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
MATEMÁTICA DISCRETA COMBINATÓRIA (4/4) Carlos Luz. EST Setúbal / IPS Março 2012
 MATEMÁTICA DISCRETA COMBINATÓRIA (4/4) Carlos Luz EST Setúbal / IPS 25 31 Março 2012 Carlos Luz (EST Setúbal / IPS) Combinatória (4/4) 25 31 Março 2012 1 / 8 Princípio da Distribuição O princípio da distribuição
MATEMÁTICA DISCRETA COMBINATÓRIA (4/4) Carlos Luz EST Setúbal / IPS 25 31 Março 2012 Carlos Luz (EST Setúbal / IPS) Combinatória (4/4) 25 31 Março 2012 1 / 8 Princípio da Distribuição O princípio da distribuição
Semana Olímpica 2019
 Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Números Primos e Criptografia RSA
 Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
Notas sobre os anéis Z m
 Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
1 TESTE TEORIA DE NÚMEROS COMPUTACIONAL
 1 TESTE TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 17 de abril de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. (a) Sem utilizar o Mathematica, calcule
1 TESTE TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 17 de abril de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. (a) Sem utilizar o Mathematica, calcule
Ordens e raízes primitivas
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 7 Ordens e raízes primitivas 1 Polinômios Dado um anel comutativo K, definimos o anel comutativo K[x] como
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 7 Ordens e raízes primitivas 1 Polinômios Dado um anel comutativo K, definimos o anel comutativo K[x] como
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
Jo ao Filipe Queir o TEORIA DOS N UMEROS Departamento de Matem atica - Universidade de Coimbra 2008
 João Filipe Queiró TEORIA DOS NÚMEROS Departamento de Matemática - Universidade de Coimbra 2008 As folhas que se seguem contêm um resumo das matérias estudadas na disciplina de Teoria dos Números. Esta
João Filipe Queiró TEORIA DOS NÚMEROS Departamento de Matemática - Universidade de Coimbra 2008 As folhas que se seguem contêm um resumo das matérias estudadas na disciplina de Teoria dos Números. Esta
Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde p é primo ímpar.
 raízes primitivas Uma raiz primitiva módulo n é um inteiro b tal que {1, b, b 2,... ( mod n)} = U(n). Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde
raízes primitivas Uma raiz primitiva módulo n é um inteiro b tal que {1, b, b 2,... ( mod n)} = U(n). Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde
Sistemas de equações lineares
 Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Valores e vectores próprios
 Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Fundamentos: Algoritmos, Inteiros e Matrizes. Inteiros e. Primos e. Divisor Comum. Inteiros e. Algoritmos. Teoria dos Centro de Informática UFPE
 , Fundamentos:, Centro de Informática UFPE , 1 2 3 4 , Sejam a e b inteiros, com a 0. a divide b se existe um inteiro c, tal que b = ac. a divide b a b Por exemplo, a = 3, b = 12 , Sejam a e b inteiros,
, Fundamentos:, Centro de Informática UFPE , 1 2 3 4 , Sejam a e b inteiros, com a 0. a divide b se existe um inteiro c, tal que b = ac. a divide b a b Por exemplo, a = 3, b = 12 , Sejam a e b inteiros,
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
Conjetura de Goldbach - Uma visão Aritmética
 Universidade dos Açores Departamento de Matemática Conjetura de Goldbach - Uma visão Aritmética José Emanuel Sousa Ponta Delgada Abril de 2013 Universidade dos Açores Departamento de Matemática Mestrado
Universidade dos Açores Departamento de Matemática Conjetura de Goldbach - Uma visão Aritmética José Emanuel Sousa Ponta Delgada Abril de 2013 Universidade dos Açores Departamento de Matemática Mestrado
Tópicos de Matemática Elementar
 Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Equa»c~oes diofantinas lineares
 7 Equa»c~oes diofantinas lineares Considere o seguinte problema. Se um trabalhador recebe 510 reais em t ³quetes de alimenta»c~ao, com valores de 20 reais ou 50 reais cada t ³quete, de quantas formas pode
7 Equa»c~oes diofantinas lineares Considere o seguinte problema. Se um trabalhador recebe 510 reais em t ³quetes de alimenta»c~ao, com valores de 20 reais ou 50 reais cada t ³quete, de quantas formas pode
Números Inteiros Algoritmo da Divisão e suas Aplicações
 Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Divisibilidade e números Inteiros
 Divisibilidade e números Inteiros Introdução à aritmética Modular Material Complementar Soluções e Observações Samuel Jurkiewicz Sumário i Capítulo 1 Material complementar A seqüência de Fibonacci A seqüência
Divisibilidade e números Inteiros Introdução à aritmética Modular Material Complementar Soluções e Observações Samuel Jurkiewicz Sumário i Capítulo 1 Material complementar A seqüência de Fibonacci A seqüência
Diagonal mais curta. Como d = mx e l = nx, teríamos: l 1 = d l = mx nx = (m n)x = n 1 x. d 1 = a:d + b:l = amx + bnx = (am + bn)x = m 1 x
 Diagonal mais curta Seja P um polígono regular de lados ( > 6), d a medida da sua diagonal mais curta e l a medida do seu lado. Supondo que d e l são comensuráveis, temos d mx e l nx, onde m e n são inteiros
Diagonal mais curta Seja P um polígono regular de lados ( > 6), d a medida da sua diagonal mais curta e l a medida do seu lado. Supondo que d e l são comensuráveis, temos d mx e l nx, onde m e n são inteiros
ALGORITMO DE EUCLIDES
 Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
Criptografia com Maple
 Criptografia com Maple - Verão/2005 Fábio Borges & Renato Portugal Criptografia com Maple p.1/32 Simétrica versus Assimétrica Simétrica Criptografia com Maple p.2/32 Simétrica versus Assimétrica Simétrica
Criptografia com Maple - Verão/2005 Fábio Borges & Renato Portugal Criptografia com Maple p.1/32 Simétrica versus Assimétrica Simétrica Criptografia com Maple p.2/32 Simétrica versus Assimétrica Simétrica
Semigrupos Numéricos e suas Características
 Universidade Federal de Goiás Instituto de Matemática e Estatística Programa de Mestrado Profissional em Matemática em Rede Nacional Semigrupos Numéricos e suas Características Leonardo Alcântara Portes
Universidade Federal de Goiás Instituto de Matemática e Estatística Programa de Mestrado Profissional em Matemática em Rede Nacional Semigrupos Numéricos e suas Características Leonardo Alcântara Portes
na Base b The Function ϕ of Euler and the Periodic Expansion Fractions in the Base b
 A Função ϕ de Euler e a Expansão Periódica de Frações na Base b The Function ϕ of Euler and the Periodic Expansion Fractions in the Base b Martinho da Costa Araujo Departamento de Matemática Universidade
A Função ϕ de Euler e a Expansão Periódica de Frações na Base b The Function ϕ of Euler and the Periodic Expansion Fractions in the Base b Martinho da Costa Araujo Departamento de Matemática Universidade
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática
 UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
Congruências I. Por exemplo, 7 2 (mod 5), 9 3 (mod 6), 37 7 (mod 10) mas 5 3 (mod 4). Veja que a b (mod m) se, e somente se, m a b.
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Sequências recorrentes e testes de primalidade
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 18 Sequências recorrentes e testes de primalidade 1 A Sequência de Fibonacci A sequência de Fibonacci é
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 18 Sequências recorrentes e testes de primalidade 1 A Sequência de Fibonacci A sequência de Fibonacci é
MATEMÁTICA DISCRETA. Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Tipo de Aulas T TP P L Tipo de disciplina ECTS
 MATEMÁTICA DISCRETA Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Engenharia Informática Língua de Ensino 2º / 1º 2017/2018 Matemática Matemática Português Responsável da Unidade Curricular (UC)
MATEMÁTICA DISCRETA Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Engenharia Informática Língua de Ensino 2º / 1º 2017/2018 Matemática Matemática Português Responsável da Unidade Curricular (UC)
MATEMÁTICA DISCRETA. Área Científica Engenharia Informática 2º / 1º 2016/2017 Matemática Matemática. Co-Responsável Carla Rodrigues
 MATEMÁTICA DISCRETA Curso Ano/Semestre Ano Lectivo Área Científica Engenharia Informática 2º / 1º 2016/2017 Matemática Matemática Dpt. Responsável da Unidade Curricular (UC) Artur Cruz Co-Responsável Carla
MATEMÁTICA DISCRETA Curso Ano/Semestre Ano Lectivo Área Científica Engenharia Informática 2º / 1º 2016/2017 Matemática Matemática Dpt. Responsável da Unidade Curricular (UC) Artur Cruz Co-Responsável Carla
Função polinomial. Pré-Cálculo. Função polinomial. Função polinomial: exemplos. Humberto José Bortolossi. Parte 6. Definição
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Função polinomial Parte 6 Parte 6 Pré-Cálculo 1 Parte 6 Pré-Cálculo 2 Função polinomial Função polinomial:
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Função polinomial Parte 6 Parte 6 Pré-Cálculo 1 Parte 6 Pré-Cálculo 2 Função polinomial Função polinomial:
37ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 37ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 3 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
37ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 3 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
TEORIA DOS NÚMEROS ****************************** Departamento de Matemática. Universidade de Aveiro
 INTRODUÇÃO À TEORIA DOS NÚMEROS Vítor Neves ****************************** Departamento de Matemática Universidade de Aveiro 2001 Introdução O presente texto resulta da evolução de um conjunto de notas
INTRODUÇÃO À TEORIA DOS NÚMEROS Vítor Neves ****************************** Departamento de Matemática Universidade de Aveiro 2001 Introdução O presente texto resulta da evolução de um conjunto de notas
MATEMÁTICA DISCRETA. Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Tipo de Aulas T TP P L Tipo de disciplina ECTS
 MATEMÁTICA DISCRETA Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Engenharia Informática Língua de Ensino 2º / 1º 2017/2018 Matemática Matemática Português Responsável da Unidade Curricular (UC)
MATEMÁTICA DISCRETA Cursos Ano/Semestre Ano Letivo Área Científica Dpt. Engenharia Informática Língua de Ensino 2º / 1º 2017/2018 Matemática Matemática Português Responsável da Unidade Curricular (UC)
Números Primos, Fatores Primos, MDC e MMC
 Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo. 1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo. 2) 17 tem apenas os divisores 1 e 17,
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo. 1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo. 2) 17 tem apenas os divisores 1 e 17,
Já sabemos como determinar todas as soluções de uma equação diofantina linear, caso esta seja resolúvel. Para conguências temos:
 Seguidamente vamos determinar valores de b (em termos de a e n) para os quais a congruência ax b (mod n) tem solução. Se a = 0 esta congruência tem solução x se e só se n b, e, neste caso, qualquer x Z
Seguidamente vamos determinar valores de b (em termos de a e n) para os quais a congruência ax b (mod n) tem solução. Se a = 0 esta congruência tem solução x se e só se n b, e, neste caso, qualquer x Z
Este material é apenas um resumo de parte do conteúdo da disciplina.
 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 11 - Seção 1.3 do livro texto da disciplina: Aritmética, A. Hefez,
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 11 - Seção 1.3 do livro texto da disciplina: Aritmética, A. Hefez,
Portal da OBMEP. Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
