1 Potências e raízes em Aritmética Modular. Seja p primo e a um inteiro primo com p; a aplicação
|
|
|
- Washington Delgado Henriques
- 6 Há anos
- Visualizações:
Transcrição
1 1 Potências e raízes em Aritmética Modular 1.1 Os Teoremas de Fermat e Euler Seja p primo e a um inteiro primo com p; a aplicação Z /p Z /p, x ax definida pela multiplicação por a (ou mais precisamente pela sua classe de congruência) é uma bijecção: de facto, como a é primo com p, existe a tal que a a 1 mod p e portanto ax ay mod p a ax a ay mod p x y mod p Por exemplo, para p = 5 e a = 2 temos x ax Se fizermos o produto dos ax para todas as classes de congruência primas com p (ou seja, todas menos a de 0) obtemos portanto a p (p 1) (a 1)(a 2) (a p 1) 1 2 (p 1) mod p uma vez que (a 1)(a 2) (a p 1) é o produto das mesmas p 1 classes de congruência por uma ordem diferente. Como 1 2 (p 1) = (p 1)! não é equivalente a 0 módulo p, podemos dividir ambos os lados por (p 1)! ( ou seja multiplicar pelo seu inverso) e concluímos que Deduzimos portanto o seguinte a p 1 1 mod p Teorema 1.1 Teorema de Fermat: Dado um primo p tem-se a p 1 1 mod p a : mdc(a, p) = 1 Note-se que o teorema pode ser enunciado de forma equivalente, e mais simples, como 1
2 Teorema 1.2 Teorema de Fermat: Dado um primo p tem-se a p a mod p a uma vez que, por um lado, a congruência anterior implica esta última para a primo com p, enquanto que para a múltiplo de p, esta é evidentemente verdadeira; e por outro, se a p a mod p e a for primo com p, então temos que p divide a p a = a(a p 1 1) e como não divide a tem que dividir o segundo factor. Exemplo 1.3 : Calcular o resto da divisão de por 17: = = ( 7 16) mod 17 e como 7 2 = mod 17, temos 7 5 ( 2) mod 17 Seja agora m um módulo qualquer e a primo com m. teorema de Fermat já não vale em geral; por exemplo e mod mod 20 O resultado do Podemos no entanto repetir o raciocínio feito para o teorema de Fermat desde que consideremos apenas as classes de congruência primas com m; designamos por Z m o conjunto das classes de congruência módulo m primas com m; por exemplo Z 12 = {1, 5, 7, 11} Notamos que o produto de duas classes primas com m é ainda uma classe prima com m. 2
3 Definição 1.4 : A função φ de Euler é definida como φ : N N, φ(m) = Z m ou seja φ(m) é o número de classes de congruência módulo m primas com m. Se a representa, mais uma vez, uma classe de congruência módulo m e prima com m, a aplicação Z /m Z /m, x ax é de novo uma bijecção, já que ax ay mod m m a(x y) e como mdc(a, m) = 1 isso implica m (x y), ou seja x e y representam a mesma classe de congruência módulo m. Se x 1,, x φ(m) representarem as classes primas com m, temos a φ(m) x 1 x φ(m) = (ax 1 ) (ax φ(m) ) x 1 x φ(m) mod m Como o produto x 1 x φ(m) é primo com m, tem um inverso módulo m e podemos multiplicar ambos os lados da congruência por esse inverso e obter o Teorema 1.5 Teorema de Euler: Se a é primo com m então a φ(m) 1 mod m Como φ(p) = p 1 para p primo, o Teorema de Fermat é de facto um caso particular deste último. 3
4 Exemplo 1.6 : Tendo em conta que, como vimos atrás, φ(12) = 4, tem-se 5 35 = = = ( 5 4) mod 12 Ou seja, qualquer potência de base a prima com m é congruente módulo m com uma potência de expoente menor que φ(m): para cada k, a k a r mod m onde 0 r < φ(m) e r k mod φ(m). Nota 1.7 : O Teorema de Euler fornece uma alternativa para resolver equações lineares: se mdc(a, m) = 1, a solução de ax b mod m pode ser calculada multiplicando ambos os lados da equação por a φ(m) 1. Para aplicar o Teorema de Euler é necessário calcular φ(m). Recorde-se que o Teorema Chinês dos Restos nos diz que se m = m 1 m k e mdc(m i, m j ) = 1 se i j, então a aplicação ψ : Z /m Z /m1 Z /mk definida por é uma bijecção. ψ(a) = (a mod m 1,, a mod m k ) Note-se também que a é primo com m se e só se o é com cada m i. Isso mostra que φ(m) = φ(m 1 ) φ(m k ) ou seja φ é uma função multiplicativa: Definição 1.8 : Uma função f : N N diz-se multiplicativa se mdc(m, n) = 1 = f(m n) = f(m)f(n) 4
5 Conclui-se que se m = p k 1 1 pk r r for a factorização de m em factores primos, ( ) φ(m) = φ φ ( ) p k r r p k 1 1 Mas é fácil verificar que, para p primo φ(p k ) = p k p k 1. De facto, as classes módulo p k que não são primas com p k são as dos múltiplos de p: 0, p, 2p,, (p k 1 1)p (o múltiplo de p seguinte seria p k 0). Portanto φ(m) = ( ) p k 1 1 pk (p k r r p k r 1 r ) r ) = m (1 1pi i=1 Exemplo 1.9 : suponhamos que queremos determinar 0 < x < 279 tal que Como 279 = 9 31, temos x (25) 681 mod 279. φ(279) = φ(9)φ(31) = 6 30 = 180. E portanto, como 25 é obviamente primo com 279, (25) 681 = (25) = ( (25) 180) 3 (25) 149 (25) 149 mod 279 Mas podemos ainda simplificar mais o cálculo desta potência: aplicando o algoritmo de Euclides, verificamos que 1 = ou seja mod 279 5
6 Usando mais uma vez o Teorema de Euler (25) 149 (25) 149 (67) 180 (25 67) 149 (67) 31 (67) 31 mod 279 que nos reduz ao cálculo de uma potência de expoente menor. Ou seja, para a primo com m e sendo b um qualquer representante da classe de congruência inversa da de a, temos a k b φ(m) k mod m que é o análogo da bem conhecida expressão a k = ( a 1) k Note-se finalmente que mesmo o cálculo da última potência poderia ser simplificado pelo uso do Teorema Chinês dos Restos: x (67) 31 mod 279 { x (67) 31 mod 9 x (67) 31 mod 31 { x 4 31 mod 9 x 5 31 mod 31 { x 4 mod 9 x 5 mod 31 onde, no último passo, voltámos a usar o Teorema de Euler. Esta aplicação do Teorema Chinês dos Restos podia, bem entendido, ter sido feita logo no início. Nota 1.10 Teorema de Euler e dízimas periódicas Os teoremas de Fermat e Euler permitem ver a uma nova luz certas propriedades elementares da representação decimal de números racionais. Embora o que se segue não desempenhe qualquer papel no desenvolvimento da teoria da aritmética modular, veremos 6
7 mais uma vez como os seus conceitos aparecem naturalmente na discussão de problemas aritméticos. Um argumento elementar (usando o Lema da Divisão) mostra que uma dízima 0.a 1 a 2 (com 0 a i < 10 para todo o i) representa um número racional se e só se a sequência a i é eventualmente periódica, ou seja, existem t 0 e n > 0 tais que a t+i+jn = a t+i para todo o 1 i n e j 0. Que racionais x têm representação decimal puramente periódica, isto é, com t = 0? Notamos que isso é equivalente à existência de um inteiro I (a parte inteira de x), de um n > 0 (o período) e de um 0 N < 10 n tais que x = I + N 10 n + N 10 2n + = I + N j jn, ou seja, usando a fórmula para a soma da série geométrica, x = I + N 10 n 1. Uma aplicação muito simples do Teorema de Euler esclarece completamente a questão. Obviamente, basta considerar o caso I = 0 e supor que x é representado por uma fracção reduzida, ou seja, com numerador e denominador primos entre si. Seja então 0 < a < 1 e suponhamos que mdc(m, 10) = 1. Então, pelo Teorema de m Euler, se φ(m) = n, temos 10 k 1 mod m, ou seja, existe M tal que 10 n 1 = Mm. Deduzimos que a = am m 10 n 1, e como se tem forçosamente am < 10n, concluímos que a m tem representação decimal puramente períodica e que o período será um divisor de φ(m) (de facto, pode acontecer que o bloco periódico de comprimento n representado por am seja a concatenação de várias cópias de um bloco de comprimento p, com p n, ou seja que am = b( p p (l 1)p ) onde n = pl e 0 < b < 10 p ). Mas, reciprocamente, se 0 < a < 1 tem representação decimal puramente períodica, m com período mínimo n, isso significa, pelo mesmo raciocínio, que existe M tal que a(10 n 1) = Mm; como mdc(a, m) = 1, temos 10 n 1 mod m e n é o menor inteiro positivo satisfazendo essa equação. Isso implica imediatamente que mdc(m, 10) = 1, mas além disso, como 10 φ(m) 1 mod m, podemos escrever φ(m) = qn + r, com 0 r < n e concluímos que também 10 r 1 mod m, o que, pela propriedade de n, implica r = 0m, ou seja, o período da representação decimal de a tem que ser um divisor de φ(m). m Terminamos esta breve digressão com duas observações. Verifica-se que quando o denominador m é primo e o período n da representação decimal é par, o bloco peri odico tem a propriedade de que a soma das suas metades é da forma Por exemplo 3 7 = = e = 999, e =
8 A justificação deste facto pode ser feita por uma aplicação igualmente simples das mesmas ideias e é deixada como exercício. A segunda observação é que nada do que se disse depende essencialmente de representarmos os números na base 10. É portanto possível deduzir propriedades semelhantes para a representação de números em qualquer base inteira b, ou seja, no caso 0 < x < 1, na forma x = i 1 c ib i. 1.2 Nota sobre o cálculo eficiente de potências Mesmo com todas as simplificações descritas anteriormente, somos irremediavelmente conduzidos, na resolução de equações modulares, à determinação da classe de congruência de potências por vezes com expoente muito grande. Naturalmente, o cálculo de potências deve ser feito iterativamente, reduzindo módulo m em cada passo; por exemplo, para calcular 2 12 módulo 19, teríamos sucessivamente 2 2 = 4; 2 3 = 8; 2 4 = 16; 2 5 = 32 13; ; ; ; ; ; ; Estes cálculos podem ainda ser simplificados e no caso de módulos e expoentes grandes, essa simplificação ganha maior importância; uma das maneiras de calcular eficientemente a n mod m passa por escrever o expoente como uma soma de potências de 2 n = 2 k k kr, k 1 < k 2 < < k r calcular a 2k mod m para cada k, levantando sucessivamente ao quadrado a potência anterior, e multiplicar os valores correspondentes. 8
9 Por exemplo, para calcular k módulo 853 mod 853, calculando primeiro as potências 7 2 = = 49 2 = = = = = = = e como 327 = , temos usando a tabela anterior Note-se que neste processo nunca usamos números superiores a m 2. Se calculássemos directamente obteríamos um número com 277 algarismos que teria depois que ser reduzido mod 853. E mesmo que reduzíssemos mod 853 a cada multiplicação, como no exemplo anterior, teríamos 327 multiplicações, enquanto que deste modo temos 12 multiplicações (mais as divisões para determinar a decomposição do expoente em soma de potências de 2). Na implementação deste algoritmo, mesmo no cálculo manual, as tarefas anteriores (determinar a representação na base 2 do expoente n n = b 0 + b b b l 2 l b i {0, 1} calcular as potências a 2k mod m e multiplicar as que correspondem a potências 2 k com b k = 1), descritas separadamente para clarificação da ideia envolvida, devem ser levadas a cabo ao mesmo tempo; eis uma descrição esquemática do algoritmo para calcular a n mod m: 1. Inincializamos variáveis j = n, x = 1 e c = a; 9
10 2. enquanto j > 0, a) se j é par, substituir j por j 2 e c por c2 e reduzir mod m; b) se j é ímpar substituir j por j 1 e x por cx e reduzir mod m 3. se j = 0, x a n mod m. A ideia do algoritmo é que se n = r i=0 b i2 i é a representação binária do expoente, se tem ( a n = a ) b 0 a 2 b 1 ( ) a 4 b 2 ( ) a 2 r br e que esses produtos se podem fazer, passo a passo, ao mesmo tempo que vamos deduzindo os b i. A variável x representa os sucessivos valores que o produto vai tomando e é naturalmente inicializado em 1; se n é ímpar, ou seja b 0 = 1, temos a n = a a n 1 enquanto que para n par (e portanto b 0 = 0) a n = (a 2 ) n/2 No primeiro caso actualizamos o produto e no segundo a base; o novo expoente é sempre menor que o anterior pelo que este processo termina. Exemplo 1.11 : Calcular 3 21 módulo 37; no quadro seguinte apresentamos à esquerda os passos do algoritmo com os sucessivos valores das variáveis, sempre reduzidos módulo 37, acompanhados à direita pela sua tradução no cálculo; note-se nesta coluna que o valor de 3 21 módulo 37 é sucessivamente representado pelo produto de um primeiro factor que corresponde ao valor de x nesse passo, e um segundo que é a parte ainda por calcular. 10
11 j c x = = = 3 (3 2 ) = 3 (3 4 ) = (3 3 4 ) (3 4 ) = (3 3 4 ) (3 8 ) = (3 3 4 ) = Testes de primalidade O Teorema de Fermat está na base de testes de primalidade: seja m > 1 e a primo com m. Se a m 1 não for congruente com 1 módulo m então m não é primo. Por exemplo, se m = 299 e a = 2, o cálculo de mod 299 dá-nos, pelo método descrito anteriormente 11
12 j c x e portanto não é primo. mod 299 comprovando que o módulo em questão Se a m 1 1 mod m então o teste é inconclusivo. Por exemplo mod 341 mas 341 não é primo, como se pode comprovar repetindo o teste com base 3 já que mod 341. No entanto, existem inteiros m compostos para os quais o teste falha para todas as bases primas com m. Esses números designam-se por números de Carmichael (em homenagem ao matemático R. Carmichael que identificou os primeiros exemplos em 1910) e o menor deles é 561 = (ver o exercício 5. da Ficha 5). A conjectura de que existem infinitos números de Carmichael (avançada pelo próprio Carmichael em 1910) foi comprovada em 1994 por Alford, Granville e Pomerance. Prova-se também o seguinte Proposição 1.12 Critério de Korselt: Um inteiro composto m é um número de Carmichael se e só se for ímpar e, para cada primo p que divida m se verificam as condições 12
13 p 2 não divide m; (p 1) (m 1); É no entanto possível deduzir critérios de primalidade mais eficazes: suponhamos que m é primo e que m 1 = 2 k q com q ímpar. Dado a primo com m, ou bem que ou então existe 0 < j k tal que a q 1 mod m a 2jq 1 mod m e a 2j 1q 1 mod m De facto, se a q não for congruente com 1, tem que existir um primeiro j tal que a 2jq 1, já que pelo menos para j = k isso acontece de certeza (sempre supondo que m é primo, bem entendido). Mas então, pondo b = a 2j 1q, temos que b 2 1 mod m o que implica b ±1 mod m (porque m é primo!). Como por hipótese b não é congruente com 1, tem que ser b 1. Este raciocínio conduz ao Proposição 1.13 Critério de Rabin-Miller: Seja m ímpar e m 1 = 2 k q com q ímpar. Se, para algum a primo com m, se verificam ambas as condições a q não é congruente com 1 módulo m, a 2jq não é congruente com 1 módulo m, para j = 0, 1,, k 1 então m é composto. Este critério é muito mais eficaz para determinar que um inteiro é composto, nomeadamente porque se pode provar que para qualquer m composto, pelo menos 3/4 de todos os a primos com m permitem verificar esse facto através do Critério de Rabin-Miller. 13
14 Um outro exemplo de aplicação do Teorema de Fermat como teste de primalidade é o seguinte: recorde-se que os números de Mersenne são os inteiros da forma 2 p 1, com p primo. Se p for razoavelmente grande, pode tornar-se extremamente difícil decidir se esse número é ou não primo. Uma primeira simplificação do problema decorre do Teorema de Fermat: suponhamos que q é um factor primo de 2 p 1, com p um primo maior que 2. O Teorema de Fermat garante também que q divide 2 q 1 1, logo q divide o máximo divisor comum de 2 p 1 e 2 q 1 1; este máximo divisor comum é de facto (ver o exercício 14. da Ficha 2) 2 mdc(p,q 1) 1; mas como p é primo temos então que mdc(p, q 1) = p ou seja q = 1+tp para algum inteiro p; note-se que t tem que ser par (p e q sã ímpares) e portanto concluímos que os factores primos de 2 p 1 são da forma 1 + 2kp. 1.4 Raizes módulo m O Teorema de Euler permite igualmente abordar a resolução de equações do tipo x k b mod m Suponhamos primeiro que b é primo com m e que k é primo com φ(m); então existem inteiros u, v tais que portanto ku φ(m)v = 1 x k b x ku b u xx φ(m)v b u mod m Mas se x for solução da equação terá que ser primo com m logo, pelo Teorema de Euler, temos x k b x b u mod m que é de facto a solução da equação: (b u ) k = b 1+φ(m)v b mod m 14
15 Proposição 1.14 : Se mdc(b, m) = 1 e mdc(k, φ(m)) = 1, a equação x k b mod m tem a solução única b u onde u é um inteiro satisfazendo ku 1 mod φ(m) Nota 1.15 : A equação anterior tem solução única mesmo se mdc(b, m) > 1, desde que mdc(k, φ(m)) = 1 e que m seja livre de quadrados, isto é, que m seja o produto de primos distintos. Sem essas condições, a solução da equação pode não existir ou não ser única, como teremos oportunidade de ver mais adiante. Exemplo 1.16 : Resolver x 29 2 mod 117 ; 117 = 13 9 e portanto φ(117) = φ(13)φ(9) = 12 6 = 72 Estamos nas condições da proposição; aplicando o algoritmo de Euclides verificamos que 1 = Logo a única solução da equação é 2 5 = 32. É claro que pode ser mais útil começar por aplicar o Teorema Chinês dos Restos: Exemplo 1.17 : Como 91 = 7 13, a resolver a equação x mod 91 é equivalente a resolver o sistema x mod 7 x 3 mod 7 x mod 13 x 7 4 mod 13 15
16 Nota 1.18 : A resolução deste tipo de equações modulares passa, como vimos, por levantar ambos os membros da equação a uma mesma potência; por exemplo, na segunda equação do exemplo anterior, temos x 7 4 mod 13 x mod13 x 4 7 mod 13, uma vez que 7 7 = 49 = Será que podemos, em geral, usar esta operação de levantar ambos os membros de uma equação a uma mesma potência para obter uma equação mais simples? Tal como na situação bem conhecida de uma equação sobre R, isso tem que ser feito com cuidado: no nosso exemplo, primeira passagem é uma equivalência porque a potência usada é prima com φ(13); se não for assim, temos apenas uma implicação. Por exemplo x 3 3 mod 5 = x 6 9 mod 5 x 2 4 mod 5; mas esta última equação tem claramente duas soluções, as classes de congruência módulo 5 de 2 e de 3, enquanto que a equação original só tem uma Aplicação à Criptografia A única dificuldade na resolução da equação x k b mod m nas condições da proposição anterior está na determinação de φ(m), que depende do conhecimento da factorização de m. Mas essa dificuldade é, de um modo geral, muito grande. O problema está em que, apesar de existirem métodos para procurar os factores de um inteiro muito mais eficazes do que tentar sistematicamente a divisão por primos, não existe ainda um algoritmo eficaz para factorizar um inteiro m > , por exemplo. Essa deficiência da Teoria dos Números acabou por ser aproveitada para a implementação de um sistema de codificação, o algoritmo RSA (dos nomes 16
17 dos seus criadores Rivest, Shamir e Andleman). Ao contrário de outros sistemas de codificação em que o método de codificar uma mensagem, a chamada chave de codificação, tem que ser mantido secreto, o RSA é um sistema de chave pública, isto é, qualquer pessoa pode codificar uma mensagem. O sistema RSA consiste muito resumidamente no seguinte: escolhem-se dois primos p e q grandes, define-se m = p q e escolhe-se um expoente k primo com φ(m) = (p 1)(q 1). Tornam-se públicos m e k que são os elementos necessários à codificação: uma mensagem é transformada numa sequência de inteiros 0 < a < m; a codificação de a é o inteiro b a k mod m. O problema de descodificar uma mensagem equivale ao de, dado um inteiro b, resolver a k b mod m Ora, para m muito grande, sem conhecer os factores de m é virtualmente impossível determinar φ(m) e portanto resolver a equção. Evidentemente, a implementação prática desta ideia geral exige vários cuidados; para mencionar apenas um, se k t 1 mod φ(m) para t pequeno, qualquer pessoa pode descoficiar uma mensagem, recodificando-a t 1 vezes. 17
3.3 Congruências e aritmética modular
 40 CHAPTER 3. ELEMENTOS DE ARITMÉTICA DOS INTEIROS 3.3 Congruências e aritmética modular Consideremos primeiro o seguinte exemplo: o que podemos dizer sobre a imagem da função f : Z Z, f(x) =x 2 + x +
40 CHAPTER 3. ELEMENTOS DE ARITMÉTICA DOS INTEIROS 3.3 Congruências e aritmética modular Consideremos primeiro o seguinte exemplo: o que podemos dizer sobre a imagem da função f : Z Z, f(x) =x 2 + x +
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1. O que podemos dizer sobre a imagem da função. f : Z Z, f(x) = x 2 + x + 1?
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Elementos de Matemática Finita ( ) Exercícios resolvidos
 Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Existem infinitos números de Carmichael, mas não provaremos isso neste curso.
 6 Pseudoprimos 6.1 O Pequeno Teorema de Fermat nos diz que, se n é primo, então temos b n b (mod n) para todo b Z. Portanto, a contrapositiva diz que se temos b n b (mod n) ( ) para algum b Z, então n
6 Pseudoprimos 6.1 O Pequeno Teorema de Fermat nos diz que, se n é primo, então temos b n b (mod n) para todo b Z. Portanto, a contrapositiva diz que se temos b n b (mod n) ( ) para algum b Z, então n
, com k 1, p 1, p 2,..., p k números primos e α i, β i 0 inteiros, as factorizações de dois números inteiros a, b maiores do que 1.
 Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ
 NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Universidade do Minho
 Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
Números Primos e Criptografia RSA
 Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
MA14 - Aritmética Unidade 20 Resumo. Teoremas de Euler e de Wilson
 MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
1 Congruência. 2. m mmc(n, m) m a b. De 1) e 2) segue que: a b mod n e a b mod m.
 1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
Se mdc(a,m) = 1, como a é invertível módulo m, a equação. ax b (mod m)
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz. EST Setúbal / IPS Maio 2012
 MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
NÚMEROS ESPECIAIS. Luciana Santos da Silva Martino. lulismartino.wordpress.com PROFMAT - Colégio Pedro II
 Sumário NÚMEROS ESPECIAIS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 27 de outubro de 2017 Sumário 1 Primos de Fermat, de Mersenne e em
Sumário NÚMEROS ESPECIAIS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 27 de outubro de 2017 Sumário 1 Primos de Fermat, de Mersenne e em
Números Inteiros Algoritmo da Divisão e suas Aplicações
 Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Teorema Chinês dos Restos. Tópicos Adicionais
 Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Notas sobre teoria dos números (3)
 1 / 21 Notas sobre teoria dos números (3) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 21 Teorema
1 / 21 Notas sobre teoria dos números (3) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 21 Teorema
11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA
 Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Note-se que pelo Teorema de Euler. a φ(n) 1 (mod n) logo existe k nas condições da definição acima e. Raízes Primitivas. Ordem de um elemento
 Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
parciais primeira parte
 MÓDULO - AULA 3 Aula 3 Técnicas de integração frações parciais primeira parte Objetivo Aprender a técnica de integração conhecida como frações parciais. Introdução A técnica que você aprenderá agora lhe
MÓDULO - AULA 3 Aula 3 Técnicas de integração frações parciais primeira parte Objetivo Aprender a técnica de integração conhecida como frações parciais. Introdução A técnica que você aprenderá agora lhe
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
RSA: ALGORITMOS DE CHAVE PÚBLICA PRIMEIRA PUBLICAÇÃO: ABRIL/1998 QUARTA REVISÃO: DEZEMBRO/2004
 Teoria e Implementação Chave Pública São algoritmos baseados em propriedades matemáticas que possibilitam o processo de criptografia (encrypt) a partir de uma chave de conhecimento público (K P ), mas
Teoria e Implementação Chave Pública São algoritmos baseados em propriedades matemáticas que possibilitam o processo de criptografia (encrypt) a partir de uma chave de conhecimento público (K P ), mas
Tópicos de Matemática Elementar
 Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido
 Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Introdução Objetivo: estudar o método
Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Introdução Objetivo: estudar o método
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
(Ciência de Computadores) 2005/ Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação
 Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
Conjuntos. Notações e Símbolos
 Conjuntos A linguagem de conjuntos é interessante para designar uma coleção de objetos. Quando os estatísticos selecionam indivíduos de uma população eles usam a palavra amostra, frequentemente. Todas
Conjuntos A linguagem de conjuntos é interessante para designar uma coleção de objetos. Quando os estatísticos selecionam indivíduos de uma população eles usam a palavra amostra, frequentemente. Todas
REVISÃO DOS CONTEÚDOS
 REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
REVISÃO DOS CONTEÚDOS As quatro operações fundamentais As operações fundamentais da matemática são quatro: Adição (+), Subtração (-), Multiplicação (* ou x ou.) e Divisão (: ou / ou ). Em linguagem comum,
Já sabemos como determinar todas as soluções de uma equação diofantina linear, caso esta seja resolúvel. Para conguências temos:
 Seguidamente vamos determinar valores de b (em termos de a e n) para os quais a congruência ax b (mod n) tem solução. Se a = 0 esta congruência tem solução x se e só se n b, e, neste caso, qualquer x Z
Seguidamente vamos determinar valores de b (em termos de a e n) para os quais a congruência ax b (mod n) tem solução. Se a = 0 esta congruência tem solução x se e só se n b, e, neste caso, qualquer x Z
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO GLOBAL Múltiplos e divisores. Critérios de divisibilidade. - Escrever múltiplos
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO GLOBAL Múltiplos e divisores. Critérios de divisibilidade. - Escrever múltiplos
Curso Satélite de. Matemática. Sessão n.º 1. Universidade Portucalense
 Curso Satélite de Matemática Sessão n.º 1 Universidade Portucalense Conceitos Algébricos Propriedades das operações de números reais Considerem-se três números reais quaisquer, a, b e c. 1. A adição de
Curso Satélite de Matemática Sessão n.º 1 Universidade Portucalense Conceitos Algébricos Propriedades das operações de números reais Considerem-se três números reais quaisquer, a, b e c. 1. A adição de
1).- Significado de congruência e de congruência numérica
 5. CONGRUÊNCIAS NUMÉRICAS 1). Significado de congruência e de congruência numérica 2). Exemplos exploratórios e a notação mod q 3). Definição geral de congruência numérica 4). Regras: somando e multiplicando
5. CONGRUÊNCIAS NUMÉRICAS 1). Significado de congruência e de congruência numérica 2). Exemplos exploratórios e a notação mod q 3). Definição geral de congruência numérica 4). Regras: somando e multiplicando
XIX Semana Olímpica de Matemática. Nível 3. Polinômios Ciclotômicos e Congruência Módulo p. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
SISTEMA DECIMAL. No sistema decimal o símbolo 0 (zero) posicionado à direita implica em multiplicar a grandeza pela base, ou seja, por 10 (dez).
 SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO ANUAL Planificação 7º ano 2010/2011 Página 1 DOMÍNIO TEMÁTICO: NÚMEROS
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO ANUAL Planificação 7º ano 2010/2011 Página 1 DOMÍNIO TEMÁTICO: NÚMEROS
Teoria dos Números e Criptografia
 Universidade Federal de São Carlos Departamento de Matemática Teoria dos Números e Criptografia Autor: Henrique Favarom Barbosa Este texto foi editado em L A TEX 2ε pelo autor, que agradece á comunidade
Universidade Federal de São Carlos Departamento de Matemática Teoria dos Números e Criptografia Autor: Henrique Favarom Barbosa Este texto foi editado em L A TEX 2ε pelo autor, que agradece á comunidade
1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL
 1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 30 de março de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. Calcule uma estimativa
1 TESTE OPÇÃO II - TEORIA DE NÚMEROS COMPUTACIONAL Licenciatura em Matemática 30 de março de 2012 duração 1h 45m Responda, justificando cuidadosamente, às seguintes questões: 1. Calcule uma estimativa
Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c.
 Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Dízimas e intervalos encaixados.
 Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Soma de Quadrados. Faculdade de Matemática, UFU, MG
 Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
S. C. COUTINHO. = 2n 2 r 2 m 1. Como 2 n 2 r = 2 r (2 n r 1) = 2 r (2 mq 1), então 2 n 2 r 2 m 1 = 2r (2 m 1)(2 mq ) Q = (2n 1) (2 r 1) 2 m 1
 DEPARTAMENTO DE CIÊNCIA DA COMPUTAÇÃO UFRJ NÚMEROS INTEIROS E CRIPTOGRAFIA RSA S. C. COUTINHO 1. Respostas dos exercícios do capítulo 1 (1) (a) mdc(14, 35) = 7; α = 2 e β = 1; (b) mdc(252, 180) = 36, α
DEPARTAMENTO DE CIÊNCIA DA COMPUTAÇÃO UFRJ NÚMEROS INTEIROS E CRIPTOGRAFIA RSA S. C. COUTINHO 1. Respostas dos exercícios do capítulo 1 (1) (a) mdc(14, 35) = 7; α = 2 e β = 1; (b) mdc(252, 180) = 36, α
D OLJHLUD UDSRVD PDUURP VDOWRX VREUH R FDFKRUUR FDQVDGR 1
 Matemática Discreta October 12, 2018 1 1 Criptografia Criptografia de chave secreta: quando remetente e destinatário concordam um código. Exemplo: Código de Caesar O que está escríto? D OLJHLUD UDSRVD
Matemática Discreta October 12, 2018 1 1 Criptografia Criptografia de chave secreta: quando remetente e destinatário concordam um código. Exemplo: Código de Caesar O que está escríto? D OLJHLUD UDSRVD
PK - Public Key RSA. Segurança RSA
 Introdução à Chave Pública PK - Public Key RSA Exponenciação rápida Segurança RSA Compartilhamento de chaves Algoritmo de chave simétrica Necessário compartilhar uma chave secreta previamente Chave que
Introdução à Chave Pública PK - Public Key RSA Exponenciação rápida Segurança RSA Compartilhamento de chaves Algoritmo de chave simétrica Necessário compartilhar uma chave secreta previamente Chave que
SISTEMA CRIPTOGRÁFICO RSA. Chave pública: (n, a) onde a N <(p 1)(q 1) e mdc(a, (p 1)(q 1)) = 1. Chave privada: (n, b)
 SISTEMA CRIPTOGRÁFICO RSA Espaço das mensagens: N
SISTEMA CRIPTOGRÁFICO RSA Espaço das mensagens: N
Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um
 FRAÇÕES Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria
FRAÇÕES Podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria
O REI MALIGNO E A PRINCESA GENEROSA: SOBRE BASES NUMÉRICAS E CRITÉRIOS DE DIVISIBILIDADE
 O REI MALIGNO E A PRINCESA GENEROSA: SOBRE BASES NUMÉRICAS E CRITÉRIOS DE DIVISIBILIDADE ANA PAULA CHAVES AND THIAGO PORTO 1. Introdução Os temas centrais deste texto - bases numéricas e critérios de divisibilidade
O REI MALIGNO E A PRINCESA GENEROSA: SOBRE BASES NUMÉRICAS E CRITÉRIOS DE DIVISIBILIDADE ANA PAULA CHAVES AND THIAGO PORTO 1. Introdução Os temas centrais deste texto - bases numéricas e critérios de divisibilidade
MA14 - Aritmética Unidade 22 Resumo. Aritmética das Classes Residuais
 MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Apontamentos de Matemática 6.º ano
 Revisão (divisores de um número) Os divisores de um número são os números naturais pelos quais podemos dividir esse número de forma exata (resto zero). Exemplos: Os divisores de 4 são 1, e 4, pois se dividirmos
Revisão (divisores de um número) Os divisores de um número são os números naturais pelos quais podemos dividir esse número de forma exata (resto zero). Exemplos: Os divisores de 4 são 1, e 4, pois se dividirmos
MA14 - Aritmética Unidade 15 - Parte 1 Resumo. Congruências
 MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
Cálculo com expressões que envolvem radicais
 Escola Secundária de Aljustrel Material de apoio para o 11. o Ano Ano Lectivo 00/003 Cálculo com expressões que envolvem radicais José Paulo Coelho Abril de 003 ... Índice... 1 Radicais: definição e propriedades.
Escola Secundária de Aljustrel Material de apoio para o 11. o Ano Ano Lectivo 00/003 Cálculo com expressões que envolvem radicais José Paulo Coelho Abril de 003 ... Índice... 1 Radicais: definição e propriedades.
Elementos de Matemática Finita ( ) Exercícios resolvidos
 Elementos de Matemática Finita (016-017 Exercícios resolvidos Ficha 7-1. ( ( 30 10 0 10. Ficha 7 -. 4 10 ( 4 10. Ficha 7-3. A resposta à primeira pergunta é (5 3 ( 5 6. A probabilidade de acertar exactamente
Elementos de Matemática Finita (016-017 Exercícios resolvidos Ficha 7-1. ( ( 30 10 0 10. Ficha 7 -. 4 10 ( 4 10. Ficha 7-3. A resposta à primeira pergunta é (5 3 ( 5 6. A probabilidade de acertar exactamente
MA14 - Aritmética Unidade 15 - Parte 2 Resumo
 MA14 - Aritmética Unidade 15 - Parte 2 Resumo Aplicações de Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante
MA14 - Aritmética Unidade 15 - Parte 2 Resumo Aplicações de Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante
Matemática A - 10 o Ano
 Matemática A - 10 o Ano Resolução da Ficha de Trabalho Álgebra - Divisão Inteira de Polinómios Grupo I 1. Considerando os polinómios p e b no enunciado temos que o termo de maior grau de p b é a nx n b
Matemática A - 10 o Ano Resolução da Ficha de Trabalho Álgebra - Divisão Inteira de Polinómios Grupo I 1. Considerando os polinómios p e b no enunciado temos que o termo de maior grau de p b é a nx n b
MATEMÁTICA MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
OBMEP 2010 Soluções da prova da 2ª Fase Nível 2. Questão 1
 Questão a) Para saber o número que deve dizer ao matemágico, Joãozinho deve fazer quatro contas: ª conta: multiplicar o número no cartão escolhido por 2; 2ª conta: somar 3 ao resultado da primeira conta;
Questão a) Para saber o número que deve dizer ao matemágico, Joãozinho deve fazer quatro contas: ª conta: multiplicar o número no cartão escolhido por 2; 2ª conta: somar 3 ao resultado da primeira conta;
1 Grupos (23/04) Sim(R 2 ) T T
 1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
Exemplos: Os números 12, 18 e 30 têm conjuntos de divisores respectivamente iguais a:
 Lista de atividades sobre MDC. Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum e o mıınimo múltiplo comum de números naturais, bem como algumas de suas propri edades.
Lista de atividades sobre MDC. Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum e o mıınimo múltiplo comum de números naturais, bem como algumas de suas propri edades.
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
Números Racionais. MAT1514 MEB 2/2016 T42 Diurno Substituição da Profa. Martha Monteiro
 Números Racionais MAT1514 MEB 2/2016 T42 Diurno Substituição da Profa. Martha Monteiro O que são números racionais? Alguma definição? Como surgiram? Relacionados a quais ideias ou situações? Representação
Números Racionais MAT1514 MEB 2/2016 T42 Diurno Substituição da Profa. Martha Monteiro O que são números racionais? Alguma definição? Como surgiram? Relacionados a quais ideias ou situações? Representação
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se
 Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira
 Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
AGRUPAMENTO DE ESCOLAS DE MIRA Escola Sec/3 Drª. Maria Cândida. PLANIFICAÇÃO ANUAL MATEMÁTICA 8º Ano Ano Letivo 2016/2017. Objetivos específicos
 1º Período TEMA 1: NÚMEROS RACIONAIS. NÚMEROS REAIS N. de blocos previstos: 15 1.1. Representação de números reais através de dízimas 1.2. Conversão em fração de uma dízima infinita periódica 1.3. Potências
1º Período TEMA 1: NÚMEROS RACIONAIS. NÚMEROS REAIS N. de blocos previstos: 15 1.1. Representação de números reais através de dízimas 1.2. Conversão em fração de uma dízima infinita periódica 1.3. Potências
1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).
![1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n). 1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).](/thumbs/98/136620653.jpg) Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
Resumo. Palavras-chave: implementações aritméticas; inverso modular; sistema de restos.
 2017, NÚMERO 1, VOLUME 5 ISSN 2319-023X Universidade Federal de Sergipe - UFS evilson@ufs.br Resumo Neste trabalho apresentamos uma implementação para execução manual do algoritmo estendido das divisões
2017, NÚMERO 1, VOLUME 5 ISSN 2319-023X Universidade Federal de Sergipe - UFS evilson@ufs.br Resumo Neste trabalho apresentamos uma implementação para execução manual do algoritmo estendido das divisões
Números primos e Criptografia
 1 Universidade de São Paulo/Faculdade de Educação Seminários de Ensino de Matemática (SEMA-FEUSP) Coordenador: Nílson José Machado novembro/2008 Números primos e Criptografia Marisa Ortegoza da Cunha marisa.ortegoza@bol.com.br
1 Universidade de São Paulo/Faculdade de Educação Seminários de Ensino de Matemática (SEMA-FEUSP) Coordenador: Nílson José Machado novembro/2008 Números primos e Criptografia Marisa Ortegoza da Cunha marisa.ortegoza@bol.com.br
Notas sobre teoria dos números (2)
 1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
Funções - Primeira Lista de Exercícios
 Funções - Primeira Lista de Exercícios Vers~ao de 0/03/00 Recomendações Não é necessário o uso de teoremas ou resultados complicados nas resoluções. Basta que você tente desenvolver suas idéias. Faltando
Funções - Primeira Lista de Exercícios Vers~ao de 0/03/00 Recomendações Não é necessário o uso de teoremas ou resultados complicados nas resoluções. Basta que você tente desenvolver suas idéias. Faltando
Equação algébrica Equação polinomial ou algébrica é toda equação na forma anxn + an 1 xn 1 + an 2 xn a 2 x 2 + a 1 x + a 0, sendo x
 EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA
 NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA NOTAS DE AULA: REPRESENTAÇÕES DECIMAIS A representação decimal é a forma como escrevemos um número em uma única base, e como essa
NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA NOTAS DE AULA: REPRESENTAÇÕES DECIMAIS A representação decimal é a forma como escrevemos um número em uma única base, e como essa
Representação decimal dos números racionais
 Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 21 de março de 2018 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta
Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 21 de março de 2018 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta
Introdução: A necessidade de ampliação dos conjuntos Numéricos. Considere incialmente o conjunto dos números naturais :
 Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
TESTES DE PRIMALIDADE
 TESTES DE PRIMALIDADE MOTIVACAO Testes de primalidade são ingredientes essenciais em sistemas de segurança computadorizados. Há uma série de sistemas de segurança que contam com a suposição que é difícil
TESTES DE PRIMALIDADE MOTIVACAO Testes de primalidade são ingredientes essenciais em sistemas de segurança computadorizados. Há uma série de sistemas de segurança que contam com a suposição que é difícil
Diagonal mais curta. Como d = mx e l = nx, teríamos: l 1 = d l = mx nx = (m n)x = n 1 x. d 1 = a:d + b:l = amx + bnx = (am + bn)x = m 1 x
 Diagonal mais curta Seja P um polígono regular de lados ( > 6), d a medida da sua diagonal mais curta e l a medida do seu lado. Supondo que d e l são comensuráveis, temos d mx e l nx, onde m e n são inteiros
Diagonal mais curta Seja P um polígono regular de lados ( > 6), d a medida da sua diagonal mais curta e l a medida do seu lado. Supondo que d e l são comensuráveis, temos d mx e l nx, onde m e n são inteiros
MA14 - Aritmética Lista 1. Unidades 1 e 2
 MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
Polos Olímpicos de Treinamento. Aula 9. Curso de Teoria dos Números - Nível 2. O Teorema de Euler. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
1 n s = s s s p s. ζ(s) = p
 Introdução A chamada série harmónica, n= n = + 2 + 3 + +... desde cedo suscitou interesse entre os 4 matemáticos. Infelizmente esta série diverge, o que se verifica por os termos termo n, apesar de tenderem
Introdução A chamada série harmónica, n= n = + 2 + 3 + +... desde cedo suscitou interesse entre os 4 matemáticos. Infelizmente esta série diverge, o que se verifica por os termos termo n, apesar de tenderem
MAT Álgebra I para Licenciatura 2 a Lista de exercícios
 MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
NÚMEROS DE FERMAT. (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal)
 NÚMEROS DE FERMAT (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal) Intrudução: O matemático francês Pierre de fermat (1601-1665) é famoso pelo seu extensivo trabalho em teoria dos números. Suas
NÚMEROS DE FERMAT (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal) Intrudução: O matemático francês Pierre de fermat (1601-1665) é famoso pelo seu extensivo trabalho em teoria dos números. Suas
Resposta:
 Gabarito - Dia 1 Exercício 1. Utilizando a Cifra de ATBASH decifre a mensagem VHHV VCVIXRXRL V UZXRO. Esse exercício é fácil. Exercício 2. Utilize o código de Políbio para codicar a mensagem Pensar é um
Gabarito - Dia 1 Exercício 1. Utilizando a Cifra de ATBASH decifre a mensagem VHHV VCVIXRXRL V UZXRO. Esse exercício é fácil. Exercício 2. Utilize o código de Políbio para codicar a mensagem Pensar é um
Este material é apenas um resumo de parte do conteúdo da disciplina.
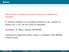 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
(Aprovado em Conselho Pedagógico de 18 de julho de 2016 ) CONHECIMENTOS CONTEÚDOS OBJETIVOS/METAS CURRICULARES CAPACIDADES
 Escola EB1 João de Deus COD. 242 937 Escola Secundária 2-3 de Clara de Resende COD. 346 779 Critérios de Avaliação Perfil de Aprendizagens Específicas (Aprovado em Conselho Pedagógico de 18 de julho de
Escola EB1 João de Deus COD. 242 937 Escola Secundária 2-3 de Clara de Resende COD. 346 779 Critérios de Avaliação Perfil de Aprendizagens Específicas (Aprovado em Conselho Pedagógico de 18 de julho de
Gabarito e Pauta de Correção ENQ
 Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
Gabarito e Pauta de Correção ENQ 015.1 Questão 01 [ 1,00 ::: (a=0,50; (b=0,50 ] (a Mostre que se x e y são números irracionais tais que x y seja racional não nulo, então x + y e x y são ambos irracionais.
Representação decimal dos números racionais
 Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 4 de abril de 2017 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta é
Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 4 de abril de 2017 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta é
NÚMEROS INTEIROS. Álgebra Abstrata - Verão 2012
 NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
Polinómios. Integração de Funções Racionais
 Polinómios. Integração de Funções Racionais Escola Superior de Tecnologia e de Gestão, Instituto Politécnico de Bragança. Mário Abrantes 2016 1 / 17 Índice de Matérias 1. Polinómios Denição Factorização
Polinómios. Integração de Funções Racionais Escola Superior de Tecnologia e de Gestão, Instituto Politécnico de Bragança. Mário Abrantes 2016 1 / 17 Índice de Matérias 1. Polinómios Denição Factorização
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Notas sobre os anéis Z m
 Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco
 MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco MÓDULO 3 Números Racionais e Operações com Frações 1.INTRODUÇÃO Quando dividimos um objeto em partes iguais, uma dessas partes ou a reunião de várias delas
MATEMÁTICA 1 ARITMÉTICA Professor Matheus Secco MÓDULO 3 Números Racionais e Operações com Frações 1.INTRODUÇÃO Quando dividimos um objeto em partes iguais, uma dessas partes ou a reunião de várias delas
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Portal da OBMEP. Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
ax + by 347 = 0 k = text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: DOCENTES: Gilda Ferreira e Ana Nunes
 text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
4 de outubro de MAT140 - Cálculo I - Método de integração: Frações Parciais
 MAT140 - Cálculo I - Método de integração: Frações Parciais 4 de outubro de 2015 Iremos agora desenvolver técnicas para resolver integrais de funções racionais, conhecido como método de integração por
MAT140 - Cálculo I - Método de integração: Frações Parciais 4 de outubro de 2015 Iremos agora desenvolver técnicas para resolver integrais de funções racionais, conhecido como método de integração por
