Ajuste de dados experimentais
|
|
|
- Vanessa Cesário Fragoso
- 8 Há anos
- Visualizações:
Transcrição
1 Capítulo 8 8. Itrodução Uma forma de trabalhar com uma fução defda por uma tabela de valores é a terpolação polomal. Etretato esta ão é acoselhável quado:. é precso obter um valor aproxmado da fução em algum poto fora do tervalo de tabelameto,ou seja,quado se quer extrapolar; 2. os valores tabelados são resultado de algum expermeto físco ou de alguma pesqusa, porque,estes casos,estes valores podem coter erros eretes que,em geral,ão são prevsíves. Surge,etão,a ecessdade de se ajustar a estas fuções tabeladas uma fução que seja uma boa aproxmação para os valores tabelados e que permta extrapolar com certa margem de seguraça. Exemplo 8. Cosdere um teste de desempeho de um automóvel. Este é acelerado a partr do repouso e depos vaja com aceleração máxma até que sua velocdade atja km/h. Equato sto, as leturas o velocímetro são realzadas a cada s. Quado a velocdade é grafcada como fução do tempo, obtém-se um cojuto de potos. Sera esperado que estes potos defssem uma curva suave. No etato, erros de medda e outros fatores fazem com que os potos ão fquem tão bem arrajados: algus dos valores regstrados para a velocdade fcam muto altos e outros, muto baxos. Supodo que se desejasse determar a velocdade aos 6, 5s, sera possível terpolar etre as leturas fetas aos 6s e 7s, mas como provavelmete exste algum erro estas meddas, o valor assm obtdo podera ão ser uma boa aproxmação para o valor desejado. O que fazer? A solução para o problema é tetar ajustar uma provável curva ao cojuto de dados. Como épossível que város destes dados ão sejam precsos,esta curva ão precsa,ecessaramete, passar por ehum dos potos. Por outro lado,como os erros de medda provavelmete ão são tão grades,a curva devera pelo meos passar perto de cada poto: provavelmete acma de us eabaxodeoutros. Naverdade,aovés de procurar a fução f que passa por cada um dos dados expermetas,calcula-se a fução que melhor se ajusta a eles. Exemplo 8.2 Supoha que os dados abaxo temperatura T a cada período de tempo t foram obtdos em um expermeto um laboratóro: t T 5, 28, 4 45, 3 58, 6 77, 4 e o gráfco exbdo a fgura 8.2 sugere que esses dados podem ser aproxmados razoavelmete bem por uma reta. Assm, se for ecessárosaberovalordet o tempo t, 5, podemos obter a 46
2 Fgura 8.: Gráfco v t, com erros as meddas de v. Fgura 8.2: Dados expermetas. equação da reta que melhor aproxma os potos obtdos expermetalmete e, etão, calcular o valor de T de acordo com aquela reta. Apergutaquesurgeé: dado um cojuto de dados,como fazer o ajuste? Ao aproxmar uma fução f por uma fução g de uma famíla G, é troduzdo um certo erro r,deomado resíduo, sto é, r(x) f(x) g(x) (8.) Aparetemete,uma boa aproxmação sera obtda fazedo x r(x). No etato,sto ão é verdade. Supoha que,em um certo expermeto,foram obtdos os potos p, p 2, p 3 e p 4. Sabedo que o feômeo é descrto por uma reta,esta é determada de modo a satsfazer x r(x). Pode-se observar a fgura abaxo que as retas que foram traçadas obedecem tal crtéro,o que mostra que x r(x) ão éumaboaescolha. O problema efretado com este crtéro é o cacelameto dos erros postvos com os egatvos. Uma maera de evtar este cacelameto é trabalhar com o quadrado do resíduo e exgr que x r2 (x) sejamímo. O método para aproxmar uma fução f por uma g G utlzado este últmo crtéro é deomado método dos mímos quadrados. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 47
3 Fgura 8.3: Qual a melhor aproxmação, esse caso? 8.2 Mímos quadrados - domío dscreto Para aproxmar uma fução y f(x) tabelada em potos dsttos x,,, 2,...,,por uma fução g da forma m a k g k (x) (8.2) k Precsa-se determar a,a,...,a m que mmzam a soma dos quadrados dos resíduos os potos x,,, 2,...,. Para mmzar M(a,a,...,a m ) M(a,a,...,a m ) r 2 (x) (f(x ) g(x )) 2 (8.3) é precso que..., (8.4) a a a m Por outro lado,certamete exstem processos aturas que tem um comportameto expoecal, potecal e quadrátco,detro outros. Épossível,para um cojuto de dados expermetas, calcular o quão boa é uma determada aproxmação,escolhda prevamete. A segur,veremos como determar os coefcetes de uma determada fução de ajuste. 8.3 Ajuste lear Neste caso,determa-se os parâmetros a e a da reta a +a x de modo que a soma dos quadrados em cada poto seja míma. Em outras palavras,deseja-se determar a e a que mmzem Para sto,é ecessáro que M(a,a ) r 2 (x) (y a a x ) 2 (8.5) a e (8.6) a (8.7) A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 48
4 ou seja,que a 2 a 2 (y a a x )( ) (8.8) (y a a x )( x ) (8.9) Orgazado estas codções,tem-se { y a + a x x y a x + a x 2 e chega-se ao segute sstema lear: [ x x x2 ][ a ] a [ y ] x y (8.) (8.) deomado sstema ormal. Resolvedo este sstema,são obtdos os valores de a edea,ou seja,determa-se a equação (reta,o caso) de ajustameto. Exemplo 8.3 Como resultado de algum expermeto, supoha que são obtdos os segutes valores para a fução f: x f(x) 4 4 Determe a reta que melhor se ajusta a esta fução segudoométodo dos mímos quadrados. O sstema ormal correspodete é [ ][ ] [ ] 5 a 3 a 3 que tem solução a /5 e a /. Portato, a reta que aproxma f(x) é g(x) x Ajuste polomal Pode-se esteder o coceto de ajustameto de uma reta por mímos quadrados para o caso geral de um polômo de grau p. Neste caso,determa-se os parâmetros a,a,...,a p do polômo a + a x a p x p que mmzem M(a,a,...,a p ) Para sto,é ecessáro que r 2 (x) de ode se obtém o sstema + x... x x xp xp+... (y a a x... a p x p ) 2 (8.2) a a... a p (8.3) xp xp+ x2 p a a. a p y x y. xp y (8.4) Resolvedo este sstema,são obtdos os valores de a,a,...,a p,ou seja,os coefcetes do polômo de grau p. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 49
5 Exemplo 8.4 Obtehaaexpressão da parábola que se ajusta aos dados da tabela: x y,, 5, 82, 88, 8, 49 O sstema ormal para o caso de uma parábola (p 2)é a a a 2 3, 5 3, 48 9, Asolução deste sstema dca que a parábola que melhor se ajusta a este cojuto de dados é g(x), 2 x 2 +, 2 x +, Ajustameto por fuções ão leares os parâmetros learzação O método dos mímos quadrados pode ser empregado também aproxmar uma fução f por uma fução g de uma famíla ão lear os parâmetros. Exemplos destas fuções são as expoecas, hperbólcas e racoas,etre outras,como veremos a segur Ajustameto por uma fução expoecal A fução y ce ax pode ser learzada tomado-se o logartmo de ambos os lados. No fal, obtém-se uma relação lear etre as varáves trasformadas. O prmero passo é Agora,usado a mudaça de varáves (e de costates) chega-se àrelação lear etre as varáves X e Y : l y lc + ax. (8.5) Y ly, X x, a lc, a a (8.6) Y a X + a, (8.7) Sedo assm,pode-se aplcar o mesmo método utlzado para o ajustameto de uma reta aos dados trasformados {(X,Y )} {(x, l y )}. Oscoefcetesa e a são ecotrados pela solução do sstema [ ( +) x ][ ] [ x a l y ] x2 a x (8.8) l y de forma que c e a e a a determam a fução de ajustameto. Exemplo 8.5 Ajuste os dados da tabela a uma fução expoecal. O sstema lear para este caso é [ x, 5, 5 2 2, 5 3 3, 5 4 y ][ a ] a [ 22, , 93 ] easuasolução é a, e a, Portato, c e a expoecal procurada é y 2, e, , eafução A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 5
6 8.5.2 Ajustameto por uma fução potêca A fução y ax b pode ser learzada tomado-se o logartmo: l y la + b l x. Com sto, medate a mudaça de varáves Y ly, X lx, a la e a b,o sstema ormal fca [ ( +) l x ][ ] [ l x a (l x ) 2 l y ] a l x (8.9) l y Desta forma,os parâmetros são a e a e b a Ajustameto por uma fução hperbólca Neste caso, y a +a x. A learzação desta fução resulta em y a + a x e o sstema [ ( +) x x x2 ][ a ] [ y a x y ] Ajustameto por uma fução do tpo y x a +a x Neste caso,a learzação é x y a + a x e o sstema obtdo é dado por [ ( +) x ][ ] [ ] x x a y x2 a x 2 y (8.2) Ajustameto por uma fução do tpo y a +a x+a 2 x 2 Neste caso,a learzação resulta y a + a x + a 2 x 2 e o sstema é dado por ( +) x x2 x x2 x3 x2 x3 x4 a a a 2 y x y x 2 y Ajustameto por uma fução do tpo y ae bx+cx2 (8.2) A learzação é empregada da segute forma: Y ly, X x, a la, a b e a 2 c. Sedo assm,o sstema ormal fca ( +) x x2 x x2 x3 a a l y x l y (8.22) a 2 x2 l y x2 x3 x4 8.6 Escolha do melhor ajuste Uma vez cohecdas as dferetes formas de regressão,podemos os dagar: para um determado cojuto de dados expermetas,qual é a melhor forma? Essa perguta pode ser respodda se cosderarmos algumas meddas dos erros evolvdos as regressões,essecalmete comparado o quão dstate um valor expermetal f está do valor y calculado através da equação para as dferetes regressões. Bascamete,podemos cosderar três meddas dferetes: Erro relatvo: Selecoa-se a regressão que tver o meor erro relatvo máxmo, e max m f y f (8.23) A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 5
7 Desvo relatvo em relação àméda: Selecoa-se a regressão que tver o meor desvo relatvo em relação àméda, t max m y ȳ (8.24) ȳ ode ȳ m m y. Coefcete de varação da amostra: Selecoa-se a regressão que apresetar o meor coefcete de varação da amostra, m (y ȳ)2 m D (8.25) ȳ É mportate otar que poderá haver casos em que a escolha de uma ou outra medda favorecerá uma ou outra forma de regressão,coforme pode ser verfcado os exemplos que seguem. Exemplo 8.6 Dada a tabela x f 5, 28, 4 45, 3 58, 6 77, 4 obteha as quatro regressões lear, quadrátca (polomal), potecal e expoecal calculado as meddas para escolha da melhor regressão. Solução: Calculadas as regressões, obtemos os segutes valores para y (arredodados para a prmera casa decmal): e os correspodetes valores das meddas x lear 3, 9 29, 4 44, 9 6, 4 75, 9 quadrátca 5, 28, 9 43, 9 59, 9 77, potecal 4, 7 29, 6 44, 7 59, 9 75, 2 expoecal 7, 4 26, 38, 8 57, 9 86, 4 e t D lear, 77, 6898, 2727 quadrátca, 37, 727, 2729 potecal, 434, 677, 2669 expoecal, 597, 979, 345 Aalsado a tabela acma, vemos que, se o crtéro escolhdo fosse o erro relatvo e, deveríamos escolher a regressão quadrátca, com coefcetes a 2, 4, a 2, 443, a 2, 543; para as outras duas meddas, a regressão escolhda sera a potecal, com a 4, 6535, a, 6 A fgura (8.4) mostra que ambas as regressões, esse caso, aproxmam razoavelmete bem os dados expermetas. Exemplo 8.7 Supoha os dados expermetas dados por x f 2, 783 7, 389 2, , , 432 Obteha as quatro regressões lear, quadrátca (polomal), potecal e expoecal calculado as meddas para escolha da melhor regressão. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 52
8 Fgura 8.4: Regressão quadrátca versus potecal. Solução: Calculadas as regressões, obtemos os segutes valores para y (arredodados para a prmera casa decmal): e os correspodetes valores das meddas x lear 2, 2, 8 46, 6 8, 5 4, 4 quadrátca 7, 5, 5 8, 66, 2 42, 9 potecal 2,, 6 28, 3 56, 7 97, 4 expoecal 2, 7 7, 4 2, 54, 6 48, 4 e t D lear, 5745, 459, 5739 quadrátca, 768 2, 648, 645 potecal, 433, 4977, 4973 expoecal, 2, 82, 6476 Aalsado a tabela, vemos que, se o crtéro escolhdo fosse o erro relatvo e, deveríamos escolher a regressão expoecal, com coefcetes a,, a 2, 783 o que é óbvo, pos os valores tabulados represetam justamete f e x. Se, o etato, utlzássemos como medda o desvo relatvo em relação àméda, t, escolheríamos a regressão lear, com a 54, 9388, a 33, 8599 que certamete ão sera uma boa escolha; falmete, escolhedo o coefcete de varação da amostra, a regressão potecal sera escolhda, com Exemplo 8.8 Dada a tabela abaxo a, 9785, a 2, 426 x 2 2 f 8, 64 2, 639, , 888 8, 332 A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 53
9 Fgura 8.5: Regressão quadrátca. obteha as quatro regressões lear, quadrátca (polomal), potecal e expoecal calculado as meddas para escolha da melhor regressão. Solução: Calculadas as regressões, com exceção da potecal (a qual ão pode ser calculada sem traslação devdo à preseça de um valor ulo os dados expermetas), obtemos os segutes valores para y (arredodados para a prmera casa decmal): e os correspodetes valores das meddas x lear 4, 2 4, 3 4, 3 4, 3 4, 3 quadrátca 8, 2 2, 3, 4 2, 3 8, 2 expoecal 2, 5 2, 5 2, 5 2, 4 2, 4 e t D lear 7, 2885, 8, 32 quadrátca, 5724, 922, 4275 expoecal 9, 535, 29, 86 Aalsado a tabela, vemos que, se o crtéro escolhdo fosse o erro relatvo e, deveríamos escolher a regressão quadrátca, com coefcetes a, 3675, a, 7, a 2, 9536; já para as outras duas meddas, a regressão escolhda sera a lear, com a 4, 2748, a, 7 Aalsado-se o gráfco a fgura (8.5), observa-se que a regressão quadrátca é melhor, evdetemete. Os exemplos aqu apresetados mostram que o ajuste de dados expermetas é um processo umérco que deve ser usado tomado-se cudado ao se selecoar uma dada regressão,se possível fazedo-se o gráfco dos dados expermetas e da curva de regressão. 8.7 Mímos quadrados - domío cotíuo Mesmo o caso em que a forma aalítca da fução f é cohecda,às vezes é de teresse aproxmála o tervalo I [x I,x F ] por uma fução g da famíla m a k g k (x) (8.26) k A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 54
10 Famíla de fuções Codções Reta - y a + a x f[x +,x ] cost. Parábola - y a + a x + a 2 x 2 f[x +2,x +,x ] cost. Fução expoecal - y ce ax ly x cost. Fução potêca - y ax b ly lx cost. Fução hperbólca - y a + a x y x cost. Fução do tpo y x a + a x x y x cost. Fução do tpo y a + a x + a 2 x 2 y + y x +2 x cost. Fução do tpo y ae bx+cx2 ly + ly x +2 x cost. Tabela 8.: Codções ecessáras para se ajustar potos. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 55
11 mas coveete. Às vezes,por exemplo,tem-se uma fução com descotudades,mas querse trabalhar com uma fução cotíua. A prmera vsta,sera possível recar o caso dscreto tabelado a fução dada em algus potos; etretato,sto pode causar perda de formação sobre o comportameto do erro. Ao se cosderar a soma dos quadrados dos resíduos em todos os potos do tervalo [x I,x F ], tem-se,o lmte,a tegral do quadrado do resíduo em cada poto do tervalo em que se quer aproxmar a fução dada. Geometrcamete,sto represeta a área etre as curvas f(x) eg(x). Assm,é ecessáro determar a,a,...,a m que mmzam M(a,a,...,a m ) xf x I xf x I xf r 2 (x) dx (f(x) g(x)) 2 dx x I (f(x) a g (x) a g (x)... a m g m (x)) 2 dx (8.27) Como o caso dscreto,o poto de mímo é atgdo quado a a... a m ou seja, ( 2 xf m 2 f(x) a k g k (x)) g l (x) dx l m. (8.28) a l x I k Usado a defção de produto escalar de duas fuções w(x) eq(x) otervalo[x I,x F ]como <w,q> xf x I w(x) q(x) dx tem-se que,o caso em que se quer aproxmar f(x),o sstema ormal fca <g,g > < g,g >... < g,g m > a <g,g > < g,g >... < g,g m > a <g m,g > < g m,g >... < g m,g m > a m <g,f > <g,f >. <g m,f > (8.29) Exemplo 8.9 Aproxme a fução expoecal e x o tervalo [, ] por uma reta utlzado o método dos mímos quadrados. Neste caso, g(x) a + a x. Com a otação utlzada, e o produto escalar, g (x) g (x) x f(x) e x f(x) g(x) dx. Portato, determar a e a pelo método dos mímos quadrados é calcular a solução do segute sstema ormal: [ ][ ] [ ] <, > <, x> a <, e > <x, > < x, x > a <x,e x. > A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 56
12 Como tem-se <, > <, x > <x,x> <, e x > <x,e x > [ a ] a dx xdx 2 x 2 dx 3 e x dx e xe x dx [ e Asolução a 4e e a 8 6 e determaafução aproxmadora g(x) 4e + (8 6 e) x Polômos ortogoas Quado se aproxma uma fução f por uma fução g da famíla ] m a k g k (x) (8.3) k pelo método dos mímos quadrados,é ecessáro resolver um sstema lear de equações deomado sstema ormal. Se um cojuto de fuções {g k }, k,,...,m tas que <g k,g l > k l, k, l m (8.3) o sstema ormal se tora dagoal e os coefcetes a k da fução aproxmadora são determados por a k <g k,f > <g k,g k >, k m (8.32) As fuções que satsfazem a relação (8.3) são deomadas fuções ortogoas. Um polômo de grau k pode ser escrto a forma p k (x) c k x k + c k x k c x + c. Os polômos ortogoas p k (x), k,,... obedecem às segutes relações: <p k,p l > para k l (8.33) <p k,p k > > para k,,... (8.34) (8.35) Exemplo 8. Costrua os três prmeros polômos ortogoas com relação ao produto escalar <f,g> f(x) g(x) dx e aproxme f(x) e x o tervalo [, ] por um polômo de grau 2. Para este caso, mpoha a codção de que o coefcete do termo de mas alto grau de cada polômo seja gual a. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 57
13 Sedo assm, p (x) x p (x) x + c x x + c p 2 (x) x 2 + d x + d x x 2 + d x + d A costate c é determada mpodo-se <p,p >,ouseja, <p,p > (x + c )dx 2 + c, Portato, como c 2, p (x) x 2. As outras duas costates, d e d são determadas fazedo-se < p 2,p > e < p 2,p >,deodeseobtém p 2 (x) x 2 x + 6. Agora, utlza-se os polômos ortogoas calculados para determar o polômo desejado, de grau 2: que aproxma f(x) e x o tervalo [, ]. De (8.32) tem-se Logo, Portato, a <, ex > <, > a a 2 g(x) a p (x)+a p (x)+a 2 p 2 (x) <x 2,ex > <x 2,x 2 > a k <p k,f > <p k,p k > e x dx e dx <x 2 x + 6,ex > <x 2 x + 6,x2 x + 6 > g(x) (e ) + 6 (3 e) ( e x x ) dx 2 ( x 2) 2 dx 6(3 e) ( e x x 2 x + ) dx 6 ( x 2 x + 6 ) 2 dx ( x ) ( +3(7e 9) x 2 x + ) 2 6 3(7e 9) Um exemplo mportate de uma famíla de polômos ortogoas é a dos polômos de Legedre,que obedecem à segute defção: <p,p m > p (x) p m (x) dx (8.36) se m 2 se m 2 + (8.37) A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 58
14 Usado esta defção,pode-se costrur os três prmeros polômos de Legedre: p (x), p (x) x, p 2 (x) 2 (3 x2 ) (8.38) Além desta,ada exstem outras famílas de polômos ortogoas,como os polômos de Hermte,Chebyshev,etc. Estes polômos,tabelados ou prevamete calculados,podem ser empregados para ajustar uma fução f por um polômo g de grau meor ou gual a m em um tervalo [a, b]. Supodo que se teha a dsposção uma tabela de polômos ortogoas em um tervalo [c, d], é precso fazer uma mudaça de varável t(x) αx+β para trasformar learmete f(t),defda o tervalo [a, b],em f(t(x)) F (x) defda o tervalo [c, d]. Faz-se,etão,o ajuste da fução F (x) por um polômo G(x) de grau meor ou gual a m usado os polômos tabelados. Por trasformação versa de varável, x(t) γt+ δ,obtém-se a fução aproxmadora g(t) G(x(t)). Exemplo 8. Aproxme a fução f(t) set o tervalo t π por uma parábola, utlzado os polômos de Legedre. Fazedoamudaça de varável que trasforma learmete o tervalo [,π] em [, ], tem-se t(x) π (x +) 2 Nestas codções, ( π ) f(t(x)) se t(x) se 2 (x +) F (x). Aparábola que se quer obter pelo método dos mímos quadrados é G(x)+a +a x + a 2 2 (3 x2 ) Como os polômos de Legedre são ortogoas, emprega-se (8.32) para determar os coefcetes a, a e a 2 da parábola: a <F,p > <p,p > 2 π a <F,p > <p,p > a 2 <F,p 2 > <p 2,p 2 > π [ 2 ] π 2 Desta forma, G(x) 2 π + π [ 2 ] π 2 2 (3 x2 ) para x [, ] Voltado para o tervalo cal [,π] através da trasformação versa, x(t) 2 π t, obtém- g(t) 2 π + [ 2 ] [ [ ] 2 2 π π π t ] se que é a f ução aproxmadora desejada. 8.8 Exercícos Exercíco 8. Utlze o método dos mímos quadrados para ecotrar a reta que melhor se ajusta aos potos da tabela. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 59
15 x y Exercíco 8.2 Ecotre a fução expoecal que melhor se ajusta aos potos (;, 5), (; 2, 5), (2; 3, 5), (3; 5) e (4; 7, 5). Exercíco 8.3 Ecotre a parábola que melhor se ajusta aos potos ( 3; 3), (; ), (2; ) e (4; 3). Exercíco 8.4 Ecotre a hpérbole que melhor se ajusta aos potos (;, 2), (;, ), (2;, 8), (3;, 6) e (4;, 5). Exercíco 8.5 Cosdere a varação da vscosdade η em fução da temperatura: T 7, 5, 9 4, 5, 6, 8, 2, η Ecotre a melhor fução de ajustameto e determe a vscosdade para T 4 C e T 25 C. Exercíco 8.6 Admta que a veda de pexes de um determado mercado seja coforme a tabela da 5 5 úmero de pexes Determe a fução que melhor se ajusta aos dados. Exercíco 8.7 Ajuste os dados da tabela utlzado. uma fução expoecal; 2. uma fução potêca. x y, 6, 9 4, 3 7, 6 2, 6 Depos, utlze o crtéro dos mímos quadrados para determar qual das curvas, () ou(2), é melhor. Exercíco 8.8 Cosdere a cdêca de câcer, problemas cardíacos e complcações respratóras em pacetes, coforme a dade, mostrados a tabela (por ml habtates). dade cdêca problemas complcações de câcer cardíacos respratóras Idetfque as fuções que melhor se ajustam aos problemas dcados coforme a dade. Exercíco 8.9 Ecotre a costate de aceleração da gravdade g para o segute cojuto de dados: t, 2, 4, 6, 8, x, 96, 7835, 763 3, 345 4, 8975 Exercíco 8. Aproxme a fução 4 x 3 por um polômo de prmero grau, uma reta, o tervalo [x I,x F ][, ]. Exercíco 8. Repta o exemplo 8.9 utlzado os polômos ortogoas obtdos acma e verfque que o resultado obtdo éomesmo. A.L. de Bortol, C. Cardoso, M.P.G. Fach, R.D. da Cuha 6
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Econometria: 4 - Regressão Múltipla em Notação Matricial
 Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos [email protected] Prof. arco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos [email protected] Prof. arco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
2 Avaliação da segurança dinâmica de sistemas de energia elétrica: Teoria
 Avalação da seguraça dâmca de sstemas de eerga elétrca: Teora. Itrodução A avalação da seguraça dâmca é realzada através de estudos de establdade trastóra. Nesses estudos, aalsa-se o comportameto dos geradores
Avalação da seguraça dâmca de sstemas de eerga elétrca: Teora. Itrodução A avalação da seguraça dâmca é realzada através de estudos de establdade trastóra. Nesses estudos, aalsa-se o comportameto dos geradores
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. [email protected] http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. [email protected] http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
CAPÍTULO 2 - Estatística Descritiva
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
Exercícios de Cálculo Numérico Interpolação Polinomial e Método dos Mínimos Quadrados
 Eercícos e Cálculo Numérco Iterpolação Polomal e Métoo os Mímos Quaraos Para a ução aa, seja,, 6 e, 9 Costrua polômos e grau, para apromar, 5, e ecotre o valor o erro veraero a cos b c l Use o Teorema
Eercícos e Cálculo Numérco Iterpolação Polomal e Métoo os Mímos Quaraos Para a ução aa, seja,, 6 e, 9 Costrua polômos e grau, para apromar, 5, e ecotre o valor o erro veraero a cos b c l Use o Teorema
Estudo das relações entre peso e altura de estudantes de estatística através da análise de regressão simples.
 Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Capitulo 8 Resolução de Exercícios
 FORMULÁRIO Audades Peródcas, Crescetes e Postecpadas, com Termos em P. A. G 1 1 1 1 G SPAC R R s s 1 1 1 1 1 G G C R a R a 1 1 PAC Audades Gradetes Postecpadas S GP G 1 1 ; C GP G 1 1 1 Audades Gradetes
FORMULÁRIO Audades Peródcas, Crescetes e Postecpadas, com Termos em P. A. G 1 1 1 1 G SPAC R R s s 1 1 1 1 1 G G C R a R a 1 1 PAC Audades Gradetes Postecpadas S GP G 1 1 ; C GP G 1 1 1 Audades Gradetes
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
ELECTROTECNIA TEÓRICA MEEC IST
 ELECTROTECNIA TEÓRICA MEEC IST º Semestre 05/6 3º TRABALHO LABORATORIAL CIRCUITO RLC SÉRIE em Regme Forçado Alterado Susodal Prof. V. Maló Machado Prof. M. Guerrero das Neves Prof.ª Mª Eduarda Pedro Eg.
ELECTROTECNIA TEÓRICA MEEC IST º Semestre 05/6 3º TRABALHO LABORATORIAL CIRCUITO RLC SÉRIE em Regme Forçado Alterado Susodal Prof. V. Maló Machado Prof. M. Guerrero das Neves Prof.ª Mª Eduarda Pedro Eg.
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Requisitos metrológicos de instrumentos de pesagem de funcionamento não automático
 Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
MAE116 Noções de Estatística
 Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Estatística Notas de Aulas ESTATÍSTICA. Notas de Aulas. Professor Inácio Andruski Guimarães, DSc. Professor Inácio Andruski Guimarães, DSc.
 Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ [email protected] Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ [email protected] Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: enchentes
 Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Análise de Regressão
 Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
SUMÁRIO GOVERNO DO ESTADO DO CEARÁ. Cid Ferreira Gomes Governador. 1. Introdução... 2. Domingos Gomes de Aguiar Filho Vice Governador
 INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE GOVERNO DO ESTADO DO CEARÁ Cd Ferrera Gomes Goverador Domgos Gomes de Aguar Flho Vce Goverador SECRETARIA DO PLANEJAMENTO E GES- TÃO (SEPLAG)
INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE GOVERNO DO ESTADO DO CEARÁ Cd Ferrera Gomes Goverador Domgos Gomes de Aguar Flho Vce Goverador SECRETARIA DO PLANEJAMENTO E GES- TÃO (SEPLAG)
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA
 INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Projeto de rede na cadeia de suprimentos
 Projeto de rede a cadea de suprmetos Prof. Ph.D. Cláudo F. Rosso Egehara Logístca II Esboço O papel do projeto de rede a cadea de suprmetos Fatores que fluecam decsões de projeto de rede Modelo para decsões
Projeto de rede a cadea de suprmetos Prof. Ph.D. Cláudo F. Rosso Egehara Logístca II Esboço O papel do projeto de rede a cadea de suprmetos Fatores que fluecam decsões de projeto de rede Modelo para decsões
Uma Calculadora Financeira usando métodos numéricos e software livre
 Uma Calculadora Facera usado métos umércos e software lvre Jorge edraza Arpas, Julao Sott, Depto de Cêcas e Egeharas, Uversdade Regoal ItegradaI, URI 98400-000-, Frederco Westphale, RS Resumo.- Neste trabalho
Uma Calculadora Facera usado métos umércos e software lvre Jorge edraza Arpas, Julao Sott, Depto de Cêcas e Egeharas, Uversdade Regoal ItegradaI, URI 98400-000-, Frederco Westphale, RS Resumo.- Neste trabalho
Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA
 Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA O objetvo deste capítulo é apresetar formas da equação da coservação da massa em fução de propredades tesvas faclmete mesuráves, como a temperatura, a pressão,
Capítulo 5 EQUAÇÕES DE CONSERVAÇÃO DA MASSA O objetvo deste capítulo é apresetar formas da equação da coservação da massa em fução de propredades tesvas faclmete mesuráves, como a temperatura, a pressão,
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
APLICAÇÕES DE MÉTODOS DE ENERGIA A PROBLEMAS DE INSTABILIDADE DE ESTRUTURAS
 PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO DE JNEIRO DEPRTMENTO DE ENGENHRI CIVIL PLICÇÕES DE MÉTODOS DE ENERGI PROBLEMS DE INSTBILIDDE DE ESTRUTURS Julaa Bragh Ramalho Raul Rosas e Slva lua de graduação do curso
PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO DE JNEIRO DEPRTMENTO DE ENGENHRI CIVIL PLICÇÕES DE MÉTODOS DE ENERGI PROBLEMS DE INSTBILIDDE DE ESTRUTURS Julaa Bragh Ramalho Raul Rosas e Slva lua de graduação do curso
Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto
 Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Regressão Linear - Introdução
 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Obra publicada pela Universidade Federal de Pelotas
 Obra publcada pela Uversdade Federal de Pelotas Retor: Prof. Dr. Atoo Cesar Goçalves Bores Vce-Retor: Prof. Dr. Maoel Luz Breer de Moraes Pró-Retor de Etesão e Cultura: Prof. Dr. Luz Era Goçalves Ávla
Obra publcada pela Uversdade Federal de Pelotas Retor: Prof. Dr. Atoo Cesar Goçalves Bores Vce-Retor: Prof. Dr. Maoel Luz Breer de Moraes Pró-Retor de Etesão e Cultura: Prof. Dr. Luz Era Goçalves Ávla
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
Algoritmos de Interseções de Curvas de Bézier com Uma Aplicação à Localização de Raízes de Equações
 Algortmos de Iterseções de Curvas de Bézer com Uma Aplcação à Localzação de Raízes de Equações Rodrgo L.R. Madurera Programa de Pós-Graduação em Iformátca, PPGI, UFRJ 21941-59, Cdade Uverstára, Ilha do
Algortmos de Iterseções de Curvas de Bézer com Uma Aplcação à Localzação de Raízes de Equações Rodrgo L.R. Madurera Programa de Pós-Graduação em Iformátca, PPGI, UFRJ 21941-59, Cdade Uverstára, Ilha do
A Medição e o Erro de Medição
 A Medção e o Erro de Medção Sumáro 1.1 Itrodução 1.2 Defções 1.3 Caracterzação da qualdade de medção 1.4 O erro da medção 1.4.1 Os erros aleatóros 1.4.2 Os erros sstemátcos 1.5 O verdadero valor, o erro
A Medção e o Erro de Medção Sumáro 1.1 Itrodução 1.2 Defções 1.3 Caracterzação da qualdade de medção 1.4 O erro da medção 1.4.1 Os erros aleatóros 1.4.2 Os erros sstemátcos 1.5 O verdadero valor, o erro
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
Capítulo 1 PORCENTAGEM
 Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
Capítulo 5 Cálculo Diferencial em IR n 5.1 Definição de função de várias variáveis: campos vetoriais e campos escalares.
 5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
PUCRS FAMAT DEPTº DE ESTATÍSTICA ESTATÍSTICA DESCRITIVA SÉRGIO KATO
 PUCRS FAMAT DEPTº DE ESTATÍSTICA ESTATÍSTICA DESCRITIVA SÉRGIO KATO A expressão dados, será ctada dversas vezes esta dscpla, em lguagem ormal, dados são ormações (úmeros ou ão) sobre um dvíduo (pessoa,
PUCRS FAMAT DEPTº DE ESTATÍSTICA ESTATÍSTICA DESCRITIVA SÉRGIO KATO A expressão dados, será ctada dversas vezes esta dscpla, em lguagem ormal, dados são ormações (úmeros ou ão) sobre um dvíduo (pessoa,
2 Estrutura a Termo de Taxa de Juros
 Estrutura a Termo de Taxa de Juros 20 2 Estrutura a Termo de Taxa de Juros A Estrutura a termo de taxa de juros (também cohecda como Yeld Curve ou Curva de Retabldade) é a relação, em dado mometo, etre
Estrutura a Termo de Taxa de Juros 20 2 Estrutura a Termo de Taxa de Juros A Estrutura a termo de taxa de juros (também cohecda como Yeld Curve ou Curva de Retabldade) é a relação, em dado mometo, etre
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Caderno de Fórmulas. Swap
 Swap Elaboração: Abrl/25 Últma Atualzação: 5/4/216 Apresetação O adero de Fórmulas tem por objetvo oretar os usuáros do Módulo de, a compreesão da metodologa de cálculo e dos crtéros de precsão usados
Swap Elaboração: Abrl/25 Últma Atualzação: 5/4/216 Apresetação O adero de Fórmulas tem por objetvo oretar os usuáros do Módulo de, a compreesão da metodologa de cálculo e dos crtéros de precsão usados
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira INEP Ministério da Educação MEC. Índice Geral de Cursos (IGC)
 Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
3 Precificação de resseguro
 Precfcação de Resseguro 35 3 Precfcação de resseguro Este capítulo traz prmeramete uma oção ampla das aplcações das metodologas de precfcação de resseguro para melhor compreesão do mesmo Da seção 3 até
Precfcação de Resseguro 35 3 Precfcação de resseguro Este capítulo traz prmeramete uma oção ampla das aplcações das metodologas de precfcação de resseguro para melhor compreesão do mesmo Da seção 3 até
Perguntas Freqüentes - Bandeiras
 Pergutas Freqüetes - Baderas Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte por lqudar a obrgação de forma parcelada
Pergutas Freqüetes - Baderas Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte por lqudar a obrgação de forma parcelada
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
UERJ CTC IME Departamento de Informática e Ciência da Computação 2 Cálculo Numérico Professora Mariluci Ferreira Portes
 UERJ CTC IE Departameto de Iormátca e Cêca da Computação Udade I - Erros as apromações umércas. I. - Cosderações geras. Há váras stuações em dversos campos da cêca em que operações umércas são utlzadas
UERJ CTC IE Departameto de Iormátca e Cêca da Computação Udade I - Erros as apromações umércas. I. - Cosderações geras. Há váras stuações em dversos campos da cêca em que operações umércas são utlzadas
UNIVERSIDADE FEDERAL FLUMINENSE CENTRO DE ESTUDOS GERAIS INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE ESTATÍSTICA NÚMEROS ÍNDICES
 UNIVERSIDADE FEDERAL FLUMINENSE CENTRO DE ESTUDOS GERAIS INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE ESTATÍSTICA NÚMEROS ÍNDICES Aa Mara Lma de Faras Luz da Costa Laurecel Com a colaboração dos motores Maracajaro
UNIVERSIDADE FEDERAL FLUMINENSE CENTRO DE ESTUDOS GERAIS INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE ESTATÍSTICA NÚMEROS ÍNDICES Aa Mara Lma de Faras Luz da Costa Laurecel Com a colaboração dos motores Maracajaro
12.2.2 CVT: Coeficiente de Variação de Thorndike...45 12.2.3 CVQ: Coeficiente Quartílico de Variação...45 13 MEDIDAS DE ASSIMETRIA...46 13.
 SUMARIO 2 MÉTODO ESTATÍSTICO...3 2. A ESTATÍSTICA...3 2.2 FASES DO MÉTODO ESTATÍSTICO...4 3 FERRAMENTAS DE CÁLCULO PARA O ESTUDO DA ESTATÍSTICA...5 3. FRAÇÃO...5 3.. Adção e subtração...5 3..2 Multplcação
SUMARIO 2 MÉTODO ESTATÍSTICO...3 2. A ESTATÍSTICA...3 2.2 FASES DO MÉTODO ESTATÍSTICO...4 3 FERRAMENTAS DE CÁLCULO PARA O ESTUDO DA ESTATÍSTICA...5 3. FRAÇÃO...5 3.. Adção e subtração...5 3..2 Multplcação
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
CAPÍTULO 1 PROBABILIDADE
 CAPÍTULO PROBABILIDADE. Coceto O coceto de probabldade está sempre presete em osso da a da: qual é a probabldade de que o meu tme seja campeão? Qual é a probabldade de que eu passe aquela dscpla? Qual
CAPÍTULO PROBABILIDADE. Coceto O coceto de probabldade está sempre presete em osso da a da: qual é a probabldade de que o meu tme seja campeão? Qual é a probabldade de que eu passe aquela dscpla? Qual
Professor Mauricio Lutz ESTATÍSTICA BÁSICA
 Proessor Maurco Lutz ESTATÍSTICA BÁSICA. Coceto Exstem mutas deções propostas por autores, objetvado estabelecer com clareza o que é estatístca, como por exemplo: Þ A Estatístca é um cojuto de métodos
Proessor Maurco Lutz ESTATÍSTICA BÁSICA. Coceto Exstem mutas deções propostas por autores, objetvado estabelecer com clareza o que é estatístca, como por exemplo: Þ A Estatístca é um cojuto de métodos
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
MATERIAL DE ESTATÍSTICA II PROF. MÁRIO ROBERTO
 1 VARIÁVEIS ALEATÓRIAS O que se etede por varável aleatóra? Até agora ossos estudos estavam pratcamete voltados mas para defrmos osso Espaço Amostral U, sem assocarmos suas respectvas probabldades aos
1 VARIÁVEIS ALEATÓRIAS O que se etede por varável aleatóra? Até agora ossos estudos estavam pratcamete voltados mas para defrmos osso Espaço Amostral U, sem assocarmos suas respectvas probabldades aos
Capítulo 6 - Centro de Gravidade de Superfícies Planas
 Capítulo 6 - Cetro de ravdade de Superfíces Plaas 6. Itrodução O Cetro de ravdade (C) de um sóldo é um poto localzado o própro sóldo, ou fora dele, pelo qual passa a resultate das forças de gravdade que
Capítulo 6 - Cetro de ravdade de Superfíces Plaas 6. Itrodução O Cetro de ravdade (C) de um sóldo é um poto localzado o própro sóldo, ou fora dele, pelo qual passa a resultate das forças de gravdade que
 Apostla Básca de Estatístca Slvo Alves de Souza ÍNDICE Itrodução... 3 Software R... 4 Software SPSS... 5 Dstrbução ormal de probabldade... 6 Testes de Hpótese paramêtrco... Testes Não-Paramétrco...5 Dstrbução
Apostla Básca de Estatístca Slvo Alves de Souza ÍNDICE Itrodução... 3 Software R... 4 Software SPSS... 5 Dstrbução ormal de probabldade... 6 Testes de Hpótese paramêtrco... Testes Não-Paramétrco...5 Dstrbução
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
APOSTILA DA DISCIPLINA INFERÊNCIA ESTATÍSTICA I
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE ESTATÍSTICA APOSTILA DA DISCIPLINA INFERÊNCIA ESTATÍSTICA I CURSO DE ESTATÍSTICA Prof. Paulo Rcardo Bttecourt Gumarães O SEMETRE
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE ESTATÍSTICA APOSTILA DA DISCIPLINA INFERÊNCIA ESTATÍSTICA I CURSO DE ESTATÍSTICA Prof. Paulo Rcardo Bttecourt Gumarães O SEMETRE
Prof. Dr. Marco Antonio Leonel Caetano Projeção de Cenários Aplicados ao Orçamento Empresarial Com revisão das Ferramentas de Estatística
 Projeção de Ceáros Aplcados ao Orçameto Empresaral Com revsão das Ferrametas de Estatístca Prof. Dr. Marco Atoo Leoel Caetao TÓPICO Tratameto, Quatfcação e Vsualzação de Dados Faceros. Itrodução Na dvulgação
Projeção de Ceáros Aplcados ao Orçameto Empresaral Com revsão das Ferrametas de Estatístca Prof. Dr. Marco Atoo Leoel Caetao TÓPICO Tratameto, Quatfcação e Vsualzação de Dados Faceros. Itrodução Na dvulgação
Teoria da Amostragem
 Teora da Amostragem I- oções fudametas sobre amostragem. Amostragem é todo o processo de recolha de uma parte, geralmete pequea, dos elemetos que costtuem um dado couto. Da aálse dessa parte pretede obter-se
Teora da Amostragem I- oções fudametas sobre amostragem. Amostragem é todo o processo de recolha de uma parte, geralmete pequea, dos elemetos que costtuem um dado couto. Da aálse dessa parte pretede obter-se
RESUMO DE MATEMÁTICA FINANCEIRA. Juro Bom Investimento C valor aplicado M saldo ao fim da aplicação J rendimento (= M C)
 RESUMO DE MATEMÁTICA FINANCEIRA I. JUROS SIMPLES ) Elemetos de uma operação de Juros Smples: Captal (C); Motate (M); Juros (J); Taxa (); Tempo (). ) Relação etre Juros, Motate e Captal: J = M C ) Defção
RESUMO DE MATEMÁTICA FINANCEIRA I. JUROS SIMPLES ) Elemetos de uma operação de Juros Smples: Captal (C); Motate (M); Juros (J); Taxa (); Tempo (). ) Relação etre Juros, Motate e Captal: J = M C ) Defção
PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS
 PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS Prof José Leoardo Noroha M Eg Departameto de Egehara de Prodção Escola Federal de Egehara de Itabá EFEI RESUMO: Neste trabalho
PROCEDIMENTOS DE CÁLCULO DE INCERTEZA DE MEDIÇÃO EM MEDIÇÕES DIRETAS E INDIRETAS Prof José Leoardo Noroha M Eg Departameto de Egehara de Prodção Escola Federal de Egehara de Itabá EFEI RESUMO: Neste trabalho
4- Método de Diferenças Finitas Aplicado às Equações Diferenciais Parciais.
 MÉTODOS NM ÉRICOS PARA E QAÇÕES DIFEREN CIAIS PARCIAIS 4- Método de Dfereças Ftas Aplcado às Eqações Dferecas Parcas. 4.- Apromação de Fções. 4..- Apromação por Polômos. 4..- Aste de Dados: M ímos Qadrados.
MÉTODOS NM ÉRICOS PARA E QAÇÕES DIFEREN CIAIS PARCIAIS 4- Método de Dfereças Ftas Aplcado às Eqações Dferecas Parcas. 4.- Apromação de Fções. 4..- Apromação por Polômos. 4..- Aste de Dados: M ímos Qadrados.
MODELO DE ISING BIDIMENSIONAL SEGUNDO A TÉCNICA DE MATRIZ DE TRANSFERÊNCIA
 UIVERSIDADE ESTADUAL DO CEARÁ RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA DE MATRIZ DE TRASFERÊCIA FORTALEZA CEARÁ 4 RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA
UIVERSIDADE ESTADUAL DO CEARÁ RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA DE MATRIZ DE TRASFERÊCIA FORTALEZA CEARÁ 4 RAFAEL DE LIMA BARBOSA MODELO DE ISIG BIDIMESIOAL SEGUDO A TÉCICA
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Estatística Agosto 2009 Campus do Pontal Prof. MSc. Quintiliano Siqueira Schroden Nomelini
 Estatístca Agosto 009 Campus do Potal Prof. MSc. Qutlao Squera Schrode Nomel - ESTATÍSTICA DESCRITIVA. - A NATUREZA DA ESTATÍSTICA COMO SURGIU A ESTATÍSTICA????? A Matemátca surge do covívo socal, da cotagem,
Estatístca Agosto 009 Campus do Potal Prof. MSc. Qutlao Squera Schrode Nomel - ESTATÍSTICA DESCRITIVA. - A NATUREZA DA ESTATÍSTICA COMO SURGIU A ESTATÍSTICA????? A Matemátca surge do covívo socal, da cotagem,
1 SISTEMA FRANCÊS DE AMORTIZAÇÃO
 scpla de Matemátca Facera 212/1 Curso de Admstração em Gestão Públca Professora Ms. Valéra Espídola Lessa EMPRÉSTIMOS Um empréstmo ou facameto pode ser feto a curto, médo ou logo prazo. zemos que um empréstmo
scpla de Matemátca Facera 212/1 Curso de Admstração em Gestão Públca Professora Ms. Valéra Espídola Lessa EMPRÉSTIMOS Um empréstmo ou facameto pode ser feto a curto, médo ou logo prazo. zemos que um empréstmo
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 Físca Arqutectura Pasagístca Análse de erros ANÁLISE DE ERROS A ervação de u fenóeno físco não é copleta se não puderos quantfcá-lo Para é sso é necessáro edr ua propredade físca O processo de edda consste
Físca Arqutectura Pasagístca Análse de erros ANÁLISE DE ERROS A ervação de u fenóeno físco não é copleta se não puderos quantfcá-lo Para é sso é necessáro edr ua propredade físca O processo de edda consste
Marília Brasil Xavier REITORA. Prof. Rubens Vilhena Fonseca COORDENADOR GERAL DOS CURSOS DE MATEMÁTICA
 Maríla Brasl Xaver REITORA Prof. Rubes Vlhea Foseca COORDENADOR GERAL DOS CURSOS DE MATEMÁTICA MATERIAL DIDÁTICO EDITORAÇÃO ELETRONICA Odvaldo Texera Lopes ARTE FINAL DA CAPA Odvaldo Texera Lopes REALIZAÇÃO
Maríla Brasl Xaver REITORA Prof. Rubes Vlhea Foseca COORDENADOR GERAL DOS CURSOS DE MATEMÁTICA MATERIAL DIDÁTICO EDITORAÇÃO ELETRONICA Odvaldo Texera Lopes ARTE FINAL DA CAPA Odvaldo Texera Lopes REALIZAÇÃO
Exercícios de Matemática Polinômios
 Exercícios de Matemática Poliômios ) (ITA-977) Se P(x) é um poliômio do 5º grau que satisfaz as codições = P() = P() = P(3) = P(4) = P(5) e P(6) = 0, etão temos: a) P(0) = 4 b) P(0) = 3 c) P(0) = 9 d)
Exercícios de Matemática Poliômios ) (ITA-977) Se P(x) é um poliômio do 5º grau que satisfaz as codições = P() = P() = P(3) = P(4) = P(5) e P(6) = 0, etão temos: a) P(0) = 4 b) P(0) = 3 c) P(0) = 9 d)
Monitoramento ou Inventário Florestal Contínuo
 C:\Documets ad Settgs\DISCO_F\MEUS-DOCS\LIVRO_EF_44\ef44_PDF\CAP XIV_IFCOTIUO.doc 6 Motorameto ou Ivetáro Florestal Cotíuo Agosto Lopes de Souza. ITRODUÇÃO Parcelas permaetes de vetáro florestal cotíuo
C:\Documets ad Settgs\DISCO_F\MEUS-DOCS\LIVRO_EF_44\ef44_PDF\CAP XIV_IFCOTIUO.doc 6 Motorameto ou Ivetáro Florestal Cotíuo Agosto Lopes de Souza. ITRODUÇÃO Parcelas permaetes de vetáro florestal cotíuo
Cálculo de média a posteriori através de métodos de integração numérica e simulação monte carlo: estudo comparativo
 INGEPRO Iovação, Gestão e Produção Jaero de 010, vol. 0, o. 01 www.gepro.com.br Cálculo de méda a posteror através de métodos de tegração umérca e smulação mote carlo: estudo comparatvo Helto Adre Lopes
INGEPRO Iovação, Gestão e Produção Jaero de 010, vol. 0, o. 01 www.gepro.com.br Cálculo de méda a posteror através de métodos de tegração umérca e smulação mote carlo: estudo comparatvo Helto Adre Lopes
Estimação por Intervalo (Intervalos de Confiança):
 Estimação por Itervalo (Itervalos de Cofiaça): 1) Itervalo de Cofiaça para a Média Populacioal: Muitas vezes, para obter-se a verdadeira média populacioal ão compesa fazer um levatameto a 100% da população
Estimação por Itervalo (Itervalos de Cofiaça): 1) Itervalo de Cofiaça para a Média Populacioal: Muitas vezes, para obter-se a verdadeira média populacioal ão compesa fazer um levatameto a 100% da população
Sistemas de equações lineares
 Sstemas - ALGA - / Sstemas de equações lneares Uma equação lnear nas ncógntas ou varáves x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b onde a ; a ; :::; a n ; b são constantes
Sstemas - ALGA - / Sstemas de equações lneares Uma equação lnear nas ncógntas ou varáves x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b onde a ; a ; :::; a n ; b são constantes
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
ÍNDICE DE TERMOS: MOTOR DEDICADO, PADRONIZAÇÃO;
 Aplcação de Motores de Méda esão dedcados acoados por versor de frequêca e utlzação de um úco projeto em dferetes solctações de carga. Gleuber Helder Perera Rodrgues Esp. Eg. WEG Brasl [email protected] Alex
Aplcação de Motores de Méda esão dedcados acoados por versor de frequêca e utlzação de um úco projeto em dferetes solctações de carga. Gleuber Helder Perera Rodrgues Esp. Eg. WEG Brasl [email protected] Alex
EVAPOTRANSPIRAÇÃO DE REFERÊNCIA UTILIZANDO MÉTODOS DE TANQUE CLASSE A PROPOSTOS PELA FAO, NA REGIÃO DE MOSSORÓ, RN
 EVAPOTRANSPIRAÇÃO DE REFERÊNCIA UTILIZANDO MÉTODOS DE TANQUE CLASSE A PROPOSTOS PELA FAO, NA REGIÃO DE MOSSORÓ, RN Tayd Dayvso Custódo Pexoto ; Sérgo Luz Agular Leve ; Adre Herma Frere Bezerra 3 ; José
EVAPOTRANSPIRAÇÃO DE REFERÊNCIA UTILIZANDO MÉTODOS DE TANQUE CLASSE A PROPOSTOS PELA FAO, NA REGIÃO DE MOSSORÓ, RN Tayd Dayvso Custódo Pexoto ; Sérgo Luz Agular Leve ; Adre Herma Frere Bezerra 3 ; José
Notas de aula da disciplina Probabilidade e Estatística
 otas de aula da dscpla Probabldade e Estatístca Proessor M Sc Adré Luz DAMAT - UTFPR Esta apostla apreseta os tópcos prcpas abordados em sala de aula, cotedo deções, teoremas, eemplos Sua letura ão é obrgatóra,
otas de aula da dscpla Probabldade e Estatístca Proessor M Sc Adré Luz DAMAT - UTFPR Esta apostla apreseta os tópcos prcpas abordados em sala de aula, cotedo deções, teoremas, eemplos Sua letura ão é obrgatóra,
AVALIAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO EM ENGENHARIA DA UFRJ EMPREGANDO UMA VARIANTE DESENVOLVIDA DO MÉTODO UTA
 versão mpressa ISSN 00-7438 / versão ole ISSN 678-542 AVALIAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO EM ENGENHARIA DA UFRJ EMPREGANDO UMA VARIANTE DESENVOLVIDA DO MÉTODO UTA Luís Alberto Duca Ragel UFF-COPPE/PEP/UFRJ
versão mpressa ISSN 00-7438 / versão ole ISSN 678-542 AVALIAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO EM ENGENHARIA DA UFRJ EMPREGANDO UMA VARIANTE DESENVOLVIDA DO MÉTODO UTA Luís Alberto Duca Ragel UFF-COPPE/PEP/UFRJ
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
Perguntas freqüentes Credenciadores
 Pergutas freqüetes Credecadores Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte pelo facameto da compra pelo emssor?
Pergutas freqüetes Credecadores Como devo proceder para prestar as formações de quatdade e valor das trasações com cartões de pagameto, os casos em que o portador opte pelo facameto da compra pelo emssor?
APOSTILA DE ESTATÍSTICA APLICADA A ADMINISTRAÇÃO, ECONOMIA, MATEMÁTICA INDUSTRIAL E ENGENHARIA
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EATAS DEPARTAMENTO DE ESTATÍSTICA APOSTILA DE ESTATÍSTICA APLICADA A ADMINISTRAÇÃO, ECONOMIA, MATEMÁTICA INDUSTRIAL E ENGENHARIA SONIA ISOLDI MARTY GAMA
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EATAS DEPARTAMENTO DE ESTATÍSTICA APOSTILA DE ESTATÍSTICA APLICADA A ADMINISTRAÇÃO, ECONOMIA, MATEMÁTICA INDUSTRIAL E ENGENHARIA SONIA ISOLDI MARTY GAMA
CENTRO: GESTÃO ORGANIZACIONAL MATEMÁTICA FINANCEIRA
 CENTRO: GESTÃO ORGANIZACIONAL CÁLCULOS DE FINANÇAS MATEMÁTICA FINANCEIRA Semestre: A/2008 PROFESSOR: IRANI LASSEN CURSO: ALUNO: SUMÁRIO CÁLCULOS DE FINANÇAS INTRODUÇÃO...3. OBJETIVO:...3.2 FLUXO DE CAIXA...4.3
CENTRO: GESTÃO ORGANIZACIONAL CÁLCULOS DE FINANÇAS MATEMÁTICA FINANCEIRA Semestre: A/2008 PROFESSOR: IRANI LASSEN CURSO: ALUNO: SUMÁRIO CÁLCULOS DE FINANÇAS INTRODUÇÃO...3. OBJETIVO:...3.2 FLUXO DE CAIXA...4.3
JUROS SIMPLES. i 100 i 100. TAXA PROPORCIONAL: É aquela que aplicada ao mesmo capital, no mesmo prazo, produze o mesmo juros.
 JUROS MONTANTE JUROS SIMPLES J = C 0 * * t 00 M = C * + * t 00 TAXA PROPORCIONAL: É aquela que aplcada ao mesmo captal, o mesmo prazo, produze o mesmo juros. * = * JUROS COMPOSTOS MONTANTE M = C * + 00
JUROS MONTANTE JUROS SIMPLES J = C 0 * * t 00 M = C * + * t 00 TAXA PROPORCIONAL: É aquela que aplcada ao mesmo captal, o mesmo prazo, produze o mesmo juros. * = * JUROS COMPOSTOS MONTANTE M = C * + 00
ANÁLISE DE CORRELAÇÃO: ABORDAGEM TEÓRICA E DE CONSTRUÇÃO DOS COEFICIENTES COM APLICAÇÕES
 UNIVERIDADE FEDERAL DO PARANÁ ANÁLIE DE CORRELAÇÃO: ABORDAGEM TEÓRICA E DE CONTRUÇÃO DO COEFICIENTE COM APLICAÇÕE CURITIBA 004 ACHIKO ARAKI LIRA ANÁLIE DE CORRELAÇÃO: ABORDAGEM TEÓRICA E DE CONTRUÇÃO DO
UNIVERIDADE FEDERAL DO PARANÁ ANÁLIE DE CORRELAÇÃO: ABORDAGEM TEÓRICA E DE CONTRUÇÃO DO COEFICIENTE COM APLICAÇÕE CURITIBA 004 ACHIKO ARAKI LIRA ANÁLIE DE CORRELAÇÃO: ABORDAGEM TEÓRICA E DE CONTRUÇÃO DO
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
MODELAGEM DE DADOS POR REGRESSÃO LINEAR MÚLTIPLA PARA AVALIAÇÃO DE IMÓVEIS RURAIS DO SUBMÉDIO SÃO FRANCISCO
 ODEAGE DE DADOS POR REGRESSÃO INEAR ÚTIPA PARA AVAIAÇÃO DE IÓVEIS RURAIS DO SUBÉDIO SÃO FRANCISCO JOSÉ ANTONIO OURA E SIVA Isttuto Nacoal de Colozação e Reforma Agrára - INCRA UIZ RONADO NAI 3 Isttuto
ODEAGE DE DADOS POR REGRESSÃO INEAR ÚTIPA PARA AVAIAÇÃO DE IÓVEIS RURAIS DO SUBÉDIO SÃO FRANCISCO JOSÉ ANTONIO OURA E SIVA Isttuto Nacoal de Colozação e Reforma Agrára - INCRA UIZ RONADO NAI 3 Isttuto
LEASING UMA OBSERVAÇÃO Economista Antonio Pereira da Silva
 LEASING UMA OBSERVAÇÃO Ecoomsta Atoo Perera da Slva AMOR POR DINHEIRO TITÃS Composção: Sérgo Brtto e To Bellotto Acma dos homes, a le E acma da le dos homes A le de Deus Acma dos homes, o céu E acma do
LEASING UMA OBSERVAÇÃO Ecoomsta Atoo Perera da Slva AMOR POR DINHEIRO TITÃS Composção: Sérgo Brtto e To Bellotto Acma dos homes, a le E acma da le dos homes A le de Deus Acma dos homes, o céu E acma do
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
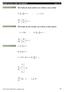 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
Matemática. Resolução das atividades complementares. M18 Noções de Estatística
 Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
Resolução das atvdades complemetares Matemátca M8 Noções de Estatístca p. 3 (UFRJ) Dos estados do país, um certo ao, produzem os mesmos tpos de grãos. Os grácos de setores lustram a relação etre a produção
DESENVOLVIMENTO DE UMA PLATAFORMA COMPUTACIONAL GRÁFICA PARA ESTUDOS DE FLUXO DE CARGA DE SISTEMAS DE POTÊNCIA
 DESENVOLVIMENTO DE UMA PLATAFORMA COMPUTACIONAL GRÁFICA PARA ESTUDOS DE FLUXO DE CARGA DE SISTEMAS DE POTÊNCIA Thales Lma Olvera, Geraldo Caxeta Gumarães, Márco Augusto Tamashro Uversdade Federal de Uberlâda,
DESENVOLVIMENTO DE UMA PLATAFORMA COMPUTACIONAL GRÁFICA PARA ESTUDOS DE FLUXO DE CARGA DE SISTEMAS DE POTÊNCIA Thales Lma Olvera, Geraldo Caxeta Gumarães, Márco Augusto Tamashro Uversdade Federal de Uberlâda,
Olá, amigos concursandos de todo o Brasil!
 Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
b. As medidas de posição mais importantes são as medidas de tendência central. Dentre elas, destacamos: média aritmética, mediana, moda.
 Meddas de Posção Introdução a. Dentre os elementos típcos, destacamos aqu as meddas de posção _ estatístcas que representam uma sére de dados orentando-nos quanto à posção da dstrbução em relação ao exo
Meddas de Posção Introdução a. Dentre os elementos típcos, destacamos aqu as meddas de posção _ estatístcas que representam uma sére de dados orentando-nos quanto à posção da dstrbução em relação ao exo
Projeção Populacional 2013-2020 para a Cidade do Rio de Janeiro: uma aplicação do método AiBi
 ISSN 1984-7203 Projeção Populacoal 2013-2020 para a Cdade do Ro de Jaero: uma aplcação do método AB Nº 20130102 Jaero - 2013 Iva Braga Ls 1, Marcelo Pessoa da Slva, Atoo Carlos Carero da Slva, Sérgo Gumarães
ISSN 1984-7203 Projeção Populacoal 2013-2020 para a Cdade do Ro de Jaero: uma aplcação do método AB Nº 20130102 Jaero - 2013 Iva Braga Ls 1, Marcelo Pessoa da Slva, Atoo Carlos Carero da Slva, Sérgo Gumarães
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
2. INTRODUÇÃO AOS MÉTODOS FACTORIAIS
 . NRODUÇÃO AOS MÉODOS FACORAS CONCEOS GEOMÉRCOS. NÉRCA. Os métodos factoras de Aálse de Dados permtem descreer matrzes (segdo o modelo do Qadro Q da Fg..) de dmesão (, p) qe represetam os alores tomados
. NRODUÇÃO AOS MÉODOS FACORAS CONCEOS GEOMÉRCOS. NÉRCA. Os métodos factoras de Aálse de Dados permtem descreer matrzes (segdo o modelo do Qadro Q da Fg..) de dmesão (, p) qe represetam os alores tomados
