2-Geometria da Programação Linear
|
|
|
- Maria Clara Caetano Gameiro
- 9 Há anos
- Visualizações:
Transcrição
1 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp
2 Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração 5. Estêca de potos etremos 6. Otmaldade de potos etremos 7. Represetação de poledros lmtados 8. Projeções de poledros: elmação de Fourer-Motzk DC-FEEC-Ucamp
3 -Poledros e cojutos coveos Defção. Um poledro é um cojuto que pode ser descrto por { R b} é uma matrz (m ) b um vetor do R m. Restrções de gualdade = b (forma padrão) é um poledro Defção. Um cojuto S R é lmtado se este uma costate K tal que o valor absoluto de toda compoete de todo elemeto de S é meor que ou gual a K. Defção.3 Seja a um vetor do R e b um escalar. (a) (b) O cojuto { R a' = b} é um hperplao. O cojuto { R a' b} é um semespaço. Um poledro é a terseção de um úmero fto de semespaços 3 DC-FEEC-Ucamp
4 a 3 ' = b 3 a ' = b H a 3 a a' < b a 4 S a 4 ' = b 4 a a 5 a ' = b S a' > b a 5 ' = b 5 a' = b a a H Poledro P = { R a ' b = 5} a H = { R a ' = b } Hperplao H e dos semespaços S e S 4 DC-FEEC-Ucamp
5 Defção.4 Um cojuto S R é coveo se para qualquer y S e qualquer λ [] temos λ + ( λ) y S. y S y Q coveo ão coveo coveo?? 5 DC-FEEC-Ucamp
6 Defção.5 Sejam k vetores em R e λ.. λ k escalares ão egatvos cuja soma é a udade. k (a) O vetor λ é a combação covea de k (b) evoltóra = covea (cove hull) dos vetores k é o cojuto de todas as combações coveas destes vetores evoltóra covea de k 6 DC-FEEC-Ucamp
7 Teorema. (a) (b) (c) (d) Iterseção de cojuto coveos é covea. Poledros são cojutos coveos. Combação covea de um úmero fto de elemetos de um cojuto coveo pertece a este mesmo cojuto Evoltóra covea de um úmero fto de vetores é um cojuto coveo. Prova : (a)sejam S Seja λ []. Como cada S λ + ( λ) y S I cojutos coveos e supoha que y I à terseção dos cojutos S é coveo e cotém e y temos o que mostra que este poto também pertece. PortatoI I S é coveo. I S. (bcd) EPC. 7 DC-FEEC-Ucamp
8 -Potos etremos vértces soluções báscas factíves Defção.6 Seja P um poledro. Um vetor P é um poto etremo de P se ão podemos ecotrar dos vetores y z P dferetes de e um escalar λ [] tal que = λy + ( λ) z. v w u P y z 8 DC-FEEC-Ucamp
9 Defção.7 Seja P um poledro. Um vetor P é um vértce de P se este algum c tal que c < c y para todo y satsfaz y P e y. w {y c y =c w} P c c {y c y =c } 9 DC-FEEC-Ucamp
10 DC-FEEC-Ucamp escalares 3 b M b M b M b R = a a a a Poledro defdo pelas segutes restrções de desgualdade e gualdade Defção.8 Se um vetor * satsfaz a * = b para algum M M M 3 etão a restrção correspodete está atva em *. 3 B C D P E
11 Teorema. Seja * um elemeto do R e I = { a * = b } o cojuto de ídces das restrções atvas. s segutes afrmações são equvaletes: (a) (b) (c) Estem vetores o cojuto {a I } que são LI. O espaço gerado pelos vetores a I é o R sto é todo elemeto do R pode ser epresso como uma combação lear dos vetores a I. O sstema de equações a = b I possu solução úca. DC-FEEC-Ucamp
12 Prova : ( ) Supoha que vetores a tem dmesão dm e são LI (Teorema. 3). ( spa({ a I gerem o R. Etão o espaço gerado por a I I})) = e destes vetores formam uma base R ( ) Supoha que dos vetores a vetores tem do R dm( spa{ a I}) = e deve ser gual ao R é uma combação lear dos vetores a I sejam LI.O subespaço gerado por estes. Logo todo elemeto I. (equvalêca (a) e (b)). Equvalêca etre (bc) EPC. a learmete depedetes restrções correspodetes são LI Teorema.(a): temos restrções LI atvas em *. DC-FEEC-Ucamp
13 Defção.9 Cosdere um poledro P defdo por restrções de gualdade e desgualdade e seja * um elemeto de R. (a) O vetor * é uma solução básca se () todas as restrções de gualdade estão atvas () etre as restrções que estão atvas em * delas são LI (b) Se * é uma solução básca que satsfaz todas as restrções etão ela é uma solução básca factível. E B D C F 3 DC-FEEC-Ucamp
14 Teorema.3 Seja P um poledro ão vazo e * P. s segutes afrmações são equvaletes: (a) (b) (c) * é um vértce. * é um poto etremo. * é uma solução básca factível. Prova :ssume P represetado por Vértce Poto etremo.supoha que * P é um vértce. Defção.7 c R Se y P z P y * z * c * < c z * mplca que c * < c ( λy + ( λ) z). Portato λy + ( λ) z a b tal que c * < c y y P y *. e λ etão c * < c y e e ão pode ser represetado por uma combação covea de dos outros elemetos de P. Logo * é poto etremo. e a = b. Poto etremo solução básca factível EPC Solução básca factível vértce EPC 4 DC-FEEC-Ucamp
15 Coroláro. Dado um úmero fto de restrções desgualdade leares este somete um úmero fto de soluções báscas ou soluções báscas factíves. Prova : Cosderar m restrções leares de desgualdade mpostas a R Estem restrções atvas learmete depetes em todas as soluções báscas. restrções atvas learmete depetes Logo soluções báscas dsttas correspodem a gualdade learmete depedetes dsttos úmero de soluções báscas tem um lmte superor que é o úmero de combações que podemos escolher restrçoes o total de m. defem um úco poto. cojutos de restrções de. OBS: úmero fto mas pode ser muto grade! Eemplo: cubo utáro { R = K} restrções soluções báscas factíves. 5 DC-FEEC-Ucamp
16 soluções báscas adjacetes: duas soluções báscas dsttas de um cojuto de restrções leares o R são adjacetes se podemos ecotrar restrções learmete depedetes que estão atvas em ambas. D E F D e E são adjacetes a B e C são adjacetes a D B C Se duas soluções báscas adjacetes também são factíves etão o segmeto de reta que as coecta e chamado de uma aresta do cojuto de soluções factíves. Eemplo: DE DC etc. 6 DC-FEEC-Ucamp
17 3-Poledros a forma padrão Poledro { R = b } matrz (m ) b vetor do R m. Hpótese: m lhas de são LI m (LD redudâca) Soluções báscas restrções atvas LI em todas elas Soluções báscas satsfazem = b m restrções atvas Para obter restrções atvas LI ( m) das varáves = ( atvas) Escolha das ( m) varáves ão pode ser arbtrára 7 DC-FEEC-Ucamp
18 Teorema.4 Cosdere as restrções = b e e assuma que a matrz (m ) tem lhas learmete depedetes. Um vetor R é uma solução básca se e somete se = b e estem ídces B() B(m) tas que (a) s coluas B() B(m) são learmete depedetes (b) Se B() B(m) etão =. Prova : ( ) Cosdere R (a) e (b). as restrções atvas m = B( ) B( ) = = Comoas coluas B( ) e supoha que estem dces B()... B( m) que satsfaçam = = b = K = e = b mplcam que são LI B( m) são úcamete determados. Logo o sstema de equações formado pelas restrções atvas possu solução úca. Pelo Teorema. estem restrções atvas LI e sso sgfca que é uma solução básca. ( ) EPC B() K 8 DC-FEEC-Ucamp
19 Procedmeto para costrução de soluções báscas.. 3. Escolher m coluas LI Seja = para todo B() K.B( m ). cujas cógtas são B() B() K K B( m) B( m) Resolver o sstema de m equações = b.. solução é ão egatva solução básca factível solução básca e factível pode ser obtda pelo procedmeto (a) Se é uma solução básca (b) B() K B( m) B() K varáves restates: varáves ão báscas coluas báscas base B( m) para or varáves m báscas. 9 DC-FEEC-Ucamp
20 DC-FEEC-Ucamp [ ] factível ão básca 6) ( báscas: factível básca 6) 4 8 ( báscas: ) ( básca matrz ) ( () ) ( () () m m B m B B B m B B B = = = = = = = B b B B M L
21 Iterpretação geométrca 3 b 4 = DC-FEEC-Ucamp
22 DC-FEEC-Ucamp. soluções báscas dferetes correspodem a bases dferetes. bases dferetes podem prover a mesma solução básca Eemplos: b = e soluções degeeradas 3. Soluções báscas adjacetes bases adjacetes Forma padrão: matrzes báscas possuem as mesmas coluas eceto uma comum em atvas LI restções ses 7 6) ( : 6) 4 8 ( : e = = = =
23 Hpótese ρ () posto pleo ( full rak) Teorema.5 Seja um poledro P = { R = b } ão vazo e uma matrz (m ) cujas lhas são a..a m. Supoha que ρ () = k < m e que as lhas a K a sejam learmete depedetes. Cosdere o poledro k Q = { a = b K a = b } k k Etão Q = P. Prova : (a) P Q pos qualquer elemeto de (b) Q P EPC P satsfaz as restrções que defem Q. 3 DC-FEEC-Ucamp
24 Soluções degeeradas Defção. Uma solução básca R é degeerada se o úmero de restrções atvas em é maor do que. B D P C E 4 DC-FEEC-Ucamp
25 Pequeas mudaças as restrções de desgualdade podem evtar soluções degeeradas P P 5 DC-FEEC-Ucamp
26 Soluções degeeradas a forma padrão Defção. Cosdere um poledro a forma padrão P = { R = b } e seja uma solução básca. Seja m o úmero de lhas de. O vetor é uma solução básca degeerada se o úmero de compoetes ulas de é maor do que ( m). 4 = P 5 = B = 6 m = 4 ( m) = 3 = = = 6 = ão degeerada B degeerada 6 DC-FEEC-Ucamp
27 Degeeração ão é uma propredade geométrca sto é ão é depedete da represetação 3 P = { ( 3 ) = = 3 > } P a forma padrão ( ) ( ) ão degeerada ( ) degeerada ( ) P = { ( 3 ) = = 3 > } P = forma ão padrão = 3 m = ( m) = ( ) ão degeerada ( ) ão degeerada 7 DC-FEEC-Ucamp
28 5-Estêca de potos etremos Defção. Um poledro P R cotém uma lha (reta) se este um vetor P e um vetor d R tal que + λd P para todo escalar λ. P Q Não cotém uma reta Possu potos etremos Cotém uma reta Não possu potos etremos 8 DC-FEEC-Ucamp
29 Teorema.6 Cosdere um poledro P = { R a b = m} ão vazo. s segutes afrmações são equvaletes: (a) (b) (c) O poledro P possu o mímo um poto etremo O poledro P ão cotém uma lha reta Etre os m vetores a a m estem deles que são LI. Prova: (a) (b) P I = { a = b } + λ * d Se a LI é solução factível básca por defção. Seão a I estão em um subespaço própo do R e este um vetor d tal que a d = I. y = + λd a y todas restrções atvas ao logo da reta y = + λd até λ = λ *. = a + λa d = b 9 DC-FEEC-Ucamp
30 (b) (a) Se P tem um poto etremo é solução factível básca (Teor..3) e estem restrções que estão atvas em com os respectvos vetores a LI. (c) (b) EPC Coroláro. Todo poledro ão vazo e lmtado e todo poledro a forma padrão possu o mímo uma solução básca factível. Prova: Poledro lmtado ão cotém uma reta. Foma padrão está o prmero quadrate { } e este ão cotém uma reta. 3 DC-FEEC-Ucamp
31 6-Otmaldade de potos etremos Teorema.7 Cosdere um problema de programação lear de mmzar c sobre um poledro P. Supoha que P teha o mímo um poto etremo e que esta uma solução ótma. Etão este uma solução ótma que é um poto etremo de P. Prova: Seja Q cojuto de todas as soluções ótmas. Seja P = Q = { R { R b} e v o valor ótmo de c. b c = v} é um poledro. P Q P e P ão cotém uma reta (Teor..6) logo Q também ão cotém uma reta e possu um poto etremo. Q * 3 DC-FEEC-Ucamp
32 Seja * poto etremo de Q. Vamos mostrar que * também é poto etremo de P Se * ão époto etremo de P etão y z P y z * λ [] * = λy + ( λ) z v = c * = λc y + ( λ) c z. Como v é o valor ótmo c y v e c z v. Logo c y = c z = v e y Q e z Q o que cotradz o fato de * é poto etremo de P. lém dsso como* Q * é umasolução ótma. 3 DC-FEEC-Ucamp
33 Teorema.8 Cosdere um problema de programação lear de mmzar c sobre um poledro P. Supoha que P teha o mímo um poto etremo. Etão ou o valor da fução objetvo é ou este um poto etremo que é a solução ótma. Prova: EPC Coroláro.3 Cosdere um problema de programação lear de mmzar c sobre um poledro ão vazo. Etão ou o valor da fução objetvo é ou este uma solução ótma. 33 DC-FEEC-Ucamp
34 7-Represetação de poledros lmtados Poledros: represetados por desgualdades Poledros: evoltóra covea de seus potos etremos Teorema.9 Um poledro ão vazo e lmtado é a evoltóra covea de seus potos etremos. Prova: EPC y z P u Q a = b * * 34 DC-FEEC-Ucamp
35 8-Projeção de poledros e elmação F-M = ( K ) R k 3 S Projeção : π k ( ) = π k ( K ) = ( K k ) Π k ( S) = { π k ( ) S} S φ Π k ( S) φ Π (S) Verfcar P R φ Π ( P) K Π ( P) Π (S) Dado P = { R j= a j b = Km} elmar e costrur Π ( P) 35 DC-FEEC-Ucamp
36 lgortmo de elmação Fourer-Motzk -Reescrever cada restrção Σ j= a j j b j a forma a a j= j j + b = Km se a dvdr ambos lados por a. Fazedo = ( - ) obtemos uma represetação de P evolvedo as segutes restrções d j d d k j + f + f k + f se se se a a a j j > < = d d j d k escalares f f j f k R - -Seja Q o poledro o R - defdo pelas restções d j d + f d k j + f k + f se se a a j > e = a j < 36 DC-FEEC-Ucamp
37 37 Eemplo algortmo de elmação reescrevedo ) ( 3) ( ) ( ) ( / / / / + + Poledro Q em R 3) ( 5 ) ( ) ( 5 3) ( 4) ( ) ( ) ( 4) ( / / / / / / / / DC-FEEC-Ucamp
38 Teorema. O poledro Q costruído pelo algortmo de elmação é gual à projeção Π - (P) de P. Coroláro.4 Seja P R +k um poledro. Etão o cojuto { R este y R k tal que (y) P} também é um poledro. Coroláro.5 Seja P R +k um poledro e uma matrz (m ). Etão o cojuto Q = { P} também é um poledro. Coroláro.6 evoltóra covea de um úmero fto de vetores é um poledro. 38 DC-FEEC-Ucamp
39 Observação Este materal refere-se às otas de aula do curso I 88 Otmzação Lear da Faculdade de Egehara Elétrca e de Computação da Ucamp. Não substtu o lvro teto as referêcas recomedadas e em as aulas epostvas. Este materal ão pode ser reproduzdo sem autorzação préva dos autores. Quado autorzado seu uso é eclusvo para atvdades de eso e pesqusa em sttuções sem fs lucratvos. 39 DC-FEEC-Ucamp
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
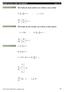 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Forma padrão do modelo de Programação Linear
 POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Métodos iterativos. Capítulo O Método de Jacobi
 Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Como CD = DC CD + DC = 0
 (9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
(9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Intervalo de Confiança para uma Média Populacional
 Estatística II Atoio Roque Aula 5 Itervalo de Cofiaça para uma Média Populacioal Um dos objetivos mais importates da estatística é obter iformação sobre a média de uma dada população. A média de uma amostra
Estatística II Atoio Roque Aula 5 Itervalo de Cofiaça para uma Média Populacioal Um dos objetivos mais importates da estatística é obter iformação sobre a média de uma dada população. A média de uma amostra
( ) ( ) ( ) ( ) ( ) 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Introdução.
 55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
Econometria: 4 - Regressão Múltipla em Notação Matricial
 Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos [email protected] Prof. arco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos [email protected] Prof. arco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Capítulo 8. Método de Rayleigh-Ritz
 Grupo : Gustavo de Souza Routma; Luís Ferado Hachch de Souza; Ale Pascoal Palombo Capítulo 8. Método de Raylegh-Rtz 8.. Itrodução Nos problemas de apromação por dfereças ftas, para apromar a solução para
Grupo : Gustavo de Souza Routma; Luís Ferado Hachch de Souza; Ale Pascoal Palombo Capítulo 8. Método de Raylegh-Rtz 8.. Itrodução Nos problemas de apromação por dfereças ftas, para apromar a solução para
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Regressão Linear - Introdução
 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
x n = n ESTATÍSTICA STICA DESCRITIVA Conjunto de dados: Organização; Amostra ou Resumo; Apresentação. População
 ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. [email protected] http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. [email protected] http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
Diferenciais Ordinárias. Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais
 Exstêca e Ucdade de Soluções de Equações Dferecas Ordáras Regaldo J Satos Departameto de Matemátca-ICEx Uversdade Federal de Mas Geras http://wwwmatufmgbr/ reg 10 de ulho de 2010 2 1 INTRODUÇÃO Sumáro
Exstêca e Ucdade de Soluções de Equações Dferecas Ordáras Regaldo J Satos Departameto de Matemátca-ICEx Uversdade Federal de Mas Geras http://wwwmatufmgbr/ reg 10 de ulho de 2010 2 1 INTRODUÇÃO Sumáro
AULA Os 4 espaços fundamentais Complemento ortogonal.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
CAP. 5 DETERMINANTES 5.1 DEFINIÇÕES DETERMINANTE DE ORDEM 2 EXEMPLO DETERMINANTE DE ORDEM 3
 DETERMINNTES CP. DETERMINNTES. DEFINIÇÕES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é por defção plcção: : M IK IK ( ) DETERMINNTES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é
DETERMINNTES CP. DETERMINNTES. DEFINIÇÕES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é por defção plcção: : M IK IK ( ) DETERMINNTES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling
![NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling](/thumbs/97/134766993.jpg) 4 INFERÊNCIA SOBRE O VETOR DE MÉDIAS 4. TESTE PARA UM VETOR DE MÉDIAS µ Lembrado o caso uvarado: H : µ = µ H : µ µ Nível de sgfcâca: α Estatístca do teste: X µ t = s/ ~ t Decsão: se t > t - (α/) rejeta-se
4 INFERÊNCIA SOBRE O VETOR DE MÉDIAS 4. TESTE PARA UM VETOR DE MÉDIAS µ Lembrado o caso uvarado: H : µ = µ H : µ µ Nível de sgfcâca: α Estatístca do teste: X µ t = s/ ~ t Decsão: se t > t - (α/) rejeta-se
CAPÍTULO III ANÁLISE DOS DADOS. Para responder à primeira pergunta, observe os dois gráficos abaixo
 CAPÍTULO III ANÁLISE DOS DADOS III.5 Idéias básicas sobre gráficos e modelos Modelos são regras matemáticas que permitem reproduzir um cojuto de valores uméricos a partir de outro ao qual correspodem.
CAPÍTULO III ANÁLISE DOS DADOS III.5 Idéias básicas sobre gráficos e modelos Modelos são regras matemáticas que permitem reproduzir um cojuto de valores uméricos a partir de outro ao qual correspodem.
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Números Complexos. 2. (IME) Seja z um número complexo de módulo unitário que satisfaz a condição z 2n 1, onde n é um número inteiro positivo.
 Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
ESTATÍSTICA APLICADA À ZOOTECNIA
 ESTATÍSTICA APLICADA À ZOOTECNIA Eucldes Braga MALHEIROS *. INTRODUÇÃO.a) Somatóras e Produtóros Sejam,, 3,...,, valores umércos. A soma desses valores (somatóra) pode ser represetada por: = = = =. e o
ESTATÍSTICA APLICADA À ZOOTECNIA Eucldes Braga MALHEIROS *. INTRODUÇÃO.a) Somatóras e Produtóros Sejam,, 3,...,, valores umércos. A soma desses valores (somatóra) pode ser represetada por: = = = =. e o
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
Vamos estudar o conceito de variabilidade absoluta considerando o conjunto de notas obtidas por cinco alunos:
 Medidas de Disperção Itrodução: - Observamos ateriormete que as medidas de tedêcia cetral são usadas para resumir, em um úico úmero, aquele parâmetro que será o represetate do cojuto de dados. Estas medidas
Medidas de Disperção Itrodução: - Observamos ateriormete que as medidas de tedêcia cetral são usadas para resumir, em um úico úmero, aquele parâmetro que será o represetate do cojuto de dados. Estas medidas
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ [email protected] Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ [email protected] Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
UNICAMP - 2004. 2ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos [email protected] Prof. Marco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos [email protected] Prof. Marco A.F.H. Cavalcat [email protected] Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
RESUMO E EXERCÍCIOS NÚMEROS COMPLEXOS ( )
 NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hipóteses Neste capítulo será estudado o segudo problema da iferêcia estatística: o teste de hipóteses. Um teste de hipóteses cosiste em verificar, a partir das observações de uma amostra,
Cap. 5. Testes de Hipóteses Neste capítulo será estudado o segudo problema da iferêcia estatística: o teste de hipóteses. Um teste de hipóteses cosiste em verificar, a partir das observações de uma amostra,
3- Autovalores e Autovetores.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
MÉTODO DOS MÍNIMOS QUADRADOS
 MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MEDIDAS E INCERTEZAS
 9//0 MEDIDAS E INCERTEZAS O Que é Medição? É um processo empírico que objetiva a desigação de úmeros a propriedades de objetos ou a evetos do mudo real de forma a descrevêlos quatitativamete. Outra forma
9//0 MEDIDAS E INCERTEZAS O Que é Medição? É um processo empírico que objetiva a desigação de úmeros a propriedades de objetos ou a evetos do mudo real de forma a descrevêlos quatitativamete. Outra forma
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. [email protected] http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. [email protected] http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Capítulo 5 Cálculo Diferencial em IR n 5.1 Definição de função de várias variáveis: campos vetoriais e campos escalares.
 5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA
 UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
Desigualdades (por Iuri de Silvio ITA-T11)
 Desigualdades (por Iuri de Silvio ITA-T) Apresetação O objetivo desse artigo é apresetar as desigualdades mais importates para quem vai prestar IME/ITA, e mostrar como elas podem ser utilizadas a resolução
Desigualdades (por Iuri de Silvio ITA-T) Apresetação O objetivo desse artigo é apresetar as desigualdades mais importates para quem vai prestar IME/ITA, e mostrar como elas podem ser utilizadas a resolução
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Cálculo Numérico. Ajuste de Curvas Método dos Mínimos Quadrados. Profa. Vanessa Rolnik 1º semestre 2015
 Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
Teoria Básica e o Método Simplex. Prof. Ricardo Santos
 Teoria Básica e o Método Simple Prof. Ricardo Santos Teoria Básica do Método Simple Por simplicidade, a teoria é desenvolvida para o problema de PL na forma padrão: Minimizar f()=c T s.a. A=b >= Considere
Teoria Básica e o Método Simple Prof. Ricardo Santos Teoria Básica do Método Simple Por simplicidade, a teoria é desenvolvida para o problema de PL na forma padrão: Minimizar f()=c T s.a. A=b >= Considere
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Apostila de Introdução Aos Métodos Numéricos
 Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
ANÁLISE DE REGRESSÃO E CORRELAÇÃO
 ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
CPV O cursinho que mais aprova na FGV
 O cursiho que mais aprova a FGV FGV ecoomia a Fase 0/dezembro/00 MATEMÁTICA 0. Se P é 0% de Q, Q é 0% de R e S é 0% de R, etão P S é igual a: 0 c 0. Dado um petágoo regular ABCDE, costrói-se uma circuferêcia
O cursiho que mais aprova a FGV FGV ecoomia a Fase 0/dezembro/00 MATEMÁTICA 0. Se P é 0% de Q, Q é 0% de R e S é 0% de R, etão P S é igual a: 0 c 0. Dado um petágoo regular ABCDE, costrói-se uma circuferêcia
Estatística Notas de Aulas ESTATÍSTICA. Notas de Aulas. Professor Inácio Andruski Guimarães, DSc. Professor Inácio Andruski Guimarães, DSc.
 Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Matrizes e Sistemas Lineares. Professor: Juliano de Bem Francisco. Departamento de Matemática Universidade Federal de Santa Catarina.
 e Aula Zero - Álgebra Linear Professor: Juliano de Bem Francisco Departamento de Matemática Universidade Federal de Santa Catarina agosto de 2011 Outline e e Part I - Definição: e Consideremos o conjunto
e Aula Zero - Álgebra Linear Professor: Juliano de Bem Francisco Departamento de Matemática Universidade Federal de Santa Catarina agosto de 2011 Outline e e Part I - Definição: e Consideremos o conjunto
Requisitos metrológicos de instrumentos de pesagem de funcionamento não automático
 Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Revisão de Estatística X = X n
 Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira INEP Ministério da Educação MEC. Índice Geral de Cursos (IGC)
 Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Macroeconometria Aula 3 Revisão de estatística e teste de hipótese
 Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Exercícios - Sequências de Números Reais (Solução) Prof Carlos Alberto S Soares
 Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
