Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
|
|
|
- Clara Balsemão Sabala
- 7 Há anos
- Visualizações:
Transcrição
1 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez
2 Matemátca Básca ara Cêcas Socas II UNIDADE INTERPOLAÇÃO. INTRODUÇÃO A terolação é uma técca de aromação de dados ou uções bastate utlzada e se alca as segutes stuações: a) quado a eressão (le de assocação) da ução ão é cohecda, orém ossuímos um cojuto de valores obtdo, or eemlo, através de dados eermetas; b) quado é dícl calcular o valor da ução, devdo a comledade da le que a dee. Nesta udade estudaremos a terolação de uções ocado o teresse a rmera stuação, ctada aterormete. Cosdere um cojuto com + elemetos relacoados, da segute orma,,,,,,,, o ode a le que dee a ução ão é cohecda. Queremos obter, or eemlo,, ode,,...,, tal que. Podemos reresetar or meo de um olômo, ara todo,,,...,. Desta orma odemos estmar através de, ou seja, Observação: o símbolo dca que se trata de um valor aromado. Gracamete tal que
3 Matemátca Básca ara Cêcas Socas II. INTERPOLAÇÃO POLINOMIAL O objetvo a terolação olomal é determar um olômo da orma a a a tal que,... a ara todo,,,...,. O olômo é chamado olômo terolador. A segur vamos obter o olômo terolador através da resolução de um sstema lear.. INTERPOLAÇÃO LINEAR A PARTIR DA SOLUÇÃO DE UM SISTEMA LINEAR Para obter um olômo ara todo,,,...,, devemos ter:, ara todo,,,...,. que terola + otos cohecdos,, Como a a a... a etão a a a a a a a a a... a... a... a. Resolvedo-se o sstema obtém-se os coecetes. a do olômo,a,..., a Observação: Quado o olômo terolador tem a orma a a um) a terolação é dta terolação lear. Eemlo : Seja a ução (grau y deda elos otos, e, Determar, or terolação lear, o valor aromado de.. Como a terolação é lear, o olômo terolador é de grau um e tem a orma:
4 Matemátca Básca ara Cêcas Socas II a. a Como e tem-se que a. a a. a. Desta orma recsamos resolver o segute sstema.a a a a. Da rmera equação do sstema temos que. Da seguda equação resulta que a a a a a. Logo. Como queremos calcular, vamos calcular... Portato é um valor aromado ara. Lembre-se que é um valor aromado em razão de que a le que dee a ução é descohecda. Além do método de terolação através da resolução de um sstema lear (ctado aterormete), estem outras ormas ara obter o olômo terolador, cohecdas como ormas de Lagrage e de Newto. Na seqüêca do teto estudaremos a orma de Newto ara terolação olomal.
5 Matemátca Básca ara Cêcas Socas II.. FORMA DE NEWTON Cosdere,,..., determar o olômo tal que ode, otos dsttos. A orma de Newto cosste em que terola através dos otos,,...,,,,.,,,......,,,,...,......,,,,,,...,,,,, são costates obtdas a artr dos otos cohecdos, chamadas oeradores dereças dvddas. A segur vejamos como determar essas costates... DIFERENÇAS DIVIDIDAS Cosdere o cojuto de otos dsttos,,,,,...,, segute orma:,, os oeradores dereças dvddas são dedos da ordem zero,,, ordem,,,, ordem,,,,, ordem,,,...,,,...,,,..., ordem
6 Matemátca Básca ara Cêcas Socas II De orma geérca odemos escrever:,,,,...,,,,,,...,.,,,,,,,,...,.,,,,,,,,,,,...,.,,...,,,...,,,,...,,.,,..., é chamada de dereça dvdda de ordem k da ução k os k+ otos dsttos.,,..., k Portato, dada uma ução tal que são cohecdos os valores, sobre ara,,,,...,, ode-se orgazar as dereças dvddas a segute tabela: X ordem ordem ordem ordem ordem,,,,,,,,,,,,,,,,,,...,
7 Matemátca Básca ara Cêcas Socas II,,,,,,, Observe que os elemetos crculados a tabela são aqueles que aarecem a eressão,,,.,,,...,,,,..., Vejamos algus eemlos: Eemlo : Cosdere a ução, tabelada a segur. Usado a orma de Newto, determe o olômo que terola os otos dados e o valor aromado de A tabela de dereças dvddas é: X ordem ordem ordem 9 6
8 Matemátca Básca ara Cêcas Socas II O olômo terolador tem a orma:,,, Portato o olômo que terola é: ou seja,. olômo terolador O valor aromado de é. Assm tem-se que: Ou ada.
9 Matemátca Básca ara Cêcas Socas II Eemlo : Cosdere a ução, tabelada a segur. Usado a orma de Newto, determe o olômo que terola os otos dados e o valor aromado de, A tabela de dereças dvddas é: ordem ordem ordem ordem ordem O olômo terolador tem a orma:,,,,,,,,,, Portato o olômo que terola é:
10 Matemátca Básca ara Cêcas Socas II O valor aromado de, é,. Assm tem-se que:,.,.,.,.,.,., 6.,.,., 6., 8. olômo terolador,.,.,.,.,.,.,9.,.,.,9. 7,,,,77 9 9,6,,,, ,,., Ou ada,,. Observação: Se os otos estão gualmete esaçados sgca,,..., que estamos em reseça de um caso artcular. Vejamos um eemlo. Eemlo : Cosdere a ução, tabelada a segur. Usado dereças dvddas, determe o olômo que terola os otos dados e o valor aromado de 8. X
11 Matemátca Básca ara Cêcas Socas II A tabela de dereças dvddas é: ordem ordem ordem O olômo terolador tem a orma:,,, Portato o olômo que terola é: 6 7 olômo terolador O valor aromado de 8 é Assm tem-se que: Ou ada ERRO NA INTERPOLAÇÃO Além dos erros de arredodameto, ao se aromar uma ução or um olômo terolador de grau, comete-se um erro E tal que
12 Matemátca Básca ara Cêcas Socas II E ara todo o tervalo,. Neste mometo, ão será eto um estudo detalhado sobre erros, tedo em vsta a ecessdade do cohecmeto de algus cocetos matemátcos ada ão estudados. Bblograa Barroso, L. C., Barroso, M. M. A., Camos Flho, F. F., Carvalho, M. L. B., Maa, M. L Cálculo Numérco, Edtora Harbra, ed. São Paulo, 98. Gomes, S. C. P. Métodos Numércos: Teora e Programação, Edtora da Furg, ed. Ro Grade, 999. Moraes, D., Mars, J. M. Cálculo Numérco Comutacoal, Teora e Pratca, Edtora Atlas, ed. São Paulo, 99. Ruggero, M. A. G., Loes, V. L. R. Cálculo Numérco, Asectos Teórcos e Comutacoas, Ed. Makro Books, ed. São Paulo, 996.
CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES
 CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES Itrodução Em dversos camos da Egehara é comum a ecessdade da determação de raízes de equações ão leares. Em algus casos artculares, como o caso de olômo, que
CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES Itrodução Em dversos camos da Egehara é comum a ecessdade da determação de raízes de equações ão leares. Em algus casos artculares, como o caso de olômo, que
4- Método de Diferenças Finitas Aplicado às Equações Diferenciais Parciais.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 4- Método de Dereças Ftas Alcado às Equações Derecas Parcas. 4.- Aromação de Fuções. 4..- Aromação or Polômos: Iterolação. 4..- Ajuste de Dados: Mímos
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 4- Método de Dereças Ftas Alcado às Equações Derecas Parcas. 4.- Aromação de Fuções. 4..- Aromação or Polômos: Iterolação. 4..- Ajuste de Dados: Mímos
CAMPUS DE GUARATINGUETÁ Computação e Cálculo Numérico: Elementos de Cálculo Numérico Prof. G.J. de Sena - Depto. de Matemática Rev.
 uesp CAMUS DE GUARATINGUETÁ Computação e Cálculo Numérco: Elemetos de Cálculo Numérco ro. G.J. de Sea - Depto. de Matemátca Rev. 5 CAÍTUO 4 INTEROAÇÃO 4. INTRODUÇÃO Cosdere a segute tabela relacoado calor
uesp CAMUS DE GUARATINGUETÁ Computação e Cálculo Numérco: Elemetos de Cálculo Numérco ro. G.J. de Sea - Depto. de Matemátca Rev. 5 CAÍTUO 4 INTEROAÇÃO 4. INTRODUÇÃO Cosdere a segute tabela relacoado calor
( ) ( ) ( ) ( ) ( ) 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Introdução.
 55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
CAP. IV INTERPOLAÇÃO POLINOMIAL
 CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts fuções são cohecds es um cojuto fto e dscreto de otos de um tervlo [,b]. Eemlo: A tbel segute relco clor esecífco d águ e temertur: temertur (ºC 5 3 35 clor
CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts fuções são cohecds es um cojuto fto e dscreto de otos de um tervlo [,b]. Eemlo: A tbel segute relco clor esecífco d águ e temertur: temertur (ºC 5 3 35 clor
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
Revisão de Estatística X = X n
 Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
ESTATÍSTICA MÓDULO 3 MEDIDAS DE TENDÊNCIA CENTRAL
 ESTATÍSTICA MÓDULO 3 MEDIDAS DE TEDÊCIA CETRAL Ídce. Meddas de Tedêca Cetral...3 2. A Méda Artmétca Smles ( μ, )...3 3. A Méda Artmétca Poderada...6 Estatístca Módulo 3: Meddas de Tedêca Cetral 2 . MEDIDAS
ESTATÍSTICA MÓDULO 3 MEDIDAS DE TEDÊCIA CETRAL Ídce. Meddas de Tedêca Cetral...3 2. A Méda Artmétca Smles ( μ, )...3 3. A Méda Artmétca Poderada...6 Estatístca Módulo 3: Meddas de Tedêca Cetral 2 . MEDIDAS
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Apostila de Introdução Aos Métodos Numéricos
 Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: enchentes
 Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Métodos tipo quadratura de Gauss
 COQ-86 Métodos Numércos ara Sstemas Algébrcos e Dferecas Métodos to quadratura de Gauss Cosderado a tegração: Método de quadratura de Gauss com otos teros I f d a ser comutada com a maor recsão ossível
COQ-86 Métodos Numércos ara Sstemas Algébrcos e Dferecas Métodos to quadratura de Gauss Cosderado a tegração: Método de quadratura de Gauss com otos teros I f d a ser comutada com a maor recsão ossível
Teoria das Comunicações
 Teora das Comucações.6ª Revsão de robabldade rof. dré Noll arreto rcíos de Comucação robabldade Cocetos áscos Eermeto aleatóro com dversos resultados ossíves Eemlo: rolar um dado Evetos são cojutos de
Teora das Comucações.6ª Revsão de robabldade rof. dré Noll arreto rcíos de Comucação robabldade Cocetos áscos Eermeto aleatóro com dversos resultados ossíves Eemlo: rolar um dado Evetos são cojutos de
Atividades Práticas Supervisionadas (APS)
 Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Momento Linear duma partícula
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
integração são difíceis de serem realizadas. Por exemplo, como calcular
 89. INTERPOAÇÃO Objetvo: Ddo um cojuto de + otos G; o lo e um cojuto de uções Ecotrr um ução gg que melhor reresete esse cojuto de ddos de cordo com lgum crtéro. Deção : Sejm os + otos. Dzemos que ução
89. INTERPOAÇÃO Objetvo: Ddo um cojuto de + otos G; o lo e um cojuto de uções Ecotrr um ução gg que melhor reresete esse cojuto de ddos de cordo com lgum crtéro. Deção : Sejm os + otos. Dzemos que ução
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES BINÔMIO DE NEWTON
 Uiversidade Federal do Rio Grade FURG Istituto de Matemática, Estatística e Física IMEF Edital CAPES BINÔMIO DE NEWTON Prof. Atôio Maurício Medeiros Alves Profª Deise Maria Varella Martiez Matemática Básica
Uiversidade Federal do Rio Grade FURG Istituto de Matemática, Estatística e Física IMEF Edital CAPES BINÔMIO DE NEWTON Prof. Atôio Maurício Medeiros Alves Profª Deise Maria Varella Martiez Matemática Básica
Sumário. Mecânica. Sistemas de partículas
 Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
CAP. IV INTERPOLAÇÃO POLINOMIAL
 CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts uções são cohecds pes um cojuto to e dscreto de potos de um tervlo [,b]. Eemplo: A tbel segute relco clor especíco d águ e tempertur: tempertur (ºC 5 5 clor
CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts uções são cohecds pes um cojuto to e dscreto de potos de um tervlo [,b]. Eemplo: A tbel segute relco clor especíco d águ e tempertur: tempertur (ºC 5 5 clor
José Álvaro Tadeu Ferreira. Cálculo Numérico. Notas de aulas
 UNIVERSIDADE FEDERAL DE OURO PRETO Isttuto de Cêcas Eatas e Bológcas Departameto de Computação José Álvaro Tadeu Ferrera Cálculo Numérco Notas de aulas Iterpolação Polomal Ouro Preto 3 (Últma revsão em
UNIVERSIDADE FEDERAL DE OURO PRETO Isttuto de Cêcas Eatas e Bológcas Departameto de Computação José Álvaro Tadeu Ferrera Cálculo Numérco Notas de aulas Iterpolação Polomal Ouro Preto 3 (Últma revsão em
Distribuições Amostrais. Estatística. 8 - Distribuições Amostrais UNESP FEG DPD
 Dstrbuções Amostras Estatístca 8 - Dstrbuções Amostras 08- Dstrbuções Amostras Dstrbução Amostral de Objetvo: Estudar a dstrbução da população costtuída de todos os valores que se pode obter para, em fução
Dstrbuções Amostras Estatístca 8 - Dstrbuções Amostras 08- Dstrbuções Amostras Dstrbução Amostral de Objetvo: Estudar a dstrbução da população costtuída de todos os valores que se pode obter para, em fução
CAP. IV INTERPOLAÇÃO POLINOMIAL
 CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts fuções são cohecds es um cojuto fto e dscreto de otos de um tervlo [,b]. Eemlo: A tbel segute relco clor esecífco d águ e temertur: temertur (ºC 5 3 35 clor
CAP. IV INTERPOLAÇÃO POLINOMIAL INTRODUÇÃO Muts fuções são cohecds es um cojuto fto e dscreto de otos de um tervlo [,b]. Eemlo: A tbel segute relco clor esecífco d águ e temertur: temertur (ºC 5 3 35 clor
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
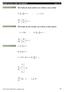 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
7 Análise de covariância (ANCOVA)
 Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Estudo do intervalo de confiança da regressão inversa utilizando o software R
 Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
Cálculo Numérico. Ajuste de Curvas Método dos Mínimos Quadrados. Profa. Vanessa Rolnik 1º semestre 2015
 Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
VI - Integração Numérica
 V - tegração Numérca C. Balsa & A. Satos. trodução São, este mometo, coecdos dos aluos métodos aalítcos para o cálculo do tegral dedo b ( d a sedo ( cotíua e tegrável o tervalo [ ab] ;. Cotudo, algumas
V - tegração Numérca C. Balsa & A. Satos. trodução São, este mometo, coecdos dos aluos métodos aalítcos para o cálculo do tegral dedo b ( d a sedo ( cotíua e tegrável o tervalo [ ab] ;. Cotudo, algumas
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
MÉTODO DE FIBONACCI. L, em que L
 Métodos de bonacc e da Seção Aúrea Adotando a notação: MÉTODO DE IBOACCI L e L L, em que L b a, resulta a: ncal orma Recursva: ara,,, - (-a) ou ara,,, - (-b) A esta equação se assoca a condção de contorno
Métodos de bonacc e da Seção Aúrea Adotando a notação: MÉTODO DE IBOACCI L e L L, em que L b a, resulta a: ncal orma Recursva: ara,,, - (-a) ou ara,,, - (-b) A esta equação se assoca a condção de contorno
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Métodos Computacionais em Engenharia DCA0304 Capítulo 3
 Métodos Comutcos em Egehr DCA4 Cítulo. Iterolção.. Itrodução Qudo se trblh com sstems ode ão é cohecd um fução que descrev seu comortmeto odemos utlzr o coceto de terolção. Há csos tmbém em que form lítc
Métodos Comutcos em Egehr DCA4 Cítulo. Iterolção.. Itrodução Qudo se trblh com sstems ode ão é cohecd um fução que descrev seu comortmeto odemos utlzr o coceto de terolção. Há csos tmbém em que form lítc
INTERPOLAÇÃO. Introdução
 INTERPOLAÇÃO Itrodução A terolção cosste em determr rtr de um cojuto de ddos dscretos um ução ou um cojuto de uções lítcs que ossm servr r determção de qulquer vlor o domío de deção. Pode-se ver terolção
INTERPOLAÇÃO Itrodução A terolção cosste em determr rtr de um cojuto de ddos dscretos um ução ou um cojuto de uções lítcs que ossm servr r determção de qulquer vlor o domío de deção. Pode-se ver terolção
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA
 INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Introdução à Estatística
 Itrodução à Estatístca Júlo Cesar de C. Balero Estatístca É a cêca que se preocupa com: () Orgazação; () Descrção; () Aálses; (v) Iterpretações. Estatístca Descrtva Estatístca Idutva ou Estatístca Ierecal
Itrodução à Estatístca Júlo Cesar de C. Balero Estatístca É a cêca que se preocupa com: () Orgazação; () Descrção; () Aálses; (v) Iterpretações. Estatístca Descrtva Estatístca Idutva ou Estatístca Ierecal
CAPÍTULO 5. Ajuste de curvas pelo Método dos Mínimos Quadrados
 CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
Momento Linear duma partícula
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Mometo lear de uma partícula e de um sstema de partículas. - Le fudametal da dâmca para um sstema de partículas. - Impulso
POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA INTRODUÇÃO
 POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos oderados (MRP) tora-se dsesável um estudo mesmo que
POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos oderados (MRP) tora-se dsesável um estudo mesmo que
Probabilidade: Diagramas de Árvore
 Probabldade: Dagramas de Árvore Ana Mara Lma de Faras Departamento de Estatístca (GET/UFF) Introdução Nesse texto apresentaremos, de forma resumda, concetos e propredades báscas sobre probabldade condconal
Probabldade: Dagramas de Árvore Ana Mara Lma de Faras Departamento de Estatístca (GET/UFF) Introdução Nesse texto apresentaremos, de forma resumda, concetos e propredades báscas sobre probabldade condconal
Objetivo Estimar uma proporção p (desconhecida) de elementos uma população, apresentando certa característica de interesse, partir
 Objetivo Estimar uma roorção (descohecida) de elemetos em uma oulação, aresetado certa característica de iteresse, a artir da iformação forecida or uma amostra. Exemlos: : roorção de aluos da USP que foram
Objetivo Estimar uma roorção (descohecida) de elemetos em uma oulação, aresetado certa característica de iteresse, a artir da iformação forecida or uma amostra. Exemlos: : roorção de aluos da USP que foram
Problema geral de interpolação
 Problema geral de terpolação Ecotrar p() que verfque as codções: f j ( ) y,,,,,, j,,, m ( j) ( ) dervada de ordem j ós valores odas Eemplo: ecotrar p() que verfque:, f () 4 3, f( 3) 3, f'(3) 4 3 p() 3
Problema geral de terpolação Ecotrar p() que verfque as codções: f j ( ) y,,,,,, j,,, m ( j) ( ) dervada de ordem j ós valores odas Eemplo: ecotrar p() que verfque:, f () 4 3, f( 3) 3, f'(3) 4 3 p() 3
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Tabela 1 Números de acidentes /mês no Cruzamento X em CG/07. N de acidentes / mês fi f
 Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
MÓDULO 8 REVISÃO REVISÃO MÓDULO 1
 MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Estudo das relações entre peso e altura de estudantes de estatística através da análise de regressão simples.
 Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Análise de Regressão
 Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
A. Equações não lineares
 A. Equações não lineares 1. Localização de raízes. a) Verifique se as equações seguintes têm pelo menos uma solução nos intervalos dados: i) (x - 2) 2 ln(x) = 0, em [1, 2] e [e, 4]. ii) 2 x cos(x) (x 2)
A. Equações não lineares 1. Localização de raízes. a) Verifique se as equações seguintes têm pelo menos uma solução nos intervalos dados: i) (x - 2) 2 ln(x) = 0, em [1, 2] e [e, 4]. ii) 2 x cos(x) (x 2)
Curso Mentor. Radicais ( ) www.cursomentor.wordpress.com. Definição. Expoente Fracionário. Extração da Raiz Quadrada. Por definição temos que:
 Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
Departamento de Informática. Modelagem Analítica do Desempenho de Sistemas de Computação. Modelagem Analítica. Disciplina:
 Deartameto de Iformátca Dscla: do Desemeho de Sstemas de Comutação Processos de ascmeto e Morte Prof. Sérgo Colcher colcher@f.uc-ro.br Processos de ascmeto e Morte CMTC Homogêea a ual trasções acotecem
Deartameto de Iformátca Dscla: do Desemeho de Sstemas de Comutação Processos de ascmeto e Morte Prof. Sérgo Colcher colcher@f.uc-ro.br Processos de ascmeto e Morte CMTC Homogêea a ual trasções acotecem
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
Regressão Simples. Parte III: Coeficiente de determinação, regressão na origem e método de máxima verossimilhança
 Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Como CD = DC CD + DC = 0
 (9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
(9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
Introdução à Estatística. Júlio Cesar de C. Balieiro 1
 Itrodução à Estatístca Júlo Cesar de C. Balero Estatístca É a cêca que se preocupa com: () Orgazação; () Descrção; () Aálses; (v) Iterpretações. Estatístca Descrtva Estatístca Idutva ou Estatístca Ierecal
Itrodução à Estatístca Júlo Cesar de C. Balero Estatístca É a cêca que se preocupa com: () Orgazação; () Descrção; () Aálses; (v) Iterpretações. Estatístca Descrtva Estatístca Idutva ou Estatístca Ierecal
a) 1,8 e 4,6. b) 2,0 e 2,2. c) 1,8 e 5,2. d) 2,0 e 4,6. e) 2,0 e 1,9.
 Questão : As otas de dez aluos, um exame, estão dadas a segur:, 5, 8, 3, 6, 5, 8, 7, 6, 0 O desvo médo e a varâca dessas otas podem ser expressos, respectvamete, por: a),8 e 4,6 b),0 e, c),8 e 5, d),0
Questão : As otas de dez aluos, um exame, estão dadas a segur:, 5, 8, 3, 6, 5, 8, 7, 6, 0 O desvo médo e a varâca dessas otas podem ser expressos, respectvamete, por: a),8 e 4,6 b),0 e, c),8 e 5, d),0
O delineamento amostral determina os processos de seleção e de inferência do valor da amostra para o valor populacional.
 Curso Aperfeçoameto em Avalação de Programas Socas ª Turma Dscpla: Téccas quattatvas de levatameto de dados: prcpas téccas de amostragem Docete: Claudete Ruas Brasíla, ovembro/005 Pesqusa por amostragem
Curso Aperfeçoameto em Avalação de Programas Socas ª Turma Dscpla: Téccas quattatvas de levatameto de dados: prcpas téccas de amostragem Docete: Claudete Ruas Brasíla, ovembro/005 Pesqusa por amostragem
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
Organização; Resumo; Apresentação.
 Prof. Lorí Val, Dr. val@ufrgs.br http://www.ufrgs.br/~val/ Grade Cojutos de Dados Orgazação; Resumo; Apresetação. Amostra ou População Defetos em uma lha de produção Lascado Deseho Torto Deseho Torto Lascado
Prof. Lorí Val, Dr. val@ufrgs.br http://www.ufrgs.br/~val/ Grade Cojutos de Dados Orgazação; Resumo; Apresetação. Amostra ou População Defetos em uma lha de produção Lascado Deseho Torto Deseho Torto Lascado
2. NOÇÕES MATEMÁTICAS
 . NOÇÕES MATEMÁTICAS Este capítulo retoma algumas oções matemátcas ecessáras para uma boa compreesão de algus aspectos que serão mecoados e detalhados o presete trabalho. Algus destes aspectos podem abstrar
. NOÇÕES MATEMÁTICAS Este capítulo retoma algumas oções matemátcas ecessáras para uma boa compreesão de algus aspectos que serão mecoados e detalhados o presete trabalho. Algus destes aspectos podem abstrar
ESTATÍSTICA MÓDULO 2 OS RAMOS DA ESTATÍSTICA
 ESTATÍSTICA MÓDULO OS RAMOS DA ESTATÍSTICA Ídce. Os Ramos da Estatístca...3.. Dados Estatístcos...3.. Formas Icas de Tratameto dos Dados....3. Notação por Ídces...5.. Notação Sgma ()...5 Estatístca Módulo
ESTATÍSTICA MÓDULO OS RAMOS DA ESTATÍSTICA Ídce. Os Ramos da Estatístca...3.. Dados Estatístcos...3.. Formas Icas de Tratameto dos Dados....3. Notação por Ídces...5.. Notação Sgma ()...5 Estatístca Módulo
Econometria: 4 - Regressão Múltipla em Notação Matricial
 Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos mcm@eco.puc-ro.br Prof. arco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Ecoometra: 4 - Regressão últpla em Notação atrcal Prof. arcelo C. ederos mcm@eco.puc-ro.br Prof. arco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
INTRODUÇÃO A ESTATÍSTICA
 Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
: 8. log 3 4 : 7 B 6 B C. B D. 1 x. t é o tempo, dado em horas, e
 Eame de Admissão de Matemática Págia de... Simpliicado a epressão. : : tem-se: Simpliicado a epressão p p p Sabedo que p p obtém-se: p p log a etão log será igual a: a a a a pp p p. Para diluir litro de
Eame de Admissão de Matemática Págia de... Simpliicado a epressão. : : tem-se: Simpliicado a epressão p p p Sabedo que p p obtém-se: p p log a etão log será igual a: a a a a pp p p. Para diluir litro de
RESUMO DE MATEMÁTICA FINANCEIRA. Juro Bom Investimento C valor aplicado M saldo ao fim da aplicação J rendimento (= M C)
 RESUMO DE MATEMÁTICA FINANCEIRA I. JUROS SIMPLES ) Elemetos de uma operação de Juros Smples: Captal (C); Motate (M); Juros (J); Taxa (); Tempo (). ) Relação etre Juros, Motate e Captal: J = M C ) Defção
RESUMO DE MATEMÁTICA FINANCEIRA I. JUROS SIMPLES ) Elemetos de uma operação de Juros Smples: Captal (C); Motate (M); Juros (J); Taxa (); Tempo (). ) Relação etre Juros, Motate e Captal: J = M C ) Defção
x n = n ESTATÍSTICA STICA DESCRITIVA Conjunto de dados: Organização; Amostra ou Resumo; Apresentação. População
 ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira INEP Ministério da Educação MEC. Índice Geral de Cursos (IGC)
 Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
Estatística: uma definição
 Prof. Lorí Val, Dr. - val@pucrs.br http://www.pucrs.br/famat/val/ Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Estatístca: uma defção Coleç Coleção de ú úmeros estatí estatístcas O ú ú mero
Prof. Lorí Val, Dr. - val@pucrs.br http://www.pucrs.br/famat/val/ Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Estatístca: uma defção Coleç Coleção de ú úmeros estatí estatístcas O ú ú mero
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
d s F = m dt Trabalho Trabalho
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
FÍSICA MODERNA I AULA 15
 Uversdde de São ulo Isttuto de Físc FÍSIC MODERN I U 5 rof. Márc de lmed Rzzutto elletro sl 0 rzzutto@f.us.br o. Semestre de 08 ág do curso: htts:edscls.us.brcoursevew.h?d=695 0008 OERDORES OBSERVÁVEIS
Uversdde de São ulo Isttuto de Físc FÍSIC MODERN I U 5 rof. Márc de lmed Rzzutto elletro sl 0 rzzutto@f.us.br o. Semestre de 08 ág do curso: htts:edscls.us.brcoursevew.h?d=695 0008 OERDORES OBSERVÁVEIS
Probabilidades e Estatística LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBiol, MEBiom, MEEC, MEFT, MEMec, MEQ
 Duração: 90 mutos Grupo I Probabldades e Estatístca LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBol, MEBom, MEEC, MEFT, MEMec, MEQ Justfque coveetemete todas as respostas 1 o semestre 018/019 10/01/019 09:00 o
Duração: 90 mutos Grupo I Probabldades e Estatístca LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBol, MEBom, MEEC, MEFT, MEMec, MEQ Justfque coveetemete todas as respostas 1 o semestre 018/019 10/01/019 09:00 o
Almeida, C. (1987) Novo método para resolução da equação dos rebaixamentos em ensaios a caudal variável
 Almeda, C. (1987) Novo método para resolução da equação dos rebaxametos em esaos a caudal varável Geols, revsta da Secção de Geologa Ec. e Aplcada, vol. I, p. 100-10. GEOLIS - Vol. I(1987) 100-10 100 NOVO
Almeda, C. (1987) Novo método para resolução da equação dos rebaxametos em esaos a caudal varável Geols, revsta da Secção de Geologa Ec. e Aplcada, vol. I, p. 100-10. GEOLIS - Vol. I(1987) 100-10 100 NOVO
Projeto e Análise de Algoritmos Recorrências. Prof. Humberto Brandão
 Projeto e Aálse de Algortmos Recorrêcas Prof. Humberto Bradão humberto@dcc.ufmg.br Uversdade Federal de Alfeas Laboratóro de Pesqusa e Desevolvmeto LP&D Isttuto de Cêcas Exatas ICEx versão da aula: 0.
Projeto e Aálse de Algortmos Recorrêcas Prof. Humberto Bradão humberto@dcc.ufmg.br Uversdade Federal de Alfeas Laboratóro de Pesqusa e Desevolvmeto LP&D Isttuto de Cêcas Exatas ICEx versão da aula: 0.
MAE 5776 ANÁLISE MULTIVARIADA. Júlia M Pavan Soler
 MAE 5776 ANÁLISE MULTIVARIADA Júla M Pava Soler ava@me.us.br º Semestre IME/09 Baco de Dados: Dados Multvarados Varáves Udades Amostras j j j j j j : Matrz de Dados resosta do -ésmo dvíduo a j-ésma varável
MAE 5776 ANÁLISE MULTIVARIADA Júla M Pava Soler ava@me.us.br º Semestre IME/09 Baco de Dados: Dados Multvarados Varáves Udades Amostras j j j j j j : Matrz de Dados resosta do -ésmo dvíduo a j-ésma varável
AV1 - MA 14-2011. (1,0) (a) Determine o maior número natural que divide todos os produtos de três números naturais consecutivos.
 Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
UNICAMP - 2004. 2ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
