1. Conjuntos Fuzzy - Fundamentos. Sistemas Nebulosos
|
|
|
- Gabriela Tomé Peixoto
- 5 Há anos
- Visualizações:
Transcrição
1 Sistemas Nebulosos Heloisa de Arruda Camargo. Conjuntos Fuzzy - Fundamentos. Conceitos básicos de conjuntos fuzzy.2 Operações em conjuntos fuzzy.3 Relações fuzzy.4 Aritmética fuzzy.5 Variáveis linguísticas 2. Conceitos básicos de conjuntos fuzzy Conjunto convencional (conjunto binário, conjunto crisp ) pode ser definido por: Função característica: enumeração {2, 4, 6, 8,,...2} propriedade dos elementos A = {x Ν x é par} B = {x Ν - x 2} função caracterísitca 3 A : {, } elementos do conjunto universo pertencem totalmente ao conjunto A: A(x) = ou não pertencem ao conjunto: A(x) = 4
2 Conjuntos fuzzy Conjuntos fuzzy Função de pertinência A: [,] - conjunto base A - conjunto fuzzy elementos do conjunto base pertencem ao conjunto com um certo grau, que usualmente varia entre e. 5 Função de pertinência mapeia elementos do conjunto base em um número real entre e,8 A: [,] x p A 6 Representação de categorias Variável temperatura baixíssima baixa média alta altíssima Intervalos conjuntos fuzzy baixíssima baixa média alta altíssima [ ]( ]( ]( ]( ] baixíssima baixa média alta altíssima
3 Representações de funções de pertinência Representação gráfica Representação analítica Representação tabular Representação por lista Formas de conjuntos fuzzy (representação gráfica e analítica) A(x) = Triangulares, se x a (x-a)/(m-a), se x [a,m] (b-x)/(b-m), se x [m,b], se x b A a m b A(x; a, m, b) = max{min[(x-a)/(m-a),(b-x)/(b-m)],} 9 Formas de conjuntos fuzzy Formas de conjuntos fuzzy Trapezoidal, se x a (x-a)/(m-a), se x [a,m] A Gaussiana A(x) = e k (x-m)2 A(x) =, se x [m,n] (b-x)/(b-n), se x [n,b] onde k >, se x > b a m n b m k A(x; a, m, n,b) = max{min[(x-a)/(m-a),, (b-x)/(b-m)],} 2
4 Formas de conjuntos fuzzy Formas de conjuntos fuzzy Função tipo -exponencial A(x) = + k(x-m) 2 FunçãoΓ, se x a A(x) = -e k(x-a)2 se x > a A k >, ou A(x) = k(x-m)2 + k(x-m) 2 k > m A(x) =, se x a k(x-a) 2 se x > a + k(x-a) 2 a k onde k > 3 4 Formas de conjuntos fuzzy Representação tabular Função S, se x a 2((x-a)/(b-a)) 2, se x [a,m] A(x) = -2((x-b)/(b-a)) 2, se x [m,b] A Para conjuntos base finitos (discretizados) Ex: conjunto base contínuo: T = [,4] conjunto base discretizado: TD = {, 5,, 5, 2, 25, 3, 35, 4}, se x > b m = a + b /2 : cruzamento da função S a b A tabela lista elementos do conjunto base e seus graus de pertinência, podendo omitir os que tem grau de pertinência zero 5 6
5 Exemplo Conceito de Temperatura alta Representação por lista Conjunto base: TD = {, 5,, 5, 2, 25, 3, 35, 4} Tabela Gráfico x TD TA(x) TA T 7 TA= {,, 5,,,, 5,, 2,.34, 25,.67, 3,, 35,, 4, } Notação de lista: TA = / + /5 + / +.34/2 +.67/25 + /3 + /35 + /4 Ou: TA =.34/2 +.67/25 + /3 + /35 + /4 8 Notações Conceitos relacionados a conjuntos fuzzy Universos finitos = {x, x 2,., x n } A = {(a i /x i ) x i ε } onde a i = A(x i ) i =,, n Corte-α (α-cut) A α = {x A(x) α} A = a /x + a 2 /x a n /x n = Σ i=,n a i /x i ou na forma de vetor: A = [a a 2.a n ] Universos contínuos Corte-α forte (strong α-cut) A α+ = {x A(x) > α } Conjunto de níveis de A ΛA = {α A(x) = α para algum x } A(x) = 9 x a/x 2
6 Conceitos Operações simples sobre conjuntos fuzzy Suporte de um conjunto fuzzy A Conjunto binário que contém todos os elementos de que tem grau de pertinência diferente de zero em A Normalização Norm_A(x) = A(x) / h(a) Altura h(a) de um conjunto fuzzy A Maior grau de pertinência obtido por qualquer elemento do conjunto Conjunto Normal Um conjunto fuzzy A é Normal quando h(a) = Concentração valores de pertinência se tonam relativamente menores Con_A(x) = A 2 (x) Dilatação valores de pertinência se tonam relativamente maiores Dil_A(x) = A.5 (x) 2 22 Operações simples sobre conjuntos fuzzy Generalização de concentração: Con_A(x) = A p (x) p> Generalização de concentração: Dil_A(x) = A r (x) r (,) Intensificação de contraste valores menores que ½ diminuem e os maiores aumentam Int_A(x) = 2A 2 (x), se A(x).5 Relações básicas igualdade e inclusão Igualdade Conjuntos fuzzy A e B A = B see A(x) = B(x) Inclusão Conjuntos fuzzy A e B A B see A(x) B(x) -2(-A(x)) 2, caso contrário 23 24
7 .2 Operações em Conjuntos Fuzzy Operações Padrão Operações padrão Complemento Fuzzy Intersecção Fuzzy União Fuzzy conjunto base Complemento: A (x) = A(x) Operações generalizadas T-normas e Intersecção generalizada T-conormas e União generalizada Dualidade e leis de De Morgan Intersecção: (A B) (x) = min(a(x), B(x)) = A(x) B(x) União: Operadores de Agregação 25 (A B) (x) = max(a(x), B(x)) = A(x) B(x) 26 Operações Padrão Complemento Padrão A (x)=-a (x) Exemplo Jovem:A Adulto:A 2 Terceira Idade:A 3 Jovem:A Adulto:A 2 Terceira Idade:A A
8 Intersecção Padrão A A 2 (x)=a (x) A 2 (x) União Padrão A A 2 (x)=a (x) A 2 (x) Jovem:A Adulto:A 2 Terceira Idade:A 3 Jovem:A Adulto:A 2 Terceira Idade:A A A 2 A A Operações Generalizadas Operações generalizadas São as operações entre conjuntos (complemento, interseção e união) que assumem formas diferentes das operações padrão No caso da interseção e união, são operações que utilizam outros operadores em substituição ao mínimo e máximo. Esses operadores pertencem a categorias denominadas genericamente por normas triangulares, as quais garantem que propriedades de operações entre conjuntos serão satisfeitas Normas triangulares: fornecem modelos genéricos para as operações de intersecção e união de conjuntos fuzzy Normas triangulares (t-normas) : intersecção Co-normas triangulares (s-normas): união 3 32
9 Normas Triangulares (t-normas) Operação binária t: [,] 2 [,] que satisfaz as propriedades: Comutatividade: x t y = y t x Exemplos de t-normas: Mínimo: x t y = min(x,y) Produto algébrico: x t 2 y = xy Diferença limitada: x t 3 y = max(, x + y ) Associatividade: x t (y t z) = (x t y) t z Monotonicidade: se x y e w z, então x t w y t z x se y = Interseção drástica: x t 4 y = y se x = caso contrário Relações entre as t-normas: x t 4 y x t y x t y Condições limite: t x =, t x = x Intersecção (produto) Jovem:A Adulto:A 2 Terceira Idade:A 3 A A 2 (x)=a (x). A 2 (x) Co-normas triangulares (snormas) Operação binária s : [,] 2 [,] que satisfaz as propriedades: Comutatividade: x s y = y s x A A 2 Associatividade: x s (y s z) = (x s y) s z Monotonicidade: se x y e w z, então x s w y s z Condições limite: x s = x, x s = 36
10 Exemplos de s-normas: União (soma algébrica) Máximo: x s y = max(x,y) Jovem:A Adulto:A 2 Terceira Idade:A 3 Soma algébrica: x s 2 y = x + y xy Soma limitada: x s 3 y = min(, x + y) x se y = União drástica: x s 4 y = y se x = caso contrário A A 2 A A 2 (x)=a (x)+a 2 (x)-(a (x).a 2 (x)) Relações entre as s-normas: x s y x s y x s 4 y Características das operações padrão Intersecção Padrão (com operador min): produz o maior Conjunto Fuzzy entre todos os produzidos por todas as possíveis intersecções (t-normas) União Padrão (com operadro max) : produz o menor Conjunto Fuzzy entre todos os produzidos por todas as possíveis uniões (s-normas) São operações idempotentes: x t x = x e x s x=x (são as únicas operações idempotentes entre as t-normas e s-normas) Dualidade e leis de De Morgan Para cada t-norma existe uma s-norma dual: x s y = (-x) t (-y) e x t y = (-x) s (-y) Escrevendo na forma: - x s y = (-x) t (-y) e - x t y = (-x) s (-y) Temos as leis de de Morgan: (A B) = A B e (A B) = A B 39 4
11 Operadores de agregação Operação de agregação sobre conjuntos fuzzy: combinam uma coleção de conjuntos fuzzy para produzir um único conjunto fuzzy É definida por h : [,] n [,] Satisfazendo: Na agregação de conjuntos fuzzy A, A 2,..., A n, a função h produz um conjunto fuzzy A operando sobre os graus de pertinência dos conjuntos dados para cada x, ou seja: A(x) = h(a (x), A 2 (x),..., A n (x)) Condições limite: h(,..., ) = e h(,..., ) = Monotonicidade: para todo x OBS: interseção e união fuzzy são operações de h(a ) h(b,..., b n ) se a i b, i =,..., n i agregação 4 42 Operadores de média São operadores que dão resultados entre a interseção fuzzy padrão (min) e a união fuzzy padrão (max) Operadores de média generalizada Classe de operadores de média que cobrem todo o intervalo entre as operações min e max. Definidos por: min (a, a 2 ) h(a, a 2 ) max (a, a 2 ) h p (a ) = (/n (a p + a 2p a np )) /p p R, p São operadores idempotentes: h(a, a,..., a) = a A função h p representa uma classe parametrizada de operadores de agregação contínuos, simétricos e idempotentes. O parâmetro p distingue os operadores de média 43 44
12 Operadores de média: Média aritmética (p = ) h(a ) = /n (a + a a n ) Média harmônica ( p = -) h(a ) = n / (/a + /a /a n ) Média geométrica ( p ) h(a ) = (a a 2... a n ) /n Operadores de média ponderados ordenados (OWA) Outra classe de operadores de média que cobrem o intervalo entre as operações de min e max Seja w = (w,..., w n ) vetor de pesos tal que w w n = Seja a seqüência de valores {a i } i=,..., n ordenada como: a a 2... a n A operação OWA associada com w é a função h w (a, a 2 ) = w a + w 2 a w n a n Alguns operadores OWA ) w = (,,..., ) operador de mínimo h w (a, a 2 ) = min(a,a 2,...,a n ) 2) w = (,,..., ) operador de máximo h w (a, a 2 ) = max(a,a 2,...,a n ) 3) w = (/n, /n,..., /n) operador de média padrão Relação entre operadores de média e normas triangulares Para um operador de média h vale a inequação: min(a ) h(a ) max(a ) para toda n-upla a Todos os operadores de agregação entre a interseção fuzzy padrão e a união fuzzy padrão (operadores de média) são idempotentes Estes são os únicos Operadores de Agregação que são idempotentes h(a ) = /n (a + a a n ) 47 48
13 Escopo dos operadores de agregação.3 Relações Fuzzy i min Operadores de intersecção (Associativos) min Operadores de média (Idempotentes) max Operadores de união (Associativos) u max Definição de relação fuzzy Operações sobre relações: projeção e extensão cilíndrica Relações fuzzy binárias Composição de relações fuzzy Algumas classes de relações fuzzy 49 5 Definição de Relação Fuzzy Relações convencionais (crisp) Relações representam a presença ou ausência de associação, interação ou interconexão entre os elementos de dois ou mais conjuntos Relação entre conjuntos, 2,..., n subconjunto do produto cartesiano dos conjuntos i A relação é também um conjunto Função característica: R(x, x 2,..., x n ) = see x, x 2,..., x n R caso contrário 5 Exemplo Relação convencional = {inglês, francês} Y = {dolar, libra, franco, marco} Z = {USA, França, Canadá, Inglaterra, Alemanha} R(, Y, Z) = { inglês, dolar, USA, francês, franco, França, inglês, dolar, Canadá, francês, dolar, Canadá, inglês, libra, Inglaterra } 52
14 Relações Fuzzy Conjuntos fuzzy definido no produto cartesiano de conjuntos convencionais, 2,..., n onde as t-uplas x, x 2,..., x n podem ter graus de pertinência variados na relação = {a, b, c} Y = {, 2} Representação matricial = {NY, Paris} Y = {Beijing, NY, Londres} Relação nebulosa representando muito longe: NY Paris Χ Y = { (a, ), (a, 2), (b, ), (b, 2), (c, ), (c, 2) } A =./(a,) +.6/(a,2) +.9/(b,) + /(b,2) + /(c,) +,2/(c,2) Beijing NY Londres Produto cartesiano de conjuntos fuzzy A e B conjuntos fuzzy sobre e Y A Χ B (produto cartesiano de A e B) é uma relação fuzzy T no conjunto Χ Y onde T(x, y) = min [A(x), B(y)] = {a, b, c} Y = {, 2, 3} A = /a +.6/b +.3/c B = / +.5/2 + /3 A Χ B = /(a,) +.5/(a,2) + /(a,3) +.6/(b,) +,5/(b,2) + /(b,3) +.3/(c,) +.3/(c,2) + /(c,3) 55 Operações sobre relações extensão cilíndrica Seja A conjunto fuzzy sobre Extensão cilíndrica de A para Χ Y : Relação fuzzy em Χ Y definida por  = A Χ Y tal que  (x,y) = A (x) Χ Y(y) = A (x) = A(x) = {a, b, c} Y = {, 2, 3} A = /a +.6/b +.3/c  = A Χ Y = /(a,) + /(a,2) + /(a,3) +.6/(b,) +.6/(b,2) +.6/(b,3) +.3/(c,) +.3/(c,2) +.3/(c,3) 56
15 Projeção A relação fuzzy sobre Χ Y Projeção de A em : Conjunto fuzzy A de A = Proj A tal que A (x) = Max y [A(x,y)] = {a, b, c} Y = {, 2, 3} A = /(a,) +.6/(a,2) +.4/(a,3) +.5/(b,) +.8/(b,2) +.2/(b,3) +.3/(c,) +.3/(c,2) +.3/(c,3) Proj A = /a +.8/b +.3/c Relações fuzzy binárias São generalizações de funções R(,Y) pode associar a cada elemento de dois ou mais elementos de Y Operações básicas de funções (inversa, composição) são aplicáveis a relações Proj Y A = / +.8/2 +.3/ Relações fuzzy binárias Relação fuzzy R(,Y) Domínio de R: conjunto fuzzy em dom R(x) = max y Y R(x,y) Co - domínio de R: conjunto fuzzy em y Co-dom R(y) = max x R(x,y) Composição de relações fuzzy Sejam P(,Y) e Q(Y,Z) Composição padrão( ou composição max-min): R(,Z) = P(,Y) Q(Y,Z) R(x,z) = [P Q](x,z) = max y Y min[p(x,y),q(y,z)] para todo x e z Z Composição max-t: R(x,z) = [P Q](x,z) = max y Y t [P(x,y),Q(y,z)] inversa de R: relação fuzzy em Y Χ Outras composições: min-max, min-s R - (y,x) = R(x,y) 59 6
16 Composição de relações binárias em termos de matrizes de pertinência P = [p ik ], Q = [q kj ], R = [r ij ], tal que R = P Q A composição pode ser escrita na notação de matrizes: [r ij ] = [p ik ] [q kj ] onde r ij = max k min (p ik, q kj ) Operação equivalente a multiplicação de matrizes, onde as operações de produto e de soma são substituídas pelas operações de min e max Exemplo composição max-min na forma matricial a b c Y Z o f g h i = 3 Z f g h i P(,Y) Q(Y,Z) R(,Z) a b c 6 62 Composição de relações fuzzy binárias - representação gráfica P.3 Y a b c.6.9 Q.8 Z α β Junção de relações fuzzy binárias Operação sobre duas relações fuzzy binárias que produz triplas em vez de pares. Sejam P(,Y) e Q(Y,Z) Junção relacional de P e Q correspondente a composição max-min: R(,Y,Z) = P(,Y) Q(Y,Z) R(,Z) R(, α) = min[p(,a),q(a, α)]= min[.7,.6] =.6 R(x,y,z) = [P Q](x,y,z) = min[p(x,y),q(y,z)] R(, β) = max{min[p(,a),q(a, β)], min[p(,b),q(b, β)]} = max{min[.7,.8], min[.5,]} = para todo x, y Y e z Z
17 Algumas classes de Relações fuzzy R sobre Χ pode ter as propriedades: reflexiva, simétrica, transitiva Relações entre conjuntos convencionais que são reflexivas, simétricas e transitivas: relações de equivalência Relações entre conjuntos fuzzy que são reflexivas, simétricas, transitivas: relações de similaridade Relações entre conjuntos convencionais que são reflexivas e simétricas: relações de compatibilidade Relações entre conjuntos fuzzy que são reflexivas e simétricas: relações de proximidade 65
Conteúdo: Operações Conjuntos Crisp Operações Conjuntos fuzzy. Operadores de Zadeh Operadores Compensatórios Operadores T-norm e T-conorm
 Conteúdo: Operações Conjuntos Crisp Operações Conjuntos fuzzy Operadores de Zadeh Operadores Compensatórios Operadores T-norm e T-conorm Operações com Conjuntos Crisp Função característica: determina se
Conteúdo: Operações Conjuntos Crisp Operações Conjuntos fuzzy Operadores de Zadeh Operadores Compensatórios Operadores T-norm e T-conorm Operações com Conjuntos Crisp Função característica: determina se
1. Conjuntos Fuzzy - Fundamentos. Sistemas Nebulosos
 Sistems Nebulosos Helois de Arrud Cmrgo. Conjuntos Fuzzy - Fundmentos. Conceitos básicos de conjuntos fuzzy.2 Operções em conjuntos fuzzy.3 Relções fuzzy.4 Aritmétic fuzzy.5 Vriáveis linguístics 2. Conceitos
Sistems Nebulosos Helois de Arrud Cmrgo. Conjuntos Fuzzy - Fundmentos. Conceitos básicos de conjuntos fuzzy.2 Operções em conjuntos fuzzy.3 Relções fuzzy.4 Aritmétic fuzzy.5 Vriáveis linguístics 2. Conceitos
CONJUNTOS NEBULOSOS. Formatos dos Conjuntos
 CONJUNTOS NEBULOSOS Conjuntos Crisp x Nebulosos Definição Representação Propriedades Formatos Operações Hedges Formatos dos Conjuntos A função verdade de um conjunto fuzzy representa as propriedades semânticas
CONJUNTOS NEBULOSOS Conjuntos Crisp x Nebulosos Definição Representação Propriedades Formatos Operações Hedges Formatos dos Conjuntos A função verdade de um conjunto fuzzy representa as propriedades semânticas
Variáveis Linguísticas CONTEÚDO. Variáveis Linguísticas. Variáveis Linguísticas. Formalismo: caracterizada por uma
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
Programa. 4. Conceitos teóricos e notação. Computação Fuzzy - PCS 5711 (capítulo 4 - Parte c)
 Computação Fuzzy - PCS 57 (capítulo 4 - Parte c) Pós-Graduação: área de Sistemas Digitais (34) Professor Marco Túlio Carvalho de ndrade PCS - Depto. de Enga. de Computação e Sistemas Digitais - EPUSP Programa.
Computação Fuzzy - PCS 57 (capítulo 4 - Parte c) Pós-Graduação: área de Sistemas Digitais (34) Professor Marco Túlio Carvalho de ndrade PCS - Depto. de Enga. de Computação e Sistemas Digitais - EPUSP Programa.
Teoria da Decisão. Modelagem de Preferência. Prof. Lucas S. Batista. lusoba
 Teoria da Decisão Modelagem de Preferência Prof. Lucas S. Batista lusoba@ufmg.br www.ppgee.ufmg.br/ lusoba Universidade Federal de Minas Gerais Escola de Engenharia Graduação em Engenharia de Sistemas
Teoria da Decisão Modelagem de Preferência Prof. Lucas S. Batista lusoba@ufmg.br www.ppgee.ufmg.br/ lusoba Universidade Federal de Minas Gerais Escola de Engenharia Graduação em Engenharia de Sistemas
Variáveis Linguísticas CONTEÚDO. Variáveis Linguísticas. Variáveis Linguísticas. Formalismo: caracterizada por uma
 ONTEÚDO Introdução Introdução, Objetivo e Histórico onceitos ásicos Definição, aracterísticas e Formas de Imprecisão onjuntos Fuzzy, Formas de Representação e Operações Lógica Fuzzy Relações, omposições,
ONTEÚDO Introdução Introdução, Objetivo e Histórico onceitos ásicos Definição, aracterísticas e Formas de Imprecisão onjuntos Fuzzy, Formas de Representação e Operações Lógica Fuzzy Relações, omposições,
Conjuntos e Relações Nebulosas (Fuzzy)
 Conjuntos e Relações Nebulosas (Fuzzy) Prof. Matheus Giovanni Pires EXA 868 Inteligência Artificial Não-Simbólica B Universidade Estadual de Feira de Santana 2 Operações Básicas Para sistemas que usam
Conjuntos e Relações Nebulosas (Fuzzy) Prof. Matheus Giovanni Pires EXA 868 Inteligência Artificial Não-Simbólica B Universidade Estadual de Feira de Santana 2 Operações Básicas Para sistemas que usam
Prof. Doutor Paulo Salgado UTAD. Doutoramento em Engª Electrotécnica e de Computadores - Prof. Paulo Salgado
 Introdução à LÓGICA DIFUSA Prof. Doutor Paulo Salgado UTAD psal@utad.pt Tópicos do Curso Introdução à LÓGICA DIFUSA (Fuzzy Logic). Operações Lógicas e Inferência difusa Técnicas automáticas de geração
Introdução à LÓGICA DIFUSA Prof. Doutor Paulo Salgado UTAD psal@utad.pt Tópicos do Curso Introdução à LÓGICA DIFUSA (Fuzzy Logic). Operações Lógicas e Inferência difusa Técnicas automáticas de geração
Soluções dos trabalhos de 1 a 7
 Universidade Federal Rural do Semiárido-UFERSA Departamento de Ciências Exatas e Naturais Curso: Bacharelado em Ciência e Tecnologia e Computação Disciplina: Álgebra Linear Aluno(a): Soluções dos trabalhos
Universidade Federal Rural do Semiárido-UFERSA Departamento de Ciências Exatas e Naturais Curso: Bacharelado em Ciência e Tecnologia e Computação Disciplina: Álgebra Linear Aluno(a): Soluções dos trabalhos
Conjuntos Fuzzy e Lógica Fuzzy
 1 Introdução Conjuntos Fuzzy e Lógica Fuzzy users.femanet.com.br/~fabri/fuzzy.htm Os Conjuntos Fuzzy e a Lógica Fuzzy provêm a base para geração de técnicas poderosas para a solução de problemas, com uma
1 Introdução Conjuntos Fuzzy e Lógica Fuzzy users.femanet.com.br/~fabri/fuzzy.htm Os Conjuntos Fuzzy e a Lógica Fuzzy provêm a base para geração de técnicas poderosas para a solução de problemas, com uma
Sistemas especialistas Fuzzy
 Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
Teoria dos Conjuntos MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES. Fundamentos de Lógica Técnicas Elementares de Prova A NOÇÃO DE CONJUNTO
 SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
A2. Cada operação é distributiva sobre a outra, isto é, para todo x, y e z em A, x (y + z) = (x y) + (x z) e x + (y z) = (x + y) (x + z)
 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
Modelos Evolucionários e Tratamento de Incertezas
 Ciência da Computação Modelos Evolucionários e Tratamento de Incertezas Aula 05 Teoria dos Conjuntos Difusos Max Pereira CONJUNTOS CLÁSSICOS Teoria dos Conjuntos é o estudo da associação entre objetos
Ciência da Computação Modelos Evolucionários e Tratamento de Incertezas Aula 05 Teoria dos Conjuntos Difusos Max Pereira CONJUNTOS CLÁSSICOS Teoria dos Conjuntos é o estudo da associação entre objetos
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos
 MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação. Inteligência Artificial. Lógica Fuzzy Aula II
 Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação Inteligência Artificial Lógica Fuzzy Aula II Introdução a Lógica Fuzzy Retomada Função de pertinência Variáveis linguísticas
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação Inteligência Artificial Lógica Fuzzy Aula II Introdução a Lógica Fuzzy Retomada Função de pertinência Variáveis linguísticas
Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos
 Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos Conjuntos Crisp x Fuzzy Conjuntos crisp ou Conjuntos clássicos: cada entidade ou objeto de um dado universo pode pertencer
Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos Conjuntos Crisp x Fuzzy Conjuntos crisp ou Conjuntos clássicos: cada entidade ou objeto de um dado universo pode pertencer
Números Reais. Víctor Arturo Martínez León b + c ad + bc. b c
 Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Notas para o Curso de Algebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009
 Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Redes Neurais e Sistemas Fuzzy
 Redes Neurais e Sistemas Fuzzy Conceitos Básicos da Lógica Fuzzy. Raciocínio aproximado Raciocínio aproximado é a forma mais conhecida de lógica fuzzy, cobrindo várias regras de inferência cujas premissas
Redes Neurais e Sistemas Fuzzy Conceitos Básicos da Lógica Fuzzy. Raciocínio aproximado Raciocínio aproximado é a forma mais conhecida de lógica fuzzy, cobrindo várias regras de inferência cujas premissas
Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy
 Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy Profa. Dra. Sarajane M. Peres e Prof. Dr. Clodoaldo A. M. Lima EACH USP http://each.uspnet.usp.br/sarajane/ } Baseado em: Dimensão Topológica
Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy Profa. Dra. Sarajane M. Peres e Prof. Dr. Clodoaldo A. M. Lima EACH USP http://each.uspnet.usp.br/sarajane/ } Baseado em: Dimensão Topológica
Matemática Discreta - 07
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Eduardo. Matemática Matrizes
 Matemática Matrizes Eduardo Definição Tabela de números dispostos em linhas e colunas. Representação ou Ordem da Matriz Se uma matriz A possui m linhas e n colunas, dizemos que A tem ordem m por n e escrevemos
Matemática Matrizes Eduardo Definição Tabela de números dispostos em linhas e colunas. Representação ou Ordem da Matriz Se uma matriz A possui m linhas e n colunas, dizemos que A tem ordem m por n e escrevemos
Curso: MAT 221- CÁLCULO DIFERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008
 Curso: MAT 221- CÁLCULO DIERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008 SÉRIES E SOMAS EM ÁLGEBRAS: C([a, b]), M n n (R), M n n (C), etc. O PRODUTO DE
Curso: MAT 221- CÁLCULO DIERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008 SÉRIES E SOMAS EM ÁLGEBRAS: C([a, b]), M n n (R), M n n (C), etc. O PRODUTO DE
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Semana 2. Primitivas. Conjunto das partes. Produto cartesiano. 1 Teoria ingênua dos conjuntos. 2 Axiomática ZFC de conjuntos. 4 Conjuntos numéricos
 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 e pertinência Conjunto é entendido como uma coleção de
Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 e pertinência Conjunto é entendido como uma coleção de
Universidade Federal Fluminense ICEx Volta Redonda Introdução a Matemática Superior Professora: Marina Sequeiros
 1. Conjuntos Objetivo: revisar as principais noções de teoria de conjuntos afim de utilizar tais noções para apresentar os principais conjuntos de números. 1.1 Conjunto, elemento e pertinência Conjunto
1. Conjuntos Objetivo: revisar as principais noções de teoria de conjuntos afim de utilizar tais noções para apresentar os principais conjuntos de números. 1.1 Conjunto, elemento e pertinência Conjunto
Matemática Discreta - 07
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Matemática Discreta Parte 11
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta Parte 11 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta Parte 11 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti
Sumário. 1 CAPÍTULO 1 Revisão de álgebra
 Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
x 1 + b a 2 a 2 : declive da recta ;
 - O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
- O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
Aula 15 Introdução à lógica fuzzy
 Organização Aula 5 Introdução à lógica fuzzy Prof. Dr. Alexandre da Silva Simões Introdução à teoria de conjuntos nebulosos Bivalência x multivalência Números fuzzy Conjuntos fuzzy Probabilidade e possibilidade
Organização Aula 5 Introdução à lógica fuzzy Prof. Dr. Alexandre da Silva Simões Introdução à teoria de conjuntos nebulosos Bivalência x multivalência Números fuzzy Conjuntos fuzzy Probabilidade e possibilidade
Histórico da Lógica Fuzzy
 Histórico da Lógica Fuzzy Lógica Fuzzy Huei Diana Lee e Newton Spolaôr Artigo de Lofti A. Zadeh Universidade da Califórnia em Berkley, EUA, 1965 Ruptura com a Lógica Aristotélica Universidade Estadual
Histórico da Lógica Fuzzy Lógica Fuzzy Huei Diana Lee e Newton Spolaôr Artigo de Lofti A. Zadeh Universidade da Califórnia em Berkley, EUA, 1965 Ruptura com a Lógica Aristotélica Universidade Estadual
Geometria Analítica. Prof Marcelo Maraschin de Souza
 Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
Redes Neurais e Sistemas Fuzzy
 Sistema de Inferência Fuzzy Redes Neurais e Sistemas Fuzzy Conceitos Básicos dos Conjuntos Fuzzy Um Sistema de Inferência Fuzzy (SIF) é um tipo especial de Sistema Baseado em Conhecimento (SBC). A Base
Sistema de Inferência Fuzzy Redes Neurais e Sistemas Fuzzy Conceitos Básicos dos Conjuntos Fuzzy Um Sistema de Inferência Fuzzy (SIF) é um tipo especial de Sistema Baseado em Conhecimento (SBC). A Base
Fundamentos de Matemática Curso: Informática Biomédica
 Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: sequências e matrizes 05 e 06/06/14 Sequências Def.: chama-se sequência finita ou n-upla toda aplicação f do
Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: sequências e matrizes 05 e 06/06/14 Sequências Def.: chama-se sequência finita ou n-upla toda aplicação f do
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos
 Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Inteligência Artificial Escola de Verão Laboratório Associado de Computação e Matemática Aplicada LAC.
 Inteligência Artificial Escola de Verão 28 Laboratório Associado de Computação e Matemática Aplicada LAC www.lac.inpe.br/~demisio/ia_lac.html Lógica Nebulosa A Lógica Nebulosa (ou Lógica Difusa Fuzzy Logic
Inteligência Artificial Escola de Verão 28 Laboratório Associado de Computação e Matemática Aplicada LAC www.lac.inpe.br/~demisio/ia_lac.html Lógica Nebulosa A Lógica Nebulosa (ou Lógica Difusa Fuzzy Logic
Exercícios e questões de Álgebra Linear
 CEFET/MG Exercícios e questões de Álgebra Linear Versão 1.2 Prof. J. G. Peixoto de Faria Departamento de Física e Matemática 25 de outubro de 2012 Digitado em L A TEX (estilo RevTEX). 2 I. À GUISA DE NOTAÇÃO
CEFET/MG Exercícios e questões de Álgebra Linear Versão 1.2 Prof. J. G. Peixoto de Faria Departamento de Física e Matemática 25 de outubro de 2012 Digitado em L A TEX (estilo RevTEX). 2 I. À GUISA DE NOTAÇÃO
1 Números Reais. 1. Simplifique as seguintes expressões (definidas nos respectivos domínios): b) x+1. d) x 2, f) 4 x 4 2 x, g) 2 x2 (2 x ) 2, h)
 Números Reais. Simplifique as seguintes expressões (definidas nos respectivos domínios): x a), x b) x+ +, x c) +x + x +x, d) x, e) ( x ), f) 4 x 4 x, g) x ( x ), h) 3 x 6 x, i) x x +, j) x x+ x, k) log
Números Reais. Simplifique as seguintes expressões (definidas nos respectivos domínios): x a), x b) x+ +, x c) +x + x +x, d) x, e) ( x ), f) 4 x 4 x, g) x ( x ), h) 3 x 6 x, i) x x +, j) x x+ x, k) log
ÁLGEBRA LINEAR I - MAT Em cada item diga se a afirmação é verdadeira ou falsa. Justifiquei sua resposta.
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
Álgebra Linear Contra-Ataca
 Contra-Ataca Prof Afonso Paiva Departamento de Matemática Aplicada e Estatística Instituto de Ciências Matemáticas e de Computação USP São Carlos Cálculo Numérico SME0104 Operações elementares Operações
Contra-Ataca Prof Afonso Paiva Departamento de Matemática Aplicada e Estatística Instituto de Ciências Matemáticas e de Computação USP São Carlos Cálculo Numérico SME0104 Operações elementares Operações
Matrizes - Matemática II /05 1. Matrizes
 Matrizes - Matemática II - 00/0 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n a uma função A de nida no conjunto f(i; j) i f1; ; ; mg e j f1; ; ; ngg e com valores
Matrizes - Matemática II - 00/0 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n a uma função A de nida no conjunto f(i; j) i f1; ; ; mg e j f1; ; ; ngg e com valores
Números Reais. Gláucio Terra. Departamento de Matemática IME - USP. Números Reais p. 1/2
 Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Lógica e Matemática Discreta
 Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 19 de Agosto de 2018 Curso de Ciência da Computação Relações Binárias Sejam A e B dois conjuntos. Definição: Chama-se relação binária
Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 19 de Agosto de 2018 Curso de Ciência da Computação Relações Binárias Sejam A e B dois conjuntos. Definição: Chama-se relação binária
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
1.2 Axioma do Supremo
 1.2 Axioma do Supremo EXERCÍCIOS RESOLVIDOS 1. Verifique que se n N é ímpar, então n 2 é também ímpar. O que pode concluir de n N sabendo que n 2 é par? RESOLUÇÃO Seja n N ímpar, com n = 2k+1, para algum
1.2 Axioma do Supremo EXERCÍCIOS RESOLVIDOS 1. Verifique que se n N é ímpar, então n 2 é também ímpar. O que pode concluir de n N sabendo que n 2 é par? RESOLUÇÃO Seja n N ímpar, com n = 2k+1, para algum
Espaços Vetoriais. () Espaços Vetoriais 1 / 17
 Espaços Vetoriais () Espaços Vetoriais 1 / 17 Espaços Vetoriais Definição Seja um conjunto V, não vazio. i. Uma adição em V é uma operação que a cada par de elementos (u, v) V V associa um elemento u +
Espaços Vetoriais () Espaços Vetoriais 1 / 17 Espaços Vetoriais Definição Seja um conjunto V, não vazio. i. Uma adição em V é uma operação que a cada par de elementos (u, v) V V associa um elemento u +
CÁLCULO I. 1 Número Reais. Objetivos da Aula
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES
 MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
Conteúdo: Hedges Relações e Composições
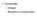 Conteúdo: Hedges Relações e Composições Hedges: Operadores semânticos Atuam na modelagem de um sistema fuzzy da mesma forma que advérbios atuam em uma sentença. Modificam a natureza de um conjunto fuzzy.
Conteúdo: Hedges Relações e Composições Hedges: Operadores semânticos Atuam na modelagem de um sistema fuzzy da mesma forma que advérbios atuam em uma sentença. Modificam a natureza de um conjunto fuzzy.
Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos
 Pode-se dizer que a é em grande parte trabalho de um único matemático: Georg Cantor (1845-1918). noção de conjunto não é suscetível de definição precisa a partir d noções mais simples, ou seja, é uma noção
Pode-se dizer que a é em grande parte trabalho de um único matemático: Georg Cantor (1845-1918). noção de conjunto não é suscetível de definição precisa a partir d noções mais simples, ou seja, é uma noção
1.4 Números Fuzzy. Números fuzzy formato. Outras formas. Casos especiais. Conjuntos fuzzy definidos no conjunto dos números reais A: R [0,1]
![1.4 Números Fuzzy. Números fuzzy formato. Outras formas. Casos especiais. Conjuntos fuzzy definidos no conjunto dos números reais A: R [0,1] 1.4 Números Fuzzy. Números fuzzy formato. Outras formas. Casos especiais. Conjuntos fuzzy definidos no conjunto dos números reais A: R [0,1]](/thumbs/87/95190949.jpg) .4 Números Fuzzy Conjuntos fuzzy definidos no conjunto dos números reais : R [0,] Conceitos intuitivos: Números próximos de um dado número real Números em torno de um dado intervalo de números reais Números
.4 Números Fuzzy Conjuntos fuzzy definidos no conjunto dos números reais : R [0,] Conceitos intuitivos: Números próximos de um dado número real Números em torno de um dado intervalo de números reais Números
Lógica Fuzzy. Lógica Fuzzy: Noções Gerais e Aplicações. apresentação. Prof a. Responsável: Graçaliz Pereira Dimuro. Disciplina: Computação Flexível
 apresentação Lógica Fuzzy Conrado Ruch. Diego Pereira. Rogério Vargas Prof a. Responsável: Graçaliz Pereira Dimuro Disciplina: Computação Flexível Programa Conrado Ruch. Diego de Pereira Pós-Graduação.
apresentação Lógica Fuzzy Conrado Ruch. Diego Pereira. Rogério Vargas Prof a. Responsável: Graçaliz Pereira Dimuro Disciplina: Computação Flexível Programa Conrado Ruch. Diego de Pereira Pós-Graduação.
2 Espaços Vetoriais. 2.1 Espaços Vetoriais Euclidianos
 2 Espaços Vetoriais 2.1 Espaços Vetoriais Euclidianos Definição: Dado n N, considere-se o conjunto de todos os n-uplos ordenados de elementos reais, isto é o conjunto de elementos da forma x = (x 1,, x
2 Espaços Vetoriais 2.1 Espaços Vetoriais Euclidianos Definição: Dado n N, considere-se o conjunto de todos os n-uplos ordenados de elementos reais, isto é o conjunto de elementos da forma x = (x 1,, x
PROVA DE MATEMÁTICA. Vestibular GAB1 Julho de CEV/UECE 03.
 PROVA DE MATEMÁTICA. Se x e y são as médias aritmética e geométrica, respectivamente, dos números, e, então a 8 razão y/x é igual a: /7 7/ C) 7/8 D) 8/7. Uma companhia de aviação alugou uma aeronave de
PROVA DE MATEMÁTICA. Se x e y são as médias aritmética e geométrica, respectivamente, dos números, e, então a 8 razão y/x é igual a: /7 7/ C) 7/8 D) 8/7. Uma companhia de aviação alugou uma aeronave de
Conjuntos Numéricos. É o conjunto no qual se encontram os elementos de todos os conjuntos estudados.
 Conjuntos Numéricos INTRODUÇÃO Conjuntos: São agrupamentos de elementos com algumas características comuns. Ex.: Conjunto de casas, conjunto de alunos, conjunto de números. Alguns termos: Pertinência Igualdade
Conjuntos Numéricos INTRODUÇÃO Conjuntos: São agrupamentos de elementos com algumas características comuns. Ex.: Conjunto de casas, conjunto de alunos, conjunto de números. Alguns termos: Pertinência Igualdade
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Prof. Lino Marcos da Silva Atividade 1 - Números Reais Objetivos De um modo geral, o objetivo dessa atividade é fomentar o estudo de conceitos relacionados aos números
Cálculo Diferencial e Integral I Prof. Lino Marcos da Silva Atividade 1 - Números Reais Objetivos De um modo geral, o objetivo dessa atividade é fomentar o estudo de conceitos relacionados aos números
Algebra Linear. 1. Espaços Vetoriais Lineares. 2. Coordenadas em Espaços Lineares. 3. Operadores Lineares. 4. Transformação de Similaridade
 Algebra Linear 1 Espaços Vetoriais Lineares Coordenadas em Espaços Lineares 3 Operadores Lineares 4 Transformação de Similaridade Matriz como Operador Norma de Vetores e Produto Interno pag1 Teoria de
Algebra Linear 1 Espaços Vetoriais Lineares Coordenadas em Espaços Lineares 3 Operadores Lineares 4 Transformação de Similaridade Matriz como Operador Norma de Vetores e Produto Interno pag1 Teoria de
Abordagem Fuzzy na Escolha de Projetos Populares
 Abordagem Fuzzy na Escolha de Projetos Populares The Fuzzy Approach in the Choice of Popular Projects Rosana Viomar de Lima Universidade Estadual do Centro-Oeste - UNICENTRO Departamento de Biologia rosanalima@unicentro.br
Abordagem Fuzzy na Escolha de Projetos Populares The Fuzzy Approach in the Choice of Popular Projects Rosana Viomar de Lima Universidade Estadual do Centro-Oeste - UNICENTRO Departamento de Biologia rosanalima@unicentro.br
Lógica Nebulosa (Fuzzy)
 Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Lógica Nebulosa (Fuzzy) Inteligência Artificial Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Lógica Nebulosa (Fuzzy) Inteligência Artificial Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
Relações Binárias, Aplicações e Operações
 Relações Binárias, Aplicações e Operações MAT 131-2018 II Pouya Mehdipour 6 de dezembro de 2018 Pouya Mehdipour 6 de dezembro de 2018 1 / 24 Referências ALENCAR FILHO, E. Teoria Elementar dos Conjuntos,
Relações Binárias, Aplicações e Operações MAT 131-2018 II Pouya Mehdipour 6 de dezembro de 2018 Pouya Mehdipour 6 de dezembro de 2018 1 / 24 Referências ALENCAR FILHO, E. Teoria Elementar dos Conjuntos,
Lista 1. 9 Se 0 < x < y e n N então 0 < x n < y n.
 UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof. José Carlos Eidam Lista 1 Em toda a lista, K denota um corpo ordenado qualquer. Corpos ordenados 1. Verifique as
UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof. José Carlos Eidam Lista 1 Em toda a lista, K denota um corpo ordenado qualquer. Corpos ordenados 1. Verifique as
1 Operações com conjuntos
 Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições)
 Exemplos Definições Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições) Matemática Elementar - EAD Departamento de Matemática Universidade Federal da Paraíba 4 de setembro de 2014
Exemplos Definições Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições) Matemática Elementar - EAD Departamento de Matemática Universidade Federal da Paraíba 4 de setembro de 2014
O espaço das Ordens de um Corpo
 O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
Pré-Cálculo. Humberto José Bortolossi. Aula 5 27 de agosto de Departamento de Matemática Aplicada Universidade Federal Fluminense
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Aula 5 27 de agosto de 200 Aula 5 Pré-Cálculo Expansões decimais: exemplo Números reais numericamente
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Aula 5 27 de agosto de 200 Aula 5 Pré-Cálculo Expansões decimais: exemplo Números reais numericamente
CONTEÚDO LÓGICA FUZZY LÓGICA FUZZY LÓGICA FUZZY. Um dos componentes mais importantes de um sistema fuzzy é o Módulo de Regras.
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
Números inteiros. Sandro Marcos Guzzo
 Números inteiros Sandro Marcos Guzzo Cascavel - Pr Agosto de 2013 1 Construção do conjunto dos números inteiros O conjunto dos números inteiros, designado por Z será aqui construído a partir do conjunto
Números inteiros Sandro Marcos Guzzo Cascavel - Pr Agosto de 2013 1 Construção do conjunto dos números inteiros O conjunto dos números inteiros, designado por Z será aqui construído a partir do conjunto
A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há
 1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
Matrizes - ALGA /05 1. Matrizes
 Matrizes - ALGA - 004/0 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n a uma função A de nida no conjunto f(i; j) : i f1; ; :::; mg e j f1; ; :::; ngg e com valores
Matrizes - ALGA - 004/0 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n a uma função A de nida no conjunto f(i; j) : i f1; ; :::; mg e j f1; ; :::; ngg e com valores
Universidade Federal do Pampa - UNIPAMPA
 Universidade Federal do Pampa - UNIPAMPA Projeto: Fundamentos Matemáticos para Computação INTRODUÇÃO À MATEMÁTICA DISCRETA 2 Introdução Praticamente qualquer estudo relacionado a computação, teórico ou
Universidade Federal do Pampa - UNIPAMPA Projeto: Fundamentos Matemáticos para Computação INTRODUÇÃO À MATEMÁTICA DISCRETA 2 Introdução Praticamente qualquer estudo relacionado a computação, teórico ou
INF 1771 Inteligência Artificial
 INF 1771 Inteligência Artificial Aula 09 Lógica Fuzzy Edirlei Soares de Lima Introdução A Lógica Fuzzy é baseada na teoria dos conjuntos fuzzy. Tradicionalmente, uma proposição lógica
INF 1771 Inteligência Artificial Aula 09 Lógica Fuzzy Edirlei Soares de Lima Introdução A Lógica Fuzzy é baseada na teoria dos conjuntos fuzzy. Tradicionalmente, uma proposição lógica
Teoria dos Conjuntos Fuzzy
 Teoria dos Conjuntos Fuzzy Francisco Carpegiani Medeiros Borges Universidade Federal do Piauí Campus Parnaíba 27 de setembro de 2011 1 / 34 Sumário Como tudo começou! 1 Como tudo começou! 2 3 4 5 6 2 /
Teoria dos Conjuntos Fuzzy Francisco Carpegiani Medeiros Borges Universidade Federal do Piauí Campus Parnaíba 27 de setembro de 2011 1 / 34 Sumário Como tudo começou! 1 Como tudo começou! 2 3 4 5 6 2 /
Parte I. Álgebra Linear. Sistemas Dinâmicos Lineares. Conteúdo de Revisão de Álgebra Linear. Vetores. Março de 2014
 Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Um Curso de Nivelamento. Instituto de Matemática UFF
 Introdução à Álgebra Linear Um Curso de Nivelamento Jorge Delgado Depto. de Matemática Aplicada Katia Frensel Depto. de Geometria Instituto de Matemática UFF Março de 2005 J. Delgado - K. Frensel ii Instituto
Introdução à Álgebra Linear Um Curso de Nivelamento Jorge Delgado Depto. de Matemática Aplicada Katia Frensel Depto. de Geometria Instituto de Matemática UFF Março de 2005 J. Delgado - K. Frensel ii Instituto
Álgebra Linear e Geometria Analítica Bacharelados e Engenharias Parte I - Matrizes
 Álgebra Linear e Geometria Analítica Bacharelados e Engenharias Parte I - Matrizes Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 Importante Material desenvolvido a partir dos livros
Álgebra Linear e Geometria Analítica Bacharelados e Engenharias Parte I - Matrizes Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 Importante Material desenvolvido a partir dos livros
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
SISTEMA ESPECIALISTA NEBULOSO (MINICURSO) Luiz Biondi Neto Pedro Henrique Gouvêa Coelho Jorge Luís Machado do Amaral Maria Helena C.
 Luiz Biondi Neto Pedro Henrique Gouvêa Coelho Jorge Luís Machado do Amaral Maria Helena C. Soares de Mello Inteligência Computacional A Inteligência Computacional (IC) é uma área de pesquisa que visa investigar
Luiz Biondi Neto Pedro Henrique Gouvêa Coelho Jorge Luís Machado do Amaral Maria Helena C. Soares de Mello Inteligência Computacional A Inteligência Computacional (IC) é uma área de pesquisa que visa investigar
CONJUNTOS FUZZY CONTEÚDO. CONJUNTOS CRISP x FUZZY. Conjuntos Crisp x Fuzzy Definição Representação Propriedades Formatos Operações Hedges
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
Algoritmos Numéricos 2 a edição
 Algoritmos Numéricos 2 a edição Capítulo 2: Sistemas lineares c 2009 FFCf 2 2.1 Conceitos fundamentais 2.2 Sistemas triangulares 2.3 Eliminação de Gauss 2.4 Decomposição LU Capítulo 2: Sistemas lineares
Algoritmos Numéricos 2 a edição Capítulo 2: Sistemas lineares c 2009 FFCf 2 2.1 Conceitos fundamentais 2.2 Sistemas triangulares 2.3 Eliminação de Gauss 2.4 Decomposição LU Capítulo 2: Sistemas lineares
Geometria Analítica. Geometria Analítica 28/08/2012
 Prof. Luiz Antonio do Nascimento luiz.anascimento@sp.senac.br www.lnascimento.com.br Conjuntos Propriedades das operações de adição e multiplicação: Propriedade comutativa: Adição a + b = b + a Multiplicação
Prof. Luiz Antonio do Nascimento luiz.anascimento@sp.senac.br www.lnascimento.com.br Conjuntos Propriedades das operações de adição e multiplicação: Propriedade comutativa: Adição a + b = b + a Multiplicação
INE Fundamentos de Matemática Discreta para a Computação
 INE543 - Fundamentos de Matemática Discreta para a Computação 5) Relações 5.) Relações e Dígrafos 5.2) Propriedades de Relações 5.3) Relações de Equivalência 5.4) Manipulação de Relações 5.5) Fecho de
INE543 - Fundamentos de Matemática Discreta para a Computação 5) Relações 5.) Relações e Dígrafos 5.2) Propriedades de Relações 5.3) Relações de Equivalência 5.4) Manipulação de Relações 5.5) Fecho de
1 Álgebra linear matricial
 MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
Programação de Computadores III
 Programação de Computadores III Aula 4 Professora Bianca (Sala 302 Bloco E) bianca@ic.uff.br http://www.ic.uff.br/~bianca/prog3/ Aula 4-14/09/2006 1 Atribuições Depois que as variáveis são declaradas,
Programação de Computadores III Aula 4 Professora Bianca (Sala 302 Bloco E) bianca@ic.uff.br http://www.ic.uff.br/~bianca/prog3/ Aula 4-14/09/2006 1 Atribuições Depois que as variáveis são declaradas,
Notas de Aula Álgebra Linear. Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte
 Notas de Aula Álgebra Linear Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte Versão 201608221232c de 22 de agosto de 2016 Parte I Espaços vetoriais
Notas de Aula Álgebra Linear Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte Versão 201608221232c de 22 de agosto de 2016 Parte I Espaços vetoriais
TP034-Tópicos Especiais de Pesquisa Operacional I
 TP34-Tópicos Especiais de Pesquisa Operacional I Conjuntos Difusos Relações Difusas Prof. Volmir Wilhelm Curitiba Paraná rasil s relações são associações entre elementos de dois ou mais conjuntos. Se o
TP34-Tópicos Especiais de Pesquisa Operacional I Conjuntos Difusos Relações Difusas Prof. Volmir Wilhelm Curitiba Paraná rasil s relações são associações entre elementos de dois ou mais conjuntos. Se o
Reticulados e Álgebras de Boole
 Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
significa ( x)[(x S P (x)) (P (x) x S)]
![significa ( x)[(x S P (x)) (P (x) x S)] significa ( x)[(x S P (x)) (P (x) x S)]](/thumbs/80/81764647.jpg) Capítulo 2 Conjuntos e Contagem 2.1 Notação S = {2, 4, 6,... } (impreciso; conjuntos finitos) 1. 2 S 2. Se n S, então (n + 2) S S = {x x é um inteiro positivo par } S = {x P (x)} significa ( x)[(x S P
Capítulo 2 Conjuntos e Contagem 2.1 Notação S = {2, 4, 6,... } (impreciso; conjuntos finitos) 1. 2 S 2. Se n S, então (n + 2) S S = {x x é um inteiro positivo par } S = {x P (x)} significa ( x)[(x S P
AXB = {(x, y) x A e y B}
 CENTRO UNIVERSITÁRIO DO NORTE PAULISTA LÓGICA E MATEMÁTICA DISCRETA 2010 1 Produto Cartesiano Par ordenado: são dois elementos em uma ordem fixa, (x,y) Produto Cartesiano: Dados dois conjuntos A e B, não
CENTRO UNIVERSITÁRIO DO NORTE PAULISTA LÓGICA E MATEMÁTICA DISCRETA 2010 1 Produto Cartesiano Par ordenado: são dois elementos em uma ordem fixa, (x,y) Produto Cartesiano: Dados dois conjuntos A e B, não
Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras. Silvia Gonçalves Santos
 Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras Silvia Gonçalves Santos Definição 1 Seja R um anel com unidade. O radical de Jacobson de R, denotado por J(R), é o ideal (à esquerda) dado pela
Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras Silvia Gonçalves Santos Definição 1 Seja R um anel com unidade. O radical de Jacobson de R, denotado por J(R), é o ideal (à esquerda) dado pela
4.1 Preliminares. No exemplo acima: Dom(R 1 ) = e Im(R 1 ) = Dom(R 2 ) = e Im(R 2 ) = Dom(R 3 ) = e Im(R 3 ) = Diagrama de Venn
 4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
SISTEMAS FUZZY CONTEÚDO CONJUNTOS FUZZY. CONJUNTOS CRISP x FUZZY
 SISTEMAS FUZZY A maioria dos fenômenos com os quais nos deparamos são imprecisos Exemplo: dia QUENTE (40, 35, 30, 29,5?) Imprecisão Intrínseca ajuda na compreensão do problema. Fuzziness é independente
SISTEMAS FUZZY A maioria dos fenômenos com os quais nos deparamos são imprecisos Exemplo: dia QUENTE (40, 35, 30, 29,5?) Imprecisão Intrínseca ajuda na compreensão do problema. Fuzziness é independente
