(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
|
|
|
- Micaela Flores Brás
- 5 Há anos
- Visualizações:
Transcrição
1 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas. Todas essas leis podem ser derivadas algebricamente a partir dos postulados. Para as formalizações apresentadas aqui, procure associar os equivalentes vistos na parte de álgebra dos conjuntos e lógica proposicional. Recomenda-se também que o leitor faça o inverso: prestar atenção como os conceitos apresentados via álgebra de conjunto podem ser formalizados (tratados de forma abstrata). Referências para esta parte do curso: [Hill and Peterson, 1981], [Garnier and Taylor, 1992], [Whitesitt, 1961], [Micheli, 1994], [Katz, 1994], entre outros. 3.1 Definição axiomática Um conjunto de elementos A, juntamente com duas operações binárias + e, é uma álgebra booleana se, e somente se, os seguintes postulados (Postulados de Huntington) são satisfeitos: (A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x (A2) Cada operação é distributiva sobre a outra, isto é, para todo x, y e z em A, x (y + z) = (x y) + (x z) e x + (y z) = (x + y) (x + z) (A3) Existem em A elementos identidade 0 e 1, distintos, com relação às operações + e, respectivamente. Ou seja, para todo x A, x + 0 = x e x 1 = x A partir disto podemos dizer que há pelo menos dois elementos distintos em A. (A4) Para cada elemento x A existe um elemento x em A tal que x + x = 1 e x x = 0 O elemento x será chamado complemento de x. Denotaremos uma álgebra booleana por uma sextupla ordenada. No caso da definição acima, temos a álgebra booleana A, +,,, 0, 1. Observação: Alguns autores incorporam outros axiomas como parte da definição de uma álgebra booleana. Vale registrar que os postulados de Huntington correspondem a um conjunto minimal de postulados, isto é, nenhum deles pode ser derivado a partir dos demais. Mais ainda, é um conjunto completo no sentido de que qualquer propriedade de uma álgebra booleana pode ser derivada/provada a partir desses postulados. Mais adiante mostraremos como a propriedade associativa (frequentemente incorporada à definição de álgebra booleana) e várias outras podem ser derivadas a partir dos postulados acima.
2 Notas de aula de MAC0329 (2003) Exemplos de álgebra booleana Exemplo 1 O conjunto B = {0, 1} onde definimos é uma álgebra booleana. 1 = 0 0 = = = = = = 0 0 = 0 1 = 1 0 = 0 Os axiomas A1, A3 e A4 são satisfeitos por definição. Para verificar o axioma A2 podemos construir uma tabela verdade com todas as possíveis combinações de valores para x, y e z. Vejamos a validade da distributividade em relaçao a, ou seja, que x (y + z) = (x y) + (x z). x y z (y + z) x (y + z) (x y) (x z) (x y) + (x z) * * Denotamos esta álgebra booleana por B, +,,, 0, 1. Exemplo 2: Dado um conjunto S, P(S) denota o conjunto das partes de S, isto é, P(S) = {X : X S}. Então, P(S),,, c,, S é uma álgebra booleana. Como já vimos na parte de álgebra dos conjuntos, os equivalentes aos 4 postulados são: (1) X Y = Y X e X Y = Y X (2) X (Y Z) = (X Y ) (X Z) e X (Y Z) = (X Y ) (X Z) (3) X = e U X = U (4) X X c = e X X c = U Exemplo 3: A lógica (ou cálculo) proposicional visto nas aulas anteriores é uma álgebra booleana. De fato, ela tem uma correspondência um-para-um com B, +,,, 0, 1, conforme mostrado a seguir: Lógica proposicional álgebra booleana B + F 0 V 1 x x
3 Notas de aula de MAC0329 (2003) 19 Como conseqüência, temos também a correspondência entre as tabelas-verdade: x y x x y x y F F V F F F V V V F V F F V F V V F V V x y x x + y x y Exemplo 4: O conjunto B n = B B... B, com as operações +, e para quaisquer (x 1, x 2,..., x n ), (y 1, y 2,..., y n ) B n, da seguinte forma herdadas de B e definidas, (x 1, x 2,..., x n ) + (y 1, y 2,..., y n ) = (x 1 + y 1, x 2 + y 2,..., x n + y n ) (x 1, x 2,..., x n ) (y 1, y 2,..., y n ) = (x 1 y 1, x 2 y 2,..., x n y n ) é uma álgebra booleana. (x 1, x 2,..., x n ) = (x 1, x 2,..., x n ) Exemplo 5: A teoria de chaveamentos, que veremos mais adiante, é uma álgebra booleana. Exercício: a) Mostre que o conjunto B n mais as operações definidas no exemplo 4 acima é uma álgebra booleana. b) Considere o conjunto dos números reais R, juntamente com as operações usuais de adição e multiplicação. Quais dos axiomas A1, A2, A3 não são satisfeitos? É possível definir uma operação unária em R tal que o axioma A4 seja satisfeito? c) Seja A = {1, 2, 3, 5, 6, 10, 15, 30}, ou seja, o conjunto de divisores de 30. Defina operações binárias + e e uma operação unária da seguinte forma: para quaiquer a 1, a 2 A, a 1 + a 2 = o menor múltiplo comum entre a 1 e a 2 a 1 a 2 = o maior fator comum entre a 1 e a 2 a 1 = 30/a 1 Quais são os elementos identidade com respeito a + e? Mostre que A com as três operações acima é uma álgebra booleana. 3.3 Leis fundamentais da álgebra booleana Princípio da dualidade: Cada expressão ou identidade algébrica dedutível a partir dos postulados em uma álgebra booleana continua válida se todas as ocorrências dos operadores + e e os elementos identidade 0 e 1 são trocados um pelo outro. De fato, o dual de cada um dos axiomas é também um axioma. Observe: Axioma 1 x y = y x x + y = y + x
4 Notas de aula de MAC0329 (2003) 20 Axioma 2 Axioma 3 Axioma 4 x (y + z) = (x y) + (x z) x + (y z) = (x + y) (x + z) x + 0 = x x 1 = x x + x = 1 x x = 0 Assim, se na prova de uma proposição E trocarmos cada proposição pela sua dual obtemos uma outra prova (válida, pois axiomas são trocadas por axiomas). Esta nova prova é uma prova da dual de E. Desta parte em diante omitiremos o símbolo na maioria das vezes; em vez de x y, escreveremos simplesmente xy. Suponha que A, +,,, 0, 1 é uma álgebra booleana. As seguintes igualdades (leis, propriedades) são válidas. [Unicidade do 0 e 1] Os elementos 0 e 1 são únicos. PROVA: Suponha que existem dois elementos zero, 0 1 e 0 2. Sejam x 1 e x 2 dois elementos quaisquer em A. Por A3, temos que x = x 1 e x = x 2 Tome, em particular, x 1 = 0 2 e x 2 = 0 1. Assim temos = 0 2 e = 0 1 Por A1 e a transitividade de =, resulta que 0 1 = 0 2. A unicidade de 1 pode ser provada usando o princípio da dualidade. [Idempotência] Para todo elemento x A, x + x = x e xx = x. PROVA: x + x = (x + x) 1 (A3) = (x + x)(x + x) (A4) = x + xx (A2) = x + 0 (A4) = x (A3) xx = xx + 0 (A3) = xx + xx (A4) = x(x + x) (A2) = x 1 (A4) = x (A3) [Identidade] Para todo x A, x + 1 = 1 e x0 = 0. x + 1 = 1 (x + 1) (A3) = (x + x)(x + 1) (A4) = x + x 1 (A2) = x + x (A3) = 1 (A4)
5 Notas de aula de MAC0329 (2003) 21 [Complemento do um (zero)] 1 = 0 e 0 = 1. 1 = 1 1 (A3) = 0 (A4) [Absorção] Para todo x, y A, x + xy = x e x(x + y) = x. x + xy = x 1 + xy (A3) = x(1 + y) (A2) = x 1 = x (A3) [Unicidade de x] O inverso de qualquer elemento x A é único, isto é, se x + y = 1 e xy = 0 para algum y A, então y = x. PROVA: Por contradição. Suponha que existem dois elementos distintos x 1 e x 2 em A tais que x + x 1 = 1 e x + x 2 = 1 e x x 1 = 0 e x x 2 = 0 [Involução] Para todo x A, x = x. x 2 = 1 x 2 (A3) = (x + x 1 )x 2 (hipótese) = xx 2 + x 1 x 2 (A2) = 0 + x 1 x 2 (hipótese) = xx 1 + x 1 x 2 (hipótese) = (x + x 2 )x 1 (A2) = 1 x 1 (hipótese) = x 1 (A3) PROVA: Seja x = y. Então, por A3 temos que xy = 0 e x + y = 1. Mas por A4, xx = 0 e x + x = 1. Por causa da unicidade do complemento, x = y = x. [Lema] Para quaisquer x, y, z A, x[(x + y) + z] = [(x + y) + z]x = x. x[(x + y) + z] = [(x + y) + z]x (A1) x[(x + y) + z] = x(x + y) + xz (A2) = x + xz (absorção) = x (absorção) [Associatividade] Para quaisquer x, y, z A, x + (y + z) = (x + y) + z e x(yz) = (xy)z. Seja Z = [(x + y) + z][x + (y + z)] = [(x + y) + z]x + [(x + y) + z](y + z) (A2) = x + [(x + y) + z](y + z) (lema) = x + {[(x + y) + z]y + [(x + y) + z]z} (A2) = x + {[(y + x) + z]y + [(x + y) + z]z} (A1) = x + {y + [(x + y) + z]z} (lema) = x + (y + z)
6 Notas de aula de MAC0329 (2003) 22 De forma similar, Logo, x + (y + z) = (x + y) + z Z = (x + y)[x + (y + z)] + z[x + (y + z)] (A2) = (x + y)[x + (y + z)] + z (lema) = {x[x + (y + z)] + y[x + (y + z)]} + z (A2) = {x[x + (y + z)] + y} + z (lema) = (x + y) + z (lema) [Teorema de DeMorgan] Para quaisquer x, y A, (x + y) = x y e x y = x + y. Vamos mostrar que (x + y) + xy = 1 e que (x + y)(xy) = 0. (x + y) + xy = [(x + y) + x][(x + y) + y] (A2) = [x + (x + y)][y + (x + y)] (A1) = [(x + x) + y)][x + (y + y)] (Identidade + A1) = 1 1 (A4) = 1 (Identidade) (x + y) xy = x(xy) + y(yx) (A2 + A1) = (xx)y + (yy)x (associativa) = 0 0 (A4) = 0 (Identidade) Portanto, pela unicidade do complemento, podemos concluir que (x + y) = x y. A igualdade dual pode ser demonstrada pelo princípio da dualidade, ou usando o fato de que as igualdades acima valem também para x e y no lugar de x e y. Note a similaridade destas propriedades com as propriedades dos conjuntos e com as da lógica proposicional. Enquanto lá fizemos uso dos diagramas de Venn e das tabelas-verdade, respectivamente, para nos convencermos da validade das propriedades, aqui as demonstrações são algébricas. Exercícios: Prove as seguintes igualdades a) x + xy = x + y (e sua dual x(x + y) = xy) b) x + y = xy (e sua dual xy = x + y) c) (x + y)(x + y) = x (e sua dual xy + xy = x) d) (Teorema do consenso) xy + yz + xz = xy + xz (e sua dual, (x + y)(y + z)(x + z) = (x + y)(x + z) e) [yx = zx yx = zx] (y = z) f) (x + y + z)(x + y) = x + y Exercícios: Simplifique as seguintes expressões a) yz(z + zx) + (x + y)(xy + xz) b) x + xyz + yzx + wx + wx + xy Exercício: Mostre que em qualquer álgebra booleana A, +,,, 0, 1, xy = 0 se, e somente se, xy = x.
7 Notas de aula de MAC0329 (2003) Álgebra booleana, ordens parciais e reticulados Seja A um conjunto não vazio. Uma relação binária R sobre A é um subconjunto de A A, isto é, R A A. Se (x, y) R, denotamos xry (lê-se x-erre-y). Relação de ordem parcial Uma relação binária sobre A é uma ordem parcial se 1. (reflexiva) x x, para todo x A 2. (anti-simétrica) Se x y e y x, então x = y, para todo x, y A 3. (transitiva) Se x y e y z então x z, para todo x, y, z A Se é uma ordem parcial em A, então a relação definida por, para quaisquer x, y A, x y se e somente se y x é também uma ordem parcial em A. Conjunto parcialmente ordenado (poset) Um conjunto A munido de uma relação de ordem parcial é denominado um conjunto parcialmente ordenado (ou poset) e denotado por (A, ). Se (A, ) é um poset, então (A, ) também é um poset. Exemplo 1: A relação de ordem usual definida no conjunto dos números reais é uma ordem parcial (na verdade é uma ordem total, pois todos os elementos são comparáveis dois a dois). A relação < não é uma ordem parcial pois ela não é reflexiva. Exemplo 2: A relação de inclusão de conjuntos é uma ordem parcial. Diagrama de Hasse Escrevemos x < y quando x y e x y. Dado um poset (A, ) e x, y A, dizemos que y cobre x se, e seomente se, x < y e não há outro elemento z A tal que x < z < y. Um diagrama de Hasse do poset (A, ) é uma representação gráfica onde vértices representam os elementos de A e dois elementos x e y são ligados por uma aresta se e somente se y cobre x. Em um diagrama de Hasse, os elementos menores (com relação a ordem parcial) são em geral desenhados abaixo dos elementos maiores. Exemplo: O diagrama de Hasse do poset ({a, b, c}, ) é mostrado na figura 1. Elementos notáveis de um poset Seja (A, ) um poset. Chama-se menor elemento de A um elemento 0 A tal que 0 x para todo x A. Chama-se maior elemento de A um elemento 1 A tal que x 1 para todo x A. Teorema: Em um poset (A, ), se existe um menor elemento, ele é único. Similarmente, se existe um maior elemento, ele é único. PROVA: Suponha que 0 1 e 0 2 são menores elementos de (A, ). Então, teríamos (pois 0 1 é menor elemento) e (pois 0 2 é menor elemento). Pela propriedade anti-simétrica da relação, concluímos que 0 1 = 0 2. A unicidade do maior elemento prova-se de forma análoga.
8 Notas de aula de MAC0329 (2003) 24 {a,b,c} {a,b} {a,c} {b,c} {a} {b} {c} { } Figura 1: Diagrama de Hasse de ({a, b, c}, ). Chama-se elemento minimal de A um elemento a A tal que elemento algum de A precede estritamente a, isto é, para qualquer x A, se x a então x = a. Chama-se elemento maximal de A um elemento a A tal que elemento algum de A sucede estritamente a, isto é, para qualquer x A, se x a então x = a. Teorema: Se 0 é o menor elemento de (A, ), então 0 é o único elemento minimal de (A, ). Seja (A, ) um poset e seja X A. Chama-se limitante inferior de X em A a todo elemento a A tal que a x para todo x X. Chama-se limitante superior de X em A a todo elemento a A tal que x a para todo x X. Chama-se ínfimo de X em A o maior elemento dos limitantes inferiores de X em A. O ínfimo de X é denotado X. O ínfimo de {x, y} é denotado x y. O operador é chamado conjunção. Chama-se supremo de X em A o menor elemento dos limitantes superiores de X em A. O supremo de X é denotado X. O supremo de {x, y} é denotado x y. O operador é chamado união. Exemplo: Seja S = {a, b, c} e considere o conjunto de todos os subconjuntos próprios de S, conforme ilustrado no diagrama abaixo. {a,b} {a,c} {b,c} {a} {b} {c} { } Este conjunto tem três elementos maximais, {a, b}, {a, c} e {b, c}. O menor elemento deste conjunto é {} e, conforme teorema acima, é o único elemento minimal. O conjunto não possui maior elemento.
9 Notas de aula de MAC0329 (2003) 25 Exercício: Mostre o teorema Se 0 é o menor elemento de (A, ), então 0 é o único elemento minimal de (A, ). Este teorema é válido com respeito ao maior elemento? Exercício: Mostre que a configuração abaixo não pode ocorrer no diagrama de Hasse de nenhum poset. c b a Exercício: Seja R uma ordem parcial sobre A e seja X A. Mostre que S = R X X é uma relação de ordem parcial. (em outras palavras, qualquer subconjunto de um poset é também um poset). Exercício: Seja a relação de divisibilidade definida sobre os inteiros positivos da seguinte forma: para quaisquer x, y inteiros positivos, x y se, e somente se, x divide y. a) Mostre que é uma relação de ordem parcial b) Desenhe o diagram de Hasse de {1, 2, 3, 4, 6, 12} com respeito à relação parcial. Exercício: Liste os elementos da relação de ordem cujo diagrama de Hasse é o seguinte: e f b c d a Reticulados Um poset (A, ) no qual cada par de elementos possui um ínfimo e um supremo em A é um reticulado (ou seja, para quaisquer x, y A, x y e x y estão em A). Um reticulado (A, ) é distributivo se as operações de união ( ) e conjunção ( ) são distributivas, isto é, para quaisquer x, y e z em A, x (y z) = (x y) (x z) e x (y z) = (x y) (x z). Um reticulado (A, ) com 0 e 1 é complementado se todo elemento em A possui um complemento, isto é, para todo x A existe x tal que x x = 1 e x x = 0.
10 Notas de aula de MAC0329 (2003) 26 Teorema: Um reticulado (A, ) distributivo e complementado é uma álgebra booleana. PROVA: Considere um reticulado distributivo e complementado (A, ) com as operações de união e conjunção como definidos acima, e complementação. Claramente e definem operações binárias em A. Sejam ainda 0 e 1 o menor e o maior elementos de (A, ). Vamos verificar que os axiomas de Huntington são satisfeitos. As operações e são comutativas por definição; são distributivas pois o reticulado é distributivo; o axioma 4 é satisfeito pois o reticulado é complementado, e o axioma 3 é satisfeito pois x 0 = x e x 1 = x para qualquer x A. Exercício: Mostre por indução que todo subconjunto finito de um reticulado tem um ínfimo e um supremo. Relação de ordem em uma álgebra booleana Seja A, +,,, 0, 1 uma álgebra booleana. Definimos uma relação binária em A da seguinte forma: x, y A, x y se e somente se x + y = y (1) A relação definida pela equação 1 é uma relação de ordem parcial. De fato, pela lei de idempotência x + x = x temos que x x para todo x A; se x y e y x, então x + y = y e y + x = x e, portanto, pela comutatividade de +, segue que x = y; se x y e y z, então z y + z (pois y z) (x + y) + z (pois x y) = x + (y + z) (associatividade de +) x + z (pois y z) Logo, x z. Exercício: Mostre que em qualquer álgebra booleana, x + y = y se, e somente se, xy = x. Expresse essa relação na álgebra dos conjuntos. Teorema: Sejam x, y elementos de uma álgebra booleana A, +,,, 0, 1. Então os elementos x + y e xy são respectivamente o supremo e o ínfimo de {x, y}. Exercício: Prove o teorema acima. Teorema: Toda álgebra booleana A, +,,, 0, 1 é um reticulado. PROVA: Qualquer subconjunto {x, y} de A tem supremo x + y e ínfimo xy (teorema anterior). Logo A, +,,, 0, 1 é um reticulado. Exercício: Mostre que em qualquer álgebra booleana a) xy x x + y, para todo x e y em A, b) 0 x 1, para todo x em A.
11 Notas de aula de MAC0329 (2003) 27 Átomo Um átomo de um reticulado (A, ) é um elemento não nulo x que não pode ser expresso na forma x = y z com x y e x z. Exemplo 1: Os átomos de P(S),,, c,, S são todos os conjuntos unitários. Exemplo 2: A álgebra booleana relativa ao conjunto B n de todas as n-uplas binárias tem como átomos as n-uplas com exatamente uma coordenada igual a 1. Teorema: Um elemento não nulo x de um reticulado (A, ) é um átomo se e somente se não há elemento y em A tal que 0 < y < x. PROVA: Suponha que x é um átomo e que y < x. Então, x = x 1 = (y x) (y y) = y (x y). Como x é um átomo, então ou y = x ou (x y) = x. Como x y por hipótese, então (x y) = x. Consequentemente y = x y = (x y) y = x (y y) = x 0 = 0. Agora suponha que não há elemento y em A tal que 0 < y < x e (suponha por absurdo) que x não é um átomo. Então, x = y z para algum y e z diferentes de x. Como y y z = x (um dos exercícios acima), temos que y < x. Além disso, y = 0 (pois caso contrário teríamos 0 < y). Logo, x = 0 z = z x (absurdo). Teorema: Seja A, +,,, 0, 1 uma álgebra booleana finita com conjunto de átomos {a 1, a 2,..., a n }. Cada elemento não nulo x de A pode ser escrito como o supremo de um conjunto de átomos x = a i1 a i2 a ik Mais ainda, tal expressão é única, a menos da ordem dos átomos. A demonstração é por contradição. Suponha que existem elementos que não são expressos como supremo de átomos. Seja x um desses elementos. Então como x não é atomo, temos que x = y z para algum y < x e z < x, e mais ainda, pelo menos y ou z não são átomos. Supondo que y não é átomo, novamente temos que ele é supremo de dois elementos menores que ele, dos quais pelo menos um não é átomo. Assim, há uma seqüência de elementos não-átomos x 0 = x > x 1 = y > x 2 >.... Mas, como A é finito, haverão índices k e m, com k < m tal que x k = x m. Pela transitividade de < em x k > x k+1 >... > x m segue que x k > x m, contradizendo x k = x m. Portanto, podemos concluir que todos os elementos não-nulos em A podem ser expressos como supremo de átomos. Para mostrar a unicidade, primeiro devemos mostrar que x = {a A : a é átomo e a x} isto é, x pode ser expresso como o supremo de todos os átomos menores ou igual a ele. (A demonstração fica como exercício). Agora, suponha que x = a i1 a i2 a ik é uma expressão de x como supremo de átomos. Então a ij x, e, portanto, a ij {a A : a é átomo}. Agora, seja a um átomo tal que a {a A : a é átomo}. Então, 0 a = a x = a (a i1 a i2 a ik ) = (a a i1 ) (a a i2 ) (a a ik ) Pelo menos um (a a ij ) precisa ser diferente de zero. Logo, a a ij = a = a ij átomos. Ou seja, a é um dos átomos em {a i1, a i2,..., a ik }. uma vez que ambos são
12 Notas de aula de MAC0329 (2003) 28 Exercício: Seja A, +,,, 0, 1 uma álgebra booleana finita com conjunto de átomos {a 1, a 2,..., a n }. Sabendo que cada elemento não nulo x de A pode ser escrito como o supremo de um conjunto de átomos x = a i1 a i2 a ik mostre que, mais especificamente, x = {a A : a é átomo e a x} isto é, x é o supremo de todos os átomos menores ou igual a ele. Dica: Comece expressando 1 como um supremo de átomos e use o fato de que x = x 1. Isomorfismo de álgebras booleanas Uma função bijetora φ entre duas álgebras booleanas A 1, + 1, 1, 1, 0 1, 1 1 e A 2, + 2, 2, 2, 0 2, 1 2 que satisfaz φ(x + 1 y) = φ(x) + 2 φ(y) φ(x 1 y) = φ(x) 2 φ(y) e φ(x) = φ(x) é um isomorfismo de álgebra booleana. Duas álgebras booleanas são isomorfas se existe um isomorfismo entre elas. Teorema: Sejam duas álgebras booleanas com o mesmo número de átomos e sejam {a 1, a 2,..., a n } e {b 1, b 2,..., b n } respectivamente os seus conjuntos de átomos. Então, existe um isomorfismo φ entre eles tal que φ(a i ) = b i, para todo i {1, 2,..., n}. Teorema: Qualquer álgebra booleana finita cujo conjunto possui n elementos é isomorfa à álgebra booleana P(S),,, c,, S onde S é um conjunto com cardinalidade n. Revisão dos principais conceitos através de um exemplo: P(S),,, c,, S. Considere a álgebra booleana A seguinte relação binária é definida em P(S): X, Y P(S), X Y X Y = Y a relação é uma ordem parcial. Logo, (P(S), ) é um poset o maior elemento de P(S) é S o menor elemento de P(S) é
13 Notas de aula de MAC0329 (2003) 29 o supremo de dois conjuntos X, Y P(S) é dado por X Y o ínfimo de dois conjuntos X, Y P(S) é dado por X Y (P(S), ) é um reticulado booleano (distributivo e complementado) os átomos de P(S),,, c,, S são os conjuntos unitários. qualquer elemento de P(S) pode ser expresso como união de conjuntos unitários 3.5 Funções Booleanas Variáveis e literais Dada uma álgebra booleana A, +,,, 0, 1, uma variável booleana é uma variável para a qual pode-se associar elementos de A, ou seja, a variável booleana toma valores em A. Dada uma variável booleana x, o complemento de x, denotado x, é uma variável booleana tal que x = a sempre que x = a para qualquer a A. Um literal é uma variável booleana x ou o seu complemento x. Expressão booleana Dada uma álgebra booleana A, +,,, 0, 1, as seguintes são expressões booleanas em n váriáveis x 1, x 2,..., x n : os elementos identidade 0 e 1, as variáveis booleanas x 1, x 2,..., x n, x + y, x y, x, onde x e y são expressões booleanas nas variáveis x 1, x 2,..., x n. Observe que uma expressão booleana em n váriáveis x 1, x 2,..., x n não necessariamente contém todas as n variáveis. Se uma expressão pode ser derivada a partir de outra aplicando-se as regras (leis) da álgebra booleana um número finito de vezes, então elas são ditas equivalentes. O valor de expressões equivalentes, para cada atribuição de valores às variáveis booleanas, é o mesmo. Expressões booleanas definem uma função. Expressões equivalentes definem uma mesma função. Função booleana Dada uma álgebra booleana A, +,,, 0, 1, uma função booleana em n variáveis x 1, x 2,..., x n é uma função f : A n A tal que f(x 1, x 2,..., x n ) é uma expressão booleana. O valor da função f para um elemento a = (a 1, a 2,..., a n ) A n é calculado substituindose cada ocorrência de x i na expressão por a i, para i = 1, 2,..., n e calculando-se o valor da expressão. No caso da álgebra booleana B,,,, 0, 1, vimos que há exatamente (2) 2n funções booleanas em n variáveis. Em geral, há ( A ) A n funções booleanas em n variáveis.
14 Notas de aula de MAC0329 (2003) 30 Exemplo: A função f : B 2 B, definida pela expressão f(x 1, x 2 ) = x 1 + x 2 pode ser representada pela tabela-verdade a seguir, à esquerda. Note que ela é igual a tabela-verdade da expressão x 1 +x 1 x 2. Logo, as expressões x 1 + x 2 e x 1 + x 1 x 2 são equivalentes (ou seja, definem uma mesma função). x 1 x 2 x 1 + x x 1 x 2 x 1 x 1 x 2 x 1 + x 1 x Há (2) 22 = 16 funções de 2 variáveis para B, +,,, 0, 1, conforme mostrados a seguir: x 1 x 2 f 0 f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 f 10 f 11 f 12 f 13 f 14 f Formas de expressão Um produto é uma expressão lógica que é ou uma literal, ou uma conjunção de duas ou mais literais, duas das quais nunca envolvem a mesma variável. Um produto q é subproduto de um produto p se cada literal que aparece em q também aparece em p. Por exemplo, xy é um subproduto de xyz. Já xy não é subproduto de xyz. Soma de produtos ou Forma normal disjuntiva (FND) Um expressão E é uma soma de produtos (SOP) se ela é um produto ou se é uma disjunção de dois ou mais produtos tais que nenhum deles é subproduto de outro. As expressões xy, x + yz, xyw + xz + yz estão na FND, enquanto que x(y + z), xy + yzx não estão. Teorema: Qualquer expressão que não é uma contradição é equivalente a uma expressão na forma SOP. Exemplos: Expressar f(x, y, z, w) = (xz + y)(zw + w) na forma SOP: f(x, y, z, w) = (xz + y)(zw + w) = (xz + y)zw + (xz + y)w (distributiva) = xzw + yzw + xzw + yw (distributiva) Expressar f(x, y, z) = [(x + y) + z](x + y)x na forma SOP: f(x, y, z) = [(x + y) + z](x + y)x = [(x + y) + z](x + y)x = [(x + y) + z](xx + yx) = [(x + y) + z]yx = xyx + yyx + zyx = zyx = xyz
15 Notas de aula de MAC0329 (2003) 31 Observação: Os nomes termo produto, produto fundamental, conjunção fundamental e produto normal também são utilizados em lugar de produto. Os nomes Soma de produtos normais e forma normal disjuntiva são também usados em vez de soma de produtos. Uma soma fundamental, ou simplesmente soma, define-se de forma análoga (é um literal ou a disjunção de dois ou mais literais, duas das quais nunca envolvem a mesma variável). Qualquer expressão é equivalente a uma expressão na forma produto de somas (POS). Mintermo (ou produto completo ou produto canônico ou produto padrão) em n variáveis x 1, x 2,..., x n é uma expressão booleana formada pelo produto de cada uma das n variáveis ou dos respectivos complementos (mas não ambas). Ou seja, consiste do produto de n literais, cada um correspondendo a uma variável (se x i está presente no produto, então x i não está, e vice-versa). Maxtermo (ou soma completa ou soma canônica) em n variáveis x 1, x 2,..., x n tem definição similar ao mintermo: em vez de produto, consiste de soma de n literais, cada um correspondendo a uma variável. Exemplo: Supondo 3 variáveis x 1, x 2, x 3, x 1 x 2 x 3 e x 1 x 2 x 3 são exemplos de mintermos, enquanto x 1 + x 2 + x 3 e x 1 + x 2 + x 3 são exemplos de maxtermos. Teorema: Há 2 n mintermos e 2 n maxtermos. Não há dois mintermos equivalentes, e similarmente, não há 2 maxtermos equivalentes. PROVA: Como um mintermo consiste de n literais, cada um podendo ser uma variável x ou o seu complemento x, há no total 2 n possíveis combinações. Denote x por x 1 e x por x 0. Assim, qualquer mintermo m pode ser expresso por m(x 1, x 2,..., x n ) = x e 1 1 xe xen n onde e i {0, 1}. Para { 1, se ei = 1, x i = 0, se e i = 0. temos m(x 1, x 2,..., x n ) = 1, pois todos os literais x e i i em m tem valor 1. Qualquer outro mintermo tem pelo menos um literal que é complemento do correspondente literal em m. Portanto, substituindo os valores de x i definidos acima neste mintermo, haverá pelo menos um zero no produto. Isto quer dizer que este mintermo vale zero para estes valores em particular. Portanto, para quaisquer dois mintermos, há sempre uma atribuição de valores às variáveis que torna um deles 1 e o outro 0. Exercício: Liste todos os mintermos em 3 variáveis. Teorema: Qualquer função booleana que não seja identicamente nulo pode ser expressa na forma de soma canônica de produtos (soma de mintermos). Teorema: Qualquer função booleana que não seja identicamente 1 pode ser expressa na forma de produto canônico de somas (produto de maxtermos).
16 Notas de aula de MAC0329 (2003) 32 Observações: Os nomes Soma padrão de produtos, forma normal disjuntiva completa ou forma mintermo também são usados em vez de soma canônica de produtos (SOP canônica). Note que alguns autores usam o nome forma normal disjuntiva em vez de forma normal disjuntiva completa. Nós usaremos soma de produtos e soma canônica de produtos; produto de somas e produto canônico de somas. Exemplos: Escrever f(x, y, z, w) = (xz + y)(zw + w) na forma SOP canônica: f(x, y, z, w) = (xz + y)zw + (xz + y)w = xzw + yzw + xzw + yw = xzw(y + y) + (x + x)yzw + x(y + y)zw + (x + x)y(z + z)w = xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xy(z + z)w + xy(z + z)w = xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xyzw = xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xyzw + xyzw Escrever x + z + yw na forma POS canônica. f(x, y, z, w) = x + z + yw = x + (z + yw) = x + (z + y)(z + w) = (x + z + y)(x + z + w) = (x + y + z + ww)(x + yy + z + w) = (x + y + z + w)((x + y + z + w)(x + y + z + w)(x + y + z + w) = (x + y + z + w)((x + y + z + w)(x + y + z + w) Exercícios: a) Escreva f(a, b, c, d, e) = (ac + d)(b + ce) na forma SOP. b) Escreva f(a, b, c, d) = (a + b)cd + (a + b)cd na forma SOP canônica. c) Escreva f(x, y, z, w) = x + z + yw na forma SOP canônica. Qual a relação entre a forma SOP canônica e a forma POS canônica? d) Lembrando que x y [(x y) (y x)], e que x y ( x y), escreva (a b) c na forma SOP canônica. e) Ache a expressão na forma SOP canônica que define a função dada pela tabela-verdade abaixo. Você consegue simplificar esta expressão e obter uma outra equivalente e mais curta? x y z f(x, y, z)
17 Notas de aula de MAC0329 (2003) 33 4 Tabela dos principais axiomas e leis x + y = y + x A1 xy = yx x(y + z) = xy + xz A2 x + yz = (x + y)(x + z) x + 0 = x A3 x 1 = x x + x = 1 A4 xx = 0 x + x = x Idempotência xx = x x + 1 = 1 Identidade x 0 = 0 Complemento do um 1 = 0 (zero) 0 = 1 x + xy = x Absorção x(x + y) = x Involução x = x x + (y + z) = (x + y) + z Associatividade x(yz) = (xy)z De Morgan x + y = xy xy = x + y xy + yz + xz = xy + xz Teorema do consenso (x + y)(y + z)(x + z) = (x + y)(x + z) Referências [Garnier and Taylor, 1992] Garnier, R. and Taylor, J. (1992). Discrete Mathematics for New Technology. Adam Hilger. [Hill and Peterson, 1981] Hill, F. J. and Peterson, G. R. (1981). Introduction to Switching Theory and Logical Design. John Wiley, 3rd edition. [Katz, 1994] Katz, R. H. (1994). Contemporary Logic Design. Benjamin Cummings. [Micheli, 1994] Micheli, G. D. (1994). Synthesis and Optimization of Digital Circuits. McGraw-Hill. [Whitesitt, 1961] Whitesitt, J. E. (1961). Boolean Algebra and its Applications. Addison-Wesley.
3.4 Álgebra booleana, ordens parciais e reticulados
 Notas de aula de MAC0329 (2003) 23 3.4 Álgebra booleana, ordens parciais e reticulados Seja A um conjunto não vazio. Uma relação binária R sobre A é um subconjunto de A A, isto é, R A A. Se (x, y) R, denotamos
Notas de aula de MAC0329 (2003) 23 3.4 Álgebra booleana, ordens parciais e reticulados Seja A um conjunto não vazio. Uma relação binária R sobre A é um subconjunto de A A, isto é, R A A. Se (x, y) R, denotamos
A2. Cada operação é distributiva sobre a outra, isto é, para todo x, y e z em A, x (y + z) = (x y) + (x z) e x + (y z) = (x + y) (x + z)
 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004)
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004) Nina S. T. Hirata Depto. de Ciência da Computação Instituto de Matemática e Estatística Universidade de São Paulo Página da disciplina: www.vision.ime.usp.br/~nina/cursos/mac0329-04/
Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004) Nina S. T. Hirata Depto. de Ciência da Computação Instituto de Matemática e Estatística Universidade de São Paulo Página da disciplina: www.vision.ime.usp.br/~nina/cursos/mac0329-04/
Álgebras Booleanas e Aplicações
 Álgebras Booleanas e Aplicações Prof. Dr. Clotilzio Moreira dos Santos IBILCE - UNESP São José do Rio Preto Outubro de 2013 Álgebras Booleanas e Aplicações Clotilzio Moreira dos Santos Sumário 1 ÁLGEBRAS
Álgebras Booleanas e Aplicações Prof. Dr. Clotilzio Moreira dos Santos IBILCE - UNESP São José do Rio Preto Outubro de 2013 Álgebras Booleanas e Aplicações Clotilzio Moreira dos Santos Sumário 1 ÁLGEBRAS
PCS 3115 (PCS2215) Sistemas Digitais I. Módulo 05 Álgebra Booleana. Prof. Dr. Edison Spina. Sobre o material do Prof. Dr. Marcos A. Simplicio Jr.
 PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Edison Sobre o material do Prof. Dr. Marcos A. Simplicio Jr. versão: 5 (Mar/28) Conceitos básicos Conteúdo Teoremas de variável Teoremas
PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Edison Sobre o material do Prof. Dr. Marcos A. Simplicio Jr. versão: 5 (Mar/28) Conceitos básicos Conteúdo Teoremas de variável Teoremas
Notas de aula de MAC0329 Álgebra Booleana e Aplicações
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
PCS 3115 (PCS2215) Conteúdo
 -Mar-8 PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Marcos A. Simplicio Jr. versão: 3. (Jan/26) Conteúdo Conceitos básicos Teoremas de variável Teoremas de 2 variáveis Teoremas
-Mar-8 PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Marcos A. Simplicio Jr. versão: 3. (Jan/26) Conteúdo Conceitos básicos Teoremas de variável Teoremas de 2 variáveis Teoremas
Teoria Elementar dos Conjuntos
 Teoria Elementar dos Conjuntos Última revisão em 27 de fevereiro de 2009 Este texto é uma breve revisão sobre teoria elementar dos conjuntos. Em particular, importam-nos os aspectos algébricos no estudo
Teoria Elementar dos Conjuntos Última revisão em 27 de fevereiro de 2009 Este texto é uma breve revisão sobre teoria elementar dos conjuntos. Em particular, importam-nos os aspectos algébricos no estudo
Sistemas Digitais I LESI :: 2º ano
 Sistemas Digitais I LESI :: 2º ano - Álgebra António Joaquim Esteves João Miguel Fernandes www.di.uminho.pt/~aje Bibliografia: secções 3. e 4., DDPP, Wakerly DEP. DE INFORMÁTICA ESCOLA DE ENGENHARIA UNIVERSIDADE
Sistemas Digitais I LESI :: 2º ano - Álgebra António Joaquim Esteves João Miguel Fernandes www.di.uminho.pt/~aje Bibliografia: secções 3. e 4., DDPP, Wakerly DEP. DE INFORMÁTICA ESCOLA DE ENGENHARIA UNIVERSIDADE
Teoria Elementar dos Conjuntos
 Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN
 ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções
 Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
O espaço das Ordens de um Corpo
 O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
O espaço das Ordens de um Corpo Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é exibir corpos com infinitas ordens e exibir uma estrutura topológica ao conjunto das ordens de um corpo.
Arquitetura e Organização de Computadores. Álgebra Booleana
 Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Números Reais. Víctor Arturo Martínez León b + c ad + bc. b c
 Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Reticulados, Álgebra Booleana e Formas Quadráticas Abstratas
 Reticulados, Álgebra Booleana e Formas Quadráticas Abstratas Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é introduzir formas quadráticas sobre reticulados. Demonstramos que a definição
Reticulados, Álgebra Booleana e Formas Quadráticas Abstratas Clotilzio Moreira dos Santos Resumo O objetivo deste trabalho é introduzir formas quadráticas sobre reticulados. Demonstramos que a definição
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
Reticulados e Álgebras de Boole
 Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Axiomas de corpo ordenado
 Axiomas de corpo ordenado 2 a lista de exercícios Análise real A abordagem axiomática dos números reais previne erros que a intuição pode ocasionar e torna mais rigoroso o processo de demonstração matemática,
Axiomas de corpo ordenado 2 a lista de exercícios Análise real A abordagem axiomática dos números reais previne erros que a intuição pode ocasionar e torna mais rigoroso o processo de demonstração matemática,
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS.
 A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
Observação: Todas as letras em negrito abaixo (x, y, z, a e b) representam números reais.
 Para mostrar que menos vezes menos dá mais precisamos admitir alguns fatos relacionados aos números reais. Vamos chamá-los de axiomas e simplesmente aceitá-los como sendo válidos: Observação: Todas as
Para mostrar que menos vezes menos dá mais precisamos admitir alguns fatos relacionados aos números reais. Vamos chamá-los de axiomas e simplesmente aceitá-los como sendo válidos: Observação: Todas as
Relações Binárias, Aplicações e Operações
 Relações Binárias, Aplicações e Operações MAT 131-2018 II Pouya Mehdipour 6 de dezembro de 2018 Pouya Mehdipour 6 de dezembro de 2018 1 / 24 Referências ALENCAR FILHO, E. Teoria Elementar dos Conjuntos,
Relações Binárias, Aplicações e Operações MAT 131-2018 II Pouya Mehdipour 6 de dezembro de 2018 Pouya Mehdipour 6 de dezembro de 2018 1 / 24 Referências ALENCAR FILHO, E. Teoria Elementar dos Conjuntos,
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Prof. Leonardo Augusto Casillo
 UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03
 RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
A B f(a, B) = A + B. A f(a ) = A
 Álgebra de Boole ESTV-ESI-Sistemas Digitais-Álgebra de Boole 1/7 A Álgebra de Boole é uma ferramenta matemática muito utilizada na representação e simplificação de funções binárias (ou lógicas), sendo
Álgebra de Boole ESTV-ESI-Sistemas Digitais-Álgebra de Boole 1/7 A Álgebra de Boole é uma ferramenta matemática muito utilizada na representação e simplificação de funções binárias (ou lógicas), sendo
Axioma dos inteiros. Sadao Massago
 Axioma dos inteiros Sadao Massago setembro de 2018 Sumário 1 Os Números 2 1.1 Notação......................................... 2 1.2 Números naturais não nulos (inteiros positivos)................... 2
Axioma dos inteiros Sadao Massago setembro de 2018 Sumário 1 Os Números 2 1.1 Notação......................................... 2 1.2 Números naturais não nulos (inteiros positivos)................... 2
Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras. Silvia Gonçalves Santos
 Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras Silvia Gonçalves Santos Definição 1 Seja R um anel com unidade. O radical de Jacobson de R, denotado por J(R), é o ideal (à esquerda) dado pela
Generalizações do Teorema de Wedderburn-Malcev e PI-álgebras Silvia Gonçalves Santos Definição 1 Seja R um anel com unidade. O radical de Jacobson de R, denotado por J(R), é o ideal (à esquerda) dado pela
Notas de aulas. álgebra abstrata
 1 Notas de aulas de álgebra abstrata UEMA LICENCIATURA EM MATEMATICA Elaborada por : Raimundo Merval Morais Gonçalves Licenciado em Matemática/UFMA Professor Assistente/UEMA Especialista em Ensino de Ciências/UEMA
1 Notas de aulas de álgebra abstrata UEMA LICENCIATURA EM MATEMATICA Elaborada por : Raimundo Merval Morais Gonçalves Licenciado em Matemática/UFMA Professor Assistente/UEMA Especialista em Ensino de Ciências/UEMA
Cálculo proposicional
 Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
Capítulo 1. Os Números. 1.1 Notação. 1.2 Números naturais não nulos (inteiros positivos) Última atualização em setembro de 2017 por Sadao Massago
 Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
12 AULA. Relações de Ordem LIVRO. META: Apresentar o conceito de relações de ordem e suas propriedades.
 2 LIVRO Relações de Ordem META: Apresentar o conceito de relações de ordem e suas propriedades. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Determinar se uma dada relação é uma relação
2 LIVRO Relações de Ordem META: Apresentar o conceito de relações de ordem e suas propriedades. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Determinar se uma dada relação é uma relação
Álgebra de Boole. João Paulo Cerquinho Cajueiro 19 de agosto de 2009
 Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/51 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/51 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
Cálculo Diferencial e Integral Química Notas de Aula
 Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Teoria intuitiva de conjuntos
 Teoria intuitiva de conjuntos.................................... 1 Relação binária............................................ 10 Lista 3................................................. 15 Teoria intuitiva
Teoria intuitiva de conjuntos.................................... 1 Relação binária............................................ 10 Lista 3................................................. 15 Teoria intuitiva
1 Conjuntos, Números e Demonstrações
 1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
Lógica e Matemática Discreta
 Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 04 de Junho de 2010 Curso de Ciência da Computação Noções básicas Um conjunto designa-se geralmente por uma letra latina maiúscula:
Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 04 de Junho de 2010 Curso de Ciência da Computação Noções básicas Um conjunto designa-se geralmente por uma letra latina maiúscula:
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
CONJUNTO DOS NÚMEROS INTEIROS
 Fundamentos de Álgebra Moderna Profª Ana Paula CONJUNTO DOS NÚMEROS INTEIROS Os números inteiros formam um conjunto, que notaremos por, no qual estão definidas duas operações, que chamaremos de adição
Fundamentos de Álgebra Moderna Profª Ana Paula CONJUNTO DOS NÚMEROS INTEIROS Os números inteiros formam um conjunto, que notaremos por, no qual estão definidas duas operações, que chamaremos de adição
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos
 MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
Números - Aula 03. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Números - Aula 03 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 28 de Fevereiro de 2014 Primeiro Semestre de 2014 Turma 2013106 - Engenharia Mecânica Corpos Vimos que o
Números - Aula 03 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 28 de Fevereiro de 2014 Primeiro Semestre de 2014 Turma 2013106 - Engenharia Mecânica Corpos Vimos que o
Capítulo 1. Os Números. 1.1 Notação. 1.2 Números naturais (inteiros positivos)
 Capítulo 1 Os Números 1.1 Notação Números naturais: N = {1, 2, 3,...}, mas existem vários autores considerando N = {0, 1, 2, 3,...}. Por isso, é recomendado dizer números positivos, números não negativos,
Capítulo 1 Os Números 1.1 Notação Números naturais: N = {1, 2, 3,...}, mas existem vários autores considerando N = {0, 1, 2, 3,...}. Por isso, é recomendado dizer números positivos, números não negativos,
Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados
 Conteúdo Conteúdo 1 1 Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados 2 1.1 Conjuntos parcialmente ordenados................ 2 1.2 Diagramas de Hasse........................ 4 1.3
Conteúdo Conteúdo 1 1 Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados 2 1.1 Conjuntos parcialmente ordenados................ 2 1.2 Diagramas de Hasse........................ 4 1.3
Teoria dos anéis 1 a parte 3
 A U L A Teoria dos anéis 1 a parte 3 Meta da aula Descrever a estrutura algébrica de anel como uma generalização de determinadas propriedades dos números inteiros. objetivos Ao final desta aula, você deverá
A U L A Teoria dos anéis 1 a parte 3 Meta da aula Descrever a estrutura algébrica de anel como uma generalização de determinadas propriedades dos números inteiros. objetivos Ao final desta aula, você deverá
Tecnologia dos Computadores 2002/2003. Exercícios
 Introdução à Álgebra de Boole 1 Introdução Em 1854, George Boole, um matemático inglês, inventou um sistema algébrico de dois valores, cujo resultado da sua evolução até aos dias de hoje se dá o nome de
Introdução à Álgebra de Boole 1 Introdução Em 1854, George Boole, um matemático inglês, inventou um sistema algébrico de dois valores, cujo resultado da sua evolução até aos dias de hoje se dá o nome de
Introdução à Computação: Álgebra Booleana
 Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Números Reais. Gláucio Terra. Departamento de Matemática IME - USP. Números Reais p. 1/2
 Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
1.1 Conjuntos parcialmente ordenados (c.p.o. s)
 Capítulo 1 PRELIMINARES Neste primeiro capítulo podemos encontrar algumas definições e proposições que para além de nos familiarizar com a notação que iremos utilizar também têm como finalidade a referência
Capítulo 1 PRELIMINARES Neste primeiro capítulo podemos encontrar algumas definições e proposições que para além de nos familiarizar com a notação que iremos utilizar também têm como finalidade a referência
Humberto José Bortolossi x 1 < 0 x2 x 12 < 0. x 1 x + 12 (x + 3)(x 4)
 SEGUNDA VERIFICAÇÃO DE APRENDIZAGEM Matemática Básica Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Nome legível: Assinatura: [0] (2.0) Resolva a inequação x 2 < x + 2 no conjunto dos
SEGUNDA VERIFICAÇÃO DE APRENDIZAGEM Matemática Básica Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Nome legível: Assinatura: [0] (2.0) Resolva a inequação x 2 < x + 2 no conjunto dos
Os números inteiros. Capítulo 2
 6 Capítulo 2 Os números inteiros Intuitivamente, o conjunto Z dos números inteiros é composto pelos números naturais e pelos "negativos". Como justificamos de uma forma simples qual a origem dos números
6 Capítulo 2 Os números inteiros Intuitivamente, o conjunto Z dos números inteiros é composto pelos números naturais e pelos "negativos". Como justificamos de uma forma simples qual a origem dos números
Aula Orientação do espaço. Observação 1
 Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
MCTB Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares. Os Exercícios 3 e 4 são os exercícios bônus dessa lista.
 MCTB002-13 Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares Os Exercícios 3 e 4 são os exercícios bônus dessa lista. Definição 1. Dados conjuntos X e Y, uma função ϕ :
MCTB002-13 Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares Os Exercícios 3 e 4 são os exercícios bônus dessa lista. Definição 1. Dados conjuntos X e Y, uma função ϕ :
Matemática Discreta Parte 11
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta Parte 11 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta Parte 11 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti
A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há
 1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
Aula 1 Conjuntos. Meta. Introduzir as noções básicas de conjunto e produto cartesiano de. conjuntos. Objetivos
 Conjuntos AULA 1 Aula 1 Conjuntos Meta conjuntos. Introduzir as noções básicas de conjunto e produto cartesiano de Objetivos Ao final desta aula, você deve ser capaz de: Definir as noções básicas de conjunto
Conjuntos AULA 1 Aula 1 Conjuntos Meta conjuntos. Introduzir as noções básicas de conjunto e produto cartesiano de Objetivos Ao final desta aula, você deve ser capaz de: Definir as noções básicas de conjunto
ELEMENTOS DE MATEMÁTICA DISCRETA Exame de Segunda Data 18/01/2011
 Uma Resolução ELEMENTOS DE MATEMÁTICA DISCRETA Exame de Segunda Data 18/01/2011 1. Seleccione e transcreva para a sua folha de exame a única opção correcta: A fórmula proposicional (p q) (p q) é a) logicamente
Uma Resolução ELEMENTOS DE MATEMÁTICA DISCRETA Exame de Segunda Data 18/01/2011 1. Seleccione e transcreva para a sua folha de exame a única opção correcta: A fórmula proposicional (p q) (p q) é a) logicamente
Teoria Ingênua dos Conjuntos (naive set theory)
 Teoria Ingênua dos Conjuntos (naive set theory) MAT 131-2018 II Pouya Mehdipour 5 de outubro de 2018 Pouya Mehdipour 5 de outubro de 2018 1 / 22 Referências ALENCAR FILHO, E. Iniciação à Lógica Matemática,
Teoria Ingênua dos Conjuntos (naive set theory) MAT 131-2018 II Pouya Mehdipour 5 de outubro de 2018 Pouya Mehdipour 5 de outubro de 2018 1 / 22 Referências ALENCAR FILHO, E. Iniciação à Lógica Matemática,
complemento para a disciplina de Matemática Discreta versão 1 - Jerônimo C. Pellegrini Relações de Equivalência e de Ordem
 Relações de Equivalência e de Ordem complemento para a disciplina de Matemática Discreta versão 1 Jerônimo C. Pellegrini 5 de agosto de 2013 ii Sumário Sumário Nomenclatura 1 Conjuntos e Relações 1 1.1
Relações de Equivalência e de Ordem complemento para a disciplina de Matemática Discreta versão 1 Jerônimo C. Pellegrini 5 de agosto de 2013 ii Sumário Sumário Nomenclatura 1 Conjuntos e Relações 1 1.1
SEGUNDA VERIFICAÇÃO DE APRENDIZAGEM. Nome legível: Assinatura:
 SEGUNDA VERIFICAÇÃO DE APRENDIZAGEM Matemática Básica Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Nome legível: Assinatura: [01] (2.0) Resolva a desigualdade 1 x 2 2 x 3 0 usando a
SEGUNDA VERIFICAÇÃO DE APRENDIZAGEM Matemática Básica Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Nome legível: Assinatura: [01] (2.0) Resolva a desigualdade 1 x 2 2 x 3 0 usando a
4.1 Preliminares. No exemplo acima: Dom(R 1 ) = e Im(R 1 ) = Dom(R 2 ) = e Im(R 2 ) = Dom(R 3 ) = e Im(R 3 ) = Diagrama de Venn
 4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
ELETRÔNICA DIGITAL Aula 4-Álgebra de Boole e Simplificações de circuitos lógicos
 ELETRÔNICA DIGITAL Aula 4-Álgebra de Boole e Simplificações de circuitos lógicos Prof.ª Eng. Msc. Patricia Pedroso Estevam Ribeiro Email: patriciapedrosoestevam@hotmail.com 08/10/2016 1 Introdução Os circuitos
ELETRÔNICA DIGITAL Aula 4-Álgebra de Boole e Simplificações de circuitos lógicos Prof.ª Eng. Msc. Patricia Pedroso Estevam Ribeiro Email: patriciapedrosoestevam@hotmail.com 08/10/2016 1 Introdução Os circuitos
Matemática Discreta - 07
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Apresentar o conceito de grupo, as primeiras definições e diversos exemplos. Aplicar as propriedades dos grupos na resolução de problemas.
 Aula 04 O CONCEITO DE GRUPO META Apresentar o conceito de grupo, as primeiras definições e diversos exemplos. OBJETIVOS Definir e exemplificar grupos e subgrupos. Aplicar as propriedades dos grupos na
Aula 04 O CONCEITO DE GRUPO META Apresentar o conceito de grupo, as primeiras definições e diversos exemplos. OBJETIVOS Definir e exemplificar grupos e subgrupos. Aplicar as propriedades dos grupos na
Teoria dos Conjuntos MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES. Fundamentos de Lógica Técnicas Elementares de Prova A NOÇÃO DE CONJUNTO
 SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
Parte 2 N Z Q R C. Não faremos a construção axiomática dos números naturais, usaremos apenas as noções intuitivas.
 Parte 2 Anéis A Matemática faz parte do nosso cotidiano e, em particular, recorremos aos números para descrever diversas situações do dia a dia. Contamos com os números naturais, repartimos um bolo usando
Parte 2 Anéis A Matemática faz parte do nosso cotidiano e, em particular, recorremos aos números para descrever diversas situações do dia a dia. Contamos com os números naturais, repartimos um bolo usando
Capítulo 1. Introdução
 Capítulo 1 Introdução O objeto de estudo de Mat-1 são as funções reais de variável real. Estudaremos nesta disciplina os conceitos de limite, continuidade, derivabilidade e integrabilidade de funções reais
Capítulo 1 Introdução O objeto de estudo de Mat-1 são as funções reais de variável real. Estudaremos nesta disciplina os conceitos de limite, continuidade, derivabilidade e integrabilidade de funções reais
Números Inteiros Axiomas e Resultados Simples
 Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
DE MATEMÁTICA I. Prof. ADRIANO CATTAI. Corpos Numéricos (Atualizada em 8 de março de 2016)
 ac COMPLEMENTOS DE MATEMÁTICA I Prof. ADRIANO CATTAI Corpos Numéricos (Atualizada em 8 de março de 2016) NOME: DATA: / / Não há ciência que fale das harmonias da natureza com mais clareza do que a matemática
ac COMPLEMENTOS DE MATEMÁTICA I Prof. ADRIANO CATTAI Corpos Numéricos (Atualizada em 8 de março de 2016) NOME: DATA: / / Não há ciência que fale das harmonias da natureza com mais clareza do que a matemática
Unidade IV. Unidade III. Na álgebra booleana, estão todos os fundamentos da eletrônica digital.
 Unidade IV 9 INTRODUÇÃO À ÁLGEBRA DE BOOLE Na álgebra booleana, estão todos os fundamentos da eletrônica digital 91 Operador binário O sistema numérico surgiu ao longo da história do desenvolvimento humano
Unidade IV 9 INTRODUÇÃO À ÁLGEBRA DE BOOLE Na álgebra booleana, estão todos os fundamentos da eletrônica digital 91 Operador binário O sistema numérico surgiu ao longo da história do desenvolvimento humano
Topologia de Zariski. Jairo Menezes e Souza. 25 de maio de Notas incompletas e não revisadas RASCUNHO
 Topologia de Zariski Jairo Menezes e Souza 25 de maio de 2013 Notas incompletas e não revisadas 1 Resumo Queremos abordar a Topologia de Zariski para o espectro primo de um anel. Antes vamos definir os
Topologia de Zariski Jairo Menezes e Souza 25 de maio de 2013 Notas incompletas e não revisadas 1 Resumo Queremos abordar a Topologia de Zariski para o espectro primo de um anel. Antes vamos definir os
Semana 2. Primitivas. Conjunto das partes. Produto cartesiano. 1 Teoria ingênua dos conjuntos. 2 Axiomática ZFC de conjuntos. 4 Conjuntos numéricos
 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 e pertinência Conjunto é entendido como uma coleção de
Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 Semana 2 1 Teoria ingênua dos conjuntos 2 Axiomática ZFC de conjuntos 3 4 e pertinência Conjunto é entendido como uma coleção de
Introdução à Teoria de Grupos Grupos cíclicos Grupos de permutações Isomorfismos
 Observação Como para k > 1 se tem (a 1, a 2,..., a k ) = (a 1, a k )(a 1, a k 1 ) (a 1, a 2 ), um ciclo de comprimento par é uma permutação ímpar e um ciclo de comprimento ímpar é uma permutação par. Proposição
Observação Como para k > 1 se tem (a 1, a 2,..., a k ) = (a 1, a k )(a 1, a k 1 ) (a 1, a 2 ), um ciclo de comprimento par é uma permutação ímpar e um ciclo de comprimento ímpar é uma permutação par. Proposição
Explorando a lógica dentro da calculadora
 Universidade Federal do Rio Grande do Norte Centro de Ciências Exatas e da Terra Mestrado Profissional em Matemática em Rede Nacional Fábio Alvaro Dantas Explorando a lógica dentro da calculadora Natal,
Universidade Federal do Rio Grande do Norte Centro de Ciências Exatas e da Terra Mestrado Profissional em Matemática em Rede Nacional Fábio Alvaro Dantas Explorando a lógica dentro da calculadora Natal,
Contando o Infinito: os Números Cardinais
 Contando o Infinito: os Números Cardinais Sérgio Tadao Martins 4 de junho de 2005 No one will expel us from the paradise that Cantor has created for us David Hilbert 1 Introdução Quantos elementos há no
Contando o Infinito: os Números Cardinais Sérgio Tadao Martins 4 de junho de 2005 No one will expel us from the paradise that Cantor has created for us David Hilbert 1 Introdução Quantos elementos há no
Álgebra de Boole binária
 Álgebra de Boole binária Fundamentação Funções lógicas de uma variável Funções lógicas de duas variáveis Princípio da dualidade Funções de n variáveis Definição formal da Álgebra de Boole Manipulação de
Álgebra de Boole binária Fundamentação Funções lógicas de uma variável Funções lógicas de duas variáveis Princípio da dualidade Funções de n variáveis Definição formal da Álgebra de Boole Manipulação de
Matemática Discreta - 07
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
1 Noções preliminares
 Álgebras, subálgebras e endomorfirsmos Ana Cristina - MAT/UFMG Durante este texto, vamos considerar F um corpo de característica zero. Iniciaremos com algumas definições da teoria de anéis que serão importantes
Álgebras, subálgebras e endomorfirsmos Ana Cristina - MAT/UFMG Durante este texto, vamos considerar F um corpo de característica zero. Iniciaremos com algumas definições da teoria de anéis que serão importantes
1. CONJUNTOS NUMÉRICOS
 . CONJUNTOS NUMÉRICOS.. INTRODUÇÃO Uma exposição sistemática dos conjuntos numéricos, utilizados na Matemática, pode ser feita a partir dos números usados para contar, chamados de números naturais. Estes
. CONJUNTOS NUMÉRICOS.. INTRODUÇÃO Uma exposição sistemática dos conjuntos numéricos, utilizados na Matemática, pode ser feita a partir dos números usados para contar, chamados de números naturais. Estes
Álgebra de Boole (ou Boleana) Circuitos Digitais Portas Lógicas e Álgebra de Boole. Álgebra de Boole: Tabela Verdade. Álgebra de Boole: funções
 6/3/2 Circuitos Digitais Portas Lógicas e Álgebra de Boole Prof. Abel Guilhermino Aula 3 (ou Boleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto
6/3/2 Circuitos Digitais Portas Lógicas e Álgebra de Boole Prof. Abel Guilhermino Aula 3 (ou Boleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto
ANÉIS. Professora: Elisandra Bär de Figueiredo
 Professora: Elisandra Bär de Figueiredo ANÉIS DEFINIÇÃO 1 Um sistema matemático (A,, ) constituído de um conjunto não vazio A e duas leis de composição interna sobre A, uma adição: (x, y) x y e uma multiplicação
Professora: Elisandra Bär de Figueiredo ANÉIS DEFINIÇÃO 1 Um sistema matemático (A,, ) constituído de um conjunto não vazio A e duas leis de composição interna sobre A, uma adição: (x, y) x y e uma multiplicação
Lógica Computacional
 Aula Teórica 9: Forma Normal Conjuntiva Departamento de Informática 21 de Março de 2011 O problema Como determinar eficazmente a validade de uma fórmula? Objectivo Determinar a validade de raciocínios
Aula Teórica 9: Forma Normal Conjuntiva Departamento de Informática 21 de Março de 2011 O problema Como determinar eficazmente a validade de uma fórmula? Objectivo Determinar a validade de raciocínios
Referências e materiais complementares desse tópico
 Notas de aula: Análise de Algoritmos Centro de Matemática, Computação e Cognição Universidade Federal do ABC Profa. Carla Negri Lintzmayer Conceitos matemáticos e técnicas de prova (Última atualização:
Notas de aula: Análise de Algoritmos Centro de Matemática, Computação e Cognição Universidade Federal do ABC Profa. Carla Negri Lintzmayer Conceitos matemáticos e técnicas de prova (Última atualização:
Números Reais. Jairo Menezes e Souza 19/09/2013 UFG/CAC
 UFG/CAC 19/09/2013 Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Chamamos de Z o conjunto dos números
UFG/CAC 19/09/2013 Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Iniciamos com o conjunto dos números naturais N = {0, 1, 2, 3, 4, 5,...} Chamamos de Z o conjunto dos números
Utiliza variáveis binárias, i.e., que só podem assumir um de dois valores: {0,1}; {Low,High}; {True,False}; etc.
 Álgebra de oole binária através do recurso à utiliação de funções booleanas (ou funções lógicas) é a principal teoria de suporte às metodologias de síntese e análise de circuitos digitais. Utilia variáveis
Álgebra de oole binária através do recurso à utiliação de funções booleanas (ou funções lógicas) é a principal teoria de suporte às metodologias de síntese e análise de circuitos digitais. Utilia variáveis
PCS 3115 Sistemas Digitais I Análise e Síntese de Circuitos Combinatórios Prof. Dr. Marcos A. Simplicio Jr.
 PCS 3115 Sistemas Digitais I Análise e Síntese de Circuitos Combinatórios Prof. Dr. Marcos A. Simplicio Jr. Adapatdo por Glauber De Bona (2018) O que vimos até agora Sistemas de numeração posicionais,
PCS 3115 Sistemas Digitais I Análise e Síntese de Circuitos Combinatórios Prof. Dr. Marcos A. Simplicio Jr. Adapatdo por Glauber De Bona (2018) O que vimos até agora Sistemas de numeração posicionais,
Ordem dos Inteiros AULA. 4.1 Introdução. 4.2 Ordem Ordem dos Inteiros
 META: Apresentar ordem nos números inteiros e os Princípio de indução e do Menor elemento. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Usar o processo de indução finita dos Inteiros. Justificar
META: Apresentar ordem nos números inteiros e os Princípio de indução e do Menor elemento. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Usar o processo de indução finita dos Inteiros. Justificar
Lógica Proposicional e Álgebra de Boole
 Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
1 Operações com conjuntos
 Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES
 MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
Introdução à Álgebra de Lie
 Introdução à Álgebra de Lie Wilian Francisco de Araujo Universidade Tecnológica Federal do Paraná e-mail: wilianfrancisco@gmail.com Estou certo, absolutamente certo de que... essas teorias será reconhecido
Introdução à Álgebra de Lie Wilian Francisco de Araujo Universidade Tecnológica Federal do Paraná e-mail: wilianfrancisco@gmail.com Estou certo, absolutamente certo de que... essas teorias será reconhecido
Lista 1. 9 Se 0 < x < y e n N então 0 < x n < y n.
 UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof. José Carlos Eidam Lista 1 Em toda a lista, K denota um corpo ordenado qualquer. Corpos ordenados 1. Verifique as
UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof. José Carlos Eidam Lista 1 Em toda a lista, K denota um corpo ordenado qualquer. Corpos ordenados 1. Verifique as
1 o semestre. 1. Símbolos lógicos e conjuntos
 CONJUNTOS E ÁLGEBRA 1 o semestre Neste curso, recordaremos inicialmente a teoria ingênua de conjuntos e um pouco de lógica. Depois, estudaremos alguns rudimentos de álgebra: relações de equivalência e
CONJUNTOS E ÁLGEBRA 1 o semestre Neste curso, recordaremos inicialmente a teoria ingênua de conjuntos e um pouco de lógica. Depois, estudaremos alguns rudimentos de álgebra: relações de equivalência e
1 Números Complexos. Seja R o conjunto dos Reais. Consideremos o produto cartesiano R R = R 2 tal que:
 Números Complexos e Polinômios Prof. Gustavo Sarturi [!] Esse documento está sob constantes atualizações, qualquer erro de ortografia, cálculo, favor comunicar. Última atualização: 01/11/2018. 1 Números
Números Complexos e Polinômios Prof. Gustavo Sarturi [!] Esse documento está sob constantes atualizações, qualquer erro de ortografia, cálculo, favor comunicar. Última atualização: 01/11/2018. 1 Números
Abaixo descreveremos 6 portas lógicas: AND, OR, NOT, NAND, NOR e XOR.
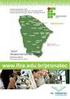 9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
CÁLCULO I. 1 Número Reais. Objetivos da Aula
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
Análise I. Notas de Aula 1. Alex Farah Pereira de Agosto de 2017
 Análise I Notas de Aula 1 Alex Farah Pereira 2 3 23 de Agosto de 2017 1 Turma de Matemática. 2 Departamento de Análise-IME-UFF 3 http://alexfarah.weebly.com ii Conteúdo 1 Conjuntos 1 1.1 Números Naturais........................
Análise I Notas de Aula 1 Alex Farah Pereira 2 3 23 de Agosto de 2017 1 Turma de Matemática. 2 Departamento de Análise-IME-UFF 3 http://alexfarah.weebly.com ii Conteúdo 1 Conjuntos 1 1.1 Números Naturais........................
