Conteúdo. Correção Exercícios Revisão para Prova
|
|
|
- Fábio Arruda Silva
- 6 Há anos
- Visualizações:
Transcrição
1 Conteúdo Correção Exercícios Revisão para Prova
2 Rosen 58 1) Transcreva as proposições abaixo para o português, em que o domínio para cada variável consista nos números reais. a) x y (x<y) b) x y (((x x y z (xy = z)
3 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. a) Todos amam Jerry
4 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. a) Todos amam Jerry y
5 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. a) Todos amam Jerry x L(x,Jerry) y
6 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. b) Todas as pessoas amam alguém?????
7 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. b) Todas as pessoas amam alguém x y L(x,y)
8 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. c) Há alguém que é amado por todos??????
9 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. c) Há alguém que é amado por todos y x L(x,y)
10 Rosen (59) 9. Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. d) Ninguém ama todos
11 Rosen (59) 9. Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. d) Ninguém ama todos Existe alguém que ama todo mundo x y L(x,y) Se isso não for verdade então Ninguém ama todos
12 Rosen (59) 9. Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. d) Ninguém ama todos ~ x y L(x,y) Existe alguém que ama todo mundo x y L(x,y) Se isso não for verdade então Ninguém ama todos
13 Rosen (59) 9. Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. d) Ninguém ama todos ~ x y L(x,y) e) Há alguém a quem Lídia não ama Reescrevendo: Lidia não ama alguém: y ~L(Lidia,y)
14 Rosen (59) 9. Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. d) Ninguém ama todos ~ x y L(x,y) e) Há alguém a quem Lídia não ama y ~L(Lidia,y) f) Há alguém a quem ninguém ama Reescrevendo: Há alguém a quem todos não amam y x ~L(x,y)
15 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. i) Todos amam a si próprio????
16 Exercícios Rosen (59) 9) Considere L(x,y) como a proposição x ama y, em que o domínio para x e y são todas as pessoas do mundo. Use quantificadores para expressar cada proposição abaixo. i) Todos amam a si próprio x L(x,x)
17 Exercícios Rosen (59) 11) Considere S(x) como o predicado x é um estudante, F(x) o predicado x é um membro da faculdade e A(x,y) o predicado x fez uma pergunta a y, em que o domínio são todas pessoas associadas a sua escola. Use quantificadores para expressar cada proposição a seguir. a) Lois fez uma pergunta ao professor Michaels
18 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} a) Lois fez uma pergunta ao professor Michaels A(x,y) Quem é?
19 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} a) Lois fez uma pergunta ao professor Michaels A(Lois,professor Michaels)
20 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} b) Todo estudante fez uma pergunta ao professor Gross A(x,y) Quem é?
21 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} b) Todo estudante fez uma pergunta ao professor Gross A(x,professor Gross) Quem é?
22 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} b) Todo estudante fez uma pergunta ao professor Gross A(x,professor Gross) Teremos que restringir o domínio...
23 Exercícios Rosen (59) 11) S(x) = x é um estudante F(x) = x é um membro da faculdade A(x,y) = x fez uma pergunta a y Domínio {todas pessoas da sua escola} b) Todo estudante fez uma pergunta ao professor Gross x(s(x) A(x,professor Gross)) Universal = Condicional!!!!
24 Exercícios Rosen (61) 26) Considere Q(x,y) como a proposição x+y = x-y. Se o domínio das duas variáveis forem todos os números inteiros, quais são os valores verdade? a) Q(1,1) =???
25 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) =????
26 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) =?????
27 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) = Falso d) xq(x,2) =????
28 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) =????
29 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) = Verdade, letra b) f ) x yq(x,y) =????
30 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) = Verdade, letra b) f ) x yq(x,y) = Verdade. Qual? g) y xq(x,y) =????
31 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso b) Q(2,0) = Verdade c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) = Verdade, letra b) f ) x yq(x,y) = Verdade. Qual? g) y xq(x,y) = Verdade. Qual?
32 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso h) y xq(x,y) = F b) Q(2,0) = Verdade i) x yq(x,y) =??? c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) = Verdade, letra b) f ) x yq(x,y) = Verdade. Qual? g) y xq(x,y) = Verdade. Qual?
33 Exercícios Rosen (61) 26) Q(x,y) = x+y = x-y Domínio = Z a) Q(1,1) = Falso h) y xq(x,y) = F b) Q(2,0) = Verdade i) x yq(x,y) = F c) yq(1,y) = Falso d) xq(x,2) = Falso e) x yq(x,y) = Verdade, letra b) f ) x yq(x,y) = Verdade. Qual? g) y xq(x,y) = Verdade. Qual?
34 Rosen (61) 30) Reescrever cada uma das proposições para que as negações apareçam apenas inseridas nos predicados (ou seja, nenhuma negação esteja do lado de fora de um quantificador ou de uma expressão que envolva conectivos lógicos). Aplicação direta das leis de De Morgan
35 O que foi visto até agora... Predicado Proposição Quantificadores Conjuntos Quantificadores com restrição Operações Lógicas com predicados Quantificadores Agrupados Negando Quantificadores Equivalências Lógicas Tradução
36 Revisão para a Prova Responda...
37 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Toda pessoa justa é formada em direito.
38 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Toda pessoa justa é formada em direito.
39 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Leonardo é delegado.
40 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Leonardo é delegado.
41 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Amanda é justa.
42 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Amanda é justa.
43 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Há pessoas formadas em direito que são justas.
44 Prova: FUNCAB Partindo das premissas: I. Todo delegado é justo. II. Todo delegado é formado em direito. III. Leonardo é justo. IV. Amanda é perita. Pode - se concluir que Há pessoas formadas em direito que são justas.
45 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis esforçados concluíram o ensino superior.
46 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis esforçados concluíram o ensino superior.
47 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: Não é verdade que nenhum policial civil esforçado concluiu o ensino superior.
48 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: Não é verdade que nenhum policial civil esforçado concluiu o ensino superior.
49 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis que não concluíram o ensino superior não são esforçados.
50 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis que não concluíram o ensino superior não são esforçados.
51 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis que concluíram o ensino superior são esforçados
52 Prova: VUNESP PC-SP Considere verdadeiras as seguintes afirmações: I. Existem policiais civis que concluíram o ensino superior. II. Todos os policiais civis são esforçados. Com base nas informações, conclui-se que: os policiais civis que concluíram o ensino superior são esforçados
53 Avaliação Interdisciplinar Em um grupo de amigos, conversando sobre profissões e carreiras, perceberam que entre eles, todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e nenhum engenheiro é cantor.
54 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Nenhum engenheiro é médico.
55 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Nenhum engenheiro é médico.
56 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Pelo menos um engenheiro é professor.
57 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Pelo menos um engenheiro é professor.
58 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Nenhum médico é cantor.
59 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Nenhum médico é cantor.
60 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Todos os programadores são médicos.
61 Avaliação Interdisciplinar Todos os médicos são, também, professores, mas nenhum professor é cantor. Todos os engenheiros são também programadores, e alguns programadores são também cantores. Como nenhum programador é professor, e como nenhum engenheiro é cantor, então, pode-se afirmar que: Todos os programadores são médicos.
62 Avaliação Interdisciplinar Conjuntos é uma estrutura discreta fundamental no estudo da computação. Algumas operações podem ser feitas com dois ou mais conjuntos, dentre elas temos a intersecção () e a diferença ( ). Considerando três conjuntos quaisquer A, B, C e o conjunto vazio, analise as afirmações a seguir.
63 Avaliação Interdisciplinar (A B C) (A B)
64 Avaliação Interdisciplinar (A B C) (A B)
65 Avaliação Interdisciplinar A (A B)
66 Avaliação Interdisciplinar A (A B)
67 Avaliação Interdisciplinar (A C) (C B ) =
68 Avaliação Interdisciplinar (A C) (C B ) =
69 Avaliação Interdisciplinar A lógica de predicados expressa adequadamente o significado das proposições em linguagem natural. Para isto ela define predicados e quantificadores, sendo o quantificador universal e o quantificador existencial.
70 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: x(c(x) ^ P(x)), onde domínio = { alunos da PUC} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
71 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: x(c(x) ^ P(x)), onde domínio = { alunos da PUC} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
72 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: P(x),onde domínio = {alunos da disciplina CMP1049} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
73 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: xp(x),onde domínio = {alunos da disciplina CMP1049} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
74 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: x(c(x) P(x)), onde domínio = { alunos da PUC} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
75 Avaliação Interdisciplinar Utilizando a lógica de predicados podemos expressar a sentença Para cada aluno da disciplina CMP1049 este foi aprovado na disciplina CMP1045 da seguinte forma: x(c(x) P(x)), onde domínio = { alunos da PUC} P(x) = x foi aprovado na disciplina CMP1045, C(x) = x é aluno da disciplina CMP1049.
76 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: O conjunto dos marinheiros contém o conjunto dos republicanos.
77 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: O conjunto dos marinheiros contém o conjunto dos republicanos.
78 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: Todos os republicanos são marinheiros.
79 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: Todos os republicanos são marinheiros.
80 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: O conjunto dos republicanos contém o conjunto dos marinheiros.
81 Avaliação Interdisciplinar Todos os marinheiros são republicanos. Com base na proposição podemos afirmar que: O conjunto dos republicanos contém o conjunto dos marinheiros.
82 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y U) (x < y) é válida.
83 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y U) (x < y) é válida.
84 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y N) (y < x) é válida.
85 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y N)(y < x) é válida.
86 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y U) (x > y) é inválida, sendo x=10 um contra-exemplo.
87 ENADE 2014 Seja o universo U={10, 20, 30, 40} e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir. ( x N)( y U) (x > y)(x > y) é inválida, sendo x=10 um contra-exemplo.
Lógica de Predicados
Lógica de Predicados Conteúdo Correção dos Exercícios (Rosen 47) Prioridade dos Quantificadores (Rosen 38) Ligando Variáveis (Rosen 38) Predicados com duas variáveis. Equivalências lógicas (Rosen 39) Negando
Matemática Discreta - 03
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 03 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
AULA 5 QUANTIFICADORES, PREDICADOS E VALIDADE
Disciplina: Matemática Computacional Prof. Diana de Barros Teles AULA 5 QUANTIFICADORES, PREDICADOS E VALIDADE Quantificadores: são frases do tipo para todo, ou para cada, ou para algum, isso é, frases
Lógica de Predicados
Lógica de Predicados Conteúdo Correção Exercícios Operações Lógicas sobre Predicados Condicional Quantificador de Unicidade (Rosen 37) Quantificadores com Restrição (Rosen 38) Tradução Português-Lógica
Noções básicas de Lógica
Noções básicas de Lógica Consideremos uma linguagem, com certos símbolos. Chamamos expressão a uma sequências de símbolos. uma expressão com significado Uma expressão pode ser expressão sem significado
= 1 1 1 1 1 1. Pontuação: A questão vale dez pontos, tem dois itens, sendo que o item A vale até três pontos, e o B vale até sete pontos.
VTB 008 ª ETAPA Solução Comentada da Prova de Matemática 0 Em uma turma de alunos que estudam Geometria, há 00 alunos Dentre estes, 30% foram aprovados por média e os demais ficaram em recuperação Dentre
Bases Matemáticas. Daniel Miranda 1. 23 de maio de 2011. sala 819 - Bloco B página: daniel.miranda
Daniel 1 1 email: daniel.miranda@ufabc.edu.br sala 819 - Bloco B página: http://hostel.ufabc.edu.br/ daniel.miranda 23 de maio de 2011 Elementos de Lógica e Linguagem Matemática Definição Uma proposição
Universidade Federal de Goiás Campus Catalão Departamento de Matemática
Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear Professor: André Luiz Galdino Aluno(a): 4 a Lista de Exercícios 1. Podemos entender transformações lineares
Lógica para computação Professor Marlon Marcon
Lógica para computação Professor Marlon Marcon INTRODUÇÃO O objetivo geral da logica formal é a mecanização do raciocnio, ou seja, A obtenção de informação a partir de informações prévias por meio de recursos
Prof. Daniela Barreiro Claro
O volume de dados está crescendo sem parar Gigabytes, Petabytes, etc. Dificuldade na descoberta do conhecimento Dados disponíveis x Análise dos Dados Dados disponíveis Analisar e compreender os dados 2
4.4 Limite e continuidade
4.4 Limite e continuidade Noções Topológicas em R : Dados dois pontos quaisquer (x 1, y 1 ) e (x, y ) de R indicaremos a distância entre eles por då(x 1, y 1 ), (x, y )è=(x 1 x ) + (y 1 y ). Definição
[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013
![[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013](/thumbs/39/19161564.jpg "[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013")
Economia I; 01/013 (º semestre) Prova da Época Recurso 3 de Julho de 013 [RESOLUÇÃO] Distribuição das respostas correctas às perguntas da Parte A (6 valores) nas suas três variantes: ER A B C P1 P P3 P4
21- EXERCÍCIOS FUNÇÕES DO SEGUNDO GRAU
1 21- EXERCÍCIOS FUNÇÕES DO SEGUNDO GRAU 1. O gráfico do trinômio y = ax 2 + bx + c. Qual a afirmativa errada? a) se a > 0 a parábola possui concavidade para cima b) se b 2 4ac > 0 o trinômio possui duas
Métodos Formais. Agenda. Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções. Relações e Funções
Métodos Formais Relações e Funções por Mauro Silva Agenda Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções MF - Relações e Funções 2 1 Relações Binárias Definição
Olimpíada Brasileira de Raciocínio Lógico Nível III Fase II 2014
1 2 Questão 1 Um dado é feito com pontos colocados nas faces de um cubo, em correspondência com os números de 1 a 6, de tal maneira que somados os pontos que ficam em cada par de faces opostas é sempre
Unidade 2. Lógica de Predicados. Objetivos:
Unidade 2 Lógica de Predicados Objetivos: Conhecer a linguagem formal Lógica de Predicados, assim como gerar fórmulas bem formadas nessa linguagem, a atribuição de valor verdade às fórmulas envolvendo
Sendo o polinômio P(x), de grau quatro e divisível por Q(x) = x 3, o resto de sua divisão por D(x) = x 5 é
Questão 01) O polinômio p(x) = x 3 + x 2 3ax 4a é divisível pelo polinômio q(x) = x 2 x 4. Qual o valor de a? a) a = 2 b) a = 1 c) a = 0 d) a = 1 e) a = 2 TEXTO: 1 Para fazer um estudo sobre certo polinômio
Nome: N.º: endereço: data: telefone: E-mail: PARA QUEM CURSA A 1 ạ SÉRIE DO ENSINO MÉDIO EM 2012. Disciplina: matemática
Nome: N.º: endereço: data: telefone: E-mail: Colégio PARA QUEM CURSA A 1 ạ SÉRIE DO ENSINO MÉDIO EM 01 Disciplina: matemática Prova: desafio nota: QUESTÃO 16 (UNESP) O gráfico a seguir apresenta dados
2º. Semestre de 2006 Marcelo Nogueira São José dos Campos - SP
(Exercício 01) Simbolize, no nível proposicional, os seguintes argumentos: (a) Os vencimentos aumentam somente se há inflação. Se há inflação, então o custo de vida aumenta. Os vencimentos não aumentaram.
MATEMÁTICA II. Aula 12. 3º Bimestre. Determinantes Professor Luciano Nóbrega
1 MATEMÁTICA II Aula 12 Determinantes Professor Luciano Nóbrega º Bimestre 2 DETERMINANTES DEFINIÇÃO A toda matriz quadrada está associado um número real ao qual damos o nome de determinante. O determinante
O erro dessa questão foi traduzir o nem como ou não, quando na verdade o correto é traduzir o nem como e não :
Resolução da Prova de Raciocínio Lógico da DPU (Nível Superior) de 2016, aplicada em 24/01/2016. Um estudante de direito, com o objetivo de sistematizar o seu estudo, criou sua própria legenda, na qual
Leis de Kepler. 4. (Epcar (Afa) 2012) A tabela a seguir resume alguns dados sobre dois satélites de Júpiter.
Leis de Kepler 1. (Ufpe 01) Um planeta realiza uma órbita elíptica com uma estrela em um dos focos. Em dois meses, o segmento de reta que liga a estrela ao planeta varre uma área A no plano da órbita do
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Raciocínio Lógico Professor: Custódio Nascimento
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Professor: Custódio Nascimento 1- Análise da prova Análise e Resolução da prova de Agente / PF Neste artigo, farei a análise das questões
Exercícios de Aprofundamento Mat Polinômios e Matrizes
. (Unicamp 05) Considere a matriz A A e A é invertível, então a) a e b. b) a e b 0. c) a 0 e b 0. d) a 0 e b. a 0 A, b onde a e b são números reais. Se. (Espcex (Aman) 05) O polinômio q(x) x x deixa resto
MATEMÁTICA POLINÔMIOS
MATEMÁTICA POLINÔMIOS 1. F.I.Anápolis-GO Seja o polinômio P(x) = x 3 + ax 2 ax + a. O valor de P(1) P(0) é: a) 1 b) a c) 2a d) 2 e) 1 2a 1 2. UFMS Considere o polinômio p(x) = x 3 + mx 20, onde m é um
RACIOCÍNIO LÓGICO Simplif icado
Sérgio Carvalho Weber Campos RACIOCÍNIO LÓGICO Simplif icado Volume 1 2ª edição Revista, atualizada e ampliada Inclui Gráficos, tabelas e outros elementos visuais para melhor aprendizado Exercícios resolvidos
Resolução da Prova de Raciocínio Lógico do STJ de 2015, aplicada em 27/09/2015.
de Raciocínio Lógico do STJ de 20, aplicada em 27/09/20. Raciocínio Lógico p/ STJ Mariana é uma estudante que tem grande apreço pela matemática, apesar de achar essa uma área muito difícil. Sempre que
Lógica Binária. Princípios
Lógica Binária Lógica Binária Proposição é toda a expressão da qual faz sentido dizer que é verdadeira ou falsa. Cada proposição tem um e um só valor lógico, Verdadeiro (1) ou Falso (0). Princípios Princípio
Módulo de Equações do Segundo Grau. Equações do Segundo Grau: Resultados Básicos. Nono Ano
Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Silogística Aristotélica
Silogística Aristotélica Prof. Paulo Margutti Com base na possibilidade de padronizar todas as sentenças de conformidade com os tipos A, E, I e O, Aristóteles considerava que todos os argumentos poderiam
Revisão para a Bimestral 8º ano
Revisão para a Bimestral 8º ano 1- Quadrado da soma de dois termos Observe: (a + b)² = ( a + b). (a + b) = a² + ab+ ab + b² = a² + 2ab + b² Conclusão: (primeiro termo)² + 2.(primeiro termo). (segundo termo)
UM JOGO BINOMIAL 1. INTRODUÇÃO
1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
CEDERJ MÉTODOS DETERMINÍSTICOS 1 - EP4. Prezado Aluno,
CEDERJ MÉTODOS DETERMINÍSTICOS 1 - EP4 Prezado Aluno, Neste EP daremos sequência ao nosso estudo da linguagem da lógica matemática. Aqui veremos o conectivo que causa mais dificuldades para os alunos e
Recorrendo à nossa imaginação podemos tentar escrever números racionais de modo semelhante: 1 2 = 1 + 3 + 32 +
1 Introdução Comecemos esta discussão fixando um número primo p. Dado um número natural m podemos escrevê-lo, de forma única, na base p. Por exemplo, se m = 15 e p = 3 temos m = 0 + 2 3 + 3 2. Podemos
Lista de Exercícios 5: Soluções Teoria dos Conjuntos
UFMG/ICEx/DCC DCC Matemática Discreta Lista de Exercícios 5: Soluções Teoria dos Conjuntos Ciências Exatas & Engenharias 2 o Semestre de 206. Escreva uma negação para a seguinte afirmação: conjuntos A,
Técnicas de Contagem I II III IV V VI
Técnicas de Contagem Exemplo Para a Copa do Mundo 24 países são divididos em seis grupos, com 4 países cada um. Supondo que a escolha do grupo de cada país é feita ao acaso, calcular a probabilidade de
Faculdade de Computação
UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra de Amo Lista de Exercícios n o 2 Revisão de Autômatos 1. Fazer os seguintes exercícios do
3.1. TRANSFORMAÇÕES LINEARES 79
31 TRANSFORMAÇÕES LINEARES 79 Exemplo 317 Mostre que existe uma função T : R R satisfazendo à condição aditiva T (x + y) =T (x)+t (y), x, y R, mas não é uma transformação linear, isto é, T (x) 6= ax, paraalgumx
AULA 1 EQUAÇÕES E SISTEMAS DO 1º GRAU
AULA EQUAÇÕES E SISTEMAS DO º GRAU EQUAÇÕES DO º GRAU Uma equação é classificada como sendo do º grau quando puder ser escrita na forma ax + b 0 onde a e b são reais com a 0. Uma equação do º grau admite
AULA 07 Distribuições Discretas de Probabilidade
1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
Módulo de Princípios Básicos de Contagem. Segundo ano
Módulo de Princípios Básicos de Contagem Combinação Segundo ano Combinação 1 Exercícios Introdutórios Exercício 1. Numa sala há 6 pessoas e cada uma cumprimenta todas as outras pessoas com um único aperto
DISTRIBUIÇÕES ESPECIAIS DE PROBABILIDADE DISCRETAS
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADES 1 1. VARIÁVEIS ALEATÓRIAS Muitas situações cotidianas podem ser usadas como experimento que dão resultados correspondentes a algum valor, e tais situações
a) Quantos estudantes não estudam nenhum desses idiomas? b) Quantos estudantes estudam apenas um desses idiomas?
Conjuntos 1- Conjuntos A, B e C são tais que A possui 10 elementos; A U B, 16 elementos; A U C, 15 elementos; A B, 5 elementos; A C, 2 elementos; B C, 6 elementos; e A B C, 2 elementos. Calcule o número
Aula 03 Proposições e Conectivos. Disciplina: Fundamentos de Lógica e Algoritmos Prof. Bruno Gomes
Aula 03 Proposições e Conectivos Disciplina: Fundamentos de Lógica e Algoritmos Prof. Bruno Gomes Agenda da Aula Proposições: Valores Lógicos; Tipos (simples e compostas). Conectivos. Revisando O que é
RACIOCÍNIO LÓGICO MATEMÁTICO ATIVIDADE DO BLOCO 1 20 QUESTÕES
RACIOCÍNIO LÓGICO MATEMÁTICO ATIVIDADE DO BLOCO 1 20 QUESTÕES As questões foram elaboradas pelo prof. Sérgio Faro e valerão apenas como exercício para o seu conhecimento. São 20 questões de múltipla escolha.
1 O gráfico no plano cartesiano expressa a alta dos preços médios de televisores de tela plana e alta definição, do modelo LCD, full HD, 32
1 O gráfico no plano cartesiano expressa a alta dos preços médios de televisores de tela plana e alta definição, do modelo LCD, full HD, 32 polegadas, antes da Copa do Mundo na África do Sul e sua queda
Resolução da Prova de Raciocínio Lógico do MPOG/ENAP de 2015, aplicada em 30/08/2015.
de Raciocínio Lógico do MPOG/ENAP de 2015, aplicada em 30/08/2015. Considerando a proposição P: Se João se esforçar o bastante, então João conseguirá o que desejar, julgue os itens a seguir. 43 A proposição
Aula 4 Função do 2º Grau
1 Tecnólogo em Construção de Edifícios Aula 4 Função do 2º Grau Professor Luciano Nóbrega GABARITO 46) f(x) = x 2 + x + 1 www.professorlucianonobrega.wordpress.com 2 FUNÇÃO POLINOMIAL DO 2º GRAU Uma função
http://rogerioaraujo.wordpress.com Série Rações Semanais Xpath e XSLT Rogério Araújo
http://rogerioaraujo.wordpress.com Série Rações Semanais Xpath e XSLT Rogério Araújo http://rogerioaraujo.wordpress.com Série Rações Semanais Xpath e XSLT Rogério Araújo Questões A persistência é o menor
ÁLGEBRA. Aula 1 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega. Maria Auxiliadora
1 ÁLGEBRA Aula 1 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega Maria Auxiliadora FUNÇÃO POLINOMIAL DO 2º GRAU 2 Uma função polinomial do 2º grau (ou simplesmente, função do 2º grau) é uma relação
AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO. Matemática. 3ª Série do Ensino Médio Turma 2º bimestre de 2015 Data / / Escola Aluno
AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 3ª Série do Ensino Médio Turma 2º bimestre de 2015 Data / / Escola Aluno Questão 1 O perímetro de um piso retangular de cerâmica mede 14 m e sua área, 12
1 Teoria de conjuntos e lógica
1 Teoria de conjuntos e lógica Estes breves apontamentos dizem respeito à parte do programa dedicada à teoria de conjuntos e à lógica matemática. Embora concebidos sem grandes formalismos e com poucas
Pronomes e quantificadores universais e indefinidos
Pronomes e quantificadores universais e indefinidos Pronomes e quantificadores indefinidos: referem uma pessoa, coisa ou fenómeno de uma forma imprecisa ou indeterminada, indicando quantidade ou diferença.
1. Uma pesquisa de mercado sobre o consumo de três marcas A, B e C de um determinado produto apresentou os seguintes resultados:
1. Uma pesquisa de mercado sobre o consumo de três marcas A, B e C de um determinado produto apresentou os seguintes resultados: A - 48% A e B - 18% B - 45% B e C - 25% C - 50% A e C - 15% nenhuma das
Fundamentos de Lógica Matemática
Webconferência 4-08/03/2012 Técnicas dedutivas Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Objetivos Maneiras
SICEEL. Simpósio de Iniciação Científica da Engenharia Elétrica. Edital de Abertura
EESC - Escola de Engenharia de São Carlos UFSCar - Universidade Federal de São Carlos SICEEL Simpósio de Iniciação Científica da Engenharia Elétrica Edital de Abertura São Carlos, 17 de Agosto de 2015
FÍSICA - 2 o ANO MÓDULO 17 ELETRODINÂMICA: CORRENTE ELÉTRICA, RESISTORES E LEI DE OHM
FÍSICA - 2 o ANO MÓDULO 17 ELETRODINÂMICA: CORRENTE ELÉTRICA, RESISTORES E LEI DE OHM A B FALTA DE CARGAS NEGATIVAS EXCESSO DE CARGAS NEGATIVAS A V A + - B V B U = V A - V B E A B U = V A - V B A + - B
Ló gica. Para Concursos Públicos. Professor Luiz Guilherme
Ló gica Para Concursos Públicos Professor Luiz Guilherme 2014 1 Lógica Para Concursos Públicos Proposição... 2 Valor Lógico das Proposições... 2 Axiomas da Lógica... 2 Tabela Verdade:... 3 Conectivos:...
I. Conjunto Elemento Pertinência
TEORI DOS CONJUNTOS I. Conjunto Elemento Pertinência Conjunto, elemento e pertinência são três noções aceitas sem definição, ou seja, são noções primitivas. idéia de conjunto é praticamente a mesma que
Disciplina: Álgebra Linear - Engenharias ], C = Basta adicionar elemento a elemento de A e B que ocupam a mesma posição na matriz.
![Disciplina: Álgebra Linear - Engenharias ], C = Basta adicionar elemento a elemento de A e B que ocupam a mesma posição na matriz.](/thumbs/41/22311260.jpg "Disciplina: Álgebra Linear - Engenharias ], C = Basta adicionar elemento a elemento de A e B que ocupam a mesma posição na matriz.")
Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear - Engenharias Professor: André Luiz Galdino Gabarito da 1 a Lista de Exercícios 1. Sejam Encontre: [ 1
8 Crie um pequeno sistema para controle automatizado de estoque, com os seguintes registros:
TRABALHO: REGISTROS 8 Crie um pequeno sistema para controle automatizado de estoque, com os seguintes registros: CLIENTES NOTAS ITENS_NOTAS PRODUTOS Cod_cliente Num_NF Num_NF Cod_produto Endereco Cod_cliente
Aula 11: Desvios e Laços
Aula 11: Desvios e Laços Nesta aula explicaremos alguns comandos que podem alterar o fluxo dos seus programas em JavaScript. Você aprenderá a estrutura dos comandos de desvios e laços. Entenderá como funcionam
Aula 03. Processadores. Prof. Ricardo Palma
Aula 03 Processadores Prof. Ricardo Palma Definição O processador é a parte mais fundamental para o funcionamento de um computador. Processadores são circuitos digitais que realizam operações como: cópia
Lógica de Primeira Ordem Quantificadores
Lógica de Primeira Ordem Quantificadores Lógica dos Quantificadores Múltiplos Quantificadores Tradução Referência: Language, Proof and Logic Jon Barwise e John Etchemendy, 1999 Capítulos: 10, 11 1 Tautologias
Regulamento Interno do Departamento de Sistemas de Informação. Escola Superior de Ciências Empresariais Instituto Politécnico de Setúbal
Regulamento Interno do Departamento de Sistemas de Informação Escola Superior de Ciências Empresariais Instituto Politécnico de Setúbal CAPÍTULO I Disposições Gerais (Artigo 1º) Definição O Departamento
Editorial Módulo: Física
1. No gráfico a seguir, está representado o comprimento L de duas barras e em função da temperatura θ. Sabendo-se que as retas que representam os comprimentos da barra e da barra são paralelas, pode-se
Aula 7 Lista de Exercícios de Raízes de Equações Polinomiais
Aula 7 Lista de Exercícios de Raízes de Equações Polinomiais Parte 1 Exercícios do Livro A Matemática do Ensino Médio Volume 3. Autores: Elon Lages Lima, Paulo Cezar Pinto Carvalho, Eduardo Wagner, Augusto
Orientações para Inscrição do Grupo e Projeto de Pesquisa
1 Orientações para Inscrição do Grupo e Projeto de Pesquisa O primeiro passo é criar um login de acesso que será com um e-mail e uma senha única para o grupo. Ao entrar no ambiente de Inscrição e selecionar
Matemática. Resolução das atividades complementares. M3 Conjuntos
Resolução das atividades complementares Matemática M Conjuntos p. (UEMG) Numa escola infantil foram entrevistadas 8 crianças, com faia etária entre e anos, sobre dois filmes, e. Verificou-se que 4 delas
Análise e Projeto Orientado a Objetos. Nazareno Andrade Baseado no material dos profs. Hyggo Almeida e Jacques Sauvé
Análise e Projeto Orientado a Objetos Nazareno Andrade Baseado no material dos profs. Hyggo Almeida e Jacques Sauvé O que veremos hoje? Análise e Projeto Definição Comparação Análise e Projeto OO Definição
AULA 1 INTRODUÇÃO A BANCO DE DADOS E VISÃO GERAL DO SQL CONCEITUANDO BANCO DE DADOS MODELO RELACIONAL
BANCO DE DADOS GERENCIAL 1 AULA 1 INTRODUÇÃO A BANCO DE DADOS E VISÃO GERAL DO SQL CONCEITUANDO BANCO DE DADOS Um banco de dados é uma coleção de dados (ou informações) organizadas de forma lógica, e que
Planejamento - 2. Definição de atividades Sequenciamento das atividades. Mauricio Lyra, PMP
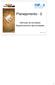Planejamento - 2 Definição de atividades Sequenciamento das atividades 1 6.1 Definir as atividades 1 Lista das atividades A lista das atividades é uma lista abrangente que inclui todas as atividades necessárias
FUNÇÃO DO 2º GRAU PROF. LUIZ CARLOS MOREIRA SANTOS
Questão 01) FUNÇÃO DO º GRAU A função definida por L(x) = x + 800x 35 000, em que x indica a quantidade comercializada, é um modelo matemático para determinar o lucro mensal que uma pequena indústria obtém
Da linha poligonal ao polígono
Polígonos Da linha poligonal ao polígono Uma linha poligonal é formada por segmentos de reta consecutivos, não alinhados. Polígono é uma superfície plana limitada por uma linha poligonal fechada. Dos exemplos
SISTEMAS DE EQUAÇÕES DO 1º GRAU
SISTEMAS DE EQUAÇÕES DO 1º GRAU I INTRODUÇÃO: Os sistemas de equação são ferramentas muito comuns na resolução de problemas em várias áreas ( matemática, química, física, engenharia,...) e aparecem sempre
REGULAMENTO I OLIMPÍADA A PRÁXIS DO SERVIÇO PÚBLICO
REGULAMENTO I OLIMPÍADA A PRÁXIS DO SERVIÇO PÚBLICO 1. Apresentação O Instituto Federal de Educação Ciência e Tecnologia da Paraíba (IFPB), Campus João Pessoa, por meio da Departamento de Gestão e Desenvolvimento
Prova de Matemática 6º Ano do Ensino Fundamental 2/6
Prova de Matemática 6º Ano do Ensino Fundamental 2/6 01. O número decimal 2,385 está compreendido entre ( A ) 2,3905 e 3,0251. ( B ) 2,3754 e 2,3828. ( C ) 2,3805 e 2,3835. ( D ) 2,3799 e 2,3849. ( E )
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Introdução ao. Script. Baltazar Tavares (Psycho Mantys) https://psychomantys.wordpress.com https://about.me/psycho_mantys
Introdução ao Script Baltazar Tavares (Psycho Mantys) https://psychomantys.wordpress.com https://about.me/psycho_mantys O que é Bash Script? O que é Bash + Script? O que é Bash? O que é Bash? Ele é um
GEOMETRIA DO TAXISTA. (a -b )² + (a -b )²
GEOMETRI O TXIST Geometria do Taxista é uma geometria não-euclidiana, no sentido em que a noção de distância não é a mesma e acordo com o desenho abaixo, suponhamos um motorista de táxi que apanha um cliente
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR. Prof. Angelo Augusto Frozza, M.Sc.
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
. B(x 2, y 2 ). A(x 1, y 1 )
Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Questões que animam a discussão e o pensar sobre a relação Universidade-ambiente-sociedade:
2º. Seminário PPGCTIA UFRRJ-UNRC 2º. Seminário PPGCTIA UFRRJ-UNRC Questões que animam a discussão e o pensar sobre a relação Universidade-ambiente-sociedade: Qual o papel da Universidade em sua relação
GEOMETRIA. sólidos geométricos, regiões planas e contornos PRISMAS SÓLIDOS GEOMÉTRICOS REGIÕES PLANAS CONTORNOS
PRISMAS Os prismas são sólidos geométricos muito utilizados na construção civil e indústria. PRISMAS base Os poliedros representados a seguir são denominados prismas. face lateral base Nesses prismas,
NOTAÇÕES. : distância do ponto P à reta r : segmento de extremidades nos pontos A e B
R C i z Rez) Imz) det A tr A : conjunto dos números reais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : parte real do número z C : parte imaginária do número z C
PROJETO ATUALIDADE EM FOCO
Centro Educacional Souza Amorim Jardim Escola Gente Sabida Sistema de Ensino PH Vila da Penha PRODUÇÃO TEXTUAL Nº3 ENTREGA: 17/ 03/ 2016 2º Ano do Ensino Médio Nome do aluno: Professor (a): DISCIPLINA:
Os passos a seguir servirão de guia para utilização da funcionalidade Acordo Financeiro do TOTVS Gestão Financeira.
Acordo Financeiro Produto : RM - Totvs Gestão Financeira 12.1.1 Processo : Acordo Financeiro Subprocesso : Template de Acordo Controle de Alçada Negociação Online Data da publicação : 29 / 10 / 2012 Os
Lista Análise Combinatória
NOME: ANO: 2º Nº: PROFESSOR(A): Ana Luiza Ozores DATA: Lista Análise Combinatória Exercícios básicos 1. Quatro times de futebol (Vasco, Atlético, Corinthians e Internacional) disputam um torneio. Quantas
Princípios e Conceitos de Desenho de Software. Projeto de Sistemas de Software Prof. Rodrigo Ribeiro
Princípios e Conceitos de Desenho de Software Projeto de Sistemas de Software Prof. Rodrigo Ribeiro Revisando... Processo Unificado PRAXIS Processo unificado: Dividido em fases e fluxos Fases Concepção,
Comecemos por relembrar as propriedades das potências: = a x c) a x a y = a x+y
. Cálculo Diferencial em IR.1. Função Exponencial e Função Logarítmica.1.1. Função Exponencial Comecemos por relembrar as propriedades das potências: Propriedades das Potências: Sejam a e b números positivos:
Inglês Prova 21 2016. 3.º Ciclo do Ensino Básico (Decreto-Lei nº17/2016, de 4 de abril) 1. Introdução. 2. Objeto de avaliação
INFORMAÇÃO PROVA DE EQUIVALÊNCIA À FREQUÊNCIA Inglês Prova 21 2016 PROVA ESCRITA E ORAL -----------------------------------------------------------------------------------------------------------------------------------------
SISTEMA DE NUMERAÇÃO NA FORMAÇÃO DO ALUNO UTILIZANDO MATERIAL CONCRETO
1 SISTEMA DE NUMERAÇÃO NA FORMAÇÃO DO ALUNO UTILIZANDO MATERIAL CONCRETO Ariana Oliveira Gomes - ariana_emanuelle@hotmail.com-uesb Christiano Santos Lima Dias - khristiano_dias@hotmail.com-uesb Evaneila
COMENTÁRIO DA PROVA DO BANCO DO BRASIL
COMENTÁRIO DA PROVA DO BANCO DO BRASIL Prezados concurseiros, segue abaixo os comentários das questões de matemática propostas pela CESPE no último concurso para o cargo de escriturário do Banco do Brasil
Construção de tabelas verdades
Construção de tabelas verdades Compreender a Lógica como instrumento da ciência e como estrutura formal do pensamento, conhecendo e compreendendo as operações com os principais conceitos proposicionais
Objetivo do Portal da Gestão Escolar
Antes de Iniciar Ambiente de Produção: É o sistema que contem os dados reais e atuais, é nele que se trabalha no dia a dia. Neste ambiente deve-se evitar fazer testes e alterações de dados sem a certeza
POTENCIAÇÃO, RADICIAÇÃO E LOGARITMAÇÂO NOS NÚMEROS REAIS. Potenciação 1
POTENCIAÇÃO, RADICIAÇÃO E LOGARITMAÇÂO NOS NÚMEROS REAIS Potenciação 1 Neste texto, ao classificarmos diferentes casos de potenciação, vamos sempre supor que a base e o expoente sejam não nulos, pois já
2 Conceitos Básicos. onde essa matriz expressa a aproximação linear local do campo. Definição 2.2 O campo vetorial v gera um fluxo φ : U R 2 R
2 Conceitos Básicos Neste capítulo são apresentados alguns conceitos importantes e necessários para o desenvolvimento do trabalho. São apresentadas as definições de campo vetorial, fluxo e linhas de fluxo.
Conclusões sobre Proposições
Lógica Programação Proposições Conclusões sobre Proposições 1 Duas proposições universais contrárias não podem ser verdadeiras ao mesmo tempo, mas podem ser falsas ao mesmo tempo. 2 Duas proposições particulares