2.3 Aplicações das Leis de Newton
|
|
|
- Rubens Back Garrau
- 8 Há anos
- Visualizações:
Transcrição
1 Aplicações das Leis de Newton Movimento tridimensional de um projétil (se despreza quaisquer efeitos do ar) Nesta seção retomamos a análise do movimento de um projétil, visando a obter algumas características novas da trajetória. Os resultados que já obtivemos serão, agora, generalizados paro o espaço de três dimensões. (Algumas noções envolvendo o movimento de um projétil em duas dimensões já foram consideradas no capítulo anterior.) O estudo do movimento de um projétil é uma das aplicações mais interessantes da Segunda lei de Newton: A força resultante sobre um corpo é igual ao produto da massa do corpo pela aceleração do corpo. Após abandonar a boca do canhão, o projétil fica só em interação com a Terra, e a força F = mg é a única força que atua sobre o corpo. Então a Segunda lei de Newton (2.L.N.) reza: ma = mg (2.3-1) As três componentes escalares desta equação vetorial têm a forma m d 2 x/dt 2 = 0 m d 2 y/dt 2 = -mg (2.3-2) m d 2 z/dt 2 = 0 O vetor da velocidade inicial é dado por v 0 = v 0 cosα i + v 0 senα j + 0 k, onde v 0x = v 0 cosα, v 0y = v 0 senα e v 0z = 0. (j é a direção vertical.) As equações (2.3-2) podem ser integradas para se obter respectivamente v x = v 0x, v y = v 0y - gt, v z = v 0z = 0 Integrando novamente, obtemos as coordenadas do corpo em função do tempo:
2 2.3-2 x = v 0x t, y = v 0y t - gt 2 /2, z = 0 onde as coordenadas iniciais do corpo são zero: x 0 = y 0 = z 0 = 0. x = v 0x t = t v 0 cosα é a componente escalar x do vetor posição r = x i + y j + z k. Para melhorar nosso entendimento do MuPAD, façamos as integrações também com ajuda desse programa: dglx:=ode({x''(t)=0,x(0)=0,x'(0)=v0*cos(a)},x(t)): x:=solve(dglx)[1]// componente escalar x do vetor posição dgly:=ode({y''(t)=-g,y(0)=0,y'(0)=v0*sin(a)},y(t)): y:=solve(dgly)[1]//componente y do vetor posição dglz:=ode({z''(t)=0,z(0)=0,z'(0)=0},z(t)): z:=solve(dglz)[1]//componente z do vetor posição dglvy:=ode({vy'(t)=-g,vy(0)=v0*sin(a)},vy(t)): vy:=solve(dglvy)[1]// componente escalar y do vetor da velocidade Esses resultados mostram que o corpo sempre se mantém no plano- xy, ou seja, a sua trajetória é plana. (O plano-xy coincide com o plano definido por v 0 e a = g.) O resultado v x = v 0x = v 0 cosα mostra que a componente da velocidade na direção x se mantém invariante no tempo, o que é consistente com o que já vimos no capítulo anterior. No entanto, a componente v y da velocidade decresce continuamente até atingir o valor nulo, quando o corpo atinge o ponto mais alto de sua trajetória.
3 2.3-3 O gráfico animado do Programa 4 no capítulo nós havia demonstrado isso com clareza considerável. O tempo necessario para o projétil alcançar o ponto mais alto é obtido pela solução da equação v y = 0: assume (g<>0): vy:=v0*sin(a)-g*t: tsub:=solve(vy=0,t) ts:=tsub[1]//tempo de subida Depois de atingir o ponto mais alto, v y se torna negativa com módulo crescente. A equação da trajetória do projétil é obtida por eliminação do tempo nas duas equações x = v ox t = t v 0 cosα e y = -g t 2 /2+ v 0 t sen(α ). Primeiramente eliminamos t da equação para x, e seguidamente substituímos o resultado na equação para y: tx:=solve(x=t*v0*cos(a),t): y:=-g*t^2/2+t*v0*sin(a): subs(y,t=tx[1]): subs(%,sin(a)=cos(a)*tan(a)) expand(%)
4 2.3-4 Então, obtivemos a equação de uma parábola: y = x tgα - g x 2 /(2 v 0 2 cos 2 α ). (Em MuPAD não é possivel utilizar cos(a) em assume, confira?trig) O tempo gasto para o projétil atingir novamente o nível y = 0, do qual foi atirado, obtemos da equação y(t) = 0. Resultado: t vôo = 2 ts = 2 v 0 senα /g. Com este tempo obtemos para o alcance horizontal a expressão R= t vôo v 0 cosα, o seja: R = 2 v 0 senα /g v 0 cosα = v 0 2 sen(2α )/g Observe que R possui seu valor máximo quando sen(2α )=1, o que corresponde a 2α =90 o ou α = 45 o. Para a altura máxima do percurso obtemos y max = v 0 2 sen 2 (α )/2g. Agora, se o operador do canhão não pretende alcançar a distância máxima de R, o seja R max = v 0 2 /g, ele pode acertar o alvo no ponto (x<r max,0) com dois ângulos de tiro. (A função trigonométrica inversa "arc sen" sempre possui duas soluções possíveis.) Esses dois ângulos possíveis têm sempre uma soma de 90 o. Eles são igualmente afastados de 45 o. Por exemplo, um alvo na distância de 800 m pode ser acertado com um dos dois ângulos que satisfazem a equação R = v 0 2 sen(2α )/g = 800. reset(): g:=9.8:v0:=100: eq:=v0*v0*sin(x)-g*800://x=2 alpha; eq=0 a1:=numeric::fsolve(eq,x=1..pi); op(a1); eval(subs(eq,a1))//deve dar zero [x = ] x = e-14 A função numeric::fsolve determina a solução de uma equação dentro de um certo intervalo a..b. Com eval(subs(eq,a1))podemos controlar a exatidão da solução. A solução x 1 = rad corresponde a 2α 1 = o, o seja, α 1 = 64,19 o.
5 2.3-5 Se utilizarmos o intervalo 0..PI, então a solução será x = , o que nos daria um ângulo de α 2 = 25,81 o. Nota-se que a soma dos dois ângulos é de 90 o, veja a seção No seguinte gráfico traçamos as trajetórias para os ângulos (30 o, 60 o ) e 45 o. As trajetórias com 30 o e 60 o cortam-se no mesmo ponto sobre o eixo x, a trajetória de 45 o é a trajetória com o alcance máximo. Se há traçada também a parábola-limite com a equação y = v 0 2 /2g -gx 2 /2v 0 2, veja mais adiante, na seção Todas as trajetorias possíveis encontram-se debaixo desta parábola-limite. Observe o método elegante que o MuPAD nos oferece para traçar varias curvas na mesma figura! (R = 565,57 m; R max = 653,06 m). reset(): v0:=80: g:=9.8: ya:=x*tan(a)-x*x*g/(2*v0*v0*cos(a)^2): k:=pi/180: alpha:=[30*k,60*k,45*k]: y1:=subs(ya,a=alpha[i])$ i=1..3: y2:=v0*v0/(2*g)-g*x*x/(2*v0*v0): plotfunc2d(y1,y2, x=0..650)
6 2.3-6 Fig Quando o alvo se encontrar num ponto (x 1,y 1 >0), a soma dos ângulos será α 1 + α 2 = π /2 + β, onde o ângulo β é a solução da equação tgβ = y 1 /x 1. Veja um pouco mais adiante, na seção Os ângulos α 1 e α 2 calculamos usando a seguinte (ver 2.3.2): (2.3-3) Exemplo: O alvo tem as coordenadas x 1 = 300m, y 1 = 100m. O canhão atira a bala com v 0 = 80 m/s. g = 9.8 m/s 2. Substituindo estes valores na equação (2.3-3), obtemos tg(α 1 )= e tg(α 2 )= Os ângulos são α 1 = arc tg(α 1 ) = 1,3061 rad = 74,8342 o e α 2 = 0,5864 rad = 33,600 o. A soma dos ângulos é 1,8925 rad e π /2 + β = 1,8925, o seja: α 1 + α 2 = π /2 + β, como haviamos dito mais acima.
7 2.3-7 Aqui você tem tudo isto demonstrado por meio de MuPAD: reset(): v0:=80: g:=9.8:x:=300:y:=100: ya:=x*tan(a)-x*x*g/(2*v0*v0*cos(a)^2): k:=pi/180: b:= arctan(y/x): alpha:=[74.834*k,pi/2+b *k]: y1:=subs(ya,a=alpha[i])$ i=1..2: y2:=v0*v0/(2*g)-g*x*x/(2*v0*v0): plotfunc2d(y1,y2, x=0..350) Fig
8 Com lápis e papel Da equação y = x tgα - g x 2 /(2 v 2 0 cos 2 α ) podemos obter a equação da parábola-limite y = v 2 0 /2g -gx 2 /2v 2 0, isto é, a equação da curva que separa as regiões acessíveis das regiões não acessíveis para o projétil. Para todo valor de x, todos os pontos que estão acima de y = v 2 0 /2g -gx 2 /2v 2 0 são inalcançáveis para a bala tirada do canhão. Para demonstrar a validade desta equação, substituímos na equação y = x tgα - g x 2 /(2 v 2 0 cos 2 α ) o termo cos 2 α por o termo equivalente 1/(1+tg 2 α). Assim fazendo, obtemos a seguinte equação de segundo grau para tg(α): (2.3-4) A solução desta equaçaõ é a equação (2.3-3). Agora, quando o discriminante na raiz quadrada da equação (2.3-3) for negativo, não existem raízes reais e tg(α) é imaginária. Isto quer dizer que não existem ângulos de tiro com v 0 4 /g 2 -x 1 2-2v 0 2 y 1 /g<0. Isso tem uma interpretação física muito conveniente: Os pontos da região acima da curva com y= v 0 2 /2g -gx 2 /2v 0 2 são inalcançáveis -como acabamos de dizer. (Da equação v 0 4 /g 2 -x 2-2v 0 2 y/g=0 podemos extrair y para obter a equação da curvalimite: y= v 0 2 /2g -gx 2 /2v 0 2 ) Falta a demonstração da relação α 1 + α 2 = π /2 +β. Vamos utilizar o teorema de Vieta (relações de Girard) sobre as raízes de uma equação de segundo grau na forma x 2 + px + q = 0: 1. O produto das raízes x 1, x 2 é igual a q 2. A soma das raízes é igual a - p (Essas relações entre raízes e coeficientes podem ser generalizadas para equações de qualquer grau.)
9 2.3-9 Daí temos tg(α 1 ) tg(α 2 ) = 1 + 2v y 1 /gx 1 tg(α 1 ) + tg(α 2 ) = 2v 2 0 /gx 1 Vamos introduzir agora a relação geral: para obter tg(α 1 +α 2 ) = -x 1 /y 1 = -cotg(β ) = tg(π /2+β ), o seja: α 1 + α 2 = π /2 +β. (β é o ângulo de inclinação da reta que passa por o origem (0,0) e por o ponto (x 1, y 1 ), o que quer dizer que o coeficiente angular é m = tg(β ) = y 1 /x 1.) Mais informações sobre gráficos Se você não quer que o MuPAD trace valores negativos, como na figura 2.3-2, então pode usar uma "procedure" (um 'procedimento', veja 2.2, Programa 5) onde se exclui os pontos debaixo do eixo x mediante uma estrutura condicional: if <condição> then <comandoverdade> else <comandofalso> ou em português: se <condição> então <comandoverdade> senão <comandofalso>
10 O programa em linguagem de MuPAD tem a seguinte aparência: reset(): f := proc(x)// procedimento begin v0:=80: a:=pi/6: // (30 o ) y:=x*tan(a)-x^2*9.8/(2*v0^2*cos(a)^2): if float(y)< 0 then hold else y end_if: end_proc: Fig
11 Para fazer uma comparação, o MuPAD pede que um numero seja do tipo ponto flutuante. Na linha if float(y)< 0 then temos a função float que transforma o objeto y num número em ponto flutuante (se a variável a for um número flutuante, por exemplo a:= , poderíamos fazer a comparação sem utilizar a função float, escreveríamos simplesmente if y < 0 then). Tecnicamente, o símbolo < (menor que) é um operador lógico que estamos utilizando para expressar uma condição: se y é menor do que 0, então a linha plot(plot::function2d(f, x = ))não será executada (hold), senão (else) a condição é falsa e o 'procedimento' f desenhará o ponto (y,x). Com o seguinte programa pode-se fazer um gráfico animado em três dimensões de uma bala lançada desde o ponto (0,0,0). (Dê um duplo clique com o botão esquerdo do maus no referencial tridimensional que o MuPAD produz e exibe na tela. O gráfico se deixa também girar: clique com o botão esquerdo do maus nele e mova-o. Observe os muitos botões na barra superior e clique neles. No lado inferior, na direita, você pode conferir as posições da câmara virtual "instalada" no programa de animação: Camera Position X, Y, Z. A função gráfica plot::curve3d([x(t),y(t),z(t)],t=tmin..tmax) permite visualizar curvas parametrizadas num sistema de referência espacial. As equações paramétricas da parábola de tiro no espaço são x = t v 0 cosα cosβ y = t v 0 cosα senβ y = t v 0 senα - gt 2 /2 (2.3-5)
12 Fig reset(): a:=75*pi/180: b:=10*pi/180: g:=9.81: v0:=20: x:=t*v0*cos(a)*cos(b): y:=t*v0*cos(a)*sin(b): z:=t*v0*sin(a)-g*t*t/2: curva:=plot::curve3d([x(t),y(t),z(t)],t=0..u,u=0..4): plot(curva)
13 Para observar a influência do valor de b sobre a trajetória, repetimos o gráfico com dois valores para b. Para b =0 obtemos um movimento no plano-xz. reset(): a:=75*pi/180: b:=20*pi/180: b1:=30*pi/180: g:=9.81: v0:=20: x0:=t*v0*cos(a)*cos(b): y0:=t*v0*cos(a)*sin(b): z0:=t*v0*sin(a)-g*t*t/2: x:=t*v0*cos(a)*cos(b1): y:=t*v0*cos(a)*sin(b1): z:=t*v0*sin(a)-g*t*t/2: curva0:=plot::curve3d([x0(t),y0(t),z0(t)],t=0..4, Color=RGB::Red): curva1:=plot::curve3d([x(t),y(t),z(t)],t=0..4): plot(curva0,curva1)
14 Fig Da forma análoga, podemos variar o valor do ângulo a para observar o seu efeito sobra a forma da trajetória. a:=60*pi/180: b:=20*pi/180: a1:=30*pi/180:// a + a1 = 90! g:=9.81: v0:=50: x0:=t*v0*cos(a)*cos(b): y0:=t*v0*cos(a)*sin(b): z0:=t*v0*sin(a)-g*t*t/2: x:=t*v0*cos(a1)*cos(b): y:=t*v0*cos(a1)*sin(b): z:=t*v0*sin(a1)-g*t*t/2:
15 curva0:=plot::curve3d([x0(t),y0(t),z0(t)],t=0..8.8, Color=RGB::Red): curva1:=plot::curve3d([x(t),y(t),z(t)],t=0..5): plot(curva0,curva1) Fig Curvas e superfícies parametrizadas Nos seguintes problemas vamos falar sobre a parametrização de curvas e superfícies e da representação delas utilizando MuPAD. 1. Descreva o movimento de uma partícula cujas coordenadas no instante t são dadas pelas equações x = cos t, y = sen t. 2. Dê uma parametrização da elipse 4x 2 + 9y 2 =1.
16 Descreva em palavras o movimento dado parametricamente por x = cos t, y = sen t, z = t e trace o gráfico. 4. Ache equações paramétricas para a reta pelo ponto (1,3,5) e paralela ao vetor 3i + 5j + 6k. O parâmetro, que usualmente denotamos por t, possa não ter significado físico. É útil de qualquer forma pensar nele como sendo o tempo. Soluções: 1. Como (cos t) 2 + (sen t) 2 = 1 temos x 2 + y 2 = 1. Isto é, a qualquer tempo t a partícula está num ponto (x,y) em algum lugar no círculo x 2 + y 2 = Como (2x) 2 + (3y) 2 = 1 ajustamos a parametrização do círculo no problema 1. Substituindo x por 2x e y por 3y dá as equações 3x = cos t, 3y = sen t. Assim uma parametrização da elipse é x = cos t/2, y = sen t/3, 0 <= t <= 2π 3. As coordenadas-x e y da partícula são as mesmas que no problema 1, que dá movimento circular no plano-xy, ao passo que a coordenada-z cresce sempre. Assim, a partícula traça uma espiral ascendente, como uma mola. Esta curva chama-se uma hélice. reset(): x:=cos(t): y:=sin(t): z:=t: curva:=plot::curve3d([x(t),y(t),z(t)],t=0..u,u=0..5 *PI): plot(curva)
17 Uma partícula eletricamente carregada sob o efeito de um campo magnético uniforme percorre uma trajetória helicoidal com velocidade de módulo constante. A partícula combina um movimento circular uniforme no plano-xy com uma velocidade também uniforme na direção z. A posição da partícula varia com o tempo na forma r(t) = r cosω t i +r senω t j + v z t k, Onde r, ω e v z são constantes positivas. MuPAD determina os seguintes expressões para velocidade e aceleração em função do tempo: x:=t->r*cos(w*t): y:=t->r*sin(w*t): z:=t->vz*t: pos:=t->(x(t),y(t),z(t)): v:=t->(x'(t),y'(t),z'(t)): a:=t->(x''(t),y''(t),z''(t)): vx:=v(t)[1]; vy:=v(t)[2]; vz:=v(t)[3]; ax:=a(t)[1]; ay:=a(t)[2]; az:=a(t)[3]:
18 A figura mostra a hélice: Fig Imaginemos uma partícula no ponto (1,3,5) no tempo t = 0 e que se move por um deslocamento 3i + 5j + 6k a cada unidade de tempo. Quando t = 0, x = 1 e x cresce por 3 unidades de tempo. Assim no tempo t a coordenada-x da partícula é dada por x = 1 + 3t. Analogamente, a coordenada-y começa em y =3 e cresce numa taxa de 5 unidades para cada unidade de tempo. A coordenada-z começa em z = 5 e cresce por 6 unidades a cada unidade de tempo. Assim as equações paramétricas da reta são x = 1+3t, y = 3+5t, z = 5+6t. Observe que a parametrização de uma reta dada acima expressa as coordenadas x, y, z como funções lineares do parâmetro t. reset(): x:=1+3*t: y:=3+5*t:
19 z:=5+6*t: reta:=plot::curve3d([x(t),y(t),z(t)],t=0..u,u=0..2* PI): plot(reta) Comentário: Acima parametrizamos um círculo no 2-espaço usando as equações x = cos t, y = sen t. No 3-espaço, o mesmo círculo no plano-xy tem equações paramétricas x = cos t, y = sen t, z =0. Acrescentamos a equação z = 0 para especificar que o círculo está no plano-xy. Se quiséssemos um círculo no plano z = 3 usaríamos as equações x = cos t, y = sen t, z = 3 Suponha agora que deixamos z variar livremente, bem como t. Obtemos círculos em cada plano horizontal, formando um cilindro. Assim, precisamos de dois parâmetros, u e v, para parametrizar o cilindro. O MuPAD possui a função plot::surface com a qual podemos traçar facilmente a superfície dum cilindro: reset(): x:=2*cos(u):// r = 2 y:=2*sin(u): z:=v: s := plot::surface([x, y, z], u = 0.. 2*PI, v = ): plot(s, Scaling= Constrained)
20 Fig A representação de uma esfera de raio 1 vemos na seguinte figura A esfera de raio 1 e centro na origem pode ser representada implicitamente pela equação x 2 + y 2 + z 2 =1 ou explicitamente pelas equações ou parametricamente por x = senα cosβ, y = senα senβ, z = cosα 0<=α <= π 0<=β <= 2 π
21 reset(): x:=cos(u)*sin(v): y:=sin(u)*sin(v): z:=cos(v): esfera := plot::surface([x, y, z], u = 0.. 2*PI, v = 0.. PI): plot(esfera, Scaling= Constrained) Fig
3.4 Movimento ao longo de uma curva no espaço (parte segunda)
 3.4-17 3.4 Movimento ao longo de uma curva no espaço (parte segunda) 3.4.4 Mais exemplos sobre curvas no espaço. No parágrafo anterior discutimos os elementos que entram na descrição de uma trajetória
3.4-17 3.4 Movimento ao longo de uma curva no espaço (parte segunda) 3.4.4 Mais exemplos sobre curvas no espaço. No parágrafo anterior discutimos os elementos que entram na descrição de uma trajetória
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
Seja D R. Uma função vetorial r(t) com domínio D é uma correspondência que associa a cada número t em D exatamente um vetor r(t) em R 3
 1 Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire Cálculo Vetorial Texto 01: Funções Vetoriais Até agora nos cursos de Cálculo só tratamos de funções cujas imagens
1 Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire Cálculo Vetorial Texto 01: Funções Vetoriais Até agora nos cursos de Cálculo só tratamos de funções cujas imagens
3.3 Espaço Tridimensional - R 3 - versão α 1 1
 1 3.3 Espaço Tridimensional - R 3 - versão α 1 1 3.3.1 Sistema de Coordenadas Tridimensionais Como vimos no caso do R, para localizar um ponto no plano precisamos de duas informações e assim um ponto P
1 3.3 Espaço Tridimensional - R 3 - versão α 1 1 3.3.1 Sistema de Coordenadas Tridimensionais Como vimos no caso do R, para localizar um ponto no plano precisamos de duas informações e assim um ponto P
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Provas Comentadas OBF/2011
 PROFESSORES: Daniel Paixão, Deric Simão, Edney Melo, Ivan Peixoto, Leonardo Bruno, Rodrigo Lins e Rômulo Mendes COORDENADOR DE ÁREA: Prof. Edney Melo 1. Um foguete de 1000 kg é lançado da superfície da
PROFESSORES: Daniel Paixão, Deric Simão, Edney Melo, Ivan Peixoto, Leonardo Bruno, Rodrigo Lins e Rômulo Mendes COORDENADOR DE ÁREA: Prof. Edney Melo 1. Um foguete de 1000 kg é lançado da superfície da
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar)
 Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
Objetivos. Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas e
 MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
Lista de exercícios nº 2
 F107 Física (Biologia) Turma B Prof. Odilon D. D. Couto Jr. Lista de exercícios nº 2 MOVIMENTO EM UMA DIMENSÃO Exercício 1: A velocidade escalar média é definida como a razão entre a distância total percorrida
F107 Física (Biologia) Turma B Prof. Odilon D. D. Couto Jr. Lista de exercícios nº 2 MOVIMENTO EM UMA DIMENSÃO Exercício 1: A velocidade escalar média é definida como a razão entre a distância total percorrida
Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta
 Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
PROGRAD / COSEAC ENGENHARIAS (CIVIL, DE PRODUÇÃO, MECÂNICA, PETRÓLEO E TELECOMUNICAÇÕES) NITERÓI - GABARITO
 Prova de Conhecimentos Específicos 1 a QUESTÃO: (1,0 ponto) Considere uma transformação linear T(x,y) em que, 5 autovetores de T com relação aos auto valores -1 e 1, respectivamente. e,7 são os Determine
Prova de Conhecimentos Específicos 1 a QUESTÃO: (1,0 ponto) Considere uma transformação linear T(x,y) em que, 5 autovetores de T com relação aos auto valores -1 e 1, respectivamente. e,7 são os Determine
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Resolução da Prova da Escola Naval 2009. Matemática Prova Azul
 Resolução da Prova da Escola Naval 29. Matemática Prova Azul GABARITO D A 2 E 2 E B C 4 D 4 C 5 D 5 A 6 E 6 C 7 B 7 B 8 D 8 E 9 A 9 A C 2 B. Os 6 melhores alunos do Colégio Naval submeteram-se a uma prova
Resolução da Prova da Escola Naval 29. Matemática Prova Azul GABARITO D A 2 E 2 E B C 4 D 4 C 5 D 5 A 6 E 6 C 7 B 7 B 8 D 8 E 9 A 9 A C 2 B. Os 6 melhores alunos do Colégio Naval submeteram-se a uma prova
Hoje estou elétrico!
 A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
Lista 2 - Vetores II. Prof. Edu Física 2. O que é necessário para determinar (caracterizar) uma: a) grandeza escalar? b) grandeza vetorial?
 Lista 2 - Vetores II O que é necessário para determinar (caracterizar) uma: a) grandeza escalar? grandeza vetorial?. Em que consiste a orientação espacial? 2. lassifique os itens abaixo em grandeza escalar
Lista 2 - Vetores II O que é necessário para determinar (caracterizar) uma: a) grandeza escalar? grandeza vetorial?. Em que consiste a orientação espacial? 2. lassifique os itens abaixo em grandeza escalar
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 4
 Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 15
 Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Universidade Federal do Paraná
 Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matematica Prof. Juan Carlos Vila Bravo Curitiba, 1 de Dezembro de 005 1. A posição de uma particula é dada por: r(t) = (sen t)i+(cost)j
Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matematica Prof. Juan Carlos Vila Bravo Curitiba, 1 de Dezembro de 005 1. A posição de uma particula é dada por: r(t) = (sen t)i+(cost)j
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
LISTA DE EXERCÍCIOS DE CAMPOS CONSERVATIVOS NO PLANO E NO ESPAÇO. CURVAS PARAMETRIZADAS, INTEGRAIS DE LINHA (COM RESPEITO A COMPRIMENTO DE ARCO).
 LISTA DE EXERCÍCIOS DE CAMPOS CONSERVATIVOS NO PLANO E NO ESPAÇO. CURVAS PARAMETRIZADAS, INTEGRAIS DE LINHA (COM RESPEITO A COMPRIMENTO DE ARCO. PROFESSOR: RICARDO SÁ EARP OBS: Faça os exercícios sobre
LISTA DE EXERCÍCIOS DE CAMPOS CONSERVATIVOS NO PLANO E NO ESPAÇO. CURVAS PARAMETRIZADAS, INTEGRAIS DE LINHA (COM RESPEITO A COMPRIMENTO DE ARCO. PROFESSOR: RICARDO SÁ EARP OBS: Faça os exercícios sobre
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
2 A Derivada. 2.1 Velocidade Média e Velocidade Instantânea
 2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
Movimento Retilíneo Uniforme (MRU) Equação Horária do MRU
 Movimento Retilíneo Uniforme (MRU) velocímetro do automóvel da figura abaixo marca sempre a mesma velocidade. Quando um móvel possui sempre a mesma velocidade e se movimenta sobre uma reta dizemos que
Movimento Retilíneo Uniforme (MRU) velocímetro do automóvel da figura abaixo marca sempre a mesma velocidade. Quando um móvel possui sempre a mesma velocidade e se movimenta sobre uma reta dizemos que
Vestibular1 A melhor ajuda ao vestibulando na Internet Acesse Agora! www.vestibular1.com.br. Cinemática escalar
 Cinemática escalar A cinemática escalar considera apenas o aspecto escalar das grandezas físicas envolvidas. Ex. A grandeza física velocidade não pode ser definida apenas por seu valor numérico e por sua
Cinemática escalar A cinemática escalar considera apenas o aspecto escalar das grandezas físicas envolvidas. Ex. A grandeza física velocidade não pode ser definida apenas por seu valor numérico e por sua
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
A abordagem do assunto será feita inicialmente explorando uma curva bastante conhecida: a circunferência. Escolheremos como y
 5 Taxa de Variação Neste capítulo faremos uso da derivada para resolver certos tipos de problemas relacionados com algumas aplicações físicas e geométricas. Nessas aplicações nem sempre as funções envolvidas
5 Taxa de Variação Neste capítulo faremos uso da derivada para resolver certos tipos de problemas relacionados com algumas aplicações físicas e geométricas. Nessas aplicações nem sempre as funções envolvidas
a) O tempo total que o paraquedista permaneceu no ar, desde o salto até atingir o solo.
 (MECÂNICA, ÓPTICA, ONDULATÓRIA E MECÂNICA DOS FLUIDOS) 01) Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80 m, antes de abrir o paraquedas. Quando este se abre, ele passa
(MECÂNICA, ÓPTICA, ONDULATÓRIA E MECÂNICA DOS FLUIDOS) 01) Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80 m, antes de abrir o paraquedas. Quando este se abre, ele passa
( ) ( ) ( ( ) ( )) ( )
 Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
A equação da posição em função do tempo t do MRUV - movimento retilíneo uniformemente variado é:
 Modellus Atividade 3 Queda livre. Do alto de duas torres, uma na Terra e outra na Lua, deixaram-se cair duas pedras, sem velocidade inicial. Considerando que cada uma das pedras leva 3,0s atingir o solo
Modellus Atividade 3 Queda livre. Do alto de duas torres, uma na Terra e outra na Lua, deixaram-se cair duas pedras, sem velocidade inicial. Considerando que cada uma das pedras leva 3,0s atingir o solo
OSCILAÇÕES: Movimento Harmônico Simples - M. H. S.
 Por Prof. Alberto Ricardo Präss Adaptado de Física de Carlos Alberto Gianotti e Maria Emília Baltar OSCILAÇÕES: Movimento Harmônico Simples - M. H. S. Todo movimento que se repete em intervelos de tempo
Por Prof. Alberto Ricardo Präss Adaptado de Física de Carlos Alberto Gianotti e Maria Emília Baltar OSCILAÇÕES: Movimento Harmônico Simples - M. H. S. Todo movimento que se repete em intervelos de tempo
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS
 INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
2 Descrição do movimento de um ponto material no espaço e no tempo
 2 Descrição do movimento de um ponto material no espaço e no tempo 2.1. Num instante t i um corpo parte de um ponto x i num movimento de translação a uma dimensão, com módulo da velocidade v i e aceleração
2 Descrição do movimento de um ponto material no espaço e no tempo 2.1. Num instante t i um corpo parte de um ponto x i num movimento de translação a uma dimensão, com módulo da velocidade v i e aceleração
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear
 Exemplos de aplicação das leis de Newton e Conservação do Momento Linear Cálculo de resultante I Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante. F 1 = 10 N 30 F
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear Cálculo de resultante I Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante. F 1 = 10 N 30 F
Exemplos de aceleração Constante 1 D
 Exemplos de aceleração Constante 1 D 1) Dada a equação de movimento de uma partícula em movimento retilíneo, s=-t 3 +3t 2 +2 obtenha: a) A velocidade média entre 1 e 4 segundos; e) A velocidade máxima;
Exemplos de aceleração Constante 1 D 1) Dada a equação de movimento de uma partícula em movimento retilíneo, s=-t 3 +3t 2 +2 obtenha: a) A velocidade média entre 1 e 4 segundos; e) A velocidade máxima;
RESUMO 2 - FÍSICA III
 RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Curso de Engenharia Civil. Física Geral e Experimental I Movimento Prof.a: Msd. Érica Muniz 1 Período
 Curso de Engenharia Civil Física Geral e Experimental I Movimento Prof.a: Msd. Érica Muniz 1 Período Posição e Coordenada de Referência Posição é o lugar no espaço onde se situa o corpo. Imagine três pontos
Curso de Engenharia Civil Física Geral e Experimental I Movimento Prof.a: Msd. Érica Muniz 1 Período Posição e Coordenada de Referência Posição é o lugar no espaço onde se situa o corpo. Imagine três pontos
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2014.2. Cinemática. Isabelle Araújo Engenharia de Produção Myllena Barros Engenharia de Produção
 CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2014.2 Cinemática Isabelle Araújo Engenharia de Produção Myllena Barros Engenharia de Produção Cinemática Na cinemática vamos estudar os movimentos sem
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2014.2 Cinemática Isabelle Araújo Engenharia de Produção Myllena Barros Engenharia de Produção Cinemática Na cinemática vamos estudar os movimentos sem
Estudaremos aqui como essa transformação pode ser entendida a partir do teorema do trabalho-energia.
 ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
CINEMÁTICA - É a parte da mecânica que estuda os vários tipos de movimento, sem se preocupar com as causas destes movimentos.
 INTRODUÇÃO À CINEMÁTICA REPOUSO OU MOVIMENTO? DEPENDE DO REFERENCIAL! CINEMÁTICA - É a parte da mecânica que estuda os vários tipos de movimento, sem se preocupar com as causas destes movimentos. REFERENCIAL.
INTRODUÇÃO À CINEMÁTICA REPOUSO OU MOVIMENTO? DEPENDE DO REFERENCIAL! CINEMÁTICA - É a parte da mecânica que estuda os vários tipos de movimento, sem se preocupar com as causas destes movimentos. REFERENCIAL.
Faculdade de Administração e Negócios de Sergipe
 Faculdade de Administração e Negócios de Sergipe Disciplina: Física Geral e Experimental III Curso: Engenharia de Produção Assunto: Gravitação Prof. Dr. Marcos A. P. Chagas 1. Introdução Na gravitação
Faculdade de Administração e Negócios de Sergipe Disciplina: Física Geral e Experimental III Curso: Engenharia de Produção Assunto: Gravitação Prof. Dr. Marcos A. P. Chagas 1. Introdução Na gravitação
Capítulo 4 Trabalho e Energia
 Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Os conceitos mais básicos dessa matéria são: Deslocamento: Consiste na distância entre dados dois pontos percorrida por um corpo.
 Os conceitos mais básicos dessa matéria são: Cinemática Básica: Deslocamento: Consiste na distância entre dados dois pontos percorrida por um corpo. Velocidade: Consiste na taxa de variação dessa distância
Os conceitos mais básicos dessa matéria são: Cinemática Básica: Deslocamento: Consiste na distância entre dados dois pontos percorrida por um corpo. Velocidade: Consiste na taxa de variação dessa distância
UNIVERSIDADE FEDERAL FLUMINENSE
 UNIVERSIDADE FEDERAL FLUMINENSE Escola de Engenharia Industrial Metalúrgica de Volta Redonda PROVAS RESOLVIDAS DE CÁLCULO VETORIAL Professora Salete Souza de Oliveira Aluna Thais Silva de Araujo P1 Turma
UNIVERSIDADE FEDERAL FLUMINENSE Escola de Engenharia Industrial Metalúrgica de Volta Redonda PROVAS RESOLVIDAS DE CÁLCULO VETORIAL Professora Salete Souza de Oliveira Aluna Thais Silva de Araujo P1 Turma
DINÂMICA. Força Resultante: É a força que produz o mesmo efeito que todas as outras aplicadas a um corpo.
 DINÂMICA Quando se fala em dinâmica de corpos, a imagem que vem à cabeça é a clássica e mitológica de Isaac Newton, lendo seu livro sob uma macieira. Repentinamente, uma maçã cai sobre a sua cabeça. Segundo
DINÂMICA Quando se fala em dinâmica de corpos, a imagem que vem à cabeça é a clássica e mitológica de Isaac Newton, lendo seu livro sob uma macieira. Repentinamente, uma maçã cai sobre a sua cabeça. Segundo
18 a QUESTÃO Valor: 0,25
 6 a A 0 a QUESTÃO FÍSICA 8 a QUESTÃO Valor: 0,25 6 a QUESTÃO Valor: 0,25 Entre as grandezas abaixo, a única conservada nas colisões elásticas, mas não nas inelásticas é o(a): 2Ω 2 V 8Ω 8Ω 2 Ω S R 0 V energia
6 a A 0 a QUESTÃO FÍSICA 8 a QUESTÃO Valor: 0,25 6 a QUESTÃO Valor: 0,25 Entre as grandezas abaixo, a única conservada nas colisões elásticas, mas não nas inelásticas é o(a): 2Ω 2 V 8Ω 8Ω 2 Ω S R 0 V energia
CINEMÁTICA VETORIAL. Observe a trajetória a seguir com origem O.Pode-se considerar P a posição de certo ponto material, em um instante t.
 CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
CPV O cursinho que mais aprova na GV
 O cursinho que mais aprova na GV FGV ADM Objetiva 06/junho/010 MATemática 01. O monitor de um notebook tem formato retangular com a diagonal medindo d. Um lado do retângulo mede 3 do outro. 4 A área do
O cursinho que mais aprova na GV FGV ADM Objetiva 06/junho/010 MATemática 01. O monitor de um notebook tem formato retangular com a diagonal medindo d. Um lado do retângulo mede 3 do outro. 4 A área do
Sumário. Prefácio... xi. Prólogo A Física tira você do sério?... 1. Lei da Ação e Reação... 13
 Sumário Prefácio................................................................. xi Prólogo A Física tira você do sério?........................................... 1 1 Lei da Ação e Reação..................................................
Sumário Prefácio................................................................. xi Prólogo A Física tira você do sério?........................................... 1 1 Lei da Ação e Reação..................................................
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Leis de Conservação. Exemplo: Cubo de gelo de lado 2cm, volume V g. =8cm3, densidade ρ g. = 0,917 g/cm3. Massa do. ρ g = m g. m=ρ.
 Leis de Conservação Em um sistema isolado, se uma grandeza ou propriedade se mantém constante em um intervalo de tempo no qual ocorre um dado processo físico, diz-se que há conservação d a propriedade
Leis de Conservação Em um sistema isolado, se uma grandeza ou propriedade se mantém constante em um intervalo de tempo no qual ocorre um dado processo físico, diz-se que há conservação d a propriedade
NUMEROS COMPLEXOS NA FORMA TRIGONOMÉTRICA
 NUMEROS COMPLEXOS NA FORMA TRIGONOMÉTRICA Na representação trigonométrica, um número complexo z = a + bi é determinado pelo módulo do vetor que o representa e pelo ângulo que faz com o semi-eixo positivo
NUMEROS COMPLEXOS NA FORMA TRIGONOMÉTRICA Na representação trigonométrica, um número complexo z = a + bi é determinado pelo módulo do vetor que o representa e pelo ângulo que faz com o semi-eixo positivo
Exercícios resolvidos P2
 Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA
 CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
Capítulo 1. x > y ou x < y ou x = y
 Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
CÁLCULO: VOLUME III MAURICIO A. VILCHES - MARIA LUIZA CORRÊA. Departamento de Análise - IME UERJ
 CÁLCULO: VOLUME III MAURICIO A. VILCHES - MARIA LUIZA CORRÊA Departamento de Análise - IME UERJ 2 Copyright by Mauricio A. Vilches Todos os direitos reservados Proibida a reprodução parcial ou total 3
CÁLCULO: VOLUME III MAURICIO A. VILCHES - MARIA LUIZA CORRÊA Departamento de Análise - IME UERJ 2 Copyright by Mauricio A. Vilches Todos os direitos reservados Proibida a reprodução parcial ou total 3
Atividade 4 Movimento circular uniforme.
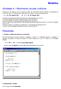 Modellus Atividade 4 Movimento circular uniforme. Amarrou-se uma pedra a um fio e pôs-se a rodar com movimento circular uniforme. As equações do movimento, para um sistemas de coordenadas com origem no
Modellus Atividade 4 Movimento circular uniforme. Amarrou-se uma pedra a um fio e pôs-se a rodar com movimento circular uniforme. As equações do movimento, para um sistemas de coordenadas com origem no
Cap. 4 - Princípios da Dinâmica
 Universidade Federal do Rio de Janeiro Instituto de Física Física I IGM1 2014/1 Cap. 4 - Princípios da Dinâmica e suas Aplicações Prof. Elvis Soares 1 Leis de Newton Primeira Lei de Newton: Um corpo permanece
Universidade Federal do Rio de Janeiro Instituto de Física Física I IGM1 2014/1 Cap. 4 - Princípios da Dinâmica e suas Aplicações Prof. Elvis Soares 1 Leis de Newton Primeira Lei de Newton: Um corpo permanece
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Lista 1 Cinemática em 1D, 2D e 3D
 UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA DEPARTAMENTO DE ESTUDOS BÁSICOS E INSTRUMENTAIS CAMPUS DE ITAPETINGA PROFESSOR: ROBERTO CLAUDINO FERREIRA DISCIPLINA: FÍSICA I Aluno (a): Data: / / NOTA: Lista
UNIVERSIDADE ESTADUAL DO SUDOESTE DA BAHIA DEPARTAMENTO DE ESTUDOS BÁSICOS E INSTRUMENTAIS CAMPUS DE ITAPETINGA PROFESSOR: ROBERTO CLAUDINO FERREIRA DISCIPLINA: FÍSICA I Aluno (a): Data: / / NOTA: Lista
Física Simples e Objetiva Mecânica Cinemática e Dinâmica Professor Paulo Byron. Apresentação
 Apresentação Após lecionar em colégios estaduais e particulares no Estado de São Paulo, notei necessidades no ensino da Física. Como uma matéria experimental não pode despertar o interesse dos alunos?
Apresentação Após lecionar em colégios estaduais e particulares no Estado de São Paulo, notei necessidades no ensino da Física. Como uma matéria experimental não pode despertar o interesse dos alunos?
Soluções das Questões de Física do Processo Seletivo de Admissão à Escola Preparatória de Cadetes do Exército EsPCEx
 Soluções das Questões de Física do Processo Seletivo de dmissão à Escola Preparatória de Cadetes do Exército EsPCEx Questão Concurso 009 Uma partícula O descreve um movimento retilíneo uniforme e está
Soluções das Questões de Física do Processo Seletivo de dmissão à Escola Preparatória de Cadetes do Exército EsPCEx Questão Concurso 009 Uma partícula O descreve um movimento retilíneo uniforme e está
MOVIMENTOS VERTICAIS NO VÁCUO
 MOVIMENTOS VERTICAIS NO VÁCUO MOVIMENTOS VERTICAIS NO VÁCUO 4.1 - INTRODUÇÃO Desde a antigüidade o estudo dos movimentos verticais era de grande importância para alguns cientistas conceituados, este era
MOVIMENTOS VERTICAIS NO VÁCUO MOVIMENTOS VERTICAIS NO VÁCUO 4.1 - INTRODUÇÃO Desde a antigüidade o estudo dos movimentos verticais era de grande importância para alguns cientistas conceituados, este era
REFLEXÃO DA LUZ: ESPELHOS 412EE TEORIA
 1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
Prof. André Motta - mottabip@hotmail.com_ 4.O gráfico apresentado mostra a elongação em função do tempo para um movimento harmônico simples.
 Eercícios Movimento Harmônico Simples - MHS 1.Um movimento harmônico simples é descrito pela função = 7 cos(4 t + ), em unidades de Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades
Eercícios Movimento Harmônico Simples - MHS 1.Um movimento harmônico simples é descrito pela função = 7 cos(4 t + ), em unidades de Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades
sendo as componentes dadas em unidades arbitrárias. Determine: a) o vetor vetores, b) o produto escalar e c) o produto vetorial.
 INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
3.4 Movimento ao longo de uma curva no espaço (terça parte)
 3.4-41 3.4 Movimento ao longo de uma curva no espaço (terça parte) Antes de começar com a nova matéria, vamos considerar um problema sobre o material recentemente visto. Problema: (Projeção de uma trajetória
3.4-41 3.4 Movimento ao longo de uma curva no espaço (terça parte) Antes de começar com a nova matéria, vamos considerar um problema sobre o material recentemente visto. Problema: (Projeção de uma trajetória
FUNÇÃO DO 1º GRAU. Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência:
 FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Universidade Federal de Viçosa Departamento de Matemática 3 a Lista de exercícios de Cálculo III - MAT 241
 Universidade Federal de Viçosa Departamento de Matemática a Lista de exercícios de Cálculo III - MAT 41 1. Calcule, se existirem, as derivadas parciais f f (0, 0) e (0, 0) sendo: x + 4 (a) f(x, ) = x,
Universidade Federal de Viçosa Departamento de Matemática a Lista de exercícios de Cálculo III - MAT 41 1. Calcule, se existirem, as derivadas parciais f f (0, 0) e (0, 0) sendo: x + 4 (a) f(x, ) = x,
Correlação e Regressão Linear
 Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
PROBLEMAS DE OTIMIZAÇÃO
 (Tóp. Teto Complementar) PROBLEMAS DE OTIMIZAÇÃO 1 PROBLEMAS DE OTIMIZAÇÃO Este teto estuda um grupo de problemas, conhecido como problemas de otimização, em tais problemas, quando possuem soluções, é
(Tóp. Teto Complementar) PROBLEMAS DE OTIMIZAÇÃO 1 PROBLEMAS DE OTIMIZAÇÃO Este teto estuda um grupo de problemas, conhecido como problemas de otimização, em tais problemas, quando possuem soluções, é
Unidade: Vetores e Forças. Unidade I:
 Unidade I: 0 Unidade: Vetores e Forças 2.VETORES 2.1 Introdução Os vetores são definidos como entes matemáticos que dão noção de intensidade, direção e sentido. De forma prática, o conceito de vetor pode
Unidade I: 0 Unidade: Vetores e Forças 2.VETORES 2.1 Introdução Os vetores são definidos como entes matemáticos que dão noção de intensidade, direção e sentido. De forma prática, o conceito de vetor pode
LANÇAMENTO OBLÍQUO (PROF. VADO)
 LANÇAMENTO OBLÍQUO (PROF. VADO) 01) PUCSP- Suponha que em uma partida de futebol, o goleiro, ao bater o tiro de meta, chuta a bola, imprimindo-lhe uma velocidade V 0 cujo vetor forma, com a horizontal,
LANÇAMENTO OBLÍQUO (PROF. VADO) 01) PUCSP- Suponha que em uma partida de futebol, o goleiro, ao bater o tiro de meta, chuta a bola, imprimindo-lhe uma velocidade V 0 cujo vetor forma, com a horizontal,
Rotação de Espelhos Planos
 Rotação de Espelhos Planos Introdução Um assunto que costuma aparecer em provas, isoladamente ou como parte de um exercício envolvendo outros tópicos, é a rotação de espelhos planos. Neste artigo, exploraremos
Rotação de Espelhos Planos Introdução Um assunto que costuma aparecer em provas, isoladamente ou como parte de um exercício envolvendo outros tópicos, é a rotação de espelhos planos. Neste artigo, exploraremos
Movimentos Periódicos: representação vetorial
 Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Professora Bruna. Caderno 13 Aula 28. Quem atinge o solo primeiro? Página 291
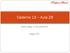 Caderno 13 Aula 28 Quem atinge o solo primeiro? Página 291 Quem atinge o solo primeiro? Vimos na aula anterior, que o tempo de queda para um corpo lançado horizontalmente não depende da sua velocidade
Caderno 13 Aula 28 Quem atinge o solo primeiro? Página 291 Quem atinge o solo primeiro? Vimos na aula anterior, que o tempo de queda para um corpo lançado horizontalmente não depende da sua velocidade
Funções algébricas do 1º grau. Maurício Bezerra Bandeira Junior
 Maurício Bezerra Bandeira Junior Definição Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados
Maurício Bezerra Bandeira Junior Definição Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados
Uma lei que associa mais de um valor y a um valor x é uma relação, mas não uma função. O contrário é verdadeiro (isto é, toda função é uma relação).
 5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
FUNÇÃO REAL DE UMA VARIÁVEL REAL
 Hewlett-Packard FUNÇÃO REAL DE UMA VARIÁVEL REAL Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luís Ano: 2015 Sumário INTRODUÇÃO AO PLANO CARTESIANO... 2 PRODUTO CARTESIANO... 2 Número de elementos
Hewlett-Packard FUNÇÃO REAL DE UMA VARIÁVEL REAL Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luís Ano: 2015 Sumário INTRODUÇÃO AO PLANO CARTESIANO... 2 PRODUTO CARTESIANO... 2 Número de elementos
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
LENTES E ESPELHOS. O tipo e a posição da imagem de um objeto, formada por um espelho esférico de pequena abertura, é determinada pela equação
 LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
A função do primeiro grau
 Módulo 1 Unidade 9 A função do primeiro grau Para início de conversa... Já abordamos anteriormente o conceito de função. Mas, a fim de facilitar e aprofundar o seu entendimento, vamos estudar algumas funções
Módulo 1 Unidade 9 A função do primeiro grau Para início de conversa... Já abordamos anteriormente o conceito de função. Mas, a fim de facilitar e aprofundar o seu entendimento, vamos estudar algumas funções
grandeza do número de elétrons de condução que atravessam uma seção transversal do fio em segundos na forma, qual o valor de?
 Física 01. Um fio metálico e cilíndrico é percorrido por uma corrente elétrica constante de. Considere o módulo da carga do elétron igual a. Expressando a ordem de grandeza do número de elétrons de condução
Física 01. Um fio metálico e cilíndrico é percorrido por uma corrente elétrica constante de. Considere o módulo da carga do elétron igual a. Expressando a ordem de grandeza do número de elétrons de condução
Vetores. Definição geométrica de vetores
 Vetores Várias grandezas físicas, tais como por exemplo comprimento, área, olume, tempo, massa e temperatura são completamente descritas uma ez que a magnitude (intensidade) é dada. Tais grandezas são
Vetores Várias grandezas físicas, tais como por exemplo comprimento, área, olume, tempo, massa e temperatura são completamente descritas uma ez que a magnitude (intensidade) é dada. Tais grandezas são
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista.
 Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista. Plantão de Atendimento Horário: terças e quintas-feiras das 14:00 às 16:00. MSN:
Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista. Plantão de Atendimento Horário: terças e quintas-feiras das 14:00 às 16:00. MSN:
Texto 07 - Sistemas de Partículas. A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica.
 Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Profa. Dra. Diana Andrade & Prof. Dr. Sergio Pilling Parte 1 - Movimento Retilíneo Coordenada de posição, trajetória,
Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Profa. Dra. Diana Andrade & Prof. Dr. Sergio Pilling Parte 1 - Movimento Retilíneo Coordenada de posição, trajetória,
São grandezas que para que a gente possa descrever 100%, basta dizer um número e a sua unidade.
 Apostila de Vetores 1 INTRODUÇÃO Fala, galera! Essa é a primeira apostila do conteúdo de Física I. Os assuntos cobrados nas P1s são: Vetores, Cinemática Uni e Bidimensional, Leis de Newton, Conservação
Apostila de Vetores 1 INTRODUÇÃO Fala, galera! Essa é a primeira apostila do conteúdo de Física I. Os assuntos cobrados nas P1s são: Vetores, Cinemática Uni e Bidimensional, Leis de Newton, Conservação
Prof. Rogério Porto. Assunto: Cinemática em uma Dimensão II
 Questões COVEST Física Mecânica Prof. Rogério Porto Assunto: Cinemática em uma Dimensão II 1. Um carro está viajando numa estrada retilínea com velocidade de 72 km/h. Vendo adiante um congestionamento
Questões COVEST Física Mecânica Prof. Rogério Porto Assunto: Cinemática em uma Dimensão II 1. Um carro está viajando numa estrada retilínea com velocidade de 72 km/h. Vendo adiante um congestionamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
4.1A Esboce o grá co de cada curva dada abaixo, indicando a orientação positiva. cos (1=t), para 0 < t 1 e y 0 (0) = 0. Sendo esta derivada
 4.1 Curvas Regulares 4.1A Esboce o grá co de cada curva dada abaixo, indicando a orientação positiva. (a) ~r (t) = t~i + (1 t)~j; 0 t 1 (b) ~r (t) = 2t~i + t 2 ~j; 1 t 0 (c) ~r (t) = (1=t)~i + t~j; 1 t
4.1 Curvas Regulares 4.1A Esboce o grá co de cada curva dada abaixo, indicando a orientação positiva. (a) ~r (t) = t~i + (1 t)~j; 0 t 1 (b) ~r (t) = 2t~i + t 2 ~j; 1 t 0 (c) ~r (t) = (1=t)~i + t~j; 1 t
