Biofísica II Turma de Biologia FFCLRP USP Prof. Antônio Roque Biologia de Populações 1 Modelo malthusiano O Modelo Malthusiano
|
|
|
- João Gabriel Taveira Canedo
- 7 Há anos
- Visualizações:
Transcrição
1 O Modelo Malthusiano Para começar nosso estudo de modelos matemáticos para populações, vamos estudar o modelo mais simples para mudanças no tamanho de uma população, que chamaremos de modelo malthusiano. Quando estudamos o tamanho N de uma população de organismos, estamos interessados em acompanhar o seu valor a intervalos de tempo iguais. Portanto, precisamos definir uma unidade de tempo. Dependendo do organismo essa unidade pode ser uma hora, um dia, um mês, um ano, etc. Para nós aqui ela será apenas indicada como unidade de tempo. Para acompanhar a mudança do tamanho da população ao longo do tempo usa-se a quantidade denotada por ΔN, que é um símbolo matemático para indicar a variação no número de indivíduos (N) da população ao final de uma unidade de tempo.
2 Se ao final de uma unidade de tempo a população cresceu ΔN será positiva, e se a população diminuiu ΔN será negativa. Note que estamos nos referindo a ΔN como a variação no tamanho N da população a uma dada unidade de tempo (um dia, mês, etc). Portanto, ΔN exprime uma taxa de variação e é medida em unidades de número de indivíduos por unidade de tempo. Para começar a modelar a variação no tamanho de uma população, deve-se primeiro modelar os fatores que causam essa variação. Uma hipótese comum é a de que a taxa de crescimento é dada pela diferença entre a taxa de adição de indivíduos devida a nascimentos e imigrações e a taxa de subtração de indivíduos devida a mortes e emigrações. Pode-se expressar essa hipótese de maneira concisa usando a fórmula matemática,
3 Δ N = B + onde B, I, D e E representam, respectivamente, as taxas de nascimentos, imigrações, mortes e emigrações por unidade de tempo. I D E, A razão pela escolha das letras vem da língua inglesa (births, immigrations, deaths e emigrations). Para progredir na análise de um modelo, costuma ser útil fazer alguns dos fatores constantes, ou eliminá-los completamente para se estudar o efeito dos fatores restantes. Usando esse método, pode-se fazer a hipótese de que a população está isolada do mundo exterior, de maneira que I = 0 e E = 0. Por exemplo, pense em uma população de insetos criada em um ambiente fechado em laboratório. Uma simplificação como essa é comum na construção de modelos matemáticos.
4 A omissão de certos detalhes em um modelo matemático não significa que eles não são importantes. A ideia é desconsiderar esses detalhes numa primeira versão do modelo para ver até onde se consegue chegar sem eles. Muitas vezes se consegue explicar muitos fenômenos observados sem considerar todos os detalhes reais de um sistema biológico. Posteriormente, depois que o modelo simples sem os detalhes foi bem entendido, os detalhes deixados de lado são incluídos para ver o que eles trazem de novo ao modelo. Para fazer uma analogia, podemos encarar um modelo com suas simplificações como um experimento controlado em que certos fatores considerados importantes pelo experimentador são eliminados ou têm sua influência reduzida no experimento, devido ao seu desenho, para que outros fatores possam ser estudados sem sofrer interferências.
5 Para continuar com a construção do modelo malthusiano, notemos que as quantidades de nascimentos e de mortes em um dado intervalo de tempo dependem do número de indivíduos na população. Quanto mais organismos houver, maiores serão os números de indivíduos que nascem e morrem. Uma maneira de reescrever a equação do modelo de modo a deixar isso explícito é usando as taxas médias de nascimentos e mortes por unidade de tempo por indivíduo da população. Elas são definidas como: e B número total de nascimentos por unidade de tempo b = = N número total de indivíduos D número total de mortes por unidade de tempo d = = N número total de indivíduos. As variáveis b e d costumam ser usadas na prática para caracterizar as taxas de nascimentos e de mortes das populações.
6 Elas são chamadas, respectivamente, de taxas de nascimento e de mortes per capita. Note que, pelas suas próprias definições, b e d devem satisfazer as condições: b 0; 0 d 1. Pense um pouco e responda, porque b pode ser maior que 1, mas d não pode? E porque os dois não podem ser menores que zero? Usando um dia como unidade de tempo, faça uma pesquisa e encontre valores típicos de b e d para elefantes, peixes, insetos e bactérias. A partir das definições de b e d podemos escrever as variáveis B e D que aparecem na equação do modelo malthusiano como, B = bn e D = dn, de maneira que a equação do modelo pode ser reescrita como
7 Δ N onde fizemos I = E = 0. = bn dn, Essa equação ainda pode ser reescrita na forma, Δ N = ( b d) N. O termo (b d) é tão importante em biologia de populações que recebe um nome e um símbolo específicos. Ele é chamado de taxa de crescimento geométrico e é denotado por R (a razão do nome geométrico será esclarecida mais tarde): R b d. Portanto, podemos escrever a equação do modelo malthusiano como, Δ N = RN. O que essa equação diz é que, dado um valor atual para a população N e taxas de fecundidade e de mortalidade per capita b e d, podemos prever a variação na população ΔN após uma unidade de tempo.
8 Por exemplo, se N = 1000, b = 0,2 e d = 0,05, a mudança no valor da população após uma unidade de tempo será: ( 0,2 0, ) = 150 ΔN =. Portanto, a população no começo da próxima unidade de tempo será N + ΔN = = Vamos passar a utilizar uma outra notação para tornar as coisas mais simples. Vamos definir: N t = N(t) = tamanho da população no instante de tempo t, de maneira que, ΔN t = N t+1 N t. Com esta nova notação podemos reescrever a equação do modelo malthusiano como ou Δ N t = RN t Nt 1 Nt = RNt Nt+ 1, = N + RN + t t ( 1 ) N. N t + 1 = + R t
9 A quantidade (1+R) também recebe o seu próprio símbolo (λ) e nome, taxa finita de crescimento: λ 1+ R = 1+ b d. A razão para o nome finita também será vista mais tarde. Finalmente, o modelo malthusiano pode agora ser sintetizado pela expressão, N = λn. t+ 1 t (1) Para os valores N 0 = 1000, b = 0,2 e d = 0,05 usados anteriormente, esta equação nos dá: N = 1,15N, N = 1000 t+ 1 t 0. A equação (1), que relaciona N t+1 com N t é de um tipo chamado em matemática de equação de diferenças finitas. Ela nos diz que: O próximo valor de N é igual a λ vezes o valor atual de N.
10 Para a equação (1) ser resolvida, é preciso saber qual o valor de N no instante em que se começa a contar o tempo (o instante inicial). A equação que dá o valor de N 0 é chamada de condição inicial. Aplicando-se a equação do modelo malthusiano várias vezes a partir do instante inicial, pode-se deduzir uma expressão que relaciona o valor de N para qualquer instante t no futuro em função do valor de N no instante inicial: N 1 = λn 0 ; N 2 = λn 1 = λ(λn 0 ) = λ 2 N 0 ; N 3 = λn 2 = λ[λ 2 N 0 ] = λ 3 N 0 ;... N t = λ t N 0. Note que esta é a equação de uma progressão geométrica (PG) de razão λ. É por isso que a quantidade R = b d foi chamada de taxa de crescimento geométrico.
11 O modelo construído prediz que a variação da população ocorre segundo uma progressão geométrica. O modelo é chamado de malthusiano porque está associado ao nome de Thomas Malthus ( ), reverendo inglês que propôs esse modelo para o crescimento da população humana. Dados valores numéricos para λ e N 0, pode-se usar a equação acima para calcular os vários valores de N para todos os instantes de tempo no futuro que sejam múltiplos da unidade de tempo. Por exemplo, para os valores do nosso exemplo (λ = 1,15 e N 0 = 1000): Tempo População
12 Note que os valores de N foram arredondados para não terem casas decimais, pois o tamanho de uma população (número de indivíduos) só pode ser um número inteiro. Os valores da tabela acima podem ser colocados em um gráfico, o que permite uma visualização da maneira como ocorre o crescimento geométrico da população. Modelo Malthusiano (Geométrico) Tamanho da População Tempo (t)
13 Modelo Malthusiano: Exemplo 1 Suponha que uma certa espécie de inseto tenha um ciclo de vida muito rígido: cada fêmea põe 200 ovos e depois todas as fêmeas adultas morrem. Após a chocagem dos ovos, apenas 3% sobrevivem para se tornar fêmeas adultas, sendo que o resto morre ou são machos. Para escrever uma equação de diferenças finitas para a população de fêmeas, vamos medir t em gerações. Pelos dados do exemplo, a taxa de mortalidade de fêmeas é d = 1 (todas as fêmeas morrem ao final de uma unidade de tempo), enquanto que a taxa de fecundidade per capita de fêmeas é b = 0,03(200) = 6. Logo, a nossa equação será: ( 1+ b d) N = ( ) N 6N. N = = t+ 1 t t t Pergunta: Segundo o modelo, a população vai crescer ou diminuir com o tempo?
14 Para responder à pergunta, devemos analisar o valor do parâmetro λ (a taxa finita de crescimento). No nosso caso, λ = 6. Observando a equação, notamos que podem haver três tipos de comportamentos diferentes para a solução da equação, dependendo do valor de λ: Decaimento: Se 0 < λ < 1 N t+1 < N t. Isto quer dizer que o tamanho da população a cada geração será menor que o tamanho da população na geração anterior. A população diminui com o tempo. O gráfico abaixo mostra um exemplo disso para o caso em que λ = 0,9 e N 0 = Exemplo: lambda = 0, N t
15 Note que eventualmente o valor de N t chega a zero, indicando que a população torna-se extinta. Crescimento: Se λ > 1 N t+1 > N t. Isto quer dizer que o tamanho da população a cada geração será maior que o tamanho da população na geração anterior. A população aumenta com o tempo. O gráfico abaixo mostra um exemplo disso para o caso em que λ = 1,1 e N 0 = Exemplo: lambda = 1, N t
16 Note que o tamanho da população cresce sem limite de geração para geração. Dizemos que o tamanho da população explode em direção ao infinito ( ). Estado Estacionário: Quando λ = 1 N t+1 = N t. Isto quer dizer que o tamanho da população permanece constante a cada geração. Esta é uma solução muito particular da nossa equação, pois ocorre apenas para um único e exato valor de λ, enquanto que os outros dois tipos de solução (decaimento e crescimento) podem ocorrer para uma faixa de valores de λ. O gráfico abaixo mostra um exemplo disso para o caso em que λ = 1 e N 0 = Exemplo: lambda = N t
17 Este tipo de comportamento em que o tamanho da população permanece constante ao longo do tempo é chamado de estado estacionário. Agora podemos responder à pergunta. Como no caso do exemplo λ = 6, que é um número maior que zero, a população cresce. Podemos ver isso pelo gráfico a seguir, onde λ = 6 e N 0 = Exemplo: lambda = 6 N t Observe que neste caso, como λ = 6 é bem maior do que 1, a explosão em direção ao infinito acontece de maneira bem mais rápida do que no exemplo anterior.
18 Note que a própria escala do eixo vertical (eixo-y) teve que ser alterada para que fosse possível visualizar alguns pontos do gráfico (o valor inicial N 0 = 1000 nem é visível na escala do gráfico, confundido-se com zero). É por isso que é conveniente usar escalas logarítmicas para representar graficamente funções que variam por muitas ordens de grandeza. Transformando a escala do eixo-y para logarítmica, o gráfico do nosso exemplo fica como abaixo:
19 Pergunta: Qual é a condição para que a população permaneça no estado estacionário? O estado estacionário é a situação em que o tamanho de população permanece constante ao longo das gerações. Vimos acima que ele só ocorre para um único valor de λ, que é λ = 1. Temos que, λ = 1+ b d = 1 b d = 0 b = d. Portanto, a condição para que exista um estado estacionário na população de fêmeas é a de que as taxas de fecundidade e de mortalidade per capita de fêmeas sejam iguais. Você deve estar se perguntando por que os machos foram ignorados neste modelo. Isto é um exemplo de simplificação de um modelo, conforme mencionado nas aulas passadas.
20 A hipótese implícita nesta simplificação é a de que, para essa espécie de insetos, o número exato de machos tem pouco efeito sobre o crescimento da população. Pode ser que se saiba que o número de machos seja sempre aproximadamente igual ao número de fêmeas, de maneira que basta conhecer o número de fêmeas para se ter a população total (2x o número de fêmeas). Ou pode ser que pouco importa se o tamanho da população de machos é maior ou menor do que o tamanho da população de fêmeas, desde que se saiba que o número de machos é sempre suficiente para manter a população de fêmeas se reproduzindo do mesmo jeito. Tanto num caso como no outro, a população de fêmeas é que é importante para se determinar o comportamento de longo termo da população de insetos.
21 Você também poderia perguntar por que o modelo não leva em consideração outros fatores que afetam a população de insetos. Por exemplo, pássaros comem insetos e, portanto, a população de insetos deve depender do tamanho da população de pássaros. E a população de pássaros, por sua vez, depende de uma série de outros fatores do ecossistema. Se quiséssemos fazer um modelo que considerasse todos os possíveis fatores que afetam a população de insetos, muito provavelmente não conseguiríamos ir muito longe. Portanto, decidiu-se começar por este modelo simplificado em que o tamanho da população de fêmeas em uma geração t + 1 depende apenas do tamanho da população de fêmeas na geração t.
22 Agora que já vimos um exemplo de uma equação de diferenças finitas, podemos tentar definir de uma maneira matematicamente mais rigorosa o que é uma equação de diferenças finitas. Uma equação de diferenças finitas é uma fórmula que expressa valores de alguma quantidade Q em termos de valores anteriores de Q, sendo que o tempo é medido em intervalos discretos (isto é, pulando de uma unidade em uma unidade, por exemplo, 1 dia, 2 dias etc). Uma equação de diferenças finitas pode ser escrita como, Q = f ( Q ), t+ 1 t onde f(x) é uma função qualquer. Q t costuma ser chamado de estado do sistema no instante t e a evolução temporal de Q t, isto é, a maneira como ele varia no tempo é chamada de dinâmica do sistema.
23 No caso do modelo malthusiano, N = λn t+ 1 t a função f(x) é uma função linear:, f ( x) = λx. Por causa disso, o modelo malthusiano de modelo linear. Se a função f(x) não fosse linear, por exemplo, uma função quadrática, f ( x) = λx 2, de maneira que, N = λ 2 ( N ), t+ 1 t teríamos um modelo não-linear. Este é um ponto para tomar cuidado: embora a solução do modelo malthusiano seja uma progressão geométrica (um crescimento exponencial), o modelo é chamado de linear, por causa da forma da equação.
24 Quando se usa equações de diferenças finitas para modelar sistemas naturais, em geral há dois problemas com os quais temos que nos deparar: (1) Como encontrar uma equação de diferenças finitas apropriada para modelar uma dada situação? Em geral, aprende-se a modelar com equações de diferenças finitas pelo estudo de modelos desse tipo desenvolvidos por outros. Mesmo assim, quando se tem que encarar um problema completamente novo costuma ser difícil encontrar um bom conjunto de equações de diferenças finitas para modelá-lo. (2) Como fazer para entender os resultados fornecidos por um modelo de equações de diferenças finitas? Isto também não é uma tarefa fácil e, em geral, não se consegue encontrar uma solução para as equações do modelo de forma explícita como no caso do modelo malthusiano. Em geral, o que se consegue fazer é organizar as possíveis soluções em classes com comportamentos típicos. Isso é uma espécie de taxonomia das soluções das equações do modelo.
25 Por exemplo, no exemplo desta aula vimos que o modelo malthusiano possui três tipos diferentes de soluções possíveis: decaimento, crescimento e estado estacionário. Vimos também que o que determina se o comportamento da solução vai ser de um tipo ou de outro é o valor do parâmetro λ: Se λ < 1 teremos um decaimento, se λ = 1 teremos um estado estacionário, e se λ > 1 teremos um crescimento. Portanto, mesmo que não fosse possível obter uma forma explícita para N t+1 em função de N t, o conhecimento do valor de λ já seria suficiente para que se pudesse ter uma idéia qualitativa de como a população de fêmeas se comportará ao longo do tempo, o que muitas vezes já é um conhecimento muito útil. Dizemos que esse tipo de conhecimento corresponde a um estudo qualitativo das soluções do modelo e existe todo um campo da matemática dedicado ao estudo qualitativo das soluções de equações.
26
O Modelo Malthusiano modelo malthusiano
 O Modelo Malthusiano Para começar nosso estudo de modelos matemáticos para populações, vamos estudar o modelo mais simples para mudanças no tamanho de uma população, que chamaremos de modelo malthusiano.
O Modelo Malthusiano Para começar nosso estudo de modelos matemáticos para populações, vamos estudar o modelo mais simples para mudanças no tamanho de uma população, que chamaremos de modelo malthusiano.
BIE Ecologia de Populações
 - Ecologia de Populações Roberto André Kraenkel http://www.ift.unesp.br/users/kraenkel Apontamentos de Cálculo e Integral Parte III Sumário 1 Sumário 1 2 Sumário 1 2 3 Sumário 1 2 3 4 Sumário 1 2 3 4 5
- Ecologia de Populações Roberto André Kraenkel http://www.ift.unesp.br/users/kraenkel Apontamentos de Cálculo e Integral Parte III Sumário 1 Sumário 1 2 Sumário 1 2 3 Sumário 1 2 3 4 Sumário 1 2 3 4 5
Escrita correta de resultados em notação
 Notas de Aula Laboratório de Física 1 e A Escrita correta de resultados em notação científica e confecção de gráficos 1 Prof. Alexandre A. C Cotta 1 Departamento de Física, Universidade Federal de Lavras,
Notas de Aula Laboratório de Física 1 e A Escrita correta de resultados em notação científica e confecção de gráficos 1 Prof. Alexandre A. C Cotta 1 Departamento de Física, Universidade Federal de Lavras,
Biomatemática - Prof. Marcos Vinícius Carneiro Vital (ICBS UFAL) - Material disponível no endereço
 Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-3 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Começando pelos exemplos. - Existem vários exemplos reais de situações
Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-3 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Começando pelos exemplos. - Existem vários exemplos reais de situações
2.1 Visualizando - Visualize um gráfico com uma função linear, y = ax + b - Neste caso, a taxa de crescimento é o valor de a, já que sabemos que:
 1. O que é uma taxa? Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Em poucas palavras, podemos descrever uma
1. O que é uma taxa? Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Em poucas palavras, podemos descrever uma
Sessão 1: Generalidades
 Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais)
 Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica. Regressão. David Menotti.
 Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica Regressão David Menotti www.inf.ufpr.br/menotti/ci171-182 Hoje Regressão Linear ( e Múltipla ) Não-Linear ( Exponencial / Logística
Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica Regressão David Menotti www.inf.ufpr.br/menotti/ci171-182 Hoje Regressão Linear ( e Múltipla ) Não-Linear ( Exponencial / Logística
, (1) onde v é o módulo de v e b 1 e b 2 são constantes positivas.
 Oscilações Amortecidas O modelo do sistema massa-mola visto nas aulas passadas, que resultou nas equações do MHS, é apenas uma idealização das situações mais realistas existentes na prática. Sempre que
Oscilações Amortecidas O modelo do sistema massa-mola visto nas aulas passadas, que resultou nas equações do MHS, é apenas uma idealização das situações mais realistas existentes na prática. Sempre que
Representação e erros numéricos
 Representação e erros numéricos Marina Andretta ICMC-USP 27 de fevereiro de 2013 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - Cálculo Numérico
Representação e erros numéricos Marina Andretta ICMC-USP 27 de fevereiro de 2013 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - Cálculo Numérico
Matemática Básica. Capítulo Conjuntos
 Capítulo 1 Matemática Básica Neste capítulo, faremos uma breve revisão de alguns tópicos de Matemática Básica necessários nas disciplinas de cálculo diferencial e integral. Os tópicos revisados neste capítulo
Capítulo 1 Matemática Básica Neste capítulo, faremos uma breve revisão de alguns tópicos de Matemática Básica necessários nas disciplinas de cálculo diferencial e integral. Os tópicos revisados neste capítulo
Representação e erros numéricos
 Representação e erros numéricos Marina Andretta/Franklina Toledo ICMC-USP 03 de Agosto de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta/Franklina Toledo (ICMC-USP)
Representação e erros numéricos Marina Andretta/Franklina Toledo ICMC-USP 03 de Agosto de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta/Franklina Toledo (ICMC-USP)
CÁLCULO I. Estabelecer a relação entre continuidade e derivabilidade; Apresentar a derivada das funções elementares. f f(x + h) f(x) c c
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 11: Derivada de uma função. Continuidade e Derivabilidade. Derivada das Funções Elementares. Objetivos da Aula Denir
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 11: Derivada de uma função. Continuidade e Derivabilidade. Derivada das Funções Elementares. Objetivos da Aula Denir
Representação e erros numéricos
 Representação e erros numéricos Marina Andretta / Franklina Toledo ICMC-USP 25 de fevereiro de 2015 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta / Franklina Toledo
Representação e erros numéricos Marina Andretta / Franklina Toledo ICMC-USP 25 de fevereiro de 2015 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta / Franklina Toledo
Home Programa Exercícios Provas Professor Links. 2.1 Representação de um número na base dois. O número binário 101,101 significa, na base dois:
 Curso de Cálculo Numérico Professor Raymundo de Oliveira Home Programa Exercícios Provas Professor Links Capítulo 2 - Representação binária de números inteiros e reais 2.1 Representação de um número na
Curso de Cálculo Numérico Professor Raymundo de Oliveira Home Programa Exercícios Provas Professor Links Capítulo 2 - Representação binária de números inteiros e reais 2.1 Representação de um número na
Representação e erros numéricos
 Representação e erros numéricos Marina Andretta ICMC-USP 29 de fevereiro de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo numérico
Representação e erros numéricos Marina Andretta ICMC-USP 29 de fevereiro de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo numérico
Universidade Federal de Pelotas. Instituto de Física e Matemática Pró-reitoria de Ensino. Módulo de Limites. Aula 01. Projeto GAMA
 Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Material Teórico - Módulo de Função Exponencial. Equações Exponenciais. Primeiro Ano - Médio
 Material Teórico - Módulo de Função Exponencial Equações Exponenciais Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 3 de novembro de 018 No material da aula
Material Teórico - Módulo de Função Exponencial Equações Exponenciais Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 3 de novembro de 018 No material da aula
Biomatemática - Prof. Marcos Vinícius Carneiro Vital (ICBS UFAL) - Material disponível no endereço
 Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Por si só, boa parte do conteúdo desta aula pode parecer mais
Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Por si só, boa parte do conteúdo desta aula pode parecer mais
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO
 CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Informática para o Ensino de Física CONTEUDISTA: Carlos Eduardo Aguiar
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Informática para o Ensino de Física CONTEUDISTA: Carlos Eduardo Aguiar
Biomatemática - Prof. Marcos Vinícius Carneiro Vital (ICBS UFAL) - Material disponível no endereço
 Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Como prever a natureza? (ou: apresentando uma função) 1.1. Visão
Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Como prever a natureza? (ou: apresentando uma função) 1.1. Visão
Funções de Correlação. Com isso, nossa amplitude de transição fica em uma forma bastante reveladora: Paremos aqui um momento para notar duas coisas:
 Teoria Quântica de Campos II 13 ( eq. 13.1 ) Com isso, nossa amplitude de transição fica em uma forma bastante reveladora: ( eq. 13.2 ) Paremos aqui um momento para notar duas coisas: (1) As equações 10.1
Teoria Quântica de Campos II 13 ( eq. 13.1 ) Com isso, nossa amplitude de transição fica em uma forma bastante reveladora: ( eq. 13.2 ) Paremos aqui um momento para notar duas coisas: (1) As equações 10.1
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
CÁLCULO I. 1 Funções. Objetivos da Aula. Aula n o 01: Funções. Denir função e conhecer os seus elementos; Reconhecer o gráco de uma função;
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 01: Funções. Objetivos da Aula Denir função e conhecer os seus elementos; Reconhecer o gráco de uma função; Denir funções compostas e inversas.
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 01: Funções. Objetivos da Aula Denir função e conhecer os seus elementos; Reconhecer o gráco de uma função; Denir funções compostas e inversas.
Tensores (Parte 1) 15 de abril de Primeira aula sobre tensores para a disciplina de CVT 2019Q1
 Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
INE Fundamentos de Matemática Discreta para a Computação
 INE5403 - Fundamentos de Matemática Discreta para a Computação ) Fundamentos.1) Conjuntos e Sub-conjuntos.) Números Inteiros.3) Funções.4) Seqüências e Somas.5) Crescimento de Funções Seqüências Uma seqüência
INE5403 - Fundamentos de Matemática Discreta para a Computação ) Fundamentos.1) Conjuntos e Sub-conjuntos.) Números Inteiros.3) Funções.4) Seqüências e Somas.5) Crescimento de Funções Seqüências Uma seqüência
1). Tipos de equações. 3). Etapas na resolução algébrica de equações numéricas. 4). Os dois grandes cuidados na resolução de equações
 1). Tipos de equações LIÇÃO 7 Introdução à resolução das equações numéricas Na Matemática, nas Ciências e em olimpíadas, encontramos equações onde a incógnita pode ser número, função, matriz ou outros
1). Tipos de equações LIÇÃO 7 Introdução à resolução das equações numéricas Na Matemática, nas Ciências e em olimpíadas, encontramos equações onde a incógnita pode ser número, função, matriz ou outros
SISTEMA DECIMAL. No sistema decimal o símbolo 0 (zero) posicionado à direita implica em multiplicar a grandeza pela base, ou seja, por 10 (dez).
 SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
O limite de uma função
 Universidade de Brasília Departamento de Matemática Cálculo 1 O ite de uma função Se s(t) denota a posição de um carro no instante t > 0, então a velocidade instantânea v(t) pode ser obtida calculando-se
Universidade de Brasília Departamento de Matemática Cálculo 1 O ite de uma função Se s(t) denota a posição de um carro no instante t > 0, então a velocidade instantânea v(t) pode ser obtida calculando-se
Para simplificar a notação, também usamos denotar uma sequência usando apenas a imagem de :
 Sequências Uma sequência é uma função f de em, ou seja. Para todo número natural i associamos um número real por meio de uma determinada regra de formação. A sequencia pode ser denotada por: Ou, por meio
Sequências Uma sequência é uma função f de em, ou seja. Para todo número natural i associamos um número real por meio de uma determinada regra de formação. A sequencia pode ser denotada por: Ou, por meio
Introdução à Neurociência Computacional (Graduação) Prof. Antônio Roque Aula 6
 Variações do modelo integra-e-dispara Nesta aula vamos apresentar algumas variações do modelo LIF visto na aula passada. Modelo integra-e-dispara com adaptação Estudos in vitro mostram que muitos tipos
Variações do modelo integra-e-dispara Nesta aula vamos apresentar algumas variações do modelo LIF visto na aula passada. Modelo integra-e-dispara com adaptação Estudos in vitro mostram que muitos tipos
CÁLCULO I. Aula n o 02: Funções. Denir função e conhecer os seus elementos; Listar as principais funções e seus grácos.
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 02: Funções. Objetivos da Aula Denir função e conhecer os seus elementos; Reconhecer o gráco de uma função; Listar as
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 02: Funções. Objetivos da Aula Denir função e conhecer os seus elementos; Reconhecer o gráco de uma função; Listar as
Cálculo Numérico. Santos Alberto Enriquez-Remigio FAMAT-UFU 2015
 Cálculo Numérico Santos Alberto Enriquez-Remigio FAMAT-UFU 2015 1 Capítulo 1 Solução numérica de equações não-lineares 1.1 Introdução Lembremos que todo problema matemático pode ser expresso na forma de
Cálculo Numérico Santos Alberto Enriquez-Remigio FAMAT-UFU 2015 1 Capítulo 1 Solução numérica de equações não-lineares 1.1 Introdução Lembremos que todo problema matemático pode ser expresso na forma de
Álgebra Matricial - Nota 03 Eliminação Gaussiana e Método de Gauss-Jordan
 Álgebra Matricial - Nota 03 Eliminação Gaussiana e Método de Gauss-Jordan Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú Curso de Licenciatura em Matemática marcio@matematicauva.org 8
Álgebra Matricial - Nota 03 Eliminação Gaussiana e Método de Gauss-Jordan Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú Curso de Licenciatura em Matemática marcio@matematicauva.org 8
Função de 2º Grau. Parábola: formas geométricas no cotidiano
 1 Função de 2º Grau Parábola: formas geométricas no cotidiano Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a 0, é denominada função do 2º grau. Generalizando
1 Função de 2º Grau Parábola: formas geométricas no cotidiano Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a 0, é denominada função do 2º grau. Generalizando
FUNÇÃO MODULAR, FUNÇÃO EXPONENCIAL E FUNÇÃO LOGARÍTMICA
 FUNÇÃO MODULAR, FUNÇÃO EXPONENCIAL E FUNÇÃO LOGARÍTMICA Função Modular Função é uma lei ou regra que associa cada elemento de um conjunto A a um único elemento de um conjunto B. O conjunto A é chamado
FUNÇÃO MODULAR, FUNÇÃO EXPONENCIAL E FUNÇÃO LOGARÍTMICA Função Modular Função é uma lei ou regra que associa cada elemento de um conjunto A a um único elemento de um conjunto B. O conjunto A é chamado
Ecologia II. Numa escala global a população muda por dois fatores: Mortes. Nascimentos
 Ecologia II Numa escala global a população muda por dois fatores: Nascimentos Mortes Ecologia II Numa escala local a população muda pelos seguintes fatores: Nascimentos Imigrações Mortes Emigrações Dispersão
Ecologia II Numa escala global a população muda por dois fatores: Nascimentos Mortes Ecologia II Numa escala local a população muda pelos seguintes fatores: Nascimentos Imigrações Mortes Emigrações Dispersão
Método de Euler. Marina Andretta/Franklina Toledo ICMC-USP. 29 de outubro de 2013
 Solução numérica de Equações Diferenciais Ordinárias: Método de Euler Marina Andretta/Franklina Toledo ICMC-USP 29 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D. Faires;
Solução numérica de Equações Diferenciais Ordinárias: Método de Euler Marina Andretta/Franklina Toledo ICMC-USP 29 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D. Faires;
Soluções dos Problemas do Capítulo 3
 48 Temas e Problemas Soluções dos Problemas do Capítulo 3. A cada período de 5 anos, a população da cidade é multiplicada por,0. Logo, em 0 anos, ela é multiplicada por,0 4 =,084. Assim, o crescimento
48 Temas e Problemas Soluções dos Problemas do Capítulo 3. A cada período de 5 anos, a população da cidade é multiplicada por,0. Logo, em 0 anos, ela é multiplicada por,0 4 =,084. Assim, o crescimento
Planificação de Matemática 9º ano. Ano letivo: 2014/15
 Planificação de 9º ano Ano letivo: 01/15 Unidades Tema Total de previstas Unidade 8 (8ºano) Sólidos Geométricos 1ºP Unidade 1 Probabilidades 65 Unidade Funções Unidade 3 Equações ºP Unidade Circunferência
Planificação de 9º ano Ano letivo: 01/15 Unidades Tema Total de previstas Unidade 8 (8ºano) Sólidos Geométricos 1ºP Unidade 1 Probabilidades 65 Unidade Funções Unidade 3 Equações ºP Unidade Circunferência
Chama-se conjunto dos números naturais símbolo N o conjunto formado pelos números. OBS: De um modo geral, se A é um conjunto numérico qualquer, tem-se
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Conjuntos Numéricos Prof.:
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Conjuntos Numéricos Prof.:
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aulas 5 e 6 03/2014 Erros Aritmética no Computador A aritmética executada por uma calculadora ou computador é diferente daquela
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aulas 5 e 6 03/2014 Erros Aritmética no Computador A aritmética executada por uma calculadora ou computador é diferente daquela
CÁLCULO I. Aula n o 02: Funções. Determinar o domínio, imagem e o gráco de uma função; Reconhecer funções pares, ímpares, crescentes e decrescentes;
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 02: Funções Objetivos da Aula Denir e reconhecer funções; Determinar o domínio, imagem e o gráco de uma função; Reconhecer funções pares,
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 02: Funções Objetivos da Aula Denir e reconhecer funções; Determinar o domínio, imagem e o gráco de uma função; Reconhecer funções pares,
Progressões aritméticas
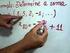 A UUL AL A Progressões aritméticas Quando escrevemos qualquer quantidade de números, um após o outro, temos o que chamamos de seqüência. As seqüências são, freqüentemente, resultado da observação de um
A UUL AL A Progressões aritméticas Quando escrevemos qualquer quantidade de números, um após o outro, temos o que chamamos de seqüência. As seqüências são, freqüentemente, resultado da observação de um
Experimento 7 Circuitos RC e RL em corrente alternada. Parte A: Circuito RC em corrente alternada
 Experimento 7 ircuitos R e RL em corrente alternada Parte A: ircuito R em corrente alternada 1 OBJETIO O objetivo desta aula é estudar o comportamento de circuitos R em presença de uma fonte de alimentação
Experimento 7 ircuitos R e RL em corrente alternada Parte A: ircuito R em corrente alternada 1 OBJETIO O objetivo desta aula é estudar o comportamento de circuitos R em presença de uma fonte de alimentação
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
Tópicos de Biologia-Matemática
 Tópicos de Biologia-Matemática Roberto André Kraenkel, IFT http://www.ift.unesp.br/users/kraenkel Aula I Instituto de Física Teórica Julho de 2012 A aula de hoje 1 Populações 2 Modelos Simples I: Malthus
Tópicos de Biologia-Matemática Roberto André Kraenkel, IFT http://www.ift.unesp.br/users/kraenkel Aula I Instituto de Física Teórica Julho de 2012 A aula de hoje 1 Populações 2 Modelos Simples I: Malthus
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano.
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano aratadano@utfpr.edu.br Aula 2 08/2014 Noções Básicas sobre Erros A resolução de problemas numericamente envolve várias fases que podem ser assim estruturadas:
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano aratadano@utfpr.edu.br Aula 2 08/2014 Noções Básicas sobre Erros A resolução de problemas numericamente envolve várias fases que podem ser assim estruturadas:
MAT 1351 : Cálculo para Funções de Uma Variável Real I. Sylvain Bonnot (IME-USP)
 MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Informações gerais Prof.: Sylvain Bonnot Email: sylvain@ime.usp.br Minha sala: IME-USP, 151-A (Bloco A) Site: ver
Biomatemática - Prof. Marcos Vinícius Carneiro Vital (ICBS UFAL) - Material disponível no endereço
 Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-3 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Uma função linear especial. 1.1. Absorção de potássio. - Para
Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-3 Biomatemática Prof. Marcos Vinícius Carneiro Vital 1. Uma função linear especial. 1.1. Absorção de potássio. - Para
Experimento 7 Circuitos RC e RL em corrente alternada. Parte A: Circuito RC em corrente alternada
 Experimento 7 Circuitos RC e RL em corrente alternada 1. OBJETIO Parte A: Circuito RC em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos RC em presença de uma fonte de alimentação
Experimento 7 Circuitos RC e RL em corrente alternada 1. OBJETIO Parte A: Circuito RC em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos RC em presença de uma fonte de alimentação
Aulas 10 e 11 / 18 e 20 de abril
 1 Conjuntos Aulas 10 e 11 / 18 e 20 de abril Um conjunto é uma coleção de objetos. Estes objetos são chamados de elementos do conjunto. A única restrição é que em geral um mesmo elemento não pode contar
1 Conjuntos Aulas 10 e 11 / 18 e 20 de abril Um conjunto é uma coleção de objetos. Estes objetos são chamados de elementos do conjunto. A única restrição é que em geral um mesmo elemento não pode contar
Primeira Lista de Exercícios de Biofísica II. c n
 Primeira Lista de Exercícios de Biofísica II 1. Considere uma célula composta por um corpo celular ao qual está preso um longo e fino processo tubular (por exemplo, o axônio de um neurônio ou o flagelo
Primeira Lista de Exercícios de Biofísica II 1. Considere uma célula composta por um corpo celular ao qual está preso um longo e fino processo tubular (por exemplo, o axônio de um neurônio ou o flagelo
Exemplo do Uso da Integração: O valor médio de uma função contínua
 Exemplo do Uso da Integração: O valor médio de uma função contínua Um problema muito comum em biologia consiste em determinar o valor médio de alguma grandeza que varia continuamente. Alguns exemplos são
Exemplo do Uso da Integração: O valor médio de uma função contínua Um problema muito comum em biologia consiste em determinar o valor médio de alguma grandeza que varia continuamente. Alguns exemplos são
Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas
 Campo Escalar e Gradiente Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas Prof. Alex G. Dias (alex.dias@ufabc.edu.br) Prof. Alysson F. Ferrari (alysson.ferrari@ufabc.edu.br) Um campo escalar
Campo Escalar e Gradiente Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas Prof. Alex G. Dias (alex.dias@ufabc.edu.br) Prof. Alysson F. Ferrari (alysson.ferrari@ufabc.edu.br) Um campo escalar
Métodos Numéricos - Notas de Aula
 Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução A interpolação é outra técnicas bem conhecida e básica do cálculo numérico. Muitas funções são conhecidas apenas em um
Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução A interpolação é outra técnicas bem conhecida e básica do cálculo numérico. Muitas funções são conhecidas apenas em um
PLANO CURRICULAR DISCIPLINAR. MATEMÁTICA 4.º Ano. Números e Operações. Relações numéricas. Números Naturais. Numeração Romana.
 PLANO CURRICULAR DISCIPLINAR MATEMÁTICA 4.º Ano 1.º Período 64 Realizar contagens progressivas e regressivas a partir de números dados. Comparar números e ordenálos em sequências crescentes e decrescentes.
PLANO CURRICULAR DISCIPLINAR MATEMÁTICA 4.º Ano 1.º Período 64 Realizar contagens progressivas e regressivas a partir de números dados. Comparar números e ordenálos em sequências crescentes e decrescentes.
Quantização por Integrais de Trajetória:
 Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Integral de Trajetória de Feynman
 Teoria Quântica de Campos II 7 No estado fundamental, ou vácuo, defindo por a energia é: Energia de ponto zero ou do vácuo Podemos definir um hamiltoniano sem esta energia de ponto zero, definindo o ordenamento
Teoria Quântica de Campos II 7 No estado fundamental, ou vácuo, defindo por a energia é: Energia de ponto zero ou do vácuo Podemos definir um hamiltoniano sem esta energia de ponto zero, definindo o ordenamento
2. Números Inteiros. A representação gráfica dos números Inteiros Os números podem ser representados numa reta horizontal, a reta numérica:
 . Números Inteiros Sempre que estamos no inverno as temperaturas caem. Algumas cidades do Sul do Brasil chegam até mesmo a nevar. Quando isso acontece, a temperatura está menor do que zero. Em Urupema,
. Números Inteiros Sempre que estamos no inverno as temperaturas caem. Algumas cidades do Sul do Brasil chegam até mesmo a nevar. Quando isso acontece, a temperatura está menor do que zero. Em Urupema,
Unidade I MATEMÁTICA. Prof. Celso Ribeiro Campos
 Unidade I MATEMÁTICA Prof. Celso Ribeiro Campos Números reais Três noções básicas são consideradas primitivas, isto é, são aceitas sem a necessidade de definição. São elas: a) Conjunto. b) Elemento. c)
Unidade I MATEMÁTICA Prof. Celso Ribeiro Campos Números reais Três noções básicas são consideradas primitivas, isto é, são aceitas sem a necessidade de definição. São elas: a) Conjunto. b) Elemento. c)
Experimento 7 Circuitos RC em corrente alternada
 1. OBJETIO Experimento 7 ircuitos R em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos R em presença de uma fonte de alimentação de corrente alternada.. 2. MATERIAL UTILIZADO
1. OBJETIO Experimento 7 ircuitos R em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos R em presença de uma fonte de alimentação de corrente alternada.. 2. MATERIAL UTILIZADO
Estatística (MAD231) Turma: IGA. Período: 2018/2
 Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim
 Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim Nestas atividades temos como objetivo abordar a definição, solução e notação de uma equação diferencial e,
Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim Nestas atividades temos como objetivo abordar a definição, solução e notação de uma equação diferencial e,
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Objetivos. Expressar o vértice da parábola em termos do discriminante e dos
 MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
Aula 14. Regra da cadeia
 Aula 14 Regra da cadeia Lembremos da Regra da Cadeia para funções de uma variável Considere duas funções diferenciáveis, y = f(x) e x = g(t) A derivada da função composta f (g(t)) é calculada por meio
Aula 14 Regra da cadeia Lembremos da Regra da Cadeia para funções de uma variável Considere duas funções diferenciáveis, y = f(x) e x = g(t) A derivada da função composta f (g(t)) é calculada por meio
UNIVERSIDADE DE SÃO PAULO
 UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ECOLOGIA Rua do Matão - Travessa 14 nº 321 - CEP 558-9 Cidade Universitária - São Paulo - Brasil http://www.ib.usp.br Instruções Gerais: 1) Responda às questões
UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ECOLOGIA Rua do Matão - Travessa 14 nº 321 - CEP 558-9 Cidade Universitária - São Paulo - Brasil http://www.ib.usp.br Instruções Gerais: 1) Responda às questões
A Integração da Morte
 A Integração da Morte Thiago de Paiva Campos No cálculo, Leibniz criou a integral mais especificamente para determinar a área sob uma curva no plano cartesiano. Mas o cálculo também pode ser utilizado
A Integração da Morte Thiago de Paiva Campos No cálculo, Leibniz criou a integral mais especificamente para determinar a área sob uma curva no plano cartesiano. Mas o cálculo também pode ser utilizado
AULA 1 Introdução aos limites 3. AULA 2 Propriedades dos limites 5. AULA 3 Continuidade de funções 8. AULA 4 Limites infinitos 10
 Índice AULA 1 Introdução aos limites 3 AULA 2 Propriedades dos limites 5 AULA 3 Continuidade de funções 8 AULA 4 Limites infinitos 10 AULA 5 Limites quando numerador e denominador tendem a zero 12 AULA
Índice AULA 1 Introdução aos limites 3 AULA 2 Propriedades dos limites 5 AULA 3 Continuidade de funções 8 AULA 4 Limites infinitos 10 AULA 5 Limites quando numerador e denominador tendem a zero 12 AULA
3. Limites e Continuidade
 3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
Elementos de Cálculo I - Conjuntos de pontos no plano 1 Prof Carlos Alberto Santana Soares
 Elementos de Cálculo I - Conjuntos de pontos no plano Prof Carlos Alberto Santana Soares Você certamente está familiarizado com o plano cartesiano desde o término do seu ensino fundamental Neste início
Elementos de Cálculo I - Conjuntos de pontos no plano Prof Carlos Alberto Santana Soares Você certamente está familiarizado com o plano cartesiano desde o término do seu ensino fundamental Neste início
1 ESTUDO DA POLUIÇÃO NUMA
 MATEMATICA 1 ESTUDO DA POLUIÇÃO NUMA AULA DE MATEMÁTICA OBJETIVO NOME ESCOLA EQUIPE SÉRIE PERÍODO DATA Esta atividade tem múltiplos objetivos: evidenciar a importância do ferramental matemático no estudo
MATEMATICA 1 ESTUDO DA POLUIÇÃO NUMA AULA DE MATEMÁTICA OBJETIVO NOME ESCOLA EQUIPE SÉRIE PERÍODO DATA Esta atividade tem múltiplos objetivos: evidenciar a importância do ferramental matemático no estudo
PLANO DE AULA IDENTIFICAÇÃO
 PLANO DE AULA IDENTIFICAÇÃO Escola: IFC Campus Avançado Sombrio Município: Sombrio Disciplina: Matemática Série: 2 ano Nível: Ensino médio Professor: Giovani Marcelo Schmidt Tempo estimado: Cinco aulas
PLANO DE AULA IDENTIFICAÇÃO Escola: IFC Campus Avançado Sombrio Município: Sombrio Disciplina: Matemática Série: 2 ano Nível: Ensino médio Professor: Giovani Marcelo Schmidt Tempo estimado: Cinco aulas
Pró-letramento Matemática Estado de Minas Gerais
 Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
Métodos Numéricos. Turma CI-202-X. Josiney de Souza.
 Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 20 (09/11/15) Interpolação: Introdução Características Interpolação Linear: Introdução Características Exercícios
Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 20 (09/11/15) Interpolação: Introdução Características Interpolação Linear: Introdução Características Exercícios
Na aula anterior vimos a noção de derivada de uma função. Suponha que uma variável y seja dada como uma função f de uma outra variável x,
 Elementos de Cálculo Dierencial Na aula anterior vimos a noção de derivada de uma unção. Supona que uma variável y seja dada como uma unção de uma outra variável, y ( ). Por eemplo, a variável y pode ser
Elementos de Cálculo Dierencial Na aula anterior vimos a noção de derivada de uma unção. Supona que uma variável y seja dada como uma unção de uma outra variável, y ( ). Por eemplo, a variável y pode ser
Lei de Decaimento Radioativo. O Decaimento Radioativo é um fenômeno Linear? Como medir o Decaimento Radioativo?
 Lei de Decaimento Radioativo O Decaimento Radioativo é um fenômeno Linear? Como medir o Decaimento Radioativo? ! Na medicina nuclear o decaimento radioativo não é observado apenas como um fenômeno, mas
Lei de Decaimento Radioativo O Decaimento Radioativo é um fenômeno Linear? Como medir o Decaimento Radioativo? ! Na medicina nuclear o decaimento radioativo não é observado apenas como um fenômeno, mas
Estatística descritiva básica: Tabelas e Gráficos
 Estatística descritiva básica: Tabelas e Gráficos ACH2021 Tratamento e Análise de Dados e Informações Marcelo de Souza Lauretto marcelolauretto@usp.br www.each.usp.br/lauretto *Parte do conteúdo baseada
Estatística descritiva básica: Tabelas e Gráficos ACH2021 Tratamento e Análise de Dados e Informações Marcelo de Souza Lauretto marcelolauretto@usp.br www.each.usp.br/lauretto *Parte do conteúdo baseada
PUC-GOIÁS - Departamento de Computação
 PUC-GOIÁS - Departamento de Computação Fundamentos IV/Enfase Clarimar J. Coelho Goiânia, 28/05/2014 O que é interpolação polinomial? Ideia básica Permite construir um novo conjunto de dados a partir de
PUC-GOIÁS - Departamento de Computação Fundamentos IV/Enfase Clarimar J. Coelho Goiânia, 28/05/2014 O que é interpolação polinomial? Ideia básica Permite construir um novo conjunto de dados a partir de
Experimento 9 Circuitos RL em corrente alternada
 1. OBJETIO Experimento 9 Circuitos RL em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos RL em presença de uma fonte de alimentação de corrente alternada. 2. MATERIAL UTILIZADO
1. OBJETIO Experimento 9 Circuitos RL em corrente alternada O objetivo desta aula é estudar o comportamento de circuitos RL em presença de uma fonte de alimentação de corrente alternada. 2. MATERIAL UTILIZADO
Tabela 1 - Minitermos e Maxtermos para uma função de 3 variáveis.
 Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 FORMAS CANÔNICAS A lógica estruturada é baseada na capacidade de escrever equações booleanas de maneira
Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 FORMAS CANÔNICAS A lógica estruturada é baseada na capacidade de escrever equações booleanas de maneira
BIO 208 Processos Evolutivos Prática 2
 Roteiro de Atividade Aula Prática Neste roteiro de aula prática iremos analisar o efeito da seleção em populações infinitas, Na aula seguinte, analisaremos resultados de processos combinados, tal como
Roteiro de Atividade Aula Prática Neste roteiro de aula prática iremos analisar o efeito da seleção em populações infinitas, Na aula seguinte, analisaremos resultados de processos combinados, tal como
O oscilador Harmônico forçado ( Nastase 7 e 8, Ramond 2.3)
 Teoria Quântica de Campos I 70 Usaremos, com muito mais frequência, uma outra definição para conectado - querendo dizer que o diagrama conecta todos os pontos externos entre si. Nesta nova definição, os
Teoria Quântica de Campos I 70 Usaremos, com muito mais frequência, uma outra definição para conectado - querendo dizer que o diagrama conecta todos os pontos externos entre si. Nesta nova definição, os
Aula 4: Gráficos lineares
 Aula 4: Gráficos lineares 1 Introdução Um gráfico é uma curva que mostra a relação entre duas variáveis medidas. Quando, em um fenômeno físico, duas grandezas estão relacionadas entre si o gráfico dá uma
Aula 4: Gráficos lineares 1 Introdução Um gráfico é uma curva que mostra a relação entre duas variáveis medidas. Quando, em um fenômeno físico, duas grandezas estão relacionadas entre si o gráfico dá uma
Matemática Básica Relações / Funções
 Matemática Básica Relações / Funções 04 1. Relações (a) Produto cartesiano Dados dois conjuntos A e B, não vazios, denomina-se produto cartesiano de A por B ao conjunto A B cujos elementos são todos os
Matemática Básica Relações / Funções 04 1. Relações (a) Produto cartesiano Dados dois conjuntos A e B, não vazios, denomina-se produto cartesiano de A por B ao conjunto A B cujos elementos são todos os
Pré-Cálculo. Humberto José Bortolossi. Parte 1. Departamento de Matemática Aplicada Universidade Federal Fluminense. Parte 1 Pré-Cálculo 1
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 1 Parte 1 Pré-Cálculo 1 Apresentação do curso Parte 1 Pré-Cálculo 2 Conteúdo do curso Números
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 1 Parte 1 Pré-Cálculo 1 Apresentação do curso Parte 1 Pré-Cálculo 2 Conteúdo do curso Números
aula ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES
 ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
Fundamentos de Matemática
 Fundamentos de Matemática Aula 1 Antonio Nascimento Plano de Ensino Conteúdos Teoria dos Conjuntos; Noções de Potenciação, Radiciação; Intervalos Numéricos; Fatoração, Equações e Inequações; Razão, Proporção,
Fundamentos de Matemática Aula 1 Antonio Nascimento Plano de Ensino Conteúdos Teoria dos Conjuntos; Noções de Potenciação, Radiciação; Intervalos Numéricos; Fatoração, Equações e Inequações; Razão, Proporção,
Capítulo 5 Derivadas Parciais e Direcionais
 Capítulo 5 Derivadas Parciais e Direcionais 1. Conceitos Sabe-se que dois problemas estão relacionados com derivadas: Problema I: Taxas de variação da função. Problema II: Coeficiente angular de reta tangente.
Capítulo 5 Derivadas Parciais e Direcionais 1. Conceitos Sabe-se que dois problemas estão relacionados com derivadas: Problema I: Taxas de variação da função. Problema II: Coeficiente angular de reta tangente.
Aula 6: Dedução Natural
 Lógica para Computação Primeiro Semestre, 2015 DAINF-UTFPR Aula 6: Dedução Natural Prof. Ricardo Dutra da Silva Em busca de uma forma de dedução mais próxima do que uma pessoa costuma fazer, foi criado
Lógica para Computação Primeiro Semestre, 2015 DAINF-UTFPR Aula 6: Dedução Natural Prof. Ricardo Dutra da Silva Em busca de uma forma de dedução mais próxima do que uma pessoa costuma fazer, foi criado
Modelagem em Sistemas Complexos
 Modelagem em Sistemas Complexos Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Março de 2012 Objetivos Nesta parte da disciplina pretendemos discutir
Modelagem em Sistemas Complexos Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Março de 2012 Objetivos Nesta parte da disciplina pretendemos discutir
MATEMÁTICA I FUNÇÕES. Profa. Dra. Amanda L. P. M. Perticarrari
 MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
Conjuntos. Notações e Símbolos
 Conjuntos A linguagem de conjuntos é interessante para designar uma coleção de objetos. Quando os estatísticos selecionam indivíduos de uma população eles usam a palavra amostra, frequentemente. Todas
Conjuntos A linguagem de conjuntos é interessante para designar uma coleção de objetos. Quando os estatísticos selecionam indivíduos de uma população eles usam a palavra amostra, frequentemente. Todas
