UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA

Transcrição

1 UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLIÉCNICA DEPARAMENO DE CONSRUÇÃO E ESRUURAS O ENSOR ENSÃO DE CAUCHY João Augusto de Lima Rocha Módulo didático: DCE MD - 02/2002

2 O ENSOR ENSÃO DE CAUCHY João Augusto de Lima Rocha 1. Introdução A idealização do sólido deformável como um meio contínuo é uma simplificação matemática adequada à aplicação do Cálculo ao estudo de seu comportamento, quando o corpo está sujeito às ações de outros corpos e a restrições impostas a seu movimento. As ações de outros corpos podem ser: de contato direto, ou de ação à distância (ação gravitacional, por exemplo). O desenvolvimento histórico dos métodos imaginados para resolver esse problema foi longo, e passou por uma fase em que se buscou resolvê-lo a partir da avaliação da interação entre as moléculas do corpo, até chegar ao método proposto pelo cientista francês Augustin Cauchy ( ) que, em 1821, introduziu o conceito de tensão. Cauchy imaginou cortar o sólido deformável segundo um plano fictício passando pelo ponto em que estava interessado em conhecer a resposta, isto é, a tensão, surgida em consequência das ações externas e das restrições impostas ao movimento do sólido. Evidentemente, podem-se passar infinitos planos de corte pelo ponto considerado. Cortado, enfim, por um desses planos fictícios (Figura 1), o corpo passa a ser considerado como composto de duas regiões que interagem entre si, exatamente através da seção de corte. Na vizinhança do ponto P, em particular, a interação da sub-região R 1 com a sub-região R 2 (Figura 2), pode ser entendida como sendo a resultante, F, das forças moleculares que, idealizadas segundo o padrão de meio contínuo, podem ser sintetizadas pela expressão: t F = lim, (1) S 0 S onde S é a medida da área de uma vizinhança de P contida no plano de corte. O vetor t, chamado de vetor de Cauchy, tem dimensão de pressão, isto é, N/m 2 ou pascal, no S. I.

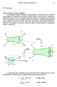
3 Figura 1 Cauchy foi adiante e imaginou representar t como uma função linear do vetor, n, normal unitário externo ao plano de corte, no ponto em estudo. al aplicação linear, que leva um elemento espaço de vetores tipo n a um elemento do espaço de vetores tipo t, é denominada tensor de tensão,, também conhecido como tensor de Cauchy. Então, vale a relação: t = n (2) Para um dado estado de carregamento e de restrições ao deslocamento do sólido, há um só valor do tensor tensão, associado a um dado ponto P do sólido. Dado um sistema cartesiano de eixos, no IR 3, é representado por uma matriz,, cujas componentes têm dimensão de pressão. Convém observar que a formulação de Cauchy preserva a erceira Lei de Newton, a da Ação e Reação. Para verificar isto, basta a observação da eq. (2), na qual, ao colocar-se o vetor n em lugar de n, tem-se t para o vetor de Cauchy (Figura 2). Vê-se na figura que t representa a ação da R 2 sobre R 1, no ponto P. Já t representa a reação

4 Figura 2 (igual em módulo e direção, mas de sentido contrário) da região R 1 sobre R 2, nesse mesmo ponto. 1.1.O significado físico das componentes do tensor tensão Considerando-se um sistema triortogonal de eixos coordenados como referência para os pontos do sólido deformável, o tensor é representado pela matriz : = (3) E F A 31 B G 12 H C D Figura 3

5 Para a interpretação das componentes ij, considere-se uma vizinhança infinitesimal, com a forma de um cubo, de um ponto genérico P, do interior do sólido, tal como mostrado na Figura 3. Considerando-se os vetores unitários, n 1, n 2 e n 3, orientados no sentido positivo dos respectivos eixos coordenados, os vetores de Cauchy correspondentes às seis faces são: Face ABCD: t 1 =n 1 =( 11, 21, 31 ), face EFGH: - t 1 = (-n 1) =(- 11, - 21, - 31 ), face BFDH: t 2 =n 2 =( 12, 22, 32 ), face AECG: - t 2 = (-n 2 )=(- 12, - 22, - 32 ), face ABEF: t 3 =n 3 =( 31, 32, 33 ) e face CDGH: -t 3 = (-n 3 )=(- 31, - 32, - 33 ). Isto significa que o equilíbrio de forças ( ou equilíbrio de translação) do cubo está assegurado por essas equações. No entanto, o equilíbrio de momentos (ou equilíbrio de rotação) ainda precisa ser estudado. Admitindo-se que o cubo da Figura 3 tenha uma aresta de comprimento a, o equilíbrio de momentos assegura que: Em torno da direção x 1 : 32. a 2.a- 23. a 2.a=0 32. = 23 Em torno da direção x 2 : 31. a 2.a- 13. a 2.a=0 31. = 13 Em torno da direção x 3 : 21. a 2.a- 12. a 2.a=0 21. = 12. Daí conclui-se que a matriz é simétrica. Como o sistema triortogonal de eixos foi escolhido arbitrariamente, então a representação do tensor tensão, em qualquer sistema de eixos desse tipo, é sempre simétrica. Esta é uma importante propriedade do tensor tensão de Cauchy. 1.2.Os invariantes do tensor Definido em cada ponto interior do sólido, o tensor possui um significado intrínseco, de natureza física, associado ao sistema de ações exercidas sobre o sólido e ao conjunto de restrições, ou vínculos, que condicionam o seu movimento. Surge, então, a pergunta:

6 e se o sistema de eixos de referência for mudado, como será possível saber se a nova matriz representativa do tensor tensão, num ponto dado, representa o mesmo tensor? Em termos concretos, imagine-se que sejam dadas duas matrizes, (1) e (2), referentes aos sistemas de eixos triortogonais de referência S 1 e S 2, respectivamente. Pergunta-se: como fazer para saber se essas duas matrizes representam, cada qual em seu sistema de referência, o mesmo tensor? Obtém-se a resposta a partir da formulação do problema de autovalor. Assim, diz-se que duas matrizes representam o mesmo tensor, se o conjunto dos autovalores (com os respectivos autovetores) de uma, for exatamente equivalente ao conjunto de autovalores e autovetores da outra. E que estes autovalores e autovetores sejam os mesmos do tensor. O problema de autovalor, para o caso, coloca-se da seguinte forma: n = λ n, (4) que é uma equação que equivale à pergunta: existe algum valor de λ para o qual o vetor de Cauchy, t, possui a mesma direção da normal ao plano em que atua? Se existir, qual a orientação desse plano? A eq. (4) pode ser escrita da seguinte forma: n = λ In, onde I é o tensor identidade. Essa equação pode ser transformada para: ( λ I)n = 0. Imaginando-se agora uma representação dessa equação num dado sistema triortogonal arbitrário de eixos, ela equivale a um sistema homogêneo de equações algébricas: Dado que n 0, esse sistema só terá solução se: det[ λ I] = 0, (5) onde e I são agora as matrizes, referentes ao sistema de eixos adotado. A eq. (3) fica:

7 11 λ det λ 23 = 0, que resolvido leva à seguinte equação de terceiro λ grau em λ, conhecida como o polinômio característico do problema de autovalor: 3 2 λ J λ + J λ J = 0. (6) Nessa expressão, as grandezas J 1, J 2 e J 3 são chamados os invariantes do tensor, e correspondem a: J 1 = tr = J 2 = det J 3 = det , + det det e A solução da eq. (6), no caso geral, dará três valores para λ, que são os autovalores do tensor. Esses valores são todos reais, em virtude de uma propriedade das matrizes simétricas. Na verdade eles correspondem às tensões principais, isto é, aos valores que multiplicados pelos respectivos vetores unitários dos planos-solução, dão os vetores t normais a esses planos. O nome tensão principal decorre do fato de que nesses planos o vetor t não possui componente tangencial ou cisalhante. 1.3.As componentes normal e tangencial do vetor t É muito conveniente, na análise de tensões, o conhecimento das componentes normal e tangencial do vetor de Cauchy, t. A projeção normal, σ n, desse vetor, é dada por seu produto escalar com a normal unitária externa,n, ao plano considerado, passando pelo ponto P do sólido, como mostra a figura 4. Assim: σ n= t. n e t n = σ n. n Onde t n é a componente de t. na direção de n. Se o sinal de σ n for positivo, tem-se uma tração. Caso contrário, tem-se compressão. Por outro lado, a componente tangencial de t será: t s = t-t n. ambém pode-se obter essa última componente a partir da projeção de t sobre um vetor unitário que esteja no plano de corte e seja coplanar a t e t n.

8 Figura 4 Exemplo: Obtenha as componentes normal e tangencial do vetor t, no plano de normal unitária n= ( 3/3; - 3/3; 3 /3), em ponto do sólido em que o tensor tensão é dado pela matriz: 20 = [ ] em MPa Solução: a) Cálculo do vetor t: = n= /3 3/3 3/3 55 = 3/ b) Cálculo da projeção σ n.e da componente normal t n σ n= t.. n = 3/3( 55;-55;10). 3/3( 1;-1;1)= 1/3( )=40 o que indica que se tem uma tração de 40 MPa. A componente normal de t será: t n = 40n= 40( 3/3 ) ( 1;-1;1) c) Cálculo da componente tangencial t st t s = t - t n= 3/3( 55;-55;10).-40( 3/3) ( 1;-1;1)= 5 3 (1;-1;-2) O módulo de t, cujo valor é 3 cisalhamento, nesse plano, no ponto P. 50 MPa dá a medida da tendência ao corte, ou