ANÁLISE DOS EFEITOS DE SEGUNDA ORDEM EM PILARES SOLICITADOS A FLEXÃO OBLÍQUA COMPOSTA. Jorge Luiz Ceccon Ricardo Leopoldo e Silva França
|
|
|
- Luzia Maria de Lourdes Capistrano Amado
- 8 Há anos
- Visualizações:
Transcrição
1 ANÁLISE DOS EFEITOS DE SEGUNDA ORDEM EM PILARES SOLICITADOS A FLEXÃO OBLÍQUA COMPOSTA Jorge Luiz Ceccon Ricardo Leopoldo e Silva França 1. Introdução Na verificação do estado limite último das estruturas reticuladas em concreto armado se tem sempre os pilares solicitados à flexão oblíqua composta, seja devido a momentos fletores transmitidos pelas vigas ou lajes ou devido a imperfeições construtivas ou por ações normais ao eixo da peça comprimida, atuantes entre seus pontos de vinculação. A NBR 6118:2004 permite que, no projeto, se substitua as imperfeições construtivas locais pela consideração de um momento mínimo de 1ª ordem dado no item Os efeitos das ações horizontais que atuam sobre a estrutura global, como a ação do vento, são determinados no cálculo da estrutura global reticulada e são considerados nos esforços transmitidos às extremidades de cada lance de pilar pelas vigas e lajes. Definem-se como efeitos de 1ª ordem os deslocamentos e esforços internos solicitantes obtidos com a análise do equilíbrio da estrutura estudado com a configuração geométrica inicial. Os efeitos de 2ª ordem são aqueles que se somam aos obtidos numa análise de 1ª ordem, quando a análise do equilíbrio passa a ser efetuada considerando a configuração deformada da estrutura. Quanto mais esbelta for a peça, maior será a importância de sua consideração. Na determinação desses efeitos deve ser considerado o comportamento não linear dos materiais. A NBR 6118:2004 no item 15.3 estabelece um limite de esbeltez abaixo do qual se podem desconsiderar os efeitos locais de 2ª ordem. A NBR 6118:2004 item apresenta alguns métodos para a determinação dos efeitos de 2ª ordem.
2 O método geral se aplica tanto ao caso de flexão normal composta quanto para flexão oblíqua composta e será detalhado ao longo deste trabalho. Esse método é obrigatório para pilares com índice de esbeltez λ > 140, segundo a NBR 6118:2004. É o processo mais exato que se dispõe até o momento mas é trabalhoso e só viável com o uso de programas de computador. Os métodos aproximados pilar-padrão com curvatura aproximada e pilar-padrão com rigidez κ aproximada são permitidos para λ 90, seção retangular constante e armadura simétrica e constante ao longo de seu eixo. Esses métodos consideram de maneira mais imediata a solicitação de flexão normal composta. O método do pilar-padrão acoplado a diagramas M N 1/r, permitido pela NBR 6118:2004 para pilares com índice de esbeltez λ 140, é aplicado de maneira mais imediata para barras solicitadas à flexão normal composta. Esse processo é mais preciso que os dois métodos aproximados citados anteriormente, por considerar a relação momento curvatura específica para a seção de concreto armado da peça, considerando não só as dimensões da seção bruta como também a armadura em área de aço e distribuição das barras, além de poder considerar a relação momento curvatura levando em conta a solicitação de flexão obliqua composta. Isto é, pode-se assim determinar a curvatura em dada direção levando em consideração a flexão existente na direção ortogonal. Mas é ainda aproximado por considerar a deformada final do eixo longitudinal como uma curva senoidal, ainda que utilizando para curvatura da seção crítica, e apenas desta, valores obtidos de diagramas M N 1/r. O método do pilar-padrão com rigidez adimensional aproximada é permitido para pilares de seção retangular submetidos à flexão obliqua composta, quando λ 90 nas duas direções principais. Nesse caso aplica-se o método do pilar-padrão em cada direção isoladamente. Os momentos totais, 1ª ordem mais 2ª ordem, podem ser considerados como sendo os momentos de 1ª ordem amplificados. A amplificação dos momentos de 1ª ordem em cada direção é diferente, pois depende de valores distintos de rigidez e esbeltez. Com o método do pilar-padrão acoplado a diagramas M N 1/r a precisão melhora, pois permite considerar as curvaturas em cada direção causadas pela solicitação de flexão obliqua composta. Entretanto, a consideração dos diagramas M N 1/r é trabalhosa e depende da utilização de programas de computador. I - 1
3 No método do pilar-padrão com rigidez aproximada, os momentos de 2ª ordem são considerados através de um coeficiente de amplificação dos momentos de 1ª ordem, utilizando uma expressão aproximada que fornece a rigidez secante adimensional obtida para a solicitação de flexão normal composta. Essa amplificação dos momentos de 1ª ordem é feita em cada direção principal, isoladamente, como se se tratasse de flexão normal composta. Ou seja, para a amplificação dos momentos de 1ª ordem em uma dada direção principal, a expressão aproximada da rigidez secante adimensional do texto da NBR 6118/2004 item não leva em consideração a atuação do momento fletor atuante na direção ortogonal. A consideração desse momento é objeto de analise neste trabalho. Uma vez obtida a distribuição de momentos totais de 1ª e 2ª ordem, em cada direção, a verificação da capacidade resistente da peça é feita em cada seção ao longo do eixo da peça através do emprego de diagramas de envoltórias de momentos resistentes para a armadura escolhida, levando em consideração a força normal solicitante (diagramas N d M xd M yd ). A NBR 6118:2004 no seu item permite que a verificação da capacidade resistente de peças solicitadas à flexão obliqua composta seja feita por uma expressão aproximada de iteração em substituição ao emprego dos diagramas de envoltórias de momentos resistentes. Nas peças solicitadas, em cada seção, à flexão obliqua composta, a deformada do eixo assume uma curva no espaço tri-dimensional e não plana. Este trabalho enfoca a análise de peças bi-apoiadas e em balanço solicitadas à flexão obliqua composta levando em conta os efeitos de segunda ordem (não linearidade geométrica) e a não linearidade física tanto do concreto quanto do aço, principalmente para seções retangulares. 2. Métodos de Cálculo dos Efeitos de Segunda ordem em Pilares 2.1. Pilares em Balanço Dados do pilar exemplo A sistemática de cálculo dos esforços solicitantes de cálculo incluindo os esforços de segunda ordem e verificação da segurança de um pilar engastado na base e livre no topo será apresentada utilizando um exemplo numérico. I - 2
4 Dados numéricos do pilar: Concreto C25: f ck =2,5 kn/cm 2 γ c = 1,4 f cd = 2,5 / 1,4 = 1,786 kn/cm 2 Aço CA-50: f yk = 50 kn/cm 2 γ s = 1,15 E s = kn/cm 2 f yd = 50 / 1,15 = 43,48 kn/cm 2 σ s,2%o= 42 kn/cm 2 Geometria: h x = 60 cm; h y = 30 cm; L = 360 cm Armadura: 12 φ 20 mm; A s = 12 * 3,14 = 37,68 cm 2 ; d = 4 cm Cobrimento da armadura longitudinal do pilar: c = d - φ/2 = 3 cm NBd HBd MBd d d L hy c hx Figura 2.1: Esquema do pilar exemplo As 37,68 Taxa geométrica de armadura: ρ = = = 2,09% A 60x30 As. f yd 37,68x43,478 Taxa mecânica de armadura: ω = = = 0, 51 A. f 30x60x1,786 Solicitações externas: N ud = 0,85.f cd.a c + σ s,2%o.a s N ud = 0,85 x 1,786 x 30 x x 37,68 N ud =4.315 kn c c cd I - 3
5 N Sd = 0,7.N ud = 0,7 x 4315 = kn θ = 30 graus Os momentos últimos considerados N Sd e θ dados, são (obtidos do programa Flexão Oblíqua composta ): M uxd = 77,86 kn.m M uyd = 134,87 kn.m Na base do pilar se considerará M Base = 60%.M ud : M Bxd = 0,6.M uxd = 0,6 x 77,86 = 46,72 kn.m M Byd = 0,6.M uyd = 0,6 x 134,87 = 80,92 kn.m No topo do pilar se considerará como dado M Topo = 40%.M Base : M Txd = 0,4.M Bxd = 0,4 x 46,72 = 18,69 kn.m M Tyd = 0,4.M Byd = 0,4 x 80,92 = 32,37 kn.m H Txd = (M Bxd M Txd ) / L = (46,72 18,69) / 3,6 = 7,79 kn H Tyd = (M Byd M Tyd ) / L = (80,92 32,37) / 3,6 = 13,49 kn Resumindo, as cargas consideradas são: N Sd 3021 N Sd = kn ν = = = 0, 940 A. f 60x30x1,786 M Txd = 18,69 kn.m M Tyd = 32,37 kn.m H Txd = 7,79 kn H Tyd = 13,49 kn c cd Solução através da Integração Numérica com rigidez secante aproximada da NBR 6118 e considerando o desacoplamento das flexões Nd=3021 kn.m Nd MBxd=18,69 kn.m Hdx=7,79 kn S6 Mxd,6 (1/r)x, 6 ϕx, 6 ax,6 Hxd MBxd S5 zi L S4 S3 S2 L fx,i fx,6 - fx,i I - 4
6 Figura 2.2: Carregamento e diagramas de primeira ordem para a direção x. Nd=3021 kn.m Nd MByd=32,37 kn.m Hdy=13,49 kn S6 Mdy,6 (1/r)y,6 ϕy,6 Hxd ay,6 MByd S5 zi L S4 S3 4 S2 L fx,i fx,6 - fx,i S1 Direção X S0 Figura 2.3: Carregamento e diagramas de primeira ordem para a direção y. A expressão da rigidez adimensional aproxima apresentada no item da ABNT NBR 6118/2004 é: M d, tot κ = ν. h NSd Mdy,o (1/r)y,o ϕy,o ay,0 Neste trabalho o momento M d,tot será substituído por M Rd κ 32 M ν. = + Rd h N Sd O momento resistente considerando a flexão normal composta na direção x, obtido dos ábacos de iteração é (desacoplamento das flexões): M Rxd = 257,51 kn.m I - 5
7 O momento resistente considerando a flexão normal composta na direção y, obtido dos ábacos de iteração é (desacoplamento das flexões):: M Ryd = 144,11 kn.m Assim κ xx = 32x 1 + 5x x0,940 κxx = 51,45 60x κ yy = 32x 1 + 5x x0,940 κyy = 53,99 30x3021 As rigidezes secantes são (EI) xx,sec = κ xx.a c.h 2 x.f cd = 51,45 x 1800 x 60 2 x 1,786 (EI) xx,sec = kn.cm 2 (EI) yy,sec = κ yy.a c.h 2 y.f cd = 53,99 x 1800 x 30 2 x 1,786 (EI) yy,sec = kn.cm 2 As curvaturas em cada seção são dadas por 1 r x M Sxd γ = ( EI) f 3 xx,sec 1 r y = M Syd ( EI) γ f 3 yy,sec As rotações em cada seção são obtidas da integração numérica dos diagramas de curvaturas. Os deslocamentos transversais são obtidos da integração numérica dos diagramas de rotações. As tabelas a seguir apresentam o cálculo dos deslocamentos por integração numérica com rigidez secante aproximada. Na iteração j os momentos de 1ª ordem na seção i são corrigidos em função dos deslocamentos da iteração anterior M Sdi,j = M Sdi,1 + N Sd.[a 6,(j-1) a i,(j-1) ] Na primeira tabela aparecem os momentos de 1ª ordem. I - 6
8 Seção zi Mdx,i 1/rx ϕx,i ax,i Mdy,i 1/ry ϕy,i ay,i i (cm) (kn.cm) (1/cm) (rad) (cm) (kn.cm) (1/cm) (rad) (cm) Iteração = ,09 2,8535E-06 1,8750E-03 0, ,73 1,8838E-05 1,2378E-02 2, ,49 3,6384E-06 1,6803E-03 0, ,13 2,4020E-05 1,1092E-02 1, ,89 4,4234E-06 1,4384E-03 0, ,53 2,9201E-05 9,4954E-03 1, ,29 5,2084E-06 1,1494E-03 0, ,93 3,4383E-05 7,5879E-03 0, ,69 5,9933E-06 8,1339E-04 0, ,33 3,9564E-05 5,3695E-03 0, ,09 6,7783E-06 4,3025E-04 0, ,73 4,4746E-05 2,8402E-03 0, ,49 7,5632E , ,13 4,9927E ,00 Seção zi Mdx,i 1/rx ϕx,i ax,i Mdy,i 1/ry ϕy,i ay,i i (cm) (kn.cm) (1/cm) (rad) (cm) (kn.cm) (1/cm) (rad) (cm) Iteração = ,09 2,8535E-06 2,2871E-03 0, ,73 1,8838E-05 2,2747E-02 4, ,41 4,1304E-06 2,0776E-03 0, ,82 3,6399E-05 2,1089E-02 3, ,76 5,3469E-06 1,7932E-03 0, ,44 5,2439E-05 1,8424E-02 2, ,37 6,4899E-06 1,4381E-03 0, ,35 6,6630E-05 1,4852E-02 1, ,49 7,5464E-06 1,0170E-03 0, ,31 7,8646E-05 1,0494E-02 0, ,36 8,5035E-06 5,3554E-04 0, ,11 8,8158E-05 5,4898E-03 0, ,21 9,3480E , ,52 9,4837E ,00 Seção zi Mdx,i 1/rx ϕx,i ax,i Mdy,i 1/ry ϕy,i ay,i i (cm) (kn.cm) (1/cm) (rad) (cm) (kn.cm) (1/cm) (rad) (cm) Iteração = ,09 2,8535E-06 2,2432E-03 0, ,73 1,8838E-05 3,2171E-02 7, ,73 3,8118E-06 2,0433E-03 0, ,81 4,7140E-05 3,0192E-02 5, ,05 5,1324E-06 1,7750E-03 0, ,78 7,3163E-05 2,6583E-02 3, ,68 6,3644E-06 1,4301E-03 0, ,86 9,5895E-05 2,1511E-02 2, ,36 7,4891E-06 1,0144E-03 0, ,55 1,1445E-04 1,5201E-02 0, ,68 8,4889E-06 5,3511E-04 0, ,87 1,2806E-04 7,9257E-03 0, ,21 9,3480E , ,58 1,3613E ,00 As duas últimas iterações são: Seção zi Mdx,i 1/rx ϕx,i ax,i Mdy,i 1/ry ϕy,i ay,i i (cm) (kn.cm) (1/cm) (rad) (cm) (kn.cm) (1/cm) (rad) (cm) Iteração = ,09 2,8535E-06 2,4156E-03 0, ,73 1,8838E-05 1,3059E-01 29, ,24 4,2678E-06 2,2020E-03 0, ,00 1,5893E-04 1,2526E-01 21, ,72 5,6306E-06 1,9050E-03 0, ,82 2,8912E-04 1,1181E-01 14, ,08 6,8908E-06 1,5294E-03 0, ,41 4,0129E-04 9,1102E-02 8, ,60 8,0370E-06 1,0816E-03 0, ,21 4,8848E-04 6,4409E-02 3, ,99 9,0503E-06 5,6893E-04 0, ,91 5,4523E-04 3,3398E-02 1, ,26 9,9140E , ,27 5,6802E ,00 Seção zi Mdx,i 1/rx ϕx,i ax,i Mdy,i 1/ry ϕy,i ay,i i (cm) (kn.cm) (1/cm) (rad) (cm) (kn.cm) (1/cm) (rad) (cm) Iteração = ,09 2,8535E-06 2,4156E-03 0, ,73 1,8838E-05 1,3062E-01 29, ,24 4,2678E-06 2,2020E-03 0, ,38 1,5896E-04 1,2528E-01 21, ,72 5,6306E-06 1,9050E-03 0, ,21 2,8918E-04 1,1184E-01 14, ,08 6,8908E-06 1,5294E-03 0, ,09 4,0139E-04 9,1124E-02 8, ,60 8,0370E-06 1,0816E-03 0, ,19 4,8859E-04 6,4424E-02 3, ,99 9,0503E-06 5,6893E-04 0, ,97 5,4536E-04 3,3406E-02 1, ,26 9,9140E , ,04 5,6816E ,00 Resultaram como valores finais: N Sd = kn M Sxd,tot = 59,0326 x 1,1 = 64,94 kn.m M Syd,tot = 887,5204 x 1,1 = 976,27 kn.m a x,final = 0,51 cm a y,final = 29,48 cm I - 7
9 Solução através da Integração Numérica com rigidez secante obtida de diagrama momento-curvatura e considerando o desacoplamento das flexões M xd - 1/r x Mxd (kn.m) GamaF3=1,0 GamaF3=1,1 Reta MRd/GamaF3 Rigidez secante ,0000 0,0100 0,0200 0,0300 0,0400 0,0500 0,0600 0,0700 0,0800 0,0900 1/r x (%o) M yd - 1/r y Myd (kn.m) GamaF3=1.0 GamaF3=1.1 Reta MRd/GamaF3 Rigidez Secante ,0000 0,0200 0,0400 0,0600 0,0800 0,1000 0,1200 0,1400 0,1600 0,1800 1/ry (%o) Do diagrama M xd 1/r x M γ Rxd f 3 = = 23410kN. cm 11, 1/r x = 2,6627x10-5 cm -1 Portanto I - 8
10 M Rxd γ f ( EI) xx, sec = = = kN. cm 5 1 2,6627x10 r x 2 Do diagrama M yd 1/r y M γ Ryd f = = 13101kN. cm 1,1 1/r y = 5,1617x10-5 cm -1 Portanto M Ryd γ f ( EI) yy, sec = = = kN. cm 5 1 5, 1617x10 r y 2 As primeiras iterações são: Verificação: Estável Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 1, ,99 1,93256E-06 0, ,25 29,43 1,16E-05 0, , ,24 2,41586E-06 0, ,18 36,79 1,45E-05 0, , ,49 2,89916E-06 0, ,12 44,14 1,74E-05 0, , ,74 3,38245E-06 0, ,07 51,50 2,03E-05 0, , ,99 3,86575E-06 0, ,03 58,86 2,32E-05 0, , ,24 4,34904E-06 0, ,01 66,22 2,61E-05 0, , ,49 4,83234E-06 0, ,00 73,58 2,9E-05 0, ,00 Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 2, ,99 1,93256E-06 0, ,29 29,43 1,16E-05 0, , ,14 2,63186E-06 0, ,21 48,18 1,9E-05 0, , ,05 3,30399E-06 0, ,14 65,51 2,58E-05 0, , ,67 3,94351E-06 0, ,08 81,11 3,2E-05 0, , ,96 4,545E-06 0, ,04 94,71 3,73E-05 0, , ,87 5,10301E-06 0, ,01 106,01 4,18E-05 0, , ,34 5,61212E-06 0, ,00 114,73 4,52E-05 0, ,00 As duas últimas iterações são: Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 9, ,99 1,93256E-06 0, ,30 29,43 1,16E-05 0, , ,49 2,67144E-06 0, ,22 61,77 2,44E-05 0, , ,72 3,38037E-06 0, ,14 91,74 3,62E-05 0, , ,62 4,05138E-06 0, ,08 118,18 4,66E-05 0, , ,12 4,67697E-06 0, ,04 140,08 5,52E-05 0, , ,16 5,2501E-06 0, ,01 156,59 6,17E-05 0, , ,68 5,76436E-06 0, ,00 167,09 6,59E-05 0, ,00 I - 9
11 Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 10, ,99 1,93256E-06 0, ,30 29,43 1,16E-05 0, , ,49 2,67144E-06 0, ,22 61,88 2,44E-05 0, , ,72 3,38037E-06 0, ,14 91,95 3,62E-05 0, , ,62 4,05138E-06 0, ,08 118,47 4,67E-05 0, , ,12 4,67697E-06 0, ,04 140,44 5,54E-05 0, , ,16 5,2501E-06 0, ,01 156,99 6,19E-05 0, , ,68 5,76436E-06 0, ,00 167,51 6,6E-05 0, ,00 Esforços Solicitantes totais finais de Cálculo: Seção NSd MSxd MSyd Teta (kn) (kn.m) (kn.m) (rad) ,10 18,69 32,37 0, ,10 25,84 68,07 0, ,10 32,69 101,14 0, ,10 39,18 130,32 0, ,10 45,23 154,48 0, ,10 50,77 172,69 0, ,10 55,75 184,26 0,2938 Esforços Resistentes de Cálculo: Seção NRd MRxd MRyd Teta (kn) (kn.m) (kn.m) (rad) ,00 77,87 134,86 0,5236 Verifica ,01 53,09 139,79 0,3630 Verifica ,00 45,53 140,77 0,3128 Verifica ,00 42,45 141,12 0,2922 Verifica ,00 41,38 141,24 0,2850 Não Verifica ,00 41,54 141,22 0,2861 Não Verifica ,00 42,71 141,09 0,2939 Não Verifica Tela de dados e resultados do programa Flexão Oblíqua Composta I - 10
12 Solução através da Integração Numérica com rigidez pontual obtida de diagrama momento-curvatura e considerando a flexão obliqua composta A rigidez (EI) yθ para cada terno de valores (N d, M xd, M yd ) é obtida dos pontos do gráfico momento-curvatura da figura abaixo. Do gráfico se percebe que as curvas praticamente coincidem. Ou seja, os momentos M xd = 40 kn.m e M xd = 50 kn.m praticamente não influem na rigidez da direção Y. Para este caso também se tem a reta que define a rigidez secante praticamente coincidindo com a curva, portanto, é de se esperar que os resultados obtidos neste item sejam muito próximos dos obtidos para a rigidez secante. Myd - 1/ry 250 Myd (kn.m) ELU Mxd=0 Mxd=40 Mxd=50 MRd/1,1 (EI)sec 0 0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 1/ry (1/1000cm) As três primeiras iterações são: Verificação: Não Verifica Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 1, ,99 1,86646E-06 0, ,24 29,43 1,13E-05 0, , ,24 2,33539E-06 0, ,18 36,79 1,41E-05 0, , ,49 2,80578E-06 0, ,12 44,14 1,69E-05 0, , ,74 3,27796E-06 0, ,07 51,50 1,98E-05 0, , ,99 3,75226E-06 0, ,03 58,86 2,26E-05 0, , ,24 4,22902E-06 0, ,01 66,22 2,55E-05 0, , ,49 4,70862E-06 0, ,00 73,58 2,84E-05 0, ,00 I - 11
13 Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 2, ,99 1,86646E-06 0, ,28 29,43 1,13E-05 0, , ,08 2,54044E-06 0, ,21 47,90 1,84E-05 0, , ,94 3,19663E-06 0, ,14 64,99 2,5E-05 0, , ,53 3,83913E-06 0, ,08 80,39 3,11E-05 0, , ,79 4,44394E-06 0, ,04 93,85 3,64E-05 0, , ,67 5,01211E-06 0, ,01 105,06 4,1E-05 0, , ,14 5,54213E-06 0, ,00 113,75 4,45E-05 0, ,00 Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 3, ,99 1,86646E-06 0, ,30 29,43 1,13E-05 0, , ,38 2,57565E-06 0, ,22 53,83 2,07E-05 0, , ,52 3,26903E-06 0, ,14 76,43 2,95E-05 0, , ,34 3,95038E-06 0, ,08 96,57 3,75E-05 0, , ,78 4,59109E-06 0, ,04 113,65 4,45E-05 0, , ,79 5,23116E-06 0, ,01 127,15 5,02E-05 0, , ,30 5,88896E-06 0, ,00 136,62 5,44E-05 0, ,00 As duas últimas iterações são: Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 6, ,99 1,86646E-06 0, ,32 29,43 1,13E-05 0, , ,54 2,59735E-06 0, ,23 60,71 2,34E-05 0, , ,84 3,32202E-06 0, ,16 89,75 3,48E-05 0, , ,81 4,02706E-06 0, ,09 115,48 4,52E-05 0, , ,39 4,80638E-06 0, ,04 136,92 5,44E-05 0, , ,49 5,75628E-06 0, ,01 153,21 6,22E-05 0, , ,04 6,6598E-06 0, ,00 163,65 6,79E-05 0, ,00 Seção Mx CurvX RotX ax My CurvY RotY ay (KN.m) (1/cm) (Rad) (cm) (kn.m) (1/cm) (Rad) (cm) Iteração: 7, ,99 1,86646E-06 0, ,32 29,43 1,13E-05 0, , ,58 2,60157E-06 0, ,24 61,60 2,37E-05 0, , ,91 3,33137E-06 0, ,16 91,47 3,55E-05 0, , ,91 4,05288E-06 0, ,09 117,94 4,62E-05 0, , ,52 4,88124E-06 0, ,04 139,96 5,58E-05 0, , ,64 5,86527E-06 0, ,01 156,63 6,4E-05 0, , ,20 6,80947E-06 0, ,00 167,20 6,99E-05 0, ,00 Os esforços totais finais de cálculo são os da última iteração multiplicados por γ f3 = 1,1. Esforços Solicitantes totais finais de Cálculo: Seção NSd MSxd MSyd Teta (kn) (kn.m) (kn.m) (rad) ,10 18,69 32,37 0, ,10 25,94 67,76 0, ,10 32,90 100,62 0, ,10 39,50 129,73 0, ,10 45,67 153,95 0, ,10 51,30 172,29 0, ,10 56,32 183,92 0,2971 I - 12
14 A análise da segurança é feita encontrando-se os pares de momentos M Rxd e M Ryd para cada valor de θ da tabela dos esforços totais finais de cálculo. Esforços Resistentes de Cálculo: Seção NRd MRxd MRyd Teta (kn) (kn.m) (kn.m) (rad) ,00 77,87 134,86 0,5236 Verifica ,00 53,52 139,73 0,3658 Verifica ,00 46,03 140,71 0,3162 Verifica ,00 42,98 141,06 0,2957 Verifica ,00 41,90 141,18 0,2885 Não Verifica ,00 42,06 141,16 0,2896 Não Verifica ,00 43,21 141,04 0,2973 Não Verifica Análise dos resultados obtidos Para este caso os resultados encontrados com a rigidez secante obtida de gráfico momento-curvatura praticamente coincidem com os encontrados com as curvaturas obtidas pontualmente. No capítulo 3 são analisados milhares de casos de pilares onde se verificou a segurança para os resultados obtidos com a rigidez secante obtida de gráfico I - 13
15 momento curvatura e com as curvaturas obtidas pontualmente daqueles gráficos. Sempre comparando os resultados desses dois processos de cálculo. No capítulo 4 são destacadas as conclusões. 3. Análise de Resultados 3.1 Geração de exemplos de pilares para análise Para finalizar este trabalho foram gerados exemplos de pilares em balanço e biapoiados para comparação dos métodos de cálculo utilizando integração numérica com desacoplamentos das solicitações de flexão e integração numérica considerando a flexão oblíqua composta sem desacoplamento. O objetivo é de se propor a solução dos pilares solicitados a flexão oblíqua composta como se se tratasse de duas flexões normais compostas independentes. Depois de encontrados os efeitos de 2ª ordem em cada direção é considerada a flexão oblíqua composta para a verificação da segurança da peça. A finalidade de se fazer assim é que para a flexão normal composta já existem ábacos de iteração que fornecem para determinadas distribuições de armadura em seções retangulares, as rigidezes em função da força normal solicitante e da taxa mecânica de armadura. Para flexão oblíqua não. Ainda, para o cálculo dos efeitos de 2ª ordem com a utilização de computadores o tempo de processamento na flexão normal composta é muito menor. Se esse desacoplamento pode ser feito se ganha em praticidade. Os milhares de exemplos rodados, no programa de computador desenvolvido ao longo deste trabalho, permitem uma análise e conclusão segura de como proceder ao desacoplamento com segurança e sem prejudicar demasiadamente a economia. Foram gerados exemplos para pilares em balanço e biapoiados. a) Pilares em balanço Os pilares em balaço têm dimensões da seção transversal h x e h y com h x h y. A dimensão h y assume os valores 14, 19, 25 e 30 cm. A dimensão h x assume valores que variam de um mínimo a um máximo sendo h x,mín = 25 cm h x,máx = 5.h y e h x = (h x,máx - h x,mín ) / 3 (12.1) I - 14
16 O comprimento de flambagem (L e ) e o próprio comprimento (L) do pilar são calculados pelo programa em função do índice de esbeltez (λ) por: L e λ. h = y (12.2) 3,46 L = 0,5.L e (12.3) A distribuição da armadura dentro da seção transversal será considerada composta de 4 barras associadas aos vértices, n x barras distribuídas nas faces de comprimento h x e n y barras distribuídas nas faces de comprimento h y. A quantidade mínima associada a um lado é definida pelo programa de modo a respeitar um espaçamento máximo de centro a centro de barras de 40 cm. A quantidade máxima associada a um lado é definida pelo programa de modo a respeitar um espaçamento mínimo entre faces de barras de 2,5 cm. Além das quantidades mínima e máxima o programa considera uma quantidade média entre a mínima e a máxima. As forças normais consideradas são funções da força normal última do pilar em compressão centrada dada por: N ud = 0,85.f cd.a c + σ s,2%o.a s (12.4) As forças normais consideradas são: N Sd,min = 0,4.N ud N Sd,máx = 0,8.N ud N Sd,méd = 0,5.(N Sd,mín + N Sd,máx ) N Sd = 0,5.(N Sd,máx - N Sd,mín ) (12.5) A inclinação do eixo de solicitação θ, é considerada variando de θ mín = 15 à θ máx = 75 com incrementos θ = 15. Para cada força normal solicitante considerada, o programa calcula os momentos resistentes (M uxd e M uyd ) do estado limite último. As solicitações de flexão são consideradas para a seção da base, em cada direção principal de inércia, como sendo M Bd,min = 0,2. M ud M Bd,méd = 0,5. M ud M Bd,máx = 0,8. M ud (12.6) As cargas no topo do pilar são: Força normal: N Sd I - 15
17 Momentos aplicados: M Txd e M Tyd Forças horizontais aplicadas: H Txd e H Tyd Os momentos aplicados no topo assumem os valores: M Td,min = 0,2.M Bd M Td,méd = 0,6.M Bd M Td,máx = 1,0.M Bd (12.7) As forças horizontais aplicadas no topo assumem os valores: H Td = (M Td M Bd ) / L (12.8) 3.2. Argumentação para a análise dos resultados Os resultados que o programa fornece para análise são referentes às solicitações totais (1ª ordem + 2ª ordem) na base do pilar, por ser a seção mais solicitada. Cada pilar é resolvido por dois processos de determinação dos efeitos de 2ª ordem, quais sejam: a) Integração numérica com a consideração da rigidez secante e do desacoplamento das flexões nas direções principais de inércia X e Y. b) Integração numérica com a consideração das curvaturas obtidas pontualmente dos diagramas momento-curvatura, construídos para a solicitação de flexão oblíqua composta, sem o desacoplamento das flexões. É de se destacar que o processo (b) com a consideração da flexão oblíqua composta é o processo mais confiável. O outro é uma aproximação. O processo (a) só merece confiança quanto à segurança se fornecer um coeficiente de segurança maior ou igual ao processo (b). Para cada processo de cálculo são obtidos os coeficientes de segurança dados pelas relações: M M Sd Rd d Momento solici tante total = Momento resistente total processo a (12.9) onde M M Sd Rd a Momento solici tante total = Momento resistente total processo b (12.10) Sd 2 Sxd 2 Syd M = M + M (12.11) I - 16
18 Rd 2 Rxd 2 Ryd M = M + M (12.12) As relações (12.9) e (12.10) indicam a condição de segurança da seção da base do pilar, respectivamente para o processo com desacoplamento das flexões e com acoplamento. Pelo processo (a) descrito acima a condição de segurança é dada por: M M Sd Rd d < 1,0 (12.13) Pelo processo (b) descrito acima a condição de segurança é dada por: M M Sd Rd a < 1,0 (12.14) O objetivo deste trabalho resultará da análise dos resultados dos milhares de pilares resolvidos e analisados tendo em vista o gráfico da figura M Sd M Rd d C D 1,0 A2 Reta s A1 B1 B2 0 1,0 1,05 M Sd M Rd a Figura 12.1: Gráfico (M Sd /M Rd ) d (M Sd /M Rd ) a Além dos valores de (M Sd /M Rd ) d e (M Sd /M Rd ) a o programa forneceu a região do gráfico da figura 12.1 onde está o ponto P, de coordenadas: M Sd M P ; M Rd a Interpretação do gráfico da figura 12.1: - A reta s separa o gráfico em três grandes regiões. Sd M Rd d I - 17
19 - A grande região definida pelas regiões A1, B1 e B2 corresponde aos pontos P para os quais a abscissa representada pela relação M Sd M Rd a é maior que a ordenada. Ou seja, a segurança com o processo com acoplamento das flexões, onde se considera a flexão oblíqua composta, é menor que no outro caso. - As regiões B1 e B2 correspondem a situações em que não existe segurança (ver eq. (12.13)) quando se considera a flexão oblíqua composta. Entretanto considerando o desacoplamento se chegaria a conclusão de haver segurança para o pilar, já que, M Sd <1. 0 M. Para essas situações do ponto P é Rd d desaconselhável o desacoplamento das flexões pois se chegaria a uma conclusão errôneas da segurança do pilar. A quantidade de casos de pilares para os quais o ponto P se localiza nas regiões B1 e B2 deveria ser nula para que o processo (a), com desacoplamento, pudesse ser empregado livremente. - A região A1 indica as posições em que estando o ponto P os dois processos garantem segurança ao pilar. Mesmo que a segurança dada pelo processo (b), flexão oblíqua composta, seja menor que a obtida pelo processo (a), com desacoplamento, a segurança do pilar está garantida. Portanto é uma região aceitável para o processo com desacoplamento. - A grande região definida pelas regiões A2 e C corresponde aos pontos P para os quais a ordenada representada pela relação M Sd M Rd d é maior que a abscissa. Ou seja, a segurança indicada pelo processo com desacoplamento das flexões, onde se consideram duas flexões normais compostas, é menor que no outro caso. Mas nestes casos a peça tem total segurança já que pelo processo mais exato se tem M Sd 1, 0 M. Rd - A região A2 é a mais interessante para se obter resultados, já que, os dois processos indicam segurança para o pilar e ainda a segurança indicada pelo processo (b), mais exato, é maior que a que se encontra pelo processo aproximado. - Na região C estão os pontos P para os quais se vai contra a economia. Para esses pontos o processo aproximado indica não haver segurança para o pilar, a I - 18
20 embora o processo exato, com a consideração da flexão oblíqua composta, garanta a segurança. Portanto são pontos que dão falsa indicação de insegurança. - Região D. Nessa região os dois processos indicam falta de segurança. Neste caso também se pode admitir estar trabalhando com o processo aproximado (a), já que, se vai concluir a falta de segurança no pilar da mesma forma que se concluiria se estivesse trabalhando com o processo mais exato. Ou seja, se chegaria à mesma conclusão. Os dois processos, aqui são equivalentes. - Regiões A1 e A2. Nessas duas regiões também é indiferente trabalhar com um ou outro processo pois, os dois levam à mesma conclusão, qual seja, o pilar tem segurança Resultados obtidos do processamento Foram resolvidos pilares pelos dois processos descritos no item anterior. As quantidades de resultados encontrados em cada região do gráfico da figura 12.1 foram: Região A1 115 resultados (0,153%) Região A resultados (23,977%) Região B1 4 resultados (0,005%) Região B2 Nenhum Região C resultados (12,372%) Região D resultados (63,493%) 4. Conclusão Da observação dos resultados tem-se a conclusão de que a solução de pilares solicitados à flexão oblíqua composta comprovadamente pode ser obtida considerando o desacoplamento das duas flexões, calculando os efeitos de 2ª ordem em cada direção independentemente, como duas flexões normais compostas, e ao final compor os momentos fletores da seção mais solicitada para a análise da segurança, que pode ser feita através de ábacos de iteração N d M xd - M yd. I - 19
Módulo 6 Pilares: Estados Limites Últimos Detalhamento Exemplo. Imperfeições Geométricas Globais. Imperfeições Geométricas Locais
 NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
e-mail: ederaldoazevedo@yahoo.com.br
 Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
CAPÍTULO IX RIGIDEZ SECANTE ADIMENSIONAL
 CAPÍTULO IX RIGIDEZ SECANTE ADIMENSIONAL 9. Rigidez Secante Adimensional 9.1. Caracterização da rigidez Na análise dos deslocamentos laterais do eixo de um prisma solicitado a flexocompressão tem papel
CAPÍTULO IX RIGIDEZ SECANTE ADIMENSIONAL 9. Rigidez Secante Adimensional 9.1. Caracterização da rigidez Na análise dos deslocamentos laterais do eixo de um prisma solicitado a flexocompressão tem papel
Artigo submetido ao Curso de Engenharia Civil da UNESC - como requisito parcial para obtenção do Título de Engenheiro Civil
 ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação
 LISTA DE FIGURAS Figura 3.1 Figura 3.2 Figura 3.3 Figura 3.5 Figura 3.6 Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação controlada Diagrama
LISTA DE FIGURAS Figura 3.1 Figura 3.2 Figura 3.3 Figura 3.5 Figura 3.6 Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação controlada Diagrama
CISALHAMENTO EM VIGAS CAPÍTULO 13 CISALHAMENTO EM VIGAS
 CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados.
 LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
Estruturas de Concreto Armado. Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com
 Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Efeito do comportamento reológico do concreto
 Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
O conhecimento das dimensões permite determinar os vãos equivalentes e as rigidezes, necessários no cálculo das ligações entre os elementos.
 PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
CÁLCULO DE VIGAS. - alvenaria de tijolos cerâmicos furados: γ a = 13 kn/m 3 ; - alvenaria de tijolos cerâmicos maciços: γ a = 18 kn/m 3.
 CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
Sistemas mistos aço-concreto viabilizando estruturas para Andares Múltiplos
 viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny
 Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Forças internas. Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro.
 Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
Caso (2) X 2 isolado no SP
 Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES
 P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES (OUTRA APRESENTAÇÃO) Prof. Almir Schäffer PORTO ALEGRE
P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES (OUTRA APRESENTAÇÃO) Prof. Almir Schäffer PORTO ALEGRE
detalhamento da armadura longitudinal da viga
 conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES
 APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES 338 Curso de Concreto Armado 1. Lajes retangulares apoiadas no contorno As tabelas A2.1 a A2.6 correspondem a lajes retangulares apoiadas ao longo de todo o contorno
APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES 338 Curso de Concreto Armado 1. Lajes retangulares apoiadas no contorno As tabelas A2.1 a A2.6 correspondem a lajes retangulares apoiadas ao longo de todo o contorno
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 2012 Duração prevista: até 4 horas.
 2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
3.6.1. Carga concentrada indireta (Apoio indireto de viga secundária)
 cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado
 BE8 Encontro Nacional Betão Estrutural 8 Guimarães 5, 6, 7 de Novembro de 8 Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado Bruna Catoia 1, Carlos A.T. Justo,
BE8 Encontro Nacional Betão Estrutural 8 Guimarães 5, 6, 7 de Novembro de 8 Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado Bruna Catoia 1, Carlos A.T. Justo,
EXERCÍCIOS DE ESTRUTURAS DE MADEIRA
 UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
2.1 O Comportamento Estrutural
 2 Vigas As vigas consistem basicamente de barras, contínuas ou não, com eixo reto ou curvo, equiibradas por um sistema de apoios, de modo a garantir que essas barras sejam, no mínimo, isostáticas. Estão
2 Vigas As vigas consistem basicamente de barras, contínuas ou não, com eixo reto ou curvo, equiibradas por um sistema de apoios, de modo a garantir que essas barras sejam, no mínimo, isostáticas. Estão
Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação?
 Assunto Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação? Artigo Segundo a NBR 6118, em seu item 22.5.1, blocos de fundação são elementos de volume através dos quais
Assunto Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação? Artigo Segundo a NBR 6118, em seu item 22.5.1, blocos de fundação são elementos de volume através dos quais
CURSO TÉCNICO DE EDIFICAÇÕES. Disciplina: Projeto de Estruturas. Aula 7
 AULA 7 CURSO TÉCNICO DE EDIFICAÇÕES Disciplina: Projeto de Estruturas CLASSIFICAÇÃO DAS ARMADURAS 1 CLASSIFICAÇÃO DAS ARMADURAS ALOJAMENTO DAS ARMADURAS Armadura longitudinal (normal/flexão/torção) Armadura
AULA 7 CURSO TÉCNICO DE EDIFICAÇÕES Disciplina: Projeto de Estruturas CLASSIFICAÇÃO DAS ARMADURAS 1 CLASSIFICAÇÃO DAS ARMADURAS ALOJAMENTO DAS ARMADURAS Armadura longitudinal (normal/flexão/torção) Armadura
Teoria das Estruturas
 Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
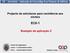
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
Facear Concreto Estrutural I
 1. ASSUNTOS DA AULA Durabilidade das estruturas, estádios e domínios. 2. CONCEITOS As estruturas de concreto devem ser projetadas e construídas de modo que, quando utilizadas conforme as condições ambientais
1. ASSUNTOS DA AULA Durabilidade das estruturas, estádios e domínios. 2. CONCEITOS As estruturas de concreto devem ser projetadas e construídas de modo que, quando utilizadas conforme as condições ambientais
ESTABILIDADE GLOBAL DAS ESTRUTURAS
 1 ESTABILIDADE GLOBAL DAS ESTRUTURAS 1. INTRODUÇÃO As considerações que se seguem estão baseadas nos capítulos 14 e 15 da NB1/000. 1.1. Tipos de análise estrutural O objetivo da análise estrutural é determinar
1 ESTABILIDADE GLOBAL DAS ESTRUTURAS 1. INTRODUÇÃO As considerações que se seguem estão baseadas nos capítulos 14 e 15 da NB1/000. 1.1. Tipos de análise estrutural O objetivo da análise estrutural é determinar
ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS
 ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS Leandro de Faria Contadini 1, Renato Bertolino Junior 2 1 Eng. Civil, UNESP-Campus de Ilha Solteira 2 Prof. Titular, Depto de Engenharia
ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS Leandro de Faria Contadini 1, Renato Bertolino Junior 2 1 Eng. Civil, UNESP-Campus de Ilha Solteira 2 Prof. Titular, Depto de Engenharia
ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES
 ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES 2. VINCULAÇÕES DAS LAJES 3. CARREGAMENTOS DAS LAJES 3.1- Classificação das lajes retangulares 3.2- Cargas acidentais
ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES 2. VINCULAÇÕES DAS LAJES 3. CARREGAMENTOS DAS LAJES 3.1- Classificação das lajes retangulares 3.2- Cargas acidentais
Módulo 4 Vigas: Estados Limites Últimos Estados Limites de Serviço Detalhamento Exemplo. Segurança em Relação aos ELU e ELS
 NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo Segurança em Relação aos ELU e ELS ELU Solicitações Normais ELU Elementos Lineares Sujeitos à Força Cortante
NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo Segurança em Relação aos ELU e ELS ELU Solicitações Normais ELU Elementos Lineares Sujeitos à Força Cortante
SUPERESTRUTURA estrutura superestrutura infra-estrutura lajes
 SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
2 Materiais e Métodos
 1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
GALPÃO. Figura 87 instabilidade lateral
 9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
A distribuição de um momento aplicado em um nó de um pórtico por parcelas de momentos fletores equilibrantes nas barras adjacentes (Seção 8.2).
 8. PROCESSO DE CROSS O Processo de Cross, ou Método da Distribuição de Momentos (White et al. 976), é um método relativamente simples para o cálculo de momentos fletores em vigas contínuas, pórticos planos,
8. PROCESSO DE CROSS O Processo de Cross, ou Método da Distribuição de Momentos (White et al. 976), é um método relativamente simples para o cálculo de momentos fletores em vigas contínuas, pórticos planos,
Artigo submetido ao Curso de Engenharia Civil da UNESC - Como requisito parcial para obtenção do Título de Engenheiro Civil
 Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
Módulo 5 Lajes: Estados Limites Últimos Estados Limites de Serviço Detalhamento Exemplo. Dimensionamento de Lajes à Punção
 NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
ESTRUTURAS METÁLICAS UFPR CAPÍTULO 5 FLEXÃO SIMPLES
 ESTRUTURAS METÁLICAS UFPR CAPÍTULO 5 FLEXÃO SIMPLES 1 INDICE CAPÍTULO 5 DIMENSIONAMENTO BARRAS PRISMÁTICAS À FLEXÃO... 1 1 INTRODUÇÃO... 1 2 CONCEITOS GERAIS... 1 2.1 Comportamento da seção transversal
ESTRUTURAS METÁLICAS UFPR CAPÍTULO 5 FLEXÃO SIMPLES 1 INDICE CAPÍTULO 5 DIMENSIONAMENTO BARRAS PRISMÁTICAS À FLEXÃO... 1 1 INTRODUÇÃO... 1 2 CONCEITOS GERAIS... 1 2.1 Comportamento da seção transversal
CAPÍTULO III CARACTERIZAÇÃO DO COMPORTAMENTO DOS MATERIAIS
 CAPÍTULO III CARACTERIZAÇÃO DO COMPORTAMENTO DOS MATERIAIS 3. Caracterização do Comportamento dos Materiais 3.1. Comportamento geral do concreto É largamente conhecido que, após atingir a resistência última,
CAPÍTULO III CARACTERIZAÇÃO DO COMPORTAMENTO DOS MATERIAIS 3. Caracterização do Comportamento dos Materiais 3.1. Comportamento geral do concreto É largamente conhecido que, após atingir a resistência última,
3. Programa Experimental
 3. Programa Experimental 3.1. Considerações Iniciais Este estudo experimental foi desenvolvido no laboratório de estruturas e materiais (LEM) da PUC- Rio e teve o propósito de estudar o comportamento de
3. Programa Experimental 3.1. Considerações Iniciais Este estudo experimental foi desenvolvido no laboratório de estruturas e materiais (LEM) da PUC- Rio e teve o propósito de estudar o comportamento de
CAPÍTULO XI VALIDAÇÃO DO PROGRAMA DESENVOLVIDO
 CAPÍTULO XI VALIDAÇÃO DO PROGRAMA DESENVOLVIDO XI-0 11. desenvolvido 11. Apresentação do programa 11.1.1. Introdução Ao longo deste trabalho foi desenvolvido um programa de computador para análise de seções
CAPÍTULO XI VALIDAÇÃO DO PROGRAMA DESENVOLVIDO XI-0 11. desenvolvido 11. Apresentação do programa 11.1.1. Introdução Ao longo deste trabalho foi desenvolvido um programa de computador para análise de seções
Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections
 Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections Universidade Federal de Viçosa - Av. P.H. Rolfs s/n - Viçosa MG - 36.570-000
Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections Universidade Federal de Viçosa - Av. P.H. Rolfs s/n - Viçosa MG - 36.570-000
Esforços axiais e tensões normais
 Esforços axiais e tensões normais (Ref.: Beer & Johnston, Resistência dos Materiais, ª ed., Makron) Considere a estrutura abaixo, construída em barras de aço AB e BC, unidas por ligações articuladas nas
Esforços axiais e tensões normais (Ref.: Beer & Johnston, Resistência dos Materiais, ª ed., Makron) Considere a estrutura abaixo, construída em barras de aço AB e BC, unidas por ligações articuladas nas
1.1 Conceitos fundamentais... 19 1.2 Vantagens e desvantagens do concreto armado... 21. 1.6.1 Concreto fresco...30
 Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS
 AULA 04 ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS Prof. Felipe Brasil Viegas Prof. Eduardo Giugliani http://www.feng.pucrs.br/professores/giugliani/?subdiretorio=giugliani 0 AULA 04 INSTABILIDADE GERAL DE EDIFÍCIOS
AULA 04 ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS Prof. Felipe Brasil Viegas Prof. Eduardo Giugliani http://www.feng.pucrs.br/professores/giugliani/?subdiretorio=giugliani 0 AULA 04 INSTABILIDADE GERAL DE EDIFÍCIOS
Detalhamento de Concreto Armado
 Detalhamento de Concreto Armado (Exemplos Didáticos) José Luiz Pinheiro Melges Ilha Solteira, março de 2009 Exercícios - Detalhamento 1 1. DIMENSIONAR E DETALHAR A VIGA ABAIXO. 1.1 DADOS A princípio, por
Detalhamento de Concreto Armado (Exemplos Didáticos) José Luiz Pinheiro Melges Ilha Solteira, março de 2009 Exercícios - Detalhamento 1 1. DIMENSIONAR E DETALHAR A VIGA ABAIXO. 1.1 DADOS A princípio, por
cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha
 cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha MULTIGRAFICA 2010 Capa: foto do predio do CRUSP em construção,
cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha MULTIGRAFICA 2010 Capa: foto do predio do CRUSP em construção,
Exemplo de projeto estrutural
 Planta de formas do pavimento tipo Exemplo de projeto estrutural P1-30x30 P2-20x50 P3-30x30 V1 L1 L2 P4-20x50 P5-40x40 P-20x50 V2 Estruturas de Concreto Armado Prof. José Milton de Araújo L3 480 cm 480
Planta de formas do pavimento tipo Exemplo de projeto estrutural P1-30x30 P2-20x50 P3-30x30 V1 L1 L2 P4-20x50 P5-40x40 P-20x50 V2 Estruturas de Concreto Armado Prof. José Milton de Araújo L3 480 cm 480
Projeção ortográfica da figura plana
 A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO
 A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
Practical formulas for calculation of deflections of reinforced concrete beams
 Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
OE Seminário Aplicação do Eurocódigo 8 ao Projecto de Edifícios Projecto de estruturas para resistência aos sismos EC8-1
 Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
PRÉ-DIMENSIONAMENTO DA ESTRUTURA
 ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES
 DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período
 UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES
 CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES No item 4.2.3. 1.C da NB-1 alerta-se que nas lajes (e vigas) deve-se limitar as flechas das estruturas. No caso das lajes maciças, (nosso caso), será
CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES No item 4.2.3. 1.C da NB-1 alerta-se que nas lajes (e vigas) deve-se limitar as flechas das estruturas. No caso das lajes maciças, (nosso caso), será
AUTOMATIZAÇÃO DA VERIFICAÇÃO DE SEÇÕES DE CONCRETO ARMADO SUBMETIDAS À FLEXÃO COMPOSTA OBLÍQUA YURI MAGALHÃES CUNHA. Aprovado por:
 AUTOMATIZAÇÃO DA VERIFICAÇÃO DE SEÇÕES DE CONCRETO ARMADO SUBMETIDAS À FLEXÃO COMPOSTA OBLÍQUA YURI MAGALHÃES CUNHA Projeto de Graduação apresentado ao corpo docente do Departamento de Mecânica Aplicada
AUTOMATIZAÇÃO DA VERIFICAÇÃO DE SEÇÕES DE CONCRETO ARMADO SUBMETIDAS À FLEXÃO COMPOSTA OBLÍQUA YURI MAGALHÃES CUNHA Projeto de Graduação apresentado ao corpo docente do Departamento de Mecânica Aplicada
ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento
 Escola Politécnica da Universidade de São Paulo Departamento de Engenharia de Estruturas e Fundações ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento Prof. Túlio Nogueira
Escola Politécnica da Universidade de São Paulo Departamento de Engenharia de Estruturas e Fundações ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento Prof. Túlio Nogueira
ANÁLISE DA INFLUÊNCIA DA DOBRA NA RESISTÊNCIA À FLEXÃO DE UM PERFIL DE AÇO FORMADO A FRIO APLICADO NO SETOR DE ESTRUTURAS METÁLICAS
 ANÁLISE DA INFLUÊNCIA DA DOBRA NA RESISTÊNCIA À FLEXÃO DE UM PERFIL DE AÇO FORMADO A FRIO APLICADO NO SETOR DE ESTRUTURAS METÁLICAS Fábio Sumara Custódio (1), Marcio Vito (2) UNESC Universidade do Extremo
ANÁLISE DA INFLUÊNCIA DA DOBRA NA RESISTÊNCIA À FLEXÃO DE UM PERFIL DE AÇO FORMADO A FRIO APLICADO NO SETOR DE ESTRUTURAS METÁLICAS Fábio Sumara Custódio (1), Marcio Vito (2) UNESC Universidade do Extremo
CI202 - Métodos Numéricos
 CI202 - Métodos Numéricos Lista de Exercícios 2 Zeros de Funções Obs.: as funções sen(x) e cos(x) devem ser calculadas em radianos. 1. Em geral, os métodos numéricos para encontrar zeros de funções possuem
CI202 - Métodos Numéricos Lista de Exercícios 2 Zeros de Funções Obs.: as funções sen(x) e cos(x) devem ser calculadas em radianos. 1. Em geral, os métodos numéricos para encontrar zeros de funções possuem
1. Definição dos Elementos Estruturais
 A Engenharia e a Arquitetura não devem ser vistas como duas profissões distintas, separadas, independentes uma da outra. Na verdade elas devem trabalhar como uma coisa única. Um Sistema Estrutural definido
A Engenharia e a Arquitetura não devem ser vistas como duas profissões distintas, separadas, independentes uma da outra. Na verdade elas devem trabalhar como uma coisa única. Um Sistema Estrutural definido
CAPÍTULO 3 PROBLEMA 3.1
 PÍTULO 3 PROLM 3.1 onsidere a placa em forma de L, que faz parte da fundação em ensoleiramento geral de um edifício, e que está sujeita às cargas indicadas. etermine o módulo, a direcção, o sentido e o
PÍTULO 3 PROLM 3.1 onsidere a placa em forma de L, que faz parte da fundação em ensoleiramento geral de um edifício, e que está sujeita às cargas indicadas. etermine o módulo, a direcção, o sentido e o
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I Estruturas II. Capítulo 5 Torção
 Capítulo 5 Torção 5.1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e
Capítulo 5 Torção 5.1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e
CAPÍTULO V CISALHAMENTO CONVENCIONAL
 1 I. ASPECTOS GERAIS CAPÍTULO V CISALHAMENTO CONVENCIONAL Conforme já foi visto, a tensão representa o efeito de um esforço sobre uma área. Até aqui tratamos de peças submetidas a esforços normais a seção
1 I. ASPECTOS GERAIS CAPÍTULO V CISALHAMENTO CONVENCIONAL Conforme já foi visto, a tensão representa o efeito de um esforço sobre uma área. Até aqui tratamos de peças submetidas a esforços normais a seção
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil. Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV
 UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE. Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.
 ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.pt 1 Mestranda e Bolseira de investigação do Departamento
ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.pt 1 Mestranda e Bolseira de investigação do Departamento
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO
 i UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO PÓS-PROCESSADOR PARA DIMENSIONAMENTO E VERIFICAÇÃO DE BARRAS DE
i UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO PÓS-PROCESSADOR PARA DIMENSIONAMENTO E VERIFICAÇÃO DE BARRAS DE
Lista de exercícios sobre barras submetidas a força normal
 RESISTÊNCIA DOS MATERIAIS I Lista de exercícios sobre barras submetidas a força normal 1) O cabo e a barra formam a estrutura ABC (ver a figura), que suporta uma carga vertical P= 12 kn. O cabo tem a área
RESISTÊNCIA DOS MATERIAIS I Lista de exercícios sobre barras submetidas a força normal 1) O cabo e a barra formam a estrutura ABC (ver a figura), que suporta uma carga vertical P= 12 kn. O cabo tem a área
Este curso consiste de uma introdução ao cálculo estrutural das vigas de concreto armado, ilustrada através do estudo de vigas retas de edifícios.
 Introdução 1 1. Introdução O objetivo do cálculo de uma estrutura de concreto armado é o de se garantir: uma segurança adequada contra a ruptura decorrente das solicitações; deformações decorrentes das
Introdução 1 1. Introdução O objetivo do cálculo de uma estrutura de concreto armado é o de se garantir: uma segurança adequada contra a ruptura decorrente das solicitações; deformações decorrentes das
ESTUDO DE PILARES DE CONCRETO ARMADO E PILARES MISTOS DE AÇO E CONCRETO TOTALMENTE REVESTIDOS
 UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE ESTRUTURAS DISSERTAÇÃO DE MESTRADO ESTUDO DE PILARES DE CONCRETO ARMADO E PILARES MISTOS DE AÇO E CONCRETO
UNIVERSIDADE FEDERAL DE MINAS GERAIS ESCOLA DE ENGENHARIA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE ESTRUTURAS DISSERTAÇÃO DE MESTRADO ESTUDO DE PILARES DE CONCRETO ARMADO E PILARES MISTOS DE AÇO E CONCRETO
PROGRAMA AUTOTRUSS 2.0
 PROGRAMA AUTOTRUSS 2.0 Universidade Estadual de Campinas Faculdade de Engenharia Civil, Arquitetura e Urbanismo Departamento de Estruturas LabMeC Autores: Prof. Dr. João Alberto Venegas Requena requena@fec.unicamp.br
PROGRAMA AUTOTRUSS 2.0 Universidade Estadual de Campinas Faculdade de Engenharia Civil, Arquitetura e Urbanismo Departamento de Estruturas LabMeC Autores: Prof. Dr. João Alberto Venegas Requena requena@fec.unicamp.br
VIGAS E LAJES DE CONCRETO ARMADO
 UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Curso: Arquitetura e Urbanismo Disciplina: 6033 - SISTEMAS ESTRUTURAIS I Notas de Aula
UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Curso: Arquitetura e Urbanismo Disciplina: 6033 - SISTEMAS ESTRUTURAIS I Notas de Aula
Flambagem de Colunas Introdução
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Flambagem de Colunas Introdução Os sistemas
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Flambagem de Colunas Introdução Os sistemas
Engº Marcelo Cuadrado Marin Engº Mounir Khalil El Debs
 CONTRIBUIÇÃO PARA A AVALIAÇÃO DA REDUÇÃO DA RIGIDEZ DE ELEMENTOS ESTRUTURAIS DE CONCRETO PRÉ-MOLDADO DE EDIFÍCIOS DE MÚLTIPLOS PAVIMENTOS PARA ANÁLISE DA ESTABILIDADE GLOBAL. Engº Marcelo Cuadrado Marin
CONTRIBUIÇÃO PARA A AVALIAÇÃO DA REDUÇÃO DA RIGIDEZ DE ELEMENTOS ESTRUTURAIS DE CONCRETO PRÉ-MOLDADO DE EDIFÍCIOS DE MÚLTIPLOS PAVIMENTOS PARA ANÁLISE DA ESTABILIDADE GLOBAL. Engº Marcelo Cuadrado Marin
PROVAESCRITA CARGO: ENGENHARIA CIVIL I
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO SUL DE MINAS GERAIS CONCURSO PÚBLICO DE DOCENTES DO QUADRO EFETIVO EDITAL
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO SUL DE MINAS GERAIS CONCURSO PÚBLICO DE DOCENTES DO QUADRO EFETIVO EDITAL
Pesquisa Operacional. Função Linear - Introdução. Função do 1 Grau. Função Linear - Exemplos Representação no Plano Cartesiano. Prof.
 Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
6 Vigas: Solicitações de Flexão
 6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
2 Sistema de Lajes com Forma de Aço Incorporado
 2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398
 Frefer System Estruturas Metálicas Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398 www.frefersystem.com.br A
Frefer System Estruturas Metálicas Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398 www.frefersystem.com.br A
5ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO FLEXÃO
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 5ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 5ª LISTA
UNIVERSIDADE DE MARÍLIA
 UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
Mecânica Aplicada. Engenharia Biomédica ESFORÇOS INTERNOS EM PEÇAS LINEARES
 Mecânica plicada Engenharia iomédica ESFORÇOS INTERNOS EM PEÇS INERES Versão 0.2 Setembro de 2008 1. Peça linear Uma peça linear é um corpo que se pode considerar gerado por uma figura plana cujo centro
Mecânica plicada Engenharia iomédica ESFORÇOS INTERNOS EM PEÇS INERES Versão 0.2 Setembro de 2008 1. Peça linear Uma peça linear é um corpo que se pode considerar gerado por uma figura plana cujo centro
MÓDULO 1 Projeto e dimensionamento de estruturas metálicas em perfis soldados e laminados
 Projeto e Dimensionamento de de Estruturas metálicas e mistas de de aço e concreto MÓDULO 1 Projeto e dimensionamento de estruturas metálicas em perfis soldados e laminados 1 Sistemas estruturais: coberturas
Projeto e Dimensionamento de de Estruturas metálicas e mistas de de aço e concreto MÓDULO 1 Projeto e dimensionamento de estruturas metálicas em perfis soldados e laminados 1 Sistemas estruturais: coberturas
Lajes de Edifícios de Concreto Armado
 Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
Relações entre tensões e deformações
 3 de dezembro de 0 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
3 de dezembro de 0 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
Miguel C. Branchtein, Delegacia Regional do Trabalho no Rio Grande do Sul
 DETERMINAÇÃO DE CONDIÇÃO DE ACIONAMENTO DE FREIO DE EMERGÊNCIA TIPO "VIGA FLUTUANTE" DE ELEVADOR DE OBRAS EM CASO DE QUEDA DA CABINE SEM RUPTURA DO CABO Miguel C. Branchtein, Delegacia Regional do Trabalho
DETERMINAÇÃO DE CONDIÇÃO DE ACIONAMENTO DE FREIO DE EMERGÊNCIA TIPO "VIGA FLUTUANTE" DE ELEVADOR DE OBRAS EM CASO DE QUEDA DA CABINE SEM RUPTURA DO CABO Miguel C. Branchtein, Delegacia Regional do Trabalho
EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO
 EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO Ao incidir em uma lente convergente, um feixe paralelo de luz, depois de passar pela lente, é concentrado em um ponto denominado foco (representado por
EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO Ao incidir em uma lente convergente, um feixe paralelo de luz, depois de passar pela lente, é concentrado em um ponto denominado foco (representado por
Efeitos dinâmicos do Vento em Edifícios Altos. Byl Farney Rodrigues da CUNHA JR¹; Frederico Martins Alves da SILVA²;
 Efeitos dinâmicos do Vento em Edifícios Altos Byl Farney Rodrigues da CUNHA JR¹; Frederico Martins Alves da SILVA²; 3 Zenón José Guzmán Nuñez DEL PRADO 1,2,3 Escola de Engenharia Civil UFG 1 farneyjr@hotmail.com,
Efeitos dinâmicos do Vento em Edifícios Altos Byl Farney Rodrigues da CUNHA JR¹; Frederico Martins Alves da SILVA²; 3 Zenón José Guzmán Nuñez DEL PRADO 1,2,3 Escola de Engenharia Civil UFG 1 farneyjr@hotmail.com,
Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr
 Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr Universidade Estadual de Campinas UNICAMP Faculdade de Engenharia Civil, Arquitetura e Urbanismo
Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr Universidade Estadual de Campinas UNICAMP Faculdade de Engenharia Civil, Arquitetura e Urbanismo
Lista de Exercícios-PRA - Estática R. C. Hibbeler I - Adição de forças vetoriais
 Lista de Exercícios-PRA - Estática R. C. Hibbeler I - Adição de forças vetoriais Forças são grandezas vetoriais, portanto são manipuladas através das regras da geometria analítica. Duas leis são válidas
Lista de Exercícios-PRA - Estática R. C. Hibbeler I - Adição de forças vetoriais Forças são grandezas vetoriais, portanto são manipuladas através das regras da geometria analítica. Duas leis são válidas
Curso de Engenharia Civil. Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CAPÍTULO 6: TORÇÃO
 Curso de Engenharia Civil Universidade Estadual de Maringá Centro de ecnologia Departamento de Engenharia Civil CPÍULO 6: ORÇÃO Revisão de Momento orçor Convenção de Sinais: : Revisão de Momento orçor
Curso de Engenharia Civil Universidade Estadual de Maringá Centro de ecnologia Departamento de Engenharia Civil CPÍULO 6: ORÇÃO Revisão de Momento orçor Convenção de Sinais: : Revisão de Momento orçor
ESTRUTURAS DE CONCRETO CAPÍTULO 2 CARACTERÍSTICAS DO CONCRETO
 ESTRUTURAS DE CONCRETO CAPÍTULO 2 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos Março de 2004 CARACTERÍSTICAS DO CONCRETO Como foi visto no capítulo anterior, a mistura em proporção adequada
ESTRUTURAS DE CONCRETO CAPÍTULO 2 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos Março de 2004 CARACTERÍSTICAS DO CONCRETO Como foi visto no capítulo anterior, a mistura em proporção adequada
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T
 DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
Análise estrutural. Objetivos da aula. Mostrar como determinar as forças nos membros de treliças usando o método dos nós e o método das seções.
 Análise estrutural Objetivos da aula Mostrar como determinar as forças nos membros de treliças usando o método dos nós e o método das seções. slide 1 Treliças simples Treliça é uma estrutura de vigas conectadas
Análise estrutural Objetivos da aula Mostrar como determinar as forças nos membros de treliças usando o método dos nós e o método das seções. slide 1 Treliças simples Treliça é uma estrutura de vigas conectadas
INDICE 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5
 INDICE 1.INTRODUÇÃO 3 2.OBJETIVO 4 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5 3.1 Caixa d`água Vazia...... 6 3.1.1 Parede XZ (Par 1 e Par 3)... 7 3.1.2. Parede YZ (Par 4 e Par
INDICE 1.INTRODUÇÃO 3 2.OBJETIVO 4 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5 3.1 Caixa d`água Vazia...... 6 3.1.1 Parede XZ (Par 1 e Par 3)... 7 3.1.2. Parede YZ (Par 4 e Par
Análise do Uso de Vigas Transversinas em Pontes de Concreto Armado
 Análise do Uso de Vigas Transversinas em Pontes de Concreto Armado João Paulo Teixeira Oliveira Rodrigues Fulgêncio 1 Fernando Amorim de Paula 2 Crysthian Purcino Bernardes Azevedo 3 Resumo O emprego de
Análise do Uso de Vigas Transversinas em Pontes de Concreto Armado João Paulo Teixeira Oliveira Rodrigues Fulgêncio 1 Fernando Amorim de Paula 2 Crysthian Purcino Bernardes Azevedo 3 Resumo O emprego de
Aula 04 Peças submetidas à flexão simples: solicitações normais.
 Aula 04 Peças submetidas à flexão simples: solicitações normais. 1. Introdução. Nas aulas anteriores foram fornecidas as bases teóricas para verificação analítica da segurança de estruturas de concreto.
Aula 04 Peças submetidas à flexão simples: solicitações normais. 1. Introdução. Nas aulas anteriores foram fornecidas as bases teóricas para verificação analítica da segurança de estruturas de concreto.
