PROBABILIDADE E ESTATÍSTICA. Profa. Dra. Yara de Souza Tadano
|
|
|
- Mafalda Benke Cabreira
- 7 Há anos
- Visualizações:
Transcrição
1 PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br
2 Aula 8 11/2014 Distribuição Normal
3 Vamos apresentar distribuições de probabilidades para variáveis aleatórias contínuas. Para ilustrar a correspondência entre área e probabilidade, vamos aprender as Em seguida, as., que ocorrem frequentemente em aplicações reais e têm papel importante nos métodos de inferência estatística. Probabilidade e Estatística 3/41
4 Distribuição Normal Se uma variável aleatória contínua tem uma distribuição com um gráfico simétrico e em forma de sino, e que pode ser descrito pela equação a seguir, dizemos que ela tem Depende apenas de µ e σ y = e 1" x µ % $ ' 2# σ & σ 2π 2 Probabilidade e Estatística 4/41
5 Distribuição Normal Padrão A tem as seguintes propriedades: 1. Seu gráfico tem forma de sino; 2. Sua média é igual a 0 (µ = 0); 3. Seu desvio-padrão é igual a 1 (σ = 1). Probabilidade e Estatística 5/41
6 Distribuições Uniformes O foco será o estudo da Distribuição de Probabilidade Normal, porém iremos começar com a, que nos dará informações para compreender estas duas propriedades importantes: 1. A área sob o gráfico de uma distribuição de probabilidades é igual a 1; 2. Há uma correspondência entre área e probabilidade (ou frequência relativa), de modo que algumas propriedades podem ser encontradas pela identificação das áreas correspondentes. Probabilidade e Estatística 6/41
7 Distribuição Uniforme Uma variável aleatória contínua tem uma se seus valores se espalham uniformemente sobre a faixa de valores possíveis. O gráfico de uma Distribuição Uniforme resulta em uma forma retangular. Probabilidade e Estatística 7/41
8 EXEMPLO A companhia de Energia fornece eletricidade com níveis de voltagem que são uniformemente distribuídos entre 123 e 125 volts. Isto é, qualquer quantidade de voltagem entre 123 e 125 volts é possível, e todos os possíveis valores são equiprováveis. Se selecionamos aleatoriamente um dos níveis de voltagem e representarmos seu valor pela variável aleatória x, então x tem uma distribuição que tem um gráfico como: Probabilidade e Estatística 8/41
9 EXEMPLO Um gráfico de uma distribuição de probabilidade contínua, como este, é chamado de. Probabilidade e Estatística 9/41
10 EXEMPLO Dada a distribuição uniforme do nível de voltagem, ache a probabilidade de que um nível de voltagem selecionado aleatoriamente seja maior do que 124,5 volts. Probabilidade e Estatística 10/41
11 Curva de Densidade Uma curva de densidade deve satisfazer os seguintes requisitos: 1. A área sob a curva tem que ser igual a Cada ponto na curva tem que ter uma altura vertical maior ou igual a 0, ou seja, a curva não pode estar abaixo do eixo x. Probabilidade e Estatística 11/41
12 Área Probabilidade Como a área total sob a curva de densidade é igual a 1, existe uma correspondência entre e. No caso da Distribuição Uniforme, a área abaixo da curva, que é facilmente calculada por: Área = Base Altura, corresponderá à probabilidade referente a esta área. Probabilidade e Estatística 12/41
13 Área Probabilidade Como a curva de densidade de uma Distribuição Normal tem a forma de sino, é mais difícil acharmos a área, porém o princípio básico é o mesmo: Há uma correspondência entre e Probabilidade e Estatística 13/41
14 Distribuição Normal Padrão A distribuição normal padrão é uma distribuição de probabilidade normal com média µ = 0 e desvio-padrão σ = 1, e a área total sob a curva de densidade é Escore z Probabilidade e Estatística 14/41
15 Distribuição Normal Padrão Não é fácil a determinação de áreas para a curva de densidade da distribuição normal padrão, então necessitamos de valores já calculados previamente e que constam na seguinte tabela: Probabilidade e Estatística 15/41
16 Distribuição Normal Padrão Ao usar a Tabela da distribuição normal padrão, temos que: 1. A tabela refere-se apenas à, que tem média 0 e desvio padrão 1; 2. A tabela é apresentada em duas páginas, uma para e a outra para ; 3. Cada valor no corpo da tabela é a até uma reta vertical sobre um valor específico do escore z; Probabilidade e Estatística 16/41
17 Distribuição Normal Padrão 4. Ao trabalhar com um gráfico, entre escores z e áreas. Escore z Distância na escala horizontal da distribuição normal padrão; refere-se à coluna à esquerda e à linha do topo da tabela. Área Região sob a curva; refere-se aos valores no corpo da tabela. Probabilidade e Estatística 17/41
18 Distribuição Normal Padrão z,00,01-3,4 0,0003 0,0003-3,3 0,0005 0,0005-3,2 0,0007 0,0007-3,1 0,0010 0,0009 Área Probabilidade e Estatística 18/41
19 EXEMPLO 1 Uma companhia de instrumentos científicos de precisão fabrica termômetros que devem informar temperaturas de 0 o C no ponto de congelamento da água. Testes em uma grande amostra desses instrumentos revelam que, no ponto de congelamento da água, alguns termômetros indicam temperaturas abaixo de 0 o C e alguns dão temperaturas acima de 0 o C. Suponha que a leitura média seja 0 o C e que o desvio-padrão das leituras seja 1,00 o C. Suponha, também, que as leituras sejam normalmente distribuídas. Se um termômetro é selecionado aleatoriamente, ache a probabilidade de que, no ponto de congelamento da água, a leitura seja menor que 1,27 o C. Probabilidade e Estatística 19/41
20 EXEMPLO 1 Gostaríamos de saber agora, qual a probabilidade de selecionarmos aleatoriamente um termômetro que apresente leitura (no ponto de congelamento da água) superior a -1,23 o C. Agora, determine a probabilidade de selecionarmos aleatoriamente um termômetro que apresente letirua (no ponto de congelamento da água) entre -2,00 o C e 1,50 o C. Probabilidade e Estatística 20/41
21 O último resultado do exemplo 1, pode ser generalizado como a seguinte regra: A área correspondente à região entre dois escores z específicos pode ser encontrada achando-se. Probabilidade e Estatística 21/41
22 Com uma distribuição de probabilidade contínua, tal como a distribuição normal, a probabilidade de se obter qualquer valor único exato é 0 (P(z=a) = 0). De modo que: P (a z b) = P (a < z < b) Então, a probabilidade de se obter um escore z no é igual à probabilidade de se obter um escore z. Probabilidade e Estatística 22/41
23 Escores z Áreas conhecidas Em muitos casos, temos que: Dada uma área (ou probabilidade), achar o escore z correspondente. Probabilidade e Estatística 23/41
24 Escores z Áreas conhecidas Procedimento para a determinação de um Escore z a partir de uma área conhecida. 1. Desenhe uma curva em forma de sino e identifique a região sob a curva que corresponde à probabilidade dada. Se a região não é uma região acumulada à esquerda, trabalhe com regiões conhecidas que sejam regiões acumuladas à esquerda. 2. Usando a área acumulada à esquerda, localize a probabilidade mais próxima no corpo da tabela da distribuição normal padrão e identifique o escore z correspondente. Probabilidade e Estatística 24/41
25 Escores z Áreas conhecidas Se um valor desejado de área o valor ; Se um valor está a tabela, selecione o ; na tabela, selecione entre dois valores da Para escores z, podemos usar como uma aproximação para a área acumulada à esquerda; Para escores z, podemos usar como uma aproximação para a área acumulada à esquerda. Probabilidade e Estatística 25/41
26 EXEMPLO 2 Use os mesmos termômetros do exemplo anterior, com leituras de temperatura no ponto de congelamento da água normalmente distribuídas, com média de 0 o C e desviopadrão de 1 o C. Ache a temperatura correspondente a P 95, o 95 o percentil. Isto é, ache a temperatura que separa os 95% inferiores dos 5% superiores. Ache, agora, as temperaturas separando os 2,5% inferiores e os 2,5% superiores. Probabilidade e Estatística 26/41
27 Valores Críticos Para uma distribuição normal, um valor crítico é um escore z na fronteira que separa os escores z que têm ocorrência provável daqueles que têm ocorrência improvável. Valores críticos comuns são z = -1,96 e z = 1,96. Os valores abaixo de 1,96 são improváveis de acontecer, pois ocorrem em apenas 2,5% dos dados, e os valores acima de z = 1,96 também são improváveis de acontecer, pois também ocorrem em apenas 2,5% das leituras. Probabilidade e Estatística 27/41
28 Valores Críticos Na expressão z α, faça α = 0,025 e ache o valor de z 0,025. A notação de z 0,025 é usada para representar o escore z com uma área de 0,025 à sua direita. Recorrendo à tabela da distribuição normal, podemos observar que z 0,025 = 1,96. Probabilidade e Estatística 28/41
29 Valores Críticos Para encontrar o valor de z α, usando a tabela de distribuição normal padrão, use o valor 1 α. Probabilidade e Estatística 29/41
30 Aplicações da distribuição normal É pouco comum encontrarmos situações que seguem uma distribuição normal padrão. As distribuições normais típicas envolvem médias diferentes de 0 e desvios-padrão diferentes de 1. Nestes casos, devemos ser capazes de encontrar probabilidades correspondentes a valores da variável x e, dado algum valor de probabilidade, devemos ser capazes de encontrar o valor correspondente da variável x. Probabilidade e Estatística 30/41
31 Aplicações da distribuição normal Para trabalhar com distribuições normais não padronizadas, simplesmente iremos padronizar os valores para usar os mesmo procedimentos aprendidos até aqui. Se convertermos valores para escores z padronizados usando a fórmula a seguir, os procedimentos usados serão os mesmos usados para a distribuição normal padrão. z = x µ σ Arredonde os escores z para 2 casas decimais Probabilidade e Estatística 31/41
32 Aplicações da distribuição normal Procedimento para achar áreas com uma distribuição normal não padronizada: 1. Esboce a curva normal, marque a média e os valores específicos de x e, então, sombreie a região que representa a probabilidade desejada; 2. Para cada valor relevante de x que representa um limite da região sombreada, converta o valor em seu escore z equivalente; 3. Consulte a tabela para achar a área da região sombreada. Probabilidade e Estatística 32/41
33 EXEMPLO 3 Uma porta típica de uma casa tem uma altura de 2 metros. Dado que as alturas de homens são normalmente distribuídas, com média de 1,725 m e desvio-padrão de 7 cm,. Ache a porcentagem de homens que passarão por uma portapadrão sem se curvar e sem bater a cabeça. Essa porcentagem é alta o bastante para que se continue a usar 2 metros como padrão de altura? Probabilidade e Estatística 33/41
34 EXEMPLO 3 O valor do escore z é 3,93, dando uma área de 0,9999. Conclui-se que a proporção de homens que podem passar pelas portas com altura-padrão de 2 m é 0,9999 ou 99,99%. Muitos poucos homens não poderão passar sem abaixarem ou baterem a cabeça. Essa porcentagem é alta o suficiente para justificar o suo de 2 m como altura-padrão para portas. Probabilidade e Estatística 34/41
35 EXEMPLO 4 Os pesos ao nascer nos Estados Unidos são distribuídos normalmente, com média de 3420 g e desvio-padrão de 495 g. O Hospital Geral de Newport exige tratamento especial para bebês que nasçam com menos de 2450 g (não usualmente leves) ou mais de 4390 g (não usualmente pesados). Qual é a porcentagem de bebês que não requerem tratamento especial por terem pesos ao nascer entre 2450 g e 4390g? Sob essas condições, muitos bebês precisam de cuidados especiais? Probabilidade e Estatística 35/41
36 EXEMPLO 4 Expressando o resultado em porcentagem, podemos concluir que 95% dos bebês não exigem cuidados especiais por terem pesos entre 2450 g e 4390 g. Segue que 5% dos bebês requerem tratamento especial por serem não usualmente leves ou pesados. A taxa de 5%, provavelmente, não é muito alta para hospitais típicos. Probabilidade e Estatística 36/41
37 Áreas conhecidas Não confunda escores z e áreas; Escolha o lado correto (direito/esquerdo) do gráfico; Um escore z tem que ser negativo sempre que se localizar na metade esquerda da distribuição normal; Áreas (ou probabilidades) são valores positivos ou nulos, mas NUNCA negativos. Probabilidade e Estatística 37/41
38 Áreas conhecidas Procedimento para achar valores a partir de áreas conhecidas 1. Esboce o gráfico da distribuição normal, introduza a probabilidade ou porcentagem dada na região apropriada do gráfico e identifique o(s) valor(es) x de interesse; 2. Use a Tabela para achar o escore z correspondente à área mais próxima e, em seguida, identifique o escore z correspondente; Probabilidade e Estatística 38/41
39 Áreas conhecidas 3. Usando a fórmula de conversão de valores para escore z, encontre o valor de x; z = x µ σ 4. Consulte o esboço da curva para verificar se a solução faz sentido no contexto do gráfico e no contexto do problema. Probabilidade e Estatística 39/41
40 EXEMPLO 5 No planejamento de um ambiente, um critério comum é que se ajuste a 95% da população. Qual a altura de uma porta se 95% dos homens devem passar por ela sem se abaixar e sem bater a cabeça? Isto é, ache o 95 º percentil das alturas dos homens, que são normalmente distribuídas, com média de 1,75m e desviopadrão de 0,07 m. Probabilidade e Estatística 40/41
41 EXEMPLO 5 O resultado é: x = 1,87 m. Isto significa que uma altura de porta de 1,87 permitiria que 95% dos homens passassem sem se curvar ou bater a cabeça. Assim, 5% dos homens não passariam por uma porta com altura de 1,87 m. Como muitos homens passam por portas com muita frequência, esta taxa de 5%, provavelmente, não seria prática. Probabilidade e Estatística 41/41
42 EXEMPLO 6 O Hospital Geral de Newport deseja redefinir os pesos ao nascer mínimo e máximo que exigem tratamento especial por serem não usualmente baixos ou altos. Depois de considerar fatores relevantes, um comitê recomenda um tratamento especial para os 3% inferiores e os 1% superiores dos pesos ao nascer. Ajude o comitê a identificar os pesos ao nascer que separam os 3% inferiores e os 1% superiores. Os pesos ao nascer, nos Estados Unidos, são normalmente distribuídos, com média de 3420 g e desvio-padrão de 495g. Probabilidade e Estatística 42/41
43 EXEMPLO 6 O Resultado nos indica que: O peso ao nascer de 2489 g (arredondado) separa os 3% inferiores dos pesos ao nascer, e 4573 (arredondado) separa o 1% superior dos pesos ao nascer. Agora, o hospital tem critérios bem definidos para determinar se um bebê recém-nascido deve receber tratamento especial relativo a um peso ao nascer não usualmente baixo ou alto. Probabilidade e Estatística 43/41
MÉTODOS EXPERIMENTAIS E TÉCNICAS DE MEDIDAS
 MÉTODOS EXPERIMENTAIS E TÉCNICAS DE MEDIDAS Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 5 Distribuição Normal Variável Aleatória Contínua Mestrado em Eng. Mecânica 3/65 Função de Probabilidade
MÉTODOS EXPERIMENTAIS E TÉCNICAS DE MEDIDAS Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 5 Distribuição Normal Variável Aleatória Contínua Mestrado em Eng. Mecânica 3/65 Função de Probabilidade
AULA 02 Distribuição de Probabilidade Normal
 1 AULA 02 Distribuição de Probabilidade Normal Ernesto F. L. Amaral 20 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
1 AULA 02 Distribuição de Probabilidade Normal Ernesto F. L. Amaral 20 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
AULA 02 Distribuição de probabilidade normal
 1 AULA 02 Distribuição de probabilidade normal Ernesto F. L. Amaral 02 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH)
1 AULA 02 Distribuição de probabilidade normal Ernesto F. L. Amaral 02 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH)
Estatística e Probabilidade Aula 06 Distribuições de Probabilidades. Prof. Gabriel Bádue
 Estatística e Probabilidade Aula 06 Distribuições de Probabilidades Prof. Gabriel Bádue Teoria A distribuição de Poisson é uma distribuição discreta de probabilidade, aplicável a ocorrências de um evento
Estatística e Probabilidade Aula 06 Distribuições de Probabilidades Prof. Gabriel Bádue Teoria A distribuição de Poisson é uma distribuição discreta de probabilidade, aplicável a ocorrências de um evento
PROBABILIDADE E ESTATÍSTICA. Profa. Dra. Yara de Souza Tadano
 PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 11/2014 Variáveis Aleatórias Variáveis Aleatórias Probabilidade e Estatística 3/41 Variáveis Aleatórias Colete
PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 11/2014 Variáveis Aleatórias Variáveis Aleatórias Probabilidade e Estatística 3/41 Variáveis Aleatórias Colete
Notas de Aula. Capítulo 6 Distribuição de Probabilidade Normal. Seção 6-1 Visão Geral. Estatística Elementar 10ª Edição. by Mario F.
 Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Copyright 2007 2007 Pearson Education, Inc Inc Publishing as as Pearson Addison-Wesley. Slide 1 Capítulo 6 Distribuição
Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Copyright 2007 2007 Pearson Education, Inc Inc Publishing as as Pearson Addison-Wesley. Slide 1 Capítulo 6 Distribuição
Notas de Aula. Estatística Elementar. by Mario F. Triola. Tradução: Denis Santos
 Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Copyright 2007 2007 Pearson Education, Inc Inc Publishing as as Pearson Addison-Wesley. Slide 1 Capítulo 6 Distribuição
Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Copyright 2007 2007 Pearson Education, Inc Inc Publishing as as Pearson Addison-Wesley. Slide 1 Capítulo 6 Distribuição
Distribuição Gaussiana
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Estatística Distribuição Gaussiana Introdução à Bioestatística Turma Nutrição Aula 7: Distribuição Normal (Gaussiana) Distribuição
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Estatística Distribuição Gaussiana Introdução à Bioestatística Turma Nutrição Aula 7: Distribuição Normal (Gaussiana) Distribuição
5- Variáveis aleatórias contínuas
 5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, atribuímos probabilidades a intervalos de valores. Exemplo 5.1 Seja a variável correspondente ao tempo de vida útil de determinado
5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, atribuímos probabilidades a intervalos de valores. Exemplo 5.1 Seja a variável correspondente ao tempo de vida útil de determinado
( x) = a. f X. = para x I. Algumas Distribuições de Probabilidade Contínuas
 Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
PROBABILIDADE E ESTATÍSTICA. Profa. Dra. Yara de Souza Tadano
 PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 4 09/2014 Estatística Descritiva Medidas de Variação Probabilidade e Estatística 3/42 Medidas de Variação Vamos
PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 4 09/2014 Estatística Descritiva Medidas de Variação Probabilidade e Estatística 3/42 Medidas de Variação Vamos
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine)
 Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
Probabilidade e Estatística
 Probabilidade e Estatística Aula 6 Distribuições Contínuas (Parte 02) Leitura obrigatória: Devore, Capítulo 4 Chap 6-1 Distribuições de Probabilidade Distribuições de Probabilidade Distribuições de Probabilidade
Probabilidade e Estatística Aula 6 Distribuições Contínuas (Parte 02) Leitura obrigatória: Devore, Capítulo 4 Chap 6-1 Distribuições de Probabilidade Distribuições de Probabilidade Distribuições de Probabilidade
Estatística I Aula 8. Prof.: Patricia Maria Bortolon, D. Sc.
 Estatística I Aula 8 Prof.: Patricia Maria Bortolon, D. Sc. MODELOS PROBABILÍSTICOS MAIS COMUNS VARIÁVEIS ALEATÓRIAS CONTÍNUAS Lembram o que vimos sobre V.A. contínua na Aula 6? Definição: uma variável
Estatística I Aula 8 Prof.: Patricia Maria Bortolon, D. Sc. MODELOS PROBABILÍSTICOS MAIS COMUNS VARIÁVEIS ALEATÓRIAS CONTÍNUAS Lembram o que vimos sobre V.A. contínua na Aula 6? Definição: uma variável
Distribuição Normal. Prof a Dr a Alcione Miranda dos Santos. Abril, 2011
 Distribuição Normal Prof a Dr a Alcione Miranda dos Santos Universidade Federal do Maranhão Programa de Pós-Graduação em Saúde Coletiva email:alcione.miranda@gmail.com Abril, 2011 1 / 18 Sumário Introdução
Distribuição Normal Prof a Dr a Alcione Miranda dos Santos Universidade Federal do Maranhão Programa de Pós-Graduação em Saúde Coletiva email:alcione.miranda@gmail.com Abril, 2011 1 / 18 Sumário Introdução
5 Distribuição normal de probabilidade. Estatística Aplicada Larson Farber
 5 Distribuição normal de probabilidade Estatística Aplicada Larson Farber Seção 5.1 Introdução às distribuições normais Propriedades de uma distribuição normal Suas média, mediana e moda são iguais. Tem
5 Distribuição normal de probabilidade Estatística Aplicada Larson Farber Seção 5.1 Introdução às distribuições normais Propriedades de uma distribuição normal Suas média, mediana e moda são iguais. Tem
5- Variáveis aleatórias contínuas
 5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, associamos probabilidades a intervalos de valores da variável. Exemplo 5.1 Seja a variável correspondente ao tempo até a cura de pacientes
5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, associamos probabilidades a intervalos de valores da variável. Exemplo 5.1 Seja a variável correspondente ao tempo até a cura de pacientes
ESTIMAÇÃO POR INTERVALO DE CONFIANÇA. Profª Sheila Oro 1
 ESTIMAÇÃO POR INTERVALO DE CONFIANÇA Profª Sheila Oro 1 DEFINIÇÃO Um itervalo de confiança (ou estimativa intervalar) é uma faixa (ou um intervalo) de valores usada para se estimar o verdadeiro valor de
ESTIMAÇÃO POR INTERVALO DE CONFIANÇA Profª Sheila Oro 1 DEFINIÇÃO Um itervalo de confiança (ou estimativa intervalar) é uma faixa (ou um intervalo) de valores usada para se estimar o verdadeiro valor de
AULA 03 Estimativas e tamanhos amostrais
 1 AULA 03 Estimativas e tamanhos amostrais Ernesto F. L. Amaral 03 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade
1 AULA 03 Estimativas e tamanhos amostrais Ernesto F. L. Amaral 03 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade
Notas de Aula. Estatística Elementar. by Mario F. Triola. Tradução: Denis Santos
 Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 7 Estimativas e Tamanhos Amostrais 7-1 Visão Geral 7-2 Estimando a Proporção Populacional 7-3 Estimando
Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 7 Estimativas e Tamanhos Amostrais 7-1 Visão Geral 7-2 Estimando a Proporção Populacional 7-3 Estimando
Aula 2 A distribuição normal
 Aula 2 A distribuição normal Objetivos: Nesta aula você estudará a distribuição normal, que é uma das mais importantes distribuições contínuas. Você verá a definição geral desta distribuição, mas, nesse
Aula 2 A distribuição normal Objetivos: Nesta aula você estudará a distribuição normal, que é uma das mais importantes distribuições contínuas. Você verá a definição geral desta distribuição, mas, nesse
Estatística Indutiva
 Estatística Indutiva MÓDULO 7: INTERVALOS DE CONFIANÇA 7.1 Conceitos básicos 7.1.1 Parâmetro e estatística Parâmetro é a descrição numérica de uma característica da população. Estatística é a descrição
Estatística Indutiva MÓDULO 7: INTERVALOS DE CONFIANÇA 7.1 Conceitos básicos 7.1.1 Parâmetro e estatística Parâmetro é a descrição numérica de uma característica da população. Estatística é a descrição
Distribuições Contínuas de Probabilidade
 Distribuições Contínuas de Probabilidade Uma variável aleatória contínua é uma função definida sobre o espaço amostral, que associa valores em um intervalo de números reais. Exemplos: Espessura de um item
Distribuições Contínuas de Probabilidade Uma variável aleatória contínua é uma função definida sobre o espaço amostral, que associa valores em um intervalo de números reais. Exemplos: Espessura de um item
Probabilidade e Estatística
 Probabilidade e Estatística Resumos e gráficos de dados Prof. Josuel Kruppa Rogenski 2 o /2017 1 VISÃO GERAL métodos de organização, resumo e obtenção de gráficos; objetivo: compreender o conjunto de dados
Probabilidade e Estatística Resumos e gráficos de dados Prof. Josuel Kruppa Rogenski 2 o /2017 1 VISÃO GERAL métodos de organização, resumo e obtenção de gráficos; objetivo: compreender o conjunto de dados
Probabilidade e Estatística
 Probabilidade e Estatística Aula 7: Intervalos de Confiança com uma amostra Leitura obrigatória: Devore, cap 7 ou Montgomery e Runger, cap 8 Chap 8-1 Objetivos Como inferir sobre um parâmetro da população,
Probabilidade e Estatística Aula 7: Intervalos de Confiança com uma amostra Leitura obrigatória: Devore, cap 7 ou Montgomery e Runger, cap 8 Chap 8-1 Objetivos Como inferir sobre um parâmetro da população,
Métodos Estatísticos
 Métodos Estatísticos 5 - Distribuição Normal Referencia: Estatística Aplicada às Ciências Sociais, Cap. 7 Pedro Alberto Barbetta. Ed. UFSC, 5ª Edição, 2002. Distribuição de Probabilidades A distribuição
Métodos Estatísticos 5 - Distribuição Normal Referencia: Estatística Aplicada às Ciências Sociais, Cap. 7 Pedro Alberto Barbetta. Ed. UFSC, 5ª Edição, 2002. Distribuição de Probabilidades A distribuição
Capítulo 3. Introdução à Probabilidade E à Inferência Estatística
 Capítulo 3 Introdução à Probabilidade E à Inferência Estatística definições e propriedades: Propriedade 5: A probabilidade condicional reflete como a probabilidade de um evento pode mudar se soubermos
Capítulo 3 Introdução à Probabilidade E à Inferência Estatística definições e propriedades: Propriedade 5: A probabilidade condicional reflete como a probabilidade de um evento pode mudar se soubermos
Capítulo 5 Distribuições de probabilidade normal Pearson Prentice Hall. Todos os direitos reservados.
 Capítulo 5 Distribuições de probabilidade normal slide 1 Descrição do capítulo 5.1 Introdução à distribuição normal e distribuição normal padrão 5.2 Distribuições normais: encontrando probabilidades 5.3
Capítulo 5 Distribuições de probabilidade normal slide 1 Descrição do capítulo 5.1 Introdução à distribuição normal e distribuição normal padrão 5.2 Distribuições normais: encontrando probabilidades 5.3
AULA 05 Teste de Hipótese
 1 AULA 05 Teste de Hipótese Ernesto F. L. Amaral 03 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução
1 AULA 05 Teste de Hipótese Ernesto F. L. Amaral 03 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução
Probabilidade, distribuição normal e uso de tabelas padronizadas. Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais
 Probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais O que é probabilidade? Perspectiva de que algo venha a ocorrer. Número
Probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais O que é probabilidade? Perspectiva de que algo venha a ocorrer. Número
Tópicos em Gestão da Informação II
 Tópicos em Gestão da Informação II Aula 04 Medidas de posição relativa Prof. Dalton Martins dmartins@gmail.com Gestão da Informação Faculdade de Informação e Comunicação Universidade Federal de Goiás Determinando
Tópicos em Gestão da Informação II Aula 04 Medidas de posição relativa Prof. Dalton Martins dmartins@gmail.com Gestão da Informação Faculdade de Informação e Comunicação Universidade Federal de Goiás Determinando
Intervalos de Confiança - Amostras Pequenas
 Intervalos de Confiança - Amostras Pequenas Prof. Eduardo Bezerra CEFET/RJ 20 de Abril de 2018 (CEFET/RJ) Intervalos de Confiança - Amostras Pequenas 1 / 26 Roteiro 1 Distribuição t de Student 2 Funções
Intervalos de Confiança - Amostras Pequenas Prof. Eduardo Bezerra CEFET/RJ 20 de Abril de 2018 (CEFET/RJ) Intervalos de Confiança - Amostras Pequenas 1 / 26 Roteiro 1 Distribuição t de Student 2 Funções
AULA 04 Teste de hipótese
 1 AULA 04 Teste de hipótese Ernesto F. L. Amaral 03 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal
1 AULA 04 Teste de hipótese Ernesto F. L. Amaral 03 de outubro de 2013 Centro de Pesquisas Quantitativas em Ciências Sociais (CPEQS) Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal
FMU- Cursos de Tecnologia Disciplina: Métodos Quantitativos em Gestão e Negócios-
 FMU- Cursos de Tecnologia Disciplina: Métodos Quantitativos em Gestão e Negócios- Memória - Teoria e Exercícios sobre Distribuição Normal de Probabilidade Distribuição Normal de Probabilidade As distribuições
FMU- Cursos de Tecnologia Disciplina: Métodos Quantitativos em Gestão e Negócios- Memória - Teoria e Exercícios sobre Distribuição Normal de Probabilidade Distribuição Normal de Probabilidade As distribuições
14. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas
 4. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas Os valores assumidos por uma variável aleatória contínua podem ser associados com medidas em uma escala contínua como, por exemplo,
4. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas Os valores assumidos por uma variável aleatória contínua podem ser associados com medidas em uma escala contínua como, por exemplo,
PROBABILIDADE E ESTATÍSTICA
 PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 3 09/2014 Estatística Descritiva Medidas de Centro Probabilidade e Estatística 3/19 Medidas de Centro Uma medida
PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 3 09/2014 Estatística Descritiva Medidas de Centro Probabilidade e Estatística 3/19 Medidas de Centro Uma medida
Estatística II Aula 2. Prof.: Patricia Maria Bortolon, D. Sc.
 Estatística II Aula Prof.: Patricia Maria Bortolon, D. Sc. Distribuições Amostrais ... vocês lembram que: Antes de tudo... Estatística Parâmetro Amostra População E usamos estatíticas das amostras para
Estatística II Aula Prof.: Patricia Maria Bortolon, D. Sc. Distribuições Amostrais ... vocês lembram que: Antes de tudo... Estatística Parâmetro Amostra População E usamos estatíticas das amostras para
LISTA 3 Introdução à Probabilidade (Profa. Cira.) OBS. Apenas os exercícios indicados como adicional não constam no livro.
 LISTA 3 Introdução à Probabilidade (Profa. Cira.) OBS. Apenas os exercícios indicados como adicional não constam no livro. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - V. A. C O N T Í N
LISTA 3 Introdução à Probabilidade (Profa. Cira.) OBS. Apenas os exercícios indicados como adicional não constam no livro. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - V. A. C O N T Í N
Exercícios de programação
 Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Cálculo das Probabilidades e Estatística I
 Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Distribuição Normal Motivação: Distribuição
Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Distribuição Normal Motivação: Distribuição
Distribuição Normal. Apontamentos para a disciplina de Estatística I. Tomás da Silva, 2003/2006
 Distribuição Normal Apontamentos para a disciplina de Estatística I Tomás da Silva, 2003/2006 Introdução: Curvas normais e distribuições normais A regra 689599,7 A distribuição normal padronizada (ou:
Distribuição Normal Apontamentos para a disciplina de Estatística I Tomás da Silva, 2003/2006 Introdução: Curvas normais e distribuições normais A regra 689599,7 A distribuição normal padronizada (ou:
AULA 17 - Distribuição Uniforme e Normal
 AULA 17 - Distribuição Uniforme e Normal Susan Schommer Introdução à Estatística Econômica - IE/UFRJ Distribuições Contínuas Em muitos problemas se torna matematicamente mais simples considerar um espaço
AULA 17 - Distribuição Uniforme e Normal Susan Schommer Introdução à Estatística Econômica - IE/UFRJ Distribuições Contínuas Em muitos problemas se torna matematicamente mais simples considerar um espaço
Estimativas e Tamanhos de Amostras
 Estimativas e Tamanhos de Amostras 1 Aspectos Gerais 2 Estimativa de uma Média Populacional: Grandes Amostras 3 Estimativa de uma Média Populacional: Pequenas Amostras 4 Tamanho Amostral Necessário para
Estimativas e Tamanhos de Amostras 1 Aspectos Gerais 2 Estimativa de uma Média Populacional: Grandes Amostras 3 Estimativa de uma Média Populacional: Pequenas Amostras 4 Tamanho Amostral Necessário para
Distribuição Normal. Estatística Aplicada I DISTRIBUIÇÃO NORMAL. Algumas característica importantes. 2πσ
 Estatística Aplicada I DISTRIBUIÇÃO NORMAL Prof a Lilian M. Lima Cunha AULA 5 09/05/017 Maio de 017 Distribuição Normal Algumas característica importantes Definida pela média e desvio padrão Media=mediana=moda
Estatística Aplicada I DISTRIBUIÇÃO NORMAL Prof a Lilian M. Lima Cunha AULA 5 09/05/017 Maio de 017 Distribuição Normal Algumas característica importantes Definida pela média e desvio padrão Media=mediana=moda
Intervalos de Confiança
 Intervalos de Confiança INTERVALOS DE CONFIANÇA.1 Conceitos básicos.1.1 Parâmetro e estatística Parâmetro é a descrição numérica de uma característica da população. Estatística é a descrição numérica de
Intervalos de Confiança INTERVALOS DE CONFIANÇA.1 Conceitos básicos.1.1 Parâmetro e estatística Parâmetro é a descrição numérica de uma característica da população. Estatística é a descrição numérica de
Contabilometria. Prof.: Patricia Maria Bortolon, D. Sc.
 Contabilometria Prof.: Patricia Maria Bortolon, D. Sc. Intervalos de Confiança Fonte: LEVINE, D. M.; STEPHAN, D. F.; KREHBIEL, T. C.; BERENSON, M. L.; Estatística Teoria e Aplicações, 5a. Edição, Editora
Contabilometria Prof.: Patricia Maria Bortolon, D. Sc. Intervalos de Confiança Fonte: LEVINE, D. M.; STEPHAN, D. F.; KREHBIEL, T. C.; BERENSON, M. L.; Estatística Teoria e Aplicações, 5a. Edição, Editora
Teorema do Limite Central
 O Teorema do limite central (TLC) demonstra a tendência de aproximação das variáveis aleatórias com a distribuição normal. 2 O teorema do limite central é básico para a maioria das aplicações do controle
O Teorema do limite central (TLC) demonstra a tendência de aproximação das variáveis aleatórias com a distribuição normal. 2 O teorema do limite central é básico para a maioria das aplicações do controle
Probabilidade e Estatística
 Probabilidade e Estatística Aula 7 Distribuição da Média Amostral Leitura obrigatória: Devore: Seções 5.3, 5.4 e 5.5 Chap 8-1 Inferência Estatística Na próxima aula vamos começar a parte de inferência
Probabilidade e Estatística Aula 7 Distribuição da Média Amostral Leitura obrigatória: Devore: Seções 5.3, 5.4 e 5.5 Chap 8-1 Inferência Estatística Na próxima aula vamos começar a parte de inferência
Estatística (MAD231) Turma: IGA. Período: 2018/2
 Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Distribuições de Probabilidade Contínuas 1/19
 all Distribuições de Probabilidade Contínuas Professores Eduardo Zambon e Magnos Martinello UFES Universidade Federal do Espírito Santo DI Departamento de Informática CEUNES Centro Universitário Norte
all Distribuições de Probabilidade Contínuas Professores Eduardo Zambon e Magnos Martinello UFES Universidade Federal do Espírito Santo DI Departamento de Informática CEUNES Centro Universitário Norte
Probabilidade, distribuição normal e uso de tabelas padronizadas
 Probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais O que é probabilidade? Número de 0 até 1 que expressa a tendência de
Probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais O que é probabilidade? Número de 0 até 1 que expressa a tendência de
Conceitos básicos, probabilidade, distribuição normal e uso de tabelas padronizadas
 Conceitos básicos, probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais Alguns conceitos População: é o conjunto de todos
Conceitos básicos, probabilidade, distribuição normal e uso de tabelas padronizadas Prof. Marcos Vinicius Pó Métodos Quantitativos para Ciências Sociais Alguns conceitos População: é o conjunto de todos
Estatística 1. Resumo Teórico
 Estatística 1 Resumo Teórico Conceitos do Curso 1. Tipos de Variáveis e Representações Gráficas a. Tipos de Variáveis b. Distribuição de Frequências c. Histograma 2. Estatística Descritiva Medidas Estatísticas
Estatística 1 Resumo Teórico Conceitos do Curso 1. Tipos de Variáveis e Representações Gráficas a. Tipos de Variáveis b. Distribuição de Frequências c. Histograma 2. Estatística Descritiva Medidas Estatísticas
GET00116 Fundamentos de Estatística Aplicada Lista de Exercícios de Revisão para a P2 Profa. Ana Maria Farias
 GET00116 Fundamentos de Estatística Aplicada Lista de Exercícios de Revisão para a P Profa. Ana Maria Farias 1. Em 00, Kaspersky Lab relatou que aproximadamente 0% de todos os e-mails são lixo ou spam.
GET00116 Fundamentos de Estatística Aplicada Lista de Exercícios de Revisão para a P Profa. Ana Maria Farias 1. Em 00, Kaspersky Lab relatou que aproximadamente 0% de todos os e-mails são lixo ou spam.
Distribuições Contínuas Prof. Walter Sousa
 Estatística Distribuições Contínuas Prof. Walter Sousa DISTRIBUIÇÕES CONTÍNUAS Uma variável aleatória XX é contínua se assumir um número infinito não numerável de valores. Assim, fica definida uma função,
Estatística Distribuições Contínuas Prof. Walter Sousa DISTRIBUIÇÕES CONTÍNUAS Uma variável aleatória XX é contínua se assumir um número infinito não numerável de valores. Assim, fica definida uma função,
7 Teste de Hipóteses
 7 Teste de Hipóteses 7-1 Aspectos Gerais 7-2 Fundamentos do Teste de Hipóteses 7-3 Teste de uma Afirmação sobre a Média: Grandes Amostras 7-4 Teste de uma Afirmação sobre a Média : Pequenas Amostras 7-5
7 Teste de Hipóteses 7-1 Aspectos Gerais 7-2 Fundamentos do Teste de Hipóteses 7-3 Teste de uma Afirmação sobre a Média: Grandes Amostras 7-4 Teste de uma Afirmação sobre a Média : Pequenas Amostras 7-5
Seção 2.1. Distribuições de freqüência e seus gráficos
 Seção 2.1 Distribuições de freqüência e seus gráficos Distribuições de freqüência Minutos gastos ao telefone 102 124 108 86 103 82 71 104 112 118 87 95 103 116 85 122 87 100 105 97 107 67 78 125 109 99
Seção 2.1 Distribuições de freqüência e seus gráficos Distribuições de freqüência Minutos gastos ao telefone 102 124 108 86 103 82 71 104 112 118 87 95 103 116 85 122 87 100 105 97 107 67 78 125 109 99
Cap. 8 - Intervalos Estatísticos para uma Única Amostra
 Intervalos Estatísticos para ESQUEMA DO CAPÍTULO 8.1 INTRODUÇÃO 8.2 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 8.3 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO
Intervalos Estatísticos para ESQUEMA DO CAPÍTULO 8.1 INTRODUÇÃO 8.2 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 8.3 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO
b) Variáveis Aleatórias Contínuas
 Disciplina: 221171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Disciplina: 221171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Amostragem Aleatória e Descrição de Dados - parte II
 Amostragem Aleatória e Descrição de Dados - parte II 2012/02 1 Diagrama de Ramo e Folhas 2 3 4 5 Objetivos Ao final deste capítulo você deve ser capaz de: Construir e interpretar disposições gráficas dos
Amostragem Aleatória e Descrição de Dados - parte II 2012/02 1 Diagrama de Ramo e Folhas 2 3 4 5 Objetivos Ao final deste capítulo você deve ser capaz de: Construir e interpretar disposições gráficas dos
Capítulo 4 Inferência Estatística
 Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a diferença de
Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a diferença de
Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina.
 Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina. De forma geral, a prova manteve o padrão das questões da
Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina. De forma geral, a prova manteve o padrão das questões da
Notas de Aula. Copyright 2007 Pearson Education, Inc Publishing as Pearson Addison-Wesley.
 Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 5 Distribuições de Probabilidades 5-1 Visão Geral 5-2 Variáveis Aleatórias 5-3 Distribuição de
Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 5 Distribuições de Probabilidades 5-1 Visão Geral 5-2 Variáveis Aleatórias 5-3 Distribuição de
Estatística Aplicada II. } Revisão: Probabilidade } Propriedades da Média Amostral
 Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Variáveis Aleatórias Contínuas
 Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
1 Distribuição Uniforme
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 03 Aula 8 Professor: Carlos Sérgio UNIDADE 4 - Distribuições Contínuas (Notas de Aula) Distribuição Uniforme
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 03 Aula 8 Professor: Carlos Sérgio UNIDADE 4 - Distribuições Contínuas (Notas de Aula) Distribuição Uniforme
Stela Adami Vayego DEST/UFPR
 Resumo 9 Modelos Probabilísticos Variável Contínua Vamos ver como criar um modelo probabilístico, o que é uma função densidade de probabilidade (fdp), e como calcular probabilidades no caso de variáveis
Resumo 9 Modelos Probabilísticos Variável Contínua Vamos ver como criar um modelo probabilístico, o que é uma função densidade de probabilidade (fdp), e como calcular probabilidades no caso de variáveis
Capítulo 5 Distribuições de Probabilidades. Seção 5-1 Visão Geral. Visão Geral. distribuições de probabilidades discretas
 Capítulo 5 Distribuições de Probabilidades 5-1 Visão Geral 5-2 Variáveis Aleatórias 5-3 Distribuição de Probabilidade Binomial 5-4 Média, Variância e Desvio Padrão da Distribuição Binomial 5-5 A Distribuição
Capítulo 5 Distribuições de Probabilidades 5-1 Visão Geral 5-2 Variáveis Aleatórias 5-3 Distribuição de Probabilidade Binomial 5-4 Média, Variância e Desvio Padrão da Distribuição Binomial 5-5 A Distribuição
Inferência. 1 Estimativa pontual de uma média 2 Estimativa intervalar de uma média. Renata Souza
 Inferência 1 Estimativa pontual de uma média 2 Estimativa intervalar de uma média Renata Souza Aspectos Gerais A estatística descritiva tem por objetivo resumir ou descrever características importantes
Inferência 1 Estimativa pontual de uma média 2 Estimativa intervalar de uma média Renata Souza Aspectos Gerais A estatística descritiva tem por objetivo resumir ou descrever características importantes
Escola Superior de Agricultura "Luiz de Queiroz", Departamento de Ciências Exatas. Modelo Normal. Cristian Villegas
 Modelo Normal Cristian Villegas clobos@usp.br http://www.lce.esalq.usp.br/arquivos/aulas/2014/lce0216/ 1 Introdução O modelo normal ocupa uma posição de grande destaque tanto a nível teórico como prático,
Modelo Normal Cristian Villegas clobos@usp.br http://www.lce.esalq.usp.br/arquivos/aulas/2014/lce0216/ 1 Introdução O modelo normal ocupa uma posição de grande destaque tanto a nível teórico como prático,
A figura 5.1 ilustra a densidade da curva normal, que é simétrica em torno da média (µ).
 Capítulo 5 Distribuição Normal Muitas variáveis aleatórias contínuas, tais como altura, comprimento, peso, entre outras, podem ser descritas pelo modelo Normal de probabilidades. Este modelo é, sem dúvida,
Capítulo 5 Distribuição Normal Muitas variáveis aleatórias contínuas, tais como altura, comprimento, peso, entre outras, podem ser descritas pelo modelo Normal de probabilidades. Este modelo é, sem dúvida,
Disciplina: Prof. a Dr. a Simone Daniela Sartorio. DTAiSeR-Ar
 Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo dos números
Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo dos números
Bioestatística e Computação I
 Bioestatística e Computação I Distribuições Teóricas de Probabilidade Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Pós Graduação em Saúde da Mulher e da Criança IFF FIOCRUZ Baseado nas aulas
Bioestatística e Computação I Distribuições Teóricas de Probabilidade Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Pós Graduação em Saúde da Mulher e da Criança IFF FIOCRUZ Baseado nas aulas
Escola Superior de Agricultura "Luiz de Queiroz", Departamento de Ciências Exatas. Modelo Normal. Cristian Villegas
 Modelo Normal Cristian Villegas clobos@usp.br Outubro de 2013 Apostila de Estatística (Cristian Villegas) 1 Introdução O modelo normal ocupa uma posição de grande destaque tanto a nível teórico como prático,
Modelo Normal Cristian Villegas clobos@usp.br Outubro de 2013 Apostila de Estatística (Cristian Villegas) 1 Introdução O modelo normal ocupa uma posição de grande destaque tanto a nível teórico como prático,
b) Variáveis Aleatórias Contínuas
 Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
P2 - parte 2 - Bioestatística Valor: 15 pontos 27/11/2018. A prova pode ser enviada para o em PDF. p k (1 p) n k (1) k
 Instrucões Leia os resumos da teoria. Estude a teoria. Data de entrega: 07/12/2018 (sexta-feira). A prova pode ser enviada para o e-mail anapaula@ana.mat.br em PDF. Distribuição Binomial O número X de
Instrucões Leia os resumos da teoria. Estude a teoria. Data de entrega: 07/12/2018 (sexta-feira). A prova pode ser enviada para o e-mail anapaula@ana.mat.br em PDF. Distribuição Binomial O número X de
GET00143 TEORIA DAS PROBABILIDADES II Variáveis Aleatórias Unidmensionais
 Universidade Federal Fluminense Instituto de Matemática e Estatística GET00143 TEORIA DAS PROBABILIDADES II Variáveis Aleatórias Unidmensionais Ana Maria Lima de Farias Jessica Quintanilha Kubrusly Mariana
Universidade Federal Fluminense Instituto de Matemática e Estatística GET00143 TEORIA DAS PROBABILIDADES II Variáveis Aleatórias Unidmensionais Ana Maria Lima de Farias Jessica Quintanilha Kubrusly Mariana
Princípios de Bioestatística
 Princípios de Bioestatística Cálculo do Tamanho de Amostra Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Depto. Estatística - ICEx - UFMG 1 / 32 2 / 32 Cálculo do Tamanho de Amostra Parte fundamental
Princípios de Bioestatística Cálculo do Tamanho de Amostra Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Depto. Estatística - ICEx - UFMG 1 / 32 2 / 32 Cálculo do Tamanho de Amostra Parte fundamental
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Intervalo Amostragem e inferência estatística População: consiste na totalidade das observações em que estamos interessados. Nº de observações na população é denominado tamanho=n.
Cap. 4 - Estimação por Intervalo Amostragem e inferência estatística População: consiste na totalidade das observações em que estamos interessados. Nº de observações na população é denominado tamanho=n.
Aula de hoje. administração. São Paulo: Ática, 2007, Cap. 3. ! Tópicos. ! Referências. ! Distribuição de probabilidades! Variáveis aleatórias
 Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
Distribuição Normal. Prof. Herondino
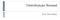 Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
IND 1115 Inferência Estatística Aula 7
 Conteúdo IND 1115 Inferência Estatística Aula 7 Setembro 2004 Por que a revisão de probabilidades até agora? A importância da distribuição Normal O Mônica Barros mbarros.com 1 mbarros.com 2 Por que uma
Conteúdo IND 1115 Inferência Estatística Aula 7 Setembro 2004 Por que a revisão de probabilidades até agora? A importância da distribuição Normal O Mônica Barros mbarros.com 1 mbarros.com 2 Por que uma
Estatística e Probabilidade Aula 08 Estimativas e Tamanho Amostral. Prof. Gabriel Bádue
 Estatística e Probabilidade Aula 08 Estimativas e Tamanho Amostral Prof. Gabriel Bádue Motivação Estatística Inferencial Conjunto de métodos e procedimentos pelo meio dos quais tiramos conclusões sobre
Estatística e Probabilidade Aula 08 Estimativas e Tamanho Amostral Prof. Gabriel Bádue Motivação Estatística Inferencial Conjunto de métodos e procedimentos pelo meio dos quais tiramos conclusões sobre
Distribuições Amostrais e Estimação Pontual de Parâmetros
 Distribuições Amostrais e Estimação Pontual de Parâmetros - parte I 19 de Maio de 2011 Introdução Objetivos Ao final deste capítulo você deve ser capaz de: Entender estimação de parâmetros de uma distribuição
Distribuições Amostrais e Estimação Pontual de Parâmetros - parte I 19 de Maio de 2011 Introdução Objetivos Ao final deste capítulo você deve ser capaz de: Entender estimação de parâmetros de uma distribuição
Bioestatística e Computação I
 Bioestatística e Computação I Distribuições Teóricas de Probabilidade Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Pós Graduação em Saúde da Mulher e da Criança IFF FIOCRUZ Baseado nas aulas
Bioestatística e Computação I Distribuições Teóricas de Probabilidade Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Pós Graduação em Saúde da Mulher e da Criança IFF FIOCRUZ Baseado nas aulas
Probabilidade e Modelos Probabilísticos
 Probabilidade e Modelos Probabilísticos 2ª Parte: modelos probabilísticos para variáveis aleatórias contínuas, modelo uniforme, modelo exponencial, modelo normal 1 Distribuição de Probabilidades A distribuição
Probabilidade e Modelos Probabilísticos 2ª Parte: modelos probabilísticos para variáveis aleatórias contínuas, modelo uniforme, modelo exponencial, modelo normal 1 Distribuição de Probabilidades A distribuição
Probabilidade. Distribuição Normal
 Probabilidade Distribuição Normal Distribuição Normal Uma variável aleatória contínua tem uma distribuição normal se sua distribuição é: simétrica apresenta (num gráfico) forma de um sino Função Densidade
Probabilidade Distribuição Normal Distribuição Normal Uma variável aleatória contínua tem uma distribuição normal se sua distribuição é: simétrica apresenta (num gráfico) forma de um sino Função Densidade
Escola Politécnica da USP Engenharia de Petróleo e Gás DISTRIBUIÇÃO DE PROBABILIDADE CONTÍNUA. Aulas 10, 11,12 e 13 - Prof. Regina Meyer Branski
 Escola Politécnica da USP Engenharia de Petróleo e Gás DISTRIBUIÇÃO DE PROBABILIDADE CONTÍNUA Aulas 10, 11,12 e 13 - Prof. Regina Meyer Branski Objetivos Distribuição Normal e Distribuição Normal Padrão
Escola Politécnica da USP Engenharia de Petróleo e Gás DISTRIBUIÇÃO DE PROBABILIDADE CONTÍNUA Aulas 10, 11,12 e 13 - Prof. Regina Meyer Branski Objetivos Distribuição Normal e Distribuição Normal Padrão
AULA 10 Estimativas e Tamanhos Amostrais
 1 AULA 10 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 18 de setembro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
1 AULA 10 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 18 de setembro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
Distribuições Amostrais e Estimação Pontual de Parâmetros
 Distribuições Amostrais e Estimação Pontual de Parâmetros - parte I 2012/02 1 Introdução 2 3 4 5 Objetivos Ao final deste capítulo você deve ser capaz de: Entender estimação de parâmetros de uma distribuição
Distribuições Amostrais e Estimação Pontual de Parâmetros - parte I 2012/02 1 Introdução 2 3 4 5 Objetivos Ao final deste capítulo você deve ser capaz de: Entender estimação de parâmetros de uma distribuição
Tópicos em Gestão da Informação II
 Tópicos em Gestão da Informação II Aula 05 Variabilidade estatística Prof. Dalton Martins dmartins@gmail.com Gestão da Informação Faculdade de Informação e Comunicação Universidade Federal de Goiás Exercício
Tópicos em Gestão da Informação II Aula 05 Variabilidade estatística Prof. Dalton Martins dmartins@gmail.com Gestão da Informação Faculdade de Informação e Comunicação Universidade Federal de Goiás Exercício
Lucas Santana da Cunha de junho de 2018 Londrina
 Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
ALGARISMOS SIGNIFICATIVOS E TRATAMENTO DE DADOS
 ALGARISMOS SIGNIFICATIVOS E TRATAMENTO DE DADOS 1.0 Objetivos Utilizar algarismos significativos. Distinguir o significado de precisão e exatidão. 2.0 Introdução Muitas observações na química são de natureza
ALGARISMOS SIGNIFICATIVOS E TRATAMENTO DE DADOS 1.0 Objetivos Utilizar algarismos significativos. Distinguir o significado de precisão e exatidão. 2.0 Introdução Muitas observações na química são de natureza
Medidas de Posição ou Tendência Central
 Medidas de Posição ou Tendência Central Medidas de Posição ou Tendência Central Fornece medidas que podem caracterizar o comportamento dos elementos de uma série; Possibilitando determinar se um valor
Medidas de Posição ou Tendência Central Medidas de Posição ou Tendência Central Fornece medidas que podem caracterizar o comportamento dos elementos de uma série; Possibilitando determinar se um valor
Métodos Experimentais em Ciências Mecânicas
 Métodos Experimentais em Ciências Mecânicas Professor Jorge Luiz A. Ferreira Função que descreve a chance que uma variável pode assumir ao longo de um espaço de valores. Uma distribuição de probabilidade
Métodos Experimentais em Ciências Mecânicas Professor Jorge Luiz A. Ferreira Função que descreve a chance que uma variável pode assumir ao longo de um espaço de valores. Uma distribuição de probabilidade
Aula 6 - Variáveis aleatórias contínuas
 Aula 6 - Variáveis aleatórias contínuas PhD. Wagner Hugo Bonat Laboratório de Estatística e Geoinformação-LEG Universidade Federal do Paraná 1/2017 Bonat, W. H. (LEG/UFPR) 1/2017 1 / 18 Variáveis aleatórias
Aula 6 - Variáveis aleatórias contínuas PhD. Wagner Hugo Bonat Laboratório de Estatística e Geoinformação-LEG Universidade Federal do Paraná 1/2017 Bonat, W. H. (LEG/UFPR) 1/2017 1 / 18 Variáveis aleatórias
Probabilidade e Estatística
 Probabilidade e Estatística Aula 9 Fundamentos de Testes de Hipóteses Leitura: Devore, Capítulo 8 Chap 9-1 Objetivos Neste capítulo, vamos aprender: Os princípios básicos de testes de hipóteses Estabelecer
Probabilidade e Estatística Aula 9 Fundamentos de Testes de Hipóteses Leitura: Devore, Capítulo 8 Chap 9-1 Objetivos Neste capítulo, vamos aprender: Os princípios básicos de testes de hipóteses Estabelecer
Notas de Aula. Estatística Elementar. by Mario F. Triola. Tradução: Denis Santos
 Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 3 Estatísticas para Descrição, Exploração e Comparação de Dados 3-1 Visão Geral 3-2 Medidas de
Notas de Aula Estatística Elementar 10ª Edição by Mario F. Triola Tradução: Denis Santos Slide 1 Capítulo 3 Estatísticas para Descrição, Exploração e Comparação de Dados 3-1 Visão Geral 3-2 Medidas de
