Sinais e Sistemas - Lista 1. Gabarito
|
|
|
- Júlio Campelo Palhares
- 6 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista 1 Gabarito 4 de outubro de Considere o sinal x(t) mostrado na figura abaixo. O sinal é zero fora do intervalo < t <. a) O gráfico a seguir representa o sinal y 1 (t). Determine uma expressão para y 1 (t) em função de x(t). 1
2 y 1 (t) = x(t + ) b) O gráfico a seguir representa o sinal y (t). Determine uma expressão para y (t) em função de x. y (t) = x(1 t) c) Considere y 3 (t) = x(t + 3). Determine todos os valores de t para os quais y 3 (t) = 1. x(t) = 1 no intervalo 0 t <. Portanto, y 3 (t) = 1 se 0 t + 3 <, logo: 3 t < 1 d) Considere que x(t) possa ser escrita como a soma de um sinal par, x p (t), e um sinal ímpar, x i (t). Encontre os valores de t para os quais x p (t) = 0. x(t) = x p (t) + x i (t) x( t) = x p ( t) + x i ( t) Pela definição de funções pares e ímpares: x( t) = x p ( t) + x i ( t) x( t) = x p (t) x i (t) Isolando o termo x p (t) em ambas as equações: Essa função pode ser plotada como: x p (t) = 1 (x(t) + x( t))
3 Pelo gráfico é fácil ver que x p (t) = 0 se t > ou t = 1. Pela definição, x(t) = 0 para t = ±. Logo, t ou t = 1.. Avalie os sistemas abaixo com relação a linearidade e causalidade: a) y(t) = x(t ) + x( t) * Linearidade: é linear. x 1 (t) y 1 (t) = x 1 (t ) + x 1 ( t) x (t) y (t) = x (t ) + x ( t) x 3 (t) = αx 1 (t) + βx (t) y 3 (t) = x 3 (t ) + x 3 ( t) y 3 (t) = αx 1 (t ) + βx (t ) + αx 1 ( t) + βx ( t) y 3 (t) = α(x 1 (t ) + x 1 ( t)) + β(x (t ) + x ( t)) = αy 1 (t) + βy (t) * Causalidade: não é causal. Para t = 0, y(0) = x( ) + x(). Ou seja, ele utiliza amostras futuras. Portanto, não é causal. b) y(t) = [cos(3t)]x (t) * Linearidade: não é linear x 1 (t) y 1 (t) = [cos(3t)]x 1 (t) x (t) y (t) = [cos(3t)]x (t) x 3 (t) = αx 1 (t) + βx (t) y 3 (t) = [cos(3t)]x 3 (t) y 3 (t) = [cos(3t)](αx 1 (t) + βx (t)) ) y 3 (t) = [cos(3t)][(αx 1 (t)) + αβx 1 (t)x (t) + (βx (t)) ] y 3 (t) = α y 1 (t) + β y (t) + [cos(3t)]αβx 1 (t)x (t) * Causalidade: é causal. c) y(t) = t x(τ)dτ 3
4 * Linearidade: x 1 (t) y 1 (t) = t x 1(τ)dτ x (t) y (t) = t x (τ)dτ x 3 (t) = αx 1 (t) + βx (t) y 3 (t) = t x 3(τ)dτ y 3 (t) = t αx 1(τ) + βx (τ)dτ y 3 (t) = α t x 1(τ)dτ + β t x (τ)dτ y 3 (t) = αy 1 (t) + βy (t) * Causalidade: Para t = 1, y( 1 ) = 1 x(τ)dτ. Ou seja, ele utiliza amostras futuras. Portanto, não é causal. { 0, t < 0 d) y(t) = x(t) + x(t ), t 0 * Linearidade: é linear. Primeira parte: y(t) = 0 é linear Segunda parte: y(t) = x(t) + x(t ) x 1 (t) y 1 (t) = x 1 (t) + x 1 (t ) x (t) y (t) = x (t) + x (t ) x 3 (t) = αx 1 (t) + βx (t) y 3 (t) = x 3 (t) + x 3 (t ) y 3 (t) = αx 1 (t) + βx (t) + αx 1 (t ) + βx (t ) y 3 (t) = α(x 1 (t) + x 1 (t )) + β(x (t) + x (t )) = αy 1 (t) + βy (t) * Causalidade: é causal. e) y[n] = x[ n] * Linearidade: x 1 [n] y 1 [n] = x 1 [ n] x [n] y [n] = x [ n] x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = x 3 [ n] y 3 [n] = αx 1 [ n] + βx [ n] = αy 1 [n] + βy [n] * Causalidade: não é causal. Para n = 1, y[ 1] = x[1]. Ou seja, ele utiliza amostras futuras. Portanto, não é causal. f) y[n] = x[n ] x[n 8] 4
5 * Linearidade: é linear. x 1 [n] y 1 [n] = x 1 [n ] x 1 [n 8] x [n] y [n] = x [n ] x [n 8] x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = x 3 [n ] x 3 [n 8] y 3 [n] = αx 1 [n ] + βx [n ] αx 1 [n 8] βx [n 8] y 3 [n] = α(x 1 [n ] x 1 [n 8]) + β(x [n ] x [n 8]) = αy 1 [n] + βy [n] * Causalidade: é causal. g) y[n] = n x[n] * Linearidade: é linear. x 1 [n] y 1 [n] = n x 1 [n] x [n] y [n] = n x [n] x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = n x 3 [n] y 3 [n] = n (αx 1 [n] + βx [n]) y 3 [n] = αn x 1 [n] + βn x [n] = αy 1 [n] + βy [n] * Causalidade:é causal. x[n], n 1 h) y[n] = 0, n = 0 x[n + 1], n 1 * Linearidade: é linear. Primeira parte: y[n] = x[n]. x 1 [n] y 1 [n] = x 1 [n] x [n] y [n] = x [n] x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = x 3 [n] y 3 [n] = αx 1 [n] + βx [n] = αy 1 [n] + βy [n] Segunda parte: y[n] = 0 é linear. Terceira parte: y[n] = x[n + 1]. x 1 [n] y 1 [n] = x 1 [n + 1] x [n] y [n] = x [n + 1] x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = x 3 [n + 1] y 3 [n] = αx 1 [n + 1] + βx [n + 1] = αy 1 [n] + βy [n] * Causalidade: não é causal. Para n = 1, y[ 1] = x[0]. Ou seja, ele utiliza amostras futuras. Portanto, não é causal. 5
6 i) y(t) = x(t/3) * Linearidade: é linear. x 1 (t) y 1 (t) = x 1 (t/3) x (t) y (t) = x (t/3) x 3 (t) = αx 1 (t) + βx (t) y 3 (t) = x 3 (t/3) y 3 (t) = αx 1 (t/3) + βx (t/3) = αy 1 (t) + βy (t) * Causalidade: Para t = 1, y( 1) = x( 1 3 ). Ou seja, ele utiliza amostras futuras. Portanto, não é causal. j) y[n] = x[4n + 1] + n * Linearidade: não é linear. x 1 [n] y 1 [n] = x 1 [4n + 1] + n x [n] y [n] = x [4n + 1] + n x 3 [n] = αx 1 [n] + βx [n] y 3 [n] = x 3 [4n + 1] + n y 3 [n] = αx 1 [4n + 1] + βx [4n + 1] + n = αx 1 [4n + 1] + y [n] * Causalidade: não é causal. 3. Considere um sistema LIT cuja resposta ao sinal de entrada x 1 (t) seja o sinal y 1 (t), mostrados na figura. Determine e esboce a resposta do sistema às entradas: a) x (t) Escrever x (t) em função de x 1 (t) e usar a propriedade de linearidade para encontrar a saída: x (t) = x 1 (t) x 1 (t ) Portanto, y (t) = y 1 (t) y 1 (t ) 6
7 b) x 3 (t) Escrever x 3 (t) em função de x 1 (t) e usar a propriedade de linearidade para encontrar a saída: x 3 (t) = x 1 (t) + x 1 (t + 1) Portanto, y 3 (t) = y 1 (t) + y 1 (t + 1) 4. Um sinal de tempo contínuo x(t) é mostrado na figura abaixo. Esboce e coloque a escala para cada um dos seguintes sinais em função da resposta impulsional da figura dada. 7
8 a) x(t 1) b) x( t) c) x(t + 1) d) x(4 t/) e) [x(t) + x( t)]u(t) f) x(t)[δ(t + 3/) δ(t 3/)] 5. Um sistema linear de tempo contínuo S com entrada x(t) e saída y(t) possui os seguintes pares entrada-saída: x(t) = e j t y(t) = e j 3t x(t) = e j t j 3t y(t) = e a) Se x 1 (t) = cos(t), determine a saída correspondente a y 1 (t) para o sistema. b) Se x (t) = cos((t 1 )), determine a saída correspondente a y (t) para o sistema. Reposta: 8
9 a) Dado x(t) = e j t y(t) = e j 3t x(t) = e j t j 3t y(t) = e E o sistema sendo linear, x 1 (t) = 1 (e j t + e j t y 1 (t) = 1 (e j 3t + e j 3t ) e: x 1 (t) = cos(t) y 1 (t) = cos(3t) b) Sabendo que x (t) pode ser escrito como: x (t) = cos((t 1 )) = e j e j t + e j j t e Usando a propriedade da linearidade, podemos reescrever: x 1 (t) = 1 (e j e j t + e j e j t ) y 1 (t) = 1 (e j e j 3t + e j e j 3t ) = cos(3t 1) então: x 1 (t) = cos((t 1/)) y 1 (t) = cos(3t 1) 6. Considere o sistema com realimentação: 9
10 a) Esboce a saída quando x[n] = δ[n] (Função impulso unitário) b) Esboce a saída quando x[n] = u[n] (Função Degrau unitário) c) Esboce a saída quando x[n] = u[n] (Função Rampa) a) e[n] = x[n] y[n] e[n] = x[n] e[n 1] y[n + 1] = x[n] y[n] para n = 0, x[n] = 1 e n 0, x[n] = 0 tem-se: y[1] = x[0] y[0] = 1 0 = 1 y[] = x[1] y[1] = 0 1 = 1 y[3] = x[] y[] = 0 ( 1) = 1... b) e[n] = x[n] y[n] e[n] = x[n] e[n 1] y[n + 1] = x[n] y[n] para n > 0, x[n] = 1 tem-se: y[1] = x[0] y[0] = 1 0 = 1 y[] = x[1] y[1] = 1 1 = 0 y[3] = x[] y[] = 1 0 = 1... c) e[n] = x[n] y[n] e[n] = x[n] e[n 1] y[n + 1] = x[n] y[n] para n > 0, x[n] = n tem-se: y[1] = x[0] y[0] = 0 0 = 0 10
11 y[] = x[1] y[1] = 1 0 = 1 y[3] = x[] y[] = 1 = 1 y[4] = x[3] y[3] = 3 1 = y[5] = x[4] y[4] = 4 = y[6] = x[5] y[5] = 5 3 = Considere o sistema descrito pela seguinte equação de diferenças: y[n] = αx[n] + βx[n 1] y[n ] Considere que o sistema inicie em repouso, e que a entrada x[n] é o sinal degrau unitário u[n]: Encontre y[119]. { 1, n 0 x[n] = u[n] = 0, caso contrário Realiza-se a iteração para resolver a equação de diferenças: 11
12 n αx[n] + βx[n 1] y[n] 0 α α 1 α + β α + β α + β β 3 α + β 0 4 α α 5 α + β α + β 6 α + β β 7 α + β k α α 4k + 1 α + β α + β 4k + α + β β 4k + 3 α + β Portanto, y[119] = y[ ] = 0 8. Dada as funções de tempo discreto descritas a seguir (gráfico das funções) calcule as convoluções abaixo: a) y[n] = u[n] u[n 3] b) y[n] = ( 1 ) n u[ n + ] u[n] c) y[n] = cos ( 1 πn) n u[ n + ] d) y[n] = x[n] z[n] e) y[n] = x[n] f [n] f) y[n] = w[n] g [n] g) y[n] = z[n] g [n] h) y[n] = f [n] g [n] 1
13 a) y[n] = u[n] u[n 3] u[n] = x 1 [n] e u[n 3] = x [n] y[n] = k= x 1 [k] x [n k] Para n 3 < 0 ou n < 3 y[n] = 0 n = 3 y[3] = 1(1) = 1 n = 4 y[4] = 1(1) + 1(1) =. n = p y[p] = (p ) y[n] = (n )u[n ] b) y[n] = ( 1 n ) u[ n + ] u[n] Para n < y[n] = 0 n y[n] = 1 ( ) n+1 y[n] = 1 ( 1 ) n u[n ] ( c) y[n] = cos ( 1 πn) n u[ n + ] x 1 [k] = cos( π k) x [k] = n k ) = 1 ( ) 1 n y[n] = cos( π k) n k k=n 1, se k =...,0,4,8,... cos( π k) = 1, se k =...,,6,10,... 0, caso contrário Considerando os termos válidos, tem-se: y[n] = k=n ( 1) k n k Substituindo e = k y[n] = n ( 1) e ( ) 1 e = n e= n y[n] = n ( 1 4 ) n y[n] = 16 9 ( 1)n+1 d) y[n] = x[n] z[n] = e= n = n ( ) ( ) 4 9 ( 4) 1 n k= ( ) 1 e 4 x[k] z[n k] Para n + 4 < 0 ou n < 4 y[n] = 0 0 n + 4 < 3 ou 4 n < 1 y[n] = n + 5 n 1 e n < 1 ou 1 n < 1 y[n] = 3 + (n + ) = n + 7 n = 1 y[n] = (1) + 3() = 8 n = y[n] = 1(1) + 3() = 7 13
14 3 n < 6 y[n] = (6 n) n 6 y[n] = 0 e) y[n] = x[n] f [n] = k= x[k] f [n k] Para n + 4 < 4 ou n < 8 y[n] = 0 y[ 8] = 4; y[ 7] = 4 3 = 7; y[ 6] = 7 = 9 y[ 5] = 9 1 = 10; y[ 4] = 10 0 = 10 y[ 3] = = 5; y[ ] = = 0 y[ 1] = = 5; y[0] = = 10 y[1] = = 10; y[] = = 9 y[3] = = 7; y[4] = 4 Para n 4 > 0 ou n > 4 y[n] = 0 f) y[n] = w[n] g [n] = k= w[k] g [n k] Para n + 5 < ou n < 7 y[n] = 0 y[ 7] = 1; y[ 6] = 1 + = 3; y[ 5] = = 6 14
15 y[ 4] = 6 + = 8; y[ 3] = = 9; y[ ] = = 8 y[ 1] = = 6; y[0] = 1 + = 3; y[1] = = y[] = + 1 = 3; y[3] = = 6; y[4] = 6 + = 8 y[5] = = 9; y[6] = 6 + = 8 y[7] = = 6; y[8] = 1 + = 3; y[9] = 1 n > 9 y[n] = 0 g) y[n] = z[n] g [n] = k= z[k] g [n k] Para n + 5 < 0 ou n < 5 y[n] = 0 y[ 5] = 1; y[ 4] = ; y[ 3] = 3; y[ ] = 3 + = 5 y[ 1] = = 7; y[0] = + (3) = 8; y[1] = 1 + (3) = 7 y[] = (3) = 6; y[3] = 1 + () = 5; y[4] = + (1) = 4 y[5] = 3(1) = 3; y[6] = + 3(1) = 5; y[7] = 3(1) + = 5 y[8] = 3() + = 8; y[9] = 3() + 1 = 7; y[10] = 3() = 6 y[11] = () = 4; y[1] = h) y[n] = f [n] g [n] = k= f [k] g [n k] Para n + 5 < 4 ou n < 9 y[n] = 0 y[ 9] = 4; y[ 8] = 4 3 = 7; y[ 7] = 7 = 9 y[ 6] = 9 1 = 10; y[ 5] = 10; y[ 4] = = 5 y[ 3] = 0; y[ ] = = 5 y[ 1] = = 6; y[0] = = 3 y[1] = 0; y[] = = 3; y[3] = = 6 15
16 y[4] = = 5; y[5] = = 0; y[6] = = 5 y[7] = = 10; y[8] = = 10; y[9] = = 9 y[10] = = 7; y[11] = 4 9. Dada as funções de tempo contínuo descritas a seguir (gráfico das funções) calcule as convoluções abaixo: a) y(t) = u(t + 1) u(t ) b) y(t) = e t u(t) u(t + ) c) y(t) = cos(πt)(u(t + 1) u(t 3)) u(t) d) y(t) = (t + t )(u(t + 1) u(t 1)) u(t + ) e) y(t) = x(t) z(t) f) y(t) = z(t) g (t) g) y(t) = z(t) f (t) 16
17 h) y(t) = f (t) g (t) x 1 (t) x (t) = x 1 (k)x (t k)dk a) y(t) = u(t + 1) u(t ) x 1 (t) = u(t + 1) e x (t) = u(t ) Para t < 1 ou t < 1 y(t) = 0 t Para t 1 y(t) = (1)(1)dk = t 1 1 y(t) = (t 1)u(t 1) x 1 (k)x (t k)dk b) y(t) = e t u(t) u(t + ) x 1 (t) = e t u(t) e x (t) = u(t + ) t+ Para t + 0 ou t y(t) = (1)e k dk = 1 (1 e (t+) ) Para t < y(t) = 0 y(t) = 1 (1 e (t+) )u(t + ) 0 c) y(t) = cos(πt)(u(t + 1) u(t 3)) u(t) x 1 (t) = cos(πt)(u(t + 1) u(t 3)) e x (t) = u(t) Para t < 1 y(t) = 0 Para 1 t < 3 y(t) = y(t) = 1 π sin(πt) u(t) t 1 = coskπdk = 1 π sinπt d) y(t) = (t + t )(u(t + 1) u(t 1)) u(t + ) x 1 (t) = (t + t )(u(t + 1) u(t 1)) e x (t) = u(t + ) Para t + < 1 ou t < 3 y(t) = 0 t+ 3 t < 1 y(t) = k + k dk 1 y(t) = (t + ) ((t + )3 + 1) y(t) = 4 3 (t + )3 + (t + ) Para t 1 y(t) = k + k dk y(t) = = 8 3 0, t < 3 4 y(t) = 3 (t + )3 + (t + ) + 1 3, 3 t < 1 8 3, t 1 e) y(t) = x(t) z(t) 1 17
18 Para t + < 1 ou t < 3 y(t) = 0 t+ Para 3 t < 1 y(t) = ( 1)dτ = (t + 3) Para 1 t < 1 y(t) = Para 1 t < 3 y(t) = Para t 3 y(t) = 0 0, t < 3 1 t 1 t 1 t 3, 3 t < 1 y(t) = t, 1 t < 1 3 t, 1 t < 3 0, t 3 f) y(t) = z(t) g (t) 1 (1)dτ + ( 1)dτ = t (1)dτ = 3 t t Para t + 1 < ou t < 3 y(t) = 0 t+1 Para 3 t < 1 y(t) = (τ t)dτ = 1 t t 3 Para 1 t < 1 y(t) = Para 1 t < 3 y(t) = Para t 3 y(t) = 0 0, t < 3 t 1 0 t 1 (τ t)dτ + 1 t t 3, 3 t < 1 y(t) = t 1, 1 t < 1 1 t + t 3, 1 t < 3 0, t 3 t+1 (t τ)dτ = 1 t + t 3 0 (t τ)dτ = t 1 18
19 g) y(t) = z(t) f (t) Para t + 1 < y(t) = 0 Para t < 1 y(t) = Para 1 t < 0 y(t) = Para 0 t < 1 y(t) = Para 1 t < y(t) = Para t < 3 y(t) = Para t 3 y(t) = 0 0, t < 0 t 1 t t 1 t 1 t t t 1 e (t τ) dτ = e (t+) 1 e (t τ) dτ = e 1 1 e (t τ) dτ + e (t+) 1, t < 1 e 1 1, 1 t < 0 y(t) = 1 + e 1 e t, 0 t < 1 1 e 1, 1 t < e ( t) e 1, t < 3 0, t 3 h) y(t) = f (t) g (t) t e (t τ) dτ = 1 e 1 e (t τ) dτ = e ( t) e 1 0 e (t τ) dτ = 1 + e 1 e t Para t + 1 < 0 ou t < 1 y(t) = 0 t+1 Para 1 t < 0 y(t) = e τ (t τ)dτ = e (t+1) + t Para 0 t < 1 y(t) = e τ (t τ)dτ = t(1 e 1 ) + e
20 Para 1 t < y(t) = Para t y(t) = 0 0, t < 1 1 t 1 e (t+1) + t 1, 1 t < 0 y(t) = t(1 e 1 ) + e 1 1, 0 t < 1 e 1 (t + ) te (t 1), 1 t < 0, t e τ (t τ)dτ = e 1 (t + ) te (t 1) 10. Para cada resposta ao impulso listada abaixo, determine se o sistema correspondente é causal e/ou estável. a) h(t) = e t u(t 1) b) h(t) = u(t + 1) u(t 1) c) h(t) = cos(πt)u(t) d) h[n] = n u[ n] e) h[n] = u[u] u[n 1] f) h[n] = sin ( 1 πn) a) h(t) = e t u(t 1) Causal e não estável b) h(t) = u(t + 1) u(t 1) Não causal e não estável c) h(t) = cos(πt)u(t) Causal e não estável d) h[n] = n u[ n] Não causal e estável e) h[n] = u[u] u[n 1] Causal e estável f) h[n] = sin ( 1 πn) Não causal e não estável 11. Considere um sistema de tempo discreto cuja entrada x[n] e a saída y[n] sejam relacionadas por: ( ) 1 y[n] = y[n 1] + x[n] a) Mostre que esse sistema satisfaz a condição de repouso inicial (isto é, se x[n] = 0 para n < n 0, então y[n] = 0 para n < n 0 ), então ele é linear e invariante no tempo. 0
21 b) Mostre que se esse sistema não satisfaz a condição inicial de repouso inicial, mas, em vez disso, obedece à condição auxiliar y[0] = 0, ele é não causal. a) Para uma entrada x 1 [n] em que x 1 [n] = 0 para n < n 1. A saída será: y 1 [n] = 1 y 1[n 1] + x 1 [n], y 1 [n] = 0 para n < n 1 (11.1) Então, considerando outra entrada x [n] em que x [n] = 0 para n < n. A saída será: y [n] = 1 y [n 1] + x [n], y [n] = 0 para n < n (11.) Multiplicando 11.1 por α e 11. por β e somando as duas equações tem-se: αy 1 [n] + βy [n] = α y 1[n 1] + β y [n 1] + αx 1 [n] + βx [n] Por inspeção, a saída é y 3 [n] = αy 1 [n] + βy [n] quando a entrada é x 3 [n] = αx 1 [n] + βx [n]. Além disso, y 3 (1) = 0 = y 1 (1) + y (1). Portanto, o sistema é linear. b) Consideramos duas entradas: x 1 [n] = 0, { para todo n 0, n < 1 x [n] = 1, n 1 Para o sistema ser linear, a resposta para x 1 [n] é y 1 [n] = 0 para todo n. A saída y [n], quando a entrada é x [n], desde que y [0] = 0, será: ) = 0, y [] = ( 1 ) = 0 y [1] = ( 1 Portanto, y [n] = 0 para n 0. Agora para n < 0, nota-se que: y [0] = ( 1 )y [ 1] + x[0]. Portanto, y [ 1] =, y [ ] = 4, y [ 3] = 8. Portanto, y [n] = ( ) 1 n u[n 1]. Desde que x 1 [n] = x [n] para todo n < 0, isto é verdade caso o sistema seja causal y 1 [n] = y [n] para n < 0. Os resultados obtidos anteriormente mostram que isso não é verdade. Portanto, o sistema é não causal. 1. Suponha que o sinal seja convoluído com o sinal x(t) = u(t + 0.5) u(t 0.5) h(t) = e j w 0t a) Determine o valor de w 0 que garante que y(0) = 0. Sendo que y(t) = x(t) h(t). b) A resposta do item anterior é única? y(t) = x(t) h(t) = Portanto, e j w 0(t τ) dτ 1
22 y(0) = e j w 0(t τ) dτ = w 0 sin( w 0 ) a) Se w 0 = π,entãoy(0) = 0. b) Não é única. Qualquer w 0 = kπ, k 0 é suficiente. 13. (Computacional) Siga as instruções: j πn a) Dado um sinal W [n] = e N, com N = 8 e n = 0,1,,...,8, expresse o número complexo na forma cartesiana b) Plote a parte real pela parte imaginária no Matlab c) Calcule W k [n] para k = 0,1,,...,8 e represente em forma matricial { 1, n = 0,1 d) Dado um segundo sinal x[n] =. Plote x[n] ao longo das amostras 0, n 0,1 de intervalo n no Matlab. e) Escreva a função X [k] = W k [n]x T [n] em forma matricial f) Calcule a fase e magnitude de X [k] e plote os gráficos g) Repita o procedimento computacional presente de a) a f) para x[n] = cos ( ) πnm N com m = 10, N = 18 e n = 0,1,,...,18. Discute os resultados. 14. (Computacional) Siga as instruções a seguir: a) Realize a convolução dos sinais abaixo usando o comando padrão do MATLAB, y = conv(x,h), e plote o resultado usando stem. Tente o inverso (y = conv(h, x)). Há diferença? x = [3,11,7,0, 1,4,] h = [,3,0, 5,,1] b) O comando padrão não nos permite localizar os sinais no tempo. Crie a função abaixo, convol ut e: function [ y, ny ] = convolute ( x, h, nx, nh) nymin = nx (1)+nh ( 1 ) ; nymax = nx ( length ( x ) ) + nh( length (h ) ) ; ny = [nymin : nymax ] ; y = conv ( x, h ) ; Em seguida, teste o seguinte e plote o resultado: nx = [ 3: 3 ] ; nh = [ 1: 4 ] ; [ y, ny ] = convolute ( x, h, nx, nh ) ; Calcule agora essa convolução e compare com o obtido na simulação. c) Agora, crie o sinal:
23 nx = [ 0 : ] ; x = sin (* pi *nx/50) + sin (0* pi *nx / 5 0 ) ; Veja o sinal x usando st em. Modifique h para ser: nh = [ 0 : 9 ] ; h=0.1* ones ( 1, 1 0 ) ; Realize a convolução entre x e h e plote o resultado. Descreva o que aconteceu. d) A melhor forma de analisar o que ocorre em c) é analisando o espectro de frequências do sinal. Analise primeiro o espectro de magnitude de x: f s = 56; freq = [ 1: 1/ f s : 1 1/ f s ] ; f x = f f t ( x, 5 1 ) ; f x = f f t s h i f t ( f x ) ; fxmag = abs ( f x ( 1 : 5 1 ) ) ; plot ( freq, fxmag ) ; Agora do sinal convoluído y: f s = 56; freq = [ 1: 1/ f s : 1 1/ f s ] ; fy= f f t ( y, 5 1 ) ; fy = f f t s h i f t ( fy ) ; fymag = abs ( fy ( 1 : 5 1 ) ) ; plot ( freq, fymag ) ; Qual o fenômeno que ocorre ao realizar essa convolução? 3
Sinais e Sistemas - Lista 1
 UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista 1 4 de setembro de 2015 1. Considere o sinal x(t) mostrado na figura abaixo. O sinal é zero no intervalo 2 < t < 2. a) O gráfico a seguir
UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista 1 4 de setembro de 2015 1. Considere o sinal x(t) mostrado na figura abaixo. O sinal é zero no intervalo 2 < t < 2. a) O gráfico a seguir
Sinais e Sistemas - Lista 3 Gabarito
 UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista Gabarito 7 de novembro de 05. Calcule a Transformada de Fourier dos seguintes sinais: a) x[n] = ( n ) u[n ] b) x[n] = ( ) n c) x[n] =
UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista Gabarito 7 de novembro de 05. Calcule a Transformada de Fourier dos seguintes sinais: a) x[n] = ( n ) u[n ] b) x[n] = ( ) n c) x[n] =
Sinais e Sistemas - Lista 3
 UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista 3 7 de novembro de 0. Calcule a Transformada de Fourier dos seguintes sinais: a) x[n] = ( n ) u[n ] b) x[n] = ( ) n c) x[n] = u[n ] u[n
UNIVERSIDADE DE BRASÍLIA, FACULDADE GAMA Sinais e Sistemas - Lista 3 7 de novembro de 0. Calcule a Transformada de Fourier dos seguintes sinais: a) x[n] = ( n ) u[n ] b) x[n] = ( ) n c) x[n] = u[n ] u[n
Caderno de Exercícios
 Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
Teste Tipo. Sinais e Sistemas (LERCI) 2004/2005. Outubro de Respostas
 Teste Tipo Sinais e Sistemas (LERCI) 2004/2005 Outubro de 2004 Respostas i Problema. Considere o seguinte integral: + 0 δ(t π/4) cos(t)dt em que t e δ(t) é a função delta de Dirac. O integral vale: 2/2
Teste Tipo Sinais e Sistemas (LERCI) 2004/2005 Outubro de 2004 Respostas i Problema. Considere o seguinte integral: + 0 δ(t π/4) cos(t)dt em que t e δ(t) é a função delta de Dirac. O integral vale: 2/2
Resumo. Sinais e Sistemas Sistemas Lineares e Invariantes no Tempo. Resposta ao Impulso. Representação de Sequências
 Resumo Sinais e Sistemas Sistemas Lineares e Invariantes no Tempo lco@ist.utl.pt Instituto Superior Técnico SLITs discretos. O somatório de convolução. SLITs contínuos. A convolução contínua. Propriedades
Resumo Sinais e Sistemas Sistemas Lineares e Invariantes no Tempo lco@ist.utl.pt Instituto Superior Técnico SLITs discretos. O somatório de convolução. SLITs contínuos. A convolução contínua. Propriedades
Parte I O teste tem uma parte de resposta múltipla (Parte I) e uma parte de resolução livre (Parte II)
 Instituto Superior Técnico Sinais e Sistemas o teste 4 de Novembro de 0 Nome: Número: Duração da prova: horas Parte I O teste tem uma parte de resposta múltipla (Parte I) e uma parte de resolução livre
Instituto Superior Técnico Sinais e Sistemas o teste 4 de Novembro de 0 Nome: Número: Duração da prova: horas Parte I O teste tem uma parte de resposta múltipla (Parte I) e uma parte de resolução livre
Sistemas lineares. Aula 3 Sistemas Lineares Invariantes no Tempo
 Sistemas lineares Aula 3 Sistemas Lineares Invariantes no Tempo SLIT Introdução Resposta de um SLIT Resposta de Entrada Nula Resposta de Estado Nulo Resposta ao Impulso Unitária Introdução Sistemas: Modelo
Sistemas lineares Aula 3 Sistemas Lineares Invariantes no Tempo SLIT Introdução Resposta de um SLIT Resposta de Entrada Nula Resposta de Estado Nulo Resposta ao Impulso Unitária Introdução Sistemas: Modelo
Exercícios para Processamento Digital de Sinal. 1 Transformada e Série de Fourier
 Exercícios para Processamento Digital de Sinal Transformada e Série de Fourier Exercício Considere o seguinte sinal x(t) = sin 2 (0πt). Encontre uma forma aditiva para este sinal e represente graficamente
Exercícios para Processamento Digital de Sinal Transformada e Série de Fourier Exercício Considere o seguinte sinal x(t) = sin 2 (0πt). Encontre uma forma aditiva para este sinal e represente graficamente
Aula sobre funções de transferência
 Aula sobre funções de transferência Matemática Aplicada II - MAT01168 maio de 2012 Sumário Sistemas lineares causais invariantes no tempo Sistemas Um sistema possui entradas e saídas. Figura : Modelo caixa-preta
Aula sobre funções de transferência Matemática Aplicada II - MAT01168 maio de 2012 Sumário Sistemas lineares causais invariantes no tempo Sistemas Um sistema possui entradas e saídas. Figura : Modelo caixa-preta
Aula 06 Representação de sistemas LIT: A soma de convolução
 Aula 06 Representação de sistemas LIT: A soma de convolução Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 47-56. HAYKIN, S. S.; VAN
Aula 06 Representação de sistemas LIT: A soma de convolução Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 47-56. HAYKIN, S. S.; VAN
1.3.2 Sistemas LIT - a integral de convolução
 Eisencraft e Loiola 1.3 Análise e transmissão de sinais 23 Figura 1.22: Propriedades da Transformada de Fourier [1]. 1.3.2 Sistemas LIT - a integral de convolução Na Seção 1.2, página 4, já foi discutido
Eisencraft e Loiola 1.3 Análise e transmissão de sinais 23 Figura 1.22: Propriedades da Transformada de Fourier [1]. 1.3.2 Sistemas LIT - a integral de convolução Na Seção 1.2, página 4, já foi discutido
Sinais e Sistemas. Sistemas Lineares Invariantes no Tempo. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Sinais e Sistemas Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Lembrando... xt () yt () ht () OK!!! xn [ ] yn [ ] hn [ ] ht (
Sinais e Sistemas Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Lembrando... xt () yt () ht () OK!!! xn [ ] yn [ ] hn [ ] ht (
Sinais e Sistemas Exame Data: 18/1/2018. Duração: 3 horas
 Sinais e Sistemas Exame Data: 8//28. Duração: 3 horas Número: Nome: Identique este enunciado e a folha de respostas com o seu número e os seus primeiro e último nomes. Para as questões a 9, indique as
Sinais e Sistemas Exame Data: 8//28. Duração: 3 horas Número: Nome: Identique este enunciado e a folha de respostas com o seu número e os seus primeiro e último nomes. Para as questões a 9, indique as
PONTÍFICIA UNIVERSIDADE CATÓLICA DE GOIÁS ESCOLA DE ENGENHARIA ENG1380 SISTEMAS LINEARES CAPÍTULO 01 LISTA DE EXERCÍCIOS PROFA. FABRÍCIA NERES BORGES
 PONTÍFICIA UNIVERSIDADE CATÓLICA DE GOIÁS ESCOLA DE ENGENHARIA ENG1380 SISTEMAS LINEARES CAPÍTULO 01 LISTA DE EXERCÍCIOS PROFA. FABRÍCIA NERES BORGES 1.1-1 Determine a energia dos sinais mostrados na Fig.
PONTÍFICIA UNIVERSIDADE CATÓLICA DE GOIÁS ESCOLA DE ENGENHARIA ENG1380 SISTEMAS LINEARES CAPÍTULO 01 LISTA DE EXERCÍCIOS PROFA. FABRÍCIA NERES BORGES 1.1-1 Determine a energia dos sinais mostrados na Fig.
Sistemas Lineares e Invariantes de Tempo Discreto
 Sistemas Lineares e Invariantes de Tempo Discreto 28 Sistemas Lineares de Tempo Discreto Um sistema linear satisfaz o teorema da superposição e implica que o sistema tem condições iniciais iguais a zero
Sistemas Lineares e Invariantes de Tempo Discreto 28 Sistemas Lineares de Tempo Discreto Um sistema linear satisfaz o teorema da superposição e implica que o sistema tem condições iniciais iguais a zero
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
04/04/ :31. Sumário. 2.1 Sistemas LIT de Tempo Discreto 2.2 Sistemas LIT de Tempo Contínuo 2.3 Propriedades dos Sistemas LIT
 Sumário 2.1 Sistemas LIT de Tempo Discreto 2.2 Sistemas LIT de Tempo Contínuo 2.3 Propriedades dos Sistemas LIT slide 1 2 Introdução Muitos processos físicos podem ser modelados como sistemas lineares
Sumário 2.1 Sistemas LIT de Tempo Discreto 2.2 Sistemas LIT de Tempo Contínuo 2.3 Propriedades dos Sistemas LIT slide 1 2 Introdução Muitos processos físicos podem ser modelados como sistemas lineares
Sinais e Sistemas. Tempo para Sistemas Lineares Invariantes no Tempo. Representações em Domínio do. Profª Sandra Mara Torres Müller.
 Sinais e Sistemas Representações em Domínio do Tempo para Sistemas Lineares Invariantes no Tempo Profª Sandra Mara Torres Müller Aula 7 Representações em Domínio do Tempo para Sistemas Lineares e Invariantes
Sinais e Sistemas Representações em Domínio do Tempo para Sistemas Lineares Invariantes no Tempo Profª Sandra Mara Torres Müller Aula 7 Representações em Domínio do Tempo para Sistemas Lineares e Invariantes
ELT032 - Introdução à Análise de Sinais
 ELT032 - Introdução à Análise de Universidade Federal de Itajubá - Campus Itajubá Engenharia Eletrônica Aula 01 Prof. Jeremias B. Machado jeremias@unifei.edu.br 24 de abril de 2015 1 / 42 Introdução Considere
ELT032 - Introdução à Análise de Universidade Federal de Itajubá - Campus Itajubá Engenharia Eletrônica Aula 01 Prof. Jeremias B. Machado jeremias@unifei.edu.br 24 de abril de 2015 1 / 42 Introdução Considere
EN2607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 2 2 quadrimestre 2011
 EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares quadrimestre 0 (P-0003D) (HAYKIN, 00, p 9) Use a equação de definição da TF para obter a representação no domínio da
EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares quadrimestre 0 (P-0003D) (HAYKIN, 00, p 9) Use a equação de definição da TF para obter a representação no domínio da
Sistemas e Sinais (LEE & LETI)
 Sistemas e Sinais (LEE & LETI) o teste - de Julho de 05 Duração da prova: hora e 30 minutos Atenção:. Identique todas as folhas.. O teste é constituído por questões de escolha múltipla e por questões de
Sistemas e Sinais (LEE & LETI) o teste - de Julho de 05 Duração da prova: hora e 30 minutos Atenção:. Identique todas as folhas.. O teste é constituído por questões de escolha múltipla e por questões de
Convolução de Sinais
 Análise de Sinais (5001) Ficha Prática Laboratorial VII Curso: Eng. Electrotécnica Duração prevista: 2 horas Convolução de Sinais I. Sinais analógicos Operações matemáticas realizadas em sinais analógicos
Análise de Sinais (5001) Ficha Prática Laboratorial VII Curso: Eng. Electrotécnica Duração prevista: 2 horas Convolução de Sinais I. Sinais analógicos Operações matemáticas realizadas em sinais analógicos
Sistemas Lineares e Invariantes: Tempo Contínuo e Tempo Discreto
 Universidade Federal da Paraíba Programa de Pós-Graduação em Engenharia Elétrica Sistemas Lineares e Invariantes: Tempo Contínuo e Tempo Discreto Prof. Juan Moises Mauricio Villanueva jmauricio@cear.ufpb.br
Universidade Federal da Paraíba Programa de Pós-Graduação em Engenharia Elétrica Sistemas Lineares e Invariantes: Tempo Contínuo e Tempo Discreto Prof. Juan Moises Mauricio Villanueva jmauricio@cear.ufpb.br
Introdução ao Processamento Digital de Sinais Soluções dos Exercícios Propostos Capítulo 1
 Introdução ao Soluções dos Exercícios Propostos Capítulo. Dados os sinais x c (t a seguir, encontre as amostras, a representação em somatórios de impulsos deslocados, e trace os gráficos de = x c (nt a
Introdução ao Soluções dos Exercícios Propostos Capítulo. Dados os sinais x c (t a seguir, encontre as amostras, a representação em somatórios de impulsos deslocados, e trace os gráficos de = x c (nt a
EN2607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 3 3 quadrimestre 2012
 EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 3 fevereiro 03 EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 3 3 quadrimestre 0
EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 3 fevereiro 03 EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 3 3 quadrimestre 0
Sistemas de Tempo Discretos
 Sistemas de Tempo Discretos Monitoria de Sinais e Sistemas Lineares 23/09/09 Monitoria de Sinais e Sistemas Lineares () Sistemas de Tempo Discretos 23/09/09 1 / 22 Tamanho de um Sinal Calcule a energia
Sistemas de Tempo Discretos Monitoria de Sinais e Sistemas Lineares 23/09/09 Monitoria de Sinais e Sistemas Lineares () Sistemas de Tempo Discretos 23/09/09 1 / 22 Tamanho de um Sinal Calcule a energia
Sinais Elementares e Operações Básicas
 Exper. 2 Sinais Elementares e Operações Básicas Objetivo Esta prática descreve como utilizar o Matlab para representar e manipular alguns sinais elementares: Estudar os sinais elementares de tempo contínuo
Exper. 2 Sinais Elementares e Operações Básicas Objetivo Esta prática descreve como utilizar o Matlab para representar e manipular alguns sinais elementares: Estudar os sinais elementares de tempo contínuo
Aula 4 Respostas de um SLIT
 Aula 4 Respostas de um SLIT Introdução Características de um SLIT Resposta ao degrau unitário Resposta a entrada nula Resposta total A convolução entre dois sinais de tempo contínuo x(t) e h(t) é dada
Aula 4 Respostas de um SLIT Introdução Características de um SLIT Resposta ao degrau unitário Resposta a entrada nula Resposta total A convolução entre dois sinais de tempo contínuo x(t) e h(t) é dada
1 o Teste Tipo. Sinais e Sistemas (LERC/LEE) 2008/2009. Maio de Respostas
 o Teste Tipo Sinais e Sistemas (LERC/LEE) 2008/2009 Maio de 2009 Respostas i Problema. (0,9v) Considere o seguinte integral: + 0 δ(t π/4) cos(t)dt em que t eδ(t) é a função delta de Dirac. O integral vale:
o Teste Tipo Sinais e Sistemas (LERC/LEE) 2008/2009 Maio de 2009 Respostas i Problema. (0,9v) Considere o seguinte integral: + 0 δ(t π/4) cos(t)dt em que t eδ(t) é a função delta de Dirac. O integral vale:
Sinais e Sistemas. Série de Fourier. Renato Dourado Maia. Faculdade de Ciência e Tecnologia de Montes Claros. Fundação Educacional Montes Claros
 Sinais e Sistemas Série de Fourier Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Lembremos da resposta de um sistema LTI discreto a uma exponencial
Sinais e Sistemas Série de Fourier Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Lembremos da resposta de um sistema LTI discreto a uma exponencial
Introdução aos Circuitos Elétricos
 1 / 47 Introdução aos Circuitos Elétricos Séries e Transformadas de Fourier Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia 2 / 47 Séries e Transformadas
1 / 47 Introdução aos Circuitos Elétricos Séries e Transformadas de Fourier Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia 2 / 47 Séries e Transformadas
Introdução ao Processamento Digital de Sinais Soluções dos Exercícios Propostos Capítulo 3
 Introdução ao Soluções dos Exercícios Propostos Capítulo 3. Calcule a transformada z, a região de convergência e a localização de pólos e zeros das sequências abaixo a) x[n] 4δ[n ]+3δ[n] δ[n+]+3δ[n+] Solução:
Introdução ao Soluções dos Exercícios Propostos Capítulo 3. Calcule a transformada z, a região de convergência e a localização de pólos e zeros das sequências abaixo a) x[n] 4δ[n ]+3δ[n] δ[n+]+3δ[n+] Solução:
Processamento de sinais digitais
 Processamento de sinais digitais Aula 2: Descrição discreta no tempo de sinais e sistemas silviavicter@iprj.uerj.br Tópicos Sequências discretas no tempo. Princípio da superposição para sistemas lineares.
Processamento de sinais digitais Aula 2: Descrição discreta no tempo de sinais e sistemas silviavicter@iprj.uerj.br Tópicos Sequências discretas no tempo. Princípio da superposição para sistemas lineares.
2/47. da matemática é ainda de grande importância nas várias áreas da engenharia. Além disso, lado de Napoleão Bonaparte. 1/47
 Introdução aos Circuitos Elétricos Séries e Transformadas de Fourier Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia Sinais: conjunto de dados ou informação
Introdução aos Circuitos Elétricos Séries e Transformadas de Fourier Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia Sinais: conjunto de dados ou informação
Sinais e Sistemas Exame Data: 11/6/2018. Duração: 3 horas
 Sinais e Sistemas Exame Data: /6/. Duração: 3 horas Número: Nome: Identique este enunciado e a folha de respostas com o seu número e os seus primeiro e último nomes. Para as questões a, indique as suas
Sinais e Sistemas Exame Data: /6/. Duração: 3 horas Número: Nome: Identique este enunciado e a folha de respostas com o seu número e os seus primeiro e último nomes. Para as questões a, indique as suas
Sinais e Sistemas. Sistemas Lineares Invariantes no Tempo. Renato Dourado Maia. Faculdade de Ciência e Tecnologia de Montes Claros
 Sinais e Sistemas Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Introdução xt () yt () ht () xn [ ] yn
Sinais e Sistemas Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Introdução xt () yt () ht () xn [ ] yn
Análise no Domínio do Tempo de Sistemas em Tempo Contínuo
 Análise no Domínio do Tempo de Sistemas em Tempo Contínuo Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise no Domínio do Tempo de Sistemas em Tempo Contínuo Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Introdução ao Processamento Digital de Sinais Soluções dos Exercícios Propostos Capítulo 2
 Introdução ao Soluções dos Exercícios Propostos Capítulo 2. Verifique se os sinais abaixo têm ou não transformada de Fourier. Em caso positivo, calcule a transformada correspondente: a) x[n] 2δ[n+2]+3δ[n]
Introdução ao Soluções dos Exercícios Propostos Capítulo 2. Verifique se os sinais abaixo têm ou não transformada de Fourier. Em caso positivo, calcule a transformada correspondente: a) x[n] 2δ[n+2]+3δ[n]
Controle de Sistemas I
 Controle de Sistemas I Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Introdução xt () y() t ht () xn [
Controle de Sistemas I Sistemas Lineares Invariantes no Tempo Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Introdução xt () y() t ht () xn [
Processamento de Sinal e Imagem Engenharia Electrotécnica e de Computadores
 António M. Gonçalves Pinheiro Departamento de Física Covilhã - Portugal pinheiro@ubi.pt Sinais Bi-dimensionais Discretos f[n, m] - sucessão complexa, Z 2 C Impulso: δ[n, m] = { 1, para (n, m) = (0, 0)
António M. Gonçalves Pinheiro Departamento de Física Covilhã - Portugal pinheiro@ubi.pt Sinais Bi-dimensionais Discretos f[n, m] - sucessão complexa, Z 2 C Impulso: δ[n, m] = { 1, para (n, m) = (0, 0)
Capítulo 2 Dinâmica de Sistemas Lineares
 Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Sistemas lineares. Aula 4 Respostas de um SLIT
 Sistemas lineares Aula 4 Respostas de um SLIT Cronograma Introdução Características de um SLIT Resposta ao degrau unitário Resposta a entrada nula Resposta total Introdução A convolução entre dois sinais
Sistemas lineares Aula 4 Respostas de um SLIT Cronograma Introdução Características de um SLIT Resposta ao degrau unitário Resposta a entrada nula Resposta total Introdução A convolução entre dois sinais
Sistemas de Controle
 Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Processamento (Digital) de Sinal. Caderno de exercícios para as horas não presenciais
 Caderno de exercícios para as horas não presenciais João Paulo Teixeira ESTiG, 014 Capítulo 1 Sinais 1. Considere o Considere o seguinte sinal contínuo: x(t) 1-1 0 1 3 t a. Represente y1(t)=x(t+1). b.
Caderno de exercícios para as horas não presenciais João Paulo Teixeira ESTiG, 014 Capítulo 1 Sinais 1. Considere o Considere o seguinte sinal contínuo: x(t) 1-1 0 1 3 t a. Represente y1(t)=x(t+1). b.
Introdução. Faculdade Pitágoras Unidade Divinópolis. Márcio Júnior Nunes. O que é um Sinal? Sinal Unidimensional Sinal Multidimensional 24/08/2016
 Faculdade Pitágoras Unidade Divinópolis Introdução Márcio Júnior Nunes O que é um Sinal? Sinal Unidimensional Sinal Multidimensional 2 1 Nível de líquido 3 Eletrocardiograma 4 2 Pressão Arterial 5 Índice
Faculdade Pitágoras Unidade Divinópolis Introdução Márcio Júnior Nunes O que é um Sinal? Sinal Unidimensional Sinal Multidimensional 2 1 Nível de líquido 3 Eletrocardiograma 4 2 Pressão Arterial 5 Índice
DFT Transformada Discreta de Fourier Representação de sinais de duração limitada
 DFT Transformada Discreta de Fourier Representação de sinais de duração limitada Luís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico DFT Transformada Discreta de Fourier p1/41 Resumo Amostragem
DFT Transformada Discreta de Fourier Representação de sinais de duração limitada Luís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico DFT Transformada Discreta de Fourier p1/41 Resumo Amostragem
Resposta em Frequência de Sistemas LTI
 Resposta em Frequência de Sistemas LTI Vimos que a resposta y(n) de um sistema LTI em estado zero é dada pela convolução linear do sinal de entrada x(n) com a sua resposta ao impulso h(n). Em particular,
Resposta em Frequência de Sistemas LTI Vimos que a resposta y(n) de um sistema LTI em estado zero é dada pela convolução linear do sinal de entrada x(n) com a sua resposta ao impulso h(n). Em particular,
Fundamentos de sinais e sistemas em tempo discreto
 Fundamentos de sinais e sistemas em tempo discreto ENGC33: Sinais e Sistemas II Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 21 de novembro de 2016 Prof. Tito Luís Maia
Fundamentos de sinais e sistemas em tempo discreto ENGC33: Sinais e Sistemas II Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 21 de novembro de 2016 Prof. Tito Luís Maia
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial
 Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Sinais e Sistemas no domínio do tempo Lista de Exercícios
 Sinais e Sistemas no domínio do tempo Lista de Exercícios Prof. Dr. Marcelo de Oliveira Rosa 10 de abril de 2012 Resumo O objetivo desta lista é reforçar alguns aspectos da análise de sistemas no domínio
Sinais e Sistemas no domínio do tempo Lista de Exercícios Prof. Dr. Marcelo de Oliveira Rosa 10 de abril de 2012 Resumo O objetivo desta lista é reforçar alguns aspectos da análise de sistemas no domínio
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Controle de Sistemas I
 Controle de Sistemas I Sinais e Sistemas - Fundamentos Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Impulso Unitário Discreto 1 Impulso Unitário
Controle de Sistemas I Sinais e Sistemas - Fundamentos Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Impulso Unitário Discreto 1 Impulso Unitário
3 o Teste (1 a data) Sistemas e Sinais (LEIC-TP) 2008/ de Junho de Respostas
 3 o Teste (1 a data) Sistemas e Sinais (LEIC-TP) 2008/2009 12 de Junho de 2009 Respostas i Problema 1. (0,75v) Considere o sinal ( n n, x(n)=cos 8 4) +π Assinale a afirmação correcta x(n) é um sinal periódico
3 o Teste (1 a data) Sistemas e Sinais (LEIC-TP) 2008/2009 12 de Junho de 2009 Respostas i Problema 1. (0,75v) Considere o sinal ( n n, x(n)=cos 8 4) +π Assinale a afirmação correcta x(n) é um sinal periódico
FACULDADE FUCAPI Processamento Digital de Sinais Parte I
 FACULDADE FUCAPI Processamento Digital de Sinais Parte I, M.Sc. Doutorando em Informática (UFAM) Mestre em Engenharia Elétrica (UFAM) Engenheiro de Telecomunicações (FUCAPI) Referências OPPENHEIM, Alan
FACULDADE FUCAPI Processamento Digital de Sinais Parte I, M.Sc. Doutorando em Informática (UFAM) Mestre em Engenharia Elétrica (UFAM) Engenheiro de Telecomunicações (FUCAPI) Referências OPPENHEIM, Alan
Sinais e Sistemas. Luis Henrique Assumpção Lolis. 21 de fevereiro de Luis Henrique Assumpção Lolis Sinais e Sistemas 1
 Sinais e Sistemas Luis Henrique Assumpção Lolis 21 de fevereiro de 2014 Luis Henrique Assumpção Lolis Sinais e Sistemas 1 Conteúdo 1 Classificação de sinais 2 Algumas funções importantes 3 Transformada
Sinais e Sistemas Luis Henrique Assumpção Lolis 21 de fevereiro de 2014 Luis Henrique Assumpção Lolis Sinais e Sistemas 1 Conteúdo 1 Classificação de sinais 2 Algumas funções importantes 3 Transformada
Resumo. Sinais e Sistemas Transformada de Fourier de Sinais Discretos. Sequência de Duração Finita. Série de Fourier
 Resumo Sinais e Sistemas Transformada de Fourier de Sinais Discretos lco@ist.utl.pt Representação de sinais aperiódicos Transformada de Fourier de sinais periódicos Propriedades da transformada de Fourier
Resumo Sinais e Sistemas Transformada de Fourier de Sinais Discretos lco@ist.utl.pt Representação de sinais aperiódicos Transformada de Fourier de sinais periódicos Propriedades da transformada de Fourier
Revisão Análise em frequência e amostragem de sinais. Hilton de Oliveira Mota
 Revisão Análise em frequência e amostragem de sinais Hilton de Oliveira Mota Introdução Análise em frequência (análise espectral): Descrição de quais frequências compõem um sinal. Por quê? Senóides são
Revisão Análise em frequência e amostragem de sinais Hilton de Oliveira Mota Introdução Análise em frequência (análise espectral): Descrição de quais frequências compõem um sinal. Por quê? Senóides são
Transformada de Laplace
 Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Processamento Digital de Sinais II Exercícios sobre Transformada z Data de entrega: 17/11/2015
 Processamento Digital de Sinais II Exercícios sobre Transformada z Data de entrega: 17/11/2015 1) Determine a transformada inversa de, aplicando: a) Desenvolvimento em série de potências b) Divisão direta
Processamento Digital de Sinais II Exercícios sobre Transformada z Data de entrega: 17/11/2015 1) Determine a transformada inversa de, aplicando: a) Desenvolvimento em série de potências b) Divisão direta
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide 1 Slide 1 Sobre Modelos para SLIT s Introdução
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide 1 Slide 1 Sobre Modelos para SLIT s Introdução
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
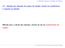 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo
 Convolução, Série de Fourier e Transformada de Fourier contínuas Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo Tópicos Sinais contínuos no tempo Função impulso Sistema
Convolução, Série de Fourier e Transformada de Fourier contínuas Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo Tópicos Sinais contínuos no tempo Função impulso Sistema
Estabilidade. 1. Estabilidade Entrada-Saída Sistemas LIT. 2. Estabilidade BIBO Sistemas LIT. 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT
 Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
Processamento Digital de Sinais - ENG420
 Processamento Digital de Sinais - ENG420 Fabrício Simões IFBA 24 de setembro de 2016 Fabrício Simões (IFBA) Processamento Digital de Sinais - ENG420 24 de setembro de 2016 1 / 19 1 Transformada Z - Conceito
Processamento Digital de Sinais - ENG420 Fabrício Simões IFBA 24 de setembro de 2016 Fabrício Simões (IFBA) Processamento Digital de Sinais - ENG420 24 de setembro de 2016 1 / 19 1 Transformada Z - Conceito
Amostragem. Processamento de Sinais 2005/6 Engenharia Aeroespacial. Sinais em tempo-contínuo. Sinais importantes: Impulso (delta Dirac): δ(t)
 Amostragem Processamento de Sinais 25/6 Engenharia Aeroespacial Sinais em tempo-contínuo Sinais importantes: Impulso (delta Dirac): δ(t) t Escalão unitário: u(t), t, t < t 2 Sinais em tempo-contínuo Rectângulo-
Amostragem Processamento de Sinais 25/6 Engenharia Aeroespacial Sinais em tempo-contínuo Sinais importantes: Impulso (delta Dirac): δ(t) t Escalão unitário: u(t), t, t < t 2 Sinais em tempo-contínuo Rectângulo-
2 - Modelos em Controlo por Computador
 Controlo Óptimo e Adaptativo 2-Modelos em Controlo por Computador 2 - Modelos em Controlo por Computador Objectivo: Introduir a classe de modelos digitais que são empregues nesta disciplina para o projecto
Controlo Óptimo e Adaptativo 2-Modelos em Controlo por Computador 2 - Modelos em Controlo por Computador Objectivo: Introduir a classe de modelos digitais que são empregues nesta disciplina para o projecto
ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS
 ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS 1. INTRODUÇÃO Sistemas dinâmicos lineares são aqueles que obedecem ao princípio da superposição, isto é, um sistema
ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS 1. INTRODUÇÃO Sistemas dinâmicos lineares são aqueles que obedecem ao princípio da superposição, isto é, um sistema
Processamento (Digital) de Sinal. Caderno de exercícios para as aulas
 Caderno de exercícios para as aulas João Paulo Teixeira ESTiG, 04 Processamento (Digital) de Sinal ESTiG - IPB Exercícios Matlab. Identificar no ambiente Matlab o Command Window, o Workspace, o Current
Caderno de exercícios para as aulas João Paulo Teixeira ESTiG, 04 Processamento (Digital) de Sinal ESTiG - IPB Exercícios Matlab. Identificar no ambiente Matlab o Command Window, o Workspace, o Current
Sinais e Sistemas. Série de Fourier. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Sinais e Sistemas Série de Fourier Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Lembremos da resposta de um sistema LTI discreto a uma exponencial complexa: x[ n] z,
Sinais e Sistemas Série de Fourier Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Lembremos da resposta de um sistema LTI discreto a uma exponencial complexa: x[ n] z,
Processamento Digital de Sinais. Notas de Aula. Transformada Z. Transformada Z - TZ
 Transformada Z Transformada Z 2 Transformada Z - TZ Processamento Digital de Sinais É uma generalização da Transformada de Fourier de Tempo Discreto (DTFT) Útil para representação e análise de sistemas
Transformada Z Transformada Z 2 Transformada Z - TZ Processamento Digital de Sinais É uma generalização da Transformada de Fourier de Tempo Discreto (DTFT) Útil para representação e análise de sistemas
Análise de Sistemas LTI através das transformadas
 Análise de Sistemas LTI através das transformadas Luis Henrique Assumpção Lolis 23 de setembro de 2013 Luis Henrique Assumpção Lolis Análise de Sistemas LTI através das transformadas 1 Conteúdo 1 Resposta
Análise de Sistemas LTI através das transformadas Luis Henrique Assumpção Lolis 23 de setembro de 2013 Luis Henrique Assumpção Lolis Análise de Sistemas LTI através das transformadas 1 Conteúdo 1 Resposta
Transformada Rápida de Fourier (FFT)
 Transformada Rápida de Fourier (FFT) A FFT é um algoritmo eficiente para calcular a DFT A DFT de uma sequência x n de comprimento finito N é definida como: N 1 N 1 X k = x n e j2π N kn = x n W N kn, 0
Transformada Rápida de Fourier (FFT) A FFT é um algoritmo eficiente para calcular a DFT A DFT de uma sequência x n de comprimento finito N é definida como: N 1 N 1 X k = x n e j2π N kn = x n W N kn, 0
Sinais e Sistemas. Conceitos Básicos. Prof.: Fábio de Araújo Leite
 Sinais e Sistemas Conceitos Básicos Prof.: Fábio de Araújo Leite Discussão do Plano do Curso As 12 normas de convivência 1. - Recomenda-se chegar à aula no horário estabelecido. 2. Evitar o uso do celular
Sinais e Sistemas Conceitos Básicos Prof.: Fábio de Araújo Leite Discussão do Plano do Curso As 12 normas de convivência 1. - Recomenda-se chegar à aula no horário estabelecido. 2. Evitar o uso do celular
Análise de Sistemas em Tempo Discreto usando a Transformada Z
 Análise de Sistemas em Tempo Discreto usando a Transformada Z Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise de Sistemas em Tempo Discreto usando a Transformada Z Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Sinais e Sistemas Discretos
 Sinais e Sistemas Discretos Luís Caldas de Oliveira Resumo 1. Sinais em Tempo Discreto 2. Sistemas em Tempo Discreto 3. Sistemas Lineares e Invariantes no Tempo 4. Representações em requência 5. A Transformada
Sinais e Sistemas Discretos Luís Caldas de Oliveira Resumo 1. Sinais em Tempo Discreto 2. Sistemas em Tempo Discreto 3. Sistemas Lineares e Invariantes no Tempo 4. Representações em requência 5. A Transformada
A TRANSFORMADA Z. Métodos Matemáticos I C. Prof. Hélio Magalhães de Oliveira, Texto por R. Menezes Campello de Souza
 A TRANSFORMADA Z Métodos Matemáticos I C Prof. Hélio Magalhães de Oliveira, Texto por R. Menezes Campello de Souza Notação x(t) é o sinal analógico x(nt) = x[n], n inteiro, é a seqüência T é o período
A TRANSFORMADA Z Métodos Matemáticos I C Prof. Hélio Magalhães de Oliveira, Texto por R. Menezes Campello de Souza Notação x(t) é o sinal analógico x(nt) = x[n], n inteiro, é a seqüência T é o período
Princípios de Comunicações Profs. André Noll Barreto / A. Judson Braga
 Prova 05/ (3/04/05) Aluno: Matrícula: Instruções A prova consiste de quatro questões discursivas A prova terá a duração de h30 A prova pode ser feita a lápis ou caneta Não é permitida consulta a notas
Prova 05/ (3/04/05) Aluno: Matrícula: Instruções A prova consiste de quatro questões discursivas A prova terá a duração de h30 A prova pode ser feita a lápis ou caneta Não é permitida consulta a notas
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período.
 Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período. sin(t) = sin (t + T), ou exp(t) = exp(t+t) em que T é o período. [sin(a) e/ou cos(a) ]+[ sin(b) e/ou cos(b)] = o periodo
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período. sin(t) = sin (t + T), ou exp(t) = exp(t+t) em que T é o período. [sin(a) e/ou cos(a) ]+[ sin(b) e/ou cos(b)] = o periodo
Equação da reta. No R 2 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 05
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 05 Assunto:Equações da reta no R 2 e no R 3, equações do plano, funções de uma variável real a valores em R n Palavras-chaves: Equação da reta,
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 05 Assunto:Equações da reta no R 2 e no R 3, equações do plano, funções de uma variável real a valores em R n Palavras-chaves: Equação da reta,
Introdução aos Sinais
 Introdução aos Sinais Pedro M. Q. Aguiar, Luís M. B. Almeida Setembro, 2012 1 Conceito de sinal Um sinal representa a variação de uma grandeza como função de uma variável independente, que designaremos
Introdução aos Sinais Pedro M. Q. Aguiar, Luís M. B. Almeida Setembro, 2012 1 Conceito de sinal Um sinal representa a variação de uma grandeza como função de uma variável independente, que designaremos
Sinais e Sistemas - ESP208
 Sinais e Sistemas - ESP208 Mestrado Profissional em Engenharia de Sistemas e Produtos Filtros Digitais FIR e IIR Fabrício Simões IFBA 01 de novembro de 2017 Fabrício Simões (IFBA) Sinais e Sistemas - ESP208
Sinais e Sistemas - ESP208 Mestrado Profissional em Engenharia de Sistemas e Produtos Filtros Digitais FIR e IIR Fabrício Simões IFBA 01 de novembro de 2017 Fabrício Simões (IFBA) Sinais e Sistemas - ESP208
Filtros IIR. 27 de outubro de 2015 IFBA. Fabrício Simões (IFBA) Filtros IIR 27 de outubro de / 49
 Filtros IIR Fabrício Simões IFBA 27 de outubro de 2015 Fabrício Simões (IFBA) Filtros IIR 27 de outubro de 2015 1 / 49 1 Filtragem Digital 2 Filtro IIR Filtros de Primeira Ordem Filtros de Segunda Ordem
Filtros IIR Fabrício Simões IFBA 27 de outubro de 2015 Fabrício Simões (IFBA) Filtros IIR 27 de outubro de 2015 1 / 49 1 Filtragem Digital 2 Filtro IIR Filtros de Primeira Ordem Filtros de Segunda Ordem
Sinais e Sistemas. Sinais e Sistemas Fundamentos. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Sinais e Sistemas Sinais e Sistemas Fundamentos Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Impulso Unitário Discreto 1 Impulso Unitário Discreto 0.9 0.8 δ[ n] 1,
Sinais e Sistemas Sinais e Sistemas Fundamentos Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Impulso Unitário Discreto 1 Impulso Unitário Discreto 0.9 0.8 δ[ n] 1,
I-6 Sistemas e Resposta em Frequência. Comunicações (6 de Dezembro de 2012)
 I-6 Sistemas e Resposta em Frequência (6 de Dezembro de 2012) Sumário 1. A função especial delta-dirac 2. Sistemas 3. Resposta impulsional e resposta em frequência 4. Tipos de filtragem 5. Associação de
I-6 Sistemas e Resposta em Frequência (6 de Dezembro de 2012) Sumário 1. A função especial delta-dirac 2. Sistemas 3. Resposta impulsional e resposta em frequência 4. Tipos de filtragem 5. Associação de
Sinais e Sistemas. Sinais e Sistemas Fundamentos. Renato Dourado Maia. Faculdade de Ciência e Tecnologia de Montes Claros
 Sinais e Sistemas Sinais e Sistemas Fundamentos Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Impulso Unitário Discreto 1 Impulso Unitário Discreto
Sinais e Sistemas Sinais e Sistemas Fundamentos Renato Dourado Maia Faculdade de Ciência e Tecnologia de Montes Claros Fundação Educacional Montes Claros Impulso Unitário Discreto 1 Impulso Unitário Discreto
TRANSFORMADA DE FOURIER. Larissa Driemeier
 TRANSFORMADA DE FOURIER Larissa Driemeier TESTE 7hs30 às 8hs00 Este não é um sinal periódico. Queremos calcular seu espectro usando análise de Fourier, mas aprendemos que o sinal deve ser periódico. O
TRANSFORMADA DE FOURIER Larissa Driemeier TESTE 7hs30 às 8hs00 Este não é um sinal periódico. Queremos calcular seu espectro usando análise de Fourier, mas aprendemos que o sinal deve ser periódico. O
Transformada Discreta de Fourier (DFT)
 Transformada Discreta de Fourier (DFT) A DFT de uma sequência x n de comprimento finito N é definida como: X k = x n e j2π N kn, 0 k N 1 A DFT mapeia uma sequência de comprimento N, x n, em outra sequência,
Transformada Discreta de Fourier (DFT) A DFT de uma sequência x n de comprimento finito N é definida como: X k = x n e j2π N kn, 0 k N 1 A DFT mapeia uma sequência de comprimento N, x n, em outra sequência,
Sistemas Lineares e Invariantes
 Universidade Federal da Paraíba Programa de Pós-Graduação em Engenharia Elétrica Sistemas Lineares e Invariantes Prof. Juan Moises Mauricio Villanueva jmauricio@cear.ufpb.br www.cear.ufpb.br/juan 1 Sistemas
Universidade Federal da Paraíba Programa de Pós-Graduação em Engenharia Elétrica Sistemas Lineares e Invariantes Prof. Juan Moises Mauricio Villanueva jmauricio@cear.ufpb.br www.cear.ufpb.br/juan 1 Sistemas
II. REVISÃO DE FUNDAMENTOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
(c) G d (z) = (d) G d (z) = A função de transferência do equivalente por invariância da resposta impulsional é = Z
 Parte I Escolha múltipla h Tópicos de resolução A função de transferência do sistema cuja resposta ao degrau unitário está representada na figura é 8 (a) G(s) = s + 6s + 4 8 (b) G(s) = s + 4s + 4 8 (c)
Parte I Escolha múltipla h Tópicos de resolução A função de transferência do sistema cuja resposta ao degrau unitário está representada na figura é 8 (a) G(s) = s + 6s + 4 8 (b) G(s) = s + 4s + 4 8 (c)
Controle e Sistemas Não lineares
 Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
Sistemas de tempo discreto
 Sistemas de tempo discreto Magno T. M. Silva EPUSP, fevereiro de Sistemas de tempo discreto p. /37 . Sistemas de tempo discreto São funções matemáticas que transformam uma seqüência de entrada s(n) em
Sistemas de tempo discreto Magno T. M. Silva EPUSP, fevereiro de Sistemas de tempo discreto p. /37 . Sistemas de tempo discreto São funções matemáticas que transformam uma seqüência de entrada s(n) em
Processamento Digital de Sinais
 Processamento Digital de Sinais Parte 2 Introdução Fabricio Ferrari Unipampa/Bagé 2009 Aplicações Astrofísica Melhora imagens espaciais Redução de ruídos Compressão de dados Análise de dados (espaciais,
Processamento Digital de Sinais Parte 2 Introdução Fabricio Ferrari Unipampa/Bagé 2009 Aplicações Astrofísica Melhora imagens espaciais Redução de ruídos Compressão de dados Análise de dados (espaciais,
Transformada de Fourier Discreta no Tempo (DTFT)
 Transformada de Fourier Discreta no Tempo (DTFT) Transformada de Fourier de um sinal discreto no tempo x(n): X e jω = x(n)e jωn n= A DTFT é uma função complexa da variável real e contínua ω. A DTFT é uma
Transformada de Fourier Discreta no Tempo (DTFT) Transformada de Fourier de um sinal discreto no tempo x(n): X e jω = x(n)e jωn n= A DTFT é uma função complexa da variável real e contínua ω. A DTFT é uma
Sinais e Sistemas. Capítulo INTRODUÇÃO 1.2 SINAIS DE TEMPO DISCRETO
 Capítulo 1 Sinais e Sistemas 1.1 INTRODUÇÃO Neste capítulo, começamos nosso estudo do processamento digital de sinais desenvolvendo as noções de sinal e sistema de tempo discreto. Vamos nos concentrar
Capítulo 1 Sinais e Sistemas 1.1 INTRODUÇÃO Neste capítulo, começamos nosso estudo do processamento digital de sinais desenvolvendo as noções de sinal e sistema de tempo discreto. Vamos nos concentrar
Capítulo 6 Filtragem, Amostragem e Reconstrução
 Capítulo 6 Filtragem, Amostragem e Reconstrução 6. Filtragem 6.2 Amostragem e reconstrução de sinais Capítulo 6 Filtragem, Amostragem e Reconstrução 6. Filtragem 6.2 Amostragem e reconstrução de sinais
Capítulo 6 Filtragem, Amostragem e Reconstrução 6. Filtragem 6.2 Amostragem e reconstrução de sinais Capítulo 6 Filtragem, Amostragem e Reconstrução 6. Filtragem 6.2 Amostragem e reconstrução de sinais
Teoria das Comunicações Prof. André Noll Barreto Prova 1 Gabarito
 Prova Gabarito Questão (4 pontos) Um pulso é descrito por: g t = t e t / u t u t, a) Esboce o pulso. Este é um sinal de energia ou de potência? Qual sua energia/potência? (,7 ponto) b) Dado um trem periódico
Prova Gabarito Questão (4 pontos) Um pulso é descrito por: g t = t e t / u t u t, a) Esboce o pulso. Este é um sinal de energia ou de potência? Qual sua energia/potência? (,7 ponto) b) Dado um trem periódico
Processamento de sinais digitais Aula 3: Transformada de Fourier (Parte 1)
 Processamento de sinais digitais Aula 3: Transformada de Fourier (Parte 1) silviavicter@iprj.uerj.br Tópicos Definição da Transformada de Fourier (TF) Propriedades importantes (ex: linearidade e periodicidade)
Processamento de sinais digitais Aula 3: Transformada de Fourier (Parte 1) silviavicter@iprj.uerj.br Tópicos Definição da Transformada de Fourier (TF) Propriedades importantes (ex: linearidade e periodicidade)
