ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do Exame Parcial 2
|
|
|
- Ana Luísa Barreiro Pinhal
- 6 Há anos
- Visualizações:
Transcrição
1 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame arcial 2 25 de Junho de 2007 Ano Lectivo: Semestre: Verão
2 ISEL è DEETC Secção de Matemática ç ALGA
3 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial 2 3 Grupo I 1 ç ara cada um dos subconjuntos seguintes, averigue se são subespaços dos espaços vectoriais indicados e, em caso afirmativo, indique uma base e a respectiva dimensão: a ç E œ ea+ -ß, +ß, -ß+, b À+ß,ß- f % (espaço vectorial real) b ç Fœ Eœ + $ß$ e c dà+ œ!, se k3 4k Ÿ f (espaço vectorial real) c ç G œeadß3ß3b ÀD f $ (espaço vectorial real) d ç G œeadß3ß3b ÀD f $ (espaço vectorial complexo) 1a ç E é um subespaço vectorial de %, como se mostra a seguir: Eœ ea+ -ß, +ß, -ß+, bà+ß,ß- f œ e+ aß ß!ß b, a!ß ß ß b - aß!ß ß! bà +ß,ß - f œ ˆ aß ß!ß bß a!ßßß bß aß!ßß! b O desenvolvimento anterior mostra que E é o subespaço gerado pela seguinte lista? de vectores de %? œ ˆ aß ß!ß bß a!ßßß bß aß!ßß! b ara determinar uma de E, basta condensar verticalmente a matriz cujas linhas são os vectores de?: Ô! Ô! Ô!! $ Ä$! $ Ä$! Õ!! Ø Õ! Ø Õ!!!! Ø ˆ aß ß!ß bß a!ßßß b é uma base de Ee dime œ. Ô!! + $ $ß$ 1b ç F é subespaço de, visto que E FÍEœ!!!, com + $ ß+ $. Õ+ $!! Ø ortanto, Ú!! + Þ Ô $ F œû!!! À+ $ ß+ $ ß ÜÕ+!! Ø $ à Ú!!!!! Þ Ô Ô œ Û + $!!! + $!!! À+ $ ß+ $ ß Ü Õ!!! Ø Õ!! Ø à ÎÔ!! Ô!!! Ñ œ!!! ß!!! ÏÕ!!! Ø Õ!! ØÒ Ano Lectivo: Semestre: Verão 2007 Junho 25
4 4 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica ÎÔ!! Ô!!! Ñ A lista,œ!!! ß!!! é linearmente independente e gera F, logo é uma ÏÕ!!! Ø Õ!! ØÒ base de F, tendo-se dimf œ. 1c ç G não é subespaço do espaço vectorial real $, porque não contém o vector nulo. 1d ç G também não é subespaço do espaço vectorial complexo $, pela mesma razão invocada na alínea anterior. $ 2 ç Considere as sequências = e = de vectores dos espaços e respectivamente = œ ˆ aß 3bß a 3ß bß a%ß! b = œ ˆ a3ß 3ß 3bß a3ß 3ß! bß a$3ß!ß! b a ç Considerando e $ como espaços vectoriais complexos, determine uma base e a dimensão dos subespaços gerados por = e =. $ b ç Considerando agora que e são espaços vectoriais reais, determine uma base e a dimensão dos subespaços gerados por = e =. 2a ç Nesta alínea, basta levar a cabo a condensação vertical das matrizes W e W cujas linhas são, respectivamente, os vectores das listas = e = : Ô 3 Ô 3 Ô 3 Ä a 3b W œ 3! 3 Ä! 3 $ Ä$ % $ Ä a 3b$ %3 Õ %! Ø Õ! %3 Ø Õ!! Ø ortanto, a lista = é -linearmente dependente (o que era óbvio, dado ter um número de vectores superior à dimensão de sobre ) e a lista, œ ˆ aß 3bß a!ß 3b é uma base de a= b e dim a a= bb œ. Isto implica que a= b œ. Quanto à lista =, temos Ô W œ 3 3! Ä 3 Ô Ô Ô Ä 3 Ä!!!! Ä $ Ä $ Ç$ $ 3$ Õ$3!! Ø $ Õ!! Ø Õ! Ø Õ!! Ø Neste caso, = é -linearmente independente e a lista ˆ aßß bß a!ßß bß a!ß!ß b é uma base escalonada de a= b, tal como a própria lista =. Temos dima a= bb œ $, o que mostra que $ $ a= b œ. Note que a dimensão de sobre é $ Junho 25 Ano Lectivo: Semestre: Verão
5 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial 2 5 2b ç Vejamos se = é -linearmente independente: com BßCßD, façamos B aß 3b C a 3ß b D a%ß! b œ a!ß! b ͈ ab C %Db 3Cß C 3B œ a!ß! b A igualdade vectorial anterior equivale ao seguinte sistema de equações lineares homogéneas nas incógnitas reais abß Cß Db: Ú Ý B C %D œ! C œ! Û Ý C œ! Ü B œ! O sistema é determinado e tem apenas a solução trivial BœCœDœ!, o que mostra que = é -linearmente independente e é uma base de a= b, cuja dimensão é dima a= bb œ $ (note que a dimensão de sobre é %, sendo ˆ aß! bßa3ß! bß a!ß bß a!ß3b uma base). Agindo de igual forma para =, temos, com BßCßD, Ba3ß 3ß 3b C a3ß 3ß! b D a$3ß!ß! b œ a!ß!ß! b Í ˆ ab C $Db3ß ab Cb3ß B3 œ a!ß!ß! b A igualdade vectorial anterior equivale ao seguinte sistema de equações lineares homogéneas nas incógnitas reais abß Cß Db: Ú B C $D œ! Û B C œ! Ü B œ! O sistema é novamente determinado, tendo apenas a solução trivial BœCœDœ!, o que mostra que = é -linearmente independente e é uma base de a= b, cuja dimensão é $ dima a= bb œ $. Note que a dimensão de sobre é ', sendo a lista $ uma base de sobre. - œ ˆ aß!ß! bß a3ß!ß! bß a!ß ß! bß a!ß 3ß! bß a!ß!ß bß a!ß!ß 3b Neste caso, podíamos imediatamente concluir que = era -linearmente independente, porque tínhamos já visto na alínea anterior que = era -linearmente independente e atendendo ao resultado teórico seguinte: Seja I um espaço vectorial complexo. Então, I é também um espaço vectorial real (com a mesma adição vectorial e com a restrição a I da multiplicação de escalar por vector) e, se /œ a/tß/tßáß/t 7 b é uma lista -linearmente dependente, então a lista / será também - linearmente dependente. Se I tem dimensão 8 sobre, então I tem dimensão 8 sobre ; mais precisamente, se / œ a/tß/tßáß/t 8b é uma base do espaço complexo I, então a lista / œ a/tß/tßáß/tß3/tß3/tßáß3/t 8 8 b é uma base do espaço real I. Ano Lectivo: Semestre: Verão 2007 Junho 25
6 6 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica 3 ç Considere, no espaço cartesiano real $, o subconjunto J œ eabß Cß DbÀ B C (D œ! %B )C &D œ! B %C $D œ! f e a sequência = œ ˆ a %ß ß $ bß aß ß & bß a!ß!ß b de vectores de $ e seja ainda K œ a= b o subespaço gerado por = : a ç Determine uma base e a dimensão de J. b ç Indique uma base e a dimensão de K e caracterize os vectores de K por meio de uma condição nas suas componentes. c ç Determine o subespaço L œ J K, indicando uma base e a dimensão de L. d ç Será J K um subespaço de $? Justifique a resposta. $ 3a ç J é o espaço das soluções do seguinte sistema de equações lineares homogéneas: Ú B C (D œ! Û %B )C &D œ! Ü B %C $D œ! As soluções do sistema obtêm-se pelo algoritmo de Gauss-Jordan: Ô (! Ô (! Ä % % ) &! Ä!! $$! Õ % $! Ø Õ!!! Ø Ô (!!!!!! Ä ( Õ!!!! Ø!!! Ä $$ $ $ Ä $ $ O sistema é simplesmente indeterminado e as incógnitas principais são arbitrário; a solução geral é abß Cß Db œ acß Cß! b œ C aß ß! bà C B e D, ficando C Então, J é o subespaço gerado pelo vector aßß! b o qual forma uma base de J (recta passando pela origem e com a direcção do vector aß ß! b): J œ ec aß ß! bà C f œ eabß Cß DbÀ B C œ! D œ! f œ ˆ aß ß! b à dimj œ 2007 Junho 25 Ano Lectivo: Semestre: Verão
7 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial 2 7 3b ç Recorremos, de novo, ao algoritmo de condensação vertical para determinar uma base e a dimensão de K, condensando a matriz W cujas linhas são os vectores de = : Ô % $ Ô % $ Ô % $ Ä Ä Wœ & $!! $!! $ Ä $ Õ!! Ø Õ!! Ø Õ!!! Ø O resultado anterior mostra que a lista = é linearmente dependente e que, œ ˆ a%ß ß $ bß a!ß!ß b constitui uma base de Kœ=à ab daqui se conclui que dimkœ. ara caracterizarmos os vectores de K, basta atender a que um vector abßcßdb pertence a Kse e só se ele for combinação linear dos vectores de, (ou de = ), pelo que a lista ˆ a%ßß $ bß a!ß!ß bßabßcßdb deverá ser linearmente dependente, ou seja, a matriz com estas linhas deverá ter característica igual a : Ô % $ Ô % $ Ô % $!! $ Ä%$ B!! $ Ä$ a$b %Db!! ÕB C D Ø Õ! B %C $B %D Ø Õ! B %C! Ø ara que a matriz anterior tenha característica igual a, deverá ser B %C œ! ou, equivalentemente, B C œ!, pelo que K é um plano vertical passando pela origem e perpendicular ao vector aß ß! b: K œ eabß Cß DbÀ B C œ! f 3c ç Quanto a L œ J K, temos, por definição de intersecção, LœeaBßCßDbÀB Cœ! Dœ! B Cœ! f œeabßcßdbàb Cœ! Dœ! f œj ortanto, temos L œj KœJ, o que equivale a J K, pelo que o vector aßß! b constitui uma base de L e diml œ dimj œ. 3d ç J K é um subespaço de $, visto que J K, tendo-se J KœK e a lista, œ ˆ a%ß ß $ bß a!ß!ß b é uma base de J K sendo dimaj Kb œ dimk œ. Ano Lectivo: Semestre: Verão 2007 Junho 25
8 8 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica Grupo II 1 ç Seja 2À Ä o endomorfismo de tal que 2 aß$ b œ aß b e 2a ß b œa ß b. Determine 2BßC a b, para qualquer abßcb. Consideremos a base / œ ˆ aß $ b, a ß b e determinemos as coordenadas de um vector genérico abß Cb em relação àquela base: abßcb œ+ aß$ b, a ß b œ a+,ß$+, b A igualdade vectorial anterior equivale a um sistema determinado de 2 equações lineares nas incógnitas a+ß, b que resolvemos a seguir: B B Ä $ $ C! & $B C Ä& &! B C Ä &! BÎ& CÎ& Ä Ê a+ß, b œ ab Cß $B b! & $B C & C! $BÎ& CÎ& & Temos, pois, abß Cb œ ab C baß $ b a $B Cba ß b & & Da igualdade vectorial anterior e atendendo à linearidade de 2, obtemos: 2aBßCb œ ab Cb2 aß$ b a $B Cb2a ß babßcb & & œ ab C baß b a $B Cba ß b œ a)b Cß B %Cb & & & 2007 Junho 25 Ano Lectivo: Semestre: Verão
9 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial ç Seja E uma matriz real do tipo $ % cujo espaço das linhas admite a base ˆ aß ß $ß! bß a!ß $ß!ß b. Indique, justificando adequadamente, o valor de verdade das proposições seguintes: a ç O espaço nulo de E tem dimensão. b ç As linhas de E são linearmente independentes. 2a ç É verdadeira. Como ˆ aß ß $ß! bß a!ß $ß!ß b é uma base do espaço das linhas, segue- se que a característica de E é < œ. A dimensão = do espaço nulo de E (nulidade de E) é o seu número de colunas ( 8œ% ) menos a característica <, ou seja, =œ8 <œ% œ (grau de indeterminação do sistema homogéneo E\ œ S). 2b ç É falsa, porque a característica é <œ $œnúmero de linhas. $ 3 ç Considere o endomorfismo :À Ä $ àabßcßdb È: abßcßdb que projecta ortogonalmente os vectores de $ sobre o plano \S^ (num referencial ortonormado S\] ^): a ç Determine : abßcßdb, para qualquer abßcßdb $ e mostre que : é linear. b ç Determine o núcleo, a imagem, a nulidade e a característica de :. c ç Tomando a mesma base no domínio e no codomínio, determine a matriz de : em relação à base / œ ˆ aß ß! bß a!ß ß bß a!ß!ß b 3a ç Os pontos do plano \S^ têm Cœ!, pelo que a projecção ortogonal de abßcßdb sobre aquele plano é o vector abß!ß Db. ortanto, : abßcßdb œabß!ßdb A função : é linear: w w w $ ñ Quanto à imagem da soma, tem-se, para quaisquer abßcßdbßabßcßd b : : ˆ w w w BßCßD BßCßD w w w w w a b a b œ: ab BßC CßD D b œab Bß!ßD D b w w w w w œabß!ßdb abß!ßd b œ: abßcßdb : abßcßd b $ ñ Quanto à imagem do produto de escalar por vector, tem-se, para! e abßcßdb : : ˆ! abßcßdb œ: a! Bß! Cß! Db œa! Bß!ß! Db œ! abß!ßdb œ!: abßcßdb Ano Lectivo: Semestre: Verão 2007 Junho 25
10 10 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica 3b ç Temos: Kera: b œ eabß Cß DbÀ abß!ß Db œ a!ß!ß! bf œ eabß Cß DbÀ B œ! D œ! f œ ea!ßcß! bàc f œec a!ßß! bàc f œ aa!ß ß! bb O vector a!ß ß! b constitui uma base do núcleo e nulidadea: b œ dimaker a: bb œ, o que mostra que : não é injectiva. Quanto a Img a: b, sabemos que ela é gerada pelas imagens por : dos vectores de qualquer base de $, por exemplo, a base canónica - œ ˆ aß!ß! bß a!ß ß! bß a!ß!ß b : Imga: b œ ˆ : aß!ß! bß: a!ßß! bß: a!ß!ß b œ ˆ aß!ß! bß a!ß!ß! bß a!ß!ß b œ ˆ aß!ß! bß a!ß!ß b A lista, œ ˆ aß!ß! bß a!ß!ß b é linearmente independente (é escalonada) e constitui uma base de Img a: b, pelo que será Img a: b œ ˆ aß!ß! bß a!ß!ß b. A característica de : é igual a dimaimg a: bb œ, o que está de acordo com o Teorema Fundamental: dimˆ Kera: b dimˆ Imga: b œ œ$œ dimˆ $ Observe-se que era óbvio que o contradomínio de : é gerado por,, visto que : abßcßdb œabß!ßdb œb aß!ß! b D a!ß!ß b à BßD 3c ç As colunas da matriz de : na base / œ ˆ aß ß! bß a!ß ß bß a!ß!ß b contêm as w w w ww ww ww coordenadas a+ß,ß - b, a+ ß, ß - b e a+ ß, ß - b dos vectores : aß ß! b, : a!ß ß b e : a!ß!ß b em relação à base /. Ora : aßß! b œ aß!ß! b œ+ aßß! b, a!ßß b - a!ß!ß b œ a+ß+,ß, -b w w w w w w w w : a!ßß b œ a!ß!ß b œ+ aßß! b, a!ßß b - a!ß!ß b œ a+ß+,ß, -b ww ww ww ww ww ww ww ww : a!ß!ß b œa!ß!ß b œ+ aßß! b, a!ßß b - a!ß!ß b œ a+ ß+, ß, - b As três igualdades vectoriais anteriores equivalem a três sistemas determinados, cada qual com três equações e três incógnitas, cuja matriz simples é comum, o que permite a sua resolução simultânea; além disso, os dois últimos sistemas são iguais, pelo que resolveremos apenas os ww ww ww w w w dois primeiros sistemas, ficando a+ß,ß-b œ a+ß,ß-b: Ô!!! Ô!!! Ô!!!!!! Ä!!! $ Ä$!!! Õ!! Ø Õ!! Ø Õ!! Ø Então, a matriz de : na base / será Ô!! Q /a: b œ!! Õ Ø 2007 Junho 25 Ano Lectivo: Semestre: Verão
11 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial 2 11 Esta matriz podia também obter-se da matriz Q -a: b de : na base canónica (a qual é imediata) e da matriz X de mudança da base canónica para a base /: -/ Ô!! Q / a: b œ X-/ Q -a: bx-/, com Q -a: b œ!!! Õ!! Ø A matriz X -/ é também imediata: X -/ Ô!! œ! Õ! Ø Ô!! A inversão de X-/ dá-nos X-/ œ X/- œ!, pelo que temos, de novo, Õ Ø Ô!! Ô!! Ô!! Q /a: b œ!!!!! Õ ØÕ!! ØÕ! Ø Ô!! Ô!! Ô!! œ!!! œ!! Õ! ØÕ! Ø Õ Ø Ano Lectivo: Semestre: Verão 2007 Junho 25
12 12 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica Grupo III 1 ç Seja 2 o endomorfismo do espaço cartesiano real $ cuja representação matricial na base canónica é a matriz Ô!! Lœ! Õ! $ Ø a ç Mostre que aßß b é um vector próprio de 2e determine o respectivo valor próprio. b ç Calcule os restantes valores próprios, bem como todos os subespaços próprios de 2 e diga, com base nos valores próprios, se 2 é um automorfismo de $. c ç Mostre que 2 é diagonalizável e determine uma matriz diagonal H e uma matriz invertível X tais que HœX LX. 1a ç Temos, trabalhando com as coordenadas dos vectores em relação à base canónica, Ô!! Ô Ô Ô! œ œ Õ! $ ØÕ Ø Õ Ø Õ Ø o que mostra, por definição, que - œ. aß ß b é um vector próprio associado ao valor próprio 1b ç O polinómio característico de 2 é -!! : 2a-b œ! - œ a- ba- ba- $ b â! $ - â As raízes do polinómio : 2 são, e $ e, sendo reais, todas são valores próprios de 2; deste modo, o espectro de 2 será: $ Ea2b œ eß ß $ f A função 2 é um automorfismo de, visto que - œ! não é valor próprio de 2 (basta observar que! é valor próprio de 2 se e só se existe um vector a+ß,ß -b Á a!ß!ß! b tal que 2 a+ß,ß-b œ! a+ß,ß-b œ a!ß!ß! b, ou seja, se e só se o núcleo de 2 contém vectores não nulos, o que equivale a dizer que 2 não é injectiva). Estes valores próprios têm multiplicidade algébrica igual a, visto serem raízes simples do polinómio característico. Existem $ valores próprios distintos e, então, sabemos que $ vectores próprios associados a cada um destes valores próprios serão linearmente independentes, formando uma base de $, na qual 2 será representada por uma matriz diagonal: 2 é diagonalizável. Representando por - a b e!- a b, respectivamente, a multiplicidade geométrica e a multiplicidade algébrica de um valor próprio - Ea2 b, sabemos que Ÿ a- b Ÿ! a-b, o que, no caso presente, nos dá Ÿ- a b Ÿ, ou seja, os valores próprios têm todos multiplicidade geométrica 2007 Junho 25 Ano Lectivo: Semestre: Verão
13 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial 2 13 igual a. Isto conduz a! $ - a b œ $ œ dima b e, de novo, à conclusão de que 2 é diagonalizável. - Ea2b As coordenadas \- œ cbcdd T dos vectores próprios de 2 na base canónica são as soluções não nulas dos sistemas homogéneos simplesmente indeterminados al - M $ b\ - œs, para cada - Ea2b. Assim, teremos: ñ ara - œ : Ô!!!! Ô!! Ç$ T!! Ä!! Ê\ œc D D Dd àd - Õ!! Ø Õ!!!! Ø Os vectores próprios pertencentes a - œ serão D aß!ß! b D a!ß ß! b D a!ß!ß b œ a Dß Dß Db œ D aß ß b à D O subespaço próprio de 2 associado a - œ é gerado pelo vector aßß b, que constitui uma base de Ia2b: I a2b œe5 aßß bà5 f œ aaßß bb Ê a b œdimai a2bb œ ñ ara - œ : Ô!!! Ô!!! Ô!!!!!! $ Ä $ Ä T!!!!!! Ê\ œc! C! d àc Ä $ $ - Õ!! Ø Õ!!! Ø Õ!!!! Ø Os vectores próprios pertencentes a - œ serão! aß!ß! b C a!ßß! b! a!ß!ß b œc a!ßß! b àc O subespaço próprio de 2 associado a - œ é gerado pelo vector a!ßß! b, que constitui uma base de Ia2b: I a2b œ ec a!ß ß! bà C f œ aa!ß ß! bb Ê a b œ dimai a2bb œ ñ ara - œ $ : Ô!!! Ô!!! Ô!!! $ Ä$!! Ä Ä T!!!! Ê\ œc! D Dd àd - Õ!!! Ø Õ!!!! Ø Õ!!!! Ø Os vectores próprios pertencentes a - œ$ serão da forma! aß!ß! b D a!ßß! b D a!ß!ß b œd a!ßß b àd O subespaço próprio de 2 associado a - œ$ é gerado pelo vector a!ßß b, que constitui uma base de I$a2b: I a2b œ ed a!ß ß bà D f œ aa!ß ß bb Ê a$ b œ dimai a2bb œ $ $ Ano Lectivo: Semestre: Verão 2007 Junho 25
14 14 Resolução do Exame arcial 2 - Álgebra Linear e Geometria Analítica A tabela seguinte resume o estudo feito: - Subespaços próprios de 2 Mult. geométrica a- b Mult. algébrica! a-b I a2b œe5 aßß bà5 f I a2b œec a!ßß! bàc f $ I$ a2b œ ed a!ß ß bàd f 1c ç Fazendo, por exemplo, 5œCœDœ nos vectores próprios da tabela anterior, obtemos os vectores próprios aß ß b, a!ß ß! b e a!ß ß b associados, respectivamente, aos valores próprios, e $. Assim, na base / œ a/tß/tß/t $ b œ ˆ aßß bß a!ßß! bß a!ßß b, a matriz de 2 será H œ diag aß ß $ b. A matriz regular X pedida é a matriz X-/ de mudança da base canónica - para a base /, cujas colunas contêm as coordenadas dos /t 3 na base canónica (ou seja, as próprias componentes dos /t 3 ): Ô!! Xœ Õ! Ø Assim, a matriz X diagonaliza L, isto é, X LX œ diag aß ß $ b œ H. odemos verificar este resultado, começando por determinar X (que é a matriz de mudança da base / para a base -): Então: Ô!!!! Ô!!!! Ä!!!! $ Ä$ Õ!!! Ø Õ!!! Ø Ô!!!! Ô!!!! ÊX œ Õ!!! Ø Õ! Ø X Ä $ Ô!! Ô!! Ô!! LX œ! Õ! ØÕ! $ ØÕ! Ø Ô!! Ô!! Ô!! œ % œ!! œ H Õ $! $ ØÕ! Ø Õ!! $ Ø Neste caso, existem $xœ' matrizes diagonais possíveis, correspondentes às ' permutações da sequência aß ß $ b dos valores próprios de 2. ara cada uma destas matrizes diagonais, existe uma infinidade de bases diagonalizadoras Junho 25 Ano Lectivo: Semestre: Verão
15 Álgebra Linear e Geometria Analítica - Resolução do Exame arcial ç Seja E uma matriz real quadrada de $ ª ordem cujo polinómio característico é : a-b œ -a- ba- b a ç Determine se E é semelhante a alguma matriz diagonal e, em caso afirmativo, indique quantas matrizes diagonais semelhantes a E existem, mostrando ainda uma delas. b ç Determine o valor da característica e da nulidade de E e justifique a sua resposta. c ç Calcule dete e diga, justificando, se E é invertível. 2a ç O espectro de E é EaEb œ e!ß ß f. Existindo 3 valores próprios distintos, quaisquer três vectores próprios pertencentes a cada um deles serão linearmente independentes e constituirão uma base de $. A matriz X cujas colunas são esses vectores próprios será diagonalizadora de E, isto é, X EX œ diaga!ß ß b Existem $xœ' matrizes diagonais semelhantes a E correspondentes às permutações da lista a!ß ß b dos valores próprios de E e, para cada uma delas, uma infinidade de matrizes X diagonalizadoras: H œ diaga!ß ß bß diaga!ß ß bß diagaß!ß bß diagaß ß! bß diagaß!ß bß diagaß ß! b 2b ç Matrizes semelhantes têm a mesma característica (por representarem o mesmo endomorfismo 0 em bases diferentes: trata-se da dimensão do contradomínio de 0). Deste modo será, por exemplo, <œcaeb œ cadiag aßß! bb œ. A nulidade de Eserá 8 <œ$ œ, que é a dimensão do núcleo de E, o qual coincide com o subespaço próprio I!aEb associado ao valor próprio - œ!. 2c ç Ora, para qualquer -, temos detae -M$ b œ : a-b œ -a- ba- b; fazendo agora - œ!, vem dete œ:! a b œ!! a ba! b œ! Deste modo, E não é invertível (o que era óbvio, visto! ser valor próprio de E) e dete œ!. Outra forma de concluir que dete œ! é atender a que matrizes semelhantes têm o mesmo determinante, pelo que!!! deteœdethœ!! œ! â!! â Ano Lectivo: Semestre: Verão 2007 Junho 25
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época Especial) 17 de Setembro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época Especial) 17 de Setembro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 1º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste Realizado em 01 de Fevereiro de 2012 Ano Lectivo: 2011-2012 Semestre: Inverno ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste Realizado em 01 de Fevereiro de 2012 Ano Lectivo: 2011-2012 Semestre: Inverno ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do Exame (Época Normal) 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do Exame (Época Normal) 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 2º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 1º Teste
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 05 de Maio de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 05 de Maio de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 1º Teste 29 de Abril de 2015; 18:30 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 1º Teste 29 de Abril de 2015; 18:30 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 1º Teste
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 07 de Maio de 2012 Ano Lectivo: 2011-2012 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução do
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 07 de Maio de 2012 Ano Lectivo: 2011-2012 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução do
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 2º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 2º Teste 30 de Junho de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 2º Teste 30 de Junho de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 20 de Fevereiro de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 20 de Fevereiro de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução da Repetição do 1º este 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução da Repetição do 1º este 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 1º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste 01 de Fevereiro de 2013 Ano Lectivo: 2012-2013 Semestre: Inverno ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste 01 de Fevereiro de 2013 Ano Lectivo: 2012-2013 Semestre: Inverno ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
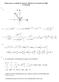 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Números Complexos Ficha 01
 Instituto Superior de Engenharia de Lisboa Departamento de Engenharia de Electrónica e elecomunicações e de Computadores Secção de Matemática Números Complexos Ficha 01 ñ A Ficha sobre Números Complexos
Instituto Superior de Engenharia de Lisboa Departamento de Engenharia de Electrónica e elecomunicações e de Computadores Secção de Matemática Números Complexos Ficha 01 ñ A Ficha sobre Números Complexos
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra linear e geometria analítica
 27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
Resolução do 1 o Teste - A (6 de Novembro de 2004)
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
{ 1 2 3, 2 4 6, T
 Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Resolução do efólio B
 Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química
 Código do Teste: 105 Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química 1. Para as matrizes A = ( 1 0 3 1 ) B = ( 5 4 1 0 2 1 3 1 ) C = 1 1 1 0 5 1
Código do Teste: 105 Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química 1. Para as matrizes A = ( 1 0 3 1 ) B = ( 5 4 1 0 2 1 3 1 ) C = 1 1 1 0 5 1
(2008/2009) Espaços vectoriais. Matemática 1º Ano - 1º Semestre 2008/2009. Mafalda Johannsen
 Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
ESPAÇOS LINEARES (ou vetoriais)
 Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
Colectânea de Exercícios
 ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
Ficha de Trabalho 02 Sistemas. Matriz Inversa. (Aulas 4 a 6).
 F I C H A D E R A B A L H O 0 Ficha de rabalho 0 Sistemas. Matriz Inversa. (Aulas 4 a 6). Sistemas de equações lineares. Equação linear. Sistema de equações lineares. Equação matricial. Soluções do sistema.
F I C H A D E R A B A L H O 0 Ficha de rabalho 0 Sistemas. Matriz Inversa. (Aulas 4 a 6). Sistemas de equações lineares. Equação linear. Sistema de equações lineares. Equação matricial. Soluções do sistema.
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003. Funções reais de várias variáveis
 EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
Geometria Analítica e Álgebra Linear
 UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof. Isabel Matos & José Amaral ALGA A - 6--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
Prof. Isabel Matos & José Amaral ALGA A - 6--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL REGIME NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA º FREQUÊNCIA de Janeiro de 8 Duração:
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL REGIME NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA º FREQUÊNCIA de Janeiro de 8 Duração:
Álgebra Linear 1 o Teste
 Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
Indicação de uma possível resolução do exame
 Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
 Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
TÓPICOS. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -1
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Instituto Universitário de Lisboa
 Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0
![1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0 1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0](/thumbs/77/76694592.jpg) 1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que:
 21002 - Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que: Verifique se o ficheiro que recebeu está correcto. O
21002 - Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que: Verifique se o ficheiro que recebeu está correcto. O
Multiplicidade geométrica
 Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
EXERCÍCIOS DE ÁLGEBRA LINEAR. Prefácio 3. Parte 1. Sistemas de equações lineares 4. Parte 2. Matrizes 10. Parte 3.
 EXERCÍCIOS DE ÁLGEBRA LINEAR PEDRO MATIAS Conteúdo Prefácio 3 Parte 1. Sistemas de equações lineares 4 Parte 2. Matrizes 10 Parte 3. Determinantes 16 Parte 4. Geometria analítica 18 Parte 5. Espaços lineares
EXERCÍCIOS DE ÁLGEBRA LINEAR PEDRO MATIAS Conteúdo Prefácio 3 Parte 1. Sistemas de equações lineares 4 Parte 2. Matrizes 10 Parte 3. Determinantes 16 Parte 4. Geometria analítica 18 Parte 5. Espaços lineares
Q1. Seja V um espaço vetorial e considere as seguintes afirmações: um conjunto de geradores de um subespaço S 2 de V, então A 1 A 2
 Q1. Seja V um espaço vetorial e considere as seguintes afirmações: (I) se A 1 é um conjunto de geradores de um subespaço S 1 de V e A 2 é um conjunto de geradores de um subespaço S 2 de V, então A 1 A
Q1. Seja V um espaço vetorial e considere as seguintes afirmações: (I) se A 1 é um conjunto de geradores de um subespaço S 1 de V e A 2 é um conjunto de geradores de um subespaço S 2 de V, então A 1 A
Álgebra Linear I - Lista 10. Matrizes e Transformações lineares. Respostas
 Álgebra Linear I - Lista 1 Matrizes e Transformações lineares Respostas 1 Sejam A e B matrizes quadradas do mesmo tamanho Dê um exemplo onde (A + B 2 A 2 + 2A B + B 2 Complete: (A + B 2 = A 2 + B 2 +?
Álgebra Linear I - Lista 1 Matrizes e Transformações lineares Respostas 1 Sejam A e B matrizes quadradas do mesmo tamanho Dê um exemplo onde (A + B 2 A 2 + 2A B + B 2 Complete: (A + B 2 = A 2 + B 2 +?
Álgebra Linear e Geometria Analítica. 7ª aula
 Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
PROBLEMAS DE ÁLGEBRA LINEAR
 PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
Referências principais (nas quais a lista foi baseada): 1. G. Strang, Álgebra linear e aplicações, 4o Edição, Cengage Learning.
 1 0 Lista de Exercício de Mat 116- Álgebra Linear para Química Turma: 01410 ( 0 semestre 014) Referências principais (nas quais a lista foi baseada): 1. G. Strang, Álgebra linear e aplicações, 4o Edição,
1 0 Lista de Exercício de Mat 116- Álgebra Linear para Química Turma: 01410 ( 0 semestre 014) Referências principais (nas quais a lista foi baseada): 1. G. Strang, Álgebra linear e aplicações, 4o Edição,
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
(a) (1,5) Obtenha os autovalores e autovetores de L. (b) (1,0) A matriz de L em relação à base canônica de M 2 2 é diagonalizável? Explique.
 Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
ÁLGEBRA LINEAR A FICHA 6. Por definição do determinante de uma matriz 3 3, tem-se det A = 7.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Testes e Sebentas. Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes)
 Testes e Sebentas Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes) Índice: 1. Matrizes 1.1. Igualdade de matrizes 3 1.2. Transposta de uma matriz 3 1.3. Multiplicação por um escalar 3
Testes e Sebentas Exercícios resolvidos de Álgebra Linear (Matrizes e Determinantes) Índice: 1. Matrizes 1.1. Igualdade de matrizes 3 1.2. Transposta de uma matriz 3 1.3. Multiplicação por um escalar 3
Universidade Federal da Paraíba Departamento de Matemática. Álgebra Linear e Geometria Analítica
 Departamento de Matemática Álgebra Linear e Geometria Analítica João Pessoa, 16 de março de 2013 AGENDA Primeira prova: 31 de janeiro de 2013 - Sistemas de Equações Lineares e Espaços Vetoriais Segunda
Departamento de Matemática Álgebra Linear e Geometria Analítica João Pessoa, 16 de março de 2013 AGENDA Primeira prova: 31 de janeiro de 2013 - Sistemas de Equações Lineares e Espaços Vetoriais Segunda
Ficha de Trabalho 08 Transformações Lineares. (Aulas 19 a 22).
 F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
ÁLGEBRA LINEAR A FICHA 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Matemática. Lic. em Enologia, 2009/2010
 Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Sebenta de exercícios de Álgebra Linear e Geometria Analítica. Curso: Eng. Topográ ca
 Sebenta de exercícios de Álgebra Linear e Geometria Analítica Curso: Eng. Topográ ca Ano Lectivo 009/010 4 de Setembro de 009 (Versão: 1.0) Índice Notações e terminologia ii 1 Revisão sobre noções elementares
Sebenta de exercícios de Álgebra Linear e Geometria Analítica Curso: Eng. Topográ ca Ano Lectivo 009/010 4 de Setembro de 009 (Versão: 1.0) Índice Notações e terminologia ii 1 Revisão sobre noções elementares
Espaços Vectoriais. Espaços Vectoriais
 Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Bases de subespaços. 5 a : aula prática (1.30h) e 08-04/2010 Bases de subespaços 5-1
 a : aula prática (.h) - e 8-/ Bases de subespaços - Instituto Superior Técnico o semestre Álgebra Linear o ano da Lics.em Engenharia Informática e de Computadores e Engenharia Química Bases de subespaços
a : aula prática (.h) - e 8-/ Bases de subespaços - Instituto Superior Técnico o semestre Álgebra Linear o ano da Lics.em Engenharia Informática e de Computadores e Engenharia Química Bases de subespaços
Sistemas lineares e matrizes, C = e C =
 1. Considere as matrizes ( 2 1 A 4 0 1 MATEMÁTICA I (M 195 (BIOLOGIA, BIOQUÍMICA E ARQUITETURA PAISAGISTA 2014/2015, B Sistemas lineares e matrizes ( 4 1 2 5 1 Verifique se está definida e, caso esteja,
1. Considere as matrizes ( 2 1 A 4 0 1 MATEMÁTICA I (M 195 (BIOLOGIA, BIOQUÍMICA E ARQUITETURA PAISAGISTA 2014/2015, B Sistemas lineares e matrizes ( 4 1 2 5 1 Verifique se está definida e, caso esteja,
Vetores e Geometria Analítica
 Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
6. Verifique detalhadamente que os seguintes conjuntos são espaços vetoriais(com a soma e produto por escalar usuais):
 a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
