Dinâmica do Movimento dos Corpos
|
|
|
- Camila Coradelli Coimbra
- 6 Há anos
- Visualizações:
Transcrição
1 2 Outras coordenadas Gil da Costa Marques 2.1 Coordenadas mais gerais 2.2 Superfícies e curvas generalizadas 2.3 Coordenadas Cartesianas 2.4 Coordenadas Cilíndricas 2.5 Coordenadas Polares 2.6 Coordenadas Esféricas 2.7 As Coordenadas Latitude e Longitude 2.8 O GPS Licenciatura em Ciências USP/ Univesp
2 Licenciatura em Ciências USP/Univesp Módulo Coordenadas mais gerais Exceto em casos especiais, como naqueles localizados ao longo de curvas, na grande maioria das vezes, estamos interessados na localização de um objeto que se situa num ponto arbitrário do espaço. Como já vimos antes, o primeiro passo para tal localização é a escolha de um referencial. Uma vez adotado um sistema particular de referência cartesiana, o próximo passo no estudo dos movimentos é fazer uma escolha de coordenadas, que é feita por uma questão de conveniência e é ditada pelas simetrias do problema em questão. A escolha de um conjunto particular de coordenadas refere-se ao uso de algum que nos permita determinar a posição de um ponto do espaço de forma. Assim, veremos que esse algoritmo faz uso de superfícies e suas intersecções, ou seja, as coordenadas são definidas a partir da intersecção de três superfícies. Observe a Figura 2.1. Figura 2.1: O ponto P e suas coordenadas são definidas a partir da intersecção de três superfícies. Embora isso não pareça óbvio, o fato é que, em três dimensões, todas as coordenadas são definidas tomando-se a intersecção de três superfícies. No espaço tridimensional, quando especificamos o valor de uma coordenada, especificamos superfícies. A localização de um ponto no espaço, em geral, dá-se mediante a procura de um ponto no espaço que seja o encontro de três superfícies. Como vimos, determinar a posição de uma partícula, do ponto de vista formal, equivale a especificar suas coordenadas. Isso pode ser feito por meio de algum tipo de algoritmo ou regra que permita associar a um conjunto de variáveis um ponto do espaço. Essa especificação implica associar a cada ponto um - e apenas um - conjunto de tais variáveis. Seja ( Q, Q, Q ) um conjunto de variáveis. Essas variáveis são agora consideradas as mais gerais possíveis, e cada uma das coordenadas mais gerais é definida como função das coordenadas cartesianas. Assim, temos: Q Q xyz,, = ( ) = ( ) = ( ) 1 1 Q Q xyz,, 2 2 Q Q xyz,,
3 24 Licenciatura em Ciências USP/Univesp Módulo 1 Um ponto P do espaço é especificado a partir de valores das coordenadas ( Q 1, Q 2, Q 3 ). Por exemplo, o ponto P 0 corresponde ao valor das coordenadas: P Q, Q, Q ( ) onde Q i0 é o valor assumido pela coordenada Q i no ponto P Superfícies e curvas generalizadas Os pontos no espaço estão associados a valores fixos das coordenadas ( Q 1, Q 2, Q 3 ). No entanto, é importante lembrar que a condição para que uma particular coordenada do espaço tenha um valor fixo se escreve como: Qi( x, yz, )= Qi0 = constante 2.3 Figura 2.2: Superfície que contém o ponto P. E, consequentemente, essa condição descreve o lugar geométrico dos pontos do espaço pertencentes a uma superfície (veja Figura 2.2). O conjunto de duas condições para valores constantes das coordenadas generalizadas do espaço, quando impostas simultaneamente, descreve a intersecção de duas superfícies: Q1( x, yz, )= Q Q ( x, yz, )= Q 2 20 Assim, o lugar geométrico dos pontos do espaço, tais que duas coordenadas generalizadas tenham um valor fixo, descreve uma curva no espaço (veja as Figuras 2.3a e 2.3b). A intersecção da curva definida com a superfície definida leva a um ponto. Observe a Figura 2.3c. 2 Outras coordenadas
4 Licenciatura em Ciências USP/Univesp Módulo 1 25 Portanto, a condição de que as três coordenadas tenham um valor bem definido se escreve como mostra a Figura 2.3: Q ( x, yz, )= Q Q ( x, yz, )= Q Q ( x, yz, )= Q a b c Figura 2.3: A intersecção de três superfícies no espaço determinam um ponto P no espaço como mostra a figura (c). As três condições definidas levam à busca do lugar geométrico caracterizado como a intersecção de três superfícies. E essa intersecção determina um ponto no espaço. A localização de um ponto no espaço, em coordenadas generalizadas, dá-se mediante a procura de um ponto no espaço que seja o ponto de encontro das superfícies associadas a valores constantes das coordenadas. 2.3 Coordenadas Cartesianas Quando especificamos que um ponto no espaço tem coordenadas ( x, y, z ) queremos dizer que esse ponto pode ser encontrado através da intersecção de três superfícies. Figura 1.35: As coordenadas cartesianas são definidas a partir de três superfícies planas.
5 26 Licenciatura em Ciências USP/Univesp Módulo 1 Quando especificamos o valor x = x estamos especificando um plano paralelo ao plano zy e que dista de um valor x 0 desse plano. O valor y = y corresponde a um plano paralelo ao plano xz, que dista dele pelo valor y 0. A intersecção desse plano, como o plano x = x 0, é uma reta. Finalmente, o plano z = z Figura 2.4: A intersecção de três superfícies planas definem um e apenas um ponto no espaço. é paralelo ao plano xy, e localizado a uma distância z 0 desse plano. A intersecção desse plano com a reta aludida acima é um ponto, o qual, dessa forma, fica perfeitamente determinado. Usualmente, isso é apresentado como linhas interceptando planos. No entanto, o procedimento mais geral é o apresentado acima. Em duas dimensões recorremos a linhas que são, na verdade, a intersecção de planos com planos. Exemplos Exemplo 01 A figura ao lado ilustra uma célula unitária de um tipo de rede cristalina. Trata-se de uma estrutura cúbica de face centrada (CFC). Os átomos localizam-se nos vértices e no centro das faces da estrutura cúbica. Considere o referencial cartesiano apresentado na Figura 2.5, e que o lado do cubo tenha 10 unidades de medida. Determine as coordenadas cartesianas dos pontos A, F, E, 1 e 2. Figura 2.5: Uma célula unitária cúbica de face centrada. 2 Outras coordenadas
6 Licenciatura em Ciências USP/Univesp Módulo 1 27 Resolução: 1 A superfície de um cubo é formada por seis superfícies planas paralelas duas a duas. São elas representadas por: ABDC e EFGH; CDEF e ABHG e ACGF e BDEH. A origem do referencial cartesiano é o ponto comum às superfícies CDEF, DBEH e GHEF. Os eixos cartesianos 0x, 0y e 0z correspondem às intersecções dessas superfícies tomadas duas a duas. 2 A superfície ABDC cruza perpendicularmente o eixo ordenado 0z no ponto D distante da origem ( E ) 10 unidades de medida; portanto, a coordenada do ponto D é z = 10. Mais ainda, todos os pontos desse lado do cubo têm a mesma coordenada z = Por razões análogas, os pontos da superfície plana GHEF têm coordenada comum z = 0 e que pertence ao plano xy do sistema cartesiano tridimensional. Figura A superfície DBEH pertence ao plano cartesiano zy. Os seus pontos têm coordenadas x = 0 (ou abscissas x = 0). E a superfície CDEF pertence ao plano xz; logo, seus pontos têm coordenadas y = 0 (ou ordenada y = 0). A tabela a seguir apresenta os valores das coordenadas dos pontos aludidos. Notação cartesiana de cada ponto x y z A(10,10,10) F(10,0,0) E(0,0,0) (5,0,5) (5,5,10) Coordenadas Cilíndricas Na Física é muito comum fazermos uso de outras coordenadas. Todas as coordenadas a serem estudadas agora são funções das coordenadas cartesianas.
7 28 Licenciatura em Ciências USP/Univesp Módulo 1 A fim de ilustrar isso e esclarecer a questão sobre a intersecção de três superfícies para localizar um ponto no espaço, consideremos o caso das coordenadas cilíndricas. As coordenadas (ρ, φ, z) cilíndricas são definidas como funções das coordenadas cartesianas a partir das seguintes expressões: As relações inversas são: ρ = x + y 2 2 ϕ = arctan z = z y x x = ρcosϕ x = ρsenϕ z = z Figura 2.8: Uma superfície cilíndrica e duas superfícies planas definem as coordenadas cilíndricas. O lugar geométrico dos pontos para os quais essas coordenadas são constantes define três superfícies no espaço. A primeira é uma superfície cilíndrica de raio ρ = ρ 0 concêntrica com o eixo 0z, e a segunda corresponde ao semiplano que contém o eixo 0z e faz um ângulo φ = φ 0 com o plano xz. E a terceira é a superfície plana paralela ao plano xy que cruza o eixo 0z no ponto (z = z 0 ). Para determinar a posição de um ponto no espaço, fazemos agora a intersecção das três superfícies. Observe a Figura 2.9. Figura 2.9: A intersecção de duas superfícies planas e uma cilíndrica define um - e apenas um - ponto no espaço. 2 Outras coordenadas
8 Licenciatura em Ciências USP/Univesp Módulo 1 29 Exemplo 2 O ponto P da Figura 2.10 ocupa o vértice de um cubo. Considere o referencial cartesiano com origem num dos vértices (Figura 2.10) e com o eixo z ao longo de uma das arestas. a. Determine as coordenadas cartesianas do ponto P. b. Expresse a posição do ponto P em coordenadas cilíndricas. Resolução: Figura 2.10: A coordenada z do ponto P é z = 20 unidades de medida. Coordenadas cartesianas do ponto P: O ponto P tem coordenada z = 20 unidades de medida; como os eixos do referencial cartesiano coincidem com três arestas do cubo, conclui-se que a aresta do cubo tem 20 unidades de medida. Portanto, a abscissa de P é x = 20 e a ordenada é y = 20. Logo, o ponto P é assim expresso: P(20, 20, 20). Coordenadas cilíndricas do ponto P: As coordenadas de um ponto P no espaço são definidas pela intersecção de três superfícies. No caso das coordenadas cilíndricas considere: Um plano (na Figura 2.11 representada por π) que passa pelo ponto P e é perpendicular ao eixo 0z. Esse plano define a coordenada z do ponto. Uma superfície cilíndrica de raio r = ρ, concêntrica com o eixo 0z e que contém o ponto P. Um semiplano (na figura, PP 0Z) que contém tanto o eixo 0z quanto o ponto P e que faz com o plano xz um ângulo φ. a b A Figura 2.11 mostra esses planos. Figura 2.11: a) Plano, semiplano e cilindro das coordenadas do ponto P. b) Vista do topo. Assim, o ponto P é representado univocamente por ρ (raio da superfície cilíndrica); por φ (ângulo que o plano PP 0Z, que contém P e o eixo 0z, faz com o plano zx ou com o eixo 0x) e pela coordenada z do ponto P. Logo, em coordenadas cilíndricas: P (ρ, φ, z). A coordenada z = 20 unidades de medida, como já foi identificado no quesito a. Resta determinar os valores de ρ e de φ. Observe que, no círculo (vista do topo) definido no plano xy, as coordenadas x e y do ponto P
9 30 Licenciatura em Ciências USP/Univesp Módulo 1 (projeção de P no plano xy ) são as mesmas de P (Figura 2.11b). Por meio de relações métricas do triângulo retângulo pontilhado, ρ (hipotenusa), x e y (catetos) e φ (ângulo oposto à ordenada y) podem ser relacionados. Assim, valem as relações: Teorema de Pitágoras: ρ² = x² + y² Relações trigonométricas: 1. senφ = y/ρ (y = ρ senφ) 2. cosφ = x/ρ (x = ρ cosφ) Do quesito a sabemos que: x = y = 20 unidades. Portanto: ρ = ( 20) + ( 20) ρ= 20 2 unidades de medida π tanϕ= = ϕ= arctan ()= ou rad 4 Portanto, em coordenadas cilíndricas, o ponto P é assim representado: P (20 2, π/4, 20). 2.5 Coordenadas Polares As coordenadas polares são úteis quando estamos descrevendo fenômenos em qualquer plano. Nesse caso, tomamos o plano xy como aquele em que estamos interessados. Para indicar um ponto no plano podemos recorrer a muitos conjuntos de coordenadas. As coordenadas polares (ρ e φ) são definidas, como função de x e y (as coordenadas cartesianas), a partir das expressões: Figura 2.12: O ponto P tem coordenadas cartesianas, x e y, e coordenadas polares, ρ e φ. ρ = x + y 2 2 ϕ = arctang y x 2.12 As relações inversas são: x = ρcosϕ y = ρsenϕ Outras coordenadas
10 Licenciatura em Ciências USP/Univesp Módulo 1 31 Portanto, elas correspondem às coordenadas cilíndricas no plano. Exemplo 3 Considere o ponto P pertencente ao plano cartesiano da Figura A sua posição pode ser expressa em função de coordenadas cartesianas e, também, em função de coordenadas polares. Em coordenadas cartesianas x = 40 m e y = 70 m e, portanto, em notação cartesiana, P (40; 70) m. Determine suas coordenadas polares. Resolução: Para representar a posição de P em coordenadas polares são necessários dois parâmetros: Figura 2.13: Coordenadas polares de um ponto P são definidas pela distância OP e pelo ângulo φ. A distância da origem até o ponto P = OP = ρ que pode ser expressa em função das coordenadas cartesianas de P, ou seja, ρ= 2 2 x + y = = m. O ângulo que o eixo polar OP faz com o eixo 0x, ou seja, φ = arctan(70/40) = arctan(1.75) = 60,26. Portanto, em coordenadas polares: P (10 65 m; 60, 26 ). 2.6 Coordenadas Esféricas Definimos as coordenadas esféricas a partir das expressões: x = rsenθcosϕ y = rsenθsenϕ z = rcosθ 2.14 Invertendo as relações acima, obtemos: r = x + y + z y ϕ = arctan x θ = arctan x + y z
11 32 Licenciatura em Ciências USP/Univesp Módulo 1 A superfície r = R (constante) 2.16 ou de modo equivalente: x + y + z = R 2.17 Figura 2.14: Uma superfície esférica, uma plana e uma cônica. corresponde a uma esfera de raio R. A superfície descrita por ϕ = ϕ ou de modo equivalente: y = xtanϕ descreve um semiplano, enquanto a equação: θ= θ x + y = z tan θ Figura 2.15: A intersecção das três superfícies definidas caracteriza um ponto no espaço. descreve um cone de ângulo θ 0. Quando dizemos que um ponto do espaço tem coordenadas (r 0, θ 0, φ 0 ), estamos nos referindo ao ponto que é a intersecção das três superfícies referidas acima. 2 Outras coordenadas
12 Licenciatura em Ciências USP/Univesp Módulo 1 33 Exemplo 4 Adotando-se um sistema de eixos, cuja origem coincida com o centro da Terra e de tal forma que o plano xz coincida com um plano que forma um ângulo de 30 com o plano associado ao meridiano de Greenwich (veja figura), determine nesse referencial a posição da cidade de Greenwich, em coordenadas polares e cartesianas, lembrando que sua latitude (ângulo acima do equador) é de aproximadamente 50. Resolução: O ponto G representa a cidade de Greenwich. Esse ponto é comum a três superfícies: 1. a superfície esférica de raio R (R é a distância de G até a origem); 2. o semiplano que contém o eixo 0z, ou seja, o meridiano que passa por G (φ é ângulo entre este plano e o plano cartesiano xz); 3. a superfície cônica de eixo concêntrico com o eixo 0z e com vértice na origem 0 (θ é a abertura do cone com relação ao eixo central). Figura 2.16: Coordenadas esféricas e as coordenadas Os valores de R, φ e θ representam as coordenadas esféricas latitude e longitude. do ponto G (no caso, a cidade de Greenwich). Considerando-se a Terra com um raio de aproximadamente km, e lembrando que a latitude da cidade de Greenwich λ = 50, a abertura θ da superfície cônica será θ = = 40. E o ângulo φ = 30, informação fornecida no enunciado da questão. Portanto, a posição de Greenwich, em coordenadas esféricas, nesse referencial adotado é P (6.400, 40 ; 30 ). Coordenadas cartesianas de P (Greenwich). Para converter as coordenadas esféricas em cartesianas, considere o esquema a seguir. Figura 2.17: Triângulos que permitem visualizar a conversão de coordenadas esféricas em cartesianas.
13 34 Licenciatura em Ciências USP/Univesp Módulo 1 Primeiramente, vamos considerar o triângulo retângulo 0ZP, onde R é a hipotenusa e 0Z = z e ZP = ρ são os catetos. Nele vale a relação: I. 0Z = z = R.cosθ e II. ZP = ρ = Rsenθ. No triângulo retângulo 0XM, pode-se escrever: III. MX = y = ρsenφ; e IV. 0X = x = ρcosφ. Substituindo II em III e em IV resulta, juntamente, com I: y = R.senθsenφ x = R.senθcosφ z = R.cosθ Substituindo-se os valores, em coordenadas cartesianas esse ponto se escreve como: Portanto, G (3.591 km, km, km) x y z G G G = 6400sen 40cos 30 = km = 6400sen40sen 30 = km = 6400cos 40= km 2.7 As Coordenadas Latitude e Longitude As coordenadas Latitude e Longitude são um bom exemplo de coordenadas generalizadas. Ao especificar que um ponto tem coordenadas que envolvem esses dois ângulos, estamos procurando o lugar geométrico sobre a superfície terrestre que corresponda à intersecção de um cone (a Figura 2.18: Intersecção de planos e superfícies cônicas na superfície da Terra. coordenada latitude) e de um semiplano (a coordenada longitude). Observe a Figura Muitas vezes ouvimos falar de pessoas que se perdem em regiões inóspitas. Estar perdido significa que alguém não sabe se localizar a partir de um ponto de referência. Dizemos que as pessoas não conhecem as coordenadas do ponto onde elas estão. Estar perdido, em nosso mundo, significa não saber as coordenadas geográficas: latitude e longitude. 2 Outras coordenadas
14 Licenciatura em Ciências USP/Univesp Módulo 1 35 As coordenadas latitude e longitude permitem determinar a posição de qualquer objeto sobre a superfície terrestre. A posição de um navio no oceano, por exemplo, pode ser determinada atribuindo-se a ele a sua latitude e sua longitude. Nesse caso, esses ângulos nos fornecem as coordenadas de um ponto na superfície terrestre. Assim, especificamos a posição de um objeto em qualquer ponto na superfície terrestre a partir do conhecimento de dois ângulos: ângulo de latitude λ e ângulo de longitude φ. Para a determinação do ângulo de longitude (φ), adota-se o meridiano de Greenwich como referência. Ele varia, portanto, entre 0 e 180 a leste (L) ou oeste (O) desse meridiano. A determinação do ângulo de latitude (λ) é feita adotando-se a linha do Equador como referência. A latitude varia, portanto, entre 0 e 90 ao sul ou ao norte do Equador. Figura 2.19: Definição da coordenada latitude λ = 1/2 θ. 2.8 O GPS O uso de satélites artificiais propiciou uma nova ferramenta voltada para a localização dos objetos na superfície terrestre. Hoje podemos localizar a posição de um objeto qualquer na superfície terrestre com grande precisão (menos de um metro). O sistema mais sofisticado que se propõe a determinar a posição (as coordenadas latitude e longitude) bem como a velocidade de um objeto na superfície terrestre ou próximo dela, com grande precisão, é o GPS (Global Positioning System). O sistema conta com 24 satélites distribuídos em 6 órbitas distintas. Os satélites ficam a uma altura aproximada de km e têm um período (duração de uma volta ao redor da Terra) de 12 horas (siderais). Figura 2.20: O sistema de posicionamento global faz o uso de satélites.
15 36 Licenciatura em Ciências USP/Univesp Módulo 1 Exemplo 5 Considere o mapa da Figura 2.21, no qual apresentamos as coordenadas Longitude e Latitude relevantes para a localização de pontos no território brasileiro. A latitude e a longitude (sem a altitude) definem um ponto na superfície esférica da Terra. Elas são também denominadas coordenadas geográficas. O sinal ( ) ou (S) na latitude significa ao sul do equador ; o sinal ( ) ou (W) na longitude, significa a oeste de Greenwich. Por exemplo, Fortaleza: Latitude: λ = 3 46 (ou 3 46 S); Longitude: φ = (38 33 W). Figura 2.21: Coordenadas de latitude e longitude do território brasileiro. a. O Brasil está inteiramente na região de latitudes negativas ou sul? Não. Uma pequena parte do território brasileiro localiza-se entre as latitudes 0 e +5, como é possível constatar no mapa. 2 Outras coordenadas
16 Licenciatura em Ciências USP/Univesp Módulo 1 37 b. Quais são as coordenadas (aproximadas) de Boa Vista (Roraima), São Luís (Maranhão) e Curitiba (Paraná)? Para as cidades mencionadas temos: Cidade Latitude (λ) Longitude (φ) Boa Vista (Roraima) +4 (Aprox.) 62 (Aprox.) São Luís (Maranhão) 2,5 (Aprox.) 44 (Aprox.) Curitiba (Paraná) 26 (Aprox.) 49 (Aprox.) c. Um avião parte de um ponto A (ver Figura 2.21) e sua rota prevê que ele voe na direção leste de forma a ter uma variação de 15 na sua longitude e, em seguida, uma variação de 10º na sua latitude em direção ao sul. Quais as coordenadas do ponto X de chegada (não considerar altitudes). De acordo com os dados, o avião parte de A(-5 ; -65 ) e chega a X(λ x ; x) Determinação da longitude λ x. O deslocamento do avião, em relação ao ponto A, foi de 15 para leste, ou seja, ele atingiu longitudes cada vez menos negativas. Logo, λ x = λ A Como λ A = 65, obtém-se λ x = = 50. Determinação da latitude x. O avião deslocou-se, em relação ao ponto A, 10 para o sul, ou seja, para latitudes cada vez mais negativas. Logo, x = A 10. Como A = 5 x = 5 10 = 15. Portanto, o ponto de chegada é X( 15 ; 50 ) ou X(15 S; 50 W). No mapa da Figura 2.21, o ponto X corresponde ao ponto C. Agora é sua vez... Acesse o Ambiente Virtual de Aprendizagem e realize a(s) atividade(s) proposta(s). Glossário Algoritmo: Um algoritmo é um conjunto finito de regras que fornece uma seqüência de operações para resolver um problema específico. Fonte: Biunívoca: Relativo à relação entre dois conjuntos em que a cada elemento do primeiro conjunto corresponde apenas um do segundo, e vice-versa.
Mecânica. Outras Coordenadas
 Mecânica Outras Coordenadas Mecânica» Outras Coordenadas 1 Coordenadas mais gerais Exceto em casos especiais, como naqueles localizados ao longo de curvas, na grande maioria das vezes, estamos interessados
Mecânica Outras Coordenadas Mecânica» Outras Coordenadas 1 Coordenadas mais gerais Exceto em casos especiais, como naqueles localizados ao longo de curvas, na grande maioria das vezes, estamos interessados
TÓPICO. Fundamentos da Matemática II APLICAÇÕES NA GEOMETRIA ANALÍTICA. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
APLICAÇÕES NA GEOMETRIA ANALÍTICA
 4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
Dinâmica do Movimento dos Corpos CINEMÁTICA VETORIAL5. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 CINEMÁTICA VETORIAL5 Gil da Costa Marques 5.1 Referenciais 5. Vetores e Referenciais Cartesianos 5.3 Referenciais Gerais 5.4 Vetores em Coordenadas Polares 5.5 Vetores Velocidade e Aceleração em coordenadas
CINEMÁTICA VETORIAL5 Gil da Costa Marques 5.1 Referenciais 5. Vetores e Referenciais Cartesianos 5.3 Referenciais Gerais 5.4 Vetores em Coordenadas Polares 5.5 Vetores Velocidade e Aceleração em coordenadas
P1 CORREÇÃO DA PROVA. GA116 Sistemas de Referência e Tempo
 P1 CORREÇÃO DA PROVA GA116 Sistemas de Referência e Tempo Profª. Érica S. Matos Departamento de Geomática Setor de Ciências da Terra Universidade Federal do Paraná -UFPR 1. Sejam dois pontos A e B cujas
P1 CORREÇÃO DA PROVA GA116 Sistemas de Referência e Tempo Profª. Érica S. Matos Departamento de Geomática Setor de Ciências da Terra Universidade Federal do Paraná -UFPR 1. Sejam dois pontos A e B cujas
Curso de Geomática Aula 2. Prof. Dr. Irineu da Silva EESC-USP
 Curso de Geomática Aula Prof. Dr. Irineu da Silva EESC-USP Sistemas de Coordenadas Determinar a posição de um ponto, em Geomática, significa calcular as suas coordenadas. Calcular as coordenadas de um
Curso de Geomática Aula Prof. Dr. Irineu da Silva EESC-USP Sistemas de Coordenadas Determinar a posição de um ponto, em Geomática, significa calcular as suas coordenadas. Calcular as coordenadas de um
3.2 Coordenadas Cilíndricas
 Exemplo 3.6 Encontre DzdV para D a região do espaço limitada pelos gráficos x = 1 z 2, x =, entre os planos y = e y = 1. Solução: observe que pela descrição da região de integração D, é mais conveniente
Exemplo 3.6 Encontre DzdV para D a região do espaço limitada pelos gráficos x = 1 z 2, x =, entre os planos y = e y = 1. Solução: observe que pela descrição da região de integração D, é mais conveniente
Capítulo 1-Sistemas de Coordenadas
 Capítulo 1-Sistemas de Coordenadas 1 Sistema Unidimensional de Coordenadas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente sobre uma reta (ou espaço unidimensional).
Capítulo 1-Sistemas de Coordenadas 1 Sistema Unidimensional de Coordenadas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente sobre uma reta (ou espaço unidimensional).
9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis
 9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis Professora: Michelle Pierri Exercício 1 Encontre o volume do sólido limitado
9 ạ Lista de Exercícios de Cálculo II Integrais Triplas: Coordenadas Retangulares, Cilíndricas e Esféricas; Mudança de Variáveis Professora: Michelle Pierri Exercício 1 Encontre o volume do sólido limitado
Ô, 04 ! ^ D. Exercícios
 O Espaço 93 O, 0,0), Q 2 (6, O, 0), Q 3 (6, 8, 0), Q 4 (0, 8,0), Q 5 (6, O, 4),
O Espaço 93 O, 0,0), Q 2 (6, O, 0), Q 3 (6, 8, 0), Q 4 (0, 8,0), Q 5 (6, O, 4),
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
Integrais Triplas em Coordenadas Polares
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Integrais Triplas em Coordenadas Polares Na aula 3 discutimos como usar coordenadas polares em integrais duplas, seja pela região
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Integrais Triplas em Coordenadas Polares Na aula 3 discutimos como usar coordenadas polares em integrais duplas, seja pela região
Geometria Analítica II - Aula
 Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
FUNÇÕES DE VÁRIAS VARIÁVEIS3
 FUNÇÕES DE VÁRIAS VARIÁVEIS3 Gil da Costa Marques 3.1 Definição 3. Funções de três ou mais variáveis 3.3 Domínios 3.4 Gráficos, curvas de nível e superfícies de nível 3.5 Funções implícitas 3.6 Funções
FUNÇÕES DE VÁRIAS VARIÁVEIS3 Gil da Costa Marques 3.1 Definição 3. Funções de três ou mais variáveis 3.3 Domínios 3.4 Gráficos, curvas de nível e superfícies de nível 3.5 Funções implícitas 3.6 Funções
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
TÓPICO. Fundamentos da Matemática II INTRODUÇÃO AO CÁLCULO VETORIAL. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 INTRODUÇÃO AO CÁLCULO VETORIAL Gil da Costa Marques TÓPICO Fundamentos da Matemática II.1 Introdução. Funções vetoriais de uma variável. Domínio e conjunto imagem.4 Limites de funções vetoriais de uma
INTRODUÇÃO AO CÁLCULO VETORIAL Gil da Costa Marques TÓPICO Fundamentos da Matemática II.1 Introdução. Funções vetoriais de uma variável. Domínio e conjunto imagem.4 Limites de funções vetoriais de uma
A TERRA ESFÉRICA. Parte I Conceitos Gerais. GA116 Sistemas de Referência e Tempo
 A TERRA ESFÉRICA Parte I Conceitos Gerais GA116 Sistemas de Referência e Tempo Profª. Érica S. Matos Departamento de Geomática Setor de Ciências da Terra Universidade Federal do Paraná -UFPR O modelo de
A TERRA ESFÉRICA Parte I Conceitos Gerais GA116 Sistemas de Referência e Tempo Profª. Érica S. Matos Departamento de Geomática Setor de Ciências da Terra Universidade Federal do Paraná -UFPR O modelo de
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
01 Referenciais e Coordenadas Cartesianas
 01 Referenciais e Coordenadas Cartesianas Exercícios Propostos Exercício 1.1 Os pontos, B e C interligados formam um triângulo no referencial cartesiano xy esquematizado. a) Representar, em notação cartesiana,
01 Referenciais e Coordenadas Cartesianas Exercícios Propostos Exercício 1.1 Os pontos, B e C interligados formam um triângulo no referencial cartesiano xy esquematizado. a) Representar, em notação cartesiana,
Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações
 Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações 1 Sistema Unidimensional de Coordenadas Cartesianas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente
Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações 1 Sistema Unidimensional de Coordenadas Cartesianas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente
3. Achar a equação da esfera definida pelas seguintes condições: centro C( 4, 2, 3) e tangente ao plano π : x y 2z + 7 = 0.
 Universidade Federal de Uerlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: Superfícies, Quádricas, Curvas e Coordenadas Professor Sato 4 a Lista de exercícios. Determinar
Universidade Federal de Uerlândia Faculdade de Matemática Disciplina : Geometria Analítica (GMA00) Assunto: Superfícies, Quádricas, Curvas e Coordenadas Professor Sato 4 a Lista de exercícios. Determinar
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
MATEMÁTICA A - 10o Ano Geometria Propostas de resolução
 MATEMÁTIA A - 10o Ano Geometria Propostas de resolução Eercícios de eames e testes intermédios 1. omo os pontos A, B e têm abcissa 1, todos pertencem ao plano de equação = 1. Assim a secção produida no
MATEMÁTIA A - 10o Ano Geometria Propostas de resolução Eercícios de eames e testes intermédios 1. omo os pontos A, B e têm abcissa 1, todos pertencem ao plano de equação = 1. Assim a secção produida no
Curso de Geometria Analítica. Hipérbole
 Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 03 - Cônicas- Circunferência, Elipse, Hipérbole e Parábola
UFGD FCA PROF. OMAR DANIEL BLOCO 1.1 NOÇÕES DE CARTOGRAFIA
 UFGD FCA PROF. OMAR DANIEL BLOCO 1.1 NOÇÕES DE CARTOGRAFIA (Copyright 1991-2006 SPRING - DPI/INPE) 1 (Para uso no SPRING) 1 - Sistemas de Coordenadas Um objeto geográfico qualquer, como uma cidade, a foz
UFGD FCA PROF. OMAR DANIEL BLOCO 1.1 NOÇÕES DE CARTOGRAFIA (Copyright 1991-2006 SPRING - DPI/INPE) 1 (Para uso no SPRING) 1 - Sistemas de Coordenadas Um objeto geográfico qualquer, como uma cidade, a foz
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Capítulo 1. Conjuntos e Relações. 1.1 Noção intuitiva de conjuntos. Notação dos conjuntos
 Conjuntos e Relações Capítulo Neste capítulo você deverá: Identificar e escrever os tipos de conjuntos, tais como, conjunto vazio, unitário, finito, infinito, os conjuntos numéricos, a reta numérica e
Conjuntos e Relações Capítulo Neste capítulo você deverá: Identificar e escrever os tipos de conjuntos, tais como, conjunto vazio, unitário, finito, infinito, os conjuntos numéricos, a reta numérica e
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
CAPÍTULO 11 ROTAÇÕES E MOMENTO ANGULAR
 O que vamos estudar? CAPÍTULO 11 ROTAÇÕES E MOMENTO ANGULAR Seção 11.1 Cinemática do corpo rígido Seção 11.2 Representação vetorial das rotações Seção 11.3 Torque Seção 11.4 Momento angular Seção 11.5
O que vamos estudar? CAPÍTULO 11 ROTAÇÕES E MOMENTO ANGULAR Seção 11.1 Cinemática do corpo rígido Seção 11.2 Representação vetorial das rotações Seção 11.3 Torque Seção 11.4 Momento angular Seção 11.5
c) F( 4, 2) r : 2x+y = 3 c) a = 3 F 1 = (0,0) F 2 = (1,1)
 Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
Lista de Exercícios Estudo Analítico das Cônicas e Quádricas 1. Determine o foco, o vértice, o parâmetro e a diretriz da parábola P e faça um esboço. a) P : y 2 = 4x b) P : y 2 +8x = 0 c) P : x 2 +6y =
5 de setembro de Gabarito. 1) Considere o ponto P = (0, 1, 2) e a reta r de equações paramétricas. r: (2 t, 1 t, 1 + t), t R.
 G1 de Álgebra Linear I 20072 5 de setembro de 2007 Gabarito 1) Considere o ponto P = (0, 1, 2) e a reta r de equações paramétricas r: (2 t, 1 t, 1 + t), t R (a) Determine a equação cartesiana do plano
G1 de Álgebra Linear I 20072 5 de setembro de 2007 Gabarito 1) Considere o ponto P = (0, 1, 2) e a reta r de equações paramétricas r: (2 t, 1 t, 1 + t), t R (a) Determine a equação cartesiana do plano
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
COORDENADAS GEOGRÁFICAS E COORDENADAS GEODÉSICAS. Professor: Leonard Niero da Silveira
 UNIVERSIDADE FEDERAL DO PAMPA CURSO DE ENGENHARIA DE AGRIMENSURA COORDENADAS GEOGRÁFICAS E COORDENADAS GEODÉSICAS Professor: Leonard Niero da Silveira leonardsilveira@unipampa.edu.br COORDENADAS GEODÉSICAS
UNIVERSIDADE FEDERAL DO PAMPA CURSO DE ENGENHARIA DE AGRIMENSURA COORDENADAS GEOGRÁFICAS E COORDENADAS GEODÉSICAS Professor: Leonard Niero da Silveira leonardsilveira@unipampa.edu.br COORDENADAS GEODÉSICAS
1. Seja θ = ang (r, s). Calcule sen θ nos casos (a) e (b) e cos θ nos casos (c) e (d): = z 3 e s : { 3x + y 5z = 0 x 2y + 3z = 1
 14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano
 Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática marcio@matematicauva.org
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática marcio@matematicauva.org
TÓPICO. Fundamentos da Matemática II INTEGRAÇÃO MÚLTIPLA10. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 INTEGAÇÃO MÚLTIPLA TÓPICO Gil da Costa Marques Fundamentos da Matemática II. Introdução. Integrais Duplas.3 Propriedades das Integrais Duplas.4 Cálculo de Integrais Duplas.5 Integrais duplas em regiões
INTEGAÇÃO MÚLTIPLA TÓPICO Gil da Costa Marques Fundamentos da Matemática II. Introdução. Integrais Duplas.3 Propriedades das Integrais Duplas.4 Cálculo de Integrais Duplas.5 Integrais duplas em regiões
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
Álgebra Linear I - Aula 9. Roteiro
 Álgebra Linear I - Aula 9 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. oteiro 1 Distância de um ponto
Álgebra Linear I - Aula 9 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. oteiro 1 Distância de um ponto
Superfícies e Curvas no Espaço
 Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Energia Solar Térmica. Prof. Ramón Eduardo Pereira Silva Engenharia de Energia Universidade Federal da Grande Dourados Dourados MS 2014
 Energia Solar Térmica Prof. Ramón Eduardo Pereira Silva Engenharia de Energia Universidade Federal da Grande Dourados Dourados MS 2014 O Sol Energia Solar Térmica - 2014 Prof. Ramón Eduardo Pereira Silva
Energia Solar Térmica Prof. Ramón Eduardo Pereira Silva Engenharia de Energia Universidade Federal da Grande Dourados Dourados MS 2014 O Sol Energia Solar Térmica - 2014 Prof. Ramón Eduardo Pereira Silva
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1. Coordenadas Aula 1
 UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas Aula 1 Recife, 2014 Sistema de Coordenadas Um dos principais objetivos da Topografia é a determinação
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas Aula 1 Recife, 2014 Sistema de Coordenadas Um dos principais objetivos da Topografia é a determinação
Álgebra Linear I - Aula 8. Roteiro
 Álgebra Linear I - Aula 8 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. 5. Distância entre duas retas.
Álgebra Linear I - Aula 8 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. 5. Distância entre duas retas.
Coordenadas Cartesianas
 1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
SISTEMAS DE COORDENADAS
 1 SISTEMAS DE COORDENADAS 2.1 Coordenadas polares no R² Fonte: Cálculo A. Funções. Limite. Derivação. Integração. Diva Marília Flemming. Mírian Buss Gonçalves. Até o presente momento, localizamos um ponto
1 SISTEMAS DE COORDENADAS 2.1 Coordenadas polares no R² Fonte: Cálculo A. Funções. Limite. Derivação. Integração. Diva Marília Flemming. Mírian Buss Gonçalves. Até o presente momento, localizamos um ponto
RETA E CIRCUNFERÊNCIA
 RETA E CIRCUNFERÊNCIA - 016 1. (Unifesp 016) Na figura, as retas r, s e t estão em um mesmo plano cartesiano. Sabe-se que r e t passam pela origem desse sistema, e que PQRS é um trapézio. a) Determine
RETA E CIRCUNFERÊNCIA - 016 1. (Unifesp 016) Na figura, as retas r, s e t estão em um mesmo plano cartesiano. Sabe-se que r e t passam pela origem desse sistema, e que PQRS é um trapézio. a) Determine
Geometria Analítica. Estudo do Plano. Prof Marcelo Maraschin de Souza
 Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
TÓPICO. Fundamentos de Matemática II FUNÇÕES DE VÁRIAS VARIÁVEIS3. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 FUNÇÕES DE VÁRIAS VARIÁVEIS3 TÓPICO Gil da Costa Marques Fundamentos de Matemática II 3.1 Definição 3. Funções de três ou mais variáveis 3.3 Domínios 3.4 Gráficos, curvas de nível e superfícies de nível
FUNÇÕES DE VÁRIAS VARIÁVEIS3 TÓPICO Gil da Costa Marques Fundamentos de Matemática II 3.1 Definição 3. Funções de três ou mais variáveis 3.3 Domínios 3.4 Gráficos, curvas de nível e superfícies de nível
Estudo Dirigido - Desvendando a Geometria Analítica: Distância entre dois pontos
 Estudo Dirigido - Desvendando a Geometria Analítica: Distância entre dois pontos Conteúdo: Plano Cartesiano Público-alvo: Alunos de Ensino Médio Competências; Modelar e resolver problemas que envolvem
Estudo Dirigido - Desvendando a Geometria Analítica: Distância entre dois pontos Conteúdo: Plano Cartesiano Público-alvo: Alunos de Ensino Médio Competências; Modelar e resolver problemas que envolvem
Cálculo II - Superfícies no Espaço
 UFJF - DEPARTAMENTO DE MATEMÁTICA Cálculo II - Superfícies no Espaço Prof. Wilhelm Passarella Freire Prof. Grigori Chapiro 1 Conteúdo 1 Introdução 4 2 Plano 6 2.1 Parametrização do plano...................................
UFJF - DEPARTAMENTO DE MATEMÁTICA Cálculo II - Superfícies no Espaço Prof. Wilhelm Passarella Freire Prof. Grigori Chapiro 1 Conteúdo 1 Introdução 4 2 Plano 6 2.1 Parametrização do plano...................................
Matemática B Extensivo V. 7
 GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA
 CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais triplas, temos funções f(x,y,z) integradas em um volume dv= dx dy dz, sendo a região de integração um paralelepípedo P=
CÁLCUL O INTEGRAIS TRIPLAS ENGENHARIA 1 INTERPRETAÇÃO GEOMÉTRICA DE Nas integrais triplas, temos funções f(x,y,z) integradas em um volume dv= dx dy dz, sendo a região de integração um paralelepípedo P=
TÓPICO. Fundamentos da Matemática II FUNÇÕES VETORIAIS DE VÁRIAS VARIÁVEIS. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 FUNÇÕES VETORIAIS DE VÁRIAS VARIÁVEIS 5 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 5. Introdução 5. Funções vetoriais de duas variáveis 5.3 Representação gráfica de funções vetoriais 5.4
FUNÇÕES VETORIAIS DE VÁRIAS VARIÁVEIS 5 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 5. Introdução 5. Funções vetoriais de duas variáveis 5.3 Representação gráfica de funções vetoriais 5.4
Integrais Múltiplas. Prof. Ronaldo Carlotto Batista. 23 de outubro de 2014
 Cálculo 2 ECT1212 Integrais Múltiplas Prof. Ronaldo Carlotto Batista 23 de outubro de 2014 Cálculo de áreas e Soma de Riemann Vamos primeiro revisar os conceitos da integral de uma função de uma variável.
Cálculo 2 ECT1212 Integrais Múltiplas Prof. Ronaldo Carlotto Batista 23 de outubro de 2014 Cálculo de áreas e Soma de Riemann Vamos primeiro revisar os conceitos da integral de uma função de uma variável.
1 Distância entre dois pontos do plano
 Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Noções Topológicas do Plano Americo Cunha André Zaccur Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro 1 Distância entre dois pontos do plano
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Álgebra Linear I - Aula 6. Roteiro
 Álgebra Linear I - Aula 6 1. Posições relativas e sistemas de equações. 2. Distância de um ponto a uma reta. 3. Distância de um ponto a um plano. Roteiro 1 Sistemas de equações lineares (posição relativa
Álgebra Linear I - Aula 6 1. Posições relativas e sistemas de equações. 2. Distância de um ponto a uma reta. 3. Distância de um ponto a um plano. Roteiro 1 Sistemas de equações lineares (posição relativa
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática
 Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GAX1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Cônicas e Quádricas Prof.
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GAX1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Cônicas e Quádricas Prof.
ELIPSE. Figura 1: Desenho de uma elipse no plano euclidiano (à esquerda). Desenho de uma elipse no plano cartesiano (à direita).
 QUÁDRICAS/CÔNICAS - Cálculo II MAT 147 FEAUSP Segundo semestre de 2018 Professor Oswaldo Rio Branco de Oliveira [ Veja também http://www.ime.usp.br/~oliveira/ele-conicas.pdf] No plano euclidiano consideremos
QUÁDRICAS/CÔNICAS - Cálculo II MAT 147 FEAUSP Segundo semestre de 2018 Professor Oswaldo Rio Branco de Oliveira [ Veja também http://www.ime.usp.br/~oliveira/ele-conicas.pdf] No plano euclidiano consideremos
Elementos de um mapa. Professora de Geografia. Thamires
 Elementos de um mapa Professora de Geografia Thamires Principais elementos de um mapa Título informa o tema, local, tempo. Legenda detalha as informações do título Escala permite visualizar a proporção
Elementos de um mapa Professora de Geografia Thamires Principais elementos de um mapa Título informa o tema, local, tempo. Legenda detalha as informações do título Escala permite visualizar a proporção
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
11/11/2013. Professor
 UniSALESIANO Centro Universitário Católico Salesiano Auxilium Curso de Engenharia Civil Disciplina: Topografia II Introdução à Geodésia Prof. Dr. André Luís Gamino Professor Definição: - Geodésia é a ciência
UniSALESIANO Centro Universitário Católico Salesiano Auxilium Curso de Engenharia Civil Disciplina: Topografia II Introdução à Geodésia Prof. Dr. André Luís Gamino Professor Definição: - Geodésia é a ciência
Unidade 1 de Física do 11º ano FQA 1 V I A G E N S C O M G P S
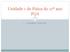 Unidade 1 de Física do 11º ano FQA 1 V I A G E N S C O M G P S 1. O sistema GPS Para indicar a posição de um lugar na superfície da Terra um modelo esférico da Terra e imaginam-se linhas: os paralelos:
Unidade 1 de Física do 11º ano FQA 1 V I A G E N S C O M G P S 1. O sistema GPS Para indicar a posição de um lugar na superfície da Terra um modelo esférico da Terra e imaginam-se linhas: os paralelos:
DADOS GEORREFERENCIADOS
 Geoprocessamento Graduação em Geografia 4º ano / 1º Semestre Profa. Dra. Fernanda Sayuri Yoshino Watanabe Departamento de Cartografia fernanda.watanabe@unesp.br 2019 DADOS GEORREFERENCIADOS GEORREFERENCIAMENTO
Geoprocessamento Graduação em Geografia 4º ano / 1º Semestre Profa. Dra. Fernanda Sayuri Yoshino Watanabe Departamento de Cartografia fernanda.watanabe@unesp.br 2019 DADOS GEORREFERENCIADOS GEORREFERENCIAMENTO
PROJEÇÕES CARTOGRÁFICAS
 Uma projeção cartográfica consiste num conjunto de linhas (paralelos e meridianos), que formam uma rede, sobre a qual são representados os elementos do mapa. Todos os mapas e/ou cartas são representações
Uma projeção cartográfica consiste num conjunto de linhas (paralelos e meridianos), que formam uma rede, sobre a qual são representados os elementos do mapa. Todos os mapas e/ou cartas são representações
Sistemas de coordenadas
 Sistemas de coordenadas Cartografia Profa. Ligia UTFPR Introdução Coordenadas Geográficas: latitude e longitude As suas bases utilizadas são a geometria esférica e o eixo de rotação da Terra. Os pólos
Sistemas de coordenadas Cartografia Profa. Ligia UTFPR Introdução Coordenadas Geográficas: latitude e longitude As suas bases utilizadas são a geometria esférica e o eixo de rotação da Terra. Os pólos
VIAGENS COM GPS. O GPS permite saber a posição de um lugar à superfície da Terra através das coordenadas geográficas (latitude, longitude e altitude).
 VIAGENS COM GPS O sistema GPS (Sistema de Posicionamento Global) é amplamente utilizado em diversas aplicações, tais como: localizar, navegar, conduzir e mapear. O GPS permite saber a posição de um lugar
VIAGENS COM GPS O sistema GPS (Sistema de Posicionamento Global) é amplamente utilizado em diversas aplicações, tais como: localizar, navegar, conduzir e mapear. O GPS permite saber a posição de um lugar
Física III IQ 2014 ( )
 Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
raio do arco: a; ângulo central do arco: θ 0; carga do arco: Q.
 Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
Álgebra Linear I - Aula 3. Roteiro
 Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Coordenadas Geográficas
 Coordenadas Geográficas Coordenadas Geográficas É a posição exata no globo terrestre Intersecção entre latitude e longitude Paralelos Linhas paralelas a Linha do Equador Trópico de Capricórnio Hemisfério
Coordenadas Geográficas Coordenadas Geográficas É a posição exata no globo terrestre Intersecção entre latitude e longitude Paralelos Linhas paralelas a Linha do Equador Trópico de Capricórnio Hemisfério
FUNÇÕES TRIGONOMÉTRICAS. Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica
 FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
PROJEÇÕES. Prof. Dr. Elódio Sebem Curso Superior de Tecnologia em Geoprocessamento Colégio Politécnico - Universidade Federal de Santa Maria
 PROJEÇÕES Prof. Dr. Elódio Sebem Curso Superior de Tecnologia em Geoprocessamento Colégio Politécnico - Universidade Federal de Santa Maria Todos os mapas são representações aproximadas da superfície terrestre.
PROJEÇÕES Prof. Dr. Elódio Sebem Curso Superior de Tecnologia em Geoprocessamento Colégio Politécnico - Universidade Federal de Santa Maria Todos os mapas são representações aproximadas da superfície terrestre.
Fundamentos de Cartografia A Rede Geográfica
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA DEPARTAMENTO DE GEOCIÊNCIAS Disciplina: Leitura e Interpretação de Cartas Fundamentos de Cartografia A Rede Geográfica Prof. Dr.
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA DEPARTAMENTO DE GEOCIÊNCIAS Disciplina: Leitura e Interpretação de Cartas Fundamentos de Cartografia A Rede Geográfica Prof. Dr.
Aula 15. Derivadas Direcionais e Vetor Gradiente. Quando u = (1, 0) ou u = (0, 1), obtemos as derivadas parciais em relação a x ou y, respectivamente.
 Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III
 UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
Geometria do Elipsoide. FGL João F Galera Monico PPGCC Abril 2018
 Geometria do Elipsoide FGL João F Galera Monico PPGCC Abril 2018 Elipsoide de Revolução Rotação de uma elipse sobre um de seus eixos! Neste caso: eixo Z Elipse no plano YZ com X = 0 Z Elipse no plano XY
Geometria do Elipsoide FGL João F Galera Monico PPGCC Abril 2018 Elipsoide de Revolução Rotação de uma elipse sobre um de seus eixos! Neste caso: eixo Z Elipse no plano YZ com X = 0 Z Elipse no plano XY
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS COIMBRA 11º ANO DE ESCOLARIDADE MATEMÁTICA A. Ficha de revisão n.º 3
 ESCOLA SECUNDÁRIA COM º CICLO D. DINIS COIMBRA 11º ANO DE ESCOLARIDADE MATEMÁTICA A Ficha de revisão n.º 1. No referencial da figura está representada uma pirâmide quadrangular regular. Sabe-se que B(6,0,0)
ESCOLA SECUNDÁRIA COM º CICLO D. DINIS COIMBRA 11º ANO DE ESCOLARIDADE MATEMÁTICA A Ficha de revisão n.º 1. No referencial da figura está representada uma pirâmide quadrangular regular. Sabe-se que B(6,0,0)
ROBÓTICA REPRESENTAÇÕES MATRICIAIS. Prof a. Dra. GIOVANA TRIPOLONI TANGERINO Tecnologia em Automação Industrial
 SP CAMPUS PIRACICABA ROBÓTICA Prof a. Dra. GIOVANA TRIPOLONI TANGERINO Tecnologia em Automação Industrial REPRESENTAÇÕES MATRICIAIS https://giovanatangerino.wordpress.com giovanatangerino@ifsp.edu.br giovanatt@gmail.com
SP CAMPUS PIRACICABA ROBÓTICA Prof a. Dra. GIOVANA TRIPOLONI TANGERINO Tecnologia em Automação Industrial REPRESENTAÇÕES MATRICIAIS https://giovanatangerino.wordpress.com giovanatangerino@ifsp.edu.br giovanatt@gmail.com
As aventuras do Geodetetive 6: GPS. Série Matemática na Escola
 As aventuras do Geodetetive 6: GPS. Série Matemática na Escola Objetivos 1. Explicar o funcionamento do GPS 2. Mostrar a matemática envolvida na programação do GPS. As aventuras do Geodetetive 6 1/12 As
As aventuras do Geodetetive 6: GPS. Série Matemática na Escola Objetivos 1. Explicar o funcionamento do GPS 2. Mostrar a matemática envolvida na programação do GPS. As aventuras do Geodetetive 6 1/12 As
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo.
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo. Trabalho de casa nº 10 1. Na figura está representado, num referencial
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Funções e Gráficos Generalidades. Funções polinomiais. Função módulo. Trabalho de casa nº 10 1. Na figura está representado, num referencial
CÁLCULO II - MAT0023. Nos exercícios de (1) a (4) encontre x e y em termos de u e v, alem disso calcule o jacobiano da
 UNIVEIDADE FEDEAL DA INTEGAÇÃO LATINO-AMEICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO II - MAT3 15 a Lista de exercícios Nos
UNIVEIDADE FEDEAL DA INTEGAÇÃO LATINO-AMEICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO II - MAT3 15 a Lista de exercícios Nos
2 Uma caixa d'água cúbica, de volume máximo, deve ser colocada entre o telhado e a laje de uma casa, conforme mostra a figura ao lado.
 MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
3. Obter a equação do plano que contém os pontos A = (3, 0, 1), B = (2, 1, 1) e C = (3, 2, 2).
 Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
as raízes de gof, e V(x v ) o vértice da parábola que representa gof no plano cartesiano. Assim sendo, 1) x x 2 = = 10 ( 4) 2) x v x 2
 MATEMÁTICA 19 c Sejam as funções f e g, de em, definidas, respectivamente, por f(x) = x e g(x) = x 1. Com relação à função gof, definida por (gof) (x) = g(f(x)), é verdade que a) a soma dos quadrados de
MATEMÁTICA 19 c Sejam as funções f e g, de em, definidas, respectivamente, por f(x) = x e g(x) = x 1. Com relação à função gof, definida por (gof) (x) = g(f(x)), é verdade que a) a soma dos quadrados de
Matemática I Cálculo I Unidade B - Cônicas. Profª Msc. Débora Bastos. IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE
 Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
Coordenadas e distância na reta e no plano
 Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Plano cartesiano, Retas e. Alex Oliveira. Circunferência
 Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
Plano cartesiano, Retas e Alex Oliveira Circunferência Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é
Primeiro Teste de CVGA
 Primeiro Teste de CVGA 31 de Março de 2005 Questão 1 [1 ponto] O triângulo com vértices em P 1 ( 2, 4, 0), P 2 (1, 2, 1) e P 3 ( 1, 1, 2) é equilátero? Questão 2 [1 ponto] O triângulo com vértices em P
Primeiro Teste de CVGA 31 de Março de 2005 Questão 1 [1 ponto] O triângulo com vértices em P 1 ( 2, 4, 0), P 2 (1, 2, 1) e P 3 ( 1, 1, 2) é equilátero? Questão 2 [1 ponto] O triângulo com vértices em P
ENTREGAR EM: 24/05/2018
 Assunto: Roteiro de recuperação da I etapa de GEOGRAFIA Tipo: U Data:25/05/2018 Ensino Médio Ano/Série: 1º Turma: TA Valor: 5,0 Nome: Nº Nota: Professor: Gilson Pinheiro Lima Ass. do Responsável: Querido(a)
Assunto: Roteiro de recuperação da I etapa de GEOGRAFIA Tipo: U Data:25/05/2018 Ensino Médio Ano/Série: 1º Turma: TA Valor: 5,0 Nome: Nº Nota: Professor: Gilson Pinheiro Lima Ass. do Responsável: Querido(a)
Preliminares de Cálculo
 Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
GEOMETRIA ANALI TICA PONTO MEDIANA E BARICENTRO PLANO CARTESIANO DISTÂNCIA ENTRE DOIS PONTOS CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS
 GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1
![INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1 INTEGRAIS MÚLTIPLAS. [a, b] e [c, d], respectivamente. O conjunto P = {(x i, y j ) i = 0,..., n, j = i=1](/thumbs/99/142468356.jpg) Teoria INTEGRAIS MÚLTIPLAS Integral Dupla: Seja o retângulo R = {(x, y) R a x b, c y d} e a = x 0 < x 1
Teoria INTEGRAIS MÚLTIPLAS Integral Dupla: Seja o retângulo R = {(x, y) R a x b, c y d} e a = x 0 < x 1
Geometria Analítica II - Aula 5 108
 Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
Geometria Analítica II - Aula 5 108 IM-UFF Aula 6 Superfícies Cilíndricas Sejam γ uma curva contida num plano π do espaço e v 0 um vetor não-paralelo ao plano π. A superfície cilíndrica S de diretriz γ
