Organização e Arquitetura de computadores
|
|
|
- Ana Beatriz Teixeira Taveira
- 8 Há anos
- Visualizações:
Transcrição
1 gaização Aquiua compuao oução Pipliigéuma écica implmação m qu váia iuçõ ão obpoa a xcução Exmplo: lavagm oupa Mlhoao o mpho com pipliig Pof. D. Luciao Joé Sg Pipliig abalho é iviio m apa ou ágio Técica pmi a mlhoa a vazão (houghpu) a aquiua S oo o ágio lvam apoximaam o mmo mpo houv abalho ufici paa aliza, ão o gaho mpho vio à écica pipli á igual ao úmo ágio o pipli uçõ MPS m cico apa Buca iução a mmóia L giao quao a iução é coificaa Excua a opação ou calcula um ço b aco a um opao a mmóia ao Ecv o ulao m um giao Pipli MPS a xploao apa 5 ágio Pipliig Dmpho ciclo úico mpho com pipli Ciclo clockpio cao igual a 200p Sm pipliig: 3 x 800 = 2400 p Com pipliig: 3 x 200 = 600 p Tmpo iuçõ = (Tmpo iuçõ m pipli)/(úmo ágio o pipli) T = 800/5 = 160 p Pipliig Pojo o cojuo iuçõ paa pipliig Toa a iuçõ MPS m o mmo amaho, aim po- buca a iuçõ o pimio ágio coificá-la o guo ágio MPS m pouco fomao iuçõ com campo giao oigm localizao o mmo luga; a imia pmi qu o guo ágio po comça a l o baco giao ao mmo mpo m qu o hawa ámiao qu ipo iução foi lia paçõ m mmóia óapacm m loa o opaoão alihao a mmóia: o ao oliciao pom afio o pocao a mmóia m um úico ágio o pipli Pipli haza Piplihazaão iuaçõ m qu a póxima iução ão po xcuaa o ciclo clock gui Tê ipo Haza uuai Haza ao Haza cool Hazauual Sigifica qu o hawa ão po amii a combiação iuçõ qu qumo xcua o mmo ciclo clock Exmplo: uma úica mmóia o acaa ao mmo mpo, o ágio 1 uma iução o ágio 5 oua iução, com a ua iuçõ o pipli
2 Pipli haza Liua m mmóia como haza uual Tim (clock cycl) Pipli haza Hazauual o aco ao baco giao Tim (clock cycl). lw Mm Rg Mm Rg Mm Rg Mm Rg Raig iucio fom mmoy Mm Rg Mm Rg Raig aa fom mmoy Mm Rg Mm Rg Mm Rg Mm Rg. a $1, 1 2 a $2,$1, Pipli haza Haza uual o aco ao baco giao. a $1, 1 2 a $2,$1, clock g ha cool gi wiig Fix gi fil acc haza by oig a i h co half of h cycl a wi i h fi half Pipli haza Haza ao com quao o piplipcia iompio poqu uma apa pcia pa aé qu oua ja cocluía Exmplo: a $0, $0, $1 ub $2, $0, $3 A iução aão cv o u ulao aéo quio ágio, igificao qu íamo qu ii ê bolha ao pipli Compilao poiam mov haza ao, ma o ulao m mo mpho iam iaifaóio A olução picipal ébaaa a obvação qu ão pciamo pa qu a iução mi a a olv o haza ao Paa a quêcia cóigo aio, aim qu a cia a oma paa o a, pomo focê-la como uma aa paa a ubação. acécimo o hawa xa paa o im qu fala a o pvio, iam o cuo io, échamao fowaig ou bypaig Pipli haza Haza ao Rpação o fowaig com ua iuçõ F: buca a iuçõ (mmóia iuçõ) D: coificação a iuçõ liua o baco giao EX: ágio xcução MEM: aco a mmóia WB: ágio paa cia o ulao Pipli haza Como pêcia m lação ao mpo cauam Haza ao a $1, ub $4,$1,$5 a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5
3 Pipli haza Como pêcia m lação ao mpo cauam Haza ao (Ra bfo wi aa haza) Pipli haza Como pêcia m lação ao mpo cauam Haza ao (Loa-u aa haza) a $1, ub $4,$1,$5 a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5. lw $1,4($2) ub $4,$1,$5 a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5 Pipli haza Foma mai impl paa olv haza ao Pipli haza Rolvo haza ao com camihamo. a $1, all all ub $4,$1,$5 a $6,$1,$7 Rolv o haza ao pla pa, ma m impaco o CP. Rolv o haza a $1, camihao (fowaig) o ulao ão logo ja ub $4,$1,$5 ipoívl paa a iuçõ qu o uilizam a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5 Pipli haza Rolvo haza ao com camihamo Pipli haza Um hazao ipo loa-ucia um ciclo aao. a $1, ub $4,$1,$5 a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5. lw $1,4($2) ub $4,$1,$5 a $6,$1,$7 o $8,$1,$9 xo $4,$1,$5
4 Pipli haza Haza ao Fowaig, apa fucioa bm a maioia a iuçõ, ão po impi oo o all o pipli Pciamo um all aé mmo com fowaig quao uma iução o fomao R apó um loaa ua o ao Pipli haza Haza cool ou vio E hazaoco a cia oma uma cião com ba o ulao um iução quao oua ão o xcuaa Solução impl: aicioa allo pipliaéqu a cia oma o vio ja calculaa Mmo com um poívl hawa xa, qu poa a o giao, calcula o ço o vio aualiza o PC o guo ágio o pipli, é cáio um all Pipli haza Haza cool S ão pumo olv o vio o guo ágio, ão íamo aao maio vio ao all Um olução épv o vio áomao ou ão A vão mai impl émp pv qu o vio ão ão omao; om quao o vio ão ão omao équ o pipli of um all Dvio ão omao Dvio omao Pipli Haza Haza cool Pviõ vio Pviõ vio pom fixa ou iâmica, quao pm o compoamo o vio uilizam um hióico vio Aualm, a quaia o ipo hióico ão xo, ulao m pvioiâmico com pcião maio qu 90% Quao a colha iv aa, o cool o pipli á qu gaai qu a iuçõ apó o vio ao ão ham fio, vo iicia o piplia pai o ço o vio apopiao Dcião aiaa Dcião aiaa (laybach) éa olução uilizaa pla aquiua MPS uçõ ão ogaizaa plo ofwa foma qu a iução imiaam poio ao alo é mp xcuaa Um camiho ao uao pipli Camiho ao Caa apa a iução po mapaa o camiho ao a qua paa a iia Úica xcçõ ão a aualização o PC a apa cia o ulao, moaa m co, qu via o ulao a ou o ao a mmóia paa a qua, paa m cio o baco giao Um camiho ao uao pipli Camiho ao Paa o valo uma iução iiviual paa u ouo ágio, o valo lio a mmóia iuçõ pcia alvo m um giao Agumo mlha aplicam o mai ágio o pipli, moo qu ão cáio giao mp qu xiim liha vicai o camiho ao PC 4 A ucio Mmoy Ra A F/D Ra A 1 Rgi Ra Ra A Daa 2 1 Fil Wi A Ra Daa 2 Wi Daa D/E X Shif lf 2 A EX/MEM A Wi Daa Daa Mmoy Ra Daa MEM/WB Sig 16 Ex 32
5 Um camiho ao uao pipli Camiho ao Écáio pva o coúo o giao io o giao io ao Um camiho ao com pipli Cool Mmo iai o camiho ao m pipli Rgiao ao amazam iai cool paa caa ágio F/D D/EX EX/MEM PC 4 ucio Mmoy Ra A A Ra A 1 Rgi Ra Ra A 2Daa 1 Fil Wi A Ra Daa 2 Wi Daa Shif lf 2 A A Wi Daa Daa Mmoy Ra Daa MEM/WB Sig 16 Ex 32 Pipliig ua uua pipli ão poívi Como olv uma iução muliplicação qu cia oi ciclo máquia? MUL Como olv o cao uma mmóia qu cia oi ciclo clock? M Rg DM1 DM2 Rg Coiaçõ fiai Pipliig Too o pocao auai uilizam pipliig Pipliig ãoajuaalaêcia umaimpl iução, ma ajua mlhoao a vazão uma caga abalho Spuppocial: a CP igual a 1 Taxa mlhoia élimiaa ao ágio piplimai lo Eágio ão balacao ciam ificiêcia mpo paa ch o mpo paa vazia o pipm impaco o mpho Haza vm cao olvio Sall afam gaivam o CP Liua comaa Pao, Davi A. Hy, Joh L. gaização Pojo Compuao: A fac Hawa/Sofwa. E. LTC, 292. E., 2004, Rio Jaio. Capíulo 6 Sli aquiua compuao Wikipia hp://.wikipia.og/wiki/ucio_pipli
Lavanderia sequencial 6 PM Pipelining: conceito natural! Lições com Pipeline. Pipeline em computadores 28/09/11
 Pipliig: cocio aual! Lavaia qucial 6 PM 7 8 9 10 11 12 Tim Exmplo a lavaia Aa, Buo, Ca@a, Davi caa um m oupa paa lava, ca paa Lava paa 30 miuo Scagm lva 40 miuo Paa lva 20 miuo A B C D T a k A B C D 30
Pipliig: cocio aual! Lavaia qucial 6 PM 7 8 9 10 11 12 Tim Exmplo a lavaia Aa, Buo, Ca@a, Davi caa um m oupa paa lava, ca paa Lava paa 30 miuo Scagm lva 40 miuo Paa lva 20 miuo A B C D T a k A B C D 30
Organização e Arquitetura de computadores
 Rvião o camiho ao com pipliig gaização Aquiua compuao Solucioao Haza o pipli Pof D Luciao Joé Sg Cool RgWi 1 Rgi 2 1 Wi Sig 16 32 Sc p Sc MmWi Mm MmoRg RgD Foma mai impl olv haza ao a $1, all all ub $,$1,$5
Rvião o camiho ao com pipliig gaização Aquiua compuao Solucioao Haza o pipli Pof D Luciao Joé Sg Cool RgWi 1 Rgi 2 1 Wi Sig 16 32 Sc p Sc MmWi Mm MmoRg RgD Foma mai impl olv haza ao a $1, all all ub $,$1,$5
Pipeline. Organização de Computadores
 Piplin Poco d Piplining (xmplo da lavandia) Ana, Buno, Cala, Luiz têm oupa uja a m lavada, cada, dobada guadada Lavadoa lva 30 minuto A B C D Scadoa lva 30 minuto Doba lva 30 minuto Guada lva 30 minuto
Piplin Poco d Piplining (xmplo da lavandia) Ana, Buno, Cala, Luiz têm oupa uja a m lavada, cada, dobada guadada Lavadoa lva 30 minuto A B C D Scadoa lva 30 minuto Doba lva 30 minuto Guada lva 30 minuto
Pipeline é Natural! Lavanderia Seqüencial Meia noite. Lavanderia pipeline. Sumário. Unidade 4* - Aulas 1/2:
 Poifíci ivi Cólic o io G o Sul iuo foáic gizção Copuo GAPH i 4* Aul 1/2: Pipli, Hz Fowig Pof. Fo Gh Mo Ny L Vil Clz Poo Alg, juho 1998 * Apo Apçõ y Kz, iviy of Bkly Suáio Pipli oução Pipli Copuo Aquiu
Poifíci ivi Cólic o io G o Sul iuo foáic gizção Copuo GAPH i 4* Aul 1/2: Pipli, Hz Fowig Pof. Fo Gh Mo Ny L Vil Clz Poo Alg, juho 1998 * Apo Apçõ y Kz, iviy of Bkly Suáio Pipli oução Pipli Copuo Aquiu
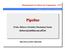 http://www.ic.uff.b/~boa/fac! 1 Ana, Buno, Cala, Luiz tê oupa uja a lavaa, caa, obaa guaaa Lavaoa lva 30 inuto Scaoa lva 30 inuto Doba lva 30 inuto Guaa lva 30 inuto A B C D 2 6 PM 7 8 9 10 11 12 1 2 AM
http://www.ic.uff.b/~boa/fac! 1 Ana, Buno, Cala, Luiz tê oupa uja a lavaa, caa, obaa guaaa Lavaoa lva 30 inuto Scaoa lva 30 inuto Doba lva 30 inuto Guaa lva 30 inuto A B C D 2 6 PM 7 8 9 10 11 12 1 2 AM
u seja, pode ser escrito como uma combinação linear de.
 Toma d Cayly-Hamilo ja x sja d I α... α poliômio caacísico d. Eão: α α... α α I Toda maiz é um zo d su poliômio caacísico., mos qu qu:... I { I,,..., } u sja, pod s scio como uma combiação lia d. Também,
Toma d Cayly-Hamilo ja x sja d I α... α poliômio caacísico d. Eão: α α... α α I Toda maiz é um zo d su poliômio caacísico., mos qu qu:... I { I,,..., } u sja, pod s scio como uma combiação lia d. Também,
Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e :
 INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
Com muito carinho para minha querida amiga e super profissional. Ale Del Vecchio
 Com muito carinho para minha querida amiga e super profissional. BA BE BI BO BU BÃO ba be bi bo bu bão BA ba boi BE be bebê BI bi Bia BO bo boi BU bu buá Nome: BA BE BI BO BU BÃO ba be bi bo bu bão BA
Com muito carinho para minha querida amiga e super profissional. BA BE BI BO BU BÃO ba be bi bo bu bão BA ba boi BE be bebê BI bi Bia BO bo boi BU bu buá Nome: BA BE BI BO BU BÃO ba be bi bo bu bão BA
Medley Forró 3. & bb b b œ œ bœ. œ bœ. œ œ œ œ. œ œ. . r. j œ œ œ. & b b b b œ. & bb b b. œ œ œ. œ œ. . œ. œ Œ. œ œ œ. œ œ. œ œ œ.
 b b b 4 2 12 Medley Foó 3 SOPRANO Vesão eduzida (2014) Baião Luiz Gonzaga q = 100 6 A 22 b b b u vou mos - ta pa vo - cês co-mo se dan-ça'o ba-ião e quem qui - se a-pen-de é fa -vo pes - ta a-ten-ção mo-e-na
b b b 4 2 12 Medley Foó 3 SOPRANO Vesão eduzida (2014) Baião Luiz Gonzaga q = 100 6 A 22 b b b u vou mos - ta pa vo - cês co-mo se dan-ça'o ba-ião e quem qui - se a-pen-de é fa -vo pes - ta a-ten-ção mo-e-na
Medley Forró 3. 6 j œ œ œ. & bb b b œ œ œ nœ. & b b b b. œ œ œ œ bœ. œ œ. œnœ. œ bœ. œ œ œ œ. œ œ œ. & bb b b. œ œ. œ œ. œ œ. . œ.
 22 27 b b b 2 7 b b b 42 47 5 b b b 72 q = 100 4 2 12 B 6 A Eu vou mos -ta pa vo - cês co-mo se dan-ça'o ba -ião e quem qui - se a - pen -de é fa -vo pes - ta a -ten-ção b mo-e -na che-gue pa cá bem un
22 27 b b b 2 7 b b b 42 47 5 b b b 72 q = 100 4 2 12 B 6 A Eu vou mos -ta pa vo - cês co-mo se dan-ça'o ba -ião e quem qui - se a - pen -de é fa -vo pes - ta a -ten-ção b mo-e -na che-gue pa cá bem un
4. VIBRAÇÃO FORÇADA - FORÇAS NÃO SENOIDAIS
 VIBRAÇÕES MEÂNIAS - APÍTULO VIBRAÇÃO ORÇADA 3. VIBRAÇÃO ORÇADA - ORÇAS NÃO SENOIDAIS No capíulo ao suou-s a vbação oçaa ssas co u gau lba, subos a oças cação oa soal. Es suo po s so paa aplcaçõs quao as
VIBRAÇÕES MEÂNIAS - APÍTULO VIBRAÇÃO ORÇADA 3. VIBRAÇÃO ORÇADA - ORÇAS NÃO SENOIDAIS No capíulo ao suou-s a vbação oçaa ssas co u gau lba, subos a oças cação oa soal. Es suo po s so paa aplcaçõs quao as
RELAÇÃO DE TURMA I D L. E. P o r t. H i s t. G e o g r.
 O UÁ U ÇÃO U 7º v 07/08 l d Bá º m º 0 B BO X X X X X X X X X X - X 004638 0 É BO X X X X X X X X X X - X 004639 03 BO O BUÃO 7 X X X X X X X X X X X - 00434 04 O O O X X X X X X X X X X - X 00470 05 O
O UÁ U ÇÃO U 7º v 07/08 l d Bá º m º 0 B BO X X X X X X X X X X - X 004638 0 É BO X X X X X X X X X X - X 004639 03 BO O BUÃO 7 X X X X X X X X X X X - 00434 04 O O O X X X X X X X X X X - X 00470 05 O
b a c v g g g t a n m p o i a a a m i o t f m p b a m p e l x m x o a a i o r a r n r c h a a s l u u u v m u c a a s n u g r l l i a a e l
 x x x z f f h h q h f z X x x x z f f h h q h f z Pó C S C Cí Nzó Lüí Aí Aó G Oá Xé Ró Lóz Bó X Mqé V Mí Lz Méz Fáz Gz Nz B Có E P C, S. L. D R Hz C ISBN13 978-84-694-1518-4 DL C 634-2011 X : TOP X : TOP
x x x z f f h h q h f z X x x x z f f h h q h f z Pó C S C Cí Nzó Lüí Aí Aó G Oá Xé Ró Lóz Bó X Mqé V Mí Lz Méz Fáz Gz Nz B Có E P C, S. L. D R Hz C ISBN13 978-84-694-1518-4 DL C 634-2011 X : TOP X : TOP
( ). ( ) ( 2.2 Valor Esperado e Momentos. Função Geratriz de Momentos Seja X uma variável aleatória, então, se o valor esperado de existe
 . Valo Espao omnos Função Gaiz omnos Sja uma vaiávl alaóia, não, s o valo spao xis paa oo valo m algum invalo ( h,h, h > 0, l é inio como a Função Gaiz omnos, noaa Fomalmn, x E. ( x x R (. caso isco x
. Valo Espao omnos Função Gaiz omnos Sja uma vaiávl alaóia, não, s o valo spao xis paa oo valo m algum invalo ( h,h, h > 0, l é inio como a Função Gaiz omnos, noaa Fomalmn, x E. ( x x R (. caso isco x
MECÂNICA. Uma força realiza trabalho quando ela transfere energia de um corpo para outro e quando transforma uma modalidade de energia em outra.
 AULA 8 MECÂNICA TRABALHO E POTÊNCIA 1- INTRODUÇÃO Uma foça ealiza abalho uano ela ansfee enegia e um copo paa ouo e uano ansfoma uma moaliae e enegia em oua. 2- TRABALHO DE UMA ORÇA CONSTANTE. A B Um copo
AULA 8 MECÂNICA TRABALHO E POTÊNCIA 1- INTRODUÇÃO Uma foça ealiza abalho uano ela ansfee enegia e um copo paa ouo e uano ansfoma uma moaliae e enegia em oua. 2- TRABALHO DE UMA ORÇA CONSTANTE. A B Um copo
Sazonais da Floresta ENQUADRAMENTO GERAL. Sazonais da Floresta
 ub ub ENQUADRAMENTO GERAL A f é um m u cm múp pu, qu ó é pív pv m m épc fc p um vgm qu pb m u p u u mm m p- pv m qu um cu f fm m cv g. Ex um g v u qu ó xm m m épc. T- pv m v pu f, qu mu v ã já u m m vu
ub ub ENQUADRAMENTO GERAL A f é um m u cm múp pu, qu ó é pív pv m m épc fc p um vgm qu pb m u p u u mm m p- pv m qu um cu f fm m cv g. Ex um g v u qu ó xm m m épc. T- pv m v pu f, qu mu v ã já u m m vu
Questionário sobre o Ensino de Leitura
 ANEXO 1 Questionário sobre o Ensino de Leitura 1. Sexo Masculino Feminino 2. Idade 3. Profissão 4. Ao trabalhar a leitura é melhor primeiro ensinar os fonemas (vogais, consoantes e ditongos), depois as
ANEXO 1 Questionário sobre o Ensino de Leitura 1. Sexo Masculino Feminino 2. Idade 3. Profissão 4. Ao trabalhar a leitura é melhor primeiro ensinar os fonemas (vogais, consoantes e ditongos), depois as
Análise Matemática IV
 Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
Compreendendo placas de interface de voz do escritório de câmbio internacional (FXO)
 Cm lc ifc z ciói câmbi icil FO I cm: Aliz m: g 6 fêci PF Imimi Fbck P Rlci Plc ifc z Cic Cic 6 Si liic Plfm Íic Iç Péqii Rqii Cm Uiliz Cç úm Rc Cfigç S à lfm Ifmç Rlci Cic lci i ic cmi Iç A ifc Fig Exchg
Cm lc ifc z ciói câmbi icil FO I cm: Aliz m: g 6 fêci PF Imimi Fbck P Rlci Plc ifc z Cic Cic 6 Si liic Plfm Íic Iç Péqii Rqii Cm Uiliz Cç úm Rc Cfigç S à lfm Ifmç Rlci Cic lci i ic cmi Iç A ifc Fig Exchg
Resolução de Matemática da Prova Objetiva FGV Administração - 06-06-10
 QUESTÃO 1 VESTIBULAR FGV 010 JUNHO/010 RESOLUÇÃO DAS 15 QUESTÕES DE MATEMÁTICA DA PROVA DA MANHÃ MÓDULO OBJETIVO PROVA TIPO A O mon i tor de um note book tem formato retangular com a di ag o nal medindo
QUESTÃO 1 VESTIBULAR FGV 010 JUNHO/010 RESOLUÇÃO DAS 15 QUESTÕES DE MATEMÁTICA DA PROVA DA MANHÃ MÓDULO OBJETIVO PROVA TIPO A O mon i tor de um note book tem formato retangular com a di ag o nal medindo
GLOSSÁRIO PREV PEPSICO
 GLOSSÁRIO PREV PEPSICO A T A A ABRAPP Aã Aã I Aí I R ANAPAR A A M A A A Lí Aá S C é ç í ê çõ 13ª í ã. Açã B E F Pê P. Cí ê, ã ê. V Cê Aã P ( á). N í, - I R P Fí (IRPF), S R F, à í á, ( 11.053 2004), çã.
GLOSSÁRIO PREV PEPSICO A T A A ABRAPP Aã Aã I Aí I R ANAPAR A A M A A A Lí Aá S C é ç í ê çõ 13ª í ã. Açã B E F Pê P. Cí ê, ã ê. V Cê Aã P ( á). N í, - I R P Fí (IRPF), S R F, à í á, ( 11.053 2004), çã.
Q ' 54 Diretora-Geral de Estatisticas da Educagao e
 MINISTERIO DA EDUCAcAo E CIENCIA Direcao-Geral de Planeamento e Gestao Financeira Exma. Senhora 001151 Q702015 ' 54 Diretora-Geral de Estatisticas da Educagao e Ciencia Av.' 24 de Julho, 134 1399-054 -
MINISTERIO DA EDUCAcAo E CIENCIA Direcao-Geral de Planeamento e Gestao Financeira Exma. Senhora 001151 Q702015 ' 54 Diretora-Geral de Estatisticas da Educagao e Ciencia Av.' 24 de Julho, 134 1399-054 -
Estratégico. III Seminário de Planejamento. Rio de Janeiro, 23 a 25 de fevereiro de 2011
 Estratégico III Seminário de Planejamento Rio de Janeiro, 23 a 25 de fevereiro de 2011 G es tão Em pre sa rial O rie nta ção pa ra om erc ado Ino vaç ão et
Estratégico III Seminário de Planejamento Rio de Janeiro, 23 a 25 de fevereiro de 2011 G es tão Em pre sa rial O rie nta ção pa ra om erc ado Ino vaç ão et
Transformada Inversa de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior
 Tanfomada Inva d Lalac Pof Eng nonio Calo Lmo Júnio GEND Tanfomada Inva d Lalac Excício Conol d Sima Mcânico Tanfomada Inva d Lalac Obivo: O obivo da ção é faz uma odução à Tanfomada Inva d Lalac ua alicação
Tanfomada Inva d Lalac Pof Eng nonio Calo Lmo Júnio GEND Tanfomada Inva d Lalac Excício Conol d Sima Mcânico Tanfomada Inva d Lalac Obivo: O obivo da ção é faz uma odução à Tanfomada Inva d Lalac ua alicação
ORAÇÃO DA NOITE. œ œ œ œ. œ œ. œ œ œ. œ. œ œ. œ J J œ œ œ œ. œ œ Amin f
 oema de EMILIANO ERNETA C Grave q = C Ami ri - B Gmi ORAÇÃO DA NOITE Resosório ara coro misto e Sorao solista a, vem re - C Ami Ma - ri - a, Ami B Gmi J J j j J J ri a, vem re - ri - a, vem - re - B G
oema de EMILIANO ERNETA C Grave q = C Ami ri - B Gmi ORAÇÃO DA NOITE Resosório ara coro misto e Sorao solista a, vem re - C Ami Ma - ri - a, Ami B Gmi J J j j J J ri a, vem re - ri - a, vem - re - B G
n o m urd ne Hel e n o mis
 Em nosso cotidiano existem infinitas tarefas que uma criança autista não é capaz de realizar sozinha, mas irá torna-se capaz de realizar qualquer atividade, se alguém lhe der instruções, fizer uma demonstração
Em nosso cotidiano existem infinitas tarefas que uma criança autista não é capaz de realizar sozinha, mas irá torna-se capaz de realizar qualquer atividade, se alguém lhe der instruções, fizer uma demonstração
Cidade Inacabada & 4 2. Œ œ œ. Andante. Manu Lafer. A b 7M/C. A ø /C. intro. 6fr. 7fr. 6fr. 7fr. 6fr.
 Cidade Inacabada Andante intro 4 2 A b M/C A ø /C 5 A b M/C A ø /C A b M/C Œ so - frer 2 A 1 11 E m 11 E ø E o b é da tu - aien - ver - ga - du - 15 D m D m/c Œ - ra lou - cu - B m 11 ra, 1 B ø é vo E
Cidade Inacabada Andante intro 4 2 A b M/C A ø /C 5 A b M/C A ø /C A b M/C Œ so - frer 2 A 1 11 E m 11 E ø E o b é da tu - aien - ver - ga - du - 15 D m D m/c Œ - ra lou - cu - B m 11 ra, 1 B ø é vo E
Resolução feita pelo Intergraus! Módulo Objetivo - Matemática FGV 2010/1-13.12.2009
 FGV 010/1-13.1.009 VESTIBULAR FGV 010 DEZEMBRO 009 MÓDULO OBJETIVO PROVA TIPO A PROVA DE MATEMÁTICA QUESTÃO 1 (Prova: Tipo B Resposta E; Tipo C Resposta C; Tipo D Resposta A) O gráfico abaio fornece o
FGV 010/1-13.1.009 VESTIBULAR FGV 010 DEZEMBRO 009 MÓDULO OBJETIVO PROVA TIPO A PROVA DE MATEMÁTICA QUESTÃO 1 (Prova: Tipo B Resposta E; Tipo C Resposta C; Tipo D Resposta A) O gráfico abaio fornece o
Proposta de Revisão Metodológica
 Proposta de Revisão Metodológica Gestão do Desempenho Dezembro de 20 DIDE/SVDC Propostas para 202 Nova sist em át ic a de pac t uaç ão e avaliaç ão de m et as set oriais e de equipe; Avaliaç ão de De s
Proposta de Revisão Metodológica Gestão do Desempenho Dezembro de 20 DIDE/SVDC Propostas para 202 Nova sist em át ic a de pac t uaç ão e avaliaç ão de m et as set oriais e de equipe; Avaliaç ão de De s
GUARITA / FACHADA GUARITA / PLANTA COBERTURA
 MP i:% MP i:% MP i:.0% ÚLMO ÁO LZ O VO: OMO FÊ L00 PLJMO LVMO O PL00 PLJMO PLJMO XÇÃO O OOL O POJO FLVOPP_Levantamento_ev0..0.0.0.0.0.0.0.00.0.0.0.0.0.0.0 MOLOG FÇÃO X V. OL FO.. PO LHO V G GÇ..0... L
MP i:% MP i:% MP i:.0% ÚLMO ÁO LZ O VO: OMO FÊ L00 PLJMO LVMO O PL00 PLJMO PLJMO XÇÃO O OOL O POJO FLVOPP_Levantamento_ev0..0.0.0.0.0.0.0.00.0.0.0.0.0.0.0 MOLOG FÇÃO X V. OL FO.. PO LHO V G GÇ..0... L
Índices Físicos ÍNDICES
 Ínice Fíico ÍNDICES = volume oal a amora; = volume a fae ólia a amora; = volume a fae líquia; a = volume a fae aoa; v = volume e vazio a amora = a + ; = peo oal a amora ; a = peo a fae aoa a amora; = peo
Ínice Fíico ÍNDICES = volume oal a amora; = volume a fae ólia a amora; = volume a fae líquia; a = volume a fae aoa; v = volume e vazio a amora = a + ; = peo oal a amora ; a = peo a fae aoa a amora; = peo
A ESTRADA E A PAISAGEM: COMO A ANTROPIZAÇÃO ATUA SOBRE O RELEVO (UM ENSAIO DE GEOMORFOLOGIA AMBIENTAL)
 A ESTRADA E A PAISAGEM: COMO A ANTROPIZAÇÃO ATUA SOBRE O RELEVO (UM ENSAIO DE GEOMORFOLOGIA AMBIENTAL) Aô C Rb Aúj Jú Pgm Eã T Gg UFPA AGB-Bém j_bz@hm.m Eêvã Jé Sv Bb Pq vbb@yh.m.b 1 - INTRODUÇÃO O ém
A ESTRADA E A PAISAGEM: COMO A ANTROPIZAÇÃO ATUA SOBRE O RELEVO (UM ENSAIO DE GEOMORFOLOGIA AMBIENTAL) Aô C Rb Aúj Jú Pgm Eã T Gg UFPA AGB-Bém j_bz@hm.m Eêvã Jé Sv Bb Pq vbb@yh.m.b 1 - INTRODUÇÃO O ém
RESPOSTA TEMPORAL. 1. Motivação. 2. Solução homogênea. Calcular a resposta temporal de sistemas dinâmicos LIT na forma SS.
 Euaro Lobo Luoa Cabral RESPOST TEMPORL. Moiação Calcular a rpoa mporal ima inâmico LT na forma SS. Rpoa mporal prmi analiar comporamno inâmico o ima no omínio o mpo. Dua oluçõ: Solução homogêna rpoa à
Euaro Lobo Luoa Cabral RESPOST TEMPORL. Moiação Calcular a rpoa mporal ima inâmico LT na forma SS. Rpoa mporal prmi analiar comporamno inâmico o ima no omínio o mpo. Dua oluçõ: Solução homogêna rpoa à
MATEMÁTICA CADERNO 6 CURSO E FRENTE 1 ÁLGEBRA. n Módulo 24 Números Complexos. n Módulo 25 Potências Naturais de i e Forma Algébrica
 MATEMÁTICA CADERNO 6 CURSO E FRENTE ÁLGEBRA n Módulo 4 Números Complexos ) (5 + 7i) ( i) = 5 0i + i 4i = 5 + i + 4 = 9 + i ) f(z) = z z + f( i) = ( i) ( i) + = = i + i + i + = i ) x + (y )i = y 4 + xi,
MATEMÁTICA CADERNO 6 CURSO E FRENTE ÁLGEBRA n Módulo 4 Números Complexos ) (5 + 7i) ( i) = 5 0i + i 4i = 5 + i + 4 = 9 + i ) f(z) = z z + f( i) = ( i) ( i) + = = i + i + i + = i ) x + (y )i = y 4 + xi,
Medley Forró 4 Tenho Sede Dominguinhos e Anastácia
 TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
B e n j a m i n C o n s t a n t B o t e l h o d e M a g a l h ã e s ( 1 8 3 6 / 1 8 9 1 )
 B e n j a m i n C o n s t a n t B o t e l h o d e M a g a l h ã e s ( 1 8 3 6 / 1 8 9 1 ) B e n ja m i n C o n s t a n t, c o m o c o s t u m a s e r r e f e r i d o, é c o n s i d e r a d o c o m o o
B e n j a m i n C o n s t a n t B o t e l h o d e M a g a l h ã e s ( 1 8 3 6 / 1 8 9 1 ) B e n ja m i n C o n s t a n t, c o m o c o s t u m a s e r r e f e r i d o, é c o n s i d e r a d o c o m o o
(Às Co missões de Re la ções Exteriores e Defesa Na ci o nal e Comissão Diretora.)
 32988 Quarta-feira 22 DIÁRIO DO SENADO FEDERAL Ou tu bro de 2003 Art. 3º O Gru po Parlamentar reger-se-á pelo seu regulamento in ter no ou, na falta deste, pela decisão da ma i o ria absoluta de seus mem
32988 Quarta-feira 22 DIÁRIO DO SENADO FEDERAL Ou tu bro de 2003 Art. 3º O Gru po Parlamentar reger-se-á pelo seu regulamento in ter no ou, na falta deste, pela decisão da ma i o ria absoluta de seus mem
Rio 40 Graus Fernanda Abreu/F.Fawcett/Laufer Û Û Û Û Û Û Û Û Û
 CONTALTO c 4 io 40 Graus Fernanda Abreu/F.Fawcett/Laufer Arrano: Edu Morelenbaum 7 10 12 15 17 20 2 24 25 26 27 i-o qua-ren-tagraus graus vi-lha pur-ga-tó-rio da be-le-za_edocaos i-o qua-ren - ta graus
CONTALTO c 4 io 40 Graus Fernanda Abreu/F.Fawcett/Laufer Arrano: Edu Morelenbaum 7 10 12 15 17 20 2 24 25 26 27 i-o qua-ren-tagraus graus vi-lha pur-ga-tó-rio da be-le-za_edocaos i-o qua-ren - ta graus
9 JUNHO. Rua Cândido dos Reis, Vila Nova de Gaia Tel.: Fax:
 ÇÃÀ 9JUNHO í çõ úãá ÕÚ õ ú ã é çã é õéá é à Rua Cândido dos Reis, 545 4400-075 Vila Nova de Gaia Tel.: 22 374 67 20 - Fax: 22 374 67 29 www.jf-santamarinha.pt 1 õ á õ à çã çõ õ á çã áí é àí àçãçã ã Á à
ÇÃÀ 9JUNHO í çõ úãá ÕÚ õ ú ã é çã é õéá é à Rua Cândido dos Reis, 545 4400-075 Vila Nova de Gaia Tel.: 22 374 67 20 - Fax: 22 374 67 29 www.jf-santamarinha.pt 1 õ á õ à çã çõ õ á çã áí é àí àçãçã ã Á à
O Sacrifício da Cruz
 O Sacrifício da ruz 6 ø 4 4 Intenso q = 61 9. r. r m b sus4 6 Ó. m Œ. r J 1.u ø. r o - lho pa - ra_o céu, bus - M7.. can - do com - preen-der o sa - cri - fí - cio do Sal - va - dor em meu lu - gar ø ø
O Sacrifício da ruz 6 ø 4 4 Intenso q = 61 9. r. r m b sus4 6 Ó. m Œ. r J 1.u ø. r o - lho pa - ra_o céu, bus - M7.. can - do com - preen-der o sa - cri - fí - cio do Sal - va - dor em meu lu - gar ø ø
Linha de Vida para Caminhão
 S md nh d Vd p Cmnhão P vq od Sm d nh d Vd p Cmnhão 10 DOIS DEZ INHA DE VIDA PARA CAMINHÃO No m d ncogm p vdd d cg dcg é conuído p d unão d m PvQ od com PvQ Rg. É compo po d ou m p cn, mã fnc un b, com
S md nh d Vd p Cmnhão P vq od Sm d nh d Vd p Cmnhão 10 DOIS DEZ INHA DE VIDA PARA CAMINHÃO No m d ncogm p vdd d cg dcg é conuído p d unão d m PvQ od com PvQ Rg. É compo po d ou m p cn, mã fnc un b, com
Índice alfabético. página: 565 a b c d e f g h i j k l m n o p q r s t u v w x y z. procura índice imprimir última página vista anterior seguinte
 Í é á: 565 á é í ú á í é á: 566 A A é, 376 A, 378 379 A á, 146 147 A, 309 310 A á, 305 A ( ), 311 A, 305 308 A á B, 470 A á, 384 385 A,, ç Bç, 338 340 A é, 337 Aé, 333 A, 410 419 A K, 466 A, 123 A, 32
Í é á: 565 á é í ú á í é á: 566 A A é, 376 A, 378 379 A á, 146 147 A, 309 310 A á, 305 A ( ), 311 A, 305 308 A á B, 470 A á, 384 385 A,, ç Bç, 338 340 A é, 337 Aé, 333 A, 410 419 A K, 466 A, 123 A, 32
COLÉGIO OBJETIVO JÚNIOR
 COLÉGIO OBJETIVO JÚNIOR NOME: N. o : 7. o ANO DATA: / /201 FOLHETO DE MATEMÁTICA (V.C. E R.V.) Este fo lhe to é um ro te i ro de es tu do para você re cu pe rar o con te ú do tra ba lha do em 201. Como
COLÉGIO OBJETIVO JÚNIOR NOME: N. o : 7. o ANO DATA: / /201 FOLHETO DE MATEMÁTICA (V.C. E R.V.) Este fo lhe to é um ro te i ro de es tu do para você re cu pe rar o con te ú do tra ba lha do em 201. Como
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Retas Cortadas por uma Transversal. Oitavo Ano
 Maial Tóico - Módulo Elmno Báico d Gomia Plana - Pa 1 Ra Coada po uma Tanval Oiavo Ano Auo: Pof. Uli Lima Pan Rvio: Pof. Anonio Caminha M. No Poal da OBMEP 1 Ra coada po uma anval Sjam dua a iuada m um
Maial Tóico - Módulo Elmno Báico d Gomia Plana - Pa 1 Ra Coada po uma Tanval Oiavo Ano Auo: Pof. Uli Lima Pan Rvio: Pof. Anonio Caminha M. No Poal da OBMEP 1 Ra coada po uma anval Sjam dua a iuada m um
Cinemática e dinâmica da partícula
 Sumáio Unia I MECÂNICA 1- a patícula Cinmática inâmica a patícula m moimntos a mais o qu uma imnsão - Rfncial to posição. - Equaçõs paaméticas o moimnto. Equação a tajtóia. - Dslocamnto, locia méia locia.
Sumáio Unia I MECÂNICA 1- a patícula Cinmática inâmica a patícula m moimntos a mais o qu uma imnsão - Rfncial to posição. - Equaçõs paaméticas o moimnto. Equação a tajtóia. - Dslocamnto, locia méia locia.
Balancete. Acumulado. Moeda - Eu r o s Cn t Me s : Ab r i l Pag. 1
 Cn t - 31. 05. 2014 Me s : Ab r i l Pag. 1 11 CA I XA 53, 384. 43 51, 010. 11 2, 374. 32 111 Ca i x a 7, 547. 50 5, 894. 50 1, 653. 00 112 Ca i x a Fa c t u r a ç ão 45, 661. 93 45, 115. 61 546. 32 113
Cn t - 31. 05. 2014 Me s : Ab r i l Pag. 1 11 CA I XA 53, 384. 43 51, 010. 11 2, 374. 32 111 Ca i x a 7, 547. 50 5, 894. 50 1, 653. 00 112 Ca i x a Fa c t u r a ç ão 45, 661. 93 45, 115. 61 546. 32 113
URBANISMO COMERCIAL EM PORTUGAL E A REVITALIZAÇÃO DO CENTRO DAS CIDADES
 LEITURAS URBANISMO COMERCIAL EM PORTUGAL E A REVITALIZAÇÃO DO CENTRO DAS CIDADES [Carlos José Lopes Balsas (1999), Gabinete de Estudos e Prospectiva Económica, Ministério da Economia, ISBN: 972-8170-55-6]
LEITURAS URBANISMO COMERCIAL EM PORTUGAL E A REVITALIZAÇÃO DO CENTRO DAS CIDADES [Carlos José Lopes Balsas (1999), Gabinete de Estudos e Prospectiva Económica, Ministério da Economia, ISBN: 972-8170-55-6]
9 a Aula. Teoria do Adensamento
 cânica do Solo Fundaçõ PEF 5 9 a ula Toia do dnamnto Rcalqu po adnamnto u dnolimnto no tmpo Camada Compíl Compão Uni-Dimional - Enaio d dnamnto Condição K o - Dfomação latal nula. Fluxo d água - tical
cânica do Solo Fundaçõ PEF 5 9 a ula Toia do dnamnto Rcalqu po adnamnto u dnolimnto no tmpo Camada Compíl Compão Uni-Dimional - Enaio d dnamnto Condição K o - Dfomação latal nula. Fluxo d água - tical
é é ç í é é é ç ó çõ é ê á çã é çã é á á ã é í á ã ó É ã ê í á á é á ã â é ó é é ã é é é á é ã ó ã á é í á é ê ã
 Ó é é ç ç ã éó éçéá éé çí é éé çóçõé ê á çã é çã é á á ã é í á ã óéãê íáá éáãâé ó é é ã éé éáé ãóã áéí á é ê ã çã é ã é çã ãíçãê éé ô í é çóã á ó ó é çãéã ú ê é á íô á ãé úóé çãçç óçãéééõé ççã çãôáíô éçé
Ó é é ç ç ã éó éçéá éé çí é éé çóçõé ê á çã é çã é á á ã é í á ã óéãê íáá éáãâé ó é é ã éé éáé ãóã áéí á é ê ã çã é ã é çã ãíçãê éé ô í é çóã á ó ó é çãéã ú ê é á íô á ãé úóé çãçç óçãéééõé ççã çãôáíô éçé
E v o lu ç ã o d o c o n c e i t o d e c i d a d a n i a. A n t o n i o P a i m
 E v o lu ç ã o d o c o n c e i t o d e c i d a d a n i a A n t o n i o P a i m N o B r a s i l s e d i me nt o u - s e u ma v is ã o e r r a d a d a c id a d a n ia. D e u m mo d o g e r a l, e s s a c
E v o lu ç ã o d o c o n c e i t o d e c i d a d a n i a A n t o n i o P a i m N o B r a s i l s e d i me nt o u - s e u ma v is ã o e r r a d a d a c id a d a n ia. D e u m mo d o g e r a l, e s s a c
CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS
 CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS. Moivaçõe Como vio o Regulado de Eado maném o iema em uma deeminada condição de egime pemanene, ou eja, ena mane o eado em uma dada condição eacionáia.
CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS. Moivaçõe Como vio o Regulado de Eado maném o iema em uma deeminada condição de egime pemanene, ou eja, ena mane o eado em uma dada condição eacionáia.
2ª Lei de Newton em forma geral ( p = mv. - momento linear, F = r r dt
 Tópios d Físia Moda 4/5 Fomuláio Mdiçõs os ~ < > i i σ i < > i σ < > ± σ < > ± 3σ < > ± g µ σ πσ mlo simaia do alo dadio a pai d mdidas - média aiméia Dsio padão aaiza a dispsão dos sulados d mdidas do
Tópios d Físia Moda 4/5 Fomuláio Mdiçõs os ~ < > i i σ i < > i σ < > ± σ < > ± 3σ < > ± g µ σ πσ mlo simaia do alo dadio a pai d mdidas - média aiméia Dsio padão aaiza a dispsão dos sulados d mdidas do
DATAPREV Divisão de Gestão Operacional e Controle - D1GC Serviço Técnico a Softwares de Produção STSP
 GIS Gertran Integration Suite Guia de T ransferência de Arquivos Entidade x DATAPREV Versão 1.0 HTTPS G I S G ui a de T ra n sf er ên ci a d e Ar qu i vo s 1/ 8 ÍNDICE ANALÍT ICO 1. INTRODU ÇÃO......4
GIS Gertran Integration Suite Guia de T ransferência de Arquivos Entidade x DATAPREV Versão 1.0 HTTPS G I S G ui a de T ra n sf er ên ci a d e Ar qu i vo s 1/ 8 ÍNDICE ANALÍT ICO 1. INTRODU ÇÃO......4
setor 1103 Aula 39 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO Então, 1. INTRODUÇÃO Duas retas r e s de um plano podem ser: Distintas: r s = Exemplo:
 to 58 Aula 9 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO. INTRODUÇÃO Dua ta d um plano podm : Ditinta: = Emplo: Então, O coficint angula ão iguai. O coficint lina ão difnt. Paalla b) ão PARALELAS COINCIDENTES.
to 58 Aula 9 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO. INTRODUÇÃO Dua ta d um plano podm : Ditinta: = Emplo: Então, O coficint angula ão iguai. O coficint lina ão difnt. Paalla b) ão PARALELAS COINCIDENTES.
1ª. Lei da Termodinâmica para um Volume de Controle
 ª. Li da Trmodinâmica ara um Volum d Conrol Grand ar do roblma d inr na ngnharia nol ima abro, ou ja, ima no quai há fluo d maa araé d ua fronira. É, orano, connin obrmo uma rão da ª. Li álida ara ima
ª. Li da Trmodinâmica ara um Volum d Conrol Grand ar do roblma d inr na ngnharia nol ima abro, ou ja, ima no quai há fluo d maa araé d ua fronira. É, orano, connin obrmo uma rão da ª. Li álida ara ima
PROCESSO SELETIVO UFES 2013
 UNIESIDADE FEDEAL DO ESPÍIO SANO OMISSÃO OODENADOA DO ESIBULA POESSO SELEIO UFES 0 As bacas laboaoas sam ob a maioia os caiaos sosas como as u sgum No ao aa a coção as ovas ouas sosas ambém oão s cosiaas
UNIESIDADE FEDEAL DO ESPÍIO SANO OMISSÃO OODENADOA DO ESIBULA POESSO SELEIO UFES 0 As bacas laboaoas sam ob a maioia os caiaos sosas como as u sgum No ao aa a coção as ovas ouas sosas ambém oão s cosiaas
Sumário e Objectivos. Placas e Cascas 7ªAula. Abril
 Sumáio Objctivos Sumáio: Placas Ciculas Objctivos a Aula: Apnsão os Métoos Solução a Equação Lagang paa Placas Ciculas cagaas apoiaas simticamnt. Abil Abil Placas Ciculas O Sistma Eixos é um sistma coonaas
Sumáio Objctivos Sumáio: Placas Ciculas Objctivos a Aula: Apnsão os Métoos Solução a Equação Lagang paa Placas Ciculas cagaas apoiaas simticamnt. Abil Abil Placas Ciculas O Sistma Eixos é um sistma coonaas
P i s cina s : 2 P i s ci n a e x te rior de á g u a d e m a r a q u e cida P i s ci n a i n te ri or d e á g u a
 E M P R IM E I R A MÃO T h e O i ta v os é o e x c lu s i v o h o te l d e 5 e s tre la s q u e co m p le t a e v a l ori za a ofe rta d a Q u i n ta d a M a ri n h a, co n s olid a n d o -a c om o d e
E M P R IM E I R A MÃO T h e O i ta v os é o e x c lu s i v o h o te l d e 5 e s tre la s q u e co m p le t a e v a l ori za a ofe rta d a Q u i n ta d a M a ri n h a, co n s olid a n d o -a c om o d e
'!"( )*+%, ( -. ) #) 01)0) 2! ' 3.!1(,,, ".6 )) -2 7! 6)) " ) 6 #$ ))!" 6) 8 "9 :# $ ( -;!: (2. ) # )
 !" #$%&& #% 1 !"# $%& '!"( )*+%, ( -. ) #) /)01 01)0) 2! ' 3.!1(,,, " 44425"2.6 )) -2 7! 6)) " ) 6 #$ ))!" 6) 4442$ ))2 8 "9 :# $ ( -;!: (2. ) # ) 44425"2 ))!)) 2() )! ()?"?@! A ))B " > - > )A! 2CDE)
!" #$%&& #% 1 !"# $%& '!"( )*+%, ( -. ) #) /)01 01)0) 2! ' 3.!1(,,, " 44425"2.6 )) -2 7! 6)) " ) 6 #$ ))!" 6) 4442$ ))2 8 "9 :# $ ( -;!: (2. ) # ) 44425"2 ))!)) 2() )! ()?"?@! A ))B " > - > )A! 2CDE)
Amostragem de sinais contínuos
 Amoragm inai conínuo 0.8 0.6 0.4 0. 0 0 0. 0. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 SS MIEIC 008/009 Programa SS Sinai Sima aula Sima Linar Invarian aula Análi Fourir (mpo conínuo 3 aula Análi Fourir (mpo icro aula
Amoragm inai conínuo 0.8 0.6 0.4 0. 0 0 0. 0. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 SS MIEIC 008/009 Programa SS Sinai Sima aula Sima Linar Invarian aula Análi Fourir (mpo conínuo 3 aula Análi Fourir (mpo icro aula
A solução mais geral da equação anterior tem a forma: α 2 2. Aplicando estes resultados na equação do MHS, temos que:
 . qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
. qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
MATEMÁTICA ATUARIAL DE VIDA Modelos de Sobrevivência
 EAC 44 Maáica Auaria II Ciêcia Auariai Nouro FEA USP Prof. Dr. Ricaro Pachco MAEMÁICA AUARIAL DE VIDA Moo Sobrvivêcia Uivria São Pauo º Sr 5 A ábua oraia u oo icro obrvivêcia. Daa a ábua Moraia hipoéica:
EAC 44 Maáica Auaria II Ciêcia Auariai Nouro FEA USP Prof. Dr. Ricaro Pachco MAEMÁICA AUARIAL DE VIDA Moo Sobrvivêcia Uivria São Pauo º Sr 5 A ábua oraia u oo icro obrvivêcia. Daa a ábua Moraia hipoéica:
# D - D - D - - -
 1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
O P a pel da M ídia no C o ntro le da s P o lític a s de S a úde
 B ra s ília, 26 de s etem bro de 2009 C o ntro le da s P o lític a s de L uiz R ibeiro FU N Ç Ã O D O J O R N A L I S M O J o r n a lis m o é a a tiv id a d e p r o fis s io n a l q u e c o n s is te e
B ra s ília, 26 de s etem bro de 2009 C o ntro le da s P o lític a s de L uiz R ibeiro FU N Ç Ã O D O J O R N A L I S M O J o r n a lis m o é a a tiv id a d e p r o fis s io n a l q u e c o n s is te e
PATR IMÔNIO PALEONTOLÓG IC O
 PATR IMÔNIO PALEONTOLÓG IC O O s depós itos fos s ilíferos, o s s ítios paleontológ icos (paleobiológicos ou fossilíferos) e o s fós s eis q u e a p r e s e n ta m valores científico, educativo o u cultural
PATR IMÔNIO PALEONTOLÓG IC O O s depós itos fos s ilíferos, o s s ítios paleontológ icos (paleobiológicos ou fossilíferos) e o s fós s eis q u e a p r e s e n ta m valores científico, educativo o u cultural
1. A TRANSFORMADA DE LAPLACE
 Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Repetindo a mesma nota. - le - ne - men - te a. trom. rar. mes. trom. mes. rar. trom. rar. mes. trom. rar. mes
 Repetindo a mesma nota A B A mes C mes D mes A A mes A trom pa to ma no trom pa to ma no trom pa to ma no trom pa to ma no ca so ta sem ca so ta sem ca so ta sem ca so ta sem le ne men te a pa rar. le
Repetindo a mesma nota A B A mes C mes D mes A A mes A trom pa to ma no trom pa to ma no trom pa to ma no trom pa to ma no ca so ta sem ca so ta sem ca so ta sem ca so ta sem le ne men te a pa rar. le
Matemática / Física. Figura 1. Figura 2
 Matemática / Fíica SÃO PAULO: CAPITAL DA VELOCIDADE Diveo título foam endo atibuído à cidade de São Paulo duante eu mai de 00 ano de fundação, como, po exemplo, A cidade que não pode paa, A capital da
Matemática / Fíica SÃO PAULO: CAPITAL DA VELOCIDADE Diveo título foam endo atibuído à cidade de São Paulo duante eu mai de 00 ano de fundação, como, po exemplo, A cidade que não pode paa, A capital da
ALFANDEGATUR - EMP.DESENV.TURIST.DE ALF.DA FE EM
 Cn t - 31. 05. 2014 Me s : Ma r ç o Pag. 1 11 CA I XA 41, 0 14. 63 37, 080. 00 3, 9 34. 6 3 111 Ca i x a 6, 0 47. 50 4, 449. 54 1, 5 97. 9 6 112 Ca i x a Fa c t u r a ç ão 34, 7 92. 13 32, 630. 46 2, 1
Cn t - 31. 05. 2014 Me s : Ma r ç o Pag. 1 11 CA I XA 41, 0 14. 63 37, 080. 00 3, 9 34. 6 3 111 Ca i x a 6, 0 47. 50 4, 449. 54 1, 5 97. 9 6 112 Ca i x a Fa c t u r a ç ão 34, 7 92. 13 32, 630. 46 2, 1
Correção da fuvest ª fase - Matemática feita pelo Intergraus
 da fuvest 009 ª fase - Matemática 08.0.009 MATEMÁTIA Q.0 Na figura ao lado, a reta r tem equação y x no plano cartesiano Oxy. Além dis so, os pontos 0,,, estão na reta r, sendo 0 = (0,). Os pontos A 0,
da fuvest 009 ª fase - Matemática 08.0.009 MATEMÁTIA Q.0 Na figura ao lado, a reta r tem equação y x no plano cartesiano Oxy. Além dis so, os pontos 0,,, estão na reta r, sendo 0 = (0,). Os pontos A 0,
III - GABARITO LISTA SALA
 cício ião Li Fíic - GBTO LST SL oáic Foç éic, po éico, Ponci, pciânci, on iênci éic Pof. D. áuio S. Soi www.cuio.oi.no.b cu@uo.co.b. cício Soução: ()..5 pf (b).5 pf p.,5 ncon foç qu u cg cooc cono, c u
cício ião Li Fíic - GBTO LST SL oáic Foç éic, po éico, Ponci, pciânci, on iênci éic Pof. D. áuio S. Soi www.cuio.oi.no.b cu@uo.co.b. cício Soução: ()..5 pf (b).5 pf p.,5 ncon foç qu u cg cooc cono, c u
Plano de Aulas. Matemática. Módulo 18 Introdução à geometria espacial
 lno de ul Memáic Módulo 18 Inodução à geomei epcil Reolução do eecício popoo Reomd do conceio ÍTULO 1 1 ) Não. b) Sim. O ê pono deeminm o plno que o conêm. c) Não peence. d) Infinio pono. O pono, e I e
lno de ul Memáic Módulo 18 Inodução à geomei epcil Reolução do eecício popoo Reomd do conceio ÍTULO 1 1 ) Não. b) Sim. O ê pono deeminm o plno que o conêm. c) Não peence. d) Infinio pono. O pono, e I e
CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA DE SÃO PAULO CEFET SP
 Diciplina: Mecânica do Fluido Aplicada Lita de Exercício Reolvido Profeor: 1 de 11 Data: 13/0/08 Caruo 1. Um menino, na tentativa de melhor conhecer o fundo do mar, pretende chegar a uma profundidade de
Diciplina: Mecânica do Fluido Aplicada Lita de Exercício Reolvido Profeor: 1 de 11 Data: 13/0/08 Caruo 1. Um menino, na tentativa de melhor conhecer o fundo do mar, pretende chegar a uma profundidade de
Módulo 6: Conteúdo programático Estudo da perda de carga distribuída Bibliografia: Bunetti, F. Mecânica dos Fluidos, São Paulo, Prentice Hall, 2007.
 Módulo 6: Contúdo programático Etudo da prda d carga ditribuída Bibliografia: Buntti, F. Mcânica do Fluido, São Paulo, Prntic Hall, 2007. PERDA DE CARGA DISTRIBUÍDA NO ESCOAMENTO Turbulnto Cao 2 O tudo
Módulo 6: Contúdo programático Etudo da prda d carga ditribuída Bibliografia: Buntti, F. Mcânica do Fluido, São Paulo, Prntic Hall, 2007. PERDA DE CARGA DISTRIBUÍDA NO ESCOAMENTO Turbulnto Cao 2 O tudo
Sistemas e Sinais (LEIC) Resposta em Frequência
 Sismas Siais (LEIC Rsposa m Frquêcia Carlos Cardira Diaposiivos para acompahamo da bibliografia d bas (Srucur ad Irpraio of Sigals ad Sysms, Edward A. L ad Pravi Varaiya Sumário Dfiiçõs Sismas sm mmória
Sismas Siais (LEIC Rsposa m Frquêcia Carlos Cardira Diaposiivos para acompahamo da bibliografia d bas (Srucur ad Irpraio of Sigals ad Sysms, Edward A. L ad Pravi Varaiya Sumário Dfiiçõs Sismas sm mmória
Análises de sistemas no domínio da frequência
 prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico
prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico
II Funções em IR n. INSTITUTO POLITÉCNICO DE TOMAR Escola Superior de Tecnologia de Tomar. Área Interdepartamental de Matemática Análise Matemática II
 INSTITUTO POLITÉCNICO DE TOMAR Ecola Supio d Tcnologia d Toma Áa Intdpatamntal d Matmática Análi Matmática II II Funçõ m IR n Dtmin o domínio da guint funçõ: b) f ( c) f ( d) f ( ) f ( ln( ln ( ) ) f)
INSTITUTO POLITÉCNICO DE TOMAR Ecola Supio d Tcnologia d Toma Áa Intdpatamntal d Matmática Análi Matmática II II Funçõ m IR n Dtmin o domínio da guint funçõ: b) f ( c) f ( d) f ( ) f ( ln( ln ( ) ) f)
Suporte à Execução. Compiladores. Procedimentos. Árvores de Ativação. Exemplo: o Quicksort. Procedimentos em ação (ativação)
 Supote à Execução Compiladoe Ambiente de upote à execução O Compilado gea código executável. Ma nem tudo etá conhecido ante que o pogama eja executado! Valoe de paâmeto e funçõe, Memóia dinamicamente alocada,
Supote à Execução Compiladoe Ambiente de upote à execução O Compilado gea código executável. Ma nem tudo etá conhecido ante que o pogama eja executado! Valoe de paâmeto e funçõe, Memóia dinamicamente alocada,
FUNDAÇÃO UNIVERSIDADE DE PERNAMBUCO. Relatório Turma/Horário
 B1 SUBTURMA : BM 25 ARQU0001 - ARQUITETURA BIANCA MARIA VASCONCELOS VALERIO* 30 QUA I08 - SALA SENHO 10:30-11:20 11:20-12:10 B2 SUBTURMA : BM 25 ARQU0001 - ARQUITETURA BIANCA MARIA VASCONCELOS VALERIO*
B1 SUBTURMA : BM 25 ARQU0001 - ARQUITETURA BIANCA MARIA VASCONCELOS VALERIO* 30 QUA I08 - SALA SENHO 10:30-11:20 11:20-12:10 B2 SUBTURMA : BM 25 ARQU0001 - ARQUITETURA BIANCA MARIA VASCONCELOS VALERIO*
Código G R$ 51,99 ICMS
 f O V - º37 - MO/JUHO/JULHO/2013 MEO 2013 Vh v E ( ul) 01 04 m x ul/ Há: 14h à 21h 15 18 m ul/ Há: 13h à 20h QUÍMEO L - Ml Quml - p 0-100 mm; - Lu 0,01 mm; - 0,02mm; - 3 õ: - lg/lg, - mm/plg, - z; - u
f O V - º37 - MO/JUHO/JULHO/2013 MEO 2013 Vh v E ( ul) 01 04 m x ul/ Há: 14h à 21h 15 18 m ul/ Há: 13h à 20h QUÍMEO L - Ml Quml - p 0-100 mm; - Lu 0,01 mm; - 0,02mm; - 3 õ: - lg/lg, - mm/plg, - z; - u
... CONTROLADOR DE TEMPERATURA/TEMPORIZADOR COM FUNÇÃO RAMPA E PATAMAR. modelo LWK48 Manual de Instalação 3 - PROCEDIMENTO DE CONFIGURAÇÃO
 M Içõ mp pív : wwwm INTÇÃ N IN m f pj p m çã pm, p m m p mgm m q é q pj p mm, m xõ é M m m m q q p g í: ) v fá ) Nã v m vçõ mp ) Nã v g v ) Nã v v pç ág f () ) mp m v ) m v v m fx m ( % %) m p m m p m
M Içõ mp pív : wwwm INTÇÃ N IN m f pj p m çã pm, p m m p mgm m q é q pj p mm, m xõ é M m m m q q p g í: ) v fá ) Nã v m vçõ mp ) Nã v g v ) Nã v v pç ág f () ) mp m v ) m v v m fx m ( % %) m p m m p m
œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ αœ œ œ œ œ œ œ œ Υ Β œ œ œ œ αœ
 ANEXO 12 - TRANSCRIÇÃO DO OFÍCIO «FESTA DE STA. MAFALDA V.» P-AR Res. Ms. 017 Ad Vésperas -Antífona - Modo VII - fl. 003r Copista: Fr. Rodrigues das Dores Transcrição: Cátia Silva Al - le - lú - ia, al
ANEXO 12 - TRANSCRIÇÃO DO OFÍCIO «FESTA DE STA. MAFALDA V.» P-AR Res. Ms. 017 Ad Vésperas -Antífona - Modo VII - fl. 003r Copista: Fr. Rodrigues das Dores Transcrição: Cátia Silva Al - le - lú - ia, al
Caminho dos Dados e Atrasos
 Caminho dos Dados e Atrasos Arquiteturas para Alto Desmpenho Prof. pauloac@ita.br Sala 110 Prédio da Computação www.comp.ita.br/~pauloac Pipeline MIPS O MIPS utiliza um pipeline com profundidade 5, porém
Caminho dos Dados e Atrasos Arquiteturas para Alto Desmpenho Prof. pauloac@ita.br Sala 110 Prédio da Computação www.comp.ita.br/~pauloac Pipeline MIPS O MIPS utiliza um pipeline com profundidade 5, porém
1 i n o 3 Outubro de Em celebração aos 73 anos da Aperam, empregados compartilham suas histórias na Empresa
 LG A 1 3 O 2017 Pçã â T ê â ó. C? C ê z? A? A ê! á.6 R... é! E çã 73 A, ó E á.5 F: E N N Sá O ê á Fçã á.2 CCQ Cç 2017 Sá G Tó á.4 Á Cç, z á.8 L é V çã. U ç ã ê á ê í. - Mí S á.8 E I A 1 I P.2 I A 1 I P.3
LG A 1 3 O 2017 Pçã â T ê â ó. C? C ê z? A? A ê! á.6 R... é! E çã 73 A, ó E á.5 F: E N N Sá O ê á Fçã á.2 CCQ Cç 2017 Sá G Tó á.4 Á Cç, z á.8 L é V çã. U ç ã ê á ê í. - Mí S á.8 E I A 1 I P.2 I A 1 I P.3
6.15 EXERCÍCIOS pg. 290
 56 6.5 EXERCÍCOS pg. 9. Da um mplo d uma fução cotíua po pat dfiida o itvalo ] [. Muito mplo podm ciado. Sgu um dl: ) ( - - f - - - - - - 6 8 y. Calcula a itgal da guit fuçõ cotíua po pat dfiida o itvalo
56 6.5 EXERCÍCOS pg. 9. Da um mplo d uma fução cotíua po pat dfiida o itvalo ] [. Muito mplo podm ciado. Sgu um dl: ) ( - - f - - - - - - 6 8 y. Calcula a itgal da guit fuçõ cotíua po pat dfiida o itvalo
! "#" $ %&& ' ( )%*)&&&& "+,)-. )/00*&&& 1+,)-. )/00*&2) (5 (6 7 36 " #89 : /&*&
 ! "#" %&& ' )%*)&&&& "+,)-. )/00*&&& 1+,)-. )/00*&2) 3 4 5 6 7 36 " #89 : /&*& #" + " ;9" 9 E" " """
! "#" %&& ' )%*)&&&& "+,)-. )/00*&&& 1+,)-. )/00*&2) 3 4 5 6 7 36 " #89 : /&*& #" + " ;9" 9 E" " """
Quadro de conteúdos. Eu Gosto M@is Integrado 1 o ano. Lição 1 As crianças e os lugares onde vivem
 Quadro de conteúdos Eu Gosto M@is Integrado 1 o ano Língua Portuguesa Matemática História Geografia Ciências Naturais Arte Inglês ABC da passarinhada O alfabeto Quantidade A ideia de quantidade Eu, criança
Quadro de conteúdos Eu Gosto M@is Integrado 1 o ano Língua Portuguesa Matemática História Geografia Ciências Naturais Arte Inglês ABC da passarinhada O alfabeto Quantidade A ideia de quantidade Eu, criança
Pipelining - analogia
 PIPELINE Pipelining - analogia Pipelining OBJECTIVO: Aumentar o desempenho pelo aumento do fluxo de instruções Program execution Time order (in instructions) lw $1, 100($0) Instruction fetch ALU Data access
PIPELINE Pipelining - analogia Pipelining OBJECTIVO: Aumentar o desempenho pelo aumento do fluxo de instruções Program execution Time order (in instructions) lw $1, 100($0) Instruction fetch ALU Data access
Modelagem de Carga Mecânica
 Univsia Fal Minas Gais Dpatamnto Engnhaia Elética ogama ós-gauação m Engnhaia Elética Molagm Caga Mcânica - Ano: 03 of. Slênio Rocha Silva Dpto. Eng. Elética slnios@.ufmg.b Dinâmica Motos Eléticos - Unia
Univsia Fal Minas Gais Dpatamnto Engnhaia Elética ogama ós-gauação m Engnhaia Elética Molagm Caga Mcânica - Ano: 03 of. Slênio Rocha Silva Dpto. Eng. Elética slnios@.ufmg.b Dinâmica Motos Eléticos - Unia
Divisão silábica e acentuação 7º ano. Professora: Allana Rauana Almeida Cortez.
 Divisão silábica e acentuação 7º ano Professora: Allana Rauana Almeida Cortez. Divisão silábica Divisão silábica Esta aula tem como objetivo revisar as regras gramaticais sobre a divisão silábica. Faremos
Divisão silábica e acentuação 7º ano Professora: Allana Rauana Almeida Cortez. Divisão silábica Divisão silábica Esta aula tem como objetivo revisar as regras gramaticais sobre a divisão silábica. Faremos
Ondas Electromagnéticas
 Facldad d ghaa Odas lcomagécas Op - MI 78 Pogama d Ópca lcomagsmo Facldad d ghaa áls coal vsão alas lcosáca Magosáca 8 alas Odas lcomagécas 6 alas Ópca Goméca 3 alas Fbas Ópcas 3 alas Lass 3 alas Op 78
Facldad d ghaa Odas lcomagécas Op - MI 78 Pogama d Ópca lcomagsmo Facldad d ghaa áls coal vsão alas lcosáca Magosáca 8 alas Odas lcomagécas 6 alas Ópca Goméca 3 alas Fbas Ópcas 3 alas Lass 3 alas Op 78
Correção da Unicamp ª fase - Matemática feita pelo Intergraus
 da Unicamp 010 ª fase - Matemática 13.01.010 UNIAMP 010 - MATEMÁTIA 1. Uma confeitaria produz dois tipos de bo los de fes ta. ada quilograma do bolo do tipo A consome 0, kg de açúcar e 0, kg de farinha.
da Unicamp 010 ª fase - Matemática 13.01.010 UNIAMP 010 - MATEMÁTIA 1. Uma confeitaria produz dois tipos de bo los de fes ta. ada quilograma do bolo do tipo A consome 0, kg de açúcar e 0, kg de farinha.
A va lia ç ã o de R is c o s A plic a da à Q ua lida de em D es envo lvim ento de S o ftw a re
 Rafael Espinha, Msc rafael.espinha@primeup.com.br +55 21 9470-9289 Maiores informações: http://www.primeup.com.br contato@primeup.com.br +55 21 2512-6005 A va lia ç ã o de R is c o s A plic a da à Q ua
Rafael Espinha, Msc rafael.espinha@primeup.com.br +55 21 9470-9289 Maiores informações: http://www.primeup.com.br contato@primeup.com.br +55 21 2512-6005 A va lia ç ã o de R is c o s A plic a da à Q ua
Visão Geral de Pipelining
 Pipeline Visão Geral de Pipelining Instruções MIPS têm mesmo tamanho Mais fácil buscar instruções no primeiro estágio e decodificar no segundo estágio IA-32 Instruções variam de 1 byte a 17 bytes Instruções
Pipeline Visão Geral de Pipelining Instruções MIPS têm mesmo tamanho Mais fácil buscar instruções no primeiro estágio e decodificar no segundo estágio IA-32 Instruções variam de 1 byte a 17 bytes Instruções
 $35(6(17$d 2Ã&/Ë1,&$ 'LDJQyVWLFRÃ FOtQLFR &ROHGRFROLWtDVH &ROHFLVWLWH 3DQFUHDWLWH &ROHGRFROLWtDVH HP UHVROXomR &ROHFLVWLWH 3DQFUHDWLWH &ROHGRFROLWtDVH HP UHVROXomR &yolfdãeloldu (FRJUDILD &ROpGRFRÃ!ÃÃFP
$35(6(17$d 2Ã&/Ë1,&$ 'LDJQyVWLFRÃ FOtQLFR &ROHGRFROLWtDVH &ROHFLVWLWH 3DQFUHDWLWH &ROHGRFROLWtDVH HP UHVROXomR &ROHFLVWLWH 3DQFUHDWLWH &ROHGRFROLWtDVH HP UHVROXomR &yolfdãeloldu (FRJUDILD &ROpGRFRÃ!ÃÃFP
=================== & 2 4 π «2. l l l. l l l l. Ó l. =================== & 2 l. l l l l l l l
 PIPOCA MODERNA aim omo o Caeano enore anarão numa região grave 2 4 π 2 3 k k k k k π 4 k k k k k 5 emper imie repeir ee 2 ompao q 70 2 aé o ompao 20, om peruão 4 bem eve quae inaudíve, Ó FÁBRICA DE ARRANJOS
PIPOCA MODERNA aim omo o Caeano enore anarão numa região grave 2 4 π 2 3 k k k k k π 4 k k k k k 5 emper imie repeir ee 2 ompao q 70 2 aé o ompao 20, om peruão 4 bem eve quae inaudíve, Ó FÁBRICA DE ARRANJOS
PROJETOHORTAEMCASA. Manualdo. Apoio. Realização CDHU PREFEITUR A DE SÃO PAULO VERDE E MEIO AMBIENTE. Instituto GEA
 M RJETHRTAEMCAA CM LANTAR E CLHER ALIMENT EM CAA 201 A Rzçã Ch Dvv Hb Ub CDHU I GEA é b REFEITUR A DE Ã AUL VERDE E MEI AMBIENTE FhTé Ebçã Tx Agô Jé Lz Ch T Nh Rh Rvã A M Dg Lz Egá j Nh Rh Rq L R Rf Tv
M RJETHRTAEMCAA CM LANTAR E CLHER ALIMENT EM CAA 201 A Rzçã Ch Dvv Hb Ub CDHU I GEA é b REFEITUR A DE Ã AUL VERDE E MEI AMBIENTE FhTé Ebçã Tx Agô Jé Lz Ch T Nh Rh Rvã A M Dg Lz Egá j Nh Rh Rq L R Rf Tv
Microcilindros. Duplo efeito: ø4 / Haste recolhida : ø2.5, ø4. Haste simples 2.5. n. recolhida. Como encomendar/duplo efeito.
 Micocilindos Duplo fio: ø / Has colhida : ø, ø Vaiaçõs Séi Funcionamno sandad B Básica mm Duplo fio Simpls Efio Has simpls Has simpls n. colhida sandad, Como ncomnda/duplo fio CJ1B U sandad do cilindo
Micocilindos Duplo fio: ø / Has colhida : ø, ø Vaiaçõs Séi Funcionamno sandad B Básica mm Duplo fio Simpls Efio Has simpls Has simpls n. colhida sandad, Como ncomnda/duplo fio CJ1B U sandad do cilindo
NPQV Variável Educação Prof. Responsáv el : Ra ph a el B i c u d o
 NPQV Variável Educação Prof. Responsáv v el :: Ra ph aa el BB ii cc uu dd o ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO 2º Semestre de 2003 ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO As atividades realizadas
NPQV Variável Educação Prof. Responsáv v el :: Ra ph aa el BB ii cc uu dd o ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO 2º Semestre de 2003 ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO As atividades realizadas
Operações comuns em transportes
 paçõ cmu m tapt Ex Wk (EXW) : aplica- a qualqu mdal d tapt; b ã tgu a dpdêcia d vdd (igm), m cagamt, ã ã dmbaaçad paa xptaçã. = ic = ut Vdd mpad ai (A): aplica- a qualqu mdal d tapt; b ã tgu a taptad digad
paçõ cmu m tapt Ex Wk (EXW) : aplica- a qualqu mdal d tapt; b ã tgu a dpdêcia d vdd (igm), m cagamt, ã ã dmbaaçad paa xptaçã. = ic = ut Vdd mpad ai (A): aplica- a qualqu mdal d tapt; b ã tgu a taptad digad
