CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS
|
|
|
- Regina de Oliveira Porto
- 8 Há anos
- Visualizações:
Transcrição
1 CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS. Moivaçõe Como vio o Regulado de Eado maném o iema em uma deeminada condição de egime pemanene, ou eja, ena mane o eado em uma dada condição eacionáia. Siema Sevo ão feio paa egui comando efeência. Em um iema evo deeja-e que a aída do iema ejam iguai à ua efeência comando, ou eja:, paa. A queão que uge é: Como fae um iema evo com um conolado po ealimenação de eado?. Regulado de eado No egulado de eado a efeência paa a aída do iema ão iguai a eo:, paa. Lei de conole do egulado: u. 3 No egulado de eado não eie inal de eo. Euua de um Regulado de Eado: C Y R U B ϕ X Noe que: φ I A e aumiu-e D.
2 3. Siema evo Dado um iema LIT na foma: & A Bu C Du 4 onde R n, u R m e R p. Aume-e que o iema A, B eja conolável e A, C eja obevável. O iema evo é obido modificando o egulado de eado paa anfoma o egulado em um iema evo é neceáio inodui epliciamene o inal de eo, e: e. 5 Pimeiamene em que edefini o veo de eado do iema de foma que a aída do iema ejam o pimeio eado do veo, ou eja, o veo de eado deve e a eguine foma: ', 6 onde é um veo de dimenão np que coném o eado do iema que não ão aída. Em geal ea anfomação do veo de eado é ivial. Conudo em alguma iuaçõe pode e neceáio uilia a Teoia de Tanfomaçõe Lineae via na aula 6. Dado o iema anfomado: &' A' ' B'u C'' Du 7 onde A, B, C e D ão a maie do iema com o novo eado. Noa-e que a mai C em a eguine foma: [ I pp n p p ] pn C' 8 O eado que não ão aída podem e obido faendo-e: C', 9
3 onde [ n p p n p n p ] n p n C I. A lei de conole do egulado eq. 3 é eecia como: ou [ ] u ' u, onde em dimenão mn, em dimenão mp e em dimenão mnp. Inoduindo o inal de efeência a lei de conole fica: e u. 3 Euua de um Siema Sevo: D R E U B ϕ X C Y X C Onde φ' I A'. Malha fechada do iema evo: Inoduindo a lei de conole eq. 3 na eq. 7 em-e: ou, &' A' ' B' C'' D [ ] [ ] ; 4
4 [ ] [ ] B' D C'' B' B' ' A' ' &. 5 Ma em-e que: '. 6 Poano, em-e a malha fechada do iema evo: D D ' C' B' ' A B' B' ' A' ' mf &. 7 Em geal no iema dinâmico a mai D, nee cao o iema evo fica: C'' B' ' A ' mf &. 8 Obevaçõe: A mai da malha fechada do iema evo é igual à do egulado de eado poano a dinâmica do iema evo é igual à dinâmica do egulado; Ee iema evo não gaane que. Poque? 4. Eemplo Eemplo : Siema SISO. Dado o eguine iema SISO: [ ] u & Pimeio deve-e edefini o veo de eado de foma que o eu pimeio elemeno eja a aída do iema, poano: T ' ' A mai de anfomação linea é dada po:
5 T Com o novo veo de eado o iema é dado po: ' CT B u T ' AT T &' o que eula em: [ ] u ' &' Conolabilidade do iema: an c c M M o iema é conolável. Pólo do iema: j ± de de, λ A' I Obeva-e que o iema é inável. Zeo do iema: de O iema poui um eo no emiplano dieio iema é de fae não mínima. Conolado po ealimenação do eado: [ ] u ' Mai da malha fechada: [ ] B A A mf
6 Pólo da malha fechada: de I A de mf Pólo da malha fechada paa e e um iema com compoameno padão Beel com empo de aenameno de egundo: λ 4,53 ±,34 j,65, ±,7 j Equação caaceíica deejada paa a malha fechada é apoimadamene dada po:,65,7 j,65,7 j 4 5,5. Compaando a equação caaceíica deejada com a equação caaceíica em função do ganho do conolado, em-e: 5,5 4 9,5 3,5 Lei de conole do egulado u 3,5' 9,5'. Tanfomando o egulado em evo lei de conole do iema evo: 9,5' u 3,5. Mai da malha fechada 5,5,5 A mf. 5,5 9,5 Dinâmica do evo & ' Amf ' B' C'' 5,5,5 3,5 ' & ' 5,5 9,5 3,5 [ ] Modelo da malha fechada no Simulin:
7 Refeencia Enada Eado Refeencia Somado 3.5 Somado ' ABu CDu Plana *u C Saida 9.5 C *u Repoa do iema evo paa um comando na foma de degau: Refeência Saída Eado.5 Ampliude Tempo egundo Obevaçõe: O eo em egime é difeene de eo; A aída eponde inicialmene em dieção opoa ao eu valo final iema fae não mínima. Eemplo : Siema MIMO. Dado o eguine iema SISO:
8 u u & Veificando a conolabilidade do iema: an 4 c c M M o iema é conolável. Pólo do iema: j ± de de, λ A' I Obeva-e que o iema é inável. Zeo do iema: de O iema poui um eo na oigem iema poui um difeenciado. Conolado po ealimenação do eado: u Mai da malha fechada: B A A mf. Pólo da malha fechada: de de mf A I
9 Pólo da malha fechada paa e e um iema com compoameno ipo Beel com empo de aenameno de egundo: λ 4,53 ±,34 j,65, ±,7 j Equação caaceíica deejada paa a malha fechada é apoimadamene dada po:,65,7 j,65,7 j 4 5,5. Compaando a equação caaceíica deejada com a equação caaceíica em função do ganho do conolado, em-e: 4 5,5 Tem-e equaçõe e 4 ganho omene ganho ão neceáio paa localia pólo. Adoando, em-e 4 5, Lei de conole do egulado:,75 u,75 6 6, Tanfomando o egulado em um evo: Como a aída do iema ão o doi eado paa anfoma o egulao em evo baa oca na lei de conole do egulado o eado pelo doi eo: u,75e,75 u 6e 6 Maie da malha fechada:.
10 4 5,5 6 mf A ;,75 6,75 D C C mf Dinâmica do evo: 6,75,75 6,75 4 5,5 & ou,75,75 6 3,5 4 5,5 & Noe que no cao e. Modelo da malha fechada no Simulin: Somado Somado Saida Refeencia Ref Ref Plana ' ABu CDu *u Eado Eo Enada C *u C *u Repoa do iema evo paa um comando na foma de degau e, paa :
11 3.5 Ref Ref Saída Saída Ampliude Tempo egundo Obevaçõe: O eo em egime ão difeene de eo; A aída eponde inicialmene em dieção opoa ao eu valo final iema fae não mínima. 3 A aída ofe um alo em peença do eo em. 5. Eecício Dado iema na foma de epaço do eado abaio: & 3. u ; Pede-e em ua o Malab a meno onde indicado: a Redefina o eado do iema de foma a coloca a dua aída do iema como endo o doi pimeio eado.
12 b Calcule o auovaloe e auoveoe do iema ue o Malab. c Calcule o eo do iema ue o Malab. d Veifique a conolabilidade e obevabilidade do iema ue o ee cláico. e Calcule o ganho do conolado po ealimenação de eado de foma que a malha fechada enha compoameno padão Beel com empo de aenameno de,5 egundo. f Tanfome o egula pojeado no iem e em um iema evo, ou eja, eceva a dinâmica da malha fechada na foma do epaço do eado. g Faça um modelo no Simulin paa imula o iema evo pojeado. h Simule o iema evo paa um veo de comando vaiando na foma de degau uniáio. Veifique o eo em egime pemanene ue o Malab. i O iema evo apeena a dinâmica epeada de um iema padão Beel? Juifique. Seja o avião F8 cuja dinâmica longiudinal é dada po:,5 &,854,5,94,8,57,344,4,6 9,5,6 u,5,87 Pede-e uando o Malab: a Pojee um egulado paa o iema uando a écnica de localiação de pólo. Localie o pólo de acodo com um iema ipo ITAE com empo de aenameno % meno do que egundo. b Tanfome o egulado em um evo. Calcule a maie da malha fechada do iema. c Faça um modelo no Simulin paa imula o iema evo pojeado. d Simule com o evo um anióio que ealia um comando vaiando na foma de degau a efeência de θ de o paa º e a efeência de γ de o paa o. e Veifique como ficou a dinâmica do iema em malha fechada calculando e analiando o auovaloe, o auoveoe e o eo do iema em malha fechada. f Qual é o eo de egime da dua aída? Comena e juifica. g O iema evo apeena a dinâmica epeada de um iema padão ITAE? Juifique.
CONTROLE INTEGRAL POR REALIMENTAÇÃO DOS ESTADOS
 ONTROLE INTEGRL POR RELIMENTÇÃO OS ESTOS. Moiaçõe Em geal a aída de m iema eo aeenam eo de egime difeene de zeo. Em geal a eecificaçõe aa m iema eo eigem qe o eo de egime ejam igai a zeo aa a aída do iema.
ONTROLE INTEGRL POR RELIMENTÇÃO OS ESTOS. Moiaçõe Em geal a aída de m iema eo aeenam eo de egime difeene de zeo. Em geal a eecificaçõe aa m iema eo eigem qe o eo de egime ejam igai a zeo aa a aída do iema.
ESPAÇO VETORIAL REAL DE DIMENSÃO FINITA
 EPÇO ETORIL REL DE DIMENÃO FINIT Defnção ejam um conjuno não ao o conjuno do númeo ea R e dua opeaçõe bnáa adção e mulplcação po ecala : : R u a u a é um Epaço eoal obe R ou Epaço eoal Real ou um R-epaço
EPÇO ETORIL REL DE DIMENÃO FINIT Defnção ejam um conjuno não ao o conjuno do númeo ea R e dua opeaçõe bnáa adção e mulplcação po ecala : : R u a u a é um Epaço eoal obe R ou Epaço eoal Real ou um R-epaço
Edital Nº. 04/2009-DIGPE 10 de maio de 2009
 Caderno de Prova CONTROLE DE PROCESSOS Edial Nº. /9-DIPE de maio de 9 INSTRUÇÕES ERAIS PARA A REALIZAÇÃO DA PROVA Ue apena canea eferográfica azul ou prea. Ecreva o eu nome compleo e o número do eu documeno
Caderno de Prova CONTROLE DE PROCESSOS Edial Nº. /9-DIPE de maio de 9 INSTRUÇÕES ERAIS PARA A REALIZAÇÃO DA PROVA Ue apena canea eferográfica azul ou prea. Ecreva o eu nome compleo e o número do eu documeno
F, V, V, F, V, F, V, V
 GOMTRI Reoluçõe apíulo 1 Geomeia de poição TIIS PR SL PÁG. 14 01 a) Poulado, poi o poulado ão conaaçõe que não neceiam e compovada paa que ejam conideada vedadeia. b) Pono, ea e plano. c) Teoema. 0 omo
GOMTRI Reoluçõe apíulo 1 Geomeia de poição TIIS PR SL PÁG. 14 01 a) Poulado, poi o poulado ão conaaçõe que não neceiam e compovada paa que ejam conideada vedadeia. b) Pono, ea e plano. c) Teoema. 0 omo
5. Transformada de Laplace
 Sinai e Siema - 5. Tanfomada de Laplace A Tanfomada de Laplace é uma impoane feamena paa a eolução de equaçõe difeenciai. Também é muio úil na epeenação e análie de iema. É uma anfomação que faz um mapeameno
Sinai e Siema - 5. Tanfomada de Laplace A Tanfomada de Laplace é uma impoane feamena paa a eolução de equaçõe difeenciai. Também é muio úil na epeenação e análie de iema. É uma anfomação que faz um mapeameno
GPS. UNIVERSIDADE FEDERAL DO PARANÁ Curso de Engenharia Cartográfica. Professor Dr. SÍLVIO ROGÉRIO CORREIA DE FREITAS HENRY MONTECINO
 UNIVERSIDDE FEDERL DO PRNÁ Cuo de Engenhaia Caogáfica GPS Pofeo D. SÍLVIO ROGÉRIO CORREI DE FREITS luno HENRY MONTECINO MRLY TEREZINH QUDRI SIMÕES D SILV NVSTR-GPS (NVigaion Saellie wih Time nd Ranging)
UNIVERSIDDE FEDERL DO PRNÁ Cuo de Engenhaia Caogáfica GPS Pofeo D. SÍLVIO ROGÉRIO CORREI DE FREITS luno HENRY MONTECINO MRLY TEREZINH QUDRI SIMÕES D SILV NVSTR-GPS (NVigaion Saellie wih Time nd Ranging)
Capítulo 1 ATIVIDADES PROPOSTAS PÁG. 14 ATIVIDADES PARA SALA PÁG. 14 GEOMETRIA. Geometria de posição. 2 a série Ensino Médio Livro 1 9.
 Reoluçõe 01 a) Poulado, poi o poulado ão conaaçõe que não neceiam e compovada paa que ejam conideada vedadeia. ) Pono, ea e plano. c) Teoema. 0 apíulo 1 Geomeia de poição TIIS PR SL PÁG. 14 omo o polongameno
Reoluçõe 01 a) Poulado, poi o poulado ão conaaçõe que não neceiam e compovada paa que ejam conideada vedadeia. ) Pono, ea e plano. c) Teoema. 0 apíulo 1 Geomeia de poição TIIS PR SL PÁG. 14 omo o polongameno
CONTROLABILIDADE E OBSERVABILIDADE
 Eduardo obo uoa Cabral CONTROABIIDADE E OBSERVABIIDADE. oiação Em um iema na forma do epaço do eado podem exiir dinâmica que não ão ia pela aída do iema ou não ão influenciada pela enrada do iema. Se penarmo
Eduardo obo uoa Cabral CONTROABIIDADE E OBSERVABIIDADE. oiação Em um iema na forma do epaço do eado podem exiir dinâmica que não ão ia pela aída do iema ou não ão influenciada pela enrada do iema. Se penarmo
TENSÕES E CORRENTES TRANSITÓRIAS E TRANSFORMADA LAPLACE
 TNSÕS CONTS TANSTÓAS TANSFOMADA D APAC PNCPAS SNAS NÃO SNODAS Degrau de ampliude - É um inal que vale vol para < e vale vol, conane, para >. Ver fig. -a. v (a) (b) v Fig. A fig. -b mora um exemplo da geração
TNSÕS CONTS TANSTÓAS TANSFOMADA D APAC PNCPAS SNAS NÃO SNODAS Degrau de ampliude - É um inal que vale vol para < e vale vol, conane, para >. Ver fig. -a. v (a) (b) v Fig. A fig. -b mora um exemplo da geração
v t Unidade de Medida: Como a aceleração é dada pela razão entre velocidade e tempo, dividi-se também suas unidades de medida.
 Diciplina de Fíica Aplicada A / Curo de Tecnólogo em Geão Ambienal Profeora M. Valéria Epíndola Lea. Aceleração Média Já imo que quando eamo andando de carro em muio momeno é neceário reduzir a elocidade,
Diciplina de Fíica Aplicada A / Curo de Tecnólogo em Geão Ambienal Profeora M. Valéria Epíndola Lea. Aceleração Média Já imo que quando eamo andando de carro em muio momeno é neceário reduzir a elocidade,
Plano de Aulas. Matemática. Módulo 18 Introdução à geometria espacial
 lno de ul Memáic Módulo 18 Inodução à geomei epcil Reolução do eecício popoo Reomd do conceio ÍTULO 1 1 ) Não. b) Sim. O ê pono deeminm o plno que o conêm. c) Não peence. d) Infinio pono. O pono, e I e
lno de ul Memáic Módulo 18 Inodução à geomei epcil Reolução do eecício popoo Reomd do conceio ÍTULO 1 1 ) Não. b) Sim. O ê pono deeminm o plno que o conêm. c) Não peence. d) Infinio pono. O pono, e I e
Exercícios propostos
 Eecícios poposos 01 Esceva uma equação da ea nos casos a segui a) passa pelo pono P(, 1,) e em a dieção do veo u (,1,1 ) b) passa pelos ponos A(1,, 1) e B(0,,) 0 Veifique, em cada um dos iens abaio, se
Eecícios poposos 01 Esceva uma equação da ea nos casos a segui a) passa pelo pono P(, 1,) e em a dieção do veo u (,1,1 ) b) passa pelos ponos A(1,, 1) e B(0,,) 0 Veifique, em cada um dos iens abaio, se
Análise Matemática IV
 Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 2ª LISTA DE EXERCÍCIOS. (Atualizada em abril de 2009)
 ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Pofesso : Humbeo Anônio Baun d Azevedo ª LISTA DE EXERCÍCIOS (Aualizada em abil de 009 1 Dados A (1, 0, -1, B (, 1,, C (1, 3, 4 e D (-3, 0, 4 Deemina: a
ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Pofesso : Humbeo Anônio Baun d Azevedo ª LISTA DE EXERCÍCIOS (Aualizada em abil de 009 1 Dados A (1, 0, -1, B (, 1,, C (1, 3, 4 e D (-3, 0, 4 Deemina: a
Campo Gravítico da Terra
 Campo Gavítico da ea 1. Condiçõe de medição eodéica O intumento com que ão efectuada a mediçõe eodéica, obe a upefície da ea, etão ujeito à foça da avidade. Paa pode intepeta coectamente o eultado da mediçõe,
Campo Gavítico da ea 1. Condiçõe de medição eodéica O intumento com que ão efectuada a mediçõe eodéica, obe a upefície da ea, etão ujeito à foça da avidade. Paa pode intepeta coectamente o eultado da mediçõe,
ESPAÇO VETORIAL REAL DE DIMENSÃO FINITA
 EPÇO ETORIL REL DE DIMENÃO FINIT Defnção ejam um conjuno não vao o conjuno do númeo ea R e dua opeaçõe bnáa adção e mulplcação po ecala : : R v u a v u v a v é um Epaço eoal obe R ou Epaço eoal Real ou
EPÇO ETORIL REL DE DIMENÃO FINIT Defnção ejam um conjuno não vao o conjuno do númeo ea R e dua opeaçõe bnáa adção e mulplcação po ecala : : R v u a v u v a v é um Epaço eoal obe R ou Epaço eoal Real ou
Quantas equações existem?
 www2.jatai.ufg.br/oj/index.php/matematica Quanta equaçõe exitem? Rogério Céar do Santo Profeor da UnB - FUP profeorrogeriocear@gmail.com Reumo O trabalho conite em denir a altura de uma equação polinomial
www2.jatai.ufg.br/oj/index.php/matematica Quanta equaçõe exitem? Rogério Céar do Santo Profeor da UnB - FUP profeorrogeriocear@gmail.com Reumo O trabalho conite em denir a altura de uma equação polinomial
Rotor bobinado: estrutura semelhante ao enrolamento de estator. Rotor em gaiola de esquilo
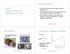 Coente altenada é fonecida ao etato dietamente; Coente altenada cicula no cicuito de oto po indução, ou ação tanfomado; A coente de etato (que poui uma etutua n-fáica) poduzem um campo giante no entefeo;!"
Coente altenada é fonecida ao etato dietamente; Coente altenada cicula no cicuito de oto po indução, ou ação tanfomado; A coente de etato (que poui uma etutua n-fáica) poduzem um campo giante no entefeo;!"
Matemática. Atividades. complementares. FUNDAMENTAL 8-º ano. Este material é um complemento da obra Matemática 8. uso escolar. Venda proibida.
 8 ENSINO FUNMENTL 8-º ano Matemática tividade complementae Ete mateial é um complemento da oba Matemática 8 Paa Vive Junto. Repodução pemitida omente paa uo ecola. Venda poibida. Samuel aal apítulo 6 Ete
8 ENSINO FUNMENTL 8-º ano Matemática tividade complementae Ete mateial é um complemento da oba Matemática 8 Paa Vive Junto. Repodução pemitida omente paa uo ecola. Venda poibida. Samuel aal apítulo 6 Ete
PARNAMIRIM - RN. Data: / / 2016
 PARNAMIRIM - RN Aluno (a) Nº: 8º ano Tuma: Daa: / / 2016 NOTA: Eecício de evião de maemáica II Timee Pofeo (a): Joeane Fenande Agoa vamo coloca em páica o eu conhecimeno maemáico e udo o que eudamo em
PARNAMIRIM - RN Aluno (a) Nº: 8º ano Tuma: Daa: / / 2016 NOTA: Eecício de evião de maemáica II Timee Pofeo (a): Joeane Fenande Agoa vamo coloca em páica o eu conhecimeno maemáico e udo o que eudamo em
ATIVIDADES PROPOSTAS PÁG. 14 ATIVIDADES PARA SALA PÁG. 14. Capítulo 1 GEOMETRIA. Geometria de posição. 2? a série Ensino Médio Livro?
 GOMTRI Reoluçõe píulo 1 Geomei de poição TIIS PR SL PÁG. 14 01 ) Pouldo, poi o pouldo ão conçõe que não neceim e compovd p que ejm conided veddei. b) Pono, e e plno. c) Teoem. 0 omo o polongmeno é infinio
GOMTRI Reoluçõe píulo 1 Geomei de poição TIIS PR SL PÁG. 14 01 ) Pouldo, poi o pouldo ão conçõe que não neceim e compovd p que ejm conided veddei. b) Pono, e e plno. c) Teoem. 0 omo o polongmeno é infinio
75$%$/+2(327(1&,$/ (/(75267È7,&2
 3 75$%$/+(37(&,$/ (/(7567È7,& Ao final deste capítulo você deveá se capa de: ½ Obte a epessão paa o tabalho ealiado Calcula o tabalho que é ealiado ao se movimenta uma caga elética em um campo elético
3 75$%$/+(37(&,$/ (/(7567È7,& Ao final deste capítulo você deveá se capa de: ½ Obte a epessão paa o tabalho ealiado Calcula o tabalho que é ealiado ao se movimenta uma caga elética em um campo elético
Movimentos bi e tridimensional 35 TRIDIMENSIONAL
 Moimenos bi e idimensional 35 3 MOVIMENTOS BI E TRIDIMENSIONAL 3.1 Inodução O moimeno unidimensional que imos no capíulo aneio é um caso paicula de uma classe mais ampla de moimenos que ocoem em duas ou
Moimenos bi e idimensional 35 3 MOVIMENTOS BI E TRIDIMENSIONAL 3.1 Inodução O moimeno unidimensional que imos no capíulo aneio é um caso paicula de uma classe mais ampla de moimenos que ocoem em duas ou
Matemática / Física. Figura 1. Figura 2
 Matemática / Fíica SÃO PAULO: CAPITAL DA VELOCIDADE Diveo título foam endo atibuído à cidade de São Paulo duante eu mai de 00 ano de fundação, como, po exemplo, A cidade que não pode paa, A capital da
Matemática / Fíica SÃO PAULO: CAPITAL DA VELOCIDADE Diveo título foam endo atibuído à cidade de São Paulo duante eu mai de 00 ano de fundação, como, po exemplo, A cidade que não pode paa, A capital da
Eletrotécnica. Módulo III Parte II - Máquina de Indução. Prof. Sidelmo M. Silva, Dr. Sidelmo M. Silva, Dr.
 1 Eletotécnica Módulo III Pate II - Máquina de Indução Pof. Máquina de Indução ou Máquina Aíncona Tipo de máquina elética otativa mai utilizado Tipo de máquina com contução mai obuta (oto em gaiola quiel
1 Eletotécnica Módulo III Pate II - Máquina de Indução Pof. Máquina de Indução ou Máquina Aíncona Tipo de máquina elética otativa mai utilizado Tipo de máquina com contução mai obuta (oto em gaiola quiel
ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS
 ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS. Intodução O conjunto dos númeos epesentáveis em uma máquina (computadoes, calculadoas,...) é finito, e potanto disceto, ou seja não é possível
ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS. Intodução O conjunto dos númeos epesentáveis em uma máquina (computadoes, calculadoas,...) é finito, e potanto disceto, ou seja não é possível
Modelo Intertemporal da Conta Corrente: Evidências para o Brasil. Resumo
 Modelo Ineempoal da Cona Coene: Evidência paa o Bail Reumo Nelon da Silva * Joaquim P. Andade ** Nee abalho eguimo o pocedimeno de Campbell (987) paa ea a popoição paa o cao baileio de que a cona coene
Modelo Ineempoal da Cona Coene: Evidência paa o Bail Reumo Nelon da Silva * Joaquim P. Andade ** Nee abalho eguimo o pocedimeno de Campbell (987) paa ea a popoição paa o cao baileio de que a cona coene
Seu pé direito nas melhores faculdades. a) Indicando os montantes finais possuídos por Carlos, Luís e Sílvio por C, L e S, respectivamente, temos:
 Seu pé dieio na melhoe faculdade. FUVEST/00 a Fae TEÁTI 0. alo, Luí e Sílvio inham, juno, 00 mil eai paa invei po um ano. alo ecolheu uma aplicação que endia ao ano. Luí, uma que endia 0% ao ano. Sílvio
Seu pé dieio na melhoe faculdade. FUVEST/00 a Fae TEÁTI 0. alo, Luí e Sílvio inham, juno, 00 mil eai paa invei po um ano. alo ecolheu uma aplicação que endia ao ano. Luí, uma que endia 0% ao ano. Sílvio
EAC 0467 Modelagem de Planos de Previdência
 DEPARTAMENTO DE CONTABILIDADE E ATUÁRIA DA FEA/USP Aula 04 Cueio de Plano BD/Cuo Suplemena Ciência Auaiai 2017 Pogama 1. Inodução 2. Cuo Suplemena 3. Aplicaçõe 2 1. Inodução Conceio de Cuo Nomal Cuo Nomal
DEPARTAMENTO DE CONTABILIDADE E ATUÁRIA DA FEA/USP Aula 04 Cueio de Plano BD/Cuo Suplemena Ciência Auaiai 2017 Pogama 1. Inodução 2. Cuo Suplemena 3. Aplicaçõe 2 1. Inodução Conceio de Cuo Nomal Cuo Nomal
Testes para comparação de médias
 7 /03/018 Rtei de Aula Aula 5 Expeimentaçã Ztécnica Pfa. Da. Amanda Liz Pacífic Manfim Peticaai Tete paa cmpaaçã de média Cntate de média: Y = c 1 m 1 + c m + + c I m I e i=1 c i = c 1 + c + +c I = 0 I
7 /03/018 Rtei de Aula Aula 5 Expeimentaçã Ztécnica Pfa. Da. Amanda Liz Pacífic Manfim Peticaai Tete paa cmpaaçã de média Cntate de média: Y = c 1 m 1 + c m + + c I m I e i=1 c i = c 1 + c + +c I = 0 I
01- A figura ABCD é um quadrado de lado 2 cm e ACE um triângulo equilátero. Calcule a distância entre os vértices B e E.
 PROFESSOR: Macelo Soae NO E QUESTÕES - MTEMÁTI - 1ª SÉRIE - ENSINO MÉIO ============================================================================================= GEOMETRI Pae 1 01- figua é um quadado
PROFESSOR: Macelo Soae NO E QUESTÕES - MTEMÁTI - 1ª SÉRIE - ENSINO MÉIO ============================================================================================= GEOMETRI Pae 1 01- figua é um quadado
PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON
 Pofa Stela Maia de Cavalho Fenandes 1 PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON Dinâmica estudo dos movimentos juntamente com as causas que os oiginam. As teoias da dinâmica são desenvolvidas com base no conceito
Pofa Stela Maia de Cavalho Fenandes 1 PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON Dinâmica estudo dos movimentos juntamente com as causas que os oiginam. As teoias da dinâmica são desenvolvidas com base no conceito
Torque Eletromagnético de Máquinas CA. com Entreferro Constante
 1. Intodução Apotila 4 Diciplina de Coneão de Enegia B Toque Eletoagnético de Máquina CA co Entefeo Contante Neta apotila ão abodado o pincipai apecto elacionado co a podução de toque e áquina de coente
1. Intodução Apotila 4 Diciplina de Coneão de Enegia B Toque Eletoagnético de Máquina CA co Entefeo Contante Neta apotila ão abodado o pincipai apecto elacionado co a podução de toque e áquina de coente
NOTAS DE AULA ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA RETAS E PLANOS ERON E ISABEL
 NOTAS DE AULA ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA RETAS E PLANOS ERON E ISABEL SALVADOR BA 7 EQUAÇÃO VETORIAL DA RETA EQUAÇÕES DA RETA DEF: Qualque eto não nulo paalelo a uma eta chama-e eto dieto dea
NOTAS DE AULA ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA RETAS E PLANOS ERON E ISABEL SALVADOR BA 7 EQUAÇÃO VETORIAL DA RETA EQUAÇÕES DA RETA DEF: Qualque eto não nulo paalelo a uma eta chama-e eto dieto dea
a) Calcule a força medida pelo dinamômetro com a chave aberta, estando o fio rígido em equilíbrio.
 UJ MÓDULO III DO PISM IÊNIO - POA DE ÍSICA PAA O DESENOLIMENO E A ESPOSA DAS QUESÕES, SÓ SEÁ ADMIIDO USA CANEA ESEOGÁICA AZUL OU PEA. Na olução da proa, ue, uando neeário, g = /, = 8 /, e = 9 - kg, π =.
UJ MÓDULO III DO PISM IÊNIO - POA DE ÍSICA PAA O DESENOLIMENO E A ESPOSA DAS QUESÕES, SÓ SEÁ ADMIIDO USA CANEA ESEOGÁICA AZUL OU PEA. Na olução da proa, ue, uando neeário, g = /, = 8 /, e = 9 - kg, π =.
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1
 Dcpna: FGE5748 Suação Copuacona de Líqudo Moecuae e 0 0 xx 0 yy 0 0 0 zz e B fxo no copo ou oécua S fxo no epaço xx yx zx xy yy zy xz yz zz e τ ω Ae Aτ A Aω oenação oque ve.angua o. angua Onde A é ua az
Dcpna: FGE5748 Suação Copuacona de Líqudo Moecuae e 0 0 xx 0 yy 0 0 0 zz e B fxo no copo ou oécua S fxo no epaço xx yx zx xy yy zy xz yz zz e τ ω Ae Aτ A Aω oenação oque ve.angua o. angua Onde A é ua az
TEOREMA DE TALES PROF. JOÃO BATISTA
 PROF. JOÃO BATISTA TEOREMA DE TALES Se um feie de paalela deemina egmeno conguene obe uma anveal, enão ee feie deemina egmeno conguene obe qualque oua anveal. Aim, um feie de paalela deemina, em dua anveai
PROF. JOÃO BATISTA TEOREMA DE TALES Se um feie de paalela deemina egmeno conguene obe uma anveal, enão ee feie deemina egmeno conguene obe qualque oua anveal. Aim, um feie de paalela deemina, em dua anveai
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Retas Cortadas por uma Transversal. Oitavo Ano
 Maeial Teóico - Módulo Elemeno áico de Geomeia Plana - Pae 1 Rea oada po uma Tanveal Oiavo no uo: Pof. Ulie Lima Paene Revio: Pof. nonio aminha M. Neo 1 Rea coada po uma anveal Sejam e dua ea iuada em
Maeial Teóico - Módulo Elemeno áico de Geomeia Plana - Pae 1 Rea oada po uma Tanveal Oiavo no uo: Pof. Ulie Lima Paene Revio: Pof. nonio aminha M. Neo 1 Rea coada po uma anveal Sejam e dua ea iuada em
2. MÉTODO DE POSICIONAMENTO RELATIVO 1. INTRODUÇÃO
 Método de poicionamento elativo po atélite GPS com coeção do efeito do multicaminho em etaçõe de efeência: fomulação matemátic eultado e análie Weley Gildo Canducci Polezel Eniuce Meneze de Souza João
Método de poicionamento elativo po atélite GPS com coeção do efeito do multicaminho em etaçõe de efeência: fomulação matemátic eultado e análie Weley Gildo Canducci Polezel Eniuce Meneze de Souza João
CONTROLE LINEAR I. Parte A Sistemas Contínuos no Tempo PROF. DR. EDVALDO ASSUNÇÃO PROF. DR. MARCELO C. M. TEIXEIRA -2013-
 CONTROLE LINEAR I Pare A Siema Conínuo no Tempo PROF. DR. EDVALDO ASSUNÇÃO PROF. DR. MARCELO C. M. TEIXEIRA -03- AGRADECIMENTOS O auore deejam agradecer ao aluno Pierre Goebel, que em uma arde de verão
CONTROLE LINEAR I Pare A Siema Conínuo no Tempo PROF. DR. EDVALDO ASSUNÇÃO PROF. DR. MARCELO C. M. TEIXEIRA -03- AGRADECIMENTOS O auore deejam agradecer ao aluno Pierre Goebel, que em uma arde de verão
Análise Energética para Sistemas Abertos (Volumes de Controles)
 UTFPR Termodinâmica 1 Análie Energéica para Siema Abero (Volume de Conrole) Princípio de Termodinâmica para Engenharia Capíulo 4 Análie Traniene Pare V Operação Traniene É a operação na qual a propriedade
UTFPR Termodinâmica 1 Análie Energéica para Siema Abero (Volume de Conrole) Princípio de Termodinâmica para Engenharia Capíulo 4 Análie Traniene Pare V Operação Traniene É a operação na qual a propriedade
4 Descrição de permutadores
 Aponameno de Pemuadoe de alo Equipameno émico 005 João Luí oe Azevedo 4 ecição de pemuadoe Nea ecção vão deceve-e o pincipai ipo de pemuadoe de calo de conaco indieco com anfeência dieca, ou eja, equipameno
Aponameno de Pemuadoe de alo Equipameno émico 005 João Luí oe Azevedo 4 ecição de pemuadoe Nea ecção vão deceve-e o pincipai ipo de pemuadoe de calo de conaco indieco com anfeência dieca, ou eja, equipameno
Credenciamento Portaria MEC 3.613, de D.O.U
 edenciamento Potaia ME 3.63, de 8..4 - D.O.U. 9..4. MATEMÁTIA, LIENIATURA / Geometia Analítica Unidade de apendizagem Geometia Analítica em meio digital Pof. Lucas Nunes Ogliai Quest(iii) - [8/9/4] onteúdos
edenciamento Potaia ME 3.63, de 8..4 - D.O.U. 9..4. MATEMÁTIA, LIENIATURA / Geometia Analítica Unidade de apendizagem Geometia Analítica em meio digital Pof. Lucas Nunes Ogliai Quest(iii) - [8/9/4] onteúdos
OPÇÕES FINANCEIRAS - Exame
 OPÇÕES FINANCEIRAS - Exame (esolução) /4/6 . (a) Aendendo a que e aplicando o lema de Iô a ln S, enão ST ln q S ds ( q) S d + S d ~ W ; Z T + d W ~ u ; () sendo : T. Na medida de pobabilidade Q, o valo
OPÇÕES FINANCEIRAS - Exame (esolução) /4/6 . (a) Aendendo a que e aplicando o lema de Iô a ln S, enão ST ln q S ds ( q) S d + S d ~ W ; Z T + d W ~ u ; () sendo : T. Na medida de pobabilidade Q, o valo
Alinhamento de Três Pontos
 ANO 0 DISIPLINA: Matemática PROFESSORA): Adiano Lima SERIE/TURMA: o Ano VALOR: ATIVIDADE TRABALHO PROVA PARIAL PROVA FINAL REUPERAÇÃO ETAPA: a Etapa SUPERVISORA: Lânia Rezende DATA: NOTA ALUNOA): N. o
ANO 0 DISIPLINA: Matemática PROFESSORA): Adiano Lima SERIE/TURMA: o Ano VALOR: ATIVIDADE TRABALHO PROVA PARIAL PROVA FINAL REUPERAÇÃO ETAPA: a Etapa SUPERVISORA: Lânia Rezende DATA: NOTA ALUNOA): N. o
MATEMÁTICA - 3o ciclo
 MATEMÁTICA - o ciclo Função afim e equação da eta ( o ano) Eecício de pova nacionai e tete intemédio. No efeencial otogonal e monomético, de oigem no ponto, da figua ao lado, etão epeentada a eta e. A
MATEMÁTICA - o ciclo Função afim e equação da eta ( o ano) Eecício de pova nacionai e tete intemédio. No efeencial otogonal e monomético, de oigem no ponto, da figua ao lado, etão epeentada a eta e. A
UNIVERSIDADE FEDERAL DE SANTA MARIA
 UNVRSDAD FDRAL D SANTA MARA CNTRO D TCNOLOGA Depaameno e uua e Conução Civil XMPLO: VRFCAÇÃO DOS STADOS LMTS D SRVÇO M VGA D CONCRTO ARMADO e exemplo eee-e ao pojeo euual a via V (iua abaixo), e eção 5cm
UNVRSDAD FDRAL D SANTA MARA CNTRO D TCNOLOGA Depaameno e uua e Conução Civil XMPLO: VRFCAÇÃO DOS STADOS LMTS D SRVÇO M VGA D CONCRTO ARMADO e exemplo eee-e ao pojeo euual a via V (iua abaixo), e eção 5cm
Campo magnético criado por uma corrente eléctrica e Lei de Faraday
 Campo magnéico ciado po uma coene elécica e Lei de Faaday 1.Objecivos (Rev. -007/008) 1) Esudo do campo magnéico de um conjuno de espias (bobine) pecoidas po uma coene elécica. ) Esudo da lei de indução
Campo magnéico ciado po uma coene elécica e Lei de Faaday 1.Objecivos (Rev. -007/008) 1) Esudo do campo magnéico de um conjuno de espias (bobine) pecoidas po uma coene elécica. ) Esudo da lei de indução
Transmissão de calor
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenhaia ansmissão de calo 3º ano Pof D. Engº Joge Nhambiu Aula. Equação difeencial de condução de calo Equação difeencial de condução de calo Dedução da equação
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenhaia ansmissão de calo 3º ano Pof D. Engº Joge Nhambiu Aula. Equação difeencial de condução de calo Equação difeencial de condução de calo Dedução da equação
Vestibular 2ª Fase Resolução das Questões Discursivas
 Vesibula ª Fase Resolução das Quesões Discusivas São apesenadas abaixo possíveis soluções paa as quesões poposas Nessas esoluções buscou-se jusifica as passagens visando uma melho compeensão do leio Quesão
Vesibula ª Fase Resolução das Quesões Discusivas São apesenadas abaixo possíveis soluções paa as quesões poposas Nessas esoluções buscou-se jusifica as passagens visando uma melho compeensão do leio Quesão
Suporte à Execução. Compiladores. Procedimentos. Árvores de Ativação. Exemplo: o Quicksort. Procedimentos em ação (ativação)
 Supote à Execução Compiladoe Ambiente de upote à execução O Compilado gea código executável. Ma nem tudo etá conhecido ante que o pogama eja executado! Valoe de paâmeto e funçõe, Memóia dinamicamente alocada,
Supote à Execução Compiladoe Ambiente de upote à execução O Compilado gea código executável. Ma nem tudo etá conhecido ante que o pogama eja executado! Valoe de paâmeto e funçõe, Memóia dinamicamente alocada,
Processamento Digital de Sinal Aula 9 4.º Ano 2.º Semestre
 Intituto Supeio Politénio de Vieu Eola Supeio de enologia de Vieu Cuo de Engenhaia de Sitema e Infomátia Poeamento Digital de Sinal Aula 9 4.º Ano.º Semete, Eng.º 1 SISEMAS DE PROCESSAMENO DIGIAL Pogama:
Intituto Supeio Politénio de Vieu Eola Supeio de enologia de Vieu Cuo de Engenhaia de Sitema e Infomátia Poeamento Digital de Sinal Aula 9 4.º Ano.º Semete, Eng.º 1 SISEMAS DE PROCESSAMENO DIGIAL Pogama:
Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista.
 Cao cusista, Todas as dúvidas deste cuso podem se esclaecidas atavés do nosso plantão de atendimento ao cusista. Plantão de Atendimento Hoáio: quatas e quintas-feias das 14:00 às 15:30 MSN: lizado@if.uff.b
Cao cusista, Todas as dúvidas deste cuso podem se esclaecidas atavés do nosso plantão de atendimento ao cusista. Plantão de Atendimento Hoáio: quatas e quintas-feias das 14:00 às 15:30 MSN: lizado@if.uff.b
Professoras: Lisiane e Suziene. Lista de Conteúdos e Exercícios Preparatórios para Exame Final 2018
 Componente Cuicula: Matemática Ano: 8º Tuma: 18 A, 18B, 18C e 18D Pofeoa: Liiane e Suziene Lita de Conteúdo e Eecício Pepaatóio paa Eame Final 018 1. Geometia. Monômio e Polinômio 3. Fatoação Algébica
Componente Cuicula: Matemática Ano: 8º Tuma: 18 A, 18B, 18C e 18D Pofeoa: Liiane e Suziene Lita de Conteúdo e Eecício Pepaatóio paa Eame Final 018 1. Geometia. Monômio e Polinômio 3. Fatoação Algébica
I~~~~~~~~~~~~~~-~-~ krrrrrrrrrrrrrrrrrr. \fy --~--.. Ação de Flexão
 Placas - Lajes Placas são estutuas planas onde duas de suas tês dimensões -lagua e compimento - são muito maioes do que a teceia, que é a espessua. As cagas nas placas estão foa do plano da placa. As placas
Placas - Lajes Placas são estutuas planas onde duas de suas tês dimensões -lagua e compimento - são muito maioes do que a teceia, que é a espessua. As cagas nas placas estão foa do plano da placa. As placas
5 Cálculo do Diâmetro e Espaçamento entre Estribos Utilizando a Formulação Proposta
 5 Cácuo do Diâmero e Epaçameno enre Erio Uiizando a Formuação ropoa 5.1. Inrodução Nee capíuo apreena-e um criério para o cácuo do diâmero e epaçameno enre erio aravé da formuação propoa e comparam-e o
5 Cácuo do Diâmero e Epaçameno enre Erio Uiizando a Formuação ropoa 5.1. Inrodução Nee capíuo apreena-e um criério para o cácuo do diâmero e epaçameno enre erio aravé da formuação propoa e comparam-e o
RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA 2 o ANO DO ENSINO MÉDIO DATA: 08/03/14 PROFESSOR: MALTEZ
 RSOLUÇÃO VLIÇÃO MTMÁTI o NO O NSINO MÉIO T: 08/03/14 PROFSSOR: MLTZ QUSTÃO 01 Na figua, a eta e ão pependiculae e a eta m e n ão paalela. m 0º n ntão a medida do ângulo, em gau, é igual a: 0º m alteno
RSOLUÇÃO VLIÇÃO MTMÁTI o NO O NSINO MÉIO T: 08/03/14 PROFSSOR: MLTZ QUSTÃO 01 Na figua, a eta e ão pependiculae e a eta m e n ão paalela. m 0º n ntão a medida do ângulo, em gau, é igual a: 0º m alteno
1. O movimento uniforme de uma partícula tem sua função horária representada no diagrama a seguir: e (m) t (s)
 . O moimeno uniforme de uma parícula em ua função horária repreenada no diagrama a eguir: e (m) - 6 7 - Deerminar: a) o epaço inicial e a elocidade ecalar; a função horária do epaço.. É dado o gráfico
. O moimeno uniforme de uma parícula em ua função horária repreenada no diagrama a eguir: e (m) - 6 7 - Deerminar: a) o epaço inicial e a elocidade ecalar; a função horária do epaço.. É dado o gráfico
EOREMA DE TALES. Assim, um feixe de paralelas determina, em duas transversais quaisquer, segmentos proporcionais. Exemplo: Quanto vale x?
 EOREMA DE TALES Se um feixe de paalela deemina egmeno conguene obe uma anveal, enão ee feixe deemina egmeno conguene obe qualque oua anveal. Aim, um feixe de paalela deemina, em dua anveai quaique, egmeno
EOREMA DE TALES Se um feixe de paalela deemina egmeno conguene obe uma anveal, enão ee feixe deemina egmeno conguene obe qualque oua anveal. Aim, um feixe de paalela deemina, em dua anveai quaique, egmeno
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação. Aula 05. Prof. Dr. Marco Antonio Leonel Caetano
 MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação Aula 5 Pof. D. Maco Antonio Leonel Caetano Guia de Estudo paa Aula 5 Poduto Vetoial - Intepetação do poduto vetoial Compaação com as funções
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação Aula 5 Pof. D. Maco Antonio Leonel Caetano Guia de Estudo paa Aula 5 Poduto Vetoial - Intepetação do poduto vetoial Compaação com as funções
Escoamentos Compressíveis. Capítulo 06 Forma diferencial das equações de conservação para escoamentos invíscidos
 Escoamenos Compessíveis Capíulo 06 Foma difeencial das equações de consevação paa escoamenos invíscidos 6. Inodução A análise de poblemas na dinâmica de fluidos eque ês passos iniciais: Deeminação de um
Escoamenos Compessíveis Capíulo 06 Foma difeencial das equações de consevação paa escoamenos invíscidos 6. Inodução A análise de poblemas na dinâmica de fluidos eque ês passos iniciais: Deeminação de um
Equações Básicas na Forma Integral - I. Prof. M. Sc. Lúcio P. Patrocínio
 Fenômenos de Tanspote Equações Básicas na Foma Integal - I Pof. M. Sc. Lúcio P. Patocínio Objetivos Entende a utilidade do teoema de Tanspote de Reynolds. Aplica a equação de consevação da massa paa balancea
Fenômenos de Tanspote Equações Básicas na Foma Integal - I Pof. M. Sc. Lúcio P. Patocínio Objetivos Entende a utilidade do teoema de Tanspote de Reynolds. Aplica a equação de consevação da massa paa balancea
Unidade 13 Noções de Matemática Financeira. Taxas equivalentes Descontos simples e compostos Desconto racional ou real Desconto comercial ou bancário
 Unidade 13 Noções de atemática Financeia Taxas equivalentes Descontos simples e compostos Desconto acional ou eal Desconto comecial ou bancáio Intodução A atemática Financeia teve seu início exatamente
Unidade 13 Noções de atemática Financeia Taxas equivalentes Descontos simples e compostos Desconto acional ou eal Desconto comecial ou bancáio Intodução A atemática Financeia teve seu início exatamente
Interbits SuperPro Web
 1. (Unesp 2013) No dia 5 de junho de 2012, pôde-se obseva, de deteminadas egiões da Tea, o fenômeno celeste chamado tânsito de Vênus, cuja póxima ocoência se daá em 2117. Tal fenômeno só é possível poque
1. (Unesp 2013) No dia 5 de junho de 2012, pôde-se obseva, de deteminadas egiões da Tea, o fenômeno celeste chamado tânsito de Vênus, cuja póxima ocoência se daá em 2117. Tal fenômeno só é possível poque
Mecânica dos Fluidos (MFL0001) CAPÍTULO 4: Equações de Conservação para Tubo de Corrente
 Mecânica do Fluido (MFL000) Curo de Engenharia Civil 4ª fae Prof. Dr. Doalcey Antune Ramo CAPÍTULO 4: Equaçõe de Conervação ara Tubo de Corrente Fonte: Bitafa, Sylvio R. Mecânica do Fluido: noçõe e alicaçõe.
Mecânica do Fluido (MFL000) Curo de Engenharia Civil 4ª fae Prof. Dr. Doalcey Antune Ramo CAPÍTULO 4: Equaçõe de Conervação ara Tubo de Corrente Fonte: Bitafa, Sylvio R. Mecânica do Fluido: noçõe e alicaçõe.
CAPÍTULO 2 DINÂMICA DA PARTÍCULA: FORÇA E ACELERAÇÃO
 13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
Material Teórico - Módulo de Geometria Anaĺıtica 1. Paralelismo e Perpendicularidade. Terceiro Ano - Médio
 Mateial Teóico - Módulo de Geometia naĺıtica 1 Paalelimo e Pependiculaidade Teceio no - Médio uto: Pof ngelo Papa Neto Revio: Pof ntonio aminha M Neto 1 Reta paalela Na aula obe a equação da eta vimo que,
Mateial Teóico - Módulo de Geometia naĺıtica 1 Paalelimo e Pependiculaidade Teceio no - Médio uto: Pof ngelo Papa Neto Revio: Pof ntonio aminha M Neto 1 Reta paalela Na aula obe a equação da eta vimo que,
AULA 2 CONDUÇÃO DE CALOR
 Noas de aula de PME 36 Pocessos de ansfeência de Calo 0 AULA CONDUÇÃO DE CALOR CONDUÇÃO DE CALOR Conduibilidade ou Conduividade éica Da Lei de Fouie da condução de calo e-se ue o fluo de calo é dieaene
Noas de aula de PME 36 Pocessos de ansfeência de Calo 0 AULA CONDUÇÃO DE CALOR CONDUÇÃO DE CALOR Conduibilidade ou Conduividade éica Da Lei de Fouie da condução de calo e-se ue o fluo de calo é dieaene
Condensador esférico Um condensador esférico é constituído por uma esfera interior de raio R e carga
 onensao esféico Um conensao esféico é constituío po uma esfea inteio e aio e caga + e uma supefície esféica exteio e aio e caga. a) Detemine o campo eléctico e a ensiae e enegia em too o espaço. b) alcule
onensao esféico Um conensao esféico é constituío po uma esfea inteio e aio e caga + e uma supefície esféica exteio e aio e caga. a) Detemine o campo eléctico e a ensiae e enegia em too o espaço. b) alcule
2. senh(x) = ex e x. 3. cos(t) = eit +e it. 4. sen(t) = eit e it 5. cos(2t) = cos 2 (t) sen 2 (t) 6. sen(2t) = 2sen(t)cos(t) 7.
 UFRGS INSTITUTO DE MATEMÁTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma D - / Segunda avaliação - Grupo 3 4 Toal Nome: Carão: Regra a obervar: Seja ucino porém compleo. Juifique odo procedimeno
UFRGS INSTITUTO DE MATEMÁTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma D - / Segunda avaliação - Grupo 3 4 Toal Nome: Carão: Regra a obervar: Seja ucino porém compleo. Juifique odo procedimeno
7 Síntese de Filtros Ativos
 7 Síntee de Filto Ativo 7. - Foma Fatoada da Função de anfeência F Bloco fundamental na íntee de filto ativo é a função iquadada Já exitem ealizaçõe ativa deta função Foma Fatoada da F em temo de ª odem
7 Síntee de Filto Ativo 7. - Foma Fatoada da Função de anfeência F Bloco fundamental na íntee de filto ativo é a função iquadada Já exitem ealizaçõe ativa deta função Foma Fatoada da F em temo de ª odem
7 Síntese de Filtros Ativos
 7 Síntee de Filto Ativo 7. - Foma Fatoada da Função de anfeência F Bloco fundamental na íntee de filto ativo é a função iquadada Já exitem ealizaçõe ativa deta função Foma Fatoada da F em temo de ª odem
7 Síntee de Filto Ativo 7. - Foma Fatoada da Função de anfeência F Bloco fundamental na íntee de filto ativo é a função iquadada Já exitem ealizaçõe ativa deta função Foma Fatoada da F em temo de ª odem
Introdução à Análise Diferencial dos Movimentos dos Fluidos
 Inodção à Análise Difeencial dos Moimenos dos Flidos Eqação de conseação de massa (coninidade) Definições ailiaes: Fnção coene Deiada maeial Aceleação Roação de flidos Eqação de Conseação de Qanidade de
Inodção à Análise Difeencial dos Moimenos dos Flidos Eqação de conseação de massa (coninidade) Definições ailiaes: Fnção coene Deiada maeial Aceleação Roação de flidos Eqação de Conseação de Qanidade de
FÍSICA GERAL E EXPERIMENTAL I RESOLUÇÃO DA LISTA II
 ÍSIC GEL E EXPEIMENTL I ESOLUÇÃO D LIST II UNIVESIDDE CTÓLIC DE GOIÁS Depatamento de Matemática e íica Diciplina: íica Geal e Epeimental I (M 01) ESOLUÇÃO D LIST II 1. + = (3 1) iˆ + ( 4 ) ˆj = ( N) iˆ
ÍSIC GEL E EXPEIMENTL I ESOLUÇÃO D LIST II UNIVESIDDE CTÓLIC DE GOIÁS Depatamento de Matemática e íica Diciplina: íica Geal e Epeimental I (M 01) ESOLUÇÃO D LIST II 1. + = (3 1) iˆ + ( 4 ) ˆj = ( N) iˆ
Associação de Professores de Matemática PROPOSTA DE RESOLUÇÃO DO EXAME DE MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS (PROVA 835) 2013 2ªFASE
 Aociação de Profeore de Matemática Contacto: Rua Dr. João Couto, n.º 7-A 1500-36 Liboa Tel.: +351 1 716 36 90 / 1 711 03 77 Fax: +351 1 716 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO
Aociação de Profeore de Matemática Contacto: Rua Dr. João Couto, n.º 7-A 1500-36 Liboa Tel.: +351 1 716 36 90 / 1 711 03 77 Fax: +351 1 716 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO
Definição: Seja a equação diferencial linear de ordem n e coeficientes variáveis:. x = +
 Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
GEOMETRIA ESPACIAL. a) Encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
 GEOMETRIA ESPACIAL ) Uma metalúgica ecebeu uma encomenda paa fabica, em gande quantidade, uma peça com o fomato de um pisma eto com base tiangula, cujas dimensões da base são 6cm, 8cm e 0cm e cuja altua
GEOMETRIA ESPACIAL ) Uma metalúgica ecebeu uma encomenda paa fabica, em gande quantidade, uma peça com o fomato de um pisma eto com base tiangula, cujas dimensões da base são 6cm, 8cm e 0cm e cuja altua
ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO
 ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO Thale Cainã do Santo Barbalho 1 ; Álvaro Daniel Tele Pinheiro 2 ; Izabelly Laria Luna
ESTUDO DINÂMICO DA PRESSÃO EM VASOS SEPARADORES VERTICAIS GÁS-LÍQUIDO UTILIZADOS NO PROCESSAMENTO PRIMÁRIO DE PETRÓLEO Thale Cainã do Santo Barbalho 1 ; Álvaro Daniel Tele Pinheiro 2 ; Izabelly Laria Luna
Total. UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Departamento de Matemática Pura e Aplicada MAT Turma D /2 Prova da área IA
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT6 - Turma D - 6/ Prova da área IA - 5 6 7 Toal Nome: Gabario Regra Gerai: Não é permiido o uo de calculadora, elefone
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT6 - Turma D - 6/ Prova da área IA - 5 6 7 Toal Nome: Gabario Regra Gerai: Não é permiido o uo de calculadora, elefone
Colégio Santa Dorotéia Área de Matemática Disciplina: Matemática Ano: 8º - Ensino Fundamental Professores: Marcus e Wuledson
 Cao(a) aluno(a), O momento de evião deve e vito como opotunidade de econtui conhecimento neceáio à continuação do poceo de apendizagem. Natualmente, a ealização dea atividade eigiá de você um envolvimento
Cao(a) aluno(a), O momento de evião deve e vito como opotunidade de econtui conhecimento neceáio à continuação do poceo de apendizagem. Natualmente, a ealização dea atividade eigiá de você um envolvimento
Formatação de fonte. Teorema da amostragem
 Formatação de ote 1 Teorema da amotragem Do aalógico para o digital A amotragem (itatâea) de um ial ou orma de oda aalógica é o proceo pelo qual o ial paa a er repreetado por um cojuto dicreto de úmero.
Formatação de ote 1 Teorema da amotragem Do aalógico para o digital A amotragem (itatâea) de um ial ou orma de oda aalógica é o proceo pelo qual o ial paa a er repreetado por um cojuto dicreto de úmero.
CAPÍTULO 4 4.1 GENERALIDADES
 CAPÍTULO 4 PRIMEIRA LEI DA TERMODINÂMICA Nota de aula pepaada a pati do livo FUNDAMENTALS OF ENGINEERING THERMODINAMICS Michael J. MORAN & HOWARD N. SHAPIRO. 4. GENERALIDADES Enegia é um conceito fundamental
CAPÍTULO 4 PRIMEIRA LEI DA TERMODINÂMICA Nota de aula pepaada a pati do livo FUNDAMENTALS OF ENGINEERING THERMODINAMICS Michael J. MORAN & HOWARD N. SHAPIRO. 4. GENERALIDADES Enegia é um conceito fundamental
CAPÍTULO 5: CISALHAMENTO
 Curo de Engenaria Civil Univeridade Eadual de Maringá Cenro de Tecnologia Deparameno de Engenaria Civil CAPÍTULO 5: CSALHAMENTO 5. Tenõe de Cialameno em iga o Flexão Hipóee Báica: a) A enõe de cialameno
Curo de Engenaria Civil Univeridade Eadual de Maringá Cenro de Tecnologia Deparameno de Engenaria Civil CAPÍTULO 5: CSALHAMENTO 5. Tenõe de Cialameno em iga o Flexão Hipóee Báica: a) A enõe de cialameno
Experimento #4. Filtros analógicos ativos LABORATÓRIO DE ELETRÔNICA
 UNIVESIDADE FEDEAL DE CAMPINA GANDE CENTO DE ENGENHAIA ELÉTICA E INFOMÁTICA DEPATAMENTO DE ENGENHAIA ELÉTICA LABOATÓIO DE ELETÔNICA Experimento #4 Filtro analógico ativo EXPEIMENTO #4 Objetivo Gerai Eta
UNIVESIDADE FEDEAL DE CAMPINA GANDE CENTO DE ENGENHAIA ELÉTICA E INFOMÁTICA DEPATAMENTO DE ENGENHAIA ELÉTICA LABOATÓIO DE ELETÔNICA Experimento #4 Filtro analógico ativo EXPEIMENTO #4 Objetivo Gerai Eta
Onde sentar no cinema?
 Onde ena no cinema? Felipe Vieia 1 felipemae@gmail.com im como muia áea da maemáica, poblema de exemo maximização ou minimização de uma cea vaiável) ão eudado á muio empo. Ee poblema, que êm deafiado maemáico
Onde ena no cinema? Felipe Vieia 1 felipemae@gmail.com im como muia áea da maemáica, poblema de exemo maximização ou minimização de uma cea vaiável) ão eudado á muio empo. Ee poblema, que êm deafiado maemáico
3. Elementos de Sistemas Elétricos de Potência
 Sistemas Eléticos de Potência. Elementos de Sistemas Eléticos de Potência..4 apacitância e Susceptância apacitiva de Linhas de Tansmissão Pofesso:. Raphael Augusto de Souza Benedito E-mail:aphaelbenedito@utfp.edu.b
Sistemas Eléticos de Potência. Elementos de Sistemas Eléticos de Potência..4 apacitância e Susceptância apacitiva de Linhas de Tansmissão Pofesso:. Raphael Augusto de Souza Benedito E-mail:aphaelbenedito@utfp.edu.b
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
Compensadores. Controle 1 - DAELN - UTFPR. Os compensadores são utilizados para alterar alguma característica do sistema em malha fechada.
 Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Conidere uma rampa plana, inclinada de um ângulo em relação à horizonal, no início da qual enconra-e um carrinho. Ele enão recebe uma pancada que o fa
 Onda acúica ão onda de compreenão, ou eja, propagam-e em meio compreívei. Quando uma barra meálica é golpeada em ua exremidade, uma onda longiudinal propaga-e por ela com velocidade v p. A grandeza E é
Onda acúica ão onda de compreenão, ou eja, propagam-e em meio compreívei. Quando uma barra meálica é golpeada em ua exremidade, uma onda longiudinal propaga-e por ela com velocidade v p. A grandeza E é
FÍSICA GERAL E EXPERIMENTAL I RESOLUÇÃO DA LISTA I
 FÍSICA GERAL E EPERIMENTAL I RESOLUÇÃO DA LISTA I UNIERSIDADE CATÓLICA DE GOIÁS Depataento de Mateática e Física Disciplina: Física Geal e Epeiental I (MAF ) RESOLUÇÃO DA LISTA II ) Consideando os deslocaentos,
FÍSICA GERAL E EPERIMENTAL I RESOLUÇÃO DA LISTA I UNIERSIDADE CATÓLICA DE GOIÁS Depataento de Mateática e Física Disciplina: Física Geal e Epeiental I (MAF ) RESOLUÇÃO DA LISTA II ) Consideando os deslocaentos,
Movimentos de satélites geoestacionários: características e aplicações destes satélites
 OK Necessito de ee esta página... Necessito de apoio paa compeende esta página... Moimentos de satélites geoestacionáios: caacteísticas e aplicações destes satélites Um dos tipos de moimento mais impotantes
OK Necessito de ee esta página... Necessito de apoio paa compeende esta página... Moimentos de satélites geoestacionáios: caacteísticas e aplicações destes satélites Um dos tipos de moimento mais impotantes
Total. UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Departamento de Matemática Pura e Aplicada MAT Turma A /2 Prova da área IIA
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
5 Estudo analítico de retas e planos
 GA3X1 - Geometia Analítica e Álgeba Linea 5 Estudo analítico de etas e planos 5.1 Equações de eta Definição (Veto dieto de uma eta): Qualque veto não-nulo paalelo a uma eta chama-se veto dieto dessa eta.
GA3X1 - Geometia Analítica e Álgeba Linea 5 Estudo analítico de etas e planos 5.1 Equações de eta Definição (Veto dieto de uma eta): Qualque veto não-nulo paalelo a uma eta chama-se veto dieto dessa eta.
Aula 08 Equações de Estado (parte I)
 Aula 8 Equaçõe de Etado (parte I) Equaçõe de Etado input S output Já vimo no capítulo 4 ( Repreentação de Sitema ) uma forma de repreentar itema lineare e invariante no tempo (SLIT) atravé de uma função
Aula 8 Equaçõe de Etado (parte I) Equaçõe de Etado input S output Já vimo no capítulo 4 ( Repreentação de Sitema ) uma forma de repreentar itema lineare e invariante no tempo (SLIT) atravé de uma função
Física Geral I - F 128 Aula 8: Energia Potencial e Conservação de Energia. 2 o Semestre 2012
 Física Geal I - F 18 Aula 8: Enegia Potencial e Consevação de Enegia o Semeste 1 Q1: Tabalho e foça Analise a seguinte afimação sobe um copo, que patindo do epouso, move-se de acodo com a foça mostada
Física Geal I - F 18 Aula 8: Enegia Potencial e Consevação de Enegia o Semeste 1 Q1: Tabalho e foça Analise a seguinte afimação sobe um copo, que patindo do epouso, move-se de acodo com a foça mostada
3 Revisão Teórica dos principais modelos de previsão
 Revião Teórica do principai modelo de previão 18 3 Revião Teórica do principai modelo de previão Denre o divero méodo e modelo de previão eine, enconramo aqui o modelo univariado e o modelo com variávei
Revião Teórica do principai modelo de previão 18 3 Revião Teórica do principai modelo de previão Denre o divero méodo e modelo de previão eine, enconramo aqui o modelo univariado e o modelo com variávei
UM SISTEMA DE GERAÇÃO EM ESCALA REDUZIDA DE 10 KVA.
 ANÁLSE EXPERMENTAL DE UM CONTROLADOR APLCADO EM UM REGULADOR DE VELOCDADE DE UM SSTEMA DE GERAÇÃO EM ESCALA REDUZDA DE 0 KVA. FLORNDO A. DE C. AYRES JR., MARCUS C. M. GOMES, ERCK M. ROCHA,WALTER BARRA
ANÁLSE EXPERMENTAL DE UM CONTROLADOR APLCADO EM UM REGULADOR DE VELOCDADE DE UM SSTEMA DE GERAÇÃO EM ESCALA REDUZDA DE 0 KVA. FLORNDO A. DE C. AYRES JR., MARCUS C. M. GOMES, ERCK M. ROCHA,WALTER BARRA
PARTE IV COORDENADAS POLARES
 PARTE IV CRDENADAS PLARES Existem váios sistemas de coodenadas planas e espaciais que, dependendo da áea de aplicação, podem ajuda a simplifica e esolve impotantes poblemas geométicos ou físicos. Nesta
PARTE IV CRDENADAS PLARES Existem váios sistemas de coodenadas planas e espaciais que, dependendo da áea de aplicação, podem ajuda a simplifica e esolve impotantes poblemas geométicos ou físicos. Nesta
Curso: Engenharia de Produção PPNL. Min (Max) f(x)
 PPNL Min (Max) f(x). a. g i (x) (,, ) b i, i 1,,m onde x (x 1,,x n ) T é o veto n-dimenional da vaiávei de decião; f (x) é a função objetivo; g i (x) ão a funçõe de etição e o b i ão contante conhecida.
PPNL Min (Max) f(x). a. g i (x) (,, ) b i, i 1,,m onde x (x 1,,x n ) T é o veto n-dimenional da vaiávei de decião; f (x) é a função objetivo; g i (x) ão a funçõe de etição e o b i ão contante conhecida.
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
