XI Encontro de Iniciação à Docência
|
|
|
- Maria de Lourdes Alves Imperial
- 8 Há anos
- Visualizações:
Transcrição
1 4CCENDFMT01 EXEMPLO DE APLICAÇÃO DE UMA METODOLOGIA PARA A SOLUÇÃO DE PROBLEMAS DE FÍSICA E MATEMÁTICA Erielson Nonato (1) e Pedro Luiz Christiano (3) Centro de Ciências Exatas e da Natureza/Departamento de Física/MONITORIA RESUMO: O presente trabalho teve sua origem na observação de que os alunos das disciplinas de física vêm encontrando enormes dificuldades na solução de problemas propostos e na impressão de que tais dificuldades são devidas à ausência de uma heurística adequada à abordagem desses problemas para ordenar a ação dos estudantes. (Objetivo) O presente trabalho visa a apresentar um exemplo de aplicação de uma metodologia proposta para facilitar a resolução de problemas de física. (Descrição Metodológica) Para melhor evidenciar a aplicação da metodologia proposta esta é trabalhada a partir de sua aplicação a um exemplo concreto, um problema clássico em cursos básicos de física. (Resultados) É apresentada de forma bastante detalhada a forma como os diferentes passos da metodologia devem ser seguidos, desde a análise do enunciado do problema até o teste final da solução. (Conclusão) A partir da utilização da metodologia explicitada neste trabalho o estudante poderá ordenar seus esforços para a solução de problemas de física, melhorando sua capacidade de resolvê-los e aprimorando seu entendimento do conteúdo. Palavras Chave: heurística, solução de problemas, Polya Introdução A habilidade em resolver problemas de matemática e de física, diferentemente do que pensa a maioria das pessoas, depende muito mais da utilização de técnica adequada para analisar o enunciado e buscar os caminhos para sua solução do que de uma habilidade natural, um dom, do indivíduo. Neste trabalho apresentamos a solução de um problema de física como um exemplo de como deve ser a abordagem desse tipo de problemas em geral. Para sua solução utilizamos uma adaptação da técnica de solução de problemas desenvolvida por G. Polya e apresentada em seu livro clássico How to Solve It, publicado inicialmente em 1945 e republicado recentemente com uma introdução de John H. Conway, que relembra as palavras de A. H. Schoenfeld a respeito do livro: Para a educação matemática e o mundo da solução de problemas, ele representa uma linha de demarcação entre duas eras, solução de problemas antes e depois de Polya. É nosso objetivo então nesse trabalho apresentar essas técnicas, devidamente adaptadas para sua utilização em problemas de física, aos nossos estudantes pois ) Bolsista, (2) Voluntário/colaborador, (3) Orientador/Coordenador, (4) Prof. colaborador, (5) Técnico colaborador.
2 acreditamos que é muito mais a ausência de técnicas adequadas do que de esforço e dedicação que fazem com que o estudo de física seja tão difícil para a maioria deles. Como a técnica já foi apresentada em outro trabalho, aqui cuidaremos apenas de ilustrá-la, mostrando a sua aplicação a um problema clássico de física básica. Como exemplo, utilizaremos o seguinte problema: Um bloco de massa M é solto de uma altura H 0 e desliza sem atrito sobre um plano inclinado, como mostrado na figura abaixo. Após descer o plano, o bloco entra em um loop, de raio R, onde também não existe atrito. Determine a força normal que atua no bloco quando o mesmo se encontra no ponto B, indicado na figura. Descrição Metodológica Como já observamos em outro trabalho, a heurística proposta para a solução de problemas de física mantém a estrutura de quatro estágios originalmente sugerida por Polya e listados abaixo. 1. Entendendo o problema a ser resolvido 2. Construindo um plano para a sua solução 3. Executando o plano 4. Revisando a solução encontrada Comecemos então a analisar nosso problema a partir do primeiro desses estágios. 1. Entendendo o problema Esse estágio consiste na identificação de diferentes aspectos do enunciado do problema, de forma a fazer com que o mesmo seja plenamente compreendido antes que se proceda à busca de sua solução. Para tanto, o estudante deve buscar as respostas às seguintes questões: Qual é a incógnita? No caso do problema que estamos considerando, a incógnita procurada é a força normal exercida pelo loop sobre o bloco quando o mesmo está passando pelo ponto A. Designaremos essa quantidade por N A. É importante que o estudante atribua à incógnita procurada uma
3 denominação, como fizemos. Deve, a seguir, escrever logo abaixo do enunciado qual a incógnita procurada vê qual foi a designação a ela atribuída, como mostrado abaixo. Incógnita: Força normal que atua sobre o bloco no ponto A (N A ) Quais são os dados? Alguns dados, como a altura em que se inicia o movimento, a massa do bloco, e o raio do loop são fornecidos de forma evidente e devem ser facilmente identificados pelo estudante. Outros, como a velocidade inicial do bloco e a altura do ponto A são fornecidos de forma menos direta: a primeira, através da afirmação de que a partícula é solta, o que implica em que sua velocidade no ponto inicial é nula e a segunda, pela indicação no desenho de que o ponto A e o centro do loop encontram-se à mesma altura. Esta então, necessariamente, é o raio R do loop. Tais dados devem ser resumidos pelo estudante, logo abaixo da identificação da incógnita, na forma mostrada abaixo. Dados: a. Massa do bloco : M b. Altura inicial : h c. Raio do loop : R d. Velocidade inicial do bloco: v 0 = 0 e. Altura do ponto A: R Quais são as condições adicionais do problema? Nesse caso o estudante deve identificar que o bloco, após ser solto, deslizará sem atrito, inicialmente por um plano inclinado e depois pelo loop. Deve observar também que, para que o bloco percorra o loop deve atuar sobre ele uma força centrípeta. O estudante deve então anotar, logo abaixo dos dados: Condições adicionais: Não existe atrito. No loop atua sobre o bloco uma força centrípeta. O passo seguinte consiste em elaborar um plano para a solução do problema. Esse plano é constituído de duas partes, uma conceitual e outra prática. Também ele deve ser construído a partir da resposta a um conjunto de perguntas. Considerando então os aspectos conceituais do plano, o estudante deve começar a responder a seguinte pergunta: 2.1 Qual o princípio básico envolvido na solução do problema? Tal pergunta, também pode ser traduzida para algo do tipo: de que trata o problema? É esse o principal momento em que se percebe mais claramente as diferenças entre principiantes e especialista. Enquanto os primeiros procuram associar o problema a seus aspectos geométricos, como a questão do problema envolver planos inclinados e movimentos circulares, o especialista tende a identificar os princípios envolvidos, no caso, o princípio da
4 conservação da energia mecânica. O estudante deve escrever então, logo abaixo das condições adicionais: Princípio básico: princípio da conservação da energia mecânica. 2.2 Porque esse princípio pode ser aplicado? Ao responder a essa pergunta, o estudante deve ser levado a identificar que é o fato de não haver atrito presente na trajetória descrita pelo bloco que faz com que o princípio da conservação da energia possa ser aplicado. 2.3 Como o princípio básico deve ser aplicado? Esse é um passo crucial no sentido de se começar a resolver o problema de forma propriamente dita. No caso, a identificação de que a energia mecânica inicial deve ser igual à energia mecânica em qualquer outro instante ou posição ocupada pelo bloco, em particular, igual à energia mecânica do bloco no ponto A, é a equação que deve conduzir à solução do problema. Tal equação pode ser escrita como: E 0 = E A Uma vez respondidas essas três perguntas, que consideram os aspectos conceituais da solução do problema, o passo seguinte consiste então na identificação dos passos práticos para a obtenção da incógnita, a partir das condições iniciais e da utilização do princípio básico. Trata-se então de obter uma conexão entre os dados e a incógnita. Para isso, o primeiro passo consiste em se verificar se essa conexão já existe. O estudante deve então responder à pergunta: 2.4 Os dados iniciais juntamente com o princípio básico levam diretamente à solução do problema? Evidentemente só nos interessa aqui o caso em que a resposta a esta questão é não pois só nesse caso o estudante deve continuar sua seu esforço para resolver o problema. O estudante deve observar que não há essa conexão direta porque nem E 0 nem E A são conhecidos diretamente e, mesmo que o fossem, não levam automaticamente à normal N A. Existem então dois caminhos complementares para se chegar à resposta: I Retropropagação da incógnita O estudante deve verificar nesse ponto que a força normal procurada é a força centrípeta responsável por fazer com que o bloco descreva um movimento circular pelo loop. Deve então fazer a identificação: N A = F cent Como a relação entre a força centrípeta e a velocidade da partícula são conhecidos, o estudante pode escrever ainda: F cent = mv 2 A /R
5 Como conhecemos M e R, nosso problema agora está reduzido à determinação de v A. É neste sentido que dizemos que houve uma retropropagação da incógnita, pois ela agora está uma passo mais próximo dos dados iniciais. II Propagação dos dados Como se sabe que a energia mecânica E é determinada pela soma das energias cinética (K) e potencial (U) o estudante pode escrever: E = K + U Por outro lado, essas energias são dadas por: K = ½ mv 2 U = mgh De modo que, com essas definições, pode-se escrever a equação fornecida pela utilização do princípio básico: como: E 0 = E A ½ mv mgh = ½ mv 2 A + mgh A Como a massa pode ser cancelada, pois está presente em todos os termos, usando-se os dados fornecidos inicialmente pode-se escrever: gh = ½ v 2 A + gh A Como v A é a única incógnita nessa equação, e ela é também a quantidade que se necessitava para a obtenção da força normal procurada, isso significa que foi encontrado um caminho conectando os dados iniciais e a incógnita e, portanto, o problema foi virtualmente resolvido. Esse caminho pode ser esquematizado como: Ou seja: dos dados iniciais m e v 0 se obtém K 0 e dos dados m e h se obtém U 0 que, juntas fornecem E 0. O valor dessa energia, juntamente com a equação fornecida pelo princípio básico e com m e H A que juntamente com m e R permitem encontrar F cent que é a força normal procurada. 3. Executando o plano Nessa etapa, as dificuldades são apenas de cálculo e, como observado por Polya, exigem apenas paciência, atenção e alguma habilidade matemática. No entanto, é também
6 uma ótima oportunidade para se testar rigorosamente cada uma das etapas do plano desenvolvido. Teremos então: K 0 = ½ mv 2 0 = 0 (pois v 0 = 0) U 0 = mgh E, então, E 0 = mgh. Como E A = ½ mv 2 A + mgh A tem-se v 2 A = 2g(h-HÁ) Dessa forma, de F cent = mv 2 A / R obtém-se F cent = 2mg(h-HÁ) / R e como F cent = N tem-se N = 2mg(h-HÁ) / R que é a resposta procurada. 4. Revisando a solução encontrada O quarto passo, como proposto por Polya, deve ser não só uma oportunidade de se testar a solução encontrada, como também para se aprender mais sobre o problema, procurando novos caminhos para resolvê-lo ou explorando casos limite interessantes. Como teste, consideremos a análise dimensional da solução. Como a normal é uma força, sua unidade deve ser o Newton. Obviamente, o lado direito da equação que a determina tem que ter a mesma unidade. Vejamos [N] = [m]. [g]([h] [H A ]) / [R] substituindo as grandezas por suas unidades obtém-se N = kg.(m/s 2 )m / m ou seja N = kg.m / s 2. como deveria ser. Como exemplo de caso limite, consideremos o que aconteceria se o bloco fosse solto da altura H A. Nesse caso, nossa solução nos indica que a normal em A seria nula. Apenas um pouco de reflexão é suficiente para verificar que isso é correto porque, tendo sido solto dessa mesma altura, no ponto A o bloco deverá parar. Nesse ponto então não se encontra descrevendo um movimento circular. Logo, não há força centrípeta e, então, também não existe nenhuma normal.
7 Resultados Com a utilização de uma heurística adequada pode-se ver como a solução de um problema de física e/ou matemática pode ser facilitada, permitindo ao estudante, além do desenvolvimento das habilidades necessárias, uma melhor compreensão do problema resolvido e, por conseqüência, dos conteúdos envolvidos. Conclusão Neste trabalho apresentamos um exemplo de aplicação de uma heurística desenvolvida para solução de problemas de física adaptada da proposta por G. Polya. A heurística apresentada visa a estruturar a abordagem iusada pelos estudantes na solução de problemas e a guiá-los no sentido de uma melhor compreensão do enunciado do problema até uma análise mais completa do resultado obtido. Referências G. Polya. How to Sole It. A new aspect of mathematical method. Princeton University Press. Princeton e Oxford, John D. Bransford, Ann L. Brown, and Rodney R. Cocking (editores). How People Learn: Brain, Mind, Experience and School. National Academy Press, Washington, E. J. S. Lima, P. Ronney e P. L. Christiano, Proposta de uma metodologia para solução de problemas de matemática e de física..
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA
 CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
Unidade 10 Teoremas que relacionam trabalho e energia. Teorema da energia cinética Teorema da energia potencial Teorema da energia mecânica
 Unidade 10 Teoremas que relacionam trabalho e energia Teorema da energia cinética Teorema da energia potencial Teorema da energia mecânica Teorema da nergia Cinética Quando uma força atua de forma favorável
Unidade 10 Teoremas que relacionam trabalho e energia Teorema da energia cinética Teorema da energia potencial Teorema da energia mecânica Teorema da nergia Cinética Quando uma força atua de forma favorável
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
Estudaremos aqui como essa transformação pode ser entendida a partir do teorema do trabalho-energia.
 ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
ENERGIA POTENCIAL Uma outra forma comum de energia é a energia potencial U. Para falarmos de energia potencial, vamos pensar em dois exemplos: Um praticante de bungee-jump saltando de uma plataforma. O
Estrategia de resolução de problemas
 Estrategia de resolução de problemas Sistemas Isolados (p. 222) Muitos problemas na física podem ser resolvidos usando-se o princípio de conservação de energia para um sistema isolado. Deve ser utilizado
Estrategia de resolução de problemas Sistemas Isolados (p. 222) Muitos problemas na física podem ser resolvidos usando-se o princípio de conservação de energia para um sistema isolado. Deve ser utilizado
Capítulo 4 Trabalho e Energia
 Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
EQUAÇÕES E INEQUAÇÕES DE 1º GRAU
 1 EQUAÇÕES E INEQUAÇÕES DE 1º GRAU Equação do 1º grau Chamamos de equação do 1º grau em uma incógnita x, a qualquer expressão matemática que pode ser escrita sob a forma: em que a e b são números reais,
1 EQUAÇÕES E INEQUAÇÕES DE 1º GRAU Equação do 1º grau Chamamos de equação do 1º grau em uma incógnita x, a qualquer expressão matemática que pode ser escrita sob a forma: em que a e b são números reais,
DINÂMICA. Força Resultante: É a força que produz o mesmo efeito que todas as outras aplicadas a um corpo.
 DINÂMICA Quando se fala em dinâmica de corpos, a imagem que vem à cabeça é a clássica e mitológica de Isaac Newton, lendo seu livro sob uma macieira. Repentinamente, uma maçã cai sobre a sua cabeça. Segundo
DINÂMICA Quando se fala em dinâmica de corpos, a imagem que vem à cabeça é a clássica e mitológica de Isaac Newton, lendo seu livro sob uma macieira. Repentinamente, uma maçã cai sobre a sua cabeça. Segundo
Múltiplos Estágios processo com três estágios Inquérito de Satisfação Fase II
 O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
Se um sistema troca energia com a vizinhança por trabalho e por calor, então a variação da sua energia interna é dada por:
 Primeira Lei da Termodinâmica A energia interna U de um sistema é a soma das energias cinéticas e das energias potenciais de todas as partículas que formam esse sistema e, como tal, é uma propriedade do
Primeira Lei da Termodinâmica A energia interna U de um sistema é a soma das energias cinéticas e das energias potenciais de todas as partículas que formam esse sistema e, como tal, é uma propriedade do
CONSERVAÇÃO DA ENERGIA MECÂNICA
 Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T3 Física Experimental I - 2007/08 CONSERVAÇÃO DA ENERGIA MECÂNICA 1. Objectivo Verificar a conservação da energia mecânica de
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T3 Física Experimental I - 2007/08 CONSERVAÇÃO DA ENERGIA MECÂNICA 1. Objectivo Verificar a conservação da energia mecânica de
2 A Derivada. 2.1 Velocidade Média e Velocidade Instantânea
 2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
A equação da posição em função do tempo t do MRUV - movimento retilíneo uniformemente variado é:
 Modellus Atividade 3 Queda livre. Do alto de duas torres, uma na Terra e outra na Lua, deixaram-se cair duas pedras, sem velocidade inicial. Considerando que cada uma das pedras leva 3,0s atingir o solo
Modellus Atividade 3 Queda livre. Do alto de duas torres, uma na Terra e outra na Lua, deixaram-se cair duas pedras, sem velocidade inicial. Considerando que cada uma das pedras leva 3,0s atingir o solo
grandeza do número de elétrons de condução que atravessam uma seção transversal do fio em segundos na forma, qual o valor de?
 Física 01. Um fio metálico e cilíndrico é percorrido por uma corrente elétrica constante de. Considere o módulo da carga do elétron igual a. Expressando a ordem de grandeza do número de elétrons de condução
Física 01. Um fio metálico e cilíndrico é percorrido por uma corrente elétrica constante de. Considere o módulo da carga do elétron igual a. Expressando a ordem de grandeza do número de elétrons de condução
APRENDER A LER PROBLEMAS EM MATEMÁTICA
 APRENDER A LER PROBLEMAS EM MATEMÁTICA Maria Ignez de Souza Vieira Diniz ignez@mathema.com.br Cristiane Akemi Ishihara crisakemi@mathema.com.br Cristiane Henriques Rodrigues Chica crischica@mathema.com.br
APRENDER A LER PROBLEMAS EM MATEMÁTICA Maria Ignez de Souza Vieira Diniz ignez@mathema.com.br Cristiane Akemi Ishihara crisakemi@mathema.com.br Cristiane Henriques Rodrigues Chica crischica@mathema.com.br
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Aula 1: Demonstrações e atividades experimentais tradicionais e inovadoras
 Aula 1: Demonstrações e atividades experimentais tradicionais e inovadoras Nesta aula trataremos de demonstrações e atividades experimentais tradicionais e inovadoras. Vamos começar a aula retomando questões
Aula 1: Demonstrações e atividades experimentais tradicionais e inovadoras Nesta aula trataremos de demonstrações e atividades experimentais tradicionais e inovadoras. Vamos começar a aula retomando questões
Cap. 4 - Princípios da Dinâmica
 Universidade Federal do Rio de Janeiro Instituto de Física Física I IGM1 2014/1 Cap. 4 - Princípios da Dinâmica e suas Aplicações Prof. Elvis Soares 1 Leis de Newton Primeira Lei de Newton: Um corpo permanece
Universidade Federal do Rio de Janeiro Instituto de Física Física I IGM1 2014/1 Cap. 4 - Princípios da Dinâmica e suas Aplicações Prof. Elvis Soares 1 Leis de Newton Primeira Lei de Newton: Um corpo permanece
Provas Comentadas OBF/2011
 PROFESSORES: Daniel Paixão, Deric Simão, Edney Melo, Ivan Peixoto, Leonardo Bruno, Rodrigo Lins e Rômulo Mendes COORDENADOR DE ÁREA: Prof. Edney Melo 1. Um foguete de 1000 kg é lançado da superfície da
PROFESSORES: Daniel Paixão, Deric Simão, Edney Melo, Ivan Peixoto, Leonardo Bruno, Rodrigo Lins e Rômulo Mendes COORDENADOR DE ÁREA: Prof. Edney Melo 1. Um foguete de 1000 kg é lançado da superfície da
Bases Matemáticas. Aula 2 Métodos de Demonstração. Rodrigo Hausen. v. 2013-7-31 1/15
 Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
Hoje estou elétrico!
 A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
A U A UL LA Hoje estou elétrico! Ernesto, observado por Roberto, tinha acabado de construir um vetor com um pedaço de papel, um fio de meia, um canudo e um pedacinho de folha de alumínio. Enquanto testava
Análise Dimensional Notas de Aula
 Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
( ) ( ) ( ( ) ( )) ( )
 Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Faculdade de Administração e Negócios de Sergipe
 Faculdade de Administração e Negócios de Sergipe Disciplina: Física Geral e Experimental III Curso: Engenharia de Produção Assunto: Gravitação Prof. Dr. Marcos A. P. Chagas 1. Introdução Na gravitação
Faculdade de Administração e Negócios de Sergipe Disciplina: Física Geral e Experimental III Curso: Engenharia de Produção Assunto: Gravitação Prof. Dr. Marcos A. P. Chagas 1. Introdução Na gravitação
Lição 5. Instrução Programada
 Instrução Programada Lição 5 Na lição anterior, estudamos a medida da intensidade de urna corrente e verificamos que existem materiais que se comportam de modo diferente em relação à eletricidade: os condutores
Instrução Programada Lição 5 Na lição anterior, estudamos a medida da intensidade de urna corrente e verificamos que existem materiais que se comportam de modo diferente em relação à eletricidade: os condutores
DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 07
 DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 07 Este é o 7º artigo da série de dicas para facilitar / agilizar os cálculos matemáticos envolvidos em questões de Raciocínio Lógico, Matemática, Matemática Financeira
DICAS PARA CÁLCULOS MAIS RÁPIDOS ARTIGO 07 Este é o 7º artigo da série de dicas para facilitar / agilizar os cálculos matemáticos envolvidos em questões de Raciocínio Lógico, Matemática, Matemática Financeira
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 4
 Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista.
 Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista. Plantão de Atendimento Horário: terças e quintas-feiras das 14:00 às 16:00. MSN:
Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista. Plantão de Atendimento Horário: terças e quintas-feiras das 14:00 às 16:00. MSN:
O degrau de potencial. Caso II: energia maior que o degrau
 O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
Lista de Exercícios - Unidade 6 Aprendendo sobre energia
 Lista de Exercícios - Unidade 6 Aprendendo sobre energia Energia Cinética e Potencial 1. (UEM 01) Sobre a energia mecânica e a conservação de energia, assinale o que for correto. (01) Denomina-se energia
Lista de Exercícios - Unidade 6 Aprendendo sobre energia Energia Cinética e Potencial 1. (UEM 01) Sobre a energia mecânica e a conservação de energia, assinale o que for correto. (01) Denomina-se energia
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar)
 Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
a) O tempo total que o paraquedista permaneceu no ar, desde o salto até atingir o solo.
 (MECÂNICA, ÓPTICA, ONDULATÓRIA E MECÂNICA DOS FLUIDOS) 01) Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80 m, antes de abrir o paraquedas. Quando este se abre, ele passa
(MECÂNICA, ÓPTICA, ONDULATÓRIA E MECÂNICA DOS FLUIDOS) 01) Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80 m, antes de abrir o paraquedas. Quando este se abre, ele passa
Fundamentos da Matemática
 Fundamentos da Matemática Aula 10 Os direitos desta obra foram cedidos à Universidade Nove de Julho Este material é parte integrante da disciplina oferecida pela UNINOVE. O acesso às atividades, conteúdos
Fundamentos da Matemática Aula 10 Os direitos desta obra foram cedidos à Universidade Nove de Julho Este material é parte integrante da disciplina oferecida pela UNINOVE. O acesso às atividades, conteúdos
Projeção ortográfica de modelos com elementos paralelos e oblíquos
 A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
INTERPRETANDO A GEOMETRIA DE RODAS DE UM CARRO: UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA
 INTERPRETANDO A GEOMETRIA DE RODAS DE UM CARRO: UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA Marcos Leomar Calson Mestrando em Educação em Ciências e Matemática, PUCRS Helena Noronha Cury Doutora em Educação
INTERPRETANDO A GEOMETRIA DE RODAS DE UM CARRO: UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA Marcos Leomar Calson Mestrando em Educação em Ciências e Matemática, PUCRS Helena Noronha Cury Doutora em Educação
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Soluções das Questões de Física do Processo Seletivo de Admissão à Escola Preparatória de Cadetes do Exército EsPCEx
 Soluções das Questões de Física do Processo Seletivo de dmissão à Escola Preparatória de Cadetes do Exército EsPCEx Questão Concurso 009 Uma partícula O descreve um movimento retilíneo uniforme e está
Soluções das Questões de Física do Processo Seletivo de dmissão à Escola Preparatória de Cadetes do Exército EsPCEx Questão Concurso 009 Uma partícula O descreve um movimento retilíneo uniforme e está
= R. Sendo m = 3,3. 10 27 kg, V = 3,0. 10 7 m/s e R = 0,45m, calcula-se a intensidade da força magnética. 3,3. 10 27. (3,0. 10 7 ) 2 = (N) 0,45
 37 a FÍSICA Em um cíclotron tipo de acelerador de partículas um deutério alcança velocidade final de 3,0 x 10 7 m/s, enquanto se move em um caminho circular de raio 0,45m, mantido nesse caminho por uma
37 a FÍSICA Em um cíclotron tipo de acelerador de partículas um deutério alcança velocidade final de 3,0 x 10 7 m/s, enquanto se move em um caminho circular de raio 0,45m, mantido nesse caminho por uma
Você sabe a regra de três?
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Você sabe a regra de três?
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Você sabe a regra de três?
UM MÓDULO DE ATIVIDADES PARA O ENSINO-APRENDIZAGEM DAS FÓRMULAS DE ÁREA DOS PRINCIPAIS POLÍGONOS CONVEXOS
 UM MÓDULO DE ATIVIDADES PARA O ENSINO-APRENDIZAGEM DAS FÓRMULAS DE ÁREA DOS PRINCIPAIS POLÍGONOS CONVEXOS Cristiane Fernandes de Souza, Ms. UFRN cristianesouza.fernandes@bol.com.br Introdução O estudo
UM MÓDULO DE ATIVIDADES PARA O ENSINO-APRENDIZAGEM DAS FÓRMULAS DE ÁREA DOS PRINCIPAIS POLÍGONOS CONVEXOS Cristiane Fernandes de Souza, Ms. UFRN cristianesouza.fernandes@bol.com.br Introdução O estudo
Fórmula versus Algoritmo
 1 Introdução Fórmula versus Algoritmo na resolução de um problema 1 Roberto Ribeiro Paterlini 2 Departamento de Matemática da UFSCar No estudo das soluções do problema abaixo deparamos com uma situação
1 Introdução Fórmula versus Algoritmo na resolução de um problema 1 Roberto Ribeiro Paterlini 2 Departamento de Matemática da UFSCar No estudo das soluções do problema abaixo deparamos com uma situação
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO
 E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear
 Exemplos de aplicação das leis de Newton e Conservação do Momento Linear Cálculo de resultante I Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante. F 1 = 10 N 30 F
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear Cálculo de resultante I Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante. F 1 = 10 N 30 F
A equação do 2º grau
 A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
A abordagem do assunto será feita inicialmente explorando uma curva bastante conhecida: a circunferência. Escolheremos como y
 5 Taxa de Variação Neste capítulo faremos uso da derivada para resolver certos tipos de problemas relacionados com algumas aplicações físicas e geométricas. Nessas aplicações nem sempre as funções envolvidas
5 Taxa de Variação Neste capítulo faremos uso da derivada para resolver certos tipos de problemas relacionados com algumas aplicações físicas e geométricas. Nessas aplicações nem sempre as funções envolvidas
Construção de tabelas verdades
 Construção de tabelas verdades Compreender a Lógica como instrumento da ciência e como estrutura formal do pensamento, conhecendo e compreendendo as operações com os principais conceitos proposicionais
Construção de tabelas verdades Compreender a Lógica como instrumento da ciência e como estrutura formal do pensamento, conhecendo e compreendendo as operações com os principais conceitos proposicionais
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
casa. Será uma casa simples, situada em terreno plano, com sala, dois quartos, cozinha, banheiro e área de serviço.
 A UUL AL A A casa Nesta aula vamos examinar a planta de uma casa. Será uma casa simples, situada em terreno plano, com, dois quartos, cozinha, banheiro e área de serviço. Introdução terreno 20 m rua 30
A UUL AL A A casa Nesta aula vamos examinar a planta de uma casa. Será uma casa simples, situada em terreno plano, com, dois quartos, cozinha, banheiro e área de serviço. Introdução terreno 20 m rua 30
Algoritmos. Objetivo principal: explicar que a mesma ação pode ser realizada de várias maneiras, e que às vezes umas são melhores que outras.
 6 6 NOME DA AULA: 6 Algoritmos Duração da aula: 45 60 minutos Tempo de preparação: 10-25 minutos (dependendo da disponibilidade de tangrans prontos ou da necessidade de cortá-los à mão) Objetivo principal:
6 6 NOME DA AULA: 6 Algoritmos Duração da aula: 45 60 minutos Tempo de preparação: 10-25 minutos (dependendo da disponibilidade de tangrans prontos ou da necessidade de cortá-los à mão) Objetivo principal:
Texto 07 - Sistemas de Partículas. A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica.
 Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.
 Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04
 ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE
 EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE NOME Nº SÉRIE : 1º EM DATA : / / BIMESTRE 3º PROFESSOR: Renato DISCIPLINA: Física 1 VISTO COORDENAÇÃO ORIENTAÇÕES: 1. O trabalho deverá ser feito em papel
EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE NOME Nº SÉRIE : 1º EM DATA : / / BIMESTRE 3º PROFESSOR: Renato DISCIPLINA: Física 1 VISTO COORDENAÇÃO ORIENTAÇÕES: 1. O trabalho deverá ser feito em papel
Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes
 Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes Para ampliar sua compreensão sobre probabilidade total e Teorema de Bayes, estude este conjunto de exercícios resolvidos sobre o tema.
Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes Para ampliar sua compreensão sobre probabilidade total e Teorema de Bayes, estude este conjunto de exercícios resolvidos sobre o tema.
Professora Bruna. Caderno 13 Aula 28. Quem atinge o solo primeiro? Página 291
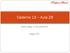 Caderno 13 Aula 28 Quem atinge o solo primeiro? Página 291 Quem atinge o solo primeiro? Vimos na aula anterior, que o tempo de queda para um corpo lançado horizontalmente não depende da sua velocidade
Caderno 13 Aula 28 Quem atinge o solo primeiro? Página 291 Quem atinge o solo primeiro? Vimos na aula anterior, que o tempo de queda para um corpo lançado horizontalmente não depende da sua velocidade
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
objetivo Exercícios Meta da aula Pré-requisitos Aplicar o formalismo quântico estudado neste módulo à resolução de um conjunto de exercícios.
 Exercícios A U L A 10 Meta da aula Aplicar o formalismo quântico estudado neste módulo à resolução de um conjunto de exercícios. objetivo aplicar os conhecimentos adquiridos nas Aulas 4 a 9 por meio da
Exercícios A U L A 10 Meta da aula Aplicar o formalismo quântico estudado neste módulo à resolução de um conjunto de exercícios. objetivo aplicar os conhecimentos adquiridos nas Aulas 4 a 9 por meio da
BRINCANDO COM GRÁFICOS E MEDINDO A SORTE
 BRINCANDO COM GRÁFICOS E MEDINDO A SORTE Elizabeth Pastor Garnier SEE/RJ Pedro Carlos Pereira - FAETEC Projeto Fundão IM/UFRJ Os Parâmetros Curriculares Nacionais propõem a introdução do tópico Tratamento
BRINCANDO COM GRÁFICOS E MEDINDO A SORTE Elizabeth Pastor Garnier SEE/RJ Pedro Carlos Pereira - FAETEC Projeto Fundão IM/UFRJ Os Parâmetros Curriculares Nacionais propõem a introdução do tópico Tratamento
Orientação a Objetos
 1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
Exercícios resolvidos sobre Definição de Probabilidade
 Exercícios resolvidos sobre Definição de Probabilidade Nesta Unidade de estudo, até este ponto você aprendeu definições de probabilidade e viu como os conceitos se aplicam a várias situações. Observe agora
Exercícios resolvidos sobre Definição de Probabilidade Nesta Unidade de estudo, até este ponto você aprendeu definições de probabilidade e viu como os conceitos se aplicam a várias situações. Observe agora
Palavras-chave: Educação Matemática; Avaliação; Formação de professores; Pró- Matemática.
 PRÓ-MATEMÁTICA 2012: UM EPISÓDIO DE AVALIAÇÃO Edilaine Regina dos Santos 1 Universidade Estadual de Londrina edilaine.santos@yahoo.com.br Rodrigo Camarinho de Oliveira 2 Universidade Estadual de Londrina
PRÓ-MATEMÁTICA 2012: UM EPISÓDIO DE AVALIAÇÃO Edilaine Regina dos Santos 1 Universidade Estadual de Londrina edilaine.santos@yahoo.com.br Rodrigo Camarinho de Oliveira 2 Universidade Estadual de Londrina
Um capacitor não armazena apenas carga, mas também energia.
 Capacitores e Dielétricos (continuação) Energia armazenada num capacitor Um capacitor não armazena apenas carga, mas também energia. A energia armazenada num capacitor é igual ao trabalho necessário para
Capacitores e Dielétricos (continuação) Energia armazenada num capacitor Um capacitor não armazena apenas carga, mas também energia. A energia armazenada num capacitor é igual ao trabalho necessário para
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
11 de maio de 2011. Análise do uso dos Resultados _ Proposta Técnica
 11 de maio de 2011 Análise do uso dos Resultados _ Proposta Técnica 1 ANÁLISE DOS RESULTADOS DO SPAECE-ALFA E DAS AVALIAÇÕES DO PRÊMIO ESCOLA NOTA DEZ _ 2ª Etapa 1. INTRODUÇÃO Em 1990, o Sistema de Avaliação
11 de maio de 2011 Análise do uso dos Resultados _ Proposta Técnica 1 ANÁLISE DOS RESULTADOS DO SPAECE-ALFA E DAS AVALIAÇÕES DO PRÊMIO ESCOLA NOTA DEZ _ 2ª Etapa 1. INTRODUÇÃO Em 1990, o Sistema de Avaliação
horizontal, se choca frontalmente contra a extremidade de uma mola ideal, cuja extremidade oposta está presa a uma parede vertical rígida.
 Exercícios: Energia 01. (UEPI) Assinale a alternativa que preenche corretamente as lacunas das frases abaixo. O trabalho realizado por uma força conservativa, ao deslocar um corpo entre dois pontos é da
Exercícios: Energia 01. (UEPI) Assinale a alternativa que preenche corretamente as lacunas das frases abaixo. O trabalho realizado por uma força conservativa, ao deslocar um corpo entre dois pontos é da
Canguru Matemático sem Fronteiras 2014
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 9. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 9. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
LISTA UERJ 2014 LEIS DE NEWTON
 1. (Pucrj 2013) Sobre uma superfície sem atrito, há um bloco de massa m 1 = 4,0 kg sobre o qual está apoiado um bloco menor de massa m 2 = 1,0 kg. Uma corda puxa o bloco menor com uma força horizontal
1. (Pucrj 2013) Sobre uma superfície sem atrito, há um bloco de massa m 1 = 4,0 kg sobre o qual está apoiado um bloco menor de massa m 2 = 1,0 kg. Uma corda puxa o bloco menor com uma força horizontal
Matemática Financeira Módulo 2
 Fundamentos da Matemática O objetivo deste módulo consiste em apresentar breve revisão das regras e conceitos principais de matemática. Embora planilhas e calculadoras financeiras tenham facilitado grandemente
Fundamentos da Matemática O objetivo deste módulo consiste em apresentar breve revisão das regras e conceitos principais de matemática. Embora planilhas e calculadoras financeiras tenham facilitado grandemente
1 m 2. Substituindo os valores numéricos dados para a análise do movimento do centro de massa, vem: Resposta: D. V = 2 10 3,2 V = 8 m/s
 01 De acordo com o enunciado, não há dissipação ou acréscimo de energia. Considerando que a energia citada seja a mecânica e que, no ponto de altura máxima, a velocidade seja nula, tem-se: ε ε = ' + 0
01 De acordo com o enunciado, não há dissipação ou acréscimo de energia. Considerando que a energia citada seja a mecânica e que, no ponto de altura máxima, a velocidade seja nula, tem-se: ε ε = ' + 0
O prof Renato Brito Comenta:
 PROVA DA UFC 009.1 COMENTADA Prof. Renato Brito R 1 = 1 x 10 6 m, Q 1 = 10.000.e R = 1 x 10 3 m Q = 10 n.e 4 n Q1 Q 10.e 10.e 1 6 3 4 π.(r 1) 4 π.(r ) (10 ) (10 ) σ = σ = = Assim, a ordem de grandeza pedida
PROVA DA UFC 009.1 COMENTADA Prof. Renato Brito R 1 = 1 x 10 6 m, Q 1 = 10.000.e R = 1 x 10 3 m Q = 10 n.e 4 n Q1 Q 10.e 10.e 1 6 3 4 π.(r 1) 4 π.(r ) (10 ) (10 ) σ = σ = = Assim, a ordem de grandeza pedida
NOME: Nº. ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA:
 NOME: Nº 1 o ano do Ensino Médio TURMA: Data: 11/ 12/ 12 DISCIPLINA: Física PROF. : Petrônio L. de Freitas ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA: INSTRUÇÕES (Leia com atenção!)
NOME: Nº 1 o ano do Ensino Médio TURMA: Data: 11/ 12/ 12 DISCIPLINA: Física PROF. : Petrônio L. de Freitas ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA: INSTRUÇÕES (Leia com atenção!)
Guia de utilização da notação BPMN
 1 Guia de utilização da notação BPMN Agosto 2011 2 Sumário de Informações do Documento Documento: Guia_de_utilização_da_notação_BPMN.odt Número de páginas: 31 Versão Data Mudanças Autor 1.0 15/09/11 Criação
1 Guia de utilização da notação BPMN Agosto 2011 2 Sumário de Informações do Documento Documento: Guia_de_utilização_da_notação_BPMN.odt Número de páginas: 31 Versão Data Mudanças Autor 1.0 15/09/11 Criação
Leis de Conservação. Exemplo: Cubo de gelo de lado 2cm, volume V g. =8cm3, densidade ρ g. = 0,917 g/cm3. Massa do. ρ g = m g. m=ρ.
 Leis de Conservação Em um sistema isolado, se uma grandeza ou propriedade se mantém constante em um intervalo de tempo no qual ocorre um dado processo físico, diz-se que há conservação d a propriedade
Leis de Conservação Em um sistema isolado, se uma grandeza ou propriedade se mantém constante em um intervalo de tempo no qual ocorre um dado processo físico, diz-se que há conservação d a propriedade
Problemas insolúveis. Um exemplo simples e concreto
 Surge agora uma outra questão. Viemos buscando algoritmos para resolver problemas. No entanto, será que sempre seria possível achar esses algoritmos? Colocando de outra forma: será que, para todo problema,
Surge agora uma outra questão. Viemos buscando algoritmos para resolver problemas. No entanto, será que sempre seria possível achar esses algoritmos? Colocando de outra forma: será que, para todo problema,
Tomada de Decisão uma arte a ser estudada Por: Arthur Diniz
 Tomada de Decisão uma arte a ser estudada Por: Arthur Diniz Tomar decisões é uma atividade que praticamos diariamente, de uma forma ou de outra. Podemos até mesmo tomar a decisão de não tomar nenhuma decisão.
Tomada de Decisão uma arte a ser estudada Por: Arthur Diniz Tomar decisões é uma atividade que praticamos diariamente, de uma forma ou de outra. Podemos até mesmo tomar a decisão de não tomar nenhuma decisão.
Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta
 Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
PARANÁ GOVERNO DO ESTADO
 A COMUNICAÇÃO NA INTERNET PROTOCOLO TCP/IP Para tentar facilitar o entendimento de como se dá a comunicação na Internet, vamos começar contando uma história para fazer uma analogia. Era uma vez, um estrangeiro
A COMUNICAÇÃO NA INTERNET PROTOCOLO TCP/IP Para tentar facilitar o entendimento de como se dá a comunicação na Internet, vamos começar contando uma história para fazer uma analogia. Era uma vez, um estrangeiro
PROJETO DE RECUPERAÇÃO EM MATEMÁTICA Manual do Professor Módulo 2 Números Racionais, Operações e Resolução de Problemas
 PROJETO DE RECUPERAÇÃO EM MATEMÁTICA Manual do Professor Módulo 2 Números Racionais, Operações e Resolução de Problemas Prezado(a) Professor(a) Este manual de orientações tem a finalidade de sugerir um
PROJETO DE RECUPERAÇÃO EM MATEMÁTICA Manual do Professor Módulo 2 Números Racionais, Operações e Resolução de Problemas Prezado(a) Professor(a) Este manual de orientações tem a finalidade de sugerir um
Departamento de Física Universidade do Algarve PÊNDULO SIMPLES
 Departamento de Física Universidade do lgarve PÊNDULO SIMPLES 1. Resumo Um pêndulo é largado de uma determinada altura, medindo-se a sua velocidade linear quando passa pela posição mais baixa. Este procedimento
Departamento de Física Universidade do lgarve PÊNDULO SIMPLES 1. Resumo Um pêndulo é largado de uma determinada altura, medindo-se a sua velocidade linear quando passa pela posição mais baixa. Este procedimento
Equações do segundo grau
 Módulo 1 Unidade 4 Equações do segundo grau Para início de conversa... Nesta unidade, vamos avançar um pouco mais nas resoluções de equações. Na unidade anterior, você estudou sobre as equações de primeiro
Módulo 1 Unidade 4 Equações do segundo grau Para início de conversa... Nesta unidade, vamos avançar um pouco mais nas resoluções de equações. Na unidade anterior, você estudou sobre as equações de primeiro
Revisão de combinatória
 A UA UL LA Revisão de combinatória Introdução Nesta aula, vamos misturar os vários conceitos aprendidos em análise combinatória. Desde o princípio multiplicativo até os vários tipos de permutações e combinações.
A UA UL LA Revisão de combinatória Introdução Nesta aula, vamos misturar os vários conceitos aprendidos em análise combinatória. Desde o princípio multiplicativo até os vários tipos de permutações e combinações.
Associação de resistores
 Associação de resistores É comum nos circuitos elétricos a existência de vários resistores, que encontram-se associados. Os objetivos de uma associação de resistores podem ser: a necessidade de dividir
Associação de resistores É comum nos circuitos elétricos a existência de vários resistores, que encontram-se associados. Os objetivos de uma associação de resistores podem ser: a necessidade de dividir
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas CMP1132 Processo e qualidade de software II Prof. Me. Elias Ferreira Sala: 402 E Quarta-Feira:
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas CMP1132 Processo e qualidade de software II Prof. Me. Elias Ferreira Sala: 402 E Quarta-Feira:
CAPACITORES. Vestibular1 A melhor ajuda ao vestibulando na Internet Acesse Agora! www.vestibular1.com.br
 CAPACITORES DEFINIÇÕES Quando as placas do capacitor estão carregadas com cargas iguais e de sinais diferentes, estabelece-se entre as placas uma diferença de potencial V que é proporcional à carga. Q
CAPACITORES DEFINIÇÕES Quando as placas do capacitor estão carregadas com cargas iguais e de sinais diferentes, estabelece-se entre as placas uma diferença de potencial V que é proporcional à carga. Q
Criatividade e Inovação Organizacional: A liderança de equipas na resolução de problemas complexos
 Criatividade e Inovação Organizacional: A liderança de equipas na resolução de problemas complexos Dizer que o grande segredo do sucesso das empresas, especialmente em tempos conturbados, é a sua adaptabilidade
Criatividade e Inovação Organizacional: A liderança de equipas na resolução de problemas complexos Dizer que o grande segredo do sucesso das empresas, especialmente em tempos conturbados, é a sua adaptabilidade
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2
 SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2 1.1 Introdução... 2 1.2 Estrutura do IP... 3 1.3 Tipos de IP... 3 1.4 Classes de IP... 4 1.5 Máscara de Sub-Rede... 6 1.6 Atribuindo um IP ao computador... 7 2
SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2 1.1 Introdução... 2 1.2 Estrutura do IP... 3 1.3 Tipos de IP... 3 1.4 Classes de IP... 4 1.5 Máscara de Sub-Rede... 6 1.6 Atribuindo um IP ao computador... 7 2
Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Matemática Financeira Professor: Custódio Nascimento
 Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Professor: Custódio Nascimento 1- Análise da prova Neste artigo, faremos a análise das questões de cobradas na prova
Análise e Resolução da prova de Auditor Fiscal da Fazenda Estadual do Piauí Disciplina: Professor: Custódio Nascimento 1- Análise da prova Neste artigo, faremos a análise das questões de cobradas na prova
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
FÍSICA PARA PRF PROFESSOR: GUILHERME NEVES
 Olá, pessoal! Tudo bem? Vou neste artigo resolver a prova de Fïsica para a Polícia Rodoviária Federal, organizada pelo CESPE-UnB. Antes de resolver cada questão, comentarei sobre alguns trechos das minhas
Olá, pessoal! Tudo bem? Vou neste artigo resolver a prova de Fïsica para a Polícia Rodoviária Federal, organizada pelo CESPE-UnB. Antes de resolver cada questão, comentarei sobre alguns trechos das minhas
A Torre de Hanói e o Princípio da Indução Matemática
 A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
