Análise Matemática III - Turma especial
|
|
|
- Kevin Capistrano
- 5 Há anos
- Visualizações:
Transcrição
1 Análise Matemática III - Turma especial Fichas 1 a 5 - Solução parcial 1.3 Seja D E k um conjunto fechado. Uma transformação T : D D diz-se uma contracção se existe c < 1 tal que para todos os x, y D se tem T (x) T (y) c x y. (a) Mostre que uma contracção é uma transformação contínua. (b) Mostre que uma contracção tem um único ponto fixo, isto é, que existe um único z D tal que T (z) = z. Solução: (a) Se x y < ɛ, então T (x) T (y) < cɛ < ɛ logo T é contínua. (b) Por indução mostra-se que T n (x) T n (y) < c n x y. Em particular, T n+1 (x) T n (x) < c n T (x) x. Assim, dado m > n, tem-se T m (x) T n (x) m 1 j=n T j+1 (x) T j (x) m 1 j=n c j T (x) x cn T (x) x 1 c Uma vez que cn 1 c 0 quando n, conclui-se que a sucessão T n (x) é uma sucessão de Cauchy (qualquer que seja x D) e portanto converge. Fixe-se x D e seja z = lim T n (x). Uma vez que D é fechado, z D. Como T é contínua tem-se T (z) = T (lim T n (x)) = lim T n+1 (x) = lim T n (x) = z, isto é, z é um ponto fixo de T em D. Se w D um ponto fixo qualquer de T. Então w z = T (w) T (z) c w z. Como c < 1 conclui-se que w z = 0, ou seja, existe um único ponto fixo de T em D. 1.5 Recorde que um conjunto K E n se diz compacto se é limitado e fechado. Uma família de conjuntos {U α E n } diz-se uma cobertura de X E n se X α U α. A cobertura diz-se aberta se cada um dos conjuntos U α é aberto. Uma subcobertura de {U α } é uma subfamília que é ainda uma cobertura. Mostre que um conjunto K é compacto se e só se toda a cobertura aberta de K admite uma subcobertura finita. Solução (do Ricardo Joel): Suponhamos que K E n é tal que toda a cobertura aberta de K admite uma subcobertura finita. A família {B n (0)} é uma cobertura aberta de E n e portanto de K. Sendo N o maior dos raios das bolas de uma subcobertura finita, tem-se K B N (0) pelo que K é limitado. 1
2 Vamos agora ver que K é fechado. Suponhamos que existe um ponto x que está na fronteira de K mas não em K. Então {E n \ B 1 (x)} é uma cobertura n aberta de K. Tomando uma subcobertura finita segue-se que existe N tal que K B 1 (x) =. Isto contradiz a hipótese de x ser um ponto fronteiro. Concluise que a fronteira de K está contida em K, ou seja K é N fechado. Suponhamos agora que K é limitado e fechado. Começamos por provar o resultado pretendido para uma cobertura particular de K, nomeadamente a cobertura {B ɛ (x) : x K} onde ɛ > 0 é um número fixo. Suponhamos que esta cobertura não tem nenhuma subcobertura finita. Então podemos escolher uma sucessão de pontos x n K com a propriedade x n+1 / n B ɛ (x k ). Pelo teorema de Bolzano-Weierstrass, a sucessão x n tem uma subsucessão convergente em D. Sem perda de generalidade podemos assumir que x n z. Sendo N tal que x n B ɛ (z) para n N, segue-se que x 2 N+1 B ɛ (x N ), o que contradiz a definição de x N+1. Isto conclui a demonstração deste caso particular. Mostramos agora que dada uma cobertura aberta {U α } de K, existe ɛ > 0 tal que para todo o x K, existe α tal que B ɛ (x) U α. Suponhamos por absurdo que tal não era o caso. Então para cada n, existe x n K tal que B 1 (x n) não está contida em nenhum U n α. Pelo teorema de Bolzano-Weierstrass a sucessão x n tem uma subsucessão convergente em D. Sem perda de generalidade, podemos assumir que a sucessão x n converge para z D. Seja α tal que z U α. Então, para n suficientemente grande, B 1 n (x n) U α o que contradiz a definição de x n. Conclui-se que existe ɛ com a propriedade desejada. Para concluir a demonstração, dada uma cobertura aberta {U α } de K escolhase ɛ como no parágrafo anterior. Então existem pontos x 1,..., x m K tais que K m B ɛ (x k ). Escolha-se α k tal que B ɛ (x k ) U αk. Então o que conclui a demonstração. K m 2.2 Suponha que n < m. Seja D E n um aberto e g : D E m uma transformação de classe C 1. Mostre que se Dg(t 0 ) é injectiva, então existe um aberto contendo t 0 tal que g é injectiva em. U αk 2
3 Solução: Dg(t 0 ) ser injectiva significa que n das linhas da matriz que representa Dg(t 0 ) são linearmente independentes. Sem perda de generalidade assumamos que as primeiras n linhas são linearmente independentes. A função h : D E n definida por h(t) = (g 1 (t),..., g n (t)) é uma função de classe C 1 em D e por hipótese det Dh(t 0 ) 0. O teorema da função inversa garante a existência de um aberto E n contendo t 0 tal que h é injectiva em. Para t, s, tem-se logo g é injectiva em. 3.2 g(t) = g(s) = h(t) = h(s) = s = t (a) Mostre que o intervalo M = {(x, 0) : 0 x 1} E 2 não é uma variedade de dimensão 1 em E 2. (b) Dê um exemplo de uma variedade M de dimensão 1 em E 2 para a qual não existe nenhuma função φ : E 2 R de classe C 1 tal que M = {x E 2 : φ(x) = 0}. Solução: (a) Se M fosse uma variedade de dimensão 1, existiria um aberto U contendo (0, 0), uma vizinhança V de 0 em R e uma função f : V R tal que U M = {(x, f(x)) : x V } ou U M = {(f(y), y) : y V }. Tal não acontece porque as funções coordenadas x e y nunca assumem valores negativos em M. Outra solução (do Ricardo Joel): Suponhamos que M era uma variedade de dimensão 1. Então existiria uma bola B ɛ ((0, 0)) e uma função φ : B ɛ ((0, 0)) R de classe C 1 tal que M B ɛ ((0, 0)) = φ 1 (0) e φ(x) 0 para todo o x M. Sejam x, y B ɛ ((0, 0)) \ M e seja γ : [0, 1] B ɛ ((0, 0)) \ M uma função contínua com γ(0) = x e γ(1) = y. Então φ γ é uma função contínua em [0, 1] que nunca se anula e portanto tem sempre o mesmo sinal. Sem perda de generalidade podemos assumir que o sinal é + e concluimos que φ(x) > 0 para todo o x B ɛ ((0, 0)) \ M. Mas então os pontos de M B ɛ ((0, 0) são pontos de mínimo de φ e portanto φ(x) = 0 para x M contráriamente ao que assumimos sobre φ. Conclui-se que M não é uma variedade de dimensão 1. (b) M = {(x, 0) : 0 < x < 1} é uma variedade de dimensão 1, já que é o gráfico da função constante 0 sobre o aberto ]0, 1[ de R. Não pode existir uma função contínua φ : E 2 R tal que φ 1 (0) = M porque φ 1 (0) é necessáriamente um conjunto fechado e M não é um subconjunto fechado de E e 4.1 O espaço vectorial das matrizes 3 3 de entradas reais M 3 (R) pode ser identificado com E 9 de forma natural. Considere o subconjunto de E 9 M = {A M 3 (R) : A t A = I} 3
4 formado pelas matrizes 3 3 ortogonais. Mostre que M é uma variedade compacta de classe C. Mostre que T I M = {A M 3 (R) : A t + A = 0}. Solução: Seja W M 3 (R) o subespaço vectorial das matrizes simétricas de M 3 (R). Defina-se F : M 3 (R) W por F (A) = A t A I. W identifica-se com E 6 tomando por exemplo as 6 entradas de uma matriz A W que não estão abaixo da diagonal. Mediante estas identificações, F é uma função de classe C já que as suas componentes são funções polinomiais. Uma vez que M = {A M 3 (R) : F (A) = 0} para ver que M é uma variedade de dimensão 3 de classe C, é suficiente ver que a derivada de F, DF (A) : M 3 (R) W é sobrejectiva para todo o A M. Como F (A + H) F (A) = A t H + H t A + H t H = A t H + H t A + o( H ) a derivada de F é dada pela fórmula DF (A)(H) = A t H + H t A. Se S é uma matriz simétrica qualquer então para qualquer A M tem-se DF (A)(AS) = A t AS + S t A t A = S + S t = 2S, logo DF (A) é sobrejectiva e portanto M é uma variedade de dimensão 3 e de classe C em E 9. Para calcular o espaço tangente a M em I, seja φ :] δ, δ[ M uma função de classe C 1 tal que φ(0) = I. Então d ( φ(s) t φ(s) ) = φ (s) t φ(s) + φ(s) t φ (s) = 0 ds Definindo H = φ (0) e avaliando a expressão anterior em s = 0 conclui-se que H + H t = 0, e portanto T I (M) {H M 3 (R) : H + H t = 0}. Uma vez que T I (M) e {H M 3 (R) : H + H t = 0} têm ambos dimensão 3, conclui-se que T I (M) = {H M 3 (R) : H + H t = 0}. 4.2 b) Seja M uma variedade compacta de dimensão n 1 em E n. Mostre que existe um intervalo J = [a 1, b 1 ] [a n, b n ] de E n com a i < b i, contendo M e cujas faces são tangentes a M. Solução: Sejam a i = min{x i : x M} e b i = max{x i : x M}, que estão bem definidos pelo Teorema de Weierstrass uma vez que M é um conjunto compacto e as funções coordenadas x i : E n R são contínuas. Por definição dos a i s e b i s, temos M [a 1, b 1 ] [a n, b n ]. Seja x M um ponto qualquer com x i = a i. Uma vez que x i é uma função diferenciável, pelo método dos multiplicadores de Lagrange, x i (x) = e i (T x M). Como M tem dimensão n 1, e i gera (T x M), portanto o hiperplano tangente a M em x é o plano {x E n : x i = a i }. De forma análoga se vê que o hiperplano 4
5 tangente aos pontos x M onde x i = b i é o hiperplano {x E n : x i = b i }. Portanto as faces do intervalo [a 1, b 1 ] [a n, b n ] são tangentes a M. Suponhamos que a i = b i para algum i. Então x i = a i para todo o x M e portanto e i (T x M) para todo o x M. Isso é impossível porque já vimos que existem pontos x M onde e j (T x M), j i e sendo M uma variedade de dimensão n 1, (T x M) tem dimensão 1 para todo o x M. Conclui-se que a i < b i para todo o i. 4.4 Seja M = {x E n : Φ(x) = 0} uma variedade, com Φ de classe C 2 tal que DΦ(x) tem característica máxima para todo o x M. Sejam f : U R uma função de classe C 2 definida num aberto contendo M, F como na regra dos multiplicadores de Lagrange e Q(x, h) = n i,j=1 F ij(x)h i h j. Mostre que (a) Se f M tem um mínimo relativo em x 0 então Q(x 0, h) 0 para todo o h T x0 M. (b) Se x 0 é um ponto de estacionariedade de F e Q(x 0, h) > 0 para todo o h T x0 M, h 0, então f M tem um mínimo relativo estrito em x 0. Solução: Primeiro note-se que F M = f M logo f M tem um extremo relativo em x 0 sse o mesmo sucede com F M. (a) Dado h T x0 M, seja φ :] δ, δ[ M uma função de classe C 2 tal que φ(0) = x 0 e 1 φ (0) = h. Uma vez que F M tem um mínimo relativo em x 0 e φ é contínua, F (φ(t)) tem um mínimo relativo em t = 0. Uma vez que F φ é de classe C 2 conclui-se que (F φ) (0) 0. Pela regra da cadeia tem-se d dt (F φ(t)) = F (φ(t)) φ (t) n = F i (φ(t))φ i (t), i=1 d 2 dt 2 (F φ(t)) = ( d n ) F i (φ(t))φ i (t) dt i=1 n = F ij (φ(t))φ i (t)φ j (t) + i,j=1 n F i (φ(t))φ i (t). O método dos multiplicadores de Lagrange garante que F (φ(0)) = F (x 0 ) = 0, pelo que (F φ) (0) = como se queria demonstrar. i=1 n F ij (x 0 )h i h j = Q(x 0, h) 0 i,j=1 1 É fácil verificar que se M é uma variedade de classe C 2 então qualquer vector tangente a M é tangente a uma curva de classe C 2 em M. 5
6 (b) Suponhamos por absurdo que x 0 não é um ponto de mínimo relativo estrito. Então existe uma sucessão de pontos y n = x 0 + h n M com h n 0, h n 0 e F (y n ) F (x 0 ). Uma vez que F é de classe C 2, F tem um desenvolvimento de Taylor de segunda ordem no ponto x 0 F (x 0 + h n ) = F (x 0 ) + F (x 0 ) h n Q(x 0 + sh n, h n ) (1) com s ]0, 1[. Uma vez que x 0 é um ponto de estacionariedade de F, o termo de primeira ordem anula-se. Vamos agora utilizar a hipótese sobre a forma quadrática Q e o facto de a direção de h n tender para a direcção de um vector tangente (num sentido que vamos tornar preciso). Considere-se a sucessão hn h n S n 1. Uma vez que S n 1 é um conjunto compacto, esta sucessão tem uma subsucessão convergente em S n 1. Sem perda de generalidade, podemos assumir que hn h h n Sn 1. Vamos ver que h T x0 M. Por definição de derivada, e porque Φ(x) = 0 para todos os pontos x M, tem-se Φ(x 0 + h n ) Φ(x 0 ) 0 = lim n h n = lim n DΦ(x 0 )h n h n = lim n DΦ(x 0) h n h n = DΦ(x 0 )h. Isto é, h pertence ao núcleo de DΦ(x 0 ) e portanto h T x0 M. Utilizando a homogeneidade de Q, a fórmula (1) implica que F (x 0 + h n ) F (x 0 ) = 1 2 h n 2 Q(x 0 + sh n, h n h n ) Uma vez que F é de classe C 2, Q é uma função contínua de ambas as variáveis, donde F (x 0 + h n ) F (x 0 ) lim n h n 2 = 1 2 Q(x 0, h). Mas isto é impossível porque, por hipótese sobre h n, o termo esquerdo tem de ser menor ou igual do que 0 enquanto que por hipótese sobre Q o termo direito é estritamente maior que 0. Notas: Conclui-se que F tem um mínimo relativo estrito em x 0. (i) Embora o argumento usado na alínea a) permita concluir que F tem um mínimo relativo estrito ao longo de cada curva em M, isso não é suficiente 6
7 para garantir imediatamente que F tem um mínimo relativo estrito em M. Por exemplo, a função g : E 2 R definida por (y 2x 2 ) 2 se y > 2x 2 g(x, y) = 0 se x 2 y 2x 2 (y x 2 ) 2 se y < x 2 tem um mínimo relativo estrito ao longo de cada recta que passa na origem mas não tem um mínimo relativo estrito na origem. De facto, se uma função g é de classe C 2 e a matriz Hessiana é definida positiva, isto não pode acontecer porque se λ > 0 for o menor dos valores próprios da matriz Hessiana de g no ponto de estacionariedade, g(x) (λ ɛ) x 2 para qualquer ɛ > 0 nalguma vizinhança do ponto (pela fórmula de Taylor). Poderia utilizar-se este facto conhecido para funções definidas em abertos de E m para demonstrar o resultado equivalente para variedades, mas para tal seria necessário considerar uma parametrização (falaremos disto mais tarde) de uma vizinhança do ponto x 0 em M e não apenas de curvas em M que passem pelo ponto x 0. (ii) A ideia básica deste resultado é a seguinte: a fórmula de Taylor (1) e a condição sobre Q garantem que a função F tem um mínimo relativo estrito quando F é restrita ao plano tangente x 0 + T x0 M. O plano tangente é uma aproximação de M a menos de um erro de ordem > 1 (para tornar isto preciso utiliza-se a fórmula de Taylor de uma parametrização de M em torno de x 0 ). Isto é, dado y = x 0 + u M, existe h T x0 M tal que y = x 0 + h + o( u ) Uma vez que o termo de primeira ordem em (1) se anula em x 0, concluise que F (y) = F (x 0 + h) + o( h 2 ), ou seja, as restrições de F a M e ao plano tangente coincidem até à segunda ordem numa vizinhança de x 0. A hipótese sobre a forma quadrática é que o termo de segunda ordem tenha um mínimo relativo estrito. Isto é suficiente para garantir que as restrições de F tanto a M como ao espaço tangente têm um mínimo relativo estrito. Note-se que não basta que a matriz Hessiana de f em x 0 seja definida positiva para que f M tenha um mínimo quando restrita a M. Como f(x 0 ) não se anula em x 0, apenas podemos garantir que as restrições de f ao plano tangente e a M diferem num termo de ordem superior a 1 em torno de x 0. Portanto a condição na Hessiana, que implica que f tenha um mínimo quando restrita ao espaço tangente, não implica o mesmo para a restrição de f a M. 5.1 Seja E a álgebra dos subconjuntos elementares de E n e V n : E [0, + ] a função aditiva definida na aula. Mostre a partir da definição de medida exterior que V n (E) V n (E). 7
8 Solução: Começamos por observar que a medida exterior pode ser definida com recurso apenas a intervalos abertos. De facto, defina-se Ṽ n (A) = inf{ V n (I k ) : I k intervalos abertos, A I k }. Então claramente, V n (A) Ṽn(A). Por outro lado, dado um intervalo I k E n limitado, existe um intervalo aberto I k I k tal que V n (I k ) < V n(i k ) + ɛ e 2 k dado um intervalo I k E n ilimitado mas com V n (I k ) = 0, existe uma família numerável {I k,l : l = 1,... } de intervalos abertos tais que I k l=1 I k,l e l=1 V n(i k,l ) < ɛ. Daqui se conclui que dado um conjunto A e uma 2 k família de intervalos I k tais que A I k e V n(i k ) <, existe uma família numerável de intervalos abertos J m tal que I k m=1j m e m=1 V n(j m ) V n(i k ) + ɛ. Isto mostra que V n (A) Ṽn(A) e portanto a medida exterior de Lebesgue pode ser definida com recurso apenas a intervalos abertos. Suponhamos agora que E é um conjunto elementar compacto e seja {I k } uma família de intervalos abertos de E n tais que E I k. Então, pelo teorema de Heine-Borel, existe N tal que E N I k. Uma vez que N I k E e V n é uma função aditiva em E, tem-se e portanto V n (E) V n (E). N V n (E) V n ( N I k ) V n (I k ) V n (I k ) Dado um conjunto elementar E arbitrário, existe uma sucessão de conjuntos elementares compactos E j tais que E j E e V n (E j ) V n (E). Uma vez que V n (E) V n (E j ) V n (E j ) conclui-se que V n (E) V n (E) o que conclui a demonstração. 5.4 a) O conjunto de Cantor C é a intersecção dos seguintes conjuntos: F 1 = [0, 1 3 ] [ 2 3, 1] F 2 = [0, 1 9 ] [ 2 9, 1 3 ] [ 2 3, 7 9 ] [ 8 9, 1] Isto é, F n+1 obtém-se de F n retirando o terço do meio de cada um dos intervalos que forma F n. Mostre que C é não numerável. Solução: A expansão de um número x [0, 1] em base 3 é, por definição, uma expressão da forma x = a k 3 k a k {0, 1, 2}. Os números que têm uma expansão finita x = N a k3 k são precisamente os múltiplos de 1 que estão entre 0 e 1 (pelo algoritmo de divisão por 3). Como 3 N 8
9 1 0 quando n, todos os números entre [0, 1] têm uma expansão em 3 N base 3. Uma vez que 2 3 k = 1 3 N (2) tem-se 0 k=n+1 k=n+1 a k 3 k 1 3 N logo os primeiros N dígitos a 1,..., a N determinam que x se encontra no intervalo [ l, l+1 ] onde l = a 3 N 3 N 1 3 N a N. A expressão (2) implica também que a expansão é única a menos do seguinte conjunto (numerável) de excepções: N a k 3 k = a k3 k sse a N = 1 ou 2, a k = a k para k < N, a N = a N 1 e a k = 2 para todo o k > N. Se convencionarmos nunca terminar uma expansão finita em 1 e nunca terminar uma expansão em 1(2), obtemos uma representação única de qualquer x [0, 1] em base 3 e não é difícil provar por indução que, utilizando esta representação, F n = {x [0, 1] : x = a k 3 k com a 1,..., a n {0, 2}}. Conclui-se que os elementos de C = F n são precisamente aqueles que têm todos os dígitos iguais a 0 ou 2. Como os elementos de C estão em correspondência bijectiva com as funções de N em {0, 2}, C é um conjunto não numerável. 5.5 Considere a seguinte relação de equivalência em R : x y sse x y Q. Seja E [0, 1] um conjunto formado escolhendo um representante de cada classe de equivalência no intervalo [0, 1]. A existência de E é assegurada por um axioma da teoria dos conjuntos chamado o axioma da escolha. (a) Seja {q n } uma enumeração dos racionais do intervalo [ 1, 1]. Mostre que [0, 1] q n + E [ 1, 2]. (b) Seja P(R) a família de todos os subconjuntos de R. Mostre que não existe nenhuma função σ-aditiva φ : P(R) [0, + ] tal que φ([0, 1]) = 1 e φ(x + A) = φ(a). (c) Mostre que E / M (isto é, E não é mensurável). Solução: 9
10 (a) Uma vez que E [0, 1] e q n [ 1, 1], tem-se q n + E [ 1, 2] para todo o n e portanto q n + E [ 1, 2]. Seja y [0, 1] e x E o representante em E da classe de equivalência de y. Então q := y x Q. Como x, y [0, 1] conclui-se que q [ 1, 1] donde y q + E q n + E. (b) Suponhamos que existe uma função φ como no enunciado. Então φ({x}) = 0 para qualquer x R. De facto, como φ é invariante por translacções φ({ 1 n }) = φ({x}) para todo o n N. Pela σ-aditividade de φ φ({x}) = φ({ 1 n }) = φ( { 1 }) φ([0, 1]) = 1, n logo φ({x}) = 0. Segue-se da aditividade e invariância por translacções de φ que φ([ 1, 2]) = φ([ 1, 0[ [0, 1] ]1, 2]) = 3. Novamente por aditividade de φ, tem-se 1 = φ([0, 1]) φ( q n + E) φ([ 1, 2]) = 3. (3) Dados q n + x q n + E e q m + y q m + E tais que q n + x = q m + y tem-se x y Q, ou seja x y. Como E contem apenas um representante de cada classe de equivalência isto implica x = y e q n = q m. Assim os conjuntos q n + E são disjuntos dois a dois e (por σ-aditividade e invariância por translacções) a equação (3) fica 1 = φ([0, 1]) φ(e) φ([ 1, 2]) = 3. (4) o que é impossível. Logo não pode existir uma função φ com as propriedades desejadas. (c) Se E fosse mensurável, o mesmo se passaria com cada uma das suas translacções e portanto com q n + E. As desigualdades (4) com φ substituído por V 1 teriam de se verificar o que é impossível. 10
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
Resumos de CDI-II. 1. Topologia e Continuidade de Funções em R n. 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto
 Resumos de CD- 1. Topologia e Continuidade de Funções em R n 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto B r (a) = {x R n : x a < r}. 2. Seja A R n um conjunto. m ponto a A diz-se: (i)
Resumos de CD- 1. Topologia e Continuidade de Funções em R n 1. A bola aberta de centro em a R n e raio r > 0 é o conjunto B r (a) = {x R n : x a < r}. 2. Seja A R n um conjunto. m ponto a A diz-se: (i)
CDI-II. Resumo das Aulas Teóricas (Semana 1) 2 Norma. Distância. Bola. R n = R R R
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 1) 1 Notação R n = R R R x R n : x = (x 1, x 2,, x n ) ; x
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 1) 1 Notação R n = R R R x R n : x = (x 1, x 2,, x n ) ; x
Capítulo Topologia e sucessões. 7.1 Considere o subconjunto de R 2 : D = {(x, y) : xy > 1}.
 Capítulo 7 Introdução à Análise em R n 7. Topologia e sucessões 7. Considere o subconjunto de R 2 : D = {(x, y) : > }.. Indique um ponto interior, um ponto fronteiro e um ponto exterior ao conjunto D e
Capítulo 7 Introdução à Análise em R n 7. Topologia e sucessões 7. Considere o subconjunto de R 2 : D = {(x, y) : > }.. Indique um ponto interior, um ponto fronteiro e um ponto exterior ao conjunto D e
1.3 Conjuntos de medida nula
 1.3 Conjuntos de medida nula Seja (X, F, µ) um espaço de medida. Um subconjunto A X é um conjunto de medida nula se existir B F tal que A B e µ(b) = 0. Do ponto de vista da teoria da medida, os conjuntos
1.3 Conjuntos de medida nula Seja (X, F, µ) um espaço de medida. Um subconjunto A X é um conjunto de medida nula se existir B F tal que A B e µ(b) = 0. Do ponto de vista da teoria da medida, os conjuntos
Introdução à Análise Funcional
 Introdução à Análise Funcional José Carlos de Sousa Oliveira Santos Departamento de Matemática Pura Faculdade de Ciências Universidade do Porto Porto Julho de 2010 Índice Índice Introdução i iii 1 Teoria
Introdução à Análise Funcional José Carlos de Sousa Oliveira Santos Departamento de Matemática Pura Faculdade de Ciências Universidade do Porto Porto Julho de 2010 Índice Índice Introdução i iii 1 Teoria
Topologia e Análise Linear. Maria Manuel Clementino, 2013/14
 Maria Manuel Clementino, 2013/14 2013/14 1 ESPAÇOS MÉTRICOS Espaço Métrico Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições,
Maria Manuel Clementino, 2013/14 2013/14 1 ESPAÇOS MÉTRICOS Espaço Métrico Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições,
Curvas e superfícies
 Análise Matemática III Curvas e superfícies Manuel Guerra Conteúdo 1 Curvas 2 2 Curvas definidas implicitamente 11 3 Superfícies 17 4 Superfícies definidas implicitamente 20 5 Anexo: A curva de Peano 21
Análise Matemática III Curvas e superfícies Manuel Guerra Conteúdo 1 Curvas 2 2 Curvas definidas implicitamente 11 3 Superfícies 17 4 Superfícies definidas implicitamente 20 5 Anexo: A curva de Peano 21
ANÁLISE MATEMÁTICA III A OUTONO 2005 PARTE I VARIEDADES EM R N. Sobre Topologia em R n
 Departamento de Matemática Secção de Álgebra e Análise Última actualização: 17/Set/005 ANÁLISE MATEMÁTICA III A OUTONO 005 PARTE I VARIEDADES EM R N EXERCÍCIOS COM POSSÍVEIS SOLUÇÕES ABREVIADAS acessível
Departamento de Matemática Secção de Álgebra e Análise Última actualização: 17/Set/005 ANÁLISE MATEMÁTICA III A OUTONO 005 PARTE I VARIEDADES EM R N EXERCÍCIOS COM POSSÍVEIS SOLUÇÕES ABREVIADAS acessível
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
[À funç~ao d chama-se métrica e aos elementos de X pontos do espaço métrico; a condiç~ao (3) designa-se por desigualdade triangular.
 Aula I - Topologia e Análise Linear 1 Espaços Métricos ESPAÇO MÉTRICO Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições, quaisquer
Aula I - Topologia e Análise Linear 1 Espaços Métricos ESPAÇO MÉTRICO Um par (X, d) diz-se um espaço métrico se X for um conjunto e d : X X R + for uma aplicação que verifica as seguintes condições, quaisquer
Cap. 5 Estabilidade de Lyapunov
 Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
O Teorema de Peano. f : D R n. uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e uma função ϕ : I R n tais que
 O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
Cálculo Diferencial e Integral II Resolução do Exame/Teste de Recuperação 02 de Julho de 2018, 15:00h - versão 2 Duração: Exame (3h), Teste (1h30)
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Cálculo Diferencial e Integral II 2012/13 1 o semestre
 Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
Análise Matemática III Resolução do 2 ō Teste e 1 ō Exame - 20 de Janeiro horas
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Análise Matemática III Resolução do ō Teste e ō Exame - de Janeiro - 9 horas. O sólido tem simetria cilíndrica em torno do
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Análise Matemática III Resolução do ō Teste e ō Exame - de Janeiro - 9 horas. O sólido tem simetria cilíndrica em torno do
3 Funções reais de variável real (Soluções)
 3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
ANÁLISE MATEMÁTICA III A TESTE 1 10 DE OUTUBRO DE :10-16H. Duração: 50 minutos
 Departamento de Matemática Secção de Álgebra e Análise Última actualização: 10/Out/2005 ANÁLISE MATEMÁTICA III A TESTE 1 10 DE OUTUBRO DE 2005 15:10-16H RESOLUÇÃO (As soluções aqui propostas não são únicas!)
Departamento de Matemática Secção de Álgebra e Análise Última actualização: 10/Out/2005 ANÁLISE MATEMÁTICA III A TESTE 1 10 DE OUTUBRO DE 2005 15:10-16H RESOLUÇÃO (As soluções aqui propostas não são únicas!)
MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos
 MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos Prof. Edson de Faria 30 de Março de 2014 Observação: O objetivo desta lista é motivar uma revisão dos conceitos e fatos básicos sobre
MAT 5798 Medida e Integração Exercícios de Revisão de Espaços Métricos Prof. Edson de Faria 30 de Março de 2014 Observação: O objetivo desta lista é motivar uma revisão dos conceitos e fatos básicos sobre
2.1 Sucessões. Convergência de sucessões
 Capítulo 2 Sucessões reais Inicia-se o capítulo introduzindo os conceitos de sucessão limitada, sucessão monótona, sucessão convergente e relacionando estes conceitos entre si. A análise da convergência
Capítulo 2 Sucessões reais Inicia-se o capítulo introduzindo os conceitos de sucessão limitada, sucessão monótona, sucessão convergente e relacionando estes conceitos entre si. A análise da convergência
Exercícios Resolvidos Variedades
 Instituto Superior Técnico Departamento de atemática Secção de Álgebra e Análise Eercícios Resolvidos Variedades Eercício 1 Considere o conjunto = {(,, ) R : + = 1 ; 0 < < 1}. ostre que é uma variedade,
Instituto Superior Técnico Departamento de atemática Secção de Álgebra e Análise Eercícios Resolvidos Variedades Eercício 1 Considere o conjunto = {(,, ) R : + = 1 ; 0 < < 1}. ostre que é uma variedade,
1 Álgebra linear matricial
 MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
(2) Seja {U α } uma família não vazia de elementos de T c. Se todos os U α são vazios, então a sua união também é e portanto pertence a T c.
 RESOLUÇÃO DOS EXERCÍCIOS DE TOPOLOGIA PARA 23/2 Munkres 3.3: Vejamos que T c = {U X : X \ U é contável ou todo o X} verifica os axiomas para uma topologia em X: () T c porque X \ é todo o X; X T c porque
RESOLUÇÃO DOS EXERCÍCIOS DE TOPOLOGIA PARA 23/2 Munkres 3.3: Vejamos que T c = {U X : X \ U é contável ou todo o X} verifica os axiomas para uma topologia em X: () T c porque X \ é todo o X; X T c porque
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3]. Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg) Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
CDI-II. Resumo das Aulas Teóricas (Semana 5) 1 Extremos de Funções Escalares. Exemplos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 5) 1 Etremos de Funções Escalares. Eemplos Nos eemplos seguintes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 5) 1 Etremos de Funções Escalares. Eemplos Nos eemplos seguintes
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Teoremas fundamentais dos espaços normados
 Capítulo 9 Teoremas fundamentais dos espaços normados 9.1 Teorema de Hahn-Banach O próximo teorema, conhecido como teorema de Hahn-Banach, é uma generalização do Teorema 4.12, o qual, recordamos para conveniência
Capítulo 9 Teoremas fundamentais dos espaços normados 9.1 Teorema de Hahn-Banach O próximo teorema, conhecido como teorema de Hahn-Banach, é uma generalização do Teorema 4.12, o qual, recordamos para conveniência
x B A x X B B A τ x B 3 B 1 B 2
 1. Definição e exemplos. Bases. Dar uma topologia num conjunto X é especificar quais dos subconjuntos de X são abertos: Definição 1.1. Um espaço topológico é um par (X, τ) em que τ é uma colecção de subconjuntos
1. Definição e exemplos. Bases. Dar uma topologia num conjunto X é especificar quais dos subconjuntos de X são abertos: Definição 1.1. Um espaço topológico é um par (X, τ) em que τ é uma colecção de subconjuntos
ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral
 Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis
 Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis Neste capítulo vamos estender as noções do cálculo diferencial a funções que dependem de mais de uma variável
Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis Neste capítulo vamos estender as noções do cálculo diferencial a funções que dependem de mais de uma variável
7.3 Diferenciabilidade
 CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
Convergência em espaços normados
 Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Sumários Alargados. Recomenda-se a leitura de: Capítulos 0 e 1 de: J. Lewin/M. Lewin, An Introduction to Mathematical Analysis;
 Sumários Alargados Capítulo I: Fundamentos o Rigor e a Demonstração em Análise 1. Operadores lógicos e quantificadores Recomenda-se a leitura de: Capítulos 0 e 1 de: J. Lewin/M. Lewin, An Introduction
Sumários Alargados Capítulo I: Fundamentos o Rigor e a Demonstração em Análise 1. Operadores lógicos e quantificadores Recomenda-se a leitura de: Capítulos 0 e 1 de: J. Lewin/M. Lewin, An Introduction
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Imersões e Mergulhos. 4 a aula,
 4 a aula, 12-04-2007 Imersões e Mergulhos Um mapa entre variedades f : X Y diz-se um mergulho sse (1) é uma imersão, i.e., Df x : T x X T f(x) Y é injectiva, para todo x X, (2) é injectiva, e (3) a inversa
4 a aula, 12-04-2007 Imersões e Mergulhos Um mapa entre variedades f : X Y diz-se um mergulho sse (1) é uma imersão, i.e., Df x : T x X T f(x) Y é injectiva, para todo x X, (2) é injectiva, e (3) a inversa
Operadores em espaços normados
 Capítulo 7 Operadores em espaços normados Neste capítulo vamos introduzir uma série de operadores em espaços normados os quais são muito úteis, nomeadamente, na resolução de equações envolvendo operadores.
Capítulo 7 Operadores em espaços normados Neste capítulo vamos introduzir uma série de operadores em espaços normados os quais são muito úteis, nomeadamente, na resolução de equações envolvendo operadores.
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Exame/Teste de Recuperação v2-8h - 29 de Junho de 215 Duração: Teste - 1h3m; Exame -
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Exame/Teste de Recuperação v2-8h - 29 de Junho de 215 Duração: Teste - 1h3m; Exame -
Apresente todos os cálculos e justificações relevantes
 Análise Matemática I 2 o Teste e o Exame Campus da Alameda 9 de Janeiro de 2006, 3 horas Licenciaturas em Engenharia do Ambiente, Engenharia Biológica, Engenharia Civil, Engenharia e Arquitectura Naval,
Análise Matemática I 2 o Teste e o Exame Campus da Alameda 9 de Janeiro de 2006, 3 horas Licenciaturas em Engenharia do Ambiente, Engenharia Biológica, Engenharia Civil, Engenharia e Arquitectura Naval,
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n
 Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
Análise Infinitesimal I. Maria Manuel Clementino, 2010/11
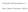 Análise Infinitesimal I Maria Manuel Clementino, 2010/11 Sumários Alargados Capítulo I: Fundamentos o Rigor e a Demonstração em Análise 1. Operadores lógicos e quantificadores Recomenda-se a leitura de:
Análise Infinitesimal I Maria Manuel Clementino, 2010/11 Sumários Alargados Capítulo I: Fundamentos o Rigor e a Demonstração em Análise 1. Operadores lógicos e quantificadores Recomenda-se a leitura de:
Análise Matemática II - 1 o Semestre 2001/ o Exame - 25 de Janeiro de h
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Questão 4 (2,0 pontos). Defina função convexa (0,5 pontos). Seja f : I R uma função convexa no intervalo aberto I. Dado c I (qualquer)
 DM IMECC UNICAMP, Análise I, Prof. Marcelo M. Santos Exame Final, 15/07/2009 Aluno: RA: Ass.: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha as suas resoluções
DM IMECC UNICAMP, Análise I, Prof. Marcelo M. Santos Exame Final, 15/07/2009 Aluno: RA: Ass.: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha as suas resoluções
Variedades diferenciáveis e grupos de Lie
 LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Resolução do Eame / Testes de Recuperação I.. (, val.)determine os ites das seguintes sucessões convergentes (i) u n n + n n e n + n, (ii) v n n + π n Resolução: i) A sucessão
Cálculo Diferencial e Integral I Resolução do Eame / Testes de Recuperação I.. (, val.)determine os ites das seguintes sucessões convergentes (i) u n n + n n e n + n, (ii) v n n + π n Resolução: i) A sucessão
FICHA DE TRABALHO 2 - RESOLUÇÃO
 Secção de Álgebra e Análise, Departamento de Matemática, Instituto Superior Técnico Análise Matemática III A - 1 o semestre de 2003/04 FICHA DE TRABALHO 2 - RESOLUÇÃO 1) Seja U R n um aberto e f : U R
Secção de Álgebra e Análise, Departamento de Matemática, Instituto Superior Técnico Análise Matemática III A - 1 o semestre de 2003/04 FICHA DE TRABALHO 2 - RESOLUÇÃO 1) Seja U R n um aberto e f : U R
3 Limites e Continuidade(Soluções)
 3 Limites e Continuidade(Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y = log y
3 Limites e Continuidade(Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y = log y
Exercício 18. Demonstre a proposição anterior. (Dica: use as definições de continuidade e mensurabilidade)
 Proposição 2.7. Sejam Y e Z espaços métricos e X um espaço mensurável. Se f : X Y é uma função mensurável e g : Y Z é uma função contínua então g f : X Z é uma função mensurável. Exercício 18. Demonstre
Proposição 2.7. Sejam Y e Z espaços métricos e X um espaço mensurável. Se f : X Y é uma função mensurável e g : Y Z é uma função contínua então g f : X Z é uma função mensurável. Exercício 18. Demonstre
Análise I Solução da 1ª Lista de Exercícios
 FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
Topologia. Fernando Silva. (Licenciatura em Matemática, 2007/2008) 13-agosto-2018
 Topologia (Licenciatura em Matemática, 2007/2008) Fernando Silva 13-agosto-2018 A última revisão deste texto está disponível em http://webpages.fc.ul.pt/~fasilva/top/ Este texto é uma revisão do texto
Topologia (Licenciatura em Matemática, 2007/2008) Fernando Silva 13-agosto-2018 A última revisão deste texto está disponível em http://webpages.fc.ul.pt/~fasilva/top/ Este texto é uma revisão do texto
Curso: MAT 221- CÁLCULO DIFERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008
 Curso: MAT 221- CÁLCULO DIERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008 SÉRIES E SOMAS EM ÁLGEBRAS: C([a, b]), M n n (R), M n n (C), etc. O PRODUTO DE
Curso: MAT 221- CÁLCULO DIERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008 SÉRIES E SOMAS EM ÁLGEBRAS: C([a, b]), M n n (R), M n n (C), etc. O PRODUTO DE
Teoria da Medida e Integração (MAT505)
 Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Gabarito da Primeira Prova MAT0234 Análise Matemática I Prof. Daniel Victor Tausk 13/09/2011
 Gabarito da Primeira Prova MAT0234 Análise Matemática I Prof. Daniel Victor Tausk 13/09/2011 Questão 1. Sejam X, X conjuntos e φ : X X uma função. (a) (valor 1,25 pontos) Mostre que se A é uma σ-álgebra
Gabarito da Primeira Prova MAT0234 Análise Matemática I Prof. Daniel Victor Tausk 13/09/2011 Questão 1. Sejam X, X conjuntos e φ : X X uma função. (a) (valor 1,25 pontos) Mostre que se A é uma σ-álgebra
Compacidade de conjuntos e operadores lineares
 Compacidade de conjuntos e operadores lineares Roberto Imbuzeiro Oliveira 13 de Janeiro de 2010 No que segue, F = R ou C e (X, X ), (Y, Y ) são Banach sobre F. Recordamos que um operador linear T : X Y
Compacidade de conjuntos e operadores lineares Roberto Imbuzeiro Oliveira 13 de Janeiro de 2010 No que segue, F = R ou C e (X, X ), (Y, Y ) são Banach sobre F. Recordamos que um operador linear T : X Y
MAT Topologia Bacharelado em Matemática 2 a Prova - 27 de maio de 2004
 MAT 317 - Topologia Bacharelado em Matemática 2 a Prova - 27 de maio de 2004 1 Nome : Número USP : Assinatura : Professor : Severino Toscano do Rêgo Melo 2 3 4 5 Total Podem tentar fazer todas as questões.
MAT 317 - Topologia Bacharelado em Matemática 2 a Prova - 27 de maio de 2004 1 Nome : Número USP : Assinatura : Professor : Severino Toscano do Rêgo Melo 2 3 4 5 Total Podem tentar fazer todas as questões.
Teoria da Medida e Integração (MAT505)
 Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Funções suaves e Variedades
 a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
CDI-II. Resumo das Aulas Teóricas (Semana 4) ; k = 1, 2,..., n.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II esumo das Aulas Teóricas (Semana 4 1 Derivadas de Ordem Superior Seja f : D n, definida num
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II esumo das Aulas Teóricas (Semana 4 1 Derivadas de Ordem Superior Seja f : D n, definida num
Análise Matemática I 1 o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI)
 Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I
 Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I 2013/2014 Exercício 1. Seja (, F) um espaço mensurável. Mostre que 1. F. 2. se A i F, i = 1, 2,... então n i=1 A i F. 3. se A i F,
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I 2013/2014 Exercício 1. Seja (, F) um espaço mensurável. Mostre que 1. F. 2. se A i F, i = 1, 2,... então n i=1 A i F. 3. se A i F,
T. Rolle, Lagrange e Cauchy
 T. Rolle, Lagrange e Cauchy EXERCÍCIOS RESOLVIDOS. Mostre que a equação 5 + 5 = 5 tem uma única solução em R. Seja f = 5 +5 5. Então f é contínua e diferenciável em R. Temos f = 5 4 + > 0, em R, logo f
T. Rolle, Lagrange e Cauchy EXERCÍCIOS RESOLVIDOS. Mostre que a equação 5 + 5 = 5 tem uma única solução em R. Seja f = 5 +5 5. Então f é contínua e diferenciável em R. Temos f = 5 4 + > 0, em R, logo f
Teorema das pré-imagens para variedades com bordo
 9 a aula, 17-05-2007 Teorema das pré-imagens para variedades com bordo Teorema das pré-imagens Sejam X, Y variedades orientadas, X com bordo e Y sem bordo tais que dim(x) dim(y ). Se c Y for um valor regular
9 a aula, 17-05-2007 Teorema das pré-imagens para variedades com bordo Teorema das pré-imagens Sejam X, Y variedades orientadas, X com bordo e Y sem bordo tais que dim(x) dim(y ). Se c Y for um valor regular
CDI-II. Limites. Continuidade
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Limites. Continuidade 1 Introdução Oassunto central docálculo emr n éoestudo defunções cujosdomínios
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Limites. Continuidade 1 Introdução Oassunto central docálculo emr n éoestudo defunções cujosdomínios
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então
 Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
ANÁLISE MATEMÁTICA III TESTE 2-9 DE JUNHO DE apresente e justifique todos os cálculos duração: hora e meia (19:00-20:30)
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA III TETE - VERÃO A 9 DE JUNHO DE apresente e justifique todos os cálculos duração: hora e meia (9: - :3
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA III TETE - VERÃO A 9 DE JUNHO DE apresente e justifique todos os cálculos duração: hora e meia (9: - :3
Resumo dos resumos de CDI-II
 Resumo dos resumos de DI-II 1 Topologia e ontinuidade de Funções em R n 1 Limites direccionais: Se lim f(x, mx) x 0 não existe, ou existe mas depende de m, então não existe lim f(x, y) (x,y) (0,0) 2 Produto
Resumo dos resumos de DI-II 1 Topologia e ontinuidade de Funções em R n 1 Limites direccionais: Se lim f(x, mx) x 0 não existe, ou existe mas depende de m, então não existe lim f(x, y) (x,y) (0,0) 2 Produto
Departamento de Matemática Faculdade de Ciências e Tecnologia Universidade de Coimbra Cálculo III - Engenharia Electrotécnica e de Computadores
 Departamento de Matemática Faculdade de Ciências e Tecnologia Universidade de Coimbra - Engenharia Electrotécnica e de Computadores Noções Fundamentais do Cálculo Diferencial e Integral ÍNDICE GERAL 1.
Departamento de Matemática Faculdade de Ciências e Tecnologia Universidade de Coimbra - Engenharia Electrotécnica e de Computadores Noções Fundamentais do Cálculo Diferencial e Integral ÍNDICE GERAL 1.
Teoria espectral de operadores lineares limitados
 Capítulo 8 Teoria espectral de operadores lineares limitados A teoria espectral é um dos ramos principais da análise funcional moderna e suas aplicações. Essencialmente consiste no inverso de certos operadores,
Capítulo 8 Teoria espectral de operadores lineares limitados A teoria espectral é um dos ramos principais da análise funcional moderna e suas aplicações. Essencialmente consiste no inverso de certos operadores,
MAT Cálculo Avançado - Notas de Aula
 bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Cálculo Diferencial e Integral II 1 o Teste (Versão A)
 Cálculo Diferencial e Integral II 1 o Teste (ersão A) LEIC-TP, LETI, LEE, LEGI 11 de Abril de 015 Justifique adequadamente todas as respostas. (5,0) 1. Seja = {(, y, z) [ 1, 1] [0, 1] R 3 : 0 z, 0 y 1}
Cálculo Diferencial e Integral II 1 o Teste (ersão A) LEIC-TP, LETI, LEE, LEGI 11 de Abril de 015 Justifique adequadamente todas as respostas. (5,0) 1. Seja = {(, y, z) [ 1, 1] [0, 1] R 3 : 0 z, 0 y 1}
Exercícios de Cálculo Diferencial e Integral I, Amélia Bastos, António Bravo, Paulo Lopes 2011
 Eercícios de Cálculo Diferencial e Integral I, Amélia Bastos, António Bravo, Paulo Lopes Introdução Neste teto apresentam-se os enunciados de conjuntos de eercícios para as aulas de problemas do curso
Eercícios de Cálculo Diferencial e Integral I, Amélia Bastos, António Bravo, Paulo Lopes Introdução Neste teto apresentam-se os enunciados de conjuntos de eercícios para as aulas de problemas do curso
TEOREMA FUNDAMENTAL DO CÁLCULO PARA INTEGRAIS MÚLTIPLOS, O TEOREMA DE GAUSS, O TEOREMA DE GREEN E O TEOREMA DE STOKES. d f (x) dx = f (b) f (a).
 TEOREMA FUNDAMENTAL DO CÁLCULO PARA INTEGRAIS MÚLTIPLOS, O TEOREMA DE GAUSS, O TEOREMA DE GREEN E O TEOREMA DE STOKES O teorema fundamental de cálculo em R diz que para uma função f de classe C 1 definida
TEOREMA FUNDAMENTAL DO CÁLCULO PARA INTEGRAIS MÚLTIPLOS, O TEOREMA DE GAUSS, O TEOREMA DE GREEN E O TEOREMA DE STOKES O teorema fundamental de cálculo em R diz que para uma função f de classe C 1 definida
Ficha de Problemas n o 6: Cálculo Diferencial (soluções) 2.Teoremas de Rolle, Lagrange e Cauchy
 Ficha de Problemas n o 6: Cálculo Diferencial soluções).teoremas de Rolle, Lagrange e Cauchy. Seja f) = 3 e. Então f é contínua e diferenciável em R. Uma vez que f) = +, f0) = conclui-se do Teorema do
Ficha de Problemas n o 6: Cálculo Diferencial soluções).teoremas de Rolle, Lagrange e Cauchy. Seja f) = 3 e. Então f é contínua e diferenciável em R. Uma vez que f) = +, f0) = conclui-se do Teorema do
) a sucessão definida por y n
 aula 05 Sucessões 5.1 Sucessões Uma sucessão de números reais é simplesmente uma função x N R. É conveniente visualizar uma sucessão como uma sequência infinita: (x(), x(), x(), ). Neste contexto é usual
aula 05 Sucessões 5.1 Sucessões Uma sucessão de números reais é simplesmente uma função x N R. É conveniente visualizar uma sucessão como uma sequência infinita: (x(), x(), x(), ). Neste contexto é usual
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA. Medida e Probabilidade
 UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
Questão 3. a) (1,5 pontos). Defina i) conjunto aberto, ii) conjunto
 DM IMECC UNICAMP Análise I Prof. Marcelo M. Santos Prova de Segunda Chamada, 08/07/2009 Aluno: Assinatura: RA: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha
DM IMECC UNICAMP Análise I Prof. Marcelo M. Santos Prova de Segunda Chamada, 08/07/2009 Aluno: Assinatura: RA: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Exercícios de Cálculo p. Informática, Ex 1-1 Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar
 Eercícios de Cálculo p. Informática, 2006-07 Números Reais. E - Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar o número dado: 7 a) b) 6 7 c) 2.(3) = 2.33 d) 2 3 e)
Eercícios de Cálculo p. Informática, 2006-07 Números Reais. E - Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar o número dado: 7 a) b) 6 7 c) 2.(3) = 2.33 d) 2 3 e)
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Funções reais de variável real.
 Capítulo 3 Funções reais de variável real. Continuidade. Diferenciabilidade. Este capítulo tem como primeiro objectivo desenvolver as bases da teoria da continuidade de funções reais de variável real.
Capítulo 3 Funções reais de variável real. Continuidade. Diferenciabilidade. Este capítulo tem como primeiro objectivo desenvolver as bases da teoria da continuidade de funções reais de variável real.
Decimaseptima áula: espaços completos e compactos
 Decimaseptima áula: espaços completos e compactos Lembramos que: Definição 0.1. Um espaço métrico (M, d) diz-se completo quando toda sequência de Cauchy é convergente. Um espaço métrico (M, d) diz-se compacto
Decimaseptima áula: espaços completos e compactos Lembramos que: Definição 0.1. Um espaço métrico (M, d) diz-se completo quando toda sequência de Cauchy é convergente. Um espaço métrico (M, d) diz-se compacto
Winding Numbers. 11 a aula, É costume chamar-se variedade fechada 1 a qualquer variedade compacta sem bordo.
 11 a aula, 31-05-2007 Winding Numbers É costume chamar-se variedade fechada 1 a qualquer variedade compacta sem bordo. Sejam X n 1 uma variedade fechada, f : X n 1 R n um mapa suave e p um ponto em R n
11 a aula, 31-05-2007 Winding Numbers É costume chamar-se variedade fechada 1 a qualquer variedade compacta sem bordo. Sejam X n 1 uma variedade fechada, f : X n 1 R n um mapa suave e p um ponto em R n
Então (τ x, ) é um conjunto dirigido e se tomarmos x U U, para cada U vizinhança de x, então (x U ) U I é uma rede em X.
 1. Redes Quando trabalhamos no R n, podemos testar várias propriedades de um conjunto A usando seqüências. Por exemplo: se A = A, se A é compacto, ou se a função f : R n R m é contínua. Mas, em espaços
1. Redes Quando trabalhamos no R n, podemos testar várias propriedades de um conjunto A usando seqüências. Por exemplo: se A = A, se A é compacto, ou se a função f : R n R m é contínua. Mas, em espaços
A forma canônica de Jordan
 A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
Professor: Carlos Eugênio da Costa Teoria Microeconômica II Monitor: Diego Santiago
 Professor: Carlos Eugênio da Costa Teoria Microeconômica II - 2012 Monitor: Diego Santiago EPGE/FGV Introdução matemática 1 Introdução Esta introdução visa familiarizar o aluno com ferramentas matemáticas
Professor: Carlos Eugênio da Costa Teoria Microeconômica II - 2012 Monitor: Diego Santiago EPGE/FGV Introdução matemática 1 Introdução Esta introdução visa familiarizar o aluno com ferramentas matemáticas
FCUP Dep. Matemática Pura
 FCUP Dep. Matemática Pura CURSO de ANÁLISE INFINITESIMAL RESUMO das Aulas Teóricas João Nuno Tavares Dept. Matemática Pura, Faculdade de Ciências, Univ. Porto, 4050 Porto, Portugal 1 1 E-mail adress: jntavar@fc.up.pt
FCUP Dep. Matemática Pura CURSO de ANÁLISE INFINITESIMAL RESUMO das Aulas Teóricas João Nuno Tavares Dept. Matemática Pura, Faculdade de Ciências, Univ. Porto, 4050 Porto, Portugal 1 1 E-mail adress: jntavar@fc.up.pt
TEOREMA DE STONE-WEIERSTRASS PARA ESPAÇOS LOCALMENTE COMPACTOS
 UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA TEOREMA DE STONE-WEIERSTRASS PARA ESPAÇOS LOCALMENTE COMPACTOS FELIPE AUGUSTO TASCA Trabalho de
UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA TEOREMA DE STONE-WEIERSTRASS PARA ESPAÇOS LOCALMENTE COMPACTOS FELIPE AUGUSTO TASCA Trabalho de
Limites e continuidade
 Limites e continuidade Limite (finito) de uma função em a Salvo indicação em contrário, quando nos referimos a uma função estamos sempre a considerar funções reais de variável real (f.r.v.r.), ou seja,
Limites e continuidade Limite (finito) de uma função em a Salvo indicação em contrário, quando nos referimos a uma função estamos sempre a considerar funções reais de variável real (f.r.v.r.), ou seja,
Sumário e Objectivos. Mecânica dos Sólidos não Linear Capítulo 2. Lúcia Dinis 2005/2006
 Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
MAT-2454 Cálculo Diferencial e Integral II EP-USP
 MAT-454 Cálculo Diferencial e Integral II EP-USP Solução da Questão da Terceira Prova 8//06 Questão (Tipo A Valor: 3, 0 pontos). a. Determine todos os pontos da superfície de nível da função g(x, y, z)
MAT-454 Cálculo Diferencial e Integral II EP-USP Solução da Questão da Terceira Prova 8//06 Questão (Tipo A Valor: 3, 0 pontos). a. Determine todos os pontos da superfície de nível da função g(x, y, z)
1. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R
 . Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
Propriedades das Funções Contínuas
 Propriedades das Funções Contínuas Prof. Doherty Andrade 2005- UEM Sumário 1 Seqüências 2 1.1 O Corpo dos Números Reais.......................... 2 1.2 Seqüências.................................... 5
Propriedades das Funções Contínuas Prof. Doherty Andrade 2005- UEM Sumário 1 Seqüências 2 1.1 O Corpo dos Números Reais.......................... 2 1.2 Seqüências.................................... 5
