Uma breve análise do movimento Browniano
|
|
|
- Vítor Gabriel Bonilha
- 5 Há anos
- Visualizações:
Transcrição
1 Universidade Federal do Espírito Santo UFES Departamento de Matemática Programa de Pós-Graduação em Matemática Uma breve análise do movimento Browniano Vitória -ES, Brasil de Dezembro de 04
2
3 Universidade Federal do Espírito Santo UFES Departamento de Matemática Programa de Pós-Graduação em Matemática Uma breve análise do movimento Browniano Oscar Mario Londoño Duque Orientador: Fábio Júlio da Silva Valentim Vitória -ES, Brasil de Dezembro de 04
4 Universidade Federal do Espírito Santo UFES Departamento de Matemática Programa de Pós-Graduação em Matemática Uma breve análise do movimento Browniano/ Universidade Federal do Espírito Santo UFES Departamento de Matemática Programa de Pós-Graduação em Matemática. Vitória -ES, Brasil, de Dezembro de 04- Orientador: Fábio Júlio da Silva Valentim Dissertação(Mestrado) Oscar Mario Londoño Duque, de Dezembro de 04.. Noções básicas de teoria da probabilidade.. Movimento browniano: Definição e propriedades de suas trajetórias. 3. Movimento Browniano e alguns processos relacionados I. Fábio Júlio da Silva Valentim. II. Universidade Federal do Espírito Santo. III. Departamento de Matemática. IV. Uma breve análise do movimento Browniano CDU 0:4:005.7
5 Agradecimentos Primeiramente, agradeço á minha família (Mãe, Pai) Não só por motivar meus estudos, sim por tudo minha vida. Dedico a vocês esta conquista. Agradeço a meus colegas do mestrado, Silvano, Vitor, Nadia e Solon pela amizade e vontade também a meus professores do PPGMAT-UFES por sua paciência e disposição para ensinar, especialmente, meu orientador o professor Fábio Júlio da Silva Valentim, a secretaria do PPGMAT-UFES, Jussára. Agradeço CAPES pelo apoio financeiro. Enquanto Deus está nos céus, todo na terra vai ficar bem
6
7 Resumo Este texto tem como objetivo principal estudar de forma introdutória o movimento browniano. Pretendemos apresentar algumas propriedades de suas trajetórias, em particular, abordando questões de continuidade, diferenciabilidade e recorrência. Ademais, identificaremos o movimento browniano como exemplo de diferentes classes de processos estocásticos, por exemplo, como um processo de Markov, gaussiano, martingal e de Lévy. Finalizamos com construção de alguns processos a partir do movimento browniano Palavras-chaves: Movimento Browniano. Processos Estocásticos. Processo Gaussiano. Martingal. Processo de Markov. Processo de Levy.
8
9 Abstract This text has as main objective to study an introductory way Brownian motion. We intend to present some properties of their trajectories, in particular, addressing questions of continuity, differentiability and recurrence. Furthermore, Brownian motion identified as an example of different classes of stochastic processes, for example, as a Markov process, Gaussian, Lévy and martingale. Finalized with construction of some processes from Brownian motion. Key-words: Brownian movement. Stochastic Processes. Gaussian process. Martingale. Markov process. Levy process.
10
11 Lista de ilustrações Figura Movimento Browniano usual em 3D Figura Relação entre os tipos de convergência Figura 3 Movimento browniano planar para 00 passos Figura 4 Movimiento browniano B t em [0, ] Figura 5 Primeira iteração X (0) t Figura 6 Segunda iteração X () t Figura 7 Terceira iteração X () (t) Figura 8 Passeio Aleatório discreto com 0 passos, simetrico +- e probabilidade Figura 9 Malha de decisão com probabilidade p e q Figura 0 Trajetória discreta simples e simétrica com 40 passos Figura Trajetória discreta não simples e não simétrica com 40 passos Figura Passeio aleatório discreto simples e simétrico com 00 passos Figura 3 Três passeios aleatórios discretos com 0 passos, e com passeio médio. 64 Figura 4 Três passeios aleatórios discretos com 00 passos, e com passeio médio 66 Figura 5 Passeio aleatório discreto com 000 passos Figura 6 Passeios aleatórios não simples e não simétrica com 5 passos Figura 7 interpolação linear de passeios aleatórios não simples e não simétrica com 000 passos Figura 8 Movimento browniano, com t [0, 0] com uma partição de Figura 9 Movimento browniano, com t [0, ] com uma partição de Figura 0 Movimento browniano B t e tb t com 00 passos, com t [0, ] Figura Movimento browniano B t e B t com 300 passos, com t [0, ] Figura Movimento browniano B t e B t+t0 B t0 com 300 passos, com t [0, ] e t 0 = tu ubt Figura 3 Martingal e com t [0, ] u =.00 e 500 passos Figura 4 Movimento browniano com ponte para T = com 500 passos Figura 5 Movimento browniano com Drift para t [0, 00], μ = 0. e σ = 0. com passos Figura 6 Movimento browniano geométrico para t [0, ], μ = 0. e σ = com 000 passos Figura 7 Processo Ornstein-Uhlenbeck para t [0, ], β =, σ = 0.0 e v = 0. com 300 passos
12 Figura 8 Movimento browniano fracionário para 000 passos com H=0. e H=0.4 e t [0, ] Figura 9 Movimento browniano fracionário para 000 passos com H=0.5, H=0.7 e H=0.8 e t [0, ]
13 Sumário Introdução Noções básicas de teoria da probabilidade Conceitos básicos de probabilidade Independência Esperança Propriedades da esperança Variância Propriedades da variância Convergência de variáveis aleatórias Lema de Borel-Cantelli Tipos de Convergência Relação entre os tipos de convergência Função característica e função geradora de momentos Leis dos Grandes Números e Teorema Central do Limite Movimento browniano: Definição e propriedades de suas trajetórias Processos estocásticos Movimento browniano Existência Movimento browniano (MB) Passeios aleatórios Movimento browniano é um processo gaussiano Propriedades das trajetórias do Movimento Browniano Movimento Browniano e alguns processos relacionados Movimento browniano é um processo de Markov Transcendência e recorrência do movimento browniano Movimento browniano é uma martingal Movimento browniano é um processo de Lévy Processos construídos a partir do movimento browniano Movimento browniano com ponte Movimento browniano com Drift Movimento browniano geométrico Processo Ornstein-Uhlenbeck Movimento browniano fracionário
14 5 Conclusões Referências
15 3 Introdução Esta dissertação tem como objetivo principal estudar de forma introdutória o movimento browniano. Pretendemos apresentar algumas propriedades de suas trajetórias, em particular, abordando questões de continuidade, diferenciabilidade e recorrência. Ademais, identificaremos o movimento browniano como exemplo de diferentes classes de processos estocásticos, por exemplo como um processo de Markov, gaussiano, martingal e de Lévy. A importância de estudar o movimento browniano radica em sua natureza "universal"dentro dos processos estocásticos que parece ser "tudo". De fato, como veremos adiante, o movimento browniano além de se identificar com as classes de processos citados no primeiro paragrafo, é utilizado na construção e representação de muitos outros. Isto reflete na utilização do movimento em diversas áreas, com por exemplo, em Física, Economia, Finanças, Matemática, Química e Biologia. Ademais, as trajetórias do movimento browniano possui uma relevante quantidade de propriedades interessantes que per se o tornam um objeto matemático interessante. O texto tem a seguinte organização:. O segundo capítulo é uma breve introdução as noções básicas de probabilidade. Em particular, abordaremos os conceitos de espaço de probabilidade, independência, esperança, variância, algumas noções de convergência, funções características. Finalizamos este capítulo com o enunciado da leis dos grandes números e o Teorema central do limite. A referência principal utilizada neste capítulo foi o livro (JAMES, 004), onde podem ser encontradas as demostrações omitidas neste capítulo.. No terceiro capítulo, nós definimos, provamos a existência do movimento Browniano e sua identificação como um processo gaussiano,e investigamos algumas propriedades de suas trajetórias. Destacamos as propriedades de não regularidade, não diferenciabilidade, auto similaridade, conjunto de zeros, invariância por escala, variação não limitada, H older continuidade dentre outros. As referências principais são os livros (ATHREYA; LAHIRI, 006), (KARATZAS; SHREVE, 99) e (LAWLER, 006). 3. Finalmente, o último capítulo é dedicado a identificar o movimento browniano como processo de Markov, martingal e processo de Lévy. Veremos a relação entre o movimento browniano e a equação do calor e como consequência, deduziremos as propriedades de recorrência e transcendência do movimento browniano. Demostraremos que todo processo de Lévy contínuo é o movimento browniano com Drift. Finalizamos este capítulo com a construção de alguns processos a partir do movimento browniano. Mais especificamente, movimento browniano com ponte ou bridge, movi-
16 4 Capítulo. Introdução mento browniano com Drift, ou com tendência, ou aritmético, movimento browniano geométrico, Processo Ornstein - Uhlenbeck, movimento browniano fracionário. As principais referências são os livros (ETHIER; KURTZ, 986), (TANKOV, 003) e (KARATZAS; SHREVE, 99). Para concluir, observamos que a ênfase no estudo do movimento browniano foi o caso unidimensional. Além de tornar a exposição mais simples na notação, a maioria das propriedades e resultados no caso d-dimensional, d, recai em essência ao caso unidimensional. de fato, um processo estocástico em R d é um movimento browniano se, e só se, cada uma de suas d componentes são movimentos brownianos unidimensionais, veja seção 3.. Para o estudo das propriedades de recorrência do movimento browniano é necessário considerar o caso d-dimensional. As figuras apresentadas no texto são de autoria própria e refletem meu interesse em simulações computacional e programação. As quais foram feitas usando a seguinte função como ideia principal: Dado um T (tempo de simulação ) e um N (numero de passos), temos Figura Movimento Browniano usual em 3D function [B]=MB(T,N) randn( state,00) % vetor de numeros aleatorios normais dt = T/N; db = sqrt(dt)*randn(,n); %vetor de incrementos B = cumsum(db); % suma acumulativa M=max(abs(B));plot([0:dt:T],[0,B], b ) % grafica W vs t grid on xlabel( t, FontSize,6) ylabel( B(t), FontSize,6) title([ MB discreto no tempo de 0 até intstr(t) com intstr(n) pasos ]) axis([0 T -M-0.5 M+0.5])
17 5 Noções básicas de teoria da probabilidade A teoria de probabilidade consiste em usar a intuição para estudar os fenômenos cotidianos. Usando o princípio básico do ser humano que é a ideia de experimento. Podemos classificar os experimentos em aleatórios (casuais) e não aleatórios (determinísticos). Os experimentos determinísticos são totalmente caracterizados a priori, ou seja, são fenômenos em que o resultado é sabido antes mesmo em que ele ocorra e desta forma, nada temos a fazer. Os experimentos que iremos estudar são os aleatórios, dos quais não sabemos o resultado a priori, ou seja, são acontecimentos cujos resultados não podem ser previstos. A seguir tratamos os termos básicos associados a modelagem dos experimentos aleatórios. Mais especificamente, neste capitulo temos vários objetivos, o primeiro é dar as noções básicas da teoria da probabilidade, que envolve as ideias de variável aleatória, probabilidade, independência, esperança, variância, covariância, convergência de v.a., a relação entre os tipos de convergência e também o conceito de função característica e finalmente a lei dos grandes números e o Teorema Central do Limite. Todo o primeiro capitulo foi feito seguindo o livro de (JAMES, 004).. Conceitos básicos de probabilidade Nesta seção vamos a introduzir a ideia de espaço de probabilidade e o conceito de função de probabilidade e suas propriedades, para depois dar uma ideia de variável aleatória, função de distribuição, função de densidade. O primeiro elemento na modelagem de um experimento é o espaço amostral, que consiste no conjunto de todos os possíveis resultados do experimento. O espaço amostral geralmente é representado como o conjunto Ω. Por exemplo, se o experimento é lançar uma moeda e verificar se a face é cara ou coroa, o espaço amostral é o conjunto Ω = {cara, coroa}. Para o lançamento de um dado de seis faces, o espaço amostral é Ω = {,, 3, 4, 5, 6}. Em estes exemplos, associamos os eventos a subconjuntos do espaço amostral. Portanto, do ponto de vista matemático, vamos definir eventos como subconjuntos do espaço amostral. O próprio espaço amostral é um evento, também conhecido como evento certo, enquanto que o evento incerto é denominado de evento vazio e denotado por. De forma mais geral, temos a seguinte definição. Definição... Um espaço de probabilidade é uma terna (Ω, I, P) formada por:
18 6 Capítulo. Noções básicas de teoria da probabilidade. Um conjunto Ω O qual chamaremos de espaço amostral.. Uma família I, de subconjuntos de Ω que tem estrutura de σ-álgebra, ou seja: i) I ii) Se A I, o complemento de A, ou seja, A c também pertence a I iii) A, A... I então i= A i I. Os elementos de I serão chamados de eventos. 3. Uma aplicação P : I [0, ] que cumpre: a) P[A] 0 b) P[ ] = 0 e P[Ω] = c) Para qualquer sequência de eventos mutuamente exclusivos A, A,..., I, isto é, eventos para os quais A i A j = quando i j, temos que [ ] P A i = P[A i ]. i= i= Quando aplicamos a função probabilidade, P, podemos interpretar da forma, P[A] = "a probabilidade do evento A ocorrer". Se P[A] =, dizemos que o evento A ocorre com probabilidade um, ou quase certamente (q.c). Nesta dissertação, a menos que seja explicitado, estamos considerando fixado um espaço de probabilidade (Ω, I, P). A seguir, apresentamos algumas propriedades elementares da função probabilidade que são obtidas diretamente se usamos o item 3a), 3b) e 3c). Algumas regras básicas para o cálculo de probabilidades: a) Se A c for o evento complementar de A, então P[A] = P[A c ]. b) A probabilidade da união de dois eventos A e B é calculada como P[A B] = P[A] + P[B] P[A B]. c) Se A, B e C são três eventos quaisquer, então P[A B C] = P[A]+P[B]+P[C] P[A B] P[A C] P[B C]+P[A B C]. d) Se A B, então P[A] P[B]. e) Se A B então P[B A] = P[B] P[A]
19 .. Conceitos básicos de probabilidade 7 f) Sejam A, A, eventos aleatórios tais que A n, ou seja, A A A 3 e ainda o lim n A n =, então P [A n ] 0. g) Sejam A, A,, A n uma sequência de eventos aleatórios, então [ n ] n P A i P[A i ]. i= i= h) (Continuidade da Probabilidade). Se A n A, então Similarmente se A n A então P[A n ] P[A]. [ n i) P j) P ] A k k= [ ] A k k= n P[A C k ]. k= P[A C k ]. k= P[A n ] P[A]. k) Se P[A n ] = 0, para n =,,, então [ ] P A n = 0. n= l) Se P[A n ] =, para n =,,, então [ ] P A n =. n= m) Se A, A, e B, B, são eventos aleatórios, tais que, P[A n ] e P[B n ] p quando n, então P[A n B n ] p. A demonstração das propriedades podem ser obtida em [(JAMES, 004) seção.]. Outro conceito importante da teoria de probabilidade é o conceito de independência entre dois eventos. Na prática, dois eventos são independentes quando a ocorrência de um evento não influência a ocorrência do outro evento. Do ponto de vista probabilístico temos a seguinte definição: Definição... Dois eventos A e B são ditos independentes se P[A B] = P[A]P[B].
20 8 Capítulo. Noções básicas de teoria da probabilidade Definição..3. (probabilidade condicional) A probabilidade de ocorrer um evento A dado que ocorreu um evento B é dada por P[A B] = P[A B]. P[B] Dessa relação sai a regra do produto que é dada no Teorema a seguir. Teorema... Considere um conjunto finito A, A,..., A n de eventos tais que os eventos condicionais A i A A... A i tenham probabilidades positivas. Então temos que [ n ] [ ] n P A i = P[A ]P[A A ]P[A 3 A A ]... P A n A i. i= i= Demonstração. Para demonstrar este Teorema escrevemos P [ n ] A i i= = P[A ] P[A A ] P[A A A 3 ]... P[A ] P[A A ] P[ n i= P[ n i= A i ], A i ] e usando a definição de probabilidade condicional, podemos reescrever o lado direito da igualdade acima como P[A ]P[A A ]P[A 3 A A ]... P [ A n ] n A i i=.. Como caso particular temos que, dados dois eventos A e B, concluímos que a probabilidade de ocorrência simultânea dos eventos A e B é igual a probabilidade de ocorrência do evento A (ou B) vezes a probabilidade de ocorrência do evento A (ou B) dado que ocorreu o evento B (ou A), ou seja, P[A B] = P[A]P[A B]. A seguir, apresentamos o Teorema da probabilidade total que é usado com frequência para calcular a probabilidade de vários eventos. Teorema... (Teorema da probabilidade total) Sejam A, A,..., A n dois a dois disjuntos que formam uma partição do espaço amostral, isto é, eventos n A i = Ω i=
21 .. Conceitos básicos de probabilidade 9 e assuma que P[A i ] > 0 para i =,,..., n. Então, para qualquer evento B, temos que n P[B] = P[A B]+ +P[A n B] = P[A ]P[B A ]+ +P[A n ]P[B A n ] = P[A i ]P[B A i ]. i= Demonstração. Para demonstrarmos esse Teorema basta observarmos que como a sequência A, A,... formam uma partição então para qualquer B Ω, temos que B = (A i i B). Como os A i são disjuntos dois a dois temos que B A i também são disjuntos e pelo item 3 da definição (..) e pelo Teorema (..) temos que P[B] = i P[A i B] = i P[A i ]P[B A i ]. Como uma consequência destes prévios resultados, temos o conhecido Teorema..3. (Teorema de Bayes) Sejam A, A,..., A n eventos que formam uma partição do espaço amostral, e assuma que P[A i ] > 0 para todo i. Então, para qualquer evento B tal que P[B] > 0, temos que P[A i B] = P[A i]p[b A i ] P[B] = P[A i ]P[B A i ] P[A ]P[B A ] P[A n ]P[B A n ]. Demonstração. Para verificar o Teorema de Bayes, basta notar que P[A i ]P[B A i ] = P[B]P[A i B] já que ambos são iguais a P[A B], o que garante a primeira igualdade. A segunda igualdade segue da aplicação do Teorema da Probabilidade Total, Teorema (..) para B. Dado um fenômeno aleatório qualquer, com um certo espaço amostral, desejamos estudar a estrutura probabilística de quantidades associadas a esse fenômeno. Por exemplo, ao descrever uma peça manufaturada podemos empregar duas classificações: "defeituosa"ou "não-defeituosa". Para facilitar a análise, vamos atribuir um número real a cada resultado do experimento. Assim podemos atribuir o valor 0 às peças não defeituosas e às defeituosas. Nós podemos entender por variável aleatória uma função que associa a cada elemento do espaço amostral um número real. Mais formalmente, temos a definição: Definição..4. (Variável aleatória) Dado um espaço de probabilidade (Ω, I, P) uma variável aleatória é uma função real X X : Ω R ω X(ω)
22 0 Capítulo. Noções básicas de teoria da probabilidade satisfazendo para todo x R [X < x] = {ω Ω : X (ω) < x} I (.) Neste texto vamos utilizar a abreviação v.a. para variável aleatória. Assim a definição nos diz que para uma v.a. X, cada um dos conjuntos [X < x], x R, pertence a σ-álgebra, I de Ω. De modo equivalente podemos definir v.a. em ternos dos borelianos de R. Denote por B(R) a menor σ-álgebra gerada pelos intervalos limitados da reta, a chamamos de σ-álgebra de Borel em R. Uma função X : Ω R é uma v.a. se, e só, se, para todo A B(R) temos X (A) I. Veja por exemplo, ((CHUNG, 00)). Assim podemos falar da probabilidade de uma v.a. X aceitar um valor menor do que x R, ou seja, escrevemos P [ω Ω : X (ω) < x] (ou ainda P [X < x]). De modo geral temos: P X [A] = P [X A] = P [ω Ω/X (ω) A] A I. Dada uma v.a. podemos associar de modo único uma função real definida nos reais a qual chamaremos de função de distribuição. Informalmente, a função de distribuição nos dá uma maneira de descrever como as probabilidades são associadas aos valores ou aos intervalos de valores de uma v.a. Formalmente, temos a definição. Definição..5. (Função de distribuição) Uma variável aleatória X em um espaço de probabilidade (Ω, I, P) a função de distribuição, F : R [0, ] de X, é dada por F X (x) = P [X x] x R. O conhecimento da função de distribuição é suficiente para entendermos o comportamento de uma v.a. Mesmo que a variável assuma valores apenas num subconjunto dos reais, a função de distribuição é definida em toda a reta. Ela é chamada de função de distribuição ou função de distribuição acumulada, pois acumula as probabilidades dos valores inferiores ou iguais a x. A função de distribuição de uma v.a. X têm três propriedades básicas:. 0 F (x), lim F (x) = 0 e lim F (x) = x x. F é não decrescente. 3. F é uma função contínua à direita e tem limite à esquerda.
23 .. Conceitos básicos de probabilidade Demonstração. item. Se x, então [X x] e assim F (x) = P[X x] 0. Se x +, então [X x] Ω e assim F (x) = P[X x]. Demonstração item. F não decrescente é equivalente a x y [X x] [X y] F (x) = P[X x] P[X y] = F (y) Demonstração item 3. F é contínua a direita é equivalente a se x n x, então [X x n ] é um sequência decrescente de eventos aleatórios e n [X x n ] = [X x], pois X x se, e somente se, X x n n. Assim, concluímos que F (x n ) = P[X x n ] P[X x] = F (x) Exemplo... Para o lançamento de uma moeda, temos que Ω = {cara, coroa} e que P(cara) = P(coroa) =. Definimos uma v.a. X, isto é, uma função de Ω em R da seguinte forma:, se ω = cara; X(ω) = 0, se ω = coroa. Vamos encontrar a função de distribuição de X. Um simples cálculo mostra que a função de distribuição de X é: 0, se x < 0; F (x) = /, se 0 x < ;, se x. Definição..6. (Função de densidade) Dizemos que X é uma v.a. absolutamente contínua se existe uma função f X : R [0, + ) denominada função densidade de probabilidade, que satisfaz às seguintes propriedades:. f(x) 0, para todo x R x e f é mensurável.. f(x)dx = Além disso, definimos para qualquer c, d R x, com c < d que P[c < X < d] = d c f(x)dx. Vale a pena notar que, da forma como a probabilidade foi definida, a probabilidade de um ponto isolado é sempre zero, ou seja, P[X = c] = c c f(x)dx = 0. Desta forma, podemos concluir que, quando X é uma v.a. contínua, a probabilidade de ocorrer um
24 Capítulo. Noções básicas de teoria da probabilidade valor especifico é zero. Observação: Se X é uma v.a. absolutamente contínua, então (quase certamente) x F X(x) = f X (x) Assim podemos ter uma relação entre a função de densidade f X e a função de distribuição F X dada por f X (x) = d F dx X(x) quase certamente. Isto significa, neste caso, que F X é contínua e derivável por partes ( F X é derivável em todo ponto exceto num número enumerável de pontos), ou seja, o conjunto dos pontos de descontinuidade da função de distribuição F X é enumerável, veja por exemplo [((CHUNG, 00)) Cap.. seção.]. Exemplo... (Normal) Seja X : Ω R uma v.a. absolutamente contínua com função distribuição de probabilidade dada por f(x) = π e x x R. (.) "padrão". Usaremos a notação X N(0, ) e diremos que v.a. X possui distribuição normal Para que f X seja uma função de densidade, basta mostrarmos que f X (s)ds =. Então, tomamos [ ] Teo Fubinni f X (s)ds = f X (x)dx f X (s)ds = π e, a partir da mudança de variáveis x = r cos θ e y = rsenθ, temos que [ ] f X (s)ds = π π 0 0 e r rdθdr = π e x +y dxdy [ ] π e r rθ dr = e u du =. 0 0 O seguinte resultado a respeito de estimativa da v.a. normal, será usado repetidas vezes adiante no texto. Lema... [(MÖRTERS; PERES, 00) Lema.5] Seja Z N(0, ). Então para todo x 0 x e x x P[Z > x] e x. (.3) + π x π Demonstração. Primeiro provemos a desigualdade da direita, sabemos que Como P[Z > x] = x π e u du. u x u x u x e u u u π π x e.
25 .. Conceitos básicos de probabilidade 3 Portanto, Assim temos que P[Z > x] = x x = [ x π π e u du π e u du ] x e u x u e u du x π u e u x du = x x π x π = e x. x π e u ( u)du Isto justifica a parte direita da desigualdade (.3). Para provar a desigualdade da esquerda, definamos a seguinte função f(x) = xe x (x + ) e mostremos que f(x) 0 para todo x 0. Note que: (i) f(0) < 0 (ii) lim x f(x) = 0. Além disso, f (x) = e x + xe x x ( x) x = ( x + x + )e x x = e x x x ( = x x e u du e u du x e Pela desigualdade da direita, obtemos que π x x e u du x 0 e u du (x + )( e x ) x ) x. e u du x e u du e x π O que nos dá que f (x) 0, para todo x 0 Assim, pelos item (i) e (ii) temos que f(x) 0, para todo x 0. segue daí que xe x (x + ) x. e u du x x (x + ) e e u du = πp[z > x] x x e x (x P[Z > x]. + ) π Isto completa a prova da expressão (.3). Assim temos que, uma v.a. normal cumpre que P[N > x] e x π x.
26 4 Capítulo. Noções básicas de teoria da probabilidade Vamos introduzir o conceito de vetor aleatório e estudar suas principais características. Por facilidade de notação, vamos considerar apenas vetores bi-dimensionais. Assim, dizemos que o par ordenado (X, Y ) é um vetor aleatório se seus componentes X e Y são variáveis aleatórias. Definimos para duas variáveis aleatórias X e Y. Um vetor Z = (X, Y ) cujos componentes X e Y são variáveis aleatórias é denominado vetor aleatório. Definição..7. (função de distribuição conjunta) A função de distribuição de Z é definida como sendo uma função F Z = F X,Y : R [0, ] tal que F X,Y (x, y) = P [{X x} {Y y}] = P [X x, Y y] x, y R. As propriedades da função de distribuição. A função de distribuição F Z é não decrescente em cada variável, isto é, se x x, então F Z (x, y) F Z (x, y) y R. F Z é contínua à direita e tem limite à esquerda em cada variável, isto é, se x n x então 3. Temos que F X (x n, y) F X (x, y) y R. lim F Z(x, y) = 0. x Esta propriedade vale para cada componente do vetor. Definição..8. Dizemos que X e Y são conjuntamente contínuas se existe uma função f(x, y) definida para todos reais x e y, tal que P [(X, Y ) (a, b ) (a, b )] = b b a a f(x, y)dxdy. Para todo < a i < b i < com i =,. A função f(x, y) é denominada função densidade de probabilidade conjunta de X e Y. Se X e Y são conjuntamente absolutamente contínuas, então elas são individualmente absolutamente contínuas e suas funções densidades de probabilidade podem ser obtidas da seguinte forma P [X A] = P [X A, Y (, )] = Onde f X (x) = A f(x, y)dydx = A f X (x)dx. f(x, y)dy é a função densidade de probabilidade de X. Similarmente, a função densidade de probabilidade de Y é dada por f Y (y) = f(x, y)dx
27 .. Independência 5. Independência Vamos estender a noção de independência para v.a. Definição... Dizemos que as variáveis aleatórias X, X,, X n, definidas em um espaço de probabilidade (Ω, I, P), são coletivamente independentes, ou simplesmente independentes, se n P [X B, X B,, X n B n ] = P [X i B i ] i= Para todo B i B(R), i =,,, n Se as v.a. X, X,, X n são independentes, então funções de famílias disjuntas das variáveis são também independentes. Por exemplo: a) X + X + X 3 e e X 4 são independentes. b) min(x, X ) e max(x 3, X 4 ) são independentes. c) X X e X + X 3 não são necessariamente independentes. Um resultado de demonstração e que nos será útil é Proposição... Sejam X, Y v.a. e sejam F X e F Y as funções de distribuição respectivas e F a função de distribuição conjunta das v.a X, Y. Então X, Y são independentes se, e somente se, F X,Y (x, y) = F X (x)f Y (y) para todo (x, y) R. A demonstração pode ser consultada em ((JAMES, 004) Cap seção.5) Proposição... Sejam X, Y v.a. e sejam f X e f Y as funções de densidade respectivas e f a função de densidade conjunta das v.a X, Y. Então X, Y são independentes se, e somente se, f X,Y (x, y) = f X (x)f Y (y) para todo (x, y) R. A demonstração pode ser consultada em ((JAMES, 004)) Teorema... Sejam X e Y duas v.a. independentes. Então, U = g(x) e V = h(y ). Também são independentes para quaisquer funções contínuas. g e h. Podemos ver a demostração em ((CHUNG, 00)) Cap. 3 seção 3.3).
28 6 Capítulo. Noções básicas de teoria da probabilidade.3 Esperança Fazendo uma tentativa de resumir o comportamento de uma v.a. vamos estudar uma medida que estuda a tendência central da v.a., chamada de esperança ou valor esperado de uma v.a. Definição.3.. Seja X uma v.a. em um espaço de probabilidade (Ω, I, P). Seja X uma v.a. e F sua função de distribuição. A esperança matemática da v.a. X, ou simplesmente esperança de X, denotada por E[X] é definida por: E[X] = xdf (x)dx = XdP, desde que a integral esteja bem definida. Note que no caso em que a v.a. X tem função de densidade f(x) temos, E[X] = e se a v.a. é discreta, temos: xdf (x)dx = xf(x)dx E[X] = x xp[x = x] = x xp(x) = i x i p(x i )..3. Propriedades da esperança. Se X = c, isto é X(ω) = c para todo ω Ω, então E[X] = c. Se X Y então E[X] E[Y ] Se as esperanças estão bem definidas. 3. (Linearidade) Se E[X] está bem definida, então E[aX + b] = ae[x] + b para todo a, b R 4. (Desigualdade de Jensen) Seja φ uma função convexa definida na reta. Se a variável aleatória (v.a.) X é integrável, então E[φ(X)] φ(e[x]) 5. Se X é uma (v.a.), então E[X k ] = x k df X (x) para k =,, Seja X é uma (v.a.) e φ(x) uma função real mensurável. Então E[φ(X)] def = ydf φ(x) (y) = φ(x)df X (x) Se X tiver função de densidade f(x), Então E[φ(X)] = φ(x)f(x)dx. A demonstração das propriedades pode ser obtida em [(JAMES, 004) Cap 3 seção 3.3]
29 .3. Esperança 7 Proposição.3.. Se X, X,..., X n são v.a. independentes e integráveis, então X X X n é integrável e E[X X...X n ] = (E[X ])(E[X ])...(E[X n ]). A demonstração pode ser obtida em ((ATHREYA; LAHIRI, 006) Cap. 7. seção 7.). A recíproca da Proposição anterior não é sempre verdadeira, isto é, E[XY ] = E[X]E[X] não implica X e Y independentes. Definição.3.. (Covariância) A covariância entre duas v.a. X e Y é definida como Cov(X, Y ) = E[(X E[X])(Y E[Y ])] = E[XY ] E[X]E[Y ]. Duas v.a. X e Y são ditas não-correlacionadas se Cov(X, Y ) = 0. Segue-se que v.a. independentes são não-correlacionadas, mas a recíproca não é necessariamente verdadeira. Tome as v.a. X, que tem distribuição uniforme, X U(, ) e Y = X. Assim temos que Cov[X, Y ] = 0 mas Y é dependente de X. Há certos casos em que não correlação implica em independência. O caso mais importante é o da Normal: Se X e Y possuem distribuição conjunta normal bivariada e são não-correlacionadas, então X e Y são independentes. Agora, definamos a esperança condicional que é um conceito fundamental, para poder definir, os conceitos de Martingal, processo de Markov, etc. Definição.3.3. A esperança condicional de uma v.a não negativa ξ com respeito a uma σ-álgebra G é denotada por E[ξ G], tal que i) E[ξ G] é G-mensurável ii) Para todo A G A ξdp = A E[ξ G] A esperanaça condicional de uma v.a qualquer ξ com respeito a uma σ-álgebra é dada por: e está definida apenas se E[ξ G] = E[ξ + G] E[ξ G] max{e[ξ + G], E[ξ G]} <
30 8 Capítulo. Noções básicas de teoria da probabilidade.4 Variância Vamos a introduzir o conceito variância, que pode ser compreendido como uma medida de dispersão que nos permitem reconhecer que tanto os dados estão dispersos ao redor do ponto central, da média. Definição.4.. (Momentos) Seja X uma v.a. Define-se o k-ésimo momento ordinário, ou centrado no zero, da v.a X, m k, como m k = E[X k ] = Assim, para uma v.a. continua temos que m k = R R x k df X (x). x k f X (x)dx Onde f X (x) é função de densidade de X Definição.4.. (Momentos Centrado) Seja X uma v.a. Define-se o k-ésimo momento central da v.a. X, M k, como M k = E[(X E[X]) k ] Assim, para uma v.a. continua temos que M k = [x E[X]] k f X (x)dx. R Onde f X (x) é função de densidade de X. Definição.4.3. (Variância) Seja X uma v.a. Define-se a variância da v.a. X, como o segundo momento central da v.a. X, e denotada por V [X] = V ar[x] = σx, ou seja, V [X] = E[(X E[X]) ], observe que V [X] = E[(X E[X]) ] = E[X ] (E[X]). Proposição.4.. A variância da v.a. Y = n X i é dada por i= V [ n ] n X i = V [X i ] + Cov(X i, X j ). i= i= i<j Corolário.4.. Se X, X,, X n são v.a. não-correlacionadas, então V [Y ] = V [ n ] n X i = V [X i ] i= i= A variância tem importantes propriedades.4. Propriedades da variância. Se C é constante, então V [C] = 0. Se a, b R, então V [ax + b] = a V [X]
31 .5. Convergência de variáveis aleatórias 9 3. (Desigualdade de Markov) Seja X uma v.a. não-negativa e seja λ > 0 uma constante. Então para todo t > 0 P[ X λ] E[ X t ] λ t (.4) 4. (Desigualdade Clássica de Chebyshev) Seja X uma variável aleatória integrável e seja λ > 0 uma constante. Então P[ X E[X] λ] V [X] λ A demonstração das propriedades pode ser obtida [(JAMES, 004) Cap 3 seção 3.5]..5 Convergência de variáveis aleatórias Considere um experimento devidamente modelado por um espaço de probabilidade (Ω, I, P). Neste espaço vamos considerar uma sequência de variáveis aleatórias X, X, X 3, Em inúmeras situações teóricas e práticas, uma pergunta natural é qual o comportamento de longo prazo da sequência (X n ) n. Dito de outra forma: quais as propriedades estatísticas de X N, sendo N suficientemente grande?. O nosso objetivo é discutir a convergência das variáveis X, X, X 3,..., X n para uma variável X quando n é grande, isto é, em qual sentido, podemos substituir X n por X ou tentar aproximar P[X n a] por P[X a], ou E[X n ] por E[X]. Nesta seção vamos apresentar um Lema muito importante, o Lema de Borel- Cantelli, que será usado com frequência nos capítulos seguintes. Também vamos introduzir alguns noções de convergência para v.a. e as relações entre os diferentes tipos de convergência e finalmente apresentamos o conceito de função característica..5. Lema de Borel-Cantelli Suponha que cada cauda de um evento tem probabilidade zero ou um, o problema é decidir qual é qual. O Lema de Borel-Cantelli é um passo importante nessa direção. Aplica-se a uma classe de eventos que inclui muitos evento-cuada. Começamos definindo o lim inf e o lim sup de uma sequência de eventos. Definição.5.. (lim sup e lim inf de eventos). Dada uma sequência de eventos aleatórios A n, definimos o evento lim sup A n, denotado por [A n infinitas vezes] ou [A n i.v.], por lim sup A n = A k. n n= k=n
32 30 Capítulo. Noções básicas de teoria da probabilidade Definimos o evento lim inf A n, denotado por [A n eventualmente], por lim inf n A n = n= k=n Observe: as seguintes interpretações. lim sup A n é o conjunto dos ω s tais que ω pertence a infinitos A n s. O evento lim sup A n significa A n acontece infinitas vezes. lim inf A n é o conjunto dos ω s tais que ω pertence a todos os A n s exceto uma quantidade finita deles. O evento lim inf A n significa A n acontece para todo n grande. De fato, lim sup A n I e lim inf A n I. Vale também que A k. lim sup A n lim inf A n e lim inf(a c n) = (lim sup A n ) c Teorema.5.. (Lema de Borel-Cantelli). Seja (Ω, I, P) um espaço de probabilidade e (A n ) n uma sequência de eventos aleatórios. Então:. Se n= P[A n ] < então [ P[A n (i.v)] = P lim sup n A n ] = 0. n= P[A n ] = e os eventos A n são independentes, então [ P[A n (i.v)] = P lim sup n A n ] = Demonstração. do item. Se como P[A n ] <, então n= P[A k ] 0, quando n. E k=n Então temos que: lim sup A n n k=n A k, Portanto como 0 P[lim sup prova do item. P[lim sup A n ] P n n [ ] A k k=n k=n P[A k ] n 0. A n ] 0, concluímos que P[lim sup n Para demonstrarmos o item basta observar que [ ] P A k = para qualquer n, k=n A n ] = 0. Isto conclui a pois interseção de eventos com probabilidade também tem probabilidade (ver propriedade k na seção (.), ou seja, se demonstrarmos que [ ] P A k = então P[lim sup A n ] = n k=n
33 .5. Convergência de variáveis aleatórias 3 e o resultado será demonstrado. Assim, seja B n = qualquer m N, e portanto B c n ( n+m k=n ( ) c A i = A c i i= i= A k ) c = e k=n n+m k=n A k, note que B n n+m k=n A k, para A c k e essa igualdade é válida pois. ( ) c A i = A c i. i= i= que são as chamadas leis de De Morgan. Logo, para todo m temos P[B n ] = P[B c n] P Como cada A i são independentes então obtemos que P [ n+m ] A c k k=n = n+m k=n P[A c k] = [ n+m ] A c k k=n n+m k=n Notemos que p e p para 0 p, então temos que: P[B n ] pois por hipótese temos que n+m k=n n= e P[A k] = exp { n+m k=n. ( P[A k ]). P[A k ] } m 0, P[A n ] =. Portanto P[B n ] =, para todo n. Teorema.5.. (Lema de Fatou). Para qualquer sequência (A n ) n de eventos vale P[lim inf n A n ] lim inf n Demonstração. Para qualquer k N e m k temos e portanto Como ( n=k P[A n ] n=k [ ] P A n P[A m ] n=k [ ] P A n inf P[A m]. m k n=k A n A m. Logo A n ) k é uma sequência crescente de eventos, temos que P[lim inf n O último termo é igual a lim inf n [ ( ) ] [ ] A n ] = P A n = lim P A n lim inf P[A k n] k n k k=0 n=k n=k P[A n ] o que termina a prova. Corolário.5.. Se P[A n (i.v)] = 0 então P[A n ] 0
34 3 Capítulo. Noções básicas de teoria da probabilidade Demonstração. Aplicando o Lema de fatou, Teorema (.5.), para a sequência (A c n) n temos que lim sup P[A n ] = lim inf P[A c n n n] = P[lim inf n donde segue o resultado. A c n] = P[lim sup A n ] = 0. n Definição.5.. (evento simétrico) Para um processo X,, X,, A I(X) dizem que é um evento simétrico se para qualquer permutação finita de índices {i, i, } de {,, } existe um conjunto B B tal que: A = {(X, X, ) B} = {(X i, X i, ) B} Sabemos que Δ é a diferença simétrica entre dois eventos por AΔB = (A B) (B A) Teorema.5.3. Hewitt Savage 0 Sejam X, X, uma sequência de variáveis aleatórias i.i.d, com B B e Um evento simétrico. Então A = {ω (X, X, ) B} P[A] = 0 ou P[A] = Demonstração. Seja A = [X B] um evento simétrico. Seja B n B(R n ), com B(R n ) a σ-álgebra de Borel do R n, tal que A n = {ω (X, X,, X n ) B n }. E sabemos que P[AΔA n ] n 0. Então P[A n ] P[A] e como A é simétrico então P[A n A n ] = P[(X, X,, X n ) B n ; (X n+,, X n ) B n ]. E pela independência dos X i temos que P[(X, X n ) B n ; (X n+, X n ) B n ] = P[(X, X n ) B n ]P[(X n+, X n ) B n ] Assim quando n temos que P[A] = P [A]. O que implica que P[A] = 0 ou P[A] =
35 .5. Convergência de variáveis aleatórias Tipos de Convergência A fim de ampliar a noção de convergência de sequências de números de sequências de v.a., existem bastantes possibilidades. Nos tipos de convergências a seguir, é considerada a sequência (X n ) n = {X, X, X 3,, X n } em que X, X, X 3,, X n e o eventual limite X da sequência (X n ) n que são v.a. definidas num mesmo espaço de probabilidade (Ω, I, P). Definição.5.3. (Convergência em probabilidade). Sejam {X, X, X 3,, X n } e X v.a. definidas num mesmo espaço de probabilidades (Ω, I, P) Dizemos que X n converge em probabilidade para X denotado por X n P X Se para todo ε > 0 P[ X n X ε] P 0 ou, equivalentemente, P[ X P n X < ε]. n n Convergência em probabilidade, significa que se n for suficientemente grande, então a probabilidade que X n seja diferente de X por mais que ε é muito pequena. A convergência em probabilidade não é uma convergência pontual. Apenas afirma que para valores grandes de n as v.a. X n e X são aproximadamente iguais, com probabilidade bem alta. Definição.5.4. (Convergência em distribuição). Sejam X, X, e X v.a. com funções de distribuição F X, F X, e F X respectivamente. Diz-se que a sequência (X n, n ) = (X, X, ) de v.a. converge em distribuição (ou em lei) para X, e denota-se por X D n X, se para todo ponto x em que F X é contínua, tem-se: lim F X n n (x) = F X (x) Definição.5.5. (Convergência quase certa (q.c)). Ou convergência em quase toda parte (q.t.p). Diz-se que a sequência de v.a. (X n, n ) = (X, X,...) converge quase q.c certamente para X, e denota-se por X n X se ) ] P[X n X] = ou equivalente P n [ ( ω Ω/X n (ω) n X(ω) =. A convergência quase certa é uma convergência pontual, isto é, uma convergência ponto a ponto. No entanto, ela permite que alguns pontos ω Ω escapem do critério de convergência. Entretanto, o conjunto desses pontos precisa ser negligenciável em termos probabilísticos, isto é, sua probabilidade deve ser zero. Definição.5.6. (Convergência em L p, p + ) Considere X uma v.a. com E[ X p ] < e {X n } n sequência de v.a. Dizemos que X n converge em L p para X se Notação: X n ou MC. lim E [ X n X p ] = 0. n L p X. Observação: quando p =, dizemos que converge em média quadrática
36 34 Capítulo. Noções básicas de teoria da probabilidade.5.3 Relação entre os tipos de convergência O seguinte Lema fornece um critério de convergência quase certa. Lema.5.. X n infinitas vezes. q.c X P[ X n X ε (i.v)] = 0, ε > 0, Onde (i.v) significa Uma referência para a prova pode ser o livro do [((CHUNG, 00)) Cap. 4. seção 4.]. Uma consequência do Lema de Borel-Cantelli é o seguinte resultado: Teorema.5.4. Sejam (X n ) n uma sequência de v.a. e X uma v.a. Se para todo ε > 0 q.c. temos P{ X n X ε} <, então X n X. n= Demonstração. Como por hipótese P{ X n X ε} <, então pelo Lema de n= Borel-Cantelli item, Teorema (.5.) segue que P{ X n X ε; i.v.} = 0. Portanto, pelo critério de convergência quase certa, Lema (.5.) temos que X n q.c. X. A seguir apresentamos mais algumas relações entre os diferentes tipos de convergência. Convergência quase certa q.c implica convergência em probabilidade, ou seja, se q.c X n X então X P n X. q.c. De fato, como por hipótese X n X, então pelo critério de convergência quase certa, Lema (.5.), temos que para todo ε > 0 Mas observe que Então, Logo, Portanto, P{ X n X ε; i.v.} = 0. { X n X ε; i.v.} = { X n X ε}. n= k=n { } lim P [ X k X ε; i.v.] = 0. n k=n ( ) n 0 P( X n X ε) P [ X k X ε] 0. k=n lim n P ( X n X ε) = 0 X n Isto conclui a justificativa desta propriedade. P X.
37 .5. Convergência de variáveis aleatórias 35. Convergência em probabilidade não implica convergência quase certa q.c, ou seja, X n P X X n q.c X. De fato basta consideramos o contra exemplo. Seja a sucessão X, X,, X n de v.a independentes com: P[X n = 0] = n e P[X n = ] = n. A ideia é provar que X n P 0 mas X n q.c 0. De fato, como ε > 0 Logo resulta que X n P 0. lim P[ X n 0 < ε] = lim [ n n n ] =. Calculemos a convergência quase certa q.c. Definamos ε > 0 com P [(A ε n) c ] = n como (A ε n) c = [ X n 0 ε] P [(A ε n) c ] = n= n= n =. Logo isto implica que P [(A ε n) c ] = 0 portantox n q.c 0. Mas podemos ter o seguinte: 3. Sejam (X n ) n uma sequência de v.a. e X uma v.a. Se X P n X, então existe uma q.c. subsequência de inteiros crescente (n k ) k tal que X nk X. Para justificar tal propriedade, primeiramente observamos que X P n X se, e somente se, X n X P 0. Assim, podemos supor, sem perda de generalidade, que X = 0. Então por hipótese para todo k > 0, temos que P { X n > } 0 quando n. k Logo, para cada k > 0, existe uma subsequência {n k } k tal que k=0 P { X nk > } k k=0 k <. Escolhida a subsequência {n k }, obtemos que P { [ X nk > k ], i.v. } = 0. Portanto, pelo Teorema (.5.4), temos que X nk q.c. 0. Este resultado nos diz que convergência em probabilidade implica em convergência quase certa ao longo de uma subsequência.
38 36 Capítulo. Noções básicas de teoria da probabilidade. Convergência em média quadrática, MC, implica convergência probabilidade, ou M.C seja. Se X n X então X P n X De fato, note que Logo tem-se que Ou seja X n X I ε [w: Xn X ε]. [ Xn X ] E E [ I [w: Xn X ε]]. ε [ Xn X ] E P [[w : X n X ε]]. ε Como por hipótese X n M.C X, temos que lim n E[ X n X ] = 0. Portanto X P n X, outra forma de provar o resultado pode ser, aplicando la desigualdade de Markov (.4) para t = e λ = ε, de fato, P[ X n X > ε] = P[ X n X > ε ] E[ X n X ] ε 0. 4) Convergência em probabilidade não implica convergência em média quadrática M.C, ou seja, X n P X X n M.C X. De fato, seja a equação X, X,, X n de v.a independentes com P[X n = 0] = 0 n e P[X n = n] = n. Provemos que X n P 0 mas, no entanto X n M.C 0. De fato, como ε > 0 Segue-se que X n lim P[ X n 0 < ε] = lim n n ( n ) =. P 0. Agora, para a convergência na média quadrática. lim n 0] n = [ lim E[X n ] = lim 0 ( n n n ) + ] n n = lim n =. n Assim, não existe convergência em média quadrática.. Convergência M.C não implica Convergência quase certamente q.c, ou seja, X n M.C X X n q.c X Demonstração. Seja (X n ) n N uma sequência de v.a. com Convergência em probabilidade, X P L n X, e Convergência em média p X p n X mas não temos Convergência q.c quase certa, X n X.
39 .5. Convergência de variáveis aleatórias 37 Definimos A n = [0, /n] e seja X n = An com P a medida de Lebesgue no [0, ]. Então para 0 < ε < lim P ( X n 0 ε) = lim P ( X n ε) = lim P ( X n = ) = /n 0. Logo converge em probabilidade para zero. Além disso, lim E[ X n 0 p ] = lim E[ X n p ] = lim P [ X n p = ] = lim P [Xn p = ] = lim P [X n = ] = lim /n = 0. Portanto converge em média p para X. Entretanto utilizando o Lema de Borel- Cantelli, Teorema (.5.) temos que P ( X n ε) = P ( X n = ) = /n =. n= n= n= O que implica que P ( X n ε, i.v.) = o que implica que X n q.c. X. 6) Convergência q.c não implica Convergência em média quadrática M.C, ou seja, X n q.c X X n M.C X Demonstração. Seja U U(0, ) variável aleatória uniforme e definimos a sucessão de v.a X n = ni {U< Verificar se a sequência converge (q.c) para zero mas não em n} média quadrática (M.C). Note-se que esta é uma sucessão de v.a. não independentes, uma vez que todos X i dependem da mesma v.a. U. Para aplicar o Lema de Borel-Cantelli, Teorema (.5.) definamos: ε > 0 (A ε n) c = { X n 0 > ε} = e sabemos que ε n > 0 { } { ni {U< n} ε = I {U< n} ε }. n [ P I {U< n} ε ] n [ ] [ = P I {U< n} = = P U < ] = n n. Logo n= P[A εc n ] = n= n =. Como esta série não é convergente, não podemos concluir que P[A ε ] =, como queríamos. Mas também não podemos concluir que P[A ε ] = 0 pois, o Lema de Borel-Cantelli segunda parte, Teorema (.5.) exige que os A ε n sejam independentes
40 38 Capítulo. Noções básicas de teoria da probabilidade e aqui isso não é verdade. No entanto, note que u > 0 todas as X n = 0 a partir de n > Logo X q.c u n 0 Consideremos a convergência em média quadrática. lim E[X n 0] = lim n n E[nI {U< n} ] = n lim n E[I {U< n} ] = lim n P[U < n n ] = lim n n n = lim n =. n Em seguida, não existe convergência em média quadrática. 7) X n D c se, e somente se, X n P c Primeiramente suponhamos que Dado ε > 0 lim F X n n (x) = 0, se x < c, se x c 0 P{ X n c ε} = P{X n c + ε} + P{X n c ε} = = P{X n < c + ε} + P{X n c ε} { P X n c + ε } + P{X n c ε} n + 0 = 0. Portanto, X n P c Reciprocamente, seja F n a função distribuição acumulada de X n, n. Fixamos x R para todo x ponto de continuidade de F. Então para todo ε > 0 P{X n x} P{X x + ε} + P{X n x ; X > x + ε} P{X x + ε} + P{ X n c > ε}. (.5) E similarmente P{X n x} P{X x ε} P{ X n c > ε}. (.6) Logo, de (.5) e (.6) obtemos que F (x ε) P{ X n c > ε} F n (x) F (x + ε) + P{ X n c > ε}. Como por hipótese temos que X n P c quando n temos que F (x ε) lim inf n F n(x) lim sup F n (x) F (x + ε), ε > 0. (.7) n Note que, para todo x R ponto de continuidade de F, temos que F (x ) = F (x). Portanto, quando ε 0 em (.7) obtemos que lim n F n (x) = F (x) ou seja, X n D c
41 .5. Convergência de variáveis aleatórias 39 8) Se X P n X então X D n X para demostrar esta afirmação, basta, usar a volta do item anterior, item 7 e trocando c por X. 9) Convergência em distribuição não implica Convergência em probabilidade, ou seja. X D n X X P n X Demonstração. Seja X N(0, ) v.a que distribui normal. Seja X n = X para n =,,... assim X n N(0, ). X n tem a mesma distribuição como função X para todo n, também, trivialmente, lim F n (x) = F (x) para todo x. Portanto, X n D X. n Mas P[ X n X > ε] = P[ X > ε] = P[ X > ε ] 0. Então X n não converge para X em probabilidade Na Figura temos um breve resumo que ilustra as implicações entre os diferentes tipos de convergências Figura Relação entre os tipos de convergência.5.4 Função característica e função geradora de momentos Definição.5.7. (Função característica) A função característica de uma v.a. X com distribuição F X é a função Φ X : R C definida por: Φ X (z) = E[e izx ] = + e izx df X (x) z R. A função característica de uma variável aleatória é caracterizada completamente por sua função de distribuição: Duas variáveis com a mesma função característica são identicamente distribuídas. Uma função característica é sempre uniformemente contínua, adicionalmente, as propriedades da suavidade da Φ X dependem da existência dos momentos m k da variável aleatória definidos em (.4.). Os momentos de uma variável aleatória pode ou não
42 40 Capítulo. Noções básicas de teoria da probabilidade existir, dependendo de quão rápido a distribuição F X decai no infinito. Os momentos de uma variável aleatória está relacionado com as derivadas em 0 da função característica. Para enunciar as propriedades vamos a considerar só o caso quando d = A função característica verifica as propriedades:. Φ X (0) =. Φ X (t) 3. Φ X (t) é uniformemente contínua. 4. Se X e Y são independentes, então Φ X+Y (t) = Φ X (t) Φ Y (t) 5. A função característica Φ X da v.a. X determina a função de distribuição de X 6. Se X e v.a. e Y = ax + b então Φ Y (t) = e itb Φ X (at) 7. Se E[ X n ] < então Φ X possui n derivadas contínuas para e Φ (k) X (t) = (ix) k e itx df X (x) k =,,..., n. (.8) Em particular, Φ (k) X (0) = i k E[X k ], de modo que a função característica é uma espécie de função geradora de momentos. A demonstração das propriedades pode ser obtida em [(JAMES, 004) Cap 6 seção 6.] Exemplo.5.. Seja uma v.a. X N(0, ). Sua função característica é Φ X (z) = e z. (.9) Mais ainda, se Y N(μ, σ ), isto é Y = σx +μ e X N(0, ). Sua função característica é (σz) izμ Φ Y (z) = e. (.0) Justifiquemos as igualdades acima. Note que pela propriedade 6., enunciada acima, basta considerar o caso X N(0, ). Usando a definição (.5.7) temos que Φ X (z) = E[e izx ] = R e izx df X (x). (.) Onde df X representa a função de densidade da normal com media μ e variância σ assim temos que df (X)(x) = ( σ (x μ) π e σ ). (.)
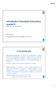
4.1. ESPERANÇA x =, x=1
 4.1. ESPERANÇA 139 4.1 Esperança Certamente um dos conceitos mais conhecidos na teoria das probabilidade é a esperança de uma variável aleatória, mas não com esse nome e sim com os nomes de média ou valor
4.1. ESPERANÇA 139 4.1 Esperança Certamente um dos conceitos mais conhecidos na teoria das probabilidade é a esperança de uma variável aleatória, mas não com esse nome e sim com os nomes de média ou valor
Capítulo 2. Variáveis Aleatórias e Distribuições
 Capítulo 2 Variáveis Aleatórias e Distribuições Experimento Aleatório Não existe uma definição satisfatória de Experimento Aleatório. Os exemplos dados são de fenômenos para os quais modelos probabilísticos
Capítulo 2 Variáveis Aleatórias e Distribuições Experimento Aleatório Não existe uma definição satisfatória de Experimento Aleatório. Os exemplos dados são de fenômenos para os quais modelos probabilísticos
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I
 Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I 2014/2015 Os exercícios assinalados com (*) têm um nível de dificuldade superior. Exercício 1. Seja (X, F) um espaço mensurável. Mostre
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte I 2014/2015 Os exercícios assinalados com (*) têm um nível de dificuldade superior. Exercício 1. Seja (X, F) um espaço mensurável. Mostre
Probabilidade IV. Ulisses U. dos Anjos. Departamento de Estatística Universidade Federal da Paraíba. Período
 Probabilidade IV Ulisses U. dos Anjos Departamento de Estatística Universidade Federal da Paraíba Período 2014.2 Ulisses Umbelino (DE-UFPB) Probabilidade IV Período 2014.2 1 / 20 Sumário 1 Apresentação
Probabilidade IV Ulisses U. dos Anjos Departamento de Estatística Universidade Federal da Paraíba Período 2014.2 Ulisses Umbelino (DE-UFPB) Probabilidade IV Período 2014.2 1 / 20 Sumário 1 Apresentação
SUMÁRIOS DE VARIÁVEIS ALEATÓRIAS CONTINUAS
 4 SUMÁRIOS DE VARIÁVEIS ALEATÓRIAS CONTINUAS Em muitos problemas de probabilidade que requerem o uso de variáveis aleatórias, uma completa especificação da função de densidade de probabilidade ou não está
4 SUMÁRIOS DE VARIÁVEIS ALEATÓRIAS CONTINUAS Em muitos problemas de probabilidade que requerem o uso de variáveis aleatórias, uma completa especificação da função de densidade de probabilidade ou não está
VARIÁVEIS ALEATÓRIAS
 UNIVERSIDADE FEDERAL DE JUIZ DE FORA INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE ESTATÍSTICA VARIÁVEIS ALEATÓRIAS Joaquim H Vianna Neto Relatório Técnico RTE-03/013 Relatório Técnico Série Ensino Variáveis
UNIVERSIDADE FEDERAL DE JUIZ DE FORA INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE ESTATÍSTICA VARIÁVEIS ALEATÓRIAS Joaquim H Vianna Neto Relatório Técnico RTE-03/013 Relatório Técnico Série Ensino Variáveis
2.4 Esperança e distribuição condicionais
 2.4. ESPERANÇA E DISTRIBUIÇÃO CONDICIONAIS 35 2.4 Esperança e distribuição condicionais Estendemos aqui o conceito de probabilidade condicional em (2.8) para obter a distribuição condicional e, posteriormente,
2.4. ESPERANÇA E DISTRIBUIÇÃO CONDICIONAIS 35 2.4 Esperança e distribuição condicionais Estendemos aqui o conceito de probabilidade condicional em (2.8) para obter a distribuição condicional e, posteriormente,
2 Conceitos de Teoria da Probabilidade
 2 Conceitos de Teoria da Probabilidade Neste capítulo, enunciaremos algumas denições e resultados de teoria de probabilidade. justicativa deste capítulo reside no fato que u objetivo nal é estimar momentos
2 Conceitos de Teoria da Probabilidade Neste capítulo, enunciaremos algumas denições e resultados de teoria de probabilidade. justicativa deste capítulo reside no fato que u objetivo nal é estimar momentos
Reviso de Teoria da Medida e Elementos Bsicos de Probabilidade
 Reviso de Teoria da Medida e Elementos Bsicos de Probabilidade Roberto Imbuzeiro Oliveira 9 de Março de 2009 Resumo Esta lista cobre o básico do básico sobre espaços e distribuições de probabilidade. Pouco
Reviso de Teoria da Medida e Elementos Bsicos de Probabilidade Roberto Imbuzeiro Oliveira 9 de Março de 2009 Resumo Esta lista cobre o básico do básico sobre espaços e distribuições de probabilidade. Pouco
Continuidade de processos gaussianos
 Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
Processos Estocásticos. Variáveis Aleatórias. Variáveis Aleatórias. Luiz Affonso Guedes. Como devemos descrever um experimento aleatório?
 Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Funções de Uma Variável Aleatória Funções de Várias Momentos e Estatística Condicional Teorema do Limite Central Processos Estocásticos
Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Funções de Uma Variável Aleatória Funções de Várias Momentos e Estatística Condicional Teorema do Limite Central Processos Estocásticos
Variáveis Aleatórias Bidimensionais &Teoremas de Limite 1/22
 all Variáveis Aleatórias Bidimensionais & Teoremas de Limite Professores Eduardo Zambon e Magnos Martinello UFES Universidade Federal do Espírito Santo DI Departamento de Informática CEUNES Centro Universitário
all Variáveis Aleatórias Bidimensionais & Teoremas de Limite Professores Eduardo Zambon e Magnos Martinello UFES Universidade Federal do Espírito Santo DI Departamento de Informática CEUNES Centro Universitário
Processos Estocásticos. Variáveis Aleatórias. Variáveis Aleatórias. Variáveis Aleatórias. Variáveis Aleatórias. Luiz Affonso Guedes
 Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Funções de Uma Variável Aleatória Funções de Várias Momentos e Estatística Condicional Teorema do Limite Central Processos Estocásticos
Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Funções de Uma Variável Aleatória Funções de Várias Momentos e Estatística Condicional Teorema do Limite Central Processos Estocásticos
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte II
 Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte II 13 de Dezembro de 2013 Exercício 1. Descreva o espaço de probabilidade associado às seguintes experiências aleatórias: 1. Uma moeda
Exercícios de Teoria da Probabilidade e Processos Estocásticos Parte II 13 de Dezembro de 2013 Exercício 1. Descreva o espaço de probabilidade associado às seguintes experiências aleatórias: 1. Uma moeda
PROBABILIDADE PGE950
 PROBABILIDADE PGE950 José J. C. Hernández DE - UFPE October 12, 2017 José J. C. Hernández (DE - UFPE) Estatística I October 12, 2017 1 / 88 1 Introdução à Probabilidade 2 Variavel Aleatória 3 Vetores Aleatórios
PROBABILIDADE PGE950 José J. C. Hernández DE - UFPE October 12, 2017 José J. C. Hernández (DE - UFPE) Estatística I October 12, 2017 1 / 88 1 Introdução à Probabilidade 2 Variavel Aleatória 3 Vetores Aleatórios
DANIEL V. TAUSK. se A é um subconjunto de X, denotamos por A c o complementar de
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
Capítulo 1. Fundamentos
 Capítulo 1 Fundamentos A probabilidade moderna se baseia fortemente na Teoria da Medida e supomos durante esse curso que o leitor esteja bem familiarizado com conceitos tais como: Medida de Lebesgue, extensões
Capítulo 1 Fundamentos A probabilidade moderna se baseia fortemente na Teoria da Medida e supomos durante esse curso que o leitor esteja bem familiarizado com conceitos tais como: Medida de Lebesgue, extensões
Processos Estocásticos. Luiz Affonso Guedes
 Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Variáveis Aleatórias Funções de Uma Variável Aleatória Funções de Várias Variáveis Aleatórias Momentos e Estatística Condicional Teorema
Processos Estocásticos Luiz Affonso Guedes Sumário Probabilidade Variáveis Aleatórias Funções de Uma Variável Aleatória Funções de Várias Variáveis Aleatórias Momentos e Estatística Condicional Teorema
Sumário. 2 Índice Remissivo 12
 i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
Probabilidade II. Departamento de Estatística. Universidade Federal da Paraíba. Prof. Tarciana Liberal (UFPB) Aula Desigualdades 02/14 1 / 31
 Probabilidade II Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Desigualdades 02/14 1 / 31 Um teorema de grande importância e bastante utilidade em probabilidade
Probabilidade II Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Desigualdades 02/14 1 / 31 Um teorema de grande importância e bastante utilidade em probabilidade
Teoria da Medida e Integração (MAT505)
 Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Teoremas de uma, duas e três séries de Kolmogorov
 Teoremas de uma, duas e três séries de Kolmogorov 13 de Maio de 013 1 Introdução Nestas notas Z 1, Z, Z 3,... é uma sequência de variáveis aleatórias independentes. Buscaremos determinar condições sob
Teoremas de uma, duas e três séries de Kolmogorov 13 de Maio de 013 1 Introdução Nestas notas Z 1, Z, Z 3,... é uma sequência de variáveis aleatórias independentes. Buscaremos determinar condições sob
Teoria da Medida e Integração (MAT505)
 Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
A estacionariedade prova-se de maneira semel- hante.
 Se por outro lado (U 1, U 2,...) é IID então mostremos que X n U 1 + + U n tem incrementos independentes e estacionários. De facto, dados n > m temos que X n X m U m+1 + + U n. Tome-se quaisquer n 1
Se por outro lado (U 1, U 2,...) é IID então mostremos que X n U 1 + + U n tem incrementos independentes e estacionários. De facto, dados n > m temos que X n X m U m+1 + + U n. Tome-se quaisquer n 1
Par de Variáveis Aleatórias
 Par de Variáveis Aleatórias Luis Henrique Assumpção Lolis 7 de abril de 2014 Luis Henrique Assumpção Lolis Par de Variáveis Aleatórias 1 Conteúdo 1 Introdução 2 Par de Variáveis Aleatórias Discretas 3
Par de Variáveis Aleatórias Luis Henrique Assumpção Lolis 7 de abril de 2014 Luis Henrique Assumpção Lolis Par de Variáveis Aleatórias 1 Conteúdo 1 Introdução 2 Par de Variáveis Aleatórias Discretas 3
Cálculo das Probabilidades e Estatística I
 Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Variáveis Aleatórias Ao descrever um espaço
Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Variáveis Aleatórias Ao descrever um espaço
Probabilidade de Ruína e Processos de Lévy α-estáveis
 Apresentação Probabilidade de Ruína e Processos de Lévy α-estáveis Universidade de São Paulo IME - USP 08 de abril, 2010 Apresentação Distribuições Estáveis e Processos de Lévy α-estáveis Convergência
Apresentação Probabilidade de Ruína e Processos de Lévy α-estáveis Universidade de São Paulo IME - USP 08 de abril, 2010 Apresentação Distribuições Estáveis e Processos de Lévy α-estáveis Convergência
Demonstração. Ver demonstração em [1]. . Para que i j se tem µ i µ j? Determine a derivada no sentido de Radon-Nikodym em cada caso.
![Demonstração. Ver demonstração em [1]. . Para que i j se tem µ i µ j? Determine a derivada no sentido de Radon-Nikodym em cada caso. Demonstração. Ver demonstração em [1]. . Para que i j se tem µ i µ j? Determine a derivada no sentido de Radon-Nikodym em cada caso.](/thumbs/61/45893652.jpg) Proposição 2.39 (Propriedades de e.). Sejam µ, λ, λ 1, λ 2 medidas no espaço mensurável (X, F). Então 1. se λ 1 µ e λ 2 µ então (λ 1 + λ 2 ) µ. 2. se λ 1 µ e λ 2 µ então (λ 1 + λ 2 ) µ. 3. se λ 1 µ e λ
Proposição 2.39 (Propriedades de e.). Sejam µ, λ, λ 1, λ 2 medidas no espaço mensurável (X, F). Então 1. se λ 1 µ e λ 2 µ então (λ 1 + λ 2 ) µ. 2. se λ 1 µ e λ 2 µ então (λ 1 + λ 2 ) µ. 3. se λ 1 µ e λ
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA. Medida e Probabilidade
 UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
Estatística Aplicada II. } Revisão: Probabilidade } Propriedades da Média Amostral
 Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Fundamentos da Teoria da Probabilidade
 Fundamentos da Teoria da Probabilidade Edmar José do Nascimento (Princípios de Comunicações) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco Sinais Aleatórios
Fundamentos da Teoria da Probabilidade Edmar José do Nascimento (Princípios de Comunicações) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco Sinais Aleatórios
Variáveis Aleatórias. Departamento de Matemática Escola Superior de Tecnologia de Viseu
 Variáveis Aleatórias Departamento de Matemática Escola Superior de Tecnologia de Viseu Exemplo No lançamento de duas moedas ao ar, os resultados possíveis são: FF, FC, CF ou CC. No entanto, o nosso interesse
Variáveis Aleatórias Departamento de Matemática Escola Superior de Tecnologia de Viseu Exemplo No lançamento de duas moedas ao ar, os resultados possíveis são: FF, FC, CF ou CC. No entanto, o nosso interesse
t X s db s, I t (X) :=
 Chapter 3 Integrais estocásticos Neste capítulo vamos definir integrais estocásticos relativamente ao movimento Browniano e estudar algumas das suas propriedades. Estes integrais também são chamados integrais
Chapter 3 Integrais estocásticos Neste capítulo vamos definir integrais estocásticos relativamente ao movimento Browniano e estudar algumas das suas propriedades. Estes integrais também são chamados integrais
Capítulo 1. Fundamentos
 Capítulo 1 Fundamentos A probabilidade moderna se baseia fortemente na Teoria da Medida e supomos durante esse curso que o leitor esteja bem familiarizado com conceitos tais como: Medida de Lebesgue, extensões
Capítulo 1 Fundamentos A probabilidade moderna se baseia fortemente na Teoria da Medida e supomos durante esse curso que o leitor esteja bem familiarizado com conceitos tais como: Medida de Lebesgue, extensões
O movimento Browniano
 O movimento Browniano R. Vilela Mendes http://label2.ist.utl.pt/vilela/ March 2010 () March 2010 1 / 35 Sumário O movimento Browniano Propriedade Markoviana Probabilidade de transição. Medida de Wiener
O movimento Browniano R. Vilela Mendes http://label2.ist.utl.pt/vilela/ March 2010 () March 2010 1 / 35 Sumário O movimento Browniano Propriedade Markoviana Probabilidade de transição. Medida de Wiener
As leis dos grandes números
 6. Introdução este capítulo estudamos algumas formulações da lei dos grandes números. Uma lei dos grandes números dá o comportamento limite, ou assimptótico, de uma média de observações aleatórias., de
6. Introdução este capítulo estudamos algumas formulações da lei dos grandes números. Uma lei dos grandes números dá o comportamento limite, ou assimptótico, de uma média de observações aleatórias., de
Escola Superior de Agricultura "Luiz de Queiroz", Departamento de Ciências Exatas. Probabilidades. Cristian Villegas
 Probabilidades Cristian Villegas clobos@usp.br Setembro de 2013 Apostila de Estatística (Cristian Villegas) 1 Introdução Escola Superior de Agricultura "Luiz de Queiroz", Departamento de Ciências Exatas
Probabilidades Cristian Villegas clobos@usp.br Setembro de 2013 Apostila de Estatística (Cristian Villegas) 1 Introdução Escola Superior de Agricultura "Luiz de Queiroz", Departamento de Ciências Exatas
MAT 461 Tópicos de Matemática II Aula 8: Resumo de Probabilidade
 MAT 461 Tópicos de Matemática II Aula 8: Resumo de Probabilidade Edson de Faria Departamento de Matemática IME-USP 28 de Agosto, 2013 Probabilidade: uma Introdução / Aula 8 1 Desigualdades de Markov e
MAT 461 Tópicos de Matemática II Aula 8: Resumo de Probabilidade Edson de Faria Departamento de Matemática IME-USP 28 de Agosto, 2013 Probabilidade: uma Introdução / Aula 8 1 Desigualdades de Markov e
3 3. Variáveis Aleatórias
 ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Departamento de Matemática Escola Superior de Tecnologia de Viseu. Engenharia e Gestão Industrial
 Variáveis Aleatórias Departamento de Matemática Escola Superior de Tecnologia de Viseu Engenharia e Gestão Industrial 1 Exemplo No lançamento de duas moedas ao ar, os resultados possíveis são: FF, FC,
Variáveis Aleatórias Departamento de Matemática Escola Superior de Tecnologia de Viseu Engenharia e Gestão Industrial 1 Exemplo No lançamento de duas moedas ao ar, os resultados possíveis são: FF, FC,
AULA 11 - Valor esperado e suas propriedades
 AULA 11 - Valor esperado e suas propriedades Susan Schommer Introdução à Estatística Econômica - IE/UFRJ O valor esperado de uma variável aleatória Como forma de resumir o comportamento de uma variável
AULA 11 - Valor esperado e suas propriedades Susan Schommer Introdução à Estatística Econômica - IE/UFRJ O valor esperado de uma variável aleatória Como forma de resumir o comportamento de uma variável
As leis dos grandes números
 As leis dos grandes números PE0708 25 de Fevereiro de 2008 Introdução este capítulo estudamos algumas formulações da lei dos grandes números. Uma lei dos grandes números dá o comportamento limite, ou assimptótico,
As leis dos grandes números PE0708 25 de Fevereiro de 2008 Introdução este capítulo estudamos algumas formulações da lei dos grandes números. Uma lei dos grandes números dá o comportamento limite, ou assimptótico,
Exercício 18. Demonstre a proposição anterior. (Dica: use as definições de continuidade e mensurabilidade)
 Proposição 2.7. Sejam Y e Z espaços métricos e X um espaço mensurável. Se f : X Y é uma função mensurável e g : Y Z é uma função contínua então g f : X Z é uma função mensurável. Exercício 18. Demonstre
Proposição 2.7. Sejam Y e Z espaços métricos e X um espaço mensurável. Se f : X Y é uma função mensurável e g : Y Z é uma função contínua então g f : X Z é uma função mensurável. Exercício 18. Demonstre
Estatística Descritiva e Exploratória
 Gledson Luiz Picharski e Wanderson Rodrigo Rocha 9 de Maio de 2008 Estatística Descritiva e exploratória 1 Váriaveis Aleatórias Discretas 2 Variáveis bidimensionais 3 Váriaveis Aleatórias Continuas Introdução
Gledson Luiz Picharski e Wanderson Rodrigo Rocha 9 de Maio de 2008 Estatística Descritiva e exploratória 1 Váriaveis Aleatórias Discretas 2 Variáveis bidimensionais 3 Váriaveis Aleatórias Continuas Introdução
Teoria da Medida e Integração (MAT505)
 Transporte de medidas Teoria da Medida e Integração (MAT505) Transporte de medidas e medidas invariantes. Teorema de Recorrência de Poincaré V. Araújo Instituto de Matemática, Universidade Federal da Bahia
Transporte de medidas Teoria da Medida e Integração (MAT505) Transporte de medidas e medidas invariantes. Teorema de Recorrência de Poincaré V. Araújo Instituto de Matemática, Universidade Federal da Bahia
Teoria Ergódica (9 a aula)
 Outubro 2012 Espaços de Sequências Seja (X, d 0 ) um espaço métrico compacto. B Z (X ) = X Z = { x = (x j ) j Z : x j X, j Z } B N (X ) = X N = { x = (x j ) j N : x j X, j N } B(X ) designa indiferentemente
Outubro 2012 Espaços de Sequências Seja (X, d 0 ) um espaço métrico compacto. B Z (X ) = X Z = { x = (x j ) j Z : x j X, j Z } B N (X ) = X N = { x = (x j ) j N : x j X, j N } B(X ) designa indiferentemente
Departamento de InformáAca - PUC- Rio. Hélio Lopes Departamento de InformáAca PUC- Rio. Probabilidade
 Introdução à Simulação Estocás5ca usando R INF2035 PUC- Rio, 2013.1 Departamento de InformáAca - PUC- Rio Hélio Lopes Departamento de InformáAca PUC- Rio Experimentos aleatórios: no estudo de probabilidade,
Introdução à Simulação Estocás5ca usando R INF2035 PUC- Rio, 2013.1 Departamento de InformáAca - PUC- Rio Hélio Lopes Departamento de InformáAca PUC- Rio Experimentos aleatórios: no estudo de probabilidade,
Aula 1 - Revisão de Probabilidade e Estatística
 Aula 1 - Revisão de Probabilidade e Estatística Matheus Rosso e Camila Steffens 1 de Março de 2018 Conteúdos 1. Introdução à probabilidade 2. Probabilidade condicional e independência 3. Variáveis aleatórias
Aula 1 - Revisão de Probabilidade e Estatística Matheus Rosso e Camila Steffens 1 de Março de 2018 Conteúdos 1. Introdução à probabilidade 2. Probabilidade condicional e independência 3. Variáveis aleatórias
Teoria das Filas aplicadas a Sistemas Computacionais. Aula 08
 Teoria das Filas aplicadas a Sistemas Computacionais Aula 08 Universidade Federal do Espírito Santo - Departamento de Informática - DI Laboratório de Pesquisas em Redes Multimidia - LPRM Teoria das Filas
Teoria das Filas aplicadas a Sistemas Computacionais Aula 08 Universidade Federal do Espírito Santo - Departamento de Informática - DI Laboratório de Pesquisas em Redes Multimidia - LPRM Teoria das Filas
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADE
 VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADE.1 INTRODUÇÃO Admita que, de um lote de 10 peças, 3 das quais são defeituosas, peças são etraídas ao acaso, juntas (ou uma a uma, sem reposição). Estamos
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADE.1 INTRODUÇÃO Admita que, de um lote de 10 peças, 3 das quais são defeituosas, peças são etraídas ao acaso, juntas (ou uma a uma, sem reposição). Estamos
No que segue, X sempre denota um espaço topológico localmente compacto
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK No que segue, sempre denota um espaço topológico localmente compacto Hausdorff. Se f : R é uma função, então supp f denota o{ suporte (relativamente
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK No que segue, sempre denota um espaço topológico localmente compacto Hausdorff. Se f : R é uma função, então supp f denota o{ suporte (relativamente
CURTA REVISÃO SOBRE PROBABILIDADE E PROCESSOS ESTOCÁSTICOS
 CURTA REVISÃO SOBRE PROBABILIDADE E PROCESSOS ESTOCÁSTICOS PARTE i Histórico Probabilidade Axiomática de Kolmogorov Variáveis Aleatórias Densidade de Probabilidade Desigualdade de Chebyshev Versão Fraca
CURTA REVISÃO SOBRE PROBABILIDADE E PROCESSOS ESTOCÁSTICOS PARTE i Histórico Probabilidade Axiomática de Kolmogorov Variáveis Aleatórias Densidade de Probabilidade Desigualdade de Chebyshev Versão Fraca
1 Probabilidade: Axiomas e Propriedades
 1 Probabilidade: Axiomas e Propriedades 1.1 Definição Frequentista Considere um experimento aleatório que consiste no lançamento de um dado honesto. O espaço amostral desse experimento é Ω = {1, 2, 3,
1 Probabilidade: Axiomas e Propriedades 1.1 Definição Frequentista Considere um experimento aleatório que consiste no lançamento de um dado honesto. O espaço amostral desse experimento é Ω = {1, 2, 3,
PARTE TEÓRICA Perguntas de escolha múltipla
 PROBABILIDADES E ESTATÍSTICA MIEEC/FEUP PARTE TEÓRICA Perguntas de escolha múltipla 1 Dada a experiência aleatória ε define-se espaço amostral associado a ε como sendo: A O espaço físico onde se realiza
PROBABILIDADES E ESTATÍSTICA MIEEC/FEUP PARTE TEÓRICA Perguntas de escolha múltipla 1 Dada a experiência aleatória ε define-se espaço amostral associado a ε como sendo: A O espaço físico onde se realiza
Construção de espaços de probabilidade. básicos
 Capítulo 2 Construção de espaços de probabilidade básicos Nessa seção descreveremos diversas maneiras diferentes de construir um espaço de probabilidade, dando diversos exemplos de como elas podem ser
Capítulo 2 Construção de espaços de probabilidade básicos Nessa seção descreveremos diversas maneiras diferentes de construir um espaço de probabilidade, dando diversos exemplos de como elas podem ser
Lista 4. Esta lista, de entrega facultativa, tem três partes e seus exercícios versam sobre séries, funções contínuas e funções diferenciáveis em R.
 UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof José Carlos Eidam Lista 4 INSTRUÇÕES Esta lista, de entrega facultativa, tem três partes e seus exercícios versam
UFPR - Universidade Federal do Paraná Departamento de Matemática CM095 - Análise I Prof José Carlos Eidam Lista 4 INSTRUÇÕES Esta lista, de entrega facultativa, tem três partes e seus exercícios versam
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática. O Teorema de Arzelá. José Renato Fialho Rodrigues
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática O Teorema de Arzelá José Renato Fialho Rodrigues Belo Horizonte - MG 1994 José Renato Fialho Rodrigues O Teorema
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática O Teorema de Arzelá José Renato Fialho Rodrigues Belo Horizonte - MG 1994 José Renato Fialho Rodrigues O Teorema
Aula 4. Aula de hoje. Aula passada
 Aula 4 Aula passada Função de distribuição Bernoulli Sequência de v.a. Binomial, Geométrica, Zeta Valor esperado Variância Distribuição conjunta Independência de v.a. Aula de hoje Valor esperado condicional
Aula 4 Aula passada Função de distribuição Bernoulli Sequência de v.a. Binomial, Geométrica, Zeta Valor esperado Variância Distribuição conjunta Independência de v.a. Aula de hoje Valor esperado condicional
TEORIA ERGÓDICA, SISTEMAS DINÂMICOS E MEDIDAS INVARIANTES
 TEORIA ERGÓDICA, SISTEMAS DINÂMICOS E MEDIDAS INVARIANTES Aluno: Juliana Arcoverde V. L. Ribeiro Orientador: Lorenzo Justiniano Díaz Casado Introdução A Teoria dos Sistemas Dinâmicos, ou mais exatamente
TEORIA ERGÓDICA, SISTEMAS DINÂMICOS E MEDIDAS INVARIANTES Aluno: Juliana Arcoverde V. L. Ribeiro Orientador: Lorenzo Justiniano Díaz Casado Introdução A Teoria dos Sistemas Dinâmicos, ou mais exatamente
Uma breve introdução a probabilidade
 Uma breve introdução a probabilidade Modelo Probabilístico Espaço amostral (S): conjunto de todos os resultados que podem ocorrer a partir de um experimento aleatório Probabilidade de eventos (P): quantificação
Uma breve introdução a probabilidade Modelo Probabilístico Espaço amostral (S): conjunto de todos os resultados que podem ocorrer a partir de um experimento aleatório Probabilidade de eventos (P): quantificação
CE085 - Estatística Inferencial
 CE085 - Estatística Inferencial Revisão: Probabilidade Básica Prof. Wagner Hugo Bonat Laboratório de Estatística e Geoinformação - LEG Curso de Bacharelado em Estatatística Universidade Federal do Paraná
CE085 - Estatística Inferencial Revisão: Probabilidade Básica Prof. Wagner Hugo Bonat Laboratório de Estatística e Geoinformação - LEG Curso de Bacharelado em Estatatística Universidade Federal do Paraná
O Teorema de Peano. f : D R n. uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e uma função ϕ : I R n tais que
 O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
Métodos Matemáticos na Ciência de Dados: Introdução Relâmpago. II
 Métodos Matemáticos na Ciência de Dados: Introdução Relâmpago. II Vladimir Pestov 1 University of Ottawa / Université d Ottawa Ottawa, Ontario, Canadá 2 Universidade Federal de Santa Catarina Florianópolis,
Métodos Matemáticos na Ciência de Dados: Introdução Relâmpago. II Vladimir Pestov 1 University of Ottawa / Université d Ottawa Ottawa, Ontario, Canadá 2 Universidade Federal de Santa Catarina Florianópolis,
Aula 11. Variáveis Aleatórias Contínuas Bidimensionais
 Aula. Variáveis Aleatórias Contínuas Bidimensionais Resumo de caso unidimensional Caso Discreto p p 2 p 3 Caso Contínuo f(x) x x 2 x 3 i p i + f x dx X x x 2 x 3 P p p 2 p 3 Caso bidimensional Caso Discreto
Aula. Variáveis Aleatórias Contínuas Bidimensionais Resumo de caso unidimensional Caso Discreto p p 2 p 3 Caso Contínuo f(x) x x 2 x 3 i p i + f x dx X x x 2 x 3 P p p 2 p 3 Caso bidimensional Caso Discreto
Métodos Estatísticos Básicos
 Aula 6 - Introdução à probabilidade Departamento de Economia Universidade Federal de Pelotas (UFPel) Maio de 2014 Experimento Experimento aleatório (E ): é um experimento que pode ser repetido indenidamente
Aula 6 - Introdução à probabilidade Departamento de Economia Universidade Federal de Pelotas (UFPel) Maio de 2014 Experimento Experimento aleatório (E ): é um experimento que pode ser repetido indenidamente
Probabilidade e Estatística
 Plano de Curso Probabilidade e Estatística UAEst/CCT/UFCG Ementa Fenômeno aleatório versus fenômeno determinístico. Espaço amostral e eventos. Introdução à teoria das probabilidades. Abordagem axiomática
Plano de Curso Probabilidade e Estatística UAEst/CCT/UFCG Ementa Fenômeno aleatório versus fenômeno determinístico. Espaço amostral e eventos. Introdução à teoria das probabilidades. Abordagem axiomática
σ-álgebras, geradores e independência
 σ-álgebras, geradores e independência Roberto Imbuzeiro M. F. de Oliveira 15 de Março de 2009 Resumo Notas sobre a σ-álgebra gerada por uma variável aleatória X e sobre as condições de independência de
σ-álgebras, geradores e independência Roberto Imbuzeiro M. F. de Oliveira 15 de Março de 2009 Resumo Notas sobre a σ-álgebra gerada por uma variável aleatória X e sobre as condições de independência de
Produtos de potências racionais. números primos.
 MATEMÁTICA UNIVERSITÁRIA n o 4 Dezembro/2006 pp. 23 3 Produtos de potências racionais de números primos Mário B. Matos e Mário C. Matos INTRODUÇÃO Um dos conceitos mais simples é o de número natural e
MATEMÁTICA UNIVERSITÁRIA n o 4 Dezembro/2006 pp. 23 3 Produtos de potências racionais de números primos Mário B. Matos e Mário C. Matos INTRODUÇÃO Um dos conceitos mais simples é o de número natural e
MP-208: Filtragem Ótima com Aplicações Aeroespaciais
 MP-208: Filtragem Ótima com Aplicações Aeroespaciais Seção 2.6: Vetores Aleatórios Davi Antônio dos Santos Departamento de Mecatrônica Instituto Tecnológico de Aeronáutica davists@ita.br São José dos Campos,
MP-208: Filtragem Ótima com Aplicações Aeroespaciais Seção 2.6: Vetores Aleatórios Davi Antônio dos Santos Departamento de Mecatrônica Instituto Tecnológico de Aeronáutica davists@ita.br São José dos Campos,
MOQ-12: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS. VA s e Distribuições
 Motivação: MOQ-2: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS VA s e Distribuições Definimos anteriormente Espaço de Probabilidades como sendo a tripla (W,, P(.)), em que, dado um eperimento, W representa
Motivação: MOQ-2: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS VA s e Distribuições Definimos anteriormente Espaço de Probabilidades como sendo a tripla (W,, P(.)), em que, dado um eperimento, W representa
Fundamentos de Estatística
 Fundamentos de Estatística Clássica Workshop Análise de Incertezas e Validação Programa de Verão 2017 Marcio Borges 1 1LABORATÓRIO NACIONAL DE COMPUTAÇÃO CIENTÍFICA mrborges@lncc.br Petrópolis, 9 de Fevereiro
Fundamentos de Estatística Clássica Workshop Análise de Incertezas e Validação Programa de Verão 2017 Marcio Borges 1 1LABORATÓRIO NACIONAL DE COMPUTAÇÃO CIENTÍFICA mrborges@lncc.br Petrópolis, 9 de Fevereiro
Probabilidades. Wagner H. Bonat Elias T. Krainski Fernando P. Mayer
 Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Estatística Matemática I
 Estatística Matemática I Roseli Aparecida Leandro e Clarice G.B. Demétrio Março de 2011 Depto. de Ciências Exatas, ESALQ/USP e-mail: raleandr@esalq.usp.br 1 Variáveis aleatórias Sejam E um experimento
Estatística Matemática I Roseli Aparecida Leandro e Clarice G.B. Demétrio Março de 2011 Depto. de Ciências Exatas, ESALQ/USP e-mail: raleandr@esalq.usp.br 1 Variáveis aleatórias Sejam E um experimento
Chamamos de evento qualquer subconjunto do espaço amostral: A é um evento A Ω.
 PROBABILIDADE 1.0 Conceitos Gerais No caso em que os possíveis resultados de um experimento aleatório podem ser listados (caso discreto), um modelo probabilístico pode ser entendido como a listagem desses
PROBABILIDADE 1.0 Conceitos Gerais No caso em que os possíveis resultados de um experimento aleatório podem ser listados (caso discreto), um modelo probabilístico pode ser entendido como a listagem desses
1 Noções de Probabilidade
 Noções de Probabilidade Já vimos que para se obter informações sobre alguma característica da população, podemos utilizar uma amostra. Estudaremos agora a probabilidade, que é uma ferramenta usada e necessária
Noções de Probabilidade Já vimos que para se obter informações sobre alguma característica da população, podemos utilizar uma amostra. Estudaremos agora a probabilidade, que é uma ferramenta usada e necessária
Variáveis Aleatórias Contínuas
 Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
3 NOÇÕES DE PROBABILIDADE
 3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
canal para sinais contínuos
 Processos estocásticos, Entropia e capacidade de canal para sinais contínuos 24 de setembro de 2013 Processos estocásticos, Entropia e capacidade de canal para1 sin Conteúdo 1 Probabilidade de sinais contínuos
Processos estocásticos, Entropia e capacidade de canal para sinais contínuos 24 de setembro de 2013 Processos estocásticos, Entropia e capacidade de canal para1 sin Conteúdo 1 Probabilidade de sinais contínuos
Estatística (MAD231) Turma: IGA. Período: 2018/2
 Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Cap. 4 - Probabilidade
 Estatística para Cursos de Engenharia e Informática Pedro Alberto Barbetta / Marcelo Menezes Reis / Antonio Cezar Bornia São Paulo: Atlas, 2004 Cap. 4 - Probabilidade APOIO: Fundação de Apoio à Pesquisa
Estatística para Cursos de Engenharia e Informática Pedro Alberto Barbetta / Marcelo Menezes Reis / Antonio Cezar Bornia São Paulo: Atlas, 2004 Cap. 4 - Probabilidade APOIO: Fundação de Apoio à Pesquisa
Movimento Browniano, Integral de Itô e Estocásticas
 Universidade Federal do Rio Grande do Sul Instituto de Matemática Programa de Pós-Graduação em Matemática Movimento Browniano, Integral de Itô e Introdução às Equações Diferenciais Estocásticas Ricardo
Universidade Federal do Rio Grande do Sul Instituto de Matemática Programa de Pós-Graduação em Matemática Movimento Browniano, Integral de Itô e Introdução às Equações Diferenciais Estocásticas Ricardo
Teoria da Medida e Integração (MAT505)
 Teoria da Medida e Integração (MAT505) Teoria de Derivação de Lebesgue. Teorema Fundamental do Cálculo. V. Araújo Mestrado em Matemática, UFBA, 204 Conteúdo Riemann. vs Lebesgue..............................2
Teoria da Medida e Integração (MAT505) Teoria de Derivação de Lebesgue. Teorema Fundamental do Cálculo. V. Araújo Mestrado em Matemática, UFBA, 204 Conteúdo Riemann. vs Lebesgue..............................2
Axiomatizações equivalentes do conceito de topologia
 Axiomatizações equivalentes do conceito de topologia Giselle Moraes Resende Pereira Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação Tutorial
Axiomatizações equivalentes do conceito de topologia Giselle Moraes Resende Pereira Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação Tutorial
Mais sobre Modelos Continuos
 Mais sobre Modelos Continuos Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo 1 / 41 Transformação Linear da Uniforme Seja X uma variável aleatória
Mais sobre Modelos Continuos Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo 1 / 41 Transformação Linear da Uniforme Seja X uma variável aleatória
Introdução aos Proc. Estocásticos - ENG 430
 Introdução aos Proc. Estocásticos - ENG 430 Fabrício Simões IFBA 16 de novembro de 2015 Fabrício Simões (IFBA) Introdução aos Proc. Estocásticos - ENG 430 16 de novembro de 2015 1 / 34 1 Motivação 2 Conceitos
Introdução aos Proc. Estocásticos - ENG 430 Fabrício Simões IFBA 16 de novembro de 2015 Fabrício Simões (IFBA) Introdução aos Proc. Estocásticos - ENG 430 16 de novembro de 2015 1 / 34 1 Motivação 2 Conceitos
Conteúdo Teórico: 04 Esperança
 ACH2053 Introdução à Estatística Conteúdo Teórico: 04 Esperança Marcelo de Souza Lauretto Sistemas de Informação EACH www.each.usp.br/lauretto Referência: Morris DeGroot, Mark Schervish. Probability and
ACH2053 Introdução à Estatística Conteúdo Teórico: 04 Esperança Marcelo de Souza Lauretto Sistemas de Informação EACH www.each.usp.br/lauretto Referência: Morris DeGroot, Mark Schervish. Probability and
Estatísticas Inferenciais Distribuições Amostrais. Estatística
 Estatística Na descrição dos conjuntos de dados x 1,..., x n, não foi feita menção ao conceito de população. Estatísticas inferenciais: preocupadas com a fonte dos dados e em tentar fazer generalizações
Estatística Na descrição dos conjuntos de dados x 1,..., x n, não foi feita menção ao conceito de população. Estatísticas inferenciais: preocupadas com a fonte dos dados e em tentar fazer generalizações
SME0801- Probabilidade II Distribuições conjuntas. Primeiras definições e propriedades
 SME0801- Probabilidade II Distribuições conjuntas. Primeiras definições e propriedades Pablo Martin Rodriguez SME ICMC USP Bacharelado em Estatística 20 Mar 2017 Vetores aleatórios Definição Sejam X 1,
SME0801- Probabilidade II Distribuições conjuntas. Primeiras definições e propriedades Pablo Martin Rodriguez SME ICMC USP Bacharelado em Estatística 20 Mar 2017 Vetores aleatórios Definição Sejam X 1,
AST203-CVR 4-1 AST203-CVR. Observação eletromagnética. Processamento de sinais importante em várias áreas, além da astronomia telecomunicações
 Bloco 4 Estatística Atualizado: 2012 4-1 Bibliografia Lena Cap. 4 (parte) - só a inspiração... Wall & Jenkins, Practical statistics for astronomers Brandt Statistical and computacional methods in data
Bloco 4 Estatística Atualizado: 2012 4-1 Bibliografia Lena Cap. 4 (parte) - só a inspiração... Wall & Jenkins, Practical statistics for astronomers Brandt Statistical and computacional methods in data
2. podemos solucionar problemas não somente probabilisticas, mas tambem qualquer
 Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
1.3 Conjuntos de medida nula
 1.3 Conjuntos de medida nula Seja (X, F, µ) um espaço de medida. Um subconjunto A X é um conjunto de medida nula se existir B F tal que A B e µ(b) = 0. Do ponto de vista da teoria da medida, os conjuntos
1.3 Conjuntos de medida nula Seja (X, F, µ) um espaço de medida. Um subconjunto A X é um conjunto de medida nula se existir B F tal que A B e µ(b) = 0. Do ponto de vista da teoria da medida, os conjuntos
3 Apresentação do processo e resultados preliminares
 3 Apresentação do processo e resultados preliminares O Capitulo 1 dá a ferramenta para construir uma cadeia de Markov a tempo contínuo, a partir de uma cadeia de Markov a tempo discreto. Agora, queremos
3 Apresentação do processo e resultados preliminares O Capitulo 1 dá a ferramenta para construir uma cadeia de Markov a tempo contínuo, a partir de uma cadeia de Markov a tempo discreto. Agora, queremos
Aula 10 Variáveis aleatórias discretas
 AULA 0 Aula 0 Variáveis aleatórias discretas Nesta aula você aprenderá um conceito muito importante da teoria de probabilidade: o conceito de variável aleatória. Você verá que as variáveis aleatórias e
AULA 0 Aula 0 Variáveis aleatórias discretas Nesta aula você aprenderá um conceito muito importante da teoria de probabilidade: o conceito de variável aleatória. Você verá que as variáveis aleatórias e
Lucas Santana da Cunha de junho de 2018 Londrina
 Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
NOTAS DA AULA REVISÃO SOBRE FUNDAMENTOS DE PROBABILIDADE. Prof.: Idemauro Antonio Rodrigues de Lara
 1 NOTAS DA AULA REVISÃO SOBRE FUNDAMENTOS DE PROBABILIDADE Prof.: Idemauro Antonio Rodrigues de Lara 2 Experimentos aleatórios Definição 1. Experimentos aleatórios são experimentos que quando executados
1 NOTAS DA AULA REVISÃO SOBRE FUNDAMENTOS DE PROBABILIDADE Prof.: Idemauro Antonio Rodrigues de Lara 2 Experimentos aleatórios Definição 1. Experimentos aleatórios são experimentos que quando executados
Aula de hoje. administração. São Paulo: Ática, 2007, Cap. 3. ! Tópicos. ! Referências. ! Distribuição de probabilidades! Variáveis aleatórias
 Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
TEOREMAS LIMITE EM PROBABILIDADE RENATO ASSUNÇÃO DCC - UFMG
 TEOREMAS LIMITE EM PROBABILIDADE RENATO ASSUNÇÃO DCC - UFMG Referência para um estudo aprofundado das questões (e demonstrações das afirmações feitas aqui) LIMITE DE NÚMEROS REAIS Sequência de números
TEOREMAS LIMITE EM PROBABILIDADE RENATO ASSUNÇÃO DCC - UFMG Referência para um estudo aprofundado das questões (e demonstrações das afirmações feitas aqui) LIMITE DE NÚMEROS REAIS Sequência de números
