3 IMPLEMENTAÇÃO DO ELEMENTO FINITO
|
|
|
- Lorenzo Sousa Castel-Branco
- 5 Há anos
- Visualizações:
Transcrição
1 3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline Hipóteses Cinemáticas a formulação do elemento foram assumidas as seguintes hipóteses: Consideram-se deslocamentos e rotações pequenas. Os segmentos perpendiculares à superfície média antes da deformação continuam retas, mas não necessariamente perpendiculares à superfície média deformada (eoria de Mindlin). Esforços normais à superfície média são desprezados. O material é considerado linear, elástico e isotrópico. 3.. ipo de Elemento e Funções de Deslocamento O elemento é do tipo subparamétrico de lados retos, definido pela coordenada local à direita, pelas coordenadas y das quatro esquinas e a espessura constante t, como indicado na Figura 3.1. Os quatro pontos dos cantos e então qualquer ponto na superfície média estão contidos no mesmo plano. Figura 3.1. Coordenadas locais do elemento.
2 9 As coordenadas de um ponto na superfície média podem ser calculadas através de uma interpolação linear e em coordenadas naturais η e ξ, com as fórmulas seguintes, onde m é o número de divisões ao longo do comprimento. = y 0 y y y1 y y3 y4 y3 y4 (3.1) η = m (3.) y 1 1 η = 1 1 m y 3 ( ξ ) 1 η = + ξ m ( 1 ) y 4 y 1 η = ξ m ( 1 ) 1 η = m ( ξ ) (3.3) O jacobiano da transformação é igual a: η J = ξ y η y ξ = η m y 1 = η m [ y ( 1 ξ ) ( y )( 1+ ξ )] 3 y4 (3.4) = 0 ξ y = ξ 1 η m ( y + y y ) + y y O determinante deste jacobiano pode ser determinado pela fórmula: det J η m m ( y + y y ) + y y = (3.5) Para que o elemento possa ser utilizado na modelagem tridimensional devemos levar em conta os seis graus de liberdade, três translações e três rotações.
3 30 Adota-se um campo de deslocamentos Lagrangiano de segundo grau no sentido transversal, pois isto atende a diferentes situações no que se refere a esforço plano e a fleão. Se um polinômio linear fosse utilizado no estado de esforço plano, vários elementos seriam necessários no sentido transversal para modelar o eemplo mais simples que é uma viga esbelta simplesmente apoiada com carregamento uniforme. Já no caso de fleão, a escolha é feita com a idéia de simplificar o elemento, já que um polinômio de terceiro grau pode ser mais efetivo, porém teríamos maior número de graus de liberdade por elemento. Com isto o campo de deslocamentos torna-se: + 1 m 1 3 i( η ) i i= 1 { δ} [ I ] [ I ] [ I ] φ { δ } = { δ} = { u v w θ θ y θz} (3.6) { } = { δ u v w θ θ θ u v w θ θ θ i i1 i1 i1 i1 yi1 zi1 i i i i yi zi... u v w θ θ θ i3 i3 i3 i3 yi3 zi3 }... a epressão acima, a matriz I é uma matriz identidade de ordem seis e δ i é o vetor de parâmetros de deslocamento que se mostram em forma esquemática na Figura 3.. Observa-se que tais parâmetros na realidade não são deslocamentos físicos. Figura 3.. Parâmetros de deslocamento.
4 Esforços e Deformações Vetor de Deformações Generalizadas Para simplificar o problema trabalha-se com um vetor de deformações generalizadas. p p p { ε} = { ε ε γ κ κ κ γ γ ε θ } y y y y z yz (3.7) As três primeiras deformações apresentadas na Equação 3.8 são produzidas por forças contidas na superfície média do elemento, considerandose esforço plano. O sobrescrito p é usado para diferenciar estas deformações das produzidas por fleão. p u p v p u v ε =, ε y =, γ y = + y y (3.8) As seguintes cinco deformações levam em conta o efeito da fleão do elemento. Segundo as hipóteses básicas assumidas e de acordo com a Figura 3.3 o campo de deslocamentos fica sendo [1]: u = z θ, v = z θ, w = w (3.9) y (, y) (, y) (, y) Aplicando as fórmulas deformação-deslocamento da teoria da elasticidade, tem-se que: ε = z θ ε = z θ ε = 0 y, y, y z γ = z θ θ γ = θ + w γ = θ + w y y, y, z y, yz, y (3.10) Figura 3.3. Elemento diferencial de placa depois do carregamento [1].
5 3 Depois de fazer a integração na espessura obtêm-se as deformações generalizadas: κ = θ γ = θ w y, z y, κ = θ γ = θ w (3.11) y, y yz, y κ = θ θ y y, y, Os sinais das deformações γ z e γ yz estão invertidos para que a fórmula tensão-deformação seja afim com a fórmula apresentada na referencia [1]. Já a última deformação generalizada leva em conta o efeito drilling e será estudada com mais detalhe num parágrafo posterior Vetor de ensões Generalizadas Os esforços ou tensões generalizadas são: g { σ } = { y y y y z yz z} M M M Q Q M (3.1) Obtêm-se os primeiros oito esforços por meio de uma integração através da espessura, sendo cada um deles calculado num comprimento unitário, com as seguintes fórmulas: t / t / t / = σ dz = σ dz = τ dz t / y t / y y t / y t / t / t / M = σ z dz M = σ z dz M = τ z dz t / y t / y y t / y t / t / Q = τ dz Q = τ dz z t / z yz t / yz (3.13) Os sinais decorrem da convenção de sentidos mostrados na Figura 3.4. Figura 3.4. Sentidos positivos dos esforços. A direção de Q z e Q yz nas faces positivas é do eio z [8] Relações esforço-deformação Para o estado de tensões plano temos a Equação 3.14, onde E é o módulo de elasticidade e ν é o coeficiente de Poisson:
6 33 p σ 1 ν 0 ε E σ = p y ν 1 0 ε y 1 ν τ 1 ν p γ y 0 0 y (3.14) Em fleão as relações generalizadas são as seguintes: D ν D ν M D D κ ( 1 ν ) κ M D y y M y = κ y Q Gt γ z z 1. Q yz γ yz Gt (3.15) a Equação 3.15 foram introduzidas as quantidades 3 E t E D = G = (3.16) 1 1 ν ( ν ) ( 1+ ) Os dois últimos termos da diagonal da matriz na Equação 3.15 dividem-se por 6/5 para permitir que a distribuição parabólica de τ z e τ yz seja substituída pela distribuição uniforme [1] Grau de Liberdade Drilling o que segue, são apresentados três procedimentos diferentes encontrados na literatura para inclusão do efeito drilling : rigidez artificial, formulação variacional e condensação cinemática Rigidez Artificial a referência [1] encontra-se uma matriz de rigidez artificial para um elemento triangular: `M z1 ` θ z1 α M z = E V θ z M θ z3 z3 (3.17) Onde V é o volume do elemento e α é um número igual o menor a 0.3.
7 34 Porém, se aplicamos uma rotação unitária em θ z1 e zero nas demais, em cada nó atuam as forças apresentadas na Figura 3.5, como se pode ver, ainda que o sistema esteja em equilíbrio, eiste uma falta de concordância entre as forças e a cinemática do elemento. Figura 3.5. Momentos resultantes para uma rotação unitária no nó 1 e zero para os demais nós Formulação Variacional A inclusão do efeito drilling na matriz de rigidez também pode ser feita através do princípio da energia potencial estacionária. Reissner, em 1965, introduz um campo de rotações na formulação variacional, que foi modificado por Hughes e Brezzi em 1989 e por Atluri em 1984 [16]. Segundo as referencias [13, 17] a energia Π pode ser escrita: 1 1 Π = ε E ε dv + Φ ( θ ω ) G z y dv W (3.18) V V a epressão acima Φ é um número diretamente relacionado com a rigidez ao efeito drilling e será determinado no primeiro eemplo do capítulo seguinte; θ z é a rotação num ponto; e ω y é um componente do tensor de pequenas rotações, dado por: 1 v u ωy = y (3.19) Fisicamente se pode entender ω y como a rotação da bissetriz de um elemento diferencial de lados inicialmente perpendiculares [18] e é chamada rotação absoluta, como se observa na Figura 3.6. O principio de energia
8 35 potencial estacionária minimiza a diferença entre a rotação num ponto e a rotação absoluta. Figura 3.6. Componente do tensor de pequenas rotações. Do anterior pode-se dizer que a deformação generalizada para o efeito drilling é: εθ = θ z ωy (3.0) E que os componentes da matriz de rigidez devidos a este efeito são: K = Φ G t B B da (3.1) θ θ θ A Redução por Condensação Cinemática Segundo a referência [] o elemento é obtido pelo seguinte método. Inicialmente tem-se um elemento de 16 graus de liberdade translacionais, mostrado na Figura 3.7a. Figura 3.7. Elemento quadrilateral com rotações normais [].
9 36 Com os seus deslocamentos definidos por: 4 8 u = u + u ( r, s) i ( r, s) i i ( r, s) i= 1 i= v = v + v ( r, s) i ( r, s) i i ( r, s) i= 1 i= 5 i i (3.) As oito funções de forma são: = (1 r) (1 s) / 4 = (1 + r) (1 s) / 4 1 = (1 + r) (1 + s) / 4 = (1 r) (1 + s) / = 6 = + 7 = + 8 = (1 r ) (1 s) / (1 r) (1 s ) / (1 r ) (1 s) / (1 r) (1 s ) / (3.3) Calculam-se as componentes normais e tangenciais dos deslocamentos dos nós 5 até 8, sendo que somente a componente normal é retida, reduzindo os graus de liberdade a 1 como na Figura 3.7b. Utilizando-se uma restrição parabólica para os deslocamentos normais ao lado do elemento se consegue introduzir as quatro rotações relativas que substituem aos deslocamentos dos nós 5 até 8. Este procedimento é realizado por meio das seguintes fórmulas e complementado pela Figura 3.8. Lij u ij = ( θ j θi ) (3.4) 8 Lij u = cosαij uij = cosαij ( θ j θi ) 8 Lij v = sinαij uij = sinαij θ j θi 8 (3.5) Figura 3.8. Lado de um elemento quadrilateral [].
10 37 Estes incrementos de deslocamento podem ser calculados para todos os lados do elemento. Substituindo a Equação 3.5 na Equação 3. obtêm-se: 4 8 u = u + M θ ( r, s) i ( r, s) i i ( r, s) i= 1 i= v = v + M θ ( r, s) i ( r, s) i yi ( r, s) i= 1 i= 5 i i (3.6) A relação deformação-deslocamento pode ser escrita em forma matricial: ε ε y = γ y u B11 B 1 (3.7) θ [ ` ] Para que o elemento cumpra com o patch test de esforço constante a matriz B 1 deve ser substituída por: 1 B = B B da A A (3.8) Finalmente para eliminar o modo de deslocamento com zero energia de deformação que se mostra na Figura 3.9, calcula-se a diferença entre a rotação absoluta e a média das rotações relativas no elemento: 4 θ = ω θ = Bo u (3.9) y i= 1 i ( 0,0) i Figura 3.9. Modo de deslocamento com zero energia []. A seguir a matriz de rigidez que leva em conta esta restrição e que é avaliada através da seguinte fórmula: Ko = Bo ko Bo dv = ko Vol Bo B o (3.30) V
11 38 Deve ser adicionada à matriz de rigidez do elemento calculada a partir das Equações 3.7 e 3.8. O valor recomendado para k O é 0.05 G. Entre estas três opções para introduzir o efeito drilling, a que melhor se adapta para o nosso elemento é aquela derivada da formulação variacional. Isto porque as deformações generalizadas já incluem ε θ e a matriz B pode ser calculada para conter B θ. Desta forma o processo de cálculo da matriz de rigidez segue a formulação geral de elementos finitos que foi apresentada no capítulo anterior Vetor de Forças. Dois tipos de cargas são considerados, carga uniforme distribuída sobre linhas nodais e carga pontual. Para calcular o vetor de forças da carga distribuída utilizamos a seguinte fórmula: A matriz L f é igual a: m+ 1 f = L q dl (3.31) L f L L 1 [ ] [ ] 3 [ ] i (3.3) Lf = I I I φ i= 1 a epressão acima, I é uma matriz identidade de ordem seis, q L o vetor de cargas distribuídas também de ordem seis, e cada componente representa um grau de liberdade. Para o vetor de forças proveniente de cargas pontuais devemos considerar a transformação de parâmetros de deslocamentos em deslocamentos reais que está definido como: δ i 1 real 1 1 δ i = δi (3.33) δ i+ 1 A conseqüência desta transformação é que somente duas terças partes da carga pontual são aplicadas no ponto de aplicação real e o restante divide-se entre o ponto anterior e posterior.
12 Condições de Contorno Para impor as condições de contorno devemos transformar os parâmetros de deslocamento em deslocamentos reais naqueles pontos nos quais vão ser aplicadas restrições. Da Equação 3.33 podemos obter: δ δ δ real real i i i δ real real i = δi = δi 4 4 δ real + 1 δ real + 1 δ i i i (3.34) A matriz se pode epandir para toda a placa, com o que depois se segue com as regras de transformação para matrizes e vetor de forças: real real K = K F = F (3.35) a verdade a matriz de transformação contém muitos zeros e então a fórmula anterior é uma representação formal. o programa deve ser utilizada uma rotina mais simples que multiplica só algumas linhas e colunas em lugar da multiplicação de matrizes especificada Matriz de Massa e Geométrica Para o cálculo da matriz de massa utiliza-se a Fórmula.13 do Capitulo, porém integrada através da espessura. Cada uma das suas submatrizes é representada por: M = L ρ L da (3.36) ik f i f k A onde as funções de forma L i foram definidas no capitulo anterior e são repetidas abaio por conveniência. 3 f i = j φi (3.37) j= 1 L ξ η A matriz ρ que contém a densidade de massa e que leva em conta a integração através da espessura é determinada pela Equação Quando se despreza a inércia à rotação somente os três primeiros termos da diagonal são diferentes de zero.
13 40 [ ρ] ρ t ρ t 0 0 ρ t = ρ t ρ t (3.38) Para o cálculo da matriz geométrica primeiro determinam-se as forças de membrana definidas na Equação 3.13 provenientes de um carregamento inicial, assumindo que estas são independentes dos deslocamentos transversais, e depois se resolve a seguinte integral: y KG = G G da A y y (3.39) Esta matriz está formada por m+3 submatrizes da forma: y KG ik = Gi Gk da A y y (3.40) onde a matriz G i é igual a: 1φi φ, i, 3 φ i, Gi = [ 0] [ 0] [ 0] [ 0] φ, φ, 3 φ i y i y i, y (3.41) 3.8. Freqüências aturais e Cargas Críticas O cálculo das freqüências naturais e respectivos modos de vibração conduz a um problema linear de autovalor e autovetor generalizado da forma ( ω ){ δ} K M = 0 (3.4) onde os autovalores representam o quadrado das freqüências naturais circulares e os autovalores os modos de vibração. Em um problema de instabilidade linearizado, em acordo com as hipóteses descritas anteriormente, o cálculo de carga crítica e do modo de flambagem também resulta em um problema de autovalor linear generalizado, na forma abaio.
14 41 ( + λ ){ δ} = 0 K K (3.43) G O autovalor λ é um fator pelo qual se deve multiplicar a carga inicial para obter a carga crítica, os autovetores são os modos de flambagem.
η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]
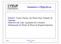
![η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ] η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]](/thumbs/100/144288148.jpg) BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas
 1 Oscar Fabricio Zuleta Inch Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas Dissertação de Mestrado Dissertação apresentada como requisito parcial para obtenção do título
1 Oscar Fabricio Zuleta Inch Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas Dissertação de Mestrado Dissertação apresentada como requisito parcial para obtenção do título
Teoria Clássica das Placas
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
EXAME NORMAL. x 2 B D. x 1 C. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
EXAME NORMAL Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) DEPARAMENO DE ENGENHARIA CIVIL SECÇÃO DE ESRUURAS Duração: h00m - (.5 val.) Considere a laje de betão armado representada
PEF 3302 Mecânica das Estruturas I Segunda Prova (22/11/2016) - duração: 160 minutos Resolver cada questão em uma folha de papel almaço distinta
 Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
P4 de Álgebra Linear I
 P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
2 Casca cilíndrica delgada
 Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486
 0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
Sumário e Objectivos. Placas e Cascas 3ªAula. Março
 Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Departamento de Engenharia Mecânica ENG Mecânica dos Sólidos II. Teoria de Vigas. Prof. Arthur Braga
 Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
2 Propagação de ondas elásticas em cilindros
 2 Propagação de ondas elásticas em cilindros 2.1 Elastodinâmica Linear As equações que governam o movimento de um corpo sólido, elástico e isotrópico são: τ ij,j + ρf i = ρ ü i (2-1) τ ij = λ ε kk δ ij
2 Propagação de ondas elásticas em cilindros 2.1 Elastodinâmica Linear As equações que governam o movimento de um corpo sólido, elástico e isotrópico são: τ ij,j + ρf i = ρ ü i (2-1) τ ij = λ ε kk δ ij
2 Aspectos Relevantes da Modelagem de Placas
 2 Aspectos Relevantes da Modelagem de Placas O presente capítulo apresenta os funcionais de energia utilizados para a obtenção da rigidez de uma placa. Além disso, desenvolve-se uma formulação matricial
2 Aspectos Relevantes da Modelagem de Placas O presente capítulo apresenta os funcionais de energia utilizados para a obtenção da rigidez de uma placa. Além disso, desenvolve-se uma formulação matricial
3 Implementação Computacional
 3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
6 MÉTODO DE ELEMENTOS FINITOS - MEF
 6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
4 Exemplos de validação
 49 4 Exemplos de validação Neste capítulo, são apresentados exemplos de validação com o objetivo de mostrar a eficiência da substituição de uma malha de elementos finitos por funções polinomiais demonstrando
49 4 Exemplos de validação Neste capítulo, são apresentados exemplos de validação com o objetivo de mostrar a eficiência da substituição de uma malha de elementos finitos por funções polinomiais demonstrando
ESTRUTURAS PARA LINHAS DE TRANSMISSÃO 6 MÉTODO DOS ELEMENTOS FINITOS
 LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas
 1 Oscar Fabricio Zuleta Inch Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas Dissertação de Mestrado Dissertação apresentada como requisito parcial para obtenção do título
1 Oscar Fabricio Zuleta Inch Elementos Finitos com Funções Spline para Instabilidade e Dinâmica de Estruturas Dissertação de Mestrado Dissertação apresentada como requisito parcial para obtenção do título
Mecânica dos Sólidos I Parte 3 Estado Plano de Tensão
 Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Sumário e Objectivos. Setembro. Elementos Finitos 2ªAula
 Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
Para poder diferenciar a formulação da placa como fina ou espessa usaremos a seguinte representação:
 4 Exemplos Neste capítulo apresentam-se exemplos de análises do comportamento estático, dinâmico e de instabilidade de placas. É considerado um comportamento elástico que está definido pelo módulo de elasticidade
4 Exemplos Neste capítulo apresentam-se exemplos de análises do comportamento estático, dinâmico e de instabilidade de placas. É considerado um comportamento elástico que está definido pelo módulo de elasticidade
Mecânica dos Sólidos II Parte 1 (Revisão)
 Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: abraga@puc-rio.br Tel:
Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: abraga@puc-rio.br Tel:
6 Formulação para Problemas da Mecânica da Fratura Linear Elástica
 58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
Equações de Navier-Stokes
 Equações de Navier-Stokes J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Equações de Navier-Stokes 1 / 16 Sumário 1 Relações constitutivas 2 Conservação do momento
Equações de Navier-Stokes J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v. 1 Equações de Navier-Stokes 1 / 16 Sumário 1 Relações constitutivas 2 Conservação do momento
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO
 4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
Método dos Elementos Finitos Aplicado à Problemas Planos
 Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS. Professores: Ronny Calixto Carbonari
 Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
O MÉTODO DOS ELEMENTOS FINITOS APLICADO A PROBLEMAS PLANOS
 O MÉTODO DOS ELEMENTOS FINITOS APLICADO A PROBLEMAS PLANOS Muitos problemas práticos (que são tri-dimensionais) podem ter sua formulação simplificada quando introduz-se algumas hipóteses. Alguns deles
O MÉTODO DOS ELEMENTOS FINITOS APLICADO A PROBLEMAS PLANOS Muitos problemas práticos (que são tri-dimensionais) podem ter sua formulação simplificada quando introduz-se algumas hipóteses. Alguns deles
Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação
 LISTA DE FIGURAS Figura 3.1 Figura 3.2 Figura 3.3 Figura 3.5 Figura 3.6 Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação controlada Diagrama
LISTA DE FIGURAS Figura 3.1 Figura 3.2 Figura 3.3 Figura 3.5 Figura 3.6 Diagramas tensão-deformação típicos de concretos, obtidos de corpos de prova cilíndricos em ensaios sob deformação controlada Diagrama
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
2 ANÁLISE LIMITE NUMÉRICA
 AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Universidade Federal do Rio de Janeiro Departamento de Engenharia Mecânica Análise Dinâmica de Estruturas - Lista de exercícios Prof.
 Universidade Federal do Rio de Janeiro Departamento de Engenharia Mecânica Análise Dinâmica de Estruturas - ista de exercícios Prof. Daniel Questão 1. Considere que a função ϕ : B B t descreve o movimento
Universidade Federal do Rio de Janeiro Departamento de Engenharia Mecânica Análise Dinâmica de Estruturas - ista de exercícios Prof. Daniel Questão 1. Considere que a função ϕ : B B t descreve o movimento
O Método dos Elementos Finitos Aplicado na Análise de Vibrações Livres de Problemas Submetidos ao Estado Plano de Tensões
 O Método dos Elementos Finitos Aplicado na Análise de Vibrações Livres de Problemas Submetidos ao Estado Plano de Tensões Ricardo Custódio Marcos Arndt PPGMNE Universidade Federal do Paraná - UFPR Curitiba/PR,
O Método dos Elementos Finitos Aplicado na Análise de Vibrações Livres de Problemas Submetidos ao Estado Plano de Tensões Ricardo Custódio Marcos Arndt PPGMNE Universidade Federal do Paraná - UFPR Curitiba/PR,
2 Teoria de Placas. Figura Placa plana retangular submetida a uma carga de superfície q z. Ref. Brush e Almroth (1975)
 2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
UFABC - Universidade Federal do ABC. ESTO Mecânica dos Sólidos I. as deformações principais e direções onde elas ocorrem.
 UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
Exame de. Licenciatura em Engenharia Civil 21 de Junho de ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre
 Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
Exame de Licenciatura em Engenharia Civil 21 de Junho de 1997 1ª Chamada 1ª Época Ano lectivo 96/97-2º Semestre Observações: Duração de 3 horas; Consulta livre; Inicie cada um dos problemas numa folha
Estruturas de Betão Armado II. 3 Lajes - Análise
 Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos
 2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
GAAL - Terceira Prova - 15/junho/2013. Questão 1: Analise se a afirmação abaixo é falsa ou verdadeira:
 GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
2 Fundamentos Teóricos
 8 Fundamentos Teóricos Todos os elementos estruturais correspondem a domínios tridimensionais, mas podem ter sua formulação simplificada quando se introduem algumas hipóteses, tais como: a. fibras paralelas
8 Fundamentos Teóricos Todos os elementos estruturais correspondem a domínios tridimensionais, mas podem ter sua formulação simplificada quando se introduem algumas hipóteses, tais como: a. fibras paralelas
Disciplina de Cálculo Automático de Estruturas. 5º ano da Licenciatura em Engenharia Civil
 ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
FLEXÃO DE PLACAS SEMI-ESPESSAS
 FLXÃO D PLACAS SMI-SPSSAS No estudo de placas semi-espessas o cisalhamento transvesal não poderá ser despreado ou seja e serão diferentes de ero. Neste caso obviamente as hipóteses de KIRCHHOFF não se
FLXÃO D PLACAS SMI-SPSSAS No estudo de placas semi-espessas o cisalhamento transvesal não poderá ser despreado ou seja e serão diferentes de ero. Neste caso obviamente as hipóteses de KIRCHHOFF não se
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
CONTEÚDOS PROGRAMADOS. (Análise Computacional de Tensões EEK 533)
 (Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
(Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
Programa de Pós-graduação em Engenharia Mecânica da UFABC. Disciplina: Fundamentos de Mecânica dos Sólidos II. Lista 2
 Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Análise Experimental de Apoios para Simulação de Condições de Contorno Livre no Espaço de Placas Retangulares
 Análise Experimental de Apoios para Simulação de Condições de Contorno Livre no Espaço de Placas Retangulares Ricardo Leiderman Benedito Luis Barbosa de Andrade Rubens Sampaio Departamento de Engenharia
Análise Experimental de Apoios para Simulação de Condições de Contorno Livre no Espaço de Placas Retangulares Ricardo Leiderman Benedito Luis Barbosa de Andrade Rubens Sampaio Departamento de Engenharia
2 Amortecimento Amortecimento viscoso ou proporcional Sistemas de um grau de liberdade
 2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
Torção de uma Barra Prismática
 Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
7 Método dos Elementos Finitos
 7 Método dos Elementos Finitos No capítulo 6 as funções usadas na aproimação são funções relacionadas à dinâmica de estruturas de formulação semelhante a de um cabo. Em problemas de dinâmica os modos de
7 Método dos Elementos Finitos No capítulo 6 as funções usadas na aproimação são funções relacionadas à dinâmica de estruturas de formulação semelhante a de um cabo. Em problemas de dinâmica os modos de
G3 de Álgebra Linear I
 G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
Efeitos de 2ª 2 Ordem
 Prof. uciano ima - lucianolima@uerj.br Eq.. Diferencial Efeitos 2ª 2 Ordem Programa de Pós-GraduaP Graduação em Engenharia Civil estrado Acadêmico Faculdade de Engenharia FEN/UERJ Professor: uciano Rodrigues
Prof. uciano ima - lucianolima@uerj.br Eq.. Diferencial Efeitos 2ª 2 Ordem Programa de Pós-GraduaP Graduação em Engenharia Civil estrado Acadêmico Faculdade de Engenharia FEN/UERJ Professor: uciano Rodrigues
1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional = 4200 knm²
 CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS
 3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS Como discutido no Capítulo 1, a análise estrutural de estruturas reticuladas está fundamentada na concepção de um modelo matemático, aqui chamado de modelo estrutural,
3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS Como discutido no Capítulo 1, a análise estrutural de estruturas reticuladas está fundamentada na concepção de um modelo matemático, aqui chamado de modelo estrutural,
4. Metodologia da Análise Numérica
 4. Metodologia da Análise Numérica Neste capítulo são apresentados tópicos referentes ao método utilizado para a realização do trabalho, com a finalidade de alcançar os objetivos descritos no item 1.3,
4. Metodologia da Análise Numérica Neste capítulo são apresentados tópicos referentes ao método utilizado para a realização do trabalho, com a finalidade de alcançar os objetivos descritos no item 1.3,
TESTE FINAL. x =2. Análise Avançada de Estruturas Sem consulta (excepto formulário fornecido) Duração: 3h00m
 ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
ESE FINAL Análise Avançada de Estruturas Sem consulta (ecepto formulário fornecido) DEARAMENO DE ENGENHARIA CIVIL Duração: h00m SECÇÃO DE ESRUURAS - (.5 val.) Considere o elemento finito unidimensional
2 Modelagem da casca cilíndrica
 odelagem da casca cilíndrica As cascas cilíndricas odem ser definidas como um coro cuja distância de qualquer onto interno deste coro a uma suerfície de referência (usualmente a suerfície média da casca)
odelagem da casca cilíndrica As cascas cilíndricas odem ser definidas como um coro cuja distância de qualquer onto interno deste coro a uma suerfície de referência (usualmente a suerfície média da casca)
5 Modelos para representação da ferrovia
 5 Modelos para representação da ferrovia O modelo adotado para análise da interação dinâmica entre trilhopalmilha-dormente-lastro é mostrado na figura (5.1). O trilho é representado por um elemento de
5 Modelos para representação da ferrovia O modelo adotado para análise da interação dinâmica entre trilhopalmilha-dormente-lastro é mostrado na figura (5.1). O trilho é representado por um elemento de
Cinemática da partícula fluida
 Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
ANÁLISE ESTRUTURAL DE PLACAS: MODELAGEM COMPUTACIONAL PARA AS TEORIAS DE REISSNER-MINDLIN E KIRCHHOFF
 ANÁLISE ESTRUTURAL DE PLACAS: MODELAGEM COMPUTACIONAL PARA AS TEORIAS DE REISSNER-MINDLIN E KIRCHHOFF Pablo Giovanni Silva Carvalho pablogscarvalho@gmail.com Aluno de mestrado em Engenharia Civil Laboratório
ANÁLISE ESTRUTURAL DE PLACAS: MODELAGEM COMPUTACIONAL PARA AS TEORIAS DE REISSNER-MINDLIN E KIRCHHOFF Pablo Giovanni Silva Carvalho pablogscarvalho@gmail.com Aluno de mestrado em Engenharia Civil Laboratório
2.1 Translação, rotação e deformação da vizinhança elementar Variação relativa do comprimento (Extensão)
 Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Revisão III: Dinâmica Estrutural Linear: Superposição Modal
 Revisão III: Dinâmica Estrutural Linear: Superposição Modal Como calcular a parcela elástica da posição do elemento de massa: p d Hipótese: flexibilidade moderada pequenos deslocamentos elásticos comportamento
Revisão III: Dinâmica Estrutural Linear: Superposição Modal Como calcular a parcela elástica da posição do elemento de massa: p d Hipótese: flexibilidade moderada pequenos deslocamentos elásticos comportamento
Prof. Dr. Eduardo Lenz Cardoso
 Elementos Finitos I Análise Estática Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Sumário Revisão de trabalho e energia; Definição de Energia Potencial Total; Princípio da Mínima Energia Potencial
Elementos Finitos I Análise Estática Prof. Dr. Eduardo Lenz Cardoso lenz@joinville.udesc.br Sumário Revisão de trabalho e energia; Definição de Energia Potencial Total; Princípio da Mínima Energia Potencial
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Caso mais simples MÉTODO DOS ELEMENTOS FINITOS. Álvaro Azevedo. Faculdade de Engenharia Universidade do Porto
 MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
MÉTODO DOS ELEMENTOS FINITOS Álvaro Azevedo http://www.fe.up.pt/~alvaro Novembro 2000 Faculdade de Engenharia Universidade do Porto 1 Caso mais simples Método dos deslocamentos Comportamento linear elástico
Vibrações Mecânicas. Sistemas Contínuos. DEMEC UFPE Ramiro Willmersdorf
 Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
Capítulo Integração de Newton-Cotes
 Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
Capítulo 8 Integração Numérica 8.1 Introdução A utilização de coordenadas locais permite simplificar os limites de integração no cálculo das matrizes e vetores de carregamento dos elementos finitos. No
Universidade de Coimbra Faculdade de Ciências e Tecnologia 2001/02 Estruturas II (aulas teóricas)
 Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
2 ANÁLISE ESTÁTICA DA ESTABILIDADE MÉTODO ANALÍTICO.
 ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
Sumário e Objectivos. Lúcia M.J.S. Dinis 2007/2008. Mecânica dos Sólidos 7ª Aula
 Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Objetivo: Determinar a equação da curva de deflexão e também encontrar deflexões em pontos específicos ao longo do eixo da viga.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Sumário e Objectivos. Método dos Elementos Finitos 3ªAula. Setembro
 Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
Sumário e Objectivos Sumário: Método dos Resíduos Pesados. Princípio Variacional. Discretização Pelo Método dos Elementos Finitos (MEF). Objectivos da Aula: Apreensão do Processo de Discretização pelo
3 Controle Passivo com Carregamento no Plano
 3 Controle Passivo com Carregamento no Plano 3.1. Conceitos Básicos Conforme visto no Capítulo 1, os mecanismos de controle passivo não são controláveis e não requerem energia para operar. Estes sistemas
3 Controle Passivo com Carregamento no Plano 3.1. Conceitos Básicos Conforme visto no Capítulo 1, os mecanismos de controle passivo não são controláveis e não requerem energia para operar. Estes sistemas
4 Análise de elementos unidimensionais
 4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
 Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
2 Formulação do Problema
 Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Curso de Engenharia Civil. Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CAPÍTULO 3: FLEXÃO
 Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
$QiOLVHHDQiOLVHGHVHQVLELOLGDGHGHHVWUXWXUDVUHWLFXODGDV
 $QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
$QiOVHHDQiOVHGHVHQVEOGDGHGHHVWUXWXUDVUHWFXODGDV,QWURGXomR Vários são os métodos para análise de estruturas. Dentre eles, o método dos elementos finitos com formulação em deslocamentos é o mais difundido
Modelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff
 Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
EXPLICIT STIFFNESS MATRIX FOR PARABOLIC PRISMATIC TRIANGULAR ELEMENT
 Blucher Mechanical Engineering Proceedings May 04, vol., num. www.proceedings.blucher.com.br/evento/0wccm EXPLICI SIFFNESS MARIX FOR PARABOLIC PRISMAIC RIANGULAR ELEMEN Marcelo R. de Matos Pedreiro a,
Blucher Mechanical Engineering Proceedings May 04, vol., num. www.proceedings.blucher.com.br/evento/0wccm EXPLICI SIFFNESS MARIX FOR PARABOLIC PRISMAIC RIANGULAR ELEMEN Marcelo R. de Matos Pedreiro a,
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Análise de Estruturas Utilizando Wavelets de Daubechies e Interpolets de Deslauriers-Dubuc
 Rodrigo Bird Burgos Análise de Estruturas Utilizando Wavelets de Daubechies e Interpolets de Deslauriers-Dubuc Tese de Doutorado Tese apresentada como requisito parcial para obtenção do título de Doutor
Rodrigo Bird Burgos Análise de Estruturas Utilizando Wavelets de Daubechies e Interpolets de Deslauriers-Dubuc Tese de Doutorado Tese apresentada como requisito parcial para obtenção do título de Doutor
Sistemas Reticulados
 6/0/017 E-US EF60 EF60 Estruturas na ruitetura III - Estruturas na ruitetura I I - Sistemas Reticulados Sistemas Reticulados e Laminares FU-US Deformações na Fleão Sistemas Reticulados (7/0/017) rofessores
6/0/017 E-US EF60 EF60 Estruturas na ruitetura III - Estruturas na ruitetura I I - Sistemas Reticulados Sistemas Reticulados e Laminares FU-US Deformações na Fleão Sistemas Reticulados (7/0/017) rofessores
Equações diferenciais
 Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1
 PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
ANÁLISE DE PLACAS LAMINADAS UTILIZANDO ELEMENTOS HÍBRIDOS DE TENSÕES TRIDIMENSIONAIS. Domingos Sávio R. Jr. (PG) & Flávio L. S.
 ANÁLISE DE PLACAS LAMINADAS UTILIZANDO ELEMENTOS HÍBRIDOS DE TENSÕES TRIDIMENSIONAIS Domingos Sávio R. Jr. (PG) & Flávio L. S. Bussamra (PQ) savio@ita.br flaviobu@ita.br RESUMO: Neste trabalho, um modelo
ANÁLISE DE PLACAS LAMINADAS UTILIZANDO ELEMENTOS HÍBRIDOS DE TENSÕES TRIDIMENSIONAIS Domingos Sávio R. Jr. (PG) & Flávio L. S. Bussamra (PQ) savio@ita.br flaviobu@ita.br RESUMO: Neste trabalho, um modelo
Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff.
 Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
Sumário e Objectivos Sumário: Tensões de Cauchy. Tensões de Piolla Kirchhoff. Objectivos da Aula: Apreensão das diferenças entre as grandes deformações e as pequenas deformações no contexto da análise
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA
 UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLIÉCNICA DEPARAMENO DE CONSRUÇÃO E ESRUURAS O ENSOR ENSÃO DE CAUCHY João Augusto de Lima Rocha Módulo didático: DCE MD - 02/2002 O ENSOR ENSÃO DE CAUCHY João Augusto
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLIÉCNICA DEPARAMENO DE CONSRUÇÃO E ESRUURAS O ENSOR ENSÃO DE CAUCHY João Augusto de Lima Rocha Módulo didático: DCE MD - 02/2002 O ENSOR ENSÃO DE CAUCHY João Augusto
Cálculo Diferencial e Integral II Resolução do Exame/Teste de Recuperação 02 de Julho de 2018, 15:00h - versão 2 Duração: Exame (3h), Teste (1h30)
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
