O MÉTODO DOS ELEMENTOS FINITOS APLICADO A PROBLEMAS PLANOS
|
|
|
- Joaquim Aquino
- 5 Há anos
- Visualizações:
Transcrição
1 O MÉTODO DOS ELEMENTOS FINITOS APLICADO A PROBLEMAS PLANOS Muitos problemas práticos (que são tri-dimensionais) podem ter sua formulação simplificada quando introduz-se algumas hipóteses. Alguns deles podem resultar em uma modelagem envolvendo problemas bi-dimensionais. Estes são os casos dos chamados problemas planos: estado plano de tensões (plane stress), estado plano de deformações (plane strain) e problemas aissimétricos. Ocorre estado plano de tensões quando as tensões segundo um dos eios é desprezível perante as restantes (que agem em um plano normal a este eio), isto é, podem ser consideradas nulas. Fisicamente, tal estado ocorre em uma placa fina, com apoios e carregamentos no próprio plano de definição da placa, conforme mostra esquematicamente a figura 8.1. Se tomarmos um sistema de eios coordenados de tal maneira que os eios e y coincidam com o plano médio da placa, o eio z será normal a tal plano. Devido as estas restrições previamente assumidas, o movimento dos pontos do plano médio da placa estarão restritos a deslocamentos no próprio plano, sendo assim, funções apenas dependentes de e y. Consequentemente, as componentes de tensões também não terão seus valores alterados na espessura, ou seja, serão funções apenas dependentes de e y. Como a placa não está carregada transversalmente, as tensões na superfície na direção z são nulas e sendo a placa fina, poderão ser assumidas como nulas em toda ela. Poderá, no entanto, pelo efeito de Poisson, ocorrer deformação na direção z. σ = 0 z y z Figura 8. A - Eemplo de estado plano de tensões 1
2 No entanto, ocorre estado plano de deformações quando as deformações segundo um dos eios podem ser consideradas nulas. Fisicamente, tal estado ocorre em estruturas longas com carregamento uniforme com mostra esquematicamente a figura 8.2. Se tomarmos um sistema de eios coordenados de tal maneira que o eio z coincida com a direção do maior comprimento, o movimento dos pontos do plano normal a z estarão restritos a deslocamentos no próprio plano, sendo assim, funções apenas dependentes de e y. Consequentemente, as componentes de tensões também não terão seus valores alterados com a variação de z, ou seja, serão funções apenas dependentes de e y. Para garantir tal estado, as tensões na direção z não são nulas, pelo efeito de Poisson. ε = 0 z y z Figura 8. B - Estado plano de deformações. Problemas aissimétricos são uma particularização do estado plano de deformações em coordenadas cilíndricas (Orθz). Neste caso eiste um eio (eio z) de simetria aial do corpo, conforme mostra esquematicamente a figura 8.3. As deformações segundo o eio θ podem ser consideradas nulas. O movimento dos pontos do plano Orz estarão restritos a deslocamentos no próprio plano, sendo assim, funções apenas dependentes de r e z. Consequentemente, as componentes de tensões também não terão seus valores alterados com a variação de θ, ou seja, serão funções apenas dependentes de r e z. Para garantir tal estado, as tensões na direção θ não são nulas, pelo efeito de Poisson. 2
3 z Figura 8. C - Problemas aissimétricos REVISÃO DE CONCEITOS DA TEORIA DA ELASTI- CIDADE E DA RESISTÊNCIA DOS MATERIAIS: ESTADO PLANO DE TENSÕES: Estudaremos o caso de uma placa fina (corpo B), de espessura t, composta de material isotrópico, elástico linear, com Módulo de Young E e Coeficiente de Poisson ν, submetida a um carregamento atuante na direção do plano médio da placa Ω, composto pelo sistema de cargas F={b,p} (onde b é uma carga de corpo, distribuída no plano médio da placa e calculada por unidade de comprimento normal ao plano e p, uma carga de linha, atuando em um contorno lateral a placa que chamaremos de contorno Γ) e a prescrição de deslocamentos homogêneas do tipo bilateral u j =0 em pontos Γ j do contorno. Supõe-se que ocorre uma transformação, ou seja, os pontos da placa sofrem deslocamentos. -SISTEMA DE COORDENADAS DE REFERÊNCIA: escolhemos um sistema cartesiano ortogonal de coordenadas Oyz cujo plano Oy coincide com o plano médio da peça. - CINEMÁTICA: Hipóteses simplificadoras: -Fibras paralelas ao plano médio ou se alongam ou se encurtam; -Seções planas e normais ao plano médio da peça permanecem planas e normais a tal plano após a deformação e paralelas às posições indeformadas; -Seções paralelas permanecem paralelas após a deformação. Campo de deslocamentos: r 3
4 Para este modelo cinemático, ou seja, quando se adotam as hipóteses cinemáticas simplificadoras listadas acima, o campo de deslocamentos possível é o que admite que o ponto distante e y da origem, após a transformação tomará a posição +u (,y) e y+u y (,y) ou seja, as componentes u e u y do vetor deslocamento segundo os eios e y serão funções dependentes apenas de e y. Na forma vetorial fica u = { u (,y) u y (,y)} T Falta identificar quais os tipos de restrições que, por hipótese, poderão ser impostas ao campo de deslocamentos. Por simplicidade, adotamos apenas restrições bilaterais e homogêneas. Por restrições bilaterais entende-se aquelas que, se o deslocamento está impedido em uma direção, também estará impedido na direção oposta. Por restrições homogêneas entende-se aquelas que impõe deslocamentos nulos, nos pontos de impedimentos j. Componentes infinitesimais de deformação: A Teoria Infinitesimal, segundo GREEN, é aquela na qual assume-se que as componentes do vetor de deslocamento (neste caso, as componentes u e u y ) e suas derivadas em relação aos eios coordenados e y e em relação ao tempo t são pequenas, de forma que pode-se negligenciar os termos não lineares se comparados com os termos lineares. Assume-se que as componentes do vetor deslocamento podem ser representadas por funções contínuas na forma u = u (,y) u y = u y (,y) Toma-se um paralelogramo infinitesimal de arestas paralelas aos eios coordenados com comprimentos d e dy, conforme mostra a figura 8.4. Com a deformação do contínuo, ocorre uma variação no comprimento de suas arestas e nos ângulos entre elas. Como os deslocamentos variam ponto a ponto no contínuo e supondo-se conhecido o deslocamento d M do ponto M, (ponto este de coordenadas (, y)) e igual a d M = u (,y) i + u y (,y)j onde i e j são os vetores unitários segundo as direções e y, respectivamente. Pode-se, por utilização da fórmula de Taylor, obter os valores dos deslocamentos em pontos próimos a M. Assim, no ponto B de coordenadas (+d, y+dy), as componentes do vetor do deslocamento ficam 4
5 u (,y) + u (,y) d + u (,y) dy u (,y) d +1 2 u (,y) dy + y 2! 2 2! y 2 u y (,y) + u y (,y) d + u y (,y) dy u y (,y) d +1 2 u y (,y) dy + y 2! 2 2! y 2 Negligenciando-se os termos de ordem superior perante os lineares, as componentes do vetor deslocamento neste ponto tomam a forma u (,y) + u (,y) d + u (,y) dy y u y (,y) + u y (,y) d + u y (,y) dy y y C B dy M A j d i Figura 8. D - Paralelogramo infinitesimal Estas relações são lineares e portanto retas paralelas são transformadas em retas paralelas. Assim o paralelogramo infinitesimal no estado final continuará sendo um paralelogramo. Já que trata-se de Teoria Linear vamos separar cada componente de deformação específicas normais ε e ε y e de corte γ y : -estudando-se inicialmente um paralelogramo sujeito a alongamento na direção, conforme mostra a figura 8.5 Como o deslocamento do ponto M é e o deslocamento do ponto A d M = u (,y) i + u y (,y) j 5
6 d A = [u (,y)+ u (,y) d ] i + [u y (,y) + u y (,y) d ] j Então d A -d M é dado por d A - d M= [ u (,y) d] i Da análise da figura 8.5, verifica-se que o segmento M'A' vale enquanto o segmento MA vale M'A' = d i + (d A - d M ) = d + u (,y) d MA = d i. Da Resistência dos Materiais sabe-se que a deformação, ou seja, o alongamento segundo a direção é dado por ou seja, ε = L = M'A' - MA = (d + u (,y)/ d) - d L MA d ε = u (,y) Fazendo o mesmo procedimento, somente que considerando agora o alongamento na direção y, tem-se ε y = u y (,y) y 6
7 C B C' B' M A M' A' y d M d A d d M - d A Figura 8. E - Paralelogramo infinitesimal antes e após a transformação. u y y dy u dy y C' B' C B M' A' u y d y M A u d Figura 8. F- Paralelogramo infinitesimal submetido a distorção angular. Na Teoria Infinitesimal as componentes de deformação específica de corte são as distorções dos ângulos retos formados pelas arestas. No problema plano, a componente não nula é γ y. Neste caso, como o deslocamento do ponto M, d M, é conhecido e vale d M = u (,y) i + u y (,y) j então o deslocamento dos pontos A, C e B serão d A = [u (,y) + u (,y) d] i + d C = [u (,y) + u (,y) dy] i + y [u y (,y) + u y (,y) d] j [u y (,y) + u y (,y) dy] j y 7
8 d B = [u (,y)+ u (,y) d+ u (,y) dy] i + [u y (,y)+ u y (,y) d+ u y (,y) dy] j y y Levando-se em conta que as deformações são infinitesimais γ y 90 - <A'M'C' = γ 1 + γ 2 e como tem-se γ 1 tg γ 1 u y (,y)/ d d γ 2 tg γ 2 u (,y)/ y dy dy γ y = u y (,y)+ u (,y) y Pode-se escrever as relações deformações-deslocamentos na forma matricial: e = D u onde e = { ε ε y ε y } T ε y = γ y/2 u = {u (,y) u y (,y) } T 2 / 0 D = 1/2 0 2 / y / y / - ESFORÇOS INTERNOS: A eistência de esforços interiores fica evidente quando observa-se que ao submeter-se um corpo deformável a ações de forças eternas, suas partículas permanecem unidas. Portanto alguma força interna deve ser responsável por este fenômeno. A título de ilustração, analisemos como se age quando se quer saber se uma correia está adequadamente tensionada. Para tal, tratamos de deslocá-la da posição inicial, e portanto impomos um alongamento da correia (ou seja, uma deformação virtual) que nos permitirá ter uma idéia da tensão na 8
9 correia através do trabalho realizado para eecutar este movimento. Portanto para o problema plano de tensões, vamos introduzir o conceito de trabalho realizado pelos esforços internos W i,, em consequência de um campo de deformações virtuais gerado a partir de um campo de deslocamentos virtuais, pela seguinte definição: W i = - (σ δε + σ y δε y + τ y δε y )db = - (σ δε + σ y δε y + τ y δε y ) dz d dy = = - t (σ δε + σ y δε y + τ y δε y ) d dy para toda (qualquer) deformação virtual δε. δε y e δε y. Na forma vetorizada: W i = - s δe d dy onde s = { σ σ y τ y } T - EQUAÇÃO CONSTITUTIVA: para um material isotrópico elástico linear submetido a processos isotérmicos e adiabáticos: s = D e sendo 1 ν 0 D= E/(1-ν 2 ) ν (1-ν) - FORÇAS EXTERNAS Imaginemos que uma determinada caia encontra-se no piso desta sala. Para termos uma idéia do seu peso, tentamos levantá-la. Portanto tal avaliação é feita através do trabalho realizado para levantar a caia. Ou seja, introduzindose um deslocamento virtual em contraposição a posição natural de repouso, pode-se avaliar o trabalho realizado e consequentemente a força necessária para levantar a caia e finalmente seu peso. Para formalizar a idéia anterior, no problema em questão, introduzimos o conceito de trabalho eterno W e realizado pelas forças eternas F={b,p} em consequência de um campo de deslocamentos virtuais δu, pela seguinte definição: W e = b δu d dy + p δu dγ 9
10 para todo (qualquer) deslocamento virtual δu e onde a carga de corpo b está distribuída na superfície b = {b (,y) b y (,y) } T e a carga de linha p está aplicada no contorno da placa Γ p = {p (,y) p y (,y) } T - EQUILÍBRIO: Para definição de equilíbrio adota-se o Princípio dos Trabalhos Virtuais, ou seja Diz-se que um corpo plano B encontra-se em equilíbrio com o sistema de forças F(b,p), se para todo deslocamento virtual δu, que satisfaça as condições cinemáticas de contorno, a distribuição de tensões s, associada ao sistema de cargas, é tal que W i + W e = 0, para todo δu ou na forma eplícita: -t s δe d dy + b δu d dy + p δu dγ= 0, para todo δu onde s é a tensão associada a deformação e pela equação constitutiva; ou seja, o trabalho virtual dos esforços internos generalizados e das cargas aplicadas é nulo para toda ação virtual de deslocamento admissível. Usando-se as relações anteriormente introduzidas s = D e e e = D u tem-se para epressão do P.T.V. -t (D u) D D δu d dy + b δu d dy + p δu dγ= 0, para todo δu ou ainda na forma matricial -t (D u) T D D δu d dy + δu T b d dy + δu T p dγ= 0, para todo δu 10
11 TENSÕES PRINCIPAIS: Admitindo-se como conhecidas as componentes em um paralelepípedo infinitesimal com faces paralelas aos eios coordenados, pode-se facilmente obter as componentes de tensão que agem em um plano com inclinação qualquer, cuja normal é dada por n = cos i + sen j τ σ σ dy ds τ y d y τ y σ y Figura 8. G - Tensões em uma face com normal n. Se ds é o comprimento da face normal a n então tem-se as relações d = ds cos dy = ds sen Se o corpo está em equilíbrio, então o somatório das forças (por unidade de comprimento normal ao plano) nas direções normais e tangenciais às faces são F n = σ ds - σ cos 2 ds - σ y sen 2 ds - 2τ y sen cos ds = 0 F t = τ ds - τ y (cos 2 - sen 2 ) ds - (σ y - σ ) sen cos ds = 0 11
12 σ d = σ cos ds σ cos 2 ds τ y = sen ds d = τ y y a) face paralela ao eio sen τcos ds y τsen y cos ds σ y sen 2 ds σ y dy = σ sen y ds τ y dy = sen τds y b) face paralela ao eio y Figura 8. H - Decomposição das forças na direção da normal n. σ d = σ cos ds σ cos sen ds τ y τ y cos ds d = τ y cos 2 ds y a) face paralela ao eio τsen y ds 2 σ y dy = σ sen ds y τ y dy = sen τds y σ y sen cos ds b) face paralela ao eio y Figura 8. I - Decomposição das forças na direção da normal n. e portanto 12
13 σ = σ cos 2 + σ y sen 2 + 2τ y sen cos τ = (σ y - σ ) sen cos - τ y (cos 2 - sen 2 ) Usando-se as seguintes relações trigonométricas cos 2 = (1 + cos 2)/2 sen 2 = (1 - cos 2)/2 cos 2 = cos 2 - sen 2 sen 2 = 2 sen cos e reagrupando-se os termos, obtém-se σ = (σ + σ y )/2 + ((σ - σ y ) cos2)/2 + τ y sen2 τ = τ y cos2 - ((σ y - σ ) sen2)/2 Verifica-se que estas componentes de tensão são funções de uma única variável e como as funções trigonométricas seno e cosseno variam de -1 a 1, estas funções passarão por valores máimos e mínimos. Procura-se então os etremos da função tensão normal σ e para tal, introduz-se a seguinte condição de valor estacionário dσ/d = 0 ou seja (σ - σ y ) sen2-2 τ y cos2 = 0 que substituída na epressão da tensão tangencial, nos fornece τ = 0 isto é, quando as tensões normais tem valores etremos, as tensões tangenciais se anulam. Da equação anterior tira-se tg 2 = 2 τ y /(σ - σ y ) Já que tg 2 = tg (p + 2) = duas direções principais perpendiculares podem ser encontradas, o que mostra que σ assume um valor mínimo ao longo de uma direção e máimo ao longo da outra. Estas direções são chamadas direções principais e suas correspondentes tensões tensões principais. Usualmente, em um estado tridimensional de tensões, estas tensões são chamadas de σ 1, σ 2 e σ 3. Suas magnitudes são obtidas por substituição e manipulações algébricas 13
14 σ 1 = σ ma = (σ + σ y )/2 + { [(σ - σ y ) 2 + 4τ y2 ]}/2 σ 1 = σ ma = (σ + σ y )/2 - { [(σ - σ y ) 2 + 4τ y2 ]}/ CRITÉRIOS DE ESCOAMENTO: É necessário definir-se critérios para os quais as tensões são admitidas como elásticas. a. CRITÉRIO DE MISES OU CRITÉRIO DA MÁXIMA ENERGIA DE DISTORÇÃO: Este critério se baseia na determinação da energia de distorção (isto é, energia relacionada a mudanças na forma) do material. Neste critério, estamos interessados na tensão equivalente σ eq = [(σ 1 - σ 2 ) 2 ]/2 Figura 8. J - Elipse de Mises. e o material é considerado no regime elástico enquanto σ eq σ Y 14
15 onde σ Y é a tensão de escoamento do material, tensão esta determinada em um ensaio de tração. Graficamente esta relação é representada pela figura 8.10, onde cada ponto, de coordenadas σ 1, σ 2 representa o estado de tensões em um ponto do corpo. A região interna a elipse de Mises indica que o ponto do corpo encontra-se no regime elástico. O contorno indica plastificação e a região eterna é inacessível. CRITÉRIO DE TRESCA OU DA MÁXIMA TENSÃO DE CISALHAMENTO: Este critério se baseia na hipótese de que o escoamento dos materiais dúcteis é causado por deslizamento do material ao longo de superfícies oblíquas, deslizamento devido principalmente a tensões cisalhantes. Neste caso, as tensões são admitidas no regime elástico enquanto se σ 1 σ 2 > 0 σ 1 σ Y σ 2 σ Y se σ 1 σ 2 < 0 σ 1 - σ 2 < σ Y As relações acima são representadas graficamente através da figura Novamente, a região interna indica que o ponto do corpo encontra-se no regime elástico. O contorno indica plastificação e a região eterna é inacessível. σ 2 σ Y + σ Y - σ Y + σ 1 σ Y - Figura 8. K - Heágono de Tresca. 15
16 8.2 - SOLUÇÕES APROXIMADAS: O Princípio dos Trabalhos Virtuais, que é um Princípio Variacional, está definido no conjunto dos deslocamentos que cumprem as condições de contorno, ou seja, dos deslocamentos cinematicamente admissíveis. Em particular, tais conjuntos são espaços vetoriais de dimensão infinita. Para obtermos soluções aproimadas, podemos defini-los em espaços de dimensão finita. Para isto, designemos por {φ i } com i=1,..., ao conjunto de funções vetoriais coordenadas ou funções de base completas para o conjunto dos deslocamentos cinematicamente admissíveis. O anterior é equivalente a dizer que, dado ε>0, arbitrariamente pequeno, sempre será possível estabelecer um número N tal que é possível definir n>n escalares A 1, A 2, A n tais que u - Σ A i φ i < ε. Portanto, para cada n gera-se um espaço aproimado de dimensão finita contido no espaço dos deslocamentos cinematicamente admissíveis. Com estas definições podemos reformular tal princípio variacional, somente que agora em espaços de dimensão finita o que nos conduzirá à resolução de sistemas de equações PRINCÍPIO DOS TRABALHOS VIRTUAIS APROXIMADO: Relembrando o Princípio dos Trabalhos Virtuais: Diz-se que um corpo plano B encontra-se em equilíbrio com o sistema de forças F(b,p), se para todo deslocamento virtual δu que satisfaça as condições de contorno, a distribuição de tensões s, associada ao sistema de cargas, é tal que W i + W e = 0, para todo δu ou na forma eplícita: -t (Du) T D Dδu d dy + δu T b d dy + δu T p dγ= 0, para todo δu ou seja, o trabalho virtual dos esforços internos generalizados e das cargas aplicadas é nulo para toda ação virtual de deslocamento admissível. 16
17 Propondo-se as interpolações: u = Σ A i φ i δu = Σ C j φ j i onde os coeficientes A i e C j são escalares arbitrários. Substituindo-se as relações acima no P.T.V. tem-se Σ Σ-t (D A i φ i ) T D D C j φ j d dy + (C j φ j ) T b d dy + (C j φ j ) T p dγ= 0 i j para todo escalar C j, j=1,2,...,n. Reagrupando-se, tem-se Σ{ Σ [-t (D φ i ) T D D φ j d dy] A i + φ jt b d dy + φ j T p dγ} C j = 0 i j para todo escalar C j, j=1,2,...,n.isto indica que cada termo entre colchetes {} deve ser nulo, obtendo-se finalmente o seguinte sistema Σ [t (D φ i ) T D D φ j d dy] A i = φ jt b d dy + φ j T p dγ i para j=1,...,n. Chamando-se k ij = t (D φ i ) T D D φ j d dy f j= φ jt b d dy + φ T j p dγ chega-se a Σ k ij A i = f j para j=1,...,n. ou ainda, matricialmente i K A = F A matriz K de dimensões [nn] é simétrica e em virtude da matriz da constantes elásticas D ser positivo definida, K é positivo definida. Portanto, eiste sua inversa K -1 e os coeficientes da solução aproimada são A = K -1 F No caso em que estamos estudando (problemas planos), as funções coordenadas φ i deverão ser funções contínuas com derivadas primeiras contínuas por partes, ou seja, o espaço dos deslocamentos cinematicamente admissíveis deverá ser um espaço de Hilbert contendo funções contínuas com derivadas primeiras quadrado integráveis. Além disso, as funções coordenadas deverão ser nulas na fronteira Γ. Se o problema fosse de outra natureza e ao invés de deslocamentos tivéssemos deslocamentos generalizados (rotações, curvatura, etc), como é o j 17
18 caso de fleão de vigas, placas e cascas, a matriz de operadores D envolverá derivadas de segunda ordem e a epressão do P.T.V. envolverá termos quadráticos em suas derivadas. Teremos assim que o conjunto dos deslocamentos será um espaço de Hilbert contendo funções contínuas com derivadas primeiras e segundas quadrado integráveis. Convém ressaltar que a variável independente que foi interpolada nesta formulação foi o deslocamento. Desta maneira ao construir-se as funções de base para o Método dos Elementos Finitos, chama-se esta formulação de Método dos Deslocamentos em contraposição ao modelo em forças ou esforços que se obtém via Princípio dos Trabalhos Virtuais Complementar. Como pudemos apreciar, a determinação das soluções aproimadas nos Princípios Variacionais anteriormente colocados recaem na solução de um sistema de equações algébricas. Para a determinação deste sistema se requer: construir funções coordenadas cujas combinações lineares definem as funções aproimantes admissíveis; para determinas os coeficientes da matriz do sistema se requer integrar uma forma bi-linear simétrica; (D φ i ) T D D φ j d dy Esta integração pode ser feita de forma analítica ou numérica; a determinação dos coeficientes do termo independente requer a interpolação de formas lineares do tipo φ jt b d dy + φ jt p dγ que também pode realizar-se de forma analítica ou numérica; é necessário ressaltar aqui que a determinação da função aproimante u pode ser uma das maiores dificuldades. Em particular, no Método dos Elementos Finitos a determinação destes aproimantes é uma tarefa simples. 18
Método dos Elementos Finitos Aplicado à Problemas Planos
 Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
Método dos Elementos Finitos Aplicado à Problemas Planos Profa Mildred Ballin Hecke, D.Sc CESEC/UFPR Método dos Elementos Finitos Aplicado a Problemas Planos 1 Introdução Ocorre ESTADO PLANO DE TENSÕES
2 Fundamentos Teóricos
 8 Fundamentos Teóricos Todos os elementos estruturais correspondem a domínios tridimensionais, mas podem ter sua formulação simplificada quando se introduem algumas hipóteses, tais como: a. fibras paralelas
8 Fundamentos Teóricos Todos os elementos estruturais correspondem a domínios tridimensionais, mas podem ter sua formulação simplificada quando se introduem algumas hipóteses, tais como: a. fibras paralelas
Teoria Clássica das Placas
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Fleão de Placas ANÁLISE DE ESTRUTURAS I PROF. EVANDRO PARENTE JUNIOR (UFC) PROF. ANTÔNIO MACÁRIO
3 IMPLEMENTAÇÃO DO ELEMENTO FINITO
 3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
3 IMPLEMEAÇÃO DO ELEMEO FIIO este capítulo apresentam-se as considerações mais importantes para a implementação do elemento finito generalizado com funções spline. 3.1. Hipóteses Cinemáticas a formulação
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Mecânica dos Sólidos I Parte 3 Estado Plano de Tensão
 Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
Mecânica dos Sólidos II Parte 1 (Revisão)
 Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: abraga@puc-rio.br Tel:
Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: abraga@puc-rio.br Tel:
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
2 Teoria de Placas. Figura Placa plana retangular submetida a uma carga de superfície q z. Ref. Brush e Almroth (1975)
 2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
2 Teoria de Placas A solução mais antiga que se tem conhecimento para o problema de estabilidade de placas planas foi dada por Bryan em 1891, em seu estudo On the Stability of a Plane Plate under Thrusts
Análise de Tensões. Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil
 Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil Disciplina: Mecânica dos Sólidos Código: ECIV3 rofessor: Eduardo Nobre Lages Análise de Tensões Maceió/AL Agosto/14 Motivação
Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil Disciplina: Mecânica dos Sólidos Código: ECIV3 rofessor: Eduardo Nobre Lages Análise de Tensões Maceió/AL Agosto/14 Motivação
ESTRUTURAS PARA LINHAS DE TRANSMISSÃO 6 MÉTODO DOS ELEMENTOS FINITOS
 LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
LINHAS DE 6 MÉTODO DOS ELEMENTOS FINITOS Método de Rayleigh - Ritz É um método de discretização, ou seja, a minimização de um conjunto restrito π = (a 1, a 2,... a n ), que depende de um número finito
, Equação ESFORÇO NORMAL SIMPLES 3.1 BARRA CARREGADA AXIALMENTE
 3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Mecânica dos Sólidos I Parte 5 Tensões de Flexão
 Departamento de Engenharia ecânica Parte 5 Tensões de Fleão Prof. Arthur. B. Braga 8.1 ecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos forças, momentos, etc. F 7 F 8 F F 3 Determinar
Departamento de Engenharia ecânica Parte 5 Tensões de Fleão Prof. Arthur. B. Braga 8.1 ecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos forças, momentos, etc. F 7 F 8 F F 3 Determinar
η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]
![η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ] η η < η j + η 0 de outro modo η η η η φ φ φ δ = δ φ, η [ η, η ]](/thumbs/100/144288148.jpg) BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
BASE TEÓRICA Este capítulo apresenta a formulação teórica do elemento finito utilizando funções spline. Com este objetivo descrevem-se primeiro as funções que definem os deslocamentos no elemento. A partir
PME Mecânica dos Sólidos I 4 a Lista de Exercícios
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
2 Formulação do Problema
 Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS
 3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS Como discutido no Capítulo 1, a análise estrutural de estruturas reticuladas está fundamentada na concepção de um modelo matemático, aqui chamado de modelo estrutural,
3. IDEALIZAÇÃO DO COMPORTAMENTO DE BARRAS Como discutido no Capítulo 1, a análise estrutural de estruturas reticuladas está fundamentada na concepção de um modelo matemático, aqui chamado de modelo estrutural,
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO
 4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
4 EXTENSÃO DAS FORMULAÇÕES AO PROBLEMA DO ACOPLAMENTO FLUIDO-MECÂNICO Neste capítulo são apresentadas as equações governantes do acoplamento fluido-mecânico para um corpo cortado por uma descontinuidade.
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #7: VASOS DE PRESSÃO DE PAREDE ESPESSA 1
 PME-2350 MECÂNICA DOS SÓLIDOS II AULA #7: VASOS DE PRESSÃO DE PAREDE ESPESSA 1 7.1. Introdução e hipóteses gerais Vimos na aula anterior as equações necessárias para a solução de um problema geral da Teoria
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #7: VASOS DE PRESSÃO DE PAREDE ESPESSA 1 7.1. Introdução e hipóteses gerais Vimos na aula anterior as equações necessárias para a solução de um problema geral da Teoria
LOM Introdução à Mecânica dos Sólidos. Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina
 LOM 3081 - Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina DEMAR USP Professores responsáveis: Viktor Pastoukhov, Carlos A.R.P. Baptista Ref. 1: F.P. BEER, E.R. JOHNSTON,
LOM 3081 - Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina DEMAR USP Professores responsáveis: Viktor Pastoukhov, Carlos A.R.P. Baptista Ref. 1: F.P. BEER, E.R. JOHNSTON,
Curso de Engenharia Civil. Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CAPÍTULO 3: FLEXÃO
 Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
CONTEÚDOS PROGRAMADOS. (Análise Computacional de Tensões EEK 533)
 (Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
(Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
PEF 3302 Mecânica das Estruturas I Segunda Prova (22/11/2016) - duração: 160 minutos Resolver cada questão em uma folha de papel almaço distinta
 Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Questão 1 (5,0) A Figura abaixo ilustra um sólido com comportamento elástico linear, solicitado por ações externas. Este sólido possui espessura t sendo t c, t L e está sem qualquer impedimento a deslocamentos
Capítulo 2 Vetores. 1 Grandezas Escalares e Vetoriais
 Capítulo 2 Vetores 1 Grandezas Escalares e Vetoriais Eistem dois tipos de grandezas: as escalares e as vetoriais. As grandezas escalares são aquelas que ficam definidas por apenas um número real, acompanhado
Capítulo 2 Vetores 1 Grandezas Escalares e Vetoriais Eistem dois tipos de grandezas: as escalares e as vetoriais. As grandezas escalares são aquelas que ficam definidas por apenas um número real, acompanhado
teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos.
 EME311 Mecânica dos Sólidos Objetivo do Curso: ornecer ao aluno os fundamentos teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos. 1-1 EME311
EME311 Mecânica dos Sólidos Objetivo do Curso: ornecer ao aluno os fundamentos teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos. 1-1 EME311
Sumário e Objectivos. Setembro. Elementos Finitos 2ªAula
 Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
Sumário e Objectivos Sumário: Revisão de Alguns Conceitos Fundamentais da Mecânica dos Sólidos. Relações Deformações Deslocamentos. Relações Tensões Deformações Equações de Equilíbrio. Objectivos da Aula:
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
FLEXÃO DE PLACAS SEMI-ESPESSAS
 FLXÃO D PLACAS SMI-SPSSAS No estudo de placas semi-espessas o cisalhamento transvesal não poderá ser despreado ou seja e serão diferentes de ero. Neste caso obviamente as hipóteses de KIRCHHOFF não se
FLXÃO D PLACAS SMI-SPSSAS No estudo de placas semi-espessas o cisalhamento transvesal não poderá ser despreado ou seja e serão diferentes de ero. Neste caso obviamente as hipóteses de KIRCHHOFF não se
Sumário e Objectivos. Placas e Cascas 3ªAula. Março
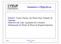 Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Sumário e Objectivos Sumário: Teoria Clássica das Placas Finas. Equação de Lagrange. Objectivos da Aula: Apreensão dos Conceitos Fundamentais da Fleão de Placas de Pequena Espessura. arço arço Sistema
Revisão, apêndice A Streeter: SISTEMAS DE FORÇAS, MOMENTOS, CENTROS DE GRAVIDADE
 UNVERSDDE FEDERL D BH ESCOL POLTÉCNC DEPRTMENTO DE ENGENHR QUÍMC ENG 008 Fenômenos de Transporte Profª Fátima Lopes FORÇS HDRÁULCS SOBRE SUPERFÍCES SUBMERSS Revisão, apêndice Streeter: SSTEMS DE FORÇS,
UNVERSDDE FEDERL D BH ESCOL POLTÉCNC DEPRTMENTO DE ENGENHR QUÍMC ENG 008 Fenômenos de Transporte Profª Fátima Lopes FORÇS HDRÁULCS SOBRE SUPERFÍCES SUBMERSS Revisão, apêndice Streeter: SSTEMS DE FORÇS,
2 Casca cilíndrica delgada
 Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
Vibrações livres não lineares de cascas cilíndricas com gradação funcional 29 2 Casca cilíndrica delgada Inicia-se este capítulo com uma pequena introdução sobre cascas e, em seguida, apresenta-se a teoria
2.1 Translação, rotação e deformação da vizinhança elementar Variação relativa do comprimento (Extensão)
 Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil º ANO EXERCICIOS PRÁTICOS Ano lectivo 005/006 Ano lectivo: 005/006.º semestre MECÂNICA APLICADA II I - Teoria do estado de
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil º ANO EXERCICIOS PRÁTICOS Ano lectivo 005/006 Ano lectivo: 005/006.º semestre MECÂNICA APLICADA II I - Teoria do estado de
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1
 PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #11: INTRODUÇÃO À TEORIA DE PLACAS E CASCAS 1 11.1. Introdução Recebem a denominação geral de folhas as estruturas nas quais duas dimensões predominam sobre uma terceira
Capítulo 6 Transformação de tensão no plano
 Capítulo 6 Transformação de tensão no plano Resistência dos Materiais I SLIDES 06 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes de tensão
Capítulo 6 Transformação de tensão no plano Resistência dos Materiais I SLIDES 06 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes de tensão
Deformação. - comportamento de um material quando carregado
 Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Tema III. TRAÇÃO E COMPRESSÃO 3.1. Introdução. Esforços solicitantes são esforços (efeitos) internos:
 Tema III. TRAÇÃO E COMRESSÃO 3.1. Introdução Esforços solicitantes são esforços (efeitos) internos: Força normal ou axial (N), É definida como força axial ou normal a carga que atua na direção do eixo
Tema III. TRAÇÃO E COMRESSÃO 3.1. Introdução Esforços solicitantes são esforços (efeitos) internos: Força normal ou axial (N), É definida como força axial ou normal a carga que atua na direção do eixo
2 ANÁLISE LIMITE NUMÉRICA
 AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
Departamento de Engenharia Mecânica ENG Mecânica dos Sólidos II. Teoria de Vigas. Prof. Arthur Braga
 Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
1 - Energia de deformação
 UFAM Desde 909 Universidade Federal do Amaonas Faculdade de Tecnologia Departamento de Construção FTC 06 Teoria das Estruturas I, Turma Período Letivo 007/ - Energia de deformação Eng Marcus inícius de
UFAM Desde 909 Universidade Federal do Amaonas Faculdade de Tecnologia Departamento de Construção FTC 06 Teoria das Estruturas I, Turma Período Letivo 007/ - Energia de deformação Eng Marcus inícius de
Lei de Gauss. O produto escalar entre dois vetores a e b, escrito como a. b, é definido como
 Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CÍTULO RESISTÊNCI DOS MTERIIS erdinand. Beer E. Russell Johnston Jr. Conceito de Tensão Capítulo 1 Conceito de Tensão 1.1 Introdução 1.2 orças e Tensões; 1.3 orças iais: Tensões Normais;
Terceira Edição CÍTULO RESISTÊNCI DOS MTERIIS erdinand. Beer E. Russell Johnston Jr. Conceito de Tensão Capítulo 1 Conceito de Tensão 1.1 Introdução 1.2 orças e Tensões; 1.3 orças iais: Tensões Normais;
4 Análise de elementos unidimensionais
 4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
4 Análise de elementos unidimensionais Neste capítulo é mostrado o desenvolvimento da formulação feita no capítulo anterior para um elemento de treliça e um elemento de viga de Timosheno com amortecimento
Física dos Materiais FMT0502 ( )
 Física dos Materiais FMT0502 (4300502) 1º Semestre de 2010 Instituto de Física Universidade de São Paulo Professor: Antonio Dominguesdos Santos E-mail: adsantos@if.usp.br Fone: 3091.6886 http://plato.if.usp.br/~fmt0502n/
Física dos Materiais FMT0502 (4300502) 1º Semestre de 2010 Instituto de Física Universidade de São Paulo Professor: Antonio Dominguesdos Santos E-mail: adsantos@if.usp.br Fone: 3091.6886 http://plato.if.usp.br/~fmt0502n/
CONCEITOS PARA USO DO SOLIDWORKS SIMULATION
 CONCEITOS PARA USO DO SOLIDWORKS SIMULATION Módulo elástico Módulo elástico nas direções globais X, Y e Z. Para um material elástico linear, o módulo elástico em uma determinada direção é definido como
CONCEITOS PARA USO DO SOLIDWORKS SIMULATION Módulo elástico Módulo elástico nas direções globais X, Y e Z. Para um material elástico linear, o módulo elástico em uma determinada direção é definido como
2.1 TENSÕES NORMAIS E DEFORMAÇÕES ESPECÍFICAS NO PONTO GENÉRICO
 2 ESTADO TRIPLO DE TENSÕES No ponto genérico de um corpo carregado, para cada plano que o contém, define-se um vetor tensão. Como o ponto contém uma família de planos, tem-se também uma família de vetores
2 ESTADO TRIPLO DE TENSÕES No ponto genérico de um corpo carregado, para cada plano que o contém, define-se um vetor tensão. Como o ponto contém uma família de planos, tem-se também uma família de vetores
Lista de Exercícios de Cálculo 3 Primeira Semana
 Lista de Exercícios de Cálculo 3 Primeira Semana Parte A 1. Se v é um vetor no plano que está no primeiro quadrante, faz um ângulo de π/3 com o eixo x positivo e tem módulo v = 4, determine suas componentes.
Lista de Exercícios de Cálculo 3 Primeira Semana Parte A 1. Se v é um vetor no plano que está no primeiro quadrante, faz um ângulo de π/3 com o eixo x positivo e tem módulo v = 4, determine suas componentes.
Capítulo 4 Propriedades Mecânicas dos Materiais
 Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
Conceitos de vetores. Decomposição de vetores
 Conceitos de vetores. Decomposição de vetores 1. Introdução De forma prática, o conceito de vetor pode ser bem assimilado com auxílio da representação matemática de grandezas físicas. Figura 1.1 Grandezas
Conceitos de vetores. Decomposição de vetores 1. Introdução De forma prática, o conceito de vetor pode ser bem assimilado com auxílio da representação matemática de grandezas físicas. Figura 1.1 Grandezas
PME Mecânica dos Sólidos II 6 a Lista de Exercícios
 Eercícios Sugeridos (Livro Teto) PME-3211 - Mecânica dos Sólidos II 6 a Lista de Eercícios Referência: Gere, J.M. & Goodno, B.J., Mecânica dos Materiais, Cengage Learning, 2010, 858 p. Deformação Plana:
Eercícios Sugeridos (Livro Teto) PME-3211 - Mecânica dos Sólidos II 6 a Lista de Eercícios Referência: Gere, J.M. & Goodno, B.J., Mecânica dos Materiais, Cengage Learning, 2010, 858 p. Deformação Plana:
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
Álgumas palavras sobre as Equações de Navier-Stokes
 Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Modelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff
 Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /ddmonnerat@yahoo.com.br A teoria clássica ou teoria de Kirchhoff
carga do fio: Q. r = r p r q figura 1
 Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Tensores cartesianos. Grandezas físicas como funções de posição e/ou de tempo
 ensores cartesianos Quantidades (grandeas) físicas: Classificação: Escalares Vectores ensores de segunda ordem... ensores de ordem ero ensores de primeira ordem ensores de segunda ordem... Relacionadas
ensores cartesianos Quantidades (grandeas) físicas: Classificação: Escalares Vectores ensores de segunda ordem... ensores de ordem ero ensores de primeira ordem ensores de segunda ordem... Relacionadas
superfície que envolve a distribuição de cargas superfície gaussiana
 Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
CAPÍTULO 3 ESFORÇO CORTANTE
 CAPÍTULO 3 ESFORÇO CORTANTE 1 o caso: O esforço cortante atuando em conjunto com o momento fletor ao longo do comprimento de uma barra (viga) com cargas transversais. É o cisalhamento na flexão ou cisalhamento
CAPÍTULO 3 ESFORÇO CORTANTE 1 o caso: O esforço cortante atuando em conjunto com o momento fletor ao longo do comprimento de uma barra (viga) com cargas transversais. É o cisalhamento na flexão ou cisalhamento
Estruturas de Betão Armado II. 3 Lajes - Análise
 Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
Estruturas de Betão Armado II 1 TEORIA DE COMPORTAMENTO ELÁSTICO DE LAJES FINAS HIPÓTESES DO MODELO DE COMPORTAMENTO (1) 1) Laje de pequena espessura (deformação por corte deprezável - h
 1) Qual propriedade de um material reproduz a lei de Hooke? Escrever a expressão que traduz a lei. 2) Um cilindro de 90,0 cm de comprimento (figura) está submetido a uma força de tração de 120 kn. Uma
1) Qual propriedade de um material reproduz a lei de Hooke? Escrever a expressão que traduz a lei. 2) Um cilindro de 90,0 cm de comprimento (figura) está submetido a uma força de tração de 120 kn. Uma
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO
 Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
ENG01140 Turma C (Prof. Alexandre Pacheco)
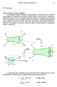 ENG01140 Turma C (rof. leandre acheco) 32 11 TENSÃO Tensão Normal e Tensão Cisalhante: Na ilustração a seguir, considera-se, primeiramente, a mesma parte seccionada do corpo rígido de forma genérica ilustrado
ENG01140 Turma C (rof. leandre acheco) 32 11 TENSÃO Tensão Normal e Tensão Cisalhante: Na ilustração a seguir, considera-se, primeiramente, a mesma parte seccionada do corpo rígido de forma genérica ilustrado
2 Propagação de ondas elásticas em cilindros
 2 Propagação de ondas elásticas em cilindros 2.1 Elastodinâmica Linear As equações que governam o movimento de um corpo sólido, elástico e isotrópico são: τ ij,j + ρf i = ρ ü i (2-1) τ ij = λ ε kk δ ij
2 Propagação de ondas elásticas em cilindros 2.1 Elastodinâmica Linear As equações que governam o movimento de um corpo sólido, elástico e isotrópico são: τ ij,j + ρf i = ρ ü i (2-1) τ ij = λ ε kk δ ij
y ds, onde ds é uma quantidade infinitesimal (muito pequena) da curva C. A curva C é chamada o
 Integral de Linha As integrais de linha podem ser encontradas em inúmeras aplicações nas iências Eatas, como por eemplo, no cálculo do trabalho realizado por uma força variável sobre uma partícula, movendo-a
Integral de Linha As integrais de linha podem ser encontradas em inúmeras aplicações nas iências Eatas, como por eemplo, no cálculo do trabalho realizado por uma força variável sobre uma partícula, movendo-a
RESISTÊNCIA DOS MATERIAIS I Curso de Eletromecânica
 Centro Federal de Educação Tecnológica de Santa Catarina CEFET/SC Unidade Araranguá RESISTÊNCIA DOS MATERIAIS I Curso de Eletromecânica Prof. Fernando H. Milanese, Dr. Eng. milanese@cefetsc.edu.br Conteúdo
Centro Federal de Educação Tecnológica de Santa Catarina CEFET/SC Unidade Araranguá RESISTÊNCIA DOS MATERIAIS I Curso de Eletromecânica Prof. Fernando H. Milanese, Dr. Eng. milanese@cefetsc.edu.br Conteúdo
MECÂNICA DO CONTÍNUO. Tópico 3. Método dos Trabalhos Virtuais
 MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
TRELIÇA C/ SISTEMA TENSOR DE CABO
 Q) RESPOSTA TRELIÇA C/ SISTEMA TENSOR DE CABO Obtidas as matrizes de rigidez dos elementos estruturais, deve-se remanejar tais coeficientes para a matriz de rigidez da estrutura (graus de liberdade ordenados).
Q) RESPOSTA TRELIÇA C/ SISTEMA TENSOR DE CABO Obtidas as matrizes de rigidez dos elementos estruturais, deve-se remanejar tais coeficientes para a matriz de rigidez da estrutura (graus de liberdade ordenados).
6 Formulação para Problemas da Mecânica da Fratura Linear Elástica
 58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
58 6 Formulação para Problemas da Mecânica da Fratura Linear Elástica Para problemas de elasticidade, a construção de soluções fundamentais é menos intuitiva e mais complexa do que para problemas de potencial,
Cinemática da partícula fluida
 Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
Cinemática da partícula fluida J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Cinemática da partícula fluida 1 / 16 Sumário 1 Descrição do movimento 2 Cinemática
TORÇÃO. Prof. Dr. Carlos A. Nadal
 TORÇÃO Prof. Dr. Carlos A. Nadal Tipo de esforços a) Tração b) Compressão c) Flexão d) Torção e) Compressão f) flambagem Esforços axiais existe uma torção quando uma seção transversal de uma peça está
TORÇÃO Prof. Dr. Carlos A. Nadal Tipo de esforços a) Tração b) Compressão c) Flexão d) Torção e) Compressão f) flambagem Esforços axiais existe uma torção quando uma seção transversal de uma peça está
3 Modelo analítico 3D para corte em rocha
 54 3 Modelo analítico 3D para corte em rocha 3.1 Cortador afiado a pressão atmosférica No caso de um corte em três dimensões, o corte é caracterizado por uma orientação lateral, chamado de ângulo de saída
54 3 Modelo analítico 3D para corte em rocha 3.1 Cortador afiado a pressão atmosférica No caso de um corte em três dimensões, o corte é caracterizado por uma orientação lateral, chamado de ângulo de saída
Sergio Persival Baroncini Proença
 ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
2 Cinemática 2.1 CINEMÁTICA DA PARTÍCULA Descrição do movimento
 2 Cinemática A cinemática tem como objeto de estudo o movimento de sistemas mecânicos procurando descrever e analisar movimento do ponto de vista geométrico, sendo, para tal, irrelevantes os fenómenos
2 Cinemática A cinemática tem como objeto de estudo o movimento de sistemas mecânicos procurando descrever e analisar movimento do ponto de vista geométrico, sendo, para tal, irrelevantes os fenómenos
26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia
 Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Sistemas Reticulados
 6/0/017 E-US EF60 EF60 Estruturas na ruitetura III - Estruturas na ruitetura I I - Sistemas Reticulados Sistemas Reticulados e Laminares FU-US Deformações na Fleão Sistemas Reticulados (7/0/017) rofessores
6/0/017 E-US EF60 EF60 Estruturas na ruitetura III - Estruturas na ruitetura I I - Sistemas Reticulados Sistemas Reticulados e Laminares FU-US Deformações na Fleão Sistemas Reticulados (7/0/017) rofessores
1 Introdução 3. 2 Estática de partículas Corpos rígidos: sistemas equivalentes SUMÁRIO. de forças 67. xiii
 SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
Capítulo O espaço R n
 Cálculo - Capítulo 1. - O espaço R n - versão 0/009 1 Capítulo 1. - O espaço R n 1..1 - Espaço R 3 1.. - Espaço R n Vamos, agora, generaliar o conceito de um espaço R primeiro para R 3 e depois para R
Cálculo - Capítulo 1. - O espaço R n - versão 0/009 1 Capítulo 1. - O espaço R n 1..1 - Espaço R 3 1.. - Espaço R n Vamos, agora, generaliar o conceito de um espaço R primeiro para R 3 e depois para R
PME-2350 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1
 PME-235 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1 6.1. Introdução O objetivo destas notas é apresentar, de forma um pouco mais detalhada,
PME-235 MECÂNICA DOS SÓLIDOS II AULA #6: SOLUÇÃO DE UM PROBLEMA GERAL DA TEORIA DA ELASTICIDADE CLÁSSICA (TEC) 1 6.1. Introdução O objetivo destas notas é apresentar, de forma um pouco mais detalhada,
Disciplina de Cálculo Automático de Estruturas. 5º ano da Licenciatura em Engenharia Civil
 ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
ALVARO. M. AZVDO lemento inito riangular Disciplina de Cálculo Automático de struturas 5º ano da Licenciatura em ngenharia Civil aculdade de ngenharia da Universidade do Porto - Portugal ovemro CAPÍULO
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento
 Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Apostila de Resistência dos Materiais II
 Departamento de Mecânica Aplicada e Computacional Faculdade de Engenharia Juiz de Fora - MG Apostila de Resistência dos Materiais II Prof. Elson Magalhães Toledo (emtc@lncc.br) Prof. Aleandre Cur (aleandre.cur@ufjf.edu.br)
Departamento de Mecânica Aplicada e Computacional Faculdade de Engenharia Juiz de Fora - MG Apostila de Resistência dos Materiais II Prof. Elson Magalhães Toledo (emtc@lncc.br) Prof. Aleandre Cur (aleandre.cur@ufjf.edu.br)
POTENCIAL ELÉTRICO. Prof. Bruno Farias
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III POTENCIAL ELÉTRICO Prof. Bruno Farias Introdução Um dos objetivos da Física é determinar
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III POTENCIAL ELÉTRICO Prof. Bruno Farias Introdução Um dos objetivos da Física é determinar
Conceito de tensões Exercícios O Tensor de tensões Exercício. Tensões. 24 de agosto de Profa. Patrícia Habib Hallak Prof Afonso Lemonge.
 24 de agosto de 2016 Profa. Patrícia Habib Hallak Prof Afonso Lemonge Conceito de tensão Conceito de tensões 2 F 2 Com os conceitos da física a pressão P no interior do duto é constante e tem valor: P=
24 de agosto de 2016 Profa. Patrícia Habib Hallak Prof Afonso Lemonge Conceito de tensão Conceito de tensões 2 F 2 Com os conceitos da física a pressão P no interior do duto é constante e tem valor: P=
Planificação Anual Matemática 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486
 0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
0RGHODJHP&RPSXWDFLRQDO$WUDYpVGR3URJUDPD$%$486 Neste capítulo apresenta-se de forma sucinta o programa de elementos finitos ABAQUS, em particular o elemento finito de placa usado neste trabalho. A seguir
SOLICITAÇÕES COMBINADAS (FLEXÃO COMPOSTA)
 Versão 2009 (FLEXÃO COMPOSTA) As chamadas Solicitações Simples são: a) Tração e Compressão (Solicitação Aial): age somente esforço normal N na seção b) Torção: age somente momento torsor T na seção c)
Versão 2009 (FLEXÃO COMPOSTA) As chamadas Solicitações Simples são: a) Tração e Compressão (Solicitação Aial): age somente esforço normal N na seção b) Torção: age somente momento torsor T na seção c)
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 04 Teoria das deformações Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 04 Teoria das deformações Eng. Civil Augusto Romanini
Elasticidade aplicada à Infraestrutura de Transportes
 SÇÃO D NSINO D NGNHARIA D FORTIFICAÇÃO CONSTRUÇÃO Pós-graduação em ngenharia de Transportes lasticidade aplicada à Infraestrutura de Transportes MAJ MONIZ D ARAGÃO PROLMAS PLANOS M COORDNADAS CARTSIANAS:
SÇÃO D NSINO D NGNHARIA D FORTIFICAÇÃO CONSTRUÇÃO Pós-graduação em ngenharia de Transportes lasticidade aplicada à Infraestrutura de Transportes MAJ MONIZ D ARAGÃO PROLMAS PLANOS M COORDNADAS CARTSIANAS:
