POTENCIAL ELÉTRICO. Prof. Bruno Farias
|
|
|
- Luiz Caldeira
- 7 Há anos
- Visualizações:
Transcrição
1 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III POTENCIAL ELÉTRICO Prof. Bruno Farias
2 Introdução Um dos objetivos da Física é determinar se uma força é conservativa, ou seja, se pode ser associada a uma energia potencial. Os físicos descobriram empiricamente que a força elétrica é conservativa, e, portanto é possível associar a ela uma energia potencial elétrica. Neste capítulo vamos definir a energia potencial elétrica a aplicá-la a alguns problemas práticos.
3 Forças Conservativas As condições para que uma força seja conservativa são expressas abaixo: A força elétrica é uma força conservativa e como consequência associar-se a ela uma energia potencial elétrica.
4 Energia Potencial Elétrica Energia potencial é a energia associada à configuração de um sistema submetido à ação de um forma conservativa. Como a força elétrica é uma força conservativa, podemos expressar o trabalho realizado pela força elétrica em função da energia potencial elétrica U. Quando um sistema se move de um estado inicial i para um estado final f, a força eletrostática realizado um trabalho W sobre as partículas, e assim a variação de energia potencial ΔU é dada por U U f U i W
5 Se a energia potencial é definida como sendo zero no infinito, a energia potencial elétrica U do sistema é dado por U W onde W é o trabalho executado pela força eletrostática sobre o sistema quando o sistema é deslocado do infinito para o ponto considerado.
6 Exemplo
7 Potencial Elétrico A energia potencial por unidade de carga em um ponto do espaço é chamada de potencial elétrico (ou simplesmente potencial) e é representada pela letra. Assim, U q O potencial elétrico é uma grandeza escalar e sua unidade no SI é volt (), onde 1 joule 1volt 1coulomb
8 Observe que a unidade para o potencial elétrico nos permite adotar uma unidade mais conveniente para o campo elétrico E, a saber: o volts por metro. A diferença de potencial elétrico Δ entre dois pontos i e f é igual à diferença entre os potencias elétricos dos dois pontos: f i U q f U q i U q
9 Como ΔU = - W, temos ainda: f i W q Se tomarmos U i = 0 no infinito como referência para a energia potencial, o potencial no infinito também será nulo. Assim o potencial elétrico em qualquer ponto do espaço é obtido através da relação: W q
10 Exemplo
11
12 Superfícies Equipotenciais É o nome dado, ao lugar geométrico dos pontos, que têm o mesmo Potencial Elétrico. Portanto, ao deslocarmos uma carga de prova entre pontos de uma mesma superfície eqüipotencial, não realizamos trabalho, veja figuras: Ao deslocarmos uma carga, pelas trajetórias I e II o trabalho é nulo, já em III e I temos trabalho sendo realizado.
13 Superfícies Equipotenciais (em laranja) Carga isolada Dipolo elétrico Obs.: O campo elétrico é sempre perpendicular à superfície equipotencial.
14 Carga Elétrico Uniforme Cargas pontuais positivas e de mesmo módulo
15 Cálculo do Potencial a partir do Campo Podemos calcular a diferença de potencial entre dois pontos i e f do espaço, determinando o trabalho realizado pelo campo elétrico sobre uma carga de prova q 0 quando a carga se desloca do ponto i até o ponto f. Considerando o sistema da figura ao lado, o trabalho elementar dw realizado sobre uma carga de prova por uma força durante um deslocamento ds é dado por: dw F ds.
16 Porém sabemos que a força elétrica é dada por F = q 0 E, assim: dw q E ds. 0 Para determinar o trabalho total W realizado pelo campo sobre a partícula quando a mesma se desloca do ponto i para o ponto f fazemos a seguinte soma por integração: W q f 0 E ds. i
17 Substituindo a expressão anterior na equação, q 0 W i f Chegamos numa expressão para calcular a diferença de potencial entre dois pontos a partir do campo elétrico, a saber:. f i i f s d E
18 E ainda, se escolhermos o potencial i = 0, podemos calcular o potencial em qualquer ponto f em relação ao potencial do ponto i através da equação: f E i ds.
19 Exemplo
20 Potencial Produzido por uma Carga Pontual Para obtermos uma expressão para o potencial elétrico criado no espaço por uma carga pontual q, vamos considerar o deslocamento de uma carga de prova q 0 do ponto P até o infinito (figura abaixo). Considerando que a carga de prova segue uma trajetória retilínea do ponto P até o infinito, temos que: E ds Edscos.
21 Como o campo elétrico E é paralelo ao deslocamento ds em toda a trajetória, θ = 0 e cos θ =1, assim: E ds Eds. Como a trajetória é retilínea, podemos fazer ds = dr, assim: E ds Edr. Substituindo a expressão acima em temos: Onde tomamos r i = R, r f =. f i R f Edr, i f E ds, i
22 Lembrando que o campo elétrico gerado por uma 1 q carga pontual é E, temos que: 4 r 0 2 q dr f i R r Finalmente, realizando a integral e tomando i = (R) = e f = ( ) = 0, ficamos com: 1 q. 4 0 R
23 E ainda, substituindo R por r, temos: 1 q. 4 0 r
24 Exemplo
25 Potencial Produzido por um Grupo de Cargas Pontuais Podemos calcular o potencial produzido em um certo ponto do espaço por um grupo de cargas pontuais utilizando o princípio da superposição, assim temos: n i1 i n i1 q. r i (n cargas pontuais)
26 Exemplo Considere o sistema formado por duas cargas puntiformes q 1 = +12 nc e q 2 = - 12 nc (conforme figura abaixo), sendo a distância entre elas igual a 10 cm. Calcule os potenciais nos pontos a, b e c.
27 Exercício
28 Potencial Produzido por uma Distribuição Contínua de Cargas Quando uma distribuição de cargas é contínua devemos escolher um elemento de carga dq, calcular o potencial d produzido por dq e integrar para toda distribuição de cargas. Tomamos o potencial no infinito como sendo nulo. Tratando o elemento de carga dq como uma carga pontual, podemos expressar d no ponto P, na forma: d 1 dq. 4 0 r onde r é a distância entre P e dq.
29 Para o calcular o potencial total no ponto P, integramos a equação anterior para todos os elementos de carga da distribuição: d dq. r
30 Linha de Cargas amos determinar o potencial elétrico produzido por uma barra fina não condutora de comprimento L no ponto P, conforme figura ao lado. Considerando um elemento de comprimento dx da barra, temos que a carga desse elemento dq é dada por: dq dx onde λ é a densidade linear de cargas.
31 Tratando o elemento dq como uma carga pontual podemos escrever o potencial d como: d 1 4 dq r x d dx O potencial total produzido pela barra no ponto P é obtido integrando a equação anterior ao longo da barra, de x = 0 a x = L, assim: L 1 dx d x d Então: 4 0 ln L 2 L d d
32 Exercício
33 Disco Carregado amos determinar o potencial elétrico em um ponto qualquer sobre o eixo central de um disco de plástico de raio R e com uma densidade superficial de cargas σ, conforme Figura ao lado. Consideramos um elemento de área da constituído por um anel de raio R e largura radial dr. A carga desse elemento é dada por: dq da ' 2 ' R dr.
34 O potencial d no ponto P produzido pelo anel citado anteriormente, pode ser escrito como: Para calcularmos o potencial total somamos as contribuições de todos os anéis, de R = 0 até R = R:
35 Cálculo do Campo Elétrico a Partir do Potencial Se conhecermos o valor do potencial elétrico numa região do espaço podemos obter o vetor campo elétrico nessa região através da equação:, ˆ ˆ ˆ z k y j x i E onde é o operador gradiente. z k y j x i ˆ ˆ ˆ
36 Exemplo
37 Exercício Em uma dada região do espaço, potencial elétrico é dado por = 5x 3x2y + 2yz 2. Encontre as expressões para as componentes x, y, e z do campo elétrico nessa região. Qual é a magnitude do campo no ponto P, cujas coordenadas são (1, 0, -2) m?
Energia potencial elétrica
 Energia potencial elétrica Foi descoberto empiricamente que a força elétrica é uma força conservativa, portanto é possível associar a ela uma energia potencial. Quando uma força eletrostática age sobre
Energia potencial elétrica Foi descoberto empiricamente que a força elétrica é uma força conservativa, portanto é possível associar a ela uma energia potencial. Quando uma força eletrostática age sobre
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III CAMPO ELÉTRICO. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III CAMPO ELÉTRICO Prof. Bruno Farias Campo Elétrico A força elétrica exercida por uma carga
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III CAMPO ELÉTRICO Prof. Bruno Farias Campo Elétrico A força elétrica exercida por uma carga
2 Diferença de Potencial e Potencial Eletrostático
 Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 3 - Potencial Eletrostático Prof. Elvis Soares Nesse capítulo, estudaremos o potencial eletrostático criado por cargas
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 3 - Potencial Eletrostático Prof. Elvis Soares Nesse capítulo, estudaremos o potencial eletrostático criado por cargas
Potencial Elétrico 1
 Potencial Elétrico 1 Vamos começar com uma revisão: Quando uma força atua sobre uma partícula que se move de um ponto a até um ponto b, o trabalho W realizado pela força é dado pela integral de linha:
Potencial Elétrico 1 Vamos começar com uma revisão: Quando uma força atua sobre uma partícula que se move de um ponto a até um ponto b, o trabalho W realizado pela força é dado pela integral de linha:
Cap. 24. Potencial Elétrico. Prof. Oscar Rodrigues dos Santos Potencial elétrico 1
 Cap. 24 Potencial Elétrico Prof. Oscar Rodrigues dos Santos [email protected] Potencial elétrico 1 Energia Potencial Elétrica... O U x x f i F( x) dx F(x) x i x x f x Na Mecânica, nós definimos
Cap. 24 Potencial Elétrico Prof. Oscar Rodrigues dos Santos [email protected] Potencial elétrico 1 Energia Potencial Elétrica... O U x x f i F( x) dx F(x) x i x x f x Na Mecânica, nós definimos
AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO. Eletromagnetismo - Instituto de Pesquisas Científicas
 ELETROMAGNETISMO AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO Se um carga elétrica se move de um ponto à outro, qual é o trabalho realizado sobre essa carga? A noção de mudança de posição nos remete
ELETROMAGNETISMO AULA 04 ENERGIA POTENCIAL E POTENCIAL ELÉTRICO Se um carga elétrica se move de um ponto à outro, qual é o trabalho realizado sobre essa carga? A noção de mudança de posição nos remete
Prof. Fábio de Oliveira Borges
 O Potencial Elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil https://cursos.if.uff.br/!fisica2-0117/doku.php
O Potencial Elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil https://cursos.if.uff.br/!fisica2-0117/doku.php
Cap. 24. Potencial Elétrico. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 Cap. 24 Potencial Elétrico Copyright 24-1 Potencial Elétrico O potencial elétrico V em um ponto P devido ao campo elétrico produzido por um objeto carregado é dado por Carga de prova q 0 no ponto P onde
Cap. 24 Potencial Elétrico Copyright 24-1 Potencial Elétrico O potencial elétrico V em um ponto P devido ao campo elétrico produzido por um objeto carregado é dado por Carga de prova q 0 no ponto P onde
F = 1/4πɛ 0 q 1.q 2 /r 2. F = G m 1.m 2 /r 2 ENERGIA POTENCIAL 04/05/2015. Bacharelado em Engenharia Civil. Física III
 ENERGIA POTENCIAL Bacharelado em Engenharia Civil Física III Prof a.: D rd. Mariana de Faria Gardingo Diniz A energia potencial é a energia que está relacionada a um corpo em função da posição que ele
ENERGIA POTENCIAL Bacharelado em Engenharia Civil Física III Prof a.: D rd. Mariana de Faria Gardingo Diniz A energia potencial é a energia que está relacionada a um corpo em função da posição que ele
Potencial Elétrico. 3.1 Energia Potencial e Forças Conservativas
 Capítulo 3 Potencial Elétrico 3.1 Energia Potencial e Forças Conservativas O trabalho W realizado por uma força F ao longo de um caminho C orientado de um ponto a um ponto P é dado por W C P P F d l (3.1)
Capítulo 3 Potencial Elétrico 3.1 Energia Potencial e Forças Conservativas O trabalho W realizado por uma força F ao longo de um caminho C orientado de um ponto a um ponto P é dado por W C P P F d l (3.1)
Lei de Gauss. O produto escalar entre dois vetores a e b, escrito como a. b, é definido como
 Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
Aula 4: O Potencial Elétrico. Curso de Física Geral III Eletricidade Básica Ana Barros
 Aula 4: O Potencial Elétrico Curso de Física Geral III Eletricidade Básica Ana Barros Potencial elétrico Como podemos relacionar a noção de força elétrica com os conceitos de energia e trabalho? Definindo
Aula 4: O Potencial Elétrico Curso de Física Geral III Eletricidade Básica Ana Barros Potencial elétrico Como podemos relacionar a noção de força elétrica com os conceitos de energia e trabalho? Definindo
Terceira Lista - Potencial Elétrico
 Terceira Lista - Potencial Elétrico FGE211 - Física III Sumário Uma força F é conservativa se a integral de linha da força através de um caminho fechado é nula: F d r = 0 A mudança em energia potencial
Terceira Lista - Potencial Elétrico FGE211 - Física III Sumário Uma força F é conservativa se a integral de linha da força através de um caminho fechado é nula: F d r = 0 A mudança em energia potencial
FÍSICA III 1/2008 Lista de Problemas 02 Campos elétricos
 FÍSICA III 1/2008 Lista de roblemas 02 Campos elétricos A C Tort 18 de Março de 2008 roblema 1 H.M. Nussenzveig: Curso de Física básica, vol. 3, Eletromagnetismo, Cap. 3, problema 4. Dois fios retilíneos
FÍSICA III 1/2008 Lista de roblemas 02 Campos elétricos A C Tort 18 de Março de 2008 roblema 1 H.M. Nussenzveig: Curso de Física básica, vol. 3, Eletromagnetismo, Cap. 3, problema 4. Dois fios retilíneos
Eletromagnetismo I. Prof. Daniel Orquiza. Eletromagnetismo I. Prof. Daniel Orquiza de Carvalho
 de Carvalho - Eletrostática Energia e Potencial Elétrico (Capítulo 4 - Páginas 75 a 84no livro texto) Energia despendida no movimento de uma carga imersa num campo Elétrico. Diferença de potencial e potencial.
de Carvalho - Eletrostática Energia e Potencial Elétrico (Capítulo 4 - Páginas 75 a 84no livro texto) Energia despendida no movimento de uma carga imersa num campo Elétrico. Diferença de potencial e potencial.
Forças de ação à distância têm atreladas a si um campo, que pode ser interpretado como uma região na qual essa força atua.
 Forças de ação à distância têm atreladas a si um campo, que pode ser interpretado como uma região na qual essa força atua. Por exemplo, a força gravitacional está relacionada a um campo gravitacional,
Forças de ação à distância têm atreladas a si um campo, que pode ser interpretado como uma região na qual essa força atua. Por exemplo, a força gravitacional está relacionada a um campo gravitacional,
Halliday Fundamentos de Física Volume 3
 Halliday Fundamentos de Física Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
Halliday Fundamentos de Física Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
Potencial Elétrico. Objetivos: Explorar o Potencial Elétrico de cargas pontuais e distribuições contínuas de cargas.
 Potencial Elétrico Objetivos: Explorar o Potencial Elétrico de cargas pontuais e distribuições contínuas de cargas. Sobre a Apresentação Todas as gravuras, senão a maioria, são dos livros: Sears & Zemansky,
Potencial Elétrico Objetivos: Explorar o Potencial Elétrico de cargas pontuais e distribuições contínuas de cargas. Sobre a Apresentação Todas as gravuras, senão a maioria, são dos livros: Sears & Zemansky,
Física 3. Resumo e Exercícios P1
 Física 3 Resumo e Exercícios P1 Resuminho Teórico e Fórmulas Parte 1 Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv
Física 3 Resumo e Exercícios P1 Resuminho Teórico e Fórmulas Parte 1 Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv
Física. Resumo Eletromagnetismo
 Física Resumo Eletromagnetismo Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv Força Elétrica Duas formas de calcular:
Física Resumo Eletromagnetismo Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv Força Elétrica Duas formas de calcular:
Potencial Elétrico. Energia. Energia pode ser vista como trabalho armazenado, ou capacidade de realizar trabalho.
 Eletricidade e Magnetismo - IME Potencial Elétrico Oliveira Ed. Basilio Jafet sala 202 [email protected] Energia Energia pode ser vista como trabalho armazenado, ou capacidade de realizar trabalho. Equipamentos
Eletricidade e Magnetismo - IME Potencial Elétrico Oliveira Ed. Basilio Jafet sala 202 [email protected] Energia Energia pode ser vista como trabalho armazenado, ou capacidade de realizar trabalho. Equipamentos
Cap. 22. Campos Elétricos. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 Cap. 22 Campos Elétricos Copyright 22-1 O Campo Elétrico? Como a partícula 1 sabe da presença da partícula 2? Isto é, uma vez que as partículas não se tocam, como pode a partícula 2 empurrar a partícula
Cap. 22 Campos Elétricos Copyright 22-1 O Campo Elétrico? Como a partícula 1 sabe da presença da partícula 2? Isto é, uma vez que as partículas não se tocam, como pode a partícula 2 empurrar a partícula
Física III-A /1 Lista 3: Potencial Elétrico
 Física III-A - 2018/1 Lista 3: Potencial Elétrico Prof. Marcos Menezes 1. Qual é a diferença de potencial necessária para acelerar um elétron do repouso até uma velocidade igual a 40% da velocidade da
Física III-A - 2018/1 Lista 3: Potencial Elétrico Prof. Marcos Menezes 1. Qual é a diferença de potencial necessária para acelerar um elétron do repouso até uma velocidade igual a 40% da velocidade da
Eletromagnetismo I - Eletrostática
 - Eletrostática Potencial de distribuições de cargas e campos conservativos (Capítulo 4 - Páginas 86 a 95) Potencial Elétrico de distribuições contínuas de cargas Gradiente do Campo Elétrico Campos conservativos
- Eletrostática Potencial de distribuições de cargas e campos conservativos (Capítulo 4 - Páginas 86 a 95) Potencial Elétrico de distribuições contínuas de cargas Gradiente do Campo Elétrico Campos conservativos
FÍSICA (ELETROMAGNETISMO) LEI DE GAUSS
 FÍSICA (ELETROMAGNETISMO) LEI DE GAUSS Carl Friedrich Gauss (1777 1855) foi um matemático, astrônomo e físico alemão que contribuiu significativamente em vários campos da ciência, incluindo a teoria dos
FÍSICA (ELETROMAGNETISMO) LEI DE GAUSS Carl Friedrich Gauss (1777 1855) foi um matemático, astrônomo e físico alemão que contribuiu significativamente em vários campos da ciência, incluindo a teoria dos
ENERGIA CINÉTICA E TRABALHO
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ENERGIA CINÉTICA E TRABALHO Prof. Bruno Farias Introdução Neste módulo concentraremos nossa
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ENERGIA CINÉTICA E TRABALHO Prof. Bruno Farias Introdução Neste módulo concentraremos nossa
superfície que envolve a distribuição de cargas superfície gaussiana
 Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Aula-2 O campo elétrico. Curso de Física Geral F semestre, 2011
 Aula- O campo elétrico Curso de Física Geral F-38 1 semestre, 11 O campo elétrico Pelo princípio da superposição, vimos que a força que um conjunto de cargas puntiformes q, 1 q,..., q n eerce sobre uma
Aula- O campo elétrico Curso de Física Geral F-38 1 semestre, 11 O campo elétrico Pelo princípio da superposição, vimos que a força que um conjunto de cargas puntiformes q, 1 q,..., q n eerce sobre uma
Fluxo do campo elétrico
 Fluxo do campo elétrico Definição: - É uma grandeza escalar que caracteriza uma medida do número de linhas de campo que atravessam uma determinada superfície. a) Linhas de um campo uniforme em magnitude
Fluxo do campo elétrico Definição: - É uma grandeza escalar que caracteriza uma medida do número de linhas de campo que atravessam uma determinada superfície. a) Linhas de um campo uniforme em magnitude
raio do arco: a; ângulo central do arco: θ 0; carga do arco: Q.
 Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
Sea um arco de circunferência de raio a e ângulo central carregado com uma carga distribuída uniformemente ao longo do arco. Determine: a) O vetor campo elétrico nos pontos da reta que passa pelo centro
E(r) = 2. Uma carga q está distribuída uniformemente por todo um volume esférico de raio R.
 1. O campo elétrico no interior de uma esfera não-condutora de raio R, com carga distribuída uniformemente em seu volume, possui direção radial e intensidade dada por E(r) = qr 4πɛ 0 R 3. Nesta equação,
1. O campo elétrico no interior de uma esfera não-condutora de raio R, com carga distribuída uniformemente em seu volume, possui direção radial e intensidade dada por E(r) = qr 4πɛ 0 R 3. Nesta equação,
7. Potencial eletrostático
 7. Potencial eletrostático Em 1989 Wolfgang Paul recebeu o prémio Nobel da física pela sua invenção da armadilha de iões que permite isolar um ião. Com essa invenção tornou-se possível estudar um átomo
7. Potencial eletrostático Em 1989 Wolfgang Paul recebeu o prémio Nobel da física pela sua invenção da armadilha de iões que permite isolar um ião. Com essa invenção tornou-se possível estudar um átomo
Potencial e trabalho da força elétrica Módulo FE.03 (página 62 à 65) Apostila 1
 Aula 03 Potencial e trabalho da força elétrica Módulo FE.03 (página 62 à 65) Apostila 1 Energia Potencial Elétrica Potencial Elétrico Diferença de Potencial Trabalho da força elétrica Relação entre potencial
Aula 03 Potencial e trabalho da força elétrica Módulo FE.03 (página 62 à 65) Apostila 1 Energia Potencial Elétrica Potencial Elétrico Diferença de Potencial Trabalho da força elétrica Relação entre potencial
Laboratório de Física
 SUPERFÍCIES EQUIPOTENCIAIS I Laboratório de Física OBJETIVOS Identificar e descrever linhas de força a partir de superfícies euipotenciais. Medir a diferença de potencial elétrico entre dois pontos. Comparar
SUPERFÍCIES EQUIPOTENCIAIS I Laboratório de Física OBJETIVOS Identificar e descrever linhas de força a partir de superfícies euipotenciais. Medir a diferença de potencial elétrico entre dois pontos. Comparar
C. -20 nc, e o da direita, com +20 nc., no ponto equidistante aos dois anéis? exercida sobre uma carga de 1,0 nc colocada no ponto equidistante?
 Profa. Dra. Ignez Caracelli (DF) 30 de outubro de 2016 LISTA DE EXERCÍCIOS 2: ASSUNTOS: FORÇA DE COULOMB, CAMPO ELÉTRICO, CAMPO ELÉTRICO PRODUZIDO POR CARGA PONTUAL - DISTRIBUIÇÃO DISCRETA DE CARGAS, CAMPO
Profa. Dra. Ignez Caracelli (DF) 30 de outubro de 2016 LISTA DE EXERCÍCIOS 2: ASSUNTOS: FORÇA DE COULOMB, CAMPO ELÉTRICO, CAMPO ELÉTRICO PRODUZIDO POR CARGA PONTUAL - DISTRIBUIÇÃO DISCRETA DE CARGAS, CAMPO
Instituto de Física UFRJ
 AC TORT 1/9 1 Instituto de Física UFRJ 1 a Avaliação a Distância de Física 3A - AD1 Soluções Pólo : Nome : Segundo Semestre de 9 Data: 1 o Q o Q 3 o Q 4 o Q Nota Assinatura : Problema 1 Considere um condutor
AC TORT 1/9 1 Instituto de Física UFRJ 1 a Avaliação a Distância de Física 3A - AD1 Soluções Pólo : Nome : Segundo Semestre de 9 Data: 1 o Q o Q 3 o Q 4 o Q Nota Assinatura : Problema 1 Considere um condutor
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundamentos de Física Eletromagnetismo Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC
Halliday & Resnick Fundamentos de Física Eletromagnetismo Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC
Capítulo 22: Campos Elétricos
 Capítulo 22: Campos Elétricos O Campo Elétrico Linhas de Campo Elétrico Campo Elétrico Produzido por uma Carga Pontual Campo Elétrico Produzido por um Dipolo Elétrico Campo Elétrico Produzido por uma Linha
Capítulo 22: Campos Elétricos O Campo Elétrico Linhas de Campo Elétrico Campo Elétrico Produzido por uma Carga Pontual Campo Elétrico Produzido por um Dipolo Elétrico Campo Elétrico Produzido por uma Linha
Letras em Negrito representam vetores e as letras i, j, k são vetores unitários.
 Lista de exercícios 4 Potencial Elétrico Letras em Negrito representam vetores e as letras i, j, k são vetores unitários. 1. Boa parte do material dos anéis de Saturno está na forma de pequenos grãos de
Lista de exercícios 4 Potencial Elétrico Letras em Negrito representam vetores e as letras i, j, k são vetores unitários. 1. Boa parte do material dos anéis de Saturno está na forma de pequenos grãos de
Lista de Exercícios 1: Eletrostática
 Lista de Exercícios 1: Eletrostática 1. Uma carga Q é distribuída uniformemente sobre um fio semicircular de raio a, que está no plano xy. Calcule a força F com que atua sobre uma carga de sinal oposto
Lista de Exercícios 1: Eletrostática 1. Uma carga Q é distribuída uniformemente sobre um fio semicircular de raio a, que está no plano xy. Calcule a força F com que atua sobre uma carga de sinal oposto
Força elétrica e Campo Elétrico
 Força elétrica e Campo Elétrico 1 Antes de Física III, um pouco de Física I... Massas e Campo Gravitacional 2 Força Gravitacional: Força radial agindo entre duas massas, m 1 e m 2. : vetor unitário (versor)
Força elétrica e Campo Elétrico 1 Antes de Física III, um pouco de Física I... Massas e Campo Gravitacional 2 Força Gravitacional: Força radial agindo entre duas massas, m 1 e m 2. : vetor unitário (versor)
Lista de Exercícios 1 Forças e Campos Elétricos
 Lista de Exercícios 1 Forças e Campos Elétricos Exercícios Sugeridos (21/03/2007) A numeração corresponde ao Livros Textos A e B. A19.1 (a) Calcule o número de elétrons em um pequeno alfinete de prata
Lista de Exercícios 1 Forças e Campos Elétricos Exercícios Sugeridos (21/03/2007) A numeração corresponde ao Livros Textos A e B. A19.1 (a) Calcule o número de elétrons em um pequeno alfinete de prata
Prof. Fábio de Oliveira Borges
 O campo elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil http://cursos.if.uff.br/fisica2-2015/ Campo elétrico
O campo elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil http://cursos.if.uff.br/fisica2-2015/ Campo elétrico
Prof. Fábio de Oliveira Borges
 O campo elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil https://cursos.if.uff.br/!fisica2-0117/doku.php Campo
O campo elétrico Prof. Fábio de Oliveira Borges Curso de Física II Instituto de Física, Universidade Federal Fluminense Niterói, Rio de Janeiro, Brasil https://cursos.if.uff.br/!fisica2-0117/doku.php Campo
Universidade de São Paulo Eletromagnetismo ( ) Prova 1
 Instituto de Física de São Carlos Universidade de São Paulo Eletromagnetismo 760001) 3 de abril de 018 Prof. D. Boito Mon.:. Carvalho 1 sem. 018: Bacharelados em Física Nome e sobrenome: n. USP: Prova
Instituto de Física de São Carlos Universidade de São Paulo Eletromagnetismo 760001) 3 de abril de 018 Prof. D. Boito Mon.:. Carvalho 1 sem. 018: Bacharelados em Física Nome e sobrenome: n. USP: Prova
Campo Elétrico [N/C] Campo produzido por uma carga pontual
![Campo Elétrico [N/C] Campo produzido por uma carga pontual Campo Elétrico [N/C] Campo produzido por uma carga pontual](/thumbs/57/40344984.jpg) Campo Elétrico Ao tentar explicar, ou entender, a interação elétrica entre duas cargas elétricas, que se manifesta através da força elétrica de atração ou repulsão, foi criado o conceito de campo elétrico,
Campo Elétrico Ao tentar explicar, ou entender, a interação elétrica entre duas cargas elétricas, que se manifesta através da força elétrica de atração ou repulsão, foi criado o conceito de campo elétrico,
Aula-2 O campo elétrico
 Aula- O campo elétrico Curso de Física Geral III - F-38 1º semestre, 14 F38 1S14 1 O Campo Elétrico Pelo princípio da superposição, vimos que a força que um conjunto de cargas puntiformes q 1, q,..., q
Aula- O campo elétrico Curso de Física Geral III - F-38 1º semestre, 14 F38 1S14 1 O Campo Elétrico Pelo princípio da superposição, vimos que a força que um conjunto de cargas puntiformes q 1, q,..., q
Halliday Fundamentos de Física Volume 3
 Halliday Fundamentos de Física Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
Halliday Fundamentos de Física Volume 3 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
1 Definição. 2 Energia potencial elétrica. 3 Relações matemáticas. 4 Legenda. 5 Gráfico do potencial elétrico. 7 Diferença de potencial (ddp)
 1 Definição 2 Energia potencial elétrica 3 Relações matemáticas 4 Legenda 5 Gráfico do potencial elétrico 6 Potencial criado por várias partículas 7 Diferença de potencial (ddp) 8 Superfície equipotencial
1 Definição 2 Energia potencial elétrica 3 Relações matemáticas 4 Legenda 5 Gráfico do potencial elétrico 6 Potencial criado por várias partículas 7 Diferença de potencial (ddp) 8 Superfície equipotencial
Eletromagnetismo I. Prof. Daniel Orquiza. Eletromagnetismo I. Prof. Daniel Orquiza de Carvalho
 de Carvalho - Eletrostática Densidade de Fluxo Elétrico e Lei de Gauss (Páginas 48 a 55 no livro texto) Experimento com esferas concêntricas Densidade de Fluxo elétrico (D) Relação entre D e E no vácuo
de Carvalho - Eletrostática Densidade de Fluxo Elétrico e Lei de Gauss (Páginas 48 a 55 no livro texto) Experimento com esferas concêntricas Densidade de Fluxo elétrico (D) Relação entre D e E no vácuo
POTENCIAL ELÉTRICO. onde. é o potencial elétrico, a energia potencial e a carga. A unidade no S.I.
 POTENCIAL ELÉTRICO Potencial elétrico é a capacidade que um corpo energizado tem de realizar trabalho, ou seja, atrair ou repelir outras cargas elétricas. Ao tomarmos uma carga de prova q e a colocarmos
POTENCIAL ELÉTRICO Potencial elétrico é a capacidade que um corpo energizado tem de realizar trabalho, ou seja, atrair ou repelir outras cargas elétricas. Ao tomarmos uma carga de prova q e a colocarmos
ENERGIA POTENCIAL. Prof. Márcio Marinho
 ENERGIA POTENCIAL Prof. Márcio Marinho Energia potencial gravitacional (Energia armazenada) Energia potencial elástica (Energia armazenada) Energia potencial elétrica (Energia armazenada) q E p = K Q q
ENERGIA POTENCIAL Prof. Márcio Marinho Energia potencial gravitacional (Energia armazenada) Energia potencial elástica (Energia armazenada) Energia potencial elétrica (Energia armazenada) q E p = K Q q
Campo Elétrico 2 Objetivos:
 Campo Elétrico 2 Objetivos: Apresentar a discretização do espaço para a resolução de problemas em coordenadas: Cartesianas; Polar; Aplicar a discretização do espaço para resolução de problemas de campo
Campo Elétrico 2 Objetivos: Apresentar a discretização do espaço para a resolução de problemas em coordenadas: Cartesianas; Polar; Aplicar a discretização do espaço para resolução de problemas de campo
ESCOLA ESTADUAL JOÃO XXIII A Escola que a gente quer é a Escola que a gente faz!
 ESCOLA ESTADUAL JOÃO XXIII A Escola que a gente quer é a Escola que a gente faz! NATUREZA DA ATIVIDADE: EXERCÍCIOS DE FIXAÇÃO - ELETROSTÁTICA DISCIPLINA: FÍSICA ASSUNTO: CAMPO ELÉTRICO, POTENCIAL ELÉTRICO,
ESCOLA ESTADUAL JOÃO XXIII A Escola que a gente quer é a Escola que a gente faz! NATUREZA DA ATIVIDADE: EXERCÍCIOS DE FIXAÇÃO - ELETROSTÁTICA DISCIPLINA: FÍSICA ASSUNTO: CAMPO ELÉTRICO, POTENCIAL ELÉTRICO,
PUC-RIO CB-CTC. Não é permitido destacar folhas da prova
 PUC-RIO CB-CTC FIS5 P DE ELETROMAGNETISMO 8.4. segunda-feira Nome : Assinatura: Matrícula: Turma: NÃO SERÃO ACEITAS RESPOSTAS SEM JUSTIFICATIVAS E CÁLCULOS EXPLÍCITOS. Não é permitido destacar folhas da
PUC-RIO CB-CTC FIS5 P DE ELETROMAGNETISMO 8.4. segunda-feira Nome : Assinatura: Matrícula: Turma: NÃO SERÃO ACEITAS RESPOSTAS SEM JUSTIFICATIVAS E CÁLCULOS EXPLÍCITOS. Não é permitido destacar folhas da
AULA 03 O FLUXO ELÉTRICO. Eletromagnetismo - Instituto de Pesquisas Científicas
 ELETROMAGNETISMO AULA 03 O FLUXO ELÉTRICO Vamos supor que exista certa superfície inserida em uma campo elétrico. Essa superfície possui uma área total A. Definimos o fluxo elétrico dφ através de um elemento
ELETROMAGNETISMO AULA 03 O FLUXO ELÉTRICO Vamos supor que exista certa superfície inserida em uma campo elétrico. Essa superfície possui uma área total A. Definimos o fluxo elétrico dφ através de um elemento
Física 3 Turma
 Física 3 Turma 09903-1 Potencial Elétrico Profa. Ignez Caracelli Física 3 1 Grandezas Grandezas a serem utilizadas devem ser entendidas e diferenciadas campo elétrico E potencial elétrico V energia potencial
Física 3 Turma 09903-1 Potencial Elétrico Profa. Ignez Caracelli Física 3 1 Grandezas Grandezas a serem utilizadas devem ser entendidas e diferenciadas campo elétrico E potencial elétrico V energia potencial
carga do fio: Q. r = r p r q figura 1
 Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A /1 Data: 24/04/2019
 Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A - 2019/1 Data: 24/04/2019 Seção 1: Múltipla Escolha (6 0,8 = 4,8 pontos) 1. Um grão de poeira
Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A - 2019/1 Data: 24/04/2019 Seção 1: Múltipla Escolha (6 0,8 = 4,8 pontos) 1. Um grão de poeira
Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A /2 Data: 17/09/2018
 Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A - 2018/2 Data: 17/09/2018 Seção 1: Múltipla Escolha (7 0,8 = 5,6 pontos) 3. O campo elétrico
Universidade Federal do Rio de Janeiro Instituto de Física Primeira Prova (Diurno) Disciplina: Física III-A - 2018/2 Data: 17/09/2018 Seção 1: Múltipla Escolha (7 0,8 = 5,6 pontos) 3. O campo elétrico
Física III Escola Politécnica GABARITO DA P1 12 de abril de 2012
 Física III - 4320301 Escola Politécnica - 2012 GABARITO DA P1 12 de abril de 2012 Questão 1 Uma distribuição de cargas com densidade linear constante λ > 0 está localizada ao longo do eio no intervalo
Física III - 4320301 Escola Politécnica - 2012 GABARITO DA P1 12 de abril de 2012 Questão 1 Uma distribuição de cargas com densidade linear constante λ > 0 está localizada ao longo do eio no intervalo
Lei de Gauss Φ = A (1) E da = q int
 Lei de Gauss Lei de Gauss: A lei de Gauss nos diz que o fluxo total do campo elétrico através de uma superfície fechada A é proporcional à carga elétrica contida no interior do volume delimitado por essa
Lei de Gauss Lei de Gauss: A lei de Gauss nos diz que o fluxo total do campo elétrico através de uma superfície fechada A é proporcional à carga elétrica contida no interior do volume delimitado por essa
FÍSICA III AULAS 6 E 7 PROFESSORA MAUREN POMALIS
 FÍSICA III AULAS 6 E 7 PROFESSORA MAUREN POMALIS [email protected] ENG. ELÉTRICA - 3 PERÍODO UNIR/Porto Velho 2017/1 SUMÁRIO Revisão Analogias Energia Potencial Elétrica Potencial Elétrico Superfícies
FÍSICA III AULAS 6 E 7 PROFESSORA MAUREN POMALIS [email protected] ENG. ELÉTRICA - 3 PERÍODO UNIR/Porto Velho 2017/1 SUMÁRIO Revisão Analogias Energia Potencial Elétrica Potencial Elétrico Superfícies
Lista 2. Física III Prof. Lucas Simões
 Lista 2 Física III Prof. Lucas Simões (A) Exercícios Energia Potencial Elétrostática e Potencial Elétrico Questão. Uma carga puntiforme q = 2,4 µc é mantida em repouso na origem. Uma segunda carga puntiforme
Lista 2 Física III Prof. Lucas Simões (A) Exercícios Energia Potencial Elétrostática e Potencial Elétrico Questão. Uma carga puntiforme q = 2,4 µc é mantida em repouso na origem. Uma segunda carga puntiforme
1 f =10 15.) q 1. σ 1. q i. ρ = q 1. 4πa 3 = 4πr 3 q i = q 1 ( r a )3 V 1 = V 2. 4πr 2 E = q 1. q = 1 3, q 2. q = 2 3 E = = q 1/4πR 2
 1 possui uma carga uniforme q 1 =+5, 00 fc e a casca Instituto de Física - UFF Física Geral e Experimental I/XVIII Prof. Hisataki Shigueoka http://profs.if.uff.br/ hisa possui uma carga q = q 1. Determine
1 possui uma carga uniforme q 1 =+5, 00 fc e a casca Instituto de Física - UFF Física Geral e Experimental I/XVIII Prof. Hisataki Shigueoka http://profs.if.uff.br/ hisa possui uma carga q = q 1. Determine
Segunda Lista - Lei de Gauss
 Segunda Lista - Lei de Gauss FGE211 - Física III 1 Sumário O fluxo elétrico que atravessa uma superfície infinitesimal caracterizada por um vetor de área A = Aˆn é onde θ é o ângulo entre E e ˆn. Φ e =
Segunda Lista - Lei de Gauss FGE211 - Física III 1 Sumário O fluxo elétrico que atravessa uma superfície infinitesimal caracterizada por um vetor de área A = Aˆn é onde θ é o ângulo entre E e ˆn. Φ e =
MOVIMENTO EM DUAS E TRÊS DIMENSÕES
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: MECÂNICA E TERMODINÂMICA MOVIMENTO EM DUAS E TRÊS DIMENSÕES Prof. Bruno Farias Introdução Neste módulo
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: MECÂNICA E TERMODINÂMICA MOVIMENTO EM DUAS E TRÊS DIMENSÕES Prof. Bruno Farias Introdução Neste módulo
Lista 01 Parte II. Capítulo 28
 Lista 01 Parte II Capítulo 28 01) Qual é o fluxo elétrico através de cada uma das superfícies (a), (b), (c) e (d) presentes na figura abaixo? 02) Uma carga positiva Q está localizada no centro de um cilindro
Lista 01 Parte II Capítulo 28 01) Qual é o fluxo elétrico através de cada uma das superfícies (a), (b), (c) e (d) presentes na figura abaixo? 02) Uma carga positiva Q está localizada no centro de um cilindro
Fundamentos de Física Clássica UFCG Prof. Ricardo. Potencial Elétrico. O que é diferença de potencial (ddp)?
 Potencial Elétrico O que é diferença de potencial (ddp)? A diferença de potencial entre dois pontos e num campo elétrico, seja ele uniforme ou não, é, por definição, o trabalho por unidade de carga (J/C
Potencial Elétrico O que é diferença de potencial (ddp)? A diferença de potencial entre dois pontos e num campo elétrico, seja ele uniforme ou não, é, por definição, o trabalho por unidade de carga (J/C
Física III-A /1 Lista 1: Carga Elétrica e Campo Elétrico
 Física III-A - 2018/1 Lista 1: Carga Elétrica e Campo Elétrico Prof. Marcos Menezes 1. Duas partículas com cargas positivas q e 3q são fixadas nas extremidades de um bastão isolante de comprimento d. Uma
Física III-A - 2018/1 Lista 1: Carga Elétrica e Campo Elétrico Prof. Marcos Menezes 1. Duas partículas com cargas positivas q e 3q são fixadas nas extremidades de um bastão isolante de comprimento d. Uma
Eletricidade e Magnetismo. Fluxo Elétrico Lei De Gauss
 Eletricidade e Magnetismo Fluxo Elétrico Lei De Gauss 1. A figura seguinte mostra uma seção de uma barra cilíndrica de plástico infinitamente longo, com uma densidade linear de carga positiva uniforme.
Eletricidade e Magnetismo Fluxo Elétrico Lei De Gauss 1. A figura seguinte mostra uma seção de uma barra cilíndrica de plástico infinitamente longo, com uma densidade linear de carga positiva uniforme.
Cap. 22. Campo Elétrico. Prof. Oscar Rodrigues dos Santos Potencial elétrico 1
 Cap. 22 Campo létrico Prof. Oscar Rodrigues dos Santos [email protected] Potencial elétrico 1 Quando ocorre a interação no vácuo entre duas partículas que possuem cargas elétricas, como é possível
Cap. 22 Campo létrico Prof. Oscar Rodrigues dos Santos [email protected] Potencial elétrico 1 Quando ocorre a interação no vácuo entre duas partículas que possuem cargas elétricas, como é possível
Primeira Prova 2º. semestre de /09/2017 ATENÇÃO LEIA ANTES DE FAZER A PROVA
 Física Teórica II Primeira Prova 2º. semestre de 2017 23/09/2017 ALUNO Gabarito NOTA DA TURMA PROF. PROVA 1 Assine a prova antes de começar. ATENÇÃO LEIA ANTES DE FAZER A PROVA 2 Os professores não poderão
Física Teórica II Primeira Prova 2º. semestre de 2017 23/09/2017 ALUNO Gabarito NOTA DA TURMA PROF. PROVA 1 Assine a prova antes de começar. ATENÇÃO LEIA ANTES DE FAZER A PROVA 2 Os professores não poderão
Física III-A /2 Lista 1: Carga Elétrica e Campo Elétrico
 Física III-A - 2018/2 Lista 1: Carga Elétrica e Campo Elétrico 1. (F) Duas partículas com cargas positivas q e 3q são fixadas nas extremidades de um bastão isolante de comprimento d. Uma terceira partícula
Física III-A - 2018/2 Lista 1: Carga Elétrica e Campo Elétrico 1. (F) Duas partículas com cargas positivas q e 3q são fixadas nas extremidades de um bastão isolante de comprimento d. Uma terceira partícula
Capítulo 23: Lei de Gauss
 Capítulo 23: Lei de Gauss O Fluxo de um Campo Elétrico A Lei de Gauss A Lei de Gauss e a Lei de Coulomb Um Condutor Carregado A Lei de Gauss: Simetria Cilíndrica A Lei de Gauss: Simetria Plana A Lei de
Capítulo 23: Lei de Gauss O Fluxo de um Campo Elétrico A Lei de Gauss A Lei de Gauss e a Lei de Coulomb Um Condutor Carregado A Lei de Gauss: Simetria Cilíndrica A Lei de Gauss: Simetria Plana A Lei de
Eletromagnetismo II. Prof. Daniel Orquiza. Prof. Daniel Orquiza de Carvalho
 Eletromagnetismo II Prof. Daniel Orquiza Eletromagnetismo II Prof. Daniel Orquiza de Carvalho Eletromagnetismo II - Eletrostática Fluxo Magnético e LGM (Capítulo 7 Páginas 207a 209) Princípio da Superposição
Eletromagnetismo II Prof. Daniel Orquiza Eletromagnetismo II Prof. Daniel Orquiza de Carvalho Eletromagnetismo II - Eletrostática Fluxo Magnético e LGM (Capítulo 7 Páginas 207a 209) Princípio da Superposição
Eletromagnetismo II. Prof. Daniel Orquiza. Prof. Daniel Orquiza de Carvalho
 Eletromagnetismo II Prof. Daniel Orquiza Eletromagnetismo II Prof. Daniel Orquiza de Carvalho Eletromagnetismo II - Eletrostática Fluxo Magnético e LGM (Capítulo 7 Páginas 207a 209) Princípio da Superposição
Eletromagnetismo II Prof. Daniel Orquiza Eletromagnetismo II Prof. Daniel Orquiza de Carvalho Eletromagnetismo II - Eletrostática Fluxo Magnético e LGM (Capítulo 7 Páginas 207a 209) Princípio da Superposição
Campo elétrico e sua relação com a força elétrica
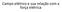 Campo elétrico e sua relação com a força elétrica Relembrando... A LEI DE COULOMB PRINCÍPIO DA SUPERPOSIÇÃO A força com a qual duas cargas interagem não é modificada pela presença de uma terceira. Em outras
Campo elétrico e sua relação com a força elétrica Relembrando... A LEI DE COULOMB PRINCÍPIO DA SUPERPOSIÇÃO A força com a qual duas cargas interagem não é modificada pela presença de uma terceira. Em outras
Segunda aula de Fundamentos de Eletromagnetismo
 Segunda aula de Fundamentos de Eletromagnetismo Prof. Vicente Barros 1- Revisão de vetores. 2- Revisão sobre carga elétrica. 3- Revisão condutores e isolantes 4- Revisão sobre Lei de Coulomb. Revisão de
Segunda aula de Fundamentos de Eletromagnetismo Prof. Vicente Barros 1- Revisão de vetores. 2- Revisão sobre carga elétrica. 3- Revisão condutores e isolantes 4- Revisão sobre Lei de Coulomb. Revisão de
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO Prof. Bruno Farias Introdução Neste capítulo vamos aprender: Como descrever a rotação
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO Prof. Bruno Farias Introdução Neste capítulo vamos aprender: Como descrever a rotação
Lista de Exercícios 2 Potencial Elétrico e Capacitância
 Lista de Exercícios 2 Potencial Elétrico e Capacitância Exercícios Sugeridos (14 de março de 2007) A numeração corresponde ao Livros Textos A e B. B25.10 Considere dois pontos numa região onde há um campo
Lista de Exercícios 2 Potencial Elétrico e Capacitância Exercícios Sugeridos (14 de março de 2007) A numeração corresponde ao Livros Textos A e B. B25.10 Considere dois pontos numa região onde há um campo
Potencial elétrico e energia potencial elétrica Capítulo
 Potencial elétrico e energia potencial elétrica Capítulo Potencial elétrico e energia potencial elétrica Potencial elétrico Se uma carga de prova q for colocada em um campo elétrico, ficará sujeita a uma
Potencial elétrico e energia potencial elétrica Capítulo Potencial elétrico e energia potencial elétrica Potencial elétrico Se uma carga de prova q for colocada em um campo elétrico, ficará sujeita a uma
Cap. 2 - Lei de Gauss
 Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 2 - Lei de Gauss Prof. Elvis Soares Nesse capítulo, descreveremos a Lei de Gauss e um procedimento alternativo para cálculo
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 2 - Lei de Gauss Prof. Elvis Soares Nesse capítulo, descreveremos a Lei de Gauss e um procedimento alternativo para cálculo
CORRENTE E RESISTÊNCIA
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III CORRENTE E RESISTÊNCIA Prof. Bruno Farias Corrente Elétrica Eletrodinâmica: estudo das
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA III CORRENTE E RESISTÊNCIA Prof. Bruno Farias Corrente Elétrica Eletrodinâmica: estudo das
Eletrostática. Antonio Carlos Siqueira de Lima. Universidade Federal do Rio de Janeiro Escola Politécnica Departamento de Engenharia Elétrica
 Eletrostática Antonio Carlos Siqueira de Lima Universidade Federal do Rio de Janeiro Escola Politécnica Departamento de Engenharia Elétrica Agosto 2008 1 Campo Elétrico Campo Elétrico Devido a Distribuições
Eletrostática Antonio Carlos Siqueira de Lima Universidade Federal do Rio de Janeiro Escola Politécnica Departamento de Engenharia Elétrica Agosto 2008 1 Campo Elétrico Campo Elétrico Devido a Distribuições
de x = decosθ = k λdθ R cosθ, de y = desenθ = k λdθ R senθ, em que já substituímos dq e simplificamos. Agora podemos integrar, cosθdθ = k λ R,
 FÍSICA BÁSICA III - LISTA 2 1 A figura 1 mostra um semicírculo carregado uniformemente na metade superior com carga +Q e na metade inferior com carga Q Calcule o campo elétrico na origem (E = Qĵ/π2 R 2
FÍSICA BÁSICA III - LISTA 2 1 A figura 1 mostra um semicírculo carregado uniformemente na metade superior com carga +Q e na metade inferior com carga Q Calcule o campo elétrico na origem (E = Qĵ/π2 R 2
Eletromagnetismo I. Prof. Daniel Orquiza. Eletromagnetismo I. Prof. Daniel Orquiza de Carvalho
 de Carvalho - Eletrostática Aplicação da Lei de Gauss e Lei de Gauss na Forma Diferencial (Páginas 56 a 70 no livro texto) Aplicação da Lei de Gauss: Linha Infinita de Cargas Condutores Coaxiais Lei de
de Carvalho - Eletrostática Aplicação da Lei de Gauss e Lei de Gauss na Forma Diferencial (Páginas 56 a 70 no livro texto) Aplicação da Lei de Gauss: Linha Infinita de Cargas Condutores Coaxiais Lei de
O potencial elétrico V em um ponto P devido ao campo elétrico produzido por um objeto carregado é dado por
 CAPÍTULO 24 Potencial Elétrico 24-1 POTENCIAL ELÉTRICO Objetivos do Aprendizado Depois de ler este módulo, você será capaz de... 24.01 Saber que a força elétrica é conservativa e, portanto, é possível
CAPÍTULO 24 Potencial Elétrico 24-1 POTENCIAL ELÉTRICO Objetivos do Aprendizado Depois de ler este módulo, você será capaz de... 24.01 Saber que a força elétrica é conservativa e, portanto, é possível
(d) E = Eŷ e V = 0. (b) (c) (f) E = Eˆx e V = (f)
 1 Universidade Federal do Rio de Janeiro Instituto de Física Física III 01/ Primeira Prova: 10/1/01 Versão: A F e = q E, E = V, E = k0 q r ˆr Seção 1 Múltipla escolha 10 0,5 = 5,0 pontos) Formulário onde
1 Universidade Federal do Rio de Janeiro Instituto de Física Física III 01/ Primeira Prova: 10/1/01 Versão: A F e = q E, E = V, E = k0 q r ˆr Seção 1 Múltipla escolha 10 0,5 = 5,0 pontos) Formulário onde
