Preferência Revelada
|
|
|
- Ágata Alencastre Borja
- 6 Há anos
- Visualizações:
Transcrição
1 Preferêcia Revelada
2 A teoria da escolha a artir das referêcias do cosumidor tem uma característica iteressate que é sua subjetividade. Dessa maeira, ão é algo observável. No etato, a escolha, em si, é algo que o aalista ecoômico ode observar. Surge, etão, a ossibilidade de se motar uma teoria a artir de algo que é itrisecamete observável, ou seja, a escolha. A artir da observação da escolha e de equeos requisitos sobre a racioalidade do idivíduo, Samuelso elaborou uma teoria que ermite chegar a coclusões muito róimas àquelas chegadas ela teoria baseada a eistêcia de um cojuto de referêcias subjetivamete determiadas. A seguir, rocuramos aresetar algus elemetos dessa teoria.
3 Suoha um cojuto de cestas X, tal que: X = R = M = { R : 0, i =,, } i A estrutura de escolha (Ɓ, C(.)) é comosta or dois igredietes: (i) Uma família Ɓ de subcojutos de X, B X, tal que B єɓ, sedo B, or coveiêcia, defiido como cojuto orçametário. Os subcojutos B єɓ são eerimetos realizados; (ii) C(.) é uma regra de escolha que desiga um subcojuto C(B) cotido em B de elemetos escolhidos ara B єɓ. Hióteses adicioais sobre o cojuto B: (i) Bes são trocados em mercados cometitivos (idivíduo ão afeta o reço) aos reços, sedo i >0 ara todo i; (ii) Eiste uma reda m à disosição do cosumidor. B, m { R; m} =.
4 Hióteses sobre C(B), o cojuto de escolha: (i) O cojuto de escolha ertece à liha orçametária, ou seja, o cosumidor gasta toda sua reda e ão mais do que sua reda. Algus autores (MasCollelet al. 995) deomiam essa hiótese de Lei de Walras(obs: a lei de Walrasafirma que os ecessos de demada se igualam a 0); (ii) O cojuto de escolha cotém aeas um comoete; (iii) A escolha atede à característica de ser homogêea de grau zero em reços e, m = α, αm reda, ou seja: ( ) ( ) A essas hióteses deve-se adicioar o aioma fraco da referêcia revelada (AFrPR): A estrutura de escolha Afirmamos, etão, relação a y. ( Β, C( B) ) satisfaz o aioma fraco da referêcia revelada se, ara todo B Β com e y B e C( B), etão, ara B Β, com e y B, y C( B). y que o cosumidor revelou diretamete sua referêcia or em Isto sigifica afirmar que se é escolhido quado y estava disoível, etão, y ão oderá ser escolhido se estiver disoível.
5 A artir dessas hióteses, odemos etrair várias roriedades da demada marshalliaatedo como úico requisito de racioalidade o atedimeto ao aioma fraco da referêcia revelada. O gráfico areseta a curva reda-cosumo (camiho de easão da reda) ara bes iferiores. Rearem que, sob quaisquer escolhas, aceitamos as hióteses a 3 sobre o cojuto de escolha, e ocorre o atedimeto ao AFrPR. O gráfico areseta a curva reço-cosumo que também atede aos ressuostos levatados acima. Curva reda-cosumo Curva reço-cosumo Gráfico Gráfico
6 O atedimeto à lei da demada comesada imede, o etato, que, uma vez tedo otado ela cesta a restrição B,m, o cosumidor veha otar ela cesta y a restrição B,m, orque a restrição cotiua disoível a restrição B,m e y estava disoível quado foi escolhida. Quado o rocesso de escolha de um cosumidor atede a testes como esse, afirmamos que o cosumidor assou o teste do aioma fraco da referêcia revelada. MasColleletal. (995:-4) mostram que, se o cosumidor atede o requisito de racioalidade a artir da teoria das referêcias subjetivas, ou seja, às hióteses de referêcias comletas e trasitivas, ele obrigatoriamete assará o teste do aioma fraco da referêcia revelada. Cotudo, o iverso só será verdadeiro se o cosumidor se cofrotar com todas as escolhas ossíveis duas a duas e assar o teste. Nesse setido, as hióteses de referêcias comletas e trasitivas são mais fortes do que o aioma forte da referêcia revelada. y B, m B, m O cosumidor atederá às hióteses de referêcias comletas e trasitivas se assar o teste do aioma forteda referêcia revelada. O aioma forte da referêcia revelada eige que se for revelada referível a ye yfor revelada referível a z, etão também será revelada referível a z, ou seja, será idiretameterevelada referível, equato o aioma fraco só imlica a revelação direta de referêcia. Gráfico 3
7 Lei da Demada Comesada Se a demada marshalliaa, (,m) é homogêea de grau zero em reços e reda e atede a lei de Walras, etão, o aioma fraco da referêcia revelada imlica a lei da demada comesada: ( -)((,m )-(,m)) 0 (), em que m =.(,m) (). Graficamete, o ajuste da reda m é reresetado or uma liha orçametária que assa ela cesta iicial (,m) e que tem sua icliação defiida or, como observado o gráfico 4 ela restrição B,m. Gráfico 4 B, m B, m O gráfico 4 também ajuda a comreeder a afirmação. Suoha que o cosumidor teha escolhido a cesta quado a restrição era B,m. Com a mudaça de reços relativos rovocada elo vetor e a comesação da reda, gera-se uma ova restrição defiida or B,m. Pela lei de Walrassabe-se que a escolha do cosumidor a ova restrição estará sobre a liha orçametária. Ao mesmo temo, sabe-se que qualquer oto da ova liha orçametária em sua arte tracejada (à direita de ) ão oderá ser escolhido dado o AFrPR, ou seja, dado que essas cestas estavam disoíveis quado foi escolhida. Assim, a escolha ou será ou será uma cesta situada a arte cotíua da ova liha orçametária.
8 Note-se que, a arte cotíua, a quatidade do bem é meor do que a quatidade ateriormete escolhida ara o bem e que a quatidade do bem é maior do que a quatidade ateriormete escolhida ara o bem. Por sua vez, os reços relativos idicam que o reço do bem é maior do que o reço aterior do bem, sedo o iverso verdadeiro ara o bem, o que cofirma a lei de demada comesada. Mais formalmete, a artir de ():.. ( (, m) (, m) ). ( (, m ) (, m) ) Sabe -se que o rimeiro termo da equação (3) é igual a 0, ela regra de comesação (). Logo : ( (, m ) (, m) ) No etato, sabe -se que se a escolhida, ou seja, com a 0 (4) cesta (, m) udesse ter sido escolhida quado (, m) foi reda. (, m), 0 etão, a sua escolha quado a reda fosse. (, m ) violaria o AFrPR, ois a cesta (, m ) ode ser cosumida com essa ova reda. Logo,. (, m ) >. (, m). (3)
9 Ídices de Preços Reare que, ela regra de ajuste da reda adotada em (), adotamos a cesta iicial (,m) como um elemeto comum as duas restrições orçametárias eostas o gráfico 4. Isso sigifica que adotamos essa cesta como um eso comum ara a formação da reda. Trata-se de um ajuste da reda que assegura que o cosumidor oderá cosumir eatamete a mesma cesta que cosumia ates. Esse critério ode ecotrar um aralelo com aquele adotado a comesação hicksiaa. A comesação hicksiaa, ao assegurar que a cesta escolhida aos ovos reços atederá o requisito de que u() u(y) garate que o cosumidor estará elo meos tão bem quato ates. Da mesma maeira, a comesação da reda adotada elo critério da equação () que deomiaremos de comesação de Slutsky, ao garatir que a cesta iicial cotiua disoível aos ovos reços também assegura que o cosumidor estará tão bem quato ates. No etato, ao cotrário do critério de Hicks em que o ível de utilidade e sua resectiva curva de idifereça ão são observáveis, a comesação de Slutskyarte da cesta iicial, ou seja, um critério observável. Esse critério é utilizado ara comor ídices de reço. Esse critério ode ser adotado ara elaboração de ídices de reços. O ídice de reços de Lasèyres adota a cesta iicialmete cosumida ara a comosição do ídice: L = Dessa maeira, o uso de ídice de Laseyresara o cálculo de variação dos reços adota um critério de oderação da imortâcia de cada um dos reços de acordo com a cesta que foi escolhida iicialmete. Como a cesta que acabou sedo cosumida o fial também é cohecida, uma forma alterativa de cálculo de variação dos reços é utilizar essa cesta fial como referêcia. Este critério é cohecido como Paasche: (5)
10 (6) P = A imortâcia dos ídices de reços está a resosta à ecessidade de aálise de variações de elemetos heterogêeos. Como comarar a imortâcia da variação dos reços de baaas e maçãs, como cotabilizar or isso? O ídice de reços ao cosumidor amlo (IPCA-5), utilizado o regime de metas de iflação, é um ídice de Laseyresque tem como referêcia a cesta de cosumo de famílias que recebem até 5 a artir da Pesquisa de Orçameto Familiar que teve sua última versão coletada em 009 e divulgada ao assado. A divulgação da ova cesta imlicou uma correção os cálculos de iflação. Já o deflatorimlícito do PIB que ermite calcular taas de crescimeto da ecoomia adota o critério de Paasche. Assim como se faz oderação ara se calcular a variação de reços, também ode ser feita a oderação ara se calcular a variação de quatidades. Esses ídices são deomiados de ídices de quatidade. Nesse caso, fica-se uma estrutura de reços de determiado mometo e aalisa-se a variação da quatidade. (7) q L = (8) q P =
TEORIA DE SISTEMAS LINEARES
 Ageda. Algebra Liear (Parte I). Ativadades IV Profa. Dra. Letícia Maria Bolzai Poehls /0/00 Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação
Ageda. Algebra Liear (Parte I). Ativadades IV Profa. Dra. Letícia Maria Bolzai Poehls /0/00 Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação
Número-índice: Conceito, amostragem e construção de estimadores
 Número-ídice: Coceito, amostragem e costrução de estimadores Objetivo Geral da aula Defiir o que são os úmeros-ídices, efatizado a sua importâcia para aálise ecoômica. Cosidere os dados apresetados a Tabela
Número-ídice: Coceito, amostragem e costrução de estimadores Objetivo Geral da aula Defiir o que são os úmeros-ídices, efatizado a sua importâcia para aálise ecoômica. Cosidere os dados apresetados a Tabela
Proposta de teste de avaliação
 Proosta de teste de avaliação Matemática A. O ANO DE ESOLARIDADE Duração: 9 miutos Data: adero (é ermitido o uso de calculadora) Na resosta aos ites de escolha múltila, selecioe a oção correta. Escreva,
Proosta de teste de avaliação Matemática A. O ANO DE ESOLARIDADE Duração: 9 miutos Data: adero (é ermitido o uso de calculadora) Na resosta aos ites de escolha múltila, selecioe a oção correta. Escreva,
O termo "linear" significa que todas as funções definidas no modelo matemático que descreve o problema devem ser lineares, isto é, se f( x1,x2
 MÓDULO 4 - PROBLEMAS DE TRANSPORTE Baseado em Novaes, Atôio Galvão, Métodos de Otimização: aplicações aos trasportes. Edgar Blücher, São Paulo, 978..CONCEITOS BÁSICOS DE PROGRAMAÇÃO LINEAR É uma técica
MÓDULO 4 - PROBLEMAS DE TRANSPORTE Baseado em Novaes, Atôio Galvão, Métodos de Otimização: aplicações aos trasportes. Edgar Blücher, São Paulo, 978..CONCEITOS BÁSICOS DE PROGRAMAÇÃO LINEAR É uma técica
INFERÊNCIA ESTATÍSTICA: ESTIMAÇÂO PONTUAL E INTERVALOS DE CONFIANÇA
 INFRÊNCIA STATÍSTICA: STIMAÇÂO PONTUAL INTRVALOS D CONFIANÇA 0 Problemas de iferêcia Iferir sigifica faer afirmações sobre algo descohecido. A iferêcia estatística tem como objetivo faer afirmações sobre
INFRÊNCIA STATÍSTICA: STIMAÇÂO PONTUAL INTRVALOS D CONFIANÇA 0 Problemas de iferêcia Iferir sigifica faer afirmações sobre algo descohecido. A iferêcia estatística tem como objetivo faer afirmações sobre
CUFSA - FAFIL. Análise Combinatória (Resumo Teórico)
 A) CONCEITOS: CUFSA - FAFIL Aálise Combiatória (Resumo Teórico) Regras Simles de Cotagem: é a maeira de determiar o úmero de elemetos de um cojuto. Na maioria das vezes é mais imortate cohecer a quatidade
A) CONCEITOS: CUFSA - FAFIL Aálise Combiatória (Resumo Teórico) Regras Simles de Cotagem: é a maeira de determiar o úmero de elemetos de um cojuto. Na maioria das vezes é mais imortate cohecer a quatidade
Grupo I. Qual é a probabilidade de o João acertar sempre no alvo, nas quatro vezes em que tem de atirar?
 Exames Nacioais EXME NCIONL DO ENSINO SECUNDÁRIO Decreto-Lei. /00, de 6 de Março Prova Escrita de Matemática. ao de Escolaridade Prova 6/.ª Fase Duração da Prova: 0 miutos. Tolerâcia: 0 miutos 008 VERSÃO
Exames Nacioais EXME NCIONL DO ENSINO SECUNDÁRIO Decreto-Lei. /00, de 6 de Março Prova Escrita de Matemática. ao de Escolaridade Prova 6/.ª Fase Duração da Prova: 0 miutos. Tolerâcia: 0 miutos 008 VERSÃO
ESTATÍSTICA E PROBABILIDADES
 ESTATÍSTICA E PROBABILIDADES Aluo(a): Turma: Professores: Data: Edu/Vicete Noções de Estatística Podemos eteder a Estatística como sedo o método de estudo de comportameto coletivo, cujas coclusões são
ESTATÍSTICA E PROBABILIDADES Aluo(a): Turma: Professores: Data: Edu/Vicete Noções de Estatística Podemos eteder a Estatística como sedo o método de estudo de comportameto coletivo, cujas coclusões são
DEPARTAMENTO DE MATEMÁTICA
 FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Camus de Lhaguee, Av. de Moçambique, km 1, Tel: +258 21401078, Fax: +258 21401082, Mauto Cursos de Liceciatura em Esio de Matemática
FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Camus de Lhaguee, Av. de Moçambique, km 1, Tel: +258 21401078, Fax: +258 21401082, Mauto Cursos de Liceciatura em Esio de Matemática
Problemas de Contagem
 Problemas de Cotagem Cotar em semre é fácil Pricíio Fudametal de Cotagem Se um certo acotecimeto ode ocorrer de 1 maeiras diferetes e se, aós este acotecimeto, um segudo ode ocorrer de 2 maeiras diferetes
Problemas de Cotagem Cotar em semre é fácil Pricíio Fudametal de Cotagem Se um certo acotecimeto ode ocorrer de 1 maeiras diferetes e se, aós este acotecimeto, um segudo ode ocorrer de 2 maeiras diferetes
CARACTERIZAÇÃO DO CONJUNTO EQUILIBRADOR PARA GRAFOS COM GAP NULO
 CARACTERIZAÇÃO DO CONJUNTO EQUILIBRADOR PARA GRAFOS COM GAP NULO Maximiliao Pito Damas Programa de Egeharia de Produção Uiversidade Federal do Rio de Jaeiro e-mail: maxdamas@hotmailcom Lilia Markezo Núcleo
CARACTERIZAÇÃO DO CONJUNTO EQUILIBRADOR PARA GRAFOS COM GAP NULO Maximiliao Pito Damas Programa de Egeharia de Produção Uiversidade Federal do Rio de Jaeiro e-mail: maxdamas@hotmailcom Lilia Markezo Núcleo
TEORIA DE SISTEMAS LINEARES
 Ageda. Algebra Liear (Parte II). Atividades V Profa. Dra. Letícia Maria Bolzai Poehls 8// Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação em
Ageda. Algebra Liear (Parte II). Atividades V Profa. Dra. Letícia Maria Bolzai Poehls 8// Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação em
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES BINÔMIO DE NEWTON
 Uiversidade Federal do Rio Grade FURG Istituto de Matemática, Estatística e Física IMEF Edital CAPES BINÔMIO DE NEWTON Prof. Atôio Maurício Medeiros Alves Profª Deise Maria Varella Martiez Matemática Básica
Uiversidade Federal do Rio Grade FURG Istituto de Matemática, Estatística e Física IMEF Edital CAPES BINÔMIO DE NEWTON Prof. Atôio Maurício Medeiros Alves Profª Deise Maria Varella Martiez Matemática Básica
CAPÍTULO 8. Exercícios Inicialmente, observamos que. não é série de potências, logo o teorema desta
 CAPÍTULO 8 Eercícios 8 Iicialmete, observamos que 0 ão é série de otêcias, logo o teorema desta seção ão se alica Como, ara todo 0, a série é geométrica e de razão, 0, etão a série coverge absolutamete
CAPÍTULO 8 Eercícios 8 Iicialmete, observamos que 0 ão é série de otêcias, logo o teorema desta seção ão se alica Como, ara todo 0, a série é geométrica e de razão, 0, etão a série coverge absolutamete
Estimadores de Momentos
 Estimadores de Mometos A média populacioal é um caso particular daquilo que chamamos de mometo. Na realidade, ela é o primeiro mometo. Se X for uma v.a. cotíua, com desidade f(x; θ 1,..., θ r ), depededo
Estimadores de Mometos A média populacioal é um caso particular daquilo que chamamos de mometo. Na realidade, ela é o primeiro mometo. Se X for uma v.a. cotíua, com desidade f(x; θ 1,..., θ r ), depededo
1. Revisão Matemática
 Sequêcias de Escalares Uma sequêcia { } diz-se uma sequêcia de Cauchy se para qualquer (depedete de ε ) tal que : ε > 0 algum K m < ε para todo K e m K Uma sequêcia { } diz-se ser limitada superiormete
Sequêcias de Escalares Uma sequêcia { } diz-se uma sequêcia de Cauchy se para qualquer (depedete de ε ) tal que : ε > 0 algum K m < ε para todo K e m K Uma sequêcia { } diz-se ser limitada superiormete
Taxas e Índices. Ana Maria Lima de Farias Dirce Uesu Pesco
 Taxas e Ídices Aa Maria Lima de Farias Dirce Uesu esco Itrodução Nesse texto apresetaremos coceitos básicos sobre ídices e taxas. Embora existam aplicações em diversos cotextos, essas otas utilizaremos
Taxas e Ídices Aa Maria Lima de Farias Dirce Uesu esco Itrodução Nesse texto apresetaremos coceitos básicos sobre ídices e taxas. Embora existam aplicações em diversos cotextos, essas otas utilizaremos
1 Cálculo combinatório e probabilidades
 álculo combiatório e robabilidades Ficha ara raticar A ( A B A ( A B Leis de De Morga Pág A ( A B B B ( A A B Proriedade associativa U B A A U U Elemeto absorvete ( A B B ( A B B Leis de De Morga ( A B
álculo combiatório e robabilidades Ficha ara raticar A ( A B A ( A B Leis de De Morga Pág A ( A B B B ( A A B Proriedade associativa U B A A U U Elemeto absorvete ( A B B ( A B B Leis de De Morga ( A B
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
CURSO DE MATEMÁTICA ANÁLISE COMBINATÓRIA & BINÔMIO DE NEWTON. a quantidade que atende ao enunciado:
 DISCIPLIN: SSUNO: SÉRIE UL CURSO DE MEMÁIC ÁLGEBR NÁLISE COMBINÓRI & BINÔMIO DE NEWON. (UERJ UENF ) Para motar um saduíche, os clietes de uma lachoete odem escolher: - um detre os tios de ão: calabresa,
DISCIPLIN: SSUNO: SÉRIE UL CURSO DE MEMÁIC ÁLGEBR NÁLISE COMBINÓRI & BINÔMIO DE NEWON. (UERJ UENF ) Para motar um saduíche, os clietes de uma lachoete odem escolher: - um detre os tios de ão: calabresa,
Técnicas de contagem 1 Introdução. 2 Sequências
 Istituto Suerior de Egeharia de Lisboa 1 Itrodução Muitos roblemas em Probabilidades e Estatística cosistem em estimar a icerteza associada a um eveto ou acotecimeto, o que imlica frequetemete determiar
Istituto Suerior de Egeharia de Lisboa 1 Itrodução Muitos roblemas em Probabilidades e Estatística cosistem em estimar a icerteza associada a um eveto ou acotecimeto, o que imlica frequetemete determiar
Economia da Informação e dos Incentivos Aplicada à Economia do Setor Público Aula 7 7. Sinalização: Akerlof
 Baseado em: Ecoomia da Iformação e dos Icetivos Alicada à Ecoomia do Setor Público 7. Sialização: Akerlof Akerlof, G. (970). The market for "lemos": Quality ucertaity ad the market mechaism, Quarterly
Baseado em: Ecoomia da Iformação e dos Icetivos Alicada à Ecoomia do Setor Público 7. Sialização: Akerlof Akerlof, G. (970). The market for "lemos": Quality ucertaity ad the market mechaism, Quarterly
INFERÊNCIA. Fazer inferência (ou inferir) = tirar conclusões
 INFERÊNCIA Fazer iferêcia (ou iferir) = tirar coclusões Iferêcia Estatística: cojuto de métodos de aálise estatística que permitem tirar coclusões sobre uma população com base em somete uma parte dela
INFERÊNCIA Fazer iferêcia (ou iferir) = tirar coclusões Iferêcia Estatística: cojuto de métodos de aálise estatística que permitem tirar coclusões sobre uma população com base em somete uma parte dela
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
FILAS PARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING PROBABILÍSTICO
 CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA PROBABILIDADES E ESTATÍSTICA
 INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA PROBABILIDADES E ESTATÍSTICA o Teste SEMESTRE PAR /7 Data: 3 de Juho de 7 Duração: h m Tóicos de Resolução.
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA PROBABILIDADES E ESTATÍSTICA o Teste SEMESTRE PAR /7 Data: 3 de Juho de 7 Duração: h m Tóicos de Resolução.
pertencente a um plano e um vetor n ( a, do plano [obviamente que P é ortogonal [normal] a qualquer vetor pertencente ao plano.
![pertencente a um plano e um vetor n ( a, do plano [obviamente que P é ortogonal [normal] a qualquer vetor pertencente ao plano. pertencente a um plano e um vetor n ( a, do plano [obviamente que P é ortogonal [normal] a qualquer vetor pertencente ao plano.](/thumbs/92/108125021.jpg) ESTUDO DO PLNO NO ESPÇO R 3 euação de um lao [o R 3 ] ode ser escrita de várias formas, sedo ue cada uma delas tem suas vatages uato à sua escolha e alicação. São elas: Euação Geral do Plao Euação Segmetária
ESTUDO DO PLNO NO ESPÇO R 3 euação de um lao [o R 3 ] ode ser escrita de várias formas, sedo ue cada uma delas tem suas vatages uato à sua escolha e alicação. São elas: Euação Geral do Plao Euação Segmetária
Teoria Microeconômica Avançada
 Teoria Microecoômica Avaçada Prof. Maurício Bugari Eco/UB 05-II Sialização: Akerlof Baseado em: Akerlof, G. (970). The market for "lemos": Quality ucertaity ad the market mechaism, Quarterly Joural of
Teoria Microecoômica Avaçada Prof. Maurício Bugari Eco/UB 05-II Sialização: Akerlof Baseado em: Akerlof, G. (970). The market for "lemos": Quality ucertaity ad the market mechaism, Quarterly Joural of
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA
 UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 206 Macroecoomia I 1º Semestre de 2018 Professor Ferado Rugitsky Lista de Exercícios 3 [1] Cosidere
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DEPARTAMENTO DE ECONOMIA EAE 206 Macroecoomia I 1º Semestre de 2018 Professor Ferado Rugitsky Lista de Exercícios 3 [1] Cosidere
ANÁLISE MULTIVARIADA DE DADOS: ESTUDOS PRELIMINARES À ANÁLISE FATORIAL CONFIRMATÓRIA (AFC)
 ANÁLISE MULTIVARIADA DE DADOS: ESTUDOS PRELIMINARES À ANÁLISE FATORIAL CONFIRMATÓRIA (AFC Débora Ferada Satos Datas (; Mylea Baia de Sousa (; Gilberto da Silva Matos (3 ( / ( Uiversidade Federal de Camia
ANÁLISE MULTIVARIADA DE DADOS: ESTUDOS PRELIMINARES À ANÁLISE FATORIAL CONFIRMATÓRIA (AFC Débora Ferada Satos Datas (; Mylea Baia de Sousa (; Gilberto da Silva Matos (3 ( / ( Uiversidade Federal de Camia
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO
 O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
 Idetifique todas as folhas Folhas ão idetificadas NÃO SERÃO COTADAS Faculdade de Ecoomia Uiversidade Nova de Lisboa EXAME DE CÁLCULO I Ao Lectivo 009-0 - º Semestre Eame Fial de ª Época em 0 de Jaeiro
Idetifique todas as folhas Folhas ão idetificadas NÃO SERÃO COTADAS Faculdade de Ecoomia Uiversidade Nova de Lisboa EXAME DE CÁLCULO I Ao Lectivo 009-0 - º Semestre Eame Fial de ª Época em 0 de Jaeiro
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
- Nominal: não há aspecto quantitativo. - Classificar espécies biológicas por nomes.
 Uiversidade Federal de Alagoas Istituto de Ciêcias e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Viícius Careiro Vital 1. Escalas. - Nomial: ão há asecto quatitativo. - Classificar esécies
Uiversidade Federal de Alagoas Istituto de Ciêcias e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Viícius Careiro Vital 1. Escalas. - Nomial: ão há asecto quatitativo. - Classificar esécies
Combinações simples e com repetição - Teoria. a combinação de m elementos tomados p a p. = (*) (a divisão por p! desconta todas as variações.
 obiações siles - Defiição obiações siles e co reetição - Teoria osidereos u cojuto X co eleetos distitos. No artigo Pricíios Multilicativos e Arrajos - Teoria, aredeos a calcular o úero de arrajos de eleetos
obiações siles - Defiição obiações siles e co reetição - Teoria osidereos u cojuto X co eleetos distitos. No artigo Pricíios Multilicativos e Arrajos - Teoria, aredeos a calcular o úero de arrajos de eleetos
CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA
 Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
1ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE 222) Prof. Benito Olivares 1 o Sem./ 2017
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE ) Prof. Beito Olivares o Sem./ 7. Classifique e costrua uma trajetória
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE ) Prof. Beito Olivares o Sem./ 7. Classifique e costrua uma trajetória
Amostragem 04/08/2014. Conceito, propriedades, métodos e cálculo. Conceitos básicos de População e Amostra. Qualidade. População;
 04/08/014 Uidade 4 : Amostragem Amostragem Coceito, propriedades, métodos e cálculo João Garibaldi Almeida Viaa Coceitos básicos de População e Amostra População; Elemetos que compõem uma população; Ceso;
04/08/014 Uidade 4 : Amostragem Amostragem Coceito, propriedades, métodos e cálculo João Garibaldi Almeida Viaa Coceitos básicos de População e Amostra População; Elemetos que compõem uma população; Ceso;
CAPITULO V. NOÇÕES TOPOLÓGICAS E SUCESSÕES EM R n
 CAPITULO V NOÇÕES TOPOLÓGICAS E SUCESSÕES EM R 1. Distâcias e vizihaças Dado um esaço vectorial E sobre o coro R dos úmeros reais, chama-se orma a qualquer alicação x x de E em R + {0} que verifique as
CAPITULO V NOÇÕES TOPOLÓGICAS E SUCESSÕES EM R 1. Distâcias e vizihaças Dado um esaço vectorial E sobre o coro R dos úmeros reais, chama-se orma a qualquer alicação x x de E em R + {0} que verifique as
Objetivo Estimar uma proporção p (desconhecida) de elementos uma população, apresentando certa característica de interesse, partir
 Objetivo Estimar uma roorção (descohecida) de elemetos em uma oulação, aresetado certa característica de iteresse, a artir da iformação forecida or uma amostra. Exemlos: : roorção de aluos da USP que foram
Objetivo Estimar uma roorção (descohecida) de elemetos em uma oulação, aresetado certa característica de iteresse, a artir da iformação forecida or uma amostra. Exemlos: : roorção de aluos da USP que foram
Séries e Equações Diferenciais Lista 02 Séries Numéricas
 Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
AULA Subespaço, Base e Dimensão Subespaço.
 Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
(aulas de 14/11/2014 e 18/11/2014) (Observação: esta aula será complementada e ilustrada no quadro de aula)
 Uiversidade do Estado do Rio de Jaeiro UERJ Istituto de atemática e Estatística Deartameto de Estatística Discilia: Processos Estocásticos I Professor: arcelo Rubes (aulas de 4//24 e 8//24) (Observação:
Uiversidade do Estado do Rio de Jaeiro UERJ Istituto de atemática e Estatística Deartameto de Estatística Discilia: Processos Estocásticos I Professor: arcelo Rubes (aulas de 4//24 e 8//24) (Observação:
arxiv: v1 [math.ho] 3 Sep 2014
![arxiv: v1 [math.ho] 3 Sep 2014 arxiv: v1 [math.ho] 3 Sep 2014](/thumbs/69/60238720.jpg) Álbum de figurihas da Copa do Mudo: uma abordagem via Cadeias de Markov Leadro Morgado IMECC, Uiversidade Estadual de Campias arxiv:409.260v [math.ho] 3 Sep 204 Cosiderações iiciais 6 de maio de 204 Com
Álbum de figurihas da Copa do Mudo: uma abordagem via Cadeias de Markov Leadro Morgado IMECC, Uiversidade Estadual de Campias arxiv:409.260v [math.ho] 3 Sep 204 Cosiderações iiciais 6 de maio de 204 Com
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Stela Adami Vayego DEST/UFPR
 Resumo 3 Resumo dos dados uméricos por meio de úmeros. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico dessa
Resumo 3 Resumo dos dados uméricos por meio de úmeros. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico dessa
Equilíbrio Químico Constante de Equilíbrio Princípio de Le Chatelier
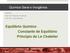 Química Geral e Iorgâica QGI0001 Eg a. de Produção e Sistemas Prof a. Dr a. Carla Dalmoli Equilíbrio Químico Costate de Equilíbrio Pricíio de Le Chatelier Eergia Livre de Gibbs Existem três codições imortates:
Química Geral e Iorgâica QGI0001 Eg a. de Produção e Sistemas Prof a. Dr a. Carla Dalmoli Equilíbrio Químico Costate de Equilíbrio Pricíio de Le Chatelier Eergia Livre de Gibbs Existem três codições imortates:
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
1- Resolução de Sistemas Lineares.
 MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
Esta folha é para si, arranque-a e leve-a consigo.
 Esta folha é para si, arraque-a e leve-a cosigo. Os aluos poderão ser pealizados por apresetação ilegível das resoluções (gatafuhos, riscos, hieróglifos, pituras rupestres, etc.) EXAME DE CÁLCULO I / Ao
Esta folha é para si, arraque-a e leve-a cosigo. Os aluos poderão ser pealizados por apresetação ilegível das resoluções (gatafuhos, riscos, hieróglifos, pituras rupestres, etc.) EXAME DE CÁLCULO I / Ao
DETERMINANDO A SIGNIFICÂNCIA ESTATÍSTICA PARA AS DIFERENÇAS ENTRE MÉDIAS
 DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS lag@if.ufrgs.br O objetivo desse texto é apresetar através de exemplos uméricos como se
DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS lag@if.ufrgs.br O objetivo desse texto é apresetar através de exemplos uméricos como se
Fundamentos de Análise Matemática Profª Ana Paula. Números reais
 Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
A DESIGUALDADE DE CHEBYCHEV
 A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
MT DEPARTAMENTO NACIONAL DE ESTRADAS DE RODAGEM. Norma Rodoviária DNER-PRO 277/97 Procedimento Página 1 de 8
 Norma Rodoviária DNER-PRO 77/97 Procedimeto Págia de 8 RESUMO Este documeto estabelece o úmero de amostras a serem utilizadas o cotrole estatístico, com base em riscos refixados, em obras e serviços rodoviários.
Norma Rodoviária DNER-PRO 77/97 Procedimeto Págia de 8 RESUMO Este documeto estabelece o úmero de amostras a serem utilizadas o cotrole estatístico, com base em riscos refixados, em obras e serviços rodoviários.
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
Capítulo 5- Introdução à Inferência estatística. (Versão: para o manual a partir de 2016/17)
 Capítulo 5- Itrodução à Iferêcia estatística. (Versão: para o maual a partir de 2016/17) 1.1) Itrodução.(222)(Vídeo 39) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar
Capítulo 5- Itrodução à Iferêcia estatística. (Versão: para o maual a partir de 2016/17) 1.1) Itrodução.(222)(Vídeo 39) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar
Estimação por Intervalo (Intervalos de Confiança):
 Estimação por Itervalo (Itervalos de Cofiaça): 1) Itervalo de Cofiaça para a Média Populacioal: Muitas vezes, para obter-se a verdadeira média populacioal ão compesa fazer um levatameto a 100% da população
Estimação por Itervalo (Itervalos de Cofiaça): 1) Itervalo de Cofiaça para a Média Populacioal: Muitas vezes, para obter-se a verdadeira média populacioal ão compesa fazer um levatameto a 100% da população
Preliminares 1. 1 lim sup, lim inf. Medida e Integração. Departamento de Física e Matemática. USP-RP. Prof. Rafael A. Rosales. 8 de março de 2009.
 Medida e Itegração. Departameto de Física e Matemática. USP-RP. Prof. Rafael A. Rosales 8 de março de 2009. 1 lim sup, lim if Prelimiares 1 Seja (x ), N, uma seqüêcia de úmeros reais, e l o limite desta
Medida e Itegração. Departameto de Física e Matemática. USP-RP. Prof. Rafael A. Rosales 8 de março de 2009. 1 lim sup, lim if Prelimiares 1 Seja (x ), N, uma seqüêcia de úmeros reais, e l o limite desta
SUCESSÕES DE NÚMEROS REAIS. Sucessões
 SUCESSÕES DE NÚMEROS REAIS Sucessões Chama-se sucessão de úmeros reais ou sucessão em IR a toda a aplicação f do cojuto IN dos úmeros aturais em IR, f : IN IR f ( ) = x IR Chamamos termos da sucessão aos
SUCESSÕES DE NÚMEROS REAIS Sucessões Chama-se sucessão de úmeros reais ou sucessão em IR a toda a aplicação f do cojuto IN dos úmeros aturais em IR, f : IN IR f ( ) = x IR Chamamos termos da sucessão aos
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina: Algumas Distribuições
 Deartameto de Iformática Discilia: do Desemeho de Sistemas de Comutação Algumas Distribuições Algumas Distribuições Discretas Prof. Sérgio Colcher colcher@if.uc-rio.br Coyright 999-8 by TeleMídia Lab.
Deartameto de Iformática Discilia: do Desemeho de Sistemas de Comutação Algumas Distribuições Algumas Distribuições Discretas Prof. Sérgio Colcher colcher@if.uc-rio.br Coyright 999-8 by TeleMídia Lab.
O QUE HÁ DE ERRADO COM O MERCADO ACIONÁRIO BRASILEIRO? - COMPARAÇÃO ENTRE OS RETORNOS MÉDIOS DO IBOVESPA E DO CDI NO PERÍODO DE 1986 A 2004
 V I I S E M E A D P E S Q U I S A Q U A N T I T A T I V A F I N A N Ç A S O QUE HÁ DE ERRADO COM O MERCADO ACIONÁRIO BRASILEIRO? - COMPARAÇÃO ENTRE OS RETORNOS MÉDIOS DO IBOVESPA E DO CDI NO PERÍODO DE
V I I S E M E A D P E S Q U I S A Q U A N T I T A T I V A F I N A N Ç A S O QUE HÁ DE ERRADO COM O MERCADO ACIONÁRIO BRASILEIRO? - COMPARAÇÃO ENTRE OS RETORNOS MÉDIOS DO IBOVESPA E DO CDI NO PERÍODO DE
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
BINÔMIO DE NEWTON. O desenvolvimento da expressão 2. a b é simples, pois exige somente quatro multiplicações e uma soma:
 07 BINÔMIO DE NEWTON O desevolvimeto da epressão a b é simples, pois eige somete quatro multiplicações e uma soma: a b a b a b a ab ba b a ab b O desevolvimeto de a b é uma tarefa um pouco mais trabalhosa,
07 BINÔMIO DE NEWTON O desevolvimeto da epressão a b é simples, pois eige somete quatro multiplicações e uma soma: a b a b a b a ab ba b a ab b O desevolvimeto de a b é uma tarefa um pouco mais trabalhosa,
Resolva os grupos do exame em folhas separadas. O uso de máquinas de calcular e telemóveis não é permitido. Não se esqueça que tudo é para justificar.
 Eame em 6 de Jaeiro de 007 Cálculo ATENÇÃO: FOLHAS DE EXAME NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eame fial 06 Jaeiro de 007 Resolva os grupos do eame em folhas separadas O uso de máquias de calcular
Eame em 6 de Jaeiro de 007 Cálculo ATENÇÃO: FOLHAS DE EXAME NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eame fial 06 Jaeiro de 007 Resolva os grupos do eame em folhas separadas O uso de máquias de calcular
Aula 3 : Somatórios & PIF
 Aula 3 : Somatórios & PIF Somatório: Somatório é um operador matemático que os permite represetar facilmete somas de um grade úmero de parcelas É represetado pela letra maiúscula do alfabeto grego sigma
Aula 3 : Somatórios & PIF Somatório: Somatório é um operador matemático que os permite represetar facilmete somas de um grade úmero de parcelas É represetado pela letra maiúscula do alfabeto grego sigma
Caderno de Exercício 2
 1 Cadero de Exercício Estimação Potual e Itervalos de Cofiaça 1. Exercícios Aulas 1. Exercício 8.6 do livro Statistics for Ecoomics ad Busiess. O úmero de adares vedidos em cada dia por uma empresa imobiliária
1 Cadero de Exercício Estimação Potual e Itervalos de Cofiaça 1. Exercícios Aulas 1. Exercício 8.6 do livro Statistics for Ecoomics ad Busiess. O úmero de adares vedidos em cada dia por uma empresa imobiliária
Análise Matemática I 2 o Exame
 Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
1.4 Determinantes. determinante é igual ao produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária.
 1.4 Determiates A teoria dos determiates surgiu quase simultaeamete a Alemaha e o Japão. Ela foi desevolvida por dois matemáticos, Gottfried Wilhelm Leibiz (1642-1716) e Seki Shisuke Kowa (1642-1708),
1.4 Determiates A teoria dos determiates surgiu quase simultaeamete a Alemaha e o Japão. Ela foi desevolvida por dois matemáticos, Gottfried Wilhelm Leibiz (1642-1716) e Seki Shisuke Kowa (1642-1708),
Capítulo 5- Introdução à Inferência estatística.
 Capítulo 5- Itrodução à Iferêcia estatística. 1.1) Itrodução.(184) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar coclusões acerca da população de ode se extraiu a amostra.
Capítulo 5- Itrodução à Iferêcia estatística. 1.1) Itrodução.(184) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar coclusões acerca da população de ode se extraiu a amostra.
CÁLCULO DO ÍNDICE DO CUSTO DA CESTA BÁSICA EM ANÁPOLIS, NO PERÍODO DE SETEMBRO DE 2008 A AGOSTO DE 2009
 CÁLCULO DO ÍNDICE DO CUSTO DA CESTA BÁSICA EM ANÁOLIS, NO ERÍODO DE SETEMBRO DE 2008 A AGOSTO DE 2009 Walquiria Cardoso de Brito 1 ;Reato Lopes dos Satos 2 ; Eliezer da Silva Freitas 2 ; Luís Ferado Barbosa
CÁLCULO DO ÍNDICE DO CUSTO DA CESTA BÁSICA EM ANÁOLIS, NO ERÍODO DE SETEMBRO DE 2008 A AGOSTO DE 2009 Walquiria Cardoso de Brito 1 ;Reato Lopes dos Satos 2 ; Eliezer da Silva Freitas 2 ; Luís Ferado Barbosa
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais Tarefa º. Desta figura, do trabalho da Olívia e da Susaa, retire duas sequêcias e imagie o processo
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais Tarefa º. Desta figura, do trabalho da Olívia e da Susaa, retire duas sequêcias e imagie o processo
Stela Adami Vayego DEST/UFPR
 Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Resumo 3 Resumo dos dados uméricos por meio de úmeros 1. Medidas de Tedêcia Cetral A tedêcia cetral da distribuição de freqüêcias de uma variável em um cojuto de dados é caracterizada pelo valor típico
Cadeias de Markov Parte I
 Cadeias de Markov arte I Defiições e Notações Defiição : Um rocesso de Markov {X t } é um processo estocástico que, dado o valor X t, os valores de X s para s>t ão são iflueciados pelos valores de X u,
Cadeias de Markov arte I Defiições e Notações Defiição : Um rocesso de Markov {X t } é um processo estocástico que, dado o valor X t, os valores de X s para s>t ão são iflueciados pelos valores de X u,
INTERVALOS DE CONFIANÇA
 INTRVALOS D CONFIANÇA stimação or itervalos,, é uma amostra aleatória de uma variável cuja distribuição deede do arâmetro Se L(,, e U(,, são duas fuções tais que L < U e P(L U =, o itervalo [L, U] é chamado
INTRVALOS D CONFIANÇA stimação or itervalos,, é uma amostra aleatória de uma variável cuja distribuição deede do arâmetro Se L(,, e U(,, são duas fuções tais que L < U e P(L U =, o itervalo [L, U] é chamado
Fundamentos de Análise Matemática Profª Ana Paula. Sequência Infinitas
 Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
OMBRO-CABEÇA-OMBRO : TESTANDO A LUCRATIVIDADE DO PADRÃO GRÁFICO DE ANÁLISE TÉCNICA NO MERCADO DE AÇÕES BRASILEIRO
 Caro parecerista, Agradecemos as sugestões e críticas ao osso artigo, as quais procuramos observar a revisão do artigo. A seguir você ecotrará um relatório descrevedo todos os ajustes realizados, a ordem
Caro parecerista, Agradecemos as sugestões e críticas ao osso artigo, as quais procuramos observar a revisão do artigo. A seguir você ecotrará um relatório descrevedo todos os ajustes realizados, a ordem
O teste de McNemar. A tabela 2x2. Depois - Antes
 Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ viali@pucrs.br O teste de McNemar O teste de McNemar para a sigificâcia de mudaças é particularmete aplicável aos experimetos do tipo "ates e depois"
Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ viali@pucrs.br O teste de McNemar O teste de McNemar para a sigificâcia de mudaças é particularmete aplicável aos experimetos do tipo "ates e depois"
TRANSFORMAÇÕES LINEARES
 rasformação Liear NSFOMÇÕES LINEES Sejam e espaços vetoriais reais Dizemos que uma fução : é uma trasformação liear se a fução preserva as operações de adição e de multiplicação por escalar isto é se os
rasformação Liear NSFOMÇÕES LINEES Sejam e espaços vetoriais reais Dizemos que uma fução : é uma trasformação liear se a fução preserva as operações de adição e de multiplicação por escalar isto é se os
Professor: Carlos Eugênio da Costa Finanças Públicas Monitor: Alexandre Sollaci
 Professor: Carlos Eugênio da Costa Finanças Públicas - 03 Monitor: Alexandre Sollaci EBEF/FGV Lista - Revisão de Microeconomia Questão. Mostre que no caso de referências quase-lineares temos a igualdade
Professor: Carlos Eugênio da Costa Finanças Públicas - 03 Monitor: Alexandre Sollaci EBEF/FGV Lista - Revisão de Microeconomia Questão. Mostre que no caso de referências quase-lineares temos a igualdade
1 a Lista de PE Solução
 Uiversidade de Brasília Departameto de Estatística 1 a Lista de PE Solução 1. a) Qualitativa omial. b) Quatitativa discreta. c) Quatitativa discreta. d) Quatitativa cotíua. e) Quatitativa cotíua. f) Qualitativa
Uiversidade de Brasília Departameto de Estatística 1 a Lista de PE Solução 1. a) Qualitativa omial. b) Quatitativa discreta. c) Quatitativa discreta. d) Quatitativa cotíua. e) Quatitativa cotíua. f) Qualitativa
1 Cálculo combinatório e probabilidades
 álculo combiatório e robabilidades Atividade de diagóstico.. a) A { x Z: x x 0 0} ± + 0 x x 0 0 x ± x x x A {,,,,, 0,,,,,, } b) B { x R: x x } x x x x x x x + 9 Pág... a) Afirmação verdadeira b) Afirmação
álculo combiatório e robabilidades Atividade de diagóstico.. a) A { x Z: x x 0 0} ± + 0 x x 0 0 x ± x x x A {,,,,, 0,,,,,, } b) B { x R: x x } x x x x x x x + 9 Pág... a) Afirmação verdadeira b) Afirmação
Disciplina: MATEMÁTICA Turma: 3º Ano Professor (a) : CÉSAR LOPES DE ASSIS INTRODUÇÃO A ESTATÍSTICA. Organização de dados
 Escola SESI de Aápolis - Judiaí Aluo (a): Disciplia: MATEMÁTICA Turma: 3º Ao Professor (a) : CÉSAR LOPES DE ASSIS Data: INTRODUÇÃO A ESTATÍSTICA A Estatística é o ramo da Matemática que coleta, descreve,
Escola SESI de Aápolis - Judiaí Aluo (a): Disciplia: MATEMÁTICA Turma: 3º Ao Professor (a) : CÉSAR LOPES DE ASSIS Data: INTRODUÇÃO A ESTATÍSTICA A Estatística é o ramo da Matemática que coleta, descreve,
Objetivo. Estimar a média de uma variável aleatória X, que representa uma característica de interesse de uma população, a partir de uma amostra.
 Objetivo Estimar a média de uma variável aleatória X, que represeta uma característica de iteresse de uma população, a partir de uma amostra. Exemplos: : peso médio de homes a faixa etária de 20 a 30 aos,
Objetivo Estimar a média de uma variável aleatória X, que represeta uma característica de iteresse de uma população, a partir de uma amostra. Exemplos: : peso médio de homes a faixa etária de 20 a 30 aos,
n O que é economia? n Princípios de um modelo: n Tudo o mais constante n Os consumidores tentam maximizar as suas utilidades
 MICROECONOMIA PARA CONCURSOS Prof. Daiel da Mata MICROECONOMIA PARA CONCURSOS Itrodução Prof. Daiel da Mata A ecoomia faz parte de ossas vidas...... As forças ecoômicas impactam o osso dia-a-dia Via impostos,
MICROECONOMIA PARA CONCURSOS Prof. Daiel da Mata MICROECONOMIA PARA CONCURSOS Itrodução Prof. Daiel da Mata A ecoomia faz parte de ossas vidas...... As forças ecoômicas impactam o osso dia-a-dia Via impostos,
Sumário. 2 Índice Remissivo 17
 i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
Probabilidades e Estatística TODOS OS CURSOS
 Duração: 90 miutos Gruo I Probabilidades e Estatística TODOS OS CURSOS Justifique coveietemete todas as resostas 1 o semestre 2017/2018 30/01/2018 15:00 2 o Teste C 10 valores 1. A variável aleatória X
Duração: 90 miutos Gruo I Probabilidades e Estatística TODOS OS CURSOS Justifique coveietemete todas as resostas 1 o semestre 2017/2018 30/01/2018 15:00 2 o Teste C 10 valores 1. A variável aleatória X
Dinâmica Estocástica
 Diâmica Estocástica Aula matriz Estocástica Balaceameto Detalhado Ifusp setembro de 6 Bibliografia: Capítulo 6 Diâmica estocástica e Irreversibilidade Tâia Tomé e Mário J. de Oliveira Edusp 4. Markov Adrei
Diâmica Estocástica Aula matriz Estocástica Balaceameto Detalhado Ifusp setembro de 6 Bibliografia: Capítulo 6 Diâmica estocástica e Irreversibilidade Tâia Tomé e Mário J. de Oliveira Edusp 4. Markov Adrei
Dessa forma, concluímos que n deve ser ímpar e, como 120 é par, então essa sequência não possui termo central.
 Resoluções das atividades adicioais Capítulo Grupo A. a) a 9, a 7, a 8, a e a 79. b) a, a, a, a e a.. a) a, a, a, a 8 e a 6. 9 b) a, a 6, a, a 9 e a.. Se a 9 e a k são equidistates dos extremos, etão existe
Resoluções das atividades adicioais Capítulo Grupo A. a) a 9, a 7, a 8, a e a 79. b) a, a, a, a e a.. a) a, a, a, a 8 e a 6. 9 b) a, a 6, a, a 9 e a.. Se a 9 e a k são equidistates dos extremos, etão existe
1. Definição e conceitos básicos de equações diferenciais
 Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Escola de Engenharia de Lorena EEL USP Departamento de Engenharia Química DEQUI Disciplina: Normalização e Controle da Qualidade NCQ
 1 Escola de Egeharia de orea EE SP Departameto de Egeharia Química DEQI Disciplia: Normalização e Cotrole da Qualidade NCQ Capítulo : Amostragem por Variáveis (MI STD 1) SEÇÃO A.1 Objetivo Este capítulo
1 Escola de Egeharia de orea EE SP Departameto de Egeharia Química DEQI Disciplia: Normalização e Cotrole da Qualidade NCQ Capítulo : Amostragem por Variáveis (MI STD 1) SEÇÃO A.1 Objetivo Este capítulo
Problema de Fluxo de Custo Mínimo
 Problema de Fluo de Custo Míimo The Miimum Cost Flow Problem Fluo de Custo Míimo O Problema de Fluo de Custo Míimo (The Miimum Cost Flow Problem) Este problema possui papel pricipal etre os modelos de
Problema de Fluo de Custo Míimo The Miimum Cost Flow Problem Fluo de Custo Míimo O Problema de Fluo de Custo Míimo (The Miimum Cost Flow Problem) Este problema possui papel pricipal etre os modelos de
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p
 ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
Parte 3: Gráfico de Gestão de Estoque. Gráficos e Cálculos Fundamentais
 Capítulo 3: Gestão de stoques Curso de Admiistração de mpresas 2º Semestre 09 Disciplia: Admiistração da Logística e Patrimôio Capítulo 03: Gestão de estoques (Partes 3 e 4) Parte : Itrodução Parte 2:
Capítulo 3: Gestão de stoques Curso de Admiistração de mpresas 2º Semestre 09 Disciplia: Admiistração da Logística e Patrimôio Capítulo 03: Gestão de estoques (Partes 3 e 4) Parte : Itrodução Parte 2:
OPERAÇÃO 1 OPERAÇÃO 2 OPERAÇÃO 3 OPERAÇÃO mês 10% a.m. 100,00 110,00 121,00
 Módulo 7 J uros Compostos Os juros compostos são cohecidos, popularmete, como juros sobre juros. 7.1 Itrodução: Etedemos por juros compostos quado o fial de cada período de capitalização, os redimetos
Módulo 7 J uros Compostos Os juros compostos são cohecidos, popularmete, como juros sobre juros. 7.1 Itrodução: Etedemos por juros compostos quado o fial de cada período de capitalização, os redimetos
6.1 Estimativa de uma média populacional: grandes amostras. Definição: Um estimador é uma característica amostral (como a média amostral
 6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6. Testes de Hipóteses Conceitos Gerais
 6. Testes de Hipóteses Coceitos Gerais Este capitulo itrodutório, pretede apresetar todas as defiições e todo o vocabulário utilizado em testes de hipóteses. Em um primeiro mometo, talvez você fique um
6. Testes de Hipóteses Coceitos Gerais Este capitulo itrodutório, pretede apresetar todas as defiições e todo o vocabulário utilizado em testes de hipóteses. Em um primeiro mometo, talvez você fique um
Análise de Informação Económica e Empresarial Prova Época Normal 17 de Junho de 2013 Duração: 2h30m (150 minutos)
 Desidade Liceciaturas Ecoomia/Fiaças/Gestão 1º Ao Ao lectivo de 01-013 Aálise de Iformação Ecoómica e Empresarial Prova Época ormal 17 de Juho de 013 Duração: h30m (150 miutos) Respoda aos grupos em Folhas
Desidade Liceciaturas Ecoomia/Fiaças/Gestão 1º Ao Ao lectivo de 01-013 Aálise de Iformação Ecoómica e Empresarial Prova Época ormal 17 de Juho de 013 Duração: h30m (150 miutos) Respoda aos grupos em Folhas
