Axioma de Arquimedes: sintético a priori ou empírico?

Transcrição

1 Axioma de Arquimedes: sintético a priori ou empírico? Rafael Tavares Juliani Doutorando - HCTE/UFRJ e bolsista Capes E-mal: rafaeljuliani@gmail.com Francisco Caruso Professor - CBPF, UERJ e HCTE/UFRJ francisco.caruso@gmail.com Resumo Um crescente número de pensadores tem rompido com a dicotomia entre a Física e a Matemática, em relação à experiência. Mas será a Matemática empírica de fato ou seus juízos são sintéticos a priori? No âmbito desta ampla discussão, focaliza-se aqui uma questão pontual: O que se pode dizer do axioma de Arquimedes, o qual foi julgado como empírico por Hilbert? É verdade que o axioma arquimediano não parece ser uma afirmação puramente matemática, por isso, resta saber se sua validade depende apenas de uma intuição dos conceitos presentes no axioma ou se sua validade vem da experiência. Dessa forma, é feita uma análise sobre o axioma arquimediano quanto às suas formulações e aos seus usos na história da Matemática, a fim de verificar a possibilidade de uma intuição da maneira sugerida por Kant. Palavras-chave Axioma de Arquimedes, empirismo, Matemática empírica, sintéticos a priori. Introdução Apesar de a Matemática ser conceituada por muitos como um saber imutável e independente do mundo sensível e dos desejos humanos, já na Antiguidade, Arquimedes usava seus conhecimentos de Estática para encontrar a medida da área de alguns objetos

2 geométricos. Contudo, acreditava-se que o método de Arquimedes era apenas heurístico, visto que na Matemática desenvolvida atualmente não se usa qualquer princípio de Mecânica. Ou seja, tais métodos estariam no contexto da descoberta, enquanto que hoje em dia só se usaria o contexto da justificação, livre de métodos empíricos. No entanto, com o passar dos tempos, cada vez mais os novos pensadores aproximam a Matemática do mundo sensível ou, pelo menos, argumentam que ela estaria relacionada a algum tipo de empirismo. Stuart Mill ( ) sustentava que a Matemática é empírica, mas seus argumentos eram bastante teóricos e não convenciam, pois muitas questões da aparente necessidade e universalidade da Matemática precisavam ainda ser respondidas (DA SILVA, 2007). Já Lakatos ( ) nos oferece inúmeros exemplos nos quais os conceitos da Matemática passam por diversas revisões de acordo com a necessidade e as novas descobertas da pesquisa matemática (LAKATOS, 1977). Além de Lakatos apresentar o caráter dinâmico dos conceitos matemáticos, Quine ( ) pensa em uma Matemática empírica, ao defender seu argumento de indispensabilidade, com o qual pretende justificar a Matemática como válida por ser indispensável às boas teorias científicas. Além disso, Quine também sustenta que todas as afirmações de um sistema, mesmo as afirmações conhecidas como a priori, passam pelo crivo da experimentação em uma revisão do sistema (QUINE, 1961). Assim, para Quine, a distinção entre a priori e a posteriori só existe como uma forma de organização estrutural, pois, o que é a priori em um sistema já foi a posteriori em um outro sistema ou, pelo menos, consultou-se a experiência para aceitá-lo como a priori de um sistema. Além desses pensadores citados, pode-se recorrer a um contemporâneo e colaborador do HCTE 1 : Gregory Chatin, o qual defende uma ruptura na distinção entre a Física e a Matemática, no que diz respeito a experimentação. Em minha opinião, a concepção de que a matemática proporciona certeza absoluta e é estática e perfeita, enquanto a física é de natureza experimental e evolui 1 HCTE - Programa de Pós-Graduação Strictu Sensu em História das Ciências e das Técnicas e Epistemologia da Universidade Federal do Rio de Janeiro (UFRJ).

3 constantemente, constitui uma falsa dicotomia. Na realidade, a matemática não difere em nada da física. Ambas são tentativas da mente humana com o fito de organizar e dar sentido à experiência humana; no caso da física, experiência no laboratório, no mundo físico; no caso da matemática, experiência no computador, na área mental da imaginação da matemática pura. (CHAITIN, 2005). Essa afirmação de Chaitin é emblemática, pois parece sugerir que a atual defesa da empiria na Matemática não está no mundo sensível. A argumentação de Lakatos se baseia em problemas internos à Matemática, embora, em última instância, as mudanças apontadas por Lakatos possam ser motivadas por questões do mundo sensível. A falsa distinção entre a priori e a posteriori defendida por Quine, porém, indica uma possível empiria no mundo sensível. No entanto, Quine não apresenta exemplos ou uma análise sobre algum caso na Matemática. Assim, não fica claro se existe empiria na Matemática ou se estamos diante dos famosos "sintéticos a priori" de Kant. Kant ( ) procurou mostrar que a Física teórica não é dependente da experimentação e que nem a Matemática é um conhecimento livre do mundo sensível como acontecia na filosofia escolástica, na qual se discutia o sexo dos anjos. Para isso, Kant sustentou a existência dos sintéticos a priori e, com isso, foi o primeiro a apresentar argumentos fortes sobre a dependência que a Matemática tem, ou precisa ter, do mundo sensível. É muito provável que o logicismo de Frege ( ) tenha sido uma tentativa de resposta aos sintéticos a priori de Kant. "Então é manifesto que o predicado está sempre, necessariamente, aderente a esses conceitos, não como pensado no próprio conceito, antes mediante uma intuição que tem de ser acrescentada ao conceito." (KANT, 2001) Os sintéticos a priori são aqueles juízos que tem a universalidade e a necessidade, que são característicos de um juízo a priori, mas que a relação entre o sujeito e o predicado não provem nem dos conceitos em si e nem da experiência, e sim da intuição que temos do mundo sensível. Poder-se-ia começar questionando a "universalidade" e a "necessidade" atribuídas aos juízos matemáticos; no entanto, não só muitos filósofos, assim como muitos matemáticos admitem essas características e, então, não abordaremos estas questões por enquanto. Voltemos à questão sobre o método de Arquimedes.

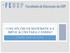
4 O Método de Arquimedes Se a falsa distinção entre a priori e a posteriori de Quine estiver correta, talvez seja possível encontrar algum falso a priori no cálculo de áreas da matemática moderna, visto que algum axioma possa ser oriundo do método empírico de Arquimedes. Tal axioma estaria camuflado e não seria explicitamente empírico, obviamente. Em seu trabalho Quadratura da Parábola (ARQUIMEDES, 1897), Arquimedes se utiliza de uma balança mental. Para descobrir a área de um segmento parabólico, ele constrói dois triângulos: um que circunscreve e outro que é inscrito no segmento parabólico. Supondo que as figuras planas são compostas pela soma de todos os segmentos de linhas que podem ser traçadas dentro dessas figuras e, também, que essas figuras têm um peso proporcional à sua área, Arquimedes colocou as linhas que formam o segmento parabólico e as que formam o triângulo circunscrito em equilíbrio em uma balança imaginária (figura 1) através de relações geométricas e, com o uso de princípios de seu "Equilíbrio dos Planos" como a lei das alavancas, ele descobre a relação entre a área do triângulo circunscrito e a do segmento parabólico. Arquimedes, também através de manipulações geométricas, descobre a relação entre as áreas dos triângulos, concluindo que a área do segmento parabólico é quatro terços da área do triângulo inscrito. Nesse método arquimediano, podemos perceber uma grande semelhança com o moderno cálculo de áreas através da integral, ou seja, com o Cálculo Integral. Ao invés de se supor que as figuras são compostas de linhas, supomos retângulos. Mas a principal diferença está na forma em que o infinito é abordado, na verdade, o infinito era o nome que não devia ser pronunciado da Matemática grega. Arquimedes, ao invés de usar uma soma de séries infinitas, usa uma dupla redução ao absurdo, o que era comum em sua época.

5 Figura 1: Balança imaginária de Arquimedes. Questões sobre o axioma de Arquimedes No prefácio da "Quadratura da Parábola", Arquimedes escreve para um matemático grego seu contemporâneo chamado Dositeo e admite o uso de uma afirmação que hoje é conhecida como axioma de Arquimedes: "que o excesso pelo qual o maior de duas áreas desiguais excede o menor pode, ao ser adicionando a si mesmo, exceder qualquer área finita". Esse axioma parece uma tentativa de Arquimedes para simular a sua balança imaginária em um contexto mais formal e abstrato, mas ele se defende afirmando que outros matemáticos também fizeram uso desse axioma; e, de fato, ele aparece no quinto livro dos Elementos de Euclides como uma definição com a seguinte redação: Magnitudes são ditas estar em razão com respeito a uma outra se, quando multiplicadas, podem exceder-se mutuamente (FITZPATRICK, 2008). No entanto, mesmo que o axioma tenha surgido antes de Arquimedes, isso não exclui que ele possa ter vindo de uma relação mais profunda com o mundo sensível, seja de experiências com balanças realizadas por outros pensadores ou com o cálculo de áreas e magnitudes na prática.

6 O axioma de Arquimedes é, também, conhecido como axioma de continuidade e garante a não existência do infinitamente grande e do infinitamente pequeno (infinitésimo). David Hilbert ( ) formulou o axioma em seu Grundlagen der Geometrie e também mostrou sua independência dos demais axiomas da Geometria (HILBERT, 2005). Além disso, Hilbert faz algumas constatações interessantes sobre o axioma de Arquimedes: o axioma das paralelas 2 não pode ser substituído por nenhuma das formulações normalmente consideradas como equivalentes se o axioma de Arquimedes não for considerado como verdadeiro. quando se exclui o axioma de Arquimedes, não se pode afirmar o axioma da geometria hiperbólica referente às infinitas paralelas a uma reta dada que podem ser traçadas, no plano, através de um único ponto. o axioma de Arquimedes é de fundamental importância para os pontos de acumulação, assim, consequentemente, também de grande importância para o Cálculo Diferencial e Integral. Hilbert, em um discurso para a Sociedade de Matemática da Suíça, alerta que o axioma de Arquimedes provem da experiência (EWALD, 2005). Ele fala da relação do axioma com a Física e apresenta alguns casos em que o axioma de continuidade é imprescindível. Conclusões Dificilmente poderíamos sustentar que o axioma arquimediano possa ter evidência apenas dentro da Matemática, visto que a continuidade não é óbvia, pois a incomensurabilidade da raiz de dois cria buracos e fez com que os gregos escolhessem a Geometria como base para os demais ramos da Matemática, porque o que os seus olhos mostravam nos diagramas 3 eram linhas contínuas. Depois disso, esse desejo de uma 2 3 O axioma das paralelas é o famoso quinto postulado dos Elementos de Euclides. Representação gráfica da Geometria.

7 Matemática contínua fez com que se desenvolvesse a teoria do números irracionais para tapar os buracos. O Cálculo Diferencial e Integral foi primeiramente desenvolvido através da ideia de infinitésimos e isso é justamente o que o axioma de Arquimedes nega. Dessa forma, percebe-se que o axioma arquimediano não é evidente dentro da Matemática. Posteriormente, foi desenvolvida a teoria do limites, que substituiu a ideia de infinitésimos. O difícil é saber se o axioma arquimediano é de fato empírico ou se ele é formado somente a partir da intuição que temos do mundo sensível, ou seja, sintético a priori. A primeira vista ele pode parecer um sintético a priori, pois nos mostra uma certa universalidade e necessidade. É difícil de imaginar que não se consiga juntar vários pedaços pequenos de um cabo de vassoura de forma que ele fique maior que qualquer outro cabo de vassoura; no entanto, não parece que se possa concluir isso apenas da intuição que se tem de um pedaço de vassoura, mas através de muitas comparações feitas na infância com vários tipos de materiais diferentes, ou seja, com a experiência. Portanto, se pode concluir que o axioma arquimediano é empírico. No entanto, não se pode esquecer que para se entender a intuição que temos de um objeto no mundo sensível, é necessário que exista algum conhecimento prévio. Mas se é difícil encontrar algum conhecimento que seja nato, como é possível fornecer uma base para os conhecimentos empíricos? A resposta a essa pergunta esclarecerá como é possível uma Matemática empírica. Referências Bibliográficas ARQUIMEDES. Quadrature of the Parabola. Tradução de T. L. HEATH, Works of Archimedes. Cambridge: Cambrigde University Press, CHAITIN, J. G. MetaMat!: em busca do ômega. Tradução de G. K. Guinsburg. São Paulo: Perspectiva, 2009.

8 DA SILVA, J. J. Filosofias da Matemática. São Paulo: UNESP, EUCLIDES. Os Elementos. Tradução de R. FITZPATRICK. Euclid s Elements of Geometry, HILBERT, D. Foundations of Geometry, The. Projeto Gutenberg. Illinois: The Open Court Publishing Company, KANT, I. Crítica da Razão Pura. Ed. 5. Tradução de M. P. Dos Santos e A. F. Morujão. Lisboa: Fundação Calouste Gulbenkian, LAKATOS, I. Proof and Refutations: the logical of Mathematical discovery. Cambridge: Cambridge Univesity Press, QUINE, W. V. O. Two Dogmas of Empiricism. Cambridge, Disponível em: < Acesso em: 22 set