GEOMETRIA ANALÍTICA E ÁLGEBRA LINEAR NOTAS DE AULAS. Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto. Universidade de São Paulo
|
|
|
- Manoela Covalski Salazar
- 7 Há anos
- Visualizações:
Transcrição
1 GEOMETRIA ANALÍTICA E ÁLGEBRA LINEAR NOTAS DE AULAS Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto Universidade de São Paulo Departamento de Computação e Matemática Prof. Dr. Jair Silvério dos Santos
2
3 Sumário 1 MATRIZES Adição de Matrizes Multiplicação de Número (Escalar) por Matrizes Propriedades da Multiplicação de Número (Escalar) por Matrizes Multiplicação de Matrizes Matriz Inversa Matriz Adjunta Clássica e Inversa Sistemas de Equações Lineares Operações Elementares GEOMETRIA Segmentos Orientados Equipolência de Segmentos Orientados Vetores Multiplicação de Número Real (escalar) Por Vetor Soma de Ponto com Vetor Dependência e Independência Linear Bases e Dimensão Produto Escalar Projeção Ortogonal de Vetores Bases Ortogonais Bases Ortonormais Produto Vetorial Geometria Analítica Retas Planos ÁLGEBRA LINEAR Espaço Vetorial Propriedades Subespços vetoriais Geradores Conjunto de Geradores Dependência Linear Soma e Intercecção de Subespaços
4 4 SUMÁRIO Base e Dimensão Coordenadas Espaços Euclidianos Produto Esalar Projeção Ortogonal de Vetores Bases Ortogonais Bases Ortonormais Ortogonalização de Gram-Schmidt Projeção Ortogonal de um Vetor sobre um Subespaço TRANSFORMAÇÕES LINEARES Kernel e Imagem de uma Transformação Linear Transformação Linear Injetora, Sobrejetora, Bijetora Teorema do Núcleo e da Imagem Matriz de uma Transformação Linear Tranformações Singulares e Não Singulares Autovalores e Autovetores Semelhança de Matrizes
5 Capítulo 1 MATRIZES Professor Doutor: Jair Silvério dos Santos Matrizes Reais Uma matriz real é o seguinte arranjo de números reais : a 11 a 12 a 13 a 1m a 21 a 22 a 23 a 2m A n m =...., a n1 a n2 a n3 a mm onde, cada entrada (elemento) a ij R, i = 1, 2,, n e j = 1, 2,, m. Definição 1.1. Chama-se Matriz Nula, a matriz cujas entradas são zero, ou seja a ij =, para i = 1, 2,, n e j = 1, 2,, m. Escolhemos a letra O para representá-la, isto é O n m =..... Seja M n m (R) o conjunto de todas as matrizes reais A n m. Note que O M n m (R) Adição de Matrizes Definição 1.2. Dadas A n m e B n m, a adição de matrizes é uma função + : M n m (R) M n m (R) M n m (R) dada por +(A, B) = A + B, onde A n m = (a ij ) n m, B n m = (b ij ) n m, A + B = (c ij ) n m e c ij = a ij + b ij, i = 1, 2,, n e j = 1, 2,, m. 1
6 2 CAPÍTULO 1. MATRIZES 1..2 Multiplicação de Número (Escalar) por Matrizes Definição 1.3. Dados α R e A n m a multiplicação de número real (escalar) por matriz é uma função : R M n m (R) M n m (R) dada por (α, A) = α A, onde A n m = (a ij ) n m, α B = (c ij ) n m e c ij = α a ij, i = 1, 2,, n e j = 1, 2,, m. Exemplo 1.1. Considremos as matrizes ( ) A 2 3 =, B = Calcule A + B e ( 1) A. ( 3 2 ) Começamos por determinar a matriz A + B, ( ) ( ) ( ) c11 c A B 2 3 = + = 12 c 13 = c 21 c 22 c 23 ( ) ( ) ( 2) = = A + B A multiplicação de número por matriz ( 1) A, ( 1) ( ) = 2 2 ( ) ( 1)1 ( 1) 1 ( 1)3 = ( 1) ( 1) 2 ( 1)2 ( ) = ( 1) A. 2 2 Propriedades da Adição de Matrizes Dadas A n m, B n m e C n m, são verdadeiras as afirmações abaixo: A1 : A + (B + C) = (A + B) + C). Associativa A2 : A + B = B + A. Comutativa A3 : A + O = A. Elemento Neutro A4 : A + ( B) = O. Elemento Simétrico O elemento A M n m (R) é o Elemento Simétrico de A em relação à Adição de Matrizes 1..3 Propriedades da Multiplicação de Número (Escalar) por Matrizes Dados α, β R, A n m e B n m, são verdadeiras as afirmações abaixo: M1 : (α + β) A = α A + β A.
7 1.1. MULTIPLICAÇÃO DE MATRIZES 3 M2 : α (A + B) = α A + α B. M3 : 1 A = A M4 : α (β A) = (αβ) A = β (α A). Observe que o conjunto M n m (R) com as operações de Adição e Multiplicação por Escalar, que aqui indicamos por (M n m (R), +, ) tem estruturas especiais com as propriedades listadas em A1, A2, A3 e A4; M1, M2, M3 e M4 o que dá ao conjunto (M n m (R), +, ) um nome diferenciado, que é o de ESPAÇO VETORIAL. 1.1 Multiplicação de Matrizes Definição 1.4. Dadas A n p e B p m, a multiplicação de matrizes é uma função : M n p (R) M p m (R) M n m (R) dada por (A, B) = A B, onde A n p = (a ij ) n p, B p m = (b jk ) p m, A B = (c ik ) n m e c ik = p (a ij b jk ). j=1 Exemplo 1.2. Considere as matrizes 1 1 A = 2 e B = 3 2 Calcule A B. ( ) Podemos utilizar umaa regra prática que consiste de posicionar as matrizes A e B e realizar a multiplicação como segue, c 11 = a 11 b 11 + a 12 b 21 + a 13 b 31 c 12 = a 11 b 12 + a 12 b 22 + a 13 b 32 c 21 = a 21 b 11 + a 22 b 21 + a 23 b 31 c 22 = a 21 b 12 + a 22 b 22 + a 23 b 32 ( c 11 = ( 1)1 + 1() + ( 3)3 1 1 c 12 = ( 1)( 1) + 1( 2) + ( 3)2 2 c 21 = (1) + 2() + ( 2)3 3 2 c 22 = ( 1) + 2( 2) + ( 2)2 ) ( ) c11 c 12 c 21 c 22 Matriz Produto Assim, obtemos a matriz A B dada por ( ) 1 7 A B =. 6 8 Definição 1.5. Dada uma matriz A n p = (a ij ) n p chama-se Matriz Transposta de A n p, outra matrix B p n == (b ij ) n n tal que b ij = a ji, para i = 1, 2 n, j = 1, 2 p e escrevemos B = A t.
8 4 CAPÍTULO 1. MATRIZES Propriedade da Transposição de Matrizes Dados α R e matrizes quadradas A e B tem-se T1 (A t ) t = A. T2 (A + B) t = A t + B t. T3 (A B) t = B t A t. T3 (αa) t = αa t. Exercício 1.1. Dadas as matrizes A = 3 4 e B = Calcule A B, (A B) t e B t A t. Dizemos que uma matriz quadrada A é SIMÉTRICA se A = A t. A é ANTI- SIMÉTRICA se A = A t. Exercício 1.2. Mostre que se A e B forem semétricas então A + B e αa são simétricas. Mostre que se A e B forem semétricas então A B é simétrica se e somente se A B = B A. Propriedades da Multiplicação de Matrizes À partir deste momento, estaremos considerando apenas as Matrizes Quadradas, isto é, matrizes A n n M n n (R). Faremos isto somente por que nossos propósitos estarão satisfeitos com com matrizes quadradas. Chama-se Matriz Identidade a matriz A n n = (a ij ) n n tal que { 1, se i = j, a ij =, se i j, esta matriz será denotada por I n e então 1 1 I n = I n n = Dadas duas matrizes A n n e B n n, dizemos que as matrizes A e B Comutam se A B = B A. Observe que a comutatividade do produto de matrizes não é sempre verdadeira, veja exemplo abaixo. Exemplo 1.3. Consideremos as matrizes ( ) 1 1 A = 2 Verifique que A B B A. e B = ( )
9 1.1. MULTIPLICAÇÃO DE MATRIZES 5 Aplique a definição 1.4 (m = n = p) e verá que A B = ( ) ( ) 1 1 = 2 ( 3 ) 1 4 e B A = ( ) ( ) 1 1 = 2 ( ) Note que A B B A. Não é dificil ver que a matriz I n comuta com qualquer A n n = (a ij ) n n Matriz Inversa Definição 1.6. Dada uma matriz quadrada A n n M n n (R) chama-se Matriz Inversa A à uma outra matriz B n n M n n (R) tal que A B = I n e B A = I n. Denotaremos a Matriz Inversa de A por A 1. A matriz A 1 é o elemento simétrico de A em relação à Multiplicação de Matrizes. Exemplo 1.4. Considere as matrizes ( ) 2 1 A = 3 e B = 1 6 ( ) Não é dificil ver que, ( ) ( ) 3 1 = 2 ( ) 1 1 e que 1 6 ( ) ( ) 2 1 = 3 ( ) 1 1 Portanto, A B = I n e B A = I n. Ou seja B é a matriz inversa de A em relação à Multiplicação de Matrizes. Propriedades da Multiplicação de Matrizes Dadas A n n, B n n e C n n, são verdadeiras as afirmações abaixo: MM1 : A (B C) = (A B) C). Associativa MM2 : A I n = A, e I n A = A. Elemento Neutro MM3 : A (A 1 ) = I n. Elemento Simétrico Propriedades de Distributividade Dadas A n n, B n n e C n n, são verdadeiras as afirmações abaixo: DM1 A (B + C) = A B + A C) e (B + C) A = B A + C A). A notação A n significa A n vezes A A.
10 6 Exemplo 1.5. Dadas as matrizes A = ( 1 2 ) e B = A t = CAPÍTULO 1. MATRIZES Uma Aplicação das Matrizes Exemplo 1.6. Uma industria produz três produtos, X, Y, e Z, utilizando dois tipos de insumos, A e B. Para a manufatura de cada kg de X são utilizados 1 grama do insumo A e 2 gramas do insumo B; para cada kg de Y são utilizados 1 grama do insumo A e 1 grama do insumo B, e cada kg de Z são utilizados 1 grama do insumo A e 4 gramas do insumo B. Usando matrizes o esquema de produção pode ser descrito da seguinte forma: gramas de A por kg gramas de B por kg AW = ( X Y Z) = A, ( ) x + y + z 2x + y + z x kg de X produzidos W = y kg de Y produzidos z kg de Z produzidos gramas de A usadas gramas de B usadas. Exercício 1.3. Dadas as matrizes A = 3 4 e B = Verifique se A B = B A. Exercício 1.4. Mostre que as matrizes A = ( ) 1 1 y y 1 onde y R, satisfazem X 2 = 2X. (X 2 = X X). Encontre os valores de y R tais que A B = B A. Nós definimos a Matriz Inversa (ver definição 1.6) e não dissemos que tipo de matriz quadrada pode ter inversa, e também, não sabemos o que fazer para determinar a inversa de uma matriz. Uma ajuda importante é dada por uma função chamada determinante. Determinantes de Uma Matrizes Ressaltamos que apenas as matrizes quadradas serão utilizadas neste momento.
11 1.1. MULTIPLICAÇÃO DE MATRIZES 7 Definição 1.7. Seja A n n = (a ij ) n n, n 2. Chamamos Menor do elemento a ij, denotado por M ij, a sub-matriz de ordem (n 1) (n 1) obtida de A suprimindo da matriz A a i-ésima linha e j-ésima coluna. Definição 1.8. O determinante de uma matriz A n n = (a ij ) n n ; é uma função que a cada matriz quadrada associa um número real, isto é, Det : M(R) n n R dada por Se n = 1 então o Det(A) = a 11. se n 2 então Det(A) = n ( 1) (i+j) a ij Det(M ij ) = i=1 n ( 1) (i+j) a ij Det(M ij ). (1.1.2) j=1 então Não é difícil ver que se ( ) a11 a A = 12, a 21 a 22 Det(A) = 2 ( 1) (i+j) a ij Det(M ij ) = i=1 ( 1) (1+1) a 11 Det(M 11 ) + ( 1) (1+2) a 12 Det(M 12 ) = a 11 a 22 a 12 a 21. Note que o determinante dado pela definição 1.8 pode ser desenvolvido por linhas ou por colunas, (ver (1.1.2)). O determinante de uma matriz nos oferece um teste infalível para saber quais são as matrizes quadradas que podem ser invertíveis ou seja que possuem inversa com relação ao produto de matrizes. Uma matriz A n n = (a ij ) n n, tem inversa em relação ao produto de matrizes se e somente se Det(A). Uma pergunta ainda se apresenta. Há um mecanismo capaz de produzir a insversa de uma matriz quadrada em relação ao produto de matriz? Veja abaixo que o determinante de uma matriz também nos ajuda responder esta questão. Definição 1.9. Seja A n n = (a ij ) n n, n 2. Chamamos Cofator do elemento a ij, denotado por A ij, o número real dado por A ij = ( 1) (i+j) Det(M ij ), i, j = 1, 2,, n, onde M ij é o Menor do elemento a ji, i, j = 1, 2,, n. À matriz formada por todos os cofatores de A chamamos Matriz dos Cofatores de A e denotamos por Cof(A). A 11 A 12 A 13 A 1n A 21 A 22 A 23 A 2n Cof(A) n m =...., A n1 A n2 A n3 A nn
12 8 CAPÍTULO 1. MATRIZES Exemplo 1.7. Considere a matriz Calcule Det(A). 1 5 A = Nós vamos calcular o determinante de A desenvolvendo pela primeira linha. 2 ( ) 6 9 Det(A) = ( 1) (1+j) a 1j Det(M 1j ) = ( 1) (1+1) Det j=1 ( ) ( ) ( 1) (1+2) 1 Det + ( 1) 2 1 (1+3) 5 Det 2 6 = = 165. Exercício 1.5. Considere a matriz 1 2 A = Calcule Cof(A), [Cof(A)] t, A [Cof(A)] t, [Cof(A)] t A e 1 Det(A) [Cof(A)]t Matriz Adjunta Clássica e Inversa Definição 1.1. Dada A n n = (a ij ) n n, chama-se Adjunta Clássica de A à matriz [Adj(A)] = [Cof(A)] t. Teorema 1.1. Dada A n n = (a ij ) n n, se DetA, então 1 Det(A) A [Adj(A)] = I n Segue facilmente da definição 1.6 que Exemplo 1.8. Considere a matriz e 1 Det(A) [Adj(A)] A = I n (1.1.3) 1 Det(A) [Adj(A)] = A 1 ( Inversa de A) A = Use (1.1.3) e calcule a martiz inversa (elemento inverso) de A em relação ao produto de matriz. Vamos calcular os cofatores dos elementos de A. ( ) ( ) A 11 = ( 1) (1+1) Det = 6; A 2 12 = ( 1) (1+2) Det = ; 2
13 1.1. MULTIPLICAÇÃO DE MATRIZES 9 ( ) ( ) A 13 = ( 1) (1+3) Det = ; A 21 = ( 1) (2+1) Det = 4; 2 ( ) ( ) A 22 = ( 1) (2+2) Det = 2; A 2 23 = ( 1) (2+3) Det = ; ( ) ( ) A 31 = ( 1) (3+1) Det = 5; A = ( 1) (3+2) Det = 2; 2 ( ) 1 2 A 33 = ( 1) (3+3) Det = 3. 3 Assim, a matriz cofatora de A será dada por 6 Cof(A) = A matriz Adjunta Clássica é a transposta de matriz cofatora de A, ou seja Adj(A) = O teorema 1.1 nos dá a matriz procurada que é A 1 = 1 DetA Adj(A) = Exemplo 1.9. Uma industria produz três produtos, X, Y, e Z, utilizando dois tipos de insumos, A e B. Para a manufatura de cada kg de X são utilizados 1 grama do insumo A e 2 gramas do insumo B; para cada kg de Y s ao utilizados 1 grama do insumo A e 1 gramas do insumo B e, cada kg de Z s ao utilizados 1 grama do insumo A e 4 gramas do insumo B. O preço de venda de um kg de cada um dos produtos X, Y e Z é R$ 2, R$ 3, e R$ 5, respectivamente. Com a venda de toda produção de X, Y e Z manufaturada com 1 kg de A e 2 kg de B, essa industria arrecadou R$ 25,. Vamos determinar quantos kg de cada produto X, Y e Z foram vendidos. Como já vimos no exemplo 1.6 usando matrizes o esquema de produção pode ser descrito da seguinte forma: gramas de A por kg gramas de B por kg preço por kg (S) AW = X Y Z x = A, W = y z x + y + z 1 2x + y + z = 2 2x + 3y + 5z 25 kg de X produzidos kg de Y produzidos kg de Z produzidos gramas de A usadas gramas de B usadas. arrecadação
14 1 CAPÍTULO 1. MATRIZES Veja que a resposta à pergunta que foi formulada no exemplo 1.6 será dada pelo conjunto solução para o Sistema de Equações (S). 1.2 Sistemas de Equações Lineares Uma Equação Linear em n variáveis x 1, x 2,, x n reais é uma equação da forma a 1 x 1 + a 2 x a n x n = b, onde a 1, a 2,, a n e b são números reais que não dependem das variáveis envolvidas na equação e são conhecidos. Um Sistema de Equações Lineares ou simplesmente Sistema Linear é um conjunto de equações lineares, ou seja (S) a 11 x 1 + a 12 x 2 + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + a 2n x n = b a m1 x 1 + a m2 x 2 + a mn x n = b m (1.2.4) onde os a ij e b i i = 1, 2, m, j = 1, 2, n são todos números reais conhecidos. Usando o produto de matrizes (ver definição 1.4) o sistema pode ser escrito como uma equação matricial, onde, AX = B, a 11 a 12 a 13 a 1m x 1 b 1 a 21 a 22 a 23 a 2m A n m =...., X = x 2. e B = b 2.. (1.2.5) a n1 a n2 a n3 a mm Uma Solução para o sistema é uma matriz s 1 s 2 S =., tal que as equações do sistema são satisfeitas quando substituimos x 1 = s 1, x 2 = s 2,, x n = s n. Exemplo 1.1. Considere o sistema linear de duas equações e duas incógnitas { x + 2y = 1 (S) 2x + y = s n x n b n
15 1.2. SISTEMAS DE EQUAÇÕES LINEARES 11 O sistema (S) pode ser escrito na forma matricial ( ) ( ) ( ) 1 2 x (S) =. 2 1 y 1 Ainda, podemos verificar facilmente que x = 1 3 e y = 2 3 sistema (S), ou seja ) S = ( formam uma solução para o é o conjunto solução de (S). Um Sistema Linear que tem solução é denominado SISTEMA POSSÍVEL. Se um Sistema Linear que não tem solução é denominado SISTEMA IMPOSSÍVEL. Mas dentre os SISTEMAS POSSÍVEIS, há aqueles que possuem mais que uma solução. Exemplo O sistema linear de duas equações e quatro incógnitas { x + 3y + z + 2w = 5 (S) x + y + z 3w = 2 tem mais que uma solução. Note que S 1 = [ 5 2 ] t e S 2 = [ 7 5 1] t são soluções para o sistema (S). Mas afinal dado um Sistema Linear (S) o que devemos fazer para decidirmos entre as três possibilidades; Sistema Possível com mais que uma solução, Sistema Possível apenas uma solução e Sistema Impossível Operações Elementares Definição Uma Operação Elementar sobre as linhas de uma matriz é uma das seguintes operações com outra linha da mesma matriz: (i) Trocar a posição de uma das linhas da matriz. (ii) Multiplicar uma linha por uma constante (escalar) diferente de zero. (iii) Somar a uma linha da matriz, um múltiplo escalar de outra linha da mesma matriz. Dado um Sistema Linear (S) como em (1.2.12) temos a Matriz A e B associada à (S). Chama-se Matriz Aumentada associada à (S) a Matriz a 11 a 12 a 13 a 1m. b 1 a [A B] = 21 a 22 a 23 a 2m. b b 1 a n1 a n2 a n3 a mm. b 1 Exemplo Considere o sistema linear de duas equações e duas incógnitas { x + 2y = 1 (S) 2x + y =
16 12 CAPÍTULO 1. MATRIZES A Matriz Aumentada associada ao sistema (S) é a matriz ( ) [A B] = Teorema 1.2. Dados dois Sistemas Lineares AX = B e CX = D tais que a Matriz Aumentada [C D] pode ser obtida da Matriz Aumentada [A B] aplicando-se apenas uma Operação Elementar (ver definição 1.11), então os dois sistemas lineares possuem o mesmo Conjunto Solução. Agora vamos utilizar o teorema 1.2 e apresentar uma maneira eficiente para encontrarmos o conjunto solução para um Sistema Linear. Método de Gauss-Jordan O método que vamos apresentar aqui para resolver Sistemas Lineares, consiste na aplicação das operações elementares às linhas da Matriz Aumentada associada ao sistema linear em estudo. Primeiro procuramos através de operações elementares obter a Matriz Aumentada de forma que na primeira linha o primeiro elemento seja não nulo, este elemento será chamado de Pivô. Vejamos um exemplo. Exemplo Considere o sistema linear (S) dado por x + y + z = 1 (S) 2x + y + 4z = 3x + 2y + 5z = 2 A Matriz Aumentada associada à S é A = L 1 = l L 1 = l L 2 = 2l 1 l L 2 = l L 3 = 3l 1 l L 3 = l 2 l (1.2.6) Note que as linhas L 1, L 2 e L 3 são linhas da matriz aumentada obtida da outra matriz aumentada (anterior) cujas linhas são l 1, l 1 e l 3 elas operações elementares indicadas (ver figura 1.2.6). EXERCÍCIOS
17 1.2. SISTEMAS DE EQUAÇÕES LINEARES De cada uma das matriz se abaixo Calcule a matriz cofatora, adjunta clássica e com a Definição 1.7 calcule o determinante. Em seguida calcule a matriz inversa caso ela exista A = 1 1, B = , C = Para cada uma das matrizes acima calcule a sua inversa usando escalonamento de matriz. Agora usando o teorema 1.2 vemos facilmente que x + y + z = 1 x + y + z = 1 (S) x + y 3z = 2 x + y 3z = 2 x + y 2z = 5 x + y + z = 3 Mas o Sistema x + y + z = 1 (S 3 ) x + y 3z = 2 x + y + z = 3 tem como conjunto solução S 3 = [11, 7, 3] t, portanto pelo teorema 1.2, o conjunto solução para o Sistema (S) é S = S 3 = [11, 7, 3] t,, Sistemas Escalonados Dada uma matriz a 1r1 a 1r1 +1 a 1r1 +2 a 1m a 2r2 a 2r2 +1 a 2m A n m =...., (1.2.7) a nrm onde, a 1r1, a 1r2, a 1rm. Se tivermos 1 r 1 < r 2 < < r m m diremos que a matriz A está escalonada. Um Sistema Linear (S) está escalonado se a matriz aumentada associada à (S) estiver na forma. a 1r1 a 1r1 +1 a 1r1 +2 a 1n. β 1 a 2r2 a 2r2 +1 a 2n. β 2 [A B] =......, (1.2.8) a mrm. β k. β k+1
18 14 CAPÍTULO 1. MATRIZES ou seja (S) onde, a 1r1, a 1r2, a 1rm. a 1r1 x 1 + a 1r1 +1x 2 + a 1n x n = β 1 x 1 + a 2r2 +1x 2 + a 2n x n = β x 1 + x 2 + a mrm x n = β k x 1 + x 2 + x n = β k (1.2.9) Discussão e Resolução de Um Sistema Linear Discutir um Sistema Linear (S) significa efetuar um estudo de (S) visando classificá-lo segundo a definição a seguir. Definição Dizemos que um Sistema Linear (S) é Incompatível se (S) não admite solução. Um Sistema Linear (S) que admite uma única solução é chamado Compatível Determinado. Se um sistema admitir mais do que uma solução então ele é denominado Compatível e Indeterminado (I) No processo de escalonamento, numa certa etapa, obtém-se (S) x 1 + x 2 + x n = β k (1.2.1) com β k, o Sistema Linear será Imcompatível ou Impossível e denoteremos por (SI) ou o conjunto solução para (S) é o conjunto vazio (ver difinição 1.12). (II) No processo de escalonamento, numa certa etapa, obtém-se (S) x 1 + a 1r1 x 2 + a 1n x n = β 1 x 1 + x 2 + a 2n x n = β x 1 + x 2 + x n = β n, (1.2.11) o sistema (S) é Compatível e Determinado (o sistema linear está escalonado e número de equações é igual ao número de incógnitas) (III) No processo de escalonamento, numa certa etapa, obtém-se (S) x 1 + a 1r1 x 2 + a 1rp x rp + a 1n x n = β 1 x 1 + x 2 + a 2rp x rp + a 2n x n = β x 1 + x 2 + x rp + a pn x n = β p, (1.2.12) onde, p < n o sistema (S) é Compatível e Indeterminado (o sistema linear está escalonado e número de equações é menor ao número de incógnitas) Se um Sistema Linear tiver mais que uma solução, então o sistema terá infinitas soluções.
19 1.2. SISTEMAS DE EQUAÇÕES LINEARES 15 Exemplo Considere o Sistema x 2y z = 1 (S) 2x + y 3z = x + 7y + z = 3 (S) x 2y z = 1 2x + y 3z = x + 7y + z = 3 L 1 = l 1 L 2 = l 2 L 3 = l 2 + l 3 L 1 = l 1 L 2 = l 2 S 3 L 3 pode ser eliminada L 1 = l 1 L 2 = 2l 1 + l 2 L 3 = l 1 + l 3 x 2y z = 1 x + 5y z = 2 x + y + z = x 2y z = 1 x + 5y z = 2 x 5y + z = 2 { x 2y z = 1 x + 5y z = 2 O teorema 1.2, garante que o conjunto solução do Sistema (S) é igual aoconjunto solução para o Sistema (S 3 ), que é S = {( z, z, z) z R}. 5 Note que o Sistema (S) tem uma quantidade infinita de soluções. Exemplo Considere o Sistema x + y + z = 1 (S) 2x + y + 5z = 3x + 2y + 5z = 2 Precedomos ao escalonamento de (S), (S) L 1 = l 1 L 2 = l 2 L 3 = l 2 l 3 L 1 = l 1 L 2 = 2l 1 l 2 L 3 = 3l 1 l 3 (S 3 ) x + y + z = 1 x + y 3z = 2 x + y 2z = 5 x + y + z = 1 x + y 3z = 2 x + y z = 3 como conjunto solução para o sistema (S 3 ) é S 3 = [ ] t, pelo teorema 1.2, o conjunto solução para o Sistema (S) é S = S 3 = [ ] t. Note que o Sistema (S) tem uma única solução e portanto (S) é Compatível e Determinado. Exemplo Considere o Sistema x + 2y + 3z = 1 (S) 3x + 6y + 9z = 3x + 2y + 5z = 2
20 16 CAPÍTULO 1. MATRIZES Precedomos ao escalonamento de (S), (S) L 1 = l 1 L 2 = 3l 1 l 2 L 3 = 3l 1 l 3 x + y + z = 1 x + y z = 3 x + y 2z = 5 Note que a segunda equção já é incompatível, e isto torna o Sistema (S) incompatível ou seja o conjunto solução de (S) é vazio.
21 Capítulo 2 GEOMETRIA RETA Dados dois pontos distintos no espaço P e Q, existe única reta que passa por P e Q. Denotaremos esta reta por P Q ou será utilizado uma letra minúscula para representar a reta, por exemplo s, t, ect.... Diremos reta P Q ou reta s por exemplo. SEGMENTO DE RETA Dada uma reta r e dois pontos distintos sobre ela, o segmento de reta AB é o conjunto dos pontos da reta r que estão entre os pontos A e B. Dada uma reta r e um ponto P fora da reta r, existe uma única reta t que passa por P que é paralela à reta r. Ainda existe uma única reta s que passa por P que é perpendicular à reta r Segmentos Orientados Definição 2.1. Um segmento orientado é um par ordenado (A, B) de pontos do espaço. Se nos for dado um segmento (A, B), tal que o ponto A seja igual ao ponto B, diremos que o segmento (A, A) ou (B, B) é o segmento nulo. O segmento orientado (A, B) consiste dse todos os pontos da reta AB que estão entre A e B, inclusive os pontos A e B, mas deve ser considerado a orientação de A para B. Um segmento orientado nulo é determinado por um par de pontos coincidentes. A reta AB que contém o segmento AB é denominada reta suporte do segmento orientado (A, B). Os pontos A e B são denominados origem e extremidade do segmento respectivamente. Geometricamente um segmento orientado será indicado por uma flexa, veja o seguinte exemplo. Exemplo 2.1. Dados quatro pontos A, B, C e D do espaço como abaixo, podemos considerar os segmentos (A, B) e (C, D) como segue C D A B. 1. Segmento Oposto 17
22 18 CAPÍTULO 2. GEOMETRIA Definição 2.2. Dado um segmento orientado (A, B), chama-se segmento orientado oposto de (A, B) o segmento orientado (B,A). Não é difícil ver que a cada segmento orientado (A, B) está associado uma três conceitos geométricas importantes que são COMPRIMENTO, DIREÇÃO e SENTIDO. À partir deste instante, estas propriedades dos segmentos orientados passam a ser o nosso objeto de estudo e veremos que, com argumentos detalhados elas poderão nos oferecer uma vizualização particularmente especial do espaço que nos cerca. Estes conceitos geométricos são aqui denominados importantes por serem conhecidos como Grandezas Vetorias e alguns dos exemplos mais populares são FORÇA, VELOCIDADE e ACELERAÇÃO. Note que, dois pontos quaisquer A e B do espaço, determinam os segmentos orientados (A, B) e (B, A), que poderão ser iguais se o ponto A coincidir com o ponto B. Igualdade de Dois Segmentos Orientados Definição 2.3. Dois segmentos orientados (A, B) e (C, D), SERÃO IGUAIS se e somente se, A B e C D. 2. Comprimento Definição 2.4. Fixada uma unidade de de comprimento, a cada segmento orientado (A, B) podemos associar um número real positivo ou zero, que será o COMPRIMENTO de (A, B). Dado um segmento orientado (A, B), a distância do ponto A até o ponto B será o comprimento do segmento orientado (A, B). Como a distância de um ponto qualquer até ele mesmo é zero, ao segmento orientado (A, A) (segmento nulo) está associado o número real zero, ou seja o comprimento do segmento orientado nulo (A, A) é exatamente zero. 3. Direção Definição 2.5. Dados dois segmentos orientados (A, B) e (C, D), diremos que eles têm a mesma DIREÇÃO se as retas AB e CD forem paralelas. Se dois segmentos orientados (A, B), e (C, D) têm mesma direção, diremos que eles são paralelos. Note que um papalelogramo ABCD determina pelo menos um par de segmentos orientados digamos (A, B), e (C, D) A B D C
23 Exemplo 2.2. Considere os dois segmentos orientados (A, B), e (C, D), de modo que as retas AB e CD sejam paralelas. B D 19 A C Pela definção 2.5 os segmentos orientados (A, B), e (C, D) têm a mesma direção. 4. Sentido Definição 2.6. Dados dois segmentos orientados (A, B) e (C, D) com mesma direção a : Se as retas AB e CD forem distintas, diremos que eles têm o mesmo SENTIDO se as segmentos de retas AC e BD tiverem interseção vazia. b : Se as retas AB e CD forem coincidentes, tome um ponto A / AB e a única reta s que passa por A e que é paralela à reta AB, em seguida tome o único ponto B s de modo que os segmentos orientados (A, B ) e (A, B) satisfaçam a parte (a) desta definição. Diremos que os segmentos orientados (A, B) e (C, D) têm o mesmo SENTIDO se (A, B ) e (C, D) tiverem o mesmo sentido. Exemplo 2.3. Considere os segmentos orientados (A, B), e (C, D) de modo que as retas AB e CD sejam paralelas e distintas, como segue A C B D Note que os segmentos de retas AC e BD têm interseção vazia, ou seja pela definição 2.6 a, os segmentos orientados (A, B), e (C, D) têm o mesmo sentido. Exemplo 2.4. Considere os segmentos orientados (A, B), e (C, D) de modo que as retas AB e CD sejam paralelas e distintas, como segue A D B C Note que os segmentos de retas AC e BD têm interseção não vazia, ou seja pela definição 2.6a os segmentos orientados (A, B), e (C, D) têm sentidos ontrários.
24 2 CAPÍTULO 2. GEOMETRIA 2..3 Equipolência de Segmentos Orientados Definição 2.7. Dois segmentos orientados (A, B), e (C, D) são EQUIPOLENTES se a : os dois forem nulos. b : os dois são não nulos e eles têm o mesmo comprimento, mesma direção e mesmo sentido. Notação (A, B) (C, D) indica que os dois segmentos orientados (E, F ), e (G, H) são equipolentes, Exemplo 2.5. Considere dois papalelogramos ABCD e EF GH suponha que eles estão representados nas figuras abaixo: A B D C E F H G Note que o fato de ABCD e EF GH serem um paralelogramos as definições 2.4 e 2.5 nos garante que os pares de segmentos orientados (A, B) e (C, D); (E, F ), e (G, H) têm mesmo comprimento, mesma direção, usando a definição 2.6 vemos que (A, B) e (C, D) têm mesmo sentido e portanto são EQUIPOLENTES. Mas os segmentos orientados (E, F ), e (G, H) que têm mesmo comprimento e mesma direção, usando a definição 2.6 vemos que eles não têm o mesmo sentido, e por isto eles não são equipolentes. Proposição 2.1. A relação de equipolência goza das seguintes propriedades: a : (A, B) (A, B) Reflexiva b : Se (A, B) (C, D), então (C, D) (A, B) Comutativa c : Se (A, B) (C, D) e (C, D) (E, F ) então (A, B) (E, F ) Transitiva A demonstração será omitida. Exemplo 2.6. Considere os segmentos orientados abaixo. Suponha que as retas AB, CD, EF e F G sejam duas a duas paralelas e que os segmentos AB, CD, EF e F G tenham o mesmo comprimento ver figura abaixo : B D E G A C F H
25 2.1. VETORES 21 Usando as definições 2.4, 2.5, 2.6 e a transitividade da relação de equipolência (ver Prop. 2.1), podemos verificar facilmente que os segmentos orientados (A, B), (C, D), (E, F ) e (G, H) têm mesmo comprimento, mesma direção e mesmo sentido, portanto eles são equipolentes (Note que verificamos a equipolência comparando grupos de dois apenas segmentos orientados). Dado um segmento orientado (A, B) podemos pensar nos segmentos orientados que são equipolentes ao segmento orientado (A, B) e estes serão muitos. Por exemplo sabe-se ao arremessar-mos um objeto de massa não nula para o alto, este objeto passará por uma quantidade enorme de pontos do espaço e a estes pontos denominamos de trajetória. Em cada ponto desta trajetória o objeto estará sujeito à Força da Gravidade, ou seja ele estará sujeito à força de atração gravitacional, que aqui em nossa linguagem o que corresponde a um conjunto de segmentos orientados representado pela letra P (Força Peso). Podemos agora pensar em todos os segmentos orientados que são equipolentes à um segmento orientado fixado. Chama-se Classe de Equipolência de um segmento orientado (A, B), ao conjunto de todos os segmentos orientados que são equipolentes ao segmento orientado )(A, B). Note que o próprio (A, B) é um segmento orientado deste conjunto. Na verdade se dois segmentos orientados (A, B) e (C, D) forem equipolentes então a Classe de Equipolência de (A, B) coincidirá com Classe de Equipolência de (C, D). 2.1 Vetores Definição 2.8. Um Vetor Geométrico é uma classe de equipolência. Cada segmento orientado da Classe de Equipolência ou do vetor será chamado de representante do vetor. A força da gravidade é um vetor, pois ela é um conjunto de segmentos orientados equipolentes ou seja ela é uma Classe de Equipolência. Representaremos os vetores por letra minúscula com uma seta sobre ela a b, u, v, w etc... ou ainda se o segmento orientado (A, B) for um representante do vetor u, por exemplo podemos indicar o vetor u por AB. Definição 2.9. Vetor Nulo. À classe de equipolência do segmento orientado nulo ( (A, A) ) chamamos Assim sendo podemos ver que (i) O vetor nulo tem comprimento zero. (ii) O vetor nulo tem a mesma direção que qualquer outro vetor. (iii) O vetor nulo tem a mesmo sentido que qualquer outro vetor. O vetor nulo será representado por. Definição 2.1. Chamamos Espaço IE 3 ao conjunto de todos os vetores geométricos. Os vetores x, y não nulos serão paralelos (indica-se x// y) se e somente se um representante (A, B) de x for paralelo a um representante (C, D) de y Chamamos Norma, Módulo ou Comprimento de um vetor ao comprimento de qualquer um de seus representantes.
26 22 CAPÍTULO 2. GEOMETRIA Dado um vetor v podemos tomar um de seus representantes, digamos (A, B) e indicarmos v por BA. Vetor Oposto Definição Se o segmento orientado (A, B) for um representante do vetor u então o segmento orientado (B, A) será um representante do vetor u denominado Vetor Oposto de u ou seja o vetor BA é o oposto do vetor AB. Indicamos oposto de BA por AB. Dado um vetor u, existe um único ponto A IE 3 tal que u tem um representante com origem em A. Neste instante temos um conjunto muito bem definido que é IE 3 e a partir deste momento nosso interesse é em explorar mais este conjunto, isto é saber quais são seus elementos, como seus elementos se relacionam com nossa vida cotidiana, particularmente algumas relações dos elementos de IE 3 com a elementos da conhecida Geometria de Euclides. ADIÇÃO DE VETORES Definição A adição de vetores é uma função que a cada par de vetores ( u, v) de IE 3 IE 3 associa um vetor de IE 3 que é chamado SOMA de u por v e indicado por u + v. A função age da seguinte forma sobre o par ( u, v): considere um representante (A, B) de u, e um representante de v com origem em B, e extremidade em C, a classe de equipolência que contém o segmento orientado (A, C) é o vetor u + v. Ver a figura abaixo: B u v A w = v + v D Esta regra de adição de vetores é conhecida como regar triangular. Há outra regra que é a conhecida como regra do paralelogramo. B u v u A w = v + v D C v Esta regra se aplica da seguinte forma : Fixamos um ponto A IE 3 e tomamos o único ponto B IE 3 tal que o segmento orientado (A, B) seja um representante do vetor u, em
27 2.1. VETORES 23 seguida com o ponto B tomamos o único ponto C IE 3 tal que o segmento orientado (B, C) seja um representante do vetor v. Analogamente, determinamos o ponto D IE 3 e em seguida um ponto C que por nossa construção coincide com o ponto C. Assim teremos o paralelogramo ABCD, e a soma dos vetores u e u é a classe de equipolência do segmento orientado (A, C). Note que o segmento AC é a diagonal principal do paralelogramo ABCD. Exercício 2.1. Mostrar que a diagonal secundária do paralelogramo ABCD nos dá a diferença dos vetores u e v. Note que o conjunto IE 3 (ver definição ) juntamente com a definição 2.12 torna-se análogo ao conjunto R (números reais) com a operação de adição de números, já bem conhecida nossa. Mas a operação adição de números reais no conjunto R TEM ELEMENTO NEUTRO (ZERO), É ASSOCIATIVA, É COMUTATIVA, CADA NÚMERO REAL TEM INVERSO (a R tem inverso a R). Uma pergunta importante: A operação adição no conjunto IE 3 (ver definição 2.12) tem as mesmas propriedades que operação adição de números reais no conjunto R? A partir deste instante o espaço IE 3 será referido como (IE 3, +) espaço IE 3 com a operção de adição PROPRIDADES DE ADIÇÃO DE VETORES Dados u, v e w em (IE 3, +), PA1 ( u + v) + w = u + ( v + w) PA2 u + v = v + u PA3 u + = u PA4 u + ( u) = u Associativa Comutativa Elemento Neutro Elemento Oposto ou Simétrico Exercício 2.2. Considere os vetores a e b cujos representantes são os segmentos orientados (A, B) e (B, C) respectivamente (ver figura abaixo) e calcule a + b e a b usando a regar do triângulo e do paralelogramo. A C B
28 24 CAPÍTULO 2. GEOMETRIA Exercício 2.3. Considere os vetores a, b e e cujos representantes são os segmentos orientados (A, B), (C, D) e (E, F ) respectivamente (ver figura abaixo) e calcule ( a + b) + e; a b e a ( b e) usando a regra do triângulo e do paralelogramo. A D E F C B Multiplicação de Número Real (escalar) Por Vetor Vamos definir uma operação externa em IE 3. Definição Multiplicação de número real ou escalar por um vetor é uma função que a cada par ordenado (α, u) R IE 3 associa um vetor w IE 3 denotado por α u, (α, u) m α u. Como a função multiplicação a associa um par ordenado, como na definição, um vetor, se faz necessário saber informar qual é o comprimento a direção e o sentido deste novo vetor. Se α = então (, u) m ou u =. Se u =, então (α, ) m ou α =. Se α, e u, então a : α u = α u b : α u // u ; (os vetores α u e u são paralelos). c : α u e u terão o mesmo sentido se α > e terão sentidos contrários se α >. Note que a multiplicação de vetor por escalar (número) pode aterar o comprimento e o sentido do vetor, mas não altera a direção. Exemplo 2.7. Dado um vetor v IE 3 com segmento orientado (A, B), tomemos retas CD, EF e GH de modo que ass retas AB CD, EF e GH sejam duas à duas paralelas e os comprimentos dos segmentos CD, EF e GH satisfaçam a relação comp( CD) = 2comp( AB) = comp( EF ) e comp( GH) = 5 2 comp( AB). (2.1.1) Usando a definição 2.5 podemos ver os segmentos orientados (A, B) (C, D), (E, F ) e (G, H) têm mesma direção, usando (2.1.1) e a definição 2.13 (Note que α ), podemos ver que segmento orientado (C, D) é representante do vetor 2 v (α = 2), segmento orientado (E, F ) é representante do vetor 2 v, (α = 2)
29 2.1. VETORES 25 segmento orientado (G, H) é representante do vetor 5 2 v, (α = 5 2 ) e com isto construir a figura abaixo. B v A 2 v C D E 2 v F G Vejamos agora como as duas operações dadas nas definições 2.12 em IE 3 IE 3, e 2.13 em R IE 3 se relacionam. H PROPRIEDADES DE MULTIPLICAÇÃO POR ESCALAR Dados u, v IE 3, α R β R, então M1 α( u + v) = α u + α v. M2 (α + β) u = α u + β u. M3 1 u = u. M2 α(β u) = (αβ) u = β(α u). A partir deste instante o espaço IE 3 será indicado por (IE 3, +, ) onde lê-se espaço IE 3 com as operções de Adição e Multiplicação por Escalar (Número real) As quatro propriedades de adição juntamente com a quatro propriedades de Multiplicação por escalar (número real) fazem uma estrutura especial dentro do conjunto IE 3 chamada Estrutura de Espaço Vetorial e por isto de agora em diante nos referiremos ao conjunto (IE 3, +, ) como um Espaço Vetorial Se α R e v R com α, será utilizado apenas a notação 1 v, de modo algum α será permitida a notação v α. Exercício 2.4. Prove a regra dos sinais a ( α) v = ( α v) para todo α R e v IE 3. b α( v) = (α v) para todo α R e v IE 3. c ( α)( v) = α v para todo α R e v IE 3. Prova a : Note que pela definição 2.11 a igualdade (a) nos diz que o vetor oposto de ( α) v é ( α v) ou seja, devemos provar que ( α) v + ( α v) =. Mas ( α) v + ( α v) M2 = ( α + α) = v 5 2 v Prova b: Agora devemos provar que α( v) + (α v) =. Mas Def 2.13 = α( v) + (α v) M1 = α( v v) = α A prova de c é deixada como exerício. Def 2.13 =.
30 26 CAPÍTULO 2. GEOMETRIA Proposição 2.2. Dado α, β R e u IE 3, se α u =, então α = ou u =. se u e α u = β u, então α = β. Prova : Priemiro vamos provar. Supponha que α então existe α 1 R tal que α 1 α = 1. Multiplicando α u = de ambos os membros por α 1 teremos αα 1 u = α 1 =, então u =. Vamos provar agora. Como α u = β u α u β u = Def 2.13 α u + (( β u)) =, Portanto, α u + ( β u) = M2 P rop 2.2 (α β) u = (α β = ) ou u =. Mas, por hipótese u, portanto α = β. Como u temos α = β. Exercício 2.5. Considere a figura abixo (o sólido ABCD é um tetraedro), e os vetores m, n e p cujos representantes são os segmentos orientados (A, B), (A, C) e (A, D) respectivamente. D C A B (i) Encontre os vetores u, v e w cujos representantes são os segmentos orientados (C, B), (C, D) e (B, D) respectivamente, como função de m, n e p. (ii) Seja M ponto médio do segmento de reta CB, exprima o vetor a com um representante dado pelo segmento orientado (A, M) em função de m e n Soma de Ponto com Vetor Neste momento nós temos dois conjuntos muito bem definidos que são o espaço no qual vivemos que denotaremos por IE ou o conjunto dos pontos do espaço e o conjunto de Vetores Geométricos (ver Def. 2.1) que estamos indicando por IE 3. Poderíamos dizer que o conjunto IE é o conjunto de dos pontos do espaço. Em verdade podemos definir uma correspondência entre estes dois conjuntos que é uma função. Veja definição a seguir.
31 2.1. VETORES 27 Definição Dado um ponto P em IE e um vetor v em IE 3, seja Q o único ponto em IE tal que o segmentos orientados (P, Q) seja um representante para o vetor v. Este ponto Q IE é denominado a Soma do Ponto P com o Vetor v, e denotamos por Q = P + v. Q v P Dados P IE e v IE 3, Q = P + v ou Q = P + P Q Usaremos a notação P v para indicar a soma do ponto P com o vetor v, e assim teremos P v = P + ( v). PROPRIEDADES DA SOMA DE PONTO COM VETOR Dados P, IE, v, u IE 3, temos PS1 P + = P, Esta é uma decorrência do imediata da definição 2.14, pois P + = P. PS2 Se P + v = P + u então v = u. Note que se Q = P + v = P + u, ent ao da defnição2.14 P P = (ver Def. 2.9) então P Q = v e P Q = u, portanto u = v. Esta propriedade permitem um tipo de Cancelamento do ponto P na igualdade P + u = P + v. PS3 (P + v) + u = P + ( v + u). Sejam Q = P + u, R = Q + v,(ver figura abaixo) então R = (P + u) + v. Ainda, segue da definição 2.14 que P Q = u, QR = v. Realizando a soma de P Q com QR teremos P Q + QR = v + u, mas P Q + QR = P R. Novamente pela definição 2.14 R = P + ( u + v) agora pela propriedade PS3 tem-se (P + u) + v = P + ( u + v). Q u v P PS4 Se P + v = Q + v, então P = Q. Como w = v + v R P + v = Q + v (P + v) v = (Q + v) v P S3 P + ( v v) = Q + ( v v) P + = Q + PS5 (P v) + v = P Esta propriedade decorre de PS3 e PS1. Pois P S1 P = Q (P v) + v = P S3 = P + ( v + ( v) = P S1 = P + = P.
32 28 CAPÍTULO 2. GEOMETRIA Neste caso se o vetor u tem como representante o segmento orientado (A, B), é comum representar o vetor AB por B A. A soma de ponto com vetor é uma relação muito importante entre os conjuntos IE e IE 3, porque ela relaciona o conjunto de pontos do espaço com o conjunto de Vetores Geométricos. Esta relação será utilizada para descrever subconjuntos de pontos do espaço, por exemplo Retas, Planos, Semi-retas, Semi-planos, e posições entre eles. Exercício 2.6. Na figura ao abaixo os pontos M, N e O são pontos médios de P Q, QR e RP respectivamente. Exprima RM, QO e P N como função P R e P Q. P M N O Resolução É fácil ver que RM = RP + P M, isto porque M é ponto médio de P Q, e pudemos nos valer da definição Mas com a definição 2.13 podemos ver que e novamente que M é ponto médio de P Q, vemos que P M = 1 P Q. Então, 2 RM = RP + 1 P Q. (2.1.2) 2 Encontramos a função de P R e P Q que procurávamos. Vamos escrever P N em função de P R e P Q. Use a defição 2.12 e note que P N Def.2.12 = P R + RN, N ponto médio de QR nos dá 2 RN = QR Def.2.12 = RP + P Q, Então, R Portanto, P N Def.2.12,2.13 = 1 ( ) P Q + RP + P 2 R MS1 = 1 P 2 Q 1 P 2 R + P R. P N = 1 P Q + 1 P R. (2.1.3) 2 2 Fica como exercício provar que QO é função P R e P Q. A conclusão do exerício 2.6 é válida mesmo quando os pontos M, N e O escolhidos não forem pontos médios, ver o exercício abaixo : Exercício 2.7. Na figura abaixo a medida de P X é a metade da medida de XR. Exprima QX em função de QP e QR. Q P X R
33 2.1. VETORES 29 Resolução O enunciado do exercício nos diz que P X = 1 XR, então 2 QX QP = P X = 1 XR 2 = 1 ) QR QX MS1 = 2( 1 QR 2 1 QX 2 Observe a primeira e última igualdade, elas no dão, QX QP = 1 QR 2 1 QX 2 Def QX = 1 2 QR + QP Def QX = 1 QR + 3 QP. (2.1.4) 3 2 Exercício 2.8. Seja ABC um triângulo, e M e N pontos médios de AC e BC respectivamente. Mostre que MN = 1 AB. 2 Exercício 2.9. Prove que se os pontos médios dos lados de um quadrilátero convexo forem vétices de um segundo quadrilátero, este será um paralelogramo Dependência e Independência Linear Observe que em (2.1.2), (2.1.3) e (3.1.4) temos os vetores RM, P N e CX, respectivamente, foram expressos como função de outros vetores, em verdade, a função que aparece no lado direito de cada uma das expressões de (2.1.2), (2.1.3) e (3.1.4) é uma Função Linear dos vetores envolvidos. Este tipo de expressão é denominado COMBINAÇÃO LINEAR ou seja, em (2.1.2) o vetor RM aparece escrito como COMBINAÇÃO LINEAR dos vetores RP e P Q; em (2.1.3) o vetor P N aparece escrito como COMBINAÇÃO LINEAR dos vetores P Q e P R; ver em (3.1.4) qual a COMBINAÇÃO LINEAR que aparece. Definição Dadas (α 1, α 2,, α n ) sequência de números reais (n-upla ordenada), e ( u 1, u 2,, u n ) sequência de vetores (n-upla de ordenada de vetores), dizemos que um vetor u inie 3 é COMBINAÇÃO LINEAR dos vetores u 1, u 2,, u n, se u = α 1 u 1 + α 2 u α n u n. (2.1.5) Exemplo 2.8. Tome na expressão CX = 1 QR + 3 QP. 3 2
34 3 CAPÍTULO 2. GEOMETRIA Observe que α 1 = 1, u 3 1 = QR, α 2 = 3 e u 2 2 = QP e se u = CX, temos a sequência de números reais (α 1, α 2 ) = ( 1, 3) e a sequência de vetores ( u 3 2 1, u 2 ) = ( QR, QP ) e u escrito como COMBINAÇÃO LINEAR dos vetores ( u 1, u 2 ) = ( QR, QP ). Exemplo 2.9. Seja P N = 1 P Q + 1 P R como em (2.1.3). 2 2 Note que se α 1 = α 2 = 1 e u 2 1 = P Q, u 2 = P R, então se u = P N teremos u escrito como COMBINAÇÃO LINEAR de u 1 e u 1. Diremos que a COMBINAÇÃO LINEAR u = α 1 u 1 + α 2 u α n u n. (2.1.6) é a COMBINAÇÃO LINEAR NULA se u = for o vetor nulo. Dada uma sequência de vetores ( u 1, u 2,, u n ), há uma maneira muito fácil, digamos trivial, de se obter a COMBINAÇÃO LINEAR NULA destes vetores, que é escolher todos os elementos da sequência de números (α 1, α 2,, α n ) = (,,, ), e assim teremos a COMBINAÇÃO LINEAR u 1 + u u n =. Exemplo 2.1. Considere os vetores u, v e w com segmentos orientados (P, Q), (Q, R) e (R, P ) respectivamente, como na figura abaixo: Q u v P w R Segue diretamente da definição 2.12 que = u + v + w ou seja, o vetor é combinação nula de u, v e w. Observação 2.1. Se dois vetores u e v forem paralelos existirá um número real α tal que u = α v. Prova Como u e v são paralelos e simultaneamente não nulos, u e v têm mesma direção. Ainda não é difícil ver que existe α R tal que u = α v. Como { α = α, se α >, α = α, se α <, então u = α v e α = u v,. Se um dos vetores u e v for o vetor nulo, por exemplo u =, então tomamos α = e poderemos escrever u = α v. Note que o vetor nulo é paralelo à qualquer outro vetor. Nas condições da observação 2.1 podemos concluir que u e v terão mesma direção se α > e sentido contrário se α <.
35 2.1. VETORES 31 Também nas condições da observação 2.1 pode-se obter a COMBINAÇÃO LINEAR NULA dos vetores, u e v ( u α v = ). Note que a sequência de números (1, α) é não nula. Vejamos qual é a relação de depenência entre α e e u e v, indnependente do valor de α. Cálculo do valor de α. O comprimento de α v e u são iguais, então u = α v Def = u = α v ; se os dois vetores forem não nulos, então v = e assim, ou seja α é unicamente determinado. α = u v, Dada uma sequência de vetores ( u 1, u 2,, u n ), tal que um deles é o vetor nulo, então existirá pelo menos uma sequência de números reais (α 1, α 2,, α n ) (,,, ) que torna possível a COMBINAÇÃO LINEAR NULA de ( u 1, u 2,, u n ). Vejamos é possível encontrar uma sequência de números reais (α 1, α 2,, α n ) não nula. Suponha que u 1. Então existe a sequência de números reais (α 1, α 2,, α n ) com α 1 por exemplo α 1 = 2, e todos os outros α s nulos, então a sequência de números reais toma a forma (2, α 2 =,, α n = ), e como u 2 =, u 3 =,, u n = a COMBINAÇÃO LINEAR dos vetores dados será dada por 2 + α 2 u α n u n = 2 + u u n Def =. Definição Uma sequência de vetores ( u 1, u 2,, u n ) será Linearmente Independente e indicaremos LI, se a única possibilidade de se obter a COMBINAÇÃO LINEAR NULA dos vetores ( u 1, u 2,, u n ) for escolher (α 1, α 2,, α n ) = (,,, ). Uma sequência com apenas vetor ( u), é Linearmente Independente se e somente se u. Prova Devemos mostrar que a COMBINAÇÃO LINEAR NULA da sequência ( u) isto é, α u = somente é possivel se α =. Mas, pela Proposição 2.2, α u = implica que α = ou u =, como a u é não nulo, α = ou seja a única sequência possível de números reais que produz a COMBINAÇÃO LINEAR NULA α u =, é (α) = (). Isto prova as duas afirmações. Definição Note que uma sequaência de vetores ( u 1, u 2,, u n ) LINEARMENTE DEPENDENTE, indicaremos por LD se ela não for LI.
36 32 CAPÍTULO 2. GEOMETRIA Dada uma sequência de vetores ( u 1, u 2,, u n ), se houver pelos menos uma maneira de se obter a COMBINAÇÃO LINEAR NULA destes vetores utilisando-se uma n-upla ordenada não nula isto é (α 1, α 2,, α n ) (,,, ), diremos que a sequência de vetores ( u 1, u 2,, u n ) é LD. Uma sequência com dois vetores ( u, v) é LD se e somente se u e v forem paralelos. Prova Se u e v forem paralelos, os comentários logo após a Obsevação 2.1 nos assegura que existe α R tal que u = α v, ou seja u α v = e isto implica que a sequência (1, α) poder ser utilizada para se obter a COMBINAÇÃO LINEAR NULA de u e v. Como (1, α) (, ), a definição nos diz que a sequência ( u, v) é LD. Se u e v forem LD então existe α R tal que u α v =, então u = α v =. A definição 2.13 assegura que u e v têm mesma direção Proposição 2.3. Uma sequência de vetores v 1, v 2,..., v n IE 3 é LD se e somente se algum destes vetores é combinação linear (CL) dos demais. Prova Suponha que { v 1, v 2,..., v n } é LD, então pela definição 2.16 existe uma n-upla de números reais (α 1, α 2,..., α n ) (,,..., ), isto é, pelo menos um dos α i para i = 1, 2,..., n, tal que α 1 v 1 + α 2 v α n v n =, como α i para algum i = 1, 2,..., n, suponhamos que α 1. Então α 1 v 1 = α 2 v 2 α n v n, e dividindo ambos os membros por α 1 teremos v 1 = α 2 α 1 v 2 α 3 α 1 v 3 α 2 α 1 v n ou seja o vetor v 1 é combinação dos demais. Suponaha agora que um dos vetores v 1, v 2,..., v n é combinação dos demais, podemos supor que seja v 1 este vetor, ou seja, pela definição existem β 1, β 2,..., β n 1 tais que v 1 = β 1 v 2 + β 2 v β n 1 v n, subtraindo v 1 em ambos os membros da igauldade acima teremos ( 1) v 1 + β 1 v 2 + β 2 v β n 1 v n =. (2.1.7) Note em (3.1.5) temos a Combinação Linear Nula dos vetores v 1, v 2,..., v n com a sequência 1, β 1, β 2,..., β n 1 de n números reais, e esta sequência é não nula, ou seja ( 1, β 1, β 2,..., β n 1 ) (,,..., ). Pela definição 2.16 os vetores v 1, v 2,..., v n são Linearmete Dependentes (LD). Uma interpretação da Proposição 2.3 Dados três vetores u, v e w em IE 3 com segmentos orientados (A, B), (A, C) e (A, D) respectivamente, os três vetores serão coplanares se existir um plano π que é paralelo aos três vetores simultaneamente, isto é os pontos A, B, C e D estiverem no mesmo plano, digamos π. Diremos que os três vetores u, v e w são COPLANARES.
2. SEGMENTOS ORIENTADOS
 FFCLRP-USP - ALGEBRA LINEAR - Vetores Geométricos 1 NOTAS DE AULAS Professor Doutor: Jair Silvério dos Santos 1 1. LEMBRETE DA GEOMETRIA DE EUCLIDES RETA Dados dois pontos distintos no espaço P e Q, existe
FFCLRP-USP - ALGEBRA LINEAR - Vetores Geométricos 1 NOTAS DE AULAS Professor Doutor: Jair Silvério dos Santos 1 1. LEMBRETE DA GEOMETRIA DE EUCLIDES RETA Dados dois pontos distintos no espaço P e Q, existe
1 NOTAS DE AULA FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA. Professor Doutor: Jair Silvério dos Santos
 FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA 1 NOTAS DE AULA Professor Doutor: Jair Silvério dos Santos (i) Matrizes Reais Uma matriz real é o seguinte arranjo de números reais : a 11 a 12 a 13 a 1m a 21
FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA 1 NOTAS DE AULA Professor Doutor: Jair Silvério dos Santos (i) Matrizes Reais Uma matriz real é o seguinte arranjo de números reais : a 11 a 12 a 13 a 1m a 21
Notas para o Curso de Algebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009
 Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Material Teórico - Módulo: Vetores em R 2 e R 3. Operações Envolvendo Vetores. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares
 FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
Notas de Aula. Gustavo Henrique Silva Sarturi. i Z (1 i m) a j1 a j2
 Notas de Aula Gustavo Henrique Silva Sarturi Matemática B - Em Ação gustavo.sarturi@ufpr.br 1 Matrizes Definição 1.1. Uma matriz A m n é um arranjo retangular de m n números reais (ou complexos) organizados
Notas de Aula Gustavo Henrique Silva Sarturi Matemática B - Em Ação gustavo.sarturi@ufpr.br 1 Matrizes Definição 1.1. Uma matriz A m n é um arranjo retangular de m n números reais (ou complexos) organizados
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
2 Igualdade e Operações com pares ordenados. 1 Conjunto R 2. 3 Vetores. 2.1 Igualdade. 1.2 Coordenadas Cartesianas no Plano
 1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Aula 3 Vetores no espaço
 MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
1. Operações com vetores no espaço
 Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
JOSÉ ROBERTO RIBEIRO JÚNIOR. 9 de Outubro de 2017
 9 de Outubro de 2017 Vetores Ferramenta matemática que é utilizada nas seguintes disciplinas dos cursos de Engenharia: Física; Mecânica Resistência dos materiais Fenômenos do transporte Consideremos um
9 de Outubro de 2017 Vetores Ferramenta matemática que é utilizada nas seguintes disciplinas dos cursos de Engenharia: Física; Mecânica Resistência dos materiais Fenômenos do transporte Consideremos um
Vetores. Laura Goulart. 21 de Julho de 2018 UESB. Laura Goulart (UESB) Vetores 21 de Julho de / 1
 Vetores Laura Goulart UESB 21 de Julho de 2018 Laura Goulart (UESB) Vetores 21 de Julho de 2018 1 / 1 Introdução Muitas grandezas físicas como força para serem completamente identicadas precisam de comprimento,
Vetores Laura Goulart UESB 21 de Julho de 2018 Laura Goulart (UESB) Vetores 21 de Julho de 2018 1 / 1 Introdução Muitas grandezas físicas como força para serem completamente identicadas precisam de comprimento,
CÁLCULO VETORIAL E GEOMETRIA ANÁLITICA
 CÁLCULO VETORIAL E GEOMETRIA ANÁLITICA Consideremos uma reta r e sejam A e B dois pontos de r Ao segmento de reta AB, podemos associar 2 sentidos : de A para B e de B para A Escrevemos AB para representar
CÁLCULO VETORIAL E GEOMETRIA ANÁLITICA Consideremos uma reta r e sejam A e B dois pontos de r Ao segmento de reta AB, podemos associar 2 sentidos : de A para B e de B para A Escrevemos AB para representar
Matrizes e sistemas de equações algébricas lineares
 Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
Capítulo 1 Matrizes e sistemas de equações algébricas lineares ALGA 2007/2008 Mest Int Eng Biomédica Matrizes e sistemas de equações algébricas lineares 1 / 37 Definições Equação linear Uma equação (algébrica)
Aula 4 Colinearidade, coplanaridade e dependência linear
 Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
NOTAS DE AULA DE MAT 137 -PRIMEIRA SEMANA Profa. Margareth Turmas 2 e 7. Atleta 1 7, ,4. Atleta Atleta 3 9 7,5 8,5 7,9
 NOTAS DE AULA DE MAT 137 -PRIMEIRA SEMANA Profa Margareth Turmas e 7 01 Motivação Num torneio de triatlon as competições: nado, corrida e ciclismo foram pontuadas com pesos x, y e z, respectivamente A
NOTAS DE AULA DE MAT 137 -PRIMEIRA SEMANA Profa Margareth Turmas e 7 01 Motivação Num torneio de triatlon as competições: nado, corrida e ciclismo foram pontuadas com pesos x, y e z, respectivamente A
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Parte 2 - Espaços Vetoriais
 Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
n. 1 Matrizes Cayley (1858) As matrizes surgiram para Cayley ligadas às transformações lineares do tipo:
 n. Matrizes Foi um dos primeiros matemáticos a estudar matrizes, definindo a ideia de operarmos as matrizes como na Álgebra. Historicamente o estudo das Matrizes era apenas uma sombra dos Determinantes.
n. Matrizes Foi um dos primeiros matemáticos a estudar matrizes, definindo a ideia de operarmos as matrizes como na Álgebra. Historicamente o estudo das Matrizes era apenas uma sombra dos Determinantes.
Produto Misto, Determinante e Volume
 15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Números Reais. Víctor Arturo Martínez León b + c ad + bc. b c
 Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2018
 MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT003 10 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT003 10 a Lista de
Vetores e Geometria Analítica
 Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
Vetores e Geometria Analítica ECT2102 Prof. Ronaldo Carlotto Batista 23 de fevereiro de 2016 AVISO O propósito fundamental destes slides é servir como um guia para as aulas. Portanto eles não devem ser
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
Fundamentos de Matemática Curso: Informática Biomédica
 Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: determinantes e sistemas 13 e 27/06/14 Determinantes Def.: Seja M uma matriz quadrada de elementos reais, de
Fundamentos de Matemática Curso: Informática Biomédica Profa. Vanessa Rolnik Artioli Assunto: determinantes e sistemas 13 e 27/06/14 Determinantes Def.: Seja M uma matriz quadrada de elementos reais, de
Geometria Analítica. Cleide Martins. Turmas E1 e E3. DMat - UFPE Cleide Martins (DMat - UFPE ) VETORES Turmas E1 e E3 1 / 22
 Geometria Analítica Cleide Martins DMat - UFPE - 2017.1 Turmas E1 e E3 Cleide Martins (DMat - UFPE - 2017.1) VETORES Turmas E1 e E3 1 / 22 Objetivos 1 Entender a denição de VETOR 2 Aprender a somar dois
Geometria Analítica Cleide Martins DMat - UFPE - 2017.1 Turmas E1 e E3 Cleide Martins (DMat - UFPE - 2017.1) VETORES Turmas E1 e E3 1 / 22 Objetivos 1 Entender a denição de VETOR 2 Aprender a somar dois
Produto interno e produto vetorial no espaço
 14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
linearmente independentes se e somente se: Exercícios 13. Determine o vetor X, tal que 3X-2V = 15(X - U).
 11 linearmente independentes se e somente se: 1.4. Exercícios 1. Determine o vetor X, tal que X-2V = 15(X - U). Figura 21 14. Determine os vetores X e Y tais que: 1.4.2 Multiplicação por um escalar. Se
11 linearmente independentes se e somente se: 1.4. Exercícios 1. Determine o vetor X, tal que X-2V = 15(X - U). Figura 21 14. Determine os vetores X e Y tais que: 1.4.2 Multiplicação por um escalar. Se
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Figura disponível em: <http://soumaisenem.com.br/fisica/conhecimentos-basicos-e-fundamentais/grandezas-escalares-egrandezas-vetoriais>.
 n. 7 VETORES vetor é um segmento orientado; são representações de forças, as quais incluem direção, sentido, intensidade e ponto de aplicação; o módulo, a direção e o sentido caracterizam um vetor: módulo
n. 7 VETORES vetor é um segmento orientado; são representações de forças, as quais incluem direção, sentido, intensidade e ponto de aplicação; o módulo, a direção e o sentido caracterizam um vetor: módulo
Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc..
 Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
Matriz, Sistema Linear e Determinante
 Matriz, Sistema Linear e Determinante 1.0 Sistema de Equações Lineares Equação linear de n variáveis x 1, x 2,..., x n é uma equação que pode ser expressa na forma a1x1 + a 2 x 2 +... + a n x n = b, onde
Matriz, Sistema Linear e Determinante 1.0 Sistema de Equações Lineares Equação linear de n variáveis x 1, x 2,..., x n é uma equação que pode ser expressa na forma a1x1 + a 2 x 2 +... + a n x n = b, onde
AULA 8- ÁLGEBRA MATRICIAL VERSÃO: OUTUBRO DE 2016
 CURSO DE ADMINISTRAÇÃO CENTRO DE CIÊNCIAS SOCIAIS APLICADAS UNIVERSIDADE CATÓLICA DE PETRÓPOLIS MATEMÁTICA 01 AULA 8- ÁLGEBRA MATRICIAL VERSÃO: 0.1 - OUTUBRO DE 2016 Professor: Luís Rodrigo E-mail: luis.goncalves@ucp.br
CURSO DE ADMINISTRAÇÃO CENTRO DE CIÊNCIAS SOCIAIS APLICADAS UNIVERSIDADE CATÓLICA DE PETRÓPOLIS MATEMÁTICA 01 AULA 8- ÁLGEBRA MATRICIAL VERSÃO: 0.1 - OUTUBRO DE 2016 Professor: Luís Rodrigo E-mail: luis.goncalves@ucp.br
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 1. Matrizes e Sistema de Equações Lineares. 1.1 Corpos
 Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
Geometria Analítica e Álgebra Linear
 NOTAS DE AULA Geometria Analítica e Álgebra Linear Vetores no Espaço Professor: Luiz Fernando Nunes, Dr. 019/Sem_01 Índice Vetores no Espaço Tridimensional... 1.1 Definição... 1. Operações com vetores...
NOTAS DE AULA Geometria Analítica e Álgebra Linear Vetores no Espaço Professor: Luiz Fernando Nunes, Dr. 019/Sem_01 Índice Vetores no Espaço Tridimensional... 1.1 Definição... 1. Operações com vetores...
Aulas práticas de Álgebra Linear
 Ficha 2 Determinantes Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores 1 o semestre 2016/17 Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto
Ficha 2 Determinantes Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores 1 o semestre 2016/17 Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto
Notas de Aula de SLC602 - Geometria Analítica. Wagner Vieira Leite Nunes Departamento de Matemática ICMC - USP
 Notas de Aula de SLC60 - Geometria Analítica Wagner Vieira Leite Nunes Departamento de Matemática ICMC - USP julho de 017 Sumário 1 Introdução 5 Vetores no plano e no espaço 7.1 Introdução.................................................
Notas de Aula de SLC60 - Geometria Analítica Wagner Vieira Leite Nunes Departamento de Matemática ICMC - USP julho de 017 Sumário 1 Introdução 5 Vetores no plano e no espaço 7.1 Introdução.................................................
MA23 - Geometria Anaĺıtica
 MA23 - Geometria Anaĺıtica Unidade 1 - Coordenadas e vetores no plano João Xavier PROFMAT - SBM 8 de agosto de 2013 Coordenadas René Descartes, matemático e filósofo, nasceu em La Have, França, em 31 de
MA23 - Geometria Anaĺıtica Unidade 1 - Coordenadas e vetores no plano João Xavier PROFMAT - SBM 8 de agosto de 2013 Coordenadas René Descartes, matemático e filósofo, nasceu em La Have, França, em 31 de
Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica. ENG1705 Dinâmica de Corpos Rígidos.
 Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica ENG1705 Dinâmica de Corpos Rígidos (Período: 2016.1) Notas de Aula Capítulo 1: VETORES Ivan Menezes ivan@puc-rio.br
Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica ENG1705 Dinâmica de Corpos Rígidos (Período: 2016.1) Notas de Aula Capítulo 1: VETORES Ivan Menezes ivan@puc-rio.br
Métodos Matemáticos II
 Sumário Métodos Matemáticos II Nuno Bastos Licenciatura em Tecnologias e Design Multimédia Escola Superior de Tecnologia de Viseu Gabinete 4 nbastos@mat.estv.ipv.pt http://www.estv.ipv.pt/paginaspessoais/nbastos.
Sumário Métodos Matemáticos II Nuno Bastos Licenciatura em Tecnologias e Design Multimédia Escola Superior de Tecnologia de Viseu Gabinete 4 nbastos@mat.estv.ipv.pt http://www.estv.ipv.pt/paginaspessoais/nbastos.
Álgebra Linear. André Arbex Hallack
 Álgebra Linear André Arbex Hallack 2017 Índice 1 Sistemas Lineares 1 1.1 Corpos............................................. 1 1.2 Sistemas de Equações Lineares............................... 3 1.3 Sistemas
Álgebra Linear André Arbex Hallack 2017 Índice 1 Sistemas Lineares 1 1.1 Corpos............................................. 1 1.2 Sistemas de Equações Lineares............................... 3 1.3 Sistemas
. f3 = 4 e 1 3 e 2. f2 = e 1 e 3, g 1 = e 1 + e 2 + e 3, 2 g 2 = e 1 + e 2,
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-457 Álgebra Linear para Engenharia I Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Dê a matriz de mudança
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-457 Álgebra Linear para Engenharia I Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Dê a matriz de mudança
Capítulo Propriedades das operações com vetores
 Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
Aula 5 - Produto Vetorial
 Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Matrizes. Lino Marcos da Silva
 Matrizes Lino Marcos da Silva lino.silva@univasf.edu.br Introdução Chamamos de matriz a uma tabela de elementos dispostos em linhas e colunas. Por exemplo, ao recolhermos os dados população, área e distância
Matrizes Lino Marcos da Silva lino.silva@univasf.edu.br Introdução Chamamos de matriz a uma tabela de elementos dispostos em linhas e colunas. Por exemplo, ao recolhermos os dados população, área e distância
ficha 2 determinantes
 Exercícios de Álgebra Linear ficha 2 determinantes Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 Determinantes 2 Sendo
Exercícios de Álgebra Linear ficha 2 determinantes Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 Determinantes 2 Sendo
com 3 Incógnitas A interseção do plano paralelo ao plano yz, passando por P, com o eixo x determina a coordenada x.
 Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Aula 25 - Espaços Vetoriais
 Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Geometria Analítica. Geometria Analítica 28/08/2012
 Prof. Luiz Antonio do Nascimento luiz.anascimento@sp.senac.br www.lnascimento.com.br Conjuntos Propriedades das operações de adição e multiplicação: Propriedade comutativa: Adição a + b = b + a Multiplicação
Prof. Luiz Antonio do Nascimento luiz.anascimento@sp.senac.br www.lnascimento.com.br Conjuntos Propriedades das operações de adição e multiplicação: Propriedade comutativa: Adição a + b = b + a Multiplicação
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
ESPAÇO VETORIAL REAL. b) Em relação à multiplicação: (ab) v = a(bv) (a + b) v = av + bv a (u + v ) = au + av 1u = u, para u, v V e a, b R
 ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
Åaxwell Mariano de Barros
 Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ö Ð Ó Å Ö Ò Ó ÒØÖÓ Ò Ü Ø Ì ÒÓÐÓ ÆÓØ ÙÐ ¹ ¼½ ÐÙÐÓ Î ØÓÖ Ð ÓÑ ØÖ Ò Ð Ø Åaxwell Mariano de Barros ËÓ ÄÙ ¹ ÅA ¾¼½½ ËÙÑ Ö Ó 1 Vetores no Espaço 2 1.1 Reta Orientada....................................
Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ö Ð Ó Å Ö Ò Ó ÒØÖÓ Ò Ü Ø Ì ÒÓÐÓ ÆÓØ ÙÐ ¹ ¼½ ÐÙÐÓ Î ØÓÖ Ð ÓÑ ØÖ Ò Ð Ø Åaxwell Mariano de Barros ËÓ ÄÙ ¹ ÅA ¾¼½½ ËÙÑ Ö Ó 1 Vetores no Espaço 2 1.1 Reta Orientada....................................
Notações e revisão de álgebra linear
 Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
ÁLGEBRA LINEAR - MAT0024
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 10 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 10 a Lista de exercícios
1 Álgebra linear matricial
 MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
x 1 3x 2 2x 3 = 0 2 x 1 + x 2 x 3 6x 4 = 2 6 x x 2 3x 4 + x 5 = 1 ( f ) x 1 + 2x 2 3x 3 = 6 2x 1 x 2 + 4x 3 = 2 4x 1 + 3x 2 2x 3 = 4
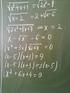 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
multiplicação de número real por matriz (operação externa):
 PÍTULO I O que é Vetor? onsiderações: O conceito de vetor é entendido quando se estuda as Estruturas lgébricas apresentadas nos cursos de Álgebra. Tomando-se um conjunto V (podendo ser conjunto de matrizes,
PÍTULO I O que é Vetor? onsiderações: O conceito de vetor é entendido quando se estuda as Estruturas lgébricas apresentadas nos cursos de Álgebra. Tomando-se um conjunto V (podendo ser conjunto de matrizes,
GA3X1 - Geometria Analítica e Álgebra Linear. Definição (Segmentos orientados de mesmo comprimento, direção e sentido):
 G3X1 - Geometria nalítica e Álgebra Linear 3 Vetores 3.1 Introdução efinição (Segmento orientado): Um segmento orientado é um par ordenado (,) de pontos do espaço. é a origem e é a etremidade do segmento
G3X1 - Geometria nalítica e Álgebra Linear 3 Vetores 3.1 Introdução efinição (Segmento orientado): Um segmento orientado é um par ordenado (,) de pontos do espaço. é a origem e é a etremidade do segmento
1 Matrizes Ortogonais
 Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de Resolva o sistema abaixo para as incógnitas x e y:
 MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
1 a Lista de Exercícios MAT 105 Geometria Analitica
 1 a Lista de Exercícios MAT 105 Geometria Analitica - 2017 1 a parte: Vetores, operações com vetores 1. Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo
1 a Lista de Exercícios MAT 105 Geometria Analitica - 2017 1 a parte: Vetores, operações com vetores 1. Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho
 Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Álgebra Linear e Geometria Analítica
 Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu wwwestvipvpt/paginaspessoais/lucas lucas@matestvipvpt 007/008 Álgebra Linear e Geometria Analítica
Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu wwwestvipvpt/paginaspessoais/lucas lucas@matestvipvpt 007/008 Álgebra Linear e Geometria Analítica
Álgebra Linear I - Aula 10. Roteiro
 Álgebra Linear I - Aula 10 1. Combinação linear de vetores. 2. Subespaços e geradores. Roteiro 1 Combinação linear de vetores Definição 1 (Combinação linear de vetores). Dada um conjunto de vetores U =
Álgebra Linear I - Aula 10 1. Combinação linear de vetores. 2. Subespaços e geradores. Roteiro 1 Combinação linear de vetores Definição 1 (Combinação linear de vetores). Dada um conjunto de vetores U =
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
G1 de Álgebra Linear I Gabarito
 G1 de Álgebra Linear I 2013.1 6 de Abril de 2013. Gabarito 1) Considere o triângulo ABC de vértices A, B e C. Suponha que: (i) o vértice B do triângulo pertence às retas de equações paramétricas r : (
G1 de Álgebra Linear I 2013.1 6 de Abril de 2013. Gabarito 1) Considere o triângulo ABC de vértices A, B e C. Suponha que: (i) o vértice B do triângulo pertence às retas de equações paramétricas r : (
1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0
![1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0 1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0](/thumbs/77/76694592.jpg) 1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
é encontrado no cruzamento da linha i com a coluna j, ou seja, o primeiro índice se refere à linha e o segundo à coluna.
 Ministério da Educação Secretaria de Educação Profissional e Tecnológica Instituto Federal De Santa Catarina Campus São José Professora: ELENIRA OLIVEIRA VILELA COMPONENTE CURRICULAR: ALG ÁLG. LINEAR MATRIZES
Ministério da Educação Secretaria de Educação Profissional e Tecnológica Instituto Federal De Santa Catarina Campus São José Professora: ELENIRA OLIVEIRA VILELA COMPONENTE CURRICULAR: ALG ÁLG. LINEAR MATRIZES
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Álgebra Linear Semana 04
 Álgebra Linear Semana 04 Diego Marcon 17 de Abril de 2017 Conteúdo 1 Produto de matrizes 1 11 Exemplos 2 12 Uma interpretação para resolução de sistemas lineares 3 2 Matriz transposta 4 3 Matriz inversa
Álgebra Linear Semana 04 Diego Marcon 17 de Abril de 2017 Conteúdo 1 Produto de matrizes 1 11 Exemplos 2 12 Uma interpretação para resolução de sistemas lineares 3 2 Matriz transposta 4 3 Matriz inversa
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Matrizes Inversas 1 Matriz Inversa e Propriedades 2 Cálculo da matriz
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Matrizes Inversas 1 Matriz Inversa e Propriedades 2 Cálculo da matriz
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Lembremos que um paralelogramo é um quadrilátero (figura geométrica com quatro lados) cujos lados opostos são paralelos.
 Capítulo 5 Vetores no plano 1. Paralelogramos Lembremos que um paralelogramo é um quadrilátero (figura geométrica com quatro lados) cujos lados opostos são paralelos. Usando congruência de triângulos,
Capítulo 5 Vetores no plano 1. Paralelogramos Lembremos que um paralelogramo é um quadrilátero (figura geométrica com quatro lados) cujos lados opostos são paralelos. Usando congruência de triângulos,
Questões. 2ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1
 ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1 Questões 1. Sejam A, B, C e D vértices de um quadrado. Quantos vetores diferentes entre si podem ser definidos
ª Lista de Exercícios (Geometria Analítica e Álgebra Linear) Prof. Helder G. G. de Lima 1 Questões 1. Sejam A, B, C e D vértices de um quadrado. Quantos vetores diferentes entre si podem ser definidos
Lista de Álgebra Linear Aplicada
 Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
I Lista de Álgebra Linear /02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple
 1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
