PERSPECTIVA ISOMÉTRICA
|
|
|
- Neuza Marinho Câmara
- 7 Há anos
- Visualizações:
Transcrição
1 PERSPECTIVA ISOMÉTRICA Aluna: Patricia Carvalho Souza Orientadora: Anna Virgínia Machado
2 Roteiro Perspectiva o Tipos de Perspectiva Perspectiva Axonométrica o Linhas Isométricas e Não Isométricas Papel Isométrico Aplicações Construção o Exercícios o Bibliografia
3 Perspectiva Perspectiva é a representação tridimensional de um objeto de forma que suas três faces principais sejam visíveis em um único plano, de forma a facilitar a visão do objeto em relação às vistas. Ela pode ser feita de várias maneiras,com resultados diferentes, que podem se assemelhar mais, ou menos à visão humana.
4 Tipos de Perspectiva As perspectivas podem ser divididas por tipos dependendo de como elas representam o objeto. 1. Paralelas: a. Axonométrica: Isométrica Dimétrica Trimétrica b. Oblíqua: Cavaleira 2. Cônica.
5 As principais maneiras de representação são:
6 Perspectiva Axonométrica Axonometria é o processo de representação no qual o objeto é perspectivado em um sistema de 3 eixos. A perspectiva axonométrica é resultante da projeção ortogonal de um objeto em estudo tendo este sofrido uma rotação em torno de um eixo vertical e inclinando-se para frente de maneira a deixar à vista três faces do objeto.
7 A representa o objeto em proporções iguais de suas reais dimensões. (largura, altura e profundidade) e é muito utilizada na representação de projeto de tubulações.
8 No caso da perspectiva isométrica, a rotação que temos é de 45 para a direita e a inclinação de 35 para frente, de modo que a diagonal principal do objeto faça 90 com o plano, resultando em 3 eixos com 120 entre si.
9 Portanto, na exata, as dimensões marcadas sobre os eixos devem ser reduzidas de 82% da dimensão real, para que possa ser obtido um volume exato do objeto. Porém na Engenharia utilizamos a simplificada, adotando as verdadeiras grandezas transferidas diretamente das vistas ortogonais apenas nas linhas paralelas aos eixos isométricos, acarretando em uma representação do objeto 23% maior que a perspectiva isométrica exata.
10 Linhas Isométricas As linhas isométricas são todas aquelas traçadas paralelamente a algum dos eixos isométricos. As retas r,s,t e u são linhas isométricas: r e s são linhas isométricas paralelas ao eixo y. t é uma linha isométrica, pois é paralela ao eixo z. u é isométrica pois é paralela ao eixo x.
11 Linhas Não Isométricas Todas as linhas não paralelas aos eixos isométricos são chamadas linhas não isométricas, por isso não serão representadas em verdadeira grandeza. Na figura temos que a reta v é uma linha não isométrica.
12 Desenhando as não isométricas As linhas não isométricas são traçadas utilizando-se dois pontos que estejam contidos na mesma. Estes pontos serão localizados através de suas coordenadas medidas sobre os eixos isométricos. Conhecendo dois pontos é possível traçar a reta.
13 Papel Isométrico Para facilitar o traçado da perspectiva isométrica à mão livre podemos utilizar o papel isométrico, composto de várias linhas isométricas previamente desenhadas.
14 Aplicações A perspectiva isométrica é a mais comumente utilizada no dia-a-dia de escritórios de projeto sejam eles de arquitetura, engenharia, design. A larga utilização desta perspectiva é devido à sua simplicidade e facilidade de compreensão. Porém, a perspectiva, apresenta desvantagens, pois alguns pontos dos objetos representados podem criar ilusões de ocupar o mesmo local no plano bidimensional apesar de terem localizações diferentes no espaço.
15 ESCHER, M.C - Belvedere 1958 ESCHER, M.C - Waterfall 1961
16 Aplicações Desenho de peças mecânicas
17 Design de Interiores
18 Arquitetura
19 Desenho de Tubulações Ver o nome do livro com o Bruno
20 Desenho de Tubulações
21 Muitos jogos antigos de computador como SimCity, também utilizavam a perspectiva isométrica como meio de simular uma realidade tridimensional
22 Construção da Constrói-se os eixos isométricos com ajuda dos esquadros
23 Marcar as medidas das dimensões do objeto em cima dos eixos, lembrando que apenas será possível visualizar três faces do objeto. Se tivermos a lateral esquerda representada na vista, esta será representada na esquerda do objeto enquanto a frontal será representada na direita, caso se tenha a lateral direita, a frontal ficará na esquerda.
24 Fechar o volume do objeto utilizando retas paralelas aos eixos com auxilio dos esquadros
25 Utilizar o mesmo procedimento para os detalhes do objeto
26 Reforçar as arestas do objeto e apagar as linhas auxiliares
27 de Circunferências A representação de circunferências é feita pela elipse isométrica, por ser de fácil construção utilizando um traçado de quatro centros. Esta elipse é um pouco menos alongada que a elipse verdadeira, porém tal imperfeição é mínima e não compromete a perspectiva.
28 Construção de elipses Inicialmente inscreve-se a circunferência em um quadrado
29 Desenhar este em perspectiva, marcando-se os pontos médios dos lados.
30 A partir dos vértices opostos mais próximos, traçamos retas passando pelos pontos médios diretamente opostos à estes, formando então quatro centros para o posicionamento do compasso.
31 Posiciona-se a ponta seca do compasso em cada um dos centros, traçando arcos a partir dos pontos médios dos lados.
32 Por fim, reforça-se os arcos, apagando as linhas auxiliares.
33 Construindo Elipses Paralelas Vamos utilizar como exemplo a construção de um cilindro. Para construirmos elipses paralelas sem ter que traçar o quadrado de base da isométrica, basta transferir os quatro centros. Esta transferência é um método bem fácil que utiliza apenas linhas isométricas e transferência de distância entre os planos que contém as elipses paralelas.
34 Traçar a elipse inicial com todos seus centros
35 Por cada um dos centros, traçar uma linha isométrica em direção perpendicular ao plano que contém a elipse.
36 Sobre estas linhas deve-se marcar a distância (d) entre os planos que contém as elipses, no caso a profundidade do objeto. Estes pontos serão os novos centros.
37 Utilizando as mesmas aberturas que na primeira elipse, e os novos centros, traçamos então a elipse paralela.
38 Para completar o cilindro devemos traçar linhas isométricas tangentes às duas elipses.
39 Por fim, reforçam-se os arcos e as linhas tangentes, apagando as linhas auxiliares.
40 Exemplo 1
41 Resposta
42 Exemplo 2
43 Resposta
44 Exemplo 3
45 Resposta
46 Exemplo 4
47 Resposta
48 Exemplo 5
49 Resposta
50 Exemplo 6
51 Resposta
52 Exemplo 7
53 Resposta
54 Exemplo 8
55 Resposta
56 Exemplo 9
57 Resposta
58 Bibliografia FELICIANO, Flávio Felix. Desenho Técnico:. Disponível em: < Acesso em: 13 maio DEMARQUI, Edgar Nogueira. Desenho Técnico I: Projeção Perspectiva. Disponível em: < erspectivas.pdf>. Acesso em: 19 maio GRANATO, Marcelo; SANTANA, Rodrigo; CLAUDINO, Rogério.. Disponível em: < Acesso em: 10 maio 2012.
59 Bibliografia LIMA, Elvana. Desenho Técnico: Lista de Exercícios. Disponível em: < Acesso em: 15 maio M.C.ESCHER. Picture Gallery. Disponível em: < Acesso em: 12 jul ESTEPHANIO, Carlos. Desenho Técnico Básico: 2º e 3º Graus. Rio de Janeiro: Ao Livro Técnico, 1984.
60 Bibliografia ESTEPHANIO, Carlos. Desenho Técnico: Uma Linguagem Básica. Terceira edição Rio de Janeiro: Editora Independente, 1994.Desenho Técnico - Uma linguagem básica - Carlos Estephanio RIGHETTO, Leonardo; PEREIRA, Manuel Augusto; MOREIRA, Roger Matsumoto.Apostila de Desenho Técnico. Rio de Janeiro: Departamento de Desenho Técnico Uff, 2000.
DESENHO TÉCNICO I. Prof. Peterson Jaeger. APOSTILA Versão 2013
 APOSTILA Versão 2013 Prof. Peterson Jaeger 1. Folhas 2. Régua paralela e esquadros 3. Distinção de traços 4. Uso do compasso 5. Construções geométricas básicas 6. Tangentes e concordantes 7. Caligrafia
APOSTILA Versão 2013 Prof. Peterson Jaeger 1. Folhas 2. Régua paralela e esquadros 3. Distinção de traços 4. Uso do compasso 5. Construções geométricas básicas 6. Tangentes e concordantes 7. Caligrafia
UNESP DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD. Parte 6/5: Prof. Víctor O. Gamarra Rosado
 UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
Projeção ortográfica e perspectiva isométrica
 Projeção ortográfica e perspectiva isométrica Introdução Para quem vai ler e interpretar desenhos técnicos, é muito importante saber fazer a correspondência entre as vistas ortográficas e o modelo representado
Projeção ortográfica e perspectiva isométrica Introdução Para quem vai ler e interpretar desenhos técnicos, é muito importante saber fazer a correspondência entre as vistas ortográficas e o modelo representado
EQUIPE DE PROFESSORES DE DESENHO UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA DEPTO. DE ENGENHARIA DE CONSTRUÇÃO CIVIL (PCC)
 PCC2110 DESENHO PARA GEOLOGIA VOL. I PERSPECTIVAS EQUIPE DE PROFESSORES DE DESENHO UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA DEPTO. DE ENGENHARIA DE CONSTRUÇÃO CIVIL (PCC) 2005 ÍNDICE: 1. PERSPECTIVA
PCC2110 DESENHO PARA GEOLOGIA VOL. I PERSPECTIVAS EQUIPE DE PROFESSORES DE DESENHO UNIVERSIDADE DE SÃO PAULO ESCOLA POLITÉCNICA DEPTO. DE ENGENHARIA DE CONSTRUÇÃO CIVIL (PCC) 2005 ÍNDICE: 1. PERSPECTIVA
Escalas ESCALAS COTAGEM
 Escalas Antes de representar objectos, modelos, peças, etc. Deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas no papel
Escalas Antes de representar objectos, modelos, peças, etc. Deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas no papel
Desenho Técnico e Geometria Descritiva Construções Geométricas. Construções Geométricas
 Desenho Técnico e Geometria Descritiva Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Bissetriz - é a reta que divide um ângulo qualquer em dois ângulos iguais, partindo do vértice deste
Desenho Técnico e Geometria Descritiva Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Bissetriz - é a reta que divide um ângulo qualquer em dois ângulos iguais, partindo do vértice deste
Construções Geométricas
 Desenho Técnico e CAD Técnico Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Ângulo - é a região plana limitada por duas semirretas de mesma origem. Classificação dos ângulos: Tipos
Desenho Técnico e CAD Técnico Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Ângulo - é a região plana limitada por duas semirretas de mesma origem. Classificação dos ângulos: Tipos
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE. Professor: João Carmo
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO O traçado de linhas retas PERPENDICULARES, PARALELAS e OBLÍQUAS é feito com o auxílio de esquadros,
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO O traçado de linhas retas PERPENDICULARES, PARALELAS e OBLÍQUAS é feito com o auxílio de esquadros,
EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA
 1 EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA 1. SEJA O CUBO DADO NA FIGURA ABAIXO CUJOS VÉRTICES AB PERTENCEM À LT. PERGUNTA-SE: A) QUE TIPO DE RETAS PASSA PELAS ARESTAS EF, EC, EG. B) QUE TIPO DE RETAS PASSA
1 EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA 1. SEJA O CUBO DADO NA FIGURA ABAIXO CUJOS VÉRTICES AB PERTENCEM À LT. PERGUNTA-SE: A) QUE TIPO DE RETAS PASSA PELAS ARESTAS EF, EC, EG. B) QUE TIPO DE RETAS PASSA
Supressão de vistas em peças prismáticas e piramidais
 Supressão de vistas em peças prismáticas e piramidais A UU L AL A Em determinadas peças, a disposição adequada das cotas, além de informar sobre o tamanho, também permite deduzir as formas das partes cotadas.
Supressão de vistas em peças prismáticas e piramidais A UU L AL A Em determinadas peças, a disposição adequada das cotas, além de informar sobre o tamanho, também permite deduzir as formas das partes cotadas.
UNIVERSIDADE FEDERAL DE SANTA MARIA PROGRAMA DE DISCIPLINA
 UNIVERSIDADE FEDERAL DE SANTA MARIA PROGRAMA DE DISCIPLINA DEPARTAMENTO: EXPRESSÃO GRÁFICA IDENTIFICAÇÃO DA DISCIPLINA: CÓDIGO NOME ( T - P ) EPG 1015 DESENHO TÉCNICO PARA AGRONOMIA (1-2) OBJETIVOS - ao
UNIVERSIDADE FEDERAL DE SANTA MARIA PROGRAMA DE DISCIPLINA DEPARTAMENTO: EXPRESSÃO GRÁFICA IDENTIFICAÇÃO DA DISCIPLINA: CÓDIGO NOME ( T - P ) EPG 1015 DESENHO TÉCNICO PARA AGRONOMIA (1-2) OBJETIVOS - ao
Construções Geométricas Usuais
 Construções Geométricas Usuais Rectas. Ângulos. Circunferência e círculo. Tangentes a circunferências. Polígonos. Rectas Duas rectas dizem-se perpendiculares quando dividem o espaço em quatro partes iguais,
Construções Geométricas Usuais Rectas. Ângulos. Circunferência e círculo. Tangentes a circunferências. Polígonos. Rectas Duas rectas dizem-se perpendiculares quando dividem o espaço em quatro partes iguais,
Sistemas de Projeção Perpectivas
 Universidade Federal de Juiz de Fora - UFJF Faculdade de Arquitetura e Urbanismo - FAU Departamento de Projeto, Representação e Tecnologia Disciplina: Representação Manual Técnica I Professor: Emmanuel
Universidade Federal de Juiz de Fora - UFJF Faculdade de Arquitetura e Urbanismo - FAU Departamento de Projeto, Representação e Tecnologia Disciplina: Representação Manual Técnica I Professor: Emmanuel
Copyright de todos artigos, textos, desenhos e lições. A reprodução parcial ou total deste ebook só é permitida através de autorização por escrito de
 1 Veja nesta aula uma introdução aos elementos básicos da perspectiva. (Mateus Machado) 1. DEFINIÇÃO INTRODUÇÃO A PERSPECTIVA Podemos dizer que a perspectiva é sem dúvida uma matéria dentro do desenho
1 Veja nesta aula uma introdução aos elementos básicos da perspectiva. (Mateus Machado) 1. DEFINIÇÃO INTRODUÇÃO A PERSPECTIVA Podemos dizer que a perspectiva é sem dúvida uma matéria dentro do desenho
O objetivo desta aula é apresentar os principais p tipos de perspectivas utilizados no desenho técnico e no desenho arquitetônico, destacando suas
 Perspectivas Prof. Cristiano Arbex Introdução O objetivo desta aula é apresentar os principais p tipos de perspectivas utilizados no desenho técnico e no desenho arquitetônico, destacando suas características
Perspectivas Prof. Cristiano Arbex Introdução O objetivo desta aula é apresentar os principais p tipos de perspectivas utilizados no desenho técnico e no desenho arquitetônico, destacando suas características
AULA 02 Normatização, Formatação, Caligrafia, Sistema de Projeções e Introdução ao Desenho técnico. 2012/02
 AULA 02 Normatização, Formatação, Caligrafia, Sistema de Projeções e Introdução ao Desenho técnico. 2012/02 Tomando como exemplo o trabalho desenvolvido anteriormente (desenho de cadeira), podemos concluir
AULA 02 Normatização, Formatação, Caligrafia, Sistema de Projeções e Introdução ao Desenho técnico. 2012/02 Tomando como exemplo o trabalho desenvolvido anteriormente (desenho de cadeira), podemos concluir
Projeções paralelas. Professor: João Carmo
 Projeções paralelas Professor: João Carmo Projeções paralelas Introdução As múltiplas vistas (projeções ortogonais) não mostram, de forma direta, a configuração tridimensional do objeto. Elas são mais
Projeções paralelas Professor: João Carmo Projeções paralelas Introdução As múltiplas vistas (projeções ortogonais) não mostram, de forma direta, a configuração tridimensional do objeto. Elas são mais
A área do triângulo OAB esboçado na figura abaixo é
 Questão 01 - (UNICAMP SP) No plano cartesiano, a reta de equação = 1 intercepta os eios coordenados nos pontos A e B. O ponto médio do segmento AB tem coordenadas (4, 4/) b) (, ) c) (4, 4/) d) (, ) Questão
Questão 01 - (UNICAMP SP) No plano cartesiano, a reta de equação = 1 intercepta os eios coordenados nos pontos A e B. O ponto médio do segmento AB tem coordenadas (4, 4/) b) (, ) c) (4, 4/) d) (, ) Questão
NBR 10126/87 CORTE TOTAL LONGITUDINAL E TRANSVERSAL
 NBR 10126/87 CORTE TOTAL LONGITUDINAL E TRANSVERSAL Podemos definir corte como sendo a representação gráfica no desenho da característica do elemento, através de linhas, símbolos, notas e valor numérico
NBR 10126/87 CORTE TOTAL LONGITUDINAL E TRANSVERSAL Podemos definir corte como sendo a representação gráfica no desenho da característica do elemento, através de linhas, símbolos, notas e valor numérico
Representação de sólidos
 110 Representação de sólidos Pirâmides e prismas regulares com base(s) contida(s) em planos verticais ou de topo Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1. diedro e com a
110 Representação de sólidos Pirâmides e prismas regulares com base(s) contida(s) em planos verticais ou de topo Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1. diedro e com a
Medida de ângulos. Há muitas situações em que uma pequena
 A UUL AL A Medida de ângulos Há muitas situações em que uma pequena mudança de ângulo causa grandes modificações no resultado final. Veja alguns casos nos quais a precisão dos ângulos é fundamental: Introdução
A UUL AL A Medida de ângulos Há muitas situações em que uma pequena mudança de ângulo causa grandes modificações no resultado final. Veja alguns casos nos quais a precisão dos ângulos é fundamental: Introdução
Universidade Federal do Espírito Santo - UFES. Centro Universitário Norte do Espírito Santo - CEUNES
 Universidade Federal do Espírito Santo - UFES Centro Universitário Norte do Espírito Santo - CEUNES APOSTILA Disciplina: Expressão Gráfica Curso: Agronomia Professor: Sidney Sára Zanetti São Mateus - ES
Universidade Federal do Espírito Santo - UFES Centro Universitário Norte do Espírito Santo - CEUNES APOSTILA Disciplina: Expressão Gráfica Curso: Agronomia Professor: Sidney Sára Zanetti São Mateus - ES
CINEMÁTICA DO PONTO MATERIAL
 1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
Perspectivas Professora Valéria Peixoto Borges
 Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Agroalimentar Perspectivas Professora Valéria Peixoto Borges INTRODUÇÃO A perspectiva é um tipo especial de projeção, na qual são
Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Agroalimentar Perspectivas Professora Valéria Peixoto Borges INTRODUÇÃO A perspectiva é um tipo especial de projeção, na qual são
Conjuntos mecânicos II
 A UU L AL A Conjuntos mecânicos II Nesta aula trataremos de outro assunto também relacionado a conjuntos mecânicos: o desenho de conjunto. Introdução Desenho de conjunto Desenho de conjunto é o desenho
A UU L AL A Conjuntos mecânicos II Nesta aula trataremos de outro assunto também relacionado a conjuntos mecânicos: o desenho de conjunto. Introdução Desenho de conjunto Desenho de conjunto é o desenho
Metrologia Professor: Leonardo Leódido
 Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
Capítulo 5 VISTAS EM CORTE
 apítulo 5 VISTS EM ORTE Definição Quando a peça a ser desenhada possuir muitos detalhes internos, detalhes invisíveis, as projeções ortogonais terão muitas linhas tracejadas e poderão dificultar a interpretação
apítulo 5 VISTS EM ORTE Definição Quando a peça a ser desenhada possuir muitos detalhes internos, detalhes invisíveis, as projeções ortogonais terão muitas linhas tracejadas e poderão dificultar a interpretação
3,00m. 3,00m. Dado o layout da planta de um quarto ou qualquer ambiente que vc queira perspectivar... escala do layout: 1:50.
 EXPRESSÃO E REPRESENTAÇÃO GRÁICA II - Prof. Carol e Neco Dado o layout da planta de um quarto ou qualquer ambiente que vc queira perspectivar... escala do layout: : método para perspectiva com um ponto
EXPRESSÃO E REPRESENTAÇÃO GRÁICA II - Prof. Carol e Neco Dado o layout da planta de um quarto ou qualquer ambiente que vc queira perspectivar... escala do layout: : método para perspectiva com um ponto
P E R S P E C T I V A S
 P E R S P E C T I V A S Definição de perspectiva : Ciência da representação gráfica dos objetos com o aspecto visto por nossos olhos. A palavra perspectiva vem do latim - Perspicere (ver através de) e
P E R S P E C T I V A S Definição de perspectiva : Ciência da representação gráfica dos objetos com o aspecto visto por nossos olhos. A palavra perspectiva vem do latim - Perspicere (ver através de) e
FEUP-DEMEGI-SDI Desenho Técnico APL-1.1. Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO. (1º ano)
 FEUP-DEMEGI-SDI Desenho Técnico APL-1.1 Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO (1º ano) (Introdução aos Sistemas e Componentes Mecânicos Normalizados de utilização corrente) Aulas Práticas
FEUP-DEMEGI-SDI Desenho Técnico APL-1.1 Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO (1º ano) (Introdução aos Sistemas e Componentes Mecânicos Normalizados de utilização corrente) Aulas Práticas
GDC I AULA TEÓRICA 06
 GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
CIRCUNFERÊNCIA. Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência. O AB s CD t T s AB 2
 CIRCUNFERÊNCIA ELEMENTOS DA CIRCUNFERÊNCIA N t T C A B D X s p Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência O AB s CD t T s AB 2 PX / Algumas
CIRCUNFERÊNCIA ELEMENTOS DA CIRCUNFERÊNCIA N t T C A B D X s p Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência O AB s CD t T s AB 2 PX / Algumas
Manual de. Geometria Descritiva. António Galrinho
 Manual de Geometria Descritiva António Galrinho FICHA TÉCNICA Título Manual de Geometria Descritiva Autor António Galrinho Grafismo Do autor Edição 1ª - 2010 APRESENTAÇÃO Este livro apresenta uma compilação
Manual de Geometria Descritiva António Galrinho FICHA TÉCNICA Título Manual de Geometria Descritiva Autor António Galrinho Grafismo Do autor Edição 1ª - 2010 APRESENTAÇÃO Este livro apresenta uma compilação
18/06/2013. Professora: Sandra Tieppo UNIOESTE Cascavel
 18/06/01 Professora: Sandra Tieppo UNIOESTE Cascavel 1 Superfícies geradas por uma geratriz (g) que passa por um ponto dado V (vértice) e percorre os pontos de uma linha dada d (diretriz), V d. Se a diretriz
18/06/01 Professora: Sandra Tieppo UNIOESTE Cascavel 1 Superfícies geradas por uma geratriz (g) que passa por um ponto dado V (vértice) e percorre os pontos de uma linha dada d (diretriz), V d. Se a diretriz
PROVA PARA OS ALUNOS DE 2º ANO DO ENSINO MÉDIO. 4 cm
 PROVA PARA OS ALUNOS DE º ANO DO ENSINO MÉDIO 1ª Questão: Um cálice com a forma de um cone contém V cm de uma bebida. Uma cereja de forma esférica com diâmetro de cm é colocada dentro do cálice. Supondo
PROVA PARA OS ALUNOS DE º ANO DO ENSINO MÉDIO 1ª Questão: Um cálice com a forma de um cone contém V cm de uma bebida. Uma cereja de forma esférica com diâmetro de cm é colocada dentro do cálice. Supondo
Luis Augusto Koenig Veiga. Fevereiro de 2015 1.2 - VERSÃO PRELIMINAR
 Notas de ula: Parcelamento/ivisão do Solo Visão Geométrica Luis ugusto Koenig Veiga Fevereiro de 2015 1.2 - VERSÃO PRELIINR PRELENTO/IVISÃO O SOLO VISÃO GEOÉTRI Engenharia artográfica e de grimensura -
Notas de ula: Parcelamento/ivisão do Solo Visão Geométrica Luis ugusto Koenig Veiga Fevereiro de 2015 1.2 - VERSÃO PRELIINR PRELENTO/IVISÃO O SOLO VISÃO GEOÉTRI Engenharia artográfica e de grimensura -
Matemática Fascículo 07 Manoel Benedito Rodrigues
 Matemática Fascículo 07 Manoel Benedito Rodrigues Índice Geometria Resumo Teórico...1 Exercícios...4 Dicas...5 Resoluções...7 Geometria Resumo Teórico 1. O volume de um prisma eodeumcilindro (retos ou
Matemática Fascículo 07 Manoel Benedito Rodrigues Índice Geometria Resumo Teórico...1 Exercícios...4 Dicas...5 Resoluções...7 Geometria Resumo Teórico 1. O volume de um prisma eodeumcilindro (retos ou
Capítulo 6 ESCALAS E DIMENSIONAMENTO
 Capítulo 6 ESCALAS E DIMENSIONAMENTO Introdução Ainda que o principal objetivo deste livro seja preparar para a leitura e interpretação de desenho técnico, é necessário abordar os princípios básicos de
Capítulo 6 ESCALAS E DIMENSIONAMENTO Introdução Ainda que o principal objetivo deste livro seja preparar para a leitura e interpretação de desenho técnico, é necessário abordar os princípios básicos de
Aula 01 Introdução à Geometria Espacial Geometria Espacial
 Aula 01 Introdução à 1) Introdução à Geometria Plana Axioma São verdades matemáticas aceitas sem a necessidade de demonstração. 1 1.1) Axioma da Existência Existem infinitos pontos em uma reta (e fora
Aula 01 Introdução à 1) Introdução à Geometria Plana Axioma São verdades matemáticas aceitas sem a necessidade de demonstração. 1 1.1) Axioma da Existência Existem infinitos pontos em uma reta (e fora
INSTITUTO DE APLICAÇÃO FERNANDO RODRIGUES DA SILVEIRA 2ª SÉRIE DO ENSINO MÉDIO PROF. ILYDIO PEREIRA DE SÁ
 INSTITUTO E PLIÇÃO FERNNO RORIGUES SILVEIR 2ª SÉRIE O ENSINO MÉIO PROF. ILYIO PEREIR E SÁ Geometria Espacial: Elementos iniciais de Geometria Espacial Introdução: Geometria espacial (euclidiana) funciona
INSTITUTO E PLIÇÃO FERNNO RORIGUES SILVEIR 2ª SÉRIE O ENSINO MÉIO PROF. ILYIO PEREIR E SÁ Geometria Espacial: Elementos iniciais de Geometria Espacial Introdução: Geometria espacial (euclidiana) funciona
Utilização dos Instrumentos de Desenho Técnico e Normas
 Universidade Regional do Cariri Departamento de Construção Civil Cursos de Tecnologia em Construção Civil DESENHO TÉCNICO 1 - TE 069 Utilização dos Instrumentos de Desenho Técnico e Normas Julho 2015 Prof.ª
Universidade Regional do Cariri Departamento de Construção Civil Cursos de Tecnologia em Construção Civil DESENHO TÉCNICO 1 - TE 069 Utilização dos Instrumentos de Desenho Técnico e Normas Julho 2015 Prof.ª
Descobrindo medidas desconhecidas (I)
 Descobrindo medidas desconhecidas (I) V ocê é torneiro em uma empresa mecânica. Na rotina de seu trabalho, você recebe ordens de serviço acompanhadas dos desenhos das peças que você tem de tornear. Vamos
Descobrindo medidas desconhecidas (I) V ocê é torneiro em uma empresa mecânica. Na rotina de seu trabalho, você recebe ordens de serviço acompanhadas dos desenhos das peças que você tem de tornear. Vamos
Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS
 Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS Definição e Pré-Requisitos Ler um desenho significa entender a forma espacial do objeto representado no desenho bidimensional resultante das projeções ortogonais.
Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS Definição e Pré-Requisitos Ler um desenho significa entender a forma espacial do objeto representado no desenho bidimensional resultante das projeções ortogonais.
Aula 4 Leitura e Interpretação de Desenhos Pearson Education do Brasil. Todos os direitos reservados.
 Aula 4 Leitura e Interpretação de Desenhos slide 1 reservados. Definição e Pré- Requisitos Ler um desenho significa entender a forma espacial do objeto representado O principal pré-requisito para fazer
Aula 4 Leitura e Interpretação de Desenhos slide 1 reservados. Definição e Pré- Requisitos Ler um desenho significa entender a forma espacial do objeto representado O principal pré-requisito para fazer
PONTO E SEGMENTO DE RETA
 1 PONTO E SEGMENTO DE RETA Neste capítulo aborda-se essencialmente o Ponto, elemento geométrico mais simples. Resultado da união de dois pontos, aborda-se também o Segmento de Reta. Com esses elementos
1 PONTO E SEGMENTO DE RETA Neste capítulo aborda-se essencialmente o Ponto, elemento geométrico mais simples. Resultado da união de dois pontos, aborda-se também o Segmento de Reta. Com esses elementos
GEOMETRIA DESCRITIVA... o que é e para que serve!
 GEOMETRIA DESCRITIVA... o que é e para que serve! Desde sempre, o homem, na sua necessidade de comunicação, procurou encontrar um meio de representar as formas dos objectos que o rodeavam. Assim, Gaspar
GEOMETRIA DESCRITIVA... o que é e para que serve! Desde sempre, o homem, na sua necessidade de comunicação, procurou encontrar um meio de representar as formas dos objectos que o rodeavam. Assim, Gaspar
IFSC - Campus São José Área de Refrigeração e Ar Condicionado Prof. Gilson Desenvolvimento de Chapas
 DESENVOLVIMENTO DE CHAPAS Desenvolvimento É o processo empregado para transformar em superfície plana, peças, reservatórios, uniões de tubulações e de dutos, normalmente feitos em chapas, razão pela qual
DESENVOLVIMENTO DE CHAPAS Desenvolvimento É o processo empregado para transformar em superfície plana, peças, reservatórios, uniões de tubulações e de dutos, normalmente feitos em chapas, razão pela qual
1 PONTOS NOTÁVEIS. 1.1 Baricentro. 1.3 Circuncentro. 1.2 Incentro. Matemática 2 Pedro Paulo
 Matemática 2 Pedro Paulo GEOMETRIA PLANA VIII 1 PONTOS NOTÁVEIS 1.1 Baricentro O baricentro é o encontro das medianas de um triângulo. Na figura abaixo, é o ponto médio do lado, é o ponto médio do lado
Matemática 2 Pedro Paulo GEOMETRIA PLANA VIII 1 PONTOS NOTÁVEIS 1.1 Baricentro O baricentro é o encontro das medianas de um triângulo. Na figura abaixo, é o ponto médio do lado, é o ponto médio do lado
MÓDULO 2 ÓPTICA E ONDAS Ronaldo Filho e Rhafael Roger
 ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
RETA. Sumário: Manual de Geometria Descritiva - António Galrinho Reta - 1
 2 RETA O alfabeto da reta é o conjunto das posições genéricas que uma reta pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
2 RETA O alfabeto da reta é o conjunto das posições genéricas que uma reta pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
AULA 09 DESENHO TÉCNICO A GEOMETRIA DESCRITIVA E O SISTEMA MONGEANO. Prof a : Karisa Lorena Carmo Barbosa Pinheiro
 AULA 09 DESENHO TÉCNICO A GEOMETRIA DESCRITIVA E O SISTEMA MONGEANO Prof a : Karisa Lorena Carmo Barbosa Pinheiro UM OLHAR NA NATUREZA As colméias têm um padrão hexagonal... As asas dos insetos têm determinadas
AULA 09 DESENHO TÉCNICO A GEOMETRIA DESCRITIVA E O SISTEMA MONGEANO Prof a : Karisa Lorena Carmo Barbosa Pinheiro UM OLHAR NA NATUREZA As colméias têm um padrão hexagonal... As asas dos insetos têm determinadas
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA
 UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: CÍRCULO TRIGONOMÉTRICO AUTORES: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR:
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: CÍRCULO TRIGONOMÉTRICO AUTORES: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR:
PROJETO DE ESTRADAS Prof o. f D r D. An A de rson on Ma M nzo zo i
 PROJETO DE ESTRADAS Prof. Dr. Anderson Manzoli CONCEITOS: Após traçados o perfil longitudinal e transversal, já se dispõe de dados necessários para uma verificação da viabilidade da locação do greide de
PROJETO DE ESTRADAS Prof. Dr. Anderson Manzoli CONCEITOS: Após traçados o perfil longitudinal e transversal, já se dispõe de dados necessários para uma verificação da viabilidade da locação do greide de
Relações métricas nos triângulos retângulos 1) Usando o teorema de Pitágoras, determine os elementos indicados por x ou y nas figuras seguintes:
 AS RESPOSTAS ESTÃO NO FINAL DOS EXERCÍCIOS. Relações métricas nos triângulos retângulos ) Usando o teorema de Pitágoras, determine os elementos indicados por ou nas figuras seguintes: d) e) f) g) h) 0
AS RESPOSTAS ESTÃO NO FINAL DOS EXERCÍCIOS. Relações métricas nos triângulos retângulos ) Usando o teorema de Pitágoras, determine os elementos indicados por ou nas figuras seguintes: d) e) f) g) h) 0
Matemática Básica Intervalos
 Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Desenho Auxiliado por Computador
 UNIVERSIDADE FEDERAL DE JUIZ DE FORA ENE073 Seminários em Eletrotécnica Desenho Auxiliado por Computador (CAD - Computer Aided Design) Prof. Flávio Vanderson Gomes E-mail: flavio.gomes@ufjf.edu.br Aula
UNIVERSIDADE FEDERAL DE JUIZ DE FORA ENE073 Seminários em Eletrotécnica Desenho Auxiliado por Computador (CAD - Computer Aided Design) Prof. Flávio Vanderson Gomes E-mail: flavio.gomes@ufjf.edu.br Aula
Paquímetro: O pessoal da empresa está chegando à quarta. Um problema. Erros de leitura
 Paquímetro: conservação A UU L AL A O pessoal da empresa está chegando à quarta aula sobre paquímetro. Nesta aula, todos vão aprender a usar corretamente o paquímetro, quais os possíveis erros de leitura
Paquímetro: conservação A UU L AL A O pessoal da empresa está chegando à quarta aula sobre paquímetro. Nesta aula, todos vão aprender a usar corretamente o paquímetro, quais os possíveis erros de leitura
Projeto Rumo ao ITA Exercícios estilo IME
 PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
Licença de uso exclusiva para Petrobrás S.A. Licença de uso exclusiva para Petrobrás S.A.
 ABNT-Associação Brasileira de Normas Técnicas Sede: Rio de Janeiro Av. Treze de Maio, 13-28º andar CEP 20003-900 - Caixa Postal 1680 Rio de Janeiro - RJ Tel.: PABX (021) 210-3122 Fax: (021) 240-8249/532-2143
ABNT-Associação Brasileira de Normas Técnicas Sede: Rio de Janeiro Av. Treze de Maio, 13-28º andar CEP 20003-900 - Caixa Postal 1680 Rio de Janeiro - RJ Tel.: PABX (021) 210-3122 Fax: (021) 240-8249/532-2143
Assunto: Estudo do ponto
 Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / Nome ; Ano/Turma ; N.º
 EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
A perspectiva geométrica é uma projeção que resulta numa imagem semelhante aquela vista pelo nosso sentido da visão.
 PERSPECTIVA GEOMÉTRICA OU EXATA A. Introdução B. Elementos C. Tipos: paralela ou axonométrica / cônica D. Projeção paralela: isométrica, militar, cavaleira. A. Na perspectiva geométrica Utilizamos os sistemas
PERSPECTIVA GEOMÉTRICA OU EXATA A. Introdução B. Elementos C. Tipos: paralela ou axonométrica / cônica D. Projeção paralela: isométrica, militar, cavaleira. A. Na perspectiva geométrica Utilizamos os sistemas
Confecção de plaina de madeira pequena sem capa. A.Etapas do processo de confecção de uma plaina de madeira:
 Confecção de plaina de madeira pequena sem capa A.Etapas do processo de confecção de uma plaina de madeira: 1. Escolha dos componentes 2. Linhas de referência 3. Corte e desbastes B.Sobre as plainas 1.
Confecção de plaina de madeira pequena sem capa A.Etapas do processo de confecção de uma plaina de madeira: 1. Escolha dos componentes 2. Linhas de referência 3. Corte e desbastes B.Sobre as plainas 1.
GEOMETRIA DESCRITIVA A (Bloco I)
 ACTIVIDADES LECTIVAS 1º Período 2º Período 3º Período para o ano lectivo Apresentação 2 ----- ----- 2 x 45 minutos Avaliação 3 Testes 3 Testes 2 Testes 16 x 45 minutos Auto-avaliação 2 2 2 6 x 45 minutos
ACTIVIDADES LECTIVAS 1º Período 2º Período 3º Período para o ano lectivo Apresentação 2 ----- ----- 2 x 45 minutos Avaliação 3 Testes 3 Testes 2 Testes 16 x 45 minutos Auto-avaliação 2 2 2 6 x 45 minutos
DESENHO TÉCNICO ( AULA 03)
 Sólidos Geométricos DESENHO TÉCNICO ( AULA 03) Você já sabe que todos os pontos de uma figura plana localizam-se no mesmo plano. Quando uma figura geométrica tem pontos situados em diferentes planos, temos
Sólidos Geométricos DESENHO TÉCNICO ( AULA 03) Você já sabe que todos os pontos de uma figura plana localizam-se no mesmo plano. Quando uma figura geométrica tem pontos situados em diferentes planos, temos
Representação de rugosidade
 Representação de rugosidade A UU L AL A Existem vários tipos de superfície de peças. Qual o melhor meio para identificar rapidamente cada um desses tipos e o estado das superfícies? Essa questão foi resolvida
Representação de rugosidade A UU L AL A Existem vários tipos de superfície de peças. Qual o melhor meio para identificar rapidamente cada um desses tipos e o estado das superfícies? Essa questão foi resolvida
Chavetas. Agora você já tem uma noção dos elementos
 A UU L AL A Chavetas Agora você já tem uma noção dos elementos de máquinas mais usados para fixar peças: rebite, pino, cavilha, contrapino ou cupilha, parafuso, porcas, arruela e anéis elásticos. Para
A UU L AL A Chavetas Agora você já tem uma noção dos elementos de máquinas mais usados para fixar peças: rebite, pino, cavilha, contrapino ou cupilha, parafuso, porcas, arruela e anéis elásticos. Para
05. COMUNICAÇÃO VISUAL EXTERNA
 05. COMUNICAÇÃO VISUAL EXTERNA 5.1 COMUNICAÇÃO VISUAL EXTERNA AGÊNCIAS Agências sem recuo em relação à calçada 1 2 3 4 Elementos de comunicação visual As fachadas das agências dos Correios, sem recuo em
05. COMUNICAÇÃO VISUAL EXTERNA 5.1 COMUNICAÇÃO VISUAL EXTERNA AGÊNCIAS Agências sem recuo em relação à calçada 1 2 3 4 Elementos de comunicação visual As fachadas das agências dos Correios, sem recuo em
Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas
 Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
6.2. Volumes. Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. APLICAÇÕES DE INTEGRAÇÃO
 APLICAÇÕES DE INTEGRAÇÃO 6.2 Volumes Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. SÓLIDOS IRREGULARES Começamos interceptando S com um plano e obtemos uma região plana
APLICAÇÕES DE INTEGRAÇÃO 6.2 Volumes Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. SÓLIDOS IRREGULARES Começamos interceptando S com um plano e obtemos uma região plana
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos
 MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
Prof. Breno Duarte Site:
 Prof. Breno Duarte Email: brenoldd@hotmail.com Site: www.fenemi.org.br/ifmec O desenho, para transmitir a ideia de três dimensões (3D - comprimento, largura e altura), precisa recorrer a um modo especial
Prof. Breno Duarte Email: brenoldd@hotmail.com Site: www.fenemi.org.br/ifmec O desenho, para transmitir a ideia de três dimensões (3D - comprimento, largura e altura), precisa recorrer a um modo especial
REPRESENTAÇÃO TÉCNICA BÁSICA DE PROJETO ARQUITETÔNICO
 REPRESENTAÇÃO TÉCNICA BÁSICA DE PROJETO ARQUITETÔNICO Reproduzir as plantas baixa, de cobertura e de localização, cortes e fachada frontal da residência apresentada abaixo. O projeto pode sofrer mudanças,
REPRESENTAÇÃO TÉCNICA BÁSICA DE PROJETO ARQUITETÔNICO Reproduzir as plantas baixa, de cobertura e de localização, cortes e fachada frontal da residência apresentada abaixo. O projeto pode sofrer mudanças,
O que é desenho técnico
 1 1 O que é desenho técnico Introdução Quando alguém quer transmitir um recado, pode utilizar a fala ou passar seus pensamentos para o papel na forma de palavras escritas. Quem lê a mensagem fica conhecendo
1 1 O que é desenho técnico Introdução Quando alguém quer transmitir um recado, pode utilizar a fala ou passar seus pensamentos para o papel na forma de palavras escritas. Quem lê a mensagem fica conhecendo
Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas:
 * 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
* 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES
 ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES Nome Nº Turma 3 EJAS Data / / Nota Disciplina Matemática Prof. Elaine e Naísa Valor 30 Instruções: TRABALHO DE
ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES Nome Nº Turma 3 EJAS Data / / Nota Disciplina Matemática Prof. Elaine e Naísa Valor 30 Instruções: TRABALHO DE
Concepção da Forma Arquitetônica_2 bares e restaurantes _ dimensionamento básico
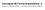 Concepção da Forma Arquitetônica_2 bares e restaurantes _ dimensionamento básico fonte: PANERO, Julius; ZELNIK, Martin. Las Dimensiones en los Espacios Interiores. Mexico: Gustavo Gili, 1996 [1979]. Pg
Concepção da Forma Arquitetônica_2 bares e restaurantes _ dimensionamento básico fonte: PANERO, Julius; ZELNIK, Martin. Las Dimensiones en los Espacios Interiores. Mexico: Gustavo Gili, 1996 [1979]. Pg
MATEMÁTICA PROFESSOR AMBRÓSIO ELIAS CÔNICAS
 QUESTÕES: CÔNICAS 01. Determine o centro, o comprimento do eixo maior, o comprimento do eixo menor, a distância focal, as coordenadas dos focos, a excentricidade e o gráfico das elipses: (x 6)² y² (y 4)²
QUESTÕES: CÔNICAS 01. Determine o centro, o comprimento do eixo maior, o comprimento do eixo menor, a distância focal, as coordenadas dos focos, a excentricidade e o gráfico das elipses: (x 6)² y² (y 4)²
MATEMÁTICA - 2 o ANO MÓDULO 01 PONTO, RETA E PLANO
 MATEMÁTICA - 2 o ANO MÓDULO 01 PONTO, RETA E PLANO r s A E B D C F α G H A B r r s r s α r P s s r α A α B C α P B r A α r α P α r P P α r A B r α A B r r r P α A B α A B F F α α=β α β = α = β α β α β
MATEMÁTICA - 2 o ANO MÓDULO 01 PONTO, RETA E PLANO r s A E B D C F α G H A B r r s r s α r P s s r α A α B C α P B r A α r α P α r P P α r A B r α A B r r r P α A B α A B F F α α=β α β = α = β α β α β
Cônicas. 2. (Fuvest 2014) Considere a circunferência λ de equação cartesiana parábola α de equação. x y 4y 0 e a. y 4 x.
 Cônicas 1. (Espcex (Aman) 014) Sobre a curva 9x + 5y 6x + 50y 164 = 0, assinale a alternativa correta. a) Seu centro é (,1). b) A medida do seu eixo maior é 5. c) A medida do seu eixo menor é 9. d) A distância
Cônicas 1. (Espcex (Aman) 014) Sobre a curva 9x + 5y 6x + 50y 164 = 0, assinale a alternativa correta. a) Seu centro é (,1). b) A medida do seu eixo maior é 5. c) A medida do seu eixo menor é 9. d) A distância
LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA. 01) Dados os vetores e, determine o valor da expressão vetorial. Resp: A=51
 1 LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA 01) Dados os vetores e, determine o valor da expressão vetorial. A=51 02) Decomponha o vetor em dois vetores tais que e, com. 03) Dados os vetores, determine
1 LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA 01) Dados os vetores e, determine o valor da expressão vetorial. A=51 02) Decomponha o vetor em dois vetores tais que e, com. 03) Dados os vetores, determine
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1. Coordenadas UTM
 UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas UTM Recife, 2014 Modelo Plano Considera a porção da Terra em estudo com sendo plana. É a simplificação
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas UTM Recife, 2014 Modelo Plano Considera a porção da Terra em estudo com sendo plana. É a simplificação
Figuras geométricas planas. Joyce Danielle. e espaciais
 Figuras geométricas planas Joyce Danielle e espaciais Figuras geométricas planas Joyce Danielle UNIVERSIDADE FEDERAL DE ALAGOAS 2 Apresentação Na geometria plana vamos então nos atentar ao método de cálculo
Figuras geométricas planas Joyce Danielle e espaciais Figuras geométricas planas Joyce Danielle UNIVERSIDADE FEDERAL DE ALAGOAS 2 Apresentação Na geometria plana vamos então nos atentar ao método de cálculo
Tecnologias no Ensino de Matemática
 Tecnologias no Ensino de Matemática Profa. Andréa Cardoso ROTEIRO DA ATIVIDADE PRÁTICA 2 Data da realização: 10 de março de 2015 Objetivo da atividade: Explorar funcionalidades do GeoGebra. ATIVIDADE 01:
Tecnologias no Ensino de Matemática Profa. Andréa Cardoso ROTEIRO DA ATIVIDADE PRÁTICA 2 Data da realização: 10 de março de 2015 Objetivo da atividade: Explorar funcionalidades do GeoGebra. ATIVIDADE 01:
. B(x 2, y 2 ). A(x 1, y 1 )
 Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
FAUTL 2012/2013 2º SEMESTRE Faculdade de arquitetura turma ED Aluna: Bruna Bergamaschi Tavares Número mecanográfico: 20128249
 FAUTL 2012/2013 2º SEMESTRE Faculdade de arquitetura turma ED Aluna: Bruna Bergamaschi Tavares Número mecanográfico: 20128249 Modelação Tridimensional exercício nº1: roofing relatório Como determinado
FAUTL 2012/2013 2º SEMESTRE Faculdade de arquitetura turma ED Aluna: Bruna Bergamaschi Tavares Número mecanográfico: 20128249 Modelação Tridimensional exercício nº1: roofing relatório Como determinado
UNIVERSIDADE VALE DO RIO DOCE
 UNIVERSIDADE VALE DO RIO DOCE DISCIPLINA: GEOMETRIA DESCRITIVA FAENGE FACULDADE DE ENGENHARIA CURSOS - ENGENHARIA CIVIL - ENGENHARIA CIVIL E AMBIENTAL 1 SUMÁRIO - Apresentação Pag 3 - Noções de Projeções
UNIVERSIDADE VALE DO RIO DOCE DISCIPLINA: GEOMETRIA DESCRITIVA FAENGE FACULDADE DE ENGENHARIA CURSOS - ENGENHARIA CIVIL - ENGENHARIA CIVIL E AMBIENTAL 1 SUMÁRIO - Apresentação Pag 3 - Noções de Projeções
FIGURAS DE LISSAJOUS
 FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
20 TANGÊNCIA E CONCORDÂNCIA 20.1 PROPRIEDADES DE TANGÊNCIA
 144 20 TNGÊNI E ONORDÂNI 20.1 PROPRIEDDES DE TNGÊNI Definições: 1) tangente a uma curva é uma reta que tem um só ponto em comum com esta curva. 2) Duas curvas são tangentes num ponto dado T, quando as
144 20 TNGÊNI E ONORDÂNI 20.1 PROPRIEDDES DE TNGÊNI Definições: 1) tangente a uma curva é uma reta que tem um só ponto em comum com esta curva. 2) Duas curvas são tangentes num ponto dado T, quando as
Programa Institucional de Bolsas de Iniciação à Docência Projeto Matemática 1 Coordenadora Professora Drª Elisangela Campos. Teorema de Pitágoras
 Programa Institucional de Bolsas de Iniciação à Docência Projeto Matemática 1 Coordenadora Professora Drª Elisangela Campos Teorema de Pitágoras Curitiba 2014 CONTEÚDO: Teorema de Pitágoras DURAÇAO: 1
Programa Institucional de Bolsas de Iniciação à Docência Projeto Matemática 1 Coordenadora Professora Drª Elisangela Campos Teorema de Pitágoras Curitiba 2014 CONTEÚDO: Teorema de Pitágoras DURAÇAO: 1
Propriedade: Num trapézio isósceles os ângulos de uma mesma base são iguais e as diagonais são também iguais.
 125 19 QUADRILÁTEROS Propriedades 1) Num quadrilátero qualquer ABCD a soma dos ângulos internos é 1800. 2) Um quadrilátero ABCD é inscritível quando seus vértices pertence a uma mesma circunferência. 3)
125 19 QUADRILÁTEROS Propriedades 1) Num quadrilátero qualquer ABCD a soma dos ângulos internos é 1800. 2) Um quadrilátero ABCD é inscritível quando seus vértices pertence a uma mesma circunferência. 3)
Equações paramétricas da Reta
 39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO 2: ILUMINAÇÃO NATURAL
 Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO : INSOLAÇÃO MÓDULO : ILUMINAÇÃO NATURAL MÓDULO : ILUMINAÇÃO DE INTERIORES Docente: Claudete Gebara J. Callegaro
Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO : INSOLAÇÃO MÓDULO : ILUMINAÇÃO NATURAL MÓDULO : ILUMINAÇÃO DE INTERIORES Docente: Claudete Gebara J. Callegaro
SOMBRAS II. Sumário: Manual de Geometria Descritiva - António Galrinho Sombras II - 1
 14 SOMBRAS II Neste capítulo mostra-se como se determinam sombras próprias e projetadas de sólidos sobre os planos de projeção, nomeadamente de pirâmides, prismas, cones e cilindros. Sumário: 2. Sombras
14 SOMBRAS II Neste capítulo mostra-se como se determinam sombras próprias e projetadas de sólidos sobre os planos de projeção, nomeadamente de pirâmides, prismas, cones e cilindros. Sumário: 2. Sombras
Por que as antenas são parabólicas?
 Por que as antenas são parabólicas? Adaptado do artigo de Eduardo Wagner A palavra parábola está, para os estudantes do ensino médio, associada ao gráfico da função polinomial do segundo grau. Embora quase
Por que as antenas são parabólicas? Adaptado do artigo de Eduardo Wagner A palavra parábola está, para os estudantes do ensino médio, associada ao gráfico da função polinomial do segundo grau. Embora quase
ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI PIBID. 16/04/2014 e 22/04/2014. Bolsistas: Mévelin Maus, Milena Poloni Pergher e Odair José Sebulsqui.
 ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI PIBID 16/04/2014 e 22/04/2014 Bolsistas: Mévelin Maus, Milena Poloni Pergher e Odair José Sebulsqui. Supervisora: Marlete Basso Roman Disciplina: Matemática
ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI PIBID 16/04/2014 e 22/04/2014 Bolsistas: Mévelin Maus, Milena Poloni Pergher e Odair José Sebulsqui. Supervisora: Marlete Basso Roman Disciplina: Matemática
GEOMETRIA DO TAXISTA. (a -b )² + (a -b )²
 GEOMETRI O TXIST Geometria do Taxista é uma geometria não-euclidiana, no sentido em que a noção de distância não é a mesma e acordo com o desenho abaixo, suponhamos um motorista de táxi que apanha um cliente
GEOMETRI O TXIST Geometria do Taxista é uma geometria não-euclidiana, no sentido em que a noção de distância não é a mesma e acordo com o desenho abaixo, suponhamos um motorista de táxi que apanha um cliente
Como fazer para deixar firme uma estante de hastes com prateleiras que está balançando para os lados?
 o triângulo é uma das figuras mais importantes da Geometria, e também uma das mais interessantes. Na nossa vida diária, existem bons exemplos de aplicação de triângulos e de suas propriedades. Quer ver
o triângulo é uma das figuras mais importantes da Geometria, e também uma das mais interessantes. Na nossa vida diária, existem bons exemplos de aplicação de triângulos e de suas propriedades. Quer ver
Projeto arquitetônico: Cortes Professora Valéria Peixoto Borges
 Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Agroalimentar Projeto arquitetônico: Cortes Professora Valéria Peixoto Borges DEFINIÇÃO Os CORTES são representações de vistas ortográficas
Universidade Federal de Campina Grande Centro de Ciências e Tecnologia Agroalimentar Projeto arquitetônico: Cortes Professora Valéria Peixoto Borges DEFINIÇÃO Os CORTES são representações de vistas ortográficas
