Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais Acopladas
|
|
|
- Brian das Neves
- 5 Há anos
- Visualizações:
Transcrição
1 Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais Acopladas Edivaldo M. Santos e João R. T. de Mello Neto Aula 5 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 1 / 34
2 Tópicos de Equações Diferenciais O método de Euler O método de Runge-Kutta de ordem 2 O método de Runge-Kutta de ordem 4 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 2 / 34
3 Equações Diferenciais São inúmeros os problemas de física, química, biologia, economia, etc, cuja resposta envolvem a solução de equações diferenciais: 1 osciladores harmônicos livres com ou sem forças de amortecimento, osciladores forçados; 2 lançamento de projéteis; 3 tensões e correntes em circuitos elétricos; 4 concentrações de substâncias em reações químicas; 5 fluxo de calor em condutores térmicos; 6 propagação de ondas mecânicas e eletromagnáticas; 7 dinâmica de populações biológicas; 8 evolução do preço de ações no mercado financeiro; Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 4 / 34
4 Equações Diferenciais A ordem de uma equação diferencial é definida pela derivada mais alta aparecendo na equação. Assim, dizemos que a equação: em que y é uma função de x é de ordem 4. a d4 y dx 4 + b d3 y dx 3 + c d2 y dx 2 + d dy + ex + f = 0 (1) dx Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 6 / 34
5 Equações Diferenciais A ordem de uma equação diferencial é definida pela derivada mais alta aparecendo na equação. Assim, dizemos que a equação: em que y é uma função de x é de ordem 4. a d4 y dx 4 + b d3 y dx 3 + c d2 y dx 2 + d dy + ex + f = 0 (1) dx Ao longo tempo, desenvolveram-se métodos para a resolução de sistemas acoplados de equações diferencial de primeira ordem. Como então aplicar tais métodos quando a equação diferencial em questão tem ordem maior do que 1? Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 6 / 34
6 Equações Diferenciais A ordem de uma equação diferencial é definida pela derivada mais alta aparecendo na equação. Assim, dizemos que a equação: em que y é uma função de x é de ordem 4. a d4 y dx 4 + b d3 y dx 3 + c d2 y dx 2 + d dy + ex + f = 0 (1) dx Ao longo tempo, desenvolveram-se métodos para a resolução de sistemas acoplados de equações diferencial de primeira ordem. Como então aplicar tais métodos quando a equação diferencial em questão tem ordem maior do que 1? Por sorte, é sempre possível transformar uma equação diferencial de ordem n num conjunto de n equações diferenciais acopladas de ordem 1. Vejamos como... Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 6 / 34
7 Equações Diferenciais Tomemos como exemplo o problema de encontrar a solução x(t) para a posição de uma partícula de massa m sujeita a uma força restauradora do tipo lei de Hook (F(x) = kx). Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 8 / 34
8 Equações Diferenciais Tomemos como exemplo o problema de encontrar a solução x(t) para a posição de uma partícula de massa m sujeita a uma força restauradora do tipo lei de Hook (F(x) = kx). A 2 a lei de Newton aplicado à partícula, fornece: m d2 x dt 2 = kx ou x d md2 + kx = 0 ou dt2 2 x dt 2 + k x = 0, (2) m que é uma equação diferencial de segunda ordem para a posição x como função do tempo t. Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 8 / 34
9 Equações Diferenciais Tomemos como exemplo o problema de encontrar a solução x(t) para a posição de uma partícula de massa m sujeita a uma força restauradora do tipo lei de Hook (F(x) = kx). A 2 a lei de Newton aplicado à partícula, fornece: m d2 x dt 2 = kx ou x d md2 + kx = 0 ou dt2 2 x dt 2 + k x = 0, (2) m que é uma equação diferencial de segunda ordem para a posição x como função do tempo t. Se definirmos uma variável y 1 = x e outra variável y 2 = dx, a solução da equação dt diferencial de segunda ordem acima é equivalente à do seguinte conjunto de 2 equações acopladas de primeira ordem: ( dy1 = y dt 2 dy 2 = k dt m y (3) 1 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 8 / 34
10 Equações Diferenciais Tomemos como exemplo o problema de encontrar a solução x(t) para a posição de uma partícula de massa m sujeita a uma força restauradora do tipo lei de Hook (F(x) = kx). A 2 a lei de Newton aplicado à partícula, fornece: m d2 x dt 2 = kx ou x d md2 + kx = 0 ou dt2 2 x dt 2 + k x = 0, (2) m que é uma equação diferencial de segunda ordem para a posição x como função do tempo t. Se definirmos uma variável y 1 = x e outra variável y 2 = dx, a solução da equação dt diferencial de segunda ordem acima é equivalente à do seguinte conjunto de 2 equações acopladas de primeira ordem: ( dy1 = y dt 2 dy 2 = k dt m y (3) 1 E não é difícil ver que o procedimento acima pode ser aplicado a uma equação de ordem arbitrária n para produzir um conjunto de n equações acopladas de ordem 1: dy i dx = f (x,y 1,...,y n) i = 1, 2,...,n (4) em que a derivada em relação a x da i-ésima variável pode, em princípio, ser uma função da variável independente x, assim como das n variáveis dependentes y i. Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais AulaAcopladas 5 8 / 34
11 Equações Diferenciais: condições de contorno Do ponto de vista formal, a solução de equação diferencial de ordem n, envolve n integrações para sair da n-ésima derivada e chegar na primitiva de ordem 0. A cada integração surge uma constante de integração. Assim, a solução completa de uma equação diferencial de ordem n envolve a especificação de n condições de contorno. 10 / 34
12 Equações Diferenciais: condições de contorno Do ponto de vista formal, a solução de equação diferencial de ordem n, envolve n integrações para sair da n-ésima derivada e chegar na primitiva de ordem 0. A cada integração surge uma constante de integração. Assim, a solução completa de uma equação diferencial de ordem n envolve a especificação de n condições de contorno. Pode-se dividir os problemas de equações diferenciais em 2 grandes categorias dependendo da natureza das condições de contorno envolvidas: 1 problemas de valores iniciais: as variáveis dependentes y i são dadas para algum valor inicial x i e propagadas até um valor final x f. 2 problemas de fronteira: as variáveis dependentes devem satisfazer condições de contorno em mais de um valor de x. Em problemas de fronteira de dois pontos, por exemplo, algumas condições (k) devem ser satisfeitas em x i e o restante (n k) em x f. 10 / 34
13 Equações Diferenciais: condições de contorno Do ponto de vista formal, a solução de equação diferencial de ordem n, envolve n integrações para sair da n-ésima derivada e chegar na primitiva de ordem 0. A cada integração surge uma constante de integração. Assim, a solução completa de uma equação diferencial de ordem n envolve a especificação de n condições de contorno. Pode-se dividir os problemas de equações diferenciais em 2 grandes categorias dependendo da natureza das condições de contorno envolvidas: 1 problemas de valores iniciais: as variáveis dependentes y i são dadas para algum valor inicial x i e propagadas até um valor final x f. 2 problemas de fronteira: as variáveis dependentes devem satisfazer condições de contorno em mais de um valor de x. Em problemas de fronteira de dois pontos, por exemplo, algumas condições (k) devem ser satisfeitas em x i e o restante (n k) em x f. Nesse curso abordaremos apenas problemas de valores iniciais. Problemas de fronteira são mais complicados que os de valores iniciais e exigem algorítmos mais sofisticados dos que os que apresentaremos aqui. 10 / 34
14 Equações Diferenciais: O método de Euler O método mais simples que pode ser utilizado para se avançar a i-ésima variável dependente y i, após n passos, de x até x + h é o de Euler, cuja fórmula é: y (n+1) i = y (n) i + h f (x n, y 1,...,y n), (5) ou seja, uma simples extrapolação linear utilizando-se a derivada de y i com respeito a x, calculada no ponto x n. 12 / 34
15 Equações Diferenciais: O método de Euler O método mais simples que pode ser utilizado para se avançar a i-ésima variável dependente y i, após n passos, de x até x + h é o de Euler, cuja fórmula é: y (n+1) i = y (n) i + h f (x n, y 1,...,y n), (5) ou seja, uma simples extrapolação linear utilizando-se a derivada de y i com respeito a x, calculada no ponto x n. O erro que se comete com esse tipo de avanço é de ordem h 2 a cada passo. O algorítmo de Euler é bastante rudimentar e na maioria dos casos, para um número de passos moderados, deve levar a erros apreciáveis. Exploremos então as limitações de tal algorítmo, para que vocês se convençam disso / 34
16 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. 14 / 34
17 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. Compile e execute o programa no seu terminal. 14 / 34
18 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. Compile e execute o programa no seu terminal. grafique no Gnuplot a posição x(t). 14 / 34
19 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. Compile e execute o programa no seu terminal. grafique no Gnuplot a posição x(t). superponha a x(t), o gráfico da velocidade v(t). 14 / 34
20 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. Compile e execute o programa no seu terminal. grafique no Gnuplot a posição x(t). superponha a x(t), o gráfico da velocidade v(t). superponha a x(t) e v(t), o gráfico da energia mecânica E = K + U. 14 / 34
21 Equações Diferenciais: o método de Euler Apliquemos então o algorítmo de Euler para a solução do problema do pêndulo simples. Baixe o código fonte mhs euler.c. Vamos analisá-lo com cuidado. Compile e execute o programa no seu terminal. grafique no Gnuplot a posição x(t). superponha a x(t), o gráfico da velocidade v(t). superponha a x(t) e v(t), o gráfico da energia mecânica E = K + U. que conclusões tirar dessas tarefas? 14 / 34
22 Equações Diferenciais: o método de Euler oscilador harmonico simples (algoritmo de Euler) 1 posicao (m) velocidade (m/s) energia (J) tempo (s) 16 / 34
23 Equações Diferenciais: Runge-Kutta de ordem 2 (RK2) Vimos que um método cujo erro no avanço a cada passo é de ordem 2, como o de Euler, leva a erros grosseiros, mesmo para sistemas de equações simples como um oscilador harmônico livre. o próximo método que analisaremos é o de Runge-Kutta de ordem 2, conhecido pela sigla RK2. 18 / 34
24 Equações Diferenciais: Runge-Kutta de ordem 2 (RK2) Vimos que um método cujo erro no avanço a cada passo é de ordem 2, como o de Euler, leva a erros grosseiros, mesmo para sistemas de equações simples como um oscilador harmônico livre. o próximo método que analisaremos é o de Runge-Kutta de ordem 2, conhecido pela sigla RK2. A diferença principal do RK2 em relação a Euler é a utilização de um passo tentativa no meio do intervalo de avanço, como representado esquematicamente na figura abaixo. Matematicamente, o algorítmo é caracterizado pelas seguintes equações (para o caso de uma única variável): k 1 = hf (x (n),y (n) ) k 2 = hf x (n) + h 2,y(n) + k «1 2 y (n+1) = y (n) + k 2 + O(h 3 ) 18 / 34
25 Equações Diferenciais: Runge-Kutta de ordem 2 (RK2) O método de Runge-Kutta de ordem 2 simula a acurácia de uma expansção em série de Taylor até ordem 2, e o erro a cada passo é de ordem 3. Vejamos como / 34
26 Equações Diferenciais: Runge-Kutta de ordem 2 (RK2) O método de Runge-Kutta de ordem 2 simula a acurácia de uma expansção em série de Taylor até ordem 2, e o erro a cada passo é de ordem 3. Vejamos como... Se tomarmos f como uma função de duas variáveis: x e y, com y = y(t), a regra da cadeia para funções de muitas variáveis implica que até ordem h: f x (n) + h 2,y(n) + k «1 = f (x (n),y (n) )+ h» df + = dy + h d 2 y 2 2 dt x (n),y (n) dx x(n),y (n) 2 dx 2 + x(n),y (n) (6) 20 / 34
27 Equações Diferenciais: Runge-Kutta de ordem 2 (RK2) O método de Runge-Kutta de ordem 2 simula a acurácia de uma expansção em série de Taylor até ordem 2, e o erro a cada passo é de ordem 3. Vejamos como... Se tomarmos f como uma função de duas variáveis: x e y, com y = y(t), a regra da cadeia para funções de muitas variáveis implica que até ordem h: f x (n) + h 2,y(n) + k «1 = f (x (n),y (n) )+ h» df + = dy + h d 2 y 2 2 dt x (n),y (n) dx x(n),y (n) 2 dx 2 + x(n),y (n) (6) Logo: y (n+1) = y(x (n) ) + h dy + h2 d 2 y dx x(n),y (n) 2 dx 2 + (7) x(n),y (n) que é a expansão de Taylor de y até ordem 2 com erro de ordem 3. Em geral, designa-se um método como sendo de ordem n se o erro a cada passo é de ordem n / 34
28 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Um refinamento do método RK2 é feito pelo algorítmo RK4. Nesse método, 4 avaliações da função f devem ser realizadas. As equações para avanço de x até x + h são: k 1 = hf (x (n),y (n) ) k 2 = hf (x (n) + h 2, y(n) + k 1 2 ) k 3 = hf (x (n) + h 2, y(n) + k 2 2 ) k 4 = hf (x (n) + h, y (n) + k 3 ) y (n+1) = y (n) + k k k k O(h5 ) 22 / 34
29 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Um refinamento do método RK2 é feito pelo algorítmo RK4. Nesse método, 4 avaliações da função f devem ser realizadas. As equações para avanço de x até x + h são: k 1 = hf (x (n),y (n) ) k 2 = hf (x (n) + h 2, y(n) + k 1 2 ) k 3 = hf (x (n) + h 2, y(n) + k 2 2 ) k 4 = hf (x (n) + h, y (n) + k 3 ) y (n+1) = y (n) + k k k k O(h5 ) Veja então que o erro a cada passo em RK4 é de ordem 5. É possível mostrar, de maneira similar a RK2, que o RK4 simula a acurária de uma expansão em série de Taylor até ordem 4. RK4 é um dos métodos mais utilizados na resolução de equações diferenciais. Acoplado a um bom algorítmo de ajuste de passo, esse método oferece boa precisão para uma grande variedade de problemas envolvendo eqs. diferenciais. Ele não é, obviamente, a palavra final quando se fala de eqs. diferenciaias. Dentre outros métodos podemos destacar: extrapolação de Richard e preditor-corretor. Para os problemas abordados nesse curso, RK4 será o método mais apropriado, pela rapidez e acurácia dos resultados. 22 / 34
30 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Baixe o código mhs rk4.c que implementa o método RK4 para resolver as equações do oscilador harmômico simples. Vamos analisá-lo com calma. 24 / 34
31 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Baixe o código mhs rk4.c que implementa o método RK4 para resolver as equações do oscilador harmômico simples. Vamos analisá-lo com calma. Compile e rode esse código. 24 / 34
32 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Baixe o código mhs rk4.c que implementa o método RK4 para resolver as equações do oscilador harmômico simples. Vamos analisá-lo com calma. Compile e rode esse código. Grafique novamente x(t), v(t) e E(t) = K + U. 24 / 34
33 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) Baixe o código mhs rk4.c que implementa o método RK4 para resolver as equações do oscilador harmômico simples. Vamos analisá-lo com calma. Compile e rode esse código. Grafique novamente x(t), v(t) e E(t) = K + U. grafique o espaço de fase v(t) x(t). 24 / 34
34 Equações Diferenciais: Runge-Kutta de ordem 4 (RK4) oscilador harmonico simples (algoritmo RK4) 1 posicao (m) velociddade (m/s) energia (J) tempo (s) 26 / 34
35 PARA FAZER EM SALA DE AULA Modifique o programa mhs rk4.c para integrar as equações de movimento de um oscilador harmônico amortecido por uma força proporcional à velocidade F a = bv, com b > 0. Aplicando-se a 2 a lei de Newton para esse sistema, chega-se à seguinte equação diferencial de segunda ordem: d 2 x dt 2 + b dx m dt + k x = 0, (8) m onde k é a constante elástica da mola e m a massa presa a ela. Grafique no gnuplot a posição x(t), v(t) e a energia mecânica E(t) = K(t) + U(t) do oscilador para a situação b = 0.2, k = 2. e m = 0.5. Grafique o espaço de fase do sistema v(t) x(t). mantendo k e m fixos nos valores acima, mude o parâmetro b para 2 e veja o acontece com a solução. mantendo k e m fixos nos valores acima, mude o parâmetro b para 3 e veja o acontece com a solução. 28 / 34
36 Variáveis externas Vimos que variáveis declaradas no interior de funções vivem somente no corpo dessa. Ao ser invocada, a sequência de instruções no interior da função são executadas. Após a execução da instrução de retorno ou da última instrução de funcções do tipo void, o fluxo de instrução volta á unidade de origem e todas as variáveis criadas no interior da funç ao são destruídas. Como não vestígio de tais variáveis locais entre uma chamada e outra da função, variáveis locais, também conhecidas como automáticas devem sempre ser inicializadas no corpo da função, pois não guardam informação de chamadas anteriores. Uma maneira de tornar certas variáveis visíveis a mais de uma função é declará-las como sendo do tipo external. Esse tipo de variável não existe dentreo de um corpo de função em específico, de forma que não são destruídas por chamadas de funções que porventura venham a acessá-las. Variáveis externas podem então ser utilizadas para comunicar dados entre várias funções. Variáveis externas devem ser declaradas UMA ÚNICA VEZ, fora de qualquer função. Além disso, toda função que deseja acessá-las deve também declará-las com auxílio da palavra-chave extern. 30 / 34
37 Variáveis externas: exemplo #include <stdio.h> #define MAXLINE 1000 /* maximum input line size */ int max; /* maximum length seen so far */ char line[maxline]; /* current input line */ char longest[maxline]; /* longest line saved here */ int getline(void); void copy(void); /* print longest input line; specialized version */ int main() { int len; extern int max; extern char longest[]; max = 0; while ((len = getline()) > 0) if (len > max) { max = len; copy(); } if (max > 0) /* there was a line */ printf("%s", longest); return 0; } 32 / 34
38 Variáveis externas e Header Files Num arquivo com extensão.h (header.h por exemplo) coloca-se: #include <stdio.h> #define MAXLINE 1000 /* maximum input line size */ int max; /* maximum length seen so far */ char line[maxline]; /* current input line */ char longest[maxline]; /* longest line saved here */ int getline(void); void copy(void); 34 / 34
39 Variáveis externas e Header Files Num arquivo com extensão.h (header.h por exemplo) coloca-se: #include <stdio.h> #define MAXLINE 1000 /* maximum input line size */ int max; /* maximum length seen so far */ char line[maxline]; /* current input line */ char longest[maxline]; /* longest line saved here */ int getline(void); void copy(void); No arquivo.c coloca-se então uma diretiva do tipo #include: #include "header.h" /* print longest input line; specialized version */ int main() { int len; extern int max; extern char longest[]; max = 0; while ((len = getline()) > 0) if (len > max) { max = len; copy(); } if (max > 0) /* there was a line */ printf("%s", longest); return 0; } 34 / 34
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
Queremos resolver uma equação diferencial da forma. dy dx. = f(x, y), (1)
 Resolução Numérica de Equações Diferenciais Método de Runge Kutta Queremos resolver uma equação diferencial da forma dy dx = f(x, y), (1) Isto é: queremos obter a função y(x) sabendo sua derivada. Numericamente:
Resolução Numérica de Equações Diferenciais Método de Runge Kutta Queremos resolver uma equação diferencial da forma dy dx = f(x, y), (1) Isto é: queremos obter a função y(x) sabendo sua derivada. Numericamente:
FENÔMENOS OSCILATÓRIOS E TERMODINÂMICA
 FENÔMENOS OSCILATÓRIOS E TERMODINÂMICA AULA 2 OSCILAÇÕES PROF.: KAIO DUTRA Movimento Harmônico Simples O movimento harmônico simples é um tipo básico de oscilação. Movimento Harmônico Simples Uma propriedade
FENÔMENOS OSCILATÓRIOS E TERMODINÂMICA AULA 2 OSCILAÇÕES PROF.: KAIO DUTRA Movimento Harmônico Simples O movimento harmônico simples é um tipo básico de oscilação. Movimento Harmônico Simples Uma propriedade
Universidade Federal do Pampa UNIPAMPA. Oscilações. Prof. Luis Armas
 Universidade Federal do Pampa UNIPAMPA Oscilações Prof. Luis Armas Que é uma oscilação? Qual é a importância de estudar oscilações? SUMARIO Movimentos oscilatórios periódicos Movimento harmônico simples
Universidade Federal do Pampa UNIPAMPA Oscilações Prof. Luis Armas Que é uma oscilação? Qual é a importância de estudar oscilações? SUMARIO Movimentos oscilatórios periódicos Movimento harmônico simples
Física 2 - Movimentos Oscilatórios. Em um ciclo da função seno ou cosseno, temos que são percorridos 2π rad em um período, ou seja, em T.
 Física 2 - Movimentos Oscilatórios Halliday Cap.15, Tipler Cap.14 Movimento Harmônico Simples O que caracteriza este movimento é a periodicidade do mesmo, ou seja, o fato de que de tempos em tempos o movimento
Física 2 - Movimentos Oscilatórios Halliday Cap.15, Tipler Cap.14 Movimento Harmônico Simples O que caracteriza este movimento é a periodicidade do mesmo, ou seja, o fato de que de tempos em tempos o movimento
Movimento Harmônico Simples - III Relação entre o MHS e o MCU Oscilações amortecidas Oscilações Forçadas e Ressonância. Prof. Ettore Baldini-Neto
 Movimento Harmônico Simples - III Relação entre o MHS e o MCU Oscilações amortecidas Oscilações Forçadas e Ressonância Prof. Ettore Baldini-Neto 1610: Galileu, usando um telescópio recém construído, descobre
Movimento Harmônico Simples - III Relação entre o MHS e o MCU Oscilações amortecidas Oscilações Forçadas e Ressonância Prof. Ettore Baldini-Neto 1610: Galileu, usando um telescópio recém construído, descobre
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
Sessão 1: Generalidades
 Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Equações Diferenciais Problemas de Valor Inicial. Computação 2º Semestre 2016/2017
 Equações Diferenciais Problemas de Valor Inicial Computação 2º Semestre 2016/2017 Equações Diferenciais Uma equação diferencial é uma equação cuja incógnita é uma função que aparece na equação sob a forma
Equações Diferenciais Problemas de Valor Inicial Computação 2º Semestre 2016/2017 Equações Diferenciais Uma equação diferencial é uma equação cuja incógnita é uma função que aparece na equação sob a forma
Modelagem Computacional. Parte 8 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Cálculo Numérico P2 EM33D
 Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto.
 Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrer turbulência
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrer turbulência
Modelos Matematicos de Sistemas
 Modelos Matematicos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações Lineares de Sistemas Físicos; Transformada de Laplace; Função de Transferência de Sistemas Lineares;
Modelos Matematicos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações Lineares de Sistemas Físicos; Transformada de Laplace; Função de Transferência de Sistemas Lineares;
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS Prof. Bruno Farias Arquivo em anexo Conteúdo Programático Bibliografia
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS Prof. Bruno Farias Arquivo em anexo Conteúdo Programático Bibliografia
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS Prof. Bruno Farias Arquivo em anexo Conteúdo Programático Bibliografia
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I INFORMAÇÕES GERAIS Prof. Bruno Farias Arquivo em anexo Conteúdo Programático Bibliografia
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais: introdução aos sistemas caóticos
 Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais: introdução aos sistemas caóticos Edivaldo M. Santos e João R. T. de Mello Neto Aula 6 Edivaldo M. Santos e João R. T.
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Equações Diferenciais: introdução aos sistemas caóticos Edivaldo M. Santos e João R. T. de Mello Neto Aula 6 Edivaldo M. Santos e João R. T.
Algoritmos Numéricos 2 a edição
 Algoritmos Numéricos 2 a edição Capítulo 7: Equaç~oes diferenciais ordinárias c 2009 FFCf 2 Capítulo 7: Equações diferenciais ordinárias 7.1 Solução numérica de EDO 7.2 Métodos de Runge-Kutta 7.3 Métodos
Algoritmos Numéricos 2 a edição Capítulo 7: Equaç~oes diferenciais ordinárias c 2009 FFCf 2 Capítulo 7: Equações diferenciais ordinárias 7.1 Solução numérica de EDO 7.2 Métodos de Runge-Kutta 7.3 Métodos
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um
 As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
Erros nas aproximações numéricas
 Erros nas aproximações numéricas Prof. Emílio Graciliano Ferreira Mercuri Departamento de Engenharia Ambiental - DEA, Universidade Federal do Paraná - UFPR emilio@ufpr.br 4 de março de 2013 Resumo: O objetivo
Erros nas aproximações numéricas Prof. Emílio Graciliano Ferreira Mercuri Departamento de Engenharia Ambiental - DEA, Universidade Federal do Paraná - UFPR emilio@ufpr.br 4 de março de 2013 Resumo: O objetivo
Modelagem Computacional. Aula 5 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 5 2 Prof. Thiago Alves de Queiroz 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 5 2 Prof. Thiago Alves de Queiroz 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Física Geral e Experimental III
 Física Geral e Experimental III Oscilações Nosso mundo está repleto de oscilações, nas quais os objetos se movem repetidamente de um lado para outro. Eis alguns exemplos: - quando um taco rebate uma bola
Física Geral e Experimental III Oscilações Nosso mundo está repleto de oscilações, nas quais os objetos se movem repetidamente de um lado para outro. Eis alguns exemplos: - quando um taco rebate uma bola
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno
 étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
3 Métodos Numéricos Análise das Equações de Movimento
 3 Métodos Numéricos A dinâmica de sistemas mecânicos normalmente é modelada como um sistema de equações diferenciais. Estas equações diferenciais devem ser resolvidas a fim de relacionar as variáveis entre
3 Métodos Numéricos A dinâmica de sistemas mecânicos normalmente é modelada como um sistema de equações diferenciais. Estas equações diferenciais devem ser resolvidas a fim de relacionar as variáveis entre
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Noções Básicas de Linguagem C
 Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Noções Básicas de Linguagem C Edivaldo M. Santos e João R. T. de Mello Neto Aula 4 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Noções Básicas de Linguagem C Edivaldo M. Santos e João R. T. de Mello Neto Aula 4 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos
Física I 2010/2011. Aula 10. Movimento Oscilatório II
 Física I 2010/2011 Aula 10 Movimento Oscilatório II Sumário Capítulo 15: Oscilações 15-3 A Energia no Movimento Harmónico Simples 15-4 Um Oscilador Harmónico Simples Angular 15-5 O Pêndulo simples 15-7
Física I 2010/2011 Aula 10 Movimento Oscilatório II Sumário Capítulo 15: Oscilações 15-3 A Energia no Movimento Harmónico Simples 15-4 Um Oscilador Harmónico Simples Angular 15-5 O Pêndulo simples 15-7
, (1) onde v é o módulo de v e b 1 e b 2 são constantes positivas.
 Oscilações Amortecidas O modelo do sistema massa-mola visto nas aulas passadas, que resultou nas equações do MHS, é apenas uma idealização das situações mais realistas existentes na prática. Sempre que
Oscilações Amortecidas O modelo do sistema massa-mola visto nas aulas passadas, que resultou nas equações do MHS, é apenas uma idealização das situações mais realistas existentes na prática. Sempre que
Equações Diferenciais
 IFBA Equações Diferenciais Versão 1 Allan de Sousa Soares Graduação: Licenciatura em Matemática - UESB Especilização: Matemática Pura - UESB Mestrado: Matemática Pura - UFMG Vitória da Conquista - BA 2013
IFBA Equações Diferenciais Versão 1 Allan de Sousa Soares Graduação: Licenciatura em Matemática - UESB Especilização: Matemática Pura - UESB Mestrado: Matemática Pura - UFMG Vitória da Conquista - BA 2013
USANDO O MODELLUS. Aula 3
 USANDO O MODELLUS Aula 3 A evolução temporal é dada pela solução numérica de equações diferenciais. Exemplo: Movimento Retilíneo Uniforme Exemplo: Movimento Retilíneo Uniformemente variado As derivadas
USANDO O MODELLUS Aula 3 A evolução temporal é dada pela solução numérica de equações diferenciais. Exemplo: Movimento Retilíneo Uniforme Exemplo: Movimento Retilíneo Uniformemente variado As derivadas
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EDOs de primeira ordem Problema de Valor Inicial (PVI) dy dx = f x, y y x 0 = y 0 Método de passo simples valor novo = valor antigo + inclinação passo Método de Euler y
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EDOs de primeira ordem Problema de Valor Inicial (PVI) dy dx = f x, y y x 0 = y 0 Método de passo simples valor novo = valor antigo + inclinação passo Método de Euler y
Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma:
 Edgard Jamhour Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma: n f x, x 0 = n=0 a n x x 0 f(x,x 0 ) = a 0 + a 1 (x-x 0 ) + a 2 (x-x
Edgard Jamhour Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma: n f x, x 0 = n=0 a n x x 0 f(x,x 0 ) = a 0 + a 1 (x-x 0 ) + a 2 (x-x
Universidade Federal Rural do Semi Árido UFERSA Pro Reitoria de Graduação PROGRAD Disciplina: Física II Professora: Subênia Medeiros
 Universidade Federal Rural do Semi Árido UFERSA Pro Reitoria de Graduação PROGRAD Disciplina: Física II Professora: Subênia Medeiros Movimento Periódico O movimento é um dos fenômenos mais fundamentais
Universidade Federal Rural do Semi Árido UFERSA Pro Reitoria de Graduação PROGRAD Disciplina: Física II Professora: Subênia Medeiros Movimento Periódico O movimento é um dos fenômenos mais fundamentais
Solução Numérica de EDOs
 Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Nota de Aula: Equações Diferenciais Ordinárias de 2 Ordem. ( Aplicações )
 Nota de Aula: Equações Diferenciais Ordinárias de Ordem ( Aplicações ) Vamos nos ater a duas aplicações de grande interesse na engenharia: Sistema massa-mola-amortecedor ( Oscilador Mecânico ) O Sistema
Nota de Aula: Equações Diferenciais Ordinárias de Ordem ( Aplicações ) Vamos nos ater a duas aplicações de grande interesse na engenharia: Sistema massa-mola-amortecedor ( Oscilador Mecânico ) O Sistema
1. Movimento Harmônico Simples
 Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
Equações diferenciais ordinárias
 Equações diferenciais ordinárias Laura Goulart UESB 9 de Abril de 2016 Laura Goulart (UESB) Equações diferenciais ordinárias 9 de Abril de 2016 1 / 13 Muitos problemas encontrados em engenharia e outras
Equações diferenciais ordinárias Laura Goulart UESB 9 de Abril de 2016 Laura Goulart (UESB) Equações diferenciais ordinárias 9 de Abril de 2016 1 / 13 Muitos problemas encontrados em engenharia e outras
Oscilador Harmônico. 8 - Oscilador Harmônico. Oscilador Harmônico. Oscilador Harmônico Simples. Oscilador harmônico simples
 Oscilador Harmônico 8 - Oscilador Harmônico Mecânica Quântica Em Física, o oscilador harmônico é qualquer sistema que apresenta movimento oscilatório, de forma harmônica, em torno de um ponto de equilíbrio.
Oscilador Harmônico 8 - Oscilador Harmônico Mecânica Quântica Em Física, o oscilador harmônico é qualquer sistema que apresenta movimento oscilatório, de forma harmônica, em torno de um ponto de equilíbrio.
MAT EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17
 MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
Aula do cap. 16 MHS e Oscilações
 Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Equações Diferenciais Ordinárias
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 2004/2005 Equações Diferenciais Ordinárias PROBLEMAS 1 Considere a equação diferencial dy dx = y(x2 1) com y(0) = 1 e x [0,
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 2004/2005 Equações Diferenciais Ordinárias PROBLEMAS 1 Considere a equação diferencial dy dx = y(x2 1) com y(0) = 1 e x [0,
O Movimento Harmônico Simples
 O Movimento Harmônico Simples Bibliografia e Figuras: Halliday, Resnick e Walker, vol 2 8 a ed, Cap 15. Todo o movimento que se repete em intervalos regulares é chamado de movimento periódico ou movimento
O Movimento Harmônico Simples Bibliografia e Figuras: Halliday, Resnick e Walker, vol 2 8 a ed, Cap 15. Todo o movimento que se repete em intervalos regulares é chamado de movimento periódico ou movimento
Física para Engenharia II
 Física para Engenharia II 430196 (FEP196) Turma 01111 Sala C-13 3as 15h00 / 5as 9h0. Prof. Antonio Domingues dos Santos Depto. Física Materiais e Mecânica IF USP Ed. Mário Schemberg, sala 05 adsantos@if.usp.br
Física para Engenharia II 430196 (FEP196) Turma 01111 Sala C-13 3as 15h00 / 5as 9h0. Prof. Antonio Domingues dos Santos Depto. Física Materiais e Mecânica IF USP Ed. Mário Schemberg, sala 05 adsantos@if.usp.br
MAP Primeiro exercício programa Osciladores Harmônicos
 MAP-11 - Primeiro exercício programa - 009 Osciladores Harmônicos Instruções gerais - Os exercícios computacionais pedidos na disciplina Cálculo Numérico têm por objetivo fundamental familiarizar o aluno
MAP-11 - Primeiro exercício programa - 009 Osciladores Harmônicos Instruções gerais - Os exercícios computacionais pedidos na disciplina Cálculo Numérico têm por objetivo fundamental familiarizar o aluno
MOVIMENTO OSCILATÓRIO
 MOVIMENTO OSCILATÓRIO 1.0 Noções da Teoria da Elasticidade A tensão é o quociente da força sobre a área aplicada (N/m²): As tensões normais são tensões cuja força é perpendicular à área. São as tensões
MOVIMENTO OSCILATÓRIO 1.0 Noções da Teoria da Elasticidade A tensão é o quociente da força sobre a área aplicada (N/m²): As tensões normais são tensões cuja força é perpendicular à área. São as tensões
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec
 Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais)
 Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
Física para Engenharia II (antiga FEP2196) Turma 09 Sala C2-09 3as 13h10 / 5as 9h20. Turma 10 Sala C2-10 3as 15h00 / 5as 7h30.
 Física para Engenharia II 4320196 (antiga FEP2196) Turma 09 Sala C2-09 3as 13h10 / 5as 9h20. Turma 10 Sala C2-10 3as 15h00 / 5as 7h30. Profa. Márcia Regina Dias Rodrigues Depto. Física Nuclear IF USP Ed.
Física para Engenharia II 4320196 (antiga FEP2196) Turma 09 Sala C2-09 3as 13h10 / 5as 9h20. Turma 10 Sala C2-10 3as 15h00 / 5as 7h30. Profa. Márcia Regina Dias Rodrigues Depto. Física Nuclear IF USP Ed.
Ondas. Lucy V. C. Assali. Física II IO
 Ondas Física II 2016 - IO O que é uma onda? Qualquer sinal que é transmitido de um ponto a outro de um meio, com velocidade definida, sem que haja transporte direto de matéria. distúrbio se propaga leva
Ondas Física II 2016 - IO O que é uma onda? Qualquer sinal que é transmitido de um ponto a outro de um meio, com velocidade definida, sem que haja transporte direto de matéria. distúrbio se propaga leva
y (n) (x) = dn y dx n(x) y (0) (x) = y(x).
 Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 10
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. ntônio Roque ula Oscilações acopladas e modos normais Os sistemas naturais não são isolados, mas interagem entre si. Em particular, se dois ou mais
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. ntônio Roque ula Oscilações acopladas e modos normais Os sistemas naturais não são isolados, mas interagem entre si. Em particular, se dois ou mais
Equa c oes Diferenciais Ordin arias - Aplica c oes Marcelo Nascimento
 Equações Diferenciais Ordinárias - Aplicações Marcelo Nascimento 2 Sumário 1 Aplicações 5 1.1 Desintegração Radioativa........................... 5 1.2 Resfriamento de um corpo..........................
Equações Diferenciais Ordinárias - Aplicações Marcelo Nascimento 2 Sumário 1 Aplicações 5 1.1 Desintegração Radioativa........................... 5 1.2 Resfriamento de um corpo..........................
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V
 Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9
 591036 Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9 A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de
591036 Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9 A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de
Seção 9: EDO s lineares de 2 a ordem
 Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
CAPÍTULO 3 DINÂMICA DA PARTÍCULA: TRABALHO E ENERGIA
 CAPÍLO 3 DINÂMICA DA PARÍCLA: RABALHO E ENERGIA Neste capítulo será analisada a lei de Newton numa de suas formas integrais, aplicada ao movimento de partículas. Define-se o conceito de trabalho e energia
CAPÍLO 3 DINÂMICA DA PARÍCLA: RABALHO E ENERGIA Neste capítulo será analisada a lei de Newton numa de suas formas integrais, aplicada ao movimento de partículas. Define-se o conceito de trabalho e energia
Física IV Poli Engenharia Elétrica: 14ª Aula (02/10/2014)
 Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
Curso de Complementos de Física
 Aula 2 Curso de Engenharia Civil Faculdade Campo Grande 27 de Agosto de 2015 Plano de Aula 1 Exemplo 1 Um bloco, preso firmemente a uma mola, oscila verticalmente uma frequência de 4 Hertz e uma amplitude
Aula 2 Curso de Engenharia Civil Faculdade Campo Grande 27 de Agosto de 2015 Plano de Aula 1 Exemplo 1 Um bloco, preso firmemente a uma mola, oscila verticalmente uma frequência de 4 Hertz e uma amplitude
Introdução à Programação. Funções e Escopo de Variáveis
 Introdução à Programação Funções e Escopo de Variáveis Funções em C Funções constituem programas em C 2 Tópicos da Aula Hoje vamos detalhar funções em C Importância Escrevendo funções Comando return Passagem
Introdução à Programação Funções e Escopo de Variáveis Funções em C Funções constituem programas em C 2 Tópicos da Aula Hoje vamos detalhar funções em C Importância Escrevendo funções Comando return Passagem
O que é o Cálculo Numérico? 05/06/13. Prof. Dr. Alexandre Passito
 Prof. Dr. Alexandre Passito passito@icomp.ufam.edu.br Parte do material cedido pelos Professores Fabíola Guerra/ Arilo DCC/UFAM. 1 } Quem sou eu? Alexandre Passito de Queiroz Doutor em Informática passito@icomp.ufam.edu.br
Prof. Dr. Alexandre Passito passito@icomp.ufam.edu.br Parte do material cedido pelos Professores Fabíola Guerra/ Arilo DCC/UFAM. 1 } Quem sou eu? Alexandre Passito de Queiroz Doutor em Informática passito@icomp.ufam.edu.br
Métodos de Runge-Kutta
 Solução numérica de Equações Diferenciais Ordinárias: Métodos de Runge-Kutta Marina Andretta/Franklina Toledo ICMC-USP 31 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D.
Solução numérica de Equações Diferenciais Ordinárias: Métodos de Runge-Kutta Marina Andretta/Franklina Toledo ICMC-USP 31 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D.
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Profa. Simone Aparecida Miloca UNIOESTE 2017 Sumario EQUAÇÕES DIFERENCIAIS ORDINÁRIAS MÉTODO DE EULER MÉTODOS DE SÉRIES DE TAYLOR MÉTODOS DE RUNGE KUTTA EQUAÇÕES DIFERENCIAIS
Equações Diferenciais Ordinárias Profa. Simone Aparecida Miloca UNIOESTE 2017 Sumario EQUAÇÕES DIFERENCIAIS ORDINÁRIAS MÉTODO DE EULER MÉTODOS DE SÉRIES DE TAYLOR MÉTODOS DE RUNGE KUTTA EQUAÇÕES DIFERENCIAIS
Introdução. Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro.
 Capitulo 16 Ondas I Introdução Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro. Ondas ondas é qualquer sinal (perturbação) que se transmite de um ponto a outro de um meio com
Capitulo 16 Ondas I Introdução Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro. Ondas ondas é qualquer sinal (perturbação) que se transmite de um ponto a outro de um meio com
SUMÁRIO PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3. PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação...
 PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
O Sistema Massa-Mola
 O Sistema Massa-Mola 1 O sistema massa mola, como vimos, é um exemplo de sistema oscilante que descreve um MHS. Como sabemos (aplicando a Segunda Lei de Newton) temos que F = ma Como sabemos, no caso massa-mola
O Sistema Massa-Mola 1 O sistema massa mola, como vimos, é um exemplo de sistema oscilante que descreve um MHS. Como sabemos (aplicando a Segunda Lei de Newton) temos que F = ma Como sabemos, no caso massa-mola
y(x n+1 ) = y(x n ) + hy (x n ) + h2 q! y (q) (x n )
 2. Método de Taylor de ordem q Seja y(x) a solução exata do p.v.i., contínua e suficientemente derivável em [a, b]. A expansão em série de Taylor para y(x n + h) em torno do ponto x n é dada por: y(x n+1
2. Método de Taylor de ordem q Seja y(x) a solução exata do p.v.i., contínua e suficientemente derivável em [a, b]. A expansão em série de Taylor para y(x n + h) em torno do ponto x n é dada por: y(x n+1
Métodos Numéricos para EDO S
 Métodos Numéricos para EDO S 9.1 Introdução O estudo das equações diferenciais foi motivado inicialmente por problemas da física, ou seja problemas de mecânica, eletricidade termodinâmica, magnetismo etc.
Métodos Numéricos para EDO S 9.1 Introdução O estudo das equações diferenciais foi motivado inicialmente por problemas da física, ou seja problemas de mecânica, eletricidade termodinâmica, magnetismo etc.
Lista de Exercícios 3 e soluções
 Lista de Exercícios 3 e soluções MAT 069 - Cálculo Numérico Prof Dagoberto Adriano Rizzotto Justo 2 de Dezembro de 2006 Calcule a integral (a) A f dx = 0 (0) = = (b) A f 0 dx = 0 (0) = = 0 (c) A ( 2 f
Lista de Exercícios 3 e soluções MAT 069 - Cálculo Numérico Prof Dagoberto Adriano Rizzotto Justo 2 de Dezembro de 2006 Calcule a integral (a) A f dx = 0 (0) = = (b) A f 0 dx = 0 (0) = = 0 (c) A ( 2 f
Tópicos de Física Clássica I Aula 2 As equações de Euler-Lagrange
 Tópicos de Física Clássica I Aula 2 As equações de Euler-Lagrange a c tort O princípio da ação mínima O que é o princípio da ação mínima? Como se usa a formulação lagrangiana da mecânica em um problema?
Tópicos de Física Clássica I Aula 2 As equações de Euler-Lagrange a c tort O princípio da ação mínima O que é o princípio da ação mínima? Como se usa a formulação lagrangiana da mecânica em um problema?
ELEMENTOS DE EQUAÇÕES DIFERENCIAIS
 ELEMENTOS DE EQUAÇÕES DIFERENCIAIS AULA 05: MODELAGEM E PROBLEMAS DIVERSOS TÓPICO 01: MODELAGEM No tópico 03 da aula 01 vimos alguns exemplos de equações diferenciais que serviam de modelo matemático para
ELEMENTOS DE EQUAÇÕES DIFERENCIAIS AULA 05: MODELAGEM E PROBLEMAS DIVERSOS TÓPICO 01: MODELAGEM No tópico 03 da aula 01 vimos alguns exemplos de equações diferenciais que serviam de modelo matemático para
Na Física (em módulo) é uma Lei
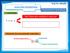 1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHRIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA ELÉTRICA. 2ª Lista de SEL0417 Fundamentos de Controle.
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHRIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA ELÉTRICA ª Lista de SEL0417 undamentos de Controle Professor: Rodrigo Andrade Ramos Questão 1 Suponha que um satélite
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHRIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA ELÉTRICA ª Lista de SEL0417 undamentos de Controle Professor: Rodrigo Andrade Ramos Questão 1 Suponha que um satélite
MODELOS MATEMÁTICOS E SIMULAÇÕES COMPUTACIONAIS DE FENÔMENOS BIOLÓGICOS
 MODELOS MATEMÁTICOS E SIMULAÇÕES COMPUTACIONAIS DE FENÔMENOS BIOLÓGICOS Prof. Dr. Robson Rodrigues da Silva robson.silva@umc.br Mogi das Cruzes Março de 2017 TÉCNICAS DE MODELAGEM 1. REGRESSÃO OU AJUSTE
MODELOS MATEMÁTICOS E SIMULAÇÕES COMPUTACIONAIS DE FENÔMENOS BIOLÓGICOS Prof. Dr. Robson Rodrigues da Silva robson.silva@umc.br Mogi das Cruzes Março de 2017 TÉCNICAS DE MODELAGEM 1. REGRESSÃO OU AJUSTE
Linearização de Modelos Matemáticos Não-Lineares. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 de Modelos Matemáticos Não-Lineares Carlos Alexandre Mello 1 Embora muitos sistemas sejam vistos como lineares eles são, de fato, lineares em intervalos Se o sistema operar em torno de um ponto de equilíbrio
de Modelos Matemáticos Não-Lineares Carlos Alexandre Mello 1 Embora muitos sistemas sejam vistos como lineares eles são, de fato, lineares em intervalos Se o sistema operar em torno de um ponto de equilíbrio
c il a ções Física 2 aula 9 2 o semestre, 2012
 Os c il a ções Física aula 9 o semestre, 1 Movimento Harmônico simples: coneão entre vibrações e ondas Energia no MHS Energia Mecânica Total: 1 1 Quando =A ou =-A (etremos): E mv k 1 1 1 E m() k( A) ka
Os c il a ções Física aula 9 o semestre, 1 Movimento Harmônico simples: coneão entre vibrações e ondas Energia no MHS Energia Mecânica Total: 1 1 Quando =A ou =-A (etremos): E mv k 1 1 1 E m() k( A) ka
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Aula 1 - Cálculo Numérico
 Aula 1 - Cálculo Numérico Conceitos básicos Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 1 - Cálculo Numérico 1 / 25 Sumário Sumário 1 Sumário 2 Motivação 3 Plano de ensino 4
Aula 1 - Cálculo Numérico Conceitos básicos Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 1 - Cálculo Numérico 1 / 25 Sumário Sumário 1 Sumário 2 Motivação 3 Plano de ensino 4
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIO #6 (1) COMPUTAÇÃO ANALÓGICA - A computação analógica
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIO #6 (1) COMPUTAÇÃO ANALÓGICA - A computação analógica
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Métodos de Monte Carlo
 Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Métodos de Monte Carlo Edivaldo M. Santos e João R. T. de Mello Neto Aula 9 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais
Métodos Computacionais em Física I (FIW234) Turmas IFA e IFB Métodos de Monte Carlo Edivaldo M. Santos e João R. T. de Mello Neto Aula 9 Edivaldo M. Santos e João R. T. de Mello Neto () Métodos Computacionais
Resolução comentada da questão 1 da P1 de 2015 da disciplina PME Mecânica dos Fluidos I
 Resolução comentada da questão 1 da P1 de 2015 da disciplina PME3230 - Mecânica dos Fluidos I Caio Cancian Março 2016 Resumo A primeira questão da P1 de 2015 da disciplina PME3230 - Mecânica dos Fluidos
Resolução comentada da questão 1 da P1 de 2015 da disciplina PME3230 - Mecânica dos Fluidos I Caio Cancian Março 2016 Resumo A primeira questão da P1 de 2015 da disciplina PME3230 - Mecânica dos Fluidos
Métodos Computacionais. Funções, Escopo de Variáveis e Ponteiros
 Métodos Computacionais Funções, Escopo de Variáveis e Ponteiros Tópicos da Aula Hoje vamos detalhar funções em C Escrevendo funções Comando return Passagem de argumentos por valor Execução de uma função
Métodos Computacionais Funções, Escopo de Variáveis e Ponteiros Tópicos da Aula Hoje vamos detalhar funções em C Escrevendo funções Comando return Passagem de argumentos por valor Execução de uma função
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto.
 Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrerem turbulência
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrerem turbulência
2. Em um sistema massa-mola temos k = 300 N/m, m = 2 kg, A = 5 cm. Calcule ω, T, f, E (12,25 rad/s; 0,51 s; 1,95 Hz; 0,38 J).
 FÍSICA BÁSICA II - LISTA 1 - OSCILAÇÕES - 2019/1 1. Em um sistema massa-mola temos k = 200 N/m, m = 1 kg, x(0) = A = 10 cm. Calcule ω, T, f, v m, a m, E (14,14 rad/s; 0,44 s; 2,25 Hz; 1,41 m/s; 20 m/s
FÍSICA BÁSICA II - LISTA 1 - OSCILAÇÕES - 2019/1 1. Em um sistema massa-mola temos k = 200 N/m, m = 1 kg, x(0) = A = 10 cm. Calcule ω, T, f, v m, a m, E (14,14 rad/s; 0,44 s; 2,25 Hz; 1,41 m/s; 20 m/s
Ordinárias. Diogo Pinheiro Fernandes Pedrosa. Universidade Federal do Rio Grande do Norte Centro de Tecnologia.
 Resolução Numérica de Equações Diferenciais Ordinárias Diogo Pinheiro Fernandes Pedrosa Universidade Federal do Rio Grande do Norte Centro de Tecnologia Departamento de Engenharia de Computação e Automação
Resolução Numérica de Equações Diferenciais Ordinárias Diogo Pinheiro Fernandes Pedrosa Universidade Federal do Rio Grande do Norte Centro de Tecnologia Departamento de Engenharia de Computação e Automação
Cálculo Numérico. Aula 5 Método Iterativo Linear e Newton-Raphson /04/2014
 Cálculo Numérico Aula 5 Método Iterativo Linear e Newton-Raphson 2014.1-15/04/2014 Prof. Rafael mesquita rgm@cin.ufpe.br Adpt. por Prof. Guilherme Amorim gbca@cin.ufpe.br O que vimos até agora? Zeros de
Cálculo Numérico Aula 5 Método Iterativo Linear e Newton-Raphson 2014.1-15/04/2014 Prof. Rafael mesquita rgm@cin.ufpe.br Adpt. por Prof. Guilherme Amorim gbca@cin.ufpe.br O que vimos até agora? Zeros de
2.1 Visualizando - Visualize um gráfico com uma função linear, y = ax + b - Neste caso, a taxa de crescimento é o valor de a, já que sabemos que:
 1. O que é uma taxa? Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Em poucas palavras, podemos descrever uma
1. O que é uma taxa? Universidade Federal de Alagoas Instituto de Ciências e Biológicas e da Saúde BIOB-003 Biomatemática Prof. Marcos Vinícius Carneiro Vital - Em poucas palavras, podemos descrever uma
Andréa Maria Pedrosa Valli
 1-24 Equações Diferenciais Ordinárias Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória,
1-24 Equações Diferenciais Ordinárias Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória,
Introdução ao Scilab 3.0 Parte 3
 Introdução ao Scilab 3.0 Parte 3 Paulo S. Motta Pires pmotta@dca.ufrn.br Departamento de Engenharia de Computação e Automação Universidade Federal do Rio Grande do Norte NATAL - RN Paulo Motta (DCA-UFRN)
Introdução ao Scilab 3.0 Parte 3 Paulo S. Motta Pires pmotta@dca.ufrn.br Departamento de Engenharia de Computação e Automação Universidade Federal do Rio Grande do Norte NATAL - RN Paulo Motta (DCA-UFRN)
Cálculo Diferencial e Integral C. Me. Aline Brum Seibel
 Cálculo Diferencial e Integral C Me. Aline Brum Seibel Em ciências, engenharia, economia e até mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenômeno
Cálculo Diferencial e Integral C Me. Aline Brum Seibel Em ciências, engenharia, economia e até mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenômeno
Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula
 Aula 3 010 Movimento Harmônico Simples: Exemplos O protótipo físico do movimento harmônico simples (MHS) visto nas aulas passadas um corpo de massa m preso a uma mola executando vibrações de pequenas amplitudes
Aula 3 010 Movimento Harmônico Simples: Exemplos O protótipo físico do movimento harmônico simples (MHS) visto nas aulas passadas um corpo de massa m preso a uma mola executando vibrações de pequenas amplitudes
Aula 04 Representação de Sistemas
 Aula 04 Representação de Sistemas Relação entre: Função de Transferência Transformada Laplace da saída y(t) - Transformada Laplace da entrada x(t) considerando condições iniciais nulas. Pierre Simon Laplace,
Aula 04 Representação de Sistemas Relação entre: Função de Transferência Transformada Laplace da saída y(t) - Transformada Laplace da entrada x(t) considerando condições iniciais nulas. Pierre Simon Laplace,
FEP Física para Engenharia II
 FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
Capítulo 4 O Oscilador Amortecido
 Capítulo 4 O Oscilador Amortecido Vamos supor que um oscilador harmônico tenha amortecimento, isto é, sofre uma resistência ao seu movimento e que esta resistência, para simplificar seja linearmente proporcional
Capítulo 4 O Oscilador Amortecido Vamos supor que um oscilador harmônico tenha amortecimento, isto é, sofre uma resistência ao seu movimento e que esta resistência, para simplificar seja linearmente proporcional
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIO #5 (1) COMPUTAÇÃO ANALÓGICA - A computação analógica
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIO #5 (1) COMPUTAÇÃO ANALÓGICA - A computação analógica
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia
 Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações Movimento Oscilatório Cinemática do Movimento Harmônico Simples (MHS) MHS e Movimento
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações Movimento Oscilatório Cinemática do Movimento Harmônico Simples (MHS) MHS e Movimento
Introdução aos Métodos Numéricos. Instituto de Computação UFF
 Introdução aos Métodos Numéricos Instituto de Computação UFF Conteúdo Erros e Aproximações Numéricas Sistemas de Equações Lineares. Métodos diretos Interpolação Ajuste de Curvas Zeros de Função Sistemas
Introdução aos Métodos Numéricos Instituto de Computação UFF Conteúdo Erros e Aproximações Numéricas Sistemas de Equações Lineares. Métodos diretos Interpolação Ajuste de Curvas Zeros de Função Sistemas
Métodos Matemáticos. O plano complexo: aplicações à cinemática e dinâmica. A C Tort 1. Instituto Física Universidade Federal do Rio de Janeiro
 Métodos Matemáticos O plano complexo: aplicações à cinemática e dinâmica A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 20 de agosto de 2012 Curvas,
Métodos Matemáticos O plano complexo: aplicações à cinemática e dinâmica A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 20 de agosto de 2012 Curvas,
Equações Ordinarias 1ªOrdem - Lineares
 Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Capítulo 7 - Equações Diferenciais Ordinárias
 Capítulo 7 - Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Química e Gestão Industrial Carlos
Capítulo 7 - Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Química e Gestão Industrial Carlos
