A Equação da Membrana

Transcrição

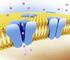
1 A Equação da Mebrana Biofísica II FFCLRP USP Prof. Antônio Roque Aula 17 Vaos considerar aqui ua aproxiação e que a célula nervosa é isopotencial, ou seja, e que o seu potencial de ebrana não varia ao longo da ebrana. Neste caso, podeos desprezar a estrutura espacial da célula e tratá-la coo u ponto. A ebrana coo u capacitor A ebrana neuronal é forada por duas caadas de lipídeos que separa os eios condutores intra e extracelular por ua fina caada isolante. Portanto, a ebrana neuronal atua coo u capacitor (veja a figura abaixo). A diferença de potencial entre as placas do capacitor é a voltage através da ebrana, V = V intra V extra. A relação entre a voltage V estabelecida entre as placas de u capacitor quando ua quantidade de carga Q é distribuída ao longo de suas placas é dada pela capacitância C: Q = CV. 1

2 Quando a voltage V varia no tepo, há ua variação na quantidade de carga Q arazenada dos dois lados da ebrana. Essa variação teporal de Q corresponde a ua corrente (I C = dq/dt) que flui para/ou das placas do capacitor, carregando-o ou descarregando-o. E teros da equação anterior, a corrente I C é dada por: I C dv ( t) = C. (1) dt É iportante notar que nunca existe u oviento de cargas através da ebrana isolante. O que ocorre é ua redistribuição de cargas nos dois lados da ebrana causada pela corrente I C que flui pelo resto do circuito. A Resistência da Mebrana: As proteínas que cruza a ebrana de u neurônio atua coo poros, ou canais iônicos, por onde corrente elétrica (íons) pode passar (íons entrando ou saindo). Ua ilustração disso é dada na figura abaixo: 2

3 Cada canal iônico (seletivo a ua dada espécie iônica) pode ser odelado por u resistor ôhico r colocado e paralelo co o capacitor que representa a ebrana (veja a figura abaixo). Segundo esta representação, a corrente iônica através de u canal pode ser escrita e teros da lei de Oh: I = V r. Esta equação pode ser reescrita e teros da condutância g do canal, coo é ais cou e neurofisiologia: I = gv. A condutância de u único canal iônico funciona coo u eleento binário, tendo valor nulo (g = 0) se o canal estiver fechado ou não nulo (= g) se o canal estiver aberto. Se o canal estiver aberto, os íons para os quais o canal é seletivo passarão através dele por difusão. Por exeplo, se o canal for u canal de K + haverá u fluxo de íons de potássio de dentro para fora da célula, pois há ua aior concentração de íons K + dentro da célula do que fora dela. 3

4 Por outro lado, se o canal for u canal de Na + haverá u fluxo de íons de sódio do exterior para o interior da célula, pois a concentração de íons de sódio é aior fora da célula do que dentro dela. Coo visto nas notas de aula sobre difusão, esse fluxo iônico irá gerar ua separação de cargas entre os dois lados da ebrana que produzirá ua diferença de potencial elétrico através dela. No equilíbrio, o valor dessa diferença de potencial é dado pelo potencial de Nernst do íon. Vaos passar a escrever esse potencial coo E íon, por exeplo, para o potássio teos E K, para o sódio teos E Na, etc: E = íon RT zf [ Íon] ln [ Íon] fora dentro. Pode-se odelar a existência de u potencial elétrico trans-ebrana provocado pelo fluxo iônico através de u canal iônico colocando-se ua bateria e série co a resistência que representa o canal iônico (lebre-se da aula 13). A voltage da bateria é o potencial de Nernst para a espécie iônica à qual o canal é seletivo (veja a figura abaixo). 4

5 Exercício: Observe na figura que o posicionaento das placas da bateria depende do íon específico. Explique porque isso é assi e porque cada bateria ostrada está co o posicionaento das suas placas indicado pela figura. As figuras acia representa u único canal iônico de u dado tipo (de sódio, potássio ou cloreto). Poré, a esa representação pode ser usada para representar todos os canais iônicos de u dado tipo e ua célula isopotencial. Para entender isto, suponha que a célula isopotencial tenha N canais iônicos para u dado tipo de íon. Então, o odelo ôhico para esse conjunto de canais iônicos é o ostrado na figura abaixo. Cada canal iônico é representado por ua resistência e série co ua bateria cuja voltage é o potencial de Nernst do íon e as N resistências estão arranjadas e paralelo na ebrana. O potencial E íon é o eso para cada resistor na figura acia porque o potencial de Nernst de u íon depende apenas da valência do íon, da teperatura e das concentrações do íon dentro e fora da célula. Ele não depende do núero N íon de canais iônicos na célula. 5

6 Coo E íon é o eso para todas as resistências e paralelo na figura acia, podeos representar o sistea de N resistores e paralelo da figura acia pelo sistea equivalente da figura abaixo. Nesta figura, o valor de R é dado pela conhecida fórula para a resistência equivalente para u conjunto de resistores e paralelo: 1 R = ! r 1 r 2 r N 1 r N Esta expressão pode ser reescrita e teros de condutâncias coo: G = g 1 + g 2 +!+ g N 1 + g N. (2) A condutância equivalente para o conjunto de N canais iônicos de u dado íon na ebrana de ua célula isopotencial é dada pela soa das condutâncias dos canais individuais. A partir de agora, vaos passar a usar condutâncias para representar canais iônicos, ao invés de resistências. Desta fora, o conjunto de N canais iônicos incrustados na ebrana de ua célula isopotencial será representado pelo eleento de circuito abaixo. 6

7 A cada instante de tepo t, ua parte dos N canais iônicos de ua dada espécie estará aberta e a outra parte estará fechada. Chaando de n a (t) o núero de canais abertos no tepo t (de aneira que o núero de canais fechados é N n a ), o valor de G íon na figura acia é dado por (note que a condutância de u canal fechado é zero): G íon (t) = g = n a (t)g, canais abertos e t onde 0 n a (t) N. O fato de que a condutância da população de N canais iônicos de ua dada espécie depende de t iplica que o odelo de circuito equivalente para essa população deve ser o da figura abaixo (a seta sobre o síbolo de resistência indica que ela é variável). 7

8 Coo visto na aula 13 (equação 2), só há corrente passando pelos canais iônicos de ua dada espécie se a voltage de ebrana V for diferente do potencial de Nernst dessa espécie iônica. Portanto, a corrente iônica passando pelos canais iônicos de ua dada espécie pode ser escrita coo: I R = V (t) E íon R íon (t) = G íon (t)( V (t) E íon ). (3) Se o potencial de ebrana V for aior que o potencial de Nernst E íon do íon, isto irá iplicar e ua corrente líquida do íon nua dada direção (para dentro ou para fora da célula, dependendo da carga do íon). Se o potencial de ebrana for enor que o potencial de Nernst, haverá ua corrente líquida do íon na direção oposta à do caso anterior. Desta fora, a direção da corrente do íon é invertida quando V passa por E íon. Por este otivo, E íon tabé é chaado de potencial de reversão do íon. Mebranas co canais iônicos cujas condutâncias varia no tepo são chaadas de ativas (por extensão, chaa-se os canais desse tipo de canais ativos e suas respectivas condutâncias de condutâncias ativas). Por outro lado, ebranas co canais iônicos cujas condutâncias não varia no tepo são chaadas de passivas (igualente, teos canais passivos e condutâncias passivas). 8

9 A aior parte das propriedades iportantes dos neurônios coo os potenciais de ação, por exeplo decorre dos efeitos não-lineares causados pelos canais ativos. Poré, vaos deixar o estudo de condutâncias ativas para aulas futuras e, nesta aula, vaos nos restringir ao estudo das propriedades de ua ebrana passiva. No caso de ua ebrana passiva, a equação (3) torna-se: I R = V (t) E íon = G íon ( V (t) E íon ). R (4) íon Cobinando os eleentos de circuito vistos até agora e u único odelo de circuito elétrico para ua ebrana neuronal passiva, teos o circuito abaixo (no caso do desenho, considerou-se apenas os canais de sódio e potássio): 9

10 A Corrente de Mebrana Quando ua corrente I passa pela ebrana, teos ua situação coo a da figura abaixo (vaos definir o sentido positivo de corrente coo sendo de dentro para fora da célula; vaos tabé considerar soente u canal iônico para não sobrecarregar a figura): Aplicando a lei das correntes de Kirchoff ao nó superior dessa figura: I dv ( t) = IC + I R = C + G( V ( t) E).. (5) dt Note que o odelo construído corresponde a u circuito RC. Podeos estiar o tepo característico τ desse circuito para u neurônio típico, coo feito a seguir: Propriedades ateriais da ebrana: 10

11 Desenrolando u pedaço de u neurônio cilíndrico de raio a, veos que a sua ebrana corresponde a u condutor de copriento b e seção reta de área A. Da figura, teos que A = 2πaL. A resistência desse pedaço de ebrana é: onde b R = ρ, A - ρ é a resistividade elétrica do aterial (unidades: Ω.c); - 1/ρ é a condutividade elétrica σ (unidades: S/c). Para ua dada ebrana de espessura b, define-se a sua resistência específica R por: R = ρb (unidades: Ω.c2), ou seja, para se saber a resistência da ebrana de ua célula de área A cuja ebrana te resistência específica R deve-se dividir R por A. Define-se a capacitância específica C de ua ebrana coo a capacitância de ua área unitária (unidades: µf/c2). Ou seja, para se saber a capacitância da ebrana de ua célula de área A deve-se ultiplicar C por A. Alguns valores típicos para essas variáveis são: C = 1 µf/c2; R = 10 kω.c2; G = 1/R = 100 µs/c2; b = 0,1 10 µ. 11

12 Exeplo: Para ua célula esférica co diâetro de 20 icrons, a sua capacitância total é: C = C.A = C.4πr 2 = ( F/c 2 )4π(10x10-4 c) 2 = 12,6 x F = 12,6 pf, e a sua resistência total é: R = R /A = (10x10 3 Ω/c 2 )/(4π.(10x10-4 c) 2 ) = 796 x 10 6 Ω = 796 MΩ. Nota: Cada ebrana possui suas propriedades ateriais, que são independentes da fora da célula. Poré, as propriedades elétricas de ua dada célula depende da sua geoetria. Co os valores de C e de R dados acia, podeos calcular a constante de tepo de ua ebrana neuronal típica: τ = R C = RC =10 s. (6) Note que a constante de tepo da ebrana neuronal não depende do taanho e da geoetria da célula. Injeção de Corrente Externa Vaos supor que se injeta corrente I inj através de u icroeletrodo diretaente dentro da nossa pequena célula isopotencial, coo na figura abaixo. Coo podeos descrever a dinâica do potencial de ebrana V (t) e resposta a essa corrente? 12

13 Usando o odelo de circuito elétrico construído acia, esta situação pode ser representada pela figura a seguir: Por conservação de corrente, a corrente de ebrana deve ser igual à corrente injetada: I = I inj : dv ( t) C G V = dt ( ( t) E) I ( t) + inj. Multiplicando abos os lados por R e usando τ = RC: dv ( t) τ = V ( t) + E RIinj( t). dt + (7) Esta é a chaada equação da ebrana. Ela descreve coo o potencial de ebrana varia no tepo e decorrência de injeção de corrente na célula para o caso de ua ebrana passiva. A equação da ebrana é ua equação diferencial ordinária de prieira orde co coeficientes constantes. Definindo-se ua condição inicial V (0), a solução da equação da ebrana nos dará ua única curva para V versus t. 13

14 Se a corrente injetada for nula, a solução da equação da ebrana é (tente ostrar coo exercício): V τ ( E V (0)) e t ( t) = E. (8) Qualquer que seja a condição inicial, o potencial de ebrana decai exponencialente para E co o tepo. Por isso, podeos chaar E de potencial de ebrana de repouso neste caso. Se V (0) = E, o potencial de ebrana peranece no valor de repouso indefinidaente. Vaos supor agora que a corrente injetada é do tipo degrau: e t = 0 injeta-se u valor de corrente I 0 que é antido constante por u longo tepo. A teoria das equações diferenciais nos ostra que a solução ais geral da equação da ebrana é do tipo: V t t) = v0 e + ( v τ, (9) onde ν 0 e ν 1 depende das condições iniciais. Substituindo esta fora geral de solução na equação da ebrana obteos a igualdade: v E + =. 1 RI 0 Vaos ipor a seguinte condição inicial: V (0) = E. Isto nos dá: E = v. 0 + v1 v0 = RI0 Substituindo ν 0 e ν 1 na solução geral (equação 9) teos: 1 V onde se definiu V = RI 0. t t ( t) = RI 0 1 τ e + E = V 1 τ e E, + (10) 14

15 U longo tepo após a aplicação do degrau de corrente (e antendo-se a corrente constante), o potencial de ebrana atinge o valor assintótico, V ( ) = V + E = RI 0 + V (0). É costue representar o potencial de ebrana de ua célula e relação ao seu potencial de repouso V rep (isto é, redefine-se o zero do potencial de aneira que ele coincida co o potencial de repouso da célula). Fazendo isso, pode-se definir ua nova variável: V = V t) V, (11) ( rep e notando que neste caso V rep = E, a solução da equação da ebrana para o degrau de corrente torna-se: V e = V t τ 1. (12) A constante V = RI 0 é chaada de potencial estacionário, pois é o valor estacionário para o qual a diferença (V (t) V rep ) tende assintóticaente e resposta ao degrau de corrente. E geral, ede-se a corrente injetada e ua célula e teros da área da ebrana que é estiulada, ou seja, ede-se a densidade de corrente (as unidades ais couns são µa/c 2 ). Para ua ebrana típica (R = 10 kω.c 2 ) estiulada co ua corrente de 5 µa/c 2, o potencial estacionário vale: V = RI 0 = (R /A)(J 0.A) = R J 0 = (10 4 Ω.c 2 ).(5 x 10-6 A/c 2 ) = 5 x 10-2 V. 15

16 E ilivolts (a unidade ais usada), deve-se ultiplicar o resultado acia por 10 3 : V = 50 V. Lebrando que V = V V rep, podeos agora escrever o valor do potencial estacionário edido e relação ao potencial externo coo (supondo, por exeplo, que V rep = 70 V): V = V + V rep = 50 V 70 V = 20 V. O gráfico abaixo ostra soluções nuéricas da equação da ebrana para diferentes valores do degrau de corrente injetado (R = 2 MΩ). O gráfico acia ostra as respostas do odelo de ebrana coo u circuito RC para quatro diferentes valores de J 0 (u negativo e três positivos). 16

17 Na escala arbitrária de tepo usada, o estíulo degrau é aplicado e t = 20 e desligado e t = 120. Note que se I 0 for positiva, V = RI 0 será positivo. Isto quer dizer que a célula foi despolarizada (V > V rep ). Já se I 0 for negativa, V será negativo, iplicando que a célula foi hiperpolarizada. Para entender isso, vejaos o diagraa da ebrana a seguir. Ua I 0 positiva corresponde a ua corrente de ebrana positiva, I > 0. Pela convenção adotada, ua corrente de ebrana positiva indica corrente saindo da célula e isto só ocorre quando a ebrana está despolarizada, isto é, o interior da célula está ais positivo do que no repouso. Isto está de acordo co o esperado, pois quando I 0 > 0 o icroeletrodo injeta corrente diretaente no interior da célula, provocando u auento de cargas positivas no interior e despolarizando a célula. Já ua I 0 negativa (I indo de fora para dentro da célula) corresponde a ua retirada de cargas positivas do interior da célula pelo icroeletrodo, hiperpolarizando a célula. 17