UM ALGORITMO EXATO PARA A OTIMIZAÇÃO DE CARTEIRAS DE INVESTIMENTO COM RESTRIÇÕES DE CARDINALIDADE
|
|
|
- Milena Sousa Abreu
- 8 Há anos
- Visualizações:
Transcrição
1 UM ALGORITMO EXATO PARA A OTIMIZAÇÃO DE CARTEIRAS DE INVESTIMENTO COM RESTRIÇÕES DE CARDINALIDADE Dssertação de mestrado em matemátca aplcada fnancada pelo CNPq IMECC - UNICAMP Pedro Ferraz Vllela Prof. Dr. Francsco de Asss Magalhães Gomes Neto - Orentador Dezembro de 2008
2
3
4 FICHA CATALOGRÁFICA ELABORADA PELA BIBLIOTECA DO IMECC DA UNICAMP Bblotecára: Crsllene Queroz Custódo CRB8a 162/2005 V715a Vllela, Pedro Ferraz Um algortmo exato para a otmzação de carteras de nvestmento com restrções de cardnaldade / Pedro Ferraz Vllela -- Campnas, [S.P. : s.n.], Orentador : Francsco de Asss Magalhães Gomes Neto Dssertação (Mestrado) - Unversdade Estadual de Campnas, Insttuto de Matemátca, Estatístca e Computação Centífca. 1. Otmzação de Carteras de Investmento. 2. Método de Lemke. 3. Algortmo Branch and Bound. 4. Restrções de cardnaldade. I. Gomes Neto, Francsco de Asss Magalhães. II. Unversdade Estadual de Campnas. Insttuto de Matemátca, Estatístca e Computação Centífca. III. Título. (cqc/mecc) Título em nglês: An exact algorthm for portfolo optmzaton wth cardnalty constrants. Palavras-chave em nglês (Keywords): 1. Portfolo optmzaton. 2. Lemke's method. 3. Branch and Bound algorthms. 4. Cardnalty constrants. Área de concentração: Otmzação Ttulação: Mestre em Matemátca Aplcada Banca examnadora: Prof. Dr. Francsco de Asss Magalhães Gomes Neto (IMECC-UNICAMP) Prof. Dr. Antono Carlos Morett (IMECC-UNICAMP) Prof. Dr. Paulo Augusto Valente Ferrera (FEEC-UNICAMP) Data da defesa: 16/12/2008 Programa de Pós-Graduação: Mestrado em Matemátca Aplcada
5
6 v
7 AGRADECIMENTOS Em prmero lugar, gostara de agradecer ao meu orentador e amgo Chco, que sempre esteve junto comgo durante todo o trabalho. Agradeço por toda a sua dsposção e pacênca ao longo desse período Também agradeço muto a mnha famíla, que sempre esteve comgo nos momentos mas dfíces, apoando-me com muto amor. Em especal aos meus pas, que se dspuseram a me ajudar até nos horáros mas ndejesáves. Sou muto grato também aos meus amgos Carlos e Rodrgo, que sempre se dsporam a me ajudar quando precso. Em especal ao Carlos, pela ajuda vtal na formatação do texto. Por últmo, agradeço ao CNPq (Conselho Naconal de Desenvolvmento Centífco e Tecnológco), pelo essencal apoo fnancero prestado durante a vgênca do trabalho. v
8 v
9 RESUMO Neste trabalho, propomos um método exato para a resolução de problemas de programação quadrátca que envolvem restrções de cardnaldade. Como aplcação, empregamos o método para a obtenção da frontera efcente de um problema (b-objetvo) de otmzação de carteras de nvestmento. Nosso algortmo é baseado no método Branch-and-Bound. A chave de seu sucesso, entretanto, resde no uso do método de Lemke, que é aplcado para a resolução dos subproblemas assocados aos nós da árvore gerada pelo Branch-and-Bound. Ao longo do texto, algumas heurístcas também são ntroduzdas, com o propósto de acelerar a convergênca do método. Os resultados computaconas obtdos comprovam que o algortmo proposto é efcente. Palavras-chave: Otmzação de carteras de nvestmento. método de Lemke. Branch-and- Bound. Restrção de cardnaldade. v
10 v
11 ABSTRACT In ths work, we propose an exact method for the resoluton of quadratc programmng problems nvolvng cardnalty restrctons. As an applcaton, the algorthm s used to generate the effectve Pareto fronter of a (b-objectve) portfolo optmzaton problem. Ths algorthm s based on the Branch-and-Bound method. The key to ts success, however, resdes n the applcaton of Lemke s method to the resoluton of the subproblems assocated to the nodes of the tree generated by the Branch-and-Bound algorthm. Throughout the text, some heurstcs are also ntroduced as a way to accelerate the performance of the method. The computatonal results acqured show that the proposed algorthm s effcent. Keywords: Portfolo optmzaton. Lemke s method. Cardnalty constrants. Branch-and-Bound algorthm x
12 x
13 SUMÁRIO RESUMO...VII ABSTRACT... IX INTRODUÇÃO...1 MODELOS DE CARTEIRAS DE INVESTIMENTO O MODELO DE MARKOWITZ OUTROS MODELOS O modelo paramétrco O modelo MAD Um modelo de programação por metas O MODELO COM RESTRIÇÃO DE CARDINALIDADE E CANALIZAÇÕES MEDIDAS DE RETORNO E RISCO A FRONTEIRA EFICIENTE PROBLEMAS DE PROGRAMAÇÃO QUADRÁTICA MISTA O MÉTODO DE LEMKE INTRODUÇÃO O PROBLEMA DE COMPLEMENTARIDADE LINEAR O MÉTODO DE LEMKE ALGORITMO EXEMPLO NUMÉRICO RESOLVENDO AS ITERAÇÕES DO MÉTODO DE LEMKE O MÉTODO BRANCH-AND-BOUND IMPLÍCITO INTRODUÇÃO O MÉTODO BRANCH-AND-BOUND PARA PROBLEMAS O MÉTODO BRANCH-AND-BOUND IMPLÍCITO ALGORITMO E EXEMPLO Algortmo Exemplo RAMIFICANDO PARA BAIXO Exemplo RAMIFICANDO PARA CIMA Exemplo PROCEDIMENTOS COMPUTACIONAIS O PROJETO ESCOLHENDO A VARIÁVEL A SER RAMIFICADA Ramfcando a varável mas próxma de um de seus lmtes Ramfcando a varável mas dstante de um de seus lmtes Ramfcando a varável mas dstante de zero e de seu lmte nferor Ramfcando quando o nó pa tem cardnaldade maor ou gual a K ESCOLHENDO UM NÓ DA LISTA DE NÓS PENDENTES x
14 4.3.1 Escolhendo o nó com melhor ζ Fazendo uma busca em profunddade Fazendo uma busca em largura APROVEITANDO A BASE NO MÉTODO DE LEMKE ATUALIZANDO A FATORAÇÃO LU DA BASE HEURÍSTICAS ADICIONAIS Lmtando o número de ramfcações para cma Determnando precocemente a nfactbldade de um subproblema RESULTADOS COMPUTACIONAIS OBJETIVOS OS PROBLEMAS DE CARTEIRAS DE INVESTIMENTO TESTANDO AS VARIANTES DO MÉTODO BRANCH-AND-BOUND Determnando a melhor estratéga de ramfcação Determnando a estratéga de ramfcação quando temos mas que K atvos Determnando a melhor estratéga de seleção do nó pendente ATUALIZANDO A FATORAÇÃO LU DA BASE Aplcando a atualzação da base à resolução de problemas de complementardade Atualzando a base em todos os subproblemas gerados pelo Branch-and-Bound COMPARANDO DOIS ALGORITMOS PARA PROGRAMAÇÃO QUADRÁTICA TESTANDO O DESEMPENHO DO PROGRAMA RESOLVENDO PROBLEMAS COM MAIS RESTRIÇÕES USANDO RESTRIÇÕES DE IGUALDADE CONCLUSÕES REFERÊNCIAS x
15 INTRODUÇÃO Esta dssertação trata do problema de otmzação de uma cartera de nvestmento, ou portfolo, que é o conjunto de atvos fnanceros nos quas se nveste. Em geral, ao montar uma cartera de nvestmento, o nvestdor procura maxmzar o lucro, bem como mnmzar o rsco de perda de captal. Para ldar com o problema, o nvestdor precsa utlzar um modelo matemátco que leve em conta esses dos objetvos antagôncos. Uma das prmeras formulações matemátcas para esse problema de nvestmento fo o modelo de Méda-Varânca proposto por Markowtz [13] nos anos 50 do século 20. Anda hoje, esse modelo tem uma boa acetação por parte dos nvestdores. Em sua forma usual, o modelo de Markowtz se resume a um problema de programação quadrátca no qual a função objetvo representa o rsco a ser mnmzado e o retorno mínmo da cartera é descrto através de uma restrção lnear. Com o passar do tempo, váras alterações foram sugerdas com o propósto de tornar o modelo de Markowtz mas compatível com o mercado fnancero real. Dentre essas alterações, destacamos a nclusão de restrções que lmtam o tamanho da cartera e de restrções que estpulam um lmte nferor para o montante aplcado em cada atvo. Com essas novas restrções, o problema de programação quadrátca passa a envolver varáves nteras, além das varáves reas que já eram usadas para representar o valor nvestdo em cada atvo. Naturalmente, com a nclusão de varáves nteras, o problema se torna NPcompleto, exgndo um grande esforço computaconal para a obtenção da solução ótma. Em vrtude da dfculdade do problema, uma alternatva prátca para a obtenção de soluções satsfatóras em um tempo acetável é a adoção de métodos heurístcos. Dentre os 1
16 2 trabalhos desta classe, podemos ctar o artgo de Chang et al. [5] que nvestga o uso de algortmos genétcos, da busca tabu e da têmpera smulada para a determnação do portfolo aproprado para cada perfl de nvestdor, contemplando desde os mas conservadores até os mas arrojados. Segundo o trabalho de Chang et al., Das [7] propôs, recentemente, um novo algortmo genétco efcente para resolver problemas de nvestmento. Outra lnha de solução do problema de carteras de atvos fnanceros envolve o emprego de métodos exatos, geralmente baseados no algortmo Branch-and-Bound alado a algum método para resolver problemas de otmzação que envolvem varáves contínuas. Dentre os trabalhos desta lnha, podemos ctar o desenvolvdo por Benstock [4], que utlza técncas de planos de corte aladas ao algortmo Branch-and-Bound. Outro trabalho gualmente mportante fo o de Bertsmas e Shoda [3], que utlza o algortmo Branch-and-Bound alado ao método de Lemke [6, 11]. Em nossa pesqusa, também desenvolvemos um algortmo exato para o problema de portfolos, combnando o algortmo Branch-and-Bound com o método de Lemke. Nosso objetvo prncpal é a obtenção de um algortmo efcente do ponto de vsta computaconal. Esta dssertação está dvdda da segunte forma: no prmero capítulo, fazemos uma ntrodução aos modelos de cartera de nvestmento, bem como apresentamos o tpo de problema problema específco que nos propomos a resolver. O Capítulo 2 é dedcado à apresentação detalhada do método de Lemke. No Capítulo 3, apresentamos o algortmo Branch-and-Bound tradconal, segudo da versão mplícta que desenvolvemos. No Capítulo 4, tratamos dos detalhes de mplementação do Branch-and-Bound e do método de Lemke. Fnalmente, o Capítulo 5 apresenta os resultados obtdos com a aplcação do nosso algortmo a problemas reas de carteras de nvestmento, que comprovam a efcênca do método que desenvolvemos.
17 CAPÍTULO 1 MODELOS DE CARTEIRAS DE INVESTIMENTO 1.1 O MODELO DE MARKOWITZ O tpo de problema de portfolo a ser estudado nesse trabalho caracterza-se pela escolha de como nvestr o captal dsponível entre as váras ações exstentes no mercado. A estratéga envolvda na resolução desse tpo de problema envolve tanto a maxmzação do lucro do nvestmento, como a mnmzação do rsco de perda de captal em vrtude das flutuações dos preços do mercado. Naturalmente, estes objetvos são contradtóros e cabe ao nvestdor decdr como combná-los. O modelo matemátco clássco para esse tpo de problema de portfolo é baseado na déas propostas por Markowtz [13] em Defndos os N dferentes atvos que compõem a cartera de nvestmento, o montante a ser nvestdo em cada atvo pode ser obtdo resolvendo-se o problema de programação quadrátca 3
18 4 mn s. a x T µ x = ρ = 1 x N T Qx x = 1 0, = 1,..., N., (1.1) onde Q NxN R é a matrz de covarânca do problema. Assm, o elemento j q da matrz representa a covarânca do atvo em relação ao atvo j. Além dsso, a matrz Q é smétrca e semdefnda postva (Q = Q T 0). x N R é o vetor de ncógntas, que ndca como o montante total dsponível deve ser dstrbuído entre os atvos. Desta forma, a componente x fornece a fração do montante a ser nvestda no atvo. N µ R é o vetor de retornos esperados. Ou seja, o elemento µ representa o retorno esperado para o atvo. ρ R é o nível desejado de retorno do portfolo. Nesse modelo, temos como objetvo mnmzar o rsco, representado pela função quadrátca baseada na matrz de covarânca, para um nível predefndo de retorno, defndo pela prmera restrção. A segunda restrção ndca apenas que desejamos gastar todo o montante dsponível, enquanto a tercera é usada para evtar que a porcentagem do dnhero gasta em cada atvo seja negatva, o que sgnfca que não permtmos a venda de atvos. Os concetos de rsco e retorno serão explcados detalhadamente na Seção 1.4. Para defnr um problema específco na forma (1.1), faz-se uma análse hstórca dos atvos fnanceros escolhdos para compor a cartera, de modo que seja possível crar tanto uma medda de rsco (em geral, a varânca), como também obter o valor esperado de retorno de captal (esperança).
19 5 1.2 OUTROS MODELOS Naturalmente, o Modelo (1.1) podera ser substtuído por outro no qual se estabelecesse um nível para a varânca e o retorno fosse mnmzado. Outra possbldade sera a adoção de uma desgualdade na restrção de retorno esperado, de modo que ρ correspondesse ao retorno mínmo admssível. Ao longo dessa seção, apresentaremos outros modelos que podem ser obtdos a partr de (1.1) O modelo paramétrco Uma modfcação possível do Modelo (1.1) corresponde a nclur, além da função de rsco, o desejo de maxmzar o retorno dentro da função objetvo. Para tanto, é precso utlzar um parâmetro λ que que pondera os objetvos confltantes de redução do rsco e aumento do retorno. Neste caso, obtemos o problema abaxo, no qual temos apenas as restrções de uso de todo o montante dsponível e de não negatvdade das varáves. mn s. a λx N = 1 x T T Qx (1 λ) µ x x = 1 0, = 1,..., N. (1.2) Tomando 0 λ 1, observamos que para λ = 0, apenas o retorno é consderado, enquanto λ = 1 corresponde à smples mnmzação do rsco. Caso a matrz Q seja postva defnda, o problema é convexo e possu solução únca, pos o únco mínmzador local exstente é também mnmzador global.
20 O modelo MAD Problemas de programação quadrátca como aqueles apresentados em (1.1) e (1.2) não são os úncos modelos utlzados na otmzação de portfolos. O modelo do desvo absoluto com relação à méda (MAD) [14], por exemplo, tem como déa a mnmzação do rsco através de uma função objetvo lnear. Neste modelo, consdera-se a exstênca de T períodos para os quas conhecemos o retorno dos atvos dsponíves para aplcação. O objetvo do modelo é mnmzar a soma do desvo absoluto do retorno de cada portfolo em relação à méda de retorno para todos os períodos. Em termos matemátcos, a função a ser mnmzada tem a forma T N 1 f ( x) = ( r, t µ ) x, T t= 1 = 1 onde r, é o retorno de um determnado atvo no período de tempo t. t auxlares Para converter o modelo em um problema de programação lnear, usamos varáves m t, de modo que cada termo que envolve o valor absoluto dá orgem a duas restrções de desgualdade. Consderando também as restrções do problema de Markowtz, chegamos ao segunte problema:
21 7 mn s. a 1 T t= 1 N = 1 N = 1 T = 1 ( r ( r x m, t, t µ x = ρ N T = 1 m t 0, x 0, t µ ) x µ ) x m t, m t, t = 1,.., T = 1,.., N. t = 1,.., T t = 1,.., T Um modelo de programação por metas Outra abordagem lnear nteressante é a que envolve programação por metas (goal programmng) [14]. Neste caso, mnmza-se tanto a chance de um retorno negatvo como a de um rsco elevado, dando um peso específco a cada uma dessas possbldades. Assm, caso o nvestdor seja arrojado, o peso sobre o retorno será maor, enquanto o nvestdor conservador rá optar por usar um peso maor sobre o rsco. Para esse modelo, utlzamos os seguntes parâmetros e varáves Parâmetros: W 1 : penaldade postva assocada ao retorno abaxo do objetvo esperado. W 2 : penaldade postva assocada ao rsco excessvo do portfolo em relação ao valor esperado. Rsk p : rsco global assocado ao portfolo defndo pelo nvestdor. Rsk : rsco assocado ao atvo defndo pelo nvestdor.
22 8 Varáves: n 1 : desvo negatvo em relação ao retorno esperado. p 1 : desvo postvo em relação ao retorno esperado. n 2 : denota o desvo negatvo em relação ao nível de rsco. p 2 : denota o desvo postvo em relação ao nível de rsco. Dessa forma, temos o segunte modelo: mn s. a W n + W p 1 N = 1 N = 1 N = 1 n, n x 1 1 x 2 = 1, p, p , = 1,2,..., N. 1 2 x µ + n p = ρ Rsk x + n p 2 = Rsk p A função objetvo procura mnmzar apenas o rsco acma da meta e o retorno abaxo da meta estabelecda. Deve-se notar que as varáves n 1 e p 1 não serão dferentes de zero ao mesmo tempo, o mesmo ocorrendo com n 2 e p 2,. 1.3 O MODELO COM RESTRIÇÃO DE CARDINALIDADE E CANALIZAÇÕES. Outra lnha de desenvolvmento de modelos para a otmzação de carteras de nvestmentos está relaconada à nclusão de restrções que tornam o problema mas compatível com as stuações encontradas na vda real. Nessa lnha, destacamos o modelo no qual se restrnge a quantdade de atvos que rão compor a cartera, uma vez que normalmente não é vável nvestr
23 9 em todos os N atvos dsponíves no mercado. Este modelo geralmente nclu também um conjunto de lmtes nferores, l, e superores, u, para as frações aplcadas a cada atvo seleconado. Para restrngr a K o número de atvos, ncluímos no modelo as varáves bnáras auxlaresδ, = 1,...,N, de modo que δ = 1 caso o atvo faça parte da cartera e δ = 0 caso contráro. Já com relação aos lmtes nferores e superores, como estes só são aplcados às varáves efetvamente ncluídas na cartera, em lugar de utlzarmos canalzações smples, recorremos a desgualdades mstas, ou seja, com varáves nteras e reas. Tomando por base o modelo de Markowtz, obtemos o segunte problema mn s. a x µ = 1 l N N = 1 x T δ T δ Qx x = ρ x = 1 x u δ, = 1,..., { 0,1}, = 1,..., N δ K, K N 0, = 1,..., N. N (1.3) Em (1.3), se δ vale 0, x também será gual a 0. Por outro lado, se δ = 1, temos l x u Como temos no máxmo K varáves nteras δ guas a 1, somos forçados a escolher no máxmo K atvos. Naturalmente, a restrção de cardnaldade pode ser ncluída em todos os problemas apresentados neste capítulo, bem como em mutos outros modelos para problemas de otmzação de carteras. Para maores nformações, sugere-se consultar o artgo de Mtra et al.[14].
24 MEDIDAS DE RETORNO E RISCO Naturalmente, não é possível medr o retorno futuro de um atvo. Assm, para estmar o retorno esperado, fazemos uma análse hstórca, na esperança de que os valores regstrados no passado recente voltem a ocorrer. Em termos matemátcos, supondo que um atvo tenho assumdo hstorcamente n valores dferentes, defnndo x como o -ésmo retorno possível e p como a respespectva probabldade de ocorrênca, uma manera de representar o retorno esperado do atvo é µ = x = E( x) = x p. n = 1 O retorno esperado pode ser vsto também como a méda dos possíves valores que o atvo assumu hstorcamente. Já o conceto de rsco é algo muto mas complexo pos não exste uma fórmula unversal para se medr o rsco de um nvestmento, uma vez que o conceto é extremamente vasto e abstrato, não podendo ser representado de manera exata. A medda de rsco mas usada e ntutva é a varânca, como vsto no modelo de Markowtz. Porém, esta é apenas uma das possíves representações do rsco. Uma manera mas geral de representar o rsco envolve o uso do que chamamos de momentos parcas [14], ou smplesmente LPM (abrevatura do termo nglês lower partal moments), apresentados a segur. Seja α o parâmetro que ndca o momento do retorno da dstrbução, τ o nível prédefndo de retorno do nvestmento, e F(x) a função de densdade de probabldade do nvestmento com retorno x. Neste caso, defnmos os momentos parcas de ordem α como τ α {( max[ 0, τ x] ) }, α 0 α Fα ( τ ) = LPMα ( τ, x) = ( τ x) f ( x) dx = E >.
25 11 O LPM pode ldar tanto com meddas smétrcas quanto assmétrcas de rsco. No caso smétrco, as meddas de rsco ncluem, por exemplo, a varânca e o desvo absoluto com relação à méda (MAD), como vemos abaxo. Varânca: defnndo o nível de retorno e o momento como τ = x e α = 2, obtemos {( x ) 2 } 2 σ = LPM 2 2( x, x) = + ( x x) f ( x) dx = E x. MAD: defnndo τ = x e α = 1, obtemos MAD = LPM ( x, x) = + x x f ( x) dx = E { x x } 1. No caso assmétrco, desprezamos da medda de rsco o retorno acma do nível desejado. Dentre as meddas assmétrcas de rsco, destacamos a semvarânca e o MAD, que são obtdas a partr das defnções acma, substtundo o lmte superor da ntegral por x, em lugar de +. Outra medda assmétrca muto usada atualmente é denomnada Valor-em-Rsco, ou VaR (do nglês Value-at-Rsk). Embora a escolha da medda de rsco seja um assunto em grande ebulção, com defensores arragados para os város modelos exstentes, utlzaremos, neste trabalho, a medda clássca, ou seja, a varânca, que anda conta com o maor número de adeptos.
26 A FRONTEIRA EFICIENTE Problemas de programação mult-objetvo, como o que temos, geralmente não possuem uma solução ótma únca. Em outras palavras, não é razoável esperar que a cartera com o maor retorno seja também aquela que tem o menor rsco. Para comparar soluções dferentes, usamos a noção de domnânca. Dzemos que uma solução x 1 domna uma outra solução x 2 se: f ( x ) f ( ) ; : 1 x2 f ( x ) f ( ). : 1 < x2 No caso de aplcações fnanceras, dzemos que um portfolo, π 1, domna outro, π 2, se π 1 possu rsco menor e retorno maor que π 2, podendo haver gualdade em uma das duas meddas. Para um problema com p objetvos, a frontera efcente de nvestmento, ou frontera de Pareto, é a curva em p R que representa o conjunto de pontos não domnados. Para o problema de carteras de nvestmentos, a frontera efcente é a curva não decrescente que contém as melhores possbldades de conclação entre rsco e retorno. Vale notar que, caso não tenhamos restrções de cardnaldade, a curva é bem comportada, pos ela é não decrescente e possu uma reta suporte. A Fgura 1.1, mostrada a segur, apresenta uma frontera efcente de nvestmento gerada a partr de atvos da bolsa de valores do Reno Undo. Nesta fgura, o exo das abscssas representa a medda de rsco do portfolo, que nesse caso é a varânca. Já o exo das ordenadas representa o retorno médo dos atvos.
27 13 Retorno Portfolo seleconado contendo 1 atvo. Portfolo seleconado contendo 30 atvos. Rsco - varânca Fgura 1.1 FEI. dos atvos da bolsa de valores do Reno Undo (UK FTSE), extraída de [5]. A análse da Fgura 1.1 revela que caso o nvestdor tenha uma grande aversão ao rsco, ele deve optar por nvestr em um portfolo que tenha város atvos, pos a possbldade de perder dnhero em todos eles é menor. Caso o nvestdor seja mas audaz e escolha prorzar o retorno, ele deve optar por nvestr em poucos atvos, em geral aqueles que apresentam o maor retorno, anda que o rsco de perda de captal seja grande devdo à volatldade do mercado fnancero. Vale notar anda, que nenhuma das soluções da frontera efcente é melhor que as outras: cada ponto dela representa a melhor solução para o nível de rsco especfcado pelo nvestdor. Para maores nformações sobre frontera efcente de nvestmentos sugere-se consultar o lvro de Luenberger [12]. Um modelo muto utlzado para a determnação da frontera efcente de nvestmento é o modelo parametrzado (1.2). Como a função objetvo desse problema é convexa, todo mínmo local é também mínmo global. Logo, cada ponto da frontera nada mas é que a solução de (1.2) para um ou mas valores de λ. Valores do parâmetro λ próxmos de zero sgnfcam que o nvestdor prorza o retorno, pouco se mportando com o rsco. Já valores de λ próxmos de um, sgnfcam que o nvestdor prorza excessvamente o rsco, dexando o retorno em segundo plano. Logo, o parâmetro λ desempenha um papel essencal no modelo, uma vez que ele mede o nível de rsco escolhdo pelo nvestdor.
28 14 Na prátca, uma manera de se construr a Frontera Efcente envolve a dscretzação dos valores λ no ntervalo [0,1] e a resolução do Problema (1.2) para cada um dos valores de λ seleconados. Em geral, essa dscretzação é feta defnndo E como o tamanho da partção e 1 2 E 1 tomando λ 0,,, L,. E 1 E 1 E 1 Quando se ncorpora a restrção de cardnaldade, a frontera efcente passa a ser descontínua. Assm, a complexdade de problemas como o (1.4), a ser apresentado na próxma seção, é muto maor do que a de (1.2). Para maores nformações sobre a frontera efcente em problemas que envolvem restrções de cardnaldade pode-se consultar Chang et al. [5] e Das [7]. 1.6 PROBLEMAS DE PROGRAMAÇÃO QUADRÁTICA MISTA Neste trabalho, nos concentramos no modelo apresentado na Seção 1.3, que nclu uma restrção de cardnaldade e lmtes nferores para os montantes a serem aplcados nos atvos da cartera. Em nosso problema, não ncluímos as restrções de lmte superor para as varáves. Para permtr um maor controle sobre a mnmzação do rsco e a maxmzação do retorno, combnamos o Modelo (1.3) com o modelo paramétrco, acrescentando o retorno parametrzado à função objetvo. Além dsso, para facltar a resolução do problema, transformamos em desgualdade a restrção de montante aplcado. Obtemos, assm, o problema
29 15 mn s. a λx = 1 x 1 δ {0,1}, = 1,..., N N = 1 x N T T Qx (1 λ ) µ x x l δ, = 1,..., N δ K, K N 0, = 1,..., N. (1.4) Com a conversão da restrção de montante aplcado em uma desgualdade, é possível que uma parte do dnhero dsponível não seja nvestda, partcularmente no caso em que λ está próxmo de 1, ou seja, quando a aversão ao rsco é grande. Em partcular, quando λ = 1, caso a matrz Q seja defnda postva, nada é nvestdo e, neste caso, a função objetvo atngrá o mínmo apenas para x = 0. Como não é razoável supor que um nvestdor mantenha em caxa grande parte de seu dnhero, podemos consderar a exstênca de um atvo lvre de rsco (como a caderneta de poupança ou as letras do tesouro amercano) que absorva o montante não aplcado nos atvos passíves de compor a cartera. Esse atvo lvre de rsco pode, nclusve, ser ntroduzdo no Modelo (1.4), o que tornara semdefnda postva a matrz Q. Com essa alteração, todo o dnhero dsponível sera aplcado, exceto no caso em que λ = 1, stuação para a qual há nfntas soluções ótmas, pos qualquer montante nvestdo no atvo lvre de rsco sera ótmo, desde que nada fosse aplcado nos demas atvos. Naturalmente, a ntrodução de um atvo lvre de rsco altera a frontera efcente, fazendo com que esta toque o exo vertcal apresentado na Fgura 1.1. A analse das restrções de (1.4) revela que lmtar o número de atvos na cartera nada mas é do que exgr que não mas que K componentes do vetor x sejam postvas. Logo, chamando de nz ( x) { x 0} o conjunto das componentes não nulas do vetor x, podemos substtur a restrção = N =1 δ K pela exgênca de que a cardnaldade de nz(x) seja, no máxmo, K, ou seja, que Card( nz( x)) K.
30 16 Para manter as restrções de lmte nferor, assm como as de postvdade, basta exgr que as varáves cujos índces estam em nz(x) satsfaçam as restrções de lmte nferor, permtndo que as demas sejam não negatvas. Sendo assm, as 4 últmas restrções de (1.4) podem ser substtuídas por Card( nz( x)) K x x l, nz( x) = 0, nz( x). Assm, podemos reescrever o problema (1.4) na forma mn s. a λ( 1 2 N = 1 1 Card( nz( x)) K x x T T x Qx) (1 λ) µ x x l, nz( x) = 0, nz( x). (1.5) Como essa mudança pode ser generalzada para qualquer problema de programçao quadrátca, de uma forma geral, escrevemos nosso problema de programação quadrátca msta 0-1 no segunte formato: mn 1 T 2 x Qx + c s. a. Ax b Card( nz( x)) K x x x l, nz( x) T = 0, nz( x), (1.6)
31 17 onde Q R N N é smétrca e defnda postva, c N R, A m N R, b m R, l N R é o vetor de lmtes nferores não negatvos de x, K é um ntero postvo, o conjunto nz(x) é defndo por nz ( x) { x 0} e Card(C) ndca a cardnaldade do conjunto C. = Além do Problema (1.5), outro tpo de problema que pode ser escrto na forma (1.6) é obtdo quando queremos construr um portfolo lmtado a um máxmo de K ações que, ao mesmo tempo, se equpare, o tanto quanto possível, a um portfolo alvo composto por N ações (N > K); mnmze os custos transaconas; lmte a mudança total de nvestmentos entre setores da economa. Suponha que dsponhamos de um portfolo atual, com frações de nvestmento em seus N atvos dadas pelo vetor x 0. Assumndo a adoção de modelo smétrco para compras e vendas, podemos mnmzar os custos assocados às alterações na cartera nclundo na função objetvo o termo quadrátco N c ( x x = 1 0 ) 2, onde c > 0 é o coefcente de mpacto relatvo à movmentação do atvo. Para lmtar o aumento ou a redução dos nvestmentos que fazem parte de um setor do mercado de ações, exgmos que B ( x x ) ε j, S j (1.7) onde ε j é a varação admssível para a soma das aplcações que pertencem ao conjunto S j, que representa o setor j da economa, e B x é fração alvo para o atvo. Dentre possíves setores da economa que poderam compor S j podemos ctar os setores bancáro, agropecuáro e petrolífero. segunte problema Transformando a Restrção (1.7) em um par de desgualdades lneares, obtemos o
32 18 ( ) ( ) ( ), 1,..., 0 ) ( )) ( ( 1 1,...,, 1,...,,. 2 1 mn N x x nz l x K x nz Card x k j x x k j x x a s x x c x x Q x x x N j S B S j S B S N B T B T j j j j = = = = = = ε ε µ onde o termo ( ) ( ) B T B x Q x x x representa o rsco do porfolo almejado se afastar do porfolo alvo. Claramente, o Problema (1.7) tem a forma (1.6), de modo que pode ser soluconado usando nossa metodologa.
33 CAPÍTULO 2 2 O MÉTODO DE LEMKE 2.1 INTRODUÇÃO Em nosso trabalho, estamos nteressados em encontrar a solução ótma exata de problemas de programação quadrátca ntera msta dados na forma (1.6). Para tanto, usaremos um método do tpo Branch-and-Bound mplícto, conforme será apresentado no Capítulo 3. A cada passo do algortmo Branch-and-Bound, precsamos resolver um problema relaxado, do qual excluímos as varáves nteras e as restções que as envolvem. Obtemos, assm, um problema na forma 1 mn 2 T x Qx + c T x s. a Ax b x 0. (2.1) Dentre as dversas alternatvas exstentes para a resolução desse problema, optamos por usar o método de Lemke, pos ele é partcularmente efcente quando começamos de uma solução nfactível próxma à solução ótma, stuação comumente encontrada durante a aplcação do método Branch-and-Bound, como será vsto no próxmo capítulo. 19
34 O PROBLEMA DE COMPLEMENTARIDADE LINEAR O método de Lemke, utlzado para otmzar os problemas relaxados assocados aos nós da árvore gerada pelo algortmo Branch-and-Bound, fo crado orgnalmente para resolver problemas de complementardade lnear (PCL), que são apresentados da segunte forma: Dados q n n n R, M R, achar z n R e w n R tas que: w = Mz + q z 0, w 0 z T w = 0. (2.2) Esse problema é conhecdo como PCL(q,M). Um vetor z é dto factível se satsfaz as duas prmeras restrções de (2.2), e é dto complementar se satsfaz a últma equação. Todo vetor z que é factível e complementar é chamado de ponto de equlíbro do PCL(q,M). Note que, devdo às restrções de não negatvdade, z e w são complementares se e somente se z w = 0, = 1,..., n. Chamamos o par z e w de par complementar. Voltando ao Subproblema (2.1), observamos que, se Q é uma matrz smétrca e defnda postva, as condções de Karush-Kuhn-Tucker são necessáras e sufcentes para a caracterzação de um mínmo global do problema. Tas condções KKT são defndas por
35 21 ( ) 0,,, = = = + + r g x x r Ax b g r g A Qx c T T T onde N m r e g R R são denomnadas varáves duas. Com o uso de um vetor auxlar m v R, podemos reescrever as condções acma como 0.,,, 0 0, = = = + + = v r g x g v x r Ax b v g A Qx c r T T T (2.3) Utlzando a representação = = = = v r w g x z A A Q M b c q T,, 0,, (2.4) é possível reescrever (2.3) na forma 0., 0 = = z w z w q Mz w T (2.5) A prmera Equação de (2.5) pode ser apresentada smplesmente como [ ], q w z I M n = (2.6)
36 22 onde I n é a matrz dentdade de ordem n = N + m. Podemos encontrar uma solução factível para (2.3) escolhendo n colunas lnearmente ndependentes da matrz [ M ] 1 I n e formando uma base B tal que B q 0. Neste caso, apenas as varáves correspondentes às colunas da base não são nulas. Sendo assm, podemos partconar o nosso vetor z x = em dos outros vetores, x B e w varíaves não nulas (báscas) e o segundo pelas varáves nulas (não báscas). x NB, sendo o prmero composto pelas Desprezando as varáves não báscas, podemos escrever (2.6) como Bx B = q. Para atender as restrções de não negatvdade de (2.3), exgmos que = B 1 q 0. Além dsso, para que as restrções de complementardade sejam satsfetas, z será básca se e somente se w não for básca, e vce-versa. Seja, então, β o conjunto dos índces de z que estão na base. Neste caso, defnmos a ésma coluna da base complementar (aquela que satsfaz as condções de complementardade) por x B B M, = e, se se β, β, onde e é a ésma coluna da matrz dentdade. Assm, cada coluna de B assocada a uma componente de z é gual a uma coluna de M com o snal trocado, enquanto as colunas de B assocadas às varáves de w são colunas da dentdade. O objetvo do método de Lemke é achar 1 uma base complementar B, tal que B q 0.
37 O MÉTODO DE LEMKE Dados q, M e um vetor h postvo defndo pelo usuáro, o método de Lemke resolve o PCL (q,m) através de uma sére de pvoteamentos. Prmeramente, verfcamos se q 0, pos, nesse caso, temos a solução trval z = 0 e w = q como solução do problema. Caso sso não aconteça, precsamos defnr uma base complementar ncal. As varáves báscas, entretanto, não precsam satsfazer a restrção de não negatvdade. A estratéga padrão, nesse caso, é fazer com que as componentes de z sejam não báscas e as de w sejam báscas, de modo que a base ncal seja a matrz dentdade. Em seguda, aumentamos o PCL(q,M), substtundo (2.4) por w = q + hz t z w = 0 w 0, z Mz 0, z 0. (2.7) Essa alteração mplca na amplação de (2.6) para z0 (2.8) w [ h M I n ] z = q, ou smplesmente n ( 2n+ 1) M x = q, com = [ h M ] R T T 2n+ 1 M e = [ z z w ] R I n x. A déa mplícta no aumento do PCL é a de que, ao ntroduzrmos no problema a coluna postva h relatva a z o e forçarmos tal varável a entrar na base, tornamos a nossa solução básca postva. 0 T
38 24 Para mostrar que sso acontece, consderemos que a base ncal seja a trval. Neste caso, queremos que w 0, o que mplca em q + hz 0 0, pos z = 0. Escolhendo o vetor h de forma adequada 1 e defnndo z = max( q / h ), 0 garantmos que a solução obtda após a transformação de z 0 em varável básca seja necessaramente postva. Nesse caso, a varável que é forçada a sar da base para a nclusão de z 0 é exatamente aquela defnda por argmax{-q /h }. A ntrodução de z 0 faz com que um par z, w ) dexe de ser complementar, pos as ( duas varáves que o compõem passam a ser não báscas. Para corrgr esse problema, o método de Lemke escolhe, a cada teração, a varável complementar àquela que sau da base na teração anteror para entrar na base da teração atual. A varável que entra na base pode ter seu valor aumentado, até que uma das varáves báscas se torne zero. A prmera varável básca a atngr o valor zero (denomnada varável de bloqueo) dexa a base. O processo de determnação da varável que sa da base é análogo ao teste da razão, utlzado na Programação Lnear. Repetmos o processo de substtução de varáves na base até que z 0 se torne a varável de bloqueo, ou até que não consgamos achar uma varável de bloqueo. No prmero caso, z 0 é retrada da base e, assm, obtemos uma solução que é ao mesmo tempo factível e complementar, de modo que dspomos da solução ótma. No segundo caso, o nosso PCL orgnal (2.5) (e, conseqüentemente, nosso problema de otmzação quadrátca) é nfactível. Na ausênca de degenerescênca e de uma regão factível vaza, podemos garantr que o método de Lemke convrgrá para uma solução do problema (2.1) caso ao menos uma das condções abaxo seja satsfeta 2 : 1 Quando se usa a base trval, uma opção smples consste em defnr h = [ ] T. 2 A demonstração desse resultado pode ser encontrada em Bazaraa et al.[2].
39 25 A matrz Q seja smétrca e semdefnda postva e c = [ ] T. A matrz Q seja smétrca defnda postva. A matrz Q seja smétrca, possua todos os elementos não negatvos e sua dagonal seja composta apenas por elementos postvos. Em nosso trabalho, supomos que a matrz Q é smétrca e defnda postva, de modo que o método de Lemke sempre convergrá para o mnmzador do problema quadrátco. Além dsso, é fácl notar que o algortmo de Lemke termna em um número fnto de passos, pos o número de bases complementares é fnto. Entretanto, a seqüênca de pvoteamentos depende dretamente da escolha do vetor h, sendo mportante a escolha de um vetor que torne o algortmo mas efcente. Durante a execução do algortmo Branch-and-Bound, aplcamos o método de Lemke para resolver uma sére de problemas quadrátcos semelhantes. Para acelerar o algortmo, aprovetamos a solução obtda para um problema como ponto ncal na resolução de outro problema. Neste caso, não é possível utlzar como base ncal, a base ótma de um problema anteror, como exposto acma, sendo necessáro defnr também um novo vetor h aproprado. Uma descrção de como ntroduzr essa alteração no método de Lemke é apresentada no Capítulo 4, no qual abordamos nossa mplementação computaconal. 2.4 ALGORITMO A segur, apresentamos o método de Lemke na forma algortmca, partndo da solução ncal trval. Supomos que sejam fornecdos os valores de q, h, e M. No algortmo abaxo, os índces de 0 a n correspondem ao vetor z, e os índces de n + 1 a 2n dzem respeto ao vetor w. Ao longo do algortmo, usaremos a notação M :, I ) para representar a submatrz de ( B M que contém apenas as colunas relaconadas aos índces do conjunto I B.
40 26 1. Se q 0, (a solução trval z = 0 é ótma) 1.1. z 0, w q Termnar o algortmo. 2. Fm Se 3. Defnr os vetores de índces: I B { n + 1,..., 2n}, I N { 0,..., n} 4. Introduzr a coluna de z 0 na base: arg { q / } max. j h j I B ( I B \ { } ) { 0}, I N ( \ { 0} ) { } B M :, I ) ( B 5. Enquanto 0 I B (a varável z 0 é básca), I N 5.1. Forçar a entrada na base da varável complementar àquela que sau na teração anteror: j + n 2 n /( n + 1) Determnar a varável que sa da base pelo teste da razão: onde arg mn{ ( B ) ( B m ), ( B m ) > 0 } m j é a j ésma coluna da matrz M Se estver defndo, Atualzar os vetores de índces e a base: 5.4. Senão, I B ( \ { } ) { j}, I N ( \ { j} ) { } I B B M :, I ) ( B O problema é nfactível Termnar o algortmo. 6. Fm Enquanto. 7. x B -1 q. q, I N k j k j k
41 EXEMPLO NUMÉRICO Para facltar a compreensão do método de Lemke, apresentamos abaxo um exemplo de aplcação do mesmo a um problema smples na forma (2.1), usando como dados de entrada os vetores e matrzes fornecdos abaxo. 2 1 A = [ 1 1], = 1 2 Q, = [ 1] 1,8 b, c =, 2,5 1 h = 1. 1 Vamos resolver o problema aumentado na forma (2.7), cuja dmensão é 7, partndo da base ncal trval. As terações serão apresentadas com o auxílo de tablôs. Nesses tablôs, as varáves báscas são aquelas ndcadas na prmera coluna, enquanto os valores dessas varáves são mostrados na últma coluna. Aplcando o Algortmo de Lemke ao problema, temos Iteração 0. VB z 0 z 1 z 2 z 3 w 1 w 2 w 3 B -1 q w ,8 w ,5 w Varável que sa da base: w 2 Varável que entra na base: z 0 Novo tablô:
42 28 VB z 0 z 1 z 2 z 3 w 1 w 2 w 3 B -1 q w ,7 z ,5 w ,5 Iteração 1. Varável que sa da base: w 1 Varável que entra na base: z 2 Novo tablô: VB z 0 z 1 z 2 z 3 w 1 w 2 w 3 B -1 q z ,7 z ,5 w ,4 Iteração 2. Varável que sa da base: w 3 Varável que entra na base: z 1 Novo tablô: VB z 0 z 1 z 2 z 3 w 1 w 2 w 3 B -1 q z ,2 0,4 0,6 0,2 0,98 z ,4 0,2 0,2 0,6 0,26 z ,2 0,6 0,4 0,2 0,28
43 29 Iteração 3. Varável que sa da base: z 0 Varável que entra na base: z 3 Novo tablô: VB z 0 z 1 z 2 z 3 w 1 w 2 w 3 B -1 q z 2 0, ,5 0,5 0,5 0,85 z 3 2, ,5 0,5 1,5 0,65 z 1 0, ,5 0,5 0,5 0,15 Iteração 4. Como z 0 sa da base, a solução atual é ótma para o nosso problema. Sabendo que as duas prmeras componentes de z correspondem ao vetor x, concluímos que x 1 = 0,15 e x 2 = 0, RESOLVENDO AS ITERAÇÕES DO MÉTODO DE LEMKE Observamos que o método de Lemke possu uma grande semelhança com o método Smplex, especalmente no que se refere ao uso de pvoteamentos e do teste da razão para determnar a varável que sa da base. Cabe notar, também, que, como na fase 1 do Smplex, tornamos factível a solução ncal nclundo uma ou mas varáves artfcas no problema. Porém, dferentemente do Smplex, o método de Lemke não lda com a função objetvo e, conseqüentemente, com os custos assocados a cada varável. Sendo assm, o crtéro de otmaldade e a estratéga usada para determnar a varável que entra na base são dferentes dos empregados na resolução do Smplex.
44 30 Dadas as semelhanças entre os algortmos, podemos adaptar ao método de Lemke váras propostas desenvolvdas para o Smplex. Como os passos computaconalmente mas caros do método estão relaconados à resolução de sstemas lneares envolvendo a matrz B, consderamos duas possbldades de mplementação do método de Lemke. A prmera envolve a decomposção LU da base sempre que uma coluna é substtuída por outra. A segunda proposta consste em efetuar a decomposção LU no níco do método, atualzando as matrzes L e U a cada teração. As duas alternatvas foram mplementadas e testadas, conforme se verá adante.
45 CAPÍTULO 3 3 O MÉTODO BRANCH- AND-BOUND IMPLÍCITO 3.1 INTRODUÇÃO Uma vez que o Problema (1.6) é equvalente a um problema de programação quadrátca ntera msta, a manera usual de encontrar sua solução exata consste em utlzar varantes do algortmo Branch-and-Bound. Dessa forma, os métodos que nvestgamos para a resolução desse tpo de problema foram: A aplcação dreta do método Branch-and-Bound, combnado com um algortmo para resolver problemas convexos de programação quadrátca. Essa estratéga, apesar de ser a mas ntutva, é mas cara, em termos de gasto computaconal, que os métodos ctados abaxo. O uso do algortmo Branch-and-Cut, que nclu no problema restrções baseadas em métodos de planos de corte, sempre que possível. Segundo essa lnha, Benstock [4] nvestgou quatro estratégas dferentes de geração de planos de corte para o problema: cortes arredondados ntero-mstos, cortes de mochla, cortes de ntersecção e cortes dsjuntos. Dentre elas, a últma se mostrou mas efcente devdo ao fato da separação ser feta de manera dreta. 31
46 32 O uso do algortmo Branch-and-Bound mplícto, combnado com o método de Lemke, para a resolução dos subproblemas quadrátcos, além de técncas de reformulação e elmnação de varáves. Dentre as estratégas descrtas, a que mas nos pareceu promssora fo a últma, uma vez que o método de Lemke pode ser faclmente adaptado à resolução dos problemas gerados a cada teração do Branch-and-Bound, problemas estes que possuem, geralmente, um número muto pequeno de restrções e para os quas dspomos de uma solução ncal quase factível. 3.2 O MÉTODO BRANCH-AND-BOUND PARA PROBLEMAS 0-1 O Branch-and-Bound é um algortmo baseado no processo de dvsão e conqusta, que consste em quebrar um problema dfícl (em geral, NP-completo) em város problemas menores, de fácl resolução, para posterormente juntar as nformações obtdas para resolver o problema orgnal. Dessa forma, é feta a enumeração sstemátca das possíves soluções, procurando sempre elmnar, ao longo do camnho, grupos de soluções menos provetosas. Em geral, esse algortmo é muto utlzado para achar a solução ótma de problemas de otmzação que envolvem varáves nteras. Neste trabalho, estamos nteressados em resolver problemas de programação quadrátca msta do tpo (1.4), em que algumas varáves são bnáras, ou seja, só podem assumr valores 0 ou 1. Para resolver esse tpo de problema usando o Branch-and-Bound, prmeramente resolvemos a versão relaxada do problema, o que no nosso caso correspondera a resolver o problema no qual todas as varáves bnáras são consderadas contínuas no ntervalo [0,1]. Feto sso, verfcamos se, na solução obtda, todas as varáves bnáras valem 0 ou 1. Se sso ocorre, já resolvemos o problema. Caso contráro, como anda não encontramos uma solução vável para o problema orgnal, guardamos uma solução vaza como a melhor soluçao ntera. Neste caso,
47 33 defnndo ζ * como o valor da função objetvo desta melhor solução, tomamos ζ * =. Em seguda, escolhemos uma das varáves bnáras que ora possue valor fraconáro e a forçamos a assumr explctamente cada um dos dos valores admssíves (0 ou 1). Geramos, assm, dos subproblemas que precsam ser resolvdos. A essa subdvsão do problema damos o nome de ramfcação. Nesse contexto, exstem 2 tpos dferentes de ramfcação: a para baxo e a para cma. Na ramfcação para baxo, a varável escolhda assume o valor 0, ao passo que na ramfcação para cma ela assume o valor 1. É fácl observar que cada ramfcação dá orgem a outras ramfcações, até que todas as varáves nteras da solução obtda possuam valor 0 ou 1. Assm, a estrutura do problema sugere a cração de uma árvore bnára para poder representar todas as possíves ramfcações a serem nvestgadas. Nessa árvore, cada subproblema gerado por uma ramfcação é chamado de nó. O prmero problema relaxado a ser resolvdo, é conhecdo como nó raz. Um nó cuja solução tenha as varáves bnáras valendo 0 ou 1 é chamado de folha, ao passo que um nó em que algumas das varáves bnáras estejam em (0,1) é chamado de ramo. Quando um nó gera um nó j va ramfcação, dzemos que o nó é o pa de j, de modo que este últmo é um nó flho de. Um nó que anda não fo resolvdo é chamado de nó pendente. O número máxmo de elementos da árvore é gual a 2 n+1 1, onde n é o número de varáves bnáras do problema. Depos de resolver o problema assocado a uma ramfcação, verfcamos se a solução é factível, no sentdo das varáves bnáras do problema assumrem apenas valores 0-1. Se sso ocorre, comparamos ζ, o valor da função objetvo, com ζ*, o valor de ζ assocado à melhor solução ntera encontrada até o momento. Se ζ < ζ*, atualzamos ζ* e dexamos de resolver todas as ramfcações pendentes cuja solução seja por que aquela que acabamos de encontrar. Por outro lado, se a solução anda nclur varáves bnáras com valores não nteros, escolhemos uma nova varável para ramfcar, gerando dos novos problemas. Salvo quando aparece uma folha, a cada teração do método, temos que armazenar 2 novos nós e decdr qual nó resolver dentre os possíves pendentes. O número de nós pendentes só dmnu quando achamos uma folha, pos, neste caso, além de não ramfcarmos, elmnamos os nós pendentes com valor de ζ maor que o da solução recém encontrada. O algortmo acaba
48 34 quando não exstem mas nós pendentes para nvestgarmos. Para facltar o entendmento do letor, apresentamos abaxo o algormo Branch-and- Bound para problemas de programação quadrátca msta Usando o método de Lemke, resolver o problema relaxado (assumndo que as varáves bnáras são contínuas no ntervalo [0,1]). 2. Se, na solução obtda, todas as varáves bnáras valerem 0 ou 1, 2.1. Termnar o algortmo (estamos no ótmo). 3. Fm Se. 4. Escolher uma varável bnára não ntera para ramfcar. 5. Crar uma lsta de nós pendentes, nosp, contendo os 2 problemas gerados pela ramfcação. 6. x * [ ] (vetor ndefndo). ζ*. 7. Enquanto nosp, 7.1. Retrar um subproblema de nosp Usando o método de Lemke, resolver este problema, obtendo x e ζ ou a ndcação de que ele é nfactível Se x possur varáves bnáras com valores fraconáros, Escolher uma varável para ramfcar Inclur em nosp os 2 subproblemas a serem resolvdos Senão, Se as varáves bnáras de x forem nteras e ζ < ζ*, x * x. ζ* ζ Para cada nó em nosp, Se ζ p p ζ*, onde ζ é o valor da função objetvo do pa do nó, Elmnar o nó de nosp Fm Se Fm Para Fm Se. 8. Fm Enquanto. 9. A solução do problema é x*, com função objetvo gual a ζ*.
49 35 Para obter maores nformações sobre o algortmo Branch-and-Bound, o letor pode consultar, por exemplo, Wolsey [16]. 3.3 O MÉTODO BRANCH-AND-BOUND IMPLÍCITO A prncpal dferença entre o Problema (1.5) ou (1.6) e um problema de programação quadrátca 0-1 convenconal é que as varáves bnáras estão mplíctas, ou seja, não aparecem, mas são necessáras para que tenhamos no máxmo K varáves postvas, ou seja, para que Card( nz( x)) K. (3.1) Essa forma mplícta de tratar as varáves bnáras pode ser estendda ao método Branch-and-Bound. Neste caso, elmnamos do problema relaxado (o nó raz da árvore bnára) a Restrção (3.1) e os lmtes x x l, = 0, nz( x) nz( x), (3.2) adotando apenas a restrção de não negatvdade x 0. Obtemos, assm, um problema clássco de programação quadrátca, na forma (2.1). A únca deferença entre este problema e o correspondente ao nó raz do Branch-and-Bound usual é N a nexstênca da restrção δ K, presente na formulação (1.4), mas não em (1.5). Anda = 1 assm, a relaxação das restrções de ntegraldade das varáves bnáras, adotada na seção anteror, também permte que a cardnaldade de nz(x) seja superor a K e que as componentes
50 36 estrtamente postvas do vetor x assumam valores abaxo de seus lmtes nferores, de modo que há grande smlardade entre os problemas abordados pelo Branch-and-Bound usual e a versão mplícta. No caso provável da solução do nó raz da árvore não satsfazer as restrções (3.1) ou (3.2), é necessáro ramfcar uma varável qualquer. É justamente na manpulação das ramfcações que as restrções gnoradas são levadas em conta, justfcando o caráter mplícto do método Branch-and-Bound. A déa é fazer com que, a cada ramfcação, as varáves estejam mas próxmas de obedecer às restrções de cardnaldade e lmte nferor. Vejamos como ramfcar uma varável x s : Habtualmente, a ramfcação para baxo corresponde à atrbução do valor 0 à varável bnára assocada a x s. Naturalmente, sso também nos obrga a adotar x s = 0. No método mplícto, essa ramfcação é obtda através da elmnação dreta de x s, o que provoca a geração de um novo subproblema com uma varável a menos. Esse subproblema é resolvdo através do método de Lemke. No problema fnancero usual, a ramfcação para cma está relaconada à nclusão forçada de um atvo na cartera. No Branch-and-Bound para problemas 0-1, sso equvale a atrbur o valor 1 à varável bnára assocada à varável x s, ao passo que, no Branch-and-Bound mplícto, tal exgênca se resume à nclusão da restrção x s l s. Esse tpo de ramfcação traz conseqüêncas não só à restrção de lmte nferor, mas também à restrção de cardnaldade, que pode passar a ser nfactível. No método mplícto, essa ramfcação é feta apenas quando x s é estrtamente postva e está abaxo do seu lmte nferor l s. Neste caso, ncluímos no problema a restrção x l e o resolvemos pelo método de Lemke. Para evtar que a s s Restrção (3.1) se torne nfactível, a ramfcação para cma não é feta se o número de varáves ramfcadas para cma for superor ou gual a K. Como veremos a segur, os prncpas concetos do algortmo Branch-and-Bound são mantdos em sua versão mplícta, que pouco dfere daquela apresentada na Seção 3.2.
51 ALGORITMO E EXEMPLO Nesta seção, para facltar a compreensão da versão mplícta do Branch-and-Bound, apresentamos o passos que compõem o algortmo, além de um exemplo numérco Algortmo 1. Usando o método de Lemke, resolver o problema relaxado, retrando as Restrções (3.1) e (3.2). 2. Se, na solução obtda, não tvermos mas que K varáves não nulas e se estas satsfzerem as restrções de lmte nferor, 2.1. Termnar o algortmo (estamos no ótmo). 3. Fm Se. 4. Escolher uma varável bnára não ntera para ramfcar. 5. Crar uma lsta de nós pendentes, nosp, contendo os 2 problemas gerados pela ramfcação. 6. x * [ ] (vetor ndefndo). ζ*. 7. Enquanto nosp, 7.1. Retrar um subproblema de nosp Usando o método de Lemke, resolver este problema, obtendo x e ζ ou a ndcação de que ele é nfactível Se x possur componentes não nulas menores que os lmtes nferores correspondentes ou se o número de componentes não nulas for maor que K, Escolher uma varável para ramfcar Inclur em nosp o problema relaconado à ramfcação para baxo Se a ramfcação para cma não volar a Restrção (3.1),
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
UM NOVO ALGORITMO GENÉTICO PARA A OTIMIZAÇÃO DE CARTEIRAS DE INVESTIMENTO COM RESTRIÇÕES DE CARDINALIDADE
 Unversdade Estadual de Campnas Insttuto de Matemátca, Estatístca e Computação Centífca Departamento de Matemátca Aplcada DISSERTAÇÃO DE MESTRADO UM NOVO ALGORITMO GENÉTICO PARA A OTIMIZAÇÃO DE CARTEIRAS
Unversdade Estadual de Campnas Insttuto de Matemátca, Estatístca e Computação Centífca Departamento de Matemátca Aplcada DISSERTAÇÃO DE MESTRADO UM NOVO ALGORITMO GENÉTICO PARA A OTIMIZAÇÃO DE CARTEIRAS
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
CURSO ON-LINE PROFESSOR: VÍTOR MENEZES
 O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
Sistemas de Filas: Aula 5. Amedeo R. Odoni 22 de outubro de 2001
 Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Problemas Associados a Cones de Segunda Ordem
 Problemas Assocados a Cones de Segunda Ordem Dense S. Trevsol, Mara A. D. Ehrhardt, Insttuto de Matemátca, Estatístca e Computação Centífca, IMECC, UNICAMP, 1383-859, Campnas, SP E-mal: ra8477@me.uncamp.br,
Problemas Assocados a Cones de Segunda Ordem Dense S. Trevsol, Mara A. D. Ehrhardt, Insttuto de Matemátca, Estatístca e Computação Centífca, IMECC, UNICAMP, 1383-859, Campnas, SP E-mal: ra8477@me.uncamp.br,
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
2 Máquinas de Vetor Suporte 2.1. Introdução
 Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Rastreando Algoritmos
 Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
RISCO. Investimento inicial $ $ Taxa de retorno anual Pessimista 13% 7% Mais provável 15% 15% Otimista 17% 23% Faixa 4% 16%
 Análse de Rsco 1 RISCO Rsco possbldade de perda. Quanto maor a possbldade, maor o rsco. Exemplo: Empresa X va receber $ 1.000 de uros em 30 das com títulos do governo. A empresa Y pode receber entre $
Análse de Rsco 1 RISCO Rsco possbldade de perda. Quanto maor a possbldade, maor o rsco. Exemplo: Empresa X va receber $ 1.000 de uros em 30 das com títulos do governo. A empresa Y pode receber entre $
Nota Técnica Médias do ENEM 2009 por Escola
 Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
CAPÍTULO 1 Exercícios Propostos
 CAPÍTULO 1 Exercícos Propostos Atenção: Na resolução dos exercícos consderar, salvo menção em contráro, ano comercal de das. 1. Qual é a taxa anual de juros smples obtda em uma aplcação de $1.0 que produz,
CAPÍTULO 1 Exercícos Propostos Atenção: Na resolução dos exercícos consderar, salvo menção em contráro, ano comercal de das. 1. Qual é a taxa anual de juros smples obtda em uma aplcação de $1.0 que produz,
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Não Lnear com Restrções Aula 9: Programação Não-Lnear - Funções de Váras Varáves com Restrções Ponto Regular; Introdução aos Multplcadores de Lagrange; Multplcadores de Lagrange e Condções
1 Programação Não Lnear com Restrções Aula 9: Programação Não-Lnear - Funções de Váras Varáves com Restrções Ponto Regular; Introdução aos Multplcadores de Lagrange; Multplcadores de Lagrange e Condções
PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS
 PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS L. G. Olvera, J. K. S. Negreros, S. P. Nascmento, J. A. Cavalcante, N. A. Costa Unversdade Federal da Paraíba,
PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS L. G. Olvera, J. K. S. Negreros, S. P. Nascmento, J. A. Cavalcante, N. A. Costa Unversdade Federal da Paraíba,
Fast Multiresolution Image Querying
 Fast Multresoluton Image Queryng Baseado no artgo proposto por: Charles E. Jacobs Adan Fnkelsten Davd H. Salesn Propõe um método para busca em um banco de dados de magem utlzando uma magem de consulta
Fast Multresoluton Image Queryng Baseado no artgo proposto por: Charles E. Jacobs Adan Fnkelsten Davd H. Salesn Propõe um método para busca em um banco de dados de magem utlzando uma magem de consulta
7 - Distribuição de Freqüências
 7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
Figura 8.1: Distribuição uniforme de pontos em uma malha uni-dimensional. A notação empregada neste capítulo para avaliação da derivada de uma
 Capítulo 8 Dferencação Numérca Quase todos os métodos numércos utlzados atualmente para obtenção de soluções de equações erencas ordnáras e parcas utlzam algum tpo de aproxmação para as dervadas contínuas
Capítulo 8 Dferencação Numérca Quase todos os métodos numércos utlzados atualmente para obtenção de soluções de equações erencas ordnáras e parcas utlzam algum tpo de aproxmação para as dervadas contínuas
Elaboração: Fevereiro/2008
 Elaboração: Feverero/2008 Últma atualzação: 19/02/2008 E ste Caderno de Fórmulas tem por objetvo esclarecer aos usuáros a metodologa de cálculo e os crtéros de precsão utlzados na atualzação das Letras
Elaboração: Feverero/2008 Últma atualzação: 19/02/2008 E ste Caderno de Fórmulas tem por objetvo esclarecer aos usuáros a metodologa de cálculo e os crtéros de precsão utlzados na atualzação das Letras
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
X = 1, se ocorre : VB ou BV (vermelha e branca ou branca e vermelha)
 Estatístca p/ Admnstração II - Profª Ana Cláuda Melo Undade : Probabldade Aula: 3 Varável Aleatóra. Varáves Aleatóras Ao descrever um espaço amostral de um expermento, não especfcamos que um resultado
Estatístca p/ Admnstração II - Profª Ana Cláuda Melo Undade : Probabldade Aula: 3 Varável Aleatóra. Varáves Aleatóras Ao descrever um espaço amostral de um expermento, não especfcamos que um resultado
3 Algoritmos propostos
 Algortmos propostos 3 Algortmos propostos Nesse trabalho foram desenvolvdos dos algortmos que permtem classfcar documentos em categoras de forma automátca, com trenamento feto por usuáros Tas algortmos
Algortmos propostos 3 Algortmos propostos Nesse trabalho foram desenvolvdos dos algortmos que permtem classfcar documentos em categoras de forma automátca, com trenamento feto por usuáros Tas algortmos
Polos Olímpicos de Treinamento. Aula 10. Curso de Teoria dos Números - Nível 2. Divisores. Prof. Samuel Feitosa
 Polos Olímpcos de Trenamento Curso de Teora dos Números - Nível 2 Prof. Samuel Fetosa Aula 10 Dvsores Suponha que n = p α 1 2...pα é a fatoração em prmos do ntero n. Todos os dvsores de n são da forma
Polos Olímpcos de Trenamento Curso de Teora dos Números - Nível 2 Prof. Samuel Fetosa Aula 10 Dvsores Suponha que n = p α 1 2...pα é a fatoração em prmos do ntero n. Todos os dvsores de n são da forma
3 Elementos de modelagem para o problema de controle de potência
 3 Elementos de modelagem para o problema de controle de potênca Neste trabalho assume-se que a rede de comuncações é composta por uma coleção de enlaces consttuídos por um par de undades-rádo ndvdualmente
3 Elementos de modelagem para o problema de controle de potênca Neste trabalho assume-se que a rede de comuncações é composta por uma coleção de enlaces consttuídos por um par de undades-rádo ndvdualmente
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Aula 7: Circuitos. Curso de Física Geral III F-328 1º semestre, 2014
 Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Programação Linear 1
 Programação Lnear 1 Programação Lnear Mutos dos problemas algortmcos são problemas de otmzação: encontrar o menor camnho, o maor fluxo a árvore geradora de menor custo Programação lnear rovê um framework
Programação Lnear 1 Programação Lnear Mutos dos problemas algortmcos são problemas de otmzação: encontrar o menor camnho, o maor fluxo a árvore geradora de menor custo Programação lnear rovê um framework
Elaboração: Novembro/2005
 Elaboração: Novembro/2005 Últma atualzação: 18/07/2011 Apresentação E ste Caderno de Fórmulas tem por objetvo nformar aos usuáros a metodologa e os crtéros de precsão dos cálculos referentes às Cédulas
Elaboração: Novembro/2005 Últma atualzação: 18/07/2011 Apresentação E ste Caderno de Fórmulas tem por objetvo nformar aos usuáros a metodologa e os crtéros de precsão dos cálculos referentes às Cédulas
Metodologia IHFA - Índice de Hedge Funds ANBIMA
 Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Universidade Estadual de Ponta Grossa/Departamento de Economia/Ponta Grossa, PR. Palavras-chave: CAPM, Otimização de carteiras, ações.
 A CONSTRUÇÃO DE CARTEIRAS EFICIENTES POR INTERMÉDIO DO CAPM NO MERCADO ACIONÁRIO BRASILEIRO: UM ESTUDO DE CASO PARA O PERÍODO 006-010 Rodrgo Augusto Vera (PROVIC/UEPG), Emerson Martns Hlgemberg (Orentador),
A CONSTRUÇÃO DE CARTEIRAS EFICIENTES POR INTERMÉDIO DO CAPM NO MERCADO ACIONÁRIO BRASILEIRO: UM ESTUDO DE CASO PARA O PERÍODO 006-010 Rodrgo Augusto Vera (PROVIC/UEPG), Emerson Martns Hlgemberg (Orentador),
CQ110 : Princípios de FQ
 CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
Hansard OnLine. Guia Unit Fund Centre
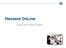 Hansard OnLne Gua Unt Fund Centre Índce Págna Introdução ao Unt Fund Centre (UFC) 3 Usando fltros do fundo 4-5 Trabalhando com os resultados do fltro 6 Trabalhando com os resultados do fltro Preços 7 Trabalhando
Hansard OnLne Gua Unt Fund Centre Índce Págna Introdução ao Unt Fund Centre (UFC) 3 Usando fltros do fundo 4-5 Trabalhando com os resultados do fltro 6 Trabalhando com os resultados do fltro Preços 7 Trabalhando
Estatística stica Descritiva
 AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
RAD1507 Estatística Aplicada à Administração I Prof. Dr. Evandro Marcos Saidel Ribeiro
 UNIVERIDADE DE ÃO PAULO FACULDADE DE ECONOMIA, ADMINITRAÇÃO E CONTABILIDADE DE RIBEIRÃO PRETO DEPARTAMENTO DE ADMINITRAÇÃO RAD1507 Estatístca Aplcada à Admnstração I Prof. Dr. Evandro Marcos adel Rbero
UNIVERIDADE DE ÃO PAULO FACULDADE DE ECONOMIA, ADMINITRAÇÃO E CONTABILIDADE DE RIBEIRÃO PRETO DEPARTAMENTO DE ADMINITRAÇÃO RAD1507 Estatístca Aplcada à Admnstração I Prof. Dr. Evandro Marcos adel Rbero
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Os modelos de regressão paramétricos vistos anteriormente exigem que se suponha uma distribuição estatística para o tempo de sobrevivência.
 MODELO DE REGRESSÃO DE COX Os modelos de regressão paramétrcos vstos anterormente exgem que se suponha uma dstrbução estatístca para o tempo de sobrevvênca. Contudo esta suposção, caso não sea adequada,
MODELO DE REGRESSÃO DE COX Os modelos de regressão paramétrcos vstos anterormente exgem que se suponha uma dstrbução estatístca para o tempo de sobrevvênca. Contudo esta suposção, caso não sea adequada,
TRABALHADORES COM DEFICIÊNCIAS EM LINHAS DE PRODUÇÃO: MODELOS, RESULTADOS E DISCUSSÕES 1
 XIV ELAVIO El Fuerte Snaloa Méxco 9-14 de agosto de 2009 TRABALHADORES COM DEFICIÊNCIAS EM LINHAS DE PRODUÇÃO: MODELOS RESULTADOS E DISCUSSÕES 1 Mayron César de O. Morera Lana Mara R. Santos Alysson M.
XIV ELAVIO El Fuerte Snaloa Méxco 9-14 de agosto de 2009 TRABALHADORES COM DEFICIÊNCIAS EM LINHAS DE PRODUÇÃO: MODELOS RESULTADOS E DISCUSSÕES 1 Mayron César de O. Morera Lana Mara R. Santos Alysson M.
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
4 Critérios para Avaliação dos Cenários
 Crtéros para Avalação dos Cenáros É desejável que um modelo de geração de séres sntétcas preserve as prncpas característcas da sére hstórca. Isto quer dzer que a utldade de um modelo pode ser verfcada
Crtéros para Avalação dos Cenáros É desejável que um modelo de geração de séres sntétcas preserve as prncpas característcas da sére hstórca. Isto quer dzer que a utldade de um modelo pode ser verfcada
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
7.4 Precificação dos Serviços de Transmissão em Ambiente Desregulamentado
 64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
Programação Dinâmica. Fernando Nogueira Programação Dinâmica 1
 Programação Dnâmca Fernando Noguera Programação Dnâmca A Programação Dnâmca procura resolver o problema de otmzação através da análse de uma seqüênca de problemas mas smples do que o problema orgnal. A
Programação Dnâmca Fernando Noguera Programação Dnâmca A Programação Dnâmca procura resolver o problema de otmzação através da análse de uma seqüênca de problemas mas smples do que o problema orgnal. A
3 Metodologia de Avaliação da Relação entre o Custo Operacional e o Preço do Óleo
 3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
IV - Descrição e Apresentação dos Dados. Prof. Herondino
 IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
3 A técnica de computação intensiva Bootstrap
 A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
Teoremas de Otimização com Restrições de Desigualdade
 Teoremas de Otmzação com Restrções de Desgualdade MAXIMIZAÇÃO COM RESTRIÇÃO DE DESIGUALDADE Consdere o segunte problema (P) de maxmzação condconada: Maxmze Fx onde x x,x,...,x R gx b As condções de Prmera
Teoremas de Otmzação com Restrções de Desgualdade MAXIMIZAÇÃO COM RESTRIÇÃO DE DESIGUALDADE Consdere o segunte problema (P) de maxmzação condconada: Maxmze Fx onde x x,x,...,x R gx b As condções de Prmera
Software. Guia do professor. Como comprar sua moto. Secretaria de Educação a Distância. Ministério da Ciência e Tecnologia. Ministério da Educação
 números e funções Gua do professor Software Como comprar sua moto Objetvos da undade 1. Aplcar o conceto de juros compostos; 2. Introduzr o conceto de empréstmo sob juros; 3. Mostrar aplcações de progressão
números e funções Gua do professor Software Como comprar sua moto Objetvos da undade 1. Aplcar o conceto de juros compostos; 2. Introduzr o conceto de empréstmo sob juros; 3. Mostrar aplcações de progressão
Y X Baixo Alto Total Baixo 1 (0,025) 7 (0,175) 8 (0,20) Alto 19 (0,475) 13 (0,325) 32 (0,80) Total 20 (0,50) 20 (0,50) 40 (1,00)
 Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
ALGORITMO E PROGRAMAÇÃO
 ALGORITMO E PROGRAMAÇÃO 1 ALGORITMO É a descrção de um conjunto de ações que, obedecdas, resultam numa sucessão fnta de passos, atngndo um objetvo. 1.1 AÇÃO É um acontecmento que a partr de um estado ncal,
ALGORITMO E PROGRAMAÇÃO 1 ALGORITMO É a descrção de um conjunto de ações que, obedecdas, resultam numa sucessão fnta de passos, atngndo um objetvo. 1.1 AÇÃO É um acontecmento que a partr de um estado ncal,
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
5 Relação entre Análise Limite e Programação Linear 5.1. Modelo Matemático para Análise Limite
 5 Relação entre Análse Lmte e Programação Lnear 5.. Modelo Matemátco para Análse Lmte Como fo explcado anterormente, a análse lmte oferece a facldade para o cálculo da carga de ruptura pelo fato de utlzar
5 Relação entre Análse Lmte e Programação Lnear 5.. Modelo Matemátco para Análse Lmte Como fo explcado anterormente, a análse lmte oferece a facldade para o cálculo da carga de ruptura pelo fato de utlzar
Análise Econômica da Aplicação de Motores de Alto Rendimento
 Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Associação de resistores em série
 Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
PARTE 1. 1. Apresente as equações que descrevem o comportamento do preço de venda dos imóveis.
 EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
ELEMENTOS DE CIRCUITOS
 MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS DO CEARÁ
 GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ADMINISTRAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ADMINISTRAÇÃO ESPECIALIZAÇÃO EM MERCADO DE CAPITAIS
 UNIVESIDADE FEDEAL DO IO GANDE DO SUL ESCOLA DE ADMINISTAÇÃO OGAMA DE ÓS-GADUAÇÃO EM ADMINISTAÇÃO ESECIALIZAÇÃO EM MECADO DE CAITAIS MODENA TEOIA DE CATEIAS: DESENVOLVIMENTO E ANÁLISE DE UM MODELO DE SELEÇÃO
UNIVESIDADE FEDEAL DO IO GANDE DO SUL ESCOLA DE ADMINISTAÇÃO OGAMA DE ÓS-GADUAÇÃO EM ADMINISTAÇÃO ESECIALIZAÇÃO EM MECADO DE CAITAIS MODENA TEOIA DE CATEIAS: DESENVOLVIMENTO E ANÁLISE DE UM MODELO DE SELEÇÃO
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
Prof. Lorí Viali, Dr.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
Lista de Exercícios de Recuperação do 2 Bimestre. Lista de exercícios de Recuperação de Matemática 3º E.M.
 Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
CAPÍTULO 2 DESCRIÇÃO DE DADOS ESTATÍSTICA DESCRITIVA
 CAPÍTULO DESCRIÇÃO DE DADOS ESTATÍSTICA DESCRITIVA. A MÉDIA ARITMÉTICA OU PROMÉDIO Defnção: é gual a soma dos valores do grupo de dados dvdda pelo número de valores. X x Soma dos valores de x número de
CAPÍTULO DESCRIÇÃO DE DADOS ESTATÍSTICA DESCRITIVA. A MÉDIA ARITMÉTICA OU PROMÉDIO Defnção: é gual a soma dos valores do grupo de dados dvdda pelo número de valores. X x Soma dos valores de x número de
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Universidade Federal do Paraná Departamento de Informática. Reconhecimento de Padrões. Classificadores Lineares. Luiz Eduardo S. Oliveira, Ph.D.
 Unversdade Federal do Paraná Departamento de Informátca Reconhecmento de Padrões Classfcadores Lneares Luz Eduardo S. Olvera, Ph.D. http://lesolvera.net Objetvos Introduzr os o conceto de classfcação lnear.
Unversdade Federal do Paraná Departamento de Informátca Reconhecmento de Padrões Classfcadores Lneares Luz Eduardo S. Olvera, Ph.D. http://lesolvera.net Objetvos Introduzr os o conceto de classfcação lnear.
Sinais Luminosos 2- CONCEITOS BÁSICOS PARA DIMENSIONAMENTO DE SINAIS LUMINOSOS.
 Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Curso de especialização em Finanças e Economia Disciplina: Incerteza e Risco Prof: Sabino da Silva Porto Júnior Sabino@ppge.ufrgs.
 Incerteza: o básco Curso de especalzação em Fnanças e Economa Dscplna: Incerteza e Rsco Prof: Sabno da Slva Porto Júnor Sabno@ppge.ufrgs.br Introdução Até agora: conseqüêncas das escolhas dos consumdores
Incerteza: o básco Curso de especalzação em Fnanças e Economa Dscplna: Incerteza e Rsco Prof: Sabno da Slva Porto Júnor Sabno@ppge.ufrgs.br Introdução Até agora: conseqüêncas das escolhas dos consumdores
Otimização de Custos de Transporte e Tributários em um Problema de Distribuição Nacional de Gás
 A pesqusa Operaconal e os Recursos Renováves 4 a 7 de novembro de 2003, Natal-RN Otmzação de ustos de Transporte e Trbutáros em um Problema de Dstrbução Naconal de Gás Fernanda Hamacher 1, Fernanda Menezes
A pesqusa Operaconal e os Recursos Renováves 4 a 7 de novembro de 2003, Natal-RN Otmzação de ustos de Transporte e Trbutáros em um Problema de Dstrbução Naconal de Gás Fernanda Hamacher 1, Fernanda Menezes
Aline Fernanda Bianco
 Alne Fernanda Banco Fltros de Kalman Robustos para Sstemas Dnâmcos Sngulares em Tempo Dscreto Tese apresentada à Escola de Engenhara de São Carlos da Unversdade de São Paulo, como parte dos requstos para
Alne Fernanda Banco Fltros de Kalman Robustos para Sstemas Dnâmcos Sngulares em Tempo Dscreto Tese apresentada à Escola de Engenhara de São Carlos da Unversdade de São Paulo, como parte dos requstos para
5 Métodos de cálculo do limite de retenção em função da ruína e do capital inicial
 5 Métodos de cálculo do lmte de retenção em função da ruína e do captal ncal Nesta dssertação serão utlzados dos métodos comparatvos de cálculo de lmte de retenção, onde ambos consderam a necessdade de
5 Métodos de cálculo do lmte de retenção em função da ruína e do captal ncal Nesta dssertação serão utlzados dos métodos comparatvos de cálculo de lmte de retenção, onde ambos consderam a necessdade de
DIAGNÓSTICO EM MODELOS LINEARES GENERALIZADOS
 DIAGNÓSTICO EM MODELOS LINEARES GENERALIZADOS 1 A análse de dagnóstco (ou dagnóstco do ajuste) confgura uma etapa fundamental no ajuste de modelos de regressão. O objetvo prncpal da análse de dagnóstco
DIAGNÓSTICO EM MODELOS LINEARES GENERALIZADOS 1 A análse de dagnóstco (ou dagnóstco do ajuste) confgura uma etapa fundamental no ajuste de modelos de regressão. O objetvo prncpal da análse de dagnóstco
Aplicando o método de mínimos quadrados ordinários, você encontrou o seguinte resultado: 1,2
 Econometra - Lsta 3 - Regressão Lnear Múltpla Professores: Hedbert Lopes, Prscla Rbero e Sérgo Martns Montores: Gustavo Amarante e João Marcos Nusdeo QUESTÃO 1. Você trabalha na consultora Fazemos Qualquer
Econometra - Lsta 3 - Regressão Lnear Múltpla Professores: Hedbert Lopes, Prscla Rbero e Sérgo Martns Montores: Gustavo Amarante e João Marcos Nusdeo QUESTÃO 1. Você trabalha na consultora Fazemos Qualquer
EXERCÍCIO: VIA EXPRESSA CONTROLADA
 EXERCÍCIO: VIA EXPRESSA CONTROLADA Engenhara de Tráfego Consdere o segmento de va expressa esquematzado abaxo, que apresenta problemas de congestonamento no pco, e os dados a segur apresentados: Trechos
EXERCÍCIO: VIA EXPRESSA CONTROLADA Engenhara de Tráfego Consdere o segmento de va expressa esquematzado abaxo, que apresenta problemas de congestonamento no pco, e os dados a segur apresentados: Trechos
Ao se calcular a média, moda e mediana, temos: Quanto mais os dados variam, menos representativa é a média.
 Estatístca Dscplna de Estatístca 0/ Curso de Admnstração em Gestão Públca Profª. Me. Valéra Espíndola Lessa e-mal: lessavalera@gmal.com Meddas de Dspersão Indcam se os dados estão, ou não, prómos uns dos
Estatístca Dscplna de Estatístca 0/ Curso de Admnstração em Gestão Públca Profª. Me. Valéra Espíndola Lessa e-mal: lessavalera@gmal.com Meddas de Dspersão Indcam se os dados estão, ou não, prómos uns dos
Ao se calcular a média, moda e mediana, temos: Quanto mais os dados variam, menos representativa é a média.
 Estatístca Dscplna de Estatístca 0/ Curso Superor de tecnólogo em Gestão Ambental Profª. Me. Valéra Espíndola Lessa e-mal: lessavalera@gmal.com Meddas de Dspersão Indcam se os dados estão, ou não, prómos
Estatístca Dscplna de Estatístca 0/ Curso Superor de tecnólogo em Gestão Ambental Profª. Me. Valéra Espíndola Lessa e-mal: lessavalera@gmal.com Meddas de Dspersão Indcam se os dados estão, ou não, prómos
MAE5778 - Teoria da Resposta ao Item
 MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
3ª AULA: ESTATÍSTICA DESCRITIVA Medidas Numéricas
 PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA DE TRASPORTES E GESTÃO TERRITORIAL PPGTG DEPARTAMETO DE EGEHARIA CIVIL ECV DISCIPLIA: TGT41006 FUDAMETOS DE ESTATÍSTICA 3ª AULA: ESTATÍSTICA DESCRITIVA Meddas umércas
PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA DE TRASPORTES E GESTÃO TERRITORIAL PPGTG DEPARTAMETO DE EGEHARIA CIVIL ECV DISCIPLIA: TGT41006 FUDAMETOS DE ESTATÍSTICA 3ª AULA: ESTATÍSTICA DESCRITIVA Meddas umércas
Controle Estatístico de Qualidade. Capítulo 8 (montgomery)
 Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
ENFRENTANDO OBSTÁCULOS EPISTEMOLÓGICOS COM O GEOGEBRA
 ENFRENTANDO OBSTÁCULOS EPISTEMOLÓGICOS COM O GEOGEBRA André Luz Souza Slva IFRJ Andrelsslva@globo.com Vlmar Gomes da Fonseca IFRJ vlmar.onseca@rj.edu.br Wallace Vallory Nunes IFRJ wallace.nunes@rj.edu.br
ENFRENTANDO OBSTÁCULOS EPISTEMOLÓGICOS COM O GEOGEBRA André Luz Souza Slva IFRJ Andrelsslva@globo.com Vlmar Gomes da Fonseca IFRJ vlmar.onseca@rj.edu.br Wallace Vallory Nunes IFRJ wallace.nunes@rj.edu.br
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Prof. Benjamin Cesar. Onde a(n, i) é o fator de valor atual de uma série de pagamentos. M: montante da renda na data do último depósito.
 Matemátca Fnancera Rendas Certas Prof. Benjamn Cesar Sére de Pagamentos Unforme e Peródca. Rendas Certas Anudades. É uma sequênca de n pagamentos de mesmo valor P, espaçados de um mesmo ntervalo de tempo
Matemátca Fnancera Rendas Certas Prof. Benjamn Cesar Sére de Pagamentos Unforme e Peródca. Rendas Certas Anudades. É uma sequênca de n pagamentos de mesmo valor P, espaçados de um mesmo ntervalo de tempo
Camila Spinassé INTRODUÇÃO À MATEMÁTICA FINANCEIRA PARA ALUNOS NA EDUCAÇÃO DE JOVENS E ADULTOS
 Camla Spnassé INTRODUÇÃO À MATEMÁTICA FINANCEIRA PARA ALUNOS NA EDUCAÇÃO DE JOVENS E ADULTOS Vtóra Agosto de 2013 Camla Spnassé INTRODUÇÃO À MATEMÁTICA FINANCEIRA PARA ALUNOS NA EDUCAÇÃO DE JOVENS E ADULTOS
Camla Spnassé INTRODUÇÃO À MATEMÁTICA FINANCEIRA PARA ALUNOS NA EDUCAÇÃO DE JOVENS E ADULTOS Vtóra Agosto de 2013 Camla Spnassé INTRODUÇÃO À MATEMÁTICA FINANCEIRA PARA ALUNOS NA EDUCAÇÃO DE JOVENS E ADULTOS
IMPLEMENTAÇÃO DO MÉTODO DE FATORAÇÃO DE INTEIROS CRIVO QUADRÁTICO
 IMPLEMENTAÇÃO DO MÉTODO DE FATORAÇÃO DE INTEIROS CRIVO QUADRÁTICO Alne de Paula Sanches 1 ; Adrana Betâna de Paula Molgora 1 Estudante do Curso de Cênca da Computação da UEMS, Undade Unverstára de Dourados;
IMPLEMENTAÇÃO DO MÉTODO DE FATORAÇÃO DE INTEIROS CRIVO QUADRÁTICO Alne de Paula Sanches 1 ; Adrana Betâna de Paula Molgora 1 Estudante do Curso de Cênca da Computação da UEMS, Undade Unverstára de Dourados;
