DISCIPLINA DE ESTRUTURAS METÁLICAS
|
|
|
- Octavio João Pedro Fontes Vilanova
- 7 Há anos
- Visualizações:
Transcrição
1 DISCIPLINA DE ESTRUTURAS METÁLICAS Estabilidade de Estruturas. Colunas e Vigas-coluna Francisco Virtuoso 2009/10 (Versão revista em Novembro de 2012)
2 INDÍCE Nota introdutória.... ii 1. Conceito de estabilidade de equilíbrio Estabilidade de estruturas constituídas por barras rígidas Equilíbrio na posição deformada. Trajectória fundamental e trajectória de pós-encurvadura. Carga crítica Critérios energéticos Análise dos efeitos das imperfeições geométricas iniciais Colunas Introdução Carga crítica de uma coluna Comprimento de encurvadura Comprimento de encurvadura de barras em estruturas trianguladas Esbelteza de uma coluna Curva de dimensionamento de uma coluna ideal Esbelteza normalizada Efeito das imperfeições geométricas Efeito das tensões residuais Verificação da segurança de colunas segundo o Eurocódigo Vigas-colunas Introdução Análise de vigas-colunas em regime elástico Dimensionamento elástico de vigas-colunas Verificação da segurança de vigas-colunas segundo o Eurocódigo Referências i
3 Nota introdutória. Este texto foi elaborado como texto de apoio ao ensino da análise plástica de estruturas na disciplina de Estruturas Metálicas do MEC (Curso de Mestrado Integrado em Engenharia Civil do Instituto Superior Técnico). A primeira versão do texto foi elaborada durante os anos lectivos de 2007/08 e 2008/09, tendo o texto original sido revisto e sofrido pequenas alterações nos anos lectivos subsequentes. Algumas partes deste documento basearam-se em textos escritos em colaboração com o Prof. António Reis e que serviram de apoio a outras disciplinas da Licenciatura e do Mestrado em Engenharia Civil. Embora este texto seja resultado de um esforço individual não posso deixar de agradecer aos meus amigos e colegas Eduardo Pereira e Luis Guerreiro pelas sugestões que fizeram e pela colaboração na revisão do texto. ii
4 1. CONCEITO DE ESTABILIDADE DE EQUILÍBRIO O conceito de estabilidade de uma estrutura está relacionado com a capacidade de uma estrutura após atingir uma posição de equilíbrio permanecer ou afastar-se dessa posição de equilíbrio. Para ilustrar este conceito considere-se uma esfera que se move sem atrito sobre superfícies côncavas, convexas e planas conforme se representa na figura 1.1a. Figura 1.1 Ilustração de situações de equilíbrio estável, instável e neutro e da correspondente variação da energia potencial Em qualquer um dos casos a esfera encontra-se em equilíbrio. No entanto as situações de equilíbrio não são todas idênticas uma vez que se a esfera for ligeiramente afastada relativamente à sua posição inicial de equilíbrio vai deslocar-se de forma diferente em função da curvatura da superfície. No caso da superfície côncava a esfera após ser afastada da sua posição de equilíbrio volta para a posição de equilíbrio inicial - diz-se nesta situação que o equilíbrio é estável. Pelo contrário, no caso da superfície convexa a esfera após ser afastada da sua posição de equilíbrio vai afastar-se cada vez mais da posição de equilíbrio inicial - diz-se nesta 1
5 situação que o equilíbrio é instável. Finalmente, no caso da superfície plana a esfera após ser afastada da equilíbrio inicial não vai ter tendência para se afastar nem para se aproximar da posição de equilíbrio inicial - diz-se neste caso que o equilíbrio é neutro ou indiferente. A avaliação do equilíbrio e da sua estabilidade pode ser efectuada através da análise das variações da energia potencial. No caso da esfera a deslocar-se sobre uma superfície a energia potencial total coincide com a energia potencial gravítica, tendo-se V = m g h (1.1) em que V representa a energia potencial total, m a massa da esfera, g a aceleração da gravidade e h a posição da esfera relativamente a uma coordenada de referência. Para as três situações referidas representa-se também a energia potencial em função de uma coordenada x, que representa o deslocamento horizontal da esfera em relação à posição de equilíbrio inicial. O equilíbrio da estrutura corresponde a um ponto de estacionaridade da energia potencial. Com efeito verifica-se para as três situações que a derivada da energia potencial em relação ao deslocamento é nula na posição de equilíbrio (x=0), ou seja dv dx x=0 =0, o que confirma que as posições iniciais da esfera constituem funções de equilíbrio. A análise da segunda derivada da energia potencial permite avaliar a estabilidade do equilíbrio. No caso da superfície côncava a segunda derivada da energia potencial é positiva, ou seja a posição de equilíbrio corresponde a um mínimo daquela energia, estando-se por isso perante uma situação de equilíbrio estável. Pelo contrário, na situação em que a superfície é convexa a segunda derivada da energia potencial é negativa, indicando assim que a posição inicial corresponde a um máximo da energia potencial, ou seja, a uma posição de equilíbrio instável. Finalmente, no caso da superfície plana a segunda derivada da energia potencial é nula, não sendo possível classificar o equilíbrio como estável ou instável, sendo por isso neutro. 2
6 2. ESTABILIDADE DE ESTRUTURAS CONSTITUÍDAS POR BARRAS RÍGIDAS 2.1. Equilíbrio na posição deformada. Trajectória fundamental e trajectória de pós-encurvadura. Carga crítica Na análise linear de estruturas admite-se que o equilíbrio se verifica na posição indeformada da própria estrutura. Quando se analisam problemas de encurvadura, ou de uma forma mais geral, problemas de estabilidade de estruturas, aquela hipótese deixa de ser admissível sendo necessário efectuar o equilíbrio na posição deformada da estrutura. Embora o objectivo final seja estudar os problemas de encurvadura em peças lineares deformáveis ao longo do seu eixo apresenta-se em seguida, através de alguns exemplos, a análise dos fenómenos de encurvadura em estruturas constituídas por barras rígidas e molas associadas às rotações e aos deslocamentos das estruturas. Estes exemplos para além de servirem para introduzir alguns conceitos fundamentais, como por exemplo o estabelecimento do equilíbrio na posição deformada, a análise de trajectórias de equilíbrio e o conceito de carga crítica, permitem a análise do problema recorrendo a conceitos de matemática muito mais simples do que no caso das barras deformáveis. Considere-se a coluna, indicada na figura 2.1, constituída por duas barras rígidas de comprimento L, ligadas por uma rótula e por uma mola com rotação de rigidez k e sujeita a uma força P aplicada segundo o eixo das barras. Figura 2.1 Coluna simplesmente apoiada composta por duas barras rígidas ligadas por uma mola 3
7 A análise linear da estrutura, em que o equilíbrio é efectuado na posição indeformada, conduz a que os deslocamentos transversais, assim como o momento na mola, sejam nulos, estando as barras da estrutura sujeitas apenas a um esforço axial de compressão com o mesmo valor da carga aplicada. Analise-se agora o equilíbrio da estrutura numa posição deformada genérica, representada na figura 2.1c, caracterizada pela rotação θ ou pelo deslocamento transversal u do nó de ligação das barras. Na figura 2.1d representa-se um diagrama de corpo livre de uma das barras na posição deformada, sendo possível analisar o problema a partir das seguintes equações: Equilíbrio (na posição deformada) P u = M (2.1) Compatibilidade u = L senθ (2.2) Relação constitutiva M = 2 k θ (2.3) Neste caso a relação de compatibilidade estabelece a relação entre o deslocamento transversal a 1/2 vão e a rotação das barras. Tratando-se de um modelo de barras rígidas a relação constitutiva refere-se apenas aos elementos deformáveis que, neste caso, é apenas a mola de rotação na ligação entre as barras. Introduzindo na equação (2.1) os valores de u e M definidos nas equações (2.2) e (2.3) obtém-se: 2 k θ P L senθ = 0 (2.4) Esta equação tem duas soluções 1ª solução θ = 0 P indeterminado (2.5a) 2ª solução θ 0 P = 2 k L θ senθ (2.5b) No gráfico apresentado na figura 2.2, em que o eixo das abcissas corresponde à rotação θ e o eixo das ordenadas à carga aplicada, representam-se as duas soluções obtidas nas equações 2.5a e 2.5b. A trajectória para a qual a rotação é nula (θ = 0) e a carga (P) indeterminada, coincidente portanto com o eixo das ordenadas, designa-se por trajectória fundamental (TF). A trajectória que corresponde a uma solução equilibrada, mas com rotações θ não nulas, designa-se por trajectória de pós-encurvadura (TPE). 4
8 Figura 2.2 Relação carga (P) rotação (θ). Trajectória fundamental (TF) e trajectória de pós-encurvadura (TPE) Os problemas em que, como no exemplo analisado, existem duas trajectórias de equilíbrio designam-se por problemas de instabilidade bifurcacional uma vez que para cargas crescentes o ponto de cruzamento das duas trajectórias corresponde a uma bifurcação da trajectória de equilíbrio. O valor de carga para o qual se dá a intersecção das duas trajectórias designa-se por carga crítica de instabilidade elástica e que, por simplicidade de apresentação, será neste texto designada apenas por carga crítica. Para a estrutura em análise tem-se P cr = 2 k L (2.6) valor este que se obtém da equação 2.5b determinando o limite de P quando θ tende para zero. No caso de se pretender obter apenas a carga crítica, a equação (2.4) pode ser linearizada na vizinhança do ponto de bifurcação, ou seja de θ = 0, admitindo que θ é pequeno, o que permite admitir senθ θ, obtendo-se 2 k θ P L θ = 0 (2 k P L) θ = 0 (2.7) Esta equação tem novamente duas soluções 1ª solução θ = 0 P indeterminado (TF) (2.8a) 2ª solução θ 0 P = 2 k L = P cr (2.8b) 5
9 Saliente-se que esta última solução, obtida da linearização da equação 2.4, corresponde à tangente à trajectória fundamental no ponto de bifurcação, o que permite determinar a carga crítica, mas não permitindo definir a trajectória de pós-encurvadura. Refira-se finalmente que a hipótese de os deslocamentos e rotações serem pequenos pode ser admitida logo desde o início da análise, obtendo-se para este problema que a equação 2.2, que representa a equação de compatibilidade, pode ser escrita na forma u = L θ, o que em conjunto com as equações 2.1 e 2.3 permite obter directamente a equação 2.7. Considere-se agora uma outra estrutura, representada na figura 2.3, constituída por uma barra rígida de comprimento L com um apoio fixo numa extremidade e com um apoio elástico de rigidez k na outra extremidade. Figura Coluna composta por uma barra rígida com um apoio fixo e um apoio elástico À semelhança do exemplo anterior a análise linear da estrutura, efectuando o equilíbrio na posição indeformada, conduz a deslocamentos transversais e forças nas molas nulos, ficando a barra sujeita apenas a esforços axiais. Se o equilíbrio for efectuado na posição deformada, conforme se representa no diagrama de corpo livre da figura 2.3c, definida em função da rotação θ ou pelo deslocamento transversal u na extremidade superior da barra, obtêm-se as seguintes equações: Equilíbrio (na posição deformada) P u = F d (2.9) Compatibilidade d = L cosθ (2.10) u = L senθ (2.11) Relação constitutiva F = k u (2.12) 6
10 Substituindo os valores de d, u e F na equação 2.9 obtém-se P L senθ = k L 2 senθ cosθ (k L cosθ - P) L senθ = 0 (2.13) Esta equação tem duas soluções Trajectória fundamental (TF) θ = 0 P indeterminado (2.14a) Trajectória de pós-encurvadura(tpe) θ 0 P = k L cosθ (2.14b) Na figura 2.3d representam-se as duas trajectórias correspondentes às equações 2.14a e 2.14b. A carga crítica corresponde ao valor da carga na intersecção dessas duas trajectórias, obtendo-se da equação 2.14b para θ = 0 P cr = k L (2.15) À semelhança do exemplo anterior a equação 2.13 pode ser linearizada na vizinhança de θ = 0, podendo admitir-se cosθ 1 e senθ 0, obtendo-se (k L P) Lθ = 0 (2.16) Esta equação tem também duas soluções: Trajectória fundamental θ = 0 P indeterminado (2.17a) Aproximação da trajectória de pós-encurvadura θ 0 P = kl = P cr (2.17b) Como se pode verificar da figura 2.3.e a linearização da equação 2.13 permite obter a tangente à trajectória de pós-encurvadura na vizinhança de θ = 0, permitindo assim determinar o valor da carga crítica, mas não a trajectória de pós-encurvadura. Da mesma forma que no exemplo anterior a hipótese de os deslocamentos e rotações serem pequenos pode ser admitida logo de início, permitindo reescrever as equações 2.10 e 2.11 (equações de compatibilidade) na forma d = L e u = L θ, respectivamente. Estas duas equações juntamente com as equações 2.9 e 2.12 permitem obter directamente a equação Nos dois exemplos apresentados ilustrou-se como é possível obter a trajectória fundamental, a trajectória de pós-encurvadura e a carga crítica. Mostrou-se ainda que através da linearização da solução na vizinhança do ponto de bifurcação se pode determinar a carga crítica e a tangente à trajectória de pós-encurvadura. Analise-se agora a estabilidade das trajectórias, começando pelas trajectórias fundamentais. Para cargas inferiores às cargas críticas as trajectórias fundamentais são 7
11 estáveis pois se for introduzida uma pequena perturbação na configuração da estrutura esta volta à sua configuração original. Para cargas superiores à carga crítica a trajectória fundamental é instável em ambos os exemplos; no segundo exemplo não existe mesmo qualquer configuração alternativa à trajectória fundamental; no primeiro exemplo existem trajectórias de pós-encurvadura com solução para o mesmo nível de carga, pelo que introduzindo uma pequena perturbação na configuração da estrutura esta vai mudar da trajectória fundamental para a trajectória de pós-encurvadura. Neste caso, para o primeiro exemplo, verifica-se que a trajectória fundamental não é estável para valores de carga superiores à carga crítica. Analise-se agora de forma qualitativa a estabilidade das trajectórias de pós-encurvadura. No primeiro exemplo a trajectória de pós-encurvadura é estável uma vez que a incrementos da rotação θ correspondem aumentos de carga. No segundo exemplo a trajectória de pós-encurvadura é instável uma vez que a incrementos da rotação θ correspondem variações negativas de cargas. Refira-se finalmente que a metodologia apresentada para a determinação das cargas críticas e as trajectórias de equilíbrio se baseia em efectuar o equilíbrio da estrutura numa posição deformada adjacente à posição indeformada inicial. 8
12 2.2. Critérios energéticos Conforme se referiu na introdução deste texto o equilíbrio e a análise de estabilidade de uma estrutura podem ser determinados através da análise de energia potencial. Considere-se novamente a estrutura do 1º exemplo analisado anteriormente e que se reproduz na figura 2.4a. Figura Coluna simplesmente apoiada composta por duas barras rígidas ligadas por uma mola Neste caso a energia potencial total V é a soma da energia potencial V e da força exterior aplicada com a energia de deformação U da mola que liga as duas barras, ou seja V = U + V e (2.18) A energia de deformação de uma mola de rotação é dada por U = 1 2 M α = 1 2 k α2 (2.19) em que M, α e K representam o momento, a rotação e a rigidez da mola, respectivamente. Tomando como referencial a posição indeformada da estrutura a energia potencial das forças exteriores, V e, tem o valor simétrico do trabalho, W, realizado por essas forças ao longo da deformação da estrutura, tendo-se V e = W (2.20) Para o problema em análise tem-se U = 1 2 k (2θ)2 = 2kθ 2 (2.21) V e = -W = - PΔ = - 2 PL (1 - cosθ) (2.22) 9
13 V = U + V e = 2kθ 2-2 PL (1 - cosθ) (2.23) salientando-se que P é a única força exterior, a qual sofre um deslocamento Δ colinear com a sua direcção. As configurações de equilíbrio correspondem a situações de estacionaridade de energia potencial ou seja Equilíbrio V = 0 4 k θ - 2 P L senθ = 0 (2.24) θ Note-se que esta equação obtida através de um critério energético é idêntica à equação 2.4, a qual foi obtida através do equilíbrio da estrutura na posição deformada. A trajectória fundamental e a trajectória de pós-encurvadura correspondem às duas soluções desta equação, tendo-se: Trajectória fundamental (TF) θ = 0 P indeterminado (2.25) Trajectória de pós-encurvadura (TPE) P = 2 k L θ senθ (2.26) Como seria de esperar estas trajectórias coincidem com as trajectórias determinadas directamente a partir do equilíbrio da estrutura na posição deformada, permitindo obter o valor da carga crítica P cr = 2 k L (2.27) Conhecidas as trajectórias de equilíbrio da estrutura pode avaliar-se se são estáveis ou instáveis. Conforme já se referiu, uma trajectória é estável ou instável consoante a segunda derivada de energia potencial seja positiva ou negativa. Para a estrutura em análise tem-se: 2 V θ 2 = 4 k - 2 P L cosθ (2.28) A trajectória fundamental (TF) é definida por θ = 0, pelo que ao longo desta trajectória se tem 2 V θ 2 = 4k - 2PL > 0 se P < P cr TF estável (2.29a) TF < 0 se P > P cr TF instável (2.29b) 10
14 permitindo assim concluir que a trajectória fundamental é estável enquanto P < P cr é instável se P > P cr. Analisando agora a estabilidade do equilíbrio ao longo da trajectória de pós-encurvadura (TPE), definida por P = 2 k L θ senθ, tem-se 2 V θ 2 = 4 k TPE 1 - θ tgθ > 0 θ TPE é estável (2.30) Conclui-se assim que para este problema a trajectória de pós-encurvadura é sempre estável. Considere-se agora o 2º exemplo analisado anteriormente e representado na figura 2.5a) Figura Coluna composta por uma barra rígida com um apoio fixo e um apoio elástico Analise-se o equilíbrio e a sua estabilidade de forma semelhante ao efectuado para o 1º exemplo. Tem-se neste caso Energia de deformação U = 1 2 k u2 (2.31) Energia potencial das forças exteriores V e = PΔ (2.32) Relação de compatibilidade u = L senθ (2.33) Δ = L (1 - cosθ) (2.34) Energia potencial total V = U + V e = 1 2 k L2 sen 2 θ - PL (1 - cosθ) (2.35) As configurações de equilíbrio correspondem a V θ = 0 k L2 senθ cosθ - P L senθ = 0 (2.36) Da solução desta equação obtém-se 11
15 Trajectória fundamental (TF) θ = 0 P indeterminado (2.37a) Trajectória de pós-encurvadura (TPE) P = k L cosθ (2.37b) Carga crítica P cr = k L (2.38) Para a análise da estabilidade de equilíbrio tem-se 2 V θ 2 = k L 2 cos 2 θ - k L 2 sen 2 θ - P L cosθ = k L 2 (2 cos 2 θ - 1) - P L cosθ (2.39) A trajectória fundamental (TF) é definida por θ = 0, pelo que ao longo desta trajectória se tem 2 V θ 2 = TF kl2 - PL > 0 se P < P cr TF estável (2.40a) < 0 se P > P cr TF instável (2.40b) permitindo assim concluir que a trajectória fundamental é estável enquanto P<P cr e instável se P>P cr. Analisando agora a estabilidade do equilíbrio ao longo da trajectória de pós-encurvadura (TPE), definida por P = k L cosθ, tem-se 2 V θ 2 = k TPE L2 (cos 2 θ - 1) < 0 θ TPE instável (2.41) Face aos resultados obtidos conclui-se que a trajectória fundamental é estável enquanto P < P cr e instável quando P > P cr, e que a trajectória de pós-encurvadura é sempre instável. Dos dois exemplos apresentados da aplicação dos métodos energéticos, e por comparação com a primeira abordagem em que se efectuou o equilíbrio na configuração deformada, pode verificar-se que a utilização dos métodos energéticos permite determinar as configurações de equilíbrio de uma forma mais sistematizável, embora de maior dificuldade de interpretação do seu significado físico. Para além disso a aplicação dos métodos energéticos apresenta como enorme vantagem o facto de permitir avaliar de uma forma explicita a estabilidade das configurações de equilíbrio através da análise do sinal da 2ª derivada da energia potencial ao longo das trajectórias de equilíbrio. 12
16 2.3. Análise dos efeitos das imperfeições geométricas iniciais Na análise dos problemas de encurvadura as imperfeições geométricas podem ter uma influência significativa, sendo importante saber avaliar a sua influência no comportamento das estruturas. Apresenta-se de seguida a análise dos efeitos das imperfeições geométricas iniciais para os dois exemplos com um grau de liberdade apresentados no 2.2. Realça-se que a análise destes problemas é de tratamento matemático relativamente simples permitindo extrapolar conclusões, ainda que apenas de forma qualitativa, para outros tipos de estruturas, nomeadamente para as barras deformáveis. Na figura 2.6a) representa-se a estrutura do primeiro exemplo anteriormente analisado, mas considerando-se agora a existência de uma imperfeição geométrica inicial com uma amplitude definida pelo ângulo θ 0. Figura 2.6 Coluna simplesmente apoiada composta por duas barras rígidas ligadas por uma mola. Análise do efeito das imperfeições geométricas iniciais A determinação das trajectórias de equilíbrio pode ser efectuada através da análise da energia potencial total, e em particular, dos seus pontos de estacionaridade, tendo-se: Energia de deformação: U = 1 2 k (2θ - 2θ 0) 2 = 2k (θ - θ 0 ) 2 (2.42) Energia potencial das forças exteriores: V e = P x Δ (2.43) Tendo em consideração que a relação de compatibilidade permite escrever que Δ = 2 L (cosθ o - cosθ) obtém-se Energia potencial total: V = U + V e = 2k (θ θ 0 ) 2 2 P L (cosθ 0 - cosθ) (2.44) Equilíbrio: V θ = 0 4k (θ θ 0) - 2 P L senθ = 0 P = 2k L θ senθ - θ 0 senθ (2.45) 13
17 Na figura 2.6c representa-se graficamente esta equação para diferentes valores de θ 0, verificando-se que o valor de θ na intersecção com os eixos das abcissas é o valor da imperfeição inicial e que as trajectórias são assimptóticas relativamente à trajectória de pós-encurvadura da estrutura perfeita (sem imperfeições). O facto de as imperfeições geométricas iniciais serem positivas ou negativas não tem qualquer consequência na resposta da estrutura a não ser definir desde logo que as deformações da estrutura terão o mesmo sinal da imperfeição. Considere-se agora o 2º exemplo já analisado, mas introduzindo uma imperfeição inicial definida pelo ângulo θ 0 conforme se representa na figura 2.7. Figura 2.7- Coluna composta por uma barra rígida com um apoio fixo e um apoio elástico. Análise do efeito das imperfeições geométricas iniciais À semelhança do caso anterior podem determinar-se as trajectórias de equilíbrio em função da imperfeição inicial θ 0, tendo-se: Energia de deformação: U = 1 2 k (u - u 0) 2 (2.46) Energia potencial das forças exteriores: V e = P x Δ (2.47) Relação compatibilidade: u 0 = L senθ 0 (2.48) u = L senθ (2.49) Δ = L (cosθ 0 - cosθ) (2.50) Energia Potencial total: V = U + V e = 1 2 kl2 (senθ senθ 0 ) 2 - PL (cosθ 0 - cosθ) (2.51) Equilíbrio: V 1 senθ - senθ 0 tgθ θ = 0 k L2 (senθ senθ 0 ) cosθ - P L senθ = 0 P = k L ( ) (2.52) 14
18 Na figura 2.7c) representam-se as trajectórias correspondentes a esta solução para diferentes valores de imperfeição geométrica inicial θ 0. Da análise das curvas verifica-se que para P = 0 se tem θ = θ 0, que as curvas são inicialmente crescentes com P, atingindo um valor máximo tanto menor quanto maior o valor absoluto da imperfeição geométrica, e que quando θ aumenta tendem assimptoticamente para a trajectória de pós-encurvadura. Da análise comparativa das figuras 2.6c) e 2.7c) verifica-se que a trajectória da estrutura com imperfeições iniciais tende em ambos os casos assimptoticamente para a trajectória de pós-encurvadura da estrutura perfeita. No entanto, o facto de esta trajectória ser estável para a primeira estrutura e instável para a segunda estrutura, traduz-se num comportamento significativamente diferente quando se consideram as imperfeições geométricas. No primeiro caso, em que a trajectória de pós-encurvadura da estrutura perfeita é estável, a consideração das imperfeições geométricas não impede que a relação carga rotação seja sempre crescente, verificando-se ser possível atingir cargas superiores à carga crítica. No segundo caso, em que a trajectória de pós-encurvadura da estrutura perfeita é instável, a consideração do efeito das imperfeições geométricas conduz a que os valores máximos da carga sejam sempre inferiores ao valor da carga crítica, sendo o valor da carga máxima tanto menor quanto maior for a amplitude da imperfeição. Esta conclusão pode ser generalizada para qualquer tipo de estruturas dizendo-se que quando as trajectórias de pós-encurvadura são estáveis as estruturas são pouco sensíveis ao efeito das imperfeições iniciais; pelo contrário, quando as trajectórias de pós-encurvadura são instáveis, as estruturas são muito sensíveis ao efeito das imperfeições iniciais. 15
19 3. COLUNAS 3.1. Introdução Neste capítulo aborda-se a encurvadura de colunas, desde os problemas de encurvadura elástica de colunas perfeitas até às curvas de dimensionamento de colunas, e a sua consideração na regulamentação actual de verificação da segurança de estruturas metálicas. No contexto da análise e verificação da segurança de elementos de estruturas metálicas entende-se por colunas as peças lineares sujeitas apenas a esforços de compressão, distinguindo-se das vigas elementos sujeitos apenas a momentos flectores e a esforços transversos, sendo nulo o esforço axial e de vigas-colunas elementos sujeitos simultaneamente a esforços axiais, momentos flectores e, em geral, esforços transversos. De uma forma geral adopta-se neste texto a convenção usual de considerar positivos os esforços axiais de tracção assim como as tensões de tracção. No entanto, e de forma a facilitar a apresentação, estando-se a abordar problemas de encurvadura, associados a esforços e tensões de compressão, optou-se em algumas situações por se fazer referência ao valor absoluto dos esforço ou tensões, deixando-se ao cuidado do leitor a interpretação do respectivo sinal. Na análise mais corrente de estruturas as equações de equilíbrio são estabelecidas na configuração inicial da estrutura, ou seja, na sua configuração indeformada, designando-se por análises geometricamente lineares. A análise da estabilidade de estruturas obriga à consideração do equilíbrio na sua posição deformada, designando-se este tipo de análises por geometricamente não lineares. Na figura 3.1 ilustra-se a diferença entre uma análise geometricamente linear e uma análise geometricamente não linear para o caso de uma coluna simplesmente apoiada, sujeita a uma carga concentrada aplicada na extremidade móvel e com a direcção do eixo da peça. No caso da análise geometricamente linear, e uma vez que o equilíbrio é estabelecido na configuração indeformada, a coluna fica sujeita apenas a esforços axiais sendo nulos os momentos flectores ao longo do seu eixo. 16
20 Figura 3.1 Coluna simplesmente apoiada sujeita a uma carga axial. Ilustração da diferença entre análises geometricamente lineares e não lineares No caso da análise geometricamente não linear o equilíbrio da estrutura é estabelecido na sua configuração deformada. Assim, e considerando uma situação genérica, admitese que a estrutura vai ter deslocamentos perpendiculares ao seu eixo que não são nulos, conduzindo a que para se garantir o equilíbrio, e como se ilustra na figura 3.1, os momentos flectores também não sejam nulos Carga crítica de uma coluna Considere-se a coluna, simplesmente apoiada e sujeita a um esforço axial de compressão P, representada na figura 3.2. Admitam-se as seguintes hipóteses: o material é elástico linear; as secções transversais têm dois eixos de simetria, sendo portanto eixos principais de inércia, e que a análise se efectua num plano definido pelo eixo da peça e por um dos eixos principais de inércia da secção; desprezam-se as deformações por esforço transverso. 17
21 De acordo com uma análise geometricamente linear, também designada por análise de 1ª ordem, a coluna apenas está sujeita a esforços e deformações axiais pelo que os deslocamentos perpendiculares ao eixo são nulos. Figura Coluna simplesmente apoiada. Equilíbrio na posição deformada. Considere-se agora a possibilidade de aqueles deslocamentos serem não nulos, ou seja w(x) 0 (figura 3.2b). Do equilíbrio do troço do elemento representado na figura 3.2c obtém-se M(x) = P w(x) (3.1) O raio de curvatura da peça deformada relaciona-se com o deslocamento transversal w(x) por 1 R = - d 2 w dx dw 3/2 - d2 w dx dx 2 (3.2) Como se admite que o material tem um comportamento elástico linear o momento flector M numa secção relaciona-se com o raio de curvatura R por M = EΙ R (3.3) em que E e Ι representam o módulo de elasticidade do material e o momento de inércia da secção transversal, respectivamente. 18
22 Tendo em consideração as equações 3.2 e 3.3 a relação entre o momento flector e o deslocamento transversal pode ser dada por M = -EΙ d2 w dx 2 (3.4) pelo que a equação 3.1 pode ser escrita na forma - EΙ d2 w dx 2 = P w d 2 w dx 2 + k2 w = 0 com k = P EΙ (3.5) A equação 3.5 é uma equação diferencial homogénea que tem como solução w = A sen(kx) + B cos(kx) (3.6) sendo as constantes A e B definidas em função das condições de fronteira. Para o caso da coluna simplesmente apoiada em análise as condições de fronteira são as correspondentes a impôr que os deslocamentos são nulos nas extremidades do elemento, ou seja w(0)=0 e w(l)=0. Destas condições obtém-se w(0) = 0 B= 0 w(x) = A sen(kx) (3.7) w(l) = 0 A sen(kl) = 0 (3.8) A primeira condição define a forma dos deslocamentos transversais. A segunda equação tem duas soluções: A sen(kl) = 0 1ª solução A = 0 (3.9a) 2ª solução A 0 sen(kl) = 0 (3.9b) No caso da 1ª solução tem-se A=0, pelo que os deslocamentos transversais de coluna são nulos, ou seja w(x)=0. Para a 2ª solução tem-se A 0, sendo assim necessário que sen(kl)=0. Tendo em consideração a periodicidade da função seno tem-se sen(kl) = 0 k L = n π (com n inteiro) (3.10) A partir da definição de k (k= qual é designado por carga crítica do modo n, e é dado por P/EΙ) obtém-se para cada valor de n um valor da carga, o P cr ( n) = n2 π 2 EΙ L 2 (3.11) A menor das cargas críticas de uma coluna simplesmente apoiada designa-se por carga de Euler (P E ), sendo dada por 19
23 P E = P cr ( 1) = π2 EΙ L 2 (3.12) A cada valor de n está também associado um modo de deformação, obtido a partir da equação 3.7 e designado por modo de encurvadura, o qual é definido por w (n) = A sen nπx L (3.13) Na figura 3.3 indicam-se as cargas críticas e representam-se os modos de encurvadura em função de n e a relação entre a carga P e o deslocamento transversal w. Figura 3.3- Cargas críticas e modos de encurvadura de uma coluna simplesmente apoiada Para A=0 a relação entre a carga e o deslocamento transversal é coincidente com o eixo das cargas (ordenadas) e designa-se por trajectória fundamental (TF). Quando a coluna encurva (A 0), a relação entre a carga e os deslocamentos transversais, representada a tracejado na figura 3.3, designa-se por trajectória de pós-encurvadura (TPE) e pode ser obtida se não se introduzir a aproximação indicada na equação 3.2. A análise da coluna anteriormente apresentada, e em consequência da simplificação introduzida na equação 3.2, apenas permite determinar as cargas críticas, não definindo a trajectória de pós-encurvadura. No entanto para as colunas, e ao contrário do que acontece com outros elementos estruturais, como por exemplo as placas, ao longo da trajectória de pós encurvadura os aumentos de carga são muito pequenos, pelo que se pode adoptar como aproximação que para a carga crítica os deslocamentos aumentam 20
24 indefinidamente. Esta hipótese é ilustrada na figura 3.3, representando-se a trajectória de pós-encurvadura a tracejado e a aproximação referida a cheio Comprimento de encurvadura Analisou-se anteriormente o caso de uma coluna simplesmente apoiada. No caso mais geral de uma coluna com quaisquer condições de apoio nas suas extremidades a determinação das cargas críticas e dos modos de encurvadura pode ser efectuada a partir da análise do modelo representado na figura 3.4. Este modelo representa uma barra genérica de comprimento L com quaisquer condições de fronteira estáticas ou cinemáticas. Figura 3.4- Caso geral de uma coluna. Equilíbrio na posição deformada. Do equilíbrio do troço da coluna representado na figura 3.4b) pode concluir-se que M(x) - P w(x) = M A + Vx (3.14) Tendo em consideração a relação entre o momento e os deslocamentos transversais (equação 3.4), a equação de equilíbrio pode escrever-se na forma EΙ d2 w dx 2 + P w = - M A - Vx (3.15) Derivando esta equação duas vezes em ordem a x obtém-se a seguinte equação diferencial homogénea com coeficientes constantes 21
25 d 4 w dx 4 + d 2 w k2 dx 2 = 0 com k= P EΙ (3.16) Esta equação diferencial tem como solução w(x) = C 1 sen(kx)+ C 2 cos(kx) + C 3 x + C 4 (3.17) A introdução das condições de fronteira nas extremidades de colunas permite, à semelhança do caso de coluna simplesmente apoiada, determinar a carga crítica e definir o modo de encurvadura. Exemplo 3.1: Considere-se a coluna encastrada-apoiada representada na figura 3.5. Determinar a menor carga crítica e o respectivo modo de encurvadura. Figura Coluna encastrada apoiada Solução: w(x) = C 1 sen(kx)+ C 2 cos(kx) + C 3 x + C 4 dw = w'(x) = C1 k cos(kx) - C2 k sen(kx) + C3 dx d 2 w dx 2 = w''(x) = - C1 k2 sen(kx) - C 2 k 2 cos(kx) Condições de fronteira: w(0) = 0 C 2 + C 4 =0 w'(0) = 0 C 1 k + C 3 =0 w(l) = 0 C 1 sen(k L) + C 2 cos(k L) + C 3 L + C 4 = 0 M(L) = 0 w''(l) = 0 -C 1 k 2 sen(k L) - C 2 k 2 cos(k L) = 0 22
26 A introdução das quatro condições de fronteira conduz a um sistema de equações cuja solução é dada por C 1 [(tg(k L) - k L) ] = 0 C 2 = - C 1tg(k L) C 3 = -C 1 k C 4 = C 1 tg(k L) Da análise da solução do sistema de equações pode concluir-se que para satisfazer a primeira equação é necessário que C 1 [(tg(k L) - k L) ] = 0 1ª solução C 1 = 0 Trajectória fundamental π 2ª solução C 1 0 tg(k L) k L = 0 k L = ,70 + nπ Refira-se que a equação [(tg(k L) - k L) ] é uma equação transcendente cuja solução só pode ser obtida numérica ou graficamente. Esta equação tem várias soluções sendo o valor de k L = π/0,70 a menor das soluções, correspondendo à menor das cargas críticas. Tendo em consideração o menor valor obtido para kl e a definição de k obtém-se para o caso da coluna encastrada-apoiada π 2 EΙ Carga crítica P cr = (0,70L) 2 Modo de encurvadura w(x) = C 1 πx sen 0,70L - tg π 0,70 cos πx 0,70L - πx 0,70L + tg π 0,70 O valor obtido para a carga crítica no caso da coluna encastrada-apoiada analisada no exemplo 3.1 permite introduzir o conceito de comprimento de encurvadura. Com efeito, a carga crítica da coluna encastrada-apoiada pode ser escrita na forma P cr = π2 EΙ L e 2 com L e = 0,70L (coluna encastrada-apoiada) (3.18) designando-se o comprimento L e por comprimento de encurvadura. Comparando a equação 3.18 com a equação 3.12, que define a carga de Euler, pode dizer-se que o comprimento de encurvadura de uma coluna é o comprimento da coluna simplesmente apoiada que tem a mesma carga crítica. Na figura 3.6 ilustra-se o conceito de comprimento de encurvadura para o caso da coluna encastrada apoiada. Definido o conceito de comprimento de encurvadura pode escrever-se, com toda a generalidade, que a carga crítica de uma coluna é dada por P cr = π2 EΙ L e 2 (3.19) 23
27 Na figura 3.7 representam-se os comprimentos de encurvadura de colunas com diversas condições de apoio, os quais podem ser determinados adoptando o mesmo procedimentos que foi apresentado no exemplo 3.1. Note-se que o comprimento de encurvadura corresponde à distância entre pontos de inflexão do modo de encurvadura. Figura Comprimento de encurvadura de uma coluna encastrada apoiada Figura Comprimento de encurvadura de colunas 24
28 Refira-se ainda que, conforme também se ilustra na figura 3.7, para a maior parte das situações analisadas é possível determinar o comprimento de encurvadura com base em condições geométricas tendo em conta as características dos apoios nas extremidades das barras. Na maior parte das estruturas as condições de fronteira das colunas dependem da rigidez dos elementos adjacentes, pelo que os valores do comprimento de encurvadura indicados na figura 3.7 não representam mais do que situações limites da rigidez de rotação dos apoios, correspondentes a uma rigidez nula (apoios simples) ou uma rigidez infinita (encastramentos ou encastramentos deslizantes). As situações intermédias podem ser analisadas a partir dos modelos representados na figura 3.8, distinguindo-se os casos em que se impede o deslocamento transversal em ambas as extremidades (figura 3.8a) e os casos em que aquele deslocamento apenas é impedido numa extremidade (figura 3.8b). Figura 3.8- Modelos para a determinação do comportamento de encurvadura no caso geral. O comprimento de encurvadura de uma coluna é função da relação entre a rigidez da coluna, K c, e a rigidez dos elementos adjacentes considerada através da rigidez das molas nas extremidades das barras, K 1 e K 2, a qual pode ser considerada a partir dos seguintes parâmetros η 1 = K c K c + K 1 η 2 = K c K c + K 2 (3.20) Para a determinação destes parâmetros a rigidez da coluna, K c, corresponde ao valor da rigidez associado à rotação numa extremidade quando estão impedidos a rotação na 25
29 outra extremidade e os deslocamentos transversais em ambas as extremidades, sendo definida por K c = 4EΙ c L c (3.21) em que I c e L c representam respectivamente o momento de inércia e o comprimento da coluna. Na figura 3.9 apresentam-se dois ábacos que permitem calcular o comprimento de encurvadura de uma coluna com base nos modelos representados na figura 3.8 e no valor dos parâmetros η 1 e η 2. 26
30 η η 2 Figura 3.9a - Ábaco para a determinação do comprimento de encurvadura de colunas com apoios elásticos no caso em que os deslocamentos transversais estão impedidos nas duas extremidades. (valores das curvas - α e; comprimento de encurvadura L e = α e L) 27
31 η η 2 Figura 3.9b - Ábaco para a determinação do comprimento de encurvadura de colunas com apoios elásticos no caso em que o deslocamento transversal está impedido apenas numa extremidade. (valores das curvas - α e; comprimento de encurvadura L e = α e L) 28
32 Exemplo 3.2: Considerem-se os pórticos representados na figura Admitindo apenas a instabilidade no plano da estrutura pretende determinar-se o comprimento de encurvadura para a situação do pórtico travado transversalmente (figura 3.10a) e não travado (figura 3.10b). Dados: E = 210 GPa Travessa Perfil HEA300 Ι t = cm4 L t = 12,00 m Montantes Perfil HEA400 Ι c = cm4 L c = 5,00 m Figura 3.10a - Pórtico travado transversalmente Figura 3.10b - Pórtico não travado transversalmente K c = 4EΙc L c = knm K 1 = EΙt 0.5L t = 6391 knm η 1 = 0,922 K 2 = η 2 = 0 K c = 4EΙc L c = knm K 1 = 3EΙt 0.5L t = knm η 1 = 0,798 K 2 = η 2 = 0 Figura 3.9a α 0,68 L e = α el c = 3,40 m Figura 3.9b α 1,55 L e = α el c = 7,75 m 29
33 3.4. Comprimento de encurvadura de barras em estruturas trianguladas De uma forma geral as estruturas trianguladas são calculadas admitindo que os seus nós funcionam como articulados pelo que os únicos esforços a considerar na verificação da segurança são esforços axiais. Os esforços podem ser calculados de forma aproximada recorrendo apenas a equações de equilíbrio ou por aplicação dos métodos de análise de estruturas. Em algumas situações a materialização das ligações entre as barras introduz algumas excentricidades entre os eixos das barras e os nós, as quais dão origem a momentos flectores que devem também ser tidos em consideração na verificação da segurança das barras embora não sejam explicitamente obtidos na análise de esforços das estruturas. Saliente-se que o facto de se calcular uma estrutura triangulada como articulada nos nós não exige que exista uma rótula nesse nó. Com efeito, a consideração apenas do esforço axial quando não existe nenhuma rótula nos nós resulta da hipótese de se desprezar a contribuição da rigidez de flexão das barras quando comparada com a sua rigidez axial. A determinação do comprimento de encurvadura de uma barra de uma estrutura triangulada depende das características da própria barra assim como das características das barras que lhe estão adjacentes. No caso de estruturas trianguladas planas o comprimento de encurvadura das barras no plano da estrutura é aproximadamente igual ao comprimento da própria barra L, medido entre nós, como se exemplifica na figura 3.11 para os casos de uma corda comprimida e de uma diagonal de uma estrutura triangulada. Na realidade a rigidez das barras adjacentes à barra em análise contribui para que o comprimento de encurvadura da barra seja menor do que o comprimento entre nós. Este cálculo pode ser efectuado de forma semelhante ao apresentado no 3.3, sendo no entanto necessário ter em consideração o efeito do esforço axial na rigidez efectiva das barras, o que introduz alguma complexidade nos cálculos [2,3]. De forma a ter em consideração o efeito do encastramento elástico nas extremidades das barras alguns regulamentos permitem que, desde que se verifiquem algumas condições relativas às características das barras e ligações, se adoptem comprimentos de encurvadura de 0,9L. Na direcção perpendicular ao plano da estrutura a triangulação deixa de influenciar o comprimento de encurvadura das barras sendo este comprimento dependente dos travamentos transversais. Neste contexto entendem-se por travamentos os sistemas estruturais adicionais que vão impedir ou restringir os deslocamentos de alguns dos nós na direcção perpendicular ao plano da estrutura. 30
34 Figura 3.11 Estruturas trianguladas. Comprimentos de encurvadura no plano da estrutura Se os nós da estrutura triangular fossem todos verdadeiramente articulados então todos esses nós teriam de ser travados na direcção perpendicular ao plano da estrutura. Nos casos mais correntes as cordas são constituídas por barras contínuas, admitindo-se que, como se exemplifica na figura 3.12, o seu comprimento de encurvadura é igual à distância entre travamentos. Figura 3.12 Estruturas trianguladas. Comprimentos de encurvadura na perpendicular ao plano da estrutura 31
35 Nalgumas situações adoptam-se estruturas triangulares tridimensionais como a que se apresenta a título de exemplo na figura Nestes casos não existe um comportamento diferenciado entre a encurvadura das barras no plano ou perpendicularmente ao plano da estrutura. Com efeito, neste caso, o carácter tridimensional da estrutura permite assegurar, com as mesmas aproximações já referidas, que o comprimento de encurvadura das barras será no máximo igual ao seu próprio comprimento. Figura 3.13 Estrutura triangulada tridimensional 3.5. Esbelteza de uma coluna Como se apresentou anteriormente qualquer coluna pode ser analisada através de uma coluna simplesmente apoiada equivalente com um comprimento igual ao comprimento de encurvadura L e. Para esta coluna equivalente define-se a carga crítica, designada por carga de Euler, P E = π 2 EΙ / L e 2 (equação 3.12). A avaliação da resistência de uma estrutura pode ser efectuada através da análise das tensões aplicadas as quais podem ser obtidas dos esforços tendo em consideração as características das secções transversais. À carga de Euler de uma coluna corresponde uma tensão σ E, designada por tensão de Euler, dada por σ E = P E A = π2 E Ι A L e 2 (3.22) Tendo em consideração a definição do raio de giração duma secção i = Ι A (3.23) 32
36 e introduzindo o parâmetro adimenional λ = L e i (3.24) a tensão crítica passa a ser dada por σ E = π2 E i 2 L e 2 = π2 E λ 2 (3.25) O parâmetro λ é adimensional, uma vez que resulta do quociente entre dois comprimentos, e designa-se por esbelteza de coluna, sendo tanto maior quanto maior o comprimento de encurvadura e tanto menor quanto menor o raio de giração de secção transversal Curva de dimensionamento de uma coluna ideal No caso de um material elasto-plástico perfeito a relação tensões deformações é a indicada na figura Figura Relação tensões deformações de um material elasto-plástico perfeito Se o material for elasto-plástico perfeito a resistência da coluna depende de qual dos fenómenos ocorre para uma carga menor, a plasticidade do material ou a encurvadura da coluna. Assim, a curva de dimensionamento de uma coluna ideal é definida pelo menor dos valores correspondentes à plastificação da secção e à carga crítica, pelo que o esforço axial resistente N R é dado por N R = A σ m com σ m = min (f y ; σ E ) (3.26) 33
37 representando σ m o valor da tensão média na secção associado ao esforço axial resistente, f y a tensão de cedência do aço e σ E a tensão de Euler. Com base no valor da tensão de cedência (f y ) e da tensão de Euler (σ E ) pode obter-se a curva de dimensionamento de uma coluna ideal, representada na figura 3.15, a qual define o valor da tensão média na secção (σ m ) associado ao esforço axial resistente em função da esbelteza λ. Analisando esta curva pode observar-se a esbelteza λ 1, que se designa por esbelteza de referência, é o valor para a qual a tensão crítica é igual à tensão de cedência, pelo que π 2 E λ 1 2 = f y λ 1 = π E f y (3.27) Figura Curva de dimensionamento de uma coluna ideal 3.7. Esbelteza normalizada A partir do valor da esbelteza de referência λ 1 pode definir-se uma nova esbelteza λ, designada por esbelteza normalizada, definida por λ L e / i λ = = = λ 1 π E / f y f y π 2 E i 2 L e 2 = f y σ E (3.28) 34
38 A esbelteza normalizada apresenta a vantagem de definir se o dimensionamento da coluna ideal é condicionado pela plastificação da secção (λ <1) ou pela encurvadura da coluna (λ >1). Saliente-se que o valor de λ =1, correspondente ao dimensionamento óptimo da coluna ideal, é independente do valor da tensão de cedência e do módulo de elasticidade do material. Na figura 3.15 representa-se também o eixo das esbeltezas definido em função de λ. Uma vez que a carga crítica da coluna N cr = Aσ E e que a resistência plástica da secção é dada por N pl = Af y, a esbelteza normalizada pode ser escrita em função daqueles dois esforços, tendo-se f y λ = = σ E N pl N cr (3.29) Verifica-se assim que a esbelteza normalizada tende para zero quando o valor relativo entre o esforço normal plástico e a carga crítica diminui. Quando o valor relativo entre o esforço normal plástico e a carga crítica aumenta a esbelteza normalizada tende para valores elevados. O valor unitário da esbelteza normalizada corresponde a situações em que o esforço axial plástico e o crítico são iguais Efeito das imperfeições geométricas Na análise apresentada anteriormente designou-se a coluna como ideal uma vez que se admitiu que na ausência de carga o seu eixo é perfeitamente rectilíneo. Nestas condições só existem deslocamentos transversais quando a carga é igual ou superior à carga crítica. No entanto, as colunas reais têm sempre imperfeições geométricas pelo que, mesmo na ausência de carga, o seu eixo não é perfeitamente recto. Considere-se a coluna representada na figura 3.16, onde w o (x) representa as imperfeições iniciais para P=0 e w(x) os deslocamentos totais para P>0. Saliente-se que w(x) representa os deslocamentos totais em relação à corda, ou seja, inclui o valor das imperfeições geométricas inicias. Do equilíbrio do troço da coluna representado na figura 3.16, e de forma semelhante ao já efectuado para a coluna ideal, obtém-se EΙ d2 w dx 2 + P w = EΙ d2 w o dx 2 (3.30) 35
39 As imperfeições geométricas podem ser representadas por uma série de Fourier na forma w o (x) = w o.m sen m π x L m=1 (3.31) em w o.m representa a amplitude da componente com a forma sen m π x L. Tendo em consideração esta definição das imperfeições geométricas e as condições de fronteira da coluna, w(0)=0 e w(l)=0, a solução da equação 3.30 é dada por w(x) = w n sen n π x L n=1 (3.32) Figura Coluna com imperfeições geométricas. Substituindo-se w o (x) e w(x) dados pelas equações 3.31 e 3.32 na equação diferencial de equilíbrio (equação 3.30) obtém-se -EΙ 2 n π + P w L n sen n π x L = - EΙ m π L 2 w o.m sen m π x L n=1 m=1 (3.33) pelo que, igualando os coeficientes que afectam cada um dos termos sinusoidais, se obtém EΙ 2 m π L w m = EΙ m π L 2 w o.m m = 1, 2, 3,..., (3.34) - P 36
40 Como a carga crítica ideal correspondente ao m ésimo modo é dada por P cr ( m) = m2 π 2 EI L 2 (ver equação 3.11) a deformada da coluna pode ser escrita na forma w(x) = m=1 m P cr ( ) m P cr ( ) - P w o.m sen m π x L (3.35) Da análise desta equação pode constatar-se que o termo de ordem m da série que define w(x) tem a forma do m-ésimo modo de encurvadura. A amplitude de cada termo é igual ao produto da componente das imperfeições iniciais nesse modo w o.m pelo coeficiente m P cr ( ) m P cr ( ) - P (3.36) O coeficiente definido na equação 3.36 designa-se por coeficiente de amplificação uma vez que amplifica a amplitude inicial w o.m em função do valor da carga P. Quando a carga se aproxima da carga crítica mais baixa P cr ( )=P E, e dada a relação entre as cargas críticas correspondentes aos diferentes modos de encurvadura, a amplificação da componente da imperfeição geométrica no 1º modo é preponderante sobre todas as outras, pelo que se pode escrever 1 w(x) w 1 sen π x L (3.37) em que w 1 = P E P E - P w 1 o.1 = w 1 - P/P o.1 (3.38) E Na figura 3.17 representa-se esquematicamente a relação entre a carga e o deslocamento transversal tendo em consideração a componente da imperfeição geométrica na forma do 1º modo de encurvadura verificando-se que coeficiente de amplificação daquela componente P/P E representa o Quando se consideram as imperfeições geométricas, a coluna fica sujeita a momentos flectores desde o início do carregamento. Tendo em consideração o equilíbrio de um troço da barra, ilustrado na figura 3.16, e considerando apenas a componente da imperfeição geométrica no 1º modo de encurvadura, o momento flector é máximo na secção de meio vão, sendo dado por M = P w 1 = P P E P E - P w 1 o.1 = P w 1 - P/P o.1 (3.39) E 37
41 Figura Influência das imperfeições geométricas na relação carga-deslocamento transversal. Tem-se assim que a secção de 1/2 vão está sujeita a um esforço axial N, igual à carga aplicada P, e a um momento flector M, função da carga P e da amplificação da amplitude da imperfeição inicial P/P E w o.1. Na figura 3.18 representa-se esquematicamente o diagrama de tensões na secção de 1/2 vão, definindo-se por c o valor absoluto da distância do centro de gravidade às fibras extremas da secção transversal. Figura 3.18 Diagrama de tensões normais na secção de 1/2 vão. A tensão máxima na secção ocorre na fibra mais comprimida. Tendo em consideração o resultado apresentado na equação 3.39 o valor absoluto da tensão máxima de compressão é dado por σ max = P A + Mc Ι = P A 1 + w o.1 c P E i 2 P E - P (3.40) 38
42 Admitindo como critério de dimensionamento que a rotura se dá quando a tensão máxima for igual à tensão de cedência, e designando por σ m a tensão média nessa situação (σ m =P/A para σ max = f y ), obtém-se da equação 3.40 f y = σ m 1 + w o.1 c σ E i 2 σ E - σ m (3.41) Resolvendo esta equação em ordem a σ m obtém-se σ m = 1 2 [ f y + σ E (1 + θ) ] - [ ] f y + σ E (1 + θ) 2-4f y σ E com θ = w o.1 c i 2 (3.42) equação esta conhecia por fórmula de Perry, na qual θ é um parâmetro adimensional proporcional à amplitude da imperfeição w o.1, A partir de medições das imperfeições em colunas reais conclui-se que o parâmetro θ pode ser considerado proporcional à esbelteza da coluna, tendo sido proposto por Robertson que se considerasse θ = λ. Introduzindo este valor do parâmetro θ na equação 3.41 obtém-se uma equação de dimensionamento, a qual é designada por fórmula de Perry-Robertson. Na figura 3.19 comparam-se as curvas de dimensionamento de uma coluna ideal e de uma coluna em que se tem em conta o efeito das imperfeições geométricas, salientando-se que as maiores diferenças se verificam exactamente na zona correspondente ao dimensionamento "óptimo" (λ =1; λ= λ 1) de uma coluna ideal. Figura Curva de dimensionamento. Efeito das imperfeições geométricas. A curva de dimensionamento representada na figura 3.19 depende do valor da tensão de cedência f y. Aquela curva pode ter um carácter mais geral se o eixo das ordenadas for adimensionalisado em relação à tensão de cedência, definindo-se um factor de redução χ = σ m f y = N N pl (3.43) 39
43 Na figura 3.20 representa-se a curva de dimensionamento de uma coluna definida através do factor de redução χ, no eixo das ordenadas, em função da esbelteza normalizada λ, no eixo das abcissas. Refira-se que o factor de redução χ permite obter o valor da tensão média σ m correspondente à resistência da coluna a partir da sua resistência máxima associada à tensão de cedência f y. Tendo em consideração a definição do factor de redução (equação 3.43), da esbelteza normalizada λ (equação 3.28) e do parâmetro de imperfeição θ = w o.m c 2, a equação 3.41 i pode ser escrita na forma 1/λ 2 1 = χ + χθ 1/λ 2 - χ (3.44) cuja solução em relação a χ é χ = 1 2 2λ 2 [ λ θ ] - [ ] λ θ - 4λ (3.45) ou 1 χ = φ + φ 2-2 λ (3.46a) em que φ = 1 [ ] θ + λ 2 (3.46b) A equação 3.46a é equivalente à equação 3.42 e corresponde à curva de dimensionamento para θ 0 representada na figura
44 Figura Curva de dimensionamento. Coeficiente de redução χ em função da esbelteza normalizada λ Efeito das tensões residuais Devido ao processo de fabrico os perfis ficam sujeitos a tensões residuais. Considere-se por exemplo o perfil Ι, de aço laminado a quente, representado na figura A distribuição de tensões residuais representada na figura 3.21 é devida à forma como se dá o arrefecimento após o processo de laminagem. Com efeito, as extremidades dos banzos e a zona intermédia da alma arrefecem primeiro do que as zonas de ligação da alma aos banzos, zona esta em que se concentra a maior parte do material e onde a superfície em contacto com o ar é menor. Assim, quando as zonas de ligação almabanzo arrefecem a sua deformação é restringida pela zona já arrefecida, gerando-se tensões residuais de compressão nas extremidades dos banzos e na zona intermédia das almas e tensões de tracção nas zonas de ligação alma-banzo. Figura Diagrama de tensões residuais numa secção de um perfil I, laminado (adaptado de Dowling [5]) Quando se aplica um esforço axial de compressão P a tensão aumenta uniformemente em toda a secção até que a tensão máxima seja igual à tensão de cedência. Para esta 41
45 situação define-se o valor de tensão média σ p, a qual representa a tensão limite da proporcionalidade de secção. Na figura 3.22 ilustra-se o efeito das tensões residuais na relação entre a tensão média (σ=p/a) e a deformação (ε). Figura Efeito das tensões residuais na relação tensão média - deformação Para tensões médias superiores à tensão limite de proporcionalidade (σ p ) a resistência à encurvadura é dada apenas pela parte de secção que permanece elástica, cuja área e momento de inércia se representam por A e e I e respectivamente. Assim, a carga crítica de uma coluna parcialmente plastificada é dada por P cr = π2 EΙ e L 2 = P E Ι e Ι (3.47) Em termos de tensão média na secção tem-se σ cr = P cr A = η σ E com η = Ι e Ι (3.48) em que η, designado por factor de redução plástica, representa a redução da carga crítica devido ao efeito das tensões residuais. O factor de redução plástica pode ser obtido a partir do parâmetro τ, o qual é função da tensão média na secção e representa a relação entre a área A e e a área total da secção A τ = τ(σ) = A e A (3.49) Este parâmetro pode ser determinado experimentalmente a partir da relação tensão média-deformação, ou analiticamente, se for conhecido o diagrama de tensões residuais. 42
46 Exemplo 3.3: Considere-se a secção I representada na figura 3.23, e admita-se como desprezável a área e a inércia da alma. Figura Efeito das tensões residuais nas curvas de dimensionamento Representando por b e a largura da zona do banzo não plastificado tem-se A = 2bt f A e = 2b et f τ = Ae A = be b Encurvadura em torno de y Encurvadura em torno de z η y = Ιy,e Ι y = 2b et h2 f 4 2b t f h2 4 = Ae A = τ Ιz,e ηz = = Ι z 3 2 be tf 12 2 b3 t f 12 = ( A e ) A 3 = τ 3 Tendo em consideração que τ 1, a redução da carga crítica devido ao efeito das tensões residuais é mais sensível para a encurvadura em torno do eixo z do que para a encurvadura em torno do eixo y. Na figura 3.23 representam-se esquematicamente as curvas de resistência de uma coluna de secção Ι reduzida aos seus banzos, e tendo em consideração apenas o efeito das tensões residuais Verificação da segurança de colunas segundo o Eurocódigo 3 De acordo com o Eurocódigo 3 (EC3) a verificação da segurança de colunas à encurvadura por flexão é efectuada garantindo que N Ed N b.rd 1,0 N Ed N b.rd (3.50) Em que N Ed e N b.rd representam os valores de cálculo do esforço axial actuante e resistente à encurvadura de uma coluna. Para as secções das classes 1 a 3, ou seja, exceptuando as secções da classe 4, o valor de cálculo do esforço axial resistente à encurvadura é dado por 43
47 N b.rd = χ A f y γ M1 (3.51) em que γ M1 é o coeficiente parcial de segurança a considerar na verificação aos estados limites últimos de encurvadura. Como já se referiu o coeficiente χ designa-se por factor de redução uma vez que define a redução do esforço axial plástico para ter em consideração a influência da esbelteza, das imperfeições geométricas e das tensões residuais. O coeficiente χ é definido em função da esbelteza normalizada (λ ) por cinco curvas (a 0, a, b; c; d), as quais se representam na figura 3.24, cuja forma reflecte a influência das imperfeições geométricas e das tensões residuais e cuja escolha depende do tipo de perfil e do eixo de flexão associado ao modo de encurvadura em análise. A esbelteza normalizada, já definida anteriormente, é dada por λ λ = = L e 1 com i = λ 1 i λ 1 Ι A e λ 1 = π E f y (3.52) representando λ a esbelteza, L e o comprimento de encurvadura da coluna, i o raio de giração da secção transversal e λ 1 a esbelteza de referência, a qual é apenas função das propriedades do material. Tomando o módulo de elasticidade do aço E=210 GPa obtémse λ 1 = 93,9ε com ε = 235 f y (f y em N/mm 2 ) (3.53) No quadro 3.1 apresentam-se os valores de λ 1 correspondentes às diferentes classes de resistência dos aços referidos no EC3. O factor de redução χ é definido de acordo com o EC3 por 1 χ = φ + φ 2-2 λ com χ 1,0 (3.54) em que φ = 1 [ ] α(λ -0,2) + 2 λ (3.55) 44
48 Curva a0 a b c d λ α = 0,13 α = 0,21 α = 0,34 α = 0,49 α = 0,76 0,2 1,000 1,000 1,000 1,000 1,000 0,3 0,986 0,977 0,964 0,949 0,923 0,4 0,970 0,953 0,926 0,897 0,850 0,5 0,951 0,924 0,884 0,843 0,779 0,6 0,928 0,890 0,837 0,785 0,710 0,7 0,896 0,848 0,784 0,725 0,643 0,8 0,853 0,796 0,724 0,662 0,580 0,9 0,796 0,734 0,661 0,600 0,521 1,0 0,725 0,666 0,597 0,540 0,467 1,1 0,648 0,596 0,535 0,484 0,419 1,2 0,573 0,530 0,478 0,434 0,376 1,3 0,505 0,470 0,427 0,389 0,339 1,4 0,446 0,418 0,382 0,349 0,306 1,5 0,395 0,372 0,342 0,315 0,277 1,6 0,352 0,333 0,308 0,284 0,251 1,7 0,315 0,299 0,278 0,258 0,229 1,8 0,283 0,270 0,252 0,235 0,209 1,9 0,256 0,245 0,229 0,214 0,192 2,0 0,232 0,223 0,209 0,196 0,177 2,1 0,212 0,204 0,192 0,180 0,163 2,2 0,194 0,187 0,176 0,166 0,151 2,3 0,178 0,172 0,163 0,154 0,140 2,4 0,164 0,159 0,151 0,143 0,130 2,5 0,151 0,147 0,140 0,132 0,121 2,6 0,140 0,136 0,130 0,123 0,113 2,7 0,130 0,127 0,121 0,115 0,106 2,8 0,122 0,118 0,113 0,108 0,100 2,9 0,114 0,111 0,106 0,101 0,094 3,0 0,106 0,104 0,099 0,095 0,088 Figura Curvas de dimensionamento de colunas do EC3 (Gráfico Figura 6.4 do EC3). 45
49 S235 S275 S355 S420 S460 λ 1 93,9 86,8 76,.4 70,2 67,1 Quadro 3.1 Valores da esbelteza de λ 1 em função da classe de resistência do aço Por comparação destas duas expressões com as equações 3.46a e b verifica-se que a curva de dimensionamento do EC3 (equação 3.54) coincide com a fórmula de Perry, bastando para isso ter em consideração que nas curvas de dimensionamento do EC3 o parâmetro de imperfeição θ = wo 1c 2 é dado por i θ = wo 1c i 2 = α(λ -0,2) (3.56) Na tabela apresentada na figura 3.24 indicam-se os valores do parâmetro α associados a cada uma das curvas de dimensionamento. Conhecidos os valores de α e as características da secção transversal é possível, através da equação 3.56, obter o valor da amplitude da imperfeição geométrica a 1/2 vão da coluna. Refira-se que este valor representa uma imperfeição geométrica equivalente ao efeito conjunto da imperfeição geométrica real da coluna e do efeito das tensões residuais. A escolha da curva de dimensionamento a utilizar é efectuada de acordo com o indicado no quadro 3.2, em função do tipo de secção, do eixo de encurvadura e em alguns casos das dimensões da secção. Na figura 3.24 apresentam-se os valores de χ para as diferentes curvas. Note-se, por exemplo, que para um perfil IPE em S235, em que a altura é maior do que 1,2 vezes a largura (h>1,2b), o valor de χ é obtido pela curva a no caso da encurvadura em torno do eixo y e pela curva b no caso da encurvadura em torno do eixo z. O EC3 não impõe limites ao valor das esbeltezas das colunas. No entanto, como o valor do esforço axial resistente é fortemente reduzido para esbeltezas muito grandes, o limite da esbelteza de uma coluna acaba por ser imposto indirectamente. Na prática raramente se utilizam colunas com esbeltezas superiores a 180, excepto no caso de elementos secundários ou de contraventamento, em que aquele limite pode ser estendido a 250. Em elementos de travamento que funcionem em geral como tirantes e que estejam comprimidos apenas quando o vento é a acção variável de base o limite da esbelteza máxima pode ser estendido a 300. Em termos da esbelteza normalizada (λ ) aqueles 46
50 limites correspondem aproximadamente aos valores indicados no quadro 3.3 sendo variáveis em função da qualidade do aço. Quadro 3.2 Selecção da curva de dimensionamento de colunas à encurvadura por flexão (tabela 6.2 EC3) 47
51 Tipo de Elementos λ S235 S275 S355 Elementos comprimidos em geral 180 1,90 2,10 2,30 Elementos secundários ou de contraventamento 250 2,60 2,90 3,20 λ Elementos de travamento que funcionem como tirantes, comprimidos apenas sob a acção do vento 300 3,20 3,50 3,80 Quadro 3.3 Limites das esbeltezas em função do tipo de elementos estruturais e da qualidade do aço Exemplo 3.4: Considere-se uma coluna com um perfil HEA200 S235 de comprimento total 6,00m simplesmente apoiada no plano xz e biencastrada no plano xy (considere-se x o eixo da peça e os eixos y e z da peça coincidentes com os mesmos eixos da secção transversal). Pretende determinar-se qual o valor de cálculo do esforço resistente à encurvadura da coluna. HEA 200: A = 5380 mm 2 ; Ι y = 3690x10 4 mm 4 ; i y = 82,8 mm; Ι z =1340x10 4 mm 4 ; i z = 49,8 mm Flexão no plano xz: L ey = 6000 mm; i y = 82,8 mm; λ y = L ey/i y = 72,5 Flexão no plano xy: L ez = 3000 mm; i z = 49,8 mm; λ z = L ez/i z = 60,2 S235 λ 1 = 93,9 λ y = 72,5/93,9 = 0,77; curva b χ y = 0,74 χ = min(χ y; χ z) = 0,74 λ z = 60,2/93,9 = 0,64; curva c χ z = 0,76 N b.rd = 0,74x5380x 235 1,00 = 936x103 N = 936 kn Exemplo 3.5: Para a coluna do exemplo 3.4 determinar a amplitude da imperfeição geométrica para a encurvadura em torno do eixo y e em torno do eixo z. Encurvadura em torno do eixo y w o,1 = α(λ -0,2) i 2 y = 0,34 x (0,77 0,20) x 82,82 Ley = 14,0 mm = z max 95,0 428 Encurvadura em torno do eixo z (representam-se por v os deslocamentos ao longo do eixo y) v o,1 = α(λ -0,2) i 2 z = 0,49 x (0,64 0,20) x 49,82 Lez = 5,4 mm = y max 100,
52 4. VIGAS-COLUNAS 4.1. Introdução Designam-se por vigas-colunas ("beam-columns" na designação anglo-saxónica) as barras solicitadas simultaneamente por esforços axiais de compressão e por momentos flectores primários. Designam-se por momentos flectores primários, M 1 (x), os momentos ao longo da barra devidos a cargas transversais ao longo do vão ou a momentos aplicados nas extremidades (ver figura 4.1a). Os deslocamentos associados aos momentos primários designam-se por deslocamentos primários, w 1 (x). Figura Momentos primários, M 1(x), e secundários, M 2(x). Deslocamentos primários, w 1(x), e secundários, w 2(x). Quando a barra, para além dos momentos nas extremidades e cargas transversais ao longo do vão, está também sujeita a esforços de compressão, desenvolvem-se acréscimos de momentos flectores, os quais se designam por momentos secundários M 2 (x) (ver figura 4.1b). Estes acréscimos de momentos resultam da excentricidade da carga aplicada relativamente ao eixo da barra na configuração deformada. Aos momentos secundários estão associados acréscimos de deslocamentos que se designam por deslocamentos secundários w 2 (x). Note-se que, quando os momentos primários tendem para zero, a viga-coluna reduz-se a uma coluna à compressão axial. Quando o esforço axial se anula, o problema reduz-se ao das vigas sujeitas ou não à encurvadura lateral por flexão-torção, dependendo do travamento lateral das vigas. 49
53 Neste capítulo apresenta-se a análise e a verificação da segurança de vigas-colunas sem ter em consideração a encurvadura lateral por flexão-torção, ou seja, admitindo-se que os travamentos dos elementos estruturais impedem a sua encurvadura no modo de flexãotorção Análise de vigas-colunas em regime elástico Considere-se a viga-coluna representada na figura 4.1b. Em cada secção a relação entre o momento flector total M(x) e a curvatura é dada por M(x) = -EΙ d2 w dx 2 (4.1) Por outro lado, o momento total na secção é igual à soma do momento primário M 1 (x) com o momento secundário M 2 (x). Este último é função do esforço axial P e do deslocamento transversal w(x), tendo-se por equilíbrio M(x) = M 1 (x) + P w(x) (4.2) Substituindo a relação entre o momento e a curvatura na equação de equilíbrio, obtém-se EΙ d2 w dx 2 + P w(x) = - M 1(x) (4.3) Note-se que esta equação é muito semelhante à equação 3.30 obtida na análise dos efeitos da imperfeições geométricas no comportamento de colunas, correspondendo o efeito dos momentos primários numa viga-coluna ao efeito das imperfeições geométricas numa coluna. Tendo em consideração o parâmetro k= P/EΙ, já definido anteriormente, obtém-se d 2 w dx 2 +k2 w(x) = - M 1(x) EI (4.4) A solução desta equação diferencial é da forma w(x) = A sen(kx) + B cos(kx) + f(x) (4.5) em f(x) é uma função dependente de M 1 (x) e as constantes A e B são determinadas impondo as condições de fronteira (w(0)=w(l)=0). 50
54 A introdução das condições de fronteira na solução da equação diferencial conduz a um resultado para o qual se pode admitir, no caso geral, a seguinte aproximação para o deslocamento máximo [1,2,5] w max w 1.max P/P E (4.6) em que w 1.max representa o deslocamento máximo devido aos momentos primários e P E representa a carga de Euler da coluna. O factor P/P E (4.7) representa o factor de amplificação dos deslocamentos primários, ou seja tem um significado semelhante ao factor de amplificação das imperfeições geométricas de uma coluna apresentado no capítulo referente à estabilidade de colunas. Admitindo que o deslocamento e o momento primário máximos se verificam na mesma secção, o momento total máximo é aproximadamente dado por M max M 1.max + P w max (4.8) Introduzindo nesta equação a aproximação do deslocamento máximo dada pela equação (4.6), obtém-se M max M 1.max 1 + ψ P/P E 1 - P/P E com ψ = P E w 1.max M 1.max - 1 (4.9) O coeficiente 1 + ψ P/P E 1 - P/P E que afecta o momento primário máximo (M 1.max ) designa-se por factor de amplificação dos momentos. Exemplo 4.1: Considere-se a viga-coluna solicitada apenas por momentos nas extremidades representada na figura 4.2. Os momentos primários são uniformes ao longo do vão (M 1(x)=M 1), sendo a flecha máxima devida a esses momentos dada por w 1.max = M1L2 8EΙ Tendo em consideração que se trata de uma viga-coluna simplesmente apoiada, a carga crítica é dada por P E = π2 EΙ L 2 pelo que se tem ψ = π2 L 2 EΙ M 1 M 1L 2 8EΙ - 1 = π2 8-1 = 0,233 51
55 Para outros tipos de carregamento a determinação do coeficiente ψ pode ser efectuada de forma análoga à apresentada no exemplo anterior. Na figura 4.2 apresentam-se os valores do coeficiente ψ para diferentes tipos de carregamento. Carga de Euler Solicitação ψ Simplesmente apoiada +0,233 P E = π2 EI L 2-0,178 +0,028-0,180 Biencastrada P E = 4π2 EI L 2 +0,200 Figura Valores do coeficiente ψ para diferentes tipos de carregamento e de condições de fronteira. 52
DISCIPLINA DE ESTRUTURAS METÁLICAS
 DECivil Departamento de Engenharia Civil e Arquitectura DISCIPLINA DE ESTRUTURAS METÁLICAS Estabilidade de Estruturas. Colunas e Vigas-colunas Francisco Virtuoso 2009/10 v5_2009 Nota Introdutória Este
DECivil Departamento de Engenharia Civil e Arquitectura DISCIPLINA DE ESTRUTURAS METÁLICAS Estabilidade de Estruturas. Colunas e Vigas-colunas Francisco Virtuoso 2009/10 v5_2009 Nota Introdutória Este
DISCIPLINA DE ESTRUTURAS METÁLICAS
 DECivil Departamento de Engenharia Civil e Arquitectura DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 INDÍCE 1. Esforço axial e flexão em regime elástico. Revisão
DECivil Departamento de Engenharia Civil e Arquitectura DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 INDÍCE 1. Esforço axial e flexão em regime elástico. Revisão
Disciplina de Estruturas Metálicas
 DECivil Departamento de Engenharia Civil e rquitectura Disciplina de Estruturas Metálicas ulas de roblemas rof. Francisco Virtuoso rof. Eduardo ereira 009/010 Capítulo 3 Encurvadura de colunas roblema
DECivil Departamento de Engenharia Civil e rquitectura Disciplina de Estruturas Metálicas ulas de roblemas rof. Francisco Virtuoso rof. Eduardo ereira 009/010 Capítulo 3 Encurvadura de colunas roblema
Resistência dos Materiais, MA, IST,
 11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
DISCIPLINA DE ESTRUTURAS METÁLICAS
 DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 (Versão revista em Outubro de 2012) INDÍCE Nota introdutória.... ii 1. Esforço axial e flexão em regime elástico.
DISCIPINA DE ESTRUTURAS METÁICAS Análise Plástica de Estruturas Francisco Virtuoso 2008/09 (Versão revista em Outubro de 2012) INDÍCE Nota introdutória.... ii 1. Esforço axial e flexão em regime elástico.
CAPÍTULO IV ASPECTOS NORMATIVOS PARA CONTENTORES
 CAPÍTULO IV ASPECTOS NORMATIVOS PARA CONTENTORES 4.1 Introdução Neste capítulo, apresentam-se as disposições normativas dos eurocódigos estruturais que podem ser usadas para verificar a segurança dos elementos
CAPÍTULO IV ASPECTOS NORMATIVOS PARA CONTENTORES 4.1 Introdução Neste capítulo, apresentam-se as disposições normativas dos eurocódigos estruturais que podem ser usadas para verificar a segurança dos elementos
Instabilidade Estrutural
 Instabilidade Estrutural Estruturas Aeroespaciais I (1036) 014 Tópicos Contextualização do problema em estruturas aeronáuticas Instabilidade em colunas e vigas Efeito de imperfeições iniciais Aspetos de
Instabilidade Estrutural Estruturas Aeroespaciais I (1036) 014 Tópicos Contextualização do problema em estruturas aeronáuticas Instabilidade em colunas e vigas Efeito de imperfeições iniciais Aspetos de
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/ Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 14ª Aula Duração - Horas Data - 13 de Novembro de 003 Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão
1/ Resistência dos Materiais 003/004 Curso de Gestão e Engenharia Industrial 14ª Aula Duração - Horas Data - 13 de Novembro de 003 Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão
Estruturas de Aço e Madeira Aula 05 Peças de Aço Comprimidas
 Estruturas de Aço e Madeira Aula 05 Peças de Aço Comprimidas - Compressão e Flambagem - Flambagem por Flexão (Global) - Dimensionamento conforme a Norma (Sem Flambagem Local) Prof. Juliano J. Scremin 1
Estruturas de Aço e Madeira Aula 05 Peças de Aço Comprimidas - Compressão e Flambagem - Flambagem por Flexão (Global) - Dimensionamento conforme a Norma (Sem Flambagem Local) Prof. Juliano J. Scremin 1
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Fundamentos de Mecânica dos Materiais
 Fundamentos de Mecânica dos Materiais - Estabilidade de estruturas Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva -, R.C. Hibbeler Índice
Fundamentos de Mecânica dos Materiais - Estabilidade de estruturas Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva -, R.C. Hibbeler Índice
Universidade de Coimbra Faculdade de Ciências e Tecnologia 2001/02 Estruturas II (aulas teóricas)
 Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
Sumário da 1ª lição: Sumário da 2ª lição: - Apresentação. - Objectivos da Disciplina. - Programa. - Avaliação. - Bibliografia. - Método dos Deslocamentos. - Introdução. - Grau de Indeterminação Cinemática.
MEMÓRIA DE CÁLCULO. Figura 1 - Dimensões e eixos considerados no provete submetido a ensaio.
 MEMÓRIA DE CÁLCULO ENSAIO EM LABORATÓRIO O ensaio experimental tem como objetivo determinar a contribuição da resina epóxido para o comportamento estrutural do tabuleiro e garantir a fiabilidade do modelo
MEMÓRIA DE CÁLCULO ENSAIO EM LABORATÓRIO O ensaio experimental tem como objetivo determinar a contribuição da resina epóxido para o comportamento estrutural do tabuleiro e garantir a fiabilidade do modelo
Verificação da Segurança de Pilares de Betão Armado em Pontes
 Verificação da Segurança de Pilares de Betão Armado em Pontes Carla Marchão Francisco Virtuoso Maio de 2007.: 1 Objectivos Implementação de uma metodologia de verificação da segurança de elementos comprimidos
Verificação da Segurança de Pilares de Betão Armado em Pontes Carla Marchão Francisco Virtuoso Maio de 2007.: 1 Objectivos Implementação de uma metodologia de verificação da segurança de elementos comprimidos
Sumário e Objectivos. Mecânica dos Sólidos 18ªAula. Lúcia M.J. S. Dinis 2007/2008
 Sumário e Objectivos Sumário: Método da Viga Conjugada. Objectivos da Aula: Ser capaz de determinar a flecha e a inclinação num ponto fazendo uso do Método da Viga Conjugada 1 Viga Flectida Estrutura de
Sumário e Objectivos Sumário: Método da Viga Conjugada. Objectivos da Aula: Ser capaz de determinar a flecha e a inclinação num ponto fazendo uso do Método da Viga Conjugada 1 Viga Flectida Estrutura de
2 ANÁLISE ESTÁTICA DA ESTABILIDADE MÉTODO ANALÍTICO.
 ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
ANÁISE ESTÁTICA DA ESTABIIDADE MÉTODO ANAÍTICO. Neste capítulo são apresentados conceitos básicos de estabilidade de estruturas, dando maior ênfase à estabilidade de arcos parabólicos com apoios elásticos
Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada.
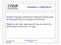 Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada.
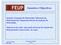 Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Sumário e Objectivos Sumário: Equação da Deformada. Obtenção da Deformada por Integração directa da equação da Deformada. Objectivos da Aula: Apreensão da forma de cálculo dos deslocamentos transversais
Módulo de elasticidade ou módulo de Young
 CAPÍTULO FLEXÃO DE VIGA Antecedendo a apresentação da formulação de diversos tipos de elementos de viga, efectua-se em seguida uma revisão dos fundamentos da flexão de vigas. Apenas são consideradas as
CAPÍTULO FLEXÃO DE VIGA Antecedendo a apresentação da formulação de diversos tipos de elementos de viga, efectua-se em seguida uma revisão dos fundamentos da flexão de vigas. Apenas são consideradas as
Nota de aula 15 - Flambagem
 Nota de aula 15 - Flambagem Flávia Bastos (retirado da apostila do rof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 1o. semestre de 2011 Flávia Bastos RESMAT II 1/22 Informações sobre este documento:
Nota de aula 15 - Flambagem Flávia Bastos (retirado da apostila do rof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF 1o. semestre de 2011 Flávia Bastos RESMAT II 1/22 Informações sobre este documento:
ESTRUTURAS DE BETÃO ARMADO I 12 EFEITOS DE SEGUNDA ORDEM PROVOCADOS POR ESFORÇO AXIAL
 fct - UL EFEITOS DE SEGUDA ORDE PROVOCADOS POR ESFORÇO AXIAL EFEITOS DE SEGUDA ORDE PROVOCADOS POR ESFORÇO AXIAL PROGRAA. Introdução ao betão armado. Bases de Projecto e Acções 3. Propriedades dos materiais:
fct - UL EFEITOS DE SEGUDA ORDE PROVOCADOS POR ESFORÇO AXIAL EFEITOS DE SEGUDA ORDE PROVOCADOS POR ESFORÇO AXIAL PROGRAA. Introdução ao betão armado. Bases de Projecto e Acções 3. Propriedades dos materiais:
Capítulo 5 Carga Axial
 Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Elementos Finitos 2014/2015 Colectânea de trabalhos, exames e resoluções
 Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Anexo 4. Resistência dos Materiais I (2º ano; 2º semestre) Objetivos. Programa
 Resistência dos Materiais I (2º ano; 2º semestre) Objetivos O aluno deverá ficar apto a conhecer os fundamentos do comportamento mecânico de sólidos deformáveis sujeitos a acções exteriores e, em particular
Resistência dos Materiais I (2º ano; 2º semestre) Objetivos O aluno deverá ficar apto a conhecer os fundamentos do comportamento mecânico de sólidos deformáveis sujeitos a acções exteriores e, em particular
1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional = 4200 knm²
 CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
8 FLAMBAGEM 8.1 ESTABILIDADE DE ESTRUTURAS
 8 FLAMBAGEM É o fenômeno que ocorre quando uma carga axial de compressão, atuando em uma barra, ocasiona uma flexão lateral, na direção do menor raio de giração de sua seção transversal, rompendo a peça
8 FLAMBAGEM É o fenômeno que ocorre quando uma carga axial de compressão, atuando em uma barra, ocasiona uma flexão lateral, na direção do menor raio de giração de sua seção transversal, rompendo a peça
RESISTÊNCIA DOS MATERIAIS II
 SEÇÃO DE ESTRUTURS DERTMENTO DE ENGENHRI IVI FUDDE DE IÊNIS E TENOOGI UNIVERSIDDE NOV DE ISO RESISTÊNI DOS MTERIIS II roblemas 1. Flexão lástica 2. orte 3. Torção 4. Solicitações ompostas e Verificação
SEÇÃO DE ESTRUTURS DERTMENTO DE ENGENHRI IVI FUDDE DE IÊNIS E TENOOGI UNIVERSIDDE NOV DE ISO RESISTÊNI DOS MTERIIS II roblemas 1. Flexão lástica 2. orte 3. Torção 4. Solicitações ompostas e Verificação
P-Δ deslocamentos horizontais dos nós da estrutura ou efeitos globais de segunda ordem;
 3 Estabilidade e Análise Estrutural O objetivo da análise estrutural é determinar os efeitos das ações na estrutura (esforços normais, cortantes, fletores, torsores e deslocamentos), visando efetuar verificações
3 Estabilidade e Análise Estrutural O objetivo da análise estrutural é determinar os efeitos das ações na estrutura (esforços normais, cortantes, fletores, torsores e deslocamentos), visando efetuar verificações
Licenciatura em Engenharia Civil MECÂNICA I
 Licenciatura em Engenharia ivil MEÂNI I Recurso 22/07/2002 NOME: 1) (3 L.) a) O que é um mecanismo? Refira as condições de ligação deste tipo de sistema. Um mecanismo é um sistema hipoestático, isto é,
Licenciatura em Engenharia ivil MEÂNI I Recurso 22/07/2002 NOME: 1) (3 L.) a) O que é um mecanismo? Refira as condições de ligação deste tipo de sistema. Um mecanismo é um sistema hipoestático, isto é,
Disciplina de Estruturas Metálicas
 Disciplina de Estruturas Metálicas Aulas de Problemas Prof. Francisco Virtuoso Prof. Eduardo Pereira Prof. Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 2 versão de
Disciplina de Estruturas Metálicas Aulas de Problemas Prof. Francisco Virtuoso Prof. Eduardo Pereira Prof. Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 2 versão de
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
, Equação ESFORÇO NORMAL SIMPLES 3.1 BARRA CARREGADA AXIALMENTE
 3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
3 ESFORÇO NORMAL SIMPLES O esforço normal simples ocorre quando na seção transversal do prisma atua uma força normal a ela (resultante) e aplicada em seu centro de gravidade (CG). 3.1 BARRA CARREGADA AXIALMENTE
Esforços Elementares em Peças Lineares
 CAPÍTULO III Esforços Elementares em Peças Lineares SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/13 Capitulo III Esforços Elementares em Peças Lineares 3.1 Definição dos esforços elementares Uma estrutura
CAPÍTULO III Esforços Elementares em Peças Lineares SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/13 Capitulo III Esforços Elementares em Peças Lineares 3.1 Definição dos esforços elementares Uma estrutura
estável indiferente instável
 UNIVESIE NOV E LISO FULE E IÊNIS E TENOLOGI USO E LIENITU EM ENGENHI GEOLÓGI esistência de Materiais (LEG): º teste Semestre par 005/00, de Junho 00, duração,5h PTE TEÓI (nota mínima valores) nota inferior
UNIVESIE NOV E LISO FULE E IÊNIS E TENOLOGI USO E LIENITU EM ENGENHI GEOLÓGI esistência de Materiais (LEG): º teste Semestre par 005/00, de Junho 00, duração,5h PTE TEÓI (nota mínima valores) nota inferior
Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial.
 Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Carga última de pilares de betão armado em situação de incêndio
 Encontro Nacional BETÃO ESTRUTURAL - BE2012 FEUP, 24-26 de outubro de 2012 Carga última de pilares de betão armado em situação de incêndio V. Dias da Silva 1 M.H.F.M. Barros 2 C. Ferreira 3 RESUMO Os elementos
Encontro Nacional BETÃO ESTRUTURAL - BE2012 FEUP, 24-26 de outubro de 2012 Carga última de pilares de betão armado em situação de incêndio V. Dias da Silva 1 M.H.F.M. Barros 2 C. Ferreira 3 RESUMO Os elementos
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I. Capítulo 6 Flexão
 Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
ESTRUTURAS METÁLICAS E DE MADEIRAS PROF.: VICTOR MACHADO
 ESTRUTURAS METÁLICAS E DE MADEIRAS PROF.: VICTOR MACHADO UNIDADE II - ESTRUTURAS METÁLICAS VIGAS DE ALMA CHEIA INTRODUÇÃO No projeto no estado limite último de vigas sujeitas à flexão simples calculam-se,
ESTRUTURAS METÁLICAS E DE MADEIRAS PROF.: VICTOR MACHADO UNIDADE II - ESTRUTURAS METÁLICAS VIGAS DE ALMA CHEIA INTRODUÇÃO No projeto no estado limite último de vigas sujeitas à flexão simples calculam-se,
Elementos de Engenharia Civil Módulo de Mecânica Estrutural (1º módulo) Apontamentos das aulas (T/P)
 DEPARTAMENTO DE ENGENHARIA CIVIL, ARQUITECTURA E GEORRECURSOS SECÇÃO DE MECÂNICA ESTRUTURAL E ESTRUTURAS Elementos de Engenharia Civil Módulo de Mecânica Estrutural (1º módulo) Apontamentos das aulas (T/P)
DEPARTAMENTO DE ENGENHARIA CIVIL, ARQUITECTURA E GEORRECURSOS SECÇÃO DE MECÂNICA ESTRUTURAL E ESTRUTURAS Elementos de Engenharia Civil Módulo de Mecânica Estrutural (1º módulo) Apontamentos das aulas (T/P)
Construções Metálicas I AULA 5 Compressão
 Universidade Federal de Ouro Preto Escola de Minas Ouro Preto - MG Construções Metálicas I AULA 5 Compressão Introdução Denomina-se coluna uma peça vertical sujeita à compressão centrada. Exemplos de peças
Universidade Federal de Ouro Preto Escola de Minas Ouro Preto - MG Construções Metálicas I AULA 5 Compressão Introdução Denomina-se coluna uma peça vertical sujeita à compressão centrada. Exemplos de peças
Sumário e Objectivos. Mecânica dos Sólidos não Linear Capítulo 2. Lúcia Dinis 2005/2006
 Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Sumário e Objectivos Sumário: Deformações. Sólido Uniaxial. Descrição Lagrangeana e Euleriana. Gradiente de Deformação. Decomposição Polar. Tensores das Deformações de Green e Lagrange. Deformação de Corte.
Turma/curso: 5º Período Engenharia Civil Professor: Elias Rodrigues Liah, Engº Civil, M.Sc.
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS I Código: ENG2032 Tópico: ENERGIA DE DEFORMAÇÃO E PRINCÍPIO DA CONSERVAÇÃO DE ENERGIA Turma/curso:
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS I Código: ENG2032 Tópico: ENERGIA DE DEFORMAÇÃO E PRINCÍPIO DA CONSERVAÇÃO DE ENERGIA Turma/curso:
ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano 2º Semestre 6 de Junho de 2011 Responsável: Prof. José Oliveira Pedro
 ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano º Semestre 6 de Junho de 0 Responsável: Prof. José Oliveira Pedro Identifique todas as folhas com o número e nome. Justifique adequadamente todas
ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano º Semestre 6 de Junho de 0 Responsável: Prof. José Oliveira Pedro Identifique todas as folhas com o número e nome. Justifique adequadamente todas
RESISTÊNCIA DOS MATERIAIS II 6º CICLO (EEM 6NA) Profa. Ms. Grace Kelly Quarteiro Ganharul
 RESISTÊNCIA DOS MATERIAIS II 6º CICLO (EEM 6NA) Profa. Ms. Grace Kelly Quarteiro Ganharul gracekellyq@yahoo.com.br grace.ganharul@aedu.com Graduação em Engenharia Mecânica Disciplina: RESISTÊNCIA DOS MATERIAIS
RESISTÊNCIA DOS MATERIAIS II 6º CICLO (EEM 6NA) Profa. Ms. Grace Kelly Quarteiro Ganharul gracekellyq@yahoo.com.br grace.ganharul@aedu.com Graduação em Engenharia Mecânica Disciplina: RESISTÊNCIA DOS MATERIAIS
DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH)
 DEPARTAMENTO DE ENGENHARIA CIVIL TEORIA DE ESTRUTURAS II 009/010 8º Semestre DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH) Problema 1 Uma mesa pesada é suportada por quatro pernas de
DEPARTAMENTO DE ENGENHARIA CIVIL TEORIA DE ESTRUTURAS II 009/010 8º Semestre DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH) Problema 1 Uma mesa pesada é suportada por quatro pernas de
4 Modelo analítico 84
 4 Modelo analítico 84 4 Modelo analítico O objetivo desta seção é apresentar uma metodologia de cálculo que servirá de base comparativa aos resultados dos métodos de elementos finitos empregados na seção
4 Modelo analítico 84 4 Modelo analítico O objetivo desta seção é apresentar uma metodologia de cálculo que servirá de base comparativa aos resultados dos métodos de elementos finitos empregados na seção
DIMENSIONAMENTO DE BARRA COMPRIMIDAS
 UNIVERSIDADE FEDERAL DOS VALES DO JEQUITINHONHA E MUCURI INSTITUTO DE CIÊNCIA, ENGENHARIA E TECNOLOGIA ENGENHARIA CIVIL ECV 113 ESTRUTURAS DE CONCRETO, METÁLICAS E DE MADEIRA DIMENSIONAMENTO DE BARRA COMPRIMIDAS
UNIVERSIDADE FEDERAL DOS VALES DO JEQUITINHONHA E MUCURI INSTITUTO DE CIÊNCIA, ENGENHARIA E TECNOLOGIA ENGENHARIA CIVIL ECV 113 ESTRUTURAS DE CONCRETO, METÁLICAS E DE MADEIRA DIMENSIONAMENTO DE BARRA COMPRIMIDAS
Tensões associadas a esforços internos
 Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 00. Esforços axiais e tensões
Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 00. Esforços axiais e tensões
26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia
 Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 010 Associação Brasileira de Métodos Computacionais em Engenharia Um Estudo sobre a Validade da Hipótese de Pequenos Deslocamentos em Projetos
Estruturas de Betão Armado II 12 Método das Escores e Tirantes
 Estruturas de Betão Armado II 12 Método das Escores e Tirantes 1 INTRODUÇÃO Método de análise de zonas de descontinuidade, baseado no Teorema Estático da Teoria da Plasticidade. Este método permite obter
Estruturas de Betão Armado II 12 Método das Escores e Tirantes 1 INTRODUÇÃO Método de análise de zonas de descontinuidade, baseado no Teorema Estático da Teoria da Plasticidade. Este método permite obter
Sergio Persival Baroncini Proença
 ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
ula n.4 : ESTUDO D FLEXÃO São Carlos, outubro de 001 Sergio Persival Baroncini Proença 3-) ESTUDO D FLEXÃO 3.1 -) Introdução No caso de barras de eixo reto e com um plano longitudinal de simetria, quando
Licenciatura em Engenharia Civil MECÂNICA II
 NOME: Não esqueça 1) (4 VAL.) de escrever o nome a) Uma partícula descreve um movimento no espaço definido pelas seguintes trajectória e lei horária: z + y 1 = 2 t = y = x + y 1 = (... e ) y s = 2 t Caracterize-o
NOME: Não esqueça 1) (4 VAL.) de escrever o nome a) Uma partícula descreve um movimento no espaço definido pelas seguintes trajectória e lei horária: z + y 1 = 2 t = y = x + y 1 = (... e ) y s = 2 t Caracterize-o
Equações diferenciais
 Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Objetivo: Determinar a equação da curva de deflexão e também encontrar deflexões em pontos específicos ao longo do eixo da viga.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
ANÁLISE DE ESTRUTURAS I Ano lectivo de 2018/2019 2º Semestre
 Exercício 6 - Método dos Deslocamentos ANÁLISE DE ESTRUTURAS I Ano lectivo de 018/019 º Semestre Problema 1 (1 de Janeiro de 000) Considere o pórtico e a acção representados na figura 1. 1.a) Indique o
Exercício 6 - Método dos Deslocamentos ANÁLISE DE ESTRUTURAS I Ano lectivo de 018/019 º Semestre Problema 1 (1 de Janeiro de 000) Considere o pórtico e a acção representados na figura 1. 1.a) Indique o
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
ESTRUTURAS DE BETÃO 2. 9 de Julho de 2007 Época de Recurso Duração: 3h
 Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE BETÃO 2 9 de Julho de 2007 Época de Recurso Duração: 3h Notas importantes: Responda com precisão e de forma
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE BETÃO 2 9 de Julho de 2007 Época de Recurso Duração: 3h Notas importantes: Responda com precisão e de forma
CIR CIR CIR m CIR 12 CIR 1. Estruturas reticuladas simples Problema
 Estruturas reticuladas simples roblema C B 4 A 3 4 m Calcule todas as reacções externas. As forças aplicadas actuam no meio das barras. Resolução (verificação da estatia: Estática) H A: libertação e a
Estruturas reticuladas simples roblema C B 4 A 3 4 m Calcule todas as reacções externas. As forças aplicadas actuam no meio das barras. Resolução (verificação da estatia: Estática) H A: libertação e a
Solução
 Uma barra homogênea e de secção constante encontra-se apoiada pelas suas extremidades sobre o chão e contra uma parede. Determinar o ângulo máximo que a barra pode formar com o plano vertical para que
Uma barra homogênea e de secção constante encontra-se apoiada pelas suas extremidades sobre o chão e contra uma parede. Determinar o ângulo máximo que a barra pode formar com o plano vertical para que
Estabilidade de Colunas de Nós com Deslocamentos Parcialmente Restringidos
 Miguel Sarmento Peres Licenciado em Ciências de Engenharia Civil Estabilidade de Colunas de Nós com Deslocamentos Parcialmente Restringidos Dissertação para obtencão do Grau de Mestre em Engenharia Civil
Miguel Sarmento Peres Licenciado em Ciências de Engenharia Civil Estabilidade de Colunas de Nós com Deslocamentos Parcialmente Restringidos Dissertação para obtencão do Grau de Mestre em Engenharia Civil
DISCIPLINA DE ESTRUTURAS METÁLICAS
 DECivil Departamento de Engenharia Civil e Arquitectura DISCIPLINA DE ESTRUTURAS METÁLICAS Análise e verificação da segurança de estruturas de aço. Resistência de secções Francisco Virtuoso 011/1 INDÍCE
DECivil Departamento de Engenharia Civil e Arquitectura DISCIPLINA DE ESTRUTURAS METÁLICAS Análise e verificação da segurança de estruturas de aço. Resistência de secções Francisco Virtuoso 011/1 INDÍCE
Instabilidade e Efeitos de 2.ª Ordem em Edifícios
 Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil Capítulo Prof. Romel Dias Vanderlei Instabilidade e Efeitos de 2.ª Ordem em Edifícios Curso: Engenharia Civil Disciplina:
Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil Capítulo Prof. Romel Dias Vanderlei Instabilidade e Efeitos de 2.ª Ordem em Edifícios Curso: Engenharia Civil Disciplina:
Licenciatura em Engenharia Civil MECÂNICA I
 Licenciatura em ngenharia Civil MCÂNICA I 2ª Chamada 08/07/2002 NOM: 1) (3 AL.) a) erifique se o sistema articulado plano ilustrado na figura é globalmente isostático. ustifique. O sistema ilustrado na
Licenciatura em ngenharia Civil MCÂNICA I 2ª Chamada 08/07/2002 NOM: 1) (3 AL.) a) erifique se o sistema articulado plano ilustrado na figura é globalmente isostático. ustifique. O sistema ilustrado na
UNIVERSIDADE NOVA DE LISBOA FACULDADE DE CIÊNCIAS E TECNOLOGIA CURSO DE LICENCIATURA EM ENGENHARIA GEOLÓGICA
 UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
Teoria da Membrana. Cascas de Revolução 9.1. Capítulo 9
 Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Teoria da Membrana. Cascas de evolução 9. Capítulo 9 Teoria de Membrana. Cascas de evolução 9. Sistema de Eixos Uma casca de revolução tem uma superfície média que forma uma superfície de revolução. Esta
Engenharia Biomédica EN2310 MODELAGEM, SIMULAÇÃO E CONTROLE APLICADOS A SISTEMAS BIOLÓGICOS. Professores: Ronny Calixto Carbonari
 Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Engenharia Biomédica EN310 MODEAGEM, SIMUAÇÃO E CONTROE APICADOS A SISTEMAS BIOÓGICOS Professores: Ronny Calixto Carbonari Janeiro de 013 Método de Elementos Finitos (MEF): Elementos de Treliça Objetivo
Figura 1 Planta e Corte A-B da estrutura de betão armado.
 Problema 1 (9,0 val.) DIMENSIONAMENTO DE ESTRUTURAS Mestrado em Engenharia Civil 4º Ano 2º Semestre 03 de Junho de 2011 Responsável: Prof. Francisco Virtuoso Identifique todas as folhas com o número e
Problema 1 (9,0 val.) DIMENSIONAMENTO DE ESTRUTURAS Mestrado em Engenharia Civil 4º Ano 2º Semestre 03 de Junho de 2011 Responsável: Prof. Francisco Virtuoso Identifique todas as folhas com o número e
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores
 Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
ANÁLISE DE ESTRUTURAS I Ano lectivo de 2015/2016 2º Semestre
 Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 05/06 º Semestre Problema (5 de Novembro de 000) onsidere a estrutura representada na figura. ssuma que todas as barras apresentam a mesma
Exercício - Método das Forças NÁLISE DE ESTRUTURS I no lectivo de 05/06 º Semestre Problema (5 de Novembro de 000) onsidere a estrutura representada na figura. ssuma que todas as barras apresentam a mesma
Disciplina de Estruturas Metálicas
 Disciplina de Estruturas Metálicas Aulas de Problemas Francisco Virtuoso, Eduardo Pereira e Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 4 versão de 2009/2010 Capítulo
Disciplina de Estruturas Metálicas Aulas de Problemas Francisco Virtuoso, Eduardo Pereira e Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 4 versão de 2009/2010 Capítulo
2 Formulação do Problema
 Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Formulação do Problema Neste capítulo apresenta-se a formulação para a obtenção do funcional de energia de deformação usando tanto uma formulação linear quanto não-linear objetivando a obtenção das equações
Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial.
 Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
5 Exemplos Numéricos do Caso Linear
 56 5 Exemplos Numéricos do Caso Linear Neste capítulo apresenta-se uma série de exemplos numéricos como parte de um estudo paramétrico para avaliar e validar a exatidão do método aproximado perante a solução
56 5 Exemplos Numéricos do Caso Linear Neste capítulo apresenta-se uma série de exemplos numéricos como parte de um estudo paramétrico para avaliar e validar a exatidão do método aproximado perante a solução
Determinação da Carga Crítica de Flambagem em Colunas do Tipo Engastada-Articulada segundo os Métodos de Newton
 Universidade Federal de São João Del-Rei MG 26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia Determinação da Carga Crítica de Flambagem em Colunas do Tipo Engastada-Articulada
Universidade Federal de São João Del-Rei MG 26 a 28 de maio de 2010 Associação Brasileira de Métodos Computacionais em Engenharia Determinação da Carga Crítica de Flambagem em Colunas do Tipo Engastada-Articulada
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Deflexão em vigas de eixo reto
 10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
CIV 1127 ANÁLISE DE ESTRUTURAS II 2º Semestre Terceira Prova 25/11/2002 Duração: 2:30 hs Sem Consulta
 CIV 1127 ANÁISE DE ESTRUTURAS II 2º Semestre 02 Terceira Prova 25/11/02 Duração: 2:30 hs Sem Consulta 1ª Questão (4,0 pontos) Para uma viga de ponte, cujo modelo estrutural é apresentado abaixo, calcule
CIV 1127 ANÁISE DE ESTRUTURAS II 2º Semestre 02 Terceira Prova 25/11/02 Duração: 2:30 hs Sem Consulta 1ª Questão (4,0 pontos) Para uma viga de ponte, cujo modelo estrutural é apresentado abaixo, calcule
CURSO DE ENGENHARIA CIVIL. Professor: Elias Rodrigues Liah, Engº Civil, M.Sc. Goiânia HIPERESTÁTICA
 CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS Tópico: Professor: Elias Rodrigues Liah, Engº Civil, M.Sc. Goiânia - 2014 O projeto estrutural tem como objetivo a concepção de uma estrutura
CURSO DE ENGENHARIA CIVIL Disciplina: TEORIA DAS ESTRUTURAS Tópico: Professor: Elias Rodrigues Liah, Engº Civil, M.Sc. Goiânia - 2014 O projeto estrutural tem como objetivo a concepção de uma estrutura
6.00 m. z (y) 3.00 m. 920 kn. 15 kn/m. Secção transversal do pilar A-B. (x) SHS 200x150x8 mm 1/29
 VIGA-OLUA Exemo : onsidere a viga-coluna A-B de suporte de um balanço B- representado na Figura abaixo A coluna é engastada na seção da base sendo a seção do topo (seção B) livre de rodar mas impedida
VIGA-OLUA Exemo : onsidere a viga-coluna A-B de suporte de um balanço B- representado na Figura abaixo A coluna é engastada na seção da base sendo a seção do topo (seção B) livre de rodar mas impedida
Lista de Exercício 3 Elastoplasticidade e Análise Liimite 18/05/2017. A flexão na barra BC ocorre no plano de maior inércia da seção transversal.
 Exercício 1 Para o sistema estrutural da figura 1a, para o qual os diagramas de momento fletor em AB e força normal em BC da solução elástica são indicados na figura 1b, estudar pelo método passo-a-passo
Exercício 1 Para o sistema estrutural da figura 1a, para o qual os diagramas de momento fletor em AB e força normal em BC da solução elástica são indicados na figura 1b, estudar pelo método passo-a-passo
PILARES EM CONCRETO ARMADO
 PILARES EM CONCRETO ARMADO DIMENSIONAMENTO E DETALHAMENTO Pilares Elementos lineares de eixo reto, usualmente dispostos na vertical, em que as forças normais de compressão são preponderantes. (ABNT NBR
PILARES EM CONCRETO ARMADO DIMENSIONAMENTO E DETALHAMENTO Pilares Elementos lineares de eixo reto, usualmente dispostos na vertical, em que as forças normais de compressão são preponderantes. (ABNT NBR
2.1 Translação, rotação e deformação da vizinhança elementar Variação relativa do comprimento (Extensão)
 Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
(1)P Para efeitos do projecto sismo-resistente, as estruturas dos edifícios são classificadas em regulares e não regulares.
 4.2.3 Critérios de regularidade estrutural 4.2.3.1 Generalidades (1)P Para efeitos do projecto sismo-resistente, as estruturas dos edifícios são classificadas em regulares e não regulares. NOTA: Nas estruturas
4.2.3 Critérios de regularidade estrutural 4.2.3.1 Generalidades (1)P Para efeitos do projecto sismo-resistente, as estruturas dos edifícios são classificadas em regulares e não regulares. NOTA: Nas estruturas
ANÁLISE DE ESTRUTURAS II
 DECivil ANÁLISE DE ESTRUTURAS II INTRODUÇÃO À ANÁLISE LIMITE DE LAJES Orlando J B A ereira 005 1 Introdução Em geral, pretende-se que as estruturas tenham um comportamento linear nas situações usuais de
DECivil ANÁLISE DE ESTRUTURAS II INTRODUÇÃO À ANÁLISE LIMITE DE LAJES Orlando J B A ereira 005 1 Introdução Em geral, pretende-se que as estruturas tenham um comportamento linear nas situações usuais de
Agrupamento de Escolas da Senhora da Hora
 Agrupamento de Escolas da Senhora da Hora Curso Profissional de Técnico de Multimédia Informação Prova da Disciplina de Física - Módulo: 1 Forças e Movimentos; Estática Modalidade da Prova: Escrita Ano
Agrupamento de Escolas da Senhora da Hora Curso Profissional de Técnico de Multimédia Informação Prova da Disciplina de Física - Módulo: 1 Forças e Movimentos; Estática Modalidade da Prova: Escrita Ano
6 Exemplos Numéricos no Domínio da Frequência
 145 6 Exemplos Numéricos no Domínio da Frequência Neste Capítulo são apresentados exemplos numéricos para validar a formulação apresentada no Capítulo 5, assim como estudar a resposta em frequência de
145 6 Exemplos Numéricos no Domínio da Frequência Neste Capítulo são apresentados exemplos numéricos para validar a formulação apresentada no Capítulo 5, assim como estudar a resposta em frequência de
FESP Faculdade de Engenharia São Paulo. Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr.
 FESP Faculdade de Engenharia São Paulo Avaliação: A2 Data: 15/set/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Duração: 85 minutos Nome: Matrícula
FESP Faculdade de Engenharia São Paulo Avaliação: A2 Data: 15/set/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Duração: 85 minutos Nome: Matrícula
Aula 04 MÉTODO DAS FORÇAS. Classi cação das estruturas quanto ao seu equilíbrio estático. ² Isostática:
 Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Universidade Federal do Ceará Centro de Tecnologia Departamento de Engenharia Estrutural e Construção Civil Disciplina: Análise Matricial de Estruturas Professor: Antônio Macário Cartaxo de Melo Aula 04
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
MECÂNICA DO CONTÍNUO. Tópico 3. Método dos Trabalhos Virtuais
 MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. eer E. Russell Johnston, Jr. Deflexão de Vigas por Integração Capítulo 7 Deflexão de Vigas por Integração 7.1 Introdução 7. Deformação de
Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. eer E. Russell Johnston, Jr. Deflexão de Vigas por Integração Capítulo 7 Deflexão de Vigas por Integração 7.1 Introdução 7. Deformação de
Resistência de Materiais I
 Resistência de Materiais I no ectivo 00/004 º exame de Janeiro de 004 uração: horas Oservações: Não podem ser consultados quaisquer elementos de estudo para além do formulário fornecido. Resolver os prolemas
Resistência de Materiais I no ectivo 00/004 º exame de Janeiro de 004 uração: horas Oservações: Não podem ser consultados quaisquer elementos de estudo para além do formulário fornecido. Resolver os prolemas
7 Exemplos Numéricos do Caso Não-Linear
 84 7 Exemplos Numéricos do Caso Não- Neste capítulo é apresentada uma série de exemplos numéricos mostrando a influência da não-linearidade da fundação na resposta do sistema, tanto para o caso de resposta
84 7 Exemplos Numéricos do Caso Não- Neste capítulo é apresentada uma série de exemplos numéricos mostrando a influência da não-linearidade da fundação na resposta do sistema, tanto para o caso de resposta
Barras prismáticas submetidas a momento fletor e força cortante
 Barras prismáticas submetidas a momento fletor e força cortante Introdução Os esforços mais comuns de incidência em vigas estruturais são a força cortante e o momento fletor, os quais são causados por
Barras prismáticas submetidas a momento fletor e força cortante Introdução Os esforços mais comuns de incidência em vigas estruturais são a força cortante e o momento fletor, os quais são causados por
Flambagem PROF. ALEXANDRE A. CURY DEPARTAMENTO DE MECÂNICA APLICADA E COMPUTACIONAL
 ROF. ALEXANDRE A. CURY DEARTAMENTO DE MECÂNICA ALICADA E COMUTACIONAL O que é e por que estudar? Onde ocorre? Que fatores influenciam? Como evitar? or que, normalmente, é desejável que a diagonal das treliças
ROF. ALEXANDRE A. CURY DEARTAMENTO DE MECÂNICA ALICADA E COMUTACIONAL O que é e por que estudar? Onde ocorre? Que fatores influenciam? Como evitar? or que, normalmente, é desejável que a diagonal das treliças
2. Revisão Bibliográfica
 . Revisão Bibliográfica.1. Considerações iniciais Neste capítulo é apresentada uma revisão bibliográfica sobre pilares de concreto armado, dividida basicamente em duas partes. A primeira apresenta alguns
. Revisão Bibliográfica.1. Considerações iniciais Neste capítulo é apresentada uma revisão bibliográfica sobre pilares de concreto armado, dividida basicamente em duas partes. A primeira apresenta alguns
