Databases. Dependências Funcionais
|
|
|
- Gabriel Henrique Frade Batista
- 8 Há anos
- Visualizações:
Transcrição
1 Databases Dependências Funcionais P. Serendero, Referências e exemplos tirados de diversas fontes, excetuando aqueles relacionados com embarcações
2 Dependências Funcionais (DF) Uma Base de Dados, para ser um modelo que bem represente a realidade, precisa de de ser depurada de anomalias, redundâncias e outros problemas que se presentam quando operamos nela: inserções, apagar, modificar, interrogar Utilizamos a Teoria da Normalização para fazer esta depuração Na base da normalização, estão as chamadas: Dependências Funcionais Utilizando os conceitos de chaves e dependências funcionais podemos desenhar boas relações numa BD As DF constituem um tipo de restrição de integridade, no desenho de BD
3 Dependências Funcionais Considere a seguinte relação: colaborador(num-empregado,num-projeto, nome-empregado, nome-projeto, num-horas) Anomalias que se podem apresentar: INSERÇÃO: Não se pode inserir um novo projeto, de não ser que um empregado seja atribuído a ele. Inversamente, não se pode inserir um novo empregado sem ter que lhe atribuir um projeto ACTUALIZAÇÃO: se mudarmos o nome dum projeto, vamos ter que atualizar em todos os muitos empregados que colaboram em dito projeto. APAGAR: Se apagarmos um projeto, vamos apagar todos os colaboradores do mesmo Portanto, NÃO É BOA PRÁTICA DE DESENHO, MISTURAR ATRIBUTOS PERTENCENTES A DISTINTAS ENTIDADES NUMA MESMA RELAÇÃO
4 Dependência Funcional Numa relação R, existe DF sse o valor dum conjunto de atributos X determinam o valor preciso dum outro atributo A X A ex: BI nome O conjunto dos atributos X determinam funcionalmente o atributo A (no ex. o nome depende do BI, mas o BI não depende do nome) X: O conjunto determinante A: o atributo dependente Por outras palavras, dados 2 tuplos em R, se os valores de X são os mesmos, então os valores de A devem ser também os mesmos DF é portanto uma declaração sobre todas as relações permitidas: uma restrição. A relação R satisfaz a depêndencia X Y
5 Dependências Funcionais Dependência Funcional Esta relação de dependência funcional também se pode expressar como subconjuntos X1,X2,..,Xm A1,...An ou X Y O símbolo da seta se lê determina, portanto o conjunto X determina o conjunto Y Isto é equivalente a dizer que a projecção π x,y R é uma função, isto é, Y é função de X Nota: A convenção em muitos textos utiliza as letras A,B,C,D, para atributos singulares e as letras X,Y,Z para conjuntos de atributos
6 Dependências Funcionais Portanto, numa tabela representando uma relação R, Se dois tuplos j e m coincidem no valor de todos os seus Tuplos atributos A1A, devem A2 também An coincidir B1em todos B2 os valores B3 dos seus atributos B Tuplo j Tuplo m Se j e m concordam aqui Também devem concordar aqui Efeitos da dependência funcional em dois tuplos Ullman, pag. 119
7 Dependências Funcionais Exemplo: Repare nos conjuntos modelo e comprimento na relação embarcação -mostrada anteriormente- : Existe um dependência entre os valores destes conjuntos. O comprimento é função do modelo. Dado um modelo de embarcação, posso encontrar o comprimento Essa dependência se expressa assim: modelo comprimento modelo Benetton I Hurrican A Benetton II Laser comprimento Isto tem uma aplicação imediata nas conhecidas chaves candidatas: Uma chave candidata é o subconjunto mínimo de atributos que determina todos os atributos numa relação
8 Dependências Funcionais Seria correto escrever a DF: comprimento modelo? Não, porque podem existir diferentes modelos com o mesmo comprimento Da mesma maneira como nome BI indicado anteriormente não é DF porque um mesmo nome (Diana por ex.) não determina um único BI O que quer dizer que se criamos uma relação com estes elementos, modelo seria a chave e comprimento o atributo Como vemos, existe normalmente DF entre a chave e os atributos numa tabela Se K é a chave primária numa relação R, então K determina funcionalmente o valor de cada um dos atributos em R. Em termos de tabelas, nunca temos dois tuplos idênticos, posto que a chave primária é única na tabela
9 Chaves nas relações Um ou mais atributos {A1, A2,...An } formam uma chave numa relação R, se: 1) Aqueles atributos determinam funcionalmente todos os outros atributos nessa relação Por outras palavras, é impossível que dois tuplos em R concordarem no valor de todos os seus atributos {A1, A2,...An } 2) Nenhum subconjunto em {A1, A2,...An } determina funcionalmente todos os outros atributos da relação R. Isto é, uma chave deve ser mínima. A esta denomina-se chave principal ou primária
10 modelo comprimento Dependências Funcionais matricula nome da embarcação num-aluno curso curso nome-curso, data-criação aluno,ano,disciplina, epoca nota Exemplos de DF na relação embarcação BI nome-pessoa Bi NIF NIF BI São estas duas dependências verdadeiras?
11 Dependências Funcionais Outro exemplo: Dada a relação R embarcação(matricula, nome, proprietario, pais, modelo, comprimento, boca, bi_proprietario), e as seguintes dependências funcionais matricula nome, matricula pais, matricula bi_proprietario matricula comprimento Estas dependências são corretas? NÃO!! o BI depende do seu proprietário, e não da matricula do seu barco. Uma pessoa que mude de bi, continuará a ser proprietário da mesma embarcação, identificada pelo número de matrícula A determinação do bi não depende funcionalmente da matrícula do barco Mais uma outra?
12 DF's Portanto um atributo é funcionalmente dependente, se o seu valor é determinado por um outro atributo que é uma CHAVE Se A B logo dado um valor para A só pode existir um valor para B Se A B e B A, logo A e B estão numa relação 1-1 Se A (B,C) logo A B e A C Se (A,B) C, não é necessariamente verdadeiro que A C e B C
13 Regras nas Dependências Funcionais A maneira de pensar sobre as dependências funcionais Splitting rule e combination rule Já foi dito que A1, A2,.., An B1, B2,...Bm isto quer dizer que: A1, A2,.., An B1 A1, A2,.., An B2... A1, A2,.., An Bm Podemos separar os atributos no lado direito tal que só 1 atributo aparece à direita de cada dependência funcional Da mesma maneira podemos substituir uma coleção de dependências com um lado esquerdo comum por uma dependência simples com o mesmo lado esquerdo e todos os lados direitos combinados num só conjunto de atributos X Y
14 Dependências Funcionais Exemplo: o conjunto de dependências: tipo-embarcação, modelo boca tipo-embarcação, modelo comprimento tipo-embarcação, modelo calado são equivalentes a dependência: tipo-embarcação, modelo boca, comprimento, calado Não existe splitting rule para o lado esquerdo da dependência Porque? tipo-embarcação boca modelo boca modelo não determina sozinho o tamanho da boca. E o tipo de embarcação também não. São precisos os dois: superchave
15 Regras nas Dependências Funcionais Em qualquer evento o novo conjunto de dependências é equivalente ao velho. Isto pode ser utilizado de diversas maneiras: substituindo A1, A2,.., An B1,B2,...Bm por A1, A2,.., An Bi para i = 1,2,..,m A esta transformação chama-se splitting rule Podemos substituir as dependências A1, A2,.., An Bi (i = 1,2,..,m) pela dependência simples: A1, A2,.., An B1,B2,...Bm Chamamos esta transformação, combination rule, regra de combinação
16 Dependências triviais Dependências Funcionais A dependência funcional A1, A2,.., An B é considerada TRIVIAL se B pertence a algum subconjunto de A Por exemplo: tipo-embarcação, modelo tipo-embarcação Portanto dependências triviais existem sempre numa relação, posto que dois tuplos que coincidem em todas as A1, A2,.., An também concordam numa delas Dependências não triviais: se pelo menos uma das B não está entre as A Dependências completamente não triviais: se nenhuma das B está entre as A
17 Dependências Funcionais Regras de inferência: propriedades das DF Axiomas de Amstrong: Reflexividade: Se A é um subconjunto de X, logo X A Augmentação: Se X A, logo XZ AZ, (XZ = X Ս Z) Transitividade: Se X A e A B, logo X B Aditividade: Se X Y, Z V, implica X U Z Y U V As primeiras 3 regras formam um conjunto completo de regras de inferência nas relações (U - união)
18 Dependências Funcionais Das regras anteriores pode-se derivar outras regras adicionais de inferência Descomposição União Se X YZ, logo X Y e X Z Se X Y e X Z, logo X YZ, onde (Y U Z) Pseudotransitividade Se X Y e WY Z, logo WX Z
19 Computando o fecho dos atributos Como sabemos se um conjunto de atributos é uma super chave? Computando o fecho dum atributo ajuda-nos a responder esta questão O fecho de Y, escrito como Y+ é o conjunto de todos os atributos X dos quais Y+ depende funcionalmente Numa DF olhemos para o lado esquerdo X. Se este determina igualmente um atributo A, então A vai fazer parte do fecho Y+. O fecho dum conjunto Y de DF é o conjunto Y+ de todas as DF que podem serem inferidas desde Y
20 Computando o fecho dos atributos Algoritmo para calcular o fecho de atributos: Começando com um conjunto de atributos, repetidamente expandimos este conjunto adicionando os lados direitos das DF dadas, na altura que incluirmos os seus lados esquerdos. Eventualmente não podemos expandir mais este conjunto. O conjunto resultante é o FECHO Algoritmo para calcular o fecho de atributos: 1. Y + = Y 2. Se A 1, A 2,..,A m B, adicionar B em Y + (adicionar uma DF) 3. Terminar quando não conseguimos adicionar mais atributos a Y + (como implementava você este algoritmo numa linguagem de programação?)
21 Computando o fecho dos atributos Y+ A B Se o subconjunto A determina um outro atributo B, adicionamos este ao fecho Y+ Novo Y+
22 Fecho dos atributos: exemplo Dada a seguinte relação R (A, B, C, D, E) e dado o seguinte conjunto de DF: A BC CD E B D E A Queremos saber se: A é ou não uma super chave desta R? Computamos o fecho A+ 1. A+ = A 2. ABC // porque A BC 3. ABCD // porque B D 4. ABCDE // porque CD E 5. ABCDE A+ = ABCDE, portanto A é uma super chave em R
23 Fecho dos atributos: exemplo Dada a mesma R (A, B, C, D, E) da página anterior e as mesmas DF: A BC CD E B D E A Será B uma super chave em R? Computamos o fecho B+ 1. B+ = B 2. BD // porque B D 3. BD B+ = BD, portanto B NÃO é uma super chave em R Se K todos os Ai numa R, então K é uma super chave As DF são uma generalização das chaves
24 Fecho de atributos - Exemplo Dado R = (A, B, C, G, H, I) e dadas DF = { A B, A C, CG H, CG I, B H } desejamos saber se AG será uma chave candidata. Portanto AG é uma super chave? ou seja AG+ R? Existe algum subconjunto de AG que seja também uma super chave? A R? é A+?, ou seja é A+ um subconjunto em R? G R? é G+?, ou seja é G+ um subconjunto em R? Para responder calculamos o fecho para AG+ 1) AG+ = AG 2) AGB //por A B 3) AGBC // por A C 4) AGBCH // por CG H 5) AGBCHI // por CG I e CG é subconjunto de AGBCH 6) ABCGHI, portanto AG é uma super chave
25 Dependências Funcionais Exemplo Dada a relação R(ABCDEF ) com as seguintes DF s: AB C BC A BC D D E CF B Qual será o fecho de (AB)+ (AB)+ = AB = ABC, porque AB C = ABCD, porque BC D = ABCDE, porque D E = ABCDE Se (AB)+ ser a chave principal desta relação, então o atributo F não é determinado funcionalmente por AB
26 Dependências funcionais Redundância entre as Dependências A C é redundante em F+ quando {A B, B C} Partes duma DF poderiam ser redundantes No lado ESQUERDO duma regra: {A B, B C, AC D} pode ser simplificada: {A B, B C, A D} No lado DIREITO duma regra: {A B, B C, A CD} Pode ser simplificada: {A B, B C, A D}
27 Dependências Funcionais Fim
Dependências Funcionais
 Dependências Funcionais Fernando Lobo Base de Dados, Universidade do Algarve 1 / 26 Motivação: Normalização Por vezes o esquema relacional tem falhas. Geralmente são derivadas de falhas no modelo conceptual.
Dependências Funcionais Fernando Lobo Base de Dados, Universidade do Algarve 1 / 26 Motivação: Normalização Por vezes o esquema relacional tem falhas. Geralmente são derivadas de falhas no modelo conceptual.
OBJETIVOS. Orientações para Projetos de BD; Dependências Funcionais (DFs): Definição de DF; Regras de inferência para DFs.
 BANCO DE DADOS Universidade do Estado de Santa Catarina Centro de Ciências Tecnológicas Departamento de Ciência da Computação Prof. Alexandre Veloso de Matos alexandre.matos@udesc.br OBJETIVOS Orientações
BANCO DE DADOS Universidade do Estado de Santa Catarina Centro de Ciências Tecnológicas Departamento de Ciência da Computação Prof. Alexandre Veloso de Matos alexandre.matos@udesc.br OBJETIVOS Orientações
Databases. Ferramentas gráficas na modelação lógica das BD. O Modelo Entidade-Relação (Associação) O Modelo de Classes no UML
 Databases Ferramentas gráficas na modelação lógica das BD O Modelo Entidade-Relação (Associação) O Modelo de Classes no UML Databases O Modelo Entidade-Relação ou Entidade-Associação 2 Modelo Entidade-Relação
Databases Ferramentas gráficas na modelação lógica das BD O Modelo Entidade-Relação (Associação) O Modelo de Classes no UML Databases O Modelo Entidade-Relação ou Entidade-Associação 2 Modelo Entidade-Relação
Microsoft Access 2010. Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento
 Microsoft Access 2010 Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento 1 Principais objetos do Access Tabelas Guardam a informação da BD (Base de Dados)
Microsoft Access 2010 Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento 1 Principais objetos do Access Tabelas Guardam a informação da BD (Base de Dados)
Dependências Multi-Valor, 4 a Forma Normal
 Normalização: Dependências Multi-Valor, 4 a Forma Normal Fernando Lobo Base de Dados, Universidade do Algarve 1 / 20 Dependências Multi-Valor (DMV s) DMV dá origem a um tipo de redundância que não está
Normalização: Dependências Multi-Valor, 4 a Forma Normal Fernando Lobo Base de Dados, Universidade do Algarve 1 / 20 Dependências Multi-Valor (DMV s) DMV dá origem a um tipo de redundância que não está
Banco de Dados Lista de Exercícios 01
 Banco de Dados Lista de Exercícios 01 Prof. Anderson Rocha & Prof. André Santanché Campinas, 24 de Setembro de 2012 Nome: RA: 1 Observações Este lista contem 20 exercícios e contempla os seguintes assuntos
Banco de Dados Lista de Exercícios 01 Prof. Anderson Rocha & Prof. André Santanché Campinas, 24 de Setembro de 2012 Nome: RA: 1 Observações Este lista contem 20 exercícios e contempla os seguintes assuntos
RELAÇÕES BINÁRIAS Produto Cartesiano A X B
 RELAÇÕES BINÁRIAS PARES ORDENADOS Um PAR ORDENADO, denotado por (x,y), é um par de elementos onde x é o Primeiro elemento e y é o Segundo elemento do par A ordem é relevante em um par ordenado Logo, os
RELAÇÕES BINÁRIAS PARES ORDENADOS Um PAR ORDENADO, denotado por (x,y), é um par de elementos onde x é o Primeiro elemento e y é o Segundo elemento do par A ordem é relevante em um par ordenado Logo, os
Lógica e Bases de Dados. Prof. Elaine Faria e Hiran Nonato Programação Lógica UFU 2012
 Lógica e Bases de Dados Prof. Elaine Faria e Hiran Nonato Programação Lógica UFU 2012 Bases de Dados Relacionais "Base de dados" Coleção de dados interrelacionados, armazenada de modo independente do programa
Lógica e Bases de Dados Prof. Elaine Faria e Hiran Nonato Programação Lógica UFU 2012 Bases de Dados Relacionais "Base de dados" Coleção de dados interrelacionados, armazenada de modo independente do programa
SISTEMAS DIGITAIS Prof. Ricardo Rodrigues Barcelar http://www.ricardobarcelar.com
 - Aula 3 - ÁLGEBRA BOOLEANA 1. Introdução O ponto de partida para o projeto sistemático de sistemas de processamento digital é a chamada Álgebra de Boole, trabalho de um matemático inglês que, em um livro
- Aula 3 - ÁLGEBRA BOOLEANA 1. Introdução O ponto de partida para o projeto sistemático de sistemas de processamento digital é a chamada Álgebra de Boole, trabalho de um matemático inglês que, em um livro
6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto
 Capítulo 6. Autômatos com Pilha 6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto Nos exemplos da seção anterior, vimos que os autômatos com pilha existem para
Capítulo 6. Autômatos com Pilha 6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto Nos exemplos da seção anterior, vimos que os autômatos com pilha existem para
- O atributo Cursos contém valores não atómicos!!!
 3. Teoria da Normalização 3.1. Dependências Funcionais 3.2. Normalização 3.2.1. Primeira Forma Normal (1FN) Uma relação está na 1ª Forma Normal se. Cada atributo contém apenas valores atómicos.. Não há
3. Teoria da Normalização 3.1. Dependências Funcionais 3.2. Normalização 3.2.1. Primeira Forma Normal (1FN) Uma relação está na 1ª Forma Normal se. Cada atributo contém apenas valores atómicos.. Não há
Aplicações de Combinatória e Geometria na Teoria dos Números
 Aplicações de Combinatória e Geometria na Teoria dos Números Nesse artigo vamos discutir algumas abordagens diferentes na Teoria dos Números, no sentido de envolverem também outras grandes áreas, como
Aplicações de Combinatória e Geometria na Teoria dos Números Nesse artigo vamos discutir algumas abordagens diferentes na Teoria dos Números, no sentido de envolverem também outras grandes áreas, como
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
OBJETIVOS. Orientações para Projetos de BD; Dependências Funcionais (DFs): Definição de DF; Regras de inferência para DFs.
 BANCO DE DADOS Universidade do Estado de Santa Catarina Centro de Ciências Tecnológicas Departamento de Ciência da Computação Prof. Alexandre Veloso de Matos alexandre.matos@udesc.br OBJETIVOS Orientações
BANCO DE DADOS Universidade do Estado de Santa Catarina Centro de Ciências Tecnológicas Departamento de Ciência da Computação Prof. Alexandre Veloso de Matos alexandre.matos@udesc.br OBJETIVOS Orientações
Normalização de Esquemas de Banco de Dados. Prof. Carlos Bazilio bazilio@ic.uff.br
 Normalização de Esquemas de Banco de Dados Prof. Carlos Bazilio bazilio@ic.uff.br Motivação Aluno (matr, nome, cr, cod) Curso (cod, nome, carga_horária) X Aluno (matr, nome, cr, cod, nome_curso, carga_horária)
Normalização de Esquemas de Banco de Dados Prof. Carlos Bazilio bazilio@ic.uff.br Motivação Aluno (matr, nome, cr, cod) Curso (cod, nome, carga_horária) X Aluno (matr, nome, cr, cod, nome_curso, carga_horária)
Tabelas vista de estrutura
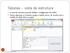 Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
MICROSOFT ACCESS MICROSOFT ACCESS. Professor Rafael Vieira Professor Rafael Vieira
 MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
Projeção ortográfica da figura plana
 A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
Introdução às Bases de Dados
 Chave primária Domínios Relação Normalizada F# F Nome Estado Cidade F1 José 20 Braga F2 João 10 Faro F3 Luís 30 Lisboa F4 Rui 30 Setúbal Atributos Tuplas Modelo Relacional Uma das regras que uma relação
Chave primária Domínios Relação Normalizada F# F Nome Estado Cidade F1 José 20 Braga F2 João 10 Faro F3 Luís 30 Lisboa F4 Rui 30 Setúbal Atributos Tuplas Modelo Relacional Uma das regras que uma relação
Modelo Relacional. Modelo Relacional. Modelo Relacional. Banco de Dados. Modelo Relacional. Modelo Relacional
 Banco de Dados Definido por E F Codd em 1970, teve sua grande aceitação comercial a partir de meados da década de 1980 Razões da grande aceitação Simplicidade dos conceitos básicos Poder dos operadores
Banco de Dados Definido por E F Codd em 1970, teve sua grande aceitação comercial a partir de meados da década de 1980 Razões da grande aceitação Simplicidade dos conceitos básicos Poder dos operadores
SISTEMAS DE BANCO DE DADOS. Prof. Adriano Pereira Maranhão
 SISTEMAS DE BANCO DE DADOS Prof. Adriano Pereira Maranhão 1 Coleção de operações usadas para manipular relações Grupos de operações Operações relacionais Seleção; projeção; junção Operações de conjunto
SISTEMAS DE BANCO DE DADOS Prof. Adriano Pereira Maranhão 1 Coleção de operações usadas para manipular relações Grupos de operações Operações relacionais Seleção; projeção; junção Operações de conjunto
Disciplina: Unidade III: Prof.: E-mail: Período:
 Encontro 08 Disciplina: Sistemas de Banco de Dados Unidade III: Modelagem Lógico de Dados Prof.: Mario Filho E-mail: pro@mariofilho.com.br Período: 5º. SIG - ADM Relembrando... Necessidade de Dados Projeto
Encontro 08 Disciplina: Sistemas de Banco de Dados Unidade III: Modelagem Lógico de Dados Prof.: Mario Filho E-mail: pro@mariofilho.com.br Período: 5º. SIG - ADM Relembrando... Necessidade de Dados Projeto
Profa. Daniela Barreiro Claro
 Profa. Daniela Barreiro Claro Modelar é criar representações do mundo real A modelagem relacional pode ser representada via MER (Modelo de Entidade Relacionamento) O MER define estruturas e restrições
Profa. Daniela Barreiro Claro Modelar é criar representações do mundo real A modelagem relacional pode ser representada via MER (Modelo de Entidade Relacionamento) O MER define estruturas e restrições
O Modelo de Entidades e Relacionamentos (MER) é um modelo conceitual usado para projeto de aplicações de banco de dados.
 Fases do Projeto de um Banco de Dados Modelo ER O Modelo de Entidades e Relacionamentos (MER) é um modelo conceitual usado para projeto de aplicações de banco de dados. É um modelo baseado na percepção
Fases do Projeto de um Banco de Dados Modelo ER O Modelo de Entidades e Relacionamentos (MER) é um modelo conceitual usado para projeto de aplicações de banco de dados. É um modelo baseado na percepção
Roteiro. Modelo de Dados Relacional. Processo de Projeto de Banco de Dados. BCC321 - Banco de Dados I. Ementa. Posicionamento.
 Roteiro Modelo de Dados Relacional Posicionamento Luiz Henrique de Campos Merschmann Departamento de Computação Universidade Federal de Ouro Preto luizhenrique@iceb.ufop.br www.decom.ufop.br/luiz Introdução
Roteiro Modelo de Dados Relacional Posicionamento Luiz Henrique de Campos Merschmann Departamento de Computação Universidade Federal de Ouro Preto luizhenrique@iceb.ufop.br www.decom.ufop.br/luiz Introdução
AJUDA DO FSYNCH. O que o FSynch faz? Como o FSynch funciona?
 AJUDA DO FSYNCH O que o FSynch faz? O FSynch é um programa para sincronizar pastas, ou seja, ele realiza alterações (cria, apaga e altera arquivos) em uma pasta para que ele fique igual a uma outra pasta
AJUDA DO FSYNCH O que o FSynch faz? O FSynch é um programa para sincronizar pastas, ou seja, ele realiza alterações (cria, apaga e altera arquivos) em uma pasta para que ele fique igual a uma outra pasta
MODELO RELACIONAL - UFMA
 MODELO RELACIONAL Universidade Federal do Maranhão - UFMA Departamento de Informática Projeto de Banco de Dados Profª.MSc Simara Rocha simararocha@gmail.com/simara@deinf.ufma.br www.deinf.ufma.br/~simara
MODELO RELACIONAL Universidade Federal do Maranhão - UFMA Departamento de Informática Projeto de Banco de Dados Profª.MSc Simara Rocha simararocha@gmail.com/simara@deinf.ufma.br www.deinf.ufma.br/~simara
Qual é Mesmo a Definição de Polígono Convexo?
 Qual é Mesmo a Definição de Polígono Convexo? Elon Lages Lima IMPA, Rio de Janeiro Quando pensamos num polígono convexo, imaginamos seus vértices todos apontando para fora, ou seja, que ele não possui
Qual é Mesmo a Definição de Polígono Convexo? Elon Lages Lima IMPA, Rio de Janeiro Quando pensamos num polígono convexo, imaginamos seus vértices todos apontando para fora, ou seja, que ele não possui
Lógica Computacional. Argumentos válidos e sólidos. Métodos de Demonstração. Demonstrações formais. Regras de Inferência Igualdade
 Lógica Computacional Argumentos válidos e sólidos Métodos de Demonstração Demonstrações formais Regras de Inferência Igualdade Não-consequências lógicas 6 Março 2013 Lógica Computacional 1 Argumentos Exemplo:
Lógica Computacional Argumentos válidos e sólidos Métodos de Demonstração Demonstrações formais Regras de Inferência Igualdade Não-consequências lógicas 6 Março 2013 Lógica Computacional 1 Argumentos Exemplo:
Projeto Conceitual Usando o Modelo-Entidade Relacionamento
 Projeto Conceitual Usando o Modelo-Entidade Relacionto 5-1 Visão Avançada do Projeto de Banco de Dados Projeto conceitual : (MER é usado neste estágio) O que são as entidades e relaciontos no cenário?
Projeto Conceitual Usando o Modelo-Entidade Relacionto 5-1 Visão Avançada do Projeto de Banco de Dados Projeto conceitual : (MER é usado neste estágio) O que são as entidades e relaciontos no cenário?
Capítulo 2. Álgebra e imagens binárias. 2.1 Subconjuntos versus funções binárias
 Capítulo 2 Álgebra e imagens binárias Em Análise de Imagens, os objetos mais simples que manipulamos são as imagens binárias. Estas imagens são representadas matematicamente por subconjuntos ou, de maneira
Capítulo 2 Álgebra e imagens binárias Em Análise de Imagens, os objetos mais simples que manipulamos são as imagens binárias. Estas imagens são representadas matematicamente por subconjuntos ou, de maneira
Introdução às Bases de Dados
 Introdução às Bases de Dados Chave primária Domínios Relação F# F Nome Estado Cidade F1 José 20 Braga F2 João 10 Faro F3 Luís 30 Lisboa F4 Rui 30 Setúbal Atributos Tuplas Introdução às Bases de Dados Modelo
Introdução às Bases de Dados Chave primária Domínios Relação F# F Nome Estado Cidade F1 José 20 Braga F2 João 10 Faro F3 Luís 30 Lisboa F4 Rui 30 Setúbal Atributos Tuplas Introdução às Bases de Dados Modelo
Microsoft Access INTRODUÇÃO. Sumário INTRODUÇÃO INTRODUÇÃO INTRODUÇÃO INTRODUÇÃO. O que é Banco de Dados?
 Microsoft Access Sumário 1. 2. ABRINDO UM BANCO DE DADOS PRONTO 3. ASSISTENTE DE BANCO DE DADOS 4. NAVEGANDO PELO BANCO DE DADOS 5. CRIANDO UM BANCO DE DADOS DESDE O INÍCIO 6. CRIANDO COSULTAS 7. CRIANDO
Microsoft Access Sumário 1. 2. ABRINDO UM BANCO DE DADOS PRONTO 3. ASSISTENTE DE BANCO DE DADOS 4. NAVEGANDO PELO BANCO DE DADOS 5. CRIANDO UM BANCO DE DADOS DESDE O INÍCIO 6. CRIANDO COSULTAS 7. CRIANDO
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Álgebra Relacional. OBS: as operações Seleção e Projeção são operações unárias porque atuam em relações únicas.
 Álgebra Relacional Álgebra Relacional é o conjunto básico de operações para o Modelo Relacional. Essas operações permitem a um usuário especificar as solicitações básicas de recuperação. O resultado de
Álgebra Relacional Álgebra Relacional é o conjunto básico de operações para o Modelo Relacional. Essas operações permitem a um usuário especificar as solicitações básicas de recuperação. O resultado de
NOÇÕES DE ÁLGEBRA LINEAR
 ESPAÇO VETORIAL REAL NOÇÕES DE ÁLGEBRA LINEAR ESPAÇOS VETORIAIS Seja um conjunto V φ no qual estão definidas duas operações: adição e multiplicação por escalar, tais que u, v V, u+v V e α R, u V, αu V
ESPAÇO VETORIAL REAL NOÇÕES DE ÁLGEBRA LINEAR ESPAÇOS VETORIAIS Seja um conjunto V φ no qual estão definidas duas operações: adição e multiplicação por escalar, tais que u, v V, u+v V e α R, u V, αu V
ARRAYS. Um array é um OBJETO que referencia (aponta) mais de um objeto ou armazena mais de um dado primitivo.
 Cursos: Análise, Ciência da Computação e Sistemas de Informação Programação I - Prof. Aníbal Notas de aula 8 ARRAYS Introdução Até agora, utilizamos variáveis individuais. Significa que uma variável objeto
Cursos: Análise, Ciência da Computação e Sistemas de Informação Programação I - Prof. Aníbal Notas de aula 8 ARRAYS Introdução Até agora, utilizamos variáveis individuais. Significa que uma variável objeto
Modelo de Dados Relacional Restrições de um Banco de Dados Relacional
 Modelo de Dados Relacional e as Restrições de um Banco de Dados Relacional Modelo de Dados Relacional Conceitos do Modelo Relacional Representa o banco de dados como uma coleção de relações. Comparação
Modelo de Dados Relacional e as Restrições de um Banco de Dados Relacional Modelo de Dados Relacional Conceitos do Modelo Relacional Representa o banco de dados como uma coleção de relações. Comparação
A lógica de programação ajuda a facilitar o desenvolvimento dos futuros programas que você desenvolverá.
 INTRODUÇÃO A lógica de programação é extremamente necessária para as pessoas que queiram trabalhar na área de programação, seja em qualquer linguagem de programação, como por exemplo: Pascal, Visual Basic,
INTRODUÇÃO A lógica de programação é extremamente necessária para as pessoas que queiram trabalhar na área de programação, seja em qualquer linguagem de programação, como por exemplo: Pascal, Visual Basic,
Banco de Dados Capítulo 2: Modelo Relacional. Bach. em Ciência da Computação UFPB/CCT Cláudio Baptista, PhD baptista@dsc.ufpb.br
 Banco de Dados Capítulo 2: Modelo Relacional Bach. em Ciência da Computação UFPB/CCT Cláudio Baptista, PhD baptista@dsc.ufpb.br 2.1 Histórico Modelo Relacional Foi introduzido por Codd (1970) Tornou-se
Banco de Dados Capítulo 2: Modelo Relacional Bach. em Ciência da Computação UFPB/CCT Cláudio Baptista, PhD baptista@dsc.ufpb.br 2.1 Histórico Modelo Relacional Foi introduzido por Codd (1970) Tornou-se
Conceitos Básicos de Banco de Dados
 Conceitos Básicos de Banco de Dados Laboratório de Bases de Dados Sistema de Banco de Dados (SBD) Sistema de armazenamento de dados Objetivos: manter informações torná-las disponível quando necessário
Conceitos Básicos de Banco de Dados Laboratório de Bases de Dados Sistema de Banco de Dados (SBD) Sistema de armazenamento de dados Objetivos: manter informações torná-las disponível quando necessário
MATEMÁTICA GEOMETRIA ANALÍTICA I PROF. Diomedes. E2) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B.
 I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
Prof. Alexandre Unterstell Banco de Dados I
 Prof. Alexandre Unterstell Banco de Dados I Etapas para o projeto de um BD Análise de requisitos Analista: Entrevista Necessidade do negócio As etapas não consideram ainda nenhuma característica específica
Prof. Alexandre Unterstell Banco de Dados I Etapas para o projeto de um BD Análise de requisitos Analista: Entrevista Necessidade do negócio As etapas não consideram ainda nenhuma característica específica
Diagrama de Classes. Um diagrama de classes descreve a visão estática do sistema em termos de classes e relacionamentos entre as classes.
 1 Diagrama de Classes Um diagrama de classes descreve a visão estática do sistema em termos de classes e relacionamentos entre as classes. Um dos objetivos do diagrama de classes é definir a base para
1 Diagrama de Classes Um diagrama de classes descreve a visão estática do sistema em termos de classes e relacionamentos entre as classes. Um dos objetivos do diagrama de classes é definir a base para
A B C F G H I. Apresente todas as soluções possíveis. Solução
 19a Olimpíada de Matemática do Estado do Rio Grande do Norte - 008 Segunda Etapa Em 7/09/008 Prova do Nível I (6 o ou 7 o Séries) (antigas 5ª ou 6ª séries) 1 a Questão: Substitua as nove letras da figura
19a Olimpíada de Matemática do Estado do Rio Grande do Norte - 008 Segunda Etapa Em 7/09/008 Prova do Nível I (6 o ou 7 o Séries) (antigas 5ª ou 6ª séries) 1 a Questão: Substitua as nove letras da figura
Principais Conceitos. Modelo Relacional representa o banco de dados como uma coleção de relações Tupla Atributos Relação Domínio
 MODELO RELACIONAL Principais Conceitos Modelo Relacional representa o banco de dados como uma coleção de relações Tupla Atributos Relação Domínio Conceitos Básicos - Relações A Álgebra Relacional fundamenta-se
MODELO RELACIONAL Principais Conceitos Modelo Relacional representa o banco de dados como uma coleção de relações Tupla Atributos Relação Domínio Conceitos Básicos - Relações A Álgebra Relacional fundamenta-se
Programação com Objectos. Processamento de Dados I. 4. Classes Abstractas
 Programação com Objectos Processamento de Dados I 4. Classes Abstractas 1 Conceito de classe abstracta Declaração de uma classe abstracta Implicações e características das classes abstractas Utilização
Programação com Objectos Processamento de Dados I 4. Classes Abstractas 1 Conceito de classe abstracta Declaração de uma classe abstracta Implicações e características das classes abstractas Utilização
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
Definida pelo American National Standard Institute (ANSI) em 1986
 2.3. Linguagens Relacionais SQL Structured Query Language Linguagem para o modelo relacional: Definida pelo American National Standard Institute (ANSI) em 1986 Adoptada em 1987 como um standard internacional
2.3. Linguagens Relacionais SQL Structured Query Language Linguagem para o modelo relacional: Definida pelo American National Standard Institute (ANSI) em 1986 Adoptada em 1987 como um standard internacional
BANCO DE DADOS I AULA 6. Wlllamys Araújo willamysaraujo7@gmail.com
 BANCO DE DADOS I AULA 6 Wlllamys Araújo willamysaraujo7@gmail.com Normalização Conjunto de regras que ajudam na definição de bancos de dados que não contenham redundância desnecessária e que permitam o
BANCO DE DADOS I AULA 6 Wlllamys Araújo willamysaraujo7@gmail.com Normalização Conjunto de regras que ajudam na definição de bancos de dados que não contenham redundância desnecessária e que permitam o
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Outras Máquinas de Turing
 Capítulo 10 Outras Máquinas de Turing 10.1. Pequenas variações da TM padrão 10.2. MT s com dispositivos de armazenamento mais complexos 10.3. MT s não-determinísticas 10.4. A Máquina de Turing Universal
Capítulo 10 Outras Máquinas de Turing 10.1. Pequenas variações da TM padrão 10.2. MT s com dispositivos de armazenamento mais complexos 10.3. MT s não-determinísticas 10.4. A Máquina de Turing Universal
Revisão de Banco de Dados
 Revisão de Banco de Dados Fabiano Baldo 1 Sistema de Processamento de Arquivos Antes da concepção dos BDs o registro das informações eram feitos através de arquivos. Desvantagens: Redundância e Inconsistência
Revisão de Banco de Dados Fabiano Baldo 1 Sistema de Processamento de Arquivos Antes da concepção dos BDs o registro das informações eram feitos através de arquivos. Desvantagens: Redundância e Inconsistência
Morfologia Matemática Binária
 Morfologia Matemática Binária Conceitos fundamentais: (Você precisa entender bem esses Pontos básicos para dominar a área! Esse será nosso game do dia!!! E nossa nota 2!!) Morfologia Matemática Binária
Morfologia Matemática Binária Conceitos fundamentais: (Você precisa entender bem esses Pontos básicos para dominar a área! Esse será nosso game do dia!!! E nossa nota 2!!) Morfologia Matemática Binária
Álgebra Booleana. Introdução ao Computador 2010/01 Renan Manola
 Álgebra Booleana Introdução ao Computador 2010/01 Renan Manola Histórico George Boole (1815-1864) Considerado um dos fundadores da Ciência da Computação, apesar de computadores não existirem em seus dias.
Álgebra Booleana Introdução ao Computador 2010/01 Renan Manola Histórico George Boole (1815-1864) Considerado um dos fundadores da Ciência da Computação, apesar de computadores não existirem em seus dias.
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
MD Teoria dos Conjuntos 1
 Teoria dos Conjuntos Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Teoria dos Conjuntos 1 Introdução O que os seguintes objetos têm em comum? um
Teoria dos Conjuntos Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Teoria dos Conjuntos 1 Introdução O que os seguintes objetos têm em comum? um
Manual de Utilizador. Caderno. Recursos da Unidade Curricular. Gabinete de Ensino à Distância do IPP. http://eweb.ipportalegre.pt. ged@ipportalegre.
 Manual de Utilizador Caderno Recursos da Unidade Curricular Gabinete de Ensino à Distância do IPP http://eweb.ipportalegre.pt ged@ipportalegre.pt Índice RECURSOS... 1 ADICIONAR E CONFIGURAR RECURSOS...
Manual de Utilizador Caderno Recursos da Unidade Curricular Gabinete de Ensino à Distância do IPP http://eweb.ipportalegre.pt ged@ipportalegre.pt Índice RECURSOS... 1 ADICIONAR E CONFIGURAR RECURSOS...
Universidade Estadual de Santa Cruz. Departamento de Ciências Exatas e Tecnológicas. Especialização em Matemática. Disciplina: Estruturas Algébricas
 1 Universidade Estadual de Santa Cruz Departamento de Ciências Exatas e Tecnológicas Especialização em Matemática Disciplina: Estruturas Algébricas Profs.: Elisangela S. Farias e Sérgio Motta Operações
1 Universidade Estadual de Santa Cruz Departamento de Ciências Exatas e Tecnológicas Especialização em Matemática Disciplina: Estruturas Algébricas Profs.: Elisangela S. Farias e Sérgio Motta Operações
UM TEOREMA QUE PODE SER USADO NA
 UM TEOREMA QUE PODE SER USADO NA PERCOLAÇÃO Hemílio Fernandes Campos Coêlho Andrei Toom PIBIC-UFPE-CNPq A percolação é uma parte importante da teoria da probabilidade moderna que tem atraído muita atenção
UM TEOREMA QUE PODE SER USADO NA PERCOLAÇÃO Hemílio Fernandes Campos Coêlho Andrei Toom PIBIC-UFPE-CNPq A percolação é uma parte importante da teoria da probabilidade moderna que tem atraído muita atenção
Fundamentos de Bancos de Dados Prova 3
 Fundamentos de Bancos de Dados Prova 3 Prof. Carlos A. Heuser 26 de janeiro de 2004 Duração: 2 horas Prova com consulta Questão 1 (Construção de modelo ER - Peso 3) Deseja-se construir uma base de dados
Fundamentos de Bancos de Dados Prova 3 Prof. Carlos A. Heuser 26 de janeiro de 2004 Duração: 2 horas Prova com consulta Questão 1 (Construção de modelo ER - Peso 3) Deseja-se construir uma base de dados
LÓGICA DE PROGRAMAÇÃO. Vitor Valerio de Souza Campos
 LÓGICA DE PROGRAMAÇÃO Vitor Valerio de Souza Campos Exemplos de algoritmos Faça um algoritmo para mostrar o resultado da multiplicação de dois números. Algoritmo em descrição narrativa Passo 1 Receber
LÓGICA DE PROGRAMAÇÃO Vitor Valerio de Souza Campos Exemplos de algoritmos Faça um algoritmo para mostrar o resultado da multiplicação de dois números. Algoritmo em descrição narrativa Passo 1 Receber
Projeção ortográfica de modelos com elementos paralelos e oblíquos
 A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
Tabela de Símbolos. Análise Semântica A Tabela de Símbolos. Principais Operações. Estrutura da Tabela de Símbolos. Declarações 11/6/2008
 Tabela de Símbolos Análise Semântica A Tabela de Símbolos Fabiano Baldo Após a árvore de derivação, a tabela de símbolos é o principal atributo herdado em um compilador. É possível, mas não necessário,
Tabela de Símbolos Análise Semântica A Tabela de Símbolos Fabiano Baldo Após a árvore de derivação, a tabela de símbolos é o principal atributo herdado em um compilador. É possível, mas não necessário,
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO)
 Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
TUTORIAL DO ACCESS PASSO A PASSO. I. Criar um Novo Banco de Dados. Passos: 1. Abrir o Access 2. Clicar em Criar um novo arquivo
 TUTORIAL DO ACCESS PASSO A PASSO I. Criar um Novo Banco de Dados Passos: 1. Abrir o Access 2. Clicar em Criar um novo arquivo 3. Clicar em Banco de Dados em Branco 4. Escrever um nome na caixa de diálogo
TUTORIAL DO ACCESS PASSO A PASSO I. Criar um Novo Banco de Dados Passos: 1. Abrir o Access 2. Clicar em Criar um novo arquivo 3. Clicar em Banco de Dados em Branco 4. Escrever um nome na caixa de diálogo
IFSP - EAD - GEOMETRIA TRIÂNGULO RETÂNGULO CONCEITUAÇÃO :
 IFSP - EAD - GEOMETRIA TRIÂNGULO RETÂNGULO CONCEITUAÇÃO : Como já sabemos, todo polígono que possui três lados é chamado triângulo. Assim, ele também possui três vértices e três ângulos internos cuja soma
IFSP - EAD - GEOMETRIA TRIÂNGULO RETÂNGULO CONCEITUAÇÃO : Como já sabemos, todo polígono que possui três lados é chamado triângulo. Assim, ele também possui três vértices e três ângulos internos cuja soma
Bases de Dados 2008/2009
 Instituto Superior Técnico Bases de Dados 2008/2009 Exame de 30 de Janeiro de 2009 Sem consulta Duração: 2h30 1. Considere o seguinte cenário relativo a um stand de compra e venda de carros usados, em
Instituto Superior Técnico Bases de Dados 2008/2009 Exame de 30 de Janeiro de 2009 Sem consulta Duração: 2h30 1. Considere o seguinte cenário relativo a um stand de compra e venda de carros usados, em
ALGORITMOS PARTE 01. Fabricio de Sousa Pinto
 ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
Feature-Driven Development
 FDD Feature-Driven Development Descrição dos Processos Requisitos Concepção e Planejamento Mais forma que conteúdo Desenvolver um Modelo Abrangente Construir a Lista de Features Planejar por
FDD Feature-Driven Development Descrição dos Processos Requisitos Concepção e Planejamento Mais forma que conteúdo Desenvolver um Modelo Abrangente Construir a Lista de Features Planejar por
Bases Matemáticas. Aula 2 Métodos de Demonstração. Rodrigo Hausen. v. 2013-7-31 1/15
 Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
,QWURGXomRDR(GLWRUGH $SUHVHQWDo}HV3RZHU3RLQW
 Universidade Federal de Viçosa Departamento de Informática,QWURGXomRDR(GLWRUGH $SUHVHQWDo}HV3RZHU3RLQW Flaviano Aguiar Liziane Santos Soares Jugurta Lisboa Filho (Orientador) PROJETO UNESC@LA Setembro
Universidade Federal de Viçosa Departamento de Informática,QWURGXomRDR(GLWRUGH $SUHVHQWDo}HV3RZHU3RLQW Flaviano Aguiar Liziane Santos Soares Jugurta Lisboa Filho (Orientador) PROJETO UNESC@LA Setembro
Alfabeto e palavras. Alfabeto conjunto finito de símbolos (Σ).
 Alfabeto e palavras Alfabeto conjunto finito de símbolos (Σ). {A,...,Z}, {α, β,... }, {a,b}, {0,1}, ASCII Palavra de Σ sequência finita de símbolos do alfabeto Σ Σ = {a, b} aabba a aaaaaaaa Comprimento
Alfabeto e palavras Alfabeto conjunto finito de símbolos (Σ). {A,...,Z}, {α, β,... }, {a,b}, {0,1}, ASCII Palavra de Σ sequência finita de símbolos do alfabeto Σ Σ = {a, b} aabba a aaaaaaaa Comprimento
BANCO DE DADOS. Eliminar redundâncias e inconsistências de um banco de dados, com reorganização mínima dos dados.
 Modelagem de Dados Normalização Objetivo: BANCO DE DADOS Eliminar redundâncias e inconsistências de um banco de dados, com reorganização mínima dos dados. Sub-Fases: Identificação das redundâncias e outros
Modelagem de Dados Normalização Objetivo: BANCO DE DADOS Eliminar redundâncias e inconsistências de um banco de dados, com reorganização mínima dos dados. Sub-Fases: Identificação das redundâncias e outros
Programação Orientada a Objetos Classes Abstratas Técnico em Informática. Prof. Marcos André Pisching, M.Sc.
 Classes Abstratas Técnico em Informática, M.Sc. Classes Abstratas 2 Classes Abstratas Abstração Devemos considerar as qualidades e comportamentos independentes dos objetos a que pertencem, isolamos seus
Classes Abstratas Técnico em Informática, M.Sc. Classes Abstratas 2 Classes Abstratas Abstração Devemos considerar as qualidades e comportamentos independentes dos objetos a que pertencem, isolamos seus
BANCO DE DADOS. Fixação dos conteúdos Integridade Referencial Normalização Exercícios
 BANCO DE DADOS Fixação dos conteúdos Integridade Referencial Normalização Exercícios BANCO DE DADOS X SGBD Banco de Dados: Um "banco de dados" pode ser definido como um conjunto de "dados" devidamente
BANCO DE DADOS Fixação dos conteúdos Integridade Referencial Normalização Exercícios BANCO DE DADOS X SGBD Banco de Dados: Um "banco de dados" pode ser definido como um conjunto de "dados" devidamente
Notas de aula número 1: Otimização *
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL UFRGS DEPARTAMENTO DE ECONOMIA CURSO DE CIÊNCIAS ECONÔMICAS DISCIPLINA: TEORIA MICROECONÔMICA II Primeiro Semestre/2001 Professor: Sabino da Silva Porto Júnior
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL UFRGS DEPARTAMENTO DE ECONOMIA CURSO DE CIÊNCIAS ECONÔMICAS DISCIPLINA: TEORIA MICROECONÔMICA II Primeiro Semestre/2001 Professor: Sabino da Silva Porto Júnior
Arquitecturas de Software Licenciatura em Engenharia Informática e de Computadores
 UNIVERSIDADE TÉCNICA DE LISBOA INSTITUTO SUPERIOR TÉCNICO Arquitecturas de Software Licenciatura em Engenharia Informática e de Computadores Primeiro Teste 21 de Outubro de 2006, 9:00H 10:30H Nome: Número:
UNIVERSIDADE TÉCNICA DE LISBOA INSTITUTO SUPERIOR TÉCNICO Arquitecturas de Software Licenciatura em Engenharia Informática e de Computadores Primeiro Teste 21 de Outubro de 2006, 9:00H 10:30H Nome: Número:
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES
 CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
FÓRMULAS DO MICROSOFT EXCEL
 FÓRMULAS DO MICROSOFT EXCEL 1. SINAIS DE OPERAÇÕES 2. SINAIS PARA CONDIÇÃO SINAL FUNÇÃO SINAL FUNÇÃO + SOMAR > MAIOR QUE - SUBTRAÇÃO < MENOR QUE * MULTIPLICAÇÃO DIFERENTE QUE / DIVISÃO >= MAIOR E IGUAL
FÓRMULAS DO MICROSOFT EXCEL 1. SINAIS DE OPERAÇÕES 2. SINAIS PARA CONDIÇÃO SINAL FUNÇÃO SINAL FUNÇÃO + SOMAR > MAIOR QUE - SUBTRAÇÃO < MENOR QUE * MULTIPLICAÇÃO DIFERENTE QUE / DIVISÃO >= MAIOR E IGUAL
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Expansão linear e geradores
 Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Espaços Vectoriais - ALGA - 004/05 4 Expansão linear e geradores Se u ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u ; u ; :::;
Banco de Dados. Modelagem de Dados com MER. Prof. Walteno Martins Parreira Jr www.waltenomartins.com.br waltenomartins@yahoo.
 Banco de Dados Modelagem de Dados com MER Prof. Walteno Martins Parreira Jr www.waltenomartins.com.br waltenomartins@yahoo.com 2015 Modelagem de Dados Modelagem de Dados tem como objetivo transformar uma
Banco de Dados Modelagem de Dados com MER Prof. Walteno Martins Parreira Jr www.waltenomartins.com.br waltenomartins@yahoo.com 2015 Modelagem de Dados Modelagem de Dados tem como objetivo transformar uma
Refinamento de Esquemas e Formas Normais
 Refinamento de Esquemas e Formas Normais Capítulo 19 UNICAMP/IC/MO410/MC536/2003-5 - Slides do livro Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke, McGrow-Hill, 2003. Cap. 19-1 Roteiro
Refinamento de Esquemas e Formas Normais Capítulo 19 UNICAMP/IC/MO410/MC536/2003-5 - Slides do livro Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke, McGrow-Hill, 2003. Cap. 19-1 Roteiro
Canguru Matema tico sem Fronteiras 2013
 Canguru Matema tico sem Fronteiras 201 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 12. ano de escolaridade Durac a o: 1h 0min Turma: Nome: Na o podes usar calculadora. Em cada questa o deves
Canguru Matema tico sem Fronteiras 201 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 12. ano de escolaridade Durac a o: 1h 0min Turma: Nome: Na o podes usar calculadora. Em cada questa o deves
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Capítulo 7. Topologia Digital. 7.1 Conexidade
 Capítulo 7 Topologia Digital A Topologia Digital estuda a aplicação das noções definidas em Topologia sobre imagens binárias. Neste capítulo vamos introduzir algumas noções básicas de Topologia Digital,
Capítulo 7 Topologia Digital A Topologia Digital estuda a aplicação das noções definidas em Topologia sobre imagens binárias. Neste capítulo vamos introduzir algumas noções básicas de Topologia Digital,
Como incluir artigos:
 Como incluir artigos: O WordPress é uma ferramenta muito flexível, com muitas variações e ajustes que podem torná-lo algo muito simples e também muito sofisticado conforme os recursos que são configurados
Como incluir artigos: O WordPress é uma ferramenta muito flexível, com muitas variações e ajustes que podem torná-lo algo muito simples e também muito sofisticado conforme os recursos que são configurados
UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA. Manual do Moodle- Sala virtual
 UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA Manual do Moodle- Sala virtual UNIFAP MACAPÁ-AP 2012 S U M Á R I O 1 Tela de Login...3 2 Tela Meus
UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA Manual do Moodle- Sala virtual UNIFAP MACAPÁ-AP 2012 S U M Á R I O 1 Tela de Login...3 2 Tela Meus
Barra de ferramentas padrão. Barra de formatação. Barra de desenho Painel de Tarefas
 Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
W o r d p r e s s 1- TELA DE LOGIN
 S U M Á R I O 1Tela de Login...2 2 Painel......3 3 Post...4 4 Ferramentas de Post...10 5 Páginas...14 6 Ferramentas de páginas...21 7 Mídias...25 8 Links......30 1 1- TELA DE LOGIN Para ter acesso ao wordpress
S U M Á R I O 1Tela de Login...2 2 Painel......3 3 Post...4 4 Ferramentas de Post...10 5 Páginas...14 6 Ferramentas de páginas...21 7 Mídias...25 8 Links......30 1 1- TELA DE LOGIN Para ter acesso ao wordpress
Múltiplos Estágios processo com três estágios Inquérito de Satisfação Fase II
 O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
(A) 30 (B) 6 (C) 200 (D) 80 (E) 20 (A) 6 (B) 10 (C) 15 (D) 8 (E) 2 (A) 15 (B) 2 (C) 6 (D) 27 (E) 4 (A) 3 (B) 2 (C) 6 (D) 27 (E) 4
 TEOREMA DE TALES. Na figura abaixo as retas r, s e t são (A) 0 (B) 6 (C) 00 (D) 80 (E) 0. Três retas paralelas são cortadas por duas Se AB = cm; BC = 6 cm e XY = 0 cm a medida, em cm, de XZ é: (A) 0 (B)
TEOREMA DE TALES. Na figura abaixo as retas r, s e t são (A) 0 (B) 6 (C) 00 (D) 80 (E) 0. Três retas paralelas são cortadas por duas Se AB = cm; BC = 6 cm e XY = 0 cm a medida, em cm, de XZ é: (A) 0 (B)
Elementos de Matemática Discreta
 Elementos de Matemática Discreta Prof. Marcus Vinícius Midena Ramos Universidade Federal do Vale do São Francisco 9 de junho de 2013 marcus.ramos@univasf.edu.br www.univasf.edu.br/~marcus.ramos Marcus
Elementos de Matemática Discreta Prof. Marcus Vinícius Midena Ramos Universidade Federal do Vale do São Francisco 9 de junho de 2013 marcus.ramos@univasf.edu.br www.univasf.edu.br/~marcus.ramos Marcus
Dependência funcional
 Dependência funcional Dependência funcional: Dados dois conjuntos de atributos A e B de uma entidade, diz-se que: B é funcionalmente dependente de A ou A determina B ou B depende de A, se a cada valor
Dependência funcional Dependência funcional: Dados dois conjuntos de atributos A e B de uma entidade, diz-se que: B é funcionalmente dependente de A ou A determina B ou B depende de A, se a cada valor
Como produzir e publicar uma apresentação online dinâmica (Prezi)
 Como produzir e publicar uma apresentação online dinâmica (Prezi) Este módulo irá ensinar-lhe como produzir e publicar uma apresentação online dinâmica usando o programa Prezi. A produção de uma apresentação
Como produzir e publicar uma apresentação online dinâmica (Prezi) Este módulo irá ensinar-lhe como produzir e publicar uma apresentação online dinâmica usando o programa Prezi. A produção de uma apresentação
ferramentas de produtividade
 ferramentas de produtividade modelização de dados normalização de dados as bases de dados 3 2002 Luis Borges Gouveia (http://www.ufp.pt/~lmbg) 1 modelização de dados 3 abordagens mínimo comum utilizar
ferramentas de produtividade modelização de dados normalização de dados as bases de dados 3 2002 Luis Borges Gouveia (http://www.ufp.pt/~lmbg) 1 modelização de dados 3 abordagens mínimo comum utilizar
Árvores Binárias Balanceadas
 Árvores Binárias Balanceadas Elisa Maria Pivetta Cantarelli Árvores Balanceadas Uma árvore é dita balanceada quando as suas subárvores à esquerda e à direita possuem a mesma altura. Todos os links vazios
Árvores Binárias Balanceadas Elisa Maria Pivetta Cantarelli Árvores Balanceadas Uma árvore é dita balanceada quando as suas subárvores à esquerda e à direita possuem a mesma altura. Todos os links vazios
