Análise Complexa. José Luis Silva Departamento de Matemática Universidade da Madeira 9000 Funchal Madeira
|
|
|
- Ayrton Pinhal Abreu
- 7 Há anos
- Visualizações:
Transcrição
1 Análise Complexa José Luis Silva Departamento de Matemática Universidade da Madeira 9000 Funchal Madeira
2 Conteúdo Números Complexos Breve nota histórica Definições e propriedades 3 3 Complexos conjugados Valores absolutos 9 4 Forma polar Potências e quocientes Exercícios 7 Funções Analíticas 0 Funções Elementares 0 Função exponencial 0 Funções trigonométricas 3 3 Função logarítmica 4 4 Potências complexas 8 5 Funções trigonométricas e hiperbólicas inversas 8 Transformações 30 3 Noções topológicas 3 4 Derivadas 36 5 Equações de Cauchy-Riemann 4 6 Funções harmónicas 45 7 Derivadas de funções elementares 47 7 Função exponencial 47 7 Funções trigonométricas Função logarítmica Potências complexas 5 Exercícios 55 i
3 ii CONTEÚDO 3 Integrais 59 3 Integral de caminho 59 3 O teorema de Cauchy-Goursat Fórmula integral de Cauchy Módulo máximo de funções analíticas 76 Exercícios 80 4 Séries de funções analíticas 83 4 Convergência de sucessões e séries 83 4 Séries de potências e teorema de Taylor Séries de Laurent e Classificação de Singularidades 97 Exercícios 3 5 Cálculo de Resíduos 7 5 Técnicas para o cálculo de resíduos 7 5 O teorema dos resíduos 3 53 Suplemento ao teorema dos resíduos 6 53 Ponto no infinito 6 53 Resíduos e comportamento no infinito 8 54 Aplicação ao cálculo de integrais reais impróprios Integrais do tipo f (x) dx Integrais impróprios envolvendo funções trigonométricas Integrais definidos de funções trigonométricas Integrais em torno de um ponto de ramificação 5 55 Soma de Séries 56 Exercícios 6
4 Capítulo Números Complexos Neste capítulo definimos o conjunto dos números complexos (denotado por C) usando o plano xy (denotado por R ) para os representar os números complexos, ideia original de J R Argand Depois de introduzirmos a soma e multiplicação de números complexos vamos provar que o conjunto dos números complexos forma um corpo, ver Teorema 4 em baixo Isto é essencialmente o conteúdo da Secção Nas Secções 3 e 4 vamos explorar outras propriedades dos números complexos usando o plano xy tais como, representação em coordenadas polares, interpretação geométrica da multiplicação de números complexos, resolução de equações envolvendo números complexos etc Resta dizer que na Secção apresentamos uma breve nota sobre o surgimento dos números complexos a qual também serve de motivação para a introdução destes números Breve nota histórica O nascimento dos números complexos pode ser datado do século XVI, quando alguns matemáticos Italianos se envolveram na tarefa de encontrar a fórmula resolvente para as equações do terceiro grau Parece ter sido Niccolo Fontana ( ) (mais conhecido por Tartáglia) o primeiro a apresentar essa fórmula, embora fosse o seu colega Gerolamo Cardano (50-576) o primeiro a publicá-la A fórmula para a equação do terceiro grau na forma x 3 px + q = 0
5 Capítulo Números Complexos é dada por x = 3 q + q Ao aplicar a fórmula () à equação 4 + p q q 4 + p3 7 () x 3 5x 4 = 0 () obtemos x = (3) A equação (), conhecida por equação Bombelli (56-573), Cardano dizia que a fórmula não se aplicava Bombelli pensou na seguinte conjectura Conjectura: Como os radicandos em (3) só diferem de um sinal, o mesmo deverá acontecer com as suas raízes cúbicas Assim resolveu o sistema 3 + = a + bi 3 = a bi obtendo as soluções a = e b = aplicando aa regras ( b) = b e ( b) 3 = b b Portanto a raiz da equação () é, segundo (3) + + = 4 Na realidade 4 é uma raiz de (), como se verifica facilmente Assim se deram os primeiros passos na criação dos números complexos
6 Definições e propriedades 3 Definições e propriedades Definição Designa-se por conjunto dos números complexos, e representa-se por C, o conjunto R dos pares ordenados de números reais com a soma vectorial e multiplicação por um escalar usuais, ie, (x, y ) + (x, y ) = (x + x, y + y ) a (x, y) = (ax, ay) e a multiplicação de números complexos definida por Observação (x, y)(u, v) = (xu yv, xv + yu) O par (x, 0) é identificado com o número real x, ie, (x, 0) x, por outras palavras, temos que R C 3 Ao par (0, ) vamos atribuir um símbolo, i, ie, Consequências z C, z = (x, y) = x + yi, pois (0, ) i x + yi (x, 0) + (y, 0)(0, ) = (x, 0) + (0, y) = (x, y); z = x + yi representação na forma algébrica, onde x é a parte real (R(z) = x) e y é a parte imaginária (I(z) = y) (ver Figura ) 3 iy = yi, pois (0, )(y, 0) = (0, y) = (y, 0)(0, ) = yi 4 i =, pois (0, )(0, ) = (, 0) 5 Dois números complexos dizem-se iguais se e só se tiverem ambos a mesma parte real e a mesma parte imaginária, ie, a + bi = c + di a = c b = d;
7 4 Capítulo Números Complexos y w z + w y = I(z) z = x + yi x = R(z) x Figura : Representação geométrica de números complexos na forma algébrica 6 bi é um imaginário puro 7 Se z C\ {(0, 0)}, então!z C : zz = Unicidade: Suponhamos que existiam z, z tais que zz = e zz = Mas, z = z = z (zz ) = (z z) z = z = z logo z é único z = z Existência: Seja z = a + bi C\ {(0, 0)} e suponhamos a 0, no caso a = 0 vem z = i b Queremos determinar z = a + b i tal que zz = Assim { { aa bb = a ab + ba = 0 = bb + a ab + b bb + = 0 a { { a = bb + a a a b + b + b b = 0 = bb + a b = b a +b { a = a a +b b = b a +b z z = a a + b + i b a + b ;
8 Definições e propriedades 5 8 z w = zw = x+yi a+bi = (x+yi)(a bi) (a+bi)(a bi) = xa+yb a +b + ya xb a +b i Exemplo 3 A partir das fórmulas para o quociente e para o produto mostre que ( a) z z = z z ), z C\ {(0, 0)} 0 z C ( )( ) b) z z = z z, z, z C\ {(0, 0)} Resolução Seja z = a + bi e z = c + di a) Por um lado tem-se por outro z ( z ) z z = ac + bd c + d ad + bc + i (4) c + d ( c di = (a + bi) c + d = (a + bi) = ) ( c c + d d ) c + d i ac + bd ad + bc + i (5) c + d c + d Como as partes reais e imaginárias de (4) e (5) são iguais, tem-se que os números são iguais b) O processo é análogo: z z = = ac bd + (ad + bc) i ac bd (ac bd) + (ad + cb) + ad cb (ac bd) + (ad + cb) i ( ) ( ) z z = = ( ) ( ) a bi c di a + b c + d ac bd ad cb + (ac bd) (ad + cb) i e a igualdade também se verifica Temos as seguintes propriedades, como consequência das propriedades de R : Propriedades da adição:
9 6 Capítulo Números Complexos z + w = w + z z + (w + s) = (z + w) + s 3 z + 0 = z 4 z + ( z) = 0, z, w, s C Propriedades da multiplicação: zw = wz z (ws) = (zw) s 3 z = z 4 zz =, z C\ {(0, 0)}, w, s C Lei distributiva: z (w + s) = zw + zs, z, w, s C Teorema 4 O conjunto dos números complexos constitui um corpo (não ordenado) Prova Fica demonstrado tendo em conta as seguintes factos Em C não se pode estabelecer uma relação de ordem, pois se assim fosse, para uma certa ordem teríamos i 0 ou i 0 mas se i 0 i 0 0 absurdo, e o mesmo se i 0 Assim não podemos ter uma ordem em C Podemos estabelecer as propriedades de corpo do conjunto C a partir do seguinte isomorfismo: (R, θ, φ) é um corpo para θ e φ definidas do seguite modo (x, y)θ (u, v) := (x + u, y + v) e (x, y)φ(u, v) := (xu yv, xv + yu)
10 Definições e propriedades 7 ie, (R, θ) e (R \ {(0, 0)}, φ) são grupos abelianos Define-se C := { z : z = a + bi; a, b R i = } e as seguintes operações em C : Seja (a + bi) + C (c + di) := a + c + i (b + d) (a + bi) C (c + di) := ac bd + i (ad + bc) f : R C, (x, y) x + yi f é um isomorfismo de (R, θ, φ) sobre (C, + C, C) ie, uma transformação que transforma a operação θ na operação + C e a operação φ na operação C Para simplificação da notação, e por abuso de linguagem representa-se + C por + e C por 3 Uma das razões da utilização dos números complexos é permitir extrair raízes quadradas de números negativos Proposição 5 Seja z C Então existe w C tal que w = z O corpo C é a menor extensão de R onde w = z tem sempre solução Note que w também satisfaz a equação Prova Seja z = a + bi Pretendemos encontrar w = x + yi tal que { a + bi = (x + yi) x y = a xy = b A existência de soluções pode ser garantida pela análise do gráfico da Figura Temos a + b = ( x y ) + 4x y = ( x + y ) x + y = a + b a + x + x = a + b x = (a + ) a + b y = ( a + a + b )
11 8 Capítulo Números Complexos y xy = b a a, b > 0 a x x y = a Figura : Exemplos de curvas de x y = a e xy = b Seja α = (a + ) a + b β = ( a + ) a + b b > 0 : (x = α y = β) (x = α y = β) b < 0 : (x = α y = β) (x = α y = β) Concluimos, pois, que para b > 0, temos ( x = a + a + b ) x = y = ( a + a + b ) y = ( a + a + b ) ( a + a + b ) e para b < 0, temos ( x = a + a + b ) ( x = a + a + b ( y = a + a + b ) ) ( y = a + a + b )
12 3 Complexos conjugados Valores absolutos 9 Exemplo 6 Resolva a equação z 4 + i = 0 Resolução Seja z = w, então w + i = 0 Substituindo na fórmula a + bi = ± (α + sgn (b) βi) com a = 0 b = sgn (b) = Assim w = ±( ) i Considerando agora a equação z = i, aplicamos novamente a fórmula, pondo a = b =, obtendo-se ( z = ± ) + + ( i ( ( ) = ± + i ( ) + = ± i Para o outro valor, w = + i, obtemos + ( ) ) + ( ) + z = ± + i ) + 3 Complexos conjugados Valores absolutos Definição 3 Dado z = x + yi C, designa-se por conjugado de z, ao número complexo z = x yi, ie, é uma simetria do ponto z em relação ao eixo dos x (ver Figura 3) Consquências: z, z C
13 0 Capítulo Números Complexos y z θ x θ z Figura 3: Representação de z e z z + z = z + z z z = z z 3 z z = z z z C\ {(0, 0)} 4 z = z z R 5 z + z = R(z) z z = ii(z) Definição 3 Dado z = x + yi C, chama-se valor absoluto de z, ao número real não negativo z = x + y Geometricamente z é o comprimento do vector (x, y), (ver Figura 4) Proposição 33 Para quaisquer z, z, z C temos z = R(z) + (I(z) z > R(z) e z I(z) 3 z z = x + y = z, z = z, z = z z 4 z z = z z 5 z z = z, z z 0
14 3 Complexos conjugados Valores absolutos y z = x + yi z = x + y x Figura 4: Representação geométrica de z 6 z + z < z + z (desigualdade triangular); 7 z z z z Prova Faremos a prova só de 7 a) z = z + (z z ) z + z z b) Mudando o papel de z com z temos: De (6) e (7) concluimos que z z z z (6) z z z z z z z z (7) z z z z z z z z z z Exemplo 34 Prove que se z =, então az + b = bz + ā para quaisquer números complexos a e b
15 Capítulo Números Complexos y z = x + yi r r sin θ θ r cos θ x Figura 5: Coordenadas polares associadas ao número complexo z = x + yi Resolução Como z = temos z = z z = z z = z Assim az + b = az + b bz + ā = z b + zā = az + b z b + za = z = 4 Forma polar Potências e quocientes Para cada número complexo z = x + yi C\ {0}, podemos associar as suas coordenadas polares r e θ, dadas por: r = z = x + y θ = arg z = arctan y x, 0 θ < π (ver Figura 5) Assim { x = r cosθ y = r sin θ r > 0, θ [0, π[
16 4 Forma polar Potências e quocientes 3 pelo que podemos escrever z = x + yi z = r (cosθ + i sin θ) Esta é a representação de z na forma polar Observação 4 Para cada z C, arg z não é único, na verdade, dado que sin θ e cos θ são funções periódicas de período π, se θ é o argumento de z, então θ + kπ, (k Z) também o é No entanto, se fixarmos um intervalo θ 0 arg z < θ 0 + π a representação é única; Quando z = 0 tem-se z = 0 e θ arbitrário; arg z = arg z Teorema 4 Dados z, z C com z = r (cosθ + i sin θ ) e z = r (cosθ + i sin θ ), então z z = r r (cos (θ + θ ) + i sin (θ + θ )), ie, z z = z z e arg (z z ) = arg z + arg z (modπ) Prova Basta multiplicar os números complexos com a representação na forma polar e usar as fórmulas trigonométricas cosθ cosθ sin θ sin θ = cos (θ + θ ) e sin θ cosθ + cos θ sin θ = sin (θ + θ ) Exemplo 43 Fixemos o intervalo [0, π[, z =, z = i Calcule z z usando a forma polar Resolução As coordenadas polares de z são: z = e arg z = π e para z temos: z = e arg z = 3 π Assim z z = z z = e arg (z z ) = arg z + arg z = 5 π
17 4 Capítulo Números Complexos y i arg( ) arg( i) arg(( )( i)) x arg( ) + arg( i) i Figura 6: Multiplicação do número complexo por i como 5 π não está no intervalo escolhido, [0, π[, devemos subtrair π para colocar o argumento de z z no intervalo [0, π[, (ver Figura 6) Observação 44 Outra forma de ver a multiplicação de números complexos é a seguinte: seja z C, define-se ψ z : C C, w zw Pelo teorema 4 sabemos que o efeito de ψ z é rodar cada número complexo de um ângulo igual a arg z no sentido contrário ao dos ponteiros do relógio e ampliando o comprimento pelo factor z ψ i simplesmente roda cada número complexo de π, (ver Figura 7) A aplicação ψ z é linear, ie, ψ z (αw + βw ) = αψ z (w ) + βψ z (w ) com α, β R e w, w C Assim ψ z pode ser representada pela sua matriz Pondo z = a + bi, sabemos da álgebra linear que a matriz de ψ z é dada por ( ) a b M (ψ z ) = b a
18 4 Forma polar Potências e quocientes 5 y iw ψ i (w) w x Figura 7: Multiplicação por i A base de C é (, 0);(0, ) A imagem de w = x + yi por meio de ψ z é dada por ( ) ( ) ( ) a b x ax by ψ z (w) = = b a y bx + ay Teorema 45 (Fórmula de De Moivre) Se z = r (cosθ + i sin θ) e n é um inteiro positivo, então Prova Pelo teorema 4 multiplicando novamente z n = r n (cos (nθ) + i sin (nθ)) z = r (cos (θ) + i sin (θ)) z 3 = r 3 (cos (3θ) + i sin (3θ)) O resultado desejado obtém-se por indução em n Seja w C ( 0) Usando a fórmula de De Moivre, tentemos resolver em ordem a z a equação z n = w Suponhamos que w = r (cosθ + i sin θ) e z = ρ (cos ψ + i sin ψ) Então pela fórmula de De Moivre z n = ρ n (cos (nψ) + i sin (nψ))
19 6 Capítulo Números Complexos e pela unicidade da representação polar, temos ρ n = r nψ = θ + kπ, k Z ρ = n r ψ = θ + kπ, k Z n Atendendo à periodicidade do seno e do co-seno, temos ψ = θ + kπ, k =,,, n n Assim ( ( ) ( )) z = n θ + kπ θ + kπ r cos + i sin, k =,, n n n Exemplo 46 Resolva a equação z 8 = Resolução Como = (cos 0 + i sin 0), então ( ( ) ( )) kπ 0 + kπ 8 = cos + i sin, k =,,, Que dá as seguintes raízes: k = 0 : z 0 = k = : z = + i k = : z = i k = 3 : z 3 = + i k = 4 : z 4 = k = 5 : z 5 = i k = 6 : z 6 = i k = 7 : z 7 = i De um modo geral as raízes n-ésimas da unidade formam um polígono convexo regular com um vértice em z = (ver Figura 8) Exemplo 47 Sendo w uma das raiz n-ésima da unidade diferente dela própria, mostre que + w + w + + w n = 0 Resolução Atendendo a que a soma em questão está em progressão geométrica de razão w, temos: n w j = wn w j= Como w é uma raiz n-ésima da unidade, então w n =, logo w n w = 0 w = 0
20 4 Forma polar Potências e quocientes 7 Figura 8: As oito raízes da unidade y i z 3 z x z 5 z 7 i Exercícios Exercício Prove que, para qualquer inteiro k i 4k =, i 4k+ = i, i 4k+ =, i 4k+3 = i Mostre como este resultado dá uma fórmula para i n, n N escrevendo n = 4k + j, 0 j 3 Calcule i 000 Exercício Determine a parte real e a parte imaginária do número complexo z + z, sabendo que z = x + yi Exercício 3 Prove que R(iz) = I(z) e que I(iz) = R(z), z C Exercício 4 Prove a seguinte igualdade zw z w = ( z )( w ), z, w C
21 8 Capítulo Números Complexos Exercício 5 Sendo z k, k = 0,,5 as raízes sextas de 8, calcule S = 5 k=0 z k Exercício 6 Prove que a hipótese x y = pode escrever-se como z + z = Exercício 7 Prove por indução a forma binomial para os números complexos, ie, z, w C temos ( ) ( ) ( ) n n n (z + w) n = z n + z n w + z n w + + zw n + w n, n onde ( n k) = n!/(k!(n k)!) Exercício 8 Prove que se a <, então z < z a āz Exercício 9 Assumindo z < ou w = e que zw, prove que z w zw = Exercício 0 Resolva as seguintes equações z 5 = 0 z 4 + i = 0 Exercício Usando a fórmula de De Moivre deduza as identidades trigonométricas cos 3θ = cos 3 θ 3 cosθ sin θ sin 3θ = 3 cos θ sin θ sin 3 θ Exercício Demonstre a desigualdade triangular para números complexos z + z z + z Em que condições se obtém a igualdade Interprete o resultado geometricamente
22 4 Forma polar Potências e quocientes 9 Exercício 3 Estabeleça a fórmula + z + z + + z n = zn+, z, n N z Use este resultado para deduzir as identidades de Lagrange + cosθ + cos θ + + cosnθ = + sin[(n + )θ], (8) sin θ sin θ + sin θ + + sin nθ = cotgθ cos[(n + )θ] sin θ Sugestão: note que o lado esquerdo de (8) é o mesmo que R( + e iθ + + e inθ ) Exercício 4 Descreva geometricamente cada uma das seguintes regiões I(z) > 0 arg(z) π 4 3 R( z ) < 4 z 4 z
23 Capítulo Funções Analíticas Neste capítulo vamos introduzir os mais importantes conceitos de funções analíticas bem como o cálculo a elas associado Na Secção definimos as funções elementares mais usuais de variável complexa, eg, exponencial, logarítmo, seno, coseno, funções hiperbólicas etc Investigamos algumas propriedades análogas ao cálculo de variável real das funções elemenatres definidas Na Secção vamos explorar os transformados de conjuntos em C por intermédio de funções de variável complexa para podermos tirar algumas conclusões sobre a função Isto porque, ao contrário das funções de variável real, neste caso não podemos fazer uma representação gráfica, pois precisamos de quatro dimensões A continuidade e diferenciabilidade de funções de variável complexa são estudadas nas Secções 3 e 4 Particular destaque é dado às equações de Cauchy-Riemann as quais desempenham um papel importante na teoria das funções analíticas Finalmente na Secção 7 apresentamos as derivadas das funções elementares mais comuns assim como o domínio de validade dessas derivadas Funções Elementares Função exponencial Pretendemos definir e z =?, com z C 0
24 Funções Elementares Sabemos que se x R, a série de Taylor da exponencial é dada por Seja z = x + yi C Temos e x = + x + x! + e z = e x e yi = e x ( + yi + (yi) + (yi)3 + (yi)4! 3! 4! ( ) ( x = e ( y! + y4 4! + i = e x (cosy + i sin y) + (yi)5 5! + ) y y3 3! + (y)5 5! )) Definição Se z = x + yi, então e z := e x (cosy + i sin y) Observação Se z é real, ie, z = x + 0i, a definição corresponde à exponencial usual Proposição 3 Propriedades da função exponencial e z+w = e z e w, z, w C e z 0, z C 3 e x+yi = e x 4 e π i = i; e πi = ; e 3 πi = i; e πi = 5 e z é uma função periódica de período kπi, k Z, ie, e z+kπi = e z, k Z 6 e z = sse z = nπi, n Z Resolução As propriedades,, 4 podem ser verificadas directamente por definição
25 Capítulo Funções Analíticas 5 Suponhamos que e z+w = e z, z C, ie, e w =, sendo w = s + ti, temos e s cost + ie s sin t = { { e s cos t = e s sin t = 0 sin t = 0 { { e s = s = 0 t = kπ, k Z t = kπ, k Z Assim w = kπi, k Z, ie, o período de e z é kπi, k Z 6 ( ) Se z = nπi e z = por 4 ( ) e z = e z+z = e z, z C z = kπi, por 5, k Z Exemplo 4 Para que valores de z se tem (e iz ) = e i z Resolução Seja z = x + yi z = x yi Temos e iz = e y+xi = e y cosx + ie y sin x logo Por outro lado Assim (e iz ) = e y cos x ie y sin x e i z = e y+xi = e y cosx + ie y sin x { e (e iz ) = e i z y cos x = e y cos x e y sin x = e y sin x { { sin x (e y + e y ) = 0 sin x = 0 { { e y = e y e y = e y (e y ) = x = kπ, k Z { y = 0 x = kπ, k Z Conclusão (e iz ) = e i z sse z = kπ, k Z
26 Funções Elementares 3 Observação 5 Dado z C, a sua representação em coordenadas polares é dada por z = z [cos (arg z) + i sin (arg z)] = z exp (i arg z) Funções trigonométricas Da representação vem que sin y = eyi e yi i e yi = cosy + i sin y cosy = eyi + e yi Definição 6 Seja z C, definimos seno e co-seno por sin z := ezi e zi i e cosz = ezi + e zi Observação 7 Novamente se z é real estas definições correspondem às definições usuais de seno e co-seno Proposição 8 As funções trigonométricas de variável complexa verificam propriedades análogas às de variável real sin z + cos z = sin (z + w) = sin z cosw + sin w cosz 3 cos (z + w) = cosz cosw sin z sin w, z, w C Prova Exercício Observação 9 As restantes funções trigonométricas definem-se pelas relações usuais com à custa do seno e do co-seno tan z = sin z cos z, cosz 0 sinh z = ez e z etc, etc cos z cotz = sin z, sin z 0 cosh z = ez + e z
27 4 Capítulo Funções Analíticas Exemplo 0 Mostre que se z = x + yi, então cosz = cos x cosh y i sin x sinh y Resolução Temos por definição cosz = ezi + e zi = [ e y (cosx + i sin x) + e y (cos x i sin x) ] = cosx ey + e y i sin x ey e y = cosxcosh y i sin x sinh y Exemplo Prove que os únicos zeros de cos z são reais Resolução Pelo exemplo 0 temos cosz = 0 cosxcosh y = 0 sin x sinh y = 0 como cosh y, então terá de ser cosx = 0 x = π + kπ, k Z Como para estes valores de x, sin x não se anula, então de sinh y sin x = 0 tira-se que sinh y = 0 y = 0 Assim os zeros de cos z são todos reais, da forma z = π + kπ, k Z 3 Função logarítmica Pretende-se estender o conceito de logarítmo a argumentos complexos, ie, log z =?, z C Um processo natural de definir o logarítmo usando propriedades reais é pela equação log z = log ( re iθ) = Logr + iθ como o argumento de z não é único, arg z = Θ + kπ, k Z, temos log z = Logr + i (Θ + kπ), pelo que a função log é multivalente
28 Funções Elementares 5 y y 0 + π A y0 y 0 x z e z v u Figura : e z é uma bijecção de A y0 em C\ {0} Proposição Consideremos o conjunto A y0 dado por A y0 = {x + yi C : x R, y 0 y < y 0 + π} Então a aplicação e z : A y0 C\ {0} é bijectiva Prova Sejam z, z A y0 (ver Figura ) e z = e z e z z = z z = kπi, k Z x x = 0 y y = kπ, k Z Como y y < π, pois z, z A y0 temos que y y = 0 Assim z = z Logo e z é injectiva Seja w C\ {0} z (=?) A y0 : e z = w Temos e x+yi = w = w e i arg(w) { e x = w e yi = e i arg(w) { x = Log w y = arg w arg w é único porque w A y0 Assim e z é sobrejectiva
29 6 Capítulo Funções Analíticas Definição 3 A função log : C\ {0} C tal que y 0 I (log z) < y 0 + π é definida por log z := Log z + i arg (z) onde arg (z) [y 0, y 0 + π[ Esta função é chamada um ramo da função logarítmo Observação 4 A função log só fica bem definida quando se especifica um intervalo de comprimento π onde arg (z) toma os seus valores Exemplo 5 Calcule log ( + i) nos seguintes ramos arg ( + i) [0, π[ arg ( + i) [π, 3π[ Resolução log ( + i) = Log + π 4 i log ( + i) = Log πi Notação 6 Log z logarítmo usual, onde z > 0 Logz = Log z + i arg (z) com π arg (z) < π ramo principal Proposição 7 A função log z é a inversa de e z no seguinte sentido: para qualquer ramo de log z temos exp (log z) = z e escolhendo a faixa y 0 y < y 0 + π então log (exp (z)) = z onde z = x + yi com y 0 y < y 0 + π Prova log z = Log z + i arg (z) Logo exp (log z) = exp (Log z )exp (i arg (z)) = z exp (i arg (z)) = z Por outro lado log e z = Log e z + i arg (e z ) = Loge x + i arg ( e x e yi) = x + yi = z
30 Funções Elementares 7 Proposição 8 Se z, z C\ {0}, então log (z z ) = log z + log z (modπ) Prova Temos log (z z ) = Log z z + i arg (z z ) onde arg (z z ) [y 0, y 0 + π[ Mas Log z z = Log ( z z ) = Log z + Log z e arg (z z ) = arg (z ) + arg (z ) (modπ) Assim log (z z ) = Log z + i arg (z ) + Log z + arg (z ) (modπ) = log z + log z (modπ) Exemplo 9 Calcule log [( i) ( i)] no ramo [0, π[ Resolução Por um lado log [( i) ( i)] = log ( ) = Log + iπ Por outro lado e log ( i) = Log + i 5 4 π log ( i) = Log + i 7 4 π Logo log [( i) ( i)] = Log + Log ( 5 + i 4 π + 7 ) 4 π = Log + i (3π) = Log + iπ
31 8 Capítulo Funções Analíticas 4 Potências complexas Pretende-se definir z w =?, quando w C e z C\ {(0, 0)} Definição 0 Seja z, w C, define-se z w := exp (w log z) com arg z [y 0, y 0 + π[ (pré-definido) Exemplo Encontre todos os valores de Resolução i i i i : = exp (i log i) [ ( ( π ) )] = exp i Log + + kπ i = exp ( π ) + kπ, k Z 5 Funções trigonométricas e hiperbólicas inversas Podemos agora definir as funções trigonométricas inversas Por exemplo, pretende-rmos definir sin z =?, z C Para tal fazemos: sin z = w sin w = z eiw e iw = z i ( e iw) ize iw = 0 e iw = iz + z Assim w = sin z = i log (iz + ) z
32 Funções Elementares 9 Com um procedimento análogo podemos provar que [ cos z = i log z + ] z Para este último, temos tan z tan z = i ( ) i + z log i z = w tan w = z eiw e iw i e iw + e = z iw ie iw + ie iw = ze iw + ze iw ie iw + i = ze iw + z ( e iw) ( i z) = z i z i e iw = i z w = i ( ) z i log i z w = i ( ) i + z log i z A dedução de outras fórmulas, como [ sinh z = log z + ] z + é deixada como exercício [ cosh z = log z + ] z tanh z = ( ) i + z log i z Exemplo Calcule todos os valores de cosh ( ) mostrando primeiro que cosh z = log [ z + ] z
33 30 Capítulo Funções Analíticas Resolução Seja cosh z = w Então temos cosh w = z ew + e w = z (e w ) ze w + = 0 e w = z + 4z 4 e w = z + [ z w = log z + ] z Assim [ cosh z = log z + ] z No caso em que z = temos ( ) ( ) cosh = log + ( ) = log ± ( ) = ± log + [ ( ) = ± Log + Transformações ] + i (kπ), k Z Ao contrário do que acontece com as funções reais de variável real, onde a representação gráfica de uma função permite tirar conclusões sobre o comportamento da função, as funções de variável complexa w = f (z) com w, z C não permitem uma tal representação, dado que precisaríamos de, pelo menos, 4 dimensões Para se tirar conclusões sobre uma função complexa, analisamos os conjuntos de pontos correspondentes a z e w em dois planos complexos, plano-z, (x, y) e plano-w, (u, v) A correspondência entre pontos dos dois planos diz-se uma aplicação, função ou ainda transformação de pontos do plano-z no plano-w
34 Transformações 3 y x z z v u Figura : Efeito da função quadrado ao primeiro quadrante Exemplo Mostre que a função f (z) = z transforma o primeiro quadrante do plano-z no semiplano superior do plano-w Resolução Sabemos que z = z e que arg (z ) = arg (z) Como z pertence ao primeiro quadrante, então 0 arg (z) π 0 arg (z) π 0 arg ( z ) π, por outro lado 0 z < 0 z < Assim temos o resultado pretendido, (ver Figura ) Exemplo Calcule os transformados das curvas x +y = c, c 0 por meio da função f (z) = x + y yi Resolução Fazendo f (z) = u + vi = x + y yi = c + ( y)i
35 3 Capítulo Funções Analíticas u y k c c v = u v = u Plano z Plano w x v k Figura 3: Imagens de circunferências por meio de f (z) = (x + y ) / yi temos u = c v = y com c y c u = c c v c u = c u v u Assim a função transforma circunferências em segmentos, (ver Figura 3) 3 Noções topológicas Definição 3 Sejam z 0 C e ǫ > 0 Chama-se vizinhança de z 0 de raio ǫ ao conjunto V ǫ (z 0 ) {z C : z z 0 < ǫ} Geometricamente (ver Figura 4) Definição 3 Um subconjunto A C diz-se aberto sse z 0 A, ǫ > 0 : V ǫ (z 0 ) A Geometricamente (ver Figura 5) Intuitivamente um conjunto aberto é um conjunto que não contém nenhum ponto da sua fronteira ou lado
36 3 Noções topológicas 33 y ǫ z 0 x Figura 4: Vizinhança de z 0 de raio ǫ y A ǫ z 0 x Figura 5: Conjunto aberto
37 34 Capítulo Funções Analíticas y y z 0 δ = ǫ w 0 x x Figura 6: Interpretação geométrica de z z 0 f (z) w 0 Definição 33 Seja f : A C C, z 0 A Diz-se que lim z z 0,z z 0 f (z) = a ( C) sse ǫ > 0 δ > 0 : 0 < z z 0 < δ (ver Figura 6) Exemplo 34 Prove que f (z) a < ǫ z lim z,z z = Resolução A função f (z) = z não está definida em z = Quando z z, (z )(z + ) f (z) = = z + z Assim f (z) = (z + ) = z Então dado ǫ > 0 basta tomar δ = ǫ ou menor Observação 35 Se f (z) = u (x, y) + iv (x, y) e lim z z0 f (z) = a = t + si, então lim u (x, y) = t lim v (x, y) = s z z 0 z z0
38 3 Noções topológicas 35 O símbolo z z 0 significa que z se aproxima de z 0 de uma forma arbitrária e não numa direcção em particular Proposição 36 Sejam f e g funções tais que Então temos lim f (z) = a e lim g (z) = b z z 0 z z0 lim z z0 [f (z) + g (z)] = a + b lim z z0 [f (z) g (z)] = ab 3 lim z z0 f(z) g(z) = a b se b 0 Prova Semelhante ao cálculo de variável real Definição 37 Seja A C aberto Dizemos que f : A C é contínua em z 0 A sse lim f (z) = f (z 0 ) z z 0 e que f é contínua em A sse é contínua em cada ponto de z 0 A Observação 38 Outras noções e propriedades, tais como, a de sucessão convergente, sucessão de Cauchy, continuidade por sucessões etc definem-se do mesmo modo como se definem para funções de variável real Exemplo 39 Indique os pontos onde a função é contínua f (z) = z + z + z 3 + Resolução Pela proposição 36 somas, produtos e quocientes de funções contínuas são contínuas, excepto nos zeros do denominador Assim f é contínua em C\{exp( πi), 3 exp(5π i), } 3
39 36 Capítulo Funções Analíticas 4 Derivadas Definição 4 Seja f : A C C, A aberto Diz-se que f é diferenciável em z 0 A se o seguinte limite f (z) f (z 0 ) lim = f (z 0 ) = df z z 0 z z 0 dz z=z0 existe Alternativamente, pondo z = z z 0, f é diferenciável se o limite f (z 0 + z) f (z 0 ) lim z 0 z (z z 0 z 0) existe Este limite é denotado por f (z 0 ) e chama-se derivada de f em z 0 f diz-se analítica ou holomorfa em z 0 A se f (z 0 ) existe e existe derivada em todos os pontos de uma vizinhança de z 0 Se f é analítica em todos os pontos de A diz-se que f é analítica em A Observação 4 A definição de derivada de uma função de variável complexa, embora muito semelhante à derivada de uma função de variável real, é muito mais rica No limite na definição de derivada (Definição 4) aparece uma divisão pelo número complexo z z 0, sendo por isso, necessário ter em conta a natureza especial da divisão de números complexos 3 O limite z z 0 é tomado para uma aproximação arbitrária de z a z 0 e não numa direcção em particular 4 A existência de f (z) permite tirar uma maior informação sobre f, nomeadamente que se f (z) existe, então também existem f, f, f (iv),, o que não acontece no caso real (Pense-se, por exemplo, na função { x se x 0 f (x) = x se x 0 Temos f (x) = x, mas f e as restantes derivadas não existem no ponto x = 0) 5 Se uma função é analítica em alguns pontos de cada vizinhança de um ponto z 0, excepto no ponto z 0, então z 0 é chamado ponto singular ou singularidade da função
40 4 Derivadas 37 Exemplo 43 Prove que se f (z) = z, então f (z 0 ) = z 0 Resolução Por definição temos f (z 0 ) := f (z) f (z 0 ) lim z z0 z z 0 = lim z z0 (z z 0 ) (z + z 0 ) z z 0 = lim z z0 z z 0 z z 0 = lim z z0 (z + z 0 ) = z 0, onde a última passagem é justificada pelo facto de os polinómios serem funções contínuas Proposição 44 Se f (z 0 ) existe e é finita, então f é contínua em z 0 Prova Provar que f é contínua em z 0 é provar que lim f (z) = f(z 0 ) z z 0 lim f (z) f (z 0 ) = 0 z z0 lim [f (z) f (z 0 )] = 0 z z0 [ ] f (z) f (z0 ) lim (z z 0 ) z z0 z z 0 = 0 f (z) f (z 0 ) lim lim (z z 0 ) = 0 z z0 z z 0 z z0 f (z 0 ) 0 = 0 0 = 0 O recíproco da proposição anterior não é verdadeiro Um contra exemplo é dado pela seguinte função: A função é contínua em C, pois f (z) = z lim f (z) = z 0 ǫ > 0 δ > 0 : z z0 < δ z z 0 f (z) z 0 < ǫ
41 38 Capítulo Funções Analíticas Temos z z 0 = ( z z 0 )( z + z 0 ) = z z 0 z + z 0 z z 0 z + z 0 δ ( z z 0 + z 0 ) δ ( z z 0 + z 0 ) Supondo 0 < δ < temos δ ( + z 0 ) = ǫ δ = ǫ + z 0 Cálculo da derivada: f f (z 0 + z) f (z 0 ) (z) = lim z 0 z z 0 + z z 0 = lim z 0 z (z 0 + z) (z 0 + z) z 0 z 0 = lim z 0 = lim z 0 ) Suponhamos que z 0 = 0, então z ( z z 0 + z + z 0 z f (z 0 ) = lim z 0 z = 0 ) Suponhamos que z 0 0 : Fazendo z 0 por diferentes direcções: a) z = x + 0i z = z Logo ) f (z 0 ) = lim z 0 (z 0 + z + z 0 ) = z 0 + z 0 b) z = 0 + yi z = z Logo f (z 0 ) = lim z 0 (z 0 z z 0 ) = z 0 z 0
42 4 Derivadas 39 Como o limite, se existir, é único, tem de ser z 0 + z 0 = z 0 z 0 z 0 = 0 absurdo, pois suposemos que z 0 0 Assim a derivada só existe em z = 0 Por definição esta função não é analítica em nenhum ponto Teorema 45 Suponhamos que f e g são analíticas em A, onde A C é um aberto Então af + bg é analítica em A e (af + bg) (z) = af (z) + bg (z), z A, a, b C fg é analítica em A e (fg) (z) = f (z) g (z) + f (z) g (z), z A 3 Se g (z) 0, z A então f/g é analítica em A e ( ) f (z) = f (z) g (z) f (z) g (z) g [g (z)], z A Prova Semelhante ao cálculo de funções de variável real Observação 46 Como consequências da proposição anterior temos que Todo o polinómio P n (z) = a o +a z + +a n z n é uma função analítica em C e P n (z) = a + a z + na n z n, z, a,, a n C Toda a função racional P n (z) Q m (z) = a o + a z + + a n z n b o + b z + + b m z m é analítica em C excepto nos zeros do denominador
43 40 Capítulo Funções Analíticas Teorema 47 (da função composta) Seja f : A C analítica e g : B C analítica, A, B abertos, com f (A) B Então g f : A C definida por (g f) (z) = g (f (z)) é analítica em A e (g f) (z) = g (f (z))f (z) Prova Sejam z, z 0 A, com f (z) = w e f (z 0 ) = w 0 Defina-se { g(w) g(w0 ) h (w) = w w 0 g (w 0 ) se w w 0 0 se w = w 0 Provemos que h é contínua Para w w 0, h está definida por uma função contínua logo contínua Para w = w 0 temos: lim w w 0 h (w) = g (w) g (w 0 ) lim lim g (w 0 ) w w 0 w w 0 w w 0 = g (w 0 ) g (w 0 ) = 0 Assim lim w w0 h (w) = h (w 0 ) = 0, ie, h é contínua Calculemos, pois Mas (g f) (z 0 ) = lim z z0 (g f) (z) (g f) (z 0 ) z z 0 () h (f (z)) = g (f (z)) g (f (z 0)) g (f (z 0 )) f (z) f (z 0 ) g (f (z)) g (f (z 0 )) = [h (f (z)) + g (f (z 0 ))] [f (z) f (z 0 )] g (f (z)) g (f (z 0)) = [h (f (z)) + g (f (z 0 ))] [f (z) f (z 0)] z z 0 z z 0 Portanto () vem (g f) (z 0 ) = lim z z0 { [h (f (z)) + g (f (z 0 ))] [f (z) f (z } 0)] z z 0 = lim z z0 [h (f (z)) + g (f (z 0 ))] lim z z0 [f (z) f (z 0 )] z z 0 = [0 + g (f (z 0 ))]f (z 0 ) Concluimos, assim, que se z A, então (g f) (z) = g (f (z))f (z)
44 5 Equações de Cauchy-Riemann 4 5 Equações de Cauchy-Riemann Teorema 5 Seja f : A C C, A aberto e z 0 A Então f (z 0 ) existe sse f = u + iv é diferenciável em z 0 = (x 0, y 0 ) no sentido de R (isto é, existem e são contínuas as derivadas parciais de u e v), e u e v satisfazem { u = v x y u = y v x equacões de Cauchy Riemann (C R) Se f (z 0 ) existe, então Prova Por definição temos f (z 0 ) = u x + i v x = f x = v y i u y = i f y f (z 0 ) := lim z z0 f (z) f (z 0 ) z z 0 Seja z = x + y 0 i Então f (z 0 ) = u (x, y 0 ) + iv (x, y 0 ) u (x 0, y 0 ) iv (x 0, y 0 ) lim z z0 x x 0 u (x, y 0 ) u (x 0, y 0 ) v (x, y 0 ) v (x 0, y 0 ) = lim + i lim x x0 x x 0 x x0 x x 0 = u x + i v x () Seja z = x 0 + yi Então f (z 0 ) = u (x 0, y) + iv (x 0, y) u (x 0, y 0 ) iv (x 0 y 0 ) lim z z0 i (y y 0 ) = i lim u (x 0, y) u (x 0, y 0 ) y y 0 y y 0 = i u y + v y + lim y y0 v (x 0, y) v (x 0, y 0 ) y y 0 = v y i u y (3)
45 4 Capítulo Funções Analíticas Como o limite quando existe é único, temos de () e (3) que f (z 0 ) = u x + i v x = v y i u y ou seja Temos ainda que { u = v x y u = y v x f x = f i y (C R) Exercício Provar que as equações de Cauchy-Riemann em coordenadas polares são dadas por { u = v r r θ v = r r e que, se f (z) existe, então ( ) ( ) u u f (z) = (cosθ i sin θ) r + i v = exp ( iθ) r r + i v r u θ Resolução Em coordenadas polares temos { x = r cos θ y = r sin θ e u x = v y u y = v x Obtemos, assim a seguinte representação para f (C R) f (r, θ) = u (x (r, θ), y (r, θ)) + iv (x (r, θ),y (r, θ)) Calculando as derivadas parciais, temos u r = u x x r + u y y r = u u cosθ + x y sin θ
46 5 Equações de Cauchy-Riemann 43 e Assim Por outro lado e Portanto Temos também que v θ = v x x θ + v y y θ = v v ( r sin θ) + (r cosθ) x y ( ) u u = r sin θ + y x cosθ = r u r u r = v r θ v r = v x x r + v y y r = v v cosθ + x y sin θ u θ = u x x = u = r x y θ u ( r sin θ) + θ + u y (r cosθ) y ( ) v v ( sin θ) y x cosθ = r u r v r = u r θ f (z) = u x + i v x onde { r = x + y θ = arctan ( ) y x
47 44 Capítulo Funções Analíticas Então ( θ v x + i r r x + v ) θ θ x = u u cosθ + ( r ) [ v r θ sin θ v + i cos θ + ( r )] r θ sin θ = u ( ) v v cosθ + r r sin θ + i u cosθ r r sin θ ( ) u = (cosθ i sin θ) r + i v r f (z) = u r r x + u θ = exp ( iθ) ( u r + i v r ) Observação 5 As condições de Cauchy-Riemann são condições necessárias para existir derivada As condições suficientes para existir derivada são, além de se ter de verificar as condições de Cauchy-Riemann as funções u, v, u, u, v, v serem contínuas x y x y Exemplo 53 Calcule a derivada das seguintes funções f (z) = z f (z) = z Resolução Neste caso temos que u (x, y) = x y v (x, y) = xy Dado que u x v = x = y u y = y = v x as condições de Cauchy-Riemann verificam-se Como u, v, u x, u y, v x, v y são contínuas em C, então f (z) existe em C e f (z) = u x + i v x = x + iy = z
48 6 Funções harmónicas 45 Temos u (x, y) = x + y v (x, y) = 0 Para se verificar as condições de Cauchy-Riemann, terá de ser: u y u x = x = v y x = 0 = y = v x y = 0 Donde se conclui, dado que u, v, u x, u y, v x, v y, são contínuas em z 0, que a derivada só existe em z = 0, (como já vimos, logo após a Proposição 44) Definição 54 Uma função analítica em C diz-se que é inteira 6 Funções harmónicas Definição 6 Seja u : A C R uma função de classe C Então u diz-se harmónica se u = u x + u = 0 (Laplaciano de u) y Proposição 6 Seja f = u + vi analítica em A, então u e v são funções harmónicas Prova Por f ser analítica temos { u = v x u = y v () y () x (C R) Derivando () em ordem a x e () em ordem a y temos u = v x x y u y = v y x u x + u y = v x y v y x = 0 Provaremos (ver Teorema 334 na pag 73) que se f é analítica, então existem todas as derivadas de f, pelo que, do cálculo de variável real sabemos que se v C (A), então v xy = v yx
49 46 Capítulo Funções Analíticas Definição 63 As funções u e v dizem-se harmónicas conjugadas sse a função f = u + vi é analítica Quando uma das funções harmónicas conjugadas é dada, podemos determinar a outra usando as condições de Cauchy-Riemann Exemplo 64 Verifique se u = y 3 3x y é harmónica em algum domínio e determine a sua harmónica conjugada Resolução Dado que e concluimos que u x = 6xy, u x = 6y u y = 3y 3x, u y = 6y u x + u y = 0 Assim, u é harmónica em C Se v é a harmónica conjugada de u, então as condições de (C-R) dizem que u x = v y 6xy = v y v (x, y) = 3xy + φ (x) Mas, pela outra equação de (C-R), vem que u y = v x 3y 3x = ( 3y + φ (x) ) φ (x) = 3x φ (x) = x 3 + k Logo v (x, y) = 3xy + x 3 + k A função correspondente é f = u + vi dada por f (z) = y 3 3x y + ( 3xy + x 3 + k ) i = (( z 3) + k ) i
50 7 Derivadas de funções elementares 47 7 Derivadas de funções elementares 7 Função exponencial Teorema 7 A aplicação f : C C, z e z é analítica em C e d dz (ez ) = e z Prova Por definição e z = e x (cosy + i sin y) de onde concluimos que u (x, y) = e x cosy v (x, y) = e x sin y que são funções infinitamente diferenciáveis Para provar que e z é analítica temos que verificar as condições de C-R: u x = ex cosy = v y u y = ex sin y = v x Como as derivadas parciais são são de classe C, então e z é analítica em C Temos ainda que d dz (ez ) = u x + i v x = ex (cos y + i sin y) = e z Exemplo 7 Calcule a derivada da função f (z) = e ez Resolução Dado que a composta de funções inteiras é uma função inteira, pela regra da função composta para a derivada temos f (z) = e z e ez
51 48 Capítulo Funções Analíticas 7 Funções trigonométricas Teorema 73 As funções sin z e cosz são inteiras com derivadas d dz (sin z) = cosz d (cosz) = sin z dz Prova Basta ter em conta a definição de sinz sin z := eiz e iz i e usar a regra da derivada da função composta O mesmo para o cosz Observação 74 As derivadas das restantes funções trigonométricas são obtidas u-sando as regras de derivação (teorema 45) e as derivadas do seno, co-seno e da exponencial tan z = sec z sinh z = cosh z tanh z = sech z cot z = csc z cosh z = sinh z coth z = csch z 73 Função logarítmica Teorema 75 Seja A = C\ {x + yi : x 0 y = 0} Define-se um ramo do logarítmo em A por log z = Log z + i arg (z), π arg (z) < π chamado ramo principal do logarítmo Então log z é analítica em A (ver Figura 7) com derivada d dz (log z) = z Prova Seja z = re iθ um elemento em A Então log z = Logr + iθ e assim obtemos u (r, θ) = Logr
52 7 Derivadas de funções elementares 49 x y Figura 7: Domínio de analiticidade de log z e v (r, θ) = θ As condições de (C-R) em coordenadas polares verificam-se, pois u r = r = r v θ v r = 0 = r u θ Como no domínio A u, v, assim como as suas derivadas, são contínuas, concluimos que log z é analítica em A, e temos, pelo Exercício que d dz (log z) = exp (iθ) ( u r + i v r ) = r exp (iθ) = z Observação 76 A razão da escolha do domínio de analiticidade de logarítmo tem a ver com o facto de o argumento de z estando no intervalo π arg z < π não ser uma função contínua sobre o eixo real negativo De facto, para um número no eixo real negativo o argumento é π, ao passo que o valor do argumento na parte superior de cada vizinhança desse número é tão próximo de π quanto se queira, ou seja, a função argumento dá um salto ao cortar o eixo real negativo
53 50 Capítulo Funções Analíticas x y Figura 8: Domínio de analiticidade de log z Os pontos do eixo real negativo, θ = π, assim como a origem são pontos singulares (ver Observação 5 na pág 36) 3 O raio θ = π chama-se corte do logarítmo, para o ramo principal, ie, é a recta ou curva de pontos singulares 4 O ponto singular z = 0 comum a todos os cortes de ramo da função multivalente log z é chamado nó de ramos ou ponto de ramificação Exemplo 77 Calcule a derivada da função log (z ) e indique o domínio de analiticidade Resolução Podemos derivar a função logarítmo desde que arg ( z ) ±π Seja arg(z) = θ arg (z ) = θ Então θ ±π θ ± π Assim em D = C\ {x + yi : x = 0, y R}, (ver Figiura 8)
54 7 Derivadas de funções elementares 5 e neste domínio temos d ( ( )) log z = dz z 74 Potências complexas Lembremos que é uma função multivalente z c := exp (c log z) Proposição 78 Para qualquer ramo da função logarítmo, a função z a z é inteira e tem derivada d dz (az ) = log (a) a z Fixando um ramo do logarítmo, por exemplo o principal, a função z z b é analítica no domínio do ramo do logarítmo escolhido e temos d ( ) z b = bz b dz 3 A função z z /n é analítica no domínio do logarítmo (ver Figura 9) e tem derivada Prova Atendendo à definição d ( ) z /n = dz n z n a z := exp (z log a) e pela derivada da função composta obtemos d dz (az ) = d dz [exp (z log a)] = d dz (z log a) exp (z log a) = log (a) az, onde log a é uma constante A derivada é válida em C
55 5 Capítulo Funções Analíticas x y Figura 9: Domínio de analiticidade de z z b e z z /n Como z b := exp (b log z), então d dz ( z b ) = d dz [exp (b log z)] = d dz (b log z) exp (b log z) = zb b z = bzb a qual é válida no domínio do logarítmo 3 Análogo a Note que se b N, então z b é analítica em C, mas em geral z b é analítica no domínio do logarítmo Exemplo 79 Explique o que está mal no seguinte raciocínio Sabemos que a z := exp (z log a) portanto d dz (az ) = a z log a Por outro lado d dz (az ) = za z (4) Assim za z = a z log a z = a log a
56 7 Derivadas de funções elementares 53 y 3π π π 3π x Figura 0: Domínio de analiticidade de (e z + ) / Resolução O que está mal é a igualdade (4), pois d dz (az ) za z dado que a derivada de a z é a z log a para qualquer ramo do logarítmo Exemplo 70 Diferencie a função z e z + indicando a região onde a função é analítica Resolução Pela proposição anterior a função é analítica no domínio do logarítmo Escolhendo o ramo principal do logarítmo que é analítica em C\ {x + yi : x 0 y = 0} A região de holomorfia de e z +, A, é tal que se z A então e z + não pode ser real negativo (ver Figura 0) Procuremos z tal que e z + R 0, ie, { e x cosy + 0 e x sin y = 0 { (e x + 0 y = kπ) ( e x + 0 y = (k + )π) y = kπ, k Z { x 0 y = (k + )π, k Z
57 54 Capítulo Funções Analíticas Assim o domínio de analiticidade de e z + é A = C\ {x + yi : x 0 y = (k + )π, k Z} e temos para z A d ( ez + ) = dz e z e z +
58 7 Derivadas de funções elementares 55 Exercícios Exercício Encontre a parte real e a parte imaginária de exp (e z ) Exercício 3 Simplifique exp (z + i) e exp (iz ), e mostre que exp (z + i) + exp ( iz ) exp (x) + exp ( yx) Exercício 4 Atendendo à definição de sinh z e cosh z, prove que cosh z sinh z = sinh(z + z ) = sinh z cosh z + cosh z sinh z 3 cosh (z + z ) = cosh z cosh z + sinh z sinh z 4 sinh (x + yi) = sinh x cosy + i cosh x sin y 5 cosh (x + yi) = cosh x cosy + i sinh x sin y Exercício 5 Use a equação sin z = sin x cosh y + i sinh y cosx onde z = x + yi para provar que sinh y sin z cosh y Exercício 6 Mostre que sin z sin x e cosz cosx Exercício 7 Encontre todas as raízes da equação exp (z) = 3 Exercício 8 Calcule todas as raízes das equações cosz = sinh z = i Exercício 9 Prove que log (z/w) = log (z) log (w) (modπ), z, w C\ {0} Exercício 0 Calcule todos os valores de log ( + i) i Exercício Calcule todos os valores de exp(log cosh () ) começando por demonstrar que [ cosh (z) = log z + ( ] z )
59 56 Capítulo Funções Analíticas Exercício Calcule todos os valores de ( + i) +i Exercício 3 Determine a imagem das faixas semi-infinitas x 0 0 y π x 0 0 y π por meio de f (z) = exp (z), exibindo os transformados das fronteiras Exercício 4 Considere a função f (z) = z Determine o conjunto de todos os pontos do plano-z que são transformados nas rectas u = c v = c no plano-w Faça c, c =, 4,, 4 Exercício 5 Prove que a função f (z) = z é contínua e não tem derivada em nenhum ponto E a função I(z)? Exercício 6 Prove que o seguinte limite não existe lim z 0 lim z z Exercício 7 Prove formalmente, por mudança de variáveis, as equações de Cauchy -Riemann em coordenadas polares u = v u r r θ θ = r v r e que a derivada de uma função em coordenadas polares é dada por ( ) u f (z) = exp ( iθ) r + i v r Augustin Louis CAUCHY ( ), engenheiro e matemático francês com enorme contribuição para o desenvolvimento da matemática e outras ciências, em especial a física, através de cerca de 8 centenas de trabalhos publicados, foi um dos fundadores da análise matemática moderna, e o seu nome está ligado a numerosos teoremas Georg Friedrich Bernhard RIEMANN (86-866), matemático alemão que sucedeu a Dirichlet como professor em Göttingen e se tornou notável pelos seus trabalhos sobre a teoria das funções analíticas (de que foi um dos fundadores), geometrias não euclidianas, teoria dos números e física matemática
60 7 Derivadas de funções elementares 57 Exercício 8 Considere a função, f, definida por f(z) = { ( z) z se z 0 0 se z = 0 Prove que as condições de Cauchy-Riemann se verificam em z = 0 mas que a derivada de f não existe nesse ponto Exercício 9 Considere a função f (z) = zi(z) Mostre que f (0) = 0 Será f (z) analítica em z = 0? Justifique Exercício 0 Prove que se f é analítica num domínio, D, então ( x + ) f(z) = 4 f (z) y Exercício Mostre que o módulo e o argumento da função analítica, f (z) = R (x, y)exp (iφ (x, y)), R, φ funções reais, verificam as seguintes relacções R x = R φ y, R y = R φ x Exercício Seja f uma função analítica num domínio D que não contém o ponto z = 0 Sendo f(z) = u(r, θ) + iv(r, θ), use as condições de Cauchy- Riemann em coordenadas polares, para mostrar que, em D, tanto u como v satisfazem a equação de Laplace 3 em coordenadas polares, admitindo que u, v C (D), r u r + r u r + u θ = 0 Exercício 3 Verifique que se f é analítica em A e u então f é constante em A + v x y = 0 em A, Exercício 4 Seja f uma função analítica em A e f(z) constante em A Mostre que f é constante em A Exercício 5 Seja f(z) = u(x, y) + iv(x, y) uma função analítica em A, tal que u + v = 0, em A Mostre que f(z) = icz + d, onde c R e x y d C\R 3 Pierre Simon de LAPLACE (749-87), astrónomo, matemático e físico francês com importantes contribuições para a mecânica celeste e teoria das probabilidades
61 58 Capítulo Funções Analíticas Exercício 6 Seja u uma função tal que u C (A) tal que u + u = 0 x y Prove que f = u x i u é analítica em A y Exercício 7 Verifique que u é harmónica em algum domínio e determine as suas harmónicas conjugadas u(x, y) = x( y) u(x, y) = sinh(x) sin y Exercício 8 Derive e indique a região de analiticidade de cada uma das seguintes funções log (e z + ) z z 3 e z 4 e az a z, a R Exercício 9 Calcule a derivada da função z e indique o domínio onde essa derivada é válida
62 Capítulo 3 Integrais Este capítulo é dedicado ao estudo dos integrais de funções complexas Neste contexto, o teorema de Cauchy desempenha um papel fundamental na teoria das funções analíticas, nomeadamante permite-nos provar que se f é analítica então existem todas as derivadas da função f Muitos dos resultados deste capítulo dependem deste teorema Não menos inportante são os resultados da Secção 33 que trata da fómula integral de Cauchy Esta fórmula é tão importante que muito dos resultados obtidos posteriormente podem ser considerados consequencia da fórmula integral de Cauchy para as derivadas Em particular destacamos os teoremas de Louville e de Morera Finalmente neste capítulo vamos abordar o módulo máximo de funções analíticas em domínios limitados, ver Secção 34 para mais pormenores 3 Integral de caminho Seja h : [a, b] R C uma função dada por h (t) = u (t) + iv (t), com u, v funções contínuas em [a, b] Definimos o integral definido por b a h (t) dt := b a u (t) dt + i b a v (t)dt C, onde b a u (t) dt e são integrais de uma variável real b a v (t) dt 59
63 60 Capítulo 3 Integrais () () (3) (b) (a) (b) (b) (a) (a) (4) (a) = (b) (b) (5) (a) Figura 3: Curvas em C () classe C ; () seccional/ classe C ; (3) suave; (4) simples fechada; (5) caminho Definição 3 Seja : [a, b] C uma curva em C diz-se de classe C se (t) existe em ]a, b[ e é contínua em [a, b] diz-se seccionalmente de classe C se (t) existe em ]a i, a i [ e é contínua em [a i, a i ], onde [a, b] = n j= [a j, a j ] 3 diz-se uma curva suave se (t) existe e (t) 0, t [a, b] 4 diz-se uma curva fechada de Jordan ou curva simples fechada se (a) = (b) e (t) (t ) t, t [a, b] \ {a, b} com (t) contínua 5 diz-se um caminho se é seccionalmente suave (Ver Fig 3) Definição 3 Seja f : A C C contínua e : [a, b] C um caminho tal que ([a, b]) A Define-se o integral de f ao longo de por f (z) dz := n i= ai a i f ( (t)) (t)dt
64 3 Integral de caminho 6 Proposição 33 Se f (z) = u (x, y) + iv (x, y), então f (z) dz = [u (x, y)dx v (x, y)dy] + i [u (x, y)dy + v (x, y)dx] Prova Seja (t) = (x (t), y (t)) = x (t) + iy (t) (t) = x (t) + iy (t) Temos b f (z) dz := [u (x (t), y (t)) + iv (x (t), y (t))] [x (t) + iy (t)]dt = a b [u (x (t), y (t)) x (t) v (x (t), y (t)) y (t)] dt a b +i a [u (x (t),y (t))y (t) + v (x (t), y (t)) x (t)] dt que, em termos de integrais de caminho reais não é mais do que u (x, y)dx v (x, y)dy + i u (x, y)dy + v (x, y)dx Este resultado pode ser obtido formalmente, calculando f (z) dz = [u (x, y) + iv (x, y)] (dx + idy) Proposição 34 Sejam f, g funções complexas contínuas, c, c C e,, cami-nhos em C Então c f + c g = c f + c g f = f 3 + f = f + f Prova Exercício Exemplo 35 Calcule o valor do integral z dz, onde é o segmento de recta que une z = 0 a z = + i, (ver Fig 3)
65 6 Capítulo 3 Integrais y + i x Figura 3: Curva de 0 a + i Resolução o Processo Seja com (t) = + i Assim z dz := 0 : [0, ] C, t t + it (t + ti) ( + i) dt = ( + i) = ( + i) (3 + 4i) = i 0 t dt = ( + i) (3 + 4i) 3 0 ( 3t + 4t i ) dt o Processo y = x com 0 x, z = x + xi dz = ( + i)dx Assim z dz = = ( ) x + x i ( + ) i dx ( + ) ( ) 34 i + i x dx = = i 0 ( + i ) ( i ) 8 3 Vamos resolver o mesmo exercício percorrendo um caminho diferente O caminho que une z = 0 a z = mais o de z = a z = +i, (ver Figura 33)
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Notas breves sobre números complexos e aplicações
 Notas breves sobre números complexos e aplicações Complementos de Análise Matemática - ESI DMat - Universidade do Minho Dezembro de 2005 1 Definição O conjunto dos números complexos, denotado por C, pode-se
Notas breves sobre números complexos e aplicações Complementos de Análise Matemática - ESI DMat - Universidade do Minho Dezembro de 2005 1 Definição O conjunto dos números complexos, denotado por C, pode-se
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1. (1) Descreva as regiões do plano complexo definidas por z i c z, onde c é um número real não negativo.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
1 Números Complexos e Plano Complexo
 UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
ANÁLISE MATEMÁTICA 3 NÚMEROS COMPLEXOS
 ANÁLISE MATEMÁTICA 3 NÚMEROS COMPLEXOS APÊNDICE Maria do Rosário de Pinho e Maria Margarida Ferreira Setembro 1998 Faculdade de Engenharia da Universidade do Porto Licenciatura em Engenharia Electrotécnica
ANÁLISE MATEMÁTICA 3 NÚMEROS COMPLEXOS APÊNDICE Maria do Rosário de Pinho e Maria Margarida Ferreira Setembro 1998 Faculdade de Engenharia da Universidade do Porto Licenciatura em Engenharia Electrotécnica
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
TURMA:12.ºA/12.ºB. O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz)
 GUIA DE ESTUDO NÚMEROS COMPLEXOS TURMA:12.ºA/12.ºB 2017/2018 (ABRIL/MAIO) Números Complexos O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz) A famosa igualdade de Euler i e 10 A
GUIA DE ESTUDO NÚMEROS COMPLEXOS TURMA:12.ºA/12.ºB 2017/2018 (ABRIL/MAIO) Números Complexos O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz) A famosa igualdade de Euler i e 10 A
Lista 1 - Métodos Matemáticos II Respostas
 Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Análise Complexa e Equações Diferenciais 1 o Semestre de 2011/ o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2011, 10h,
 Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Fichas de Análise Matemática III
 Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
SUMÁRIO CAPÍTULO 1 CAPÍTULO 2
 SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
MATEMÁTICA A - 12o Ano N o s Complexos - Equações e problemas Propostas de resolução
 MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
Álgebra. Exercícios de auto-avaliação
 Universidade Eduardo Mondlane Faculdade de Ciências Departamento de Matemática e Informática Álgebra Para Estudantes do Ensino à Distância do Curso de Licenciatura em Matemática, ano 01 Unidade 1 Números
Universidade Eduardo Mondlane Faculdade de Ciências Departamento de Matemática e Informática Álgebra Para Estudantes do Ensino à Distância do Curso de Licenciatura em Matemática, ano 01 Unidade 1 Números
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Análise Complexa e Equações Diferenciais 1 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Lista 2 - Métodos Matemáticos II Respostas
 Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
Lista - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele fornecer
1 Números Complexos. Seja R o conjunto dos Reais. Consideremos o produto cartesiano R R = R 2 tal que:
 Números Complexos e Polinômios Prof. Gustavo Sarturi [!] Esse documento está sob constantes atualizações, qualquer erro de ortografia, cálculo, favor comunicar. Última atualização: 01/11/2018. 1 Números
Números Complexos e Polinômios Prof. Gustavo Sarturi [!] Esse documento está sob constantes atualizações, qualquer erro de ortografia, cálculo, favor comunicar. Última atualização: 01/11/2018. 1 Números
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
MATEMÁTICA A - 12o Ano N o s Complexos - Equações e problemas Propostas de resolução
 MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
ANÁLISE MATEMÁTICA IV
 ANÁLISE MATEMÁTICA IV (2 ō semestre 2006/07) LEC e LEGM Professor Responsvel: Maria João Borges http://www.math.ist.utl.pt/ mborges/amiv Sumários das Aulas Teóricas Aula 37: (05/06) Aula 36: (04/06) Continuação
ANÁLISE MATEMÁTICA IV (2 ō semestre 2006/07) LEC e LEGM Professor Responsvel: Maria João Borges http://www.math.ist.utl.pt/ mborges/amiv Sumários das Aulas Teóricas Aula 37: (05/06) Aula 36: (04/06) Continuação
Análise Complexa Derivação e Analiticidade Turma EIA /2011
 Análise Complexa Derivação e Analiticidade Turma EIA+4 00/0 No que segue, consideramos f uma função complexa de variável complexa definidanumconjuntoabertod Cez 0 Dumnúmerocomplexo. Sef temderivadaemz
Análise Complexa Derivação e Analiticidade Turma EIA+4 00/0 No que segue, consideramos f uma função complexa de variável complexa definidanumconjuntoabertod Cez 0 Dumnúmerocomplexo. Sef temderivadaemz
1 a Lista de Exercícios de Métodos Matemáticos II
 a Lista de Exercícios de Métodos Matemáticos II. Simplifique: [ ] + i a Re + i i b Im 4 i + i 6 i + i d i 4 e eπi i e πi f e +πi. Encontre todos os valores de C tais que: a i 0 b + i + i d 6 + 64 0 e i
a Lista de Exercícios de Métodos Matemáticos II. Simplifique: [ ] + i a Re + i i b Im 4 i + i 6 i + i d i 4 e eπi i e πi f e +πi. Encontre todos os valores de C tais que: a i 0 b + i + i d 6 + 64 0 e i
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Conjunto dos Números Complexos
 Conjunto dos Unidade Imaginária Seja a equação: x + 0 Como sabemos, no domínio dos números reais, esta equação não possui solução, criou-se então um número cujo quadrado é. Esse número, representado pela
Conjunto dos Unidade Imaginária Seja a equação: x + 0 Como sabemos, no domínio dos números reais, esta equação não possui solução, criou-se então um número cujo quadrado é. Esse número, representado pela
Análise Complexa e Equações Diferenciais 2 ō Semestre 2009/2010
 Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
! " # $ % & ' # % ( # " # ) * # +
 a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Introdução: A necessidade de ampliação dos conjuntos Numéricos. Considere incialmente o conjunto dos números naturais :
 Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
Introdução: A necessidade de ampliação dos conjuntos Numéricos Considere incialmente o conjunto dos números naturais : Neste conjunto podemos resolver uma infinidade de equações do tipo A solução pertence
Prova Substitutiva de MAT Cálculo IV - IFUSP 2 ō semestre de /12/2009 Prof. Oswaldo Rio Branco de Oliveira
 Prova Substitutiva de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009-8/2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : GABARITO Q 2 3 4 5 6 7 8 9 0 2 Total N JUSTIFIQUE TODAS AS PASSAGENS
Prova Substitutiva de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009-8/2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : GABARITO Q 2 3 4 5 6 7 8 9 0 2 Total N JUSTIFIQUE TODAS AS PASSAGENS
Pequena Introdução à Trigonometria Hiperbólica
 Pequena Introdução à Trigonometria Hiperbólica (Filipe Oliveira, 9) 1 Motivação Consideremos o plano euclidiano munido de um referencial ortonormado (, e 1, e ). Quando θ percorre o intervalo [; π[, o
Pequena Introdução à Trigonometria Hiperbólica (Filipe Oliveira, 9) 1 Motivação Consideremos o plano euclidiano munido de um referencial ortonormado (, e 1, e ). Quando θ percorre o intervalo [; π[, o
MATEMÁTICA A - 12o Ano N o s Complexos - Potências e raízes Propostas de resolução
 MATEMÁTICA A - 1o Ano N o s Complexos - Potências e raízes Propostas de resolução Exercícios de exames e testes intermédios 1. Escrevendo 1 + i na f.t. temos 1 + i ρ cis θ, onde: ρ 1 + i 1 + 1 1 + 1 tg
MATEMÁTICA A - 1o Ano N o s Complexos - Potências e raízes Propostas de resolução Exercícios de exames e testes intermédios 1. Escrevendo 1 + i na f.t. temos 1 + i ρ cis θ, onde: ρ 1 + i 1 + 1 1 + 1 tg
Variável Complexa
 Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
GABARITO. 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan
 GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Funções do Plano Complexo(MAT162) Notas de Aulas Prof Carlos Alberto S Soares
 Funções do Plano Complexo(MAT62) Notas de Aulas 2-209 Prof Carlos Alberto S Soares O Plano Complexo Considerando a nossa definição de número complexo, é claro que existe uma correspondênca biunívoca entre
Funções do Plano Complexo(MAT62) Notas de Aulas 2-209 Prof Carlos Alberto S Soares O Plano Complexo Considerando a nossa definição de número complexo, é claro que existe uma correspondênca biunívoca entre
Análise Complexa e Equações Diferenciais Guia 3 João Pedro Boavida. 21 a 28 de Setembro
 2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
Funções analíticas LISTA DE EXERCÍCIOS
 LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Funções Elementares do Cálculo Complexos 2
 Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
RESOLUÇÃO DO PRIMEIRO TESTE 31 DE OUTUBRO DE 2015 MEMEC,LEAN. f(x + iy) = x + x 3 + i(1 + y + y 2 )
 ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
NÚMEROS COMPLEXOS CAPÍTULO
 NÚMEROS COMPLEXOS CAPÍTULO 1 Neste capítulo, exploramos as estruturas algébrica e geométrica do sistema dos números complexos, para o que supomos conhecidas várias propriedades correspondentes dos números
NÚMEROS COMPLEXOS CAPÍTULO 1 Neste capítulo, exploramos as estruturas algébrica e geométrica do sistema dos números complexos, para o que supomos conhecidas várias propriedades correspondentes dos números
1 o Semestre 2018/2019 MEC
 ACED Análise Complea e Equações Diferenciais o Semestre 208/209 MEC Conteúdo I. Números compleos, funções compleas........... II. Transformações conformes e diferenciabilidade de funções compleas.............................
ACED Análise Complea e Equações Diferenciais o Semestre 208/209 MEC Conteúdo I. Números compleos, funções compleas........... II. Transformações conformes e diferenciabilidade de funções compleas.............................
Capítulo 2 Funções de uma variável complexa. A origem dos números complexos repousa na solução de equações algébricas
 Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
Funções Elementares do Cálculo Complexos 1
 Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
1. Polinómios e funções racionais
 Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
Análise Complexa e Equações Diferenciais
 Instituto Superior Técnico Departamento de Matemática Análise Complexa e Equações Diferenciais Cursos: MEMec,LEAN (25/6, Semestre ) Apontamentos das aulas teóricas. Introdução Este texto consiste numa
Instituto Superior Técnico Departamento de Matemática Análise Complexa e Equações Diferenciais Cursos: MEMec,LEAN (25/6, Semestre ) Apontamentos das aulas teóricas. Introdução Este texto consiste numa
Gr aficos de Fun c oes Elementares
 Gráficos de Funções Elementares O gráfico de uma f.r.v.r. é uma curva ou uma união de curvas. Para a sua determinação é necessário conhecer o comportamento da função. Entre os vários aspectos da teoria
Gráficos de Funções Elementares O gráfico de uma f.r.v.r. é uma curva ou uma união de curvas. Para a sua determinação é necessário conhecer o comportamento da função. Entre os vários aspectos da teoria
ANÁLISE MATEMÁTICA IV 1 o Teste (LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ) Justifique cuidadosamente todas as respostas.
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
3 ā Prova de MAT Cálculo IV - IFUSP 2 ō semestre de /12/2009 Prof. Oswaldo Rio Branco de Oliveira
 3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
Análise Complexa e Equações Diferenciais
 Instituto Superior Técnico Departamento de Matemática Análise Complexa e Equações Diferenciais Cursos: MEC,LEGM (24/5, Semestre ) Apontamentos das aulas teóricas. Introdução Este texto consiste numa transcrição
Instituto Superior Técnico Departamento de Matemática Análise Complexa e Equações Diferenciais Cursos: MEC,LEGM (24/5, Semestre ) Apontamentos das aulas teóricas. Introdução Este texto consiste numa transcrição
Polinómio e série de Taylor
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
Análise Matemática IV Problemas para as Aulas Práticas
 Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Lista 3 - Métodos Matemáticos II
 Lista 3 - Métodos Matemáticos II Prof. Jorge Delgado. Seja a curva poligonal de vértices 2( + i), 2( + i), 2( + i) e 2( i) orientada positivamente. Use a fórmula integral de auchy para verificar que: e
Lista 3 - Métodos Matemáticos II Prof. Jorge Delgado. Seja a curva poligonal de vértices 2( + i), 2( + i), 2( + i) e 2( i) orientada positivamente. Use a fórmula integral de auchy para verificar que: e
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
PROVAS DE ANÁLISE COMPLEXA
 PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
PROVAS DE ANÁLISE COMPLEXA PROFESSOR RICARDO SA EARP () Seja Ω um domínio do plano complexo. Sejam f e g funções holomorfas em Ω. Assuma que g nunca se anule em Ω e que f(z) ( ) R, para todo z Ω. g(z)
Parte II. Análise funcional II
 Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Trabalho feito e apresentado para a disciplina de matemática em: Instituto Estadual de Educação - 3º ano(306)
 Trabalho feito e apresentado para a disciplina de matemática em: Instituto Estadual de Educação - 3º ano(306) Colocado na internet Estude e se baseie nesse trabalho para os seus, mas não copie. Plágio
Trabalho feito e apresentado para a disciplina de matemática em: Instituto Estadual de Educação - 3º ano(306) Colocado na internet Estude e se baseie nesse trabalho para os seus, mas não copie. Plágio
Análise Complexa e Equações Diferenciais. Apontamentos das aulas teóricas
 Análise Complexa e Equações Diferenciais Apontamentos das aulas teóricas 2 Índice Introdução 3. Revisões sobre números complexos 3 2. Representação trigonométrica dos números complexos 4 3. Noções topológicas
Análise Complexa e Equações Diferenciais Apontamentos das aulas teóricas 2 Índice Introdução 3. Revisões sobre números complexos 3 2. Representação trigonométrica dos números complexos 4 3. Noções topológicas
1. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R
 . Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
Mais Alguns Aspectos da Derivação Complexa
 Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Variável Complexa
 Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Pre-calculo 2013/2014
 . Números reais, regras básicas de cálculo com fracções, expoentes e radicais Sumário: Número reais, regras básicas de cálculo com fracções, expoentes e radicais. Ler secções. e. do livro adoptado.. Pre-calculo
. Números reais, regras básicas de cálculo com fracções, expoentes e radicais Sumário: Número reais, regras básicas de cálculo com fracções, expoentes e radicais. Ler secções. e. do livro adoptado.. Pre-calculo
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
MÉTODOS MATEMÁTICOS. Claudia Mazza Dias Sandra Mara C. Malta
 MÉTODOS MATEMÁTICOS Claudia Mazza Dias Sandra Mara C. Malta 1 Métodos Matemáticos Aulas: De 03/11 a 08/11-8:30 as 11:00h Ementa: 1. Funções 2. Eq. Diferenciais Ordinárias de 1 a ordem 3. Sistemas de Equações
MÉTODOS MATEMÁTICOS Claudia Mazza Dias Sandra Mara C. Malta 1 Métodos Matemáticos Aulas: De 03/11 a 08/11-8:30 as 11:00h Ementa: 1. Funções 2. Eq. Diferenciais Ordinárias de 1 a ordem 3. Sistemas de Equações
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Séries de Laurent e Teoremas de Cauchy
 Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Números Complexos. Cálculo Diferencial e Integral III WELLINGTON JOSÉ CORRÊA. Campo Mourão, Paraná. Brasil. Universidade Tecnológica Federal do Paraná
 Ministério da Educação Universidade Tecnológica Federal do Paraná ampus ampo Mourão Números omplexos álculo Diferencial e Integral III WELLINGTON JOSÉ ORRÊA ampo Mourão, Paraná Brasil Sumário Wellington
Ministério da Educação Universidade Tecnológica Federal do Paraná ampus ampo Mourão Números omplexos álculo Diferencial e Integral III WELLINGTON JOSÉ ORRÊA ampo Mourão, Paraná Brasil Sumário Wellington
(a + bi) - (c + di) = a - c + (b - d)i. zz"' = l. (a + bi)(.x + yi) = 1. a -b x =,v= -j. a~+b~ a + b~ a 2 + b 2 a 2 +b 2
 174 Geometria Analítica \ O oposto do número complexo z- a + bié o número -z = (-l)z = -a - bi, enquanto que o seu conjugado éz = a-bi. Na Figura 6.1, aparecem o número 2 + o seu oposto -2 - / e o seu
174 Geometria Analítica \ O oposto do número complexo z- a + bié o número -z = (-l)z = -a - bi, enquanto que o seu conjugado éz = a-bi. Na Figura 6.1, aparecem o número 2 + o seu oposto -2 - / e o seu
2 Funções exponencial e logarítmica complexas
 Equações reais, Soluções imaginárias. 1 Introdução Carlos A. Gomes UFRN Na última edição da RPM número 77) há um artigo Por que e iθ = cosθ + i.senθ?, do professor José Paulo Carneiro, onde é exibida uma
Equações reais, Soluções imaginárias. 1 Introdução Carlos A. Gomes UFRN Na última edição da RPM número 77) há um artigo Por que e iθ = cosθ + i.senθ?, do professor José Paulo Carneiro, onde é exibida uma
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Cálculo Diferencial e Integral Química Notas de Aula
 Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
1.1 Função Exponencial
 VARIÁVEL COMPLEXA 3. AS FUNÇÕES ELEMENTARES 1.1 Função Exponencial 1. Escreva as funções abaixo sob a forma u (x; y) + iv (x; y) : (a) w = exp (2z) (b) w = exp z 2 (c) w = exp (iz) : 2. Em cada caso, determine
VARIÁVEL COMPLEXA 3. AS FUNÇÕES ELEMENTARES 1.1 Função Exponencial 1. Escreva as funções abaixo sob a forma u (x; y) + iv (x; y) : (a) w = exp (2z) (b) w = exp z 2 (c) w = exp (iz) : 2. Em cada caso, determine
Revisão do Teorema de Green
 Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Tópicos de Matemática Elementar
 Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Análise Complexa e Equações Diferenciais
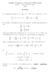 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: Matemática DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias ANO:12º
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: Matemática DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias ANO:12º
Capítulo 5. séries de potências
 Capítulo 5 Séries numéricas e séries de potências Inicia-se o capítulo com a definição de série numérica e com oção de convergência de séries numéricas, indicando-se exemplos, em particular o exemplo da
Capítulo 5 Séries numéricas e séries de potências Inicia-se o capítulo com a definição de série numérica e com oção de convergência de séries numéricas, indicando-se exemplos, em particular o exemplo da
NÚMEROS COMPLEXOS CAPÍTULO
 NÚMEROS COMPLEXOS CAPÍTULO 1 Neste capítulo, exploramos as estruturas algébrica e geométrica do sistema dos números complexos, para o que supomos conhecidas várias propriedades correspondentes dos números
NÚMEROS COMPLEXOS CAPÍTULO 1 Neste capítulo, exploramos as estruturas algébrica e geométrica do sistema dos números complexos, para o que supomos conhecidas várias propriedades correspondentes dos números
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Sucessões. , ou, apenas, u n. ,u n n. Casos Particulares: 1. Progressão aritmética de razão r e primeiro termo a: o seu termo geral é u n a n1r.
 Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
Concluímos esta secção apresentando alguns exemplos que constituirão importantes limites de referência. tan θ. sin θ
 aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Análise Complexa e Equações Diferenciais Guia 6 João Pedro Boavida. 19 a 28 de Outubro
 19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ano 01-1 a Fase Proposta de resolução GRUPO I 1. Sabemos que P B A P B A P A P B A P B A P A Como P A 0,, temos que P A 1 P A 1 0, 0,6 Como P B A 0,8 e P A 0,6, temos
Prova Escrita de MATEMÁTICA A - 1o Ano 01-1 a Fase Proposta de resolução GRUPO I 1. Sabemos que P B A P B A P A P B A P B A P A Como P A 0,, temos que P A 1 P A 1 0, 0,6 Como P B A 0,8 e P A 0,6, temos
Universidade Federal de Pelotas. Instituto de Física e Matemática Pró-reitoria de Ensino. Módulo de Limites. Aula 01. Projeto GAMA
 Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
