Dep. Matemática Pura. FCUP ÁLGEBRA LINEAR II
|
|
|
- Suzana Terra Corte-Real
- 7 Há anos
- Visualizações:
Transcrição
1 Dep. Matemática Pura. FCUP ÁLGEBRA LINEAR II Resumo das aulas teóricas e práticas 1. o ano da licenciatura em Matemática Ano lectivo de 005/06 João Nuno Tavares
2 ÍNDICE: 1 Determinantes. Produtos vectorial e misto (ou triplo) em IR Determinantes Produto vectorial. Produto misto (ou triplo) em IR 3. Interpretação geométrica do determinante Interpretação geométrica do det A Espaços vectoriais com produto interno 10.1 Espaços Euclideanos reais Espaços Hermitianos (ou Unitários) complexos Norma Ortogonalidade Aplicações à geometria Bases ortonormadas num espaço vectorial com produto interno Método de ortogonalização de Gram-Schmidt Decomposição ortogonal. Teorema da aproximação óptima Aplicações. Mínimos quadrados Exercícios Subespaços invariantes. Subespaços próprios. Valores próprios Conjugação Subespaços invariantes Valores e vectores próprios de um operador linear. Operadores diagonalizáveis Cálculo de valores e vectores próprios Sistemas dinâmicos lineares discretos Exercícios Transformações ortogonais e unitárias Transformações ortogonais e unitárias. Exemplos Isometrias em IR. Os grupos O() e SO()
3 1 4.3 Isometrias em IR 3. Rotações. Ângulos de Euler. Os grupos O(3) e SO(3) Transformações unitárias em C. Os grupos U() e SU() Exercícios Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Operadores auto-adjuntos (simétricos e hermitianos) Teorema espectral para operadores auto-adjuntos Diagonalização de formas quadráticas reais Diagonalização simultânea de duas formas quadráticas reais Exercícios Cónicas e quádricas afins Parábola, Elipse e Hipérbole Quádricas Cónicas e quádricas afins Redução à forma canónica da equação geral de uma cónica Quaterniões e Rotações 95 Referências 1. T.M. Apostol: Calculus, vol.1 e vol.. Xerox College Publishing International Textbook series, Postnikov M.: Leçons de Géométrie, vol.1 e. Éditions MIR, Moscou, Banchoff T., Wermer J.. Linear Algebra through Geometry. UTM, Springer- Verlag, New York, Smith L.: Linear Algebra. UTM, Springer-Verlag, New York, Curtis C.W.: Linear Algebra, An Introductory Approach. UTM, Springer- Verlag, New York, Lipschutz S.: Linear Algebra. Schaum s Outline Series. McGraw-Hill Book Company, Hernández E.: Álgebra y Geometría (. a edicion). Addison-Wesley/Universidad Autónoma de Madrid, 1994.
4 Capítulo 1 Determinantes. Produtos vectorial e misto (ou triplo) em IR Determinantes [ a b 1.1 Matrizes... Dada uma matriz A =, com entradas em Ik, definimos o c d seu determinante det A, como sendo o escalar: [ a b det A = det = ad bc Ik (1.1.1) c d Representemos por A 1 = [ a c Um cálculo directo mostra que: e ainda que: e A = [ b d as colunas da matriz A, de tal forma que: det A = det [A 1 A = ad bc (1.1.) det [A 1 A 0 sse A 1, A são linearmente independentes (1.1.3) det [A 1 A = det [A A 1 (1.1.4) det [A 1 + A 1 A = det [A 1 A + det [A 1 A (1.1.5) det [A 1 A + A = det [A 1 A + det [A 1 A (1.1.6) onde A t é a transposta de A. det [λ A 1 A = λ det [A 1 A = det [A 1 λ A λ Ik (1.1.7) det I = 1 (1.1.8) det (AB) = det A det B (1.1.9) det (A 1 ) = (det A) 1 A GL(; Ik) (1.1.10) det (P 1 A P ) = det A P GL(; Ik) (1.1.11) det (A) = det (A t ) (1.1.1)
5 1.1. Determinantes 3 Além disso é possível provar que para uma matriz A M, (Ik): A é inversível se e só se det A 0 e, nesse caso: [ A 1 a b = c d 1 = 1 [ det A d c b a (1.1.13) Finalmente, se L : V V é um operador linear num espaço vectorial V de dimensão, sobre Ik, define-se o respectivo determinante det L, como sendo o determinante da matriz de L, relativamente a uma qualquer base de V. Por (1.1.10), esta definição não depende da base escolhida. Veremos en breve uma interpretação geométrica para det L, no caso real. 1. Matrizes Dada uma matriz A =, com entradas em Ik, definimos o seu determinante det A, como sendo o escalar: a b c det A = det d e f g h k [ [ e f d f = a det b det h k g k Representemos por: A 1 = as colunas da matriz A, de tal forma que: a d g, A = É possível mostrar as seguintes propriedades do det : b e h a b c d e f g h k [ d e + c det g h e A 3 = c f k Ik (1.1.14) det A = det [A 1 A A 3 (1.1.15) (i). det [A 1 A A 3 0 sse A 1, A, A 3 são linearmente independentes. (ii). det [A 1 A A 3 muda de sinal, sempre que se permuta um par de colunas. (iii). det [A 1 + A 1 A A 3 = det [A 1 A A 3 + det [A 1 A A 3 (1.1.16) det [A 1 A + A A 3 = det [A 1 A A 3 + det [A 1 A A 3 (1.1.17) det [A 1 A A 3 + A 3 = det [A 1 A A 3 + det [A 1 A A 3 (1.1.18) det [λ A 1 A A 3 = λ det [A 1 A A 3 = det [A 1 λ A A 3 = det [A 1 A λ A 3 λ Ik (1.1.19)
6 1.1. Determinantes 4 e ainda que: (iv). onde A t é a transposta de A. det I = 1 (1.1.0) det (AB) = det A det B (1.1.1) det (A 1 ) = (det A) 1 A GL(3; Ik) (1.1.) det (P 1 A P ) = det A P GL(3; Ik) (1.1.3) det (A) = det (A t ) (1.1.4) (v). Além disso é possível provar que para uma matriz A M 3,3 (Ik): Nesse caso, a inversa de A = A é inversível se e só se det A 0 a b c d e f g h k lugar definimos a chamada matriz adjunta de A, adj A, através de: pode ser calculada da seguinte forma: em primeiro adj A = e h b h b e f k c k c f d g a g a d f k c k c f d g a g a d e h b h b e t (1.1.5) Esta matriz é pois obtida substituindo cada entrada de A pelo determinante, chamado o cofactor dessa entrada, obtido por remoção da linha e coluna que contêm essa entrada, afectado de um sinal + ou, como está indicado. Finalmente: A 1 = 1 adj A (1.1.6) det A Se L : V V é um operador linear num espaço vectorial de dimensão 3, sobre Ik, define-se o respectivo determinante det L, como sendo o determinante da matriz de L, relativamente a uma qualquer base de V. Por (1.1.3), esta definição não depende da base escolhida. Veremos en breve uma interpretação geométrica para det L, no caso real. 1.3 Matrizes n n... A generalização da função determinante para matrizes quaisquer n n, está contida no teorema seguinte, cuja demonstração omitimos. Dada uma matriz A M n (Ik), digamos A = [A i j, representemos por A 1, A,, A n as respectivas n colunas. A matriz A será escrita na forma: A = [A 1 A A n
7 1.1. Determinantes Teorema... Existe uma única aplicação det : det : M n (Ik) Ik A det A (1.1.7) que satisfaz as seguintes três propriedades: det [A 1 A i A j A n = det [A 1 A j A i A n det [A 1 A i + λ A i A n = det [A 1 A i A n + λ det [A 1 A i A n det 1 n = 1, onde 1 n é a matriz identidade n n. Esta função determinante verifica, além disso, as seguintes propriedades: 1. det (AB) = det A det B. det (A t ) = det A 3. det A 0 se e só se A fôr inversível. 4. Se A fôr inversível, então det (A 1 ) = (det A) 1 5. det (P 1 AP ) = det A, se P fôr inversível. 6. Se à se obtem a partir de A, usando as transformações elementares sobre A então: det à = λdet A, se à se obtem a partir de A multiplicando uma linha (ou uma coluna) por λ Ik. det à = det A, se à se obtem a partir de A permutando duas linhas (ou duas colunas). det à = det A, se à se obtem a partir de A substituindo uma linha (respectivamente, uma coluna) pela que se obtem somando a essa linha (respectivamente, coluna) um múltiplo escalar de uma outra. 7. O det A pode ser obtido pela seguinte regra de Laplace: fixamos uma qualquer linha i da matriz A = [A i j e desenvolvemos segundo esta linha : det A = n ( 1) i+j A i j det Âi j (1.1.8) j=1 onde Âi j representa a matriz (n 1) (n 1) que se obtem a partir de A, omitindo a linha i e a coluna j.. Estas propriedades serão usadas sistemàticamente no cálculo prático de determinantes. Finalmente, se L : V V é um operador linear num espaço vectorial de dimensão n, sobre Ik, define-se o respectivo determinante det L, como sendo o determinante da matriz de L, relativamente a uma qualquer base de V. Como det (P 1 LP ) = det L, se P fôr inversível, esta definição não depende da base escolhida.
8 1.. Produto vectorial. Produto misto (ou triplo) em IR 3. Interpretação geométrica do determinante 6 1. Produto vectorial. Produto misto (ou triplo) em IR 3. Interpretação geométrica do determinante 1.5 Produto vectorial em IR 3... Comecemos por recordar o que é o produto vectorial x x de dois vectores em IR 3. Dados dois vectores x = y z e x = y z, em IR 3, define-se o produto vectorial x x, de x por x, como sendo o seguinte vector de IR 3 : x x def = (yz y z) i + (zx z x) j + (xy x y) k (1..1) O produto vectorial x y, pode ser obtido desenvolvendo segundo a primeira linha, o determinante formal: i j k x y = det x y z x y z 1.6 Propriedades... A seguir indicam-se as propriedades mais importantes deste produto vectorial, todas elas de demonstração simples (que deve ser feita como exercício). O produto vectorial é bilinear: (x + y) z = x z + y z x (y + z) = x y + x z λ x y = x λ y = λ (x y), λ IR, x, y, z IR 3 (1..) O produto vectorial é antissimétrico: x y = y x (1..3) Além disso, se x IR 3 e y IR 3, são ambos não nulos, então: 1. x y é perpendicular a x e a y, i.e.:. (x y) x = 0 = (x y) y (1..4) Se x e y são linearmente independentes, x y é perpendicular ao plano gerado por x e y. x y = x y sin θ (1..5) onde θ é o ângulo entre x e y. Portanto, x y é igual à área do paralelogramo cujos lados adjacentes são x e y. 3. x y = 0 x e y são linearmente dependentes.
9 1.. Produto vectorial. Produto misto (ou triplo) em IR 3. Interpretação geométrica do determinante 7 4. O produto vectorial não é associativo. De facto: (x y) z = (x z)y (y z)x (1..6) enquanto que: x (y z) = (x z)y (x y)z (1..7) Em particular, se consideramos o paralelogramo de lados adjacentes x = contido no plano z = 0, vemos que a respectiva área é dada por: x x = = i j k det x y 0 x y 0 [ x y det x y = xy x y x y 0 e x = = área do paralelogramo gerado por x e x (1..8) x y 0, Uma equação (cartesiana) para o plano vectorial span IR {u, v}, gerado por dois vectores u, v IR 3 {0}, linearmente independentes, é: (u v) x = 0 (1..9) 1.7 Produto misto (ou triplo) em IR 3... produto misto (ou triplo). Definamos agora, ainda em IR 3, o chamado Dados três vectores x, y, z em IR 3, define-se o produto misto (ou triplo) [x, y, z, de x, y e z (por esta ordem), através de: É fácil ver que [x, y, z é dado por: [x, y, z x (y z) (1..10) [x, y, z = det [x y z x 1 y 1 z 1 = det x y z (1..11) x 3 y 3 z Propriedades... Eis algumas propriedades do produto triplo: São válidas as igualdades seguintes, que se deduzem das propriedades sobre determinantes: [x, y, z = [y, z, x = [z, x, y = [y, x, z = [x, z, y = [z, y, x (1..1)
10 1.3. Interpretação geométrica do det A 8 O volume vol (x, y, z), do paralelipípedo de lados adjacentes x, y, z IR 3, é igual ao módulo do produto misto: vol (x, y, z) = [x, y, z (1..13) Com efeito, o volume de um paralelipípedo é igual ao produto da área da base pela sua altura. A base é o paralelogramo de lados adjacentes x e y, e por isso, a sua área é x y. A altura é igual à norma da projecção de z sobre um vector perpendicular à base. Mas x y é perpendicular à base, e, portanto, a projecção de z sobre x y, é igual a: donde se deduz fàcilmente o resultado. z (x y) x y (x y) (1..14) Quando x 1, x e x 3 são linearmente independentes, de tal forma que: det [x 1 x x 3 0 dizemos que a base ordenada {x 1, x, x 3 } é positiva se det [x 1 x x 3 > 0, e negativa se det [x 1 x x 3 < Interpretação geométrica do det A Consideremos agora uma aplicação linear A : IR 3 IR 3. A imagem do cubo Q IR 3, gerado pelos vectores da base canónica (que é positiva) {e 1, e, e 3 }: Q = {ae 1 + be + ce 3 : 0 a, b, c 1} é o paralelipípedo A(Q), de lados adjacentes A(e 1 ), A(e ) e A(e 3 ). a 1 Pondo A(e 1 ) = a 1 1 e 1 + a 1 e + a 3 1 e 1 a 1 3 = a 1, A(e ) = a 1 a 3 e 1 + a e + a 3 e 3 = a, e 1 a 3 a 1 A(e 3 ) = a 1 3 e 1 + a 3 e + a 3 3 e 3 3 = a 3 sabemos que o volume deste paralelipípedo é igual a: a 3 3 Portanto: vol A(Q) = [A(e 1 ), A(e ), A(e 3 ) = det [A(e 1 ) A(e ) A(e 3 ) a 1 = det 1 a 1 a 1 3 a 1 a a 3 a 3 1 a 3 a 3 3 = det A (1.3.1) vol A(Q) = det A (1.3.) Mais geralmente, se P é um paralelipípedo gerado pelos vectores x, y e z, então a imagem A(P) é o paralelipípedo gerado por A(x), A(y) e A(z), e é fácil provar que o volume dessa imagem é igual a: vol A(P) = [A(x), A(y), A(z) = det [A(x) A(y) A(z) = det A vol (P) (1.3.3)
11 1.3. Interpretação geométrica do det A 9 Em particular, se os vectores x, y e z são linearmente independentes, de tal forma que vol P 0, então: vol A(P) det A = (1.3.4) vol P Diz-se que uma aplicação linear inversível A : IR 3 IR 3 preserva a orientação (ou é positiva) se det A > 0, e que inverte a orientação (ou é negativa) se det A < 0.
12 Capítulo Espaços vectoriais com produto interno.1 Espaços Euclideanos reais.1 Definição... Seja V um espaço vectorial real. Um produto interno em V é, por definição, uma aplicação: : V V IR (.1.1) (u, v) u v que satisfaz as três propriedades seguintes: [PI1. é uma forma bilinear: (u + v) w = u w + v w u (v + w) = u w + u w λu v = u λv = λ u v (.1.) [PI. é uma forma simétrica: u v = v u (.1.3) [PI3. é não degenerada: u v = 0 v V u = 0 (.1.4) u, v, w V, λ IR. Um produto interno diz-se um produto interno Euclideano, se satisfaz além disso a seguinte propriedade: [PI4. é uma forma definida positiva: u u 0, u V (.1.5) Um espaço vectorial real, munido de um produto interno Euclideano chama-se um espaço Euclideano. Outras notações muito comuns para u v são por exemplo u, v, β(u, v), g(u, v), u v ou ainda u v. 10
13 .1. Espaços Euclideanos reais 11. Exemplo [Produto interno Euclideano usual em IR n... Dados dois vectores x = [x i e y = [y i, em IR n, define-se o respectivo produto interno (Euclideano), como sendo o escalar x y IR, dado por: x y def = n x i y i = x 1 y 1 + x y + + x n y n i=1 = x t y em notação matricial (.1.6) O espaço vectorial IR n, munido deste produto interno Euclideano, diz-se o espaço Euclideano usual e nota-se por IE n..3 Exemplo [Produto interno L em C o ([a, b, IR)... Consideremos o espaço vectorial real constituído pelas funções contínuas reais, definidas no intervalo [a, b IR. Dadas duas funções f, g C o ([a, b, IR), define-se o respectivo produto interno L, como sendo o escalar f g IR, dado por: f g def = b a f(t)g(t) dt (.1.7).4 Exemplo [Produto interno de Minkowski em IR 4... Dados dois vectores x = x 0 y 0 x 1 x e y = y 1 y, em IR4, define-se o respectivo produto interno de Minkowski, como x 3 y 3 sendo o escalar x y IR, dado por: x y = x 0 y 0 + x 1 y 1 + x y + x 3 y 3 y 0 = [ x 0 x 1 x x 3 y 1 y y 3 = x t η y (.1.8) onde η representa a matriz simétrica: (.1.9) O produto interno de Minkowski não é definido positivo, isto é, não é verdade que x x 0, x IR 4. Com efeito, por exemplo o vector e 0 = (1, 0, 0, 0), satisfaz e 0 e 0 = 1. Note no entanto que a restrição do produto escalar de Minkowski ao hiperplano {0} IR 3 = {x = (x α ) IR 4 : x 0 = 0} = IR 3, é um produto interno euclideano, portanto em particular definido positivo..5 Expressões matriciais... Seja (V, ) um espaço vectorial real, de dimensão n, com um produto interno Euclideano.
14 .1. Espaços Euclideanos reais 1 Seja C = [ e 1 e e n uma base qualquer para V, escrita como um vector-linha com entradas vectoriais e i. Se u, v V podemos escrever: onde [v C = v 1. v n v = i v i e i = [ e 1 e e n v 1 v. v n = C [v C (.1.10) é o vector-coluna das componentes do vector v na base C. Analogamente: u = i u i e i = C [u C Calculemos agora o produto interno u v : u v = u i e i v j e j i j = u i v j e i e j i,j = i,j g ij u i v j = [u T C G C [v C (.1.11) onde definimos a chamada matriz de Gram, G C = [g ij, do produto interno, na base C através de: def = e i e j (.1.1) g ij Como u v = v u, deduzimos que a matriz de Gram G C é simétrica, isto é: G T C = G C Como v v > 0, v 0 V deduzimos que a matriz de Gram G C é definida positiva, isto é: [v T C G C [v C = i,j g ij v i v j > 0, v i não simultâneamente nulos É possível provar os critérios seguintes (necessários e suficientes) para decidir quando uma matriz simétrica G = [g ij é definida positiva: n = g ij > 0, g 11 g 1 g 1 g > 0 n = 3 g ij > 0, g 11 g 1 g 1 g > 0, g 11 g 1 g 13 g 1 g g 3 g 31 g 3 g 33 > 0
15 .. Espaços Hermitianos (ou Unitários) complexos 13. Espaços Hermitianos (ou Unitários) complexos.6 Definição... Seja V um espaço vectorial complexo. Um produto interno Hermitiano em V é, por definição, uma aplicação: : V V C (u, v) u v (..1) que satisfaz as propriedades seguintes: [PH1. é uma forma sesquilinear, isto é, é linear na primeira variável e semi-linear na segunda variável 1 : (u + v) w = u w + v w u (v + w) = u w + u w (..) λu v = λ u v u λv = λ u v (..3) [PH. é uma forma Hermitiana: u v = v u (..4) [PH3. é não degenerada: u v = 0 v V u = 0 (..5) [PH4. é definida positiva: u, v, w V, λ C. u u 0 (..6) Um espaço vectorial complexo, munido de um produto interno Hermitiano chama-se um espaço Hermitiano ou um espaço unitário..7 Exemplo [Produto interno Hermitiano usual em C n... Dados dois vectores z = [z i e w = [w i, em C n, define-se o respectivo produto interno (Hermitiano), como sendo o escalar x y C, dado por: z w def = n z i w i = z 1 w 1 + z w + + z n w n i=1 = [z 1 z z n w 1 w. w n = z t w em notação matricial (..7) O espaço vectorial C n, munido deste produto interno Euclideano, diz-se o espaço unitário usual e nota-se por U n. 1 em Física, nomeadamente em Mecânica Quântica, é usual considerar outra convenção - linearidade na segunda variável e semi-linearidade na primeira variável!
16 .3. Norma 14.8 Exemplo [Produto interno L em C o ([a, b, C)... Consideremos o espaço vectorial real constituído pelas funções contínuas complexas, definidas no intervalo [a, b IR. Dadas duas funções f, g C o ([a, b, C), define-se o respectivo produto interno L, como sendo o escalar f g C, dado por:.3 Norma f g def = b a f(t)g(t) dt (..8).9 Definição [Norma... Seja (V, ) um espaço com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo). Define-se a norma v, de um vector v V, através da fórmula: v def = v v (.3.1).10 A norma verifica as propriedades seguintes: [N1. é positiva e não degenerada: v 0 e v = 0 sse v = 0 (.3.) [N. é homogénea (positiva): λv = λ v (.3.3) [N3. satisfaz a desigualdade triangular seguinte: v, w V, λ Ik = IR ou C. v + w v + w (.3.4) Todas as propriedades são de demonstração imediata com excepção da desigualdade triangular, que resulta da seguinte proposição:.11 Proposição [Desigualdade de Cauchy-Schwarz... v w v w, v, w V (.3.5) Dem.: Se w = 0 a desigualdade é trivial. Se w 0 consideremos o vector: u = v v w w w de tal forma que u w = 0. Temos então que: ( 0 u = v v w ) ( w w v v w ) w w o que demonstra a desigualdade. = v v v w w v w = v v w w (.3.6)
17 .4. Ortogonalidade 15.1 Demonstremos agora a desigualdade triangular (.3.4): u + v = u + v u + v = u u + u v + v u + v v = u + u v + u v + v = u + Re u v + v u + u v + v u + u v + v, pela desigualdade de Cauchy-Schwarz (.3.5) = ( u + v ) e portanto u + v u + v, como se pretendia..13 Exemplos... (i). No espaço Euclideano IE n, a norma de um vector x = (x i ) IR n é dada pelo teorema de Pitágoras: x = [ n 1/ x t x = (x i ) (.3.7) (ii). No espaço Unitário U n, a norma de um vector z = (z i ) C n é dada por: i=1 z = [ n 1/ z t z = z i (.3.8) (iii). No espaço Unitário C o ([a, b, C), munido do produto interno L, dado por (..8): def f g = b a f(t)g(t) dt, a norma de uma função f Co ([a, b, C) é dada por: i=1 f = [ b 1/ f f = f(t) dt (.3.9) Neste exemplo, a desigualdade de Cauchy-Schwarz toma o aspecto: b a [ b f(t)g(t) dt enquanto que a desigualdade triangular tem o aspecto seguinte: [ b 1/ [ b f(t) + g(t) dt.4 Ortogonalidade a a a 1/ 1/ [ b dt f(t) dt g(t) (.3.10) a a 1/ [ b 1/ f(t) dt + g(t) dt (.3.11) a.14 Definição... Seja (V, ) um espaço com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo). Dois vectores u, v V dizem-se ortogonais se: u v = 0 (.4.1)
18 .4. Ortogonalidade Ângulo não orientado... Suponhamos agora que (V, ) é um espaço real Euclideano. Dados dois vectores não nulos u, v V, deduzimos da desigualdade de Cauchy-Schwarz que: 1 u v u v 1 (.4.) o que permite definir o ângulo (não orientado) θ = θ(u, v) [0, π, entre os referidos vectores não nulos u, v V, como sendo o único θ [0, π, tal que: cos θ = u v u v [ 1, 1 (.4.3) Portanto: u v = u v cos θ(u, v) (.4.4) Como vimos antes, dois vectores u, v V dizem-se ortogonais se u v = 0. Se ambos são não nulos isto significa que o ângulo θ(u, v) é igual a π/..16 Definição [Ortogonal de um subconjunto... Seja (V, ) um espaço com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo). Se S é um subconjunto não vazio de V, define-se o ortogonal de S como sendo o subconjunto S de V constituído por todos os vectores que são ortogonais a todos os vectores de S: S def = {u V : u s = 0, s S} (.4.5) Vamos verificar que S é um subespaço de V. De facto, se u, v S, então u s = 0 e v s = 0, s S e portanto u + v s = u s + v s = 0, s S, i.e., u + v S. Anàlogamente λu S, λ Ik, se u S..17 Hiperplanos vectoriais... No espaço Euclideano IE n, dado um vector não nulo u IR n {0}, o conjunto dos vectores x IE n que são ortogonais a u: {x IE n : x u = 0} (.4.6) formam um subespaço em IE n, que se diz o hiperplano (vectorial) ortogonal a u. Se x = (x i ) é um ponto genérico desse hiperplano, e se u = (u i ), a equação x u = 0, é equivalente à seguinte equação cartesiana: u i x i = u 1 x 1 + u x + + u n x n = 0 (.4.7) i.18 Hiperplanos afins em IE n...
19 .5. Aplicações à geometria 17 No espaço Euclideano IE n, com a estrutura afim canónica, dado um ponto A e um vector não nulo u IR n {0}, o conjunto dos pontos P IE n tais que AP = P A é ortogonal a u: {P IE n : AP u = 0} (.4.8) diz o hiperplano (afim) ortogonal a u, que passa em A. Se OA = (a i ), u = (u i ) e se OP = (xi ) é um ponto genérico desse hiperplano, a equação AP u = 0, é equivalente a: 0 = ( OP OA) u = OP u OA u = u i x i a i u i i i e portanto à seguinte equação cartesiana: u i x i = u 1 x 1 + u x + + u n x n = c (.4.9) onde c = OA) u = i a iu i. i.19 Teorema [Pitágoras... Seja (V, ) um espaço com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo), e u, v V dois vectores ortogonais. Então: Dem.: u + v = u + v (.4.10) u + v = u + v u + v = u + v + u v + v u = u + v (.4.11).5 Aplicações à geometria.0 Exemplo... As diagonais de um losango intersectam-se perpendicularmente. Dem.: Como OQRP é um losango, u = v. Pretendese provar que QP OR, isto é que, (u v) (u + v) = 0. Mas: (u v) (u + v) = u v = 0
20 .5. Aplicações à geometria 18.1 Exemplo [Lei dos cossenos... Num triângulo plano (ABC), onde a = BC, etc. tem-se que: c = a + b ab cos C Dem.: Escolhamos um referencial com origem em C, e ponhamos u = CA e v = CB. Então AB = v u, e daí que: AB = v u = v u v + u ou, com as notações referidas: c = a + b ab cos C. Exemplo... Se R é um ponto sobre um círculo de diâmetro P OQ, mostre que P R QR. Dem.: Seja u = OQ, v = OR. Então P R = OR OP = u + v QR = OR OQ = v u Sabe-se que u = v e portanto: P R QR = (u + v) (v u) = v u = 0.3 Exemplo... As alturas de um triângulo intersectam-se num único ponto (chamado o ortocentro do triângulo). Dem.: Pretende-se encontrar um ponto X tal que: AX BC = 0, BX CA = 0, CX AB = 0 Identificando um ponto P com o seu vector de posição OP, relativamente a uma origem fixa O no plano, é fácil verificar a identidade seguinte: (X A) (C B)+(X B) (A C)+(X C) (B A) = 0 (.5.1) Seja X o ponto de intersecção de duas das alturas, digamos, das alturas partindo de A e de B. Temos então que, lembrando que AX = X A, etc: (X A) (C B) = 0 (.5.) (X B) (A C) = 0 (.5.3)
21 .5. Aplicações à geometria 19 Subtraindo (.5.) e (.5.3) de (.5.1), obtemos: como se pretendia. (X C) (B A) = 0.4 Exemplo... Dados dois pontos distintos A B no plano, mostrar que o lugar geométrico dos pontos P cuja distância a A é o dobro da distância a B é um círculo..5 Exemplo... Calcular a distância entre um ponto P e um hiperplano afim em IE n. Res... Suponhamos que esse hiperplano é perpendicular ao vector u 0 e passa num ponto a e, portanto, tem equação: (x a) u = 0 ou x u + c = 0, c = a u A recta que passa em P OP = p e tem a direcção do vector u, tem equação: x(t) = p + tu O ponto desta recta que pertence ao plano referido, corresponde ao valor do parâmetro t que verifica: 0 = x(t) u + c = (p + tu) u + c = p u + t u + c t = p u + c u A distância entre um ponto P p e o hiperplano afim é pois dada por: d = p x(t) = p p + p u + c u u p u + c = u Assim por exemplo: No plano, a distância entre um ponto P = (α, β) e a recta afim ax + by + c = 0 é: d = p u + c u = (α, β) (a, b) + c (a, b) = aα + bβ + c (a + b ) 1/ No espaço, a distância entre um ponto P = (α, β, γ) e o plano afim ex + fy + gz + h = 0 é: d = p u + c u = (α, β, γ) (e, f, g) + h (e, f, g) = eα + fβ + gγ + h (e + f + g ) 1/.6 Exemplo... Calcular a distância entre um ponto P e uma recta afim em IE 3, quando: 1. essa recta é definida parametricamente.. essa recta é definida como intersecção de dois planos afins.
22 .6. Bases ortonormadas num espaço vectorial com produto interno 0.6 Bases ortonormadas num espaço vectorial com produto interno.7 Definição [Base ortonormada... Seja (V, ) um espaço vectorial de dimensão n com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo). Uma base {e 1,, e n } diz-se uma base ortonormada para V se: { def 1 se i = j e i e j = δ ij = 0 se i j (.6.1).8 Proposição... Seja (V, ) um espaço vectorial de dimensão n com um produto interno (Euclideano se V é real ou Hermitiano se V é complexo) e {e 1,, e n } uma base ortonormada para V. Então v V: n v = v e i e i (.6.) e: Dem.: Cálculo directo. v = i=1 n v e i (.6.3) i=1.7 Método de ortogonalização de Gram-Schmidt.9 Ortogonalização de Gram-Schmidt... Dada uma base qualquer {f 1,, f n }, para V, é possível construir, a partir dela, uma base ortogonal {e 1,, e n }, para V: e i e j = 0, i j através do chamado processo de ortogonalização de Gram-Schmidt, que passamos a descrever: [1. Em primeiro lugar pômos: [. e 1 = f 1 (.7.1) Em segundo lugar, começamos por calcular a chamada projecção ortogonal de f sobre a recta gerada por f 1 = e 1. Esta projecção ortogonal, por estar na recta gerada por f 1 = e 1, vai ser um vector do tipo λe 1, onde λ Ik é calculado pela condição de que f λe 1 e 1 = 0. Obtemos então: λ = f e 1 e 1 Pômos agora e igual a: e = f f e 1 e 1 e 1 (.7.)
23 .7. Método de ortogonalização de Gram-Schmidt 1 [3. Em terceiro lugar, começamos por calcular a chamada projecção ortogonal de f 3 sobre o plano gerado por {f 1, f }, que é também o plano gerado por {e 1, e }. Esta projecção ortogonal, por estar no plano gerado por {e 1, e }, vai ser um vector do tipo λe 1 + ηe, onde λ, η Ik são calculados pela condição de que f 3 (λe 1 + ηe ) e 1 = 0 e f 3 (λe 1 +ηe ) e = 0. Fazendo os cálculos, atendendo a que e 1 e, obtemos: λ = f 3 e 1 e 1, η = f 3 e e Portanto a projecção ortogonal de f 3 sobre o plano gerado por {e 1, e } é dada por: f 3 e 1 e 1 e 1 + f 3 e e e Pômos agora e 3 igual a: e 3 = f 3 f 3 e 1 e 1 e 1 f 3 e e e (.7.3) [k. o processo decorre agora indutivamente: se supômos já construídos os vectores ortogonais {e 1,..., e k }, de tal forma que: span{e 1,..., e k } = span{f 1,..., f k } o vector e k+1 será construído da seguinte forma - começamos por calcular a chamada projecção ortogonal de f k+1 sobre o subespaço gerado por {e 1,..., e k }. Esta projecção ortogonal é dada por: k f k+1 e i e i e i Pômos agora e k+1 igual a: i=1 e k+1 = f k+1 k i=1 f k+1 e i e i e i (.7.4) É claro que a base ortogonal assim obtida, pode ser transformada numa base ortonormada, normalizando os vectores e i, isto é, dividindo cada um deles pela respectiva norma..30 Polinómios de Legendre... Consideremos o espaço vectorial V constituído por todas as funções polinomiais de grau n, definidas no intervalo [ 1, 1, munido do produto interno L : p q = 1 1 p(t)q(t) dt
24 .8. Decomposição ortogonal. Teorema da aproximação óptima Uma base para V é {1, t, t,, t n }. Quando aplicamos o processo de ortogonalização de Gram- Schmidt a esta base obtemos os chamados polinómios de Legendre {ψ 0, ψ 1, ψ,, ψ n }. Vejamos como. Em primeiro lugar pômos: Depois pômos: Em seguida: ψ 0 (t) = 1 ψ 1 = t t = t t dt dt 1 = t (.7.5) ψ = t t t t t t 1 1 t dt = t = t dt t3 dt 1 1 t dt t (.7.6) e procedendo da mesma forma: ψ 3 = t t ψ 4 = t t (.7.7) Quando normalizamos estes polinómios obtemos os chamados polinómios de Legendre normalizados {ϕ 0, ϕ 1, ϕ,, ϕ n }: 1 ϕ 0 = 3 ϕ 1 = t ϕ = 1 5 (3t 1) ϕ 3 = 1 7 (5t3 3t). (.7.8).8 Decomposição ortogonal. Teorema da aproximação óptima.31 Teorema [Decomposição ortogonal... Consideremos um espaço vectorial com um produto interno (V, ) (Euclideano se V é real ou Hermitiano se V é complexo), e seja S um
25 .8. Decomposição ortogonal. Teorema da aproximação óptima 3 subespaço de dimensão finita. Então: V = S S (.8.1) isto é, qualquer vector v V pode ser representado de maneira única como uma soma de dois vectores: v = s + (v s), onde s S e v s S (.8.) Além disso: v = s + v s (.8.3) Dem.: Como S tem dimensão finita, existe uma base ortonormada {e 1,..., e m } para S, onde m = dim S. Dado um vector qualquer v V, definamos: s def = m v e i e i (.8.4) i=1 É claro que s S. Por outro lado, como: v s e j = v e j s e j = v e j v e j = 0, j = 1,..., m o que significa que v s está em S. Obtemos portanto a decomposição (.8.). Mostremos agora que esta decomposição é única. Isto é equivalente a provar, como já sabemos, que S S = {0}. Suponhamos então que 0 u S S. Então, por definição de S, e como u S, u é ortogonal a todo o vector de S. Em particular é ortogonal a si próprio, isto é, 0 = u u = u, o que implica que u = 0. Finalmente (.8.3) deduz-se do Teorema de Pitágoras (ver o teorema.19)..3 Projectores... Consideremos de novo um espaço vectorial com um produto interno (V, ) (Euclideano se V é real ou Hermitiano se V é complexo), e suponhamos que S é um subespaço de dimensão finita em V. Então, como V = S S, podemos ainda definir uma aplicação linear: P S : V V (.8.5) chamada a projecção ortogonal sobre S da seguinte forma. Por definição de soma directa, todo o vector v V admite uma decomposição única da forma: v = s + (v s), onde s S e v s S. Pômos então P S (v) = s. É fácil ver que P S verifica as propriedades seguintes: im P S = S ker P S = S P S = P S P S (v) v, v V Se {e 1,, e m } é uma base ortonormada para S, então: P S (v) = m v e i e i (.8.6) i=1
26 .8. Decomposição ortogonal. Teorema da aproximação óptima 4.33 Exemplo [Projecção ortogonal sobre uma recta, em IE 3... Sejam a 0 e x dois vectores em IR 3, com a não nulo. Então existe um único vector u, na recta gerada por a, e um único vector v, ortogonal a a, tais que x = u + v. O vector u, notado por P a (x), diz-se a projecção ortogonal de x sobre a recta gerada por a, e é dado por: P a (x) = x a a a (.8.7) A aplicação P a : IR 3 IR 3 definida por (4.1.1), é linear. Note que P a = P a. Por outro lado, se considerarmos um qualquer vector b 0 ortogonal a a (i.e.: a b = 0), vemos que P a (b) = 0 e portanto: ker P a = span{b} = {b IR 3 : b a = 0} = a é o plano vectorial ortogonal a a..34 Exemplo [Projecção ortogonal sobre um plano vectorial, em IE 3... Consideremos um plano vectorial ortogonal a um vector n IR 3 {0} (se esse plano é gerado por dois vectores u, v linearmente independentes, podemos tomar n = u v). Notemos esse plano por π = n. Dado um vector x IR 3, ao vector: P n x P n (x) chamamos a projecção ortogonal de x sobre o plano vectorial ortogonal a n. De acordo com (4.1.1), temos que: P n x P n (x) = x x n n n (.8.8) A aplicação P n : IR 3 IR 3 definida por (4.1.13), é linear. Note que P n = P n. Se x n = 0, i.e., se x é ortogonal a n, então P n (x) = x, enquanto que, por outro lado, P n (n) = 0. Portanto vemos que: ker P n = span{n} e: P n (x) = x x n
27 .8. Decomposição ortogonal. Teorema da aproximação óptima 5.35 Teorema [da aproximação óptima... Consideremos um espaço vectorial com um produto interno (V, ) (Euclideano se V é real ou Hermitiano se V é complexo), e seja S um subespaço de dimensão finita. Dado um vector v V, a projecção ortogonal de v sobre S: s = P S (v) S é o vector de S que está mais perto de v, isto é: v P S (v) v u, u S (.8.9) e v P S (v) = v u, com u S se e só se u = P S (v). Dem.: Por (.8.), temos que v = s + (v s), onde s = P S (v) S e v s S. Como u S se tem: v u = (s u) + (v s) }{{}}{{} S S esta é a decomposição ortogonal de v u. Pelo teorema de Pitágoras: v u = s u + v s v s sendo a igualdade válida sse s u = 0, isto é, sse s = u..36 Exemplo (Aproximação de funções contínuas em [0, π por polinómios trigonométricos)... Seja V = C o ([0, π; IR) o espaço das funções reais contínuas definidas em [0, π, munido do produto L : f g = π 0 f(t)g(t) dt e S n o subespaço de dimensão n + 1 seguinte: { S n = span IR ϕ 0 (t) = 1 } cos kt sin kt, ϕ k 1 (t) =, ϕ k (t) = : k = 1,, n π π (.8.10) As n + 1 funções {ϕ 0, ϕ 1,, ϕ n 1, ϕ n }, chamadas polinómios trigonométricos, formam uma base ortonormada para S (mostrar isto ). Se f C o ([0, π; IR), representemos por F n (f) a projecção ortogonal de f sobre S n. De acordo com a fórmula da projecção ortogonal (.8.6), temos que: Usar as relações trigonométricas seguintes: F n (f) = n k=0 cos A cos B = 1 {cos(a B) + cos(a + B)} sin A sin B = 1 {cos(a B) cos(a + B)} sin A cos B = 1 {sin(a B) + sin(a + B)} f ϕ k ϕ k (.8.11)
28 .8. Decomposição ortogonal. Teorema da aproximação óptima 6 onde: f ϕ k = π 0 f(t)ϕ k (t) dt (.8.1) são os chamados coeficientes de Fourier de f. Usando a definição das funções ϕ k, podemos escrever as fórmulas anteriores na forma: F n (f) = 1 a 0 + n (a k cos kt + b k sin kt) (.8.13) k=1 onde os coeficientes de Fourier são dados por: a k = 1 π b k = 1 π π 0 π 0 f(t) cos kt dt f(t) sin kt dt (.8.14) para k = 0, 1,,..., n. O teorema da aproximação óptima diz-nos que o polinómio trigonométrico F n (f) S n, dado por (.8.13), aproxima f melhor que qualquer outro polinómio trigonométrico em S n, no sentido em que f F n (f) é o menor possível..37 Exemplo (Aproximação de funções contínuas em [ 1, 1 por polinómios de grau n )... Seja V = C o ([ 1, 1; IR) o espaço das funções reais contínuas definidas em [ 1, 1, munido do produto L : f g = 1 1 f(t)g(t) dt e S n o subespaço de dimensão n + 1 gerado pelos polinómios de Legendre normalizados, introduzidos no exemplo.30: S n = span IR {ϕ o, ϕ 1,, ϕ n } (.8.15) É claro que S é o subespaço constituído por todas as funções polinomiais de grau n, definidas no intervalo [ 1, 1. f C o ([ 1, 1; IR), representemos por P n (f) a projecção ortogonal de f sobre S n. De acordo com a fórmula da projecção ortogonal (.8.6), temos que: n P n (f) = f ϕ k ϕ k, onde f ϕ k = k=0 1 1 f(t)ϕ k (t) dt (.8.16) que é o polinómio de grau n, para o qual f P n (f) é o menor possível. Por exemplo, se f(t) = sin πt, os coeficientes f ϕ k são dados por: f ϕ k = 1 1 sin πtϕ k (t) dt Em particular, f ϕ 0 = 0 E. f ϕ 1 = t sin πt dt = π
29 .9. Aplicações. Mínimos quadrados 7.9 Aplicações. Mínimos quadrados.38 Solução dos mínimos quadrados... Seja: Ax = b (.9.1) um sistema de equações lineares, não homogéneo, escrito em forma matricial. A é uma matriz m n, x IR n e b IR m é um vector fixo. Uma solução dos mínimos quadrados do sistema (.9.1) é, por definição, um vector x, que satisfaz: A x b é mínimo (.9.) Interpretando A como a matriz de uma aplicação linear A : IR n IR m, relativamente às bases canónicas de cada um destes espaços, vemos que o significado de uma solução dos mínimos quadrados é o seguinte: é um vector x IR n cuja imagem está mais próxima de b..39 Quando ker A = {0} a solução x é única. Quando b im A, x é uma solução exacta do sistema. Quando b / im A, e ker A = {0} a solução x é dada por: x = A 1 P im A (b) (.9.3) Isto é, para calcular a solução dos mínimos quadrados do sistema (.9.1) procede-se da seguinte forma: 1. Calcula-se a projecção ortogonal ŷ im A, de b sobre a imagem de A. Pelo teorema da aproximação óptima, este será o vector da imagem de A, que melhor aproxima b.. Calcula-se x tal que A x = ŷ.40 Exemplo... Calcular a solução dos mínimos quadrados do sistema: x + y = 1 3x y + z = 0 x + y + z = 1 x y z = x + y z = (.9.4) e o erro correspondente..41 Aproximação de dados por uma recta pelo método dos mínimos quadrados...
30 .9. Aplicações. Mínimos quadrados 8 Suponhamos que se fazem n medições de uma certa grandeza y, em n instantes t i, i = 1,..., n, obtendo os resultados: t 1 t t 3 t n y 1 y y 3 y n (.9.5) Representemos os n pontos (t i, y i ) no plano em IR t,y,e suponhamos que se pretende calcular uma recta do tipo: y = αt + β (.9.6) que melhor ajuste esses dados. Em que sentido deve ser entendido este melhor ajustamento? Para cada t i, o erro e i entre o valor medido y i e o valor estimado a partir da recta referida (supondo que ela está já calculada) é igual a: e i = y i (αt i + β), i = 1,,, n onde: Em forma matricial: e = e 1 e. e n, y = y 1 y. y n e = y Ax (.9.7), A = t 1 1 t. t n n, x = e é o chamado vector de erro e y o vector dos dados. Os coeficientes α, β - as incógnitas do problema - são as componentes do vector x. Se os dados se ajustassem exactamente, y i = αt i + β, os erros seriam todos nulos e i = 0, e poderíamos resolver o sistema Ax = y. Por outras palavras, os dados estarão todos numa linha recta sse y im A. Se eles não forem colineares então devemos procurar a recta para a qual o erro total: e = ( e e n ) 1/ seja mínimo. Em linguagem vectorial, procuramos pois o vector x = ) que minimiza a norma Euclideana do vector erro: e = Ax y ( α β ( α β ) que é exactamente a situação que caracteriza a procura da solução dos mínimos quadrados para o sistema Ax = y, que foi explicada no ponto anterior..4 Exemplo... Calcular a recta de aproximação dos mínimos quadrados para os dados seguintes: t i (.9.8) y i Solução: y = 1/7(1 + t).
31 .9. Aplicações. Mínimos quadrados 9.43 Exemplo... Considere a aplicação linear A : IR IR 3 definida por: A(x, y) = (x + y, x y, x) a.) Calcule o ortogonal da imagem de A em IR 3, com a estrutura Euclideana usual. b.) Calcule a solução dos mínimos quadrados do sistema: x + y = 1 x y = 1 x = 0 Calcule o erro associado a essa solução e explique qual o seu significado geométrico (da solução e do seu erro). Resolução... a.) A imagem de A é constituída por todos os vectores (X, Y, Z) IR 3 tais que: (X, Y, Z) = A(x, y) = (x + y, x y, x) para algum vector (x, y) IR. A questão é pois: quais os vectores (X, Y, Z) IR 3 para os quais existe (x, y) tal que: x + y = X x y = Y? x = Z Resolvendo o sistema em ordem a x, y (com X, Y, Z como parâmetros), vem que: x = Z y = X Z 0 = X + Y Z Portanto a imagem de A é o plano X + Y Z = 0 em IR 3. O seu ortogonal é a recta gerada pelo vector n = (1, 1, ). b.) Por definição (e pelo teorema da aproximação óptima), a solução dos mínimos quadrados é a solução do sistema: Ax = P im A (b) onde P im A (b) é a projecção ortogonal do vector b = (1, 1, 0) sobre o plano imagem de A: X + Y Z = 0. Essa projecção pode ser calculada pela seguinte fórmula: P im A (1, 1, 0) = (1, 1, 0) Logo a solução procurada é a solução do sistema: (1, 1, 0) (1, 1, ) (1, 1, ) (1, 1, ) = (1, 1, 1) 3 x + y = /3 x y = /3 x = /3
32 .9. Aplicações. Mínimos quadrados 30 que é: x = /3, y = 0 O erro associado é, por definição, igual à distância entre o ponto (1, 1, 0) e a P im A (b): e = (1, 1, 0) 3 (1, 1, 1) = 6/3.44 Exemplo... Considere o espaço vectorial IR 3 [t das funções polinomiais p(t), de grau 3, de coeficientes reais, munido do produto interno: p(t) q(t) = +1 0 p(t)q(t) dt a.) Mostre que: S = {p(t) IR 3 [t : p(t) = p( t) } é um subespaço vectorial. Calcule dim S e determine uma base ortonormada para S. b.) Calcule o polinómio de S que está mais próximo do polinómio p(t) = t. c.) Calcule o ortogonal de T = span{1} em IR 3 [t. d.) Calcule o núcleo e a imagem da aplicação linear: T : IR 3 [t IR 3 [t p(t) T[p(t) = p (t) tp (t) Resolução... a.) Se p, q S então (p + q)(t) = p(t) + q(t) = p( t) + q( t) = (p + q)( t) e portanto p + q S. Se p S e λ IR então (λp)(t) = λp(t) = λp( t) = λp( t) e portanto λp S. Se p(t) = a + bt + ct + dt 3 S então a + bt + ct + dt 3 = p(t) = p( t) = a bt + ct dt 3, isto é, bt + dt 3 = 0 e portanto b = d = 0. Logo: S = {p(t) = a + bt + ct + dt 3 IR 3 [t : b = d = 0 } = {p(t) = a + ct IR 3 [t : a, c IR } = span{1, t } e dim S =. Os polinómios p(t) 1 e q(t) = t constituem uma base para S. Uma base ortonormada obtem-se pelo processo de Gram-Schmidt. 1 = dt = 1 e t t 1 1 = t t dt = t 1/3. Além disso t 1/3 = 1 0 (t 1/3) dt = 4/45. Logo os polinómios 1 e (3 5/)(t 1/3) constituem uma base ortonormada para S. b.) Pelo teorema da aproximação óptima esse polinómio é dado pela projecção ortogonal de t sobre S: P S (t) = t t (3 5/)(t 1/3) (3 5/)(t 1/3) 1 ( 1 ) = t dt + (45/4) t(t 1/3) dt (t 1/3) 0 = 1/ + (45/48)(t 1/3) 0
33 .10. Exercícios 31 c.) Um polinómio p(t) = a+bt+ct +dt 3 IR 3 [t estará em T sse (a+bt+ct +dt 3 ) 1 = 0 isto é, sse a + b/ + c/3 + d/4 = 0. Portanto: T = {p(t) = a + bt + ct + dt 3 IR 3 [t : a + b/ + c/3 + d/4 = 0 } que é um hiperplano em IR 3 [t. d.) Um polinómio p(t) = a + bt + ct + dt 3 IR 3 [t estará em ker T sse: 0 = T[p(t) = p (t) tp (t) = (a + bt + ct + dt 3 ) t(a + bt + ct + dt 3 ) = (c + 6dt) t(b + ct + 3dt ) = c + (6d b)t 4ct 6dt 3 donde c = 0, 6d b = 0, 4c = 0, 6d = 0, isto é, b = c = d = 0. Portanto o ker T é constituídio pelos polinómios p(t) = a + bt + ct + dt 3 IR 3 [t tais que b = c = d = 0, isto é, ker T = {a : a IR} = span{1}. im T é constituídia pelos polinómios P (t) = A + Bt + Ct + Dt 3 IR 3 [t tais que: T(a + bt + ct + dt 3 ) = A + Bt + Ct + Dt 3 para algum polinómio p(t) = a+bt+ct +dt 3 IR 3 [t. Como T[p(t) = c+(6d b)t 4ct 6dt 3, vem que: c + (6d b)t 4ct 6dt 3 = A + Bt + Ct + Dt 3 isto é: c = A b + 6d = B 4c = C 6d = D b + 6d = B c = A 6d = D 0 = A + C e portanto im T = {P (t) = A + Bt + Ct + Dt 3 IR 3 [t : A + C = 0}..10 Exercícios Exercício.1... Verifique quais das seguintes funções são produtos internos Euclidianos em IR ou IR 3 : a) u, v = x 1 y 1 x 1 y x y 1 + 3x y, sabendo que u = (x 1, x ), e v = (y 1, y ). b) u, v = x 1 y 1 + x 1 y x y 1 + 3x y, sabendo que u = (x 1, x ), e v = (y 1, y ). c) u, v = 6x 1 y 1 + x y, sabendo que u = (x 1, x ), e v = (y 1, y ). d) u, v = x 1 y 1 + 3x y + 4x 3 y 3, sabendo que u = (x 1, x, x 3 ), e v = (y 1, y, y 3 ). e) u, v = x 1 y 1 +3x y +4x 3 y 3 x 1 y y 1 x, sabendo que u = (x 1, x, x 3 ), e v = (y 1, y, y 3 ). Exercício.... Calcule em cada caso u, v usando o produto interno Euclidiano usual e o produto interno definido em.1-a). Depois, calcule u e v recorrendo também a cada um desses dois produtos internos. a) u = (1, 1), v = ( 1, 1); b) u = (1, 0), v = (1, ); c) u = (, 1), v = (4, 1);
34 .10. Exercícios 3 Exercício.3... Calcule em cada caso u, v usando o produto interno euclidiano usual e o produto interno definido em.1-d). Depois, calcule u e v recorrendo também a cada um destes dois produtos internos. a) u = (1, 1, 1), v = ( 1, 1, ); b) u = (1, 0, 1), v = (3, 1, ); c) u = (0, 0, 1), v = ( 1, 4, 6); Exercício.4... Determine todos os valores reais de k para os quais u, v é um produto interno Euclidiano em IR : u, v = x 1 y 1 3x 1 y 3x y 1 + kx y Exercício.5... Determine todos os valores reais de a, b, c, d para os quais u, v é um produto interno Euclidiano em IR : u, v = ax 1 y 1 + bx 1 y + cx y 1 + dx y Exercício.6... Sejam, u = (z 1, z ) e v = (w 1, w ) elementos de C. Verifique que a função que se segue é um produto interno Hermitiano em C : f(u, v) = z 1 w 1 + (1 + i)z 1 w + (1 i)z w 1 + 3z w Calcule a norma de v = (1 i, + 3i) usando o produto interno Hermitiano usual e depois o produto interno definido neste exercício. Exercício.7... Em cada caso, determine o cos do ângulo θ entre os vectores u e v : a) u = (1, 3, ), v = (, 1, 5) em IR 3, usando o produto interno euclidiano usual e o produto interno definido em.1-d). b) u = t 1, v = t em IR [t, usando o produto interno Euclidiano definido no exercício.14. Exercício.8... No espaço linear IR [t verifique se f, g é um produto interno. a) f, g = f(1)g(1) b) f, g = 1 0 f(t)g(t) dt c) f, g = 1 0 f (t)g (t) dt ( ) ( 1 ) d) f, g = 0 f(t) dt 1 0 g(t) dt Exercício.9... No espaço vectorial real das funções contínuas em [ 1, 1, seja f, g = 1 1 f(t)g(t) dt. Considere as três funções u 1, u, u 3 dadas por: u 1 (t) = 1, u (t) = t, u 3 (t) = 1 + t. Mostre que duas delas são ortogonais, duas fazem um angulo de π 3 fazem um ângulo de π 6 entre si. entre si e as outras duas
35 .10. Exercícios 33 Exercício Prove cada uma das afirmações das alíneas seguintes e interprete-as geométricamente no caso do produto interno usual em IR ou IR 3. a) x, y = 0 x + y = x + y. b) x, y = 0 x + y = x y. c) x, y = 0 x + cy x para todo o real c. d) x + y, x y = 0 x = y. Exercício Calcule o ângulo que o vector (1, 1,, 1) de IR n faz com os vectores coordenados unitários de IR n. Exercício.1... Como se sabe, num espaço Euclidiano real com produto interno x, y fica definida ume norma por x = x, x 1. Dê uma fórmula para obter o produto interno x, y a partir de normas de vectores apropriados. Exercício Seja V um espaço linear real normado e designe-se a norma de x V por x. Prove que se a norma se pode obter de um produto interno na forma x = x, y 1 então: x y + x + y = x + y Esta identidade é conhecida por lei do paralelogramo. Verifique que corresponde a afirmar que para um paralelogramo a soma dos quadrados dos comprimentos dos lados é igual à soma dos quadrados dos comprimentos das diagonais. Exercício Considere o espaço vectorial real IR [t no qual está definido o seguinte produto interno: f, g = 1 0 f(t)g(t) dt. Seja f(t) = t + e g(t) = t t 3. Determine : a) f, g b) f c) Um vector unitário com a direcção de g. Exercício Seja E um espaço vectorial no qual está definido um produto escalar. Mostre que : a) u + v + u v = u + v b) u, v = 1 4 u + v 1 4 u v Exercício Em cada um dos casos, determine uma base ortonormada do subespaço de IR 3 gerado pelos seguintes vectores: a) x 1 = (1, 1, 1), x = (1, 0, 1), x 3 = (3,, 3). b) x 1 = (1, 1, 1), x = ( 1, 1, 1), x 3 = (1, 0, 1). Exercício Em cada um dos casos, determine uma base ortonormada do subespaço de IR 4 gerado pelos seguintes vectores: a) x 1 = (1, 1, 0, 0), x = (0, 1, 1, 0), x 3 = (0, 0, 1, 1), x 4 = (1, 0, 0, 1). b) x 1 = (1, 1, 0, 1), x = (1, 0,, 1), x 3 = (1,,, 1).
36 .10. Exercícios 34 Exercício No espaço vectorial real IR [t, com o produto interno x, y = 1 0 x(t)y(t) dt, mostre que as funções que se seguem formam uma base ortonormada do subespaço por elas gerado: y 1 (t) = 1, y (t) = 3(t 1), y 3 (t) = 5(6t 6t + 1). Exercício Seja S um subespaço de um espaço vectorial V. Mostre que o S é o conjunto dos vectores ortogonais a todos os vectores de uma base de S. Exercício.0... Seja W o subespaço de IR 5 gerado pelos vectores u = (1,, 3, 1, ) e v = (, 4, 7,, 1). Determine uma base do complemento ortogonal W de W. Exercício.1... Determine uma base do subespaço W de IR 4 ortogonal a u 1 = (1,, 3, 4) e u = (3, 5, 7, 8). Exercício.... Considere o espaço vectorial real IR [t no qual está definido o produto interno f, g = 1 0 f(t)g(t) dt. a) Determine uma base do subespaço W ortogonal a h(t) = t + 1. b) Aplique o método de ortogonalização de Gram-Schmidt à base (1, t, t ) para obter uma base ortonormada (u 1 (t), u (t), u 3 (t)) de IR [X. Exercício.3... Seja V o espaço linear das matrizes de componentes reais, com as operações usuais. Prove que fica definido um produto interno em V por: A, B = a 11 b 11 + a 1 b 1 + a 1 b 1 + a b onde A = (a ij ) e B = (b ij ). ( a b Calcule a matriz da forma b a ). ( ), com a, b IR, mais próxima da matriz A = Exercício.4... Considere o subespaço S de IR 3 gerado pelos vectores (1, 0, 0) e (0, 1, 0). a) Verifique que fica definido em IR 3 um produto interno por: x, y = x 1 y 1 + x 1 y + x y 1 + x y + x 3 y 3, onde x = (x 1, x, x 3 ) e y = (y 1, y, y 3 ). b) Determine uma base ortonormal para o subespaço S, com este produto interno. c) Determine o elemento de S mais próximo do ponto (0, 0, 1),usando o produto interno de a). d) Calcule um vector diferente de zero e ortogonal a S usando o produto interno de a). Exercício.5... No espaço vectorial real das funções contínuas definidas em [0,, com o produto interno f, g = 0 f(x)g(x) dx, seja f(x) = exp(x). Mostre que, o polinómio constante g, mais próximo de f é g = 1 (exp() 1). Calcule g f.
37 .10. Exercícios 35 Exercício.6... Usando os produtos internos usuais em IR e IR 3, calcule em cada caso a projecção ortogonal P u (v), de v sobre a recta gerada pr u: a) u=(1,1), v=(,3); b) u=(4,3), v=(0,1); c) u=(1,1,1), v=(1,-1,0); d) u=(1,0,0), v=(0,1,). Exercício.7... Determine as projecções ortogonais seguintes: a) v = (1, 1, ), w = (0, 1, 1) sobre F = { (x, y, z) IR 3 : x + y + z = 0 } usando o produto interno Euclidiano usual de IR 3. b) v = t 1, w = t sobre IR 1 [t usando o produto interno L.
38 Capítulo 3 Subespaços invariantes. Subespaços próprios. Valores próprios 3.1 Conjugação 3.1 Mudança de base... Suponhamos que V é um espaço vectorial e que: C = [ e 1 e e n é uma base qualquer, escrita como um vector-linha com entradas vectoriais e i. Se v V é um vector qualquer em V, designemos por v i as suas componentes na base C, isto é: v = i v i e i = [ e 1 e e n v 1 v. v n = C [v C (3.1.1) Suponhamos agora que mudamos de base: que escrevemos na forma matricial seguinte: ou muito simplesmente: C C P = C = [ ê 1 ê ê n [ [ ê1 ê ê n = e1 e e n C = C P P 1 1 P 1 P 1 n P 1 P P n... P1 n P n Pn n Se v i são as componentes do mesmo vector v na base C, isto é, se: (3.1.) (3.1.3) v = i v i ê i = C [v C (3.1.4) 36
Álgebra Linear e Geometria Analítica em R 3
 Módulo 2 Álgebra Linear e Geometria Analítica em R 3 Neste segundo módulo vamos generalizar os conceitos aprendidos no módulo 1, e também no ensino secundário, estudando Álgebra Linear e Geometria Analítica
Módulo 2 Álgebra Linear e Geometria Analítica em R 3 Neste segundo módulo vamos generalizar os conceitos aprendidos no módulo 1, e também no ensino secundário, estudando Álgebra Linear e Geometria Analítica
Um curso rápido de ALGA apenas em R 2
 Módulo 1 Um curso rápido de ALGA apenas em R 2 Neste primeiro módulo vamos retomar alguns conceitos ensinados no ensino secundário, e fazer uma ponte para os assuntos mais sofisticados que precisamos de
Módulo 1 Um curso rápido de ALGA apenas em R 2 Neste primeiro módulo vamos retomar alguns conceitos ensinados no ensino secundário, e fazer uma ponte para os assuntos mais sofisticados que precisamos de
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Apontamentos III. Espaços euclidianos. Álgebra Linear aulas teóricas. Lina Oliveira Departamento de Matemática, Instituto Superior Técnico
 Apontamentos III Espaços euclidianos Álgebra Linear aulas teóricas 1 o semestre 2017/18 Lina Oliveira Departamento de Matemática, Instituto Superior Técnico Índice Índice i 1 Espaços euclidianos 1 1.1
Apontamentos III Espaços euclidianos Álgebra Linear aulas teóricas 1 o semestre 2017/18 Lina Oliveira Departamento de Matemática, Instituto Superior Técnico Índice Índice i 1 Espaços euclidianos 1 1.1
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral
 Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Dep. Matemática FCUP. ÁLGEBRA LINEAR e GEOMETRIA ANALÍTICA
 ******************************************************* ******************************************************* Dep. Matemática FCUP ******************************************************* *******************************************************
******************************************************* ******************************************************* Dep. Matemática FCUP ******************************************************* *******************************************************
Introdução à Geometria
 Introdução à Geometria - 2007-2008 Algumas noções 1. Norma de um vector Seja E um espaço vectorial real de dimensão finita E munido de um produto interno (u, v) u v. Dado um vector v E chama-se norma ou
Introdução à Geometria - 2007-2008 Algumas noções 1. Norma de um vector Seja E um espaço vectorial real de dimensão finita E munido de um produto interno (u, v) u v. Dado um vector v E chama-se norma ou
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Capítulo 2. Ortogonalidade e Processo de Gram-Schmidt. Curso: Licenciatura em Matemática
 Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Espaços vectoriais com produto interno. ALGA 2008/2009 Mest. Int. Eng. Electrotécnica e de Computadores Espaços vectoriais com produto interno 1 / 19
 Capítulo 6 Espaços vectoriais com produto interno ALGA 2008/2009 Mest. Int. Eng. Electrotécnica e de Computadores Espaços vectoriais com produto interno 1 / 19 Definição e propriedades ALGA 2008/2009 Mest.
Capítulo 6 Espaços vectoriais com produto interno ALGA 2008/2009 Mest. Int. Eng. Electrotécnica e de Computadores Espaços vectoriais com produto interno 1 / 19 Definição e propriedades ALGA 2008/2009 Mest.
Produto interno e produto vetorial no espaço
 14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
14 Produto interno e produto vetorial no espaço Sumário 14.1 Produto interno.................... 14. Produto vetorial.................... 5 14..1 Interpretação geométrica da norma do produto vetorial.......................
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Capítulo Propriedades das operações com vetores
 Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
1 a Lista de Exercícios de MAT3458 Escola Politécnica 2 o semestre de 2016
 1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
1. Não temos um espaço vetorial, pois a seguinte propriedade (a + b) v = a v + b v não vale. De fato:
 Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Produto interno, externo e misto
 Produto interno, externo e misto Definição: Chama-se norma (ou comprimento) do vector u ao comprimento do segmento de recta [OP ] e representa-se por u. Definição: Sejam a = OA e b = OB dois vectores não
Produto interno, externo e misto Definição: Chama-se norma (ou comprimento) do vector u ao comprimento do segmento de recta [OP ] e representa-se por u. Definição: Sejam a = OA e b = OB dois vectores não
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2018
 MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
MAT3457 ÁLGEBRA LINEAR PARA ENGENHARIA I a Lista de Exercícios - o semestre de 8 Exercícios -8: os espaços V e V 3. Exercícios 9-7: dependência, independência linear, bases. Exercícios 8-48: sistemas lineares.
Capítulo 5. Operadores Auto-adjuntos. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
Aula 19 Operadores ortogonais
 Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá. 21 de outubro de 2011
 APLICAÇÕES DA DIAGONALIZAÇÃO Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá IEFF-ITA 21 de outubro de 2011 Roteiro 1 2 3 Roteiro 1 2 3 Introdução Considere a equação de uma cônica: Forma Geral Ax 2 + Bxy
APLICAÇÕES DA DIAGONALIZAÇÃO Álgebra Linear (MAT-27) Ronaldo Rodrigues Pelá IEFF-ITA 21 de outubro de 2011 Roteiro 1 2 3 Roteiro 1 2 3 Introdução Considere a equação de uma cônica: Forma Geral Ax 2 + Bxy
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
4 a LISTA DE EXERCÍCIOS Produto Interno Álgebra Linear - 2 o Semestre /2005 LEE, LEGI, LEIC-TP, LERCI
 4 a LISTA DE EXERCÍCIOS Produto Interno Álgebra Linear - 2 o Semestre - 2004/2005 LEE, LEGI, LEIC-TP, LERCI Problema 1. Seja u, w um produto interno num espaço linear V. Mostre que i) para qualquer vector
4 a LISTA DE EXERCÍCIOS Produto Interno Álgebra Linear - 2 o Semestre - 2004/2005 LEE, LEGI, LEIC-TP, LERCI Problema 1. Seja u, w um produto interno num espaço linear V. Mostre que i) para qualquer vector
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
MAT ÁLGEBRA LINEAR PARA ENGENHARIA II 1 a Lista de Exercícios - 2 o semestre de 2006
 MAT 2458 - ÁLGEBRA LINEAR PARA ENGENHARIA II 1 a Lista de Exercícios - 2 o semestre de 2006 1. Sejam u = (x 1, x 2 ) e v = (y 1, y 2 ) vetores de R 2. Para que valores de t R a funcão u, v = x 1 y 1 +
MAT 2458 - ÁLGEBRA LINEAR PARA ENGENHARIA II 1 a Lista de Exercícios - 2 o semestre de 2006 1. Sejam u = (x 1, x 2 ) e v = (y 1, y 2 ) vetores de R 2. Para que valores de t R a funcão u, v = x 1 y 1 +
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Lista 8 de Álgebra Linear /01 Produto Interno
 Lista 8 de Álgebra Linear - / Produto Interno. Sejam u = (x x e v = (y y. Mostre que temos um produto interno em R nos seguintes casos: (a u v = x y + x y. (b u v = x y x y x y + x y.. Sejam u = (x y z
Lista 8 de Álgebra Linear - / Produto Interno. Sejam u = (x x e v = (y y. Mostre que temos um produto interno em R nos seguintes casos: (a u v = x y + x y. (b u v = x y x y x y + x y.. Sejam u = (x y z
Produto interno no espaço vectorial R n
 ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
Diagonalização unitária e diagonalização ortogonal. (Positividade do produto interno) Raíz quadrada. Formas quadráticas.
 Aplicações: Diagonalização unitária e diagonalização ortogonal (Positividade do produto interno) Raíz quadrada Formas quadráticas Mínimos quadrados Produto externo e produto misto (Área do paralelogramo.
Aplicações: Diagonalização unitária e diagonalização ortogonal (Positividade do produto interno) Raíz quadrada Formas quadráticas Mínimos quadrados Produto externo e produto misto (Área do paralelogramo.
Capítulo 6. Operadores Ortogonais. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
- identificar operadores ortogonais e unitários e conhecer as suas propriedades;
 DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
Álgebra Linear e suas Aplicações Notas de Aula. Petronio Pulino = Q
 Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino 1 3 4 3 1 0 4 0 1 = Q 4 1 6 Qt Q t Q = 1 1 1 PULINUS Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino Departamento de Matemática
Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino 1 3 4 3 1 0 4 0 1 = Q 4 1 6 Qt Q t Q = 1 1 1 PULINUS Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino Departamento de Matemática
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Produto interno no espaço vectorial R n
 ALGA - 008/09 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
ALGA - 008/09 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
Introduzir os conceitos de base e dimensão de um espaço vetorial. distinguir entre espaços vetoriais de dimensão fnita e infinita;
 META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
Produto Misto, Determinante e Volume
 15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
Álgebra linear A Primeira lista de exercícios
 Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Geometria Analítica e Álgebra Linear
 Geometria Analítica e Álgebra Linear por PAULO XAVIER PAMPLONA UFCG-UATA 2011 Conteúdo 1 Vetores 4 1.1 Introdução..................................... 4 1.2 Vetores no Plano.................................
Geometria Analítica e Álgebra Linear por PAULO XAVIER PAMPLONA UFCG-UATA 2011 Conteúdo 1 Vetores 4 1.1 Introdução..................................... 4 1.2 Vetores no Plano.................................
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
Notações e revisão de álgebra linear
 Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Álgebra Linear /2 Turma EM1 (unificada)
 Álgebra Linear 2 2013/2 Turma EM1 (unificada) Planejamento preliminar (última revisão: 3/4/2013) Os exercícios correspondentes a cada aula serão discutidos na aula seguinte e não valem nota Este planejamento
Álgebra Linear 2 2013/2 Turma EM1 (unificada) Planejamento preliminar (última revisão: 3/4/2013) Os exercícios correspondentes a cada aula serão discutidos na aula seguinte e não valem nota Este planejamento
23 e 24. Forma Quadrática e Equação do Segundo Grau em R 3. Sumário
 23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
x 1 3x 2 2x 3 = 0 2 x 1 + x 2 x 3 6x 4 = 2 6 x x 2 3x 4 + x 5 = 1 ( f ) x 1 + 2x 2 3x 3 = 6 2x 1 x 2 + 4x 3 = 2 4x 1 + 3x 2 2x 3 = 4
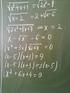 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de Resolva o sistema abaixo para as incógnitas x e y:
 MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I 1 a Lista de Exercícios - 1 o semestre de 2015 1 Determine x em função de u e v na equação 2 x 3 u = 10( x + v 2 Resolva o sistema abaixo para as incógnitas x e
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - ula 2 1. Vetores. 2. Distâncias. 3. Módulo de um vetor. Roteiro 1 Vetores Nesta seção lembraremos brevemente os vetores e suas operações básicas. Definição de vetor. Vetor determinado
Álgebra Linear I - ula 2 1. Vetores. 2. Distâncias. 3. Módulo de um vetor. Roteiro 1 Vetores Nesta seção lembraremos brevemente os vetores e suas operações básicas. Definição de vetor. Vetor determinado
Prof. Drª Marília Brasil Xavier REITORA. Profª. Drª. Maria das Graças Silva VICE-REITORA
 Prof. Drª Marília Brasil Xavier REITORA Profª. Drª. Maria das Graças Silva VICE-REITORA Prof. Dr. Ruy Guilherme Castro de Almeida PRÓ-REITOR DE ENSINO E GRADUAÇÃO Profª. M.Sc. Maria José de Souza Cravo
Prof. Drª Marília Brasil Xavier REITORA Profª. Drª. Maria das Graças Silva VICE-REITORA Prof. Dr. Ruy Guilherme Castro de Almeida PRÓ-REITOR DE ENSINO E GRADUAÇÃO Profª. M.Sc. Maria José de Souza Cravo
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
Transformações geométricas planas
 9 Transformações geométricas planas Sumário 9.1 Introdução....................... 2 9.2 Transformações no plano............... 2 9.3 Transformações lineares................ 5 9.4 Operações com transformações...........
9 Transformações geométricas planas Sumário 9.1 Introdução....................... 2 9.2 Transformações no plano............... 2 9.3 Transformações lineares................ 5 9.4 Operações com transformações...........
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
1 a Lista de Exercícios de MAT2457 Escola Politécnica 1 o semestre de (b)
 a Lista de Exercícios de MAT457 Escola Politécnica o semestre de 04 Resolva os seguintes sistemas: x + x x 3 + 3x 4 = a 3x + x x 3 + x 4 = 4 3x + 3x + 3x 3 3x 4 = 5 c x + x 3 + x 5 = x + x 3 + x 5 + x
a Lista de Exercícios de MAT457 Escola Politécnica o semestre de 04 Resolva os seguintes sistemas: x + x x 3 + 3x 4 = a 3x + x x 3 + x 4 = 4 3x + 3x + 3x 3 3x 4 = 5 c x + x 3 + x 5 = x + x 3 + x 5 + x
MATEMÁTICA A - 12o Ano N o s Complexos - Equações e problemas Propostas de resolução
 MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
MATEMÁTICA A - 1o Ano N o s Complexos - Equações e problemas Propostas de resolução Exercícios de exames e testes intermédios 1. Simplificando as expressões de z 1 e z, temos que: Como i 19 i + i i, vem
PROBLEMAS DE ÁLGEBRA LINEAR
 PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
O Plano no Espaço. Sumário
 17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
ESPAÇO VETORIAL REAL. b) Em relação à multiplicação: (ab) v = a(bv) (a + b) v = av + bv a (u + v ) = au + av 1u = u, para u, v V e a, b R
 ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
10. Determine as equações cartesianas das famílias de retas que fazem um ângulo de π/4 radianos com a reta y = 2x + 1.
 Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Geometria Analítica. 1. Determine as posições relativas e as interseções entre os conjuntos em R abaixo. Em cada item também faça um esboço dos dois conjuntos dados no mesmo sistema de eixos. (a) C : (x
Aula 4 Produto Interno
 MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
MÓDULO 1 - AULA 4 Objetivos Aula 4 Produto Interno Definir as noções de ângulo entre dois vetores, a norma de um vetor e a operação de produto interno. Compreender as propriedades básicas da norma e do
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
7 temos que e u =
 Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Colectânea de Exercícios
 ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Álgebra Linear e Geometria Anaĺıtica
 Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa
 MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
